Estimation of Canopy Structure of Field Crops Using Sentinel-2 Bands with Vegetation Indices and Machine Learning Algorithms
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area and Field Measurements
2.2. PROSAIL Model Application
2.3. Simulation of Sentinel-2 Bands
2.4. Vegetation Indices
2.5. Machine Learning Algorithms and Statistical Analysis
2.5.1. Implementation and Optimization
2.5.2. Random Forest (RF)
2.5.3. Support Vector Machine (SVM)
2.5.4. Multilayer Perceptron (MLP)
2.5.5. Partial Least Squares Regression (PLSR)
2.5.6. Statistical Analysis
3. Results
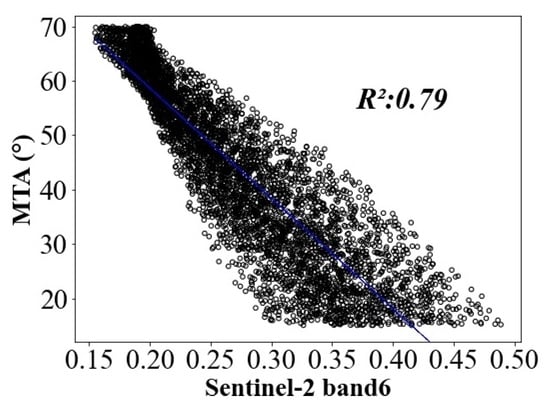
3.1. Correlations between Canopy Structural Characteristics and Remotely Sensed Data
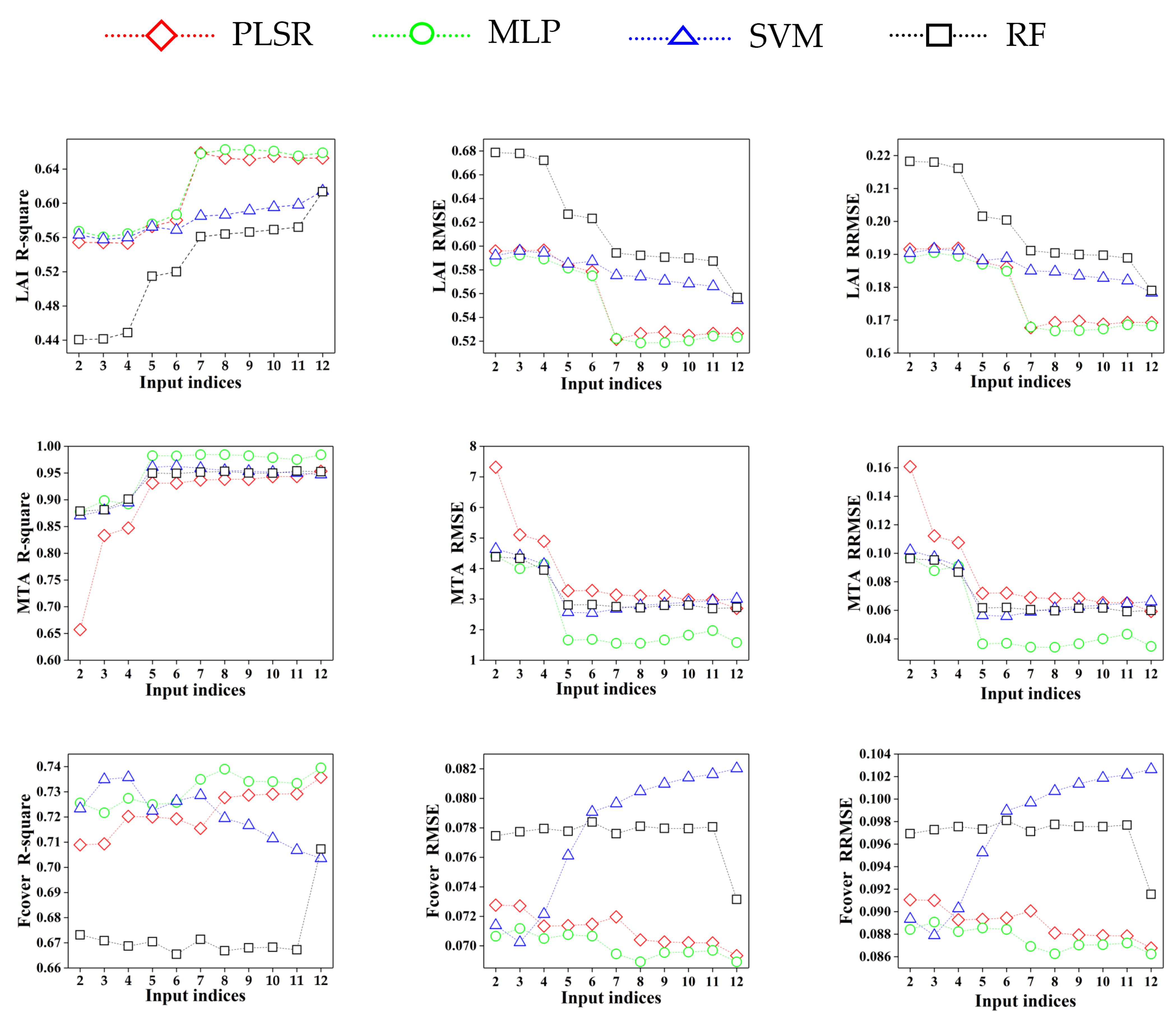
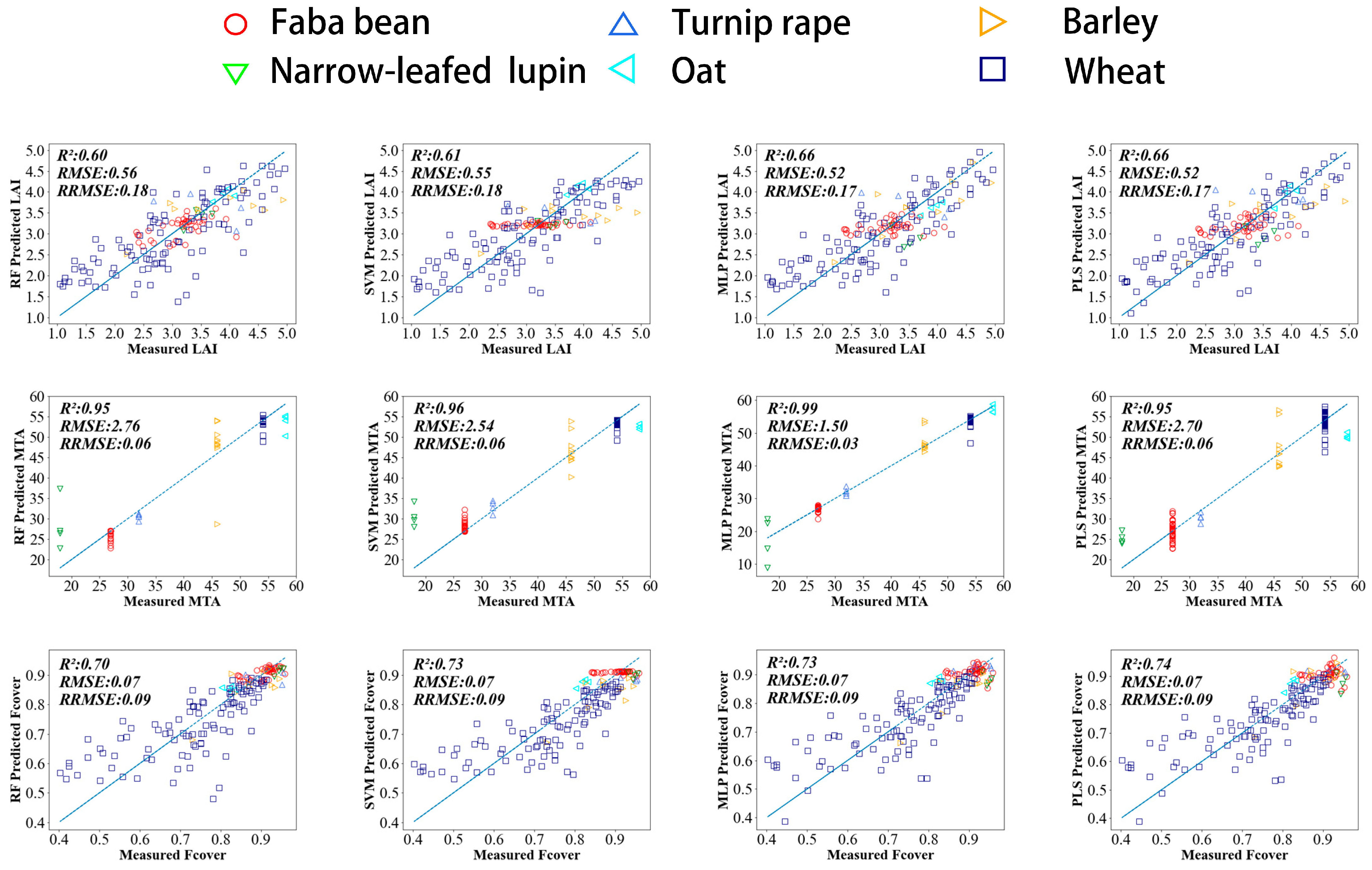
3.2. Performance of Machine Learning Algorithms with Individual Band Combinations
3.3. Performance of Machine Learning Algorithms with Vegetation Indices
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kanning, M.; InsaKühling, T.D.; Jarmer, T. High-Resolution UAV-Based Hyperspectral Imagery for LAI and Chlorophyll Estimations from Wheat for Yield Prediction. Remote Sens. 2018, 10, 2000. [Google Scholar] [CrossRef] [Green Version]
- Mao, L.; Zhang, L.; Zhao, X.; Liu, S.; Werf, W.; Zhang, S.; Spiertz, H.; Li, Z. Crop growth, light utilization and yield of relay intercropped cotton as affected by plant density and a plant growth regulator. Field Crops Res. 2014, 155, 67–76. [Google Scholar] [CrossRef]
- Duan, T.; Chapman, S.C.; Holland, E.; Rebetzke, G.J.; Guo, Y.; Zheng, B. Dynamic quantification of canopy structure to characterize early plant vigour in wheat genotypes. J. Exp. Bot. 2016, 67, 4523–4534. [Google Scholar] [CrossRef] [PubMed]
- Ross, J. The Radiation Regime and Architecture of Plants Stands. In Tasks for Vegetation Science; Springer: Medford, MA, USA, 1981; Volume 3, pp. 122–123. [Google Scholar]
- Lang, A.R.G.; Xiang, Y.Q.; Norman, J.M. Crop structure and the penetration of direct sunlight—ScienceDirect. Agric. For. Meteorol. 1985, 35, 83–101. [Google Scholar] [CrossRef]
- Watson, D.J. Comparative Physiological Studies on the Growth of Field Crops: I. Variation in Net Assimilation Rate and Leaf Area between Species and Varieties, and within and between Years. Ann. Bot. 1947, 11, 41–76. [Google Scholar] [CrossRef]
- Mulla; David, J. Twenty five years of remote sensing in precision agriculture: Key advances and remaining knowledge gaps. Biosyst. Eng. 2013, 114, 358–371. [Google Scholar] [CrossRef]
- Comba, L.; Biglia, A.; Aimonino, D.R.; Tortia, C.; Gay, P. Leaf Area Index evaluation in vineyards using 3D point clouds from UAV imagery. Precis. Agric. 2020, 21, 881–896. [Google Scholar] [CrossRef] [Green Version]
- Thorp, K.R.; Wang, G.; West, A.L.; Moran, M.S.; Bronson, K.F.; White, J.W.; Mon, J. Estimating crop biophysical properties from remote sensing data by inverting linked radiative transfer and ecophysiological models. Remote Sens. Environ. 2012, 124, 224–233. [Google Scholar]
- Su, W.; Huang, J.; Liu, D.; Zhang, M. Retrieving Corn Canopy Leaf Area Index from Multitemporal Landsat Imagery and Terrestrial LiDAR Data. Remote Sens. 2019, 11, 572. [Google Scholar] [CrossRef] [Green Version]
- Huete, A.R. A soil adjusted vegetation index (SAVI). National Space Centre Applications Development Programme. Remote Sens. Environ. 1988, 9, 295–309. [Google Scholar] [CrossRef]
- Moulin, S.; Guerif, M. Impacts of model parameter uncertainties on crop reflectance estimates: A regional case study on wheat. Int. J. Remote Sens. 1999, 20, 213–218. [Google Scholar] [CrossRef]
- Nguy-Robertson, A.L.; Peng, Y.; Gitelson, A.A.; Arkebauer, T.J.; Pimstein, A.; Herrmann, I.; Karnieli, A.; Rundquist, D.C.; Bonfil, D.J. Estimating green LAI in four crops: Potential of determining optimal spectral bands for a universal algorithm. Agric. For. Meteorol. 2014, 192, 140–148. [Google Scholar] [CrossRef]
- Gitelson, A.; Solovchenko, A. Generic algorithms for estimating foliar pigment content. Geophys. Res. Lett. 2017, 44, 9293–9298. [Google Scholar] [CrossRef]
- Sun, Y.; Ren, H.; Zhang, T.; Zhang, C.; Qin, Q. Crop leaf area index retrieval based on inverted difference vegetation index and NDVI. IEEE Geosci. Remote Sens. 2018, 15, 1662–1666. [Google Scholar] [CrossRef]
- Hansen, P.M.; Schjoerring, J.K. Reflectance measurement of canopy biomass and nitrogen status in wheat crops using normalized difference vegetation indices and partial least squares regression. Remote Sens.Environ. 2003, 86, 542–553. [Google Scholar] [CrossRef]
- An, G.; Xing, M.; He, B.; Liao, C.; Kang, H. Using Machine Learning for Estimating Rice Chlorophyll Content from In Situ Hyperspectral Data. Remote Sens. 2020, 12, 3104. [Google Scholar] [CrossRef]
- Li, Z.; Xin, X.; Tang, H.; Yang, F.; Chen, B.; Zhang, B. Estimating grassland LAI using the Random Forests approach and Landsat imagery in the meadow steppe of Hulunber, China. J. Integr. Agric. 2017, 16, 286–297. [Google Scholar] [CrossRef]
- Neinavaz, E.; Skidmore, A.K.; Darvishzadeh, R.; Groen, T.A. Retrieval of leaf areaindex in different plant species using thermal hyperspectraldata. ISPRS J. Photogramm. Remote Sens. 2016, 119, 390–401. [Google Scholar] [CrossRef]
- Riihimäki, H.; Luoto, M.; Heiskanen, J. Estimating fractional cover of tundra vegetation at multiple scales using unmanned aerial systems and optical satellite data. Remote Sens. Environ. 2019, 224, 119–132. [Google Scholar] [CrossRef]
- Zou, X.; Mõttus, M. Retrieving crop leaf tilt angle from imaging spectroscopy data. Agric. For. Meteorol. 2015, 205, 73–82. [Google Scholar] [CrossRef]
- Marshall, M.; Thenkabail, P. Developing in situ non-destructive estimates of crop biomass to address issues of scale in remote sensing. Remote Sens. 2015, 7, 808–835. [Google Scholar] [CrossRef] [Green Version]
- Hill, M.J. Vegetation index suites as indicators of vegetation state in grassland and savanna: An analysis with simulated SENTINEL 2 data for a North American transect. Remote Sens. Environ. 2013, 137, 94–111. [Google Scholar] [CrossRef]
- Jönsson, P.; Cai, Z.; Melaas, E.; Friedl, M.A.; Eklundh, L. A method for robust estimation of vegetation seasonality from Landsat and Sentinel-2 time series data. Remote Sens. 2018, 10, 635. [Google Scholar] [CrossRef] [Green Version]
- Sun, Y.; Qin, Q.; Ren, H.; Zhang, T.; Chen, S. Red-edge band vegetation indices for leaf area index estimation from sentinel-2/msiimagery. IEEE Trans. Geosci. Remote Sens. 2019, 58, 826–840. [Google Scholar] [CrossRef]
- Zou, X.; Mõttus, M.; Tammeorg, P.; Torres, C.L.; Takala, T.; Pisek, J.; Mäkelä, P.; Stoddard, F.L.; Pellikka, P. Photographic measurement of leaf angles in field crops. Agric. For. Meteorol. 2014, 184, 137–146. [Google Scholar] [CrossRef] [Green Version]
- Prey, L.; Schmidhalter, U. Simulation of satellite reflectance data using high-frequency ground based hyperspectral canopy measurements for in-season estimation of grain yield and grain nitrogen status in winter wheat. ISPRS J. Photogramm.Remote Sens. 2019, 149, 176–187. [Google Scholar] [CrossRef]
- Huang, S.; Miao, Y.; Yuan, F.; Gnyp, M.L.; Yao, Y.; Cao, Q.; Lenz-Wiedemann, V.I.S.; Bareth, G. Potential of RapidEye and WorldView-2 satellite data for improvingrice nitrogen monitoring at different growth stages. Remote Sens. 2017, 9, 227. [Google Scholar] [CrossRef] [Green Version]
- Campbell, G.S.; Norman, J.M. An Introduction to Environmental Biophysics; Springer: New York, NY, USA, 1998; pp. 147–165. [Google Scholar]
- McNeil, B.E.; Pisek, J.; Lepisk, H.; Flamenco, E.A. Measuring leaf angle distribution in broadleaf canopies using UAVs. Agric. For. Meteorol. 2016, 218–219, 204–208. [Google Scholar] [CrossRef]
- Pisek, J.; Sonnentag, O.; Richardson, A.D.; Mõttus, M. Is the spherical leaf inclination angle distribution a valid assumption for temperate and boreal broadleaf tree species? Agric. For. Meteorol. 2013, 169, 186–194. [Google Scholar] [CrossRef]
- Webb, N.; Nichol, C.; Wood, J.; Potter, E. User Manual for the SunScan Canopy Analysis System—Type SS1, version 2.0; Delta-T Devices Limited: Winster, UK, 2008; p. 83. [Google Scholar]
- Walthall, C.L.; Norman, J.M.; Welles, J.M.; Campbell, G.; Blad, B.L. Simple Equationto Approximate the Bidirectional Reflectance from Vegetative Canopies and Bare SoilSurfaces. Appl. Opt. 1985, 24, 383–387. [Google Scholar] [CrossRef]
- Nilson, T.; Kuusk, A. A Reflectance Model for the Homogeneous Plant Canopy and ItsInversion. Remote Sens. Environ. 1989, 27, 157–167. [Google Scholar] [CrossRef]
- Feret, J.B.; François, C.; Asner, G.P.; Gitelson, A.A.; Martin, R.E.; Bidel, L.P.R.; Ustin, S.L.; le Maire, G.; Jacquemoud, S. PROSPECT-4 and 5: Advances in the leaf optical properties model separating photosynthetic pigments. Remote Sens. Environ. 2008, 112, 3030–3043. [Google Scholar] [CrossRef]
- Verhoef, W. Light scattering by leaf layers with application to canopy reflectance modeling: The SAIL model. Remote Sens. Environ. 1984, 16, 125–141. [Google Scholar] [CrossRef] [Green Version]
- Kuusk, A. The Hot Spot Effect in Plant Canopy Reflectance. In Photon-Vegetation Interactions; Myneni, R.B., Ross, J., Eds.; Springer: Berlin/Heidelberg, Germany, 1991; pp. 139–159. [Google Scholar]
- Hosgood, B.; Jacquemoud, S.; Andreoli, G.; Verdebout, J.; Pedrini, G.; Schmuck, G. Leaf Optical PropertiesExperiment 93 (Lopex93); Office for Official Publications of the European Communities: Luxembourg, 1994. [Google Scholar]
- Mäkelä, P.; Kleemola, J.; Jokinen, K.; Mantila, J.; Pehu, E.; Peltonen-Sainio, P. Growth response of pea andsummer turnip rape to foliar application of glycinebetaine. Acta Agric. Scand. Sect. B Soil Plant Sci. 1997, 47, 168–175. [Google Scholar]
- Dennett, M.D.; Ishag, K.H.M. Use of the Expolinear Growth Model to Analyse the Growth of Faba bean, Peas and Lentils at Three Densities: Predictive Use of the Model. Ann. Bot. 1998, 82, 507–512. [Google Scholar] [CrossRef] [Green Version]
- Pinheiro, C.; Rodrigues, A.P.; de Carvalho, I.S.; Chaves, M.M.; Ricardo, C.P. Sugar metabolism in developinglupin seeds is affected by a short-term water deficit. J. Exp. Bot. 2005, 56, 2705–2712. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vile, D.; Garnier, E.; Shipley, B.; Laurent, G.; Navas, M.L.; Roumet, C.; Lavorel, S.; Diaz, S.; Hodgson, J.G.; Lloret, F.; et al. Specific leaf area and dry matter content estimate thickness in laminar leaves. Ann. Bot. 2005, 96, 1129–1136. [Google Scholar] [CrossRef]
- Haboudane, D.; Miller, J.; Pattery, E.; Zarco, P.; Strachan, B. Hyperspectral vegetation indices and novel algorithms for predicting green LAI of crop canopies: Modeling and validation in the context of precision agriculture. Remote Sens. Environ. 2004, 90, 337–352. [Google Scholar] [CrossRef]
- Rouse, W.; Haas, R.; Schell, A.; Deering, D.; Harlan, J. Monitoring the Vernal Advancement of Retrogradation(Green Wave Effect) of Natural Vegetation; NASA/GSFC, Type III; Final Report; NASA: Greenbelt, MD, USA, 1974.
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.; Gao, X.; Ferreira, L. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Jiang, Z.; Huete, A.; Didan, K.; Miura, T. Development of a two-band enhanced vegetation index without a blue band. Remote Sens. Environ. 2008, 112, 3833–3845. [Google Scholar] [CrossRef]
- Rondeaux, G.; Steven, M.; Baret, F. Optimization of soil-adjusted vegetation indices. Remote Sens. Environ. 1996, 55, 95–107. [Google Scholar] [CrossRef]
- Gitelson, A.A. Wide Dynamic Range Vegetation Index for remote quantification of biophysical characteristicsof vegetation. J. Plant Physiol. 2004, 161, 165–173. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Peng, Y.; Gitelson, A.A. Application of chlorophyll-related vegetation indices for remote estimation of maizeproductivity. Agric. For. Meteorol. 2011, 151, 1267–1276. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Merzlyak, M.N. Spectral reflectance changes associated with autumn senescence of Aesculushippocastanum L. and Acer platanoides L. leaves. Spectral features and relation to chlorophyll estimation. J. Plant Physiol. 1994, 143, 286–292. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Gritz, Y.; Merzlyak, M.N. Relationships between leaf chlorophyll content and spectral reflectance and algorithms for non-destructive chlorophyll assessment in higher plant leaves. J. Plant Physiol. 2003, 160, 271–282. [Google Scholar] [CrossRef]
- Wu, C.; Niu, Z.; Tang, Q.; Huang, W. Estimating chlorophyll content from hyperspectral vegetation indices: Modeling and validation. Agric. For. Meteorol. 2008, 148, 1230–1241. [Google Scholar] [CrossRef]
- Chen, J.M. Evaluation of vegetation indices and a modified simple ratio for boreal applications. Can. J. Remote Sens. 1996, 22, 229–242. [Google Scholar] [CrossRef]
- Fernández, M.A.; Fernández, M.O.; Quintano, C. SENTINEL-2A red-edge spectral indices suitability for discriminating burn severity. Int. J. Appl. Earth Obs. Geoinf. 2016, 50, 170–175. [Google Scholar] [CrossRef]
- Frampton, W.J.; Dash, J.; Watmough, G.; Milton, E.J. Evaluating the capabilities of Sentinel-2 for quantitative estimation of biophysical variables in vegetation. ISPRS J. Photogram. Remote Sens. 2013, 82, 83–92. [Google Scholar] [CrossRef] [Green Version]
- Volpe, V.; Manzoni, S.; Marani, M.; Katul, G. Leave-One-Out Cross-Validation. In Encyclopedia of Machine Learning; Springer US: Boston, MA, USA, 2010; pp. 600–601. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Belgiu, M.; Dragu, L. Random forest in remote sensing: A review of applications and future directions. ISPRS J. Photogramm.Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- Vapnik, V.N. The Nature of Statistical Learning Theory; Springer: New York, NY, USA, 1995; pp. 123–180. [Google Scholar]
- Mountrakis, G.; Im, J.; Ogole, C. Support vector machines in remote sensing: A review. ISPRS J. Photogramm.Remote Sens. 2011, 66, 247–259. [Google Scholar] [CrossRef]
- Abdi, H. Partial least squares regression and projection on latent structure regression(PLS regression). WIREs Comp. Stat. 2010, 2, 97–106. [Google Scholar] [CrossRef]
- De Grave, C.; Verrelst, J.; MorcilloPallrés, P.; Pipia, L.; RiveraCaicedo, J.P.; Amin, E.; Moreno, J. Quantifying vegetation biophysical variables from the Sentinel-3/FLEX tandem mission: Evaluation of the synergy of OLCI and FLORIS data sources. Remote Sens. Environ. 2020, 251, 112101. [Google Scholar] [CrossRef]
- Berger, K.; Atzberger, C.; Danner, M.; Wocher, M.; Mauser, W.; Hank, T. Model-Based Optimization of Spectral Sampling for the Retrieval of Crop Variables with the PROSAIL Model. Remote Sens. 2018, 10, 2063. [Google Scholar] [CrossRef] [Green Version]
- Kaplan, G.; Rozenstein, O. Spaceborne Estimation of Leaf Area Index in Cotton, Tomato, and Wheat Using Sentinel-2. Land 2021, 10, 505. [Google Scholar] [CrossRef]
- Baret, F.; Guyot, G. Potentials and limits of vegetation indices for LAI and APAR assessment. Remote Sens. Environ. 1991, 35, 161–173. [Google Scholar] [CrossRef]
- Clevers, J.G.P.W.; Verhoef, W. LAI estimation by means of the WDVI: A sensitivity analysis with a combined PROSPECT-SAIL model. Remote Sens. Rev. 1993, 7, 43–64. [Google Scholar] [CrossRef]
- Zou, X.; Hernández-Clemente, R.; Tammeorg, P.; Lizarazo Torres, C.; Stoddard, F.L.; Mäkelä, P.; Pellikka, P.; Mõttus, M. Retrieval of leaf chlorophyll content in field crops using narrow-band indices: Effects of leaf area index and leaf mean tilt angle. Int. J. Remote Sens. 2015, 36, 6031–6055. [Google Scholar] [CrossRef]
- Peppo, D.M.; Taramelli, A.; Boschetti, M.; Mantino, A.; Volpi, I.; Filipponi, F.; Tornato, A.; Valentini, E.; Ragaglini, G. Non-Parametric Statistical Approaches for Leaf Area Index Estimation from Sentinel-2 Data: A Multi-Crop Assessment. Remote Sens. 2021, 13, 2841. [Google Scholar] [CrossRef]
- Xie, Q.; Dash, J.; Huang, W.; Peng, D.; Qin, Q.; Mortimer, H.; Casa, R.; Pignatti, S.; Laneve, G.; Pascucci, S. Vegetation indices combining the red and red-edge spectral information for leaf area index retrieval. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2018, 11, 1482–1493. [Google Scholar] [CrossRef] [Green Version]
- Dong, T.; Liu, J.; Shang, J.; Qian, B.; Ma, B.; Kovacs, J.M.; Walters, D.; Jiao, X.; Geng, X.; Shi, Y. Assessment of red-edge vegetation indices for crop leaf area index estimation. Remote Sens. Environ. 2018, 222, 133–143. [Google Scholar] [CrossRef]
- Verrelst, J.; Muñoz, J.; Alonso, L.; Delegido, J.; Rivera, J.P.; Camps-Valls, G.; Moreno, J. Machine learning regression algorithms for biophysical parameter retrieval: Opportunities for Sentinel-2 and-3. Remote Sens. Environ. 2012, 118, 127–139. [Google Scholar] [CrossRef]
- Kganyago, M.; Odindi, J.; Adjorlolo, C.; Mhangara, P. Evaluating the capability of landsat 8 oli and spot 6 for discriminating invasive alien species in the african savanna landscape. Int. J. Appl. Earth Obs. Geoinf. 2018, 67, 10–19. [Google Scholar] [CrossRef]





| Model | Variable | Symbol | Value or Range | Unit |
|---|---|---|---|---|
| PROSPECT | Leaf structure parameter | N | 1.55 | - |
| Leaf chlorophyll a + b content | Cab | 25–100 | μg cm−2 | |
| Equivalent water thickness | Cw | 0.001 | cm | |
| Leaf dry matter content | Cm | 0.005 | g cm−2 | |
| Brown pigment content | Cbp | 0 | μg cm−2 | |
| Leaf carotenoid content | Car | 0.2 × Cab | μg cm−2 | |
| SAIL | Leaf area index | LAI | 1–5 | - |
| Leaf mean tilt angle | MTA | 15–70 | ° | |
| Hot spot parameter | hspot | 0.01 | - | |
| Solar zenith angle | SZA | 49.4 | ° | |
| Observer zenith angle | OZA | 9 | ° | |
| Relativeazimuth angle | RAA | 90 | ° | |
| Fraction of incident diffuse sky radiation | skyl | Calculated from 6S atmosphere radiative transfer model | - | |
| Soil reflectance | ρsoil | ASD measurement, corrected by soil reflectance model | - |
| Number | Central Wavelength (nm) | Name | Width (nm) | Spatial Resolution (m) |
|---|---|---|---|---|
| 2 | 490 | Blue | 65 | 10 |
| 3 | 560 | Green | 50 | 10 |
| 4 | 665 | Red | 30 | 10 |
| 5 | 705 | RE1 | 15 | 20 |
| 6 | 740 | RE2 | 15 | 20 |
| 7 | 783 | NIR | 20 | 20 |
| 8 | 842 | 115 | 10 | |
| 8A | 865 | 20 | 20 |
| Index(Abbreviation) | Original Equation | References |
|---|---|---|
| Visible–NIR reflectance based VIs | ||
| NDVI | [44] | |
| EVI | [45] | |
| EVI2 | [46] | |
| MTVI2 | [43] | |
| OSAVI | [47] | |
| WDRVI | [48,49] | |
| Red-edge reflectance based VIs | ||
| NDVIRE | [50] | |
| CIRE | 1 | [51] |
| WDRVIRE | [49] | |
| MSRRE | ()/ | [52,53,54] |
| IRECI | ()/() | [55] |
| S2REP | [55] | |
| Band Number | Model Simulation | Field Measurements | ||||
|---|---|---|---|---|---|---|
| LAI | MTA (°) | Fcover | LAI | MTA (°) | Fcover | |
| 2 | 0.47 | 0.20 | 0.86 | 0.34 | 0.00 | 0.22 |
| 3 | 0.33 | 0.07 | 0.50 | 0.18 | 0.05 | 0.06 |
| 4 | 0.43 | 0.31 | 0.91 | 0.40 | 0.08 | 0.47 |
| 5 | 0.26 | 0.00 | 0.30 | 0.00 | 0.77 | 0.18 |
| 6 | 0.07 | 0.79 | 0.47 | 0.06 | 0.87 | 0.44 |
| 7 | 0.21 | 0.77 | 0.69 | 0.15 | 0.78 | 0.57 |
| 8 | 0.20 | 0.77 | 0.68 | 0.15 | 0.77 | 0.57 |
| 8A | 0.20 | 0.78 | 0.67 | 0.16 | 0.76 | 0.57 |
| Vegetation Indices | Model Simulation | Field Measurement | ||||
|---|---|---|---|---|---|---|
| LAI | MTA (°) | Fcover | LAI | MTA (°) | Fcover | |
| NDVI | 0.35 | 0.43 | 0.90 | 0.45 | 0.25 | 0.67 |
| EVI | 0.27 | 0.71 | 0.83 | 0.26 | 0.65 | 0.67 |
| EVI2 | 0.30 | 0.68 | 0.85 | 0.28 | 0.63 | 0.69 |
| OSAVI | 0.32 | 0.58 | 0.90 | 0.37 | 0.46 | 0.72 |
| WDRVI | 0.43 | 0.46 | 0.92 | 0.41 | 0.31 | 0.64 |
| MTVI2 | 0.28 | 0.66 | 0.86 | 0.28 | 0.62 | 0.70 |
| NDVIRE | 0.36 | 0.28 | 0.75 | 0.55 | 0.07 | 0.57 |
| CIRE | 0.32 | 0.21 | 0.55 | 0.57 | 0.05 | 0.54 |
| WDRVIRE | 0.35 | 0.25 | 0.65 | 0.56 | 0.06 | 0.55 |
| IRECI | 0.31 | 0.47 | 0.68 | 0.24 | 0.67 | 0.66 |
| S2REP | 0.21 | 0.00 | 0.14 | 0.19 | 0.52 | 0.00 |
| MSRRE | 0.35 | 0.25 | 0.64 | 0.56 | 0.06 | 0.55 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zou, X.; Zhu, S.; Mõttus, M. Estimation of Canopy Structure of Field Crops Using Sentinel-2 Bands with Vegetation Indices and Machine Learning Algorithms. Remote Sens. 2022, 14, 2849. https://doi.org/10.3390/rs14122849
Zou X, Zhu S, Mõttus M. Estimation of Canopy Structure of Field Crops Using Sentinel-2 Bands with Vegetation Indices and Machine Learning Algorithms. Remote Sensing. 2022; 14(12):2849. https://doi.org/10.3390/rs14122849
Chicago/Turabian StyleZou, Xiaochen, Sunan Zhu, and Matti Mõttus. 2022. "Estimation of Canopy Structure of Field Crops Using Sentinel-2 Bands with Vegetation Indices and Machine Learning Algorithms" Remote Sensing 14, no. 12: 2849. https://doi.org/10.3390/rs14122849
APA StyleZou, X., Zhu, S., & Mõttus, M. (2022). Estimation of Canopy Structure of Field Crops Using Sentinel-2 Bands with Vegetation Indices and Machine Learning Algorithms. Remote Sensing, 14(12), 2849. https://doi.org/10.3390/rs14122849