Identifying Spatial and Temporal Variations in Concrete Bridges with Ground Penetrating Radar Attributes
Abstract
1. Introduction
2. Data Description
- 1.
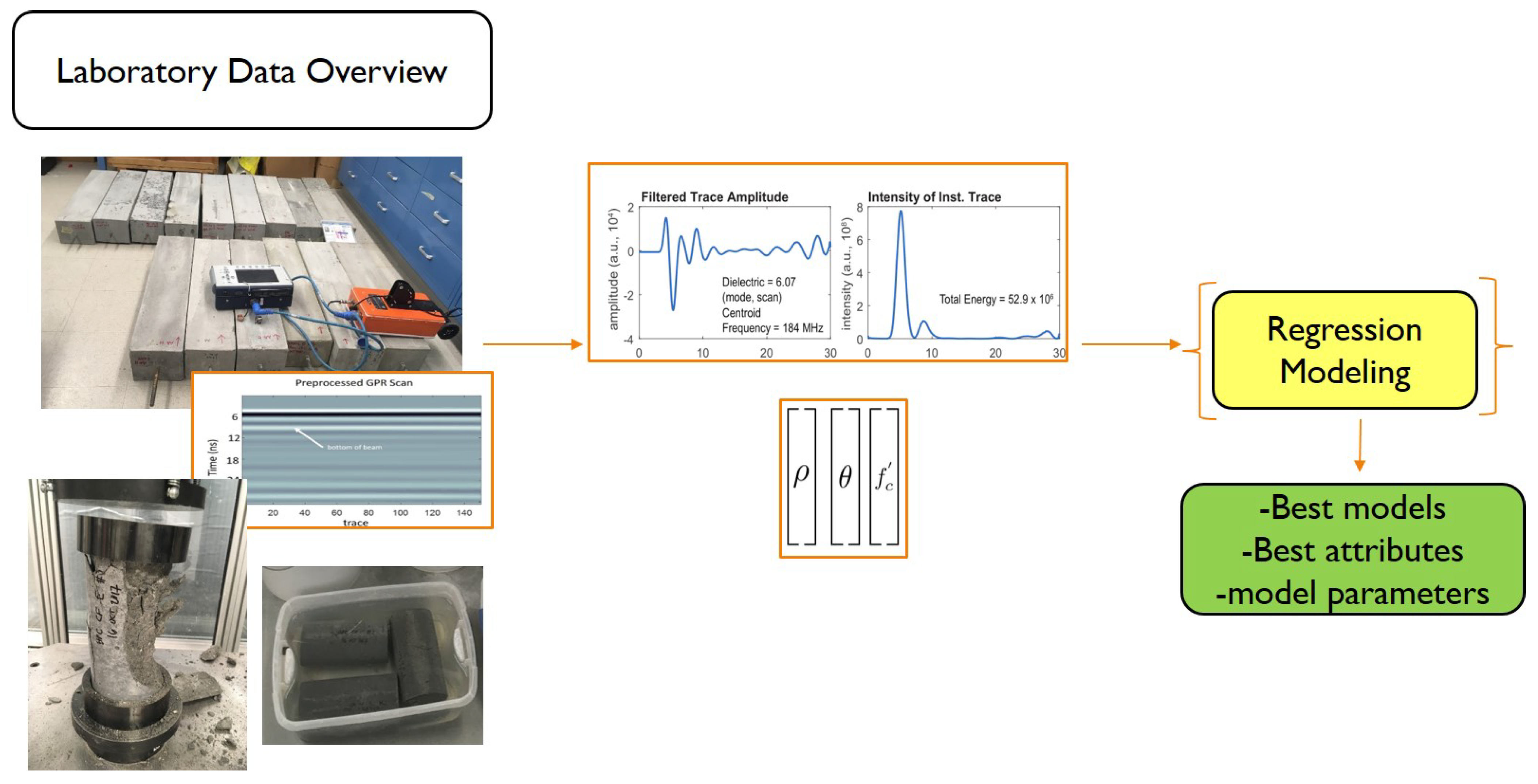
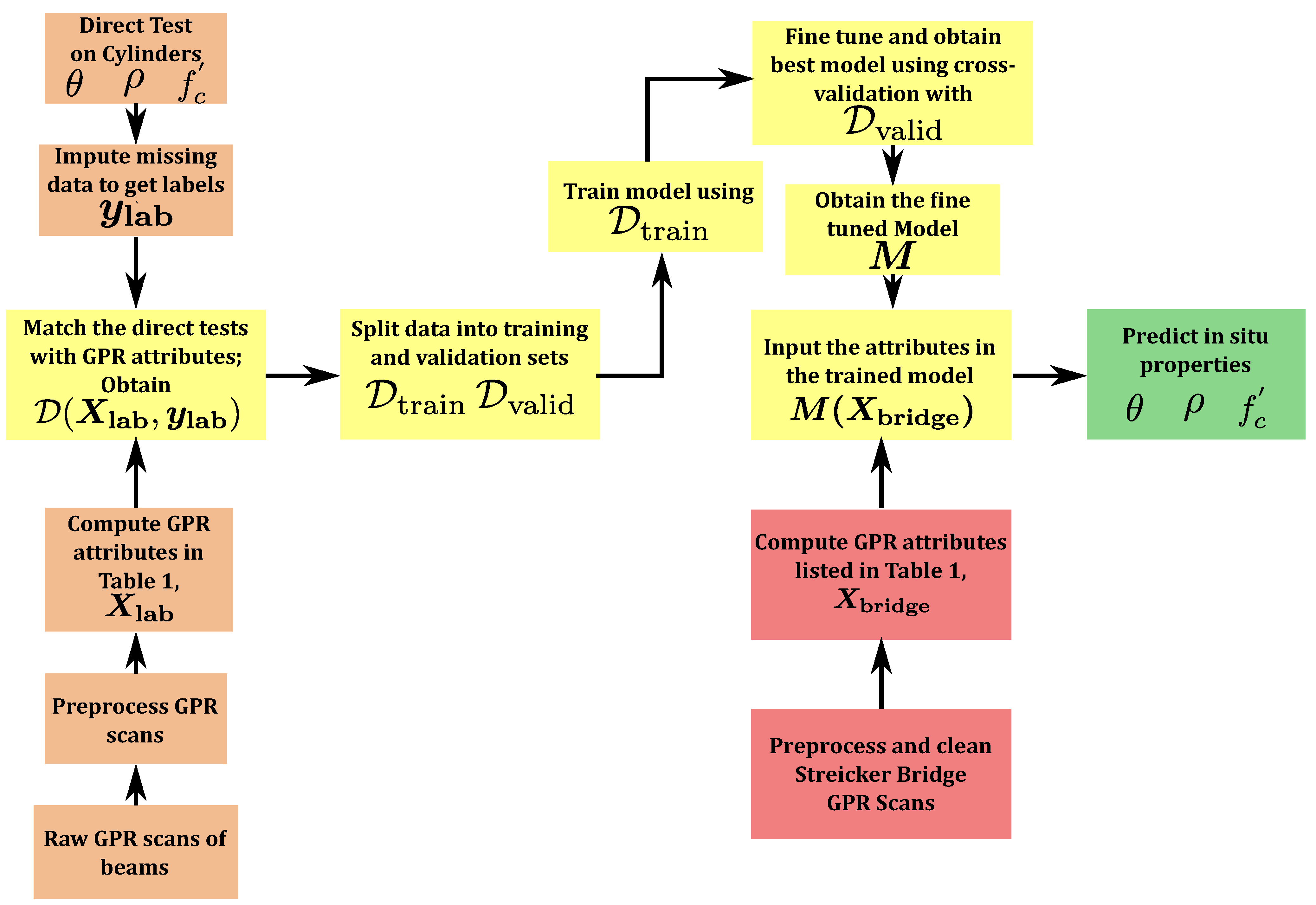
- Laboratory data: Concrete cylinders of 3in diameter and 6in height as per ASTM testing standards, and beams (15 × 15 cm × 90 cm) made of various industrial mixes and cured under different conditions were fabricated and tested. Direct tests were used to obtain values for density, porosity, and compressive strength and the corresponding beams were scanned using a 900-MHz GSSI antenna. The direct test values and calculated attributes from scans were used to develop machine learning models to predict the material properties on Streicker bridge in Section 4. The details of data collection can be found in the previous work by the authors [54]; the lab data and connection with the modeling pipeline (Section 3) are summarized in Figure 1.
- 2.
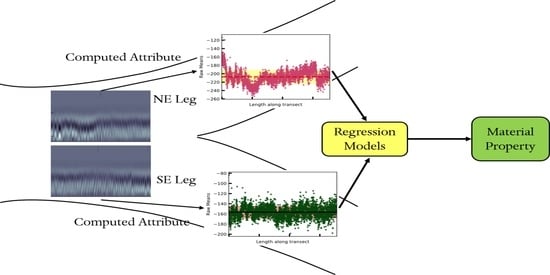
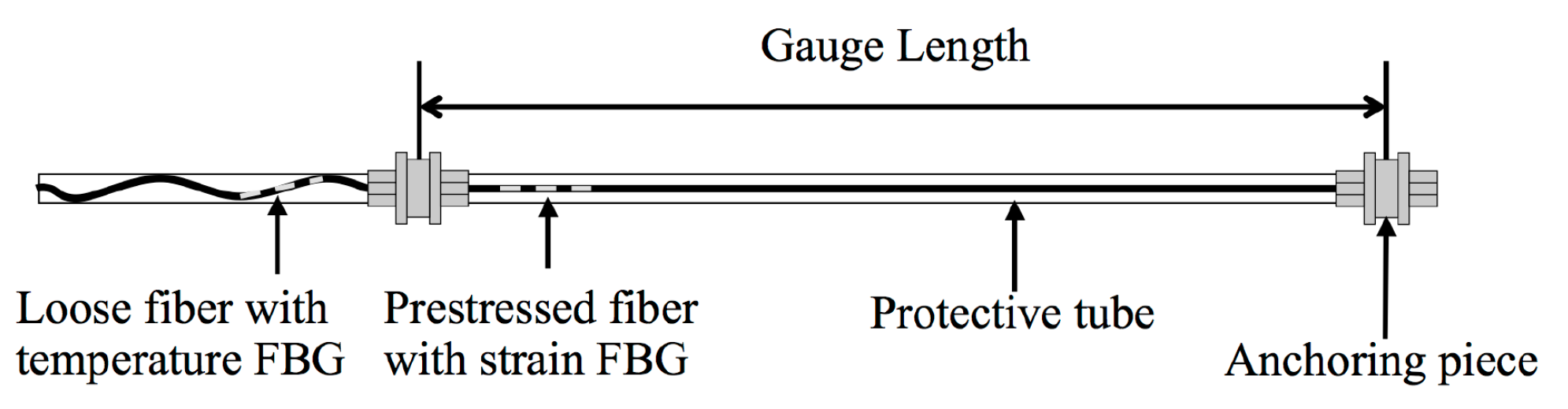
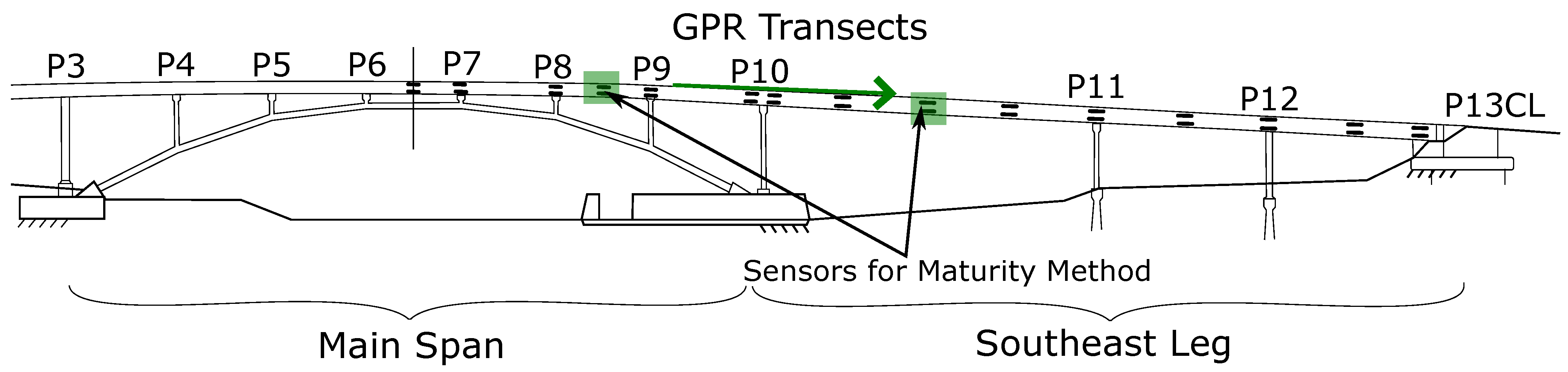
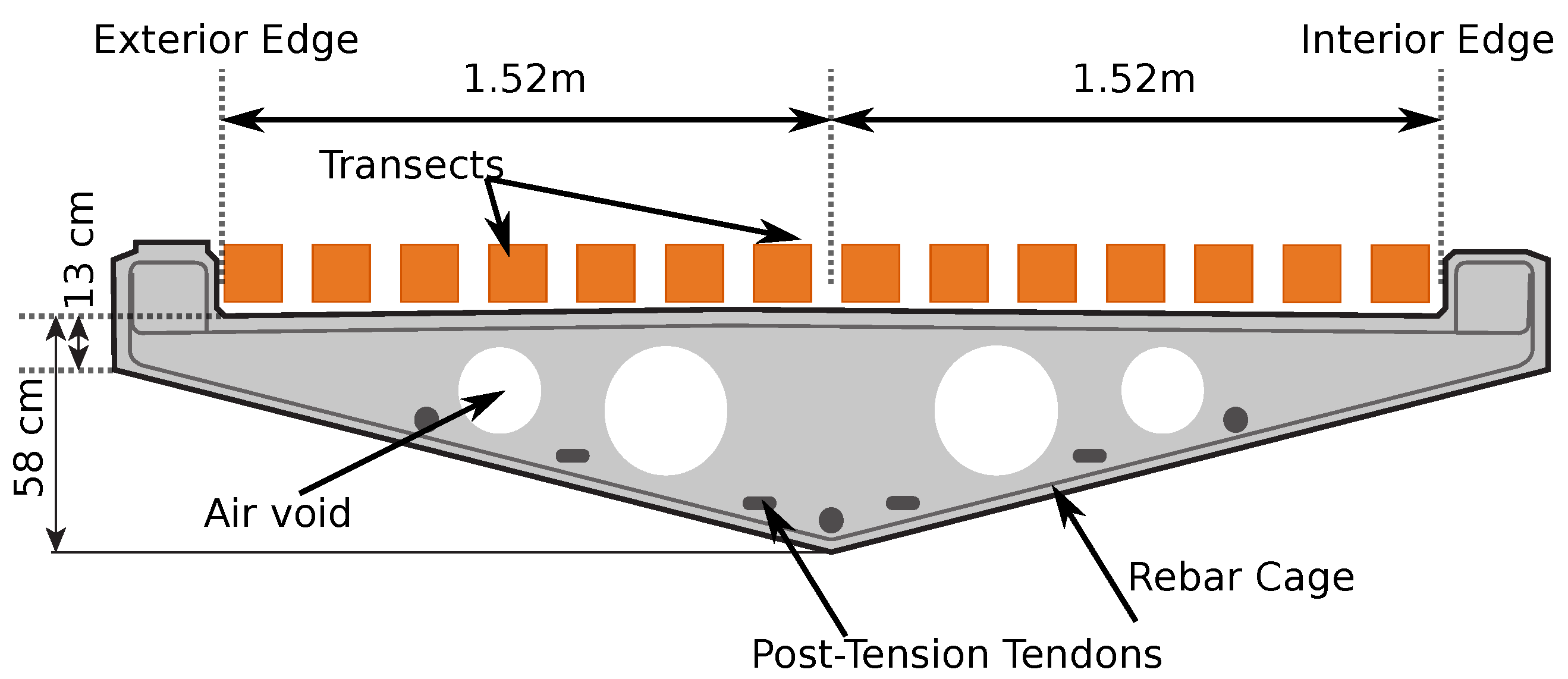
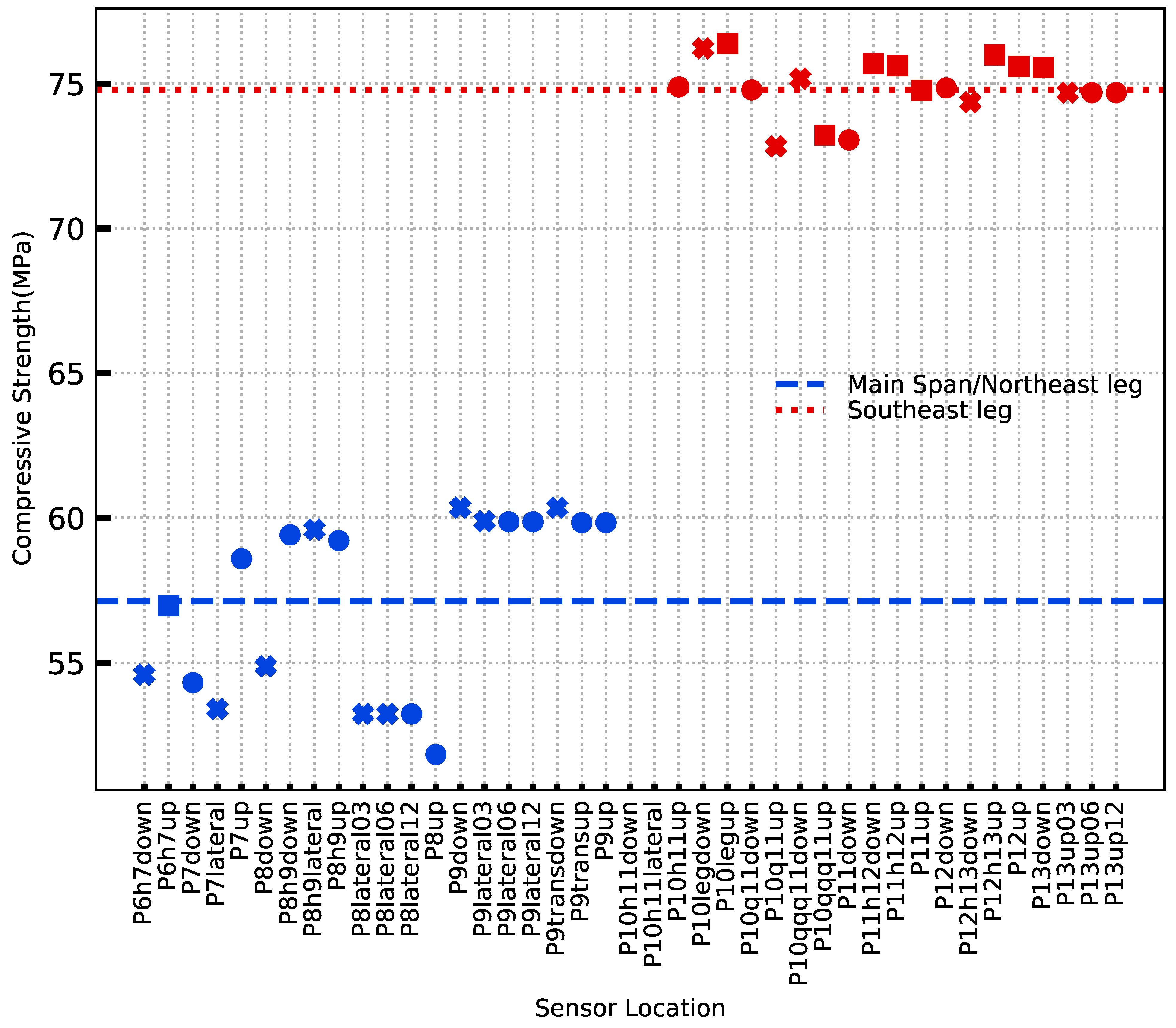
- Streicker bridge: Streicker bridge at Princeton University is the real-life application structure for this paper. The pedestrian bridge provides strategic connection between the east and west ends of the campus. It is a post-tensioned prestressed bridge in the shape of a chromosome. It is 105 m long and consists of a 35 m deck-stiffened arch (the main span) and four approach legs. The approach legs are continuous curved concrete girders. The front view of the bridge is shown in Figure 2. The main span and all legs except the southeast leg were constructed in August 2009. The southeast leg was constructed in October of that year using the same specified concrete mix (Class A HPC with design strength of 41 MPa at 28 days).Streicker bridge was instrumented with long-gage fiber optic sensors at the time of construction for research and teaching purposes. A schematic of Fiber Bragg Grating (FBG) sensor used for temperature monitoring is shown in Figure 3. A brief description of the working is as follows: When a light is sent from the reading unit, specific wavelengths of the light are reflected back by the Bragg gratings in the fiber. Depending on the strain in the fiber, the reflected wavelength changes. The fiber optic sensors installed in Streicker bridge measure both the temperature and strain.The sensor locations along the main span and southeast leg are shown in Figure 4 by black boxes. The sensors have been continuously monitoring strain and temperature with periodic interruptions for maintenance since their installation in 2009. These sensors are installed at various locations on the bridge which provide the temperature data that are required for the maturity index calculations. The temperature readings have an uncertainty of 0.14 C. These sensors are used for compressive strength calculations based on the maturity method. Two typical locations are also highlighted in Figure 4. The GPR attributes collected on Streicker bridge in 2016 and 2020 are used to identify the spatial and temporal variation in concrete in a structure. There are two types of data sets used from previous studies for validation of those predicted values:
- (a)
- Temperature measurements: Streicker bridge is instrumented with Fiber Bragg Grating (FBG) fiber-optic sensors which have been regularly collecting temperature and strain data from the time of construction in 2009. The sensor locations along the main span and southeast leg are shown in Figure 4 by black boxes. The sensors have been continuously monitoring strain and temperature with periodic interruptions for maintenance since their installation in 2009. These sensors are installed at various locations on the bridge which provide the temperature data that are used for the maturity index estimates of compressive strength. The temperature readings have an uncertainty of 0.14 C. The location of the typical sensors in the main span (P8h9) and southeast leg (P10h11) are highlighted in Figure 4.
- (b)
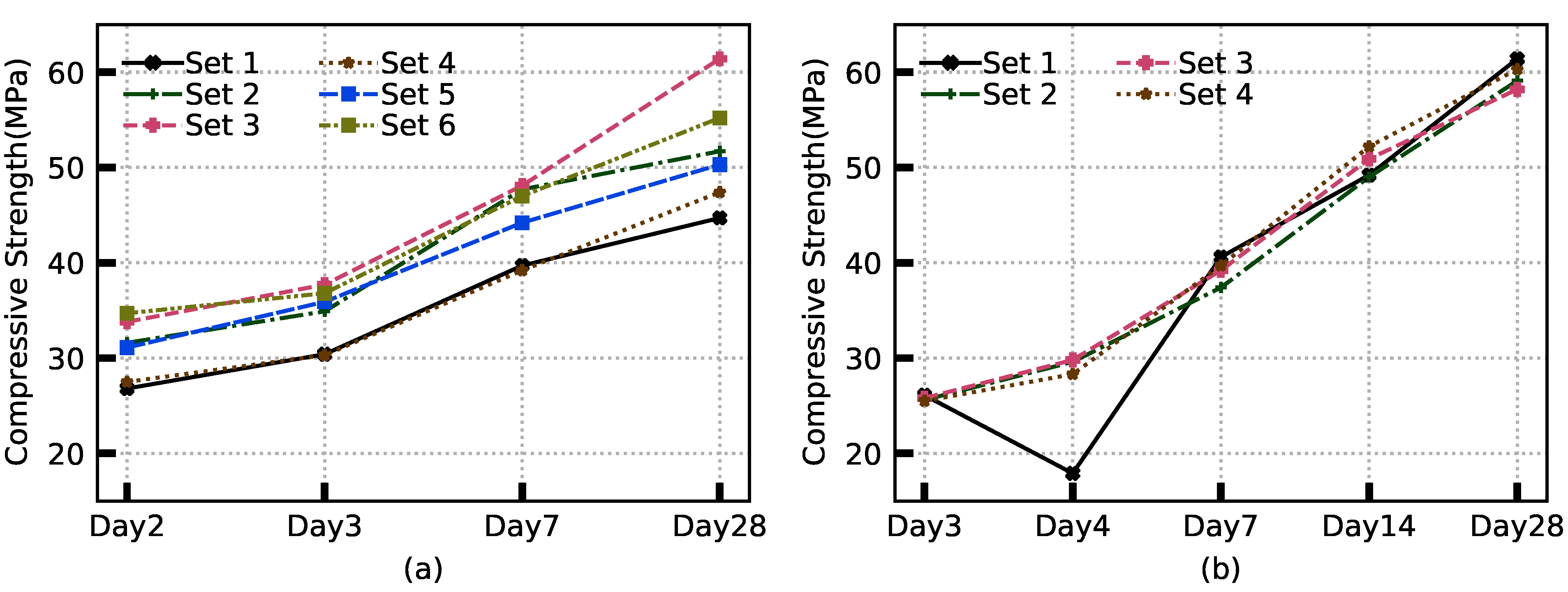
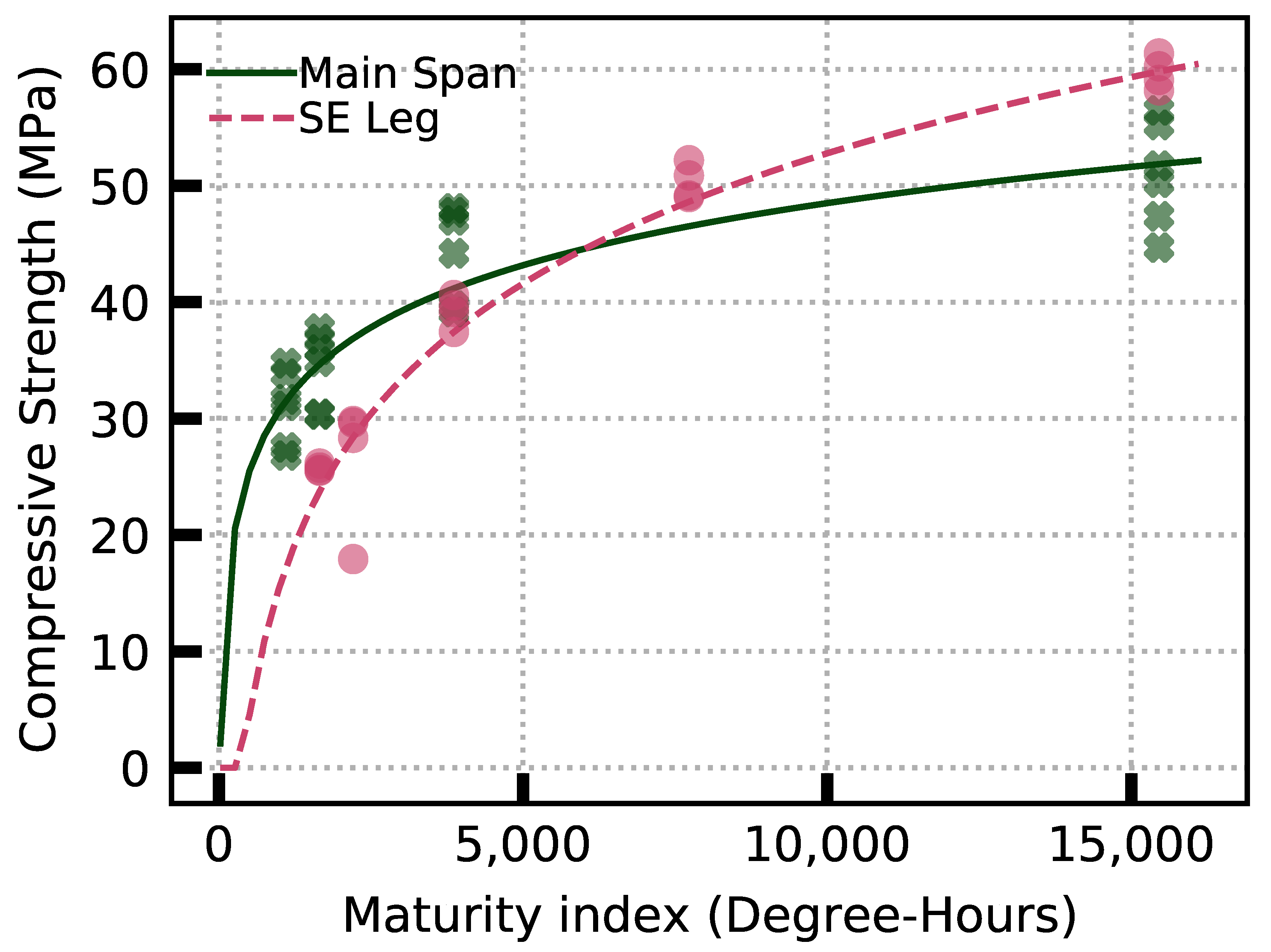
- Core reserves: Class A HPC concrete with a design strength of 41 MPa (at 28 days) was used for the construction of the bridge. The bridge was constructed in two phases; one in August 2009 (main span and northeast leg included) and the other in October 2009 (southeast leg). Even though the design strengths were the same for the two construction phases, the measured compressive strength on the reserved cores indicate a nominal compressive strength of 51 MPa for the main span (MS) and northeast (NE) leg and 59 MPa for southeast (SE) leg at 28 days [56]. Figure 5 shows the compressive strengths of the reserved cores based on the strength tests performed at US Laboratories Inc. (Broomall, PA, USA). Six samples were tested for the concrete poured in August (MS and NE leg) at 2, 3, 7, and 28 days and four samples were tested for the October pour (SE leg) at 3, 4, 7, 14, and 28 days. In this work, we try to identify the spatial variation using GPR attributes.
2.1. GPR Survey of Streicker Bridge
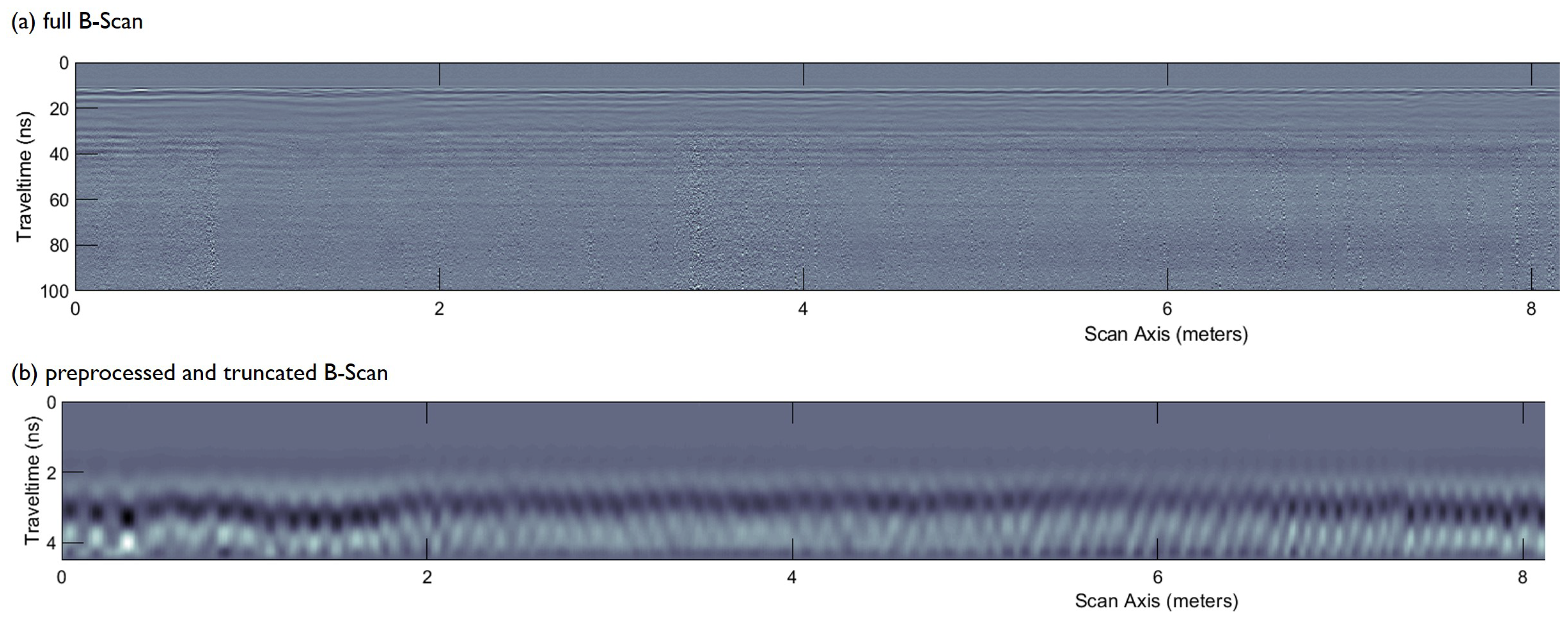
2.2. Data Processing
3. Modeling
3.1. Machine Learning Pipeline
- 1.
- Data imputation: The total samples tested directly in the laboratory for density, compressive strength, and porosity were 219, 146, and 73, respectively. Since the number of samples tested for compressive strength and porosity were small, a data imputation was performed. Mean substitution was chosen as it is a standard practice in data science even if it sometimes results in statistically correlated samples [64].
- 2.
- Stratified split of train-validation data: For a small sample set such as ours, stratified splitting of training and validation sets avoids overfitting. The stratified approach further guarantees that a sample in the validation set would have the same mix of concrete in the training set while preserving the distribution of properties [63].
- 3.
- Feature selection: Since many of the attributes had more than 500 features, feature selection was adopted to improve the computational efficiency of the machine learning models. The feature selection was performed using the score. The top “n” features were chosen heuristically based on the scores.
- 4.
- Model tuning approach: All the machine learning models were first trained using a baseline set of hyper-parameters. These hyper-parameters were then fine-tuned to improve the predictions using randomized search and grid search [65]. The cross-validation score was used to determine the best parameters in all these cases.
3.2. Maturity Index Model
4. Results
4.1. GPR Attributes: Qualitative Spatial and Temporal Variation
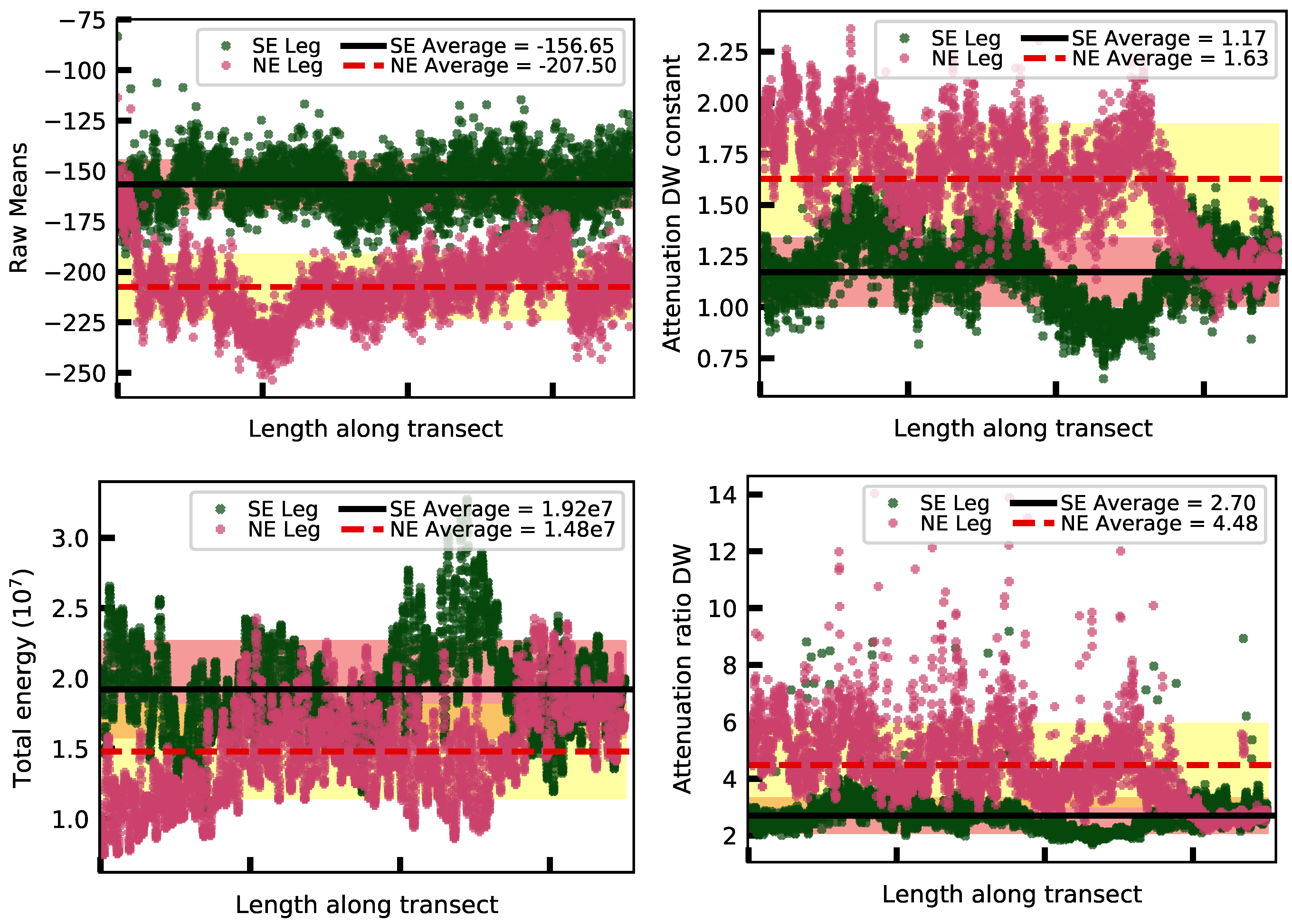
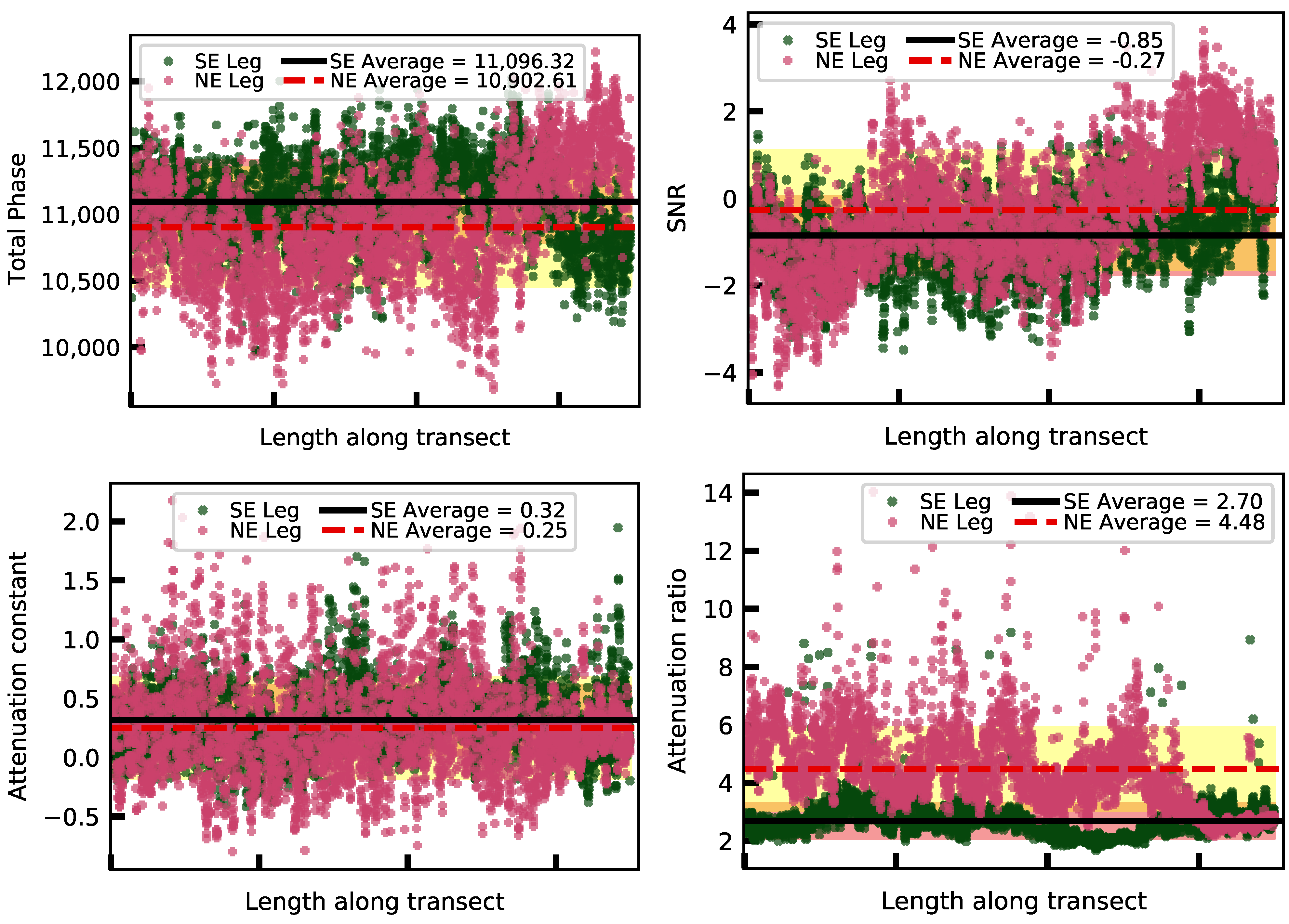
4.1.1. Spatial Variation
4.1.2. Temporal Variation
4.2. Quantitative Differences between Legs
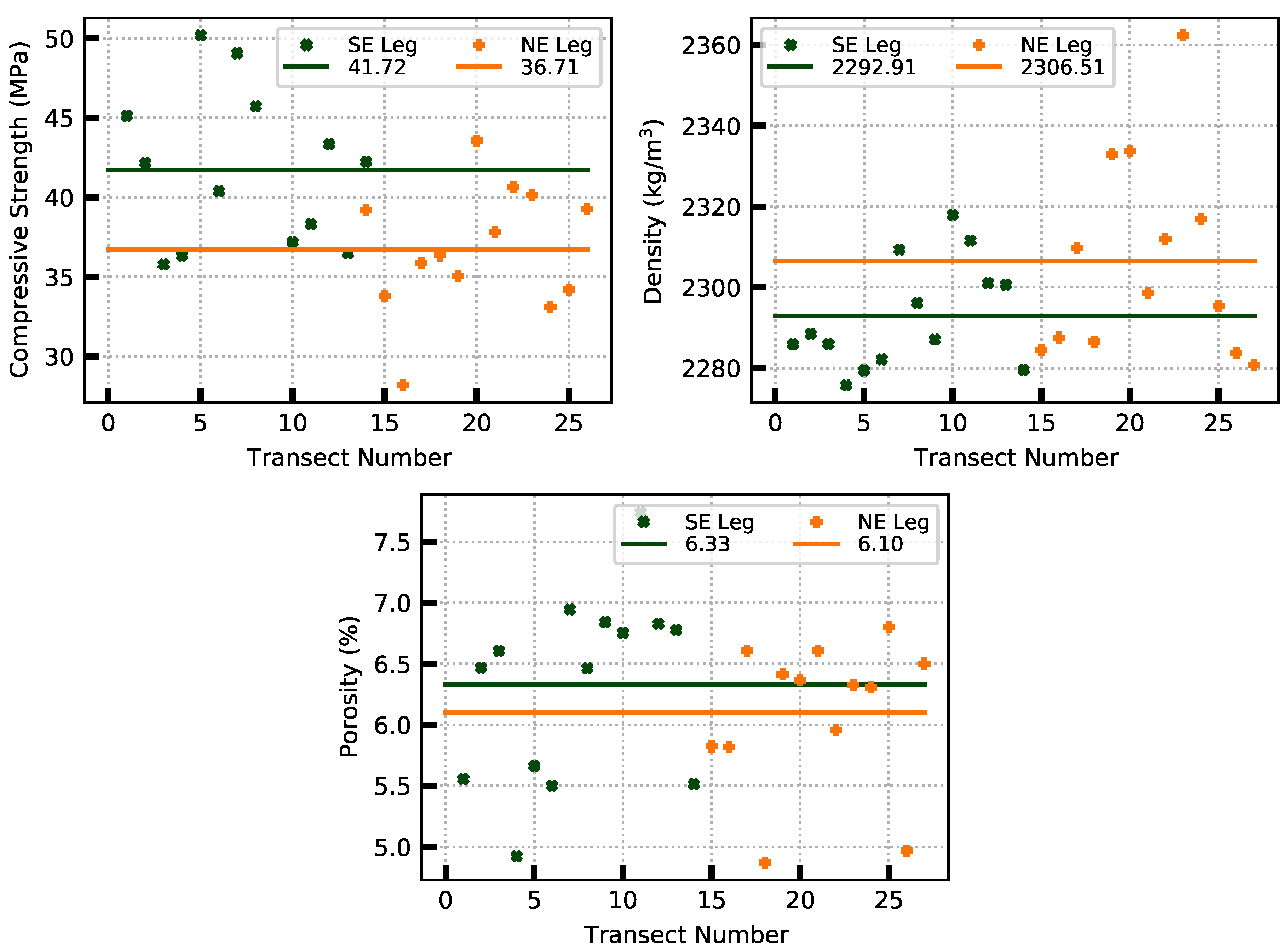
4.2.1. In Situ Property Estimation Using GPR Attributes
4.2.2. Compressive Strength Calculation Using Maturity Method
5. Conclusions and Discussion
- 1.
- Instantaneous amplitude and summary attributes can statistically distinguish between the concrete in Streicker bridge on the basis of relative material properties.
- 2.
- Spatial variation in the physical properties of the two phases of concrete is identified with amplitude-based attributes such as raw means, total energy, and two different measures of attenuation.
- 3.
- Temporal variation in the physical properties over a four-year period is difficult to determine due to the use of different antennas and seasonal differences, but the comparison does identify how sensitive attributes are to the antenna relative to the different concrete.
- 4.
- The GPR attributes predict a 5.01 MPa difference in the mean compressive strength, a 13.6 kg/m difference in density, and a 0.23% difference in porosity between the southeast and northeast legs of the bridge.
- 5.
- The quantitative strength predictions from the GPR attributes are reasonable and fall between the lower bound of the 28-day reserved concrete core strength and the upper bound from the maturity method and temperature history of the concrete.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Betti, R. Aging Infrastructure: Issues, Research, and Technology. Buildings and Infrastructure Protection Series. Infrastructure Protection and Disaster Management Division; Science & Technology Directorate, US Department of Homeland Security: Wahsington, DC, USA, 2010.
- ASCE. 2021 Infrastructure Report Card; ASCE: Reston, VA, USA, 2021. [Google Scholar]
- ASCE. Failure to Act: Economic Impacts of Status Quo Investment Across Infrastructure Systems; Technical Report; ASCE: Reston, VA, USA, 2021; Available online: https://www.asce.org/failuretoact/ (accessed on 2 February 2021).
- Glisic, B.; Inaudi, D. Fibre Optic Methods for Structural Health Monitoring; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Scott, M.; Rezaizadeh, A.; Delahaza, A.; Santos, C.; Moore, M.; Graybeal, B.; Washer, G. A comparison of nondestructive evaluation methods for bridge deck assessment. NDT E Int. 2003, 36, 245–255. [Google Scholar] [CrossRef]
- Rehman, S.K.U.; Ibrahim, Z.; Memon, S.A.; Jameel, M. Nondestructive test methods for concrete bridges: A review. Constr. Build. Mater. 2016, 107, 58–86. [Google Scholar] [CrossRef]
- Alani, A.M.; Aboutalebi, M.; Kilic, G. Applications of ground penetrating radar (GPR) in bridge deck monitoring and assessment. J. Appl. Geophys. 2013, 97, 45–54. [Google Scholar] [CrossRef]
- An, Y.; Chatzi, E.; Sim, S.H.; Laflamme, S.; Blachowski, B.; Ou, J. Recent progress and future trends on damage identification methods for bridge structures. Struct. Control. Health Monit. 2019, 26, e2416. [Google Scholar] [CrossRef]
- Chen, Z.; Zhou, X.; Wang, X.; Dong, L.; Qian, Y. Deployment of a smart structural health monitoring system for long-span arch bridges: A review and a case study. Sensors 2017, 17, 2151. [Google Scholar] [CrossRef] [PubMed]
- Ko, J.; Ni, Y.Q. Technology developments in structural health monitoring of large-scale bridges. Eng. Struct. 2005, 27, 1715–1725. [Google Scholar] [CrossRef]
- Cao, W.; Liu, W.; Koh, C.G.; Smith, I.F. Exploring potential benefits of bridge condition assessment in highway operations. In Proceedings of the IABSE Congress 2019, New York, NY, USA, 4–6 September 2019; IABSE: Zurich, Switzerland, 2019. [Google Scholar]
- Fu, G.; Devaraj, D. Bridge Management Using Pontis and Improved Concepts. In Bridge Engineering Handbook, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2014; pp. 233–246. [Google Scholar]
- Kim, J.; Ahn, Y.; Yeo, H. A comparative study of time-based maintenance and condition-based maintenance for optimal choice of maintenance policy. Struct. Infrastruct. Eng. 2016, 12, 1525–1536. [Google Scholar] [CrossRef]
- Ni, Y.; Wong, K. Integrating bridge structural health monitoring and condition-based maintenance management. In Proceedings of the 4th International Workshop on Civil Structural Health Monitoring, Berlin, Germany, 6–8 November 2012; pp. 6–8. [Google Scholar]
- Rens, K.L.; Wipf, T.J.; Klaiber, F.W. Review of nondestructive evaluation techniques of civil infrastructure. J. Perform. Constr. Facil. 1997, 11, 152–160. [Google Scholar] [CrossRef]
- Giannini, R.; Sguerri, L.; Paolacci, F.; Alessandri, S. Assessment of concrete strength combining direct and NDT measures via Bayesian inference. Eng. Struct. 2014, 64, 68–77. [Google Scholar] [CrossRef]
- Li, Z.; Li, F.; Zdunek, A.; Landis, E.; Shah, S.P. Application of acoustic emission technique to detection of rebar corrosion in concrete. Mater. J. 1998, 95, 68–81. [Google Scholar]
- Rhazi, J.; Kharrat, Y.; Ballivy, G.; Rivest, M. Application of acoustical imaging to the evaluation of concrete in operating structures. Spec. Publ. 1997, 168, 221–232. [Google Scholar]
- Holford, K.M.; Davies, A.; Pullin, R.; Carter, D. Damage location in steel bridges by acoustic emission. J. Intell. Mater. Syst. Struct. 2001, 12, 567–576. [Google Scholar] [CrossRef]
- Maser, K.R.; Roddis, W.K. Principles of thermography and radar for bridge deck assessment. J. Transp. Eng. 1990, 116, 583–601. [Google Scholar] [CrossRef]
- Clark, M.; McCann, D.; Forde, M. Application of infrared thermography to the non-destructive testing of concrete and masonry bridges. NDT E Int. 2003, 36, 265–275. [Google Scholar] [CrossRef]
- Chang, Y.F.; Wang, C.Y. A 3-D image detection method of a surface opening crack in concrete using ultrasonic transducer arrays. J. Nondestruct. Eval. 1997, 16, 193–203. [Google Scholar] [CrossRef]
- Mohamed, O.A.; Rens, K.L. Ultrasonic testing of properties of 50 year old concrete. Mater. Eval. 2001, 59, 1426–1430. [Google Scholar]
- Shiotani, T.; Aggelis, D.G.; Makishima, O. Global monitoring of large concrete structures using acoustic emission and ultrasonic techniques: Case study. J. Bridge Eng. 2009, 14, 188–192. [Google Scholar] [CrossRef]
- Rens, K.L.; Greimann, L.F. Ultrasonic approach for nondestructive testing of civil infrastructure. J. Perform. Constr. Facil. 1997, 11, 97–104. [Google Scholar] [CrossRef]
- Davis, A.; Ansari, F.; Gaynor, R.; Lozen, K.; Rowe, T.; Caratin, H.; Heidbrink, F.; Malhotra, V.; Simons, B.; Carino, N. Nondestructive Test Methods for Evaluation of Concrete in Structures; American Concrete Institute, ACI: Farmington Hills, MI, USA, 1998; Volume 228. [Google Scholar]
- Ervin, B.L.; Kuchma, D.A.; Bernhard, J.T.; Reis, H. Monitoring corrosion of rebar embedded in mortar using high-frequency guided ultrasonic waves. J. Eng. Mech. 2009, 135, 9–19. [Google Scholar] [CrossRef]
- Azari, H.; Nazarian, S.; Yuan, D. Assessing sensitivity of impact echo and ultrasonic surface waves methods for nondestructive evaluation of concrete structures. Constr. Build. Mater. 2014, 71, 384–391. [Google Scholar] [CrossRef]
- Krause, M.; Milmann, B.; Mielentz, F.; Streicher, D.; Redmer, B.; Mayer, K.; Langenberg, K.J.; Schickert, M. Ultrasonic imaging methods for investigation of post-tensioned concrete structures: A study of interfaces at artificial grouting faults and its verification. J. Nondestruct. Eval. 2008, 27, 67–82. [Google Scholar] [CrossRef]
- Hsieh, K.H.; Halling, M.W.; Barr, P.J. Overview of vibrational structural health monitoring with representative case studies. J. Bridge Eng. 2006, 11, 707–715. [Google Scholar] [CrossRef]
- Samman, M.M.; Biswas, M. Vibration testing for nondestructive evaluation of bridges. I: Theory. J. Struct. Eng. 1994, 120, 269–289. [Google Scholar] [CrossRef]
- Kazemi, M.; Madandoust, R.; de Brito, J. Compressive strength assessment of recycled aggregate concrete using Schmidt rebound hammer and core testing. Constr. Build. Mater. 2019, 224, 630–638. [Google Scholar] [CrossRef]
- Breccolotti, M.; Bonfigli, M.F.; Materazzi, A.L. Influence of carbonation depth on concrete strength evaluation carried out using the SonReb method. NDT E Int. 2013, 59, 96–104. [Google Scholar] [CrossRef]
- Cristofaro, M.; Viti, S.; Tanganelli, M. New predictive models to evaluate concrete compressive strength using the SonReb method. J. Build. Eng. 2020, 27, 100962. [Google Scholar] [CrossRef]
- Diamanti, N.; Annan, A.P.; Redman, J.D. Concrete bridge deck deterioration assessment using ground penetrating radar (GPR). J. Environ. Eng. Geophys. 2017, 22, 121–132. [Google Scholar] [CrossRef]
- Chen, D.H.; Wimsatt, A. Inspection and condition assessment using ground penetrating radar. J. Geotech. Geoenviron. Eng. 2010, 136, 207–214. [Google Scholar] [CrossRef]
- Maser, K.R. Condition assessment of transportation infrastructure using ground-penetrating radar. J. Infrastruct. Syst. 1996, 2, 94–101. [Google Scholar] [CrossRef]
- Barnes, C.L.; Trottier, J.F. Ground-penetrating radar for network-level concrete deck repair management. J. Transp. Eng. 2000, 126, 257–262. [Google Scholar] [CrossRef]
- Sbartaï, Z.; Laurens, S.; Viriyametanont, K.; Balayssac, J.; Arliguie, G. Non-destructive evaluation of concrete physical condition using radar and artificial neural networks. Constr. Build. Mater. 2009, 23, 837–845. [Google Scholar] [CrossRef]
- Sbartaï, Z.M.; Laurens, S.; Elachachi, S.M.; Payan, C. Concrete properties evaluation by statistical fusion of NDT techniques. Constr. Build. Mater. 2012, 37, 943–950. [Google Scholar] [CrossRef]
- Ploix, M.A.; Garnier, V.; Breysse, D.; Moysan, J. NDE data fusion to improve the evaluation of concrete structures. NDT E Int. 2011, 44, 442–448. [Google Scholar] [CrossRef]
- Villain, G.; Sbartaï, Z.M.; Dérobert, X.; Garnier, V.; Balayssac, J.P. Durability diagnosis of a concrete structure in a tidal zone by combining NDT methods: Laboratory tests and case study. Constr. Build. Mater. 2012, 37, 893–903. [Google Scholar] [CrossRef]
- Völker, C.; Shokouhi, P. Multi sensor data fusion approach for automatic honeycomb detection in concrete. NDT E Int. 2015, 71, 54–60. [Google Scholar] [CrossRef]
- Dérobert, X.; Lataste, J.F.; Balayssac, J.P.; Laurens, S. Evaluation of chloride contamination in concrete using electromagnetic non-destructive testing methods. NDT E Int. 2017, 89, 19–29. [Google Scholar] [CrossRef]
- Hugenschmidt, J.; Mastrangelo, R. GPR inspection of concrete bridges. Cem. Concr. Compos. 2006, 28, 384–392. [Google Scholar] [CrossRef]
- Maierhofer, C. Nondestructive evaluation of concrete infrastructure with ground penetrating radar. J. Mater. Civ. Eng. 2003, 15, 287–297. [Google Scholar] [CrossRef]
- Morris, I.; Abdel-Jaber, H.; Glisic, B. Quantitative attribute analyses with ground penetrating radar for infrastructure assessments and structural health monitoring. Sensors 2019, 19, 1637. [Google Scholar] [CrossRef]
- Jazayeri, S.; Kruse, S.; Hasan, I.; Yazdani, N. Reinforced concrete mapping using full-waveform inversion of GPR data. Constr. Build. Mater. 2019, 229, 117102. [Google Scholar] [CrossRef]
- Clemena, G.G.; Sprinkel, M.M.; Long, R.R., Jr. Use of Ground-Penetrating Radar for Detecting Voids under a Jointed Concrete Pavement; Transportation Research Record: Washington, DC, USA, 1987. [Google Scholar]
- Anderson, N.L.; Ismael, A.M.; Thitimakorn, T. Ground-penetrating radar: A tool for monitoring bridge scour. Environ. Eng. Geosci. 2007, 13, 1–10. [Google Scholar] [CrossRef]
- Laurens, S.; Balayssac, J.; Rhazi, J.; Klysz, G.; Arliguie, G. Non-destructive evaluation of concrete moisture by GPR: Experimental study and direct modeling. Mater. Struct. 2005, 38, 827–832. [Google Scholar] [CrossRef]
- Dérobert, X.; Iaquinta, J.; Klysz, G.; Balayssac, J.P. Use of capacitive and GPR techniques for the non-destructive evaluation of cover concrete. NDT E Int. 2008, 41, 44–52. [Google Scholar] [CrossRef]
- Plati, C.; Loizos, A. Estimation of in-situ density and moisture content in HMA pavements based on GPR trace reflection amplitude using different frequencies. J. Appl. Geophys. 2013, 97, 3–10. [Google Scholar] [CrossRef]
- Morris, I.M.; Kumar, V.; Glisic, B. Predicting material properties of concrete from ground-penetrating radar attributes. Struct. Health Monit. 2020, 1475921720976999. [Google Scholar]
- Rodés, J.P.; Pérez-Gracia, V.; Martínez-Reguero, A. Evaluation of the GPR frequency spectra in asphalt pavement assessment. Constr. Build. Mater. 2015, 96, 181–188. [Google Scholar] [CrossRef]
- Sigurdardottir, D.H. Strain-Based Monitoring Methods for Beam-Like Structures. Ph.D. Thesis, Princeton University, Princeton, NJ, USA, 2015. [Google Scholar]
- Morris, I.M.; Abdel-Jaber, H.; Glisic, B. Ground penetrating radar as a monitoring tool: Mapping internal features with attribute analysis. In Proceedings of the SHMII 8, Brisbane, Australia, 5–8 December 2017. [Google Scholar]
- Allroggen, N.; Tronicke, J. Attribute-based analysis of time-lapse ground-penetrating radar data. Geophysics 2016, 81, H1–H8. [Google Scholar] [CrossRef]
- Annan, A. Ground Penetrating Radar Principles, Procedures, and Applications; Sensors and Software Inc.: Mississauga, ON, Canada, 2003; p. 285. [Google Scholar]
- Allen, R. Automatic earthquake recognition and timing from single traces. Bull. Seismol. Soc. Am. 1978, 68, 1521–1531. [Google Scholar]
- Wong, P.T.; Lai, W.W.; Sham, J.F.; Poon, C.S. Hybrid non-destructive evaluation methods for characterizing chloride-induced corrosion in concrete. NDT E Int. 2019, 107. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Kohavi, R. A study of cross-validation and bootstrap for accuracy estimation and model selection. In Proceedings of the IJCAI, Montreal, QC, Canada, 20–25 August 1995; Volume 14, pp. 1137–1145. [Google Scholar]
- Rubin, L.; Witkiewitz, K.; Andre, J.; Reilly, S. Methods for handling missing data in the behavioral neurosciences: Don’t throw the baby rat out with the bath water. J. Undergrad. Neurosci. Educ. 2007, 5, A71. [Google Scholar] [PubMed]
- Bergstra, J.; Bengio, Y. Random search for hyper-parameter optimization. J. Mach. Learn. Res. 2012, 13, 281–305. [Google Scholar]
- C1074-19e1. Standard Practice for Estimating Concrete Strength by the Maturity Method; ASTM International: West Conshohocken, PA, USA, 2019. [Google Scholar]
- Plowman, J.M. Maturity and the strength of concrete. Mag. Concr. Res. 1956, 8, 13–22. [Google Scholar] [CrossRef]
- Carino, N.J. The Maturity Method. In Handbook on Nondestructive Testing of Concrete; Malhotra, V.M., Carino, N.J., Eds.; CRC Press: West Conshohocken, PA, USA, 2003; pp. 5.1–5.47. [Google Scholar]
- Ruxton, G.D. The unequal variance t-test is an underused alternative to Student’s t-test and the Mann–Whitney U test. Behav. Ecol. 2006, 17, 688–690. [Google Scholar] [CrossRef]
- Past Weather in Princeton, NJ, USA. Available online: https://www.timeanddate.com/weather/@5102922/historic (accessed on 24 April 2021).
- Morris, I.M.; Kumar, V.; Lopez, S.A.; Glisic, B. Comparing predicted in situ 8-year concrete strength by ground penetrating radar attributes and maturity method. In Nondestructive Characterization and Monitoring of Advanced Materials, Aerospace, Civil Infrastructure, and Transportation XV; Yu, T.Y., Gyekenyesi, A.L., Eds.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 2021; Volume 11592, pp. 38–47. [Google Scholar] [CrossRef]



| Main Attribute | Equation | Derived Attribute | Equation |
|---|---|---|---|
| Instantaneous Amplitude | Total energy | ||
| Intensity | Raw average amplitude | Average(A) | |
| Phase | Signal-to-Noise (SNR) | ||
| Dielectric Constant () | |||
| Span | ||
|---|---|---|
| Main Span | 1116.3 | −3198.7 |
| South-east Leg | 2249.7 | −12,951.9 |
| Attribute | Range SE Leg | Range NE Leg |
|---|---|---|
| Raw Means | [−542.13, 196.38] | [−464.25, 60.93] |
| Attenuation DW constant | [−0.73, 6.16] | [−0.47, 6.23] |
| Denergy | [] | [] |
| Attenuation DW ratio | [0.58, 101.32] | [0.70, 107.22] |
| Total Phase | [] | [] |
| SNR | [−16.797, 12.224] | [−16.899, 14.009] |
| Attenuation constant | [−6.51, 15.00] | [−6.18, 20.17] |
| Dielectric constant | [3.01, 78.74] | [3.10, 93.71] |
| Attribute | Welch’s t-Score | p-Value | Mann–Whitney U-Score | p-Value |
|---|---|---|---|---|
| Raw Means | 154.52 | 0.0 | 0.0 | |
| Attenuation DW constant | 86.57 | 0.0 | 0.0 | |
| Denergy | 55.60 | 0.0 | 0.0 | |
| Attenuation DW ratio | −67.88 | 0.0 | 0.0 | |
| Total Phase | 21.19 | |||
| SNR | 21.06 | |||
| Attenuation constant | 7.73 | |||
| Dielectric constant | −22.41 | |||
| Attenuation ratio | −11.42 |
| Attribute | Southeast Leg | Northeast Leg | Ratio SE/NE | |||
|---|---|---|---|---|---|---|
| 2016 | 2020 | 2016 | 2020 | 2016 | 2020 | |
| Raw Means | −160.4 | −156.65 | −169.5 | −207.50 | 0.95 | 0.75 |
| Attenuation constant (DW) | −0.60 | 1.17 | −1.29 | 1.63 | 0.46 | 0.72 |
| Total energy | 1.0 | 1.30 | ||||
| Attenuation ratio (DW) | 3.41 | 2.70 | 1.84 | 4.48 | 1.85 | 0.60 |
| Total Phase | 0.93 | 1.01 | ||||
| Attenuation constant | −1.07 | −0.36 | 2.97 | 1.28 | ||
| Attenuation ratio | 21.72 | 25.64 | 0.85 | 0.59 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kumar, V.; Morris, I.M.; Lopez, S.A.; Glisic, B. Identifying Spatial and Temporal Variations in Concrete Bridges with Ground Penetrating Radar Attributes. Remote Sens. 2021, 13, 1846. https://doi.org/10.3390/rs13091846
Kumar V, Morris IM, Lopez SA, Glisic B. Identifying Spatial and Temporal Variations in Concrete Bridges with Ground Penetrating Radar Attributes. Remote Sensing. 2021; 13(9):1846. https://doi.org/10.3390/rs13091846
Chicago/Turabian StyleKumar, Vivek, Isabel M. Morris, Santiago A. Lopez, and Branko Glisic. 2021. "Identifying Spatial and Temporal Variations in Concrete Bridges with Ground Penetrating Radar Attributes" Remote Sensing 13, no. 9: 1846. https://doi.org/10.3390/rs13091846
APA StyleKumar, V., Morris, I. M., Lopez, S. A., & Glisic, B. (2021). Identifying Spatial and Temporal Variations in Concrete Bridges with Ground Penetrating Radar Attributes. Remote Sensing, 13(9), 1846. https://doi.org/10.3390/rs13091846