Next Article in Journal
An Optical and SAR Based Fusion Approach for Mapping Surface Water Dynamics over Mainland China
Next Article in Special Issue
Review of Works Combining GNSS and InSAR in Europe
Previous Article in Journal
Ambient Seismic Noise and Microseismicity Monitoring of a Prone-To-Fall Quartzite Tower (Ormea, NW Italy)
Previous Article in Special Issue
Multi-Segment Rupture Model of the 2016 Kumamoto Earthquake Revealed by InSAR and GPS Data
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 13
Issue 9
10.3390/rs13091665
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Ground Deformation Modelling of the 2020 Mw6.9 Samos Earthquake (Greece) Based on InSAR and GNSS Data

by
Vassilis Sakkas
Department of Geophysics-Geothermics, National Kapodistrian University of Athens, Panepistimiopolis Zografou, 15784 Athens, Greece
Remote Sens. 2021, 13(9), 1665; https://doi.org/10.3390/rs13091665
Submission received: 19 March 2021 / Revised: 19 April 2021 / Accepted: 22 April 2021 / Published: 24 April 2021
(This article belongs to the Special Issue Ground Deformation Patterns Detection by InSAR and GNSS Techniques)
Browse Figures
Versions Notes

Abstract

:
Modelling of combined Global Navigation Satellite System (GNSS) and Interferometric Synthetic Aperture Radar (InSAR) data was performed to characterize the source of the Mw6.9 earthquake that occurred to the north of Samos Island (Aegean Sea) on 30 October 2020. Pre-seismic analysis revealed an NNE–SSW extensional regime with normal faults along an E–W direction. Co-seismic analysis showed opening of the epicentral region with horizontal and vertical displacements of ~350 mm and ~90 mm, respectively. Line-of-sight (LOS) interferometric vectors were geodetically corrected using the GNSS data and decomposed into E–W and vertical displacement components. Compiled interferometric maps reveal that relatively large ground displacements had occurred in the western part of Samos but had attenuated towards the eastern and southern parts. Alternating motions occurred along and across the main geotectonic units of the island. The best-fit fault model has a two-segment listric fault plane (average slip 1.76 m) of normal type that lies adjacent to the northern coastline of Samos. This fault plane is 35 km long, extends to 15 km depth, and dips to the north at 60° and 40° angles for the upper and lower parts, respectively. A predominant dip-slip component and a substantial lateral one were modelled.

Graphical Abstract

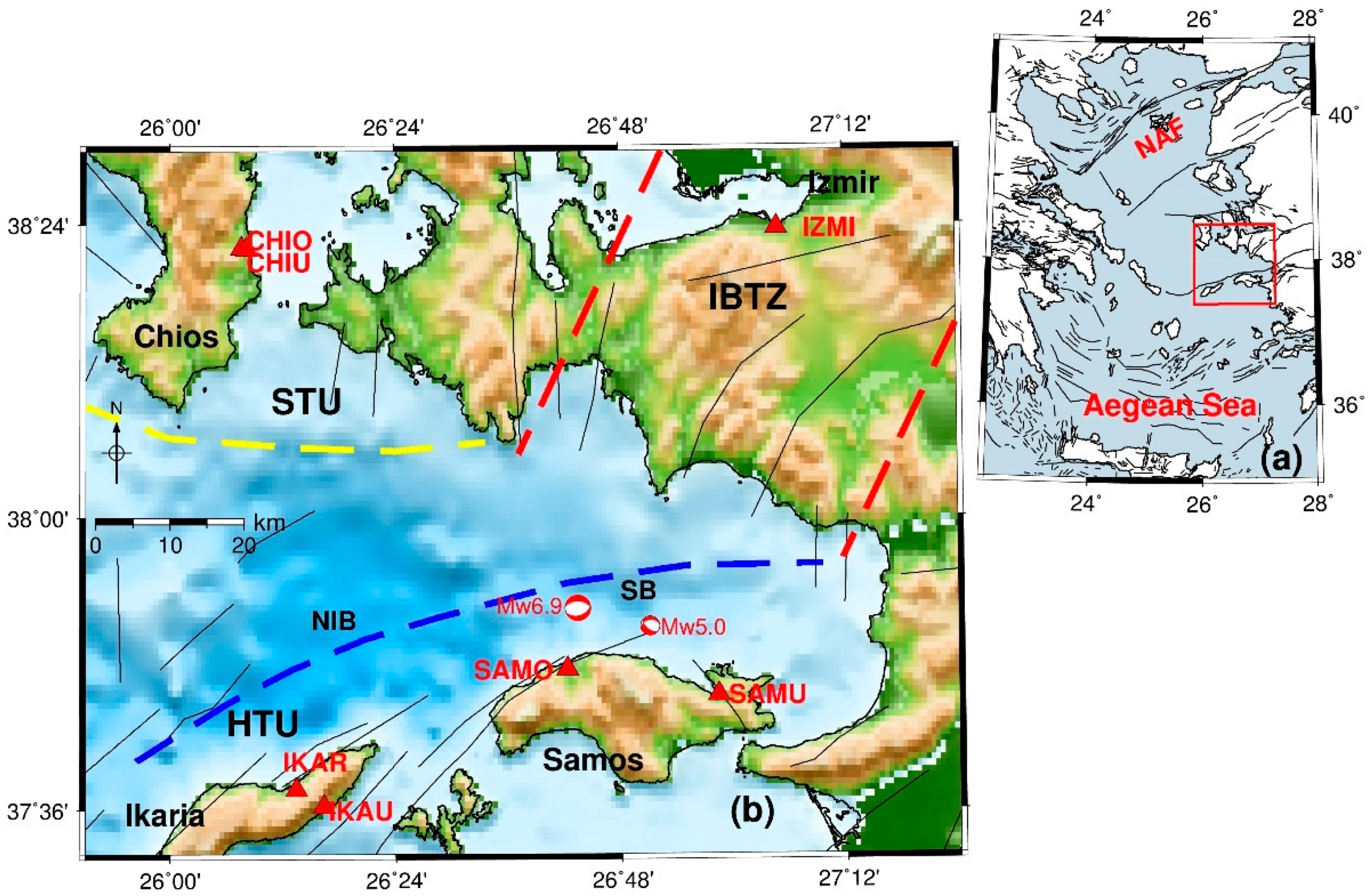
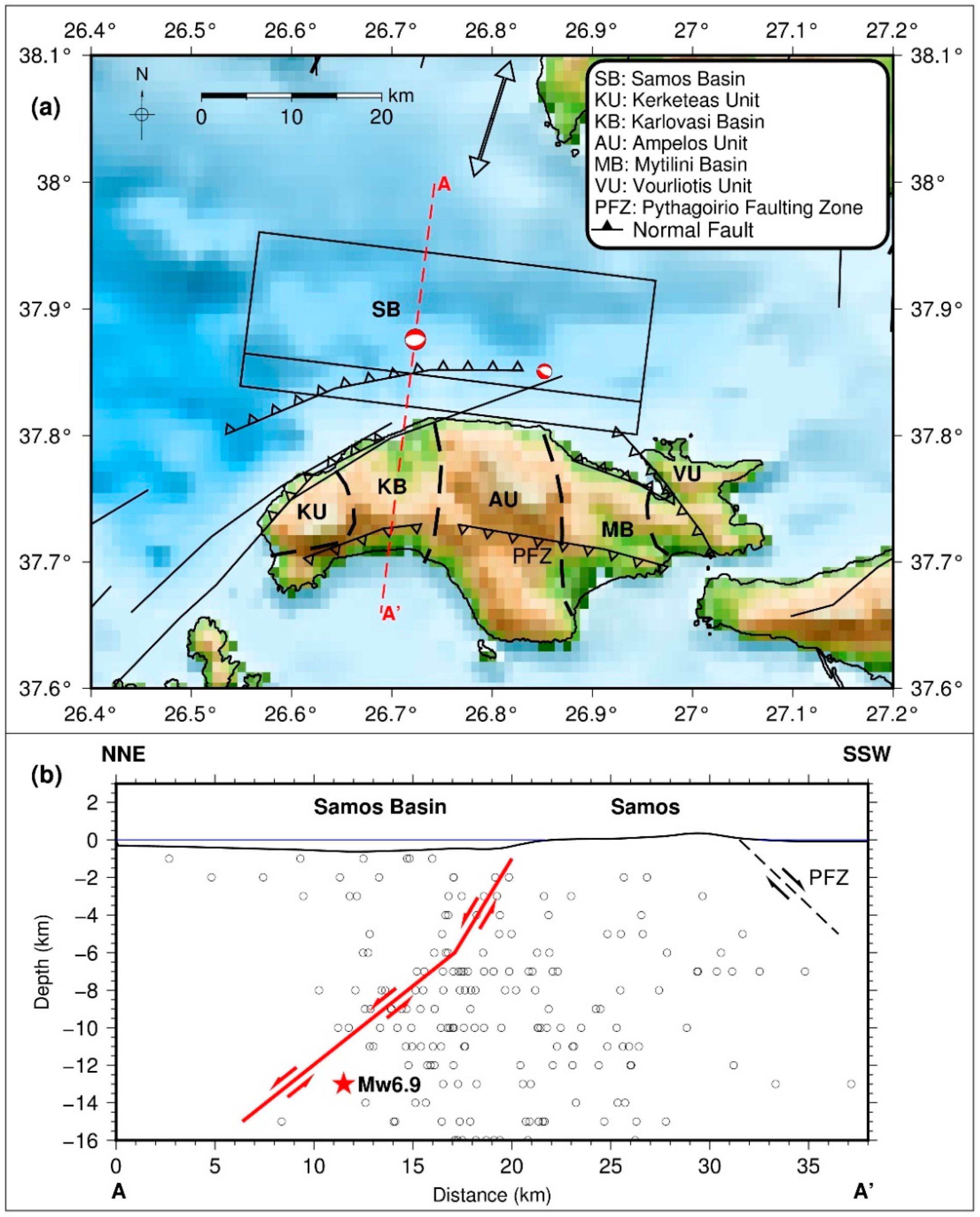
1. Introduction

The Northern Aegean Sea (Greece) is characterized by a complex geotectonic setting with intense seismic activity (Figure 1). The area that is bordered by the Northern Anatolian Fault (NAF) zone to the north and the Hellenic Trench to the south exhibits a strong extensional regime consistent with major continental extension [1,2]. The kinematic and dynamic models of the area are compatible with plate tectonic motions [3,4] and highlight the occurrence of strong ground deformation and intense seismicity. The NE–SW trending, dextral, strike-slip faulting in the northern Aegean Sea is associated with and linked to the NAF, which trends parallel to the North Aegean Trough [5,6,7]. However, the eastern part of the Aegean Sea has diverse fault trends and character. This region accommodates several E–W trending fault zones that exhibit normal-type motions, which are consistent with the extensional stress field [3,8].
The study area of Samos Island—located in the eastern part of the northern Aegean Sea—is subject to extensional forces. It is situated to the south of a NE–SW trending, dextral, strike-slip transfer zone called the Izmir Balikesir Transfer Zone (IBTZ) [1,9], as well as a zone of E–W normal faulting near Izmir Bay (Turkey). East of the IBTZ is the Sakarya Tectonic Unit (STU), which includes Chios Island [10], while in the south the islands of Samos and Ikaria are part of the tectono-metamorphic belt of the Hellenides Tectonic Unit (HTU) [10]. This broad region represents the transition between western Turkey and the Aegean domains [10,11,12].
The geology of the island consists of four main tectono-metamorphic units that are mainly covered by Mio-Pliocene sedimentary basins [11,12,13,14]. Based on geological and seismological studies, there are five active fault zones that have the potential to generate large-magnitude earthquakes [15]. These zones are oriented approximately E–W. Two of them are located in the northern coastal part, and two in the southern central part of Samos. Their dip angles vary between 50 and 75°. The longest fault zone (~27 km) occurs to the north and offshore of the island; it is a normal fault that dips to the north at an angle of 40°. This fault zone is located in the southern part of the Samos Basin (SB) [14]. This basin extends westward towards the deeper (1600 m depth) North Ikarian Basin (NIB).
Several large-magnitude earthquakes have occurred over the last few years in this part of the Aegean [19,20]. The most recent one occurred to the north of Samos on 30 October 2020. This earthquake caused extensive damage on the island and the surrounding areas, as well as significant co-seismic displacements. Combined GNSS and InSAR techniques have been proved effective in precisely measuring the ground deformation. The GNSS technique can provide an absolute 3D vector of ground displacement (estimated errors ~2–3 mm and ~5–8 mm for the horizontal and vertical component, respectively), but it is limited to point-wise coverage. The InSAR provides spatial coverage, but the information is in the line-of-sight (LOS) direction, and further multi-geometrical analysis is required to obtain the true ground motion components. Moreover, the conventional differential interferometry may detect displacements of at least ~28 mm, which is half the wavelength of the radar signal. Thus, joint application of GNSS and InSAR data can effectively determine the real ground displacement field.
The purpose of the present work is to study the ground deformation associated with the Mw6.9 earthquake by combining GNSS and InSAR data for analysis. The methodology has been previously applied to other tectonically active areas of Greece [21,22,23]. This study aims to quantitatively determine the pre- and co-seismic displacements in the Samos area and produce a model of the activated fault that describes its geometrical and kinematic characteristics.

2. Seismological Data

The Mw6.9 earthquake that occurred ~10 km to the north and offshore of Samos (Figure 2) devastated the island and the broader area of Izmir; there were several fatalities. The main event was followed by intense post-seismic activity with more than 200 aftershocks of M ≥ 3 over the next forty days. The strongest aftershock occurred about three hours after the earthquake [24].
Real-time waveform data from the Hellenic Unified Seismological network were used for the seismological analysis, together with data from other available seismological networks in the area [25,26,27]. The hypocenters were initially located by using the HypoInverse code [28] and a custom velocity model that was formed for this sequence, which started with a 1-D model for the region of Karaburun (Erythres), Turkey [24,29]. The hypocenters presented herein are relocated events that were extracted using the double-difference method HypoDD [30]. Further details of the processing procedure are found in [19].
The analysis of the earthquake and the strongest aftershock reveals a nearly E–W oriented, dip-slip, normal fault plane (Table 1). The most prominent features of post-seismic activity were the formation of two distinctive clusters. One large group of aftershocks extended eastward from the epicenter, mainly along the northern coast of the island. A smaller cluster occurred west of the epicenter and terminated at the SE margin of the NIB, which itself is characterized by en echelon faults of strike-slip character [17]. The spatial evolution of aftershocks revealed that the seismicity extended over a broader area of ~60 km by ~20 km in the east–west and north–south directions, respectively. The hypocenter depth of the strongest aftershocks (M ≥ 4.5) was located mainly within a zone of 10–15 km depth, which also encompasses the hypocenter depth of the earthquake and the main aftershock. It is noted that all of the post-seismic events with M ≥ 4.5 occurred up to 31 October, and that the seismicity was significantly decreased about eight days after the main event (i.e., less than three events of M ≥ 3 per day). The last significant seismic activity with ~M4 occurred between late January (M4.3 near the epicenter) and early February (M4 near the western-formed cluster) 2021. Furthermore, less than twenty events of 3.0 < M ≤ 4.3 occurred over the broader region between January and February 2021.

3. GNSS Data

Over the past few decades, the Global Navigation Satellite System (GNSS) technique has been used to study the crustal velocity field, as well as ground deformations due to seismic, volcanic, geologic, or anthropogenic activity [31,32,33,34,35]. Several continuous GNSS stations have been installed in the vicinity of Samos, mainly by the commercial sector (Figure 1). Daily data covering the period before and after the earthquake from four continuous stations were available and processed, namely SAMO, IKAR, and CHIO, which belong to the METRICA S.A commercial network [36], and IZMI, which is an International GNSS Service (IGS) station (https://www.igs.org; accessed on 23 April 2021) (Figure 3).
Daily data from three more stations—SAMU, IKAU, and CHIU—were available from the Uranus commercial network for the co-seismic period (26 October to 1 November) [37]. The stations SAMO and SAMU are located in the northern part of Samos at ~9 km and ~25 km, respectively, from the earthquake’s epicenter. The stations IKAR and IKAU are located on the nearby island of Ikaria, which lies to the west of Samos and ~45 km to the WSW of the epicenter. The stations CHIO and CHIU operate on the island of Chios at ~80 km to the NW of Samos. Finally, station IZMI is located near Izmir (Turkey) at ~65 km to the NE of the epicenter. Data were also processed from GNSS stations that are located on the islands of Lesvos (~140 km to the north of Samos), Leros, and Kalymnos (~65 km and ~86 km to the south of Samos, respectively) [36,37] (Figures S1 and S2). Inspection of the GNSS stations that are located close to the epicenter did not reveal any structural damage after the earthquake [38,39,40].
The raw GNSS data were processed using Bernese v5.2 GNSS s/w (Astronomical Institute of the University of Bern, Bern, Switzerland) [41]. The coordinates for the local continuous GNSS stations were estimated on the global ITRF2014 reference frame. The processing yielded high-precision datasets of station coordinates, time series of daily coordinates, annual velocities, and co-seismic displacements. Further processing details are provided in Appendix A.

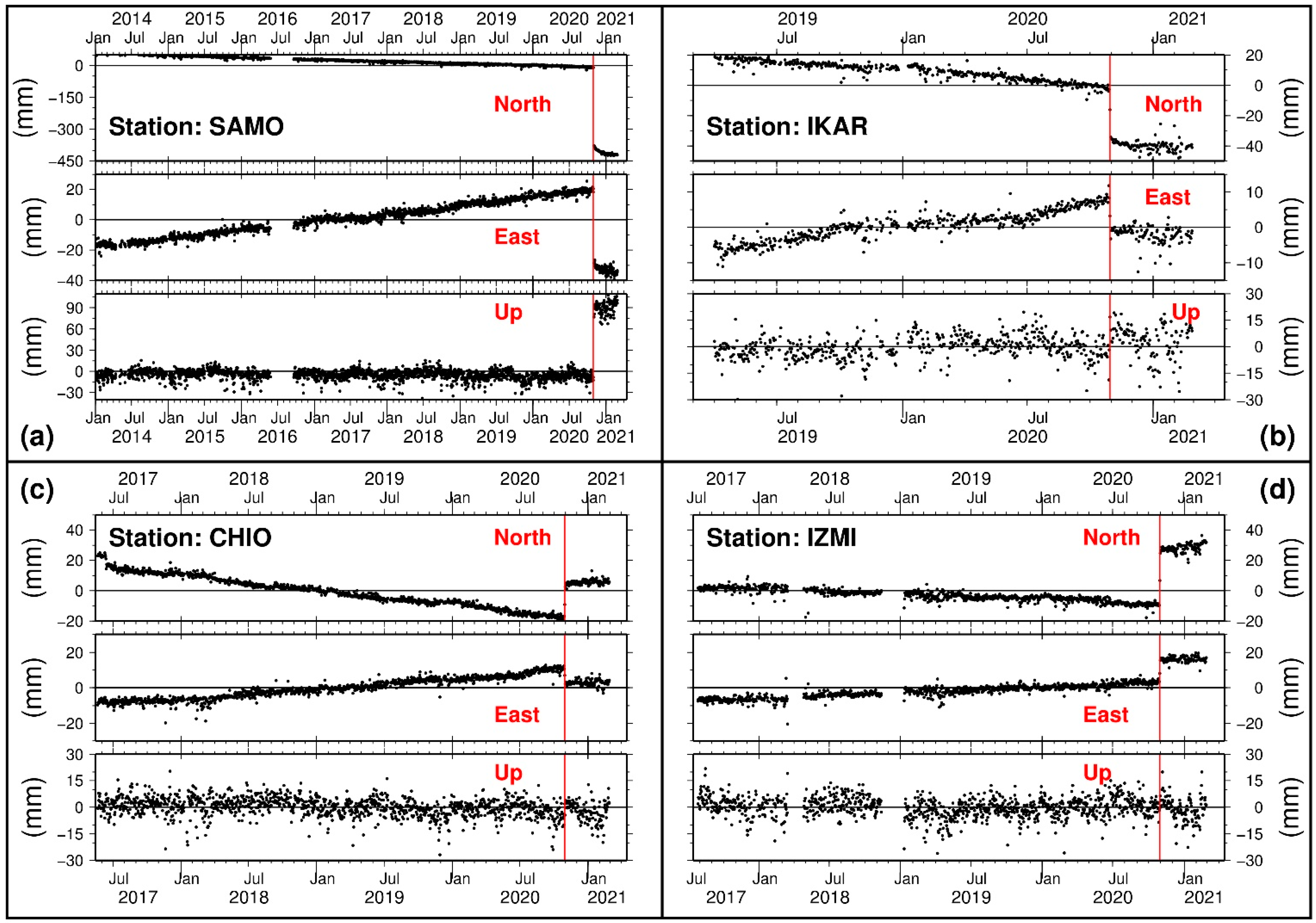
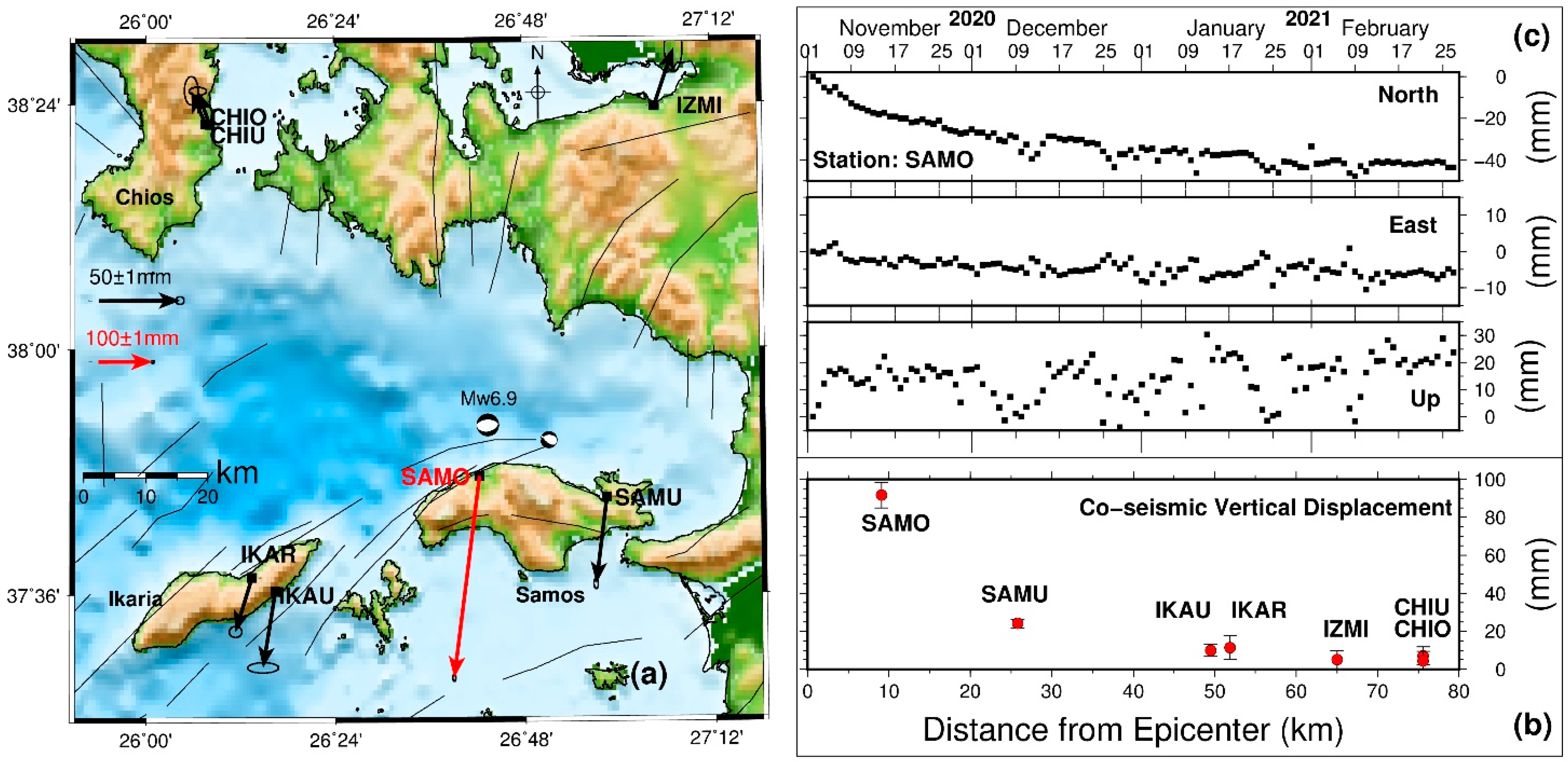
3.1. Pre-Seismic Period

Baselines changes between the four local GNSS stations were compiled to assess local deformation prior to the earthquake (Figure 4a). Moreover, differential velocities were calculated relative to station IZMI, and the regional strain field was estimated (Figure 4b). It is noted that station IKAR was only briefly operating before the earthquake (being established on 1 April 2019). However, its calculated velocity vector is in agreement with another station on Ikaria (belonging to Hellenic Cadaster), where data were available for the period from 2013 to 2017. The pre-earthquake deformational field confirms the extensional dynamic conditions of the area [1,8,42].
The baseline change between two stations was estimated based on the daily coordinates of the selected sites. Baselines were formed only when data were available for both sites and for a period exceeding 24 h. From the triangle formed by the stations SAMO, IZMI, and CHIO, it is evident that a significant lengthening occurred between SAMO and IZMI, which had a baseline change velocity of 3.81 ± 0.07 mm/yr. Conversely, the distance between IZMI and CHIO was shortened by a smaller value (v = −2.28 ± 0.06 mm/yr). The distance between CHIO and SAMO remained almost unchanged (v = −0.61 ± 0.07 mm/yr). Station IKAR’s kinematic behavior indicates lengthening relative to CHIO (v = 2.96 ± 0.23 mm/yr) but shortening with respect to SAMO (v = −1.02 ± 0.16 mm/yr).
The strain tensor was calculated for the pre-seismic period based on the local GNSS station’s horizontal differential velocities relative to station IZMI. The strain field represents the dynamic forces in active tectonic areas; it is independent of the reference frame and reveals the changes of dimensions or shape of a deformed area. Due to the large average distance between the stations, the strain tensor was computed on a central point of the network using the algorithm of [43]. The strain tensor of the area has a principal strain direction of 17.5° CWN and an extensional behavior eigenvalue of 60.2 ± 4.8 nstrain/yr, while the minimum eigenvalue was computed to be −39.3 ± 2.5 nstrain/yr (negative for compression). These values are consistent with the aforementioned baseline changes.

3.2. Co-Seismic Period

The normal-fault character of the earthquake—as shown by the focal mechanism solution—dominates the pattern and the amplitude of the co-seismic deformational field, as recorded at the GNSS stations (Figure 5). As previously noted, data from three more GNSS stations were included in the processing for the co-seismic deformation. For the computation of the pre-seismic location of the stations, the coordinates from four days prior to the earthquake were averaged up to 11:00 UTC 30 October. The co-seismic location was determined by averaging the estimated coordinates from 12:00 UTC 30 to 31 October, thus avoiding inclusion of more days after the earthquake. Post-seismic motions did occur, as will be presented later.
For station SAMO, the post-seismic location was estimated for the days 2 and 3 November, since the station stopped working during the earthquake and re-operated on 2 November, 11:50 UTC. Thus, the co-seismic deformation for this station, as deduced from the analysis, is slightly overestimated since it encompasses motions for about two days after the earthquake. For the days 2–6 November, the station exhibited a near linear post-seismic motion for both horizontal and vertical components (Figure 5c). For this short period, velocity vectors of ~1.5 ± 0.2 mm/day to the south and ~4.5 ± 0.8 mm/day for the vertical were estimated. Presuming a linear motion (at least for the first few days), the co-seismic motion at the station was overestimated by ~5 mm and ~10 mm for the horizontal and vertical components, respectively.
The stations located to the south and closer to the epicenter exhibited higher co-seismic horizontal and vertical displacements than the northern stations (CHIO, CHIU, and IZMI) (Table 2). Co-seismic displacements were also observed at the stations on the islands of Lesvos to the north and Leros and Kalymnos on the south (Figure S1). Two stations on Lesvos showed displacements of ~9 mm to the north, while stations on Leros and Kalymnos exhibited displacements of ~20 mm and ~10 mm to the south, respectively.
The most prominent feature of the co-seismic displacement is the large horizontal (~370 mm) and vertical (~90 mm) displacements at station SAMO when compared to the other station on the island, SAMU. The two stations on Ikaria had similar vectors with small differences attributed to local tectonic characteristics. The stations on Chios also had similar co-seismic motions. Lastly, station IZMI had a displacement of >35 mm to the NE, which was associated with the severe damage in the urban area of Izmir.
The relaxation period for the region was expected to last for at least 4–6 months after the earthquake. Processing of the GNSS data for almost four months after the earthquake (up to February 2021) showed continued strong deformation at least at station SAMO (Figure 5c) and adjacent stations where data are available (Figure 3). Station SAMO showed southward horizontal motion at ~1.5 mm/day for about 15 days after the earthquake, which reduced to ~0.5 mm/day up to 12 December. The vertical component exhibited an uplift rate of ~3.5 mm/day till 7 November (8 days after the earthquake), then flattened afterwards. The curve for the east component is almost flat, showing no motion in this direction. It is noted that most of the post-seismic activity (number of events and magnitude) occurred during the first fortnight after the main tremor.

4. InSAR Data

During the period of the earthquake, co-seismic deformation over the whole island was captured by the Sentinel-1 Synthetic Aperture Radar (SAR) satellites that are maintained by the European Space Agency. Interferometric processing of the acquired SAR images was performed using the Geohazards Exploitation Platform (https://geohazards-tep.eu; accessed on 23 April 2021) and the provided Diapason module, which is being commercially developed by TRE ALTMiRA (Milano, Italy). The interferograms that are presented and post-processed in this study are the final products from the online platform. The SAR images were of ascending and descending orbital trajectory, which yielded three differential interferograms of the deformed region (Table 3).
The coherence of the formed differential interferograms depends mainly on the temporal and spatial decorrelation between the reference and the repeat SAR scenes [44]. The small time separation between the acquired images (only few days), and the use of Sentinel-1 data that have a small and well-controlled orbital tube (ensuing in small spatial baselines), result in the composition of differential interferograms of good coherence, and consequently obtain precise co-seismic ground deformation.
The ascending interferogram that was produced from the 24 and 30 October images (Figure 6a) is of good quality with ~34% coherence at ≥0.6. The largest aftershock occurred three hours after the earthquake and is not expected to have contributed to the displacement that is depicted by the interferogram. This assumption is supported by the GNSS data from station SAMU (24-h, 30s interval, continuous data for 30 October), which reveals the total observed co-seismic static displacement occurred during the earthquake and not afterwards (Figure S3. Therefore, this interferogram solely describes the co-seismic deformation given that the repeat scene was acquired just 4 h after the earthquake.
The descending interferogram (24 October and 5 November) exhibited the highest coherence when compared to the others (40% at ≥0.6), as well as low tropospheric disturbances (Figure 6c). The strong aftershocks (~M4) that occurred up to 31 October are not expected to have produced measurable deformation. Note that the post-seismic displacement at station SAMO was ~23 mm during the six days after the earthquake, which is less than the sensitivity of the InSAR method (i.e., ~28 mm, which is half the wavelength of the radar signal).
The second ascending interferogram (24 October and 5 November) had similar coherence as the first ascending one (Figure 6b). It was generated to be directly compared to the descending interferogram, since both have the same time span from the earthquake’s occurrence. Other interferograms that were created for longer periods and dates, and overlapping the three presented pairs, proved to be of lower quality and were not considered for further interpretation.
The interferograms obtained from all the SAR pairs showed discrete fringes. Significant deformation occurred along the northern coast of Samos, and less towards its southern part. A lack of information due to low coherence was observed in all interferograms in the northern central part of the island. The deterioration is attributed to poor decorrelation caused by dense vegetation of the area. The most intense fringes (i.e., similar number, type (color sequence linked to phase differences), and shape) on all three interferograms were located in a narrow zone in the northern central coastal area. The phase differences in this zone are compatible to increased line-of-sight (LOS) distance between the repeat and the reference scenes. In the western and eastern parts of Samos, both ascending interferograms showed similar shape and type of deformational fringes and were significantly different than the descending interferogram. This difference is due to the horizontal kinematic character of the ground motions depicted from the two orbital geometries, which are associated with changes in range along the LOS direction.

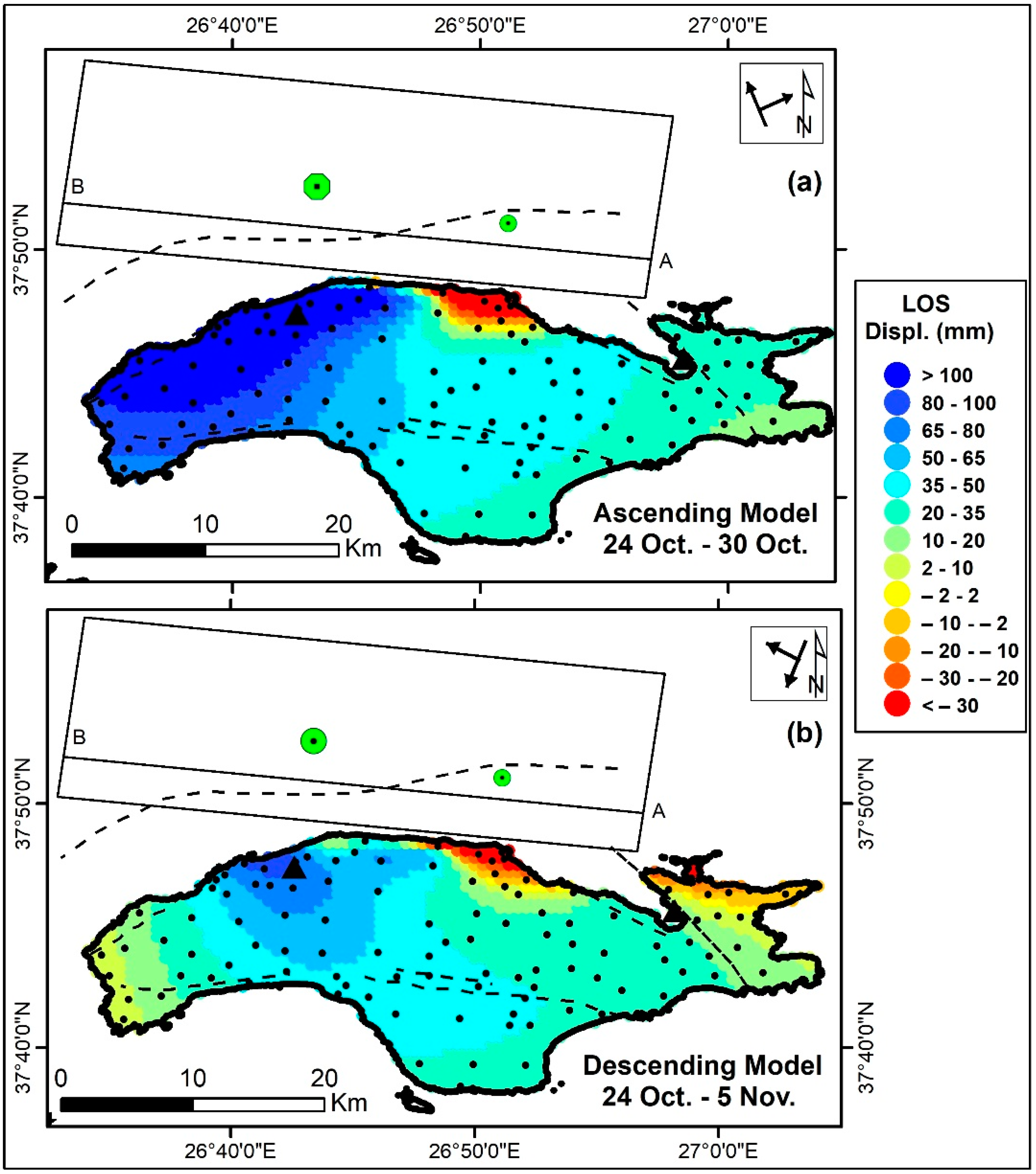
4.1. LOS Displacement Vector

The phase interferograms were unwrapped and the LOS deformational vectors were estimated. They revealed that large co-seismic displacements occurred mainly in the northern and western parts of Samos. Spatial unwrapping provides “relative” information about deformations. To obtain “absolute” values of ground displacements, the GNSS data from the two stations on the island could be used to calibrate the LOS displacement vectors. The differences between the deformation recorded by InSAR and GNSS data are aligned, which creates a smooth surface-of-displacement correction by means of a set of correction for each GNSS station [45,46,47]. However, the GNSS stations should not be used where intense geodynamic deformation has occurred (as is the present case) [47]. Thus, station SAMO was excluded from the InSAR geodetic correction because of its close proximity to the epicenter; it was inoperable for about two days after the earthquake. Conversely, the station SAMU is located away from the epicenter. It operated continuously after the earthquake, and the produced interferograms exhibit good coherence (≥0.6) in the adjacent area. Therefore, this station was used to define the offset calibration of the InSAR LOS displacement vector. The 3D GNSS derived vector for station SAMU was projected on the LOS direction for ascending and descending acquisition orbits (see Appendix B for details). A cloud of InSAR points around the station that was distributed to a radius of ~200 m of good coherence (≥0.6) was used to calculate the interferometric LOS displacement (dSAR) of the area and to be compared with the projected on LOS direction GNSS vector (dGNSS). Then the offset calibration (dSAROC) of the InSAR data based on the GNSS observations was performed as the difference of the LOS displacement determined by the two techniques: dSAROC = dGNSS – dSAR The resultant geodetically corrected LOS displacement maps of the three interferometric pairs are presented in Figure 7.

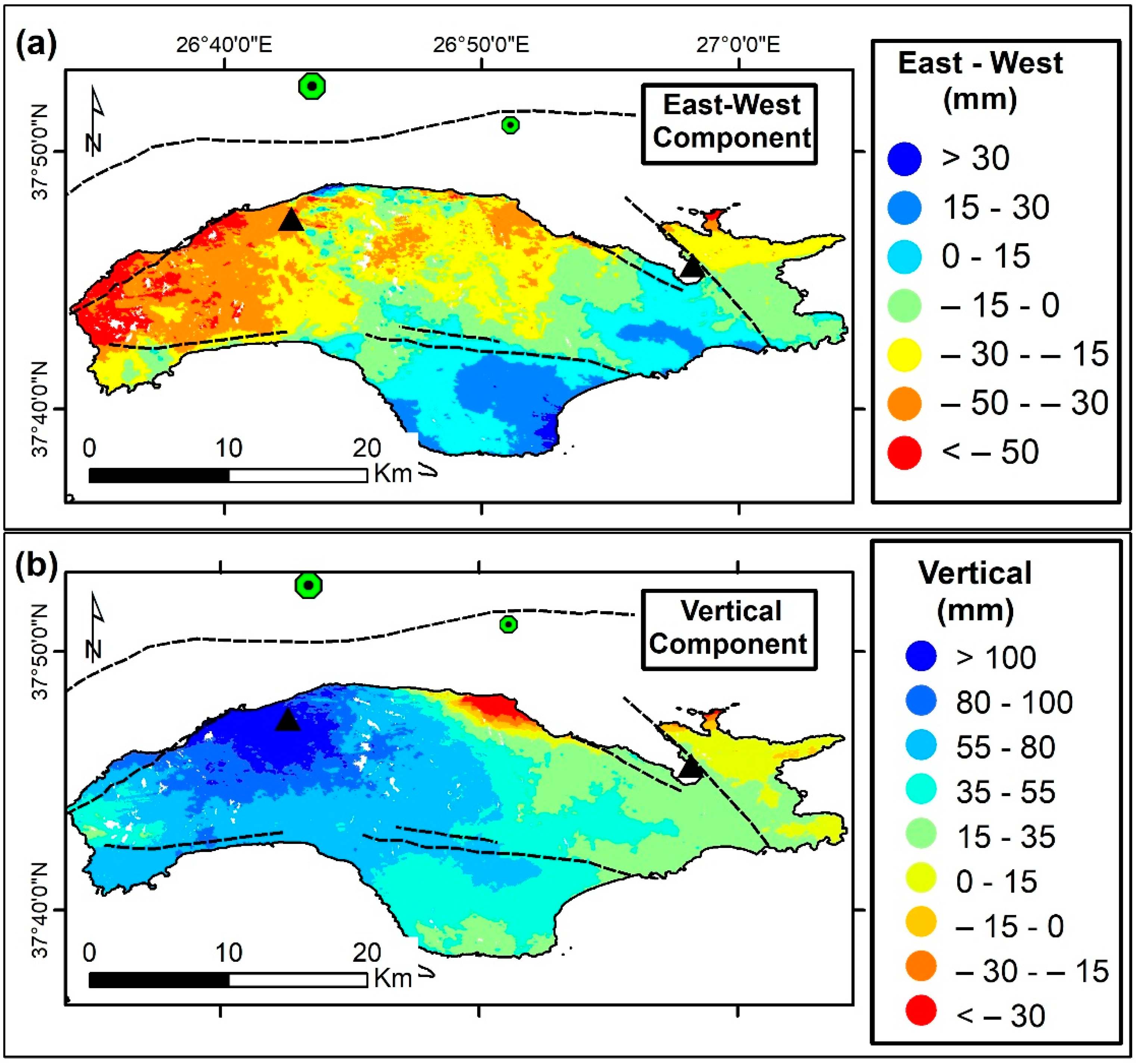
4.2. Decomposition of LOS Vector

The LOS displacement vector is composed of projection vectors of the real E–W, N–S, and vertical displacements of a ground target in the direction of the radar wave. Based on the geometry of the SAR imagery, the projection of the LOS displacement vector on the 3D-motion components is defined by the incidence angle θ and the azimuth angle φ of the satellite heading (measured clockwise from North) [48,49] (Appendix B). The LOS vector has different sensitivity for each component. For the present case, the sensitivities of the ascending and descending tracks were 74–83%, 36–65%, and 10–12% for the vertical, E–W, and N–S components, respectively. It is evident that the InSAR technique was more sensitive in detecting vertical displacement rather than E–W motions and was limited in the N–S direction.
The aim of multi-geometry SAR processing is to combine LOS displacement measurements from two or more acquisition geometries in order to estimate the horizontal and vertical components of the recorded displacement signal [49]. Accordingly, displacement data from the first ascending (24–30 October 2020) and the descending interferograms were decomposed to estimate displacement motion for the E–W and vertical directions. The variation of incidence angle θ along the range was considered in the calculation. The variation of θ was about ±2° for the ascending pair and about ±1.5° for the descending; these variations were introduced to the fuse procedure. The azimuth angle φ of the satellite heading was treated as constant for each track, since it is usually about 1° over the extent of a radar image.
Efforts to use all of the three formed interferograms to retrieve the N–S displacement component were unsuccessful. The estimated N–S components in target points close to GNSS stations (which were acting as control points) were excessively high and of different sign (northward or southward) concerning the GNSS results. Odd and inconsistent behavior was observed also on several other neighboring targets, where both amplitude and sign of the N–S component were unrealistically changing. A plausible explanation could be the limited sensitivity of the InSAR method on the N–S component, especially on Samos where this is the prominent deformational component, as shown by the GNSS data. A more accurate way to illustrate the poorly constrained N–S component is the calculation of the condition number of the coefficient matrix (cond(A)) that is used in the decompositional process [49]. The resultant cond(A) for the three produced interferograms has a high value (146.9 ≫ 1), indicating an ill-conditioned linear system (i.e., cond(A) value close to 1 is considered as well-conditioned), whereas, the condition number of the coefficient matrix has a small value (1.25) when neglecting the N–S component from the linear equation system, thus demonstrating a well-constrained linear system. Based on the above issue, the N–S component was excluded from the decompositional process.
The downsampling procedure of the calibrated unwrapped interferograms was performed spatially for the whole island (Figure 8). The results were evaluated for points in the vicinity of the two GNSS stations. There was an overestimation of about 20% and 10% on the vertical and the E–W components, respectively, for the InSAR points close to station SAMO, while the points in the vicinity of station SAMU yielded almost identical results as those of the GNSS observations.
The deformational map of the E–W component (Figure 8a) shows significant westward motion on the western part of Samos, while the vertical component describes intense uplift (Figure 8b). In the central southern part of the island, a differential type of motion (westward to the north and eastward to the south) is evident from the E–W component map. Significant subsidence (up to 80 mm) was observed on the narrow-deformed zone in the central northern coastal region, as was concluded from both wrapped and unwrapped interferograms. Subsidence (~15 mm) was also observed at the northeastern part of the island. The overall maps of the E–W and vertical components highlight the gradual decrease of the co-seismic displacements towards the eastern and southern parts of Samos, which is more clearly depicted in the two ascending interferograms.

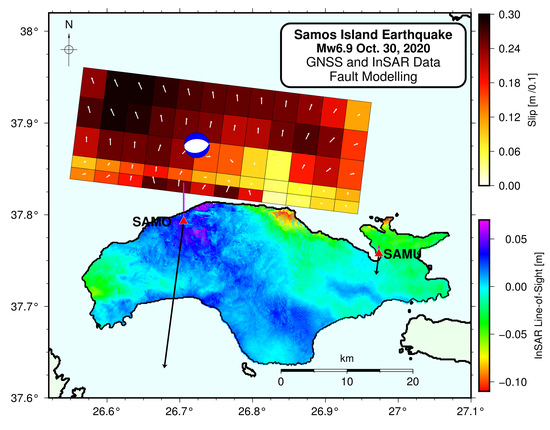
5. Fault Modelling

Forward and inverse modelling of a rectangular fault surface was performed to define the source, the magnitude, and the type of earthquake that caused the displacements on Samos, as were recorded by the GNSS and SAR data. Displacements that were embedded in a non-uniform slip model were calculated using an inversion algorithm [50,51,52]. The displacement vectors (together with their error estimates) that were derived from all of the available GNSS stations in the area were used in modelling.
Several of the highly correlated data points in the unwrapped calibrated interferograms were down-sampled using an approach similar to [53] to facilitate the modelling. For each orbital trajectory, LOS displacement values from the calibrated interferograms were numerically extracted by manually picking selected pixels. These pixels had high coherence (≥0.6), were located along formed fringes, and uniformly covered the island. Points/targets were selected that were close to the two GNSS stations for quality control. Some targets were picked from areas of low coherence (<0.6) in order to gain insight about the displacement in these areas and to attain better spatial coverage of the island. Approximately 160 and 190 points/targets from the ascending and descending interferograms, respectively, were chosen that met the above criteria. Finally, 110 points/targets that were common to both tracks were selected from the two data sets and used in modelling. An error of 10% was added to the LOS components. This error was considered sufficient to describe the sensitivity of the LOS vector to the true ground motion along the horizontal component, and to account for the differences between the GNSS and the InSAR data for the selected points in the vicinity of the two stations.
The two data sets were weighted unequally in the joint inversion. The GNSS data points were weighted at 1.0, while a weighting factor that ranged from 0.6 to 1.0 was applied to the InSAR data points based on the coherence levels of the selected points.

5.1. Fault Geometry

Determining simultaneously the fault geometry and the slip distribution on the fault plane is computationally expensive [32]. For this reason, inversion was performed only to define the slip distribution on the fault plane. The location, geometry, and characteristics of the model fault plane were derived from (i) the fault traces proposed by [15], (ii) the amplitude and the direction of the GNSS displacement vectors, (iii) the spatial deformation from the interferometric maps, (iv) the information derived from and the constraints imposed by the focal mechanism solution of the earthquake (Table 1) and the spatial distribution of the aftershocks (Figure 2), and (v) the iterative attempts to fit the observed data. The geometrical parameters of the best-fit model are presented in Table 4.
The observed ground deformation indicates that the source of the earthquake was a fault plane to the north and offshore of the island. The gradual attenuation of ground displacements eastward and to the southern part of the island indicated a near E–W striking plane. This explains the spatial distribution of the post-seismic activity along the northern coast of Samos. Intense uplift occurred mainly in the northern and western parts with a large southward displacement component. This describes a normal fault with the activated part dipping to the north such that the mainland of Samos rests on the footwall block. These observations clarify which one of the two possible nodal plane solutions for the centroid moment tensor is the actual one.
The length of the fault plane along the strike direction was set to ~35 km, which extends to the areas of the most intense displacements and the majority of aftershocks. The width of the plane was estimated from the expected ruptured surface for a ~M7 earthquake [54]. The depth distribution of the earthquake and aftershocks was considered when assigning the width and the locking depth of the fault plane. The locking depth was set to 15 km, which takes into account that most of the strong aftershocks (M ≥ 4.5) happened in this zone. The tsunami that formed after the earthquake [55] indicates that the fault plane likely reaches close to the sea bottom. Thus, a 1 km vertical burial depth was assumed. Nevertheless, the burial depth was altered several times to assess the sensitivity of the model to this parameter.
The dip angle of the fault plane was examined by fixing the location and the extent of the fault plane and then searching for the optimal angle that minimized the data misfit between observed and predicted surface displacements. Treating the fault as a single plane produced the general pattern and amplitude of ground displacement. However, this approach could not account for the observed intense subsidence along a narrow zone in the northern central part of the island. The motions in this area indicate a hanging-wall block of the fault. Assuming a two-segment fault plane along the width yielded a better fit to the observed vertical displacement.
The characteristics of the two segments along the width (i.e., extension and dip angles) were determined by trial and error inversion. Ultimately, dip angles of 60° and 40° were defined for the upper and lower segments, respectively. The horizontal boundary between the two parts was estimated to 6 km vertical depth, which marks the transition from an area of moderate seismicity (<6 km depth) to a zone where the main seismic activity was recorded (6–15 km depth). The dip angle for the upper segment coincides with the characteristics of tectonic faults in the area, which are described as high-angle normal faults [11]. The modelled dip angle of the lower segment is consistent with the focal mechanism solution and errors on its estimation.

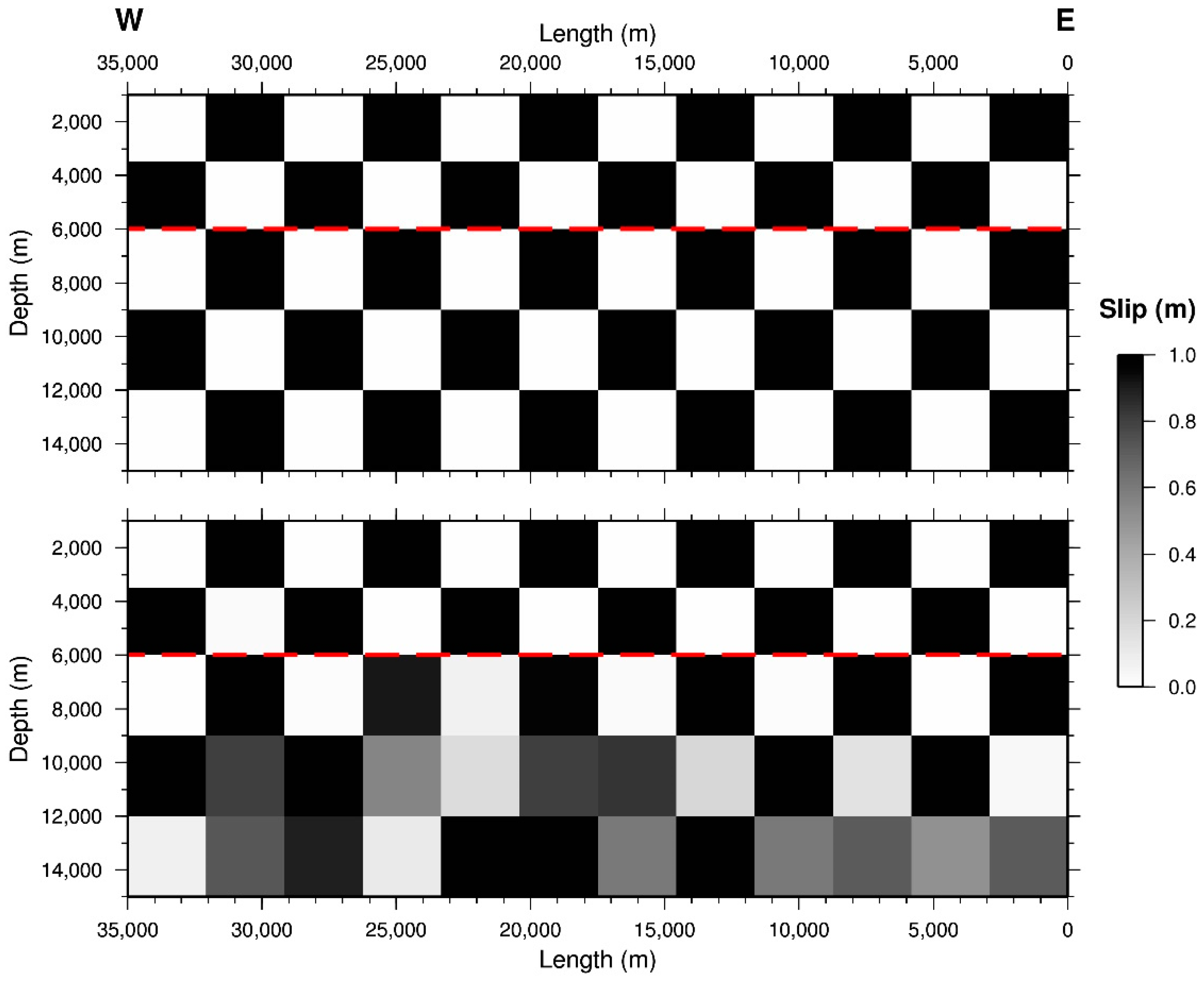
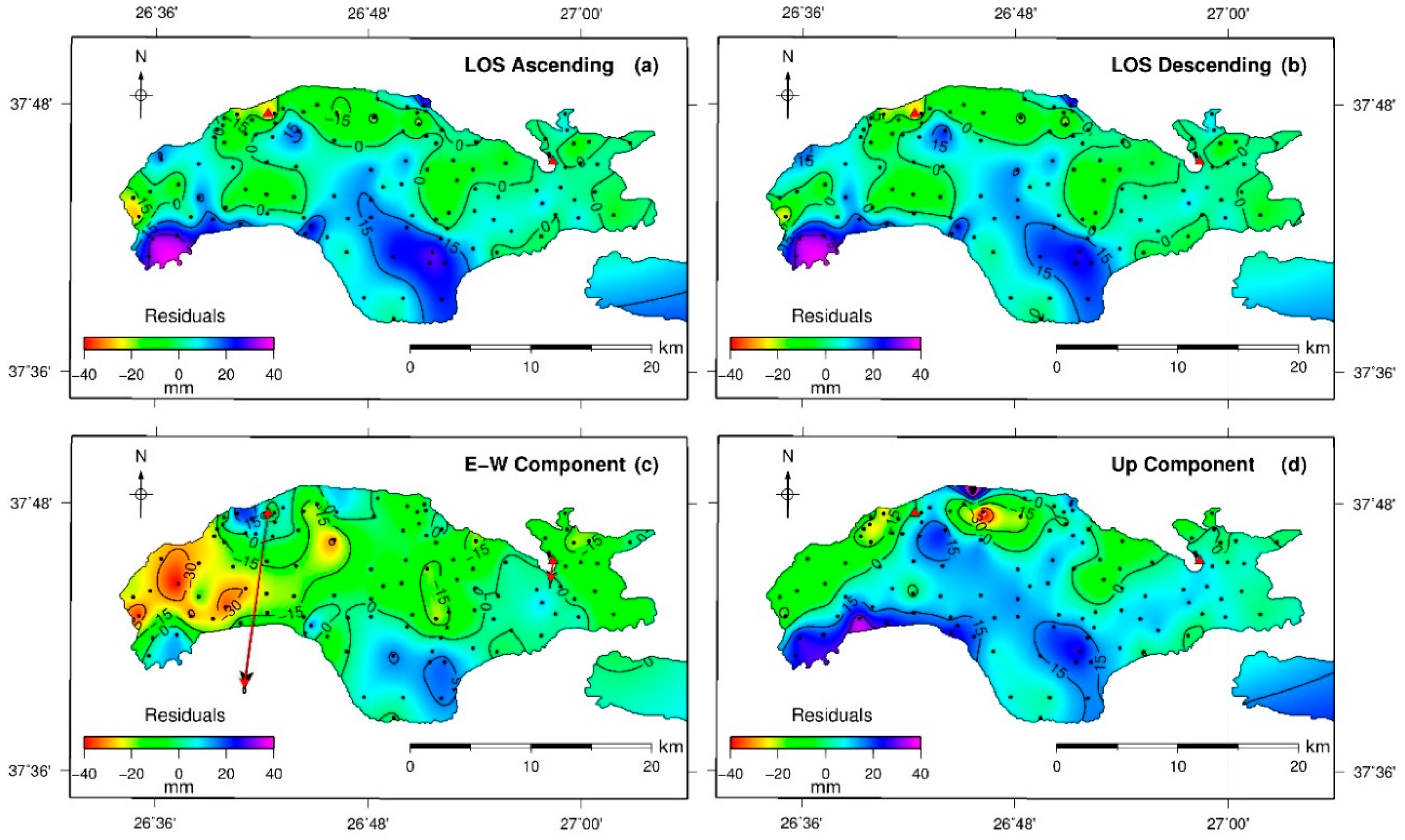
5.2. Slip Distribution

After the geometry of the activated fault was determined, the plane was discretized to horizontal (rows) and vertical (columns) subsegments and then inverted to define the slip distribution along the plane. The average spacing of the data points close to the epicentral area (i.e., northern Samos) was ~3 km. Therefore, a grid of 5 rows × 12 columns was deemed adequate. Two rows along the dip direction were assigned to the upper segment and three rows to the lower one. The grid has cells of ~3 km along the strike direction and ~2.5 km and ~3.0 km along the dip direction for the upper and lower segments, respectively.
A checkerboard resolution test was performed to assess the ability of the discretized plane to resolve the observed data (Appendix C). The test was applied to a fault plane with the same geometrical characteristics as described above. For forward modelling, alternating dip-slip values of 0 m and 1 m were assigned to the cells, and then the 3D displacement vector was calculated to produce synthetic observational data. Next, these data were used to resolve the slip of a uniform slip model. It was found that the model recovered the slip on all of the cells of the upper three rows but lost resolution for the deeper cells (fully resolved at ~60%).
A smoothing factor, k, was introduced to constrain irregular oscillations of the slip distribution along adjacent cells [49] and to control the roughness of the model. Increasing k results in a smoother distribution of slip motion but increases the misfit. Thus, there is no unique solution. A wide range of values for k was applied during the inversion process. The preferred model for slip distribution has k = 3000 in the inflation corner with the trade-off curve between roughness and misfit.
Concerning the limitations on slip, the modelling allowed all cells to include a lateral strike-slip component (range from −1.0 m to 1.0 m, where negative sign indicates left-lateral motion). However, the modelling focused on determining the magnitude of dip-slip motion. Accordingly, the range of dip-slip was set free but with an absolute magnitude of less than 2.5 m, which was based on the focal mechanism of the earthquake and studies by [54]. The slip distribution of the best-fit model is presented in Figure 9.
The preferred slip-distribution model shows an average slip of 1.76 m along the entire fault plane. The slip on the upper and lower segments of the plane was computed to 0.48 m and 1.28 m, respectively. The average slip value is significantly higher than the expected value of ~0.8 m that is based on the scaling law presented by [54]. Scaling relationships also relate the ruptured surface, the length, and the width of the plane to the moment magnitude. The theoretical values for the Samos earthquake are much higher than those of the best-fit model. The use of a larger fault plane was precluded by lack of model resolution (as shown by the checkerboard test), which may account for the difference.
The resultant geodetic seismic moment of 3.67·× 1019 N-m was higher than the seismic one (Table 1), but within the range calculated by others (USGS United States Geological Survey [56]; GFZ—GeoForschungsZentrum [57]; GCMT: Global Centroid Moment Tensor [58]). The latter value indicates a slightly larger moment magnitude (Mw7.01) from the one publicized here for the earthquake. Note that the predominant slip occurs in the lower zone of the fault plane (i.e., >6 km depth), which coincides with the main shock zone. Although this zone lacks good resolution (as shown by the checkerboard test), the slip vectors have a strong dip-slip component and a moderate lateral component. The latter is consistent with the focal mechanism for the dip-slip but contradicts the almost pure dip-slip character of the source. The upper eastern part of the plane exhibits a small slip amplitude (<0.5 m), which is in the area where the plane is running offshore and away from the modelled points. In the western end of the fault plane, the misfit deteriorates but shows intense slip motion (>2 m), which may be attributed to the algorithm’s effort to fit the observed deformations at the limits of the data. A quite distinctive feature that emerges from the fault-plane solution is the decreased slip motion on the eastern upper part of the plane. This decrease may indicate a possible deepening of the fault’s upper edge there to depths greater than 1 km.
For direct comparison to InSAR results, the 3D modelled vector was computed on a grid of 500 m × 500 m that covered Samos. This vector was projected on the LOS direction for the ascending and descending acquired pairs by using the geometric characteristics for each track at time of acquisition (Figure 10).
The RMS misfit is 0.012 m for all of the data points (GNSS and LOS vectors) that were used in the inversion process for the preferred slip model. The mean scatter between observed and calculated LOS values is 3.61 mm and 3.26 mm for the ascending and descending orbits, respectively (Figure 11a,b). The residuals between the observed and modelled data for both orbital geometries showed larger deviations in the western and southern parts of Samos, as well as for points/targets of low coherence level. In the same areas, the east–west and vertical components also showed the largest discrepancies between observed and calculated values (Figure 11c,d). The mean scatter for the east–west component was −8.1 mm; modeled values were overestimated mainly in the western part. For the vertical component, the mean scatter was 7.2 mm; the larger differences were located in western and southern Samos, as well as in the narrow subsiding zone in the north.
The modelled values for the N–S displacement component for the two GNSS stations SAMO and SAMU were underestimated by 4 mm and 8 mm, respectively. The fits for the two Ikarian stations were also underestimated but significantly worse. For the GNSS stations that are located to the north of the epicenter (i.e., CHIO, CHIU, and IZMI), the matching was better with only overestimation (~7 mm) at station IZMI.

6. Discussion

The present ground-deformation study is based on joint interpretation of GNSS observations and InSAR data, both before and after the earthquake. In the following, the results of modelling the seismogenic source are discussed in terms of the overall tectonic status of the study area (Figure 12).

6.1. Regional Deformational Characteristics

The pre-seismic kinematic study that was based on continuous GNSS observations over the broad area of Samos reveals a predominant extensional regime, in agreement with previous works [1,2,6,8,10]. The strain field tensor is parallel to the IBTZ, which comprises the main tectonic unit of the Izmir region of western Turkey [7]. This ophiolitic unit is a NE–SW trending zone that is bounded by dextral strike-slip faults that terminate to the northeast of Samos. It lies between the STU to the north and the continental European foreland to the south [10]. The GNSS-derived velocity vectors reveal differential motion along stations CHIO, SAMO, and IKAR to the west and station IZMI to the east, which are compatible with the tectonic regime. Note that Chios is located in the STU, while Samos and Ikaria are in the European foreland [10]. The latter explains the increasing distance between the islands of Ikaria and Chios as described by the baseline changes, while the shortening between Ikaria and Samos is attributable to strike-slip faults in the southern margin of the NIB [17]. The overall extensional condition in the area has resulted in the formation of E–W trending faults, the reactivation of older structures [15], and subsequent triggering of the Mw6.9 earthquake.
The modelling of the earthquake shows that it took place on an almost E–W trending normal fault that dips to the north and lies adjacent to the northern coastal zone of Samos. The extent of the observed deformations from Lesvos to Kalymnos (Figure S1) indicates that the main event was associated with regional tectonic conditions. This conclusion is supported by the magnitude and the regional tectonic characteristics of the area [10], which features Samos at a key position for the dynamic evolution of the Aegean Sea [12]. However, the dimensions of the modelled fault plane are smaller than expected for the given magnitude [54,59].
The displacements that were recorded at the GNSS stations described a strong NNE–SSW extension due to an E–W trending normal fault (Figure 5). The displacement vector from station IZMI reveals a NNE co-seismic motion, while station CHIO reveals a NNW motion, i.e., an opening in-between the two sites, which is opposite to the shortening that occurred during the pre-seismic period. The latter describes the compressional regime in the inter-seismic periods, whereas extensional forces are at play during seismic events. The displacement vectors observed at Ikarian stations are almost parallel to the ones at Samos. This similarity imposes a uniform spatial southward motion for the broader region to the south of the epicentral area, even though the tectonic characteristics and the pre-seismic motion presumed a more distinctive co-seismic differentiation between Samos and Ikaria.

6.2. Local Deformational Characteristics

The strongest co-seismic displacement occurred at the western GNSS station SAMO (Table 2), which is close to the epicenter. Its displacement was almost an order of magnitude larger than at the eastern station SAMU. It may be argued that the latter is more distant from the epicenter; however, it had nearly the same horizontal displacement as the station IKAU, which is located at twice the distance from the epicenter. Similarly, the InSAR analysis shows intense deformation in the western part of Samos on both ascending and descending orbits but which substantially attenuates towards the eastern and southern parts (Figure 7). These observations suggest that the activated faulting is less extended towards the east than indicated by post-seismic activity. There are formations in the eastern part of Samos that may inhibit ground motion. Recent studies [14] have revealed a hummocky volcanic relief that is located offshore of the eastern part of Samos; these formations may act as a kinematic discontinuity that effectively reduces ground deformation as exhibited by the GNSS data.
The displacement field from the InSAR analysis highlights the main tectonic units on Samos that have been described in previous works [11,12,14]. Alternating LOS motions between the central (positive values) and the eastern (negative values) parts of the island clearly delineate the area that forms the Vourliotes nappe to the east of Mytilini Basin [12]. The area is marked by a NW–SE normal fault zone (Figure 12). The intense deformation in the central and western parts of Samos coincides with the Ampelos Unit and Karlovasi Basin in the center and to the west, respectively [12]. Another distinct geological unit that shows an alternating LOS pattern is the Kerketeas Unit [12,14]. It is at the westernmost part of Samos and is mapped clearly in the descending interferogram. It is also in NW Samos where both techniques show intense amplitudes on the vertical component (>100 mm), which coincides with intense uplift (100–200 mm) that has been documented along the shoreline [60].
Differential LOS displacement is also apparent in the central southern part of Samos across the Pythagorean fault zone, which is a normal fault that dips to the south at a 45° angle [14,15] (Figure 12). However, the kinematic variation is more apparent in the East–West component map (Figure 8a) and not in the vertical one. The whole area shows a gradual decreasing of uplift towards the south (Figure 8b), which has been verified from shoreline measurements [60].
The intense negative LOS displacement observed on the narrow north central zone may be due to a hanging-wall block of the seismogenic fault, which is bounded by high angle normal faults, as have been mapped by [11]. The modelling reveals that the observed displacement occurs most probably in an area that is north of the surficial extension of the fault plane, which has been modelled to a depth of 1 km depth, such that the subsidence describes the effect of the hanging wall motion to the surface.
When comparing the image of the vertical displacement map (Figure 8b) to field measurements along the coastal zone of Samos [60], an exceptionally good agreement is observed. The discrepancies between the geodetic and the field data are less than 10% for most of the ground-truth points, which verifies the procedure for geodetic correction.
Two segments were modelled along the dipping direction of the modelled fault plane. The dip angle decreased with depth from 60° to 40° from the upper to lower segments, respectively. This change defines the transition from an upper less activated area to a deeper zone where the earthquake and the strongest aftershocks occurred (Figure 12b). The dip-slip motion along the plane is the main component of slip. However, a significant lateral slip is included on the vector, and a strike-slip component does exist for the seismogenic fault, which is consistent with previous studies [17]. The latter does not agree with the focal mechanism solution, which describes a pure dip-slip motion. The checkerboard test shows that the slip distribution along the fault plane is well constrained in the upper segment but less so on the lower one (Appendix C).
Examining the slip distribution on the upper cells in the eastern section of the model fault plane, smaller slip amplitudes (~1 m) are observed compared to the deeper cells (~2.5 m). The latter value may indicate a deepening of the upper edge of the fault to depths larger than the modelled 1 km. This is the area where the hummocky formations were found on SB [14]. The extension of the fault plane to the west terminates close to the NIB and coincides with the decay of seismicity in that direction (Figure 2). It may be considered that the modelled seismogenic fault links together all the main active faults that have been described in the area by [12]. It represents a large fault zone, the activation of which has been triggered by the regional dynamics of the northern Aegean Sea.
Concerning the post-seismic deformations measured by the GNSS data, the period after the earthquake shows that the area is slowly and gradually relaxing. The co-seismic deformation was followed by intense post-seismic relaxation of high deformational rates (~3 mm/day) for the first few days. After the first month, the deformation slowed down and seemed to attain the pre-seismic levels (Figure 5). However, this period may not mark the end of the relaxation period, which is normally expected to last a bit longer in time.

7. Conclusions

Pre-seismic geodetic data for the broader region of Samos clearly confirm the NNE–SSW extensional tectonic setting that is expressed by dominant E–W striking normal fault zones. Co-seismic displacements that were recorded by GNSS stations during the Mw6.9 earthquake defined an almost N–S opening of the area, which correlates to the activation of an E–W striking normal fault. The GNSS data from two stations on Samos were used to measure the absolute displacement, and to geodetically correct co-seismic interferograms. Both GNSS and InSAR data exhibited intense displacements in the northern and western parts of the island, but which decay towards its eastern and southern parts. The pattern and amplitude of the InSAR LOS displacement vectors, and the decomposed E–W and vertical components highlighted distinct and differential motions along and across the main geotectonic units.
GNSS data and InSAR deformational maps provided powerful constraints on the fault geometry and slip distribution of the seismogenic plane during the modelling procedure. The best-fit model describes a north dipping listric fault of normal type, which is located to the north and offshore of Samos. The modelled plane is comprised of two segments along the dipping direction, 60° for the upper segment up to 6 km depth, and 40° for the lower one (6–15 km depth). The lower segment is associated with the bulk of aftershocks. The strike direction of the fault (277° CWN) is nearly perpendicular to the pre-seismic extensional field of the region. The length of the plane (~35 km) matches partially with the spatial expansion of the aftershocks. The eastern end of the plane coincides with hummocky relief structures defined in the area, while its western end is situated close to the NIB. The rupture surface is smaller than the estimated one based on scaling laws, while the average slip (1.76 m) is larger. The slip distribution on the modelled plane reveals greater slip on the lower segment, with its upper edge deepening towards the east (i.e., depth > 1 km). The dip-slip component is the dominant one, but a lateral-slip component is also noted. The resultant geodetic seismic moment (3.67·1019 N-m) indicates an earthquake with a higher magnitude (Mw7.01) than the seismologically calculated one of Mw6.9.
The geodetic observations and the derived deformation field together with the modelling results undoubtedly defined the nodal plane solution of the centroid moment tensor. Areas of strong co-seismic motions were mapped that could possibly be taken into consideration in the civil engineering. Moreover, the slip distribution model could provide vital information to the generation of strong motion synthetic waveforms [61] in case of unavailable near-field strong motion records, contributing to the seismic hazard and risk assessment of Samos Island.

Supplementary Materials

The following are available online at https://www.mdpi.com/article/10.3390/rs13091665/s1, Figure S1: Deformational map for the broader area of Samos, where GNSS data have been processed to define co-seismic displacements, including the islands of Lesvos, Leros, and Kalymnos, Figure S2: Time series of the coordinates for the GNSS stations on Kalymnos and Lesvos islands; Figure S3: Time series at 30-s time interval of the coordinates of station SAMU for 30 October 2020.

Funding

This research received no external funding.

Acknowledgments

The author would like to thank E. Lagios (Department of Geology and Geoenvironment, NKUA, Greece) and B. Damiata (Cotsen Institute of Archaeology, UCLA, USA) for their constructive comments and proof-reading of the manuscript, as well as K. Pavlou and S. Vassilopoulou (Department of Geology and Geoenvironment, NKUA, Greece) for their help with the ArcGIS s/w. Continuous GNSS data were provided by METRICA SA (HexagonSmartNet), and Uranus commercial networks. The seismological analysis was performed by the personnel of the Seismological Laboratory, NKUA (Greece) [25]. Figures were made using the Generic Mapping Tool S/w [62].

Conflicts of Interest

The authors declare no conflict of interest.

Appendix A

BERNESE s/w was used to process the GNSS data [41]. Data from 25 GNSS stations of the EUropean REference Frame (EUREF) and IGS were processed together with the available daily 30s RINEX local GNSS data. For pre-processing, cycle slips and outliers were detected from the RINEX files and phase measurements were used to smooth the code observations. Next, baselines were formed in to single-difference observation files. Lastly, cycle slips were resolved, outliers removed, and ambiguities added to the phase observation files.
The data were then reduced to a Precise Point Positioning (PPP) mode [63] to obtain a priori coordinate solutions that were subsequently introduced to the double-difference method, as a more precise method for static mode solutions [41]. The absolute antenna phase center corrections were used in the processing. Precise orbital solutions were obtained from the Center for Orbit Determination in Europe (CODE). The FES2004 model (http://holt.oso.chalmers.se/loading; accessed on 23 April 2021) was used for the tide loading corrections [64]. The Vienna Mapping Function (http://ggosatm.hg.tuwien.ac.at; accessed on 23 April 2021) and the Neill mapping function were applied for the tropospheric modelling [65]. Ambiguity resolution was applied using several strategies depending on the baseline length between the stations [41]: code-based wide- and narrow-lane techniques for very long baselines (<6000 km), phase-based wide- and narrow-lane for medium baselines (<200 km), and a quasi-ionosphere-free (QIF) strategy for long baselines (<1000–2000 km). The calculated coordinates were evaluated for the repeatability error on a weekly basis and values excluded in cases of large deviations from the weekly solution.

Appendix B

The LOS displacement vector is composed of projection vectors dE, dN, and dU in the direction of radar wave. The LOS displacement vector on the 3D motion components is defined by the incidence angle θ and the azimuth angle φ of the satellite heading. The LOS displacement DLOS can be expressed as a function of the real 3D ground surface motion components (dE, dN, and dU) and the SAR imaging angular parameters (θ and φ) as
D LOS = ( − sin θ cos φ sin θ sin φ cos θ )   ( d E d N d U )
D LOS = − d E sin θ cos φ +   d N sin θ sin φ + d U cos θ
The LOS displacement vector can estimate the motion components at a target by combining ascending and descending SAR images. The decomposition equation, presuming there are available data from three interferometric pairs (1, 2, 3) of ascending and descending tracks (i.e., DLOS1, DLOS2, and DLOS3), can be written as y = A·x and analytically by [48]
[ D LOS 1 D LOS 2 D LOS 3 ] = A [ d E d N d U ]
where
A = [ a 1 b 1 c 1 a 2 b 2 c c a 3 b 3 c 3 ] a i = − sin θ i cos φ i ,   b i = sin θ i sin φ i ,   c ι = cos θ i ,   ( ι = 1 ,   2 ,   3 )
Since the sensitivity of the method on the N–S component is limited, the N component may be omitted, and the second column of the matrix A can be eliminated [49]. Assuming that LOS data are available from only one ascending and descending pair, the linear Equation (A2) reduces to
[ D LOS   asc D LOS   desc ] = [ − sin θ a s c cos φ a s c cos θ a s c − sin θ d e s c cos φ d e s c cos θ d e s c ] [ d E d U ]
where “asc” and “desc” stand for ascending and descending orbital trajectory, respectively. To decompose the LOS displacement vector to the E–W and vertical components, Equation (A3) is solved by inversion (x = A−1y).

Appendix C

A checkerboard test was performed for the fault plane to examine the resolution of the slip distribution that was derived from inversion, and to define the optimal discretization for modelling. In Figure A1, the upper part represents the inputted synthetic slip distribution; the lower part shows output from the best-fit slip distribution that was inverted from the synthetic surface deformation and assuming a smoothing factor k = 100. A synthetic fault plane that has the same geometric characteristics as the best-fit model was assumed.
Remotesensing 13 01665 g0a1 550
Figure A1. Results of checkerboard test (smoothing factor k = 100) for the optimal plane discretization. Red dashed line defines the limits of segments along the dip direction. The grey scale gives the magnitude of dip-slip variation.
Figure A1. Results of checkerboard test (smoothing factor k = 100) for the optimal plane discretization. Red dashed line defines the limits of segments along the dip direction. The grey scale gives the magnitude of dip-slip variation.
Remotesensing 13 01665 g0a1

References

  1. Çirmik, A.; Doğru, F.; Gönenç, T.; Pamukçu, O. The Stress/Strain Analysis of Kinematic Structure at Gülbahçe Fault and Uzunkuyu Intrusive (İzmir, Turkey). Pure Appl. Geophys. 2017, 174, 1425–1440. [Google Scholar] [CrossRef]
  2. D’Agostino, N.; Métois, M.; Koci, R.; Duni, L.; Kuka, N.; Ganas, A.; Georgiev, I.; Jouanne, F.; Kaludjerovic, N.; Kandić, R. Active crustal deformation and rotations in the southwestern Balkans from continuous GPS measurements. Earth Planet. Sci. Lett. 2020, 539, 116246. [Google Scholar] [CrossRef]
  3. Reilinger, R.; McClusky, S.; Paradissis, D.; Ergintav, S.; Vernant, P. Geodetic constraints on the tectonic evolution of the Aegean region and strain accumulation along the Hellenic subduction zone. Tectonophysics 2010, 488, 22–30. [Google Scholar] [CrossRef]
  4. Le Pichon, X.; Kreemer, C. The miocene-to-present kinematic evolution of the eastern mediterranean and middle east and its implications for dynamics. Annu. Rev. Earth Planet. Sci. 2010, 38, 323–351. [Google Scholar] [CrossRef]
  5. Roumelioti, Z.; Kiratzi, A.; Melis, N. Relocation of the 26 July 2001 Skyros Island (Greece) earthquake sequence using the double-difference technique. Phys. Earth Planet. Inter. 2003, 138, 231–239. [Google Scholar] [CrossRef]
  6. Kreemer, C.; Chamot-Rooke, N.; Le Pichon, X. Constraints on the evolution and vertical coherency of deformation in the Northern Aegean from a comparison of geodetic, geologic and seismologic data. Earth Planet. Sci. Lett. 2004, 225, 329–346. [Google Scholar] [CrossRef]
  7. Kreemer, C.; Holt, W.E.; Haines, A.J. An integrated global model of present-day plate motions and plate boundary deformation. Geophys. J. Int. 2003, 154, 8–34. [Google Scholar] [CrossRef] [Green Version]
  8. Müller, M.; Geiger, A.; Kahle, H.-G.; Veis, G.; Billiris, H.; Paradissis, D.; Felekis, S. Velocity and deformation fields in the North Aegean domain, Greece, and implications for fault kinematics, derived from GPS data 1993–2009. Tectonophysics 2013, 597–598, 34–49. [Google Scholar] [CrossRef]
  9. Coskun, S.; Dondurur, D.; Cifci, G.; Aydemir, A.; Gungor, T.; Drahor, M.G. Investigation on the tectonic significance of Izmir, Uzunada Fault Zones and other tectonic elements in the Gulf of Izmir, western Turkey, using high resolution seismic data. Mar. Pet. Geol. 2017, 83, 73–83. [Google Scholar] [CrossRef]
  10. Schmid, S.M.; Fügenschuh, B.; Kounov, A.; Maţenco, L.; Nievergelt, P.; Oberhänsli, R.; Pleuger, J.; Schefer, S.; Schuster, R.; Tomljenović, B.; et al. Tectonic units of the Alpine collision zone between Eastern Alps and western Turkey. Gondwana Res. 2020, 78, 308–374. [Google Scholar] [CrossRef]
  11. Ring, U.; Okrusch, M.; Will, T. Samos Island, Part I: Metamorphosed and non-metamorphosed nappes, and sedimentary basins. J. Virtual Explor. 2007, 27, 5. [Google Scholar] [CrossRef]
  12. Roche, V.; Jolivet, L.; Papanikolaou, D.; Bozkurt, E.; Menant, A.; Rimmelé, G. Slab fragmentation beneath the Aegean/Anatolia transition zone: Insights from the tectonic and metamorphic evolution of the Eastern Aegean region. Tectonophysics 2019, 754, 101–129. [Google Scholar] [CrossRef]
  13. Ring, U.; Laws, S.; Bernet, M. Structural analysis of a complex nappe sequence and late-orogenic basins from the Aegean Island of Samos, Greece. J. Struct. Geol. 1999, 21, 1575–1601. [Google Scholar] [CrossRef]
  14. Nomikou, P.; Evangelidis, D.; Papanikolaou, D.; Lampridou, D.; Litsas, D.; Tsaparas, Y.; Koliopanos, I. Morphotectonic Analysis along the Northern Margin of Samos Island, Related to the Seismic Activity of October 2020, Aegean Sea, Greece. Geosciences 2021, 11, 102. [Google Scholar] [CrossRef]
  15. Chatzipetros, A.; Kiratzi, A.; Sboras, S.; Zouros, N.; Pavlides, S. Active faulting in the north-eastern Aegean Sea Islands. Tectonophysics 2013, 597–598, 106–122. [Google Scholar] [CrossRef]
  16. Kokkalas, S.; Aydin, A. Is there a link between faulting and magmatism in the south-central Aegean Sea? Geol. Mag. 2013, 150, 193–224. [Google Scholar] [CrossRef]
  17. Sakellariou, D.; Tsampouraki-Kraounaki, K. Plio-quaternary extension and strike-slip tectonics in the Aegean. Transform. Plate Boundaries Fract. Zones 2018, 339, 374. [Google Scholar]
  18. Kassaras, I.; Kapetanidis, V.; Ganas, A.; Tzanis, A.; Kosma, C.; Karakonstantis, A.; Valkaniotis, S.; Chailas, S.; Kouskouna, V.; Papadimitriou, P. The New Seismotectonic Atlas of Greece (v1.0) and Its Implementation. Geosciences 2020, 10, 447. [Google Scholar] [CrossRef]
  19. Papadimitriou, P.; Kassaras, I.; Kaviris, G.; Tselentis, G.-A.; Voulgaris, N.; Lekkas, E.; Chouliaras, G.; Evangelidis, C.; Pavlou, K.; Kapetanidis, V.; et al. The 12th June 2017 Mw=6.3 Lesvos earthquake from detailed seismological observations. J. Geodyn. 2018, 115, 23–42. [Google Scholar] [CrossRef]
  20. Ganas, A.; Elias, P.; Kapetanidis, V.; Valkaniotis, S.; Briole, P.; Kassaras, I.; Argyrakis, P.; Barberopoulou, A.; Moshou, A. The July 20, 2017 M6.6 Kos Earthquake: Seismic and Geodetic Evidence for an Active North-Dipping Normal Fault at the Western End of the Gulf of Gökova (SE Aegean Sea). Pure Appl. Geophys. 2019, 176, 4177–4211. [Google Scholar] [CrossRef]
  21. Sakkas, V.; Lagios, E. Fault modelling of the early-2014 ~M6 Earthquakes in Cephalonia Island (W. Greece) based on GPS measurements. Tectonophysics 2015, 644, 184–196. [Google Scholar] [CrossRef]
  22. Lagios, E.; Sakkas, V.; Novali, F.; Bellotti, F.; Ferretti, A.; Vlachou, K.; Dietrich, V. SqueeSAR™ and GPS ground deformation monitoring of Santorini Volcano (1992–2012): Tectonic implications. Tectonophysics 2013, 594, 38–59. [Google Scholar] [CrossRef]
  23. Lagios, E.; Papadimitriou, P.; Novali, F.; Sakkas, V.; Fumagalli, A.; Vlachou, K.; Del Conte, S. Combined Seismicity Pattern Analysis, DGPS and PSInSAR studies in the broader area of Cephalonia (Greece). Tectonophysics 2012, 524–525, 43–58. [Google Scholar] [CrossRef]
  24. Papadimitriou, P.; Kapetanidis, V.; Karakonstantis, A.; Spingos, I.; Kassaras, I.; Sakkas, V.; Kouskouna, V.; Karatzetzou, A.; Pavlou, K.; Kaviris, G.; et al. First Results on the Mw = 6.9 Samos Earthquake of 30 October 2020. Bull. Geol. Soc. Greece 2020, 56, 251–279. [Google Scholar] [CrossRef]
  25. Greece Earthquake Catalogue Search. Available online: http://www.geophysics.geol.uoa.gr (accessed on 23 April 2021).
  26. Geodynamics Institute of the National Observatory of Athens (GI-NOA). Available online: www.gein.noa.gr (accessed on 23 April 2021).
  27. Turkish Disaster and Emergency Management Presidency AFAD. Available online: https://deprem.afad.gov.tr (accessed on 23 April 2021).
  28. Klein, F.W. User’s guide to HYPOINVERSE-2000: A Fortran program to solve for earthquake locations and magnitudes. U.S. Geol. Surv. Prof. Pap 2002, 1–123. [Google Scholar] [CrossRef] [Green Version]
  29. Karakonstantis, A. 3-D simulation of Crust and Upper Mantle Structure in the Broader Hellenic Area through Seismic Tomography. Ph.D. Thesis, National and Kapodistrian University of Athens, Athens, Greece, 2017. [Google Scholar]
  30. Waldhauser, F. HypoDD-A Program to Compute Double-Difference Hypocenter Locations. U.S. Geol. Surv. Open File Rep. 2001, 25. [Google Scholar] [CrossRef]
  31. Caporali, A.; Floris, M.; Chen, X.; Nurce, B.; Bertocco, M.; Zurutuza, J. The November 2019 seismic sequence in Albania: Geodetic constraints and fault interaction. Remote Sens. 2020, 12, 846. [Google Scholar] [CrossRef] [Green Version]
  32. He, Z.; Chen, T.; Wang, M.; Li, Y. Multi-segment rupture model of the 2016 Kumamoto earthquake revealed by InSAR and GPS data. Remote Sens. 2020, 12, 3721. [Google Scholar] [CrossRef]
  33. Tzanis, A.; Chailas, S.; Sakkas, V.; Lagios, E. Tectonic Deformation in the Santorini Volcanic Complex (Greece) as inferred by joint analysis of Gravity, Magnetotelluric and DGPS Observations. Geophys. J. Int. 2020, 220, 461–489. [Google Scholar] [CrossRef]
  34. Boixart, G.; Cruz, L.F.; Cruz, R.M.; Euillades, P.A.; Euillades, L.D.; Battaglia, M. Source model for Sabancaya Volcano constrained by DInSAR and GNSS surface deformation observation. Remote Sens. 2020, 12, 1852. [Google Scholar] [CrossRef]
  35. Gatsios, T.; Cigna, F.; Tapete, D.; Sakkas, V.; Pavlou, K.; Parcharidis, I. Copernicus sentinel-1 MT-InSAR, GNSS and seismic monitoring of deformation patterns and trends at the Methana Volcano, Greece. Appl. Sci. 2020, 10, 6445. [Google Scholar] [CrossRef]
  36. HexagonSmartNet METRICA S.A. Available online: https://hxgnsmartnet.com (accessed on 23 April 2021).
  37. URANUS Net. Available online: http://www.uranus.gr (accessed on 23 April 2021).
  38. Onder Cetin, K.; Mylonakis, G.; Sextos, A.; Stewart, J.P. Seismological and Engineering Effects of the M 7.0 Samos Island (Aegean Sea) Earthquake; Hellenic Association of Earthquake Engineering: Athens, Greece, 2020. [Google Scholar]
  39. Lekkas, E.; Mavroulis, S.; Gogou, M.; Papadopoulos, G.A.; Triantafyllou, I.; Katsetsiadou, K.-N.; Kranis, H.; Skourtsos, E.; Carydis, P.; Voulgaris, N.; et al. The October 30, 2020, Mw 6.9 Samos (Greece) earthquake. Newsl. Environ. Disaster Cris. Manag. Strateg. 2020, 21, 1–156. [Google Scholar]
  40. EUREF Permanent GNSS Network–Station Log. Available online: https://www.epncb.oma.be/ftp/station/log_9char/izmi00tur_20201111.log (accessed on 23 April 2021).
  41. Dach, R.; Lutz, S.; Walser, P.; Fridez, P. Bernese GNSS Software Version 5.2; User Manual; Astronomical Institute, University of Bern, Bern Open Publishing: Bern, Switzerland, 2015. [Google Scholar]
  42. Nocquet, J.-M. Present-day kinematics of the Mediterranean: A comprehensive overview of GPS results. Tectonophysics 2012, 579, 220–242. [Google Scholar] [CrossRef]
  43. Pesci, A.; Teza, G. Strain rate analysis over the central Apennines from GPS velocities: The development of a new free software. Boll. Di Geod. E Sci. Affin. 2007, 56, 69–88. [Google Scholar]
  44. Hanssen, R.F. Radar Interferometry: Data Interpretation and Error Analysis; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2001. [Google Scholar]
  45. Comerci, V.; Vittori, E. The Need for a Standardized Methodology for Quantitative Assessment of Natural and Anthropogenic Land Subsidence: The Agosta (Italy) Gas Field Case. Remote Sens. 2019, 11, 1178. [Google Scholar] [CrossRef] [Green Version]
  46. Farolfi, G.; Del Soldato, M.; Bianchini, S.; Casagli, N. A procedure to use GNSS data to calibrate satellite PSI data for the study of subsidence: An example from the north-western Adriatic coast (Italy). Eur. J. Remote Sens. 2019, 52, 54–63. [Google Scholar] [CrossRef] [Green Version]
  47. Farolfi, G.; Bianchini, S.; Casagli, N. Integration of GNSS and Satellite InSAR Data: Derivation of Fine-Scale Vertical Surface Motion Maps of Po Plain, Northern Apennines, and Southern Alps, Italy. IEEE Trans. Geosci. Remote. Sens. 2019, 57, 319–328. [Google Scholar] [CrossRef]
  48. Dai, K.; Liu, G.; Li, Z.; Li, T.; Yu, B.; Wang, X.; Singleton, A. Extracting vertical displacement rates in Shanghai (China) with multi-platform SAR images. Remote Sens. 2015, 7, 9542–9562. [Google Scholar] [CrossRef] [Green Version]
  49. Fuhrmann, T.; Garthwaite, M.C. Resolving three-dimensional surface motion with InSAR: Constraints from multi-geometry data fusion. Remote Sens. 2019, 11, 241. [Google Scholar] [CrossRef] [Green Version]
  50. Chen, T.; Newman, A.V.; Feng, L.; Fritz, H.M. Slip distribution from the 1 April 2007 Solomon Islands earthquake: A unique image of near-trench rupture. Geophys. Res. Lett. 2009, 36, L16307. [Google Scholar] [CrossRef] [Green Version]
  51. Feng, L.; Newman, A.V.; Protti, M.; González, V.; Jiang, Y.; Dixon, T.H. Active deformation near the Nicoya Peninsula, northwestern Costa Rica, between 1996 and 2010: Interseismic megathrust coupling. J. Geophys. Res. 2012, 117, B06407. [Google Scholar] [CrossRef] [Green Version]
  52. GTdef. Available online: https://avnewman.github.io/GTDef/ (accessed on 8 March 2021).
  53. Valkaniotis, S.; Briole, P.; Ganas, A.; Elias, P.; Kapetanidis, V.; Tsironi, V.; Fokaefs, A.; Partheniou, H.; Paschos, P. The Mw = 5.6 Kanallaki earthquake of 21 March 2020 in west Epirus, Greece: Reverse fault model from InSAR data and seismotectonic implications for Apulia-Eurasia collision. Geosciences 2020, 10, 454. [Google Scholar] [CrossRef]
  54. Thingbaijam, K.K.S.; Mai, P.M.; Goda, K. New empirical earthquake source-scaling laws. Bull. Seismol. Soc. Am. 2017, 107, 2225–2246. [Google Scholar] [CrossRef] [Green Version]
  55. Triantafyllou, I.; Gogou, M.; Mavroulis, S.; Lekkas, E.; Papadopoulos, G.A.; Thravalos, M. The Tsunami Caused by the 30 October 2020 Samos (Aegean Sea) Mw7.0 Earthquake: Hydrodynamic Features, Source Properties and Impact Assessment from Post-Event Field Survey and Video Records. J. Mar. Sci. Eng. 2021, 9, 68. [Google Scholar] [CrossRef]
  56. USGS Earthquakes Hazards Program. Available online: https://earthquake.usgs.gov/earthquakes/ (accessed on 23 April 2021).
  57. GFZ GEOFON. Available online: http://geofon.gfz-potsdam.de/eqinfo/ (accessed on 23 April 2021).
  58. Global CMT Web Page. Available online: https://www.globalcmt.org (accessed on 23 April 2021).
  59. Wells, D.I.; Coppersmith, K.J. New empirical relationships among magnitude, rupture length, rupture area and surface displacement. Bull. Seismol. Soc. Am. 1994, 84, 974–1002. [Google Scholar]
  60. Evelpidou, N.; Karkani, A.; Kampolis, I. Relative Sea Level Changes and Morphotectonic Implications Triggered by the Samos Earthquake of 30th October 2020. J. Mar. Sci. Eng. 2021, 9, 40. [Google Scholar] [CrossRef]
  61. Pischiutta, M.; Akinci, A.; Tinti, H.A. Broad-band ground-motion simulation of 2016 Amatrice earthquake, Central Italy. Geophys. J. Int. 2021, 224, 1753–1779. [Google Scholar] [CrossRef]
  62. Wessel, P.; Smith, W.H.F.; Scharroo, R.; Luis, J.; Wobbe, F. Generic Mapping Tools: Improved Version Released. Eos Trans. Agu 2013, 94, 409–410. [Google Scholar] [CrossRef] [Green Version]
  63. Zumberge, J.; Heflin, M.; Jefferson, D.; Watkins, M.; Webb, F.H. Precise point positioning for the efficient and robust analysis of GPS data from large networks. J. Geophys. Res. 1997, 102, 5005–5017. [Google Scholar] [CrossRef] [Green Version]
  64. Métois, M.; D’Agostino, N.; Avallone, A.; Chamot-Rooke, N.; Rabaute, A.; Duni, L.; Kuka, N.; Koci, R.; Georgiev, I. Insights on continental collisional processes from GPS data: Dynamics of the peri-Adriatic belts. J. Geophys. Res. Solid Earth 2015, 120, 8701–8719. [Google Scholar] [CrossRef] [Green Version]
  65. Nykiel, G.; Wolak, P.; Figurski, M. Atmospheric opacity estimation based on IWV derived from GNSS observations for VLBI applications. Gps Solut. 2018, 22, 9. [Google Scholar] [CrossRef] [Green Version]
Remotesensing 13 01665 g001 550
Figure 1. (a) Index map and (b) relief map of the broader area of Samos, which shows the location of continuous Global Navigation Satellite System (GNSS) sites that were used in this study (red triangles), together with the focal mechanism solutions of the Mw6.9 earthquake and its major aftershock. Faults (black lines) were taken from [15,16,17,18]. Red dashed lines define the Izmir Balikesir Transfer Zone (IBTZ); yellow dashed line marks the Sakarya Tectonic Unit (STU); blue dashed line defines the Hellenides Tectonic Unit (HTU); NIB: North Ikaria Basin; SB: Samos Basin; NAF: North Anatolian Fault zone.
Figure 1. (a) Index map and (b) relief map of the broader area of Samos, which shows the location of continuous Global Navigation Satellite System (GNSS) sites that were used in this study (red triangles), together with the focal mechanism solutions of the Mw6.9 earthquake and its major aftershock. Faults (black lines) were taken from [15,16,17,18]. Red dashed lines define the Izmir Balikesir Transfer Zone (IBTZ); yellow dashed line marks the Sakarya Tectonic Unit (STU); blue dashed line defines the Hellenides Tectonic Unit (HTU); NIB: North Ikaria Basin; SB: Samos Basin; NAF: North Anatolian Fault zone.
Remotesensing 13 01665 g001
Remotesensing 13 01665 g002 550
Figure 2. (a) Post-seismic activity (M ≥ 3) following the Mw6.9 earthquake (black circle) and its spatial distribution for the period 30 October 2020 to 28 February 2021. (b) Depth distribution of the aftershocks (M ≥ 3) along an E–W striking profile. Only earthquakes with M ≥ 3 are presented, since events of smaller magnitude have negligible or even no contribution to the ground displacement.
Figure 2. (a) Post-seismic activity (M ≥ 3) following the Mw6.9 earthquake (black circle) and its spatial distribution for the period 30 October 2020 to 28 February 2021. (b) Depth distribution of the aftershocks (M ≥ 3) along an E–W striking profile. Only earthquakes with M ≥ 3 are presented, since events of smaller magnitude have negligible or even no contribution to the ground displacement.
Remotesensing 13 01665 g002
Remotesensing 13 01665 g003 550
Figure 3. Time series of four GNSS stations: (a) SAMO, (b) IKAR, (c) CHIO, and (d) IZMI. Red line marks the day of the earthquake. The reference frame is ITRF2014.
Figure 3. Time series of four GNSS stations: (a) SAMO, (b) IKAR, (c) CHIO, and (d) IZMI. Red line marks the day of the earthquake. The reference frame is ITRF2014.
Remotesensing 13 01665 g003
Remotesensing 13 01665 g004 550
Figure 4. (a) The daily baseline changes between the four local continuous GNSS stations for the period before the Mw6.9 earthquake, normalized to an average value. (b) Map of the strain tensor (blue arrow for extension, red arrow for compression) and the horizontal velocity vectors (black arrows) for the GNSS stations relative to station IZMI. Error ellipses in all figures have been drawn to the 95% confidence interval.
Figure 4. (a) The daily baseline changes between the four local continuous GNSS stations for the period before the Mw6.9 earthquake, normalized to an average value. (b) Map of the strain tensor (blue arrow for extension, red arrow for compression) and the horizontal velocity vectors (black arrows) for the GNSS stations relative to station IZMI. Error ellipses in all figures have been drawn to the 95% confidence interval.
Remotesensing 13 01665 g004
Remotesensing 13 01665 g005 550
Figure 5. (a) Map showing the focal mechanism of the earthquake together with the co-seismic horizontal displacement vectors of seven GNSS stations located near the epicenter (station SAMO’s vector is at a different scale compared to the others). (b) Diagram showing the co-seismic vertical displacements (and error estimates) as a function of distance from the epicenter. (c) Time series of the daily coordinates of station SAMO for the period following the earthquake (2 November 2020 to 28 February 2021).
Figure 5. (a) Map showing the focal mechanism of the earthquake together with the co-seismic horizontal displacement vectors of seven GNSS stations located near the epicenter (station SAMO’s vector is at a different scale compared to the others). (b) Diagram showing the co-seismic vertical displacements (and error estimates) as a function of distance from the epicenter. (c) Time series of the daily coordinates of station SAMO for the period following the earthquake (2 November 2020 to 28 February 2021).
Remotesensing 13 01665 g005
Remotesensing 13 01665 g006 550
Figure 6. Wrapped phase InSAR maps derived from the Sentinel 1 satellites on (a,b) ascending and (c) descending orbital trajectory. Color scale (−π to π) describes one cycle of phase difference between the reference and repeat SAR images in the line-of-sight direction (LOS), which represents 28 mm of ground displacement along this direction. Black triangles mark the two GNSS stations on Samos (SAMO to the west and SAMU to the east). Green polygons mark the earthquake and the strongest aftershock. Inset arrows indicate the heading azimuth and look direction of the radar satellites.
Figure 6. Wrapped phase InSAR maps derived from the Sentinel 1 satellites on (a,b) ascending and (c) descending orbital trajectory. Color scale (−π to π) describes one cycle of phase difference between the reference and repeat SAR images in the line-of-sight direction (LOS), which represents 28 mm of ground displacement along this direction. Black triangles mark the two GNSS stations on Samos (SAMO to the west and SAMU to the east). Green polygons mark the earthquake and the strongest aftershock. Inset arrows indicate the heading azimuth and look direction of the radar satellites.
Remotesensing 13 01665 g006
Remotesensing 13 01665 g007 550
Figure 7. LOS displacement maps that were geodetically corrected by GNSS station SAMU for ascending (a,b) and descending (c) orbital acquisition geometry. Black triangles mark the two GNSS stations on Samos (SAMO to the west and SAMU to the east). Dashed lines represent active fault zones from [15]. Green polygons mark the earthquake (Mw6.9) and main aftershock (Mw5.0).
Figure 7. LOS displacement maps that were geodetically corrected by GNSS station SAMU for ascending (a,b) and descending (c) orbital acquisition geometry. Black triangles mark the two GNSS stations on Samos (SAMO to the west and SAMU to the east). Dashed lines represent active fault zones from [15]. Green polygons mark the earthquake (Mw6.9) and main aftershock (Mw5.0).
Remotesensing 13 01665 g007
Remotesensing 13 01665 g008 550
Figure 8. Multi-geometry data decomposition of the calibrated unwrapped interferometric displacements maps for the (a) E–W and (b) vertical co-seismic components. Negative values on the E–W component represent westward motion. Black triangles mark the two GNSS stations on Samos (SAMO to the west and SAMU to the east).
Figure 8. Multi-geometry data decomposition of the calibrated unwrapped interferometric displacements maps for the (a) E–W and (b) vertical co-seismic components. Negative values on the E–W component represent westward motion. Black triangles mark the two GNSS stations on Samos (SAMO to the west and SAMU to the east).
Remotesensing 13 01665 g008
Remotesensing 13 01665 g009 550
Figure 9. Slip distribution along the fault plane for the preferred model. The upper segment (2 rows) has a dipping angle of 60° and the lower one (3 rows) of 40°. White arrows on the fault plane describe the unit slip vector. Pink arrows on the data points are the modelled horizontal displacement vectors. The focal mechanisms of the earthquake, and the main aftershock are also presented.
Figure 9. Slip distribution along the fault plane for the preferred model. The upper segment (2 rows) has a dipping angle of 60° and the lower one (3 rows) of 40°. White arrows on the fault plane describe the unit slip vector. Pink arrows on the data points are the modelled horizontal displacement vectors. The focal mechanisms of the earthquake, and the main aftershock are also presented.
Remotesensing 13 01665 g009
Remotesensing 13 01665 g010 550
Figure 10. Modelled LOS displacement maps after projecting the calculated 3D vector on the LOS direction for the (a) ascending and (b) descending orbital geometry. Black dots show the InSAR data points used in the inversion process. The rectangle shows the projection of the fault plane on to the surface. Line AB marks the change of the dip angle from 60° to 40° on upper and lower segments, respectively.
Figure 10. Modelled LOS displacement maps after projecting the calculated 3D vector on the LOS direction for the (a) ascending and (b) descending orbital geometry. Black dots show the InSAR data points used in the inversion process. The rectangle shows the projection of the fault plane on to the surface. Line AB marks the change of the dip angle from 60° to 40° on upper and lower segments, respectively.
Remotesensing 13 01665 g010
Remotesensing 13 01665 g011 550
Figure 11. Residual maps showing the difference between observed and calculated data for the LOS modelled displacement vectors for (a) ascending and (b) descending orbits. (c,d) Residual maps of E–W and vertical components for the 110-modelled points/targets (black circles). The fit of the GNSS horizontal displacement vectors are included in (c) where black arrows are observed, and red arrows are modelled.
Figure 11. Residual maps showing the difference between observed and calculated data for the LOS modelled displacement vectors for (a) ascending and (b) descending orbits. (c,d) Residual maps of E–W and vertical components for the 110-modelled points/targets (black circles). The fit of the GNSS horizontal displacement vectors are included in (c) where black arrows are observed, and red arrows are modelled.
Remotesensing 13 01665 g011
Remotesensing 13 01665 g012 550
Figure 12. (a) Map of Samos Island showing the modelled fault plane that has been projected to the surface (black rectangle). Dashed lines delineate the main geotectonic units. The double headed arrow shows the direction of the pre-seismic, regional, extensional strain tensor. (b) Cross section along the AA’ line showing the modelled plane of the listric fault, which dips to the north (red line). The black circles represent the aftershocks (M ≥ 3) and their primary association with the lower fault segment.
Figure 12. (a) Map of Samos Island showing the modelled fault plane that has been projected to the surface (black rectangle). Dashed lines delineate the main geotectonic units. The double headed arrow shows the direction of the pre-seismic, regional, extensional strain tensor. (b) Cross section along the AA’ line showing the modelled plane of the listric fault, which dips to the north (red line). The black circles represent the aftershocks (M ≥ 3) and their primary association with the lower fault segment.
Remotesensing 13 01665 g012
Table
Table 1. Focal mechanism parameters of earthquake and strongest aftershock [25].
Table 1. Focal mechanism parameters of earthquake and strongest aftershock [25].
Mw6.9Mw5.0
Date30 October 202030 October 2020
Time (UTC)11:5115:14
Latitude (°N)37.875937.8507
Longitude (°E)26.723526.8522
Depth (km)1315
Strike (°) CWN270264
Dip (°)5037
Rake (°)−81−126
Seismic Moment (N-m)2.81 × 10193.9 × 1016
Table
Table 2. Co-Seismic displacements from the GNSS stations (the reference frame is ITRF2014). Notation: D, displacement; STDV, standard deviation; E, east–west; N, north–south; and U, vertical/up.
Table 2. Co-Seismic displacements from the GNSS stations (the reference frame is ITRF2014). Notation: D, displacement; STDV, standard deviation; E, east–west; N, north–south; and U, vertical/up.
StationLongitude (°)Latitude (°)DE (mm)DN (mm)DU (mm)STDVE (mm)STDVN (mm)STDVU (mm)
SAMO26.705337.7928−48.94−371.2791.701.152.756.71
SAMU26.973537.7575−6.95−53.2724.100.521.292.27
IKAR26.224237.6282−10.22−33.1611.351.581.376.28
IKAU26.273337.6054−7.69−46.6510.033.871.303.19
CHIO26.127238.3679−8.7520.597.101.723.534.71
CHIU26.136038.3665−7.3020.834.442.191.014.92
IZMI27.081838.394812.2135.205.032.206.054.71
Table
Table 3. Synthetic Aperture Radar (SAR) interferometric pairs.
Table 3. Synthetic Aperture Radar (SAR) interferometric pairs.
Pairs24 October–30 October 202024 October–5 November 202024 October–5 November 2020
SensorS1B-S1AS1B-S1BS1A-S1A
OrbitAscendingAscendingDescending
Track13113136
B┴ (m) *36.0322.8345.47
BT (time) **4 h 13 min6 days6 days
Incidence Angle, θ (°)36.851333.741241.5633
Azimuth Angle, φ (°) CWN349349191
* B┴ represents the perpendicular baseline between the orbits; ** BT is the time interval between the occurrences of the earthquake and acquisition of the repeat image.
Table
Table 4. Fault parameters of the best-fit model.
Table 4. Fault parameters of the best-fit model.
Location 1Length (km)Width (km)Strike (°) (CWN)Dip (°)Burial Depth (km)Locking Depth (km)Geodetic Moment (N-m)
26.9435° E 35 ± 319.7277 ± 3 1.0 ± 0.315.0 ± 3.03.67 × 1019
37.7956° N
Upper Segment 5.7 60 ± 31.0 ± 0.36.0 ± 0.51.01 × 1019
Lower Segment 14.0 40 ± 56.0 ± 0.515.0 ± 3.02.66 × 1019
1 The location (longitude and latitude) indicates the eastern top-most point of the fault plane. The rigidity was assumed to be 30·GPa.
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Sakkas, V. Ground Deformation Modelling of the 2020 Mw6.9 Samos Earthquake (Greece) Based on InSAR and GNSS Data. Remote Sens. 2021, 13, 1665. https://doi.org/10.3390/rs13091665

AMA Style

Sakkas V. Ground Deformation Modelling of the 2020 Mw6.9 Samos Earthquake (Greece) Based on InSAR and GNSS Data. Remote Sensing. 2021; 13(9):1665. https://doi.org/10.3390/rs13091665

Chicago/Turabian Style

Sakkas, Vassilis. 2021. "Ground Deformation Modelling of the 2020 Mw6.9 Samos Earthquake (Greece) Based on InSAR and GNSS Data" Remote Sensing 13, no. 9: 1665. https://doi.org/10.3390/rs13091665

APA Style

Sakkas, V. (2021). Ground Deformation Modelling of the 2020 Mw6.9 Samos Earthquake (Greece) Based on InSAR and GNSS Data. Remote Sensing, 13(9), 1665. https://doi.org/10.3390/rs13091665

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop