Assessing Marginal Shallow-Water Bathymetric Information Content of Lidar Sounding Attribute Data and Derived Seafloor Geomorphometry
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area and Instrumentation
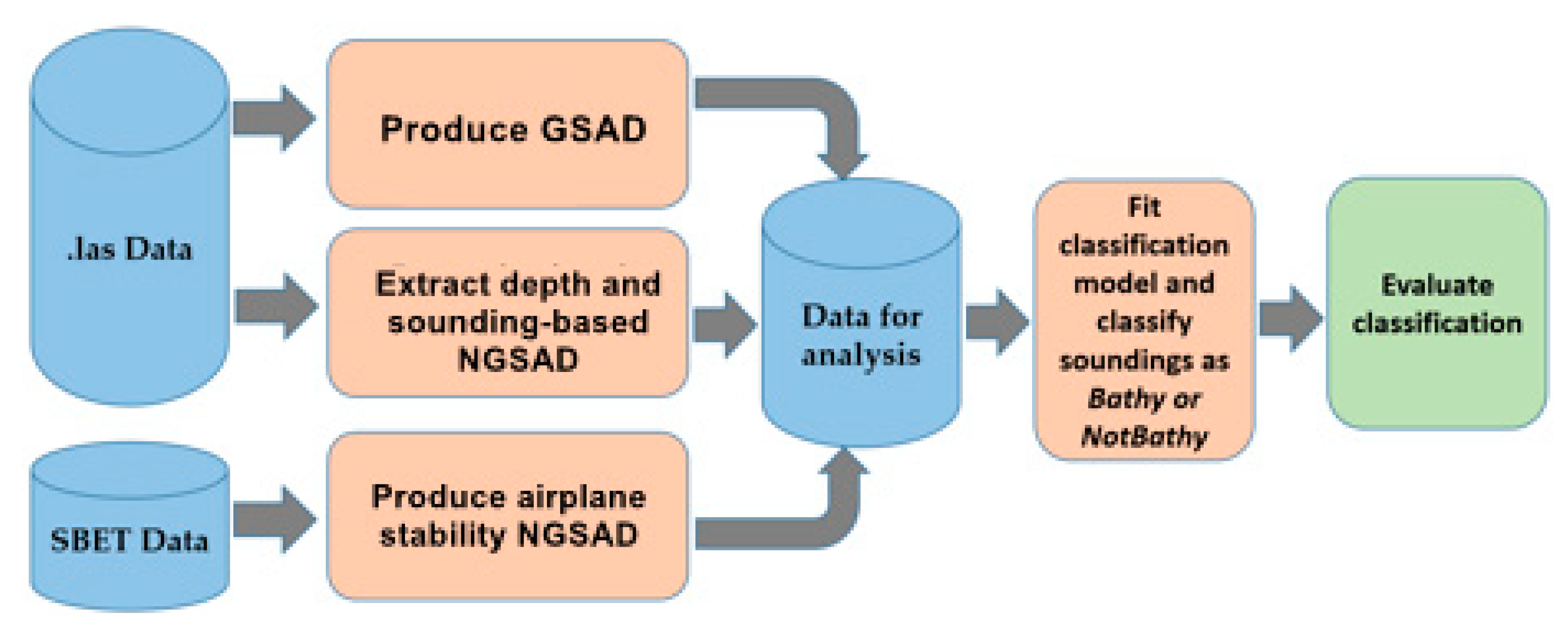
2.2. Data
2.2.1. Predicted/Dependent Variable: Sounding Classification
2.2.2. Predictor/Independent Variables
Depth
Non-Geomorphometric Sounding Attribute Data (NGSAD)
Geomorphometric Sounding Attribute Data (GSAD)
Base Geomorphometry
Orthographic Geomorphometry
2.3. Modelling and Analysis
2.3.1. Model Fitting
2.3.2. Model Evaluation (Depth, NGSAD, and GSAD Assessment)
2.3.3. Individual Variable Evaluation
3. Results
3.1. Model Evaluation (Depth, NGSAD, and GSAD Assessment
- The GSAD variable suite had the lowest predictive ability for bathymetry on its own (‘GSAD only’ models) and provided little or no additional marginal benefit when incorporated into models with depth and/or the NGSAD variable suite.
- Depth was consistently the strongest stand-alone indicator of bathymetry. However, in shallow areas, the bathymetric signal strength in the NGSAD variable suite alone was comparable to the signal strength in depth alone. Nonetheless, in shallow areas, it was the combination of depth and the NGSAD variable suite that provided the best bathymetry extraction.
- The models with the greatest bathymetry predictive power and that were most efficient, i.e., fewest variables for a given accuracy, were the models that employed depth and the NGSAD variable suite.
3.2. Individual Variable Evaluation
- At least 10 variables were important in all models (Column 2, Table 3)
- Last was the second most important variable in the Shallow, Deeper, and Deepest CSs; further analyses indicated that not being the first (sounding) return from a lidar pulse increased p(Bathy).
- SBET variables (particularly stdXYZ) describing airplane/platform stability—and therefore presumably local wind and surface reflectance characteristics—were among the five most important variables in all models.
- The presence of azim2pls in models for two CSs (Deep and Deepest) may also have captured a bathymetric signal related to momentary surface or ocean conditions since there was no instrumental or other reason that a particular azimuth would be better or worse for identifying bathymetry.
- Inciangle (the 20° instrument angle corrected for yaw, pitch, and roll) was important for all CSs except the Deepest CS; this may also relate to how the dynamics of light reflection and/or penetration relate to bathymetry in lidar data.
- Surprisingly, intensity was only among the five most important variables for two CSs, suggesting that other NGSAD related more to the bathymetric signal of soundings.
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Acronym | Definition |
| ADASYN | Adaptive Synthetic Sampling Approach |
| CHRT | CUBE with Hierarchical Resolution Techniques |
| CS | Case Study |
| EN | Estimation Node |
| FNR/FPR | False Negative/Positive Rate |
| GSAD | Geomorphometric Sounding Attribute Data |
| LAS | Not an acronym; a file containing lidar data |
| MBES | Multi-Beam Echo Sounder |
| ML | Machine Learning |
| MSL | Mean Sea Level |
| NOAA | National Oceanic and Atmospheric Administration (United States) |
| NGSAD | Non-Geomorphometric Sounding Attribute Data |
| ODT | Optimal Decision Threshold |
| P(Bathy) | Probability of an individual sounding being Bathy |
| PDT | Probability Decision Threshold |
| RMSE | Root mean square error |
| SAD | Sounding Attribute Data |
| SMOTE | Synthetic Minority Oversampling Technique |
| TIN | Triangulated Irregular Network |
| TNR/TPR | True Negative/Positive Rate |
| UTM | Universal Transverse Mercator |
| XGB | Extreme Gradient Boosting |
References
- Allouis, T.; Bailly, J.-S.; Pastol, Y.; Le Roux, C. Comparison of LiDAR waveform processing methods for very shallow water bathymetry using Raman, near-infrared and green signals. Earth Surf. Process. Landf. 2010, 35, 640–650. [Google Scholar] [CrossRef]
- Dix, M.; Abd-Elrahman, A.; Dewitt, B.; Nash, L., Jr. Accuracy evaluation of terrestrial LIDAR and multibeam sonar systems mounted on a survey vessel. J. Surv. Eng. 2012, 138, 203–213. [Google Scholar] [CrossRef]
- Calder, B.; Mayer, L. Automatic processing of high-rate, high-density multibeam echosounder data. Geochem. Geophys. Geosystems 2003, 4, 22. [Google Scholar] [CrossRef]
- Calder, B.; Rice, G. Computationally efficient variable resolution depth estimation. Comput. Geosci. 2017, 106, 49–59. [Google Scholar] [CrossRef]
- Fischler, M.; Bolles, J. Random sample consensus—A paradigm for model fitting with applications to image analysis and automated cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Nayegandhi, A.; Brock, J.; Wright, C. Small-footprint, waveform-resolving lidar estimation of submerged and sub-canopy topography in coastal environments. Int. J. Remote Sens. 2009, 30, 861–878. [Google Scholar] [CrossRef]
- Nagle, D.; Wright, C. Algorithms Used in the Airborne Lidar Processing System (ALPS); Dept. of the Interior/U.S. Geological Survey Open File Report 2016–1046; United States Geological Survey: Reston, VA, USA, 2016; p. 45.
- Pe’eri, S.; Gardner, J.; Ward, L.; Morrison, J. The seafloor: A key factor in lidar bottom detection. IEEE Trans. Geosci. Remote Sens. 2011, 49, 1150–1157. [Google Scholar] [CrossRef]
- Niroumand-Jadidi, M.; Vitti, A.; Lyzenga, D. Multiple optimal depth predictors analysis (MODPA) for river bathymetry: Findings from spectroradiometry, simulations, and satellite imagery. Remote Sens. Environ. 2018, 218, 132–147. [Google Scholar] [CrossRef]
- Collin, A.; Archambault, P.; Long, B. Mapping shallow water seabed habitat with the SHOALS. IEEE Trans. Geosci. Remote Sens. 2008, 46, 2947–2955. [Google Scholar] [CrossRef]
- Wedding, L.; Friedlander, A.; McGranaghan, M.; Yost, R.; Monaco, M. Using bathymetric lidar to define nearshore benthic habitat complexity: Implications for management of reef fish assemblages in Hawaii. Remote Sens. Environ. 2008, 112, 4159–4165. [Google Scholar] [CrossRef]
- Lecours, V.; Dolan, M.; Micallef, A.; Lucieer, V. A review of marine geomorphometry, the quantitative study of the sea floor. Hydrol. Earth Syst. Sci. 2016, 20, 3207–3244. [Google Scholar] [CrossRef]
- White, M.; Mohn, C.; Orren, M. Physical processes and seamount productivity. In Seamounts: Ecology, Fisheries and Conservation; Blackwell Publishing: Oxford, UK, 2007; pp. 65–84. [Google Scholar]
- Kunze, E.; Llewellyn Smith, S. The role of small-scale topography in turbulent mixing of the global ocean. Oceanography 2004, 17, 55–64. [Google Scholar] [CrossRef]
- McArthur, M.; Brooke, B.; Przeslawski, R.; Ryan, D.; Lucieer, V.; Nichol, S.; McCallum, A.; Mellin, C.; Cresswell, I.; Radke, L. On the use of abiotic surrogates to describe marine benthic biodiversity. Estuar. Coast. Shelf Sci. 2010, 88, 21–32. [Google Scholar] [CrossRef]
- Eren, F.; Pe’eri, S.; Rzhanov, Y.; Ward, L. Bottom characterization by using airborne lidar bathymetry (ALB) waveform feature obtained from bottom return residual analysis. Remote Sens. Environ. 2018, 206, 260–274. [Google Scholar] [CrossRef]
- Wang, C.-K.; Philpot, W. Using airborne bathymetric lidar to detect bottom type variation in shallow waters. Remote Sens. Environ. 2007, 106, 123–135. [Google Scholar] [CrossRef]
- Wang, C.; Li, Q.; Liu, Y.; Wu, G.; Liu, P.; Ding, X. A comparison of waveform processing algorithms for single-wavelength LiDAR bathymetry. Isprs J. Photogramm. Remote Sens. 2015, 101, 22–35. [Google Scholar] [CrossRef]
- Lucieer, V.; Lecours, V.; Dolan, M. Charting the course for future developments in marine geomorphometry: An introduction to the special issue. Geosciences 2018, 8, 477. [Google Scholar] [CrossRef]
- Tulldahl, H.; Wikström, S. Classification of aquatic macrovegetation and substrates with airborne lidar. Remote Sens. Environ. 2012, 121, 347–357. [Google Scholar] [CrossRef]
- American Society for Photogrammetry and Remote Sensing. Las Specification Version 1.4-R13; American Society for Photogrammetry and Remote Sensing: Bethesda, MD, USA, 2013; pp. 15–18. [Google Scholar]
- Fernandez-Diaz, F.; Glennie, C.; Carter, W.; Shrestha, R.; Sartori, M.; Singhania, A.; Legleiter, C.; Overstreet, B. Early results of simultaneous terrain and shallow water bathymetry mapping using a single-wavelength airborne LiDAR sensor. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 623–635. [Google Scholar] [CrossRef]
- Lowell, K.; Calder, B. Measuring shallow-water bathymetric signal strength in lidar point attribute data using machine learning. Int. J. Geogr. Inf. Sci. 2020, in press. [Google Scholar] [CrossRef]
- Pittman, S.; Costa, B.; Battista, T. Using lidar bathymetry and boosted regression trees to predict the diversity and abundance of fish and corals. J. Coast. Res. 2009, 53, 27–38. [Google Scholar] [CrossRef]
- Höfle, B.; Rutzinger, M. Topographic airborne LiDAR in geomorphology: A technological perspective. Z. Geomorphol. 2011, 55, 1–29. (In English) [Google Scholar] [CrossRef]
- Sarala, P.; Räisänen, J.; Johansson, P.; Eskola, K. Aerial LiDAR analysis in geomorphological mapping and geochronological determination of surficial deposits in the Sodankylä region, northern Finland. GFF 2015, 137, 293–303. [Google Scholar] [CrossRef]
- Andersen, M.; Gergely, A.; Al-Hamdani, Z.; Steinbacher, F.; Larsen, L.; Ernstsen, V. Processing and performance of topobathymetric lidar data for geomorphometric and morphological classification in a high-energy tidal environment. Hydrol. Earth Syst. Sci. 2017, 21, 43–63. [Google Scholar] [CrossRef]
- Koppal, S. Lambertian reflectance. Encyclopedia of Computer Vision; Katsushi, I., Ed.; Springer: London, UK, 2014; pp. 441–443. [Google Scholar]
- Chen, T.; Guestrin, C. XGBoost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD ’16), San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Friedman, J. Greedy function approximation: A gradient boosting machine (1999 Reitz Lecture). Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Chawla, N.; Bowyer, K.; Hall, L.; Kegelmeyer, W. SMOTE: Synthetic minority over-sampling technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- He, H.; Bai, Y.; Garcia, E.; Li, S. ADASYN: Adaptive synthetic sampling approach for imbalanced learning. In Proceedings of the IEEE International Joint Conference on Neural Networks (IJCNN 2008), Hong Kong, China, 1–8 June 2008; pp. 1322–1328. [Google Scholar] [CrossRef]
- McFadden, D. Conditional logit analysis of qualitative choice behavior. In Frontiers in Econometrics; Zarembka, P., Ed.; Academic Press: Cambridge, UK, 1974; pp. 105–142. [Google Scholar]
- Measures, R. Laser Remote Sensing: Fundamentals and Applications; Krieger: Melbourne, FL, USA, 1992; p. 510. [Google Scholar]
- Linklater, M.; Hamylton, S.; Brooke, B.; Nichol, S.; Jordan, A.; Woodroffe, C. Development of a Seamless, High-Resolution Bathymetric Model to Compare Reef Morphology around the Subtropical Island Shelves of Lord Howe Island and Balls Pyramid, Southwest Pacific Ocean. Geosciences 2018, 8, 11. [Google Scholar] [CrossRef]
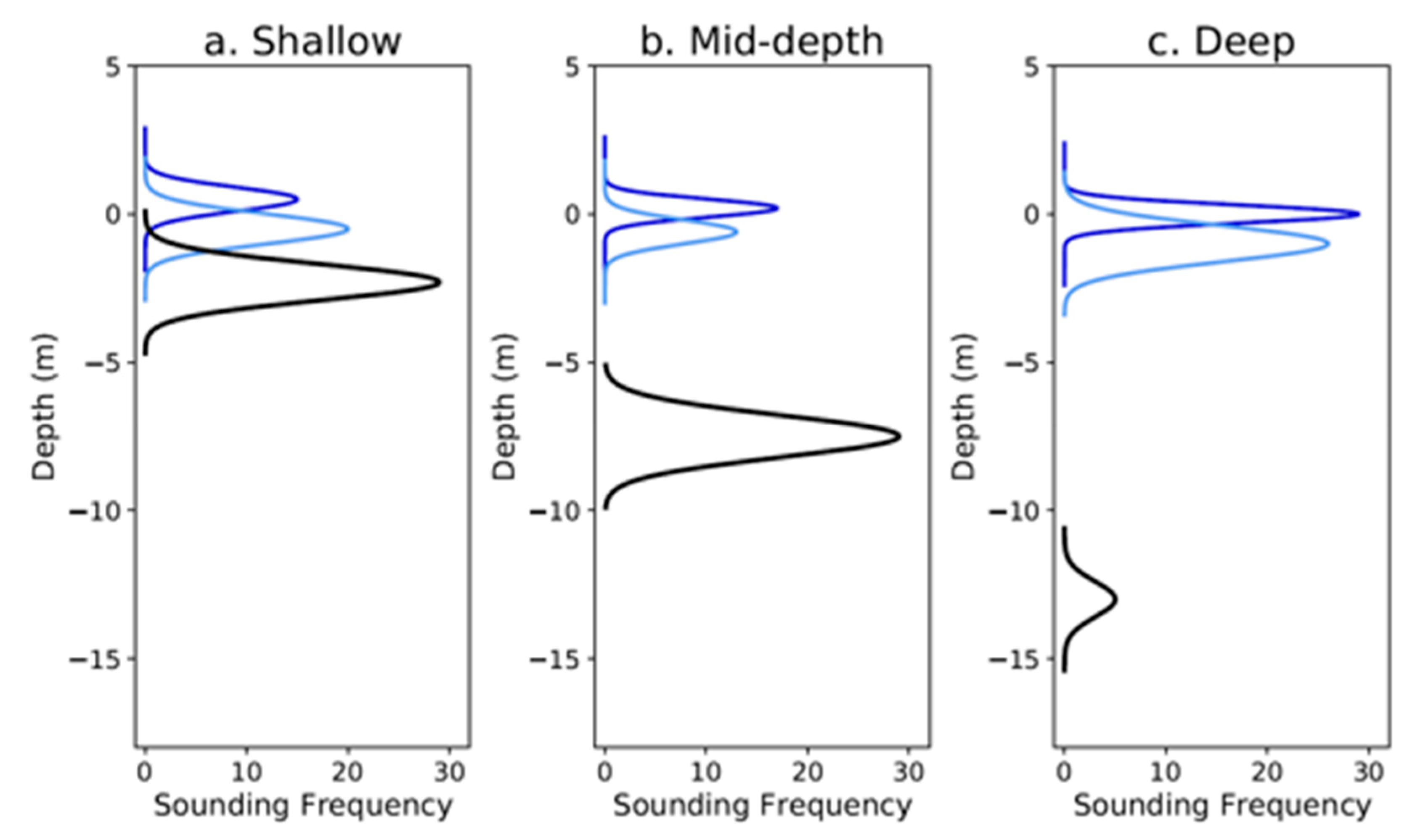
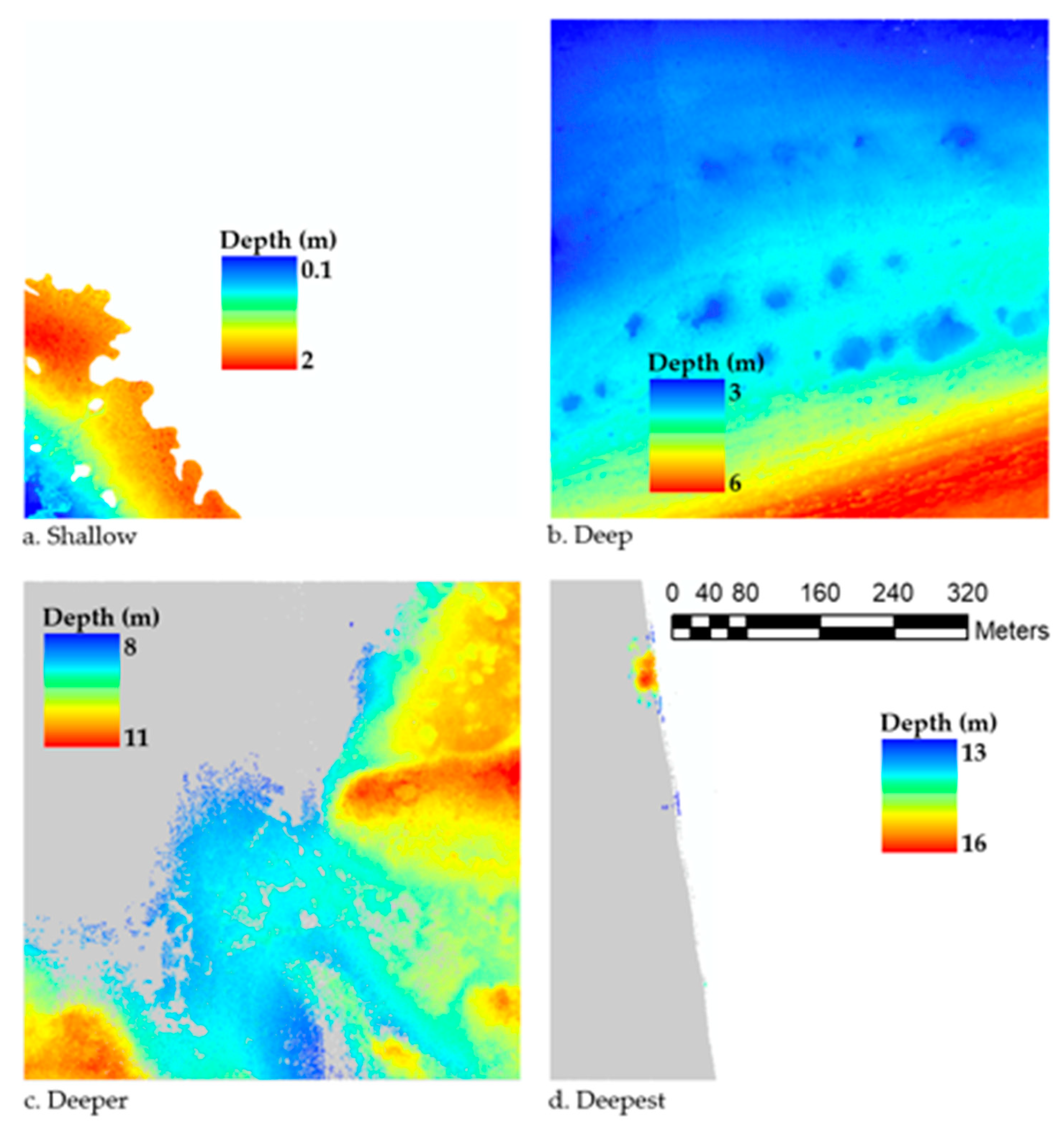

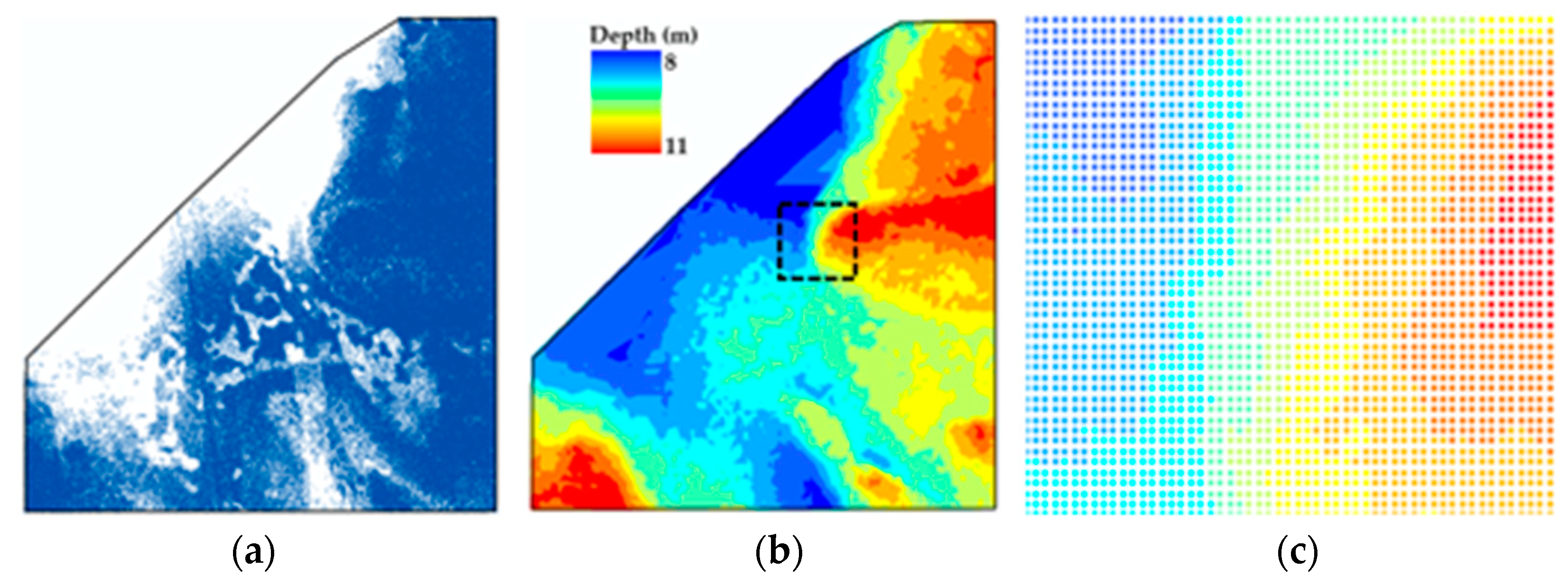

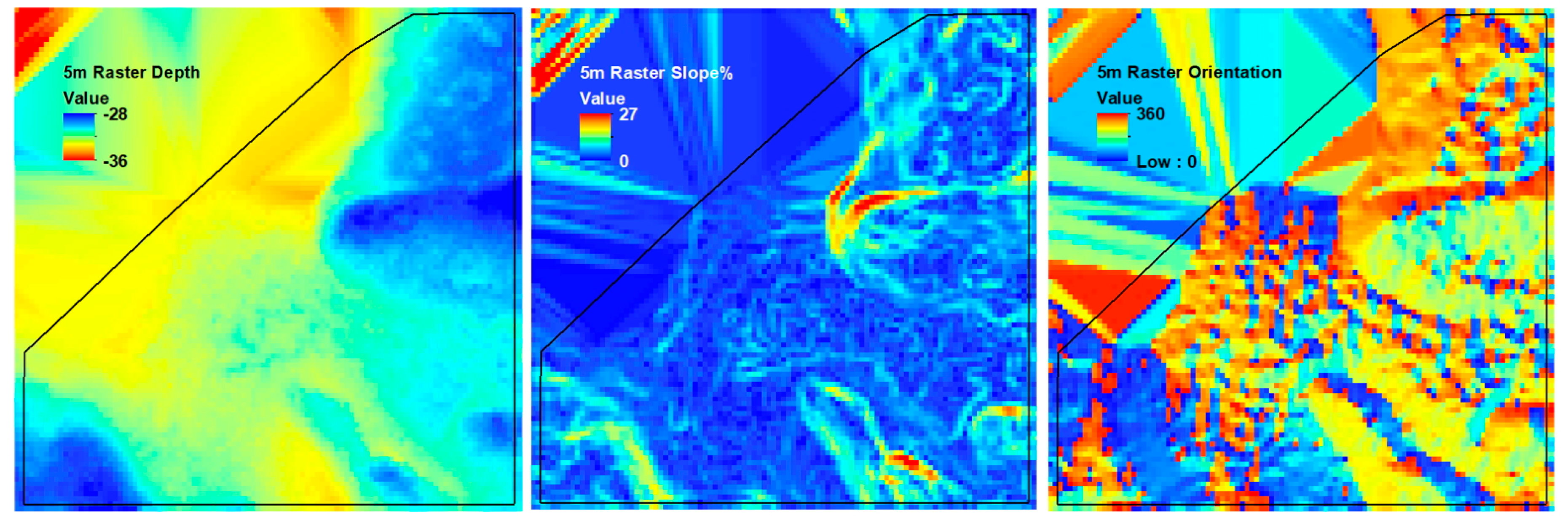
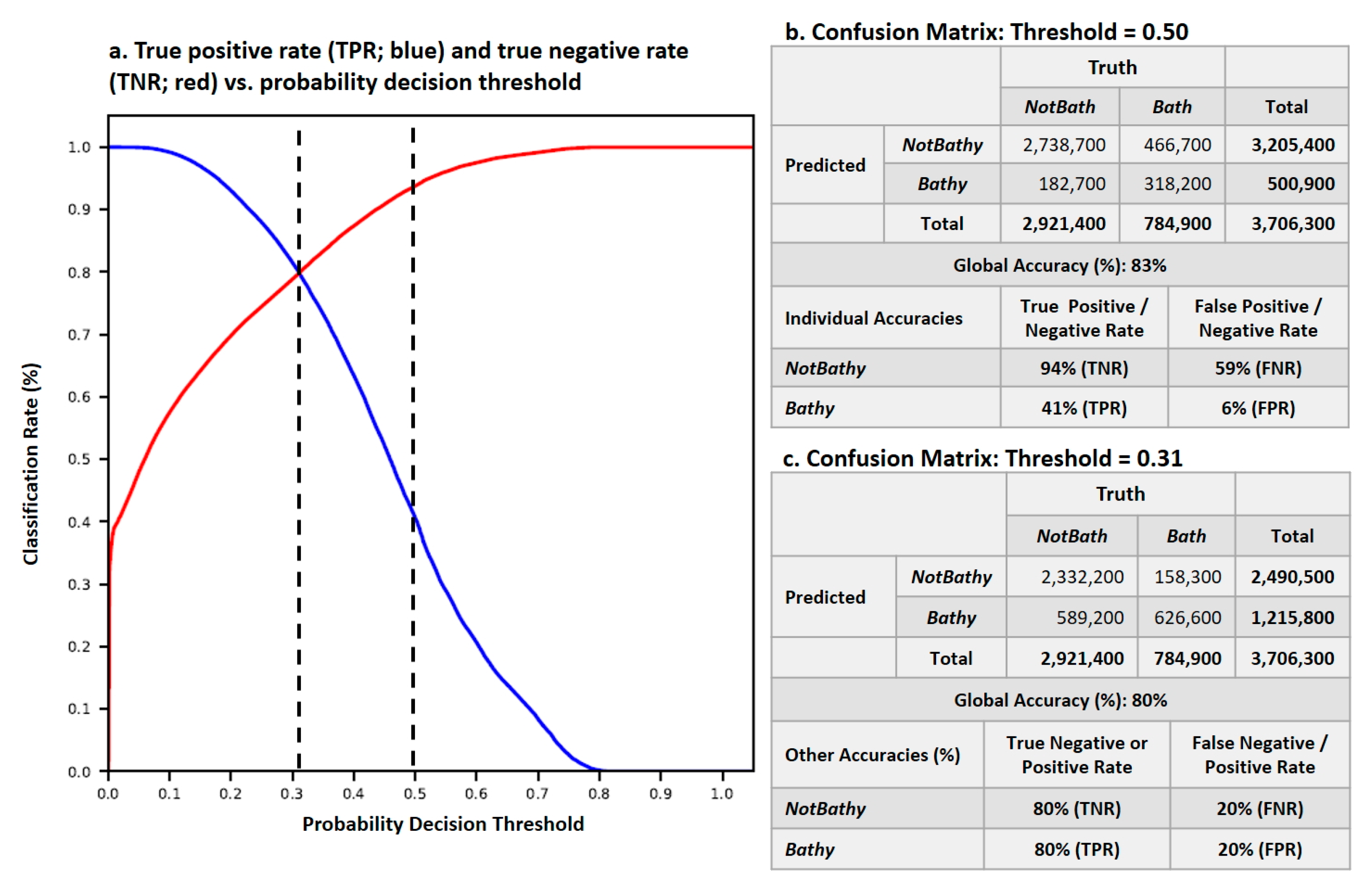

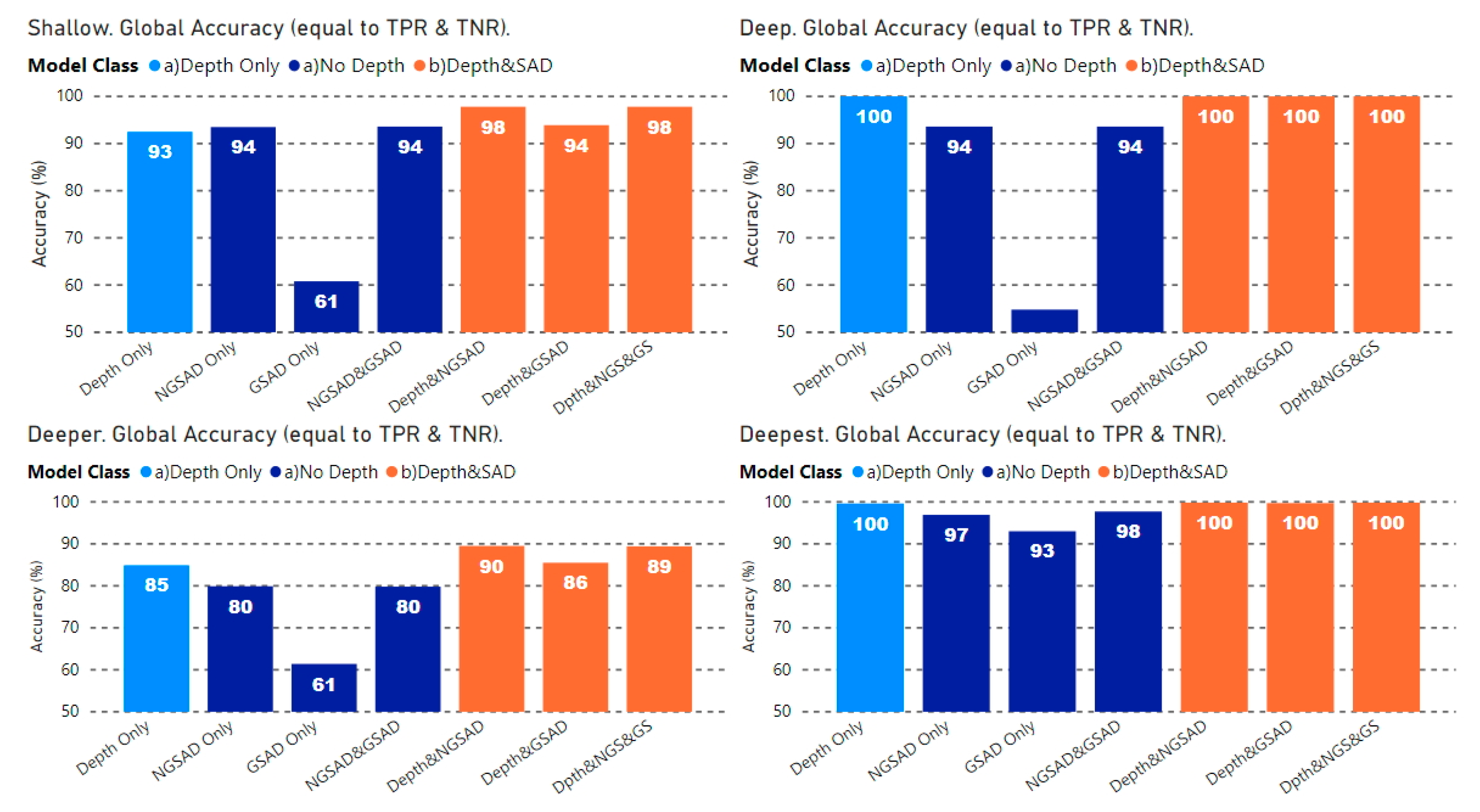

| Identifier/Rel. Depth | Shallow | Deep | Deeper | Deepest |
|---|---|---|---|---|
| Latitude/Longitude | 24°35′08″/81°42′31″ | 24°28′39″/81°41′18″ | 24°40′00″/81°47′00″ | 24°40′00″/81°47′00″ |
| Description | Shallow—only the southwest is below mean sea level (MSL) | Gradual slope with a few ‘dimples’ approximately 1 m tall throughout. | Gradually sloped and cut by relatively shallow channels with bathymetry sparse in the northwest | Long fairly flat trapezoid with small lower depth “mound’ in northeast. Bathymetry extremely sparse and clustered. |
| Area covered (m2) | 30,000 | 250,000 | 250,000 | 75,000 |
| Approx. depth range below MSL (m) | From −2 to 0 | From −6 to −3 | From −11 to −8 | From −16 to −13 |
| Total Returns (million) | 0.6 | 7.6 | 3.7 | 1.0 |
| Return density (pts/m2) | 27.6 | 30.4 | 14.8 | 13.3 |
| % Bathymetry | 78 | 76 | 21 | 0.4 |
| Number of flight paths | 5 | 7 | 7 | 2 |
| Type | Nature | Variable (Name) |
|---|---|---|
| Depth | Depth |
|
| NGSAD: Sounding-based | Sounding-specific |
|
| NGSAD: Airplane stability | SBET |
|
| Edge-based |
|
| CS | Number of Variables with Importance > 0.00 1 | Variables with Importance = 0.0 | Five Most Important Contributing Variables 2 | Cumulative Importance of 5 Most Important |
|---|---|---|---|---|
| Shallow | 12 | Num_returns, first_of_many (2) | Depth, intensity, last, stdXYZ, inciangle | 0.83 |
| Deep | 11 | Return_no, first_of_many, last_of_many (3) | Depth, intensity, stdXYZ, inciangle, azim2pls | 0.97 |
| Deeper | 11 | Return_no, first_of_many, scandirect (3) | Depth, last, stdYwPtRl, stdXYZ, inciangle | 0.80 |
| Deepest | 10 | Num_returns, first_of_many, last_of_many, inciangle (4) | Depth, last, stdXYZ, pls_frm_hdng, azim2pls | 0.89 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lowell, K.; Calder, B. Assessing Marginal Shallow-Water Bathymetric Information Content of Lidar Sounding Attribute Data and Derived Seafloor Geomorphometry. Remote Sens. 2021, 13, 1604. https://doi.org/10.3390/rs13091604
Lowell K, Calder B. Assessing Marginal Shallow-Water Bathymetric Information Content of Lidar Sounding Attribute Data and Derived Seafloor Geomorphometry. Remote Sensing. 2021; 13(9):1604. https://doi.org/10.3390/rs13091604
Chicago/Turabian StyleLowell, Kim, and Brian Calder. 2021. "Assessing Marginal Shallow-Water Bathymetric Information Content of Lidar Sounding Attribute Data and Derived Seafloor Geomorphometry" Remote Sensing 13, no. 9: 1604. https://doi.org/10.3390/rs13091604
APA StyleLowell, K., & Calder, B. (2021). Assessing Marginal Shallow-Water Bathymetric Information Content of Lidar Sounding Attribute Data and Derived Seafloor Geomorphometry. Remote Sensing, 13(9), 1604. https://doi.org/10.3390/rs13091604





