Interpretation of Spectral LiDAR Backscattering off the Florida Coast
Abstract
:1. Introduction
2. Materials and Methods
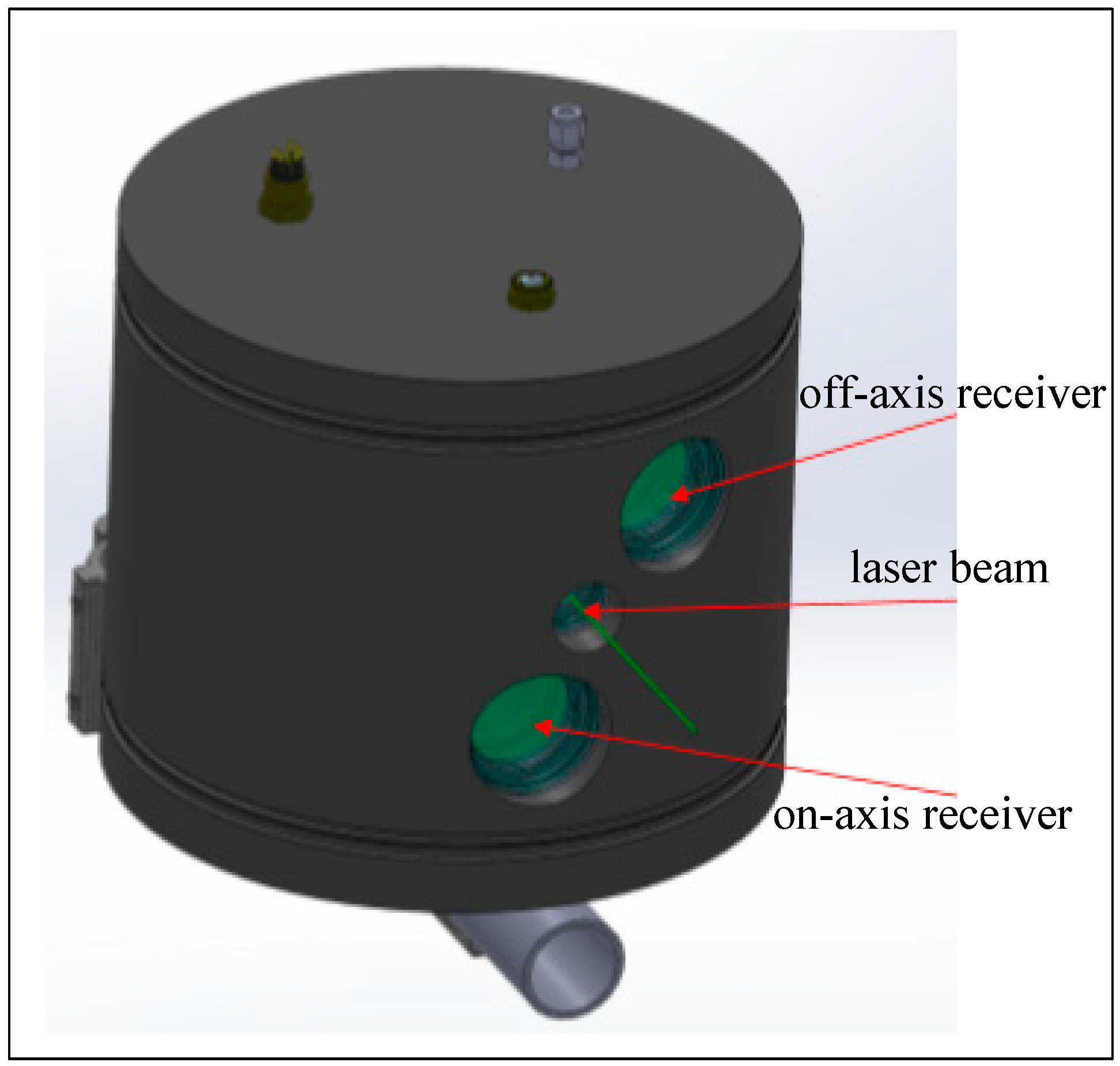
2.1. The LiDAR System
2.2. Field Experiments
2.3. Direct and Diffuse Scattering Components
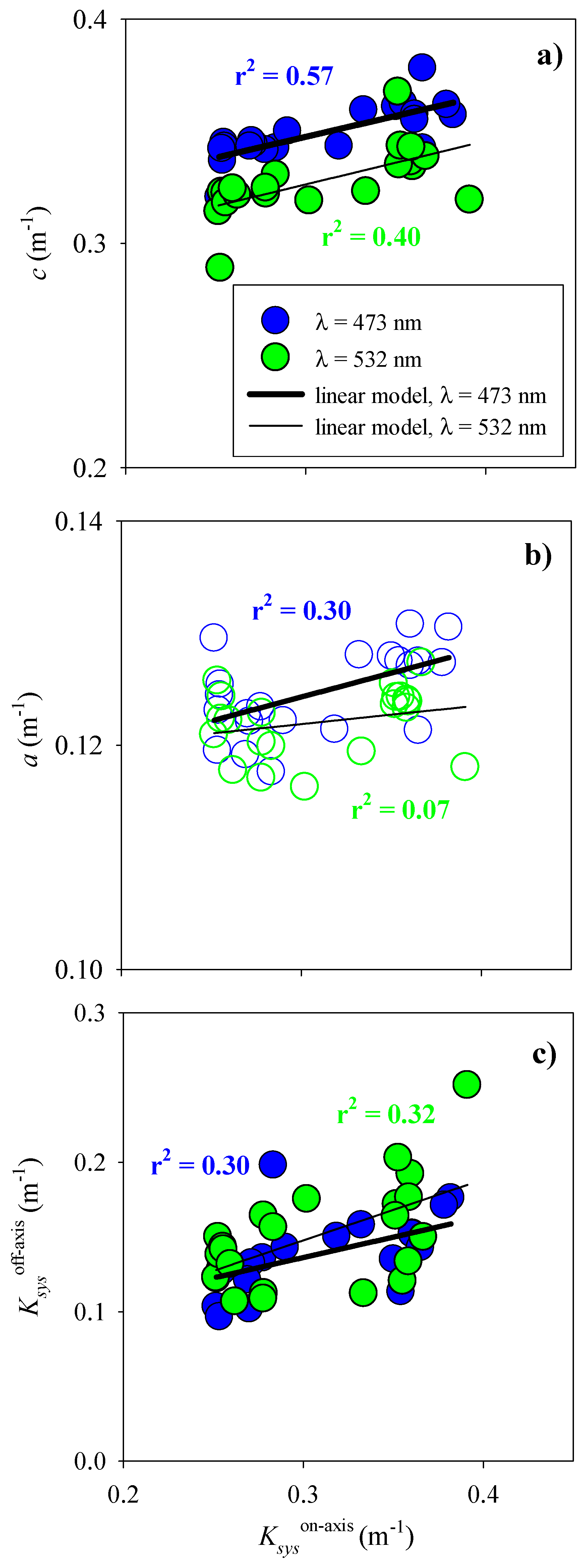
2.4. Relationships between Ksys and IOPs
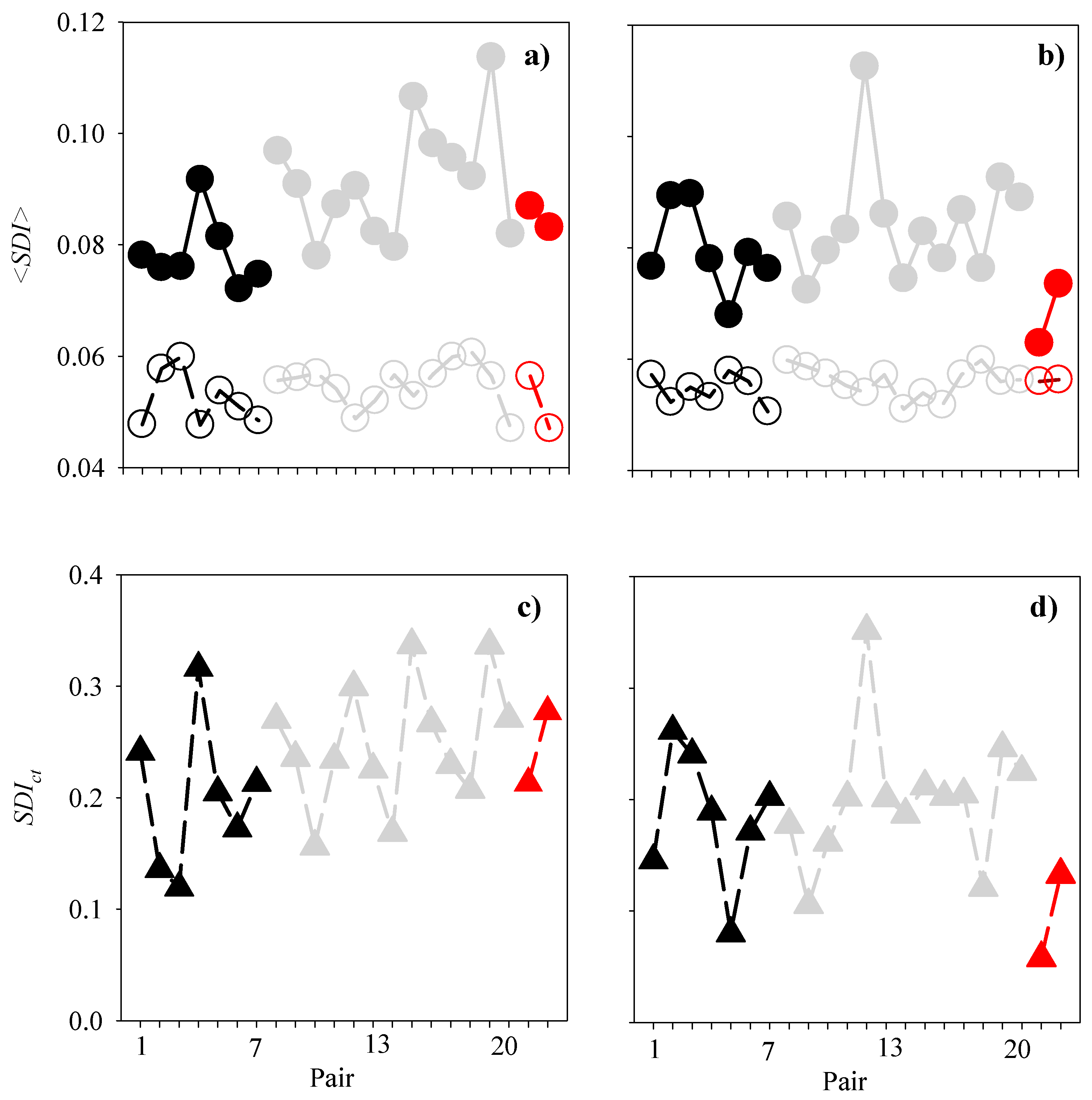
2.5. SDI
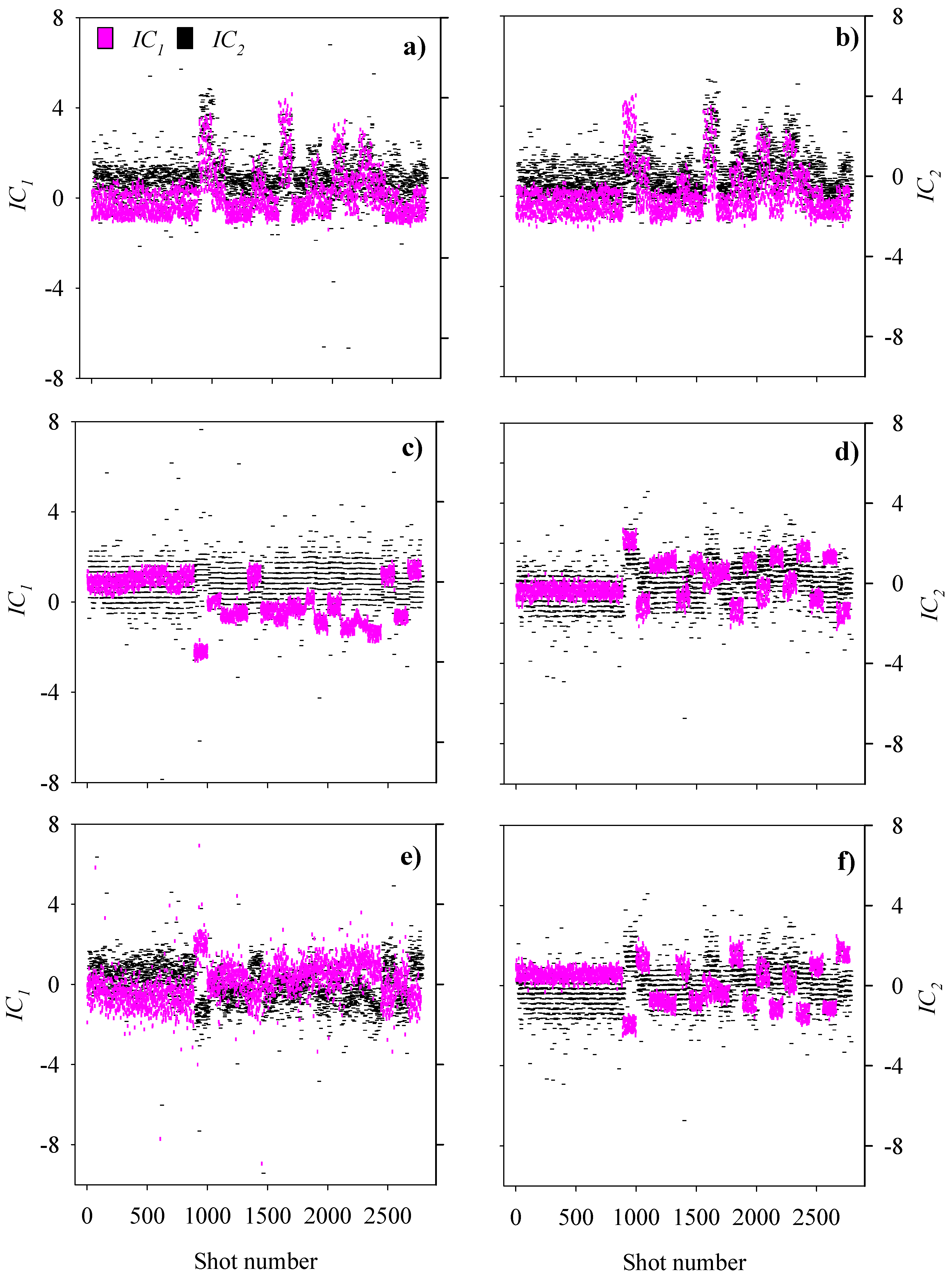
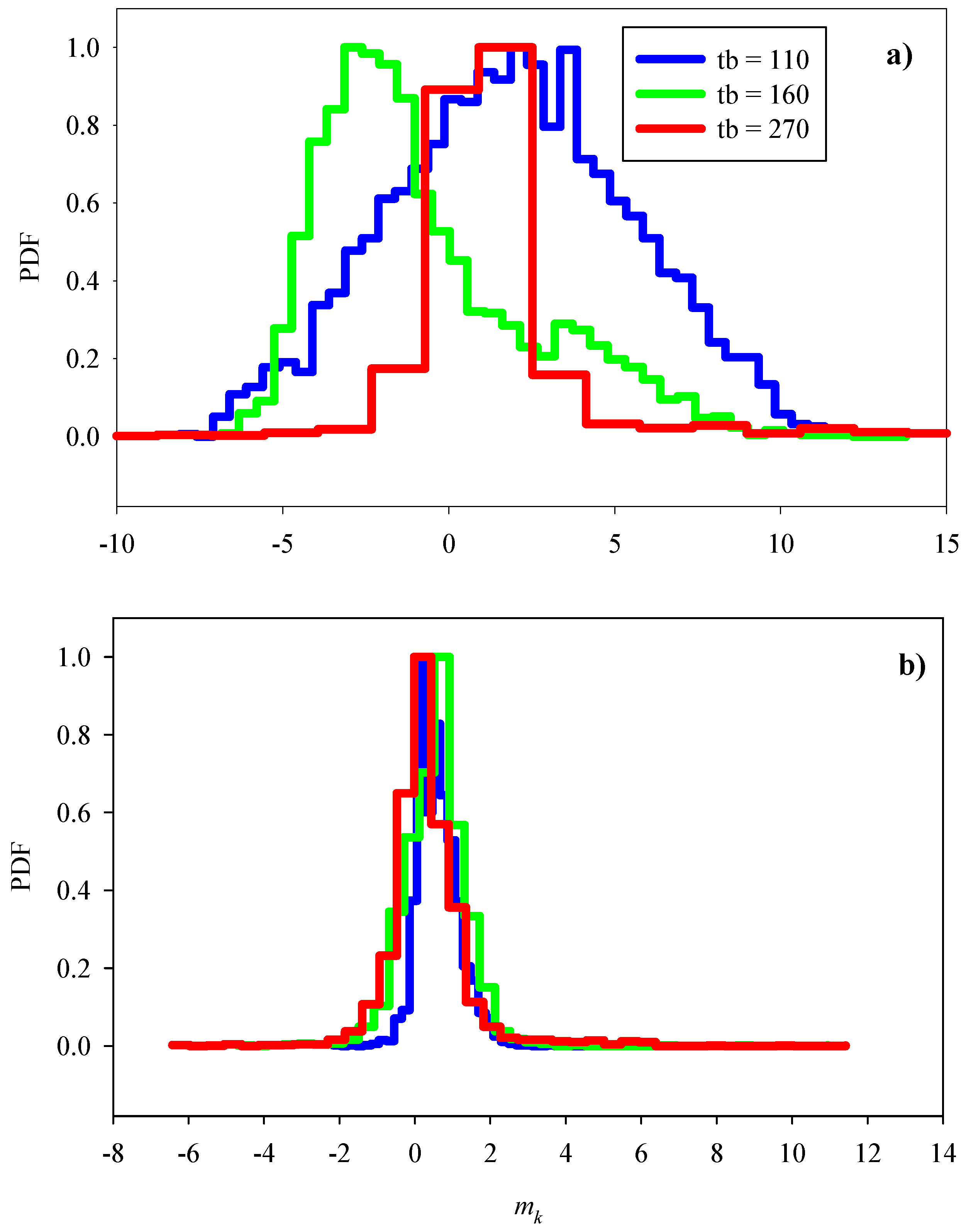
2.6. The Spectral Slope of LiDAR Backscattering
3. Results
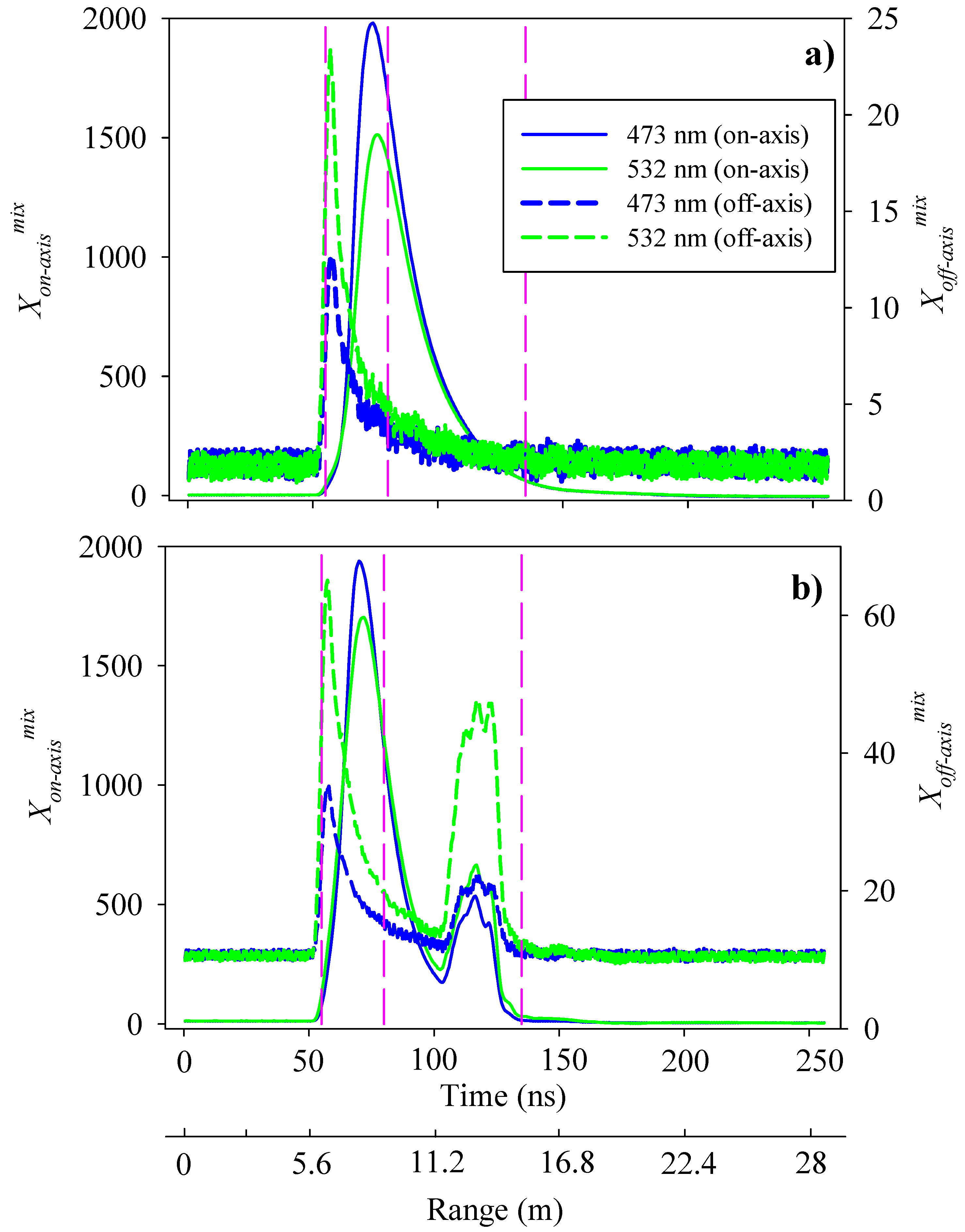
3.1. Scattering Processes and Shape of Waveforms
3.2. Response of Ksys to IOPs
3.3. Structural Dissimilarity
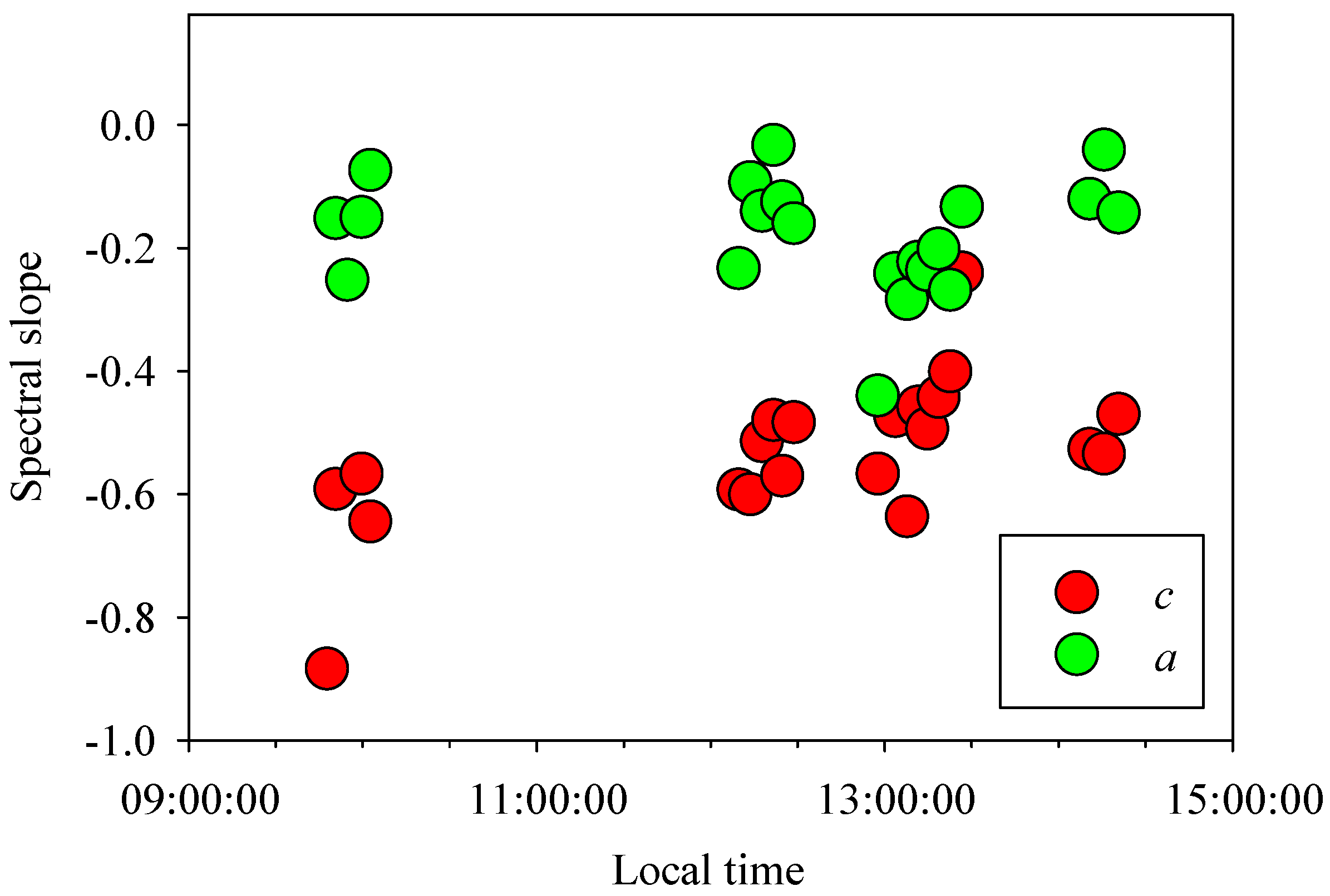
3.4. Spectral Slopes of LiDAR Backscattering
4. Discussion
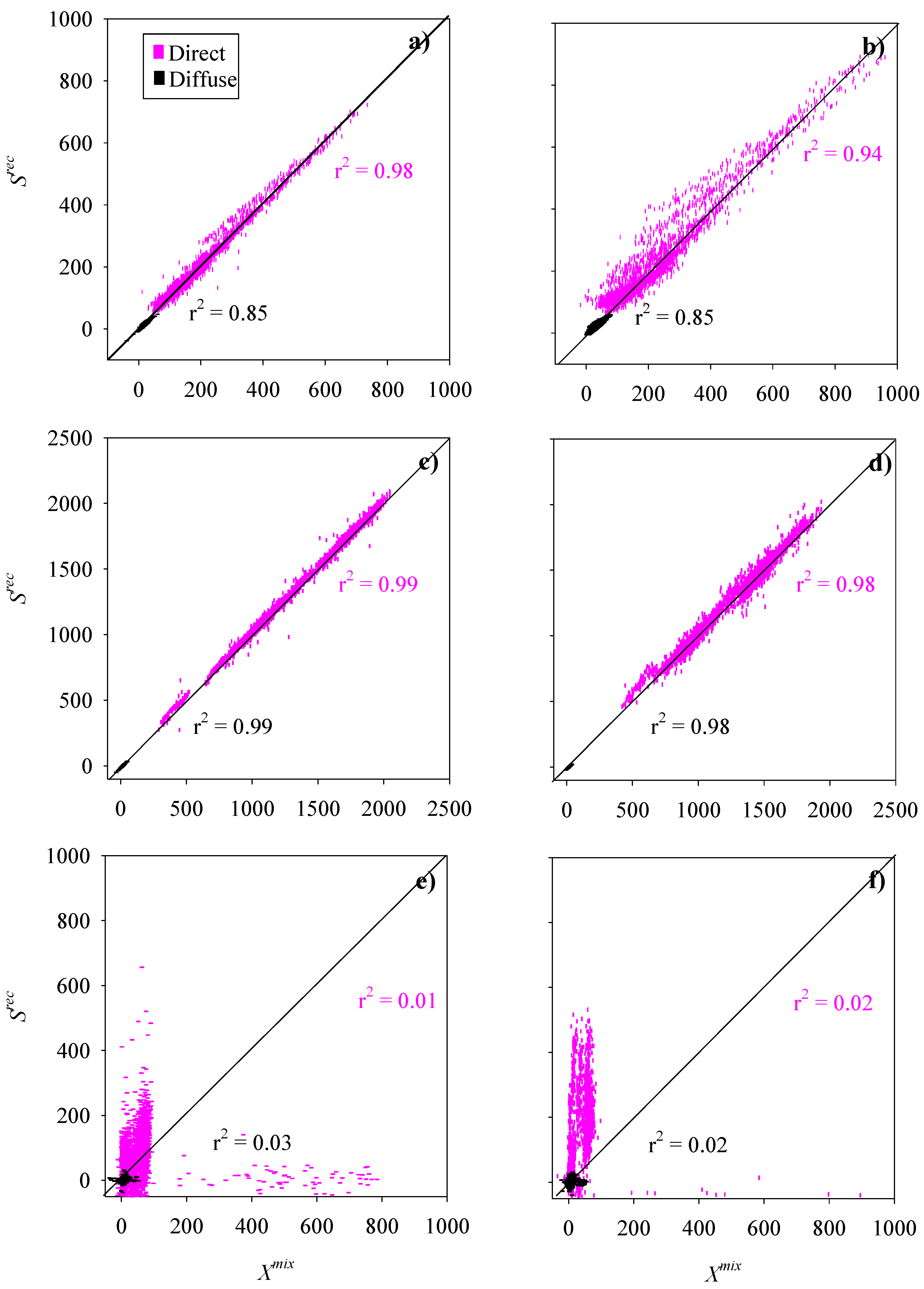
4.1. Direct/Diffuse Backscattering Components
4.2. LiDAR vs Ac-9 Optical Properties
4.3. Diel and Spatial Patterns of Scatterers
4.4. Spectral Backscattering Variations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Hoge, C.W.F.E.; Wright, W.B.; Krabill, R.R.; Buntzen, G.D.; Gilbert, R.N.; Swift, R.N.; Yungel, J.K.; Berry, R.E. Airborne lidar detection of subsurface oceanic scattering layers. App. Opt. 1998, 27, 3969–3977. [Google Scholar] [CrossRef]
- Churnside, J.H.; Donaghay, P.L. Thin scattering layers observed by airborne lidar. ICES J. Mar. Sci. 2009, 66, 778–789. [Google Scholar] [CrossRef]
- Montes-Hugo, M.A.; Churnside, J.H.; Gould, R.W.; Arnone, R.A.; Foy, R. Spatial coherence between remotely sensed ocean color data and vertical distribution of lidar backscattering in coastal stratified waters. Remote Sens. Environ. 2010, 114, 2584–2593. [Google Scholar] [CrossRef]
- Montes, M.A.; Churnside, J.; Lee, Z.; Gould, R.; Arnone, R.; Weidemann, A. Relationships between water attenuation coefficients derived from active and passive remote sensing: A case study from two coastal environments. Appl. Opt. 2011, 50, 2990–2999. [Google Scholar] [CrossRef]
- Montes, M.A.; Vuorenkoski, A.K.; Dalgleish, F.R.; Ouyang, B. Characterization of underwater scattering layers based on variance components of LiDAR backscattering. Opt. Exp. 2019, 27, A1084–A1108. [Google Scholar] [CrossRef] [PubMed]
- Brown, E.D.; Churnside, J.H.; Collins, R.L.; Veenstra, T.; Wilson, J.J.; Abnett, K. Remote sensing of capelin and other biological features in the North Pacific using lidar and video technology. ICES J. Mar. Sci. 2002, 59, 1120–1130. [Google Scholar] [CrossRef]
- Churnside, J.H.; Marchbanks, R.D.; Donaghay, P.L.; Sullivan, J.M.; Graham, W.M.; Wells, R.J.D. Hollow aggregations of moon jellyfish (Aurelia spp.). J. Plank. Res. 2016, 38, 122–130. [Google Scholar] [CrossRef] [Green Version]
- Clavano, W.J.; Boss, E.S.; Karp-Boss, L. Inherent optical properties of non-spherical marine-like particles -from theory to observation. Oceanogr. Mar. Biol. 2007, 245, 11–38. [Google Scholar]
- Montes, M.; Carder, K. Monte Carlo simulations as a tool to optimize target detection by AUV/ROV laser line scanners. In Proceedings of the SPIE—The International Society for Optical Engineering, Orlando, FL, USA, 19 May 2005; p. 5799. [Google Scholar]
- Strait, C.; Twardowski, M.; Dalgleish, F.; Tonizzo, A.; Vuorenkoski, A. Development and assessment of lidar modeling to retrieve IOPs. In Proceedings of the SPIE: Ocean Sensing and Monitoring X, Orlando, FL, USA, 25 May 2018; p. 10631. [Google Scholar]
- Montes-Hugo, M.A.; Gould, R.; Arnone, R.; Ducklow, H.; Carder, K.; English, D.; Schofield, O.; Kerfoot, J. Beyond the first optical depth: Fusing optical data from ocean color imagery and gliders. In Proceedings of the SPIE 7459, Ocean Remote Sensing: Methods and Applications, San Diego, CA, USA, 19 August 2009; p. 74590N. [Google Scholar]
- Aulicino, G.; Cotroneo, Y.; Lacava, T.; Sileo, G.; Fusco, G.; Carlon, R.; Satriano, V.; Pergola, N.; Tramutoli, V.; Budillon, G. Results of the first Wave Glider experiment in the Southern Tyrrhenian Sea. Adv. Oceanogr. Limnol. 2016, 7, 16–35. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Bovik, A.; Sheikh, H.; Simoncelli, E. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Slade, W.H.; Boss, E. Spectral attenuation and backscattering as indicators of average particle size. App. Opt. 2015, 54, 7264–7277. [Google Scholar] [CrossRef] [PubMed]
- Hyvärinen, A.; Oja, E. Independent Component Analysis: Algorithms and Applications. Neural Netw. 2000, 13, 411–430. [Google Scholar] [CrossRef] [Green Version]
- Luchinin, A.G.; Kirillin, M.Y.; Dolin, L.S. Backscatter signals in underwater lidars: Temporal and frequency features. Appl. Opt. 2018, 57, 673–677. [Google Scholar] [CrossRef]
- Mohammadpour, G.; Gagné, J.P.; Larouche, P.; Montes-Hugo, M. Optical properties of size fractions of suspended particulate matter in littoral waters of Quebec. Biogeosciences 2017, 14, 5297–5312. [Google Scholar] [CrossRef] [Green Version]
- Walker, R.E.; McLean, J.W. Lidar equations for turbid media with pulse stretching. Appl. Opt. 1999, 38, 2384–2397. [Google Scholar] [CrossRef] [PubMed]
- Gordon, H.R. Interpretation of airborne oceanic lidar: Effects of multiple scattering. Appl. Opt. 1982, 21, 2996–3001. [Google Scholar] [CrossRef]
- Sokal, R.R.; Rohlf, J. Biometry: The Principles and Practices of Statistics in Biological Research, 3rd ed.; W.H. Freeman: New York, USA, 2009; 880p. [Google Scholar]
- Gray, D.; Anderson, J.; Nelson, J.; Edwards, J. Using a multiwavelength LiDAR for improved remote sensing of natural waters. Appl. Opt. 2015, 54, F232–F242. [Google Scholar] [CrossRef]
- Boss, E.; Pegau, W.S.; Lee, M.; Twardowski, M.; Shybanov, E.; Korotaev, G.; Baratange, F. Particulate backscattering ratio at LEO 15 and its use to study particle composition and distribution. J. Geophys. Res. Atm. 2004, 109. [Google Scholar] [CrossRef] [Green Version]
- Montes, M.; Vuorenkoski, A.K.; Dalgleish, F.R.; Ouyang, B. Weibull approximation of LiDAR waveforms for estimating the beam attenuation coefficient. Opt. Expr. 2016, 24, 22670–22681. [Google Scholar] [CrossRef] [PubMed]
- Boss, E.; Twardowski, M.S.; Herring, S. Shape of the particulate beam attenuation spectrum and its inversion to obtain the shape of particulate size distribution. Appl. Opt. 2001, 40, 4885–4893. [Google Scholar] [CrossRef]
- Dubrovinskaya, E.; Dalgleish, F.; Ouyang, B.; Casari, P. Underwater LiDAR Signal Processing for Enhanced Detection and Localization of Marine Life. In Proceedings of the MTS/IEEE OCEANS, Kobe, Japan, 28–31 May 2018. [Google Scholar]
- Lindeman, K.C. Development of Grunts and Snappers of Southeast Florida; Crossshelf Distributions and Effects of Beach Management Alternatives. Ph.D. Thesis, University of Miami, Coral Gables, FL, USA, 1997. Unpublished. [Google Scholar]
- Van der Zande, D.; Green, J.; Ruddick, K. JellySpec: Feasibility study for determining the spectral characteristics of jellyfish from Belgian waters. In Proceedings of the Ocean Optics XXII Conference, Portland, OR, USA, 26–31 October 2014. [Google Scholar]
- Loisel, H.; Nicolas, J.M.; Sciandra, A.; Stramski, D.; Poteau, A. Spectral dependency of optical backscattering by marine particles from satellite remote sensing of the global ocean. J. Geophys. Res. 2006, 111, C09024. [Google Scholar] [CrossRef]

| Definition | Units | |
|---|---|---|
| FOV | Field-of-View | |
| IOP | Inherent optical property | |
| ICA | Independent Component Analysis | |
| SSI | Structural Similarity Index | dimensionless |
| SDI | Structural Dissimilarity Index | dimensionless |
| SDIct | SDI contrast | dimensionless |
| lum | Luminance | dimensionless |
| ct | Contrast | dimensionless |
| st | Structure | dimensionless |
| λ | Wavelength of LiDAR source | Nm |
| A | Total absorption coefficient | m−1 |
| c | Beam attenuation coefficient | m−1 |
| nw | Refractive index of seawater | dimensionless |
| np | Refractive index of particulates | dimensionless |
| Ksys | System attenuation coefficient | m−1 |
| Kd | Diffuse attenuation coefficient of downwelling irradiance | m−1 |
| Xmix | Backscattering power | Relative units |
| mk | Spectral slope of Xmix | dimensionless |
| S | Source signal | Relative units |
| Srec | Reconstructed source signal | Relative units |
| λ (nm) | Receiver | Waveform Portion | Time Bin Range |
|---|---|---|---|
| 473 | On-axis | Leading | 107–142 |
| Off-axis | 100–113 | ||
| On-axis | Exponential attenuation | 138–300 | |
| Off-axis | 115–200 | ||
| On-axis | Trailing | 240–363 | |
| Off-axis | 139–290 | ||
| 532 | On-axis | Leading | 104–146 |
| Off-axis | 105–115 | ||
| On-axis | Exponential attenuation | 146–300 | |
| Off-axis | 117–200 | ||
| On-axis | Trailing | 250–350 | |
| Off-axis | 142–280 |
| Time Bin | Receiver | Morning | Noon-Afternoon | ||
|---|---|---|---|---|---|
| <mk> | S/N | <mk> | S/N | ||
| 110 | on-axis | 1.84 | 2.2 | 3.92 | 2.8 |
| off-axis | 0.64 | 1.20 | |||
| 160 | on-axis | −3.16 | 17.8 | 0.06 | 12.5 |
| off-axis | 0.16 | 0.42 | |||
| 270 | on-axis | −0.38 | 1.6 | 1.40 | 1.4 |
| off-axis | −0.04 | 0.18 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Montes, M.A.; Vuorenkoski, A.K.; Metzger, B.; Botson, B. Interpretation of Spectral LiDAR Backscattering off the Florida Coast. Remote Sens. 2021, 13, 2475. https://doi.org/10.3390/rs13132475
Montes MA, Vuorenkoski AK, Metzger B, Botson B. Interpretation of Spectral LiDAR Backscattering off the Florida Coast. Remote Sensing. 2021; 13(13):2475. https://doi.org/10.3390/rs13132475
Chicago/Turabian StyleMontes, Martin A., Anni K. Vuorenkoski, Ben Metzger, and Bryan Botson. 2021. "Interpretation of Spectral LiDAR Backscattering off the Florida Coast" Remote Sensing 13, no. 13: 2475. https://doi.org/10.3390/rs13132475
APA StyleMontes, M. A., Vuorenkoski, A. K., Metzger, B., & Botson, B. (2021). Interpretation of Spectral LiDAR Backscattering off the Florida Coast. Remote Sensing, 13(13), 2475. https://doi.org/10.3390/rs13132475





