Weighted Information Models for the Quantitative Prediction and Evaluation of the Geothermal Anomaly Area in the Plateau: A Case Study of the Sichuan–Tibet Railway
Abstract
1. Introduction
2. Study Area
3. Methodology
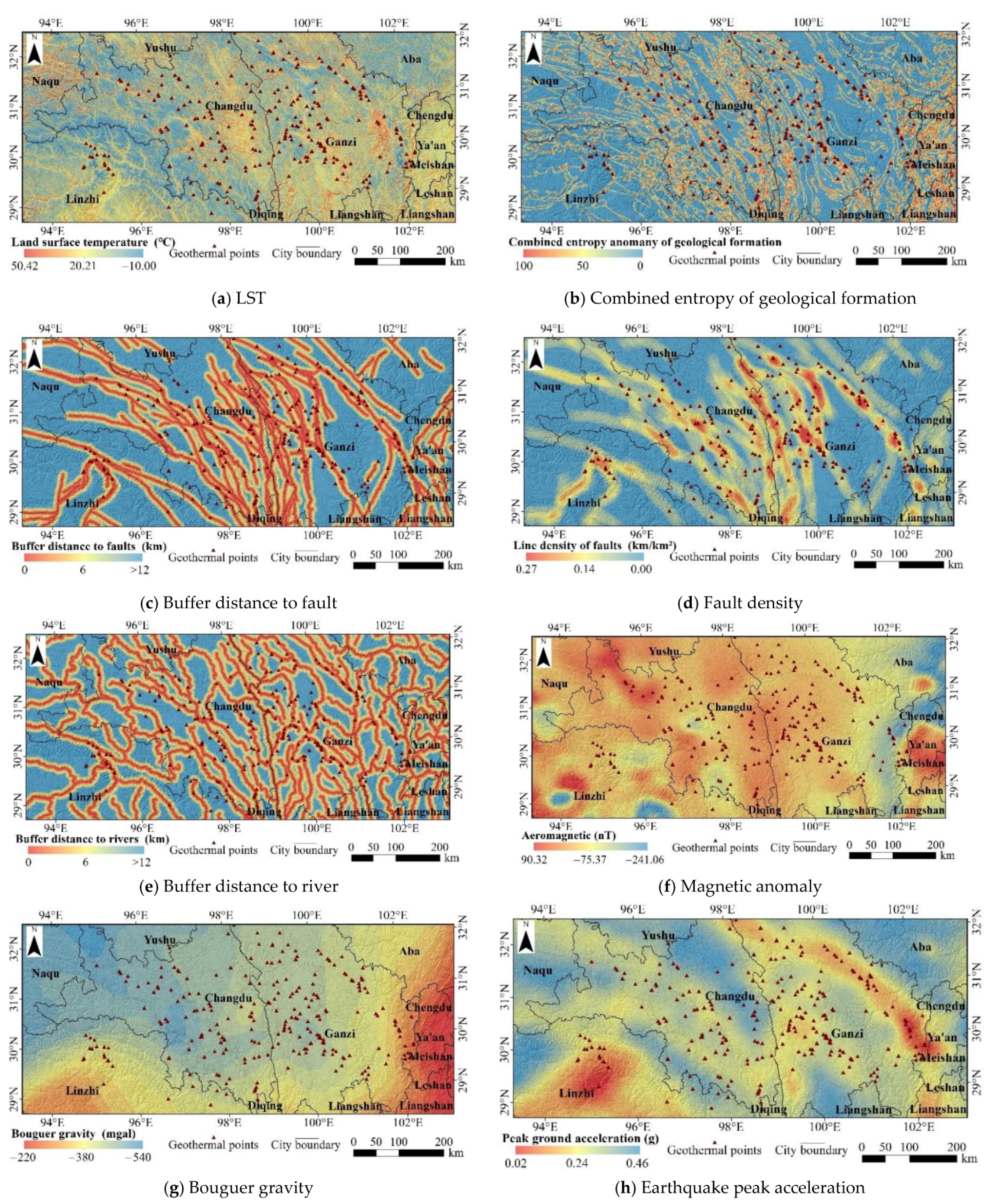
3.1. Factor Selection
3.1.1. Geothermal Points
3.1.2. Land Surface Temperature
3.1.3. Combined Entropy of Geological Formation
3.1.4. Buffer Distance to Fault and Fault Density
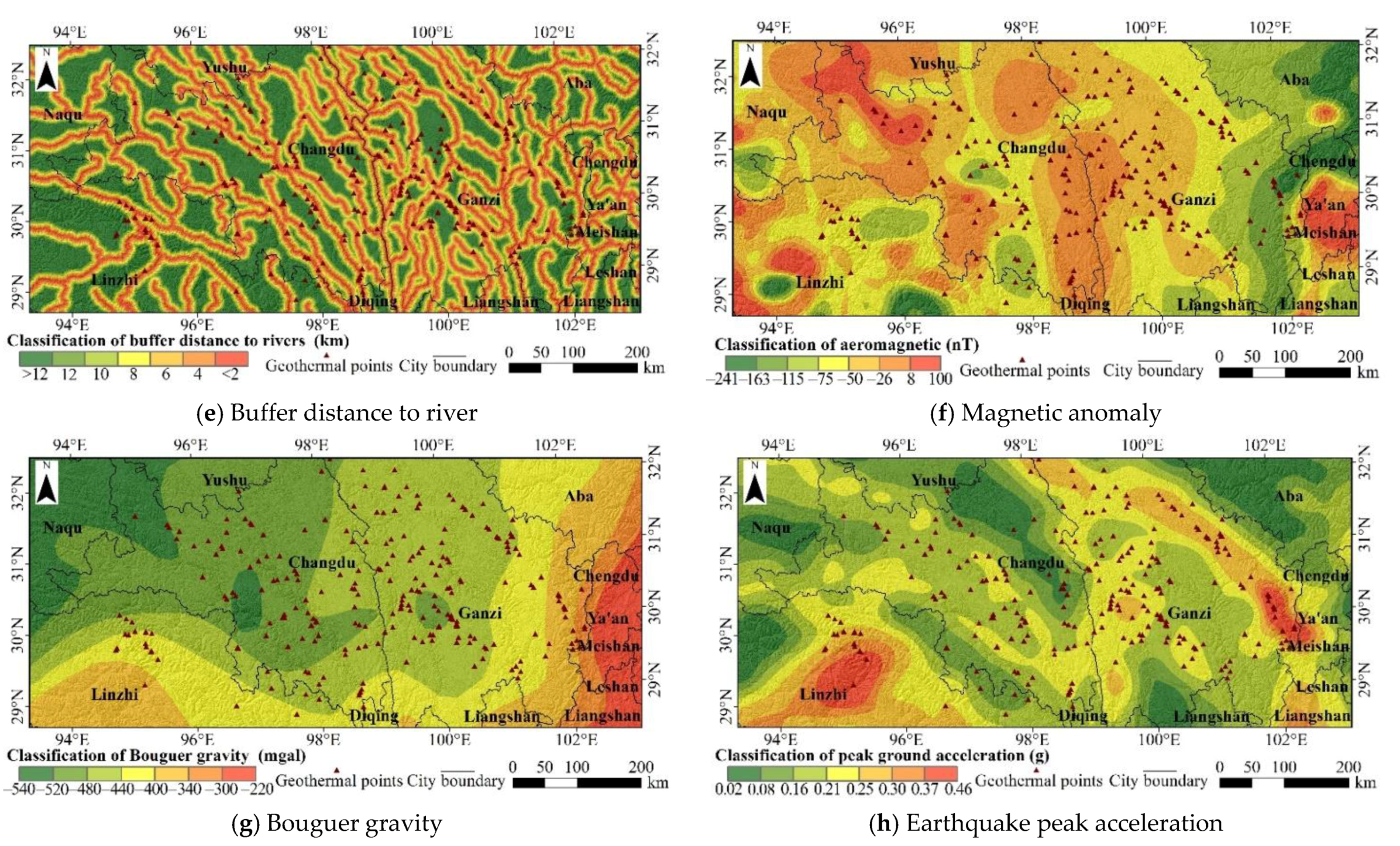
3.1.5. Buffer Distance to River
3.1.6. Magnetic Anomaly
3.1.7. Bouguer Gravity
3.1.8. Earthquake Peak Acceleration
3.2. Factor Reclassification and Independence
3.2.1. Factor Reclassification
3.2.2. Independence Test
3.3. Model Establishment
3.3.1. Information Model
3.3.2. Index-Overlay Information Model
3.3.3. Weights of Entropy Information Model
3.3.4. Weights of Evidence Information Model
3.3.5. Classification Maps of Prediction
4. Model Assessment
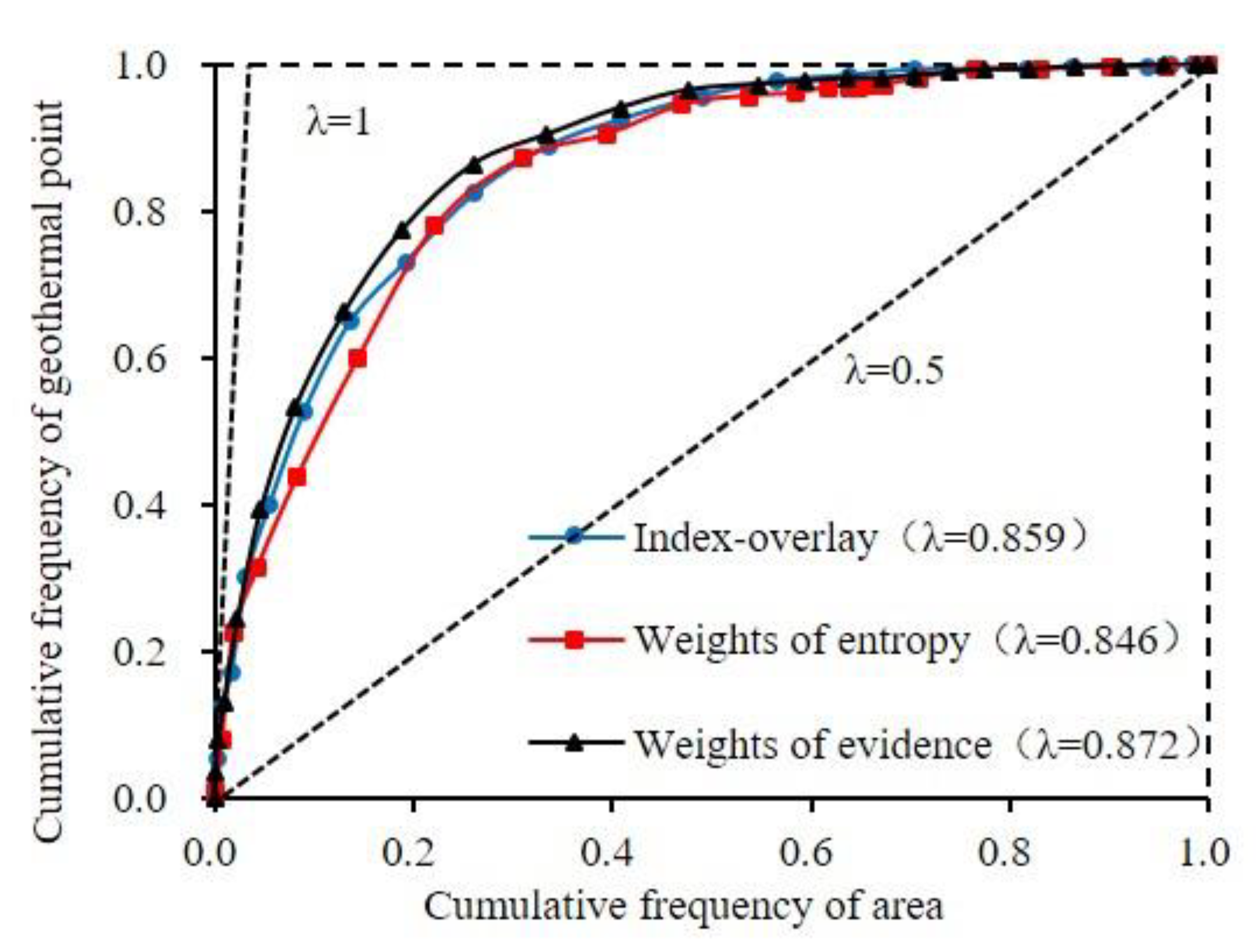
4.1. Analysis of Success Index
4.2. Analysis of Area Ratio
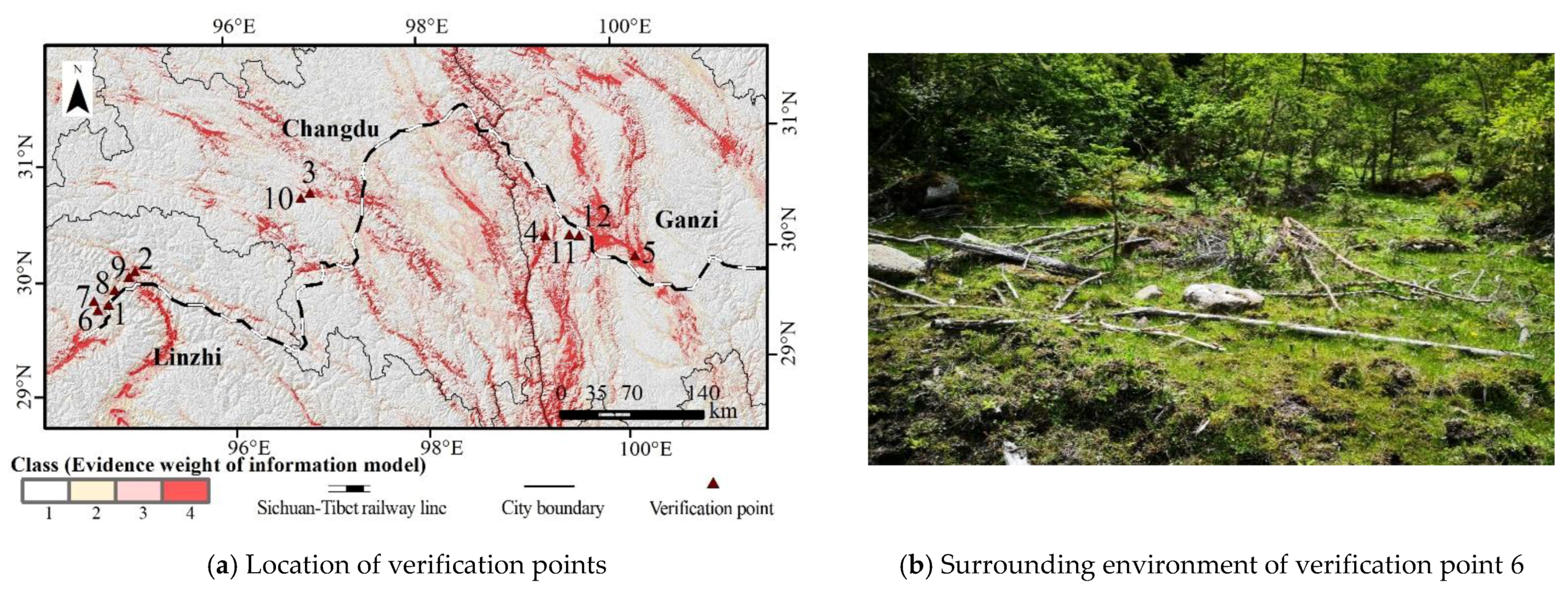
4.3. Ground Verification
5. Discussion and Conclusions
5.1. Discussion
5.2. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Peng, J.B.; Cui, P.; Zhuang, J.Q. Challenges to engineering geology of Sichuan-Tibet railway. Chin. J. Rock Mech. Eng. 2020, 39, 1–13. [Google Scholar] [CrossRef]
- Guo, C.; Zhang, Y.; Jiang, L.; Shi, J. Discussion on the environmental and engineering geological problems along the Sichuan-Tibet railway and its adjacent area. Geoscience 2017, 31, 4–16. [Google Scholar] [CrossRef]
- Lu, C.; Cai, C. Challenges and countermeasures for construction safety during the Sichuan–Tibet railway project. Engineering 2019, 5, 833–838. [Google Scholar] [CrossRef]
- Jiang, L.W.; Li, Y.S.; Yi, S.J.; Huang, C.; Liu, K. Engineering Geological Research in Formations-structural features of the Sichuan-Tibet Railway Plate Collision Junction. In Proceedings of the 2016 Academic Exchange Conference on Challenges and Countermeasures of Sichuan-Tibet Railway Construction; People’s Communications Press: Beijing, China, 2016. [Google Scholar]
- Xu, Y.D.; Yao, L.K. Some cognitions and thinking about the specific geo-environmental problems along the Sichuan-Tibet railway. J. Railw. Eng. Soc. 2017, 34, 1–5. [Google Scholar] [CrossRef]
- Zhu, Y. The Sichuan-Tibet Railway Construction Challenges and Countermeasures; China Communications Press: Beijing, China, 2017. [Google Scholar]
- Zheng, Z.X.; Sun, Q.Q. The tunneling engineering of Sichuan-Tibet railway. Tunn. Constr. 2017, 37, 138–143. [Google Scholar]
- Yan, J.; He, C.; Wang, B.; Meng, W.; Wu, F.Y. Inoculation and characters of rock bursts in extra-long and deep tunnels located on Yarlung Zangbo suture. Chin. J. Rock Mech. Rock Eng. 2019, 38, 769–781. [Google Scholar] [CrossRef]
- Watson, T.; Kruse, F.A.; Hummer, M.S. Thermal Infrared Exploration in the Carlin Trend. Geophysics 1990, 55, 70–79. [Google Scholar] [CrossRef]
- Rodgers, J.L. The Epistemology of Mathematical and Statistical Modeling. Am. Psychol. 2010, 65, 1–12. [Google Scholar] [CrossRef]
- Criss, R.E.; Champion, D.E. Magnetic Properties of Granitic Rocks from the Southern Half of the Idaho Batholith: Influences of Hydrothermal Alteration and Implications for Aeromagnetic Interpretation. J. Geophys. Res. Solid Earth 1984, 89, 7061–7076. [Google Scholar] [CrossRef]
- Yan, B.Z.; Qiu, S.W.; Xiao, C.L.; Liang, X.J. Potential Geothermal Fields Remote Sensing Identification in Changbai Mountain Basalt Area. J. Jilin Univ. 2017, 47, 1819–1828. [Google Scholar] [CrossRef]
- Chen, J.P.; Lu, P.; Wu, W.; Zhao, H.Q. A 3D method for predicting blind orebodies, based on a 3D visualization model and its application. Earth Sci. Front. 2017, 47, 1819–1828. [Google Scholar] [CrossRef]
- Hou, J. Spatial assessment for groundwater quality based on GIS and improved fuzzy comprehensive assessment with entropy weights. Chin. J. Popul. Resour. Environ. 2013, 11, 135–141. [Google Scholar] [CrossRef]
- Fan, L.F.; Hu, R.L.; Zeng, F.C.; Wang, S.S.; Zhang, X.Y. Application of Weighted Information Value Model to Landslide Susceptibility Assessment-A Case Study of Enshi City, Hubei Province. J. Eng. Geol. 2012, 20, 508–513. [Google Scholar] [CrossRef]
- Ding, E.J.; Xie, D.T.; Wei, C.F.; Ni, J.P. MUSLE-Based Agricultural Nonpoint Source Pollution Risk Assessment in the Three Gorges Reservoir Area of Chongqing. J. Southwest Univ. 2010, 32, 96–101. [Google Scholar]
- Prol-Ledesma, R.M. Evaluation of the reconnaissance results in geothermal exploration using GIS. Geothermics 2000, 29, 83–103. [Google Scholar] [CrossRef]
- Coolbaugh, M.F.; Raines, G.L.; Zehner, R.E. Assessment of exploration bias in data-driven predictive models and the estimation of undiscovered resources. Nat. Resour. Res. 2007, 16, 199–207. [Google Scholar] [CrossRef]
- Tüfekçi, N.; Süzen, M.L.; Güleç, N. GIS based geothermal potential assessment: A case study from Western Anatolia, Turkey. Energy 2010, 35, 246–261. [Google Scholar] [CrossRef]
- Noorollahi, Y.; Itoi, R.; Fujii, H.; Tanaka, T. GIS model for geothermal resource exploration in Akita and Iwate prefectures, northern Japan. Comput. Geosci. 2007, 33, 1008–1021. [Google Scholar] [CrossRef]
- Yousefi, R.; Muhamad, M.R. Effects of gold catalysts and thermal evaporation method modifications on the growth process of Zn1-x MgxO nanowires. J. Solid State Chem. 2010, 183, 1733–1739. [Google Scholar] [CrossRef]
- Moghaddam, M.; Pourbaige, M.; Tabar, H.K.; Farhadi, N.; Hosseini, S.M.A. Composition and Antifungal Activity of Peppermint (Mentha piperita) Essential Oil from Iran. J. Essent. Oil Bear. Plants 2013, 506–512. [Google Scholar] [CrossRef]
- Moghaddam, T.B.; Soltani, M.; Karim, M.R. Evaluation of permanent deformation characteristics of unmodified and Polyethylene Terephthalate modified asphalt mixtures using dynamic creep test. Mater. Des. 2014, 53, 317–324. [Google Scholar] [CrossRef]
- Li, J.M.; Zhang, Y.J. GIS based information model for assessment of geothermal potential: Case study of Tengchong county, southwest China. J. Eng. Geol. 2018, 26, 540–550. [Google Scholar] [CrossRef]
- Lachenbruch, A.H. Heat flow in the Basin and Range province and thermal effects of tectonic extension. Pure Appl. Geophys. 1978, 117, 34–50. [Google Scholar] [CrossRef]
- Vlassova, L.; Perezcabello, F.; Nieto, H.; Martín, P.; Riano, D. Assessment of methods for land surface temperature retrieval from Landsat-5 TM images applicable to multiscale tree-grass ecosystem modeling. Remote Sens. 2014, 6, 4345–4368. [Google Scholar] [CrossRef]
- Johnson, L.R. Source mechanisms of induced earthquakes at the Geysers geothermal reservoir. Pure Appl. Geophys. 2014, 171, 1641–1668. [Google Scholar] [CrossRef]
- Mcguire, J.J.; Lohman, R.B.; Catchings, R.D.; Rymer, M.J.; Goldman, M.R. Relationships among seismic velocity, metamorphism, and seismic and aseismic fault slip in the Salton Sea Geothermal Field region. Geophys. Res. Solid Earth 2015, 120, 2600–2615. [Google Scholar] [CrossRef]
- Crespo, E.; Lillo, J.; Oyarzun, R.; Cubas, P.; Leal, M. The Mazarron basin, SE Spain: A study of mineralization processes, evolving magmatic series, and geothermal activity. Int. Geol. Rev. 2013, 55, 1978–1990. [Google Scholar] [CrossRef]
- Kang, S.C.; Xu, Y.W.; You, Q.L.; Flugel, W.A.; Pepin, N.; Yao, T.D. Review of climate and cryospheric change in the Tibetan Plateau. Env. Res. Lett. 2010, 5, 8. [Google Scholar] [CrossRef]
- Yang, D.H. Analysis of Main Engineering Geological Problems in Changdu to Linzhi Section of Sichuan-Tibet Railway. Railw. Stand. Des. 2019, 63, 1622–1627. [Google Scholar] [CrossRef]
- Vlassova, L.; Perezcabello, F.; Mimbrero, M.; Llovería, R.M.; García-Martín, A. Analysis of the relationship between land surface temperature and wildfire severity in a series of landsat images. Remote Sens. 2014, 6, 6136–6162. [Google Scholar] [CrossRef]
- Jiménez-Muñoz, J.C.; Sobrino, J.A. A generalized single-channel method for retrieving land surface temperature from remote sensing data. J. Geophys. Res. Atmos. 2003, 108. [Google Scholar] [CrossRef]
- Becker, F.; Li, Z.L. Temperature-independent spectral indices in thermal infrared bands. Remote Sens. Environ. 1990, 32, 17–33. [Google Scholar] [CrossRef]
- Sobrino, J.; Jiménez-Muñoz, J.C.; Paolini, L. Land surface temperature retrieval from LANDSAT TM 5. Remote Sens. Environ. 2004, 90, 434–440. [Google Scholar] [CrossRef]
- Wan, Z.M.; Li, Z.L. A physics-based algorithm for retrieving land-surface emissivity and temperature from EOS/MODIS data. IEEE Trans. Geosci. Remote Sens. 1997, 35, 980–996. [Google Scholar] [CrossRef]
- Wang, N.; Wu, H.; Nerry, F.; Li, C.R.; Li, Z.L. Temperature and emissivity retrievals from hyperspectral thermal infrared data using linear spectral emissivity constraint. IEEE Trans. Geosci. Remote Sens. 2001, 49, 1291–1303. [Google Scholar] [CrossRef]
- Qin, Z.H.; Zhang, M.H.; Arnon, K. Mono-window Algorithm for Retrieving Land Surface Temperature from Landsat TM6 data. Acta Geogr. Sin. 2001, 456–466. [Google Scholar] [CrossRef]
- Jin, D.D.; Gong, Z.N. Algorithms Comparison of Land Surface Temperature Retrieval from Landsat Series Data: A Case Study in Qiqihar, China. Remote Sens. Technol. Appl. 2018, 33, 830–841. [Google Scholar] [CrossRef]
- Zhao, P.D.; Chi, S.D. Preliminary view on geological anomaly. Earth Sci. J. China Univ. Geosci. 1991, 16, 241–248. [Google Scholar]
- Chi, S.D.; Zhao, P.D. Application of Combined-entropy Anomany of Geological Formations to Delineation of Preferable Ore-finding Area. Geoscience 2000, 423–428. [Google Scholar] [CrossRef]
- Revil, A.; Pezard, P.A. Streaming electrical potential anomaly along faults in geothermal areas. Geophys. Res. Lett. 1998, 25, 3197–3200. [Google Scholar] [CrossRef]
- Zhang, F.W.; Wang, G.L.; Hou, X.W.; Li, J.H.; Li, Y.J. An Analysis of the Formation of Geothermal Resources and the Effects of Groundwater Circulation on the Wall Rock Temperature Field-Taking the Pingdingshan Mining Field as an Example. Acta Geosci. Sin. 2000, 21, 142–146. [Google Scholar]
- Hochstein, M.P.; Hunt, T.M. Seismic, gravity and magnetic studies, Broadlands geothermal field. Geothermics 1970, 2, 333–346. [Google Scholar] [CrossRef]
- Institute of Geography; CAS. Atlas of Qinghai-Tibet Plateau; Science Press: Beijing, China, 2015. [Google Scholar]
- Aydogan, D. Extraction of lineaments from gravity anomaly maps using the gradient calculation: Application to Central Anatolia. Earth Planets Space 2011, 63, 903–913. [Google Scholar] [CrossRef]
- Wang, D.F. Aeromagnetic Series Maps and Specifications of Qinghai-Tibet Plateau and Adjacent Areas; Geological Publishing House: Beijing, China, 2013. [Google Scholar]
- Gutenberg, B.; Richter, C.F. Frequency of earthquakes in California. Bull. Seismol. Soc. Am. 1945, 34, 185–188. [Google Scholar] [CrossRef]
- Bayrak, Y.; Bayrak, E. Regional variations and correlations of Gutenberge-Richter parameters and fractal dimension for the different seismogenic zones in Western Anatolia. J. Asian Earth Sci. 2012, 58, 98–107. [Google Scholar] [CrossRef]
- Tang, G.A.; Yang, X. Experimental Course of Spatial Analysis of ArcGIS; Science Press: Beijing, China, 2004. [Google Scholar]
- Zhao, H.; Song, E.X. Improved Information Value Model and Its Application in the Spatial Prediction of Landslides. J. Civ. Archit. Environ. Eng. 2011, 33, 38–44. [Google Scholar] [CrossRef]
- Zhang, X.M. Hazard Assessment and Zoning Research of Landslide in Shanxi Province Based on GIS; Chang’an University: Xi’an, China, 2019. [Google Scholar]
- Ye, C.F.; Zhang, Y.C.; Xiong, J.N.; Qin, J.X. Hazard Assessment of Mountain Torrent Disaster in Small Watersheds of the Hilly Areas of Hunan Province. J. Geo-Inf. Sci. 2017, 19, 1593–1603. [Google Scholar] [CrossRef]
- Tziritis, E.; Lombardo, L. Estimation of intrinsic aquifer vulnerability with index-overlay and statistical methods: The case of eastern Kopaida, central Greece. Appl. Water Sci. 2016. [Google Scholar] [CrossRef]
- Shannon, C.E.; Weaver, W. The Mathematical Theory of Communication; The University of Illinois Press: Urbana, IL, USA, 1947. [Google Scholar] [CrossRef]
- Tangestani, M.H.; Moore, F. Porphyry copper potential mapping using the weights-of- evidence model in a GIS, northern Shahr-e-Babak, Iran. Aust. J. Earth Sci. 2002, 48, 695–701. [Google Scholar] [CrossRef]
- Lee, S.; Talib, J.A. Probabilistic landslide susceptibility and factor effect analysis. Environ. Geol. 2005, 47, 982–990. [Google Scholar] [CrossRef]
- Cong, W.Q.; Li, T.F. Study on the key problems of landslide and debris flow hazard zoning based on GIS. Earth Sci. Front. 2006, 13, 185–190. [Google Scholar] [CrossRef]
- Xiao, K.Y.; Zhang, X.H.; Chen, Z.H. Comparison of evidence weight method and information quantity method in metallogenic prediction. Calc. Technol. Geophys. Geochem. Explor. 1999, 21, 223–226. [Google Scholar] [CrossRef]
- He, Z.C.; Chi, C.X. Effects of spatial resolution and sampling methods on watershed feature extraction from DEM. J. Glaciol. Geocryol. 2004, 26, 610–616. [Google Scholar] [CrossRef]
- Dahal, R.K.; Hasegawa, S.; Bhandary, N.P.; Poudel, P.P.; Nonomura, A.; Yatabe, R. A replication of landslide hazard mapping at catchment scale. Geomat. Nat. Hazards Risk 2012, 3, 161–192. [Google Scholar] [CrossRef]
- Romero-Calcerrada, R.; Novillo, C.J.; Millington, J.D.A.; Gomez-Jimenez, I. GIS analysis of spatial patterns of human-caused wildfire ignition risk in the SW of Madrid (Central Spain). Landsc. Ecol. 2008, 23, 341–354. [Google Scholar] [CrossRef]






| Impact Factors | Class | ||||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| LST (°C) | −10.00–6.21 | −6.21–0.69 | 0.69–6.83 | 6.83–11.75 | 11.75–16.02 | 16.02–23.54 | 23.54–50.42 |
| Combined entropy of geological formation | 0–10 | 10–20 | 20–40 | 40–50 | 50–60 | 60–80 | 80–100 |
| Buffer distance to fault (km) | 0–2 | 2–4 | 4–6 | 6–8 | 8–10 | 10–12 | >12 |
| Fault density (km/km2) | 0.000–0.019 | 0.019–0.047 | 0.047–0.069 | 0.069–0.092 | 0.092–0.117 | 0.117–0.148 | 0.148–0.266 |
| Buffer distance to river (km) | 0–2 | 2–4 | 4–6 | 6–8 | 8–10 | 10–12 | >12 |
| Magnetic anomaly (nT) | −241–−163 | −163–−115 | −115–−75 | −75–−50 | −50–−26 | −26–8 | 8–100 |
| Bouguer gravity (mgal) | −540–−520 | −520–−480 | −480–−440 | −440–−400 | −400–−340 | −340–−300 | −300–−220 |
| Earthquake peak acceleration (g). | 0.02–0.08 | 0.08–0.14 | 0.14–0.20 | 0.20–0.24 | 0.24–0.30 | 0.30–0.34 | 0.34–0.40 |
| Study Area (km2) | Scale | Grid Size (m) |
|---|---|---|
| ≥100,000 | ≤1:250,000 | ≥100 × 100 |
| 10,000–100,000 | 1:250,000–1:100,000 | ≥50 × 50 |
| 1000–10,000 | 1:100,000–1:50,000 | ≥25 × 25 |
| <10,000 | >1:50,000 | ≥5 × 5 |
| Impact Factors | LST | Combined Entropy | Buffer Distance to Fault | Fault Density | Buffer Distance to River | Magnetic Anomaly | Bouguer Gravity | Earthquake Peak Acceleration |
|---|---|---|---|---|---|---|---|---|
| LST | 1.000 | −0.062 | 0.127 | −0.152 | 0.038 | 0.053 | 0.089 | −0.006 |
| Combined entropy | −0.062 | 1.000 | −0.158 | 0.175 | −0.157 | 0.035 | −0.079 | −0.037 |
| Buffer distance to fault | 0.127 | −0.158 | 1.000 | −0.771 | 0.064 | 0.171 | −0.021 | 0.263 |
| Fault density | −0.152 | 0.175 | −0.771 | 1.000 | −0.085 | −0.160 | −0.031 | −0.246 |
| Buffer distance to river | 0.038 | −0.157 | 0.064 | −0.085 | 1.000 | −0.034 | 0.150 | 0.051 |
| Magnetic anomaly | 0.053 | 0.035 | 0.171 | −0.160 | −0.034 | 1.000 | −0.406 | −0.016 |
| Bouguer gravity | 0.089 | −0.079 | −0.021 | −0.031 | 0.150 | −0.406 | 1.000 | 0.292 |
| Earthquake peak acceleration | −0.006 | −0.037 | 0.263 | −0.246 | 0.051 | −0.016 | 0.292 | 1.000 |
| Impact factors | Class | Points | Grids | Iij | Hi | Wi |
|---|---|---|---|---|---|---|
| LST | 1 | 2 | 7,459,893 | −3.145 | 0.803 | 2.462 |
| 2 | 2 | 6,526,266 | −3.012 | |||
| 3 | 26 | 6,864,561 | −0.497 | |||
| 4 | 55 | 7,272,770 | 0.194 | |||
| 5 | 85 | 6,157,522 | 0.796 | |||
| 6 | 51 | 3,924,683 | 0.736 | |||
| 7 | 28 | 1,781,793 | 0.926 | |||
| Combined entropy of geological formation | 1 | 53 | 21,710,503 | −0.936 | 0.955 | 0.568 |
| 2 | 18 | 2,378,633 | 0.195 | |||
| 3 | 42 | 4,703,793 | 0.360 | |||
| 4 | 26 | 2,538,350 | 0.498 | |||
| 5 | 37 | 2,590,893 | 0.830 | |||
| 6 | 50 | 4,408,954 | 0.599 | |||
| 7 | 23 | 1,656,362 | 0.802 | |||
| Fault density | 1 | 40 | 5,387,518 | 0.176 | 0.932 | 0.847 |
| 2 | 55 | 4,568,425 | 0.659 | |||
| 3 | 34 | 3,905,275 | 0.335 | |||
| 4 | 44 | 3,325,438 | 0.754 | |||
| 5 | 33 | 2,855,477 | 0.618 | |||
| 6 | 30 | 2,452,899 | 0.675 | |||
| 7 | 13 | 17,492,456 | −2.126 | |||
| Buffer distance to river | 1 | 112 | 5,920,266 | 1.111 | 0.869 | 1.647 |
| 2 | 36 | 5,608,909 | 0.030 | |||
| 3 | 22 | 5,273,756 | −0.401 | |||
| 4 | 20 | 4,772,597 | −0.396 | |||
| 5 | 18 | 4,150,553 | −0.362 | |||
| 6 | 13 | 3,479,987 | −0.511 | |||
| 7 | 28 | 10,781,420 | −0.875 | |||
| Magnetic anomaly | 1 | 5 | 1,393,066 | −0.551 | 0.964 | 0.457 |
| 2 | 9 | 2,079,263 | −0.364 | |||
| 3 | 20 | 5,555,534 | −0.548 | |||
| 4 | 70 | 9,336,800 | 0.186 | |||
| 5 | 88 | 11,748,298 | 0.185 | |||
| 6 | 52 | 7,902,464 | 0.055 | |||
| 7 | 5 | 1,972,063 | −0.899 | |||
| Earthquake peak acceleration | 1 | 7 | 4,149,900 | −1.306 | 0.980 | 0.254 |
| 2 | 13 | 6,921,418 | −1.199 | |||
| 3 | 69 | 13,669,294 | −0.210 | |||
| 4 | 83 | 9,371,586 | 0.352 | |||
| 5 | 52 | 3,792,104 | 0.789 | |||
| 6 | 23 | 1,108,662 | 1.203 | |||
| 7 | 2 | 974,524 | −1.110 |
| Impact Factors | Class | Cij | Ci | ||
|---|---|---|---|---|---|
| LST | 1 | −0.346 | 0.198 | −0.544 | 3.547 |
| 2 | −0.312 | 0.170 | −0.482 | ||
| 3 | −0.498 | 0.078 | −0.576 | ||
| 4 | 0.194 | −0.049 | 0.243 | ||
| 5 | 0.896 | −0.350 | 1.246 | ||
| 6 | 1.535 | −0.226 | 1.761 | ||
| 7 | 1.725 | −0.174 | 1.899 | ||
| Combined entropy of geological formation | 1 | −0.924 | 0.529 | −1.453 | 2.203 |
| 2 | 0.195 | −0.014 | 0.208 | ||
| 3 | 0.360 | −0.060 | 0.420 | ||
| 4 | 0.497 | −0.045 | 0.542 | ||
| 5 | 0.830 | −0.094 | 0.924 | ||
| 6 | 0.599 | −0.107 | 0.706 | ||
| 7 | 0.802 | −0.055 | 0.856 | ||
| Fault density | 1 | −1.021 | 0.416 | −1.437 | 3.383 |
| 2 | −0.160 | 0.050 | −0.211 | ||
| 3 | 0.283 | −0.038 | 0.321 | ||
| 4 | 0.586 | −0.091 | 0.677 | ||
| 5 | 0.978 | −0.091 | 1.069 | ||
| 6 | 1.310 | −0.095 | 1.406 | ||
| 7 | 1.515 | −0.042 | 1.557 | ||
| Buffer distance to river | 1 | 1.111 | −0.737 | 1.848 | 1.324 |
| 2 | 0.730 | −0.650 | 1.380 | ||
| 3 | −0.101 | 0.049 | −0.150 | ||
| 4 | −0.096 | 0.043 | −0.140 | ||
| 5 | −0.262 | 0.035 | −0.297 | ||
| 6 | −0.411 | 0.137 | −0.549 | ||
| 7 | −0.574 | 0.195 | −0.768 | ||
| Magnetic anomaly | 1 | −0.251 | 0.015 | −0.266 | 0.862 |
| 2 | −0.164 | 0.017 | −0.181 | ||
| 3 | −0.448 | 0.036 | −0.484 | ||
| 4 | 0.685 | −0.464 | 1.149 | ||
| 5 | 0.707 | −0.397 | 1.104 | ||
| 6 | 0.455 | −0.314 | 0.769 | ||
| 7 | −0.699 | 0.530 | −1.229 | ||
| Earthquake peak acceleration | 1 | −1.443 | 0.089 | −1.532 | 1.183 |
| 2 | −0.556 | 0.128 | −0.684 | ||
| 3 | 0.063 | −0.034 | 0.097 | ||
| 4 | 0.290 | −0.109 | 0.398 | ||
| 5 | 0.576 | −0.185 | 0.761 | ||
| 6 | 0.623 | −0.278 | 0.901 | ||
| 7 | 0.905 | −0.337 | 1.242 |
| Model | Class | |||
|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |
| Index-overlay information model | −1.99–0.00 | 0.00–0.24 | 0.24–0.57 | 0.57–1.32 |
| Weights of entropy information model | −16.21–0.00 | 0.00–6.50 | 6.50–7.21 | 7.21–8.81 |
| Weights of evidence information model | −31.72–0.00 | 0.00–3.84 | 3.84–8.41 | 8.41–18.94 |
| Class | Index-Overlay | Weights of Entropy | Weights of Evidence | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Grids | Points | Index | Grids | Points | Index | Grids | Points | Index | |
| 4 | 1,689,379 | 74 | 0.44% | 2,696,687 | 106 | 0.39% | 1,814,461 | 96 | 0.53% |
| 3 | 3,764,914 | 77 | 0.21% | 5,649,918 | 84 | 0.15% | 4,127,875 | 75 | 0.18% |
| 2 | 4,397,731 | 52 | 0.12% | 5,009,384 | 31 | 0.06% | 5,189,797 | 41 | 0.08% |
| 1 | 29,611,165 | 46 | 0.02% | 26,107,200 | 28 | 0.01% | 28,331,056 | 37 | 0.01% |
| Number | Measurement Date | Coordinate | Altitude (m) | Temperature (°C) |
|---|---|---|---|---|
| 1 | 12 June 2019 | 94°44′19″ E, | 3175 | 30.8–39.7 |
| 29°48′56″ N | ||||
| 2 | 12 June 2019 | 95°02′22″ E, | 2033 | 50.3–64.6 |
| 30°03′54″ N | ||||
| 5 | 9 June 2019 | 100°08′29″ E, | 3971 | 31.4–52.3 |
| 30°02′16″ N | ||||
| 10 | 12 June 2019 | 96°50′44″ E, | 4377 | 19.3–33.2 |
| 30°42′49″ N | ||||
| 11 | 9 June 2019 | 99°20′24″ E, | 3297 | 17.9–23.9 |
| 30°16′55″ N |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, W.; Dong, Q.; Chen, Z.; Feng, T.; Wang, D.; Jiang, L.; Du, S.; Zhang, X.; Meng, D.; Bian, M.; et al. Weighted Information Models for the Quantitative Prediction and Evaluation of the Geothermal Anomaly Area in the Plateau: A Case Study of the Sichuan–Tibet Railway. Remote Sens. 2021, 13, 1606. https://doi.org/10.3390/rs13091606
Zhao W, Dong Q, Chen Z, Feng T, Wang D, Jiang L, Du S, Zhang X, Meng D, Bian M, et al. Weighted Information Models for the Quantitative Prediction and Evaluation of the Geothermal Anomaly Area in the Plateau: A Case Study of the Sichuan–Tibet Railway. Remote Sensing. 2021; 13(9):1606. https://doi.org/10.3390/rs13091606
Chicago/Turabian StyleZhao, Wenbo, Qing Dong, Zhe Chen, Tao Feng, Dong Wang, Liangwen Jiang, Shihui Du, Xiaoyu Zhang, Deli Meng, Min Bian, and et al. 2021. "Weighted Information Models for the Quantitative Prediction and Evaluation of the Geothermal Anomaly Area in the Plateau: A Case Study of the Sichuan–Tibet Railway" Remote Sensing 13, no. 9: 1606. https://doi.org/10.3390/rs13091606
APA StyleZhao, W., Dong, Q., Chen, Z., Feng, T., Wang, D., Jiang, L., Du, S., Zhang, X., Meng, D., Bian, M., & Chen, J. (2021). Weighted Information Models for the Quantitative Prediction and Evaluation of the Geothermal Anomaly Area in the Plateau: A Case Study of the Sichuan–Tibet Railway. Remote Sensing, 13(9), 1606. https://doi.org/10.3390/rs13091606







