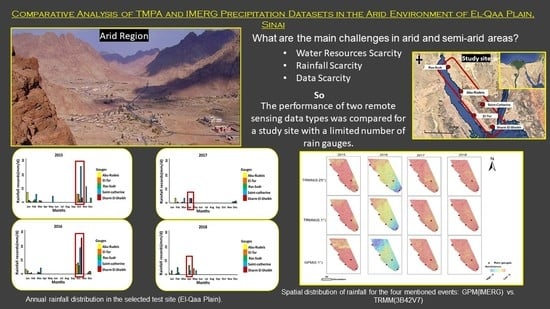
Comparative Analysis of TMPA and IMERG Precipitation Datasets in the Arid Environment of El-Qaa Plain, Sinai
Abstract
1. Introduction
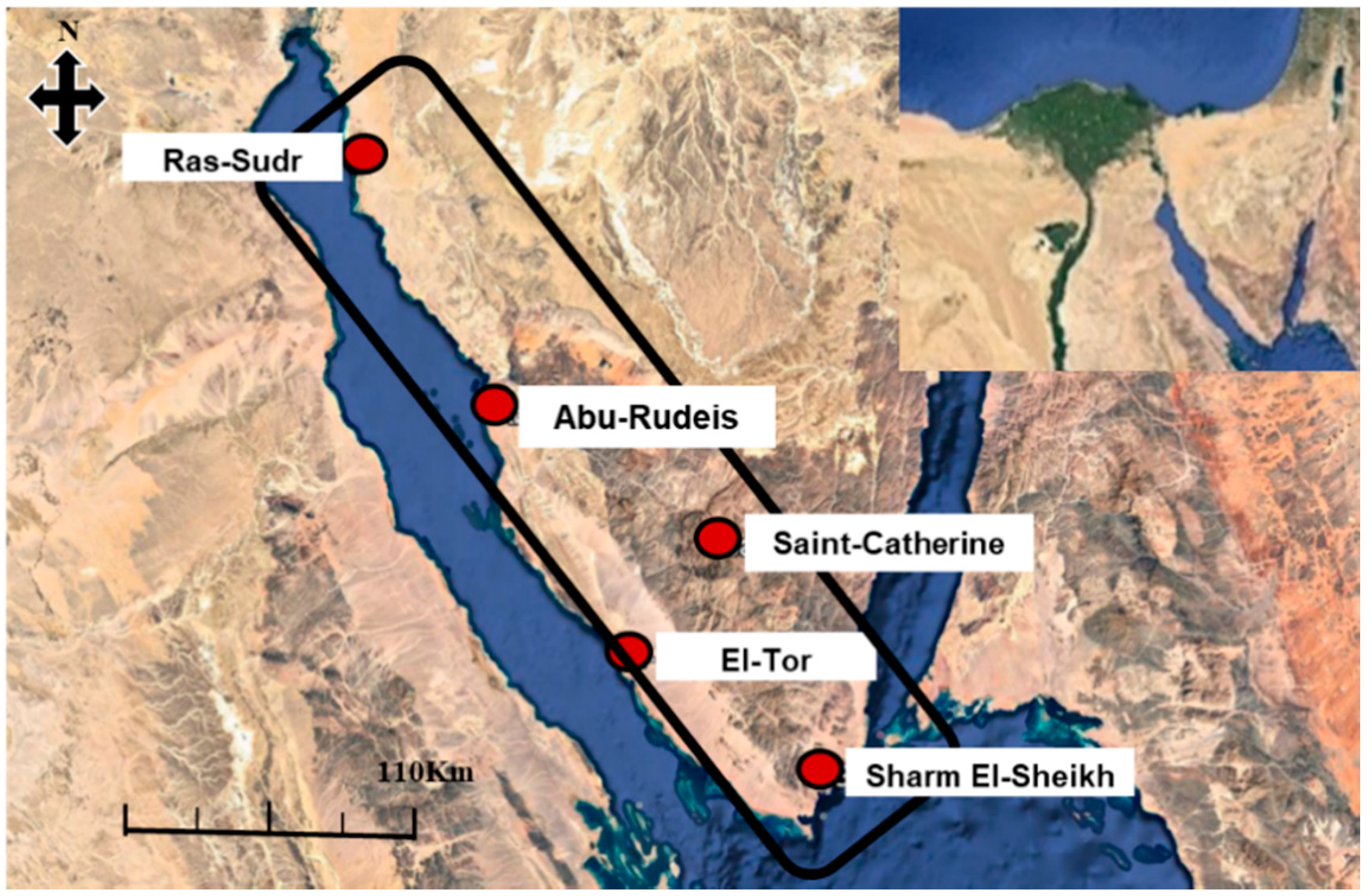
2. Study Area
3. Materials
3.1. TRMM Multi-Satellite Precipitation Analysis (TMPA)
3.2. Integrated Multi-Satellite Retrievals for GPM (IMERG)
3.3. In Situ Rain Gauge Data
4. Methods
Classification of Rainfall Events
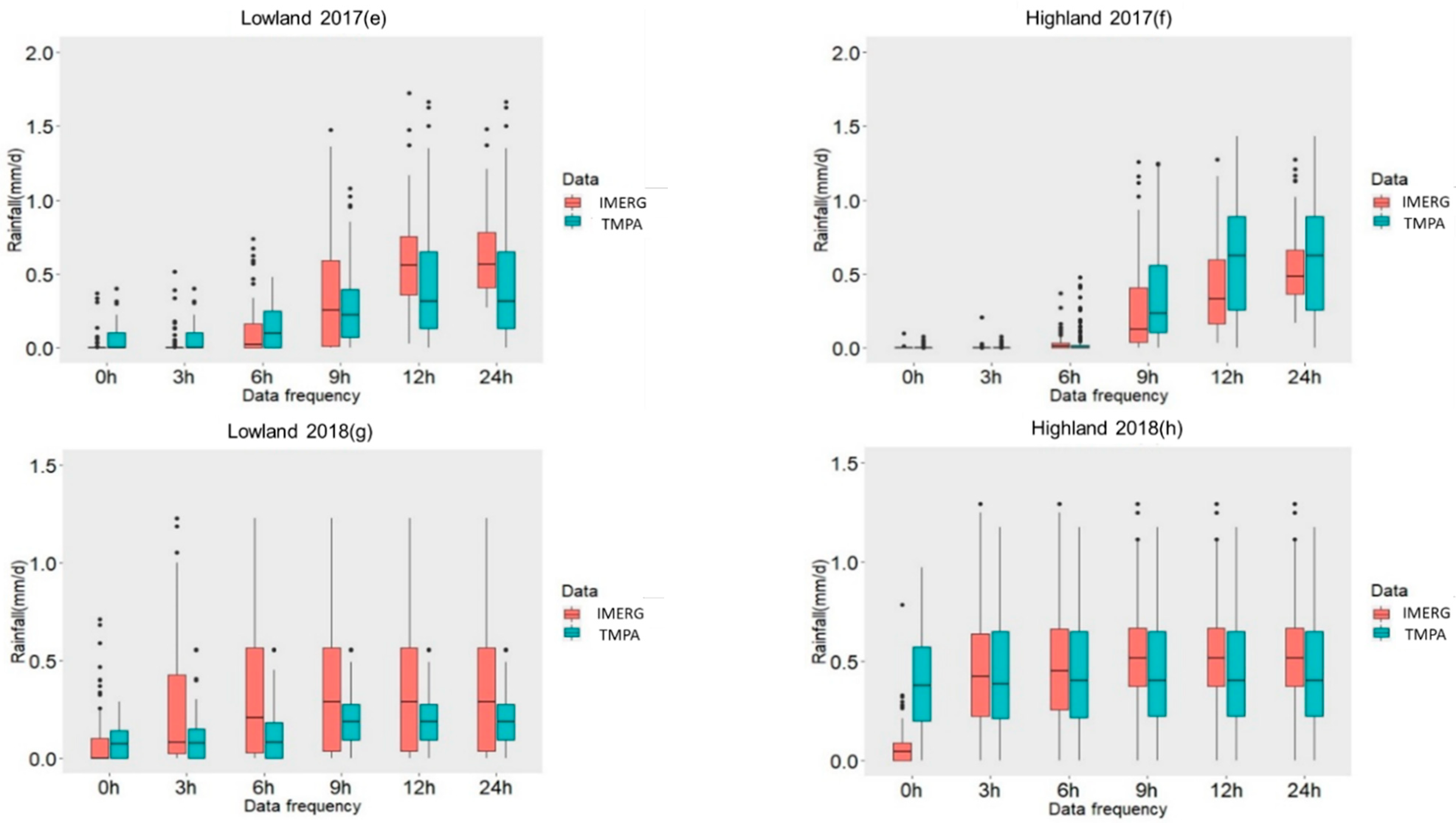
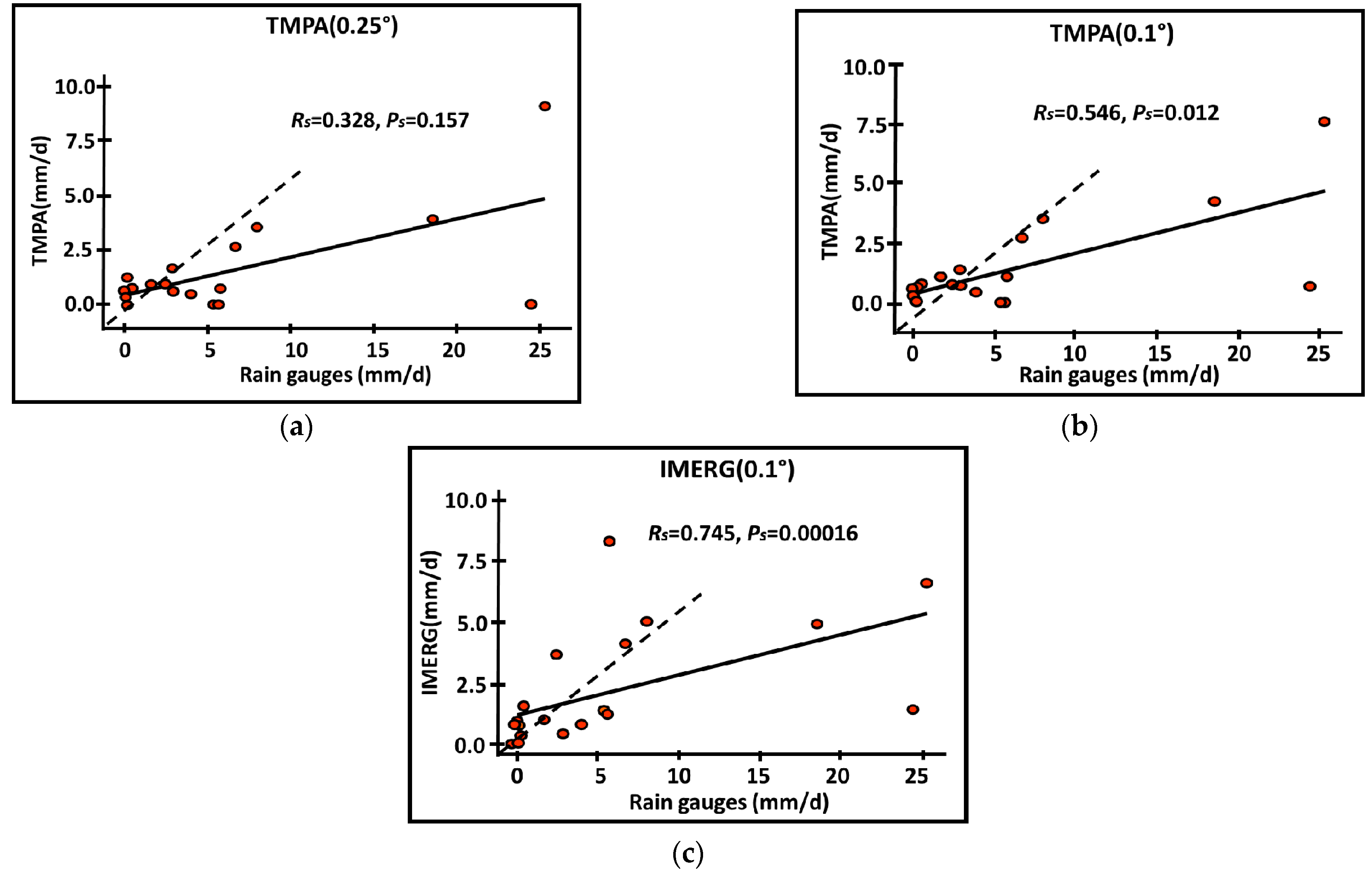
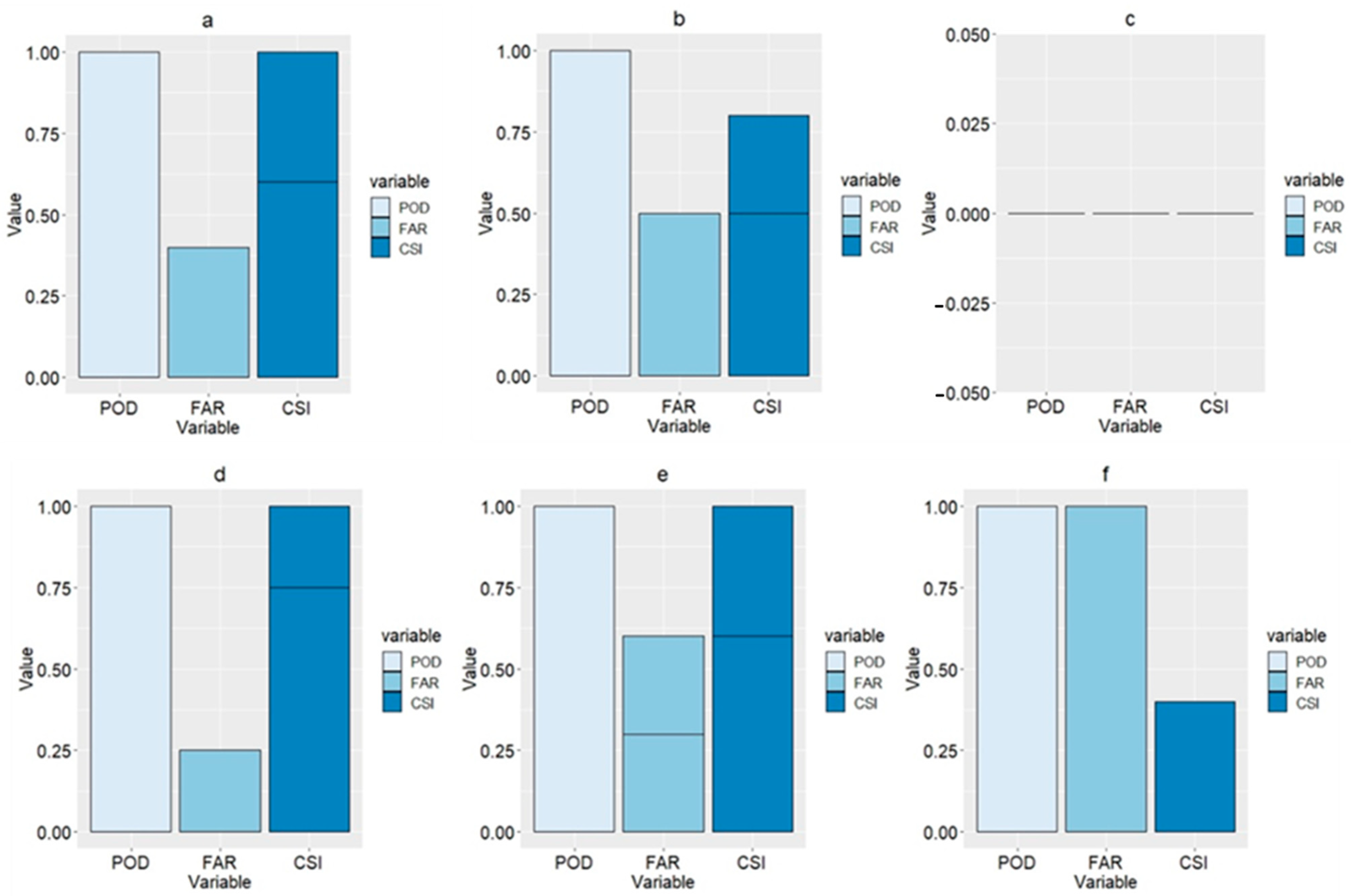
5. Results and Discussion
5.1. TMPA and IMERG
5.2. Satellite-Based Versus In-Situ Data
6. Concluding Remarks
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Statistical Metrics
References
- Ebert, E.E.; Janowiak, J.E.; Kidd, C. Comparison of near-real-time precipitation estimates from satellite observations and numerical models. Bull. Am. Meteorol. Soc. 2007, 88, 47–64. [Google Scholar] [CrossRef]
- Yong, B.; Hong, Y.; Ren, L.-L.; Gourley, J.J.; Huffman, G.J.; Chen, X.; Wang, W.; Khan, S.I. Assessment of evolving TRMM-based multisatellite real-time precipitation estimation methods and their impacts on hydrologic prediction in a high latitude basin. J. Geophys. Res. D Atmos. 2012, 117, D09108. [Google Scholar] [CrossRef]
- Guo, H.; Chen, S.; Bao, A.; Behrangi, A.; Hong, Y.; Ndayisaba, F.; Hu, J.; Stepanian, P.M. Early assessment of integrated multi-satellite retrievals for global precipitation measurement over China. Atmos. Res. 2016, 176–177, 121–133. [Google Scholar] [CrossRef]
- Tang, G.Q.; Ma, Y.Z.; Long, D.; Zhong, L.; Hong, Y. Evaluation of GPM Day-1 IMERG and TMPA version-7 legacy products over mainland China at multiple spatiotemporal scales. J. Hydrol. 2016, 533, 152–167. [Google Scholar] [CrossRef]
- Kidd, C.; Levizzani, V. Status of satellite precipitation retrievals. Hydrol. Earth Syst. Sci. 2011, 15, 1109–1116. [Google Scholar] [CrossRef]
- Kidd, C.; Bauer, P.; Turk, J.; Huffman, G.J.; Joyce, R.; Hsu, K.-L.; Braithwaite, D. Intercomparison of high resolution precipitation products over northwest Europe. J. Hydrometeorol. 2012, 13, 67–83. [Google Scholar] [CrossRef]
- Hou, A.Y.; Kakar, R.K.; Neeck, S.; Azarbarzin, A.A.; Kummerow, C.D.; Kojima, M.; Oki, R.; Nakamura, K.; Iguchi, T. The Global Precipitation Measurement Mission. Bull. Am. Meteorol. Soc. 2014, 95, 701–722. [Google Scholar] [CrossRef]
- Chen, C.; Li, Z.; Song, Y.; Duan, Z.; Mo, K.; Wang, Z.; Chen, Q. Performance of multiple satellite precipitation estimates over a typical arid mountainous area of China: Spatiotemporal patterns and extremes. J. Hydrometeorol. 2020, 21, 533–550. [Google Scholar] [CrossRef]
- Abdulkadir, A.; Wuddivira, M.N.; Abdu, N.; Mudiare, O.J. Use of Horton infiltration model in estimating infiltration characteristics of an alfisol in the Northern Guinea Savanna of Nigeria. J. Agric. Sci. Technol. 2011, A1, 925–931. [Google Scholar] [CrossRef]
- Asoka, A.; Gleeson, T.; Wada, Y.; Mishra, V. Relative contribution of monsoon precipitation and pumping to changes in groundwater storage in India. Nat. Geosci. 2017, 10, 109–117. [Google Scholar] [CrossRef]
- Tapiador, F.J.; Turk, F.J.; Petersen, W.; Hou, A.Y.; García-Ortega, E.; Machado, L.A.; Angelis, C.F.; Salio, P.; Kidd, C.; Huffman, G.J.; et al. Global precipitation measurement: Methods, datasets and applications. Atmos. Res. 2012, 104, 70–97. [Google Scholar] [CrossRef]
- Niu, G.Y.; Yang, Z.-L. Assessing a land surface model’s improvement with GRACE estimates. Geophys. Res. Lett. 2006, 33, L07401. [Google Scholar] [CrossRef]
- Niu, G.Y.; Yang, Z.-L. Effects of frozen soil on snowmelt runoff and soil water storage at a continental scale. J. Hydrometeorol. 2006, 7, 937–952. [Google Scholar] [CrossRef]
- Kiros, G.; Shetty, A.; Nandagiri, L. Analysis of variability and trends in rainfall over northern Ethiopia. Arabian J. Geosci. 2016, 9, 451. [Google Scholar] [CrossRef]
- Marques, M.J.; Bienes, R.; Jiménez, L.; Pérez-Rodríguez, R. Effect of vegetal cover on runoff and soil erosion under light intensity events. Rainfall simulation over USLE plots. Sci. Total Environ. 2007, 378, 161–165. [Google Scholar] [CrossRef]
- Stomph, T.J.; De Ridder, N.; Van de Giesen, N.C. A flume design for the study of slope length effects on runoff. Earth Surface Processes and Landforms. J. Br. Geomorphol. Res. Group 2001, 26, 647–655. [Google Scholar] [CrossRef]
- Kim, K.; Park, J.; Baik, J.; Choi, M. Evaluation of topographical and seasonal feature using GPM IMERG and TRMM 3B42 over Far-East Asia. Atmos. Res. 2017, 187, 95–105. [Google Scholar] [CrossRef]
- Kneis, D.; Chatterjee, C.; Singh, R. Evaluation of TRMM rainfall estimates over a large Indian river basin (Mahanadi). Hydrol. Earth Syst. Sci. 2014, 11, 1169–1201. [Google Scholar] [CrossRef]
- Sun, Q.; Miao, C.; Duan, Q.; Ashouri, H.; Sorooshian, S.; Hsu, K.L. A review of global precipitation data sets: Data sources, estimation, and intercomparisons. Rev. Geophys. 2018, 56, 79–107. [Google Scholar] [CrossRef]
- Das, R.K.; Prakash, N.R. Design of an improvised tipping bucket rain gauge for measurement of rain and snow precipitation. Int. J. Instrum. Technol. 2011, 1, 44–59. [Google Scholar] [CrossRef]
- Poméon, T.; Diekkrüger, B.; Kumar, R. Computationally efficient multivariate calibration and validation of a grid-based hydrologic model in sparsely gauged west African river basins. Water 2018, 10, 1418. [Google Scholar] [CrossRef]
- Khan, A.; Chatterjee, S.; Bisai, D.; Barman, N.K. Analysis of change point in surface temperature time series using cumulative sum chart and bootstrapping for Asansol weather observation station, West Bengal, India. Am. J. Clim. Chang. 2014, 3, 83–94. [Google Scholar] [CrossRef]
- EL-Refai, A.A. Water Resources of Southern Sinai, Egypt. (Geomorphological and Hydrogeological Studies). Ph.D. Thesis, Faculty of Science, University of Cairo, Giza, Egypt, 1992; p. 357. [Google Scholar]
- El-Fakharany, M.A. Geophysical and hydrogeochemical investigations of the Quaternary aquifer at the middle part of El Qaa Plain SW Sinai, Egypt. Egypt. J. Geol. 2016, 47, 1003–1022. [Google Scholar]
- Wahid, A.; Madden, M.; Khalaf, F.; Fathy, I. Geospatial analysis for the determination of hydro-morphological characteristics and assessment of flash flood potentiality in Arid Coastal Plains: A case in Southwestern Sinai, Egypt. Earth Sci. Res. J. 2016, 20, 1–9. [Google Scholar] [CrossRef]
- Sherief, Y. Flash Floods and Their Effects on the Development in El-Qaá Plain Area in South Sinai, Egypt, a Study in Applied Geomorphology Using GIS and Remote Sensing. Ph.D. Thesis, Mainz University, Mainz, Germany, 2008. Available online: https://openscience.ub.uni-mainz.de/handle/20.500.12030/2211 (accessed on 20 October 2020).
- Lonfat, M. Tropical Cyclone Rainfall: An Observational and Numerical Study of the Structure and Governing Physical Processes. Ph.D. Thesis, University of Miami, ProQuest Dissertations Publishing, Miami, FL, USA, 2004; p. 135. [Google Scholar]
- Lau, K.M.; Zhou, Y.P.; Wu, H.T. Have tropical cyclones been feeding more extreme rainfall? J. Geophys. Res. Atmos. 2008, 113. [Google Scholar] [CrossRef]
- Marchok, T.; Rogers, R.; Tuleya, R. Validation schemes for tropical cyclone quantitative precipitation forecasts: Evaluation of operational models for US landfalling cases. Weather Forecast. 2007, 22, 726–746. [Google Scholar] [CrossRef]
- Tuleya, R.E.; De Maria, M.; Kuligowski, R.J. Evaluation of GFDL and simple statistical model rainfall forecasts for US landfalling tropical storms. Weather Forecast. 2007, 22, 56–70. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Wolff, D.B.; Adler, R.F.; Gu, G.; Hong, Y.; Bowman, K.P.; Stocker, E.F. The TRMM multisatellite precipitation analysis (TMPA): Quasi-global, multiyear, combined-sensor precipitation estimates at fine scales. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Braithwaite, D.; Hsu, K.; Joyce, R.; Kidd, C.; Nelkin, E.J.; Sorooshian, S.; Stocker, E.F.; Tan, J.; et al. Integrated multi-satellite retrievals for the Global Precipitation Measurement (GPM) mission (IMERG). In Satellite Precipitation Measurement; Levizzani, V., Kidd, C., Kirschbaum, D., Kummerow, C., Nakamura, K., Turk, F.J., Eds.; Springer Nature: Dordrecht, The Netherlands, 2020; pp. 343–354. ISBN1 978-3-030-24567-2. ISBN2 978-3-030-24568-9. [Google Scholar] [CrossRef]
- Chen, F.R.; Li, X. Evaluation of IMERG and TRMM 3B43 monthly precipitation products over mainland China. Remote Sens. 2016, 8, 472. [Google Scholar] [CrossRef]
- Fang, J.; Yang, W.; Luan, Y.; Du, J.; Lin, A.; Zhao, L. Evaluation of the TRMM 3B42 and GPM IMERG products for extreme precipitation analysis over China. Atmos. Res. 2019, 223, 24–38. [Google Scholar] [CrossRef]
- Wang, S.; Liu, J.; Wang, J.; Qiao, X.; Zhang, J. Evaluation of GPM IMERG V05B and TRMM 3B42V7 Precipitation Products over High Mountainous Tributaries in Lhasa with Dense Rain Gauges. Remote Sens. 2019, 11, 2080. [Google Scholar] [CrossRef]
- Wu, Y.; Zhang, Z.; Huang, Y.; Jin, Q.; Chen, X.; Chang, J. Evaluation of the GPM IMERG v5 and TRMM 3B42 v7 Precipitation Products in the Yangtze River Basin, China. Water 2019, 11, 1459. [Google Scholar] [CrossRef]
- Manz, B.; Páez-Bimos, S.; Horna, N.; Buytaert, W.; Ochoa-Tocachi, B.; Lavado-Casimiro, W.; Willems, B. Comparative ground validation of IMERG and TMPA at variable spatiotemporal scales in the Tropical Andes. J. Hydrometeorol. 2017, 18, 2469–2489. [Google Scholar] [CrossRef]
- Tan, M.L.; Duan, Z. Assessment of GPM and TRMM precipitation products over Singapore. Remote Sens. 2017, 9, 720. [Google Scholar] [CrossRef]
- Xu, R.; Tian, F.; Yang, L.; Hu, H.; Lu, H.; Hou, A. Ground validation of GPM IMERG and TRMM 3B42V7 rainfall products over southern Tibetan Plateau based on a high-density rain gauge network. J. Geophys. Res. D Atmos. 2017, 122, 910–924. [Google Scholar] [CrossRef]
- Zhang, S.; Wand, D.; Qin, Z.; Zheng, Y.; Guo, J. Assessment of the GPM and TRMM precipitation products using the rain gauge network over the Tibetan Plateau. J. Meteorol. Res. 2018, 32, 324–336. [Google Scholar] [CrossRef]
- Anjum, M.N.; Ding, Y.; Shangguan, D.; Ahmad, I.; Ijaz, M.W.; Farid, H.U.; Yagoub, Y.E.; Zaman, M.; Adnan, M. Performance evaluation of latest integrated multi-satellite retrievals for Global Precipitation Measurement (IMERG) over the northern highlands of Pakistan. Atmos. Res. 2018, 205, 134–146. [Google Scholar] [CrossRef]
- Tan, M.L.; Santo, H. Comparison of GPM IMERG, TMPA 3B42 and PERSIANN-CDR satellite precipitation products over Malaysia. Atmos. Res. 2018, 202, 63–76. [Google Scholar] [CrossRef]
- Anjum, M.N.; Ahmad, I.; Ding, Y.; Shangguan, D.; Zaman, M.; Ijaz, M.W.; Sarwar, K.; Han, H.; Yang, M. Assessment of IMERG-V06 precipitation product over different hydro-climatic regimes in the Tianshan mountains, North-Western China. Remote Sens. 2019, 11, 2314. [Google Scholar] [CrossRef]
- Palomino-Ángel, S.; Anaya-Acevedo, J.A.; Botero, B.A. Evaluation of 3B42V7 and IMERG daily-precipitation products for a very high-precipitation region in northwestern South America. Atmos. Res. 2019, 217, 37–48. [Google Scholar] [CrossRef]
- Zhang, Z.; Tian, J.; Huang, Y.; Chen, X.; Chen, S.; Duan, Z. Hydrologic evaluation of TRMM and GPM IMERG satellite-based precipitation in a humid basin of China. Remote Sens. 2019, 11, 431. [Google Scholar] [CrossRef]
- Rashed, M.; Sauck, W.; Soliman, F. Gravity, magnetic, and geoelectric survey on El-Qaa plain, southwest Sinai, Egypt. In Proceedings of the 8th Conference Geology of Sinai for Development, Ismailia, Egypt, 3 December 2007; pp. 15–20. [Google Scholar]
- Sayed, M.A.A.; El-Fakharany, M.A.; Hamed, M.F. Integrated geophysical and hydrogeological studies on the Quaternary aquifer at the middle part of El Qaa plain, SW Sinai, Egypt. Egypt. Geophys. Soc. J. 2004, 2, 135–145. [Google Scholar]
- Sauck, W.; Kehew, A.; Soliman, F.; Smart, L.; Mesbah, M. Basin definition with gravity and resistivity (VES) in the central El Qaa Plain, Sinai, Egypt. Geophys. Res. Abstr. 2005, 7. Available online: https://www.cosis.net/abstracts/EGU05/00066/EGU05-J-00066.pdf (accessed on 20 October 2020).
- Ahmed, M.; Sauck, W.; Sultan, M.; Yan, E.; Soliman, F.; Rashed, M. Geophysical constraints on the hydrogeologic and structural settings of the Gulf of Suez rift-related basins: Case study from the El Qaa Plain, Sinai, Egypt. Surv. Geophys. 2014, 35, 415–430. [Google Scholar] [CrossRef]
- Ghodeif, K.; Gorski, J. Protection of fresh ground water in El-Qaa Quaternary aquifer, Sinai, Egypt. In New Approaches Characterizing Groundwater Flow; Seiler, K.-P., Wohnlich, S., Eds.; Swets & Zeitlinger: Lisse, The Netherlands, 2001; pp. 71–76. ISBN 90-2651-848-X. [Google Scholar]
- Han, S.C.; Yeo, I.Y.; Alsdorf, D.; Bates, P.; Boy, J.P.; Kim, H.; Oki, T.; Rodell, M. Movement of Amazon surface water from time-variable satellite gravity measurements and implications for water cycle parameters in land surface models. Geochem. Geophys. Geosyst. 2010, 11, Q09007. [Google Scholar] [CrossRef]
- Said, R. The Geology of Egypt; Elsevier Publishing, Co.: New York, NY, USA, 1962. [Google Scholar]
- Prat, O.P.; Nelson, B.R. Evaluation of precipitation estimates over CONUS derived from satellite, radar, and rain gauge datasets (2002–2012). Hydrol. Earth Syst. Sci. 2015, 11, 11489–11531. [Google Scholar] [CrossRef]
- Chen, Y.; Huang, J.; Sheng, S.; Mansaray, L.R.; Liu, Z.; Wu, H.; Wang, X. A new downscaling-integration framework for high-resolution monthly precipitation estimates: Combining rain gauge observations, satellite-derived precipitation data and geographical ancillary data. Remote Sens. Environ. 2018, 214, 154–172. [Google Scholar] [CrossRef]
- Kummerow, C.; Barnes, W.; Kozu, T.; Shiue, J.; Simpson, J. The tropical rainfall measuring mission (TRMM) sensor package. J. Atmos. Oceanic Technol. 1998, 15, 809–817. [Google Scholar] [CrossRef]
- Fensterseifer, C.; Allasia, D.G.; Paz, A.R. Assessment of the TRMM 3B42 precipitation product in southern Brazil. J. Am. Water Resourc. Assoc. 2016, 52, 367–375. [Google Scholar] [CrossRef]
- Guo, H.; Bao, A.; Ndayisaba, F.; Liu, T.; Kurban, A.; De Maeyer, P. Systematical evaluation of satellite precipitation estimates over central Asia using an improved error-component procedure. J. Geophys. Res. D Atmos. 2017, 122, 10906–10927. [Google Scholar] [CrossRef]
- Retalis, A.; Katsanos, D.; Tymvios, F.; Michaelides, S. Validation of the first years of GPM operation over Cyprus. Remote Sens. 2018, 10, 1520. [Google Scholar] [CrossRef]
- Skofronick-Jackson, G.; Petersen, W.A.; Berg, W.; Kidd, C.; Stocker, E.F.; Kirschbaum, D.B.; Kakar, R.; Braun, S.A.; Huffman, G.J.; Iguchi, T.; et al. The Global Precipitation Measurement (GPM) mission for science and society. Bull. Am. Meteorol. Soc. 2017, 98, 1679–1695. [Google Scholar] [CrossRef]
- Skofronick-Jackson, G.; Kirschbaum, D.; Petersen, W.; Huffman, G.; Kidd, C.; Stocker, E.; Kakar, R. The Global Precipitation Measurement (GPM) mission’s scientific achievements and societal contributions: Reviewing four years of advanced rain and snow observations. Q. J. Roy. Meteorol. Soc. 2018, 144, 27–48. [Google Scholar] [CrossRef]
- Shapiro, S.S.; Wilk, M.B. An analysis of variance test for normality (complete samples). Biometrika 1965, 52, 591–611. [Google Scholar] [CrossRef]
- Wilcoxon, F. Individual comparisons by ranking methods. Biom. Bull. 1945, 1, 80–83. [Google Scholar] [CrossRef]
- Wu, L.; Xu, Y.; Wang, S. Comparison of TMPA-3B42RT legacy product and the equivalent IMERG products over mainland China. Remote Sens. 2018, 10, 1778. [Google Scholar] [CrossRef]
- Chen, C.; Chen, Q.; Duan, Z.; Zhang, J.; Mo, K.; Li, Z.; Tang, G. Multiscale Comparative Evaluation of the GPM IMERG v5 and TRMM 3B42 v7 Precipitation Products from 2015 to 2017 over a Climate Transition Area of China. Remote Sens. 2018, 10, 944. [Google Scholar] [CrossRef]
- Yuan, F.; Zhang, L.; Win, K.W.W.; Ren, L.; Zhao, C.; Zhu, Y.; Jiang, S.; Liu, Y. Assessment of GPM and TRMM Multi-Satellite Precipitation Products in Streamflow Simulations in a Data-Sparse Mountainous Watershed in Myanmar. Remote Sens. 2017, 9, 302. [Google Scholar] [CrossRef]
- Retalis, A.; Katsanos, D.; Tymvios, T.; Michaelides, S. Comparison of GPM IMERG and TRMM 3B43 Products over Cyprus. Remote Sens. 2020, 12, 3212. [Google Scholar] [CrossRef]


| Product | Temporal Resolution | Spatial Resolution | Spatial Coverage | Time of Image | Official Start | Product Main Data Sources |
|---|---|---|---|---|---|---|
| TMPA | 3 h | 0.25° | 50°N–50°S | Time ± 1.5 h | 1 January 1998 | Geostationary IR (Infra Red), TMI (TRMM Microwave Imager), TCI (Temperature Condition Index), SSMI (Special Sensor Microwave Imager),AMSR-E (Advanced Microwave Scanning Radiometer for Earth Observing System), AMSU (Advanced Microwave Sounding Unit), SSMI/S (The Special Sensor Microwave Imager), MHS (Microwave Humidity Sounder) |
| IMERG | 0.5 h | 0.10° | 60°N–60°S | Start time | 12 March 2014 | Geostationary IR, GMI (Global Monitoring Mode Image), GCI (Ground Controlled Interception), TMI,SSMI/S, AMSR2 (Advanced Microwave Scanning Radiometer 2), MHS, GPCC (Global Precipitation Climatology Centre) |
| Event | Region | Time (Hours) | Wilcoxon p-Value | Spearman Correlation | Spearman p-Value |
|---|---|---|---|---|---|
| pw | Rs | ps | |||
| 2015 | Lowland | 0 | ND [0.1873] | −0.16 | VW [0.1922] |
| 3 | ND [0.5814] | 0.61 | VS [8.919 × 10−8] | ||
| 6 | D [3.325 × 10−6] | 0.39 | VS [0.0015] | ||
| 9 | D [3.189 × 10−15] | 0.28 | S [0.0228] | ||
| 12 | D [1.62 × 10−15] | 0.43 | VS [0.0003] | ||
| 24 | D [2.894 × 10−16] | 0.46 | VS [0.0001] | ||
| Highland | 0 | D [0.0002] | −0.04 | VW [0.6976] | |
| 3 | D [0.0002] | −0.03 | VW [0.7823] | ||
| 6 | D [9.49 × 10−14] | −0.33 | VS [0.0003] | ||
| 9 | D [2.2 × 10−16] | −0.52 | VS [9.125 × 10−10] | ||
| 12 | D [2.2 × 10−16] | −0.44 | VS [3.934 × 10−7] | ||
| 24 | D [2.2 × 10−16] | −0.28 | VS [0.0018] | ||
| 2016 | Lowland | 0 | D [1.722 × 10−7] | 0.68 | VS [3.609 × 10−10] |
| 3 | ND [0.0630] | 0.44 | VS [0.0002] | ||
| 6 | D [7.602 × 10−6] | 0.03 | VW [0.7942] | ||
| 9 | D [1.763 × 10−12] | −0.51 | VS [1.097 × 10−5] | ||
| 12 | D [1.641 × 10−13] | −0.52 | VS [7.236 × 10−6] | ||
| 24 | D [1.641 × 10−13] | −0.52 | VS [7.236 × 10−6] | ||
| Highland | 0 | D [2.2 × 10−16] | 0.87 | VS [2.2 × 10−16] | |
| 3 | ND [0.4478] | 0.91 | VS [2.2 × 10−16] | ||
| 6 | D [1.541 × 10−7] | 0.49 | VS [3.234 × 10−8] | ||
| 9 | D [2.2 × 10−16] | −0.14 | VW [0.1266] | ||
| 12 | D [2.2 × 10−16] | −0.21 | S [0.0244] | ||
| 24 | D [2.2 × 10−16] | −0.1 | S [0.0244] | ||
| 2017 | Lowland | 0 | ND [0.2178] | 0.56 | VS [1.06 × 10−6] |
| 3 | D [0.02497 | 0.38 | VS [0.0020] | ||
| 6 | ND [0.7156] | 0.52 | VS [8.462 × 10−6] | ||
| 9 | ND [0.9647] | −0.27 | W [0.0294] | ||
| 12 | D [0.0004] | 0.14 | VW [0.2550] | ||
| 24 | D [2.039 × 10−6] | 0.23 | VW [0.0671] | ||
| Highland | 0 | D [0.0012] | 0.15 | VW [0.1070] | |
| 3 | ND [0.1134] | 0.01 | VW [0.9563] | ||
| 6 | D [8.091 × 10−6] | −0.02 | VW [0.8219] | ||
| 9 | D [0.0001] | −0.55 | VS [1.234 × 10−10] | ||
| 12 | D [0.0002] | −0.46 | VS [1.133 × 10−7] | ||
| 24 | ND [0.261] | −0.10 | VW [0.2988] | ||
| 2018 | Lowland | 0 | ND [0.0612] | 0.42 | VS [0.0085] |
| 3 | ND [0.0556] | 0.71 | VS [0.0002] | ||
| 6 | D [0.0046] | 0.70 | VS [5.82 × 10−5] | ||
| 9 | ND [0.1368] | 0.64 | VS [0.0007] | ||
| 12 | ND [0.1368] | 0.64 | VS [0.0007] | ||
| 24 | ND [0.1368] | 0.64 | VS [0.0007] | ||
| Highland | 0 | D [2.2 × 10−16] | 0.42 | VS [1.776 × 10−6] | |
| 3 | ND [0.7851] | 0.71 | VS [2.2 × 10−16] | ||
| 6 | ND [0.3289] | 0.70 | VS [2.2 × 10−16] | ||
| 9 | D [0.0329] | 0.64 | VS [2.2 × 10−16] | ||
| 12 | D [0.0329] | 0.64 | VS [2.2 × 10−16] | ||
| 24 | D [0.03293] | 0.64 | VS [2.2 × 10−16] |
| Event (Product) | Metric | ||
|---|---|---|---|
| RMSE (mm) | MAE (mm) | BIAS (%) | |
| 2015 (TMPA 0.25°) | 11.51 | 7.45 | 0.63 |
| 2015 (TMPA 0.1°) | 11.23 | 7.35 | 0.64 |
| 2015 (IMERG 0.1°) | 10.67 | 6.72 | −0.00 |
| 2016 (TMPA 0.25°) | 10.43 | 8.93 | 0.69 |
| 2016 (TMPA 0.1°) | 10.72 | 9.03 | 0.68 |
| 2016 (IMERG 0.1°) | 10.56 | 8.07 | 0.36 |
| 2017 (TMPA 0.25°) | 0.82 | 0.72 | −1.62 |
| 2017 (TMPA 0.1°) | 0.76 | 0.57 | −0.81 |
| 2017 (IMERG 0.1°) | 1.20 | 0.89 | −1.71 |
| 2018 (TMPA 0.25°) | 1.94 | 1.47 | 0.96 |
| 2018 (TMPA 0.1°) | 1.91 | 1.37 | 1.01 |
| 2018 (IMERG 0.1°) | 1.88 | 1.36 | 1.01 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Morsy, M.; Scholten, T.; Michaelides, S.; Borg, E.; Sherief, Y.; Dietrich, P. Comparative Analysis of TMPA and IMERG Precipitation Datasets in the Arid Environment of El-Qaa Plain, Sinai. Remote Sens. 2021, 13, 588. https://doi.org/10.3390/rs13040588
Morsy M, Scholten T, Michaelides S, Borg E, Sherief Y, Dietrich P. Comparative Analysis of TMPA and IMERG Precipitation Datasets in the Arid Environment of El-Qaa Plain, Sinai. Remote Sensing. 2021; 13(4):588. https://doi.org/10.3390/rs13040588
Chicago/Turabian StyleMorsy, Mona, Thomas Scholten, Silas Michaelides, Erik Borg, Youssef Sherief, and Peter Dietrich. 2021. "Comparative Analysis of TMPA and IMERG Precipitation Datasets in the Arid Environment of El-Qaa Plain, Sinai" Remote Sensing 13, no. 4: 588. https://doi.org/10.3390/rs13040588
APA StyleMorsy, M., Scholten, T., Michaelides, S., Borg, E., Sherief, Y., & Dietrich, P. (2021). Comparative Analysis of TMPA and IMERG Precipitation Datasets in the Arid Environment of El-Qaa Plain, Sinai. Remote Sensing, 13(4), 588. https://doi.org/10.3390/rs13040588