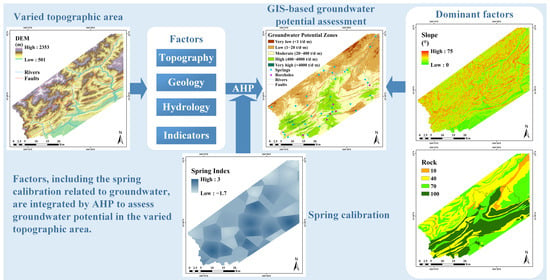
GIS-Based Groundwater Potential Assessment in Varied Topographic Areas of Mianyang City, Southwestern China, Using AHP
Abstract
1. Introduction
2. Materials and Methods
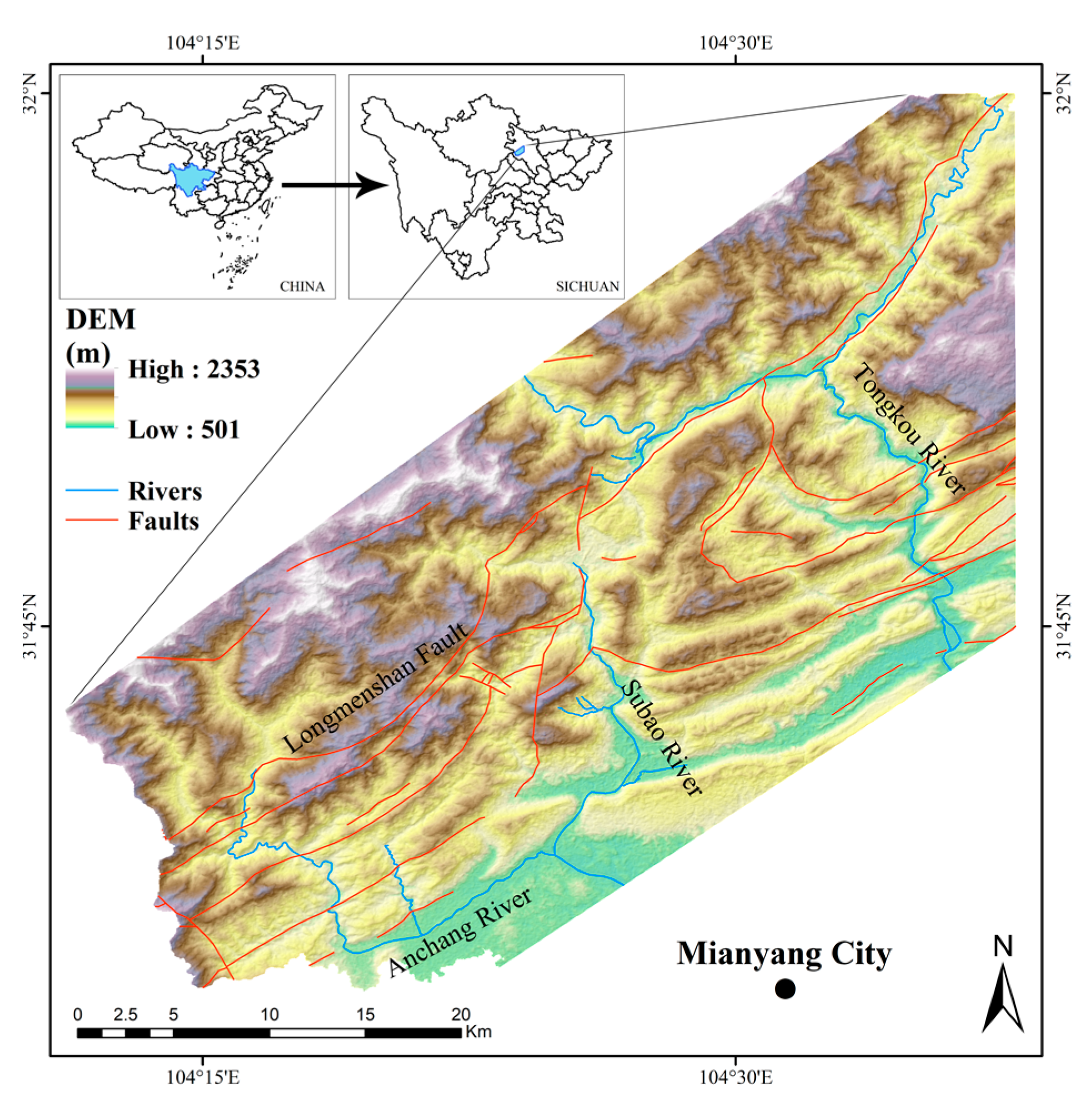
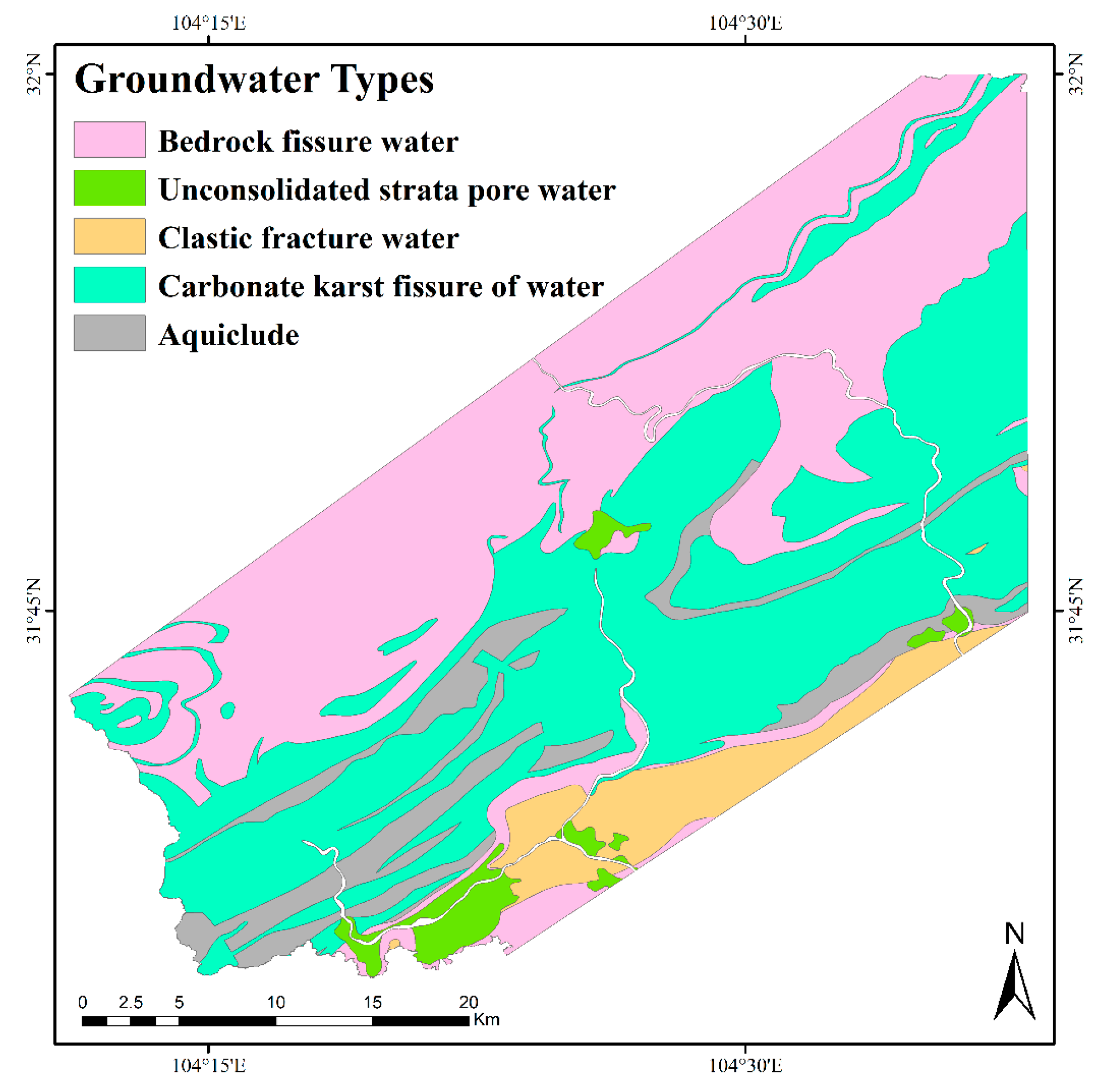
2.1. Study Area
2.2. Evaluation Method
2.2.1. Weighting Method and Overlay Analysis
2.2.2. Validation
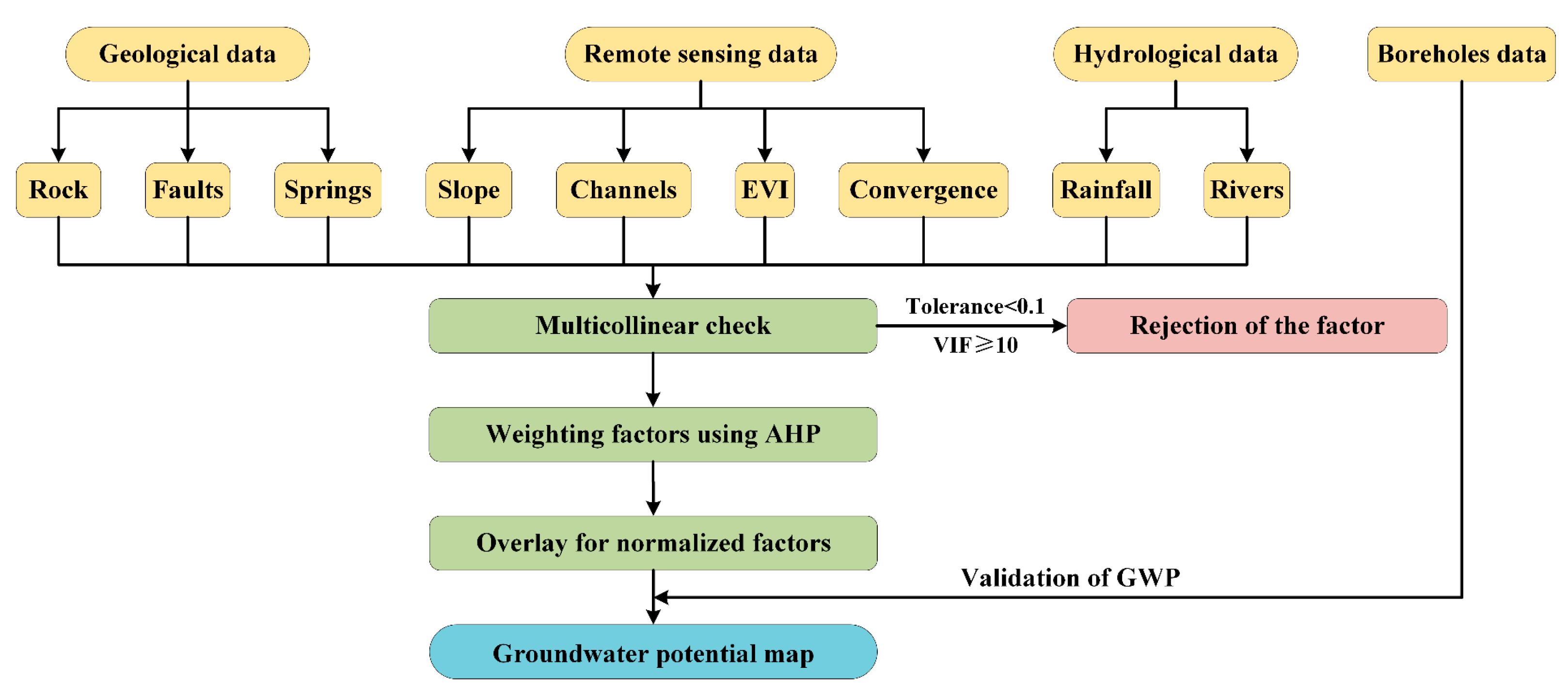
2.3. Data
2.3.1. Data Description
2.3.2. Factor Analysis
3. Results
3.1. Multicollinear Analysis
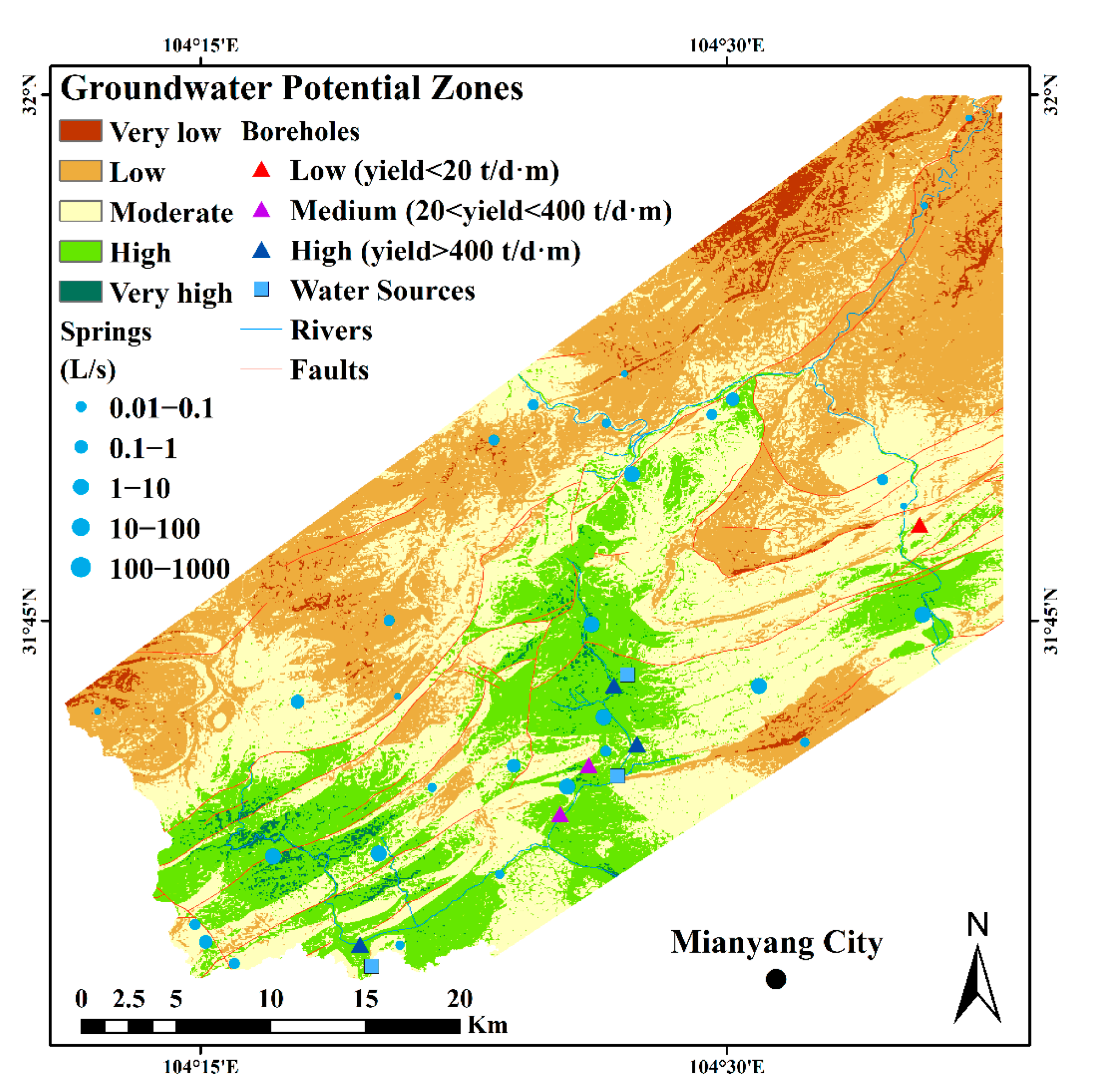
3.2. Groundwater Potential Map
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Stratum | Abbreviation | Description |
|---|---|---|
| Quaternary Holocene modern fluvial alluvium | Sand and gravel. | |
| Quaternary Holocene floodplain terrace | Clayey sand and sandy pebble alluvium. | |
| Quaternary Holocene deluvial and alluvial deposits | Deluvial and alluvial deposits. | |
| Quaternary Middle Pleistocene Ya’an formation | Alluvium and diluvium of clay and gravel pebbles. | |
| Lianhuakou formation of Upper Jurassic | Deposition of conglomerate, sandstone, and mudstone. The bottom is often a very thick gravel layer. | |
| Suining formation of Middle Jurassic | Mudstone, argillaceous siltstone, sandstone, marl, and conglomerate. | |
| Shaximiao formation of Middle Jurassic | ||
| Qianfoyan formation of Middle Jurassic | ||
| Lower part of Xujiahe formation of Upper Triassic | Sandstone, siltstone, and shale. | |
| Tianjingshan formation of Middle Triassic | The upper limestone is intercalated with dolomitic limestone and calcareous dolomite, and the lower dolomite is intercalated with limestone, dolomitic limestone, and argillaceous dolomite. | |
| Jialingjiang formation and Leikoupo formation of Middle Triassic | ||
| Feixianguan formation and Tongjiezi formation of Lower Triassic | The upper part is shale and argillaceous limestone; the lower part is interbedded with mudstone and siltstone; the bottom is limestone. The middle and upper parts are argillaceous strata. | |
| Upper Permian | Limestone intercalated with carbonaceous shale and calcareous shale. | |
| Lower Permian | ||
| Huanglong group and Chuanshan group of Upper and Middle Carboniferous | Limestone, intercalated with shale and iron sandstone at the lower part. | |
| Zongchanggou group of Lower Carboniferous | ||
| Tangwangzhai group of Upper Devonian | Dolomite intercalated with limestone and dolomitic limestone. | |
| Guanwushan formation, Baishipu group, Middle Devonian | Limestone, sandy limestone, and sand shale. | |
| Yangmaba formation, Baishipu group, Middle Devonian | ||
| Ganxi formation, Baishipu group, Middle Devonian | Upper siltstone, quartz sandstone, shale intercalated with argillaceous limestone and limestone. The lower quartzite sandstone is intercalated with siltstone and carbonaceous shale. | |
| Pingyipu group of Lower Devonian | ||
| The first part of the third subgroup, Maoxian group, Upper and Middle Silurian | Sericite phyllite, sandstone, slate with limestone. | |
| The second subgroup of Maoxian group, Upper and Middle Silurian | Sandy limestone, limestone, phyllite, sandstone. | |
| The first subgroup of Maoxian group, Upper and Middle Silurian | Shale intercalated with limestone and phyllite. | |
| Luojiaping group and Shamao group of Upper and Middle Silurian system | Shale mixed with sandstone and limestone. | |
| Longmaxi group of Lower Silurian | Carbonaceous slate and siliceous rock. | |
| Baota formation of Middle Ordovician | Marl, argillaceous limestone, limestone. | |
| Qingping formation of Lower Cambrian | Siltstone, siliceous rock, phosphorous marl, and phosphorous limestone. | |
| Qiujiahe formation of Upper Sinian | Shale, siliceous rock, dolomite, and limestone. | |
| Diabase dyke | ||
| Unexplored strata at rivers or lakes | unknown |
References
- Watto, M.A. The Economics of Groundwater Irrigation in the Indus Basin, Pakistan: Tube-Well Adoption, Technical and Ir-rigation Water Efficiency and Optimal Allocation. Ph.D. Thesis, University of Western Australia, Perth, Australia, 2015. [Google Scholar]
- Oke, S.A.; Fourie, F. Guidelines to groundwater vulnerability mapping for Sub-Saharan Africa. Groundw. Sustain. Dev. 2017, 5, 168–177. [Google Scholar] [CrossRef]
- Wang, Z.; Yi, F.C. AHP-based evaluation of occurrence easiness of geological disasters in Mianyang City. J. Nat. Disasters 2009, 18, 14–23. [Google Scholar] [CrossRef]
- Vadiati, M.; Asghari-Moghaddam, A.; Nakhaei, M.; Adamowski, J.; Akbarzadeh, A. A fuzzy-logic based decision-making approach for identification of groundwater quality based on groundwater quality indices. J. Environ. Manag. 2016, 184, 255–270. [Google Scholar] [CrossRef]
- Lan, Y.; Jin, M.; Yan, C.; Zou, Y. Schemes of groundwater exploitation for emergency water supply and their environmental impacts on Jiujiang City, China. Environ. Earth Sci. 2014, 73, 2365–2376. [Google Scholar] [CrossRef]
- Naghibi, S.A.; Moghaddam, D.D.; Kalantar, B.; Pradhan, B.; Kisi, O. A comparative assessment of GIS-based data mining models and a novel ensemble model in groundwater well potential mapping. J. Hydrol. 2017, 548, 471–483. [Google Scholar] [CrossRef]
- Sichuan Hydrology and Water Resources Survey Bureau. Water Resources Bulletin of Sichuan Province, China; Sichuan Provincial Water Resources Department: Sichuan, China, 2019. [Google Scholar]
- Russoniello, C.J.; Michael, H.A.; Fernandez, C.; Andres, A.S.; He, C.; Madsen, J.A. Investigation of Submarine Groundwater Discharge at Holts Landing State Park, Delaware: Hydrogeologic Framework, Groundwater Level and Salinity Observations; Delaware Geological Survey, University of Delaware: Newark, DE, USA, 2017. [Google Scholar]
- Helaly, A.S. Assessment of groundwater potentiality using geophysical techniques in Wadi Allaqi basin, Eastern Desert, Egypt—Case study. NRIAG J. Astron. Geophys. 2017, 6, 408–421. [Google Scholar] [CrossRef]
- Moss, R.; Moss, G.E. Handbook of Ground Water Development; Wiley-Interscience: New York, NY, USA, 1990. [Google Scholar]
- Patra, S.; Mishra, P.; Mahapatra, S.C. Delineation of groundwater potential zone for sustainable development: A case study from Ganga Alluvial Plain covering Hooghly district of India using remote sensing, geographic information system and analytic hierarchy process. J. Clean. Prod. 2018, 172, 2485–2502. [Google Scholar] [CrossRef]
- Nampak, H.; Pradhan, B.; Manap, M.A. Application of GIS based data driven evidential belief function model to predict groundwater potential zonation. J. Hydrol. 2014, 513, 283–300. [Google Scholar] [CrossRef]
- Lee, S.; Lee, C.-W.; Kim, J.-C. Groundwater productivity potential mapping using logistic regression and boosted tree models: The case of Okcheon City in Korea. Arab. J. Geosci. 2019, 305–307. [Google Scholar] [CrossRef]
- Park, S.-H.; Jung, H.-S.; Choi, J.; Jeon, S. A quantitative method to evaluate the performance of topographic correction models used to improve land cover identification. Adv. Space Res. 2017, 60, 1488–1503. [Google Scholar] [CrossRef]
- Baek, W.-K.; Jung, H.-S.; Jo, M.-J.; Lee, W.-J.; Zhang, L. Ground subsidence observation of solid waste landfill park using multi-temporal radar interferometry. Int. J. Urban Sci. 2019, 23, 406–421. [Google Scholar] [CrossRef]
- Kim, J.-C.; Kim, D.-H.; Park, S.-H.; Jung, H.-S.; Shin, H.-S. Application of Landsat images to Snow Cover Changes by volcanic activities at Mt. Villarrica and Mt. Llaima, Chile. Korean J. Remote. Sens. 2014, 30, 341–350. [Google Scholar] [CrossRef][Green Version]
- Tweed, S.O.; Leblanc, M.; Webb, J.; Lubczynski, M.W. Remote sensing and GIS for mapping groundwater recharge and discharge areas in salinity prone catchments, southeastern Australia. Hydrogeol. J. 2006, 15, 75–96. [Google Scholar] [CrossRef]
- Aluko, O.E.; Igwe, O. An integrated geomatics approach to groundwater potential delineation in the Akoko-Edo Area, Nigeria. Environ. Earth Sci. 2017, 76, 240. [Google Scholar] [CrossRef]
- Goodchild, M.F. Geographic information systems. In Encyclopedia of Theoretical Ecology; University of California Press: Oakland, CA, USA, 2012; pp. 341–345. [Google Scholar] [CrossRef]
- Elfadaly, A.; Attia, W.; Lasaponara, R. Monitoring the environmental risks around Medinet Habu and Ramesseum Temple at West Luxor, Egypt, using remote sensing and GIS techniques. J. Archaeol. Method Theory 2017, 25, 587–610. [Google Scholar] [CrossRef]
- Elmahdy, S.I.; Mohamed, M.M. Automatic detection of near surface geological and hydrological features and investigating their influence on groundwater accumulation and salinity in southwest Egypt using remote sensing and GIS. Geocarto Int. 2014, 30, 1–13. [Google Scholar] [CrossRef]
- Das, N.; Mukhopadhyay, S. Application of multi-criteria decision making technique for the assessment of groundwater potential zones: A study on Birbhum district, West Bengal, India. Environ. Dev. Sustain. 2018, 22, 931–955. [Google Scholar] [CrossRef]
- Anbarasu, S.; Brindha, K.; Elango, L. Multi-influencing factor method for delineation of groundwater potential zones using remote sensing and GIS techniques in the western part of Perambalur district, southern India. Earth Sci. Inform. 2019, 13, 317–332. [Google Scholar] [CrossRef]
- Lee, S.; Hyun, Y.; Lee, M.-J. Groundwater potential mapping using data mining models of big data analysis in Goyang-si, South Korea. Sustainability 2019, 11, 1678. [Google Scholar] [CrossRef]
- Al-Abadi, A.M. Modeling of groundwater productivity in northeastern Wasit Governorate, Iraq using frequency ratio and Shannon’s entropy models. Appl. Water Sci. 2017, 7, 699–716. [Google Scholar] [CrossRef]
- Rahmati, O.; Pourghasemi, H.R.; Melesse, A.M. Application of GIS-based data driven random forest and maximum entropy models for groundwater potential mapping: A case study at Mehran Region, Iran. Catena 2016, 137, 360–372. [Google Scholar] [CrossRef]
- Golkarian, A.; Naghibi, S.A.; Kalantar, B.; Pradhan, B. Groundwater potential mapping using C5.0, random forest, and multivariate adaptive regression spline models in GIS. Environ. Monit. Assess. 2018, 190, 149. [Google Scholar] [CrossRef] [PubMed]
- Park, S.; Hamm, S.-Y.; Jeon, H.-T.; Kim, J. Evaluation of logistic regression and multivariate adaptive regression spline models for groundwater potential mapping using R and GIS. Sustainability 2017, 9, 1157. [Google Scholar] [CrossRef]
- Kim, J.-C.; Jung, H.-S.; Lee, S. Spatial mapping of the groundwater potential of the geum river basin using ensemble models based on remote sensing images. Remote Sens. 2019, 11, 2285. [Google Scholar] [CrossRef]
- Panahi, M.; Sadhasivam, N.; Pourghasemi, H.R.; Rezaie, F.; Lee, S. Spatial prediction of groundwater potential mapping based on convolutional neural network (CNN) and support vector regression (SVR). J. Hydrol. 2020, 588, 125033. [Google Scholar] [CrossRef]
- Pradhan, A.M.S.; Kim, Y.-T.; Shrestha, S.; Huynh, T.-C.; Nguyen, B.-P. Application of deep neural network to capture groundwater potential zone in mountainous terrain, Nepal Himalaya. Environ. Sci. Pollut. Res. 2021, 28, 18501–18517. [Google Scholar] [CrossRef] [PubMed]
- Kord, M.; Moghaddam, A.A. Spatial analysis of Ardabil plain aquifer potable groundwater using fuzzy logic. J. King Saud Univ. Sci. 2014, 26, 129–140. [Google Scholar] [CrossRef]
- Aouragh, M.H.; Essahlaoui, A.; El Ouali, A.; El Hmaidi, A.; Kamel, S. Groundwater potential of Middle Atlas plateaus, Morocco, using fuzzy logic approach, GIS and remote sensing. Geomat. Nat. Hazards Risk 2017, 8, 194–206. [Google Scholar] [CrossRef]
- Das, S. Comparison among influencing factor, frequency ratio, and analytical hierarchy process techniques for groundwater potential zonation in Vaitarna basin, Maharashtra, India. Groundw. Sustain. Dev. 2019, 8, 617–629. [Google Scholar] [CrossRef]
- Quan, H.-C.; Lee, B.-G. GIS-based landslide susceptibility mapping using analytic hierarchy process and artificial neural network in Jeju (Korea). KSCE J. Civ. Eng. 2012, 16, 1258–1266. [Google Scholar] [CrossRef]
- Lu, Z.; Deng, Z.; Wang, D.; Zhao, H.; Wang, G.; Xu, H. Overview of the research progress of groundwater resources assessment technology based on remote sensing. Geol. Surv. China 2021, 114–124. [Google Scholar] [CrossRef]
- Saaty, T.L. Decision making—The analytic hierarchy and network processes (AHP/ANP). J. Syst. Sci. Syst. Eng. 2004, 13, 1–35. [Google Scholar] [CrossRef]
- Brunelli, M. Introduction to the Analytic Hierarchy Process; Springer: Singapore, 2015. [Google Scholar]
- Saaty, R. The analytic hierarchy process—What it is and how it is used. Math. Model. 1987, 9, 161–176. [Google Scholar] [CrossRef]
- Mu, E.; Pereyra-Rojas, M. Understanding the analytic hierarchy process. In Practical Decision Making; Springer: Cham, Switzerland, 2017; pp. 7–22. [Google Scholar] [CrossRef]
- Murmu, P.; Kumar, M.; Lal, D.; Sonker, I.; Singh, S.K. Delineation of groundwater potential zones using geospatial techniques and analytical hierarchy process in Dumka district, Jharkhand, India. Groundw. Sustain. Dev. 2019, 9, 100239. [Google Scholar] [CrossRef]
- Kumar, V.A.; Mondal, N.C.; Ahmed, S. Identification of groundwater potential zones using RS, GIS and AHP techniques: A case study in a part of Deccan Volcanic Province (DVP), Maharashtra, India. J. Indian Soc. Remote Sens. 2020, 48, 497–511. [Google Scholar] [CrossRef]
- Andualem, T.G.; Demeke, G.G. Groundwater potential assessment using GIS and remote sensing: A case study of Guna tana landscape, upper blue Nile Basin, Ethiopia. J. Hydrol. Reg. Stud. 2019, 24, 100610. [Google Scholar] [CrossRef]
- Dar, T.; Rai, N.; Bhat, A. Delineation of potential groundwater recharge zones using analytical hierarchy process (AHP). Geol. Ecol. Landsc. 2020, 1–16. [Google Scholar] [CrossRef]
- Lee, S.; Song, K.-Y.; Kim, Y.; Park, I. Regional groundwater productivity potential mapping using a geographic information system (GIS) based artificial neural network model. Hydrogeol. J. 2012, 20, 1511–1527. [Google Scholar] [CrossRef]
- Pinto, D.; Shrestha, S.; Babel, M.S.; Ninsawat, S. Delineation of groundwater potential zones in the Comoro watershed, Timor Leste using GIS, remote sensing and analytic hierarchy process (AHP) technique. Appl. Water Sci. 2017, 7, 503–519. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, X.; Hua, Q.; Su, L.; Feng, C.; Qiu, Y.; Liang, C.; Su, J.; Gu, Y.; Jin, Z. Segmentation characteristics of the Longmenshan fault—Constrained from dense focal mechanism data. Chin. J. Geophys. 2021, 64, 1181–1205. [Google Scholar]
- Mu, H.; Chen, H.; Zhang, Z.; Zhang, B. China national digital hydrogeological map (At 1:200,000 Scale) spatial database. Geol. China 2021, 48, 124–138. [Google Scholar] [CrossRef]
- Ishizaka, A.; Nemery, P. Multi-Criteria Decision Analysis: Methods and Software; Wiley: Hoboken, NJ, USA, 2013. [Google Scholar]
- Kaur, L.; Rishi, M.S.; Singh, G.; Thakur, S.N. Groundwater potential assessment of an alluvial aquifer in Yamuna sub-basin (Panipat region) using remote sensing and GIS techniques in conjunction with analytical hierarchy process (AHP) and catastrophe theory (CT). Ecol. Indic. 2020, 110, 105850. [Google Scholar] [CrossRef]
- Arshad, A.; Zhang, Z.; Zhang, W.; Dilawar, A. Mapping favorable groundwater potential recharge zones using a GIS-based analytical hierarchical process and probability frequency ratio model: A case study from an agro-urban region of Pakistan. Geosci. Front. 2020, 11, 1805–1819. [Google Scholar] [CrossRef]
- Mukherjee, I.; Singh, U. Delineation of groundwater potential zones in a drought-prone semi-arid region of east India using GIS and analytical hierarchical process techniques. Catena 2020, 194, 104681. [Google Scholar] [CrossRef]
- Saha, S. Groundwater potential mapping using analytical hierarchical process: A study on Md. Bazar Block of Birbhum District, West Bengal. Spat. Inf. Res. 2017, 25, 615–626. [Google Scholar] [CrossRef]
- Tamura, R.; Kobayashi, K.; Takano, Y.; Miyashiro, R.; Nakata, K.; Matsui, T. Mixed integer quadratic optimization formulations for eliminating multicollinearity based on variance inflation factor. J. Glob. Optim. 2018, 73, 431–446. [Google Scholar] [CrossRef]
- Dormann, C.F.; Elith, J.; Bacher, S.; Buchmann, C.; Carl, G.; Carré, G.; Marquéz, J.R.G.; Gruber, B.; Lafourcade, B.; Leitão, P.J.; et al. Collinearity: A review of methods to deal with it and a simulation study evaluating their performance. Ecography 2013, 36, 27–46. [Google Scholar] [CrossRef]
- Li, C.; Wang, X.; He, C.; Wu, X.; Kong, Z.; Li, X. China national digital geological map (Public Version at 1:200,000 Scale) spatial database. Geol. China 2019, 46, 1–10. [Google Scholar] [CrossRef]
- Geospatial Data Cloud. Available online: www.gscloud.cn (accessed on 3 March 2021).
- Earthdata. Available online: Search.earthdata.nasa.gov/search (accessed on 3 March 2021).
- GSMaP Global Satellite Mapping of Precipitation. Available online: Sharaku.eorc.jaxa.jp/GSMaP/index.htm (accessed on 6 May 2021).
- OpenStreetMap. Available online: Download.geofabrik.de (accessed on 3 May 2021).
- Oikonomidis, D.; Dimogianni, S.; Kazakis, N.; Voudouris, K. A GIS/Remote Sensing-based methodology for groundwater potentiality assessment in Tirnavos area, Greece. J. Hydrol. 2015, 525, 197–208. [Google Scholar] [CrossRef]
- Shao, Z.; Huq, E.; Cai, B.; Altan, O.; Li, Y. Integrated remote sensing and GIS approach using Fuzzy-AHP to delineate and identify groundwater potential zones in semi-arid Shanxi Province, China. Environ. Model. Softw. 2020, 134, 104868. [Google Scholar] [CrossRef]
- Serele, C.; Pérez-Hoyos, A.; Kayitakire, F. Mapping of groundwater potential zones in the drought-prone areas of south Madagascar using geospatial techniques. Geosci. Front. 2020, 11, 1403–1413. [Google Scholar] [CrossRef]
- Lee, S.; Hyun, Y.; Lee, S.; Lee, M.-J. Groundwater potential mapping using remote sensing and GIS-based machine learning techniques. Remote Sens. 2020, 12, 1200. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, H.; Ren, C.; Nan, Z.; Wei, X.; Li, C. A cross-reconstruction method for step-changed runoff series to implement frequency analysis under changing environment. Int. J. Environ. Res. Public Health 2019, 16, 4345. [Google Scholar] [CrossRef]
- Naghibi, S.A.; Hashemi, H.; Berndtsson, R.; Lee, S. Application of extreme gradient boosting and parallel random forest algorithms for assessing groundwater spring potential using DEM-derived factors. J. Hydrol. 2020, 589, 125197. [Google Scholar] [CrossRef]
- Conoscenti, C.; Ciaccio, M.; Caraballo-Arias, N.A.; Gómez-Gutiérrez, A.; Rotigliano, E.; Agnesi, V. Assessment of susceptibility to earth-flow landslide using logistic regression and multivariate adaptive regression splines: A case of the Belice River basin (western Sicily, Italy). Geomorphology 2015, 242, 49–64. [Google Scholar] [CrossRef]
- Conrad, O.; Bechtel, B.; Bock, M.; Dietrich, H.; Fischer, E.; Gerlitz, L.; Wehberg, J.; Wichmann, V.; Böhner, J. System for automated geoscientific analyses (SAGA) v. 2.1.4. Geosci. Model. Dev. 2015, 8, 1991–2007. [Google Scholar] [CrossRef]
- Villeneuve, S.; Cook, P.; Shanafield, M.; Wood, C.; White, N. Groundwater recharge via infiltration through an ephemeral riverbed, central Australia. J. Arid. Environ. 2015, 117, 47–58. [Google Scholar] [CrossRef]
- Rahmati, O.; Melesse, A.M. Application of Dempster–Shafer theory, spatial analysis and remote sensing for groundwater potentiality and nitrate pollution analysis in the semi-arid region of Khuzestan, Iran. Sci. Total Environ. 2016, 568, 1110–1123. [Google Scholar] [CrossRef]
- Horton, R.E. Drainage-basin characteristics. Trans. Am. Geophys. Union 1932, 13, 350–361. [Google Scholar] [CrossRef]
- Zhong, R.; Wang, P.; Mao, G.; Chen, A.; Liu, J. Spatiotemporal variation of enhanced vegetation index in the Amazon Basin and its response to climate change. Phys. Chem. Earth Parts ABC 2021, 123, 103024. [Google Scholar] [CrossRef]
- Al-Djazouli, M.O.; Elmorabiti, K.; Rahimi, A.; Amellah, O.; Fadil, O.A.M. Delineating of groundwater potential zones based on remote sensing, GIS and analytical hierarchical process: A case of Waddai, eastern Chad. Geojournal 2021, 86, 1881–1894. [Google Scholar] [CrossRef]



| Scale | Degree of Preference | Description |
|---|---|---|
| 1 | Equally | When two parameters contribute equally to the objective |
| 2 | Intermediate | Preference between 1 and 3 |
| 3 | Moderately | The judgment slightly to-moderately favor one parameter |
| 4 | Intermediate | Preference between 3 and 5 |
| 5 | Strongly | The judgment strongly or essentially favors one parameter |
| 6 | Intermediate | Preference between 5 and 7 |
| 7 | Very strongly | Very strong preference or importance |
| 8 | Intermediate | Preference between 7 and 9 |
| 9 | Extremely | Quite preferred or quite important |
| Order of the Matrix | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| RCI | 0 | 0 | 0.58 | 0.90 | 1.12 | 1.24 | 1.32 | 1.41 | 1.45 |
| Category | Factor | Source Data | Data Precision |
|---|---|---|---|
| Geology | Rock | Geological Map | 1:200,000 |
| Fault density | |||
| Topography | Slope | ASTER-GDEM V2 | 30 m |
| Drainage density | |||
| Convergence index | |||
| Hydrology | Rainfall | GSMaP | 0.1° × 0.1° |
| Distance from rivers | Open Street Map | ||
| Indicators | Enhanced vegetation index | Moderate-resolution Imaging Spectroradiometer | 250 m |
| Spring index | Hydrogeological Map | 1:200,000 |
| Factor | Description | Characteristics |
|---|---|---|
| Rock | Geological formations | Regional strata affect the porosity and permeability of aquifers. |
| Fault density | Line density of faults | The faults are conducive to the infiltration of groundwater. |
| Slope | The degree of steepness of the surface unit | The infiltration of surface water is inversely correlated with the slope. |
| Drainage density | The channel length per unit area | Seepage from surface water channels facilitates groundwater recharge. |
| Convergence index | The concavity or convexity of the landscape at a smaller spatial scale. | A negative convergence refers to concavities (e.g., valleys), whereas positive values reflect convex features (e.g., ridges). |
| Rainfall | Annual rainfall | Rainfall is an important source of groundwater recharge. |
| Distance from rivers | The distance of each grid to the nearest river | Aquifers close to rivers exhibit high recharge rates. |
| Enhanced vegetation index | Measurements of surface vegetation condition | Vegetation is a surface indicator of groundwater in varied topographic areas. |
| Spring index | Index calculated from actual spring locations and flow rates | The spring index provides a visual representation of the groundwater conditions in the study area. |
| Factor | Tolerance | VIF | Factor | Tolerance | VIF | ||
|---|---|---|---|---|---|---|---|
| 1 | Rock | 0.816 | 1.225 | 6 | EVI | 0.805 | 1.242 |
| 2 | Fault density | 0.936 | 1.068 | 7 | Convergence index | 0.984 | 1.016 |
| 3 | Spring index | 0.739 | 1.353 | 8 | Rainfall | 0.871 | 1.148 |
| 4 | Slope | 0.909 | 1.100 | 9 | Distance from rivers | 0.783 | 1.277 |
| 5 | Drainage density | 0.782 | 1.279 |
| Rock | SL | CI | SI | FD | DD | DR | RAIN | EVI | Priority | CI | CR | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Rock | 1 | 1 | 9/8 | 9/8 | 9/7 | 9/6 | 9/6 | 9/5 | 9/4 | 0.145 | 9 | 0 | 0 |
| SL | 1 | 1 | 9/8 | 9/8 | 9/7 | 9/6 | 9/6 | 9/5 | 9/4 | 0.145 | |||
| CI | 8/9 | 8/9 | 1 | 1 | 8/7 | 8/6 | 8/6 | 8/5 | 8/4 | 0.129 | |||
| SI | 8/9 | 8/9 | 1 | 1 | 8/7 | 8/6 | 8/6 | 8/5 | 8/4 | 0.129 | |||
| FD | 7/9 | 7/9 | 7/8 | 7/8 | 1 | 7/6 | 7/6 | 7/5 | 7/4 | 0.113 | |||
| DD | 6/9 | 6/9 | 6/8 | 6/8 | 6/7 | 1 | 1 | 6/5 | 6/4 | 0.097 | |||
| DR | 6/9 | 6/9 | 6/8 | 6/8 | 6/7 | 1 | 1 | 6/5 | 6/4 | 0.097 | |||
| RAIN | 5/9 | 5/9 | 5/8 | 5/8 | 5/7 | 5/6 | 5/6 | 1 | 5/4 | 0.081 | |||
| EVI | 4/9 | 4/9 | 4/8 | 4/8 | 4/7 | 4/6 | 4/6 | 4/5 | 1 | 0.065 | |||
| Sum | 6.889 | 6.889 | 7.75 | 7.75 | 8.857 | 10.333 | 10.333 | 12.4 | 15.5 |
| Yield (t/d·m) | GWP | Potentiality | Water Source Level | GWP | Potentiality |
|---|---|---|---|---|---|
| 2 | 0.48 | Low | 2 | 0.62 | High |
| 41.8 | 0.58 | Moderate | 3 | 0.69 | High |
| 148.3 | 0.59 | Moderate | 3 | 0.73 | Very high |
| 468.6 | 0.63 | High | |||
| 1464.4 | 0.64 | High | |||
| 2541.9 | 0.69 | High |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Q.; Zhang, S.; Zhang, Y.; Li, M.; Wei, Y.; Chen, M.; Zhang, Z.; Dai, Z. GIS-Based Groundwater Potential Assessment in Varied Topographic Areas of Mianyang City, Southwestern China, Using AHP. Remote Sens. 2021, 13, 4684. https://doi.org/10.3390/rs13224684
Zhang Q, Zhang S, Zhang Y, Li M, Wei Y, Chen M, Zhang Z, Dai Z. GIS-Based Groundwater Potential Assessment in Varied Topographic Areas of Mianyang City, Southwestern China, Using AHP. Remote Sensing. 2021; 13(22):4684. https://doi.org/10.3390/rs13224684
Chicago/Turabian StyleZhang, Qing, Shuangxi Zhang, Yu Zhang, Mengkui Li, Yu Wei, Meng Chen, Zeyi Zhang, and Zhouqing Dai. 2021. "GIS-Based Groundwater Potential Assessment in Varied Topographic Areas of Mianyang City, Southwestern China, Using AHP" Remote Sensing 13, no. 22: 4684. https://doi.org/10.3390/rs13224684
APA StyleZhang, Q., Zhang, S., Zhang, Y., Li, M., Wei, Y., Chen, M., Zhang, Z., & Dai, Z. (2021). GIS-Based Groundwater Potential Assessment in Varied Topographic Areas of Mianyang City, Southwestern China, Using AHP. Remote Sensing, 13(22), 4684. https://doi.org/10.3390/rs13224684