Identifying Surface Urban Heat Island Drivers and Their Spatial Heterogeneity in China’s 281 Cities: An Empirical Study Based on Multiscale Geographically Weighted Regression
Abstract
:1. Introduction
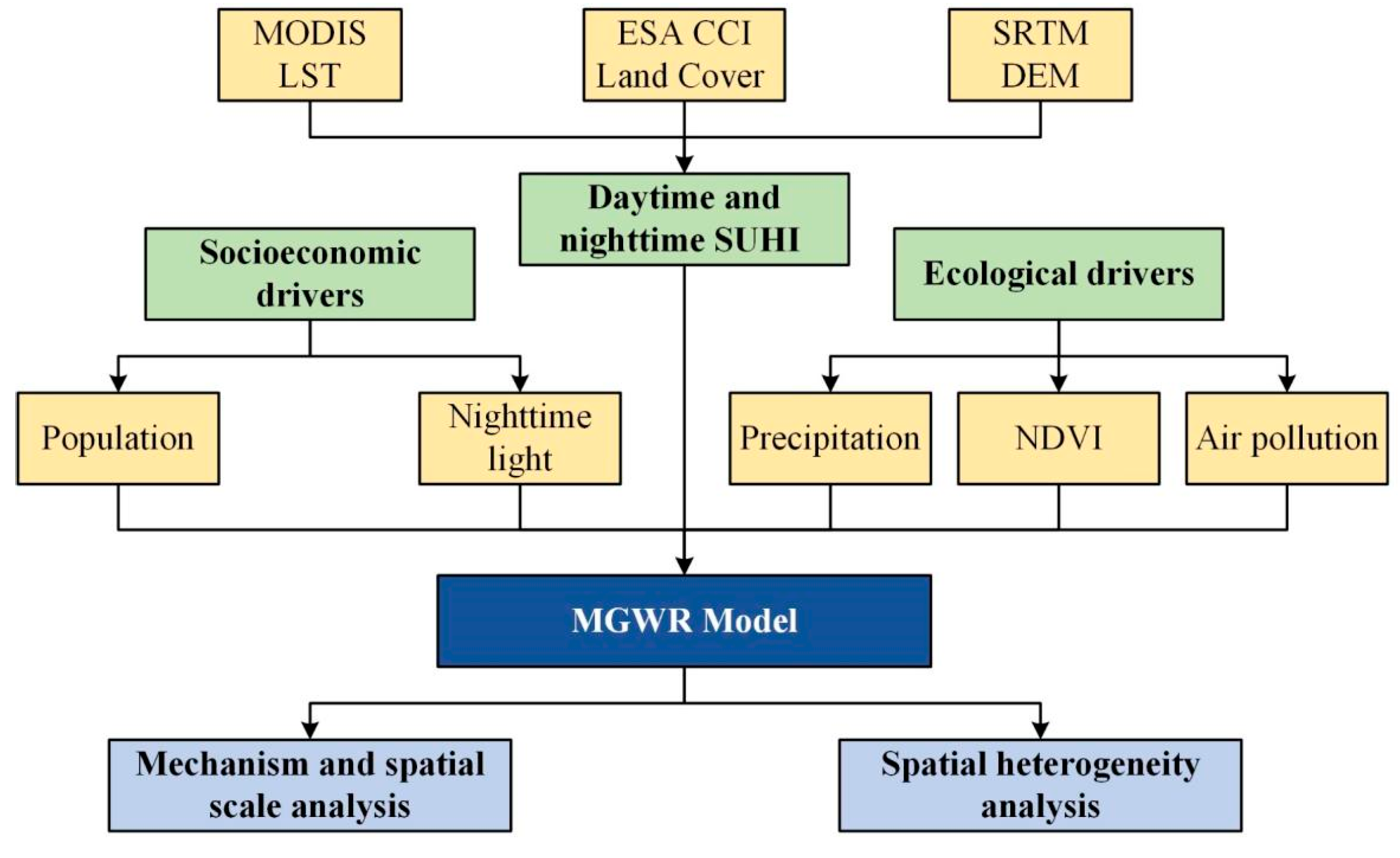
2. Study Area and Data
2.1. Study Area
2.2. Data
2.2.1. CSUHI Dataset
- The LST data from 2001 to 2018 were provided by the Terra/Aqua MODIS 8-day 1 km LST/LSE products (MOD11A2 for Terra MODIS and MYD11A2 v006 for Aqua MODIS and the data of MYD11A2 are from 2003) [51].
- The European Space Agency’s Climate Change Initiative (ESA CCI) land cover data at 300 m resolution from 2001 to 2018 [52] were employed to delineate urban and rural areas.
- Shuttle Radar Topography Mission (SRTM) data at 90 m resolution from 2000 was employed to determine the elevation of urban and rural areas.
- The above 281 cities’ administrative areas were defined based on data from the National Geomatics Center of China (NGCC).
2.2.2. Variable Selection and Data Source
- ΔNDVI was derived from the 16-day 1 km MODIS NDVI products (MYD13A2 v006) in 2005, 2010, 2015, and 2018 [53].
- ΔPre was derived from the monthly 1 km precipitation raster product (National Tibetan Plateau Data Center. Available online: http://data.tpdc.ac.cn (accessed on 21 October 2021)) in 2005, 2010, 2015, and 2018, which was spatially downscaled from the Climatic Research Unit (CRU) time-series dataset combined with the climatology dataset of WorldClim [54].
- ΔPM2.5 was derived from the yearly 1 km ChinaHighAirPollutants (CHAP) dataset, which was constructed from the MODIS/Terra+Aqua multiangle implementation of atmospheric correction (MAIAC) aerosol optical depth products together with abundant natural and human factors using the Space–Time Extra-Trees (STET) model [55,56].
- An integrated and consistent annual NTL product was employed from a harmonized global nighttime light dataset [57] for 2005, 2010, 2015, and 2018. This dataset employed Defense Meteorological Satellite Program (DMSP) data and simulated DMSP-like NTL observations from Visible Infrared Imaging Radiometer Suite (VIIRS) data to harmonize the intercalibrated NTL observations and showed consistent temporal trends. This study only used pixels with more than seven digital number (DN) values to improve the data’s reliability.
- Population data was extracted from the China Urban Statistical Yearbook for 2005, 2010, 2015, and 2018.
3. Methods
3.1. SUHI Intensity Calculation
3.2. Ordinary Least Square Model
3.3. Multiscale Geographically Weighted Regression Model
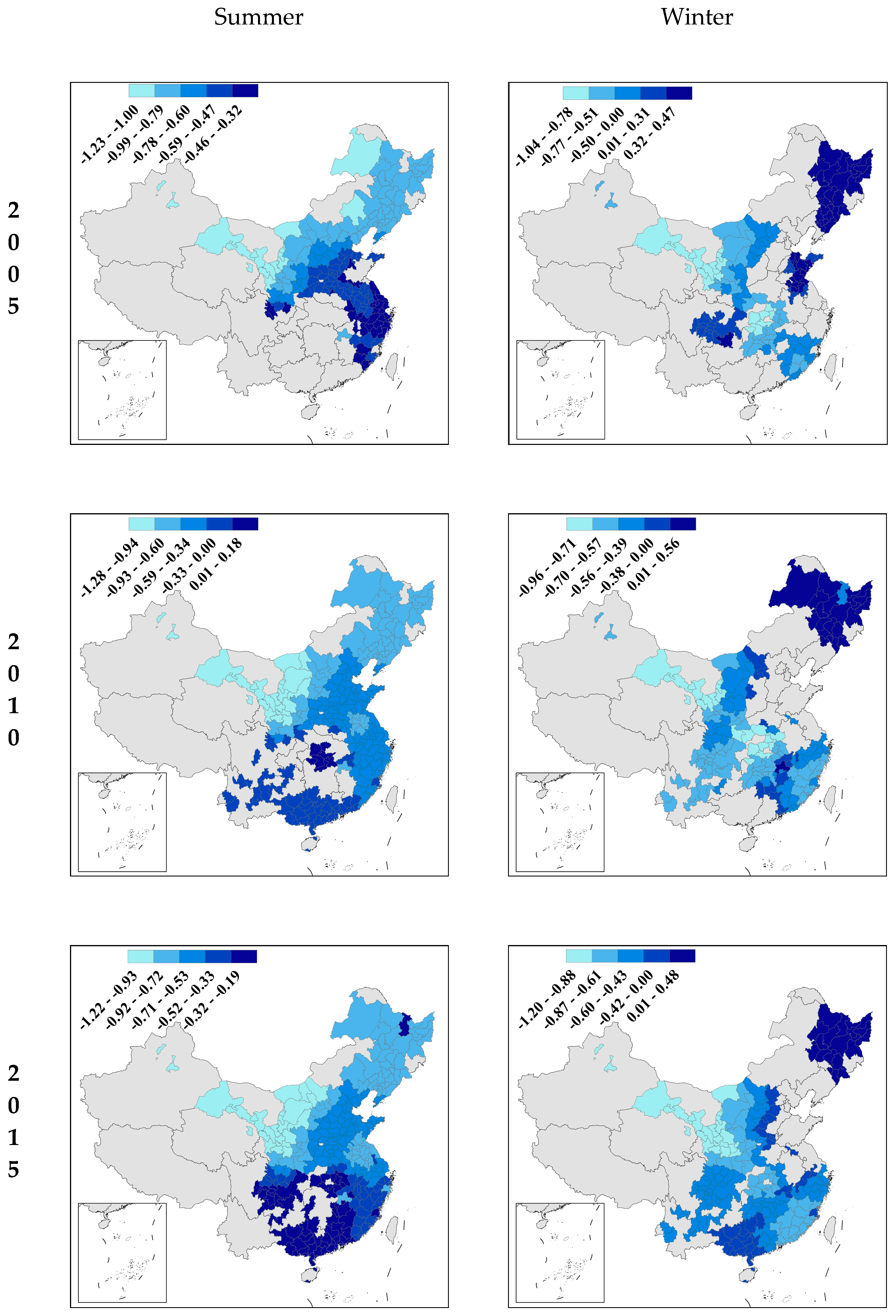
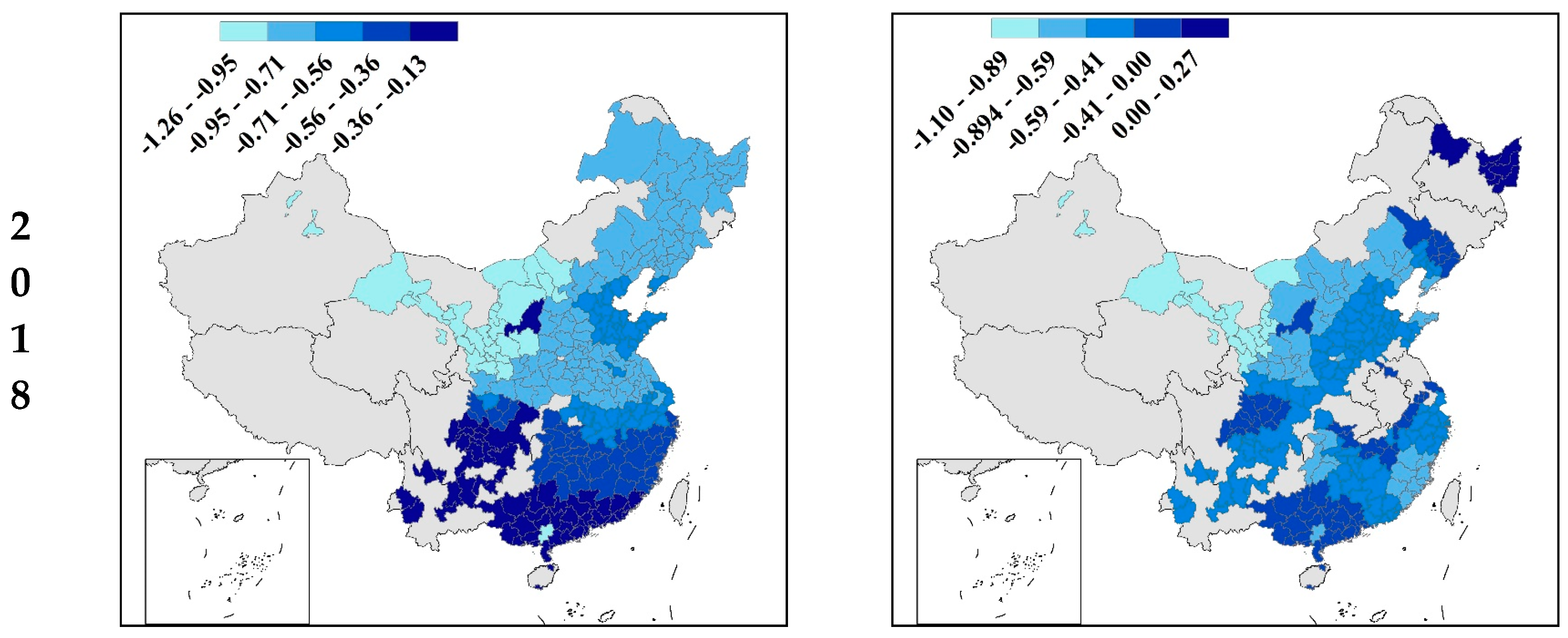
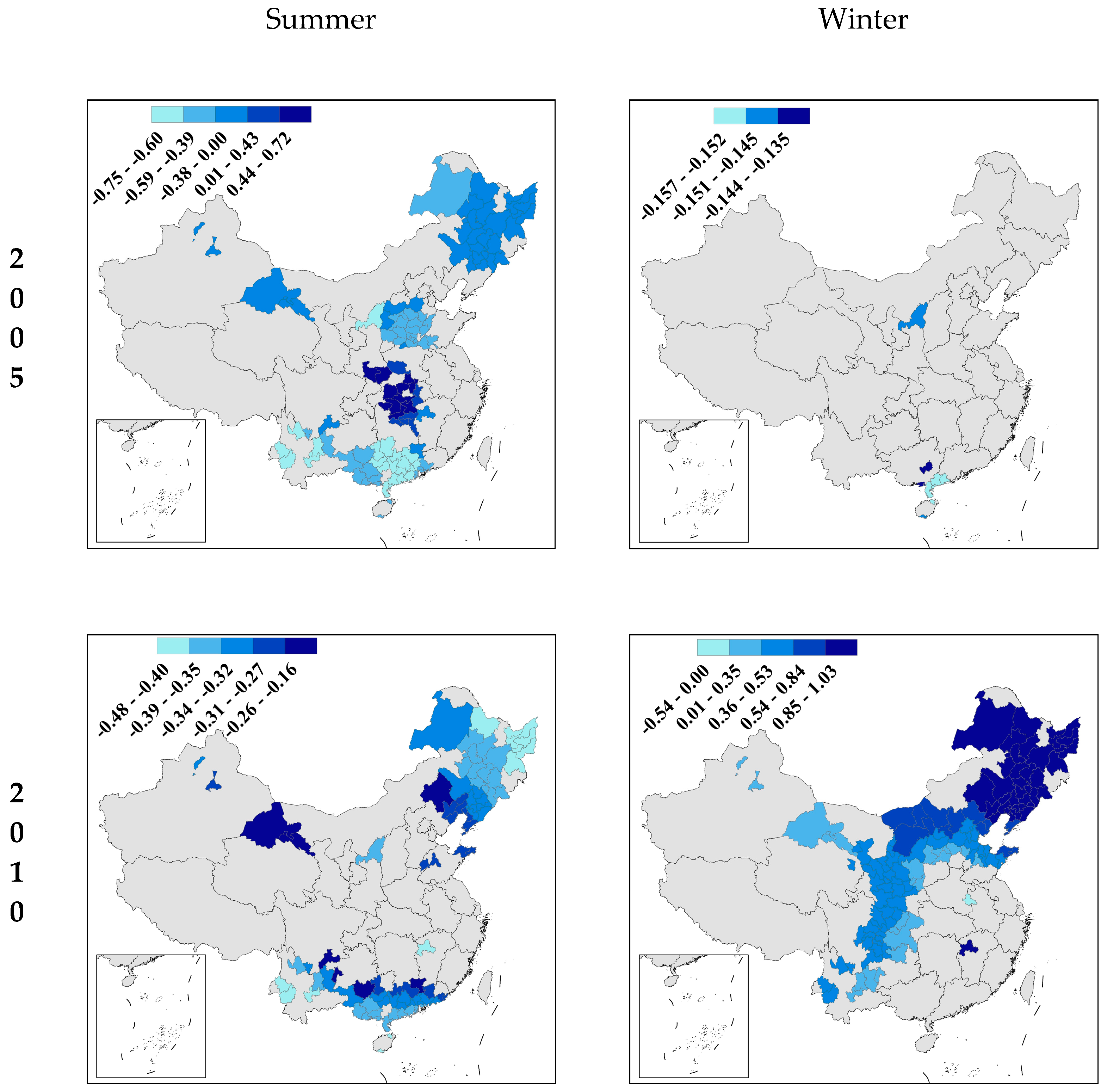
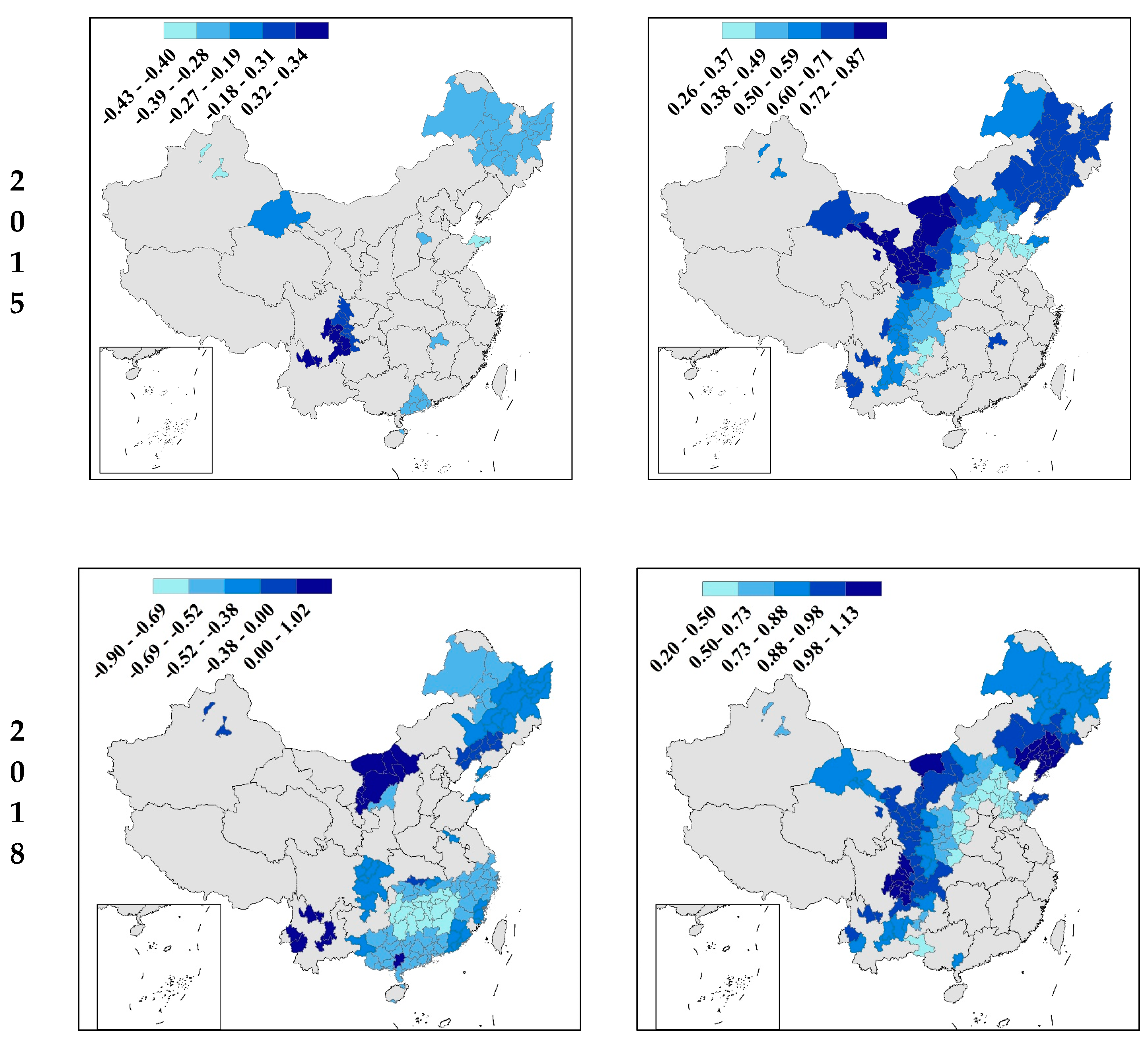
4. Results
4.1. Results of the OLS Analysis
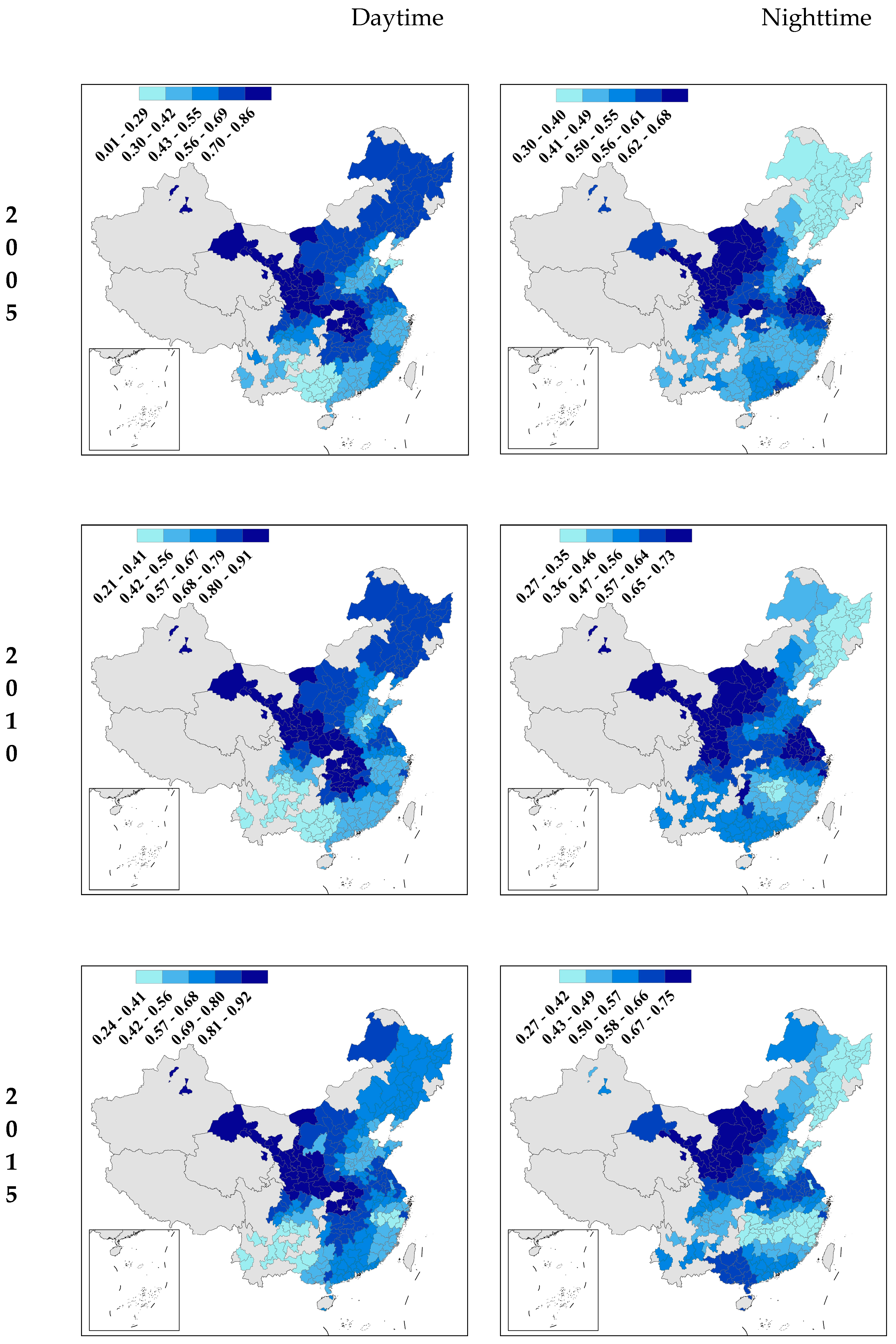
4.2. MGWR Results
5. Discussion
5.1. Multiscale Extensions of Geographically Weighted Regression
5.2. Seasonal Variation of SUHIs and Vegetation
5.3. Spatial Context and Population
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhou, L.; Dickinson, R.E.; Tian, Y.; Fang, J.; Li, Q.; Kaufmann, R.K.; Tucker, C.J.; Myneni, R.B. Evidence for a significant urbanization effect on climate in China. Proc. Natl. Acad. Sci. USA 2004, 101, 9540–9544. [Google Scholar] [CrossRef] [Green Version]
- Kalnay, E.; Cai, M. Impact of urbanization and land-use change on climate. Nature 2003, 423, 528–531. [Google Scholar] [CrossRef]
- Deng, J.S.; Wang, K.; Hong, Y.; Qi, J.G. Spatio-temporal dynamics and evolution of land use change and landscape pattern in response to rapid urbanization. Landsc. Urban Plan. 2009, 92, 187–198. [Google Scholar] [CrossRef]
- Oke, T.R. City size and the urban heat island. Atmos. Environ. 1973, 7, 769–779. [Google Scholar] [CrossRef]
- Howard, L. Climate of London deduced from meteorological observation. Harvey Darton 1833, 1, 1–24. [Google Scholar]
- Kolokotroni, M.; Ren, X.; Davies, M.; Mavrogianni, A. London’s urban heat island: Impact on current and future energy consumption in office buildings. Energy Build. 2012, 47, 302–311. [Google Scholar] [CrossRef] [Green Version]
- Kikegawa, Y.; Genchi, Y.; Kondo, H.; Hanaki, K. Impacts of city-block-scale countermeasures against urban heat-island phenomena upon a building’s energy-consumption for air-conditioning. Appl. Energy 2006, 83, 649–668. [Google Scholar] [CrossRef]
- Parker, J. The Leeds urban heat island and its implications for energy use and thermal comfort. Energy Build. 2021, 235, 110636. [Google Scholar] [CrossRef]
- Sarrat, C.; Lemonsu, A.; Masson, V.; Guedalia, D. Impact of urban heat island on regional atmospheric pollution. Atmos. Environ. 2006, 40, 1743–1758. [Google Scholar] [CrossRef]
- Li, H.; Meier, F.; Lee, X.; Chakraborty, T.; Liu, J.; Schaap, M.; Sodoudi, S. Interaction between urban heat island and urban pollution island during summer in Berlin. Sci. Total Environ. 2018, 636, 818–828. [Google Scholar] [CrossRef] [PubMed]
- Čeplová, N.; Kalusová, V.; Lososová, Z. Effects of settlement size, urban heat island and habitat type on urban plant biodiversity. Landsc. Urban Plan. 2017, 159, 15–22. [Google Scholar] [CrossRef]
- Géron, C.; Lembrechts, J.J.; Nijs, I.; Monty, A. Shielded environments reduce stress in alien Asteraceae species during hot and dry summers along urban-to-rural gradients. Ecol. Evol. 2021, 11, 10613–10626. [Google Scholar] [CrossRef]
- Tan, J.; Zheng, Y.; Tang, X.; Guo, C.; Li, L.; Song, G.; Zhen, X.; Yuan, D.; Kalkstein, A.J.; Li, F. The urban heat island and its impact on heat waves and human health in Shanghai. Int. J. Biometeorol. 2010, 54, 75–84. [Google Scholar] [CrossRef]
- Goggins, W.B.; Chan, E.Y.; Ng, E.; Ren, C.; Chen, L. Effect modification of the association between short-term meteorological factors and mortality by urban heat islands in Hong Kong. PLoS ONE 2012, 7, e38551. [Google Scholar]
- He, B.-J.; Wang, J.; Liu, H.; Ulpiani, G. Localized synergies between heat waves and urban heat islands: Implications on human thermal comfort and urban heat management. Environ. Res. 2021, 193, 110584. [Google Scholar] [CrossRef]
- Oke, T.R. The energetic basis of the urban heat island. Q. J. R. Meteorol. Soc. 1982, 108, 1–24. [Google Scholar] [CrossRef]
- Stewart, I.; Mills, G. The Urban Heat Island: A Guidebook; Elsevier: Amsterdam, The Netherlands, 2021. [Google Scholar]
- Clinton, N.; Gong, P. MODIS detected surface urban heat islands and sinks: Global locations and controls. Remote Sens. Environ. 2013, 134, 294–304. [Google Scholar] [CrossRef]
- Lai, J.; Zhan, W.; Huang, F.; Voogt, J.; Bechtel, B.; Allen, M.; Peng, S.; Hong, F.; Liu, Y.; Du, P. Identification of typical diurnal patterns for clear-sky climatology of surface urban heat islands. Remote Sens. Environ. 2018, 217, 203–220. [Google Scholar] [CrossRef]
- Runnalls, K.; Oke, T. Dynamics and controls of the near-surface heat island of Vancouver, British Columbia. Phys. Geogr. 2000, 21, 283–304. [Google Scholar] [CrossRef]
- De Faria Peres, L.; de Lucena, A.J.; Rotunno Filho, O.C.; de Almeida França, J.R. The urban heat island in Rio de Janeiro, Brazil, in the last 30 years using remote sensing data. Int. J. Appl. Earth Obs. Geoinf. 2018, 64, 104–116. [Google Scholar] [CrossRef]
- Imhoff, M.L.; Zhang, P.; Wolfe, R.E.; Bounoua, L. Remote sensing of the urban heat island effect across biomes in the continental USA. Remote Sens. Environ. 2010, 114, 504–513. [Google Scholar] [CrossRef] [Green Version]
- Schwarz, N.; Lautenbach, S.; Seppelt, R. Exploring indicators for quantifying surface urban heat islands of European cities with MODIS land surface temperatures. Remote Sens. Environ. 2011, 115, 3175–3186. [Google Scholar] [CrossRef]
- Bhang, K.J.; Park, S.-S. Evaluation of the surface temperature variation with surface settings on the urban heat island in Seoul, Korea, using Landsat-7 ETM+ and SPOT. IEEE Geosci. Remote Sens. Lett. 2009, 6, 708–712. [Google Scholar] [CrossRef]
- Khamchiangta, D.; Dhakal, S. Physical and non-physical factors driving urban heat island: Case of Bangkok Metropolitan Administration, Thailand. J. Environ. Manag. 2019, 248, 109285. [Google Scholar] [CrossRef] [PubMed]
- Stewart, I.D.; Oke, T.R. Local climate zones for urban temperature studies. Bull. Am. Meteorol. Soc. 2012, 93, 1879–1900. [Google Scholar] [CrossRef]
- Li, Z.-L.; Si, M.; Leng, P. A Review of Remotely Sensed Surface Urban Heat Islands from the Fresh Perspective of Comparisons Among Different Regions (Invited Review). Prog. Electromagn. Res. C 2020, 102, 31–46. [Google Scholar] [CrossRef]
- Peng, S.; Piao, S.; Ciais, P.; Friedlingstein, P.; Ottle, C.; Bréon, F.-M.; Nan, H.; Zhou, L.; Myneni, R.B. Surface Urban Heat Island Across 419 Global Big Cities. Environ. Sci. Technol. 2012, 46, 696–703. [Google Scholar] [CrossRef]
- Zhao, L.; Lee, X.; Smith, R.B.; Oleson, K. Strong contributions of local background climate to urban heat islands. Nature 2014, 511, 216–219. [Google Scholar] [CrossRef]
- Manoli, G.; Fatichi, S.; Schläpfer, M.; Yu, K.; Crowther, T.W.; Meili, N.; Burlando, P.; Katul, G.G.; Bou-Zeid, E. Magnitude of urban heat islands largely explained by climate and population. Nature 2019, 573, 55–60. [Google Scholar] [CrossRef]
- Priyankara, P.; Ranagalage, M.; Dissanayake, D.; Morimoto, T.; Murayama, Y. Spatial process of surface urban heat island in rapidly growing Seoul metropolitan area for sustainable urban planning using Landsat data (1996–2017). Climate 2019, 7, 110. [Google Scholar] [CrossRef] [Green Version]
- Moellering, H.; Tobler, W. Geographical variances. Geogr. Anal. 1972, 4, 34–50. [Google Scholar] [CrossRef]
- Liverman, D. Who governs, at what scale and at what price? Geography, environmental governance, and the commodification of nature. Ann. Assoc. Am. Geogr. 2004, 94, 734–738. [Google Scholar]
- Fotheringham, A.S.; Yang, W.; Kang, W. Multiscale geographically weighted regression (MGWR). Ann. Am. Assoc. Geogr. 2017, 107, 1247–1265. [Google Scholar] [CrossRef]
- Yang, Q.; Huang, X.; Li, J. Assessing the relationship between surface urban heat islands and landscape patterns across climatic zones in China. Sci. Rep. 2017, 7, 1–11. [Google Scholar] [CrossRef]
- Zhou, D.; Zhao, S.; Zhang, L.; Liu, S. Remotely sensed assessment of urbanization effects on vegetation phenology in China’s 32 major cities. Remote Sens. Environ. 2016, 176, 272–281. [Google Scholar] [CrossRef] [Green Version]
- Sun, R.; Lü, Y.; Yang, X.; Chen, L. Understanding the variability of urban heat islands from local background climate and urbanization. J. Clean. Prod. 2019, 208, 743–752. [Google Scholar] [CrossRef]
- Niu, L.; Tang, R.; Jiang, Y.; Zhou, X. Spatiotemporal patterns and drivers of the surface urban heat island in 36 major cities in China: A comparison of two different methods for delineating rural areas. Sustainability 2020, 12, 478. [Google Scholar] [CrossRef] [Green Version]
- Zhou, D.; Zhao, S.; Liu, S.; Zhang, L.; Zhu, C. Surface urban heat island in China’s 32 major cities: Spatial patterns and drivers. Remote Sens. Environ. 2014, 152, 51–61. [Google Scholar] [CrossRef]
- Li, Y.; Sun, Y.; Li, J.; Gao, C. Socioeconomic drivers of urban heat island effect: Empirical evidence from major Chinese cities. Sustain. Cities Soc. 2020, 63, 102425. [Google Scholar] [CrossRef]
- Liu, S.; Zhang, J.; Li, J.; Li, Y.; Zhang, J.; Wu, X. Simulating and mitigating extreme urban heat island effects in a factory area based on machine learning. Build. Environ. 2021, 202, 108051. [Google Scholar] [CrossRef]
- Yoo, S. Investigating important urban characteristics in the formation of urban heat islands: A machine learning approach. J. Big Data 2018, 5, 1–24. [Google Scholar] [CrossRef] [Green Version]
- Li, K.; Chen, Y.; Wang, M.; Gong, A. Spatial-temporal variations of surface urban heat island intensity induced by different definitions of rural extents in China. Sci. Total Environ. 2019, 669, 229–247. [Google Scholar] [CrossRef] [PubMed]
- Szymanowski, M.; Kryza, M. Local regression models for spatial interpolation of urban heat island—An example from Wrocław, SW Poland. Theor. Appl. Climatol. 2012, 108, 53–71. [Google Scholar] [CrossRef] [Green Version]
- Zhao, C.; Jensen, J.; Weng, Q.; Weaver, R. A geographically weighted regression analysis of the underlying factors related to the surface urban heat island phenomenon. Remote Sens. 2018, 10, 1428. [Google Scholar] [CrossRef] [Green Version]
- Li, L.; Zha, Y.; Zhang, J. Spatially non-stationary effect of underlying driving factors on surface urban heat islands in global major cities. Int. J. Appl. Earth Obs. Geoinf. 2020, 90, 102131. [Google Scholar] [CrossRef]
- Stewart Fotheringham, A.; Li, Z.; Wolf, L.J. Scale, Context, and Heterogeneity: A Spatial Analytical Perspective on the 2016 US Presidential Election. Ann. Am. Assoc. Geogr. 2021, 111, 1602–1621. [Google Scholar]
- Li, J.-J.; Wang, X.-R.; Wang, X.-J.; Ma, W.-C.; Zhang, H. Remote sensing evaluation of urban heat island and its spatial pattern of the Shanghai metropolitan area, China. Ecol. Complex. 2009, 6, 413–420. [Google Scholar] [CrossRef]
- Peng, S.; Feng, Z.; Liao, H.; Huang, B.; Peng, S.; Zhou, T. Spatial-temporal pattern of, and driving forces for, urban heat island in China. Ecol. Indic. 2019, 96, 127–132. [Google Scholar] [CrossRef]
- Niu, L.; Peng, Z.; Tang, R.; Zhang, Z. Development of a long-term dataset of China surface urban heat island for policy making: Spatio-temporal characteristics. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021; pp. 6928–6931. [Google Scholar]
- Wan, Z. New refinements and validation of the MODIS land-surface temperature/emissivity products. Remote Sens. Environ. 2008, 112, 59–74. [Google Scholar] [CrossRef]
- Bontemps, S.; Defourny, P.; Radoux, J.; Van Bogaert, E.; Lamarche, C.; Achard, F.; Mayaux, P.; Boettcher, M.; Brockmann, C.; Kirches, G. Consistent global land cover maps for climate modelling communities: Current achievements of the ESA’s land cover CCI. In Proceedings of the ESA Living Planet Symposium, Edinburgh, UK, 9–13 September 2013; pp. 9–13. [Google Scholar]
- Lunetta, R.S.; Knight, J.F.; Ediriwickrema, J.; Lyon, J.G.; Worthy, L.D. Land-cover change detection using multi-temporal MODIS NDVI data. Remote Sens. Environ. 2006, 105, 142–154. [Google Scholar] [CrossRef]
- Peng, S.; Ding, Y.; Liu, W.; Li, Z. 1 km monthly temperature and precipitation dataset for China from 1901 to 2017. Earth Syst. Sci. Data 2019, 11, 1931–1946. [Google Scholar] [CrossRef] [Green Version]
- Wei, J.; Li, Z.; Cribb, M.; Huang, W.; Xue, W.; Sun, L.; Guo, J.; Peng, Y.; Li, J.; Lyapustin, A. Improved 1 km resolution PM2.5 estimates across China using enhanced space–time extremely randomized trees. Atmos. Chem. Phys. 2020, 20, 3273–3289. [Google Scholar] [CrossRef] [Green Version]
- Wei, J.; Li, Z.; Lyapustin, A.; Sun, L.; Peng, Y.; Xue, W.; Su, T.; Cribb, M. Reconstructing 1-km-resolution high-quality PM2.5 data records from 2000 to 2018 in China: Spatiotemporal variations and policy implications. Remote Sens. Environ. 2021, 252, 112136. [Google Scholar] [CrossRef]
- Li, X.; Zhou, Y.; Zhao, M.; Zhao, X. A harmonized global nighttime light dataset 1992–2018. Sci. Data 2020, 7, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.L.; Zhao, H.M.; Li, P.X.; Yin, Z.Y. Remote sensing image-based analysis of the relationship between urban heat island and land use/cover changes. Remote Sens. Environ. 2006, 104, 133–146. [Google Scholar] [CrossRef]
- Rani, M.; Kumar, P.; Pandey, P.C.; Srivastava, P.K.; Chaudhary, B.; Tomar, V.; Mandal, V.P. Multi-temporal NDVI and surface temperature analysis for Urban Heat Island inbuilt surrounding of sub-humid region: A case study of two geographical regions. Remote Sens. Appl. Soc. Environ. 2018, 10, 163–172. [Google Scholar] [CrossRef]
- Yang, Y.; Zheng, Z.; Yim, S.Y.; Roth, M.; Ren, G.; Gao, Z.; Wang, T.; Li, Q.; Shi, C.; Ning, G. PM2.5 pollution modulates wintertime urban heat island intensity in the Beijing-Tianjin-Hebei Megalopolis, China. Geophys. Res. Lett. 2020, 47, e2019GL084288. [Google Scholar] [CrossRef] [Green Version]
- Pandey, P.; Kumar, D.; Prakash, A.; Masih, J.; Singh, M.; Kumar, S.; Jain, V.K.; Kumar, K. A study of urban heat island and its association with particulate matter during winter months over Delhi. Sci. Total Environ. 2012, 414, 494–507. [Google Scholar] [CrossRef]
- Zhong, S.; Qian, Y.; Zhao, C.; Leung, R.; Wang, H.; Yang, B.; Fan, J.; Yan, H.; Yang, X.-Q.; Liu, D. Urbanization-induced urban heat island and aerosol effects on climate extremes in the Yangtze River Delta region of China. Atmos. Chem. Phys. 2017, 17, 5439–5457. [Google Scholar] [CrossRef] [Green Version]
- Peng, J.; Liu, Q.; Xu, Z.; Lyu, D.; Du, Y.; Qiao, R.; Wu, J. How to effectively mitigate urban heat island effect? A perspective of waterbody patch size threshold. Landsc. Urban Plann. 2020, 202, 103873. [Google Scholar] [CrossRef]
- Chakraborty, T.; Lee, X. A simplified urban-extent algorithm to characterize surface urban heat islands on a global scale and examine vegetation control on their spatiotemporal variability. Int. J. Appl. Earth Obs. Geoinf. 2019, 74, 269–280. [Google Scholar] [CrossRef]
- Chakraborty, T.; Hsu, A.; Manya, D.; Sheriff, G. A spatially explicit surface urban heat island database for the United States: Characterization, uncertainties, and possible applications. ISPRS J. Photogramm. Remote Sens. 2020, 168, 74–88. [Google Scholar] [CrossRef]
- Cui, W.; Li, J.; Xu, W.; Güneralp, B. Industrial electricity consumption and economic growth: A spatio-temporal analysis across prefecture-level cities in China from 1999 to 2014. Energy 2021, 222, 119932. [Google Scholar] [CrossRef]
- Fotheringham, A.S.; Brunsdon, C.; Charlton, M. Geographically Weighted Regression: The Analysis of Spatially Varying Relationships; John Wiley & Sons: Hoboken, NJ, USA, 2003. [Google Scholar]
- Paschalis, A.; Chakraborty, T.; Fatichi, S.; Meili, N.; Manoli, G. Urban forests as main regulator of the evaporative cooling effect in cities. AGU Adv. 2021, 2, e2020AV000303. [Google Scholar] [CrossRef]
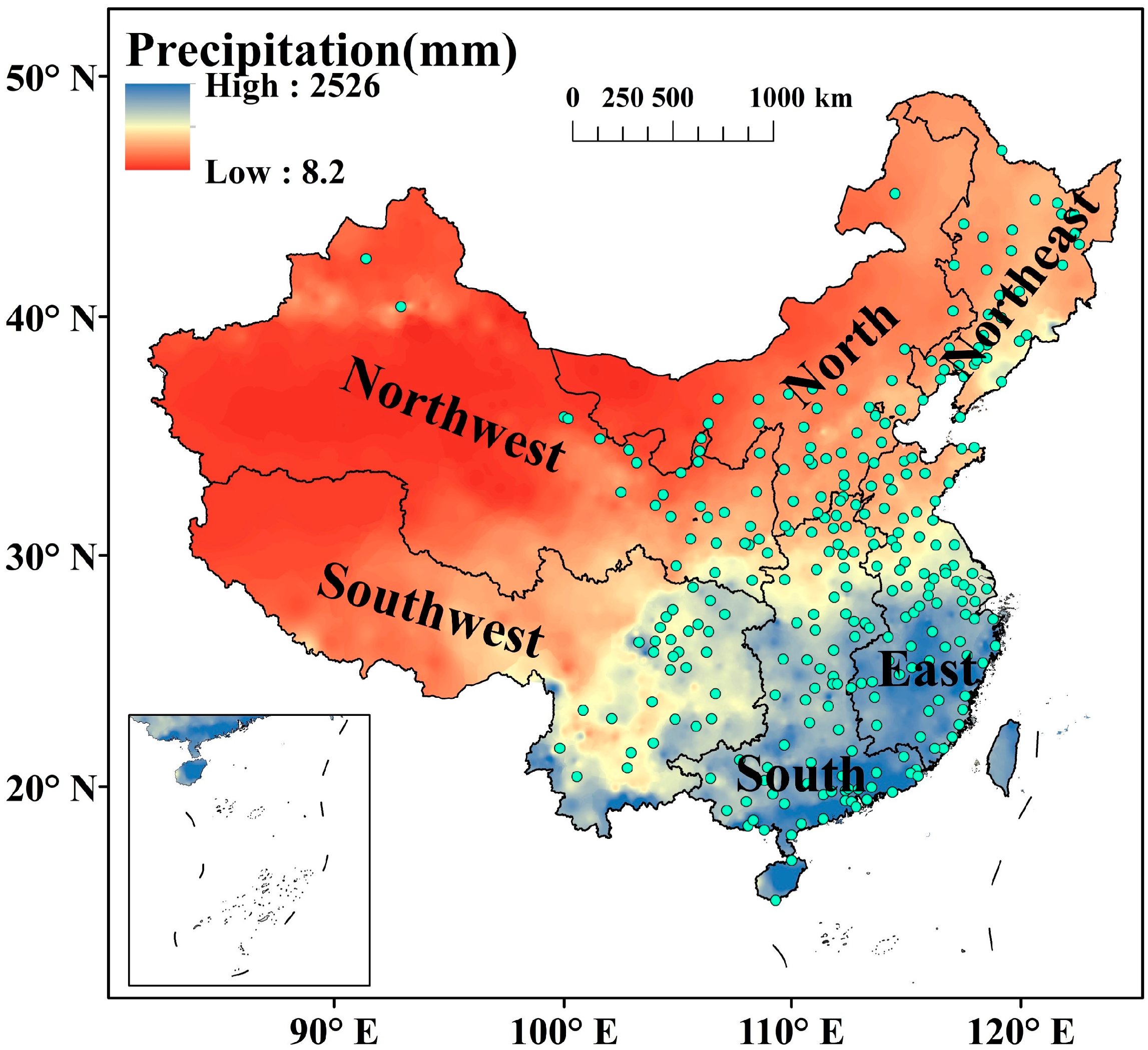
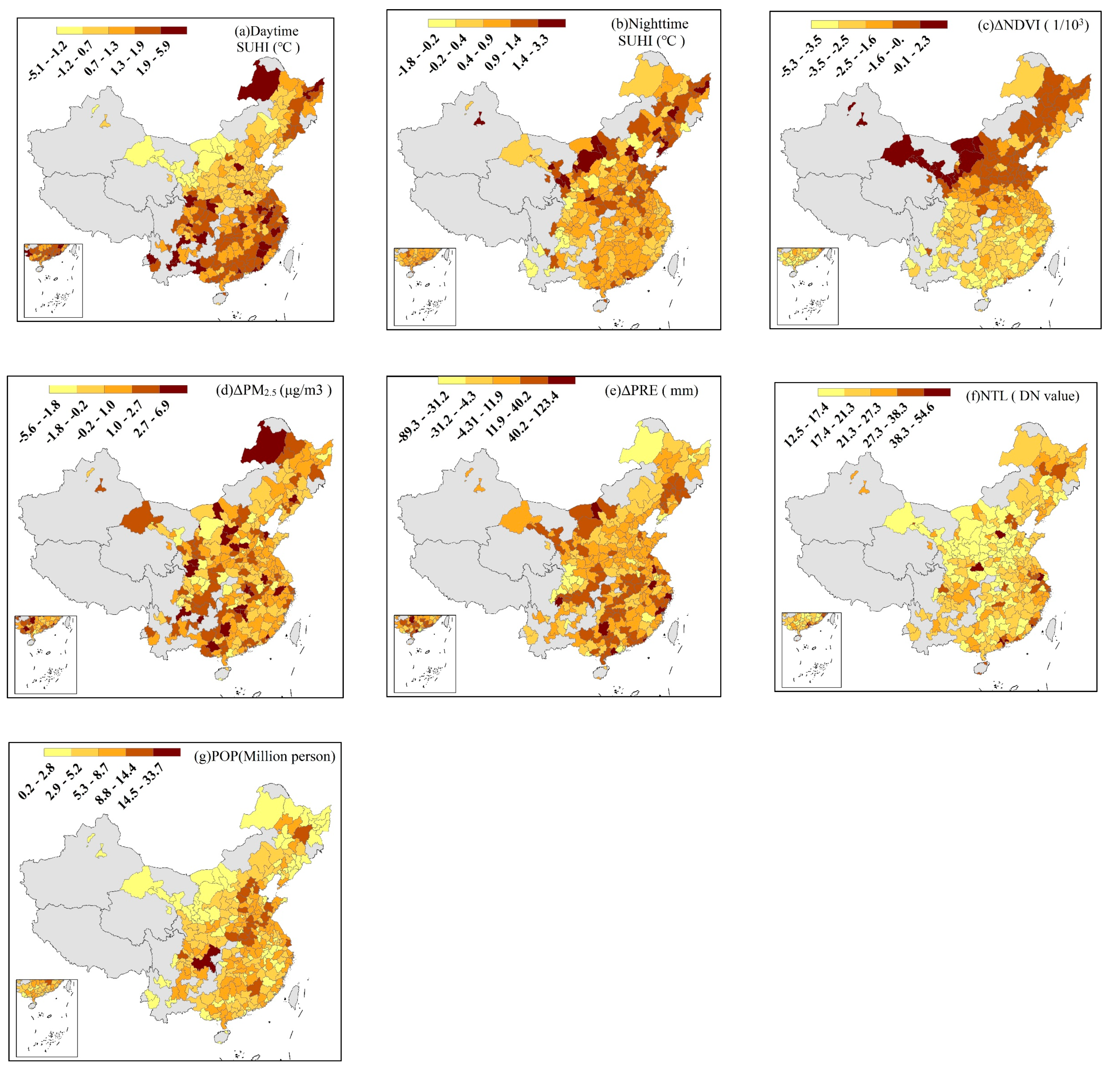
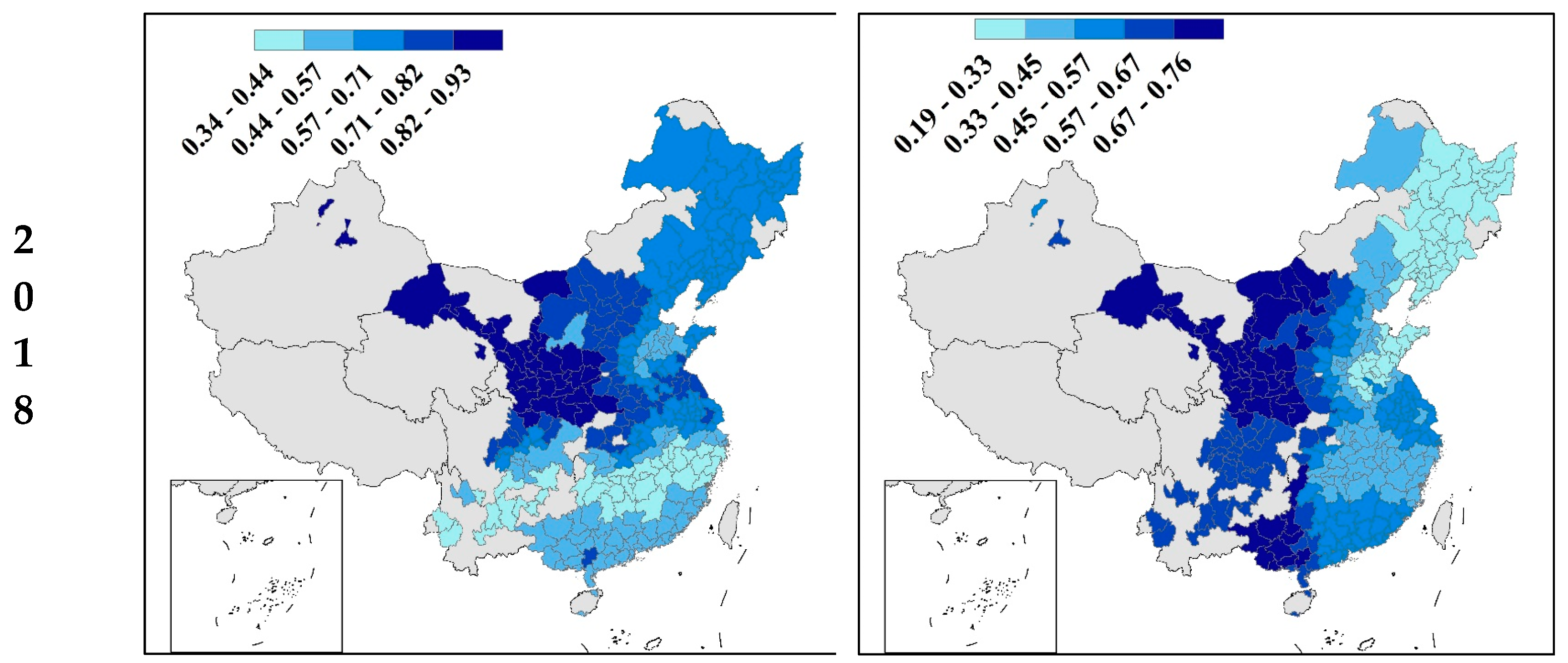
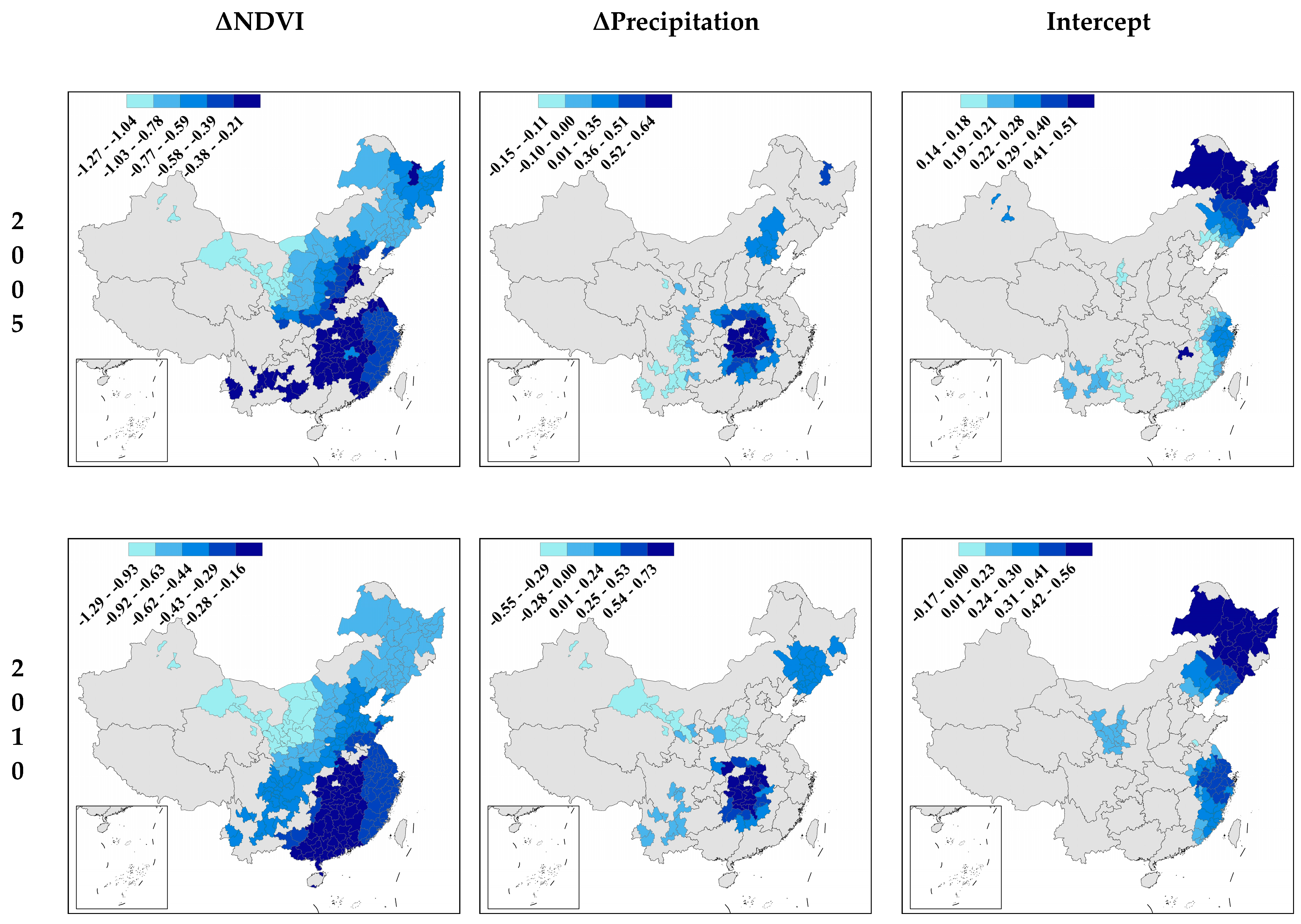

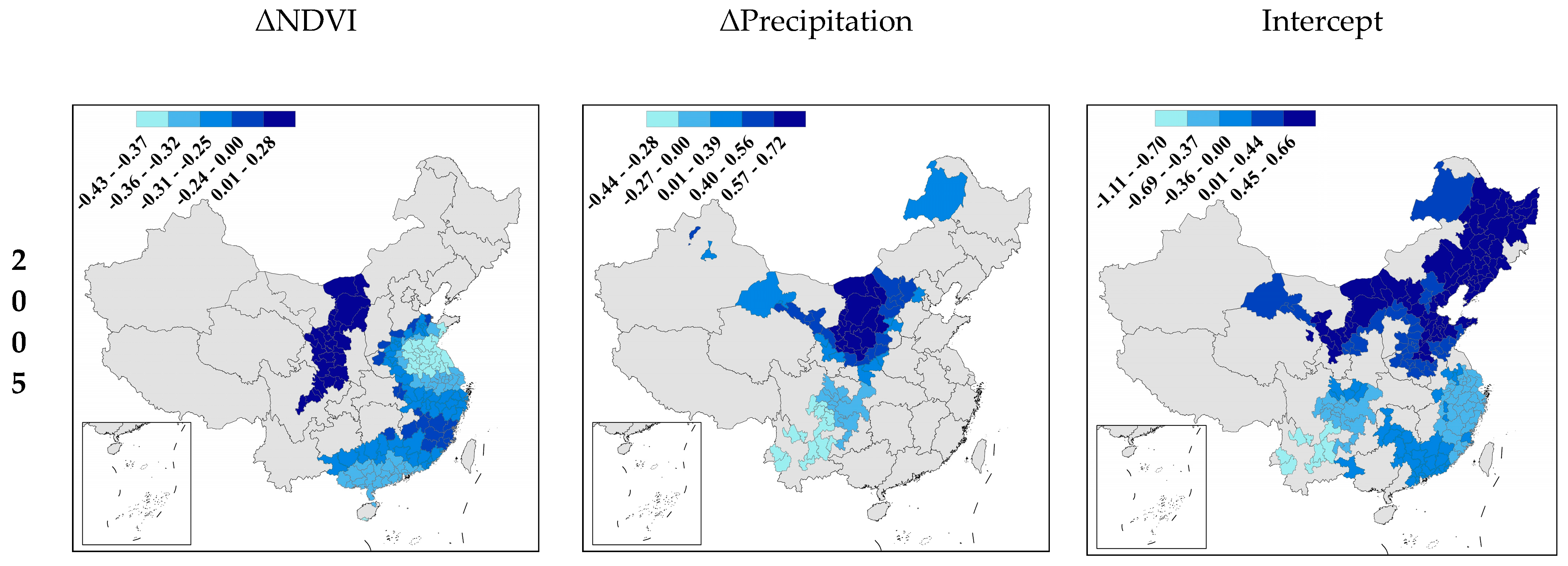
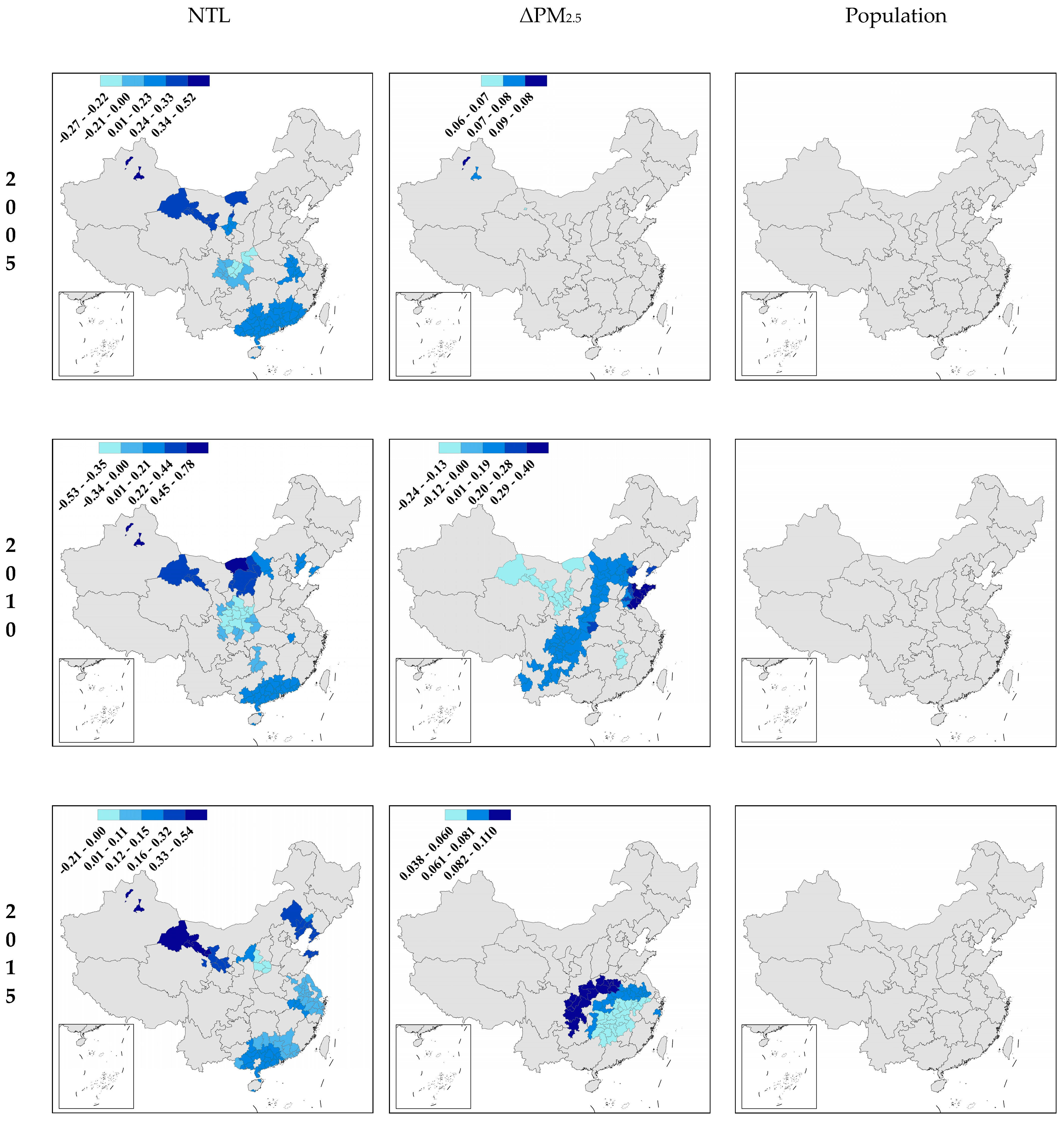
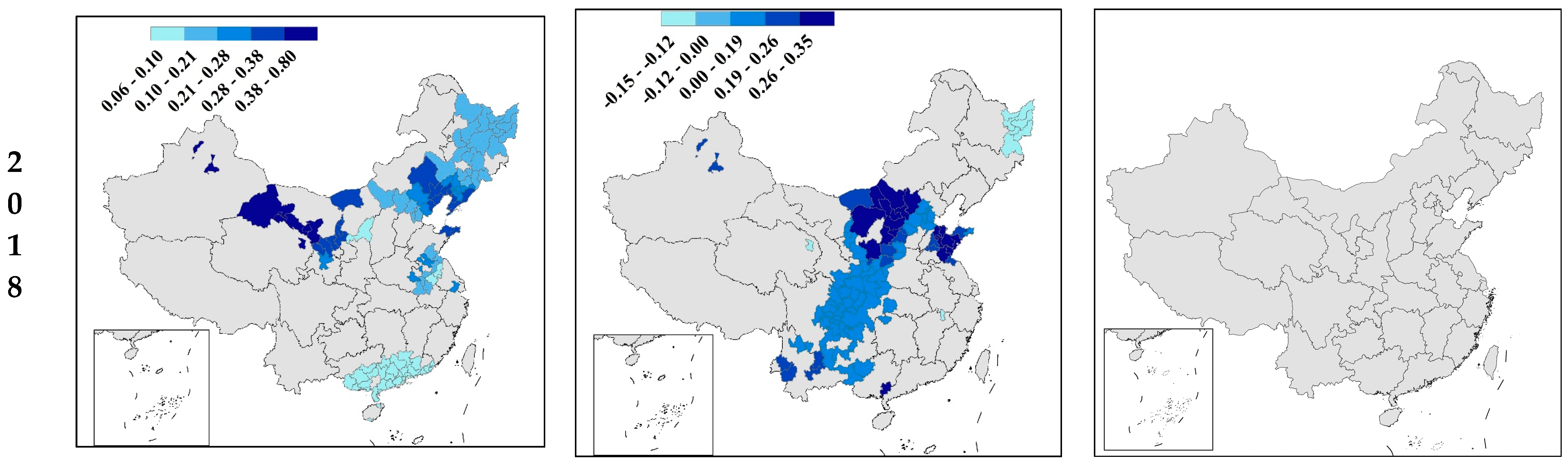
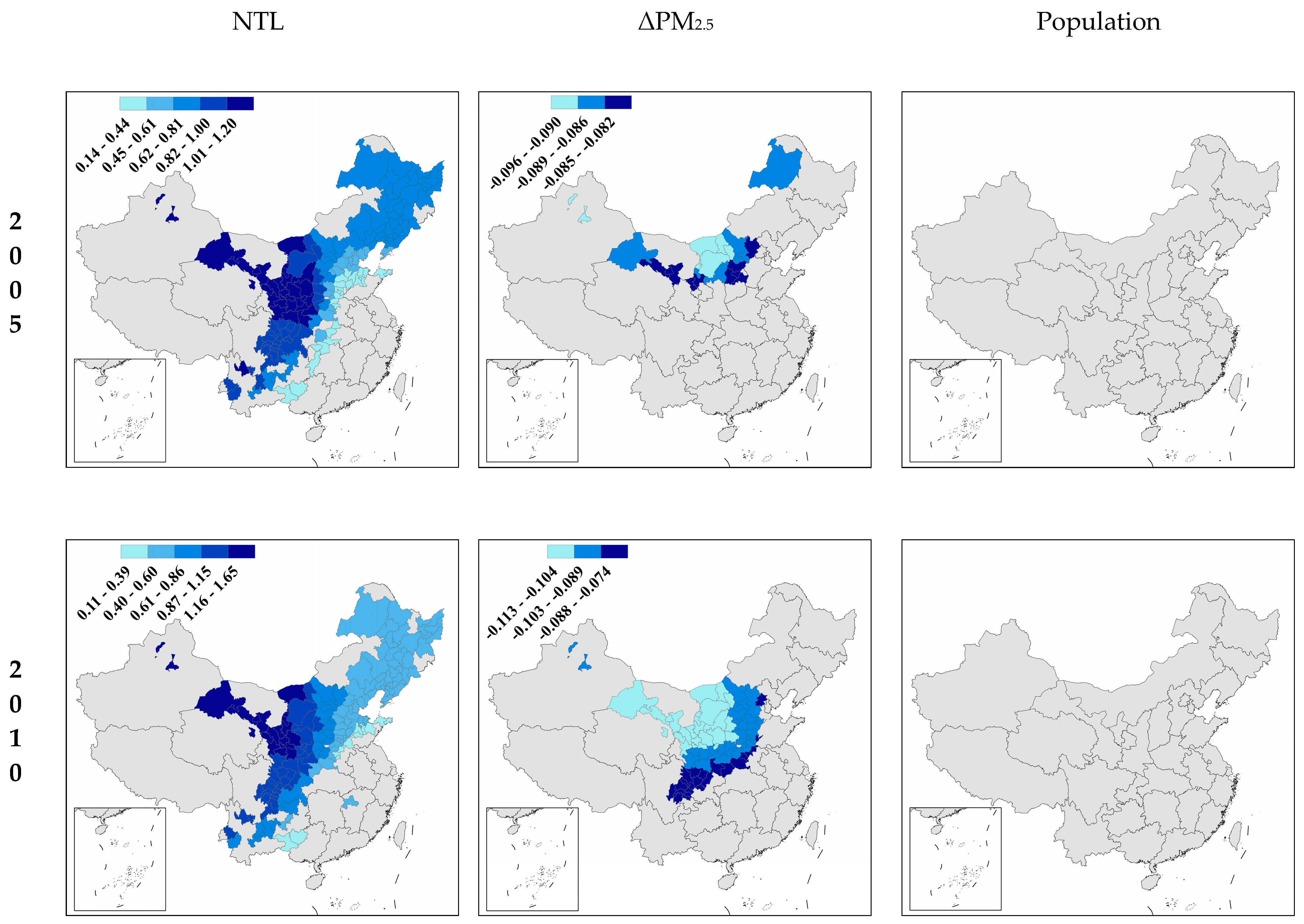
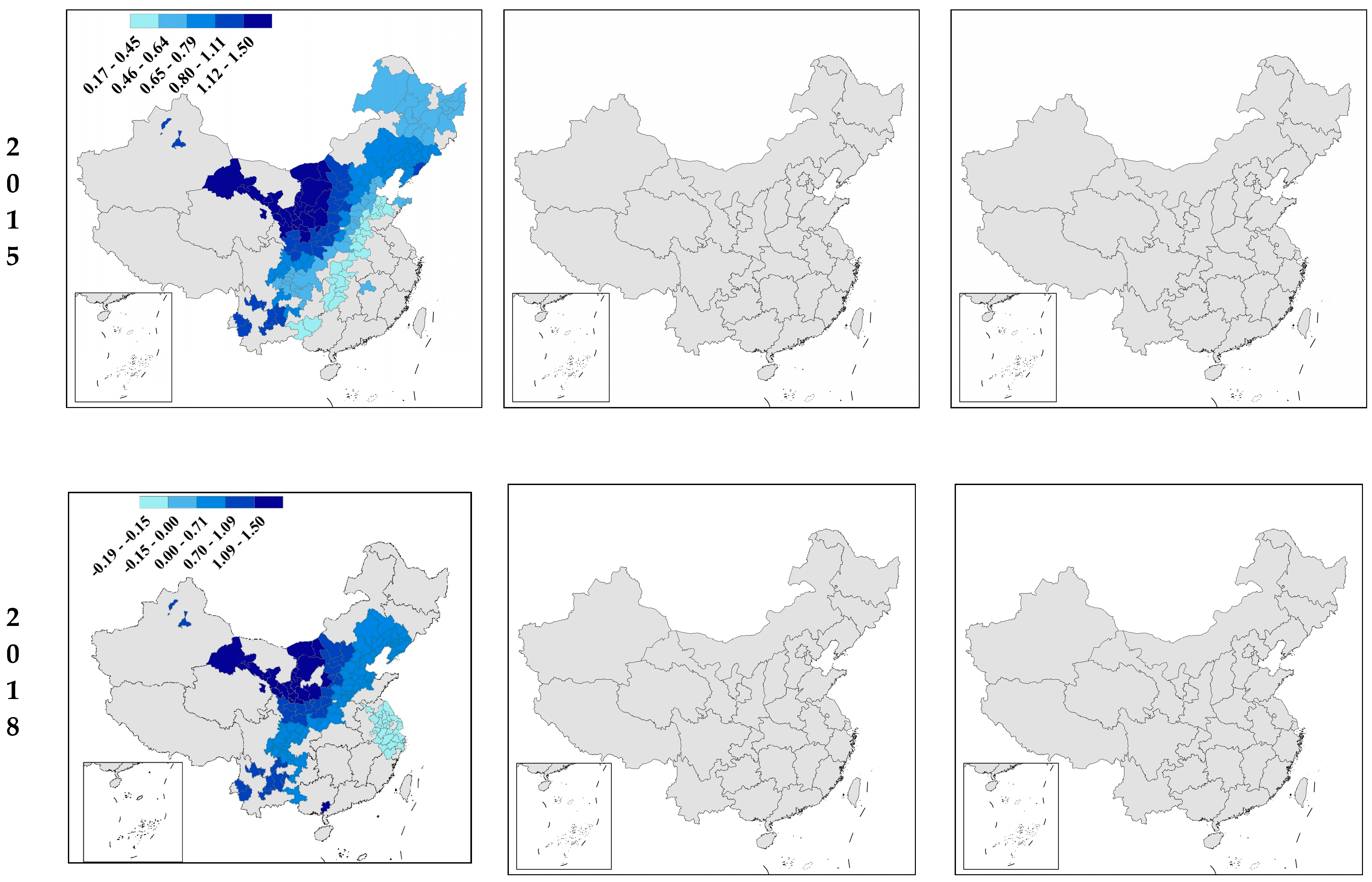
| Variable | Number of Observations | Mean | STD | 1st Quartile | 2nd Quartile | 3rd Quartile | Reference | |
|---|---|---|---|---|---|---|---|---|
| SUHI (°C) | Daytime | 281 | 0.856 | 1.125 | 0.470 | 1.033 | 1.465 | - |
| Nighttime | 281 | 0.703 | 0.571 | 0.439 | 0.702 | 0.966 | ||
| ΔNDVI (1/103) | 281 | −2.218 | 1.171 | −3.027 | −2.377 | −1.502 | [58,59] | |
| ΔPM2.5 (μg/m3) | 281 | 0.303 | 2.108 | −0.757 | 0.241 | 1.319 | [60,61] | |
| ΔPre (mm) | 281 | 4.939 | 24.033 | −5.315 | 5.218 | 15.210 | [30,62] | |
| NTL (DN value) | 281 | 20.70 | 5.607 | 17.502 | 19.255 | 21.968 | [28,63] | |
| Pop (104 Person) | 281 | 4.328 | 3.073 | 2.382 | 3.664 | 5.675 | [4,40] | |
| 2005 | 2010 | 2015 | 2018 | |||||
|---|---|---|---|---|---|---|---|---|
| Daytime | Nighttime | Daytime | Nighttime | Daytime | Nighttime | Daytime | Daytime | |
| ΔNDVI | −0.735 *** | 0.208 *** | −0726 *** | 0.337 *** | −0.790 *** | 0.399 *** | −0.776 *** | 0.386 *** |
| ΔPRE | −0.013 | −0.014 | 0.068 * | 0.063 | 0.037 | 0.100 | −0.008 | 0.132 ** |
| NTL | 0.082 ** | 0.205 *** | 0.083 ** | 0.056 ** | 0.121 *** | 0.139 *** | 0.131 *** | 0.059 |
| ΔPM2.5 | 0.000 | −0.012 | −0.036 | −0.043 | 0.068 | −0.02 | 0.092 *** | 0.055 |
| POP | 0.003 | 0.001 | 0.019 | 0.012 | 0.034 | 0.06 | 0.04 | 0.074 |
| R2 | 0.545 | 0.087 | 0.540 | 0.135 | 0.666 | 0.181 | 0.658 | 0.176 |
| Adj. R2 | 0.537 | 0.071 | 0.532 | 0.120 | 0.660 | 0.166 | 0.652 | 0.161 |
| AICC | 592.758 | 788.989 | 595.728 | 773.649 | 505.325 | 758.541 | 510.183 | 757.353 |
| RSS | 128.370 | 257.435 | 129.729 | 243.806 | 94.148 | 231 | 96.043 | 231.459 |
| 2005 | 2010 | 2015 | 2018 | |||||
|---|---|---|---|---|---|---|---|---|
| Day | Night | Day | Night | Day | Night | Day | Night | |
| Moran’s Index | 0.408 | 0.261 | 0.475 | 0.334 | 0.544 | 0.246 | 0.546 | 0.260 |
| Z-score | 17.31 | 11.06 | 20.19 | 16.06 | 22.93 | 10.402 | 22.08 | 10.538 |
| p-value | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 |
| 2005 | 2010 | 2015 | 2018 | |||||
|---|---|---|---|---|---|---|---|---|
| Daytime | Nighttime | Daytime | Daytime | Nighttime | Nighttime | Daytime | Nighttime | |
| Bandwidth | 73 | 88 | 63 | 86 | 74 | 98 | 83 | 78 |
| R2 | 0.804 | 0.588 | 0.851 | 0.868 | 0.632 | 0.609 | 0.861 | 0.619 |
| Adj. R2 | 0.756 | 0.508 | 0.810 | 0.842 | 0.545 | 0.543 | 0.832 | 0.535 |
| AICC | 479.856 | 662.772 | 421.886 | 342.88 | 652.109 | 634.155 | 362.921 | 655.341 |
| RSS | 55.396 | 116.224 | 41.919 | 36.968 | 103.365 | 110.241 | 39.175 | 107.310 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Niu, L.; Zhang, Z.; Peng, Z.; Liang, Y.; Liu, M.; Jiang, Y.; Wei, J.; Tang, R. Identifying Surface Urban Heat Island Drivers and Their Spatial Heterogeneity in China’s 281 Cities: An Empirical Study Based on Multiscale Geographically Weighted Regression. Remote Sens. 2021, 13, 4428. https://doi.org/10.3390/rs13214428
Niu L, Zhang Z, Peng Z, Liang Y, Liu M, Jiang Y, Wei J, Tang R. Identifying Surface Urban Heat Island Drivers and Their Spatial Heterogeneity in China’s 281 Cities: An Empirical Study Based on Multiscale Geographically Weighted Regression. Remote Sensing. 2021; 13(21):4428. https://doi.org/10.3390/rs13214428
Chicago/Turabian StyleNiu, Lu, Zhengfeng Zhang, Zhong Peng, Yingzi Liang, Meng Liu, Yazhen Jiang, Jing Wei, and Ronglin Tang. 2021. "Identifying Surface Urban Heat Island Drivers and Their Spatial Heterogeneity in China’s 281 Cities: An Empirical Study Based on Multiscale Geographically Weighted Regression" Remote Sensing 13, no. 21: 4428. https://doi.org/10.3390/rs13214428
APA StyleNiu, L., Zhang, Z., Peng, Z., Liang, Y., Liu, M., Jiang, Y., Wei, J., & Tang, R. (2021). Identifying Surface Urban Heat Island Drivers and Their Spatial Heterogeneity in China’s 281 Cities: An Empirical Study Based on Multiscale Geographically Weighted Regression. Remote Sensing, 13(21), 4428. https://doi.org/10.3390/rs13214428









