Determination of Navigation System Positioning Accuracy Using the Reliability Method Based on Real Measurements
Abstract
:1. Introduction
- The calculations are based on simple Root Mean Square (RMS) determination relationships;
- Gross errors and outliers significantly affect RMS (φ) and RMS (λ), causing a change in the 2DRMS measure;
- Errors are analysed, not as a function of time, but as a function of the subsequent measurement error. The navigation process runs as a function of time. The problem of missing synchronisation with time will emerge in the case of erroneous measurements (recording errors, which have to be removed from the dataset).
- The calculations are quite complex;
- Gross errors and outliers affect the life and failure times in the same way as the other measurements;
- The analysis is carried out as a function of time, similar to the navigation process.
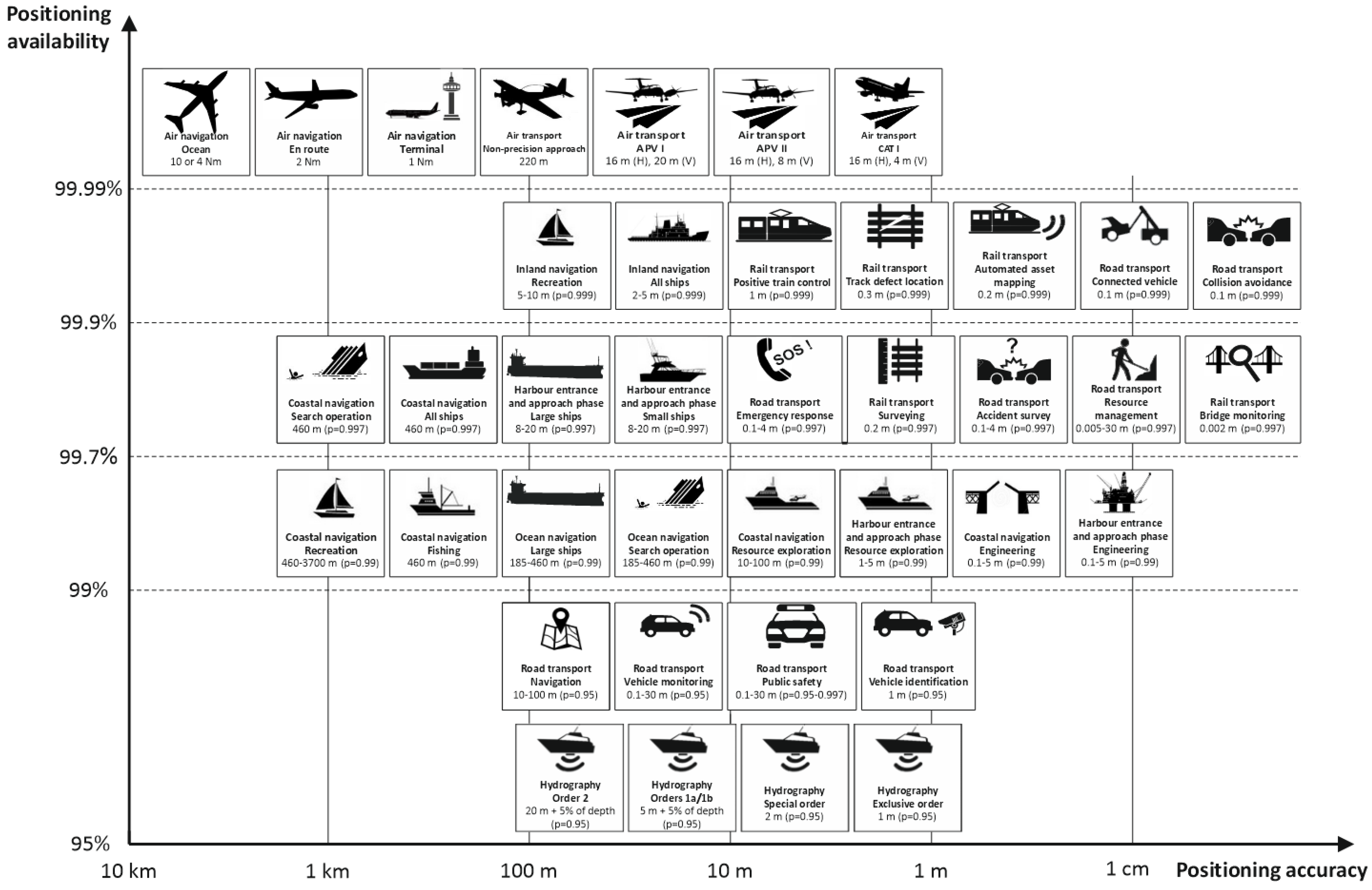
- To propose a new (reliability-based) method to calculate position error values for a navigation system with a probability of 95%;
- To verify which method (classical or reliability) produces results closer to empirical data;
- To check, based on empirical data, the actual measurements of GPS, DGPS and EGNOS systems, whether the distributions of life and failure times for position errors are, in fact, exponential. The other distributions most commonly used in statistics will be tested: beta, Cauchy, chi-square, exponential, gamma, Laplace, logistic, lognormal, normal, Pareto, Rayleigh, Student’s and Weibull.
2. Materials and Methods
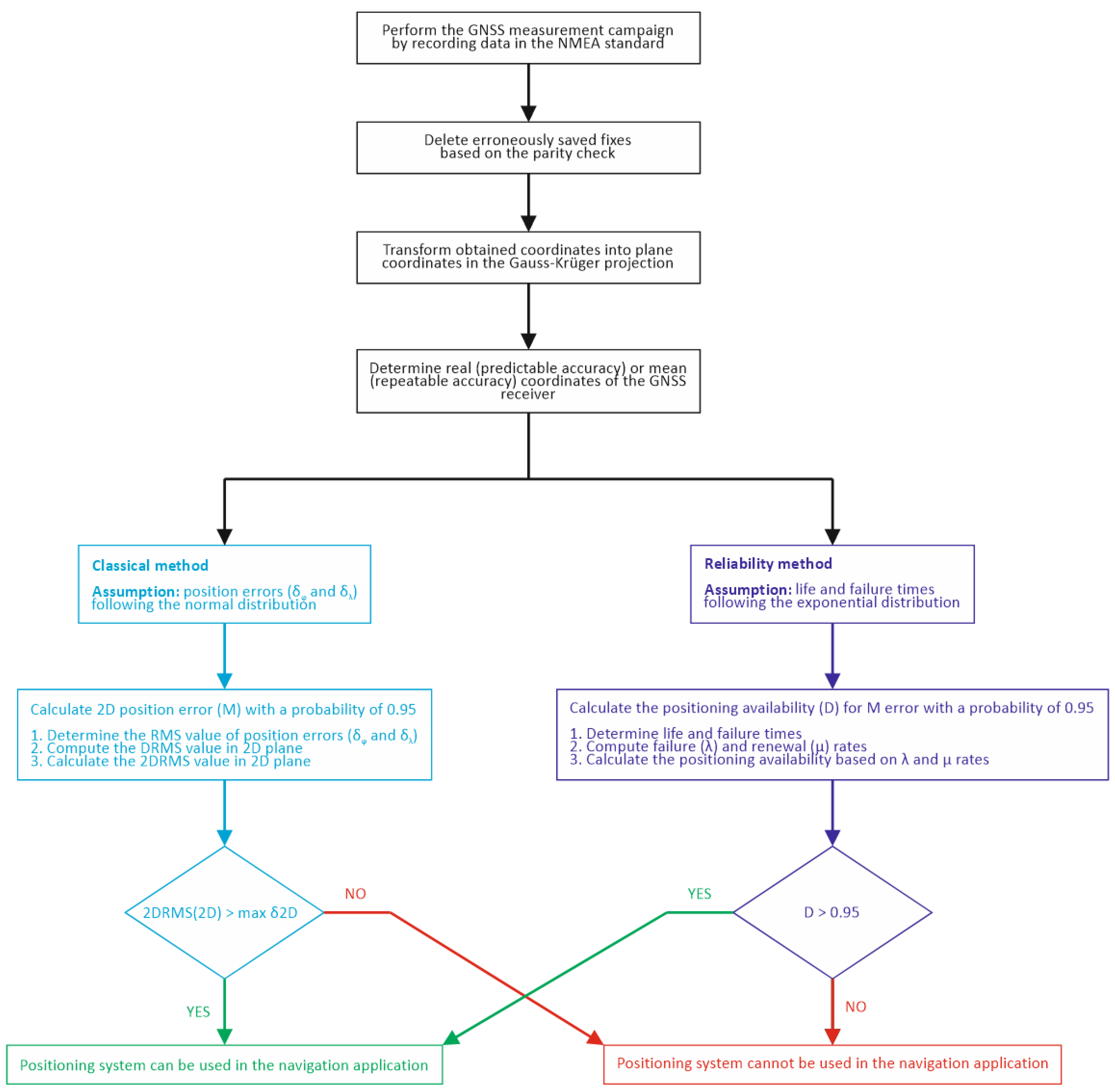
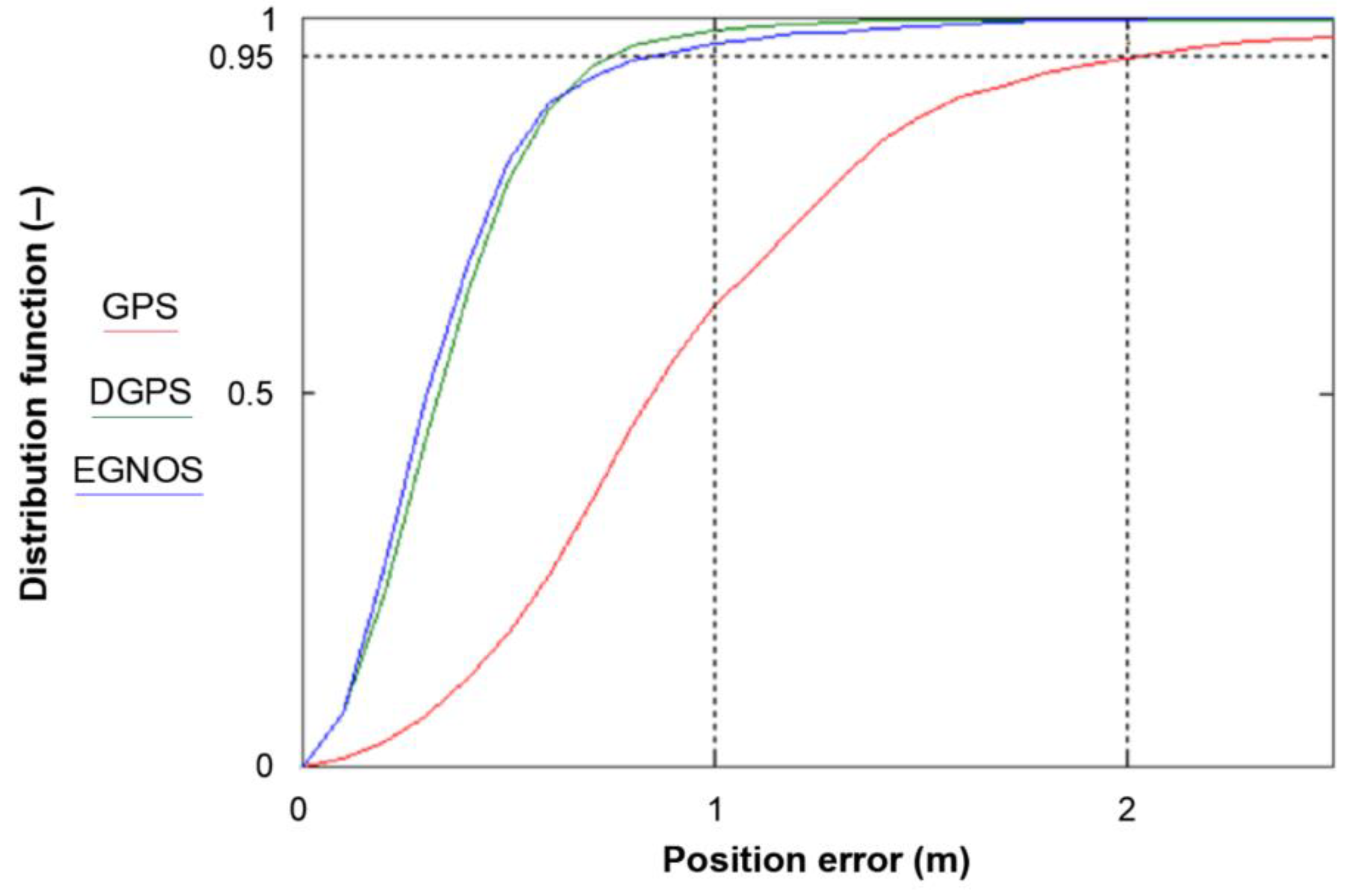
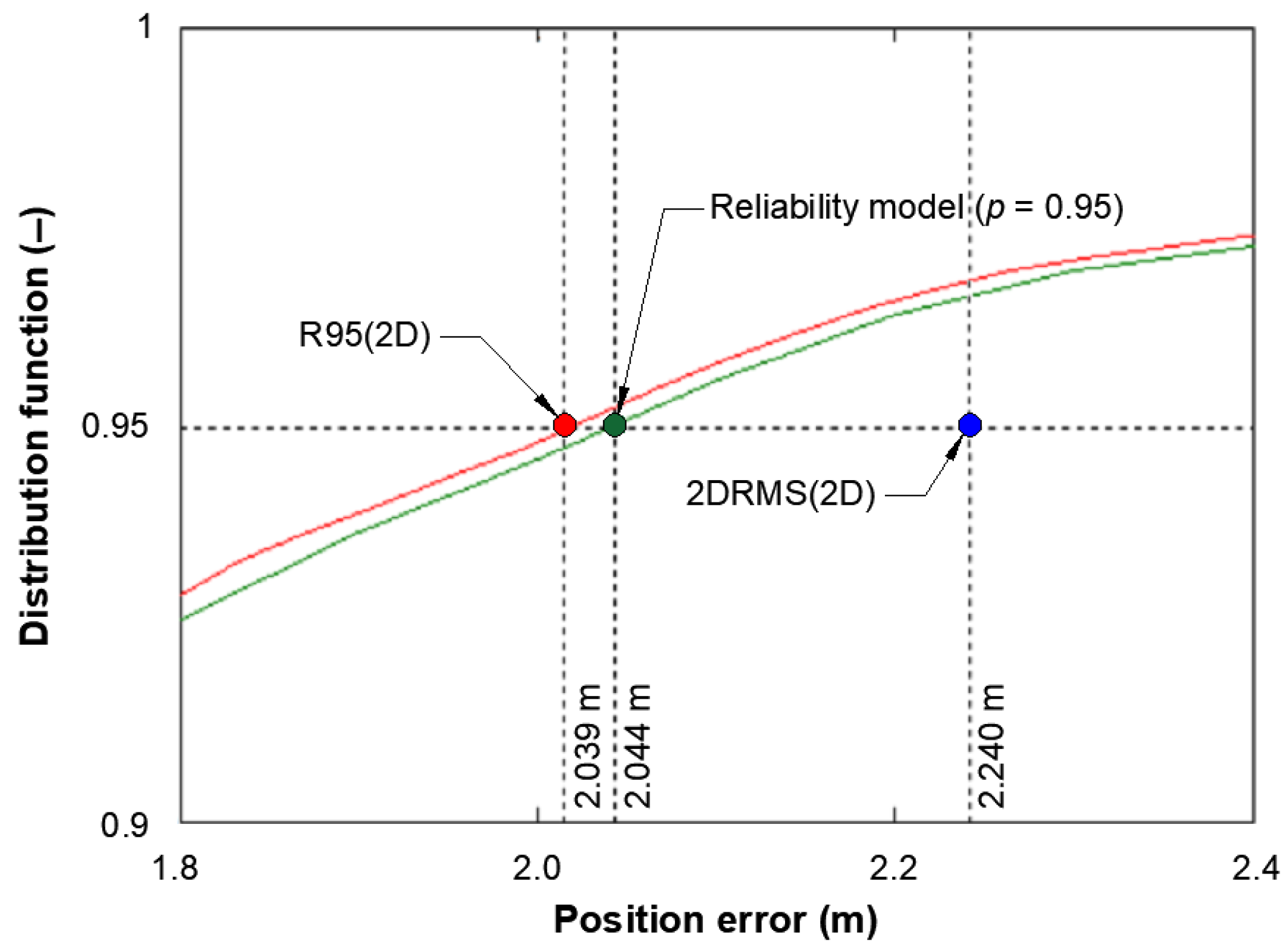
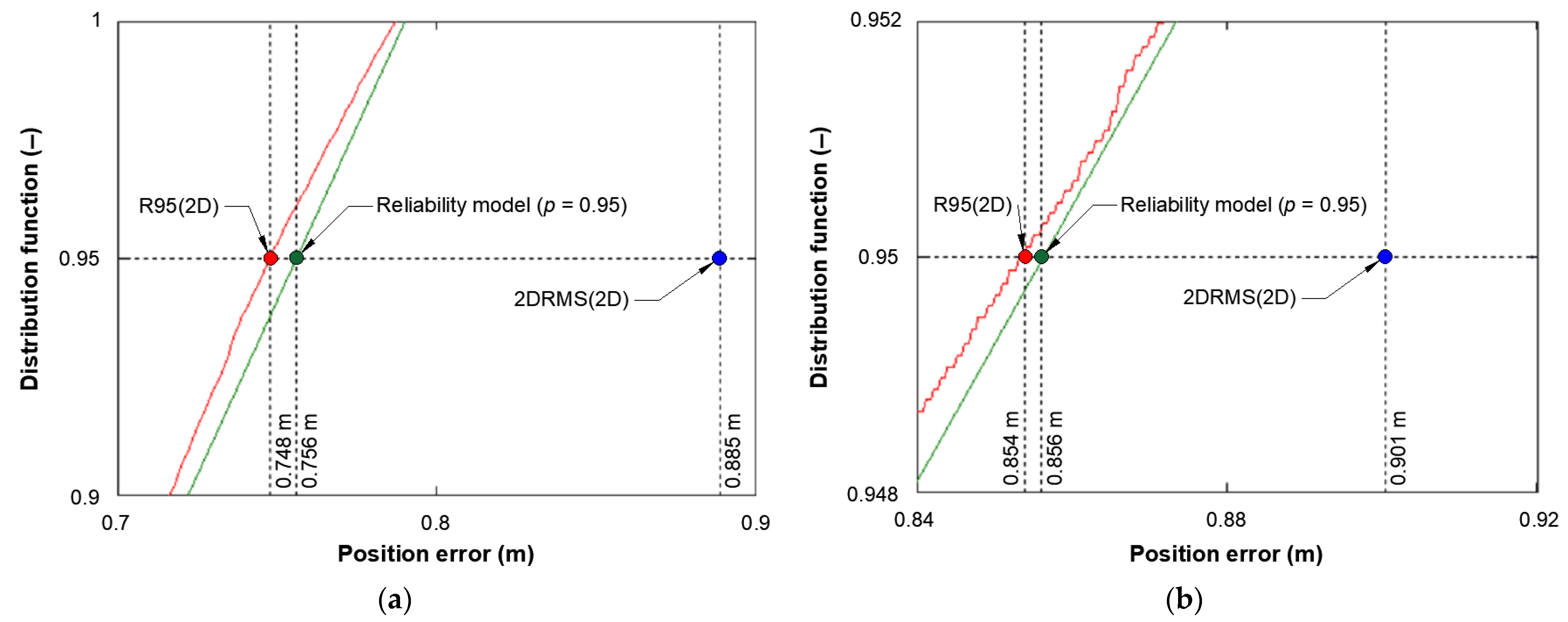
2.1. Classical Method for Determining the Positioning Accuracy of a Navigation System with 95% Probability
2.2. Reliability Method for Determining the Positioning Accuracy of a Navigation System with 95% Probability
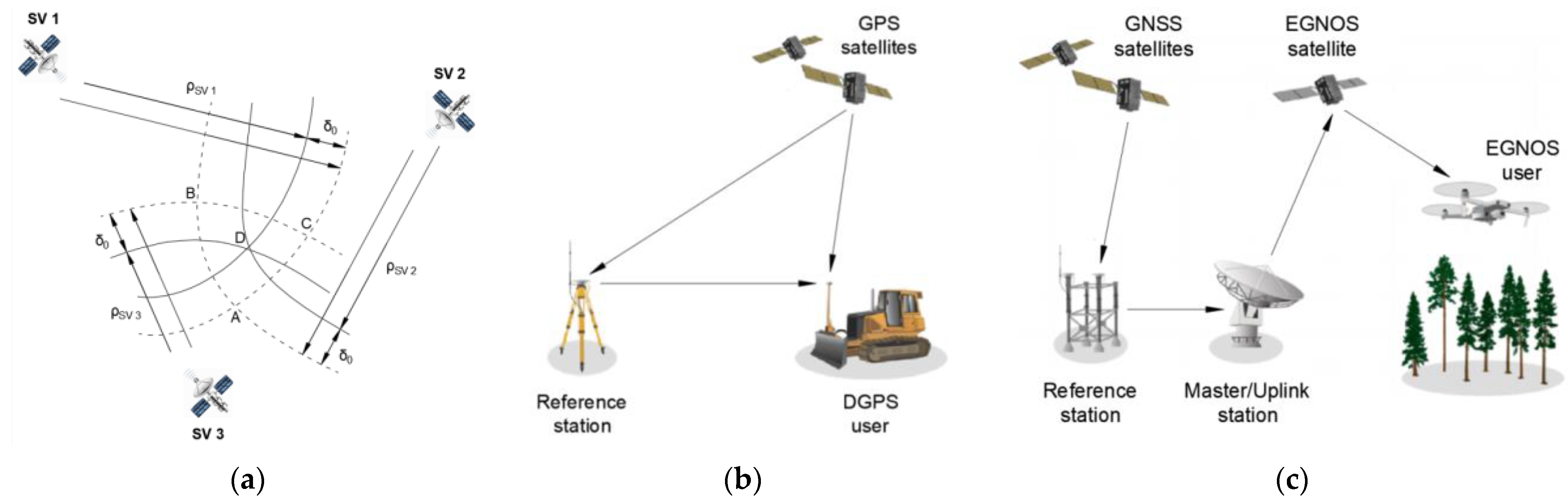
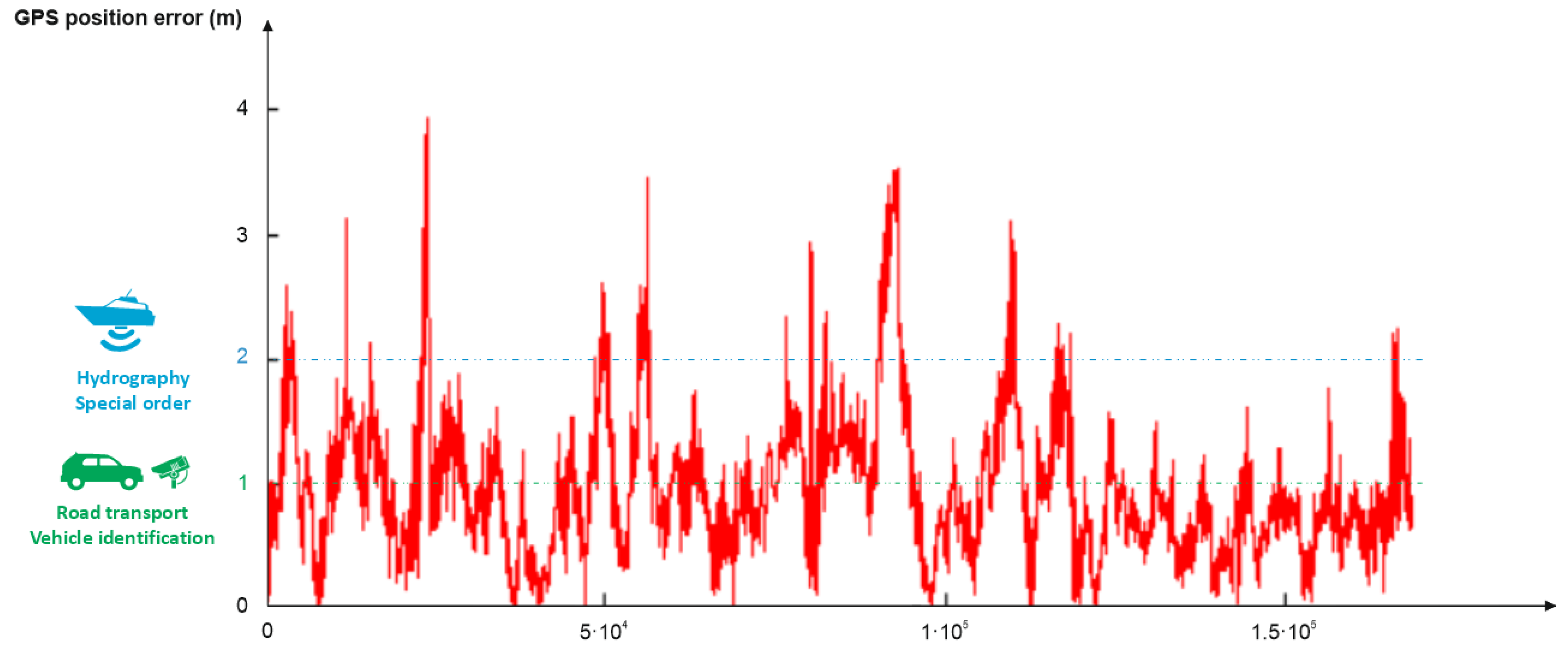
2.3. Description of GPS, DGPS and EGNOS Measurement Campaigns
- The GPS measurements were carried out at a point with coordinates: φ = 54°32.585029′ N and λ = 18°32.741505′ E (Poland). In March 2013, 168′286 fixes were recorded with a recording frequency of 1 Hz. A typical 12-channel GPS code receiver was used in the study;
- The DGPS measurements were carried out at a point with coordinates: φ = 54°31.756087′ N, λ = 18°33.574138′ E and h = 68.070 m (Poland). In April 2014, 951′698 fixes were recorded with a recording frequency of 1 Hz. 900′000 fixes were used for the analyses, which were the same as for EGNOS. A typical marine DGPS code receiver was used in the study;
- The EGNOS measurements were carried out at a point with coordinates: φ = 54°31.756087′ N, λ = 18°33.574138′ E and h = 68.070 m (Poland). In April 2014, 927′553 fixes were recorded with a recording frequency of 1 Hz. 900′000 fixes were used for the analyses, which were the same as for DGPS. A typical land EGNOS code receiver was used in the study.
3. Results
- Do the empirical (actual) distributions of life and failure times for position errors follow an exponential distribution?
- Are there distributions other than exponential with a better fit?
- Depending on the value of the error determining the fitness status (maximum permissible position error for a navigation application), will the statistical distribution of life times change or not?
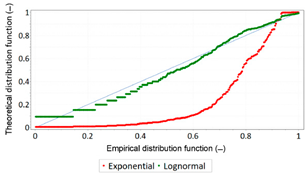
- The analysis of GPS data indicates that the lognormal distribution reflects the course of the PDF of life and failure times determined for navigation system position errors significantly better than the exponential distribution;
- For values above 0.9, the fit between theoretical and empirical distributions (exponential distribution) is very good in all the analysed cases;
- The results obtained from the GPS system also prove that increasing the decision threshold from 1 m to 2 m causes a previously predictable change in the distributions of life and failure times, which does not explicitly prove that this will affect the final results of positioning accuracy calculations;
- Similarly, as in the case of GPS and DGPS systems, EGNOS exhibits similar properties when it comes to fit between the normal distribution and the empirical data.
4. Discussion
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Brodin, G.; Cooper, J.; Walsh, D.; Stevens, J. The Effect of Helicopter Rotors on GPS Signal Reception. J. Navig. 2005, 58, 433–450. [Google Scholar] [CrossRef]
- Krasuski, K.; Ciećko, A.; Bakuła, M.; Wierzbicki, D. New Strategy for Improving the Accuracy of Aircraft Positioning Based on GPS SPP Solution. Sensors 2020, 20, 4921. [Google Scholar] [CrossRef]
- Krasuski, K.; Savchuk, S. Accuracy Assessment of Aircraft Positioning Using the Dual-frequency GPS Code Observations in Aviation. Commun. Sci. Lett. Univ. Zilina 2020, 22, 23–30. [Google Scholar] [CrossRef] [Green Version]
- Lachapelle, G.; Cannon, M.E.; Qiu, W.; Varner, C. Precise Aircraft Single-point Positioning Using GPS Post-mission Orbits and Satellite Clock Corrections. J. Geod. 1996, 70, 562–571. [Google Scholar] [CrossRef]
- Ochieng, W.Y.; Sauer, K.; Walsh, D.; Brodin, G.; Griffin, S.; Denney, M. GPS Integrity and Potential Impact on Aviation Safety. J. Navig. 2003, 56, 51–65. [Google Scholar] [CrossRef]
- Elhajj, M.; Ochieng, W. Impact of New GPS Signals on Positioning Accuracy for Urban Bus Operations. J. Navig. 2020, 73, 1284–1305. [Google Scholar] [CrossRef]
- MacLean, G. Weak GPS Signal Detection in Animal Tracking. J. Navig. 2009, 62, 1–21. [Google Scholar] [CrossRef]
- Naranjo, J.E.; Jiménez, F.; Aparicio, F.; Zato, J. GPS and Inertial Systems for High Precision Positioning on Motorways. J. Navig. 2009, 62, 351–363. [Google Scholar] [CrossRef]
- Ojeda, L.; Borenstein, J. Non-GPS Navigation for Security Personnel and First Responders. J. Navig. 2007, 60, 391–407. [Google Scholar] [CrossRef] [Green Version]
- Sun, Q.C.; Odolinski, R.; Xia, J.C.; Foster, J.; Falkmer, T.; Lee, H. Validating the Efficacy of GPS Tracking Vehicle Movement for Driving Behaviour Assessment. Travel Beh. Soc. 2017, 6, 32–43. [Google Scholar] [CrossRef]
- Bhatti, J.; Humphreys, T.E. Hostile Control of Ships via False GPS Signals: Demonstration and Detection. Navig. J. Inst. Navig. 2017, 64, 51–66. [Google Scholar] [CrossRef]
- Glomsvoll, O.; Bonenberg, L.K. GNSS Jamming Resilience for Close to Shore Navigation in the Northern Sea. J. Navig. 2017, 70, 33–48. [Google Scholar] [CrossRef] [Green Version]
- Han, J.; Park, J.; Kim, J.; Son, N.-S. GPS-less Coastal Navigation Using Marine Radar for USV Operation. IFAC-Papers OnLine 2016, 49, 598–603. [Google Scholar] [CrossRef]
- Ramesh, R.; Jyothi, V.B.N.; Vedachalam, N.; Ramadass, G.A.; Atmanand, M.A. Development and Performance Validation of a Navigation System for an Underwater Vehicle. J. Navig. 2016, 69, 1097–1113. [Google Scholar] [CrossRef] [Green Version]
- Specht, C. Radio Navigation Systems: Definitions and Classifications. J. Navig. 2021, 74, 945–954. [Google Scholar] [CrossRef]
- EC. European Radio Navigation Plan; Version 1.1; EC: Luxembourg, 2018. [Google Scholar]
- GLA. GLA Radio Navigation Plan; GLA: London, UK, 2007. [Google Scholar]
- SMA. Swedish Radio Navigation Plan, Policy and Plans; SMA: Norrköping, Sweden, 2009. [Google Scholar]
- U. S. DoD. 2019 Federal Radionavigation Plan; U.S. DoD: Springfield, VA, USA, 2019. [Google Scholar]
- GSA. Report on Rail User Needs and Requirements; Version 1.0; GSA: Prague, Czech Republic, 2018. [Google Scholar]
- IALA. NAVGUIDE 2018 Marine Aids to Navigation Manual, 8th ed.; IALA: Saint-Germain-en-Laye, France, 2018. [Google Scholar]
- ICAO. Convention on International Civil Aviation of 7th December 1944; ICAO: Montreal, QC, Canada, 1944. [Google Scholar]
- IHO. IHO Standards for Hydrographic Surveys; Special Publication No. 44, 6th ed.; IHO: Monaco, Monaco, 2020. [Google Scholar]
- Reid, T.G.R.; Houts, S.E.; Cammarata, R.; Mills, G.; Agarwal, S.; Vora, A.; Pandey, G. Localization Requirements for Autonomous Vehicles. In Proceedings of the WCX SAE World Congress Experience 2019, Detroit, MI, USA, 9–11 April 2019. [Google Scholar]
- Specht, C. System GPS; Bernardinum Publishing House: Pelplin, Poland, 2007. (In Polish) [Google Scholar]
- Specht, M. Method of Evaluating the Positioning System Capability for Complying with the Minimum Accuracy Requirements for the International Hydrographic Organization Orders. Sensors 2019, 19, 3860. [Google Scholar] [CrossRef] [Green Version]
- Bowditch, N. American Practical Navigator, 2019 ed.; Paradise Cay Publications: Blue Lake, CA, USA, 2019; Volumes 1–2. [Google Scholar]
- U.S. DoD. Global Positioning System Standard Positioning Service Signal Specification, 1st ed.; U.S. DoD: Arlington County, VA, USA, 1993. [Google Scholar]
- Van Diggelen, F. GPS Accuracy: Lies, Damn Lies, and Statistics. GPS World 1998, 9, 1–6. [Google Scholar]
- Specht, C.; Pawelski, J.; Smolarek, L.; Specht, M.; Dąbrowski, P. Assessment of the Positioning Accuracy of DGPS and EGNOS Systems in the Bay of Gdansk Using Maritime Dynamic Measurements. J. Navig. 2019, 72, 575–587. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Zhang, X.; Ren, X.; Fritsche, M.; Wickert, J.; Schuh, H. Precise Positioning with Current Multi-constellation Global Navigation Satellite Systems: GPS, GLONASS, Galileo and BeiDou. Sci. Rep. 2021, 5, 8328. [Google Scholar] [CrossRef]
- Specht, C.; Dąbrowski, P.S.; Pawelski, J.; Specht, M.; Szot, T. Comparative Analysis of Positioning Accuracy of GNSS Receivers of Samsung Galaxy Smartphones in Marine Dynamic Measurements. Adv. Space Res. 2019, 63, 3018–3028. [Google Scholar] [CrossRef]
- Szot, T.; Specht, C.; Specht, M.; Dabrowski, P.S. Comparative Analysis of Positioning Accuracy of Samsung Galaxy Smartphones in Stationary Measurements. PLoS ONE 2019, 14, e0215562. [Google Scholar] [CrossRef]
- NovAtel Positioning Leadership. GPS Position Accuracy Measures. Available online: https://www.novatel.com/assets/Documents/Bulletins/apn029.pdf (accessed on 2 November 2021).
- Specht, M. Consistency Analysis of Global Positioning System Position Errors with Typical Statistical Distributions. J. Navig. 2021, 1–18. [Google Scholar] [CrossRef]
- Specht, M. Consistency of the Empirical Distributions of Navigation Positioning System Errors with Theoretical Distributions—Comparative Analysis of the DGPS and EGNOS Systems in the Years 2006 and 2014. Sensors 2021, 21, 31. [Google Scholar] [CrossRef]
- Specht, M. Statistical Distribution Analysis of Navigation Positioning System Errors—Issue of the Empirical Sample Size. Sensors 2020, 20, 7144. [Google Scholar] [CrossRef]
- Cardano, G. The Book on Games of Chance; Princeton University Press: Princeton, NJ, USA, 1953. [Google Scholar]
- Bellhouse, D. Decoding Cardano’s Liber de Ludo Aleae. Hist. Math. 2005, 32, 180–202. [Google Scholar] [CrossRef] [Green Version]
- Huygens, C. De Ratiociniis in Ludo Aleae. In Francisci a Schooten Exercitationum Mathematicarum libri Quinque; van Schooten, F., Ed.; Elsevier: Leiden, Netherlands, 1657; pp. 517–524. [Google Scholar]
- Laplace, P.S. Théorie Analytique des Probabilités; Courcier: Paris, France, 1812. (In French) [Google Scholar]
- Kolmogorov, A. Sulla Determinazione Empirica di una Legge di Distribuzione. Giornale dell’Istituto Italiano degli Attuari 1933, 4, 83–91. (In Italian) [Google Scholar]
- Montgomery, D.C.; Runger, G.C. Applied Statistics and Probability for Engineers, 5th ed.; John Wiley & Sons, Inc: Hoboken, NJ, USA, 2010. [Google Scholar]
- Hong, Y. Probability and Statistics for Economists; World Scientific: Singapore, 2017. [Google Scholar]
- Baron, M. Probability and Statistics for Computer Scientists, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar]
- Mertikas, S.P. Error Distributions and Accuracy Measures in Navigation: An Overview. Available online: https://unbscholar.lib.unb.ca/islandora/object/unbscholar%3A8708 (accessed on 2 November 2021).
- Kendall, M.G.; Buckland, W.R. A Dictionary of Statistical Terms, 4th ed.; Longman: Harlow, UK, 1982. [Google Scholar]
- Feller, W. An Introduction to Probability Theory and its Applications, 3rd ed.; John Wiley & Sons Inc: Hoboken, NJ, USA, 1968; Volume 1. [Google Scholar]
- Specht, C.; Rudnicki, J. A Method for the Assessing of Reliability Characteristics Relevant to an Assumed Position-fixing Accuracy in Navigational Positioning Systems. Pol. Marit. Res. 2016, 23, 20–27. [Google Scholar] [CrossRef] [Green Version]
- Barlow, R.E.; Proschan, F. Statistical Theory of Reliability and Life Testing: Probability Models; Holt, Rinehart and Winston: New York, NY, USA, 1974. [Google Scholar]
- Specht, C. Availability, Reliability and Continuity Model of Differential GPS Transmission. Annu. Navig. 2003, 5, 1–85. [Google Scholar]
- U.S. DoD. Global Positioning System Standard Positioning Service Performance Standard, 5th ed.; U.S. DoD: Arlington County, VA, USA, 2020. [Google Scholar]
- IALA. Performance and Monitoring of DGNSS Services in the Frequency Band 283.5-325kHz; IALA: Saint-Germain-en-Laye, France, 2015. [Google Scholar]
- Ketchum, R.L.; Lemmon, J.J.; Hoffman, J.R. Site Selection Plan and Installation Guidelines for a Nationwide Differential GPS Service; ITS: Boulder, CO, USA, 1997. [Google Scholar]
- GSA. EGNOS Open Service (OS) Service Definition Document; Version 2.3; GSA: Prague, Czech Republic, 2017. [Google Scholar]
- Keefe, R.F.; Wempe, A.M.; Becker, R.M.; Zimbelman, E.G.; Nagler, E.S.; Gilbert, S.L.; Caudill, C.C. Positioning Methods and the Use of Location and Activity Data in Forests. Forests 2019, 10, 458. [Google Scholar] [CrossRef] [Green Version]
- EC-DG Enterprise and Industry. EGNOS Safety of Life (SoL) Service Definition Document; Version 3.3; EC-DG Enterprise and Industry: Brussels, Belgium; Luxembourg, 2019. [Google Scholar]


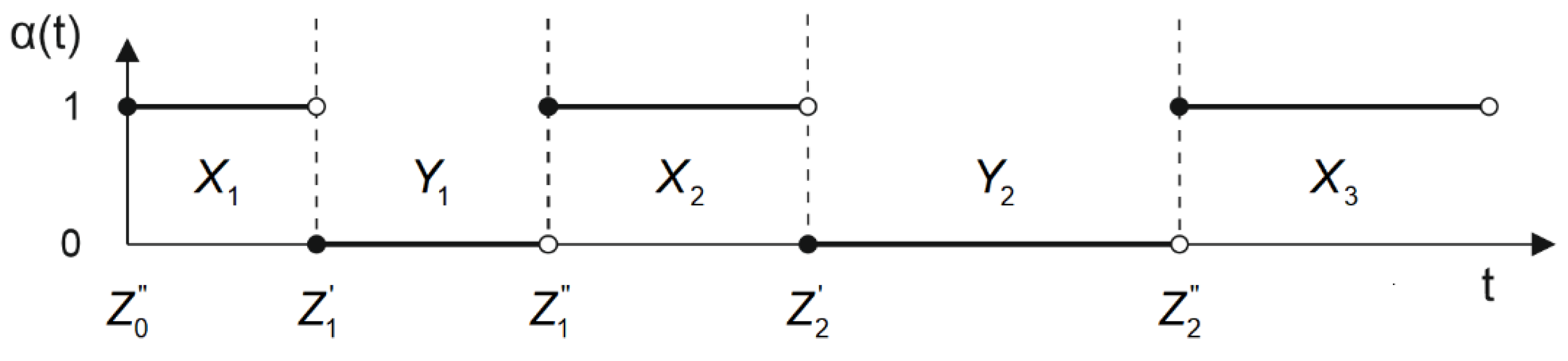

| GPS | |||
|---|---|---|---|
| P-P Plot: Life Time for the Position Error Amounted to 1 m | P-P Plot: Failure Time for the Position Error Amounted to 1 m | ||
 |  |  |  |
| P-P Plot: Life Time for the Position Error Amounted to 2 m | P-P Plot: Failure Time for the Position Error Amounted to 2 m | ||
 |  |  | 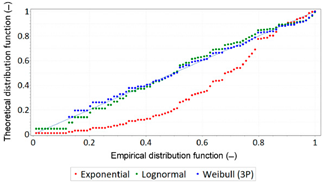 |
| DGPS | |||
|---|---|---|---|
| PDF: Life Time for the Position Error Amounted to 1 m | PDF: Failure Time for the Position Error Amounted to 1 m | ||
 | 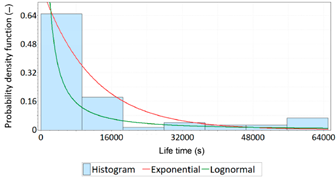 |  | 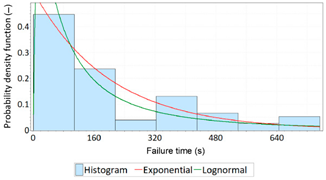 |
| P-P Plot: Life Time for the Position Error Amounted to 1 m | P-P Plot: Failure Time for the Position Error Amounted to 1 m | ||
 |  |  | 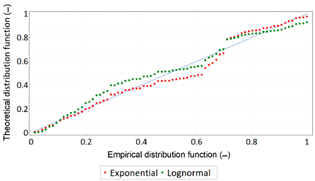 |
| EGNOS | |||
| P-P Plot: Life Time for the Position Error Amounted to 1 m | P-P Plot: Failure Time for the Position Error Amounted to 1 m | ||
 | 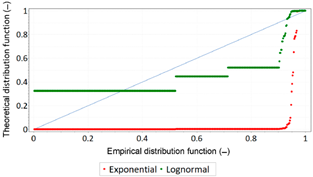 |  | 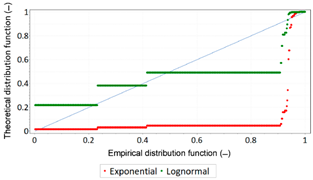 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Specht, M. Determination of Navigation System Positioning Accuracy Using the Reliability Method Based on Real Measurements. Remote Sens. 2021, 13, 4424. https://doi.org/10.3390/rs13214424
Specht M. Determination of Navigation System Positioning Accuracy Using the Reliability Method Based on Real Measurements. Remote Sensing. 2021; 13(21):4424. https://doi.org/10.3390/rs13214424
Chicago/Turabian StyleSpecht, Mariusz. 2021. "Determination of Navigation System Positioning Accuracy Using the Reliability Method Based on Real Measurements" Remote Sensing 13, no. 21: 4424. https://doi.org/10.3390/rs13214424
APA StyleSpecht, M. (2021). Determination of Navigation System Positioning Accuracy Using the Reliability Method Based on Real Measurements. Remote Sensing, 13(21), 4424. https://doi.org/10.3390/rs13214424






