Influence of Varying Solar Zenith Angles on Land Surface Phenology Derived from Vegetation Indices: A Case Study in the Harvard Forest
Abstract
:1. Introduction
2. Study Area and Data
2.1. Study Area
2.2. Data
2.2.1. Ground Measurements
2.2.2. Remote Sensing Data
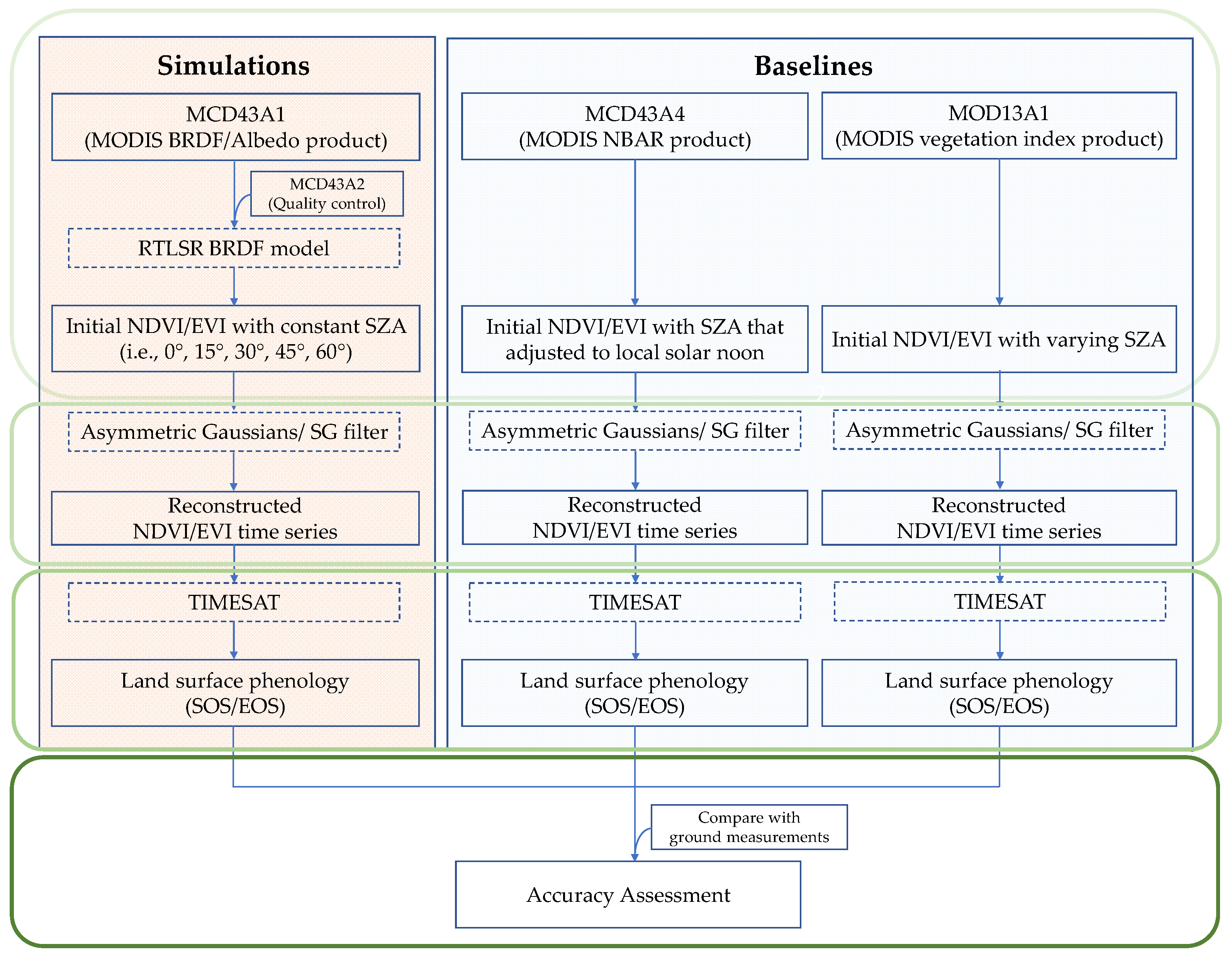
3. Methods
3.1. NDVI/EVI Time Series Simulation Based on the Kernel-Driven Model
3.2. Reconstructing NDVI/EVI Time Series
3.3. Deriving Land Surface Phenology
3.4. Accuracy Assessment
4. Results
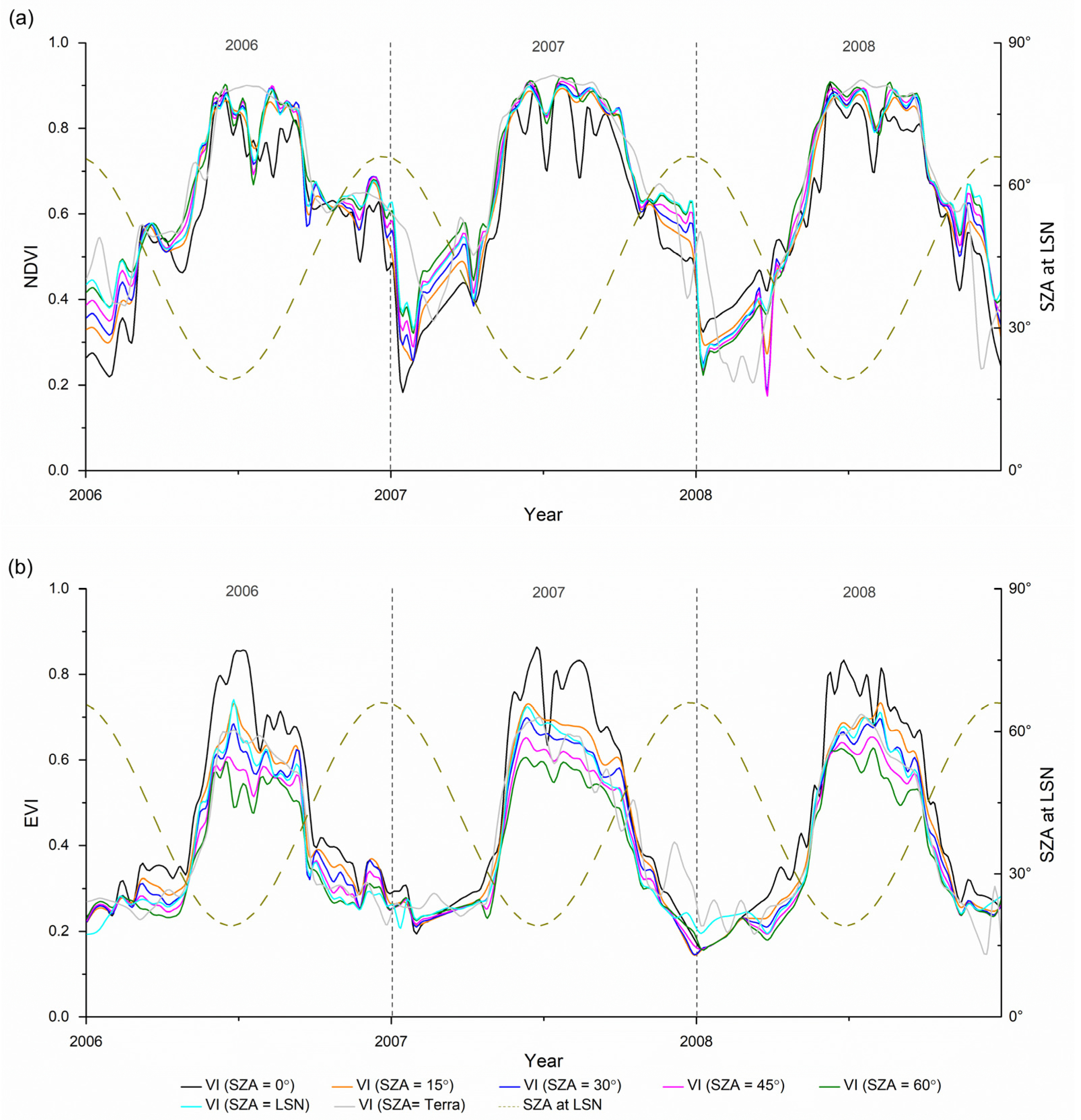
4.1. NDVI and EVI Time Series
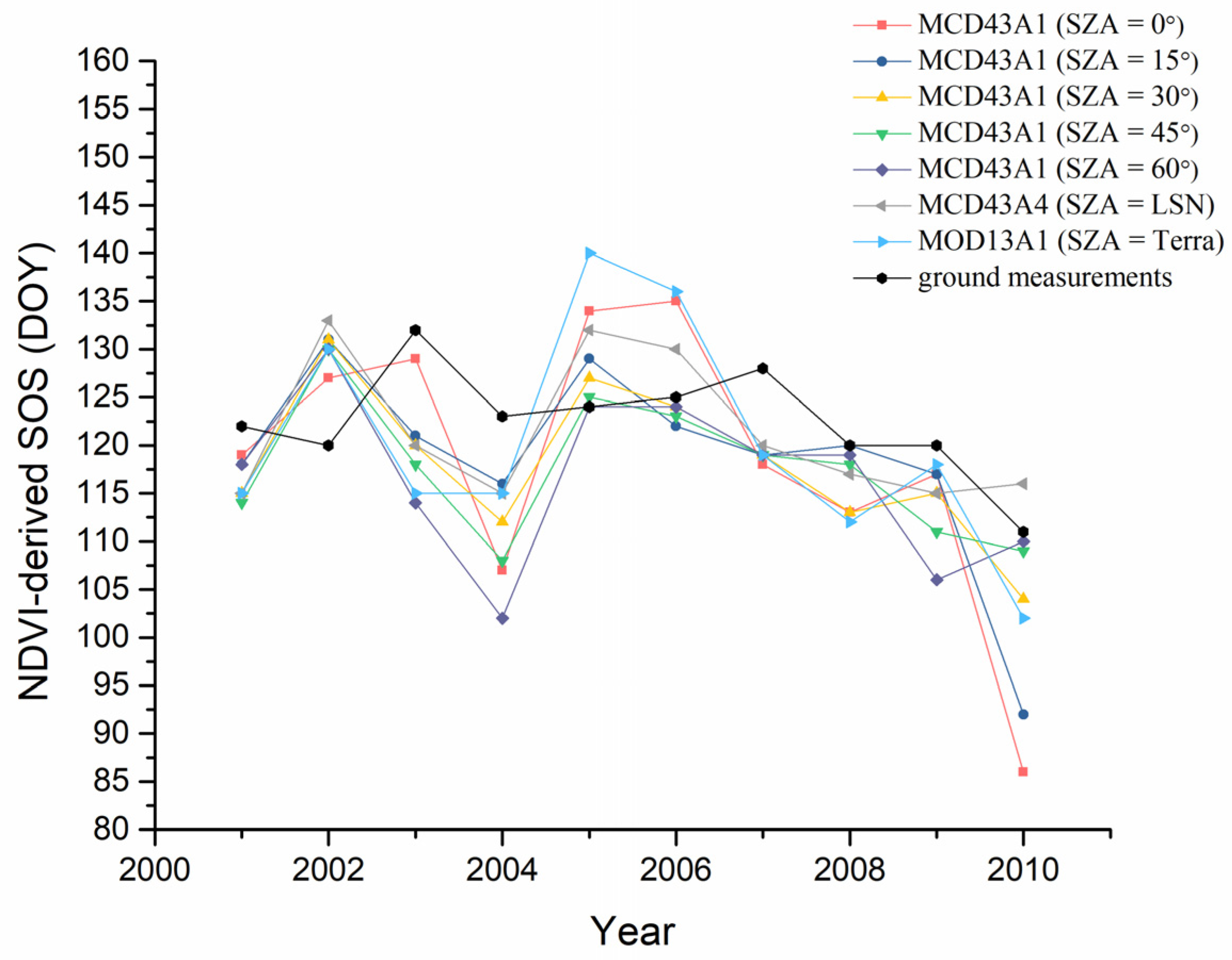
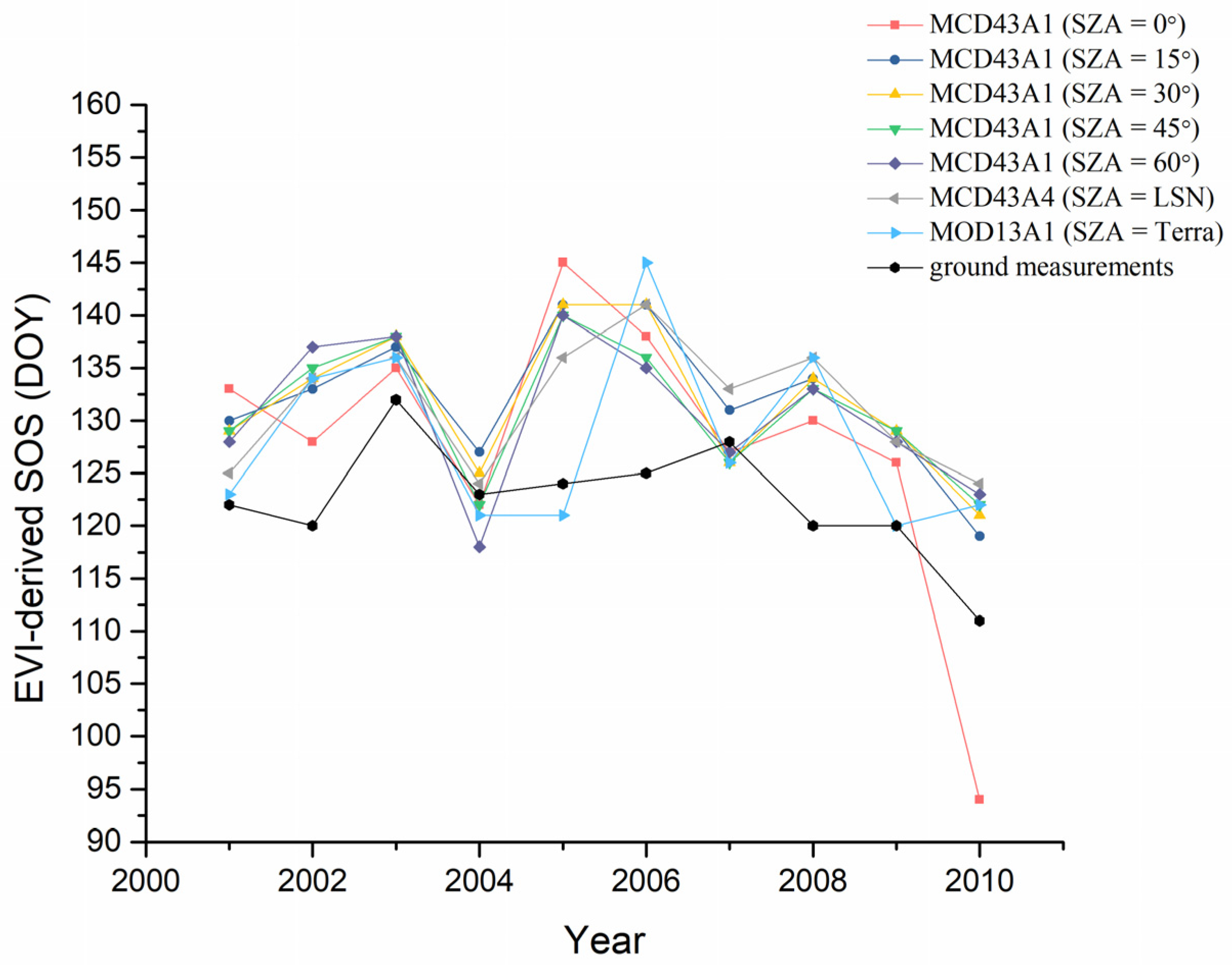
4.2. SOS Derived from NDVI and EVI Time Series
4.2.1. SOS Derived from NDVI Time Series
4.2.2. SOS Derived from EVI Time Series
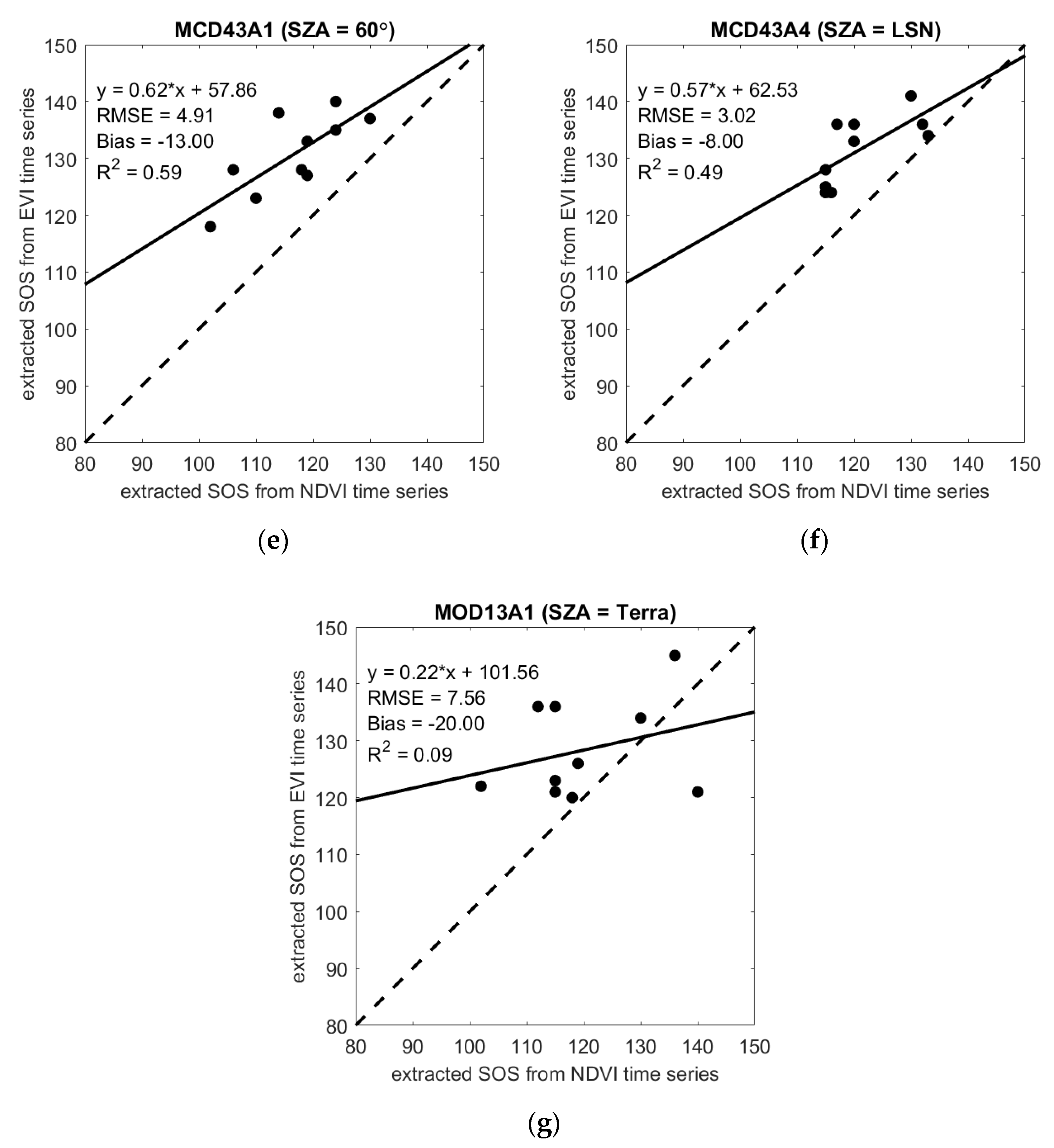
4.2.3. Comparison of SOS Derived from NDVI and EVI Time Series
4.3. EOS Derived from NDVI and EVI Time Series
4.3.1. EOS Derived from NDVI Time Series
4.3.2. EOS Derived from EVI Time Series
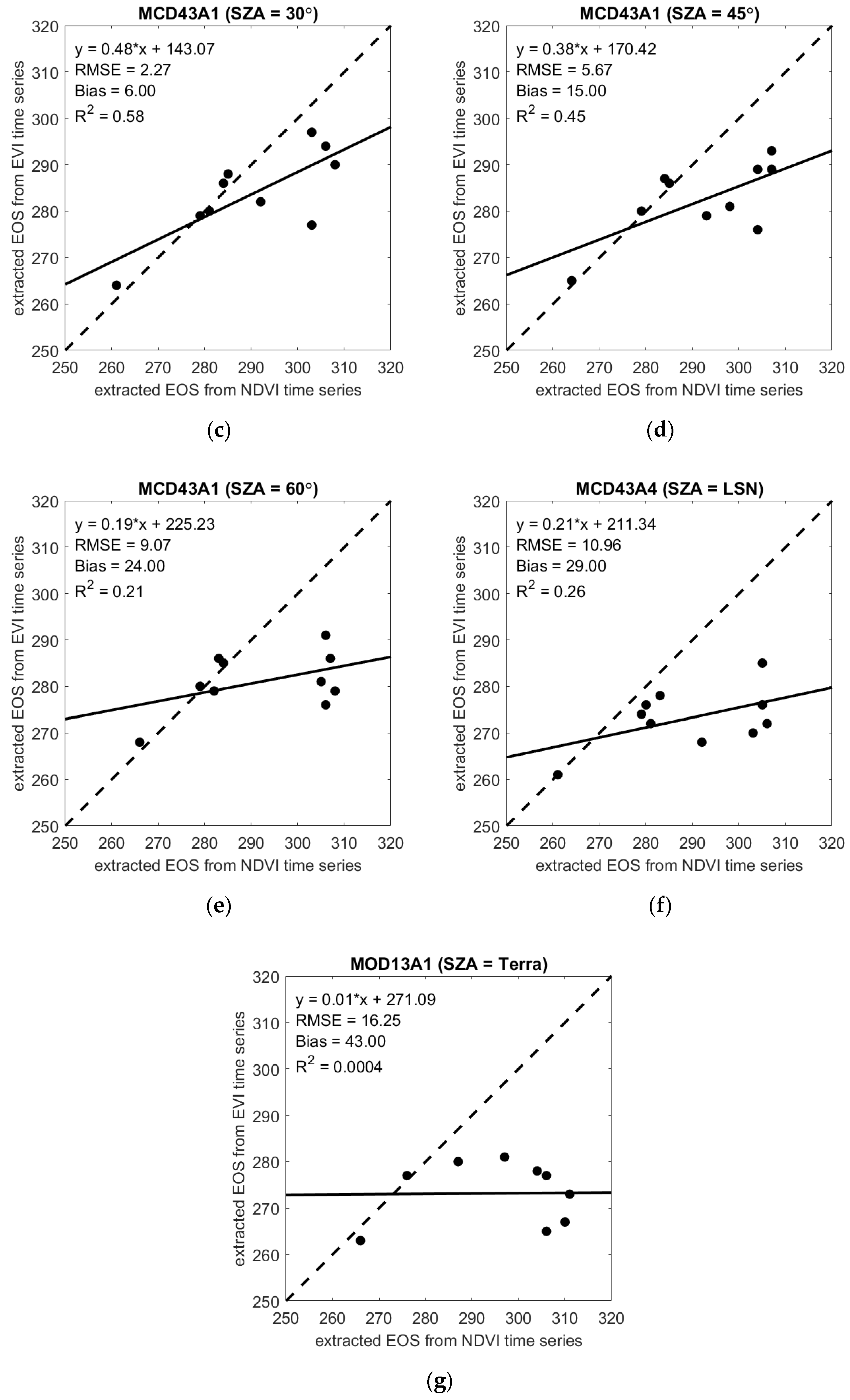
4.3.3. Comparison of EOS Derived from NDVI and EVI Time Series
5. Discussion
5.1. NDVI and EVI Time Series
5.2. Comparison of VI-Derived Land Surface Phenology Metrics
5.3. Impacts from Illumination Geometry on Deriving Land Surface Phenology Metrics
5.4. Uncertainties
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| NDVI | Normalized Difference Vegetation Index |
| EVI | Enhanced Vegetation Index |
| LSP | Land Surface Phenology |
| SOS | Start of Season |
| EOS | End of Season |
| DOY | Day of Year |
| SZA | Solar Zenith Angle |
| LSN | Local Solar Noon |
| BRDF | Bidirectional Reflectance Distribution Function |
| NBAR | Nadir BRDF-Adjusted Reflectance |
References
- Schwartz, M.D. Phenology: An Integrative Environmental Science, 2nd ed.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2003. [Google Scholar]
- Ryu, Y.; Lee, G.; Jeon, S.; Song, Y.; Kimm, H. Monitoring Multi-Layer Canopy Spring Phenology of Temperate Deciduous and Evergreen Forests Using Low-Cost Spectral Sensors. Remote Sens. Environ. 2014, 149, 227–238. [Google Scholar] [CrossRef]
- Helm, B.; Ben-Shlomo, R.; Sheriff, M.J.; Hut, R.A.; Foster, R.; Barnes, B.M.; Dominoni, D. Annual Rhythms That Underlie Phenology: Biological Time-Keeping Meets Environmental Change. Proc. R. Soc. B Biol. Sci. 2013, 280, 20130016. [Google Scholar] [CrossRef] [Green Version]
- Donaldson, J.R.; Lindroth, R.L. Effects of Variable Phytochemistry and Budbreak Phenology on Defoliation of Aspen during a Forest Tent Caterpillar Outbreak. Agric. For. Entomol. 2008, 10, 399–410. [Google Scholar] [CrossRef]
- Zhang, X.; Friedl, M.A.; Schaaf, C.B.; Strahler, A.H.; Hodges, J.C.F.; Gao, F.; Reed, B.C.; Huete, A. Monitoring Vegetation Phenology Using MODIS. Remote Sens. Environ. 2003, 84, 471–475. [Google Scholar] [CrossRef]
- Peñuelas, J.; Rutishauser, T.; Filella, I. Phenology Feedbacks on Climate Change. Science 2009, 324, 887–888. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, X.; Zhou, Y.; Meng, L.; Asrar, G.; Sapkota, A.; Coates, F. Characterizing the Relationship between Satellite Phenology and Pollen Season: A Case Study of Birch. Remote Sens. Environ. 2019, 222, 267–274. [Google Scholar] [CrossRef]
- Sapkota, A.; Dong, Y.; Li, L.; Asrar, G.; Zhou, Y.; Li, X.; Coates, F.; Spanier, A.J.; Matz, J.; Bielory, L.; et al. Association Between Changes in Timing of Spring Onset and Asthma Hospitalization in Maryland. JAMA Netw. Open 2020, 3, e207551. [Google Scholar] [CrossRef]
- Chen, J.M.; Menges, C.H.; Leblanc, S.G. Global Mapping of Foliage Clumping Index Using Multi-Angular Satellite Data. Remote Sens. Environ. 2005, 97, 447–457. [Google Scholar] [CrossRef]
- Jiao, Z.; Dong, Y.; Schaaf, C.B.; Chen, J.M.; Román, M.; Wang, Z.; Zhang, H.; Ding, A.; Erb, A.; Hill, M.J.; et al. An Algorithm for the Retrieval of the Clumping Index (CI) from the MODIS BRDF Product Using an Adjusted Version of the Kernel-Driven BRDF Model. Remote Sens. Environ. 2018, 209, 594–611. [Google Scholar] [CrossRef]
- Cui, L.; Jiao, Z.; Dong, Y.; Sun, M.; Zhang, X.; Yin, S.; Ding, A.; Chang, Y.; Guo, J.; Xie, R. Estimating Forest Canopy Height Using MODIS BRDF Data Emphasizing Typical-Angle Reflectances. Remote Sens. 2019, 11, 2239. [Google Scholar] [CrossRef] [Green Version]
- Jiao, Z.; Hill, M.J.; Schaaf, C.B.; Zhang, H.; Wang, Z.; Li, X. An Anisotropic Flat Index (AFX) to Derive BRDF Archetypes from MODIS. Remote Sens. Environ. 2014, 141, 168–187. [Google Scholar] [CrossRef]
- Galvão, L.S.; Breunig, F.M.; Teles, T.S.; Gaida, W.; Balbinot, R. Investigation of Terrain Illumination Effects on Vegetation Indices and VI-Derived Phenological Metrics in Subtropical Deciduous Forests. GISci. Remote Sens. 2016, 53, 360–381. [Google Scholar] [CrossRef]
- Karkauskaite, P.; Tagesson, T.; Fensholt, R. Evaluation of the Plant Phenology Index (PPI), NDVI and EVI for Start-of-Season Trend Analysis of the Northern Hemisphere Boreal Zone. Remote Sens. 2017, 9, 485. [Google Scholar] [CrossRef] [Green Version]
- Peng, D.; Wu, C.; Li, C.; Zhang, X.; Liu, Z.; Ye, H.; Luo, S.; Liu, X.; Hu, Y.; Fang, B. Spring Green-up Phenology Products Derived from MODIS NDVI and EVI: Intercomparison, Interpretation and Validation Using National Phenology Network and AmeriFlux Observations. Ecol. Indic. 2017, 77, 323–336. [Google Scholar] [CrossRef]
- Tan, B.; Morisette, J.T.; Wolfe, R.E.; Gao, F.; Ederer, G.A.; Nightingale, J.; Pedelty, J.A. Vegetation Phenology Metrics Derived from Temporally Smoothed and Gap-Filled MODIS Data. In Proceedings of the IGARSS 2008 IEEE International Geoscience and Remote Sensing Symposium, Boston, MA, USA, 6–11 July 2008; Volume 3, pp. III-593–III-596. [Google Scholar]
- Li, X.; Zhou, Y.; Meng, L.; Asrar, G.R.; Lu, C.; Wu, Q. A Dataset of 30 m Annual Vegetation Phenology Indicators (1985–2015) in Urban Areas of the Conterminous United States. Earth Syst. Sci. Data Online 2019, 11, 881–894. [Google Scholar] [CrossRef] [Green Version]
- Gao, F.; Anderson, M.; Daughtry, C.; Karnieli, A.; Hively, D.; Kustas, W. A Within-Season Approach for Detecting Early Growth Stages in Corn and Soybean Using High Temporal and Spatial Resolution Imagery. Remote Sens. Environ. 2020, 242, 111752. [Google Scholar] [CrossRef]
- Xie, Y.; Wilson, A.M. Change Point Estimation of Deciduous Forest Land Surface Phenology. Remote Sens. Environ. 2020, 240, 111698. [Google Scholar] [CrossRef]
- Zhao, K.; Wulder, M.A.; Hu, T.; Bright, R.; Wu, Q.; Qin, H.; Li, Y.; Toman, E.; Mallick, B.; Zhang, X.; et al. Detecting Change-Point, Trend, and Seasonality in Satellite Time Series Data to Track Abrupt Changes and Nonlinear Dynamics: A Bayesian Ensemble Algorithm. Remote Sens. Environ. 2019, 232, 111181. [Google Scholar] [CrossRef]
- Li, X.; Zhou, Y.; Asrar, G.R.; Meng, L. Characterizing Spatiotemporal Dynamics in Phenology of Urban Ecosystems Based on Landsat Data. Sci. Total Environ. 2017, 605–606, 721–734. [Google Scholar] [CrossRef] [PubMed]
- Jeong, S.-J.; Schimel, D.; Frankenberg, C.; Drewry, D.T.; Fisher, J.B.; Verma, M.; Berry, J.A.; Lee, J.-E.; Joiner, J. Application of Satellite Solar-Induced Chlorophyll Fluorescence to Understanding Large-Scale Variations in Vegetation Phenology and Function over Northern High Latitude Forests. Remote Sens. Environ. 2017, 190, 178–187. [Google Scholar] [CrossRef]
- Motohka, T.; Nasahara, K.N.; Oguma, H.; Tsuchida, S. Applicability of Green-Red Vegetation Index for Remote Sensing of Vegetation Phenology. Remote Sens. 2010, 2, 2369–2387. [Google Scholar] [CrossRef] [Green Version]
- Testa, S.; Soudani, K.; Boschetti, L.; Borgogno Mondino, E. MODIS-Derived EVI, NDVI and WDRVI Time Series to Estimate Phenological Metrics in French Deciduous Forests. Int. J. Appl. Earth Obs. Geoinf. 2018, 64, 132–144. [Google Scholar] [CrossRef]
- Fu, Y.H.; Piao, S.; de Beeck, M.O.; Cong, N.; Zhao, H.; Zhang, Y.; Menzel, A.; Janssens, I.A. Recent Spring Phenology Shifts in Western Central Europe Based on Multiscale Observations. Glob. Ecol. Biogeogr. 2014, 23, 1255–1263. [Google Scholar] [CrossRef]
- Liang, L.; Schwartz, M.D.; Fei, S. Validating Satellite Phenology through Intensive Ground Observation and Landscape Scaling in a Mixed Seasonal Forest. Remote Sens. Environ. 2011, 115, 143–157. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, J.; Gao, F.; Liu, Y.; Schaaf, C.; Friedl, M.; Yu, Y.; Jayavelu, S.; Gray, J.; Liu, L.; et al. Exploration of Scaling Effects on Coarse Resolution Land Surface Phenology. Remote Sens. Environ. 2017, 190, 318–330. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Friedl, M.A.; Schaaf, C.B. Sensitivity of Vegetation Phenology Detection to the Temporal Resolution of Satellite Data. Int. J. Remote Sens. 2009, 30, 2061–2074. [Google Scholar] [CrossRef]
- Klosterman, S.; Melaas, E.; Wang, J.A.; Martinez, A.; Frederick, S.; O’Keefe, J.; Orwig, D.A.; Wang, Z.; Sun, Q.; Schaaf, C.; et al. Fine-Scale Perspectives on Landscape Phenology from Unmanned Aerial Vehicle (UAV) Photography. Agric. For. Meteorol. 2018, 248, 397–407. [Google Scholar] [CrossRef]
- Nasahara, K.N.; Nagai, S. Review: Development of an in situ Observation Network for Terrestrial Ecological Remote Sensing: The Phenological Eyes Network (PEN). Ecol. Res. 2015, 30, 211–223. [Google Scholar] [CrossRef]
- Richardson, A.D.; Hufkens, K.; Milliman, T.; Aubrecht, D.M.; Chen, M.; Gray, J.M.; Johnston, M.R.; Keenan, T.F.; Klosterman, S.T.; Kosmala, M.; et al. Tracking Vegetation Phenology across Diverse North American Biomes Using PhenoCam Imagery. Sci. Data 2018, 5, 180028. [Google Scholar] [CrossRef]
- Hu, T.; Zhao, T.; Zhao, K.; Shi, J. A Continuous Global Record of Near-Surface Soil Freeze/Thaw Status from AMSR-E and AMSR2 Data. Int. J. Remote Sens. 2019, 40, 6993–7016. [Google Scholar] [CrossRef]
- Gao, F.; He, T.; Masek, J.G.; Shuai, Y.; Schaaf, C.B.; Wang, Z. Angular Effects and Correction for Medium Resolution Sensors to Support Crop Monitoring. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 4480–4489. [Google Scholar] [CrossRef]
- Fensholt, R.; Sandholt, I.; Stisen, S.; Tucker, C. Analysing NDVI for the African Continent Using the Geostationary Meteosat Second Generation SEVIRI Sensor. Remote Sens. Environ. 2006, 101, 212–229. [Google Scholar] [CrossRef]
- Fensholt, R.; Sandholt, I.; Proud, S.R.; Stisen, S.; Rasmussen, M.O. Assessment of MODIS Sun-Sensor Geometry Variations Effect on Observed NDVI Using MSG SEVIRI Geostationary Data. Int. J. Remote Sens. 2010, 31, 6163–6187. [Google Scholar] [CrossRef]
- Lindström, J.; Eklundh, L.; Holst, J.; Holst, U. Influence of Solar Zenith Angles on Observed Trends in the NOAA/NASA 8-km Pathfinder Normalized Difference Vegetation Index over the African Sahel. Int. J. Remote Sens. 2006, 27, 1973–1991. [Google Scholar] [CrossRef]
- Roy, D.P.; Li, Z.; Zhang, H.K.; Huang, H. A Conterminous United States Analysis of the Impact of Landsat 5 Orbit Drift on the Temporal Consistency of Landsat 5 Thematic Mapper Data. Remote Sens. Environ. 2020, 240, 111701. [Google Scholar] [CrossRef]
- Galvão, L.S.; de Souza, A.A.; Breunig, F.M. A Hyperspectral Experiment over Tropical Forests Based on the EO-1 Orbit Change and PROSAIL Simulation. GISci. Remote Sens. 2020, 57, 74–90. [Google Scholar] [CrossRef]
- Hao, D.; Wen, J.; Xiao, Q.; Wu, S.; Lin, X.; Dou, B.; You, D.; Tang, Y. Simulation and Analysis of the Topographic Effects on Snow-Free Albedo over Rugged Terrain. Remote Sens. 2018, 10, 278. [Google Scholar] [CrossRef] [Green Version]
- Matsushita, B.; Yang, W.; Chen, J.; Onda, Y.; Qiu, G. Sensitivity of the Enhanced Vegetation Index (EVI) and Normalized Difference Vegetation Index (NDVI) to Topographic Effects: A Case Study in High-Density Cypress Forest. Sensors 2007, 7, 2636–2651. [Google Scholar] [CrossRef] [Green Version]
- Teles, T.S.; Galvão, L.S.; Breunig, F.M.; Balbinot, R.; Gaida, W. Relationships between MODIS Phenological Metrics, Topographic Shade, and Anomalous Temperature Patterns in Seasonal Deciduous Forests of South Brazil. Int. J. Remote Sens. 2015, 36, 4501–4518. [Google Scholar] [CrossRef]
- Bolton, D.K.; Gray, J.M.; Melaas, E.K.; Moon, M.; Eklundh, L.; Friedl, M.A. Continental-Scale Land Surface Phenology from Harmonized Landsat 8 and Sentinel-2 Imagery. Remote Sens. Environ. 2020, 240, 111685. [Google Scholar] [CrossRef]
- Franch, B.; Vermote, E.; Skakun, S.; Roger, J.-C.; Masek, J.; Ju, J.; Villaescusa-Nadal, J.L.; Santamaria-Artigas, A. A Method for Landsat and Sentinel 2 (HLS) BRDF Normalization. Remote Sens. 2019, 11, 632. [Google Scholar] [CrossRef] [Green Version]
- Griffiths, P.; Nendel, C.; Hostert, P. Intra-Annual Reflectance Composites from Sentinel-2 and Landsat for National-Scale Crop and Land Cover Mapping. Remote Sens. Environ. 2019, 220, 135–151. [Google Scholar] [CrossRef]
- Berman, E.E.; Graves, T.A.; Mikle, N.L.; Merkle, J.A.; Johnston, A.N.; Chong, G.W. Comparative Quality and Trend of Remotely Sensed Phenology and Productivity Metrics across the Western United States. Remote Sens. 2020, 12, 2538. [Google Scholar] [CrossRef]
- Kowalski, K.; Senf, C.; Hostert, P.; Pflugmacher, D. Characterizing Spring Phenology of Temperate Broadleaf Forests Using Landsat and Sentinel-2 Time Series. Int. J. Appl. Earth Obs. Geoinf. 2020, 92, 102172. [Google Scholar] [CrossRef]
- Bhandari, S.; Phinn, S.; Gill, T. Assessing Viewing and Illumination Geometry Effects on the MODIS Vegetation Index (MOD13Q1) Time Series: Implications for Monitoring Phenology and Disturbances in Forest Communities in Queensland, Australia. Int. J. Remote Sens. 2011, 32, 7513–7538. [Google Scholar] [CrossRef]
- Ji, L.; Brown, J.F. Effect of NOAA Satellite Orbital Drift on AVHRR-Derived Phenological Metrics. Int. J. Appl. Earth Obs. Geoinf. 2017, 62, 215–223. [Google Scholar] [CrossRef]
- Breunig, F.M.; Galvão, L.S.; dos Santos, J.R.; Gitelson, A.A.; de Moura, Y.M.; Teles, T.S.; Gaida, W. Spectral Anisotropy of Subtropical Deciduous Forest Using MISR and MODIS Data Acquired under Large Seasonal Variation in Solar Zenith Angle. Int. J. Appl. Earth Obs. Geoinf. 2015, 35, 294–304. [Google Scholar] [CrossRef]
- Ma, X.; Huete, A.; Tran, N.N. Interaction of Seasonal Sun-Angle and Savanna Phenology Observed and Modelled Using MODIS. Remote Sens. 2019, 11, 1398. [Google Scholar] [CrossRef] [Green Version]
- Xin, Q.; Broich, M.; Zhu, P.; Gong, P. Modeling Grassland Spring Onset across the Western United States Using Climate Variables and MODIS-Derived Phenology Metrics. Remote Sens. Environ. 2015, 161, 63–77. [Google Scholar] [CrossRef]
- O’Keefe, J. Phenology of Woody Species at Harvard Forest since 1990. Harvard Forest Data Archive: HF003. Available online: https://harvardforest1.fas.harvard.edu/exist/apps/datasets/showData.html?id=HF003 (accessed on 1 October 2021).
- Friedl, M.A.; Gray, J.M.; Melaas, E.K.; Richardson, A.D.; Hufkens, K.; Keenan, T.F.; Bailey, A.; O’Keefe, J. A Tale of Two Springs: Using Recent Climate Anomalies to Characterize the Sensitivity of Temperate Forest Phenology to Climate Change. Environ. Res. Lett. 2014, 9, 054006. [Google Scholar] [CrossRef]
- Keenan, T.F.; Gray, J.; Friedl, M.A.; Toomey, M.; Bohrer, G.; Hollinger, D.Y.; Munger, J.W.; O’Keefe, J.; Schmid, H.P.; Wing, I.S.; et al. Net Carbon Uptake Has Increased through Warming-Induced Changes in Temperate Forest Phenology. Nat. Clim. Chang. 2014, 4, 598–604. [Google Scholar] [CrossRef]
- Keenan, T.F.; Davidson, E.A.; Munger, J.W.; Richardson, A.D. Rate My Data: Quantifying the Value of Ecological Data for the Development of Models of the Terrestrial Carbon Cycle. Ecol. Appl. 2013, 23, 273–286. [Google Scholar] [CrossRef] [Green Version]
- Xu, H.; Twine, T.E.; Yang, X. Evaluating Remotely Sensed Phenological Metrics in a Dynamic Ecosystem Model. Remote Sens. 2014, 6, 4660–4686. [Google Scholar] [CrossRef] [Green Version]
- Keenan, T.F.; Richardson, A.D. The Timing of Autumn Senescence Is Affected by the Timing of Spring Phenology: Implications for Predictive Models. Glob. Chang. Biol. 2015, 21, 2634–2641. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hadley, J.L.; O’Keefe, J.; Munger, J.W.; Hollinger, D.Y.; Richardson, A.D. Phenology of Forest-Atmosphere Carbon Exchange for Deciduous and Coniferous Forests in Southern and Northern New England. In Phenology of Ecosystem Processes; Springer: New York, NY, USA, 2009; pp. 119–141. [Google Scholar]
- Richardson, A.D.; Hollinger, D.Y.; Dail, D.B.; Lee, J.T.; Munger, J.W.; O’keefe, J. Influence of Spring Phenology on Seasonal and Annual Carbon Balance in Two Contrasting New England Forests. Tree Physiol. 2009, 29, 321–331. [Google Scholar] [CrossRef]
- Yang, X.; Mustard, J.F.; Tang, J.; Xu, H. Regional-Scale Phenology Modeling Based on Meteorological Records and Remote Sensing Observations. J. Geophys. Res. Biogeosci. 2012, 117. [Google Scholar] [CrossRef]
- Schaaf, C.B.; Gao, F.; Strahler, A.H.; Lucht, W.; Li, X.; Tsang, T.; Strugnell, N.C.; Zhang, X.; Jin, Y.; Muller, J.-P.; et al. First Operational BRDF, Albedo Nadir Reflectance Products from MODIS. Remote Sens. Environ. 2002, 83, 135–148. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Schaaf, C.B.; Strahler, A.H.; Chopping, M.J.; Román, M.O.; Shuai, Y.; Woodcock, C.E.; Hollinger, D.Y.; Fitzjarrald, D.R. Evaluation of MODIS Albedo Product (MCD43A) over Grassland, Agriculture and Forest Surface Types during Dormant and Snow-Covered Periods. Remote Sens. Environ. 2014, 140, 60–77. [Google Scholar] [CrossRef] [Green Version]
- Shuai, Y.; Schaaf, C.B.; Strahler, A.H.; Liu, J.; Jiao, Z. Quality Assessment of BRDF/Albedo Retrievals in MODIS Operational System. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Jin, H.; Eklundh, L. A Physically Based Vegetation Index for Improved Monitoring of Plant Phenology. Remote Sens. Environ. 2014, 152, 512–525. [Google Scholar] [CrossRef]
- Liu, L.; Liang, L.; Schwartz, M.D.; Donnelly, A.; Wang, Z.; Schaaf, C.B.; Liu, L. Evaluating the Potential of MODIS Satellite Data to Track Temporal Dynamics of Autumn Phenology in a Temperate Mixed Forest. Remote Sens. Environ. 2015, 160, 156–165. [Google Scholar] [CrossRef]
- Ahl, D.E.; Gower, S.T.; Burrows, S.N.; Shabanov, N.V.; Myneni, R.B.; Knyazikhin, Y. Monitoring Spring Canopy Phenology of a Deciduous Broadleaf Forest Using MODIS. Remote Sens. Environ. 2006, 104, 88–95. [Google Scholar] [CrossRef] [Green Version]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the Radiometric and Biophysical Performance of the MODIS Vegetation Indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Shi, H.; Li, L.; Eamus, D.; Huete, A.; Cleverly, J.; Tian, X.; Yu, Q.; Wang, S.; Montagnani, L.; Magliulo, V.; et al. Assessing the Ability of MODIS EVI to Estimate Terrestrial Ecosystem Gross Primary Production of Multiple Land Cover Types. Ecol. Indic. 2017, 72, 153–164. [Google Scholar] [CrossRef] [Green Version]
- Jiao, Z.; Schaaf, C.B.; Dong, Y.; Román, M.; Hill, M.J.; Chen, J.M.; Wang, Z.; Zhang, H.; Saenz, E.; Poudyal, R.; et al. A Method for Improving Hotspot Directional Signatures in BRDF Models Used for MODIS. Remote Sens. Environ. 2016, 186, 135–151. [Google Scholar] [CrossRef] [Green Version]
- Jin, Y.; Schaaf, C.B.; Gao, F.; Li, X.; Strahler, A.H.; Lucht, W.; Liang, S. Consistency of MODIS Surface Bidirectional Reflectance Distribution Function and Albedo Retrievals: 1. Algorithm Performance. J. Geophys. Res. Atmos. 2003, 108. [Google Scholar] [CrossRef]
- Stroeve, J.; Box, J.E.; Gao, F.; Liang, S.; Nolin, A.; Schaaf, C. Accuracy Assessment of the MODIS 16-Day Albedo Product for Snow: Comparisons with Greenland in Situ Measurements. Remote Sens. Environ. 2005, 94, 46–60. [Google Scholar] [CrossRef]
- Dong, Y.; Jiao, Z.; Yin, S.; Zhang, H.; Zhang, X.; Cui, L.; He, D.; Ding, A.; Chang, Y.; Yang, S. Influence of Snow on the Magnitude and Seasonal Variation of the Clumping Index Retrieved from MODIS BRDF Products. Remote Sens. 2018, 10, 1194. [Google Scholar] [CrossRef] [Green Version]
- Privette, J.L.; Eck, T.F.; Deering, D.W. Estimating Spectral Albedo and Nadir Reflectance through Inversion of Simple BRDF Models with AVHRR/MODIS-like Data. J. Geophys. Res. Atmos. 1997, 102, 29529–29542. [Google Scholar] [CrossRef]
- Roujean, J.-L.; Leroy, M.; Deschamps, P.-Y. A Bidirectional Reflectance Model of the Earth’s Surface for the Correction of Remote Sensing Data. J. Geophys. Res. Atmos. 1992, 97, 20455–20468. [Google Scholar] [CrossRef]
- Wanner, W.; Li, X.; Strahler, A.H. On the Derivation of Kernels for Kernel-Driven Models of Bidirectional Reflectance. J. Geophys. Res. Atmos. 1995, 100, 21077–21089. [Google Scholar] [CrossRef]
- Gao, F.; Schaaf, C.B.; Strahler, A.H.; Jin, Y.; Li, X. Detecting Vegetation Structure Using a Kernel-Based BRDF Model. Remote Sens. Environ. 2003, 86, 198–205. [Google Scholar] [CrossRef]
- Zhang, H.; Jiao, Z.; Chen, L.; Dong, Y.; Zhang, X.; Lian, Y.; Qian, D.; Cui, T. Quantifying the Reflectance Anisotropy Effect on Albedo Retrieval from Remotely Sensed Observations Using Archetypal BRDFs. Remote Sens. 2018, 10, 1628. [Google Scholar] [CrossRef] [Green Version]
- Ross, J. The Radiation Regime and Architecture of Plant Stands; Wilhelm Junk: The Hague, The Netherlands, 1981. [Google Scholar]
- Li, X.; Strahler, A.H. Geometric-Optical Bidirectional Reflectance Modeling of the Discrete Crown Vegetation Canopy: Effect of Crown Shape and Mutual Shadowing. IEEE Trans. Geosci. Remote Sens. 1992, 30, 276–292. [Google Scholar] [CrossRef]
- Lucht, W.; Schaaf, C.B.; Strahler, A.H. An Algorithm for the Retrieval of Albedo from Space Using Semiempirical BRDF Models. IEEE Trans. Geosci. Remote Sens. 2000, 38, 977–998. [Google Scholar] [CrossRef] [Green Version]
- Maignan, F.; Bréon, F.-M.; Lacaze, R. Bidirectional Reflectance of Earth Targets: Evaluation of Analytical Models Using a Large Set of Spaceborne Measurements with Emphasis on the Hot Spot. Remote Sens. Environ. 2004, 90, 210–220. [Google Scholar] [CrossRef]
- Xie, Y.; Zhang, X.; Ding, X.; Liu, S.; Zhang, C. Salt-Marsh Geomorphological Patterns Analysis Based on Remote Sensing Images and Lidar-Derived Digital Elevation Model: A Case Study of Xiaoyangkou, Jiangsu. In Proceedings of the International Symposium on Lidar and Radar Mapping 2011: Technologies and Applications, Nanjing, China, 26–29 May 2011; International Society for Optics and Photonics: Bellingham, WA, USA, 2001; Volume 8286, p. 828626. [Google Scholar]
- Jönsson, P.; Eklundh, L. TIMESAT—A Program for Analyzing Time-Series of Satellite Sensor Data. Comput. Geosci. 2004, 30, 833–845. [Google Scholar] [CrossRef] [Green Version]
- Li, R.; Zhang, X.; Liu, B.; Zhang, B. Review on Methods of Remote Sensing Time-Series Data Reconstruction. J. Remote Sens. 2009, 13, 335–341. [Google Scholar]
- Song, C.; Huang, B.; You, S. Comparison of Three Time-Series NDVI Reconstruction Methods Based on TIMESAT. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; pp. 2225–2228. [Google Scholar]
- Gao, F.; Morisette, J.T.; Wolfe, R.E.; Ederer, G.; Pedelty, J.; Masuoka, E.; Myneni, R.; Tan, B.; Nightingale, J. An Algorithm to Produce Temporally and Spatially Continuous MODIS-LAI Time Series. IEEE Geosci. Remote Sens. Lett. 2008, 5, 60–64. [Google Scholar] [CrossRef]
- Reed, B.C.; Brown, J.F.; VanderZee, D.; Loveland, T.R.; Merchant, J.W.; Ohlen, D.O. Measuring Phenological Variability from Satellite Imagery. J. Veg. Sci. 1994, 5, 703–714. [Google Scholar] [CrossRef]
- Jeganathan, C.; Dash, J.; Atkinson, P.M. Remotely Sensed Trends in the Phenology of Northern High Latitude Terrestrial Vegetation, Controlling for Land Cover Change and Vegetation Type. Remote Sens. Environ. 2014, 143, 154–170. [Google Scholar] [CrossRef]
- Piao, S.; Liu, Q.; Chen, A.; Janssens, I.A.; Fu, Y.; Dai, J.; Liu, L.; Lian, X.; Shen, M.; Zhu, X. Plant Phenology and Global Climate Change: Current Progresses and Challenges. Glob. Chang. Biol. 2019, 25, 1922–1940. [Google Scholar] [CrossRef]
- White, K.; Pontius, J.; Schaberg, P. Remote Sensing of Spring Phenology in Northeastern Forests: A Comparison of Methods, Field Metrics and Sources of Uncertainty. Remote Sens. Environ. 2014, 148, 97–107. [Google Scholar] [CrossRef]
- Meng, L.; Mao, J.; Zhou, Y.; Richardson, A.D.; Lee, X.; Thornton, P.E.; Ricciuto, D.M.; Li, X.; Dai, Y.; Shi, X.; et al. Urban Warming Advances Spring Phenology but Reduces the Response of Phenology to Temperature in the Conterminous United States. Proc. Natl. Acad. Sci. USA 2020, 117, 4228–4233. [Google Scholar] [CrossRef]
- Li, X.; Zhou, Y.; Asrar, G.R.; Mao, J.; Li, X.; Li, W. Response of Vegetation Phenology to Urbanization in the Conterminous United States. Glob. Chang. Biol. 2017, 23, 2818–2830. [Google Scholar] [CrossRef]
- Eklundh, L.; Jönsson, P. TIMESAT 3.3 with Seasonal Trend Decomposition and Parallel Processing Software Manual; Lund University: Lund, Sweden, 2017. [Google Scholar]
- Stanimirova, R.; Cai, Z.; Melaas, E.K.; Gray, J.M.; Eklundh, L.; Jönsson, P.; Friedl, M.A. An Empirical Assessment of the MODIS Land Cover Dynamics and TIMESAT Land Surface Phenology Algorithms. Remote Sens. 2019, 11, 2201. [Google Scholar] [CrossRef] [Green Version]
- Zheng, Z.; Zhu, W. Uncertainty of Remote Sensing Data in Monitoring Vegetation Phenology: A Comparison of MODIS C5 and C6 Vegetation Index Products on the Tibetan Plateau. Remote Sens. 2017, 9, 1288. [Google Scholar] [CrossRef] [Green Version]
- Wu, C.; Peng, D.; Soudani, K.; Siebicke, L.; Gough, C.M.; Arain, M.A.; Bohrer, G.; Lafleur, P.M.; Peichl, M.; Gonsamo, A.; et al. Land Surface Phenology Derived from Normalized Difference Vegetation Index (NDVI) at Global FLUXNET Sites. Agric. For. Meteorol. 2017, 233, 171–182. [Google Scholar] [CrossRef]
- Liu, Y.; Wu, C.; Peng, D.; Xu, S.; Gonsamo, A.; Jassal, R.S.; Altaf Arain, M.; Lu, L.; Fang, B.; Chen, J.M. Improved Modeling of Land Surface Phenology Using MODIS Land Surface Reflectance and Temperature at Evergreen Needleleaf Forests of Central North America. Remote Sens. Environ. 2016, 176, 152–162. [Google Scholar] [CrossRef]
- Richardson, A.D.; Keenan, T.F.; Migliavacca, M.; Ryu, Y.; Sonnentag, O.; Toomey, M. Climate Change, Phenology, and Phenological Control of Vegetation Feedbacks to the Climate System. Agric. For. Meteorol. 2013, 169, 156–173. [Google Scholar] [CrossRef]
- Nagai, S.; Inoue, T.; Ohtsuka, T.; Kobayashi, H.; Kurumado, K.; Muraoka, H.; Nasahara, K.N. Relationship between Spatio-Temporal Characteristics of Leaf-Fall Phenology and Seasonal Variations in near Surface- and Satellite-Observed Vegetation Indices in a Cool-Temperate Deciduous Broad-Leaved Forest in Japan. Int. J. Remote Sens. 2014, 35, 3520–3536. [Google Scholar] [CrossRef]
- Pastor-Guzman, J.; Dash, J.; Atkinson, P.M. Remote Sensing of Mangrove Forest Phenology and Its Environmental Drivers. Remote Sens. Environ. 2018, 205, 71–84. [Google Scholar] [CrossRef] [Green Version]
- Evans, S.G.; Small, E.E.; Larson, K.M. Comparison of Vegetation Phenology in the Western USA Determined from Reflected GPS Microwave Signals and NDVI. Int. J. Remote Sens. 2014, 35, 2996–3017. [Google Scholar] [CrossRef]
- Chang, Q.; Xiao, X.; Jiao, W.; Wu, X.; Doughty, R.; Wang, J.; Du, L.; Zou, Z.; Qin, Y. Assessing Consistency of Spring Phenology of Snow-Covered Forests as Estimated by Vegetation Indices, Gross Primary Production, and Solar-Induced Chlorophyll Fluorescence. Agric. For. Meteorol. 2019, 275, 305–316. [Google Scholar] [CrossRef]
- Gao, F.; Jin, Y.; Schaaf, C.B.; Strahler, A.H. Bidirectional NDVI and Atmospherically Resistant BRDF Inversion for Vegetation Canopy. IEEE Trans. Geosci. Remote Sens. 2002, 40, 1269–1278. [Google Scholar] [CrossRef]
- Goodin, D.G.; Gao, J.; Henebry, G.M. The Effect of Solar Illumination Angle and Sensor View Angle on Observed Patterns of Spatial Structure in Tallgrass Prairie. IEEE Trans. Geosci. Remote Sens. 2004, 42, 154–165. [Google Scholar] [CrossRef]
- Zhang, H.K.; Roy, D.P. Landsat 5 Thematic Mapper Reflectance and NDVI 27-Year Time Series Inconsistencies Due to Satellite Orbit Change. Remote Sens. Environ. 2016, 186, 217–233. [Google Scholar] [CrossRef] [Green Version]
- De Moura, Y.M.; Galvão, L.S.; Hilker, T.; Wu, J.; Saleska, S.; do Amaral, C.H.; Nelson, B.W.; Lopes, A.P.; Wiedeman, K.K.; Prohaska, N.; et al. Spectral Analysis of Amazon Canopy Phenology during the Dry Season Using a Tower Hyperspectral Camera and Modis Observations. ISPRS J. Photogramm. Remote Sens. 2017, 131, 52–64. [Google Scholar] [CrossRef]
- Galvão, L.S.; dos Santos, J.R.; Roberts, D.A.; Breunig, F.M.; Toomey, M.; de Moura, Y.M. On Intra-Annual EVI Variability in the Dry Season of Tropical Forest: A Case Study with MODIS and Hyperspectral Data. Remote Sens. Environ. 2011, 115, 2350–2359. [Google Scholar] [CrossRef]
- Aguado, E.; Burt, J.E. Energy Balance and Temperature. In Understanding Weather and Climate; Pearson Education Inc.: London, UK, 2014. [Google Scholar]
- Reed, B.C.; Schwartz, M.D.; Xiao, X. Remote Sensing Phenology. In Phenology of Ecosystem Processes: Applications in Global Change Research; Noormets, A., Ed.; Springer: New York, NY, USA, 2009; pp. 231–246. [Google Scholar]
- Zhang, X.; Friedl, M.A.; Schaaf, C.B. Global Vegetation Phenology from Moderate Resolution Imaging Spectroradiometer (MODIS): Evaluation of Global Patterns and Comparison with in situ Measurements. J. Geophys. Res. Biogeosci. 2006, 111. [Google Scholar] [CrossRef]
- Hmimina, G.; Dufrêne, E.; Pontailler, J.-Y.; Delpierre, N.; Aubinet, M.; Caquet, B.; de Grandcourt, A.; Burban, B.; Flechard, C.; Granier, A.; et al. Evaluation of the Potential of MODIS Satellite Data to Predict Vegetation Phenology in Different Biomes: An Investigation Using Ground-Based NDVI Measurements. Remote Sens. Environ. 2013, 132, 145–158. [Google Scholar] [CrossRef]
- Pisek, J.; Erb, A.; Korhonen, L.; Biermann, T.; Carrara, A.; Cremonese, E.; Cuntz, M.; Fares, S.; Gerosa, G.; Grünwald, T.; et al. Retrieval and Validation of Forest Background Reflectivity from Daily Moderate Resolution Imaging Spectroradiometer (MODIS) Bidirectional Reflectance Distribution Function (BRDF) Data across European Forests. Biogeosciences 2021, 18, 621–635. [Google Scholar] [CrossRef]
- Richardson, A.D.; O’Keefe, J. Phenological Differences Between Understory and Overstory. In Phenology of Ecosystem Processes: Applications in Global Change Research; Noormets, A., Ed.; Springer: New York, NY, USA, 2009; pp. 87–117. ISBN 978-1-4419-0026-5. [Google Scholar]




| Dataset | Purposes |
|---|---|
| MODIS BRDF/Albedo product (MCD43A1) | To simulate reflectance under a set of constant SZAs |
| MODIS BRDF/Albedo Quality product (MCD43A2) | Quality control |
| MODIS NBAR product (MCD43A4) | A baseline product with SZA adjusted to LSN |
| MODIS vegetation index product (MOD13A1) | A baseline product with inconsistent SZAs |
| NDVI Product (with Constant SZAs) | RMSE (Days) | ρ |
|---|---|---|
| MCD43A1 (SZA = 0°) | 11.4 | 0.661 |
| MCD43A1 (SZA = 15°) | 8.9 | 0.442 |
| MCD43A1 (SZA = 30°) | 8.1 | 0.539 |
| MCD43A1 (SZA = 45°) | 8.7 | 0.442 |
| MCD43A1 (SZA = 60°) | 10.8 | 0.285 |
| MCD43A4 (SZA = LSN) | 8.0 | 0.382 |
| MOD13A1 (SZA = Terra) | 10.5 | 0.491 |
| EVI Product (with Constant SZAs) | RMSE (Days) | ρ |
|---|---|---|
| MCD43A1 (SZA = 0°) | 11.1 | 0.709 |
| MCD43A1 (SZA = 15°) | 10.8 | 0.830 |
| MCD43A1 (SZA = 30°) | 11.0 | 0.758 |
| MCD43A1 (SZA = 45°) | 10.3 | 0.709 |
| MCD43A1 (SZA = 60°) | 10.6 | 0.588 |
| MCD43A4 (SZA = LSN) | 10.7 | 0.842 |
| MOD13A1 (SZA = Terra) | 10.0 | 0.345 |
| NDVI Product (with Constant SZAs) | RMSE (Days) | ρ |
|---|---|---|
| MCD43A1 (SZA = 0°) | 6.5 | 0.091 |
| MCD43A1 (SZA = 15°) | 16.6 | 0.321 |
| MCD43A1 (SZA = 30°) | 21.3 | 0.321 |
| MCD43A1 (SZA = 45°) | 6.6 | 0.382 |
| MCD43A1 (SZA = 60°) | 33.7 | 0.248 |
| MCD43A4 (SZA = LSN) | 16.0 | 0.03 |
| MOD13A1 (SZA = Terra) | 5.2 | −0.04 |
| EVI Product (with Constant SZAs) | RMSE (Days) | ρ |
|---|---|---|
| MCD43A1 (SZA = 0°) | 13.3 | 0.927 |
| MCD43A1 (SZA = 15°) | 10.1 | 0.527 |
| MCD43A1 (SZA = 30°) | 8.5 | 0.345 |
| MCD43A1 (SZA = 45°) | 8.5 | 0.515 |
| MCD43A1 (SZA = 60°) | 16.6 | 0.709 |
| MCD43A4 (SZA = LSN) | 5.4 | 0.345 |
| MOD13A1 (SZA = Terra) | 7.4 | 0.818 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Jiao, Z.; Zhao, K.; Dong, Y.; Zhou, Y.; Zeng, Y.; Xu, H.; Zhang, X.; Hu, T.; Cui, L. Influence of Varying Solar Zenith Angles on Land Surface Phenology Derived from Vegetation Indices: A Case Study in the Harvard Forest. Remote Sens. 2021, 13, 4126. https://doi.org/10.3390/rs13204126
Li Y, Jiao Z, Zhao K, Dong Y, Zhou Y, Zeng Y, Xu H, Zhang X, Hu T, Cui L. Influence of Varying Solar Zenith Angles on Land Surface Phenology Derived from Vegetation Indices: A Case Study in the Harvard Forest. Remote Sensing. 2021; 13(20):4126. https://doi.org/10.3390/rs13204126
Chicago/Turabian StyleLi, Yang, Ziti Jiao, Kaiguang Zhao, Yadong Dong, Yuyu Zhou, Yelu Zeng, Haiqing Xu, Xiaoning Zhang, Tongxi Hu, and Lei Cui. 2021. "Influence of Varying Solar Zenith Angles on Land Surface Phenology Derived from Vegetation Indices: A Case Study in the Harvard Forest" Remote Sensing 13, no. 20: 4126. https://doi.org/10.3390/rs13204126
APA StyleLi, Y., Jiao, Z., Zhao, K., Dong, Y., Zhou, Y., Zeng, Y., Xu, H., Zhang, X., Hu, T., & Cui, L. (2021). Influence of Varying Solar Zenith Angles on Land Surface Phenology Derived from Vegetation Indices: A Case Study in the Harvard Forest. Remote Sensing, 13(20), 4126. https://doi.org/10.3390/rs13204126










