Estimating Vertical Distribution of Leaf Water Content within Wheat Canopies after Head Emergence
Abstract
:1. Introduction
2. Materials and Methods
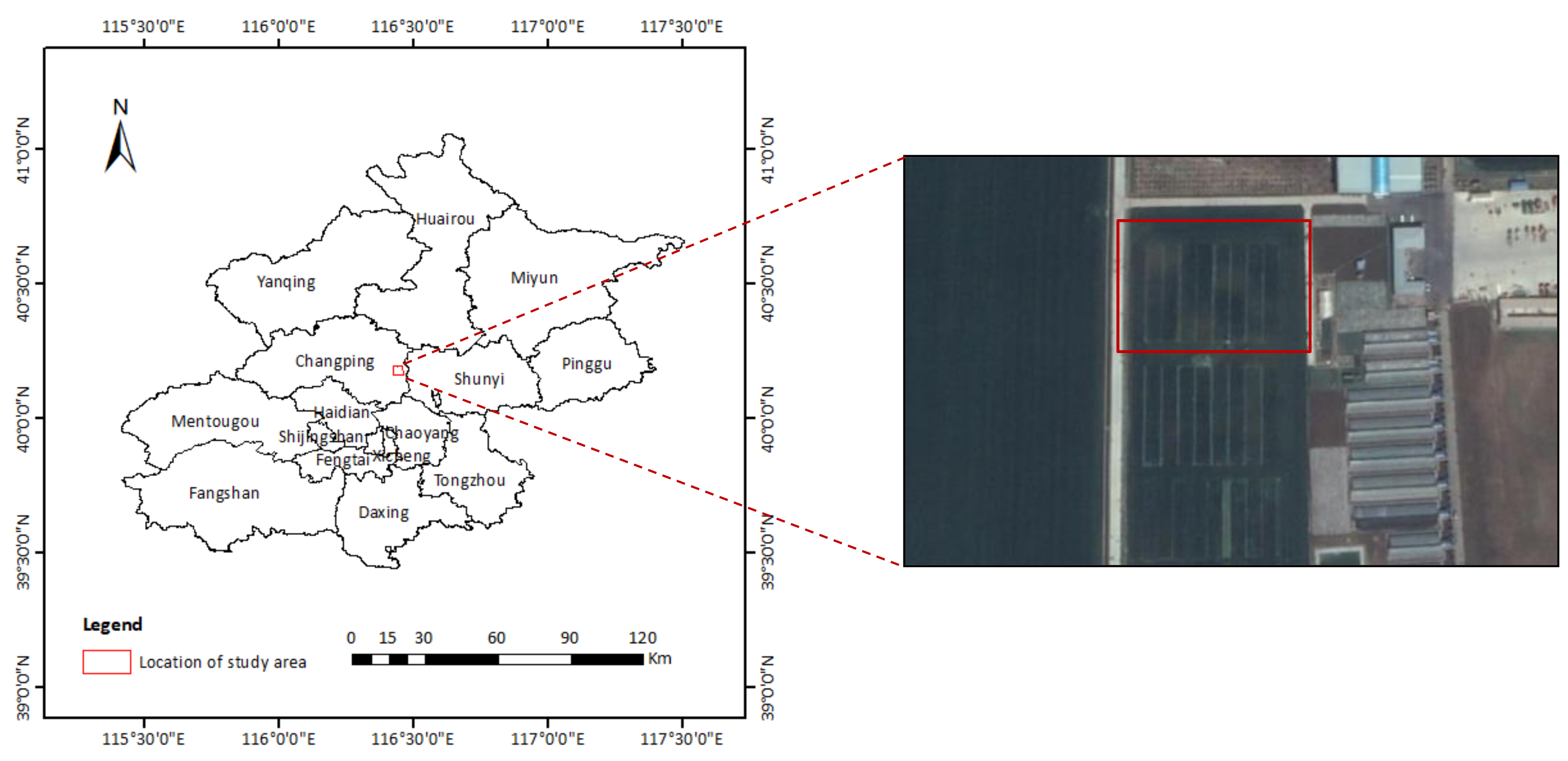
2.1. Field Experiments
2.2. Canopy Spectral Reflectance Measurement
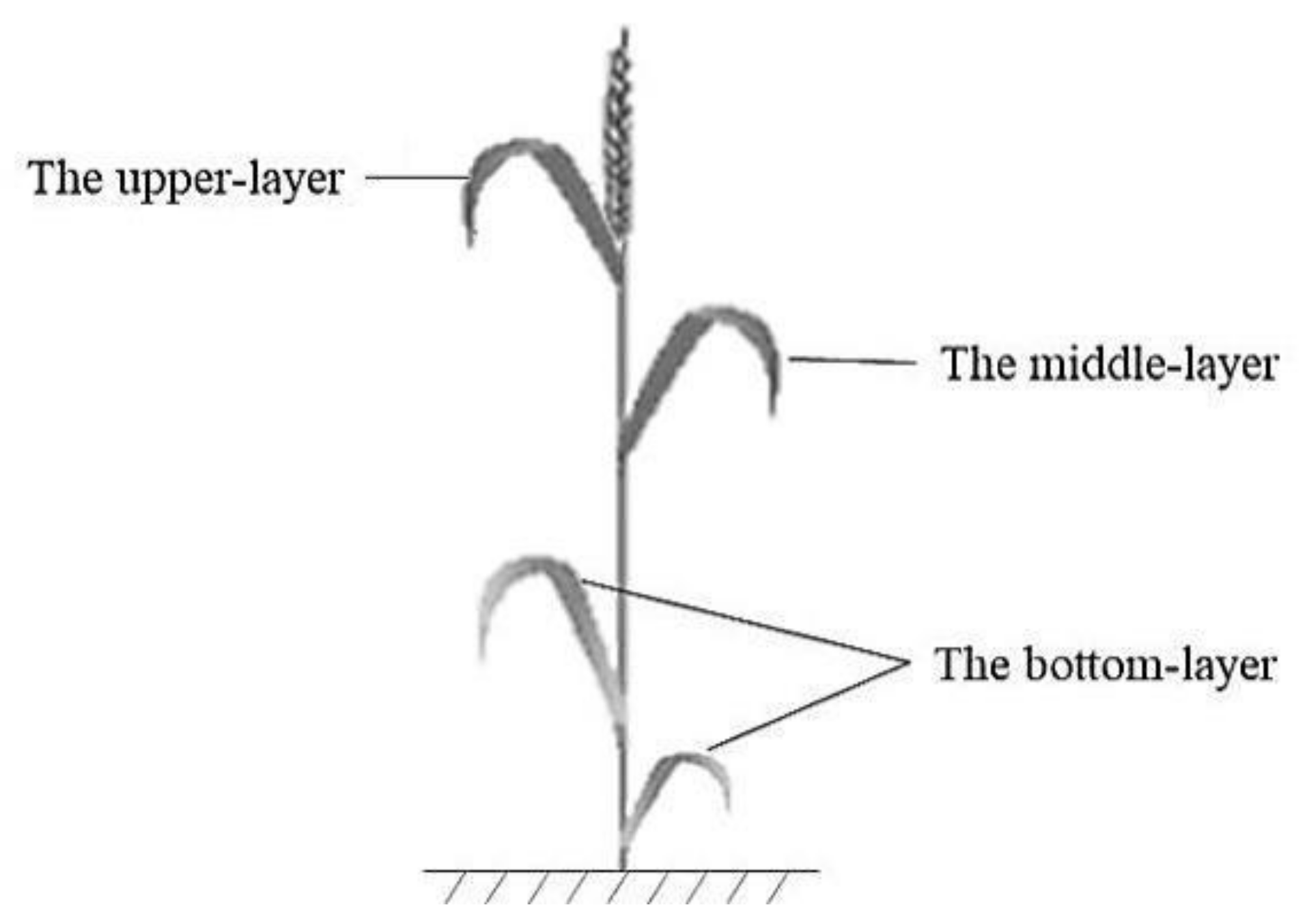
2.3. Vertical Leaf Water Content Distribution Measurement
2.4. Published Spectral Indices
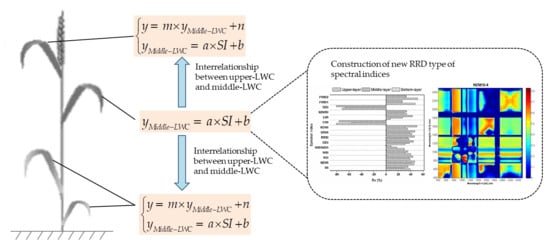
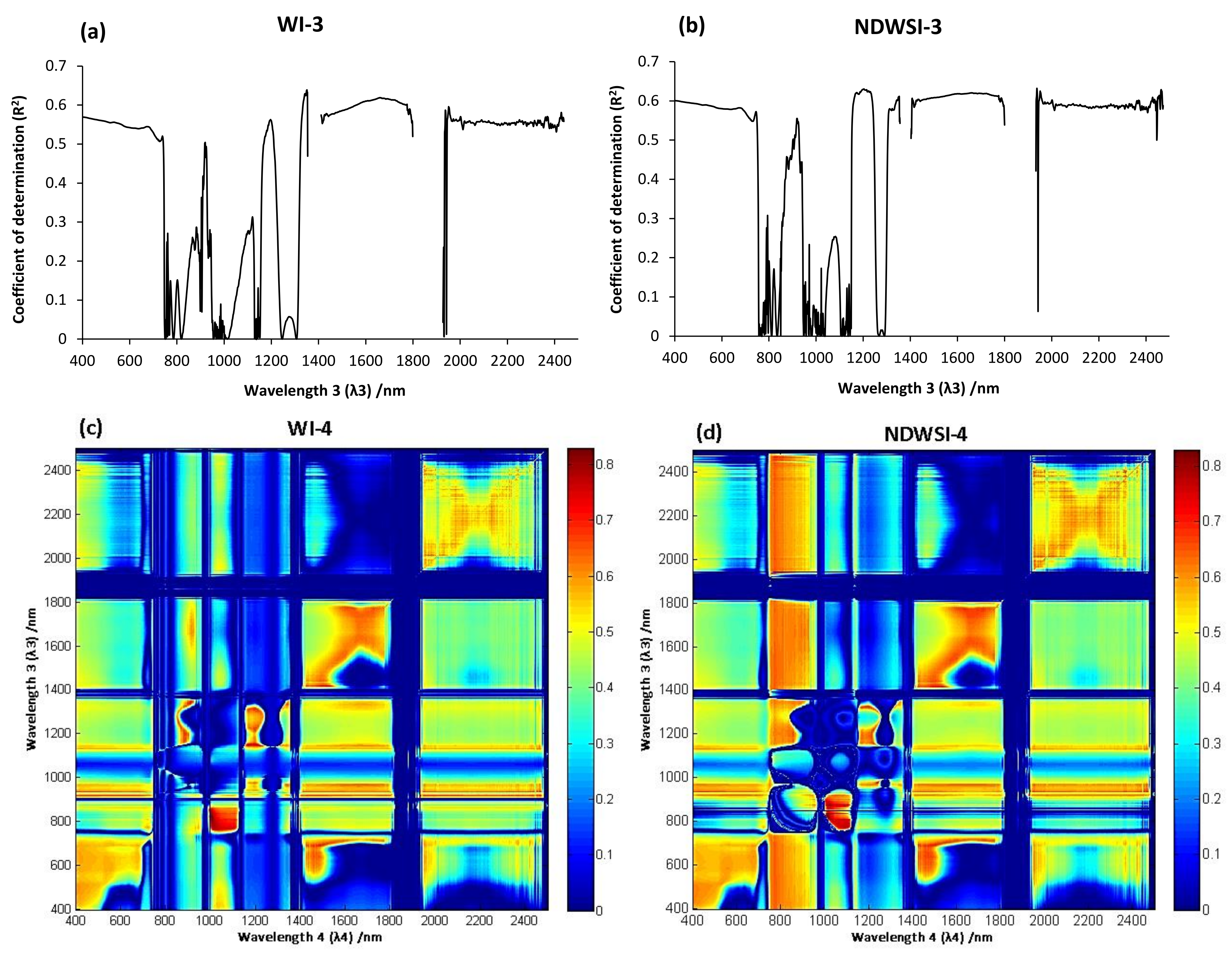
2.5. Construction of New RRD Type of Spectral Indices
2.6. Data Analysis
3. Results
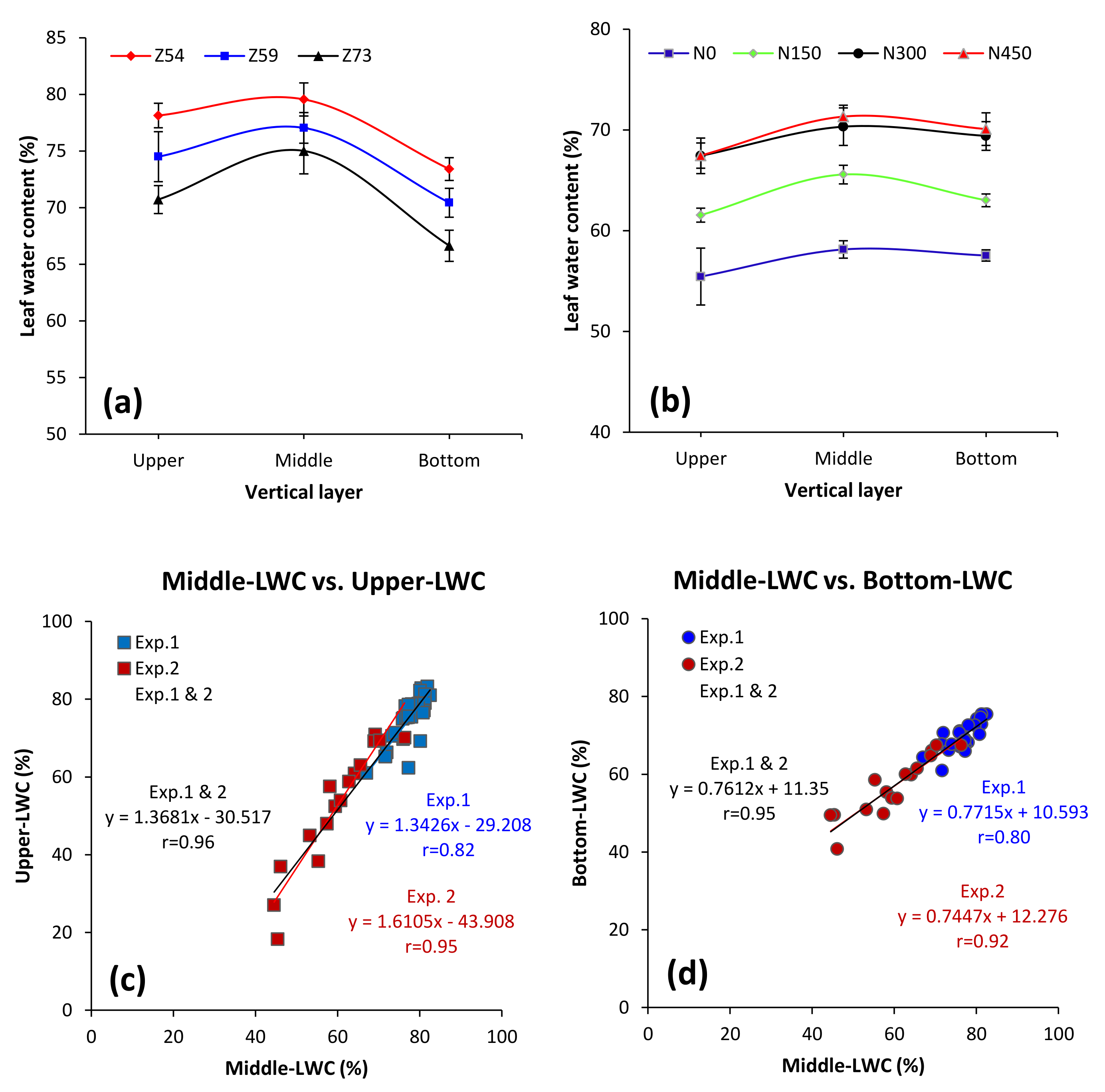
3.1. Vertical Variation of LWC within Wheat Canopies
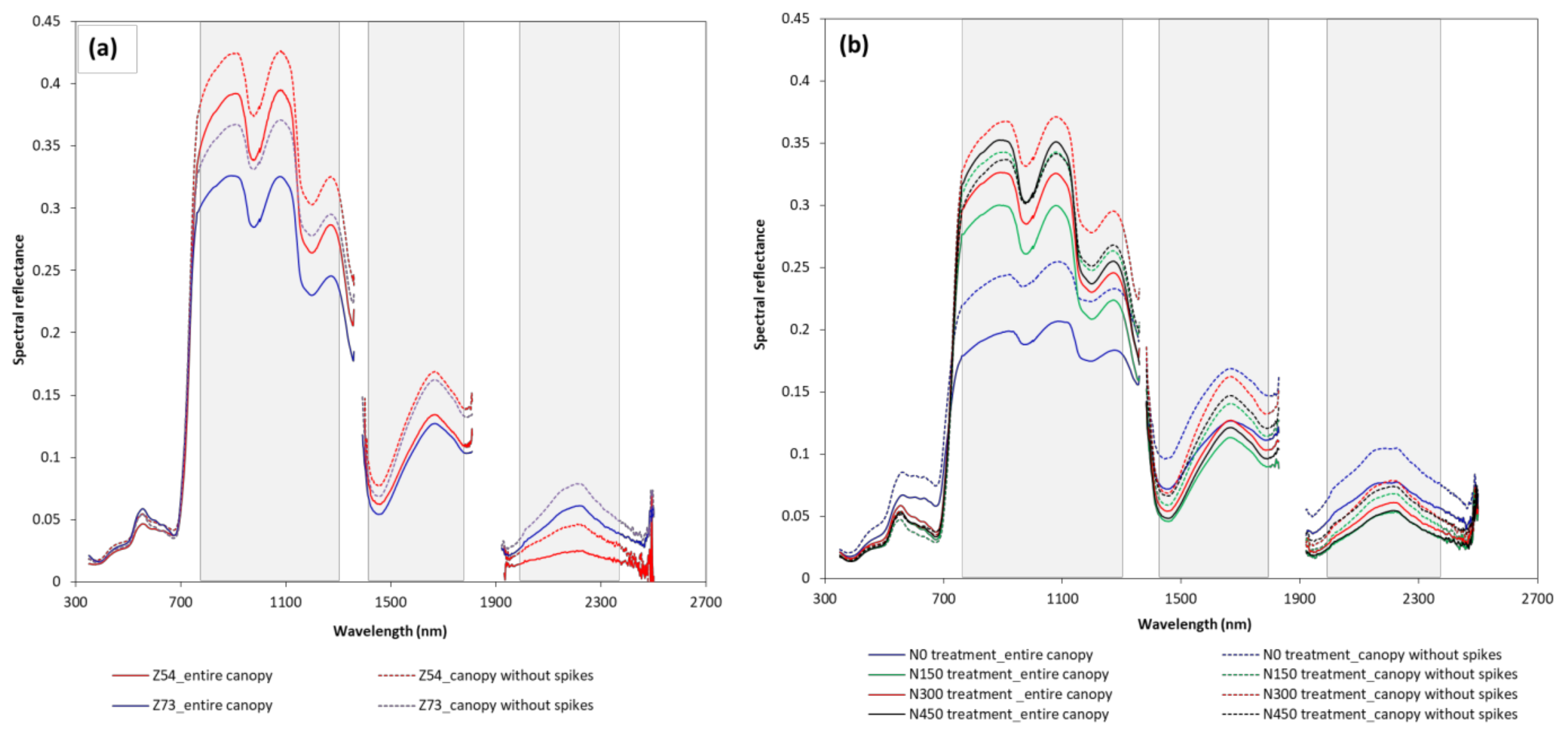
3.2. Effects of Wheat Spikes on Canopy Spectral Reflectance
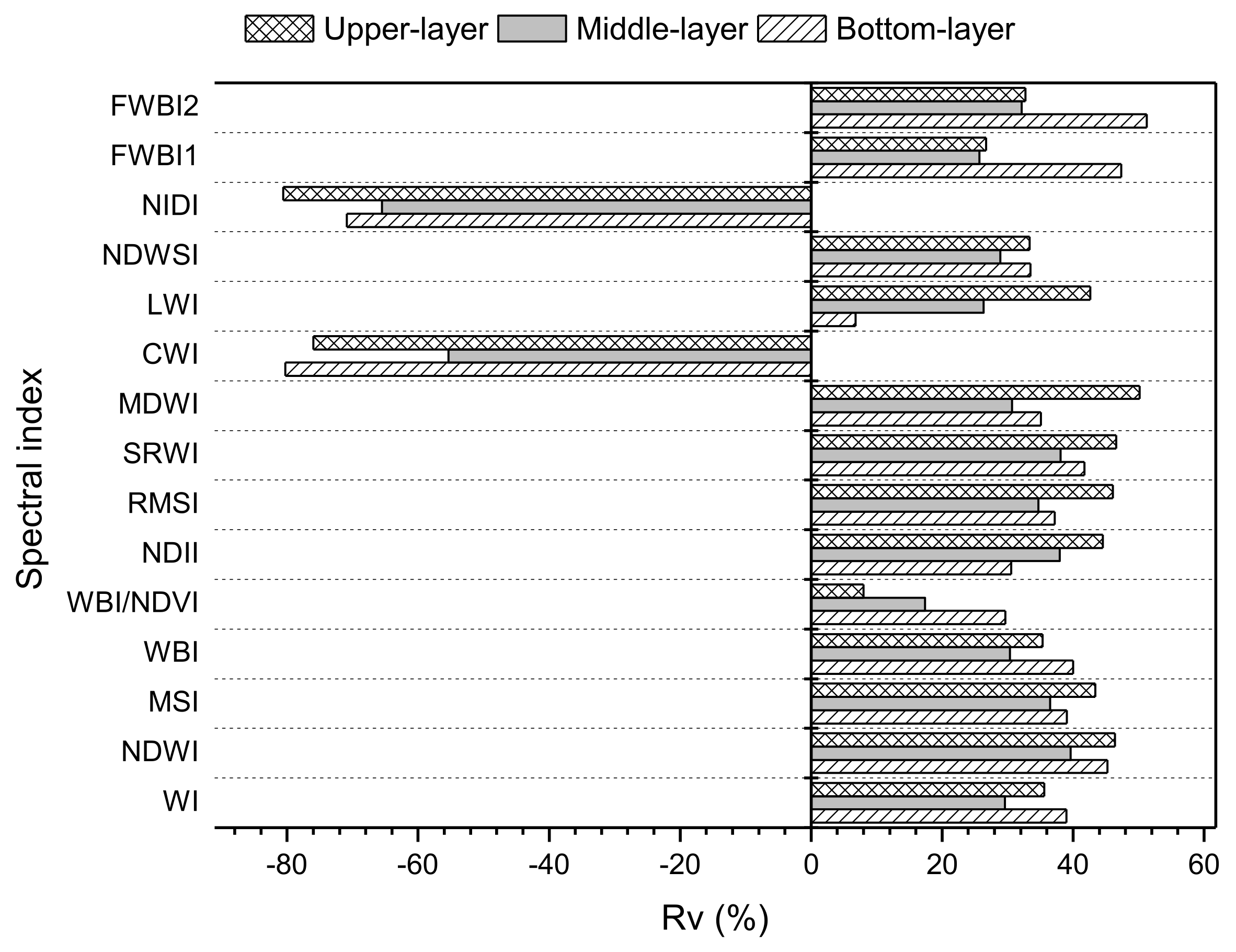
3.3. Effects of Wheat Spikes on Relationships between Published Spectral Indices and LWC in Vertical Layers
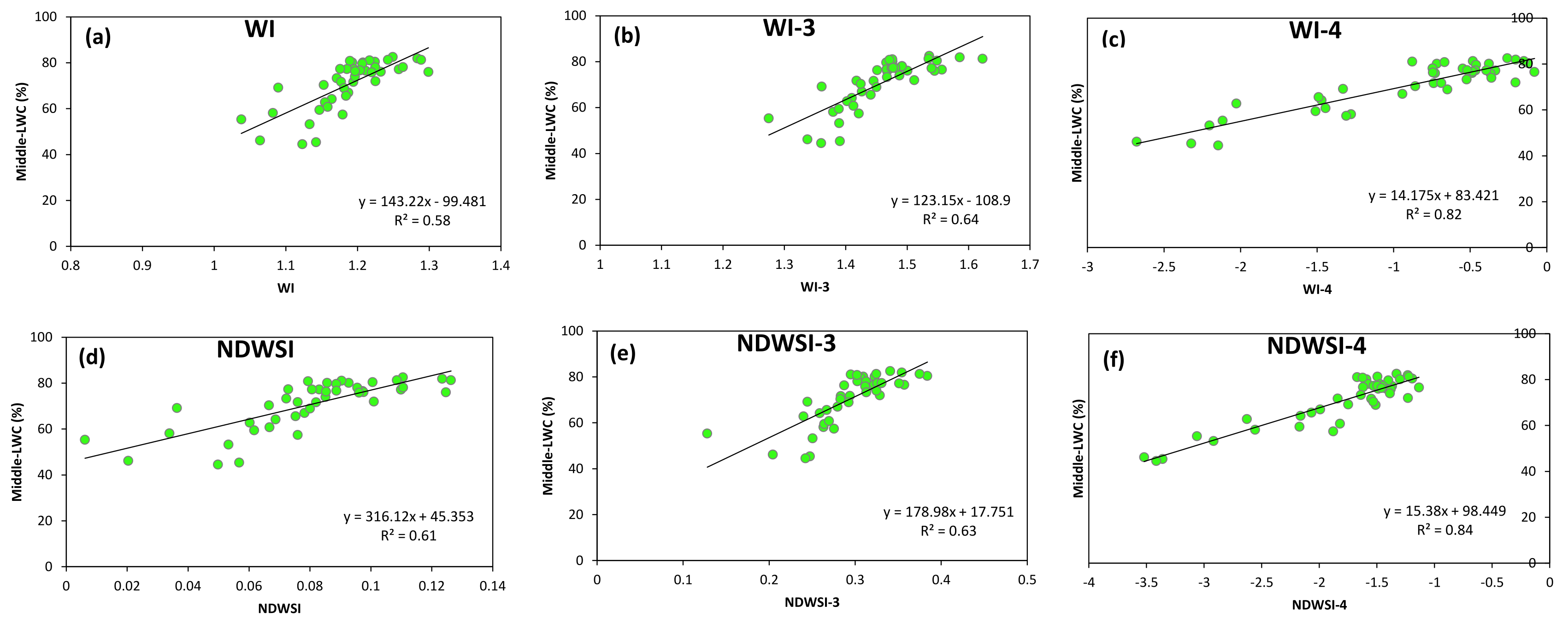
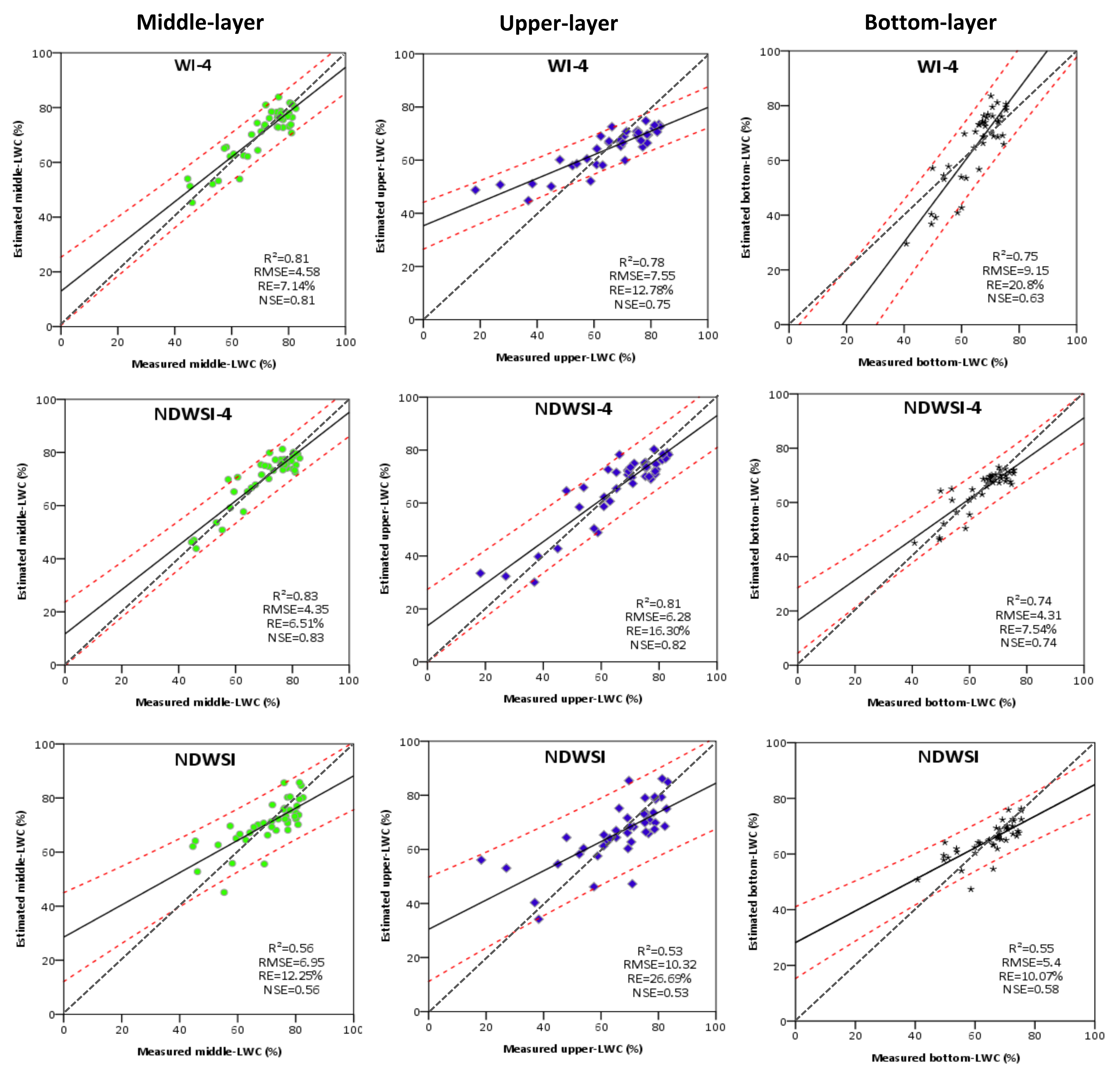
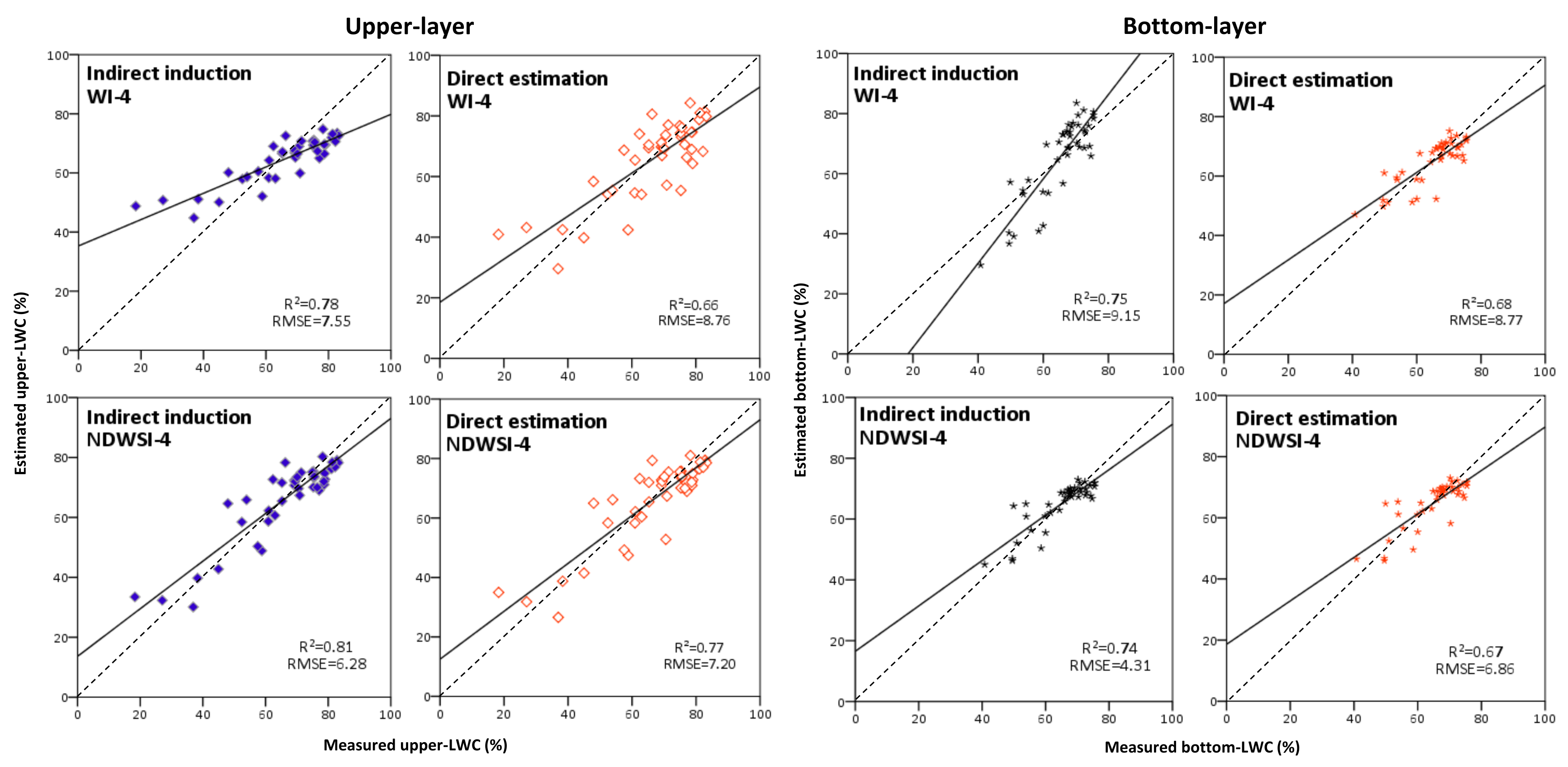
3.4. Estimation of Vertical LWC Distribution of Wheat Using a Method of Indirect Induction
3.5. Validation of Vertical LWC Distribution Models
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sydoruk, V.A.; Fiorani, F.; Jahnke, S.; Krause, H.-J. Design and characterization of microwave cavity resonators for noninvasive monitoring of plant water distribution. IEEE Trans. Microw. Theory Tech. 2016, 64, 2894–2904. [Google Scholar] [CrossRef]
- Brown, S.C.; Keatinge, J.D.H.; Gregory, P.J.; Cooper, P.J.M. Effects of fertilizer, variety and location on barley production under rainfed conditions in northern syria 1. Root and shoot growth. Field Crop. Res. 1987, 16, 53–66. [Google Scholar] [CrossRef]
- Cooper, P.J.M.; Gregory, P.J.; Keatinge, J.D.H.; Brown, S.C. Effects of fertilizer, variety and location on barley production under rainfed conditions in northern syria 2. Soil water dynamics and crop water use. Field Crop. Res. 1987, 16, 67–84. [Google Scholar] [CrossRef]
- Quintero, J.M.; Fournier, J.M.; Benlloch, M. Water transport in sunflower root systems: Effects of aba, ca2+ status and hgcl2. J. Exp. Bot. 1999, 50, 1607–1612. [Google Scholar] [CrossRef]
- Lawlor, D.W.; Cornic, G. Photosynthetic carbon assimilation and associated metabolism in relation to water deficits in higher plants. Plant Cell Environ. 2002, 25, 275–294. [Google Scholar] [CrossRef] [Green Version]
- Araus, J.L.; Slafer, G.A.; Royo, C.; Dolores Serret, M. Breeding for yield potential and stress adaptation in cereals. Crit. Rev. Plant Sci. 2008, 27, 377–412. [Google Scholar] [CrossRef]
- Sims, D.A.; Gamon, J.A. Relationships between leaf pigment content and spectral reflectance across a wide range of species, leaf structures and developmental stages. Remote Sens. Environ. 2002, 81, 337–354. [Google Scholar] [CrossRef]
- Haboudane, D.; Miller, J.R.; Pattey, E.; Zarco-Tejada, P.J.; Strachan, I.B. Hyperspectral vegetation indices and novel algorithms for predicting green lai of crop canopies: Modeling and validation in the context of precision agriculture. Remote Sens. Environ. 2004, 90, 337–352. [Google Scholar] [CrossRef]
- Clevers, J.; Kooistra, L. Using hyperspectral remote sensing data for retrieving canopy chlorophyll and nitrogen content. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 574–583. [Google Scholar] [CrossRef]
- Campos-Taberner, M.; Garcia-Haro, F.J.; Camps-Valls, G.; Grau-Muedra, G.; Nutini, F.; Crema, A.; Boschetti, M. Multitemporal and multiresolution leaf area index retrieval for operational local rice crop monitoring. Remote Sens. Environ. 2016, 187, 102–118. [Google Scholar] [CrossRef]
- Ihuoma, S.O.; Madramootoo, C.A. Recent advances in crop water stress detection. Comput. Electron. Agric. 2017, 141, 267–275. [Google Scholar] [CrossRef]
- Peng, Z.G.; Lin, S.Z.; Zhang, B.Z.; Wei, Z.; Liu, L.; Han, N.N.; Cai, J.B.; Chen, H. Winter wheat canopy water content monitoring based on spectral transforms and “three-edge” parameters. Agric. Water Manag. 2020, 240, 106306. [Google Scholar] [CrossRef]
- Rasheed, F.; Delagrange, S.; Lorenzetti, F. Detection of plant water stress using leaf spectral responses in three poplar hybrids prior to the onset of physiological effects. Int. J. Remote Sens. 2020, 41, 5127–5146. [Google Scholar] [CrossRef]
- Penuelas, J.; Pinol, J.; Ogaya, R.; Filella, I. Estimation of plant water concentration by the reflectance water index wi (r900/r970). Int. J. Remote Sens. 1997, 18, 2869–2875. [Google Scholar] [CrossRef]
- Gao, B.C. Ndwi—A normalized difference water index for remote sensing of vegetation liquid water from space. Remote Sens. Environ. 1996, 58, 257–266. [Google Scholar] [CrossRef]
- Zarco-Tejada, P.J.; Rueda, C.A.; Ustin, S.L. Water content estimation in vegetation with modis reflectance data and model inversion methods. Remote Sens. Environ. 2003, 85, 109–124. [Google Scholar] [CrossRef]
- Ciganda, V.; Gitelson, A.; Schepers, J. Vertical profile and temporal variation of chlorophyll in maize canopy: Quantitative “crop vigor” indicator by means of reflectance-based techniques. Agron. J. 2008, 100, 1409–1417. [Google Scholar] [CrossRef] [Green Version]
- Widlowski, J.L.; Taberner, M.; Pinty, B.; Bruniquel-Pinel, V.; Disney, M.; Fernandes, R.; Gastellu-Etchegorry, J.P.; Gobron, N.; Kuusk, A.; Lavergne, T.; et al. Third radiation transfer model intercomparison (rami) exercise: Documenting progress in canopy reflectance models. J. Geophys. Res.-Atmos. 2007, 112. [Google Scholar] [CrossRef] [Green Version]
- Huang, W.J.; Yang, Q.Y.; Pu, R.L.; Yang, S.Y. Estimation of nitrogen vertical distribution by bi-directional canopy reflectance in winter wheat. Sensors 2014, 14, 20347–20359. [Google Scholar] [CrossRef] [Green Version]
- He, J.Y.; Zhang, X.B.; Guo, W.T.; Pan, Y.Y.; Yao, X.; Cheng, T.; Zhu, Y.; Cao, W.X.; Tian, Y.C. Estimation of vertical leaf nitrogen distribution within a rice canopy based on hyperspectral data. Front. Plant Sci. 2020, 10, 1802. [Google Scholar] [CrossRef]
- Wang, Q.; Li, P.H. Canopy vertical heterogeneity plays a critical role in reflectance simulation. Agric. For. Meteorol. 2013, 169, 111–121. [Google Scholar] [CrossRef]
- Ye, H.C.; Huang, W.J.; Huang, S.Y.; Wu, B.; Dong, Y.Y.; Cui, B. Remote estimation of nitrogen vertical distribution by consideration of maize geometry characteristics. Remote Sens. 2018, 10, 17. [Google Scholar] [CrossRef] [Green Version]
- Li, H.; Zhao, C.; Yang, G.; Feng, H. Variations in crop variables within wheat canopies and responses of canopy spectral characteristics and derived vegetation indices to different vertical leaf layers and spikes. Remote Sens. Environ. 2015, 169, 358–374. [Google Scholar] [CrossRef]
- Ciganda, V.S.; Gitelson, A.A.; Schepers, J. How deep does a remote sensor sense? Expression of chlorophyll content in a maize canopy. Remote Sens. Environ. 2012, 126, 240–247. [Google Scholar] [CrossRef]
- Luo, J.H.; Ma, R.H.; Feng, H.H.; Li, X.C. Estimating the total nitrogen concentration of reed canopy with hyperspectral measurements considering a non-uniform vertical nitrogen distribution. Remote Sens. 2016, 8, 789. [Google Scholar] [CrossRef] [Green Version]
- Zhao, C.J.; Li, H.L.; Li, P.S.; Yang, G.J.; Gu, X.H.; Lan, Y.B. Effect of vertical distribution of crop structure and biochemical parameters of winter wheat on canopy reflectance characteristics and spectral indices. IEEE Geosci. Remote Sens. Mag. 2017, 55, 236–247. [Google Scholar] [CrossRef]
- Li, L.; Jakli, B.; Lu, P.; Ren, T.; Ming, J.; Liu, S.; Wang, S.; Lu, J. Assessing leaf nitrogen concentration of winter oilseed rape with canopy hyperspectral technique considering a non-uniform vertical nitrogen distribution. Ind. Crop. Prod. 2018, 116, 1–14. [Google Scholar] [CrossRef]
- Liu, S.S.; Peng, Y.; Du, W.; Le, Y.; Li, L. Remote estimation of leaf and canopy water content in winter wheat with different vertical distribution of water-related properties. Remote Sens. 2015, 7, 4626–4650. [Google Scholar] [CrossRef] [Green Version]
- Slaton, M.R.; Hunt, E.R.; Smith, W.K. Estimating near-infrared leaf reflectance from leaf structural characteristics. Am. J. Bot. 2001, 88, 278–284. [Google Scholar] [CrossRef]
- Gutierrez, M.; Paul Reynolds, M.; Klatt, A.R. Effect of leaf and spike morphological traits on the relationship between spectral reflectance indices and yield in wheat. Int. J. Remote Sens. 2015, 36, 701–718. [Google Scholar] [CrossRef]
- Gaju, O.; DeSilva, J.; Carvalho, P.; Hawkesford, M.J.; Griffiths, S.; Greenland, A.; Foulkes, M.J. Leaf photosynthesis and associations with grain yield, biomass and nitrogen-use efficiency in landraces, synthetic-derived lines and cultivars in wheat. Field Crop. Res. 2016, 193, 1–15. [Google Scholar] [CrossRef]
- Li, H.; Zhao, C.; Huang, W.; Yang, G. Non-uniform vertical nitrogen distribution within plant canopy and its estimation by remote sensing: A review. Field Crop. Res. 2013, 142, 75–84. [Google Scholar] [CrossRef]
- Jones, C.L.; Weckler, P.R.; Maness, N.O.; Stone, M.L.; Jayasekara, R. Estimating water stress in plants using hyperspectral sensing. System 2004. [Google Scholar] [CrossRef]
- Hunt, E.R., Jr.; Rock, B.N. Detection of changes in leaf water content using near- and middle-infrared reflectances. Remote Sens. Environ. 1989, 30, 43–54. [Google Scholar]
- Xu, H.R.; Ying, Y.B.; Fu, X.P.; Zhu, S.P. Near-infrared spectroscopy in detecting leaf miner damage on tomato leaf. Biosyst. Eng. 2007, 96, 447–454. [Google Scholar] [CrossRef]
- Hardisky, M.; Klemas, V.; Smart, R. The influence of soil salinity, growth form, and leaf moisture on the spectral radiance of spartina alterniflora canopies. Photogramm. Eng. Remote Sens. 1983, 49, 77–83. [Google Scholar]
- Eitel, J.U.H.; Gessler, P.E.; Smith, A.M.S.; Robberecht, R. Suitability of existing and novel spectral indices to remotely detect water stress in populus spp. For. Ecol. Manag. 2006, 229, 170–182. [Google Scholar] [CrossRef]
- Seelig, H.-D.; Hoehn, A.; Stodieck, L.S.; Klaus, D.M.; Adams, W.W.; Emery, W.J. Plant water parameters and the remote sensing r (1300)/r (1450) leaf water index: Controlled condition dynamics during the development of water deficit stress. Irrig. Sci. 2009, 27, 357–365. [Google Scholar] [CrossRef]
- Hunt, E.R.; Daughtry, C.S.T.; Eitel, J.U.H.; Long, D.S. Remote sensing leaf chlorophyll content using a visible band index. Agron. J. 2011, 103, 1090–1099. [Google Scholar] [CrossRef] [Green Version]
- Kim, D.M.; Zhang, H.; Zhou, H.; Du, T.; Wu, Q.; Mockler, T.C.; Berezin, M.Y. Highly sensitive image-derived indices of water-stressed plants using hyperspectral imaging in swir and histogram analysis. Sci. Rep. 2015, 5, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Strachan, I.B.; Pattey, E.; Boisvert, J.B. Impact of nitrogen and environmental conditions on corn as detected by hyperspectral reflectance. Remote Sens. Environ. 2002, 80, 213–224. [Google Scholar] [CrossRef]
- Harris, A.; Bryant, R.G.; Baird, A.J. Mapping the effects of water stress on sphagnum: Preliminary observations using airborne remote sensing. Remote Sens. Environ. 2006, 100, 363–378. [Google Scholar] [CrossRef]
- Datt, B. Remote sensing of water content in eucalyptus leaves. Aust. J. Bot. 1999, 47, 909–923. [Google Scholar] [CrossRef]
- Geladi, P.; Macdougall, D.; Martens, H. Linearization and scatter-correction for near-infrared reflectance spectra of meat. Appl. Spectrosc. 1985, 39, 491–500. [Google Scholar] [CrossRef]
- Richter, K.; Atzberger, C.; Hank, T.B.; Mauser, W. Derivation of biophysical variables from earth observation data: Validation and statistical measures. J. Appl. Remote Sens. 2012, 6, 063557. [Google Scholar] [CrossRef]
- Jamieson, P.D.; Porter, J.R.; Wilson, D.R. A test of the computer-simulation model arc-wheat1 on wheat crops grown in new zealand. Field Crop. Res. 1991, 27, 337–350. [Google Scholar] [CrossRef]
- Yu, K.; Lenz-Wiedemann, V.; Chen, X.; Bareth, G. Estimating leaf chlorophyll of barley at different growth stages using spectral indices to reduce soil background and canopy structure effects. ISPRS J. Photogramm. Remote Sens. 2014, 97, 58–77. [Google Scholar] [CrossRef]
- Raj, R.; Walker, J.P.; Pingale, R.; Nandan, R.; Naik, B.; Jagarlapudi, A. Leaf area index estimation using top-of-canopy airborne rgb images. Int. J. Appl. Earth Obs. Geoinf. 2021, 96, 102282. [Google Scholar] [CrossRef]
- Yu, K.Q.; Zhao, Y.R.; Li, X.L.; Shao, Y.N.; Liu, F.; He, Y. Hyperspectral imaging for mapping of total nitrogen spatial distribution in pepper plant. PLoS ONE 2014, 9, e116205. [Google Scholar] [CrossRef]
- He, J.; Zhang, N.; Su, X.; Lu, J.; Yao, X.; Cheng, T.; Zhu, Y.; Cao, W.; Tian, Y. Estimating leaf area index with a new vegetation index considering the influence of rice panicles. Remote Sens. 2019, 11, 1809. [Google Scholar] [CrossRef] [Green Version]
- Grant, L. Diffuse and specular characteristics of leaf reflectance. Remote Sens. Environ. 1987, 22, 309–322. [Google Scholar] [CrossRef]
- Kong, W.; Huang, W.; Casa, R.; Zhou, X.; Ye, H.; Dong, Y. Off-nadir hyperspectral sensing for estimation of vertical profile of leaf chlorophyll content within wheat canopies. Sensors 2017, 17, 2711. [Google Scholar] [CrossRef] [Green Version]
- Roosjen, P.P.J.; Brede, B.; Suomalainen, J.M.; Bartholomeus, H.M.; Kooistra, L.; Clevers, J.G.P.W. Improved estimation of leaf area index and leaf chlorophyll content of a potato crop using multi-angle spectral data—potential of unmanned aerial vehicle imagery. Int. J. Appl. Earth Obs. Geoinf. 2018, 66, 14–26. [Google Scholar] [CrossRef]
- Verrelst, J.; Schaepman, M.E.; Koetz, B.; Kneubuehler, M. Angular sensitivity analysis of vegetation indices derived from chris/proba data. Remote Sens. Environ. 2008, 112, 2341–2353. [Google Scholar] [CrossRef]
- Jacquemoud, S.; Bacour, C.; Poilve, H.; Frangi, J.P. Comparison of four radiative transfer models to simulate plant canopies reflectance: Direct and inverse mode. Remote Sens. Environ. 2000, 74, 471–481. [Google Scholar] [CrossRef]
- Dash, J.; Curran, P.J. The meris terrestrial chlorophyll index. Int. J. Remote. Sens. 2004, 25, 5403–5413. [Google Scholar] [CrossRef]
- Penuelas, J.; Baret, F.; Filella, I. Semiempirical indices to assess carotenoids chlorophyll a ratio from leaf spectral reflectance. Photosynthetica 1995, 31, 221–230. [Google Scholar]
- Li, X.A.; Sun, Z.Q.; Lu, S.; Omasa, K.J. A multi-angular invariant spectral index for the estimation of leaf water content across a wide range of plant species in different growth stages. Remote Sens. Environ. 2021, 253, 19. [Google Scholar] [CrossRef]
| Spectral Index | Formula | Reference |
|---|---|---|
| Water index (WI) | [14] | |
| Normalized difference water index (NDWI) | [15] | |
| Moisture stress index (MSI) | [34] | |
| Water band index (WBI) | [35] | |
| WBI/normalized difference vegetation index (WBI/NDVI) | [14] | |
| Normalized difference infrared index (NDII) | [36] | |
| Reciprocal of moisture stress index (RMSI) | [36] | |
| Simple ratio water index (SRWI) | [16] | |
| Maximum difference water index (MDWI) | [37] | |
| Composite water index (CWI) | [13] | |
| Leaf water index (LWI) | [38] | |
| Normalized different water stress index (NDWSI) | [39] | |
| Novel image-derived index (NIDI) | [40] | |
| Floating-position water band index (FWBI1) | [41] | |
| Floating-position water band index (FWBI2) | [42] |
| Excellent | Good | Fair | Unsuitable | |
|---|---|---|---|---|
| RE | <10% | 10%–20% | 20–30% | >30% |
| NSE | ≥0.9 | 0.5–0.8 | - | 0.1–0.4 |
| Spectral Index | R2entire canopy | R2canopy without spikes | ||||
|---|---|---|---|---|---|---|
| Upper-Layer | Middle-Layer | Bottom-Layer | Upper-Layer | Middle-Layer | Bottom-Layer | |
| WI | 0.39 | 0.47 | 0.29 | 0.53 | 0.61 | 0.4 |
| NDWI | 0.36 | 0.44 | 0.28 | 0.53 | 0.61 | 0.4 |
| MSI | 0.32 | 0.4 | 0.28 | 0.46 | 0.55 | 0.39 |
| WBI | 0.38 | 0.47 | 0.29 | 0.52 | 0.6 | 0.4 |
| WBI/NDVI | 0.36 | 0.41 | 0.28 | 0.39 | 0.48 | 0.36 |
| NDII | 0.34 | 0.41 | 0.3 | 0.48 | 0.56 | 0.39 |
| RMSI | 0.36 | 0.45 | 0.31 | 0.53 | 0.6 | 0.39 |
| SRWI | 0.37 | 0.45 | 0.32 | 0.55 | 0.62 | 0.4 |
| MDWI | 0.27 | 0.38 | 0.24 | 0.4 | 0.49 | 0.32 |
| CWI | 0.46 | 0.38 | 0.44 | 0.11 | 0.17 | 0.09 |
| LWI | 0.29 | 0.39 | 0.25 | 0.41 | 0.49 | 0.27 |
| NDWSI | 0.44 | 0.5 | 0.37 | 0.58 | 0.65 | 0.41 |
| NIDI | 0.32 | 0.34 | 0.26 | 0.08 | 0.12 | 0.06 |
| FWBI1 | 0.38 | 0.5 | 0.33 | 0.57 | 0.63 | 0.42 |
| FWBI2 | 0.38 | 0.48 | 0.33 | 0.56 | 0.63 | 0.44 |
| Spectral Index | Upper-Layer | Middle-Layer | Bottom-Layer |
|---|---|---|---|
| WI | 0.56 | 0.58 | 0.54 |
| NDWI | 0.47 | 0.47 | 0.45 |
| MSI | 0.40 | 0.42 | 0.38 |
| WBI | 0.55 | 0.58 | 0.54 |
| WBI/NDVI | 0.42 | 0.49 | 0.44 |
| NDII | 0.42 | 0.44 | 0.41 |
| RMSI | 0.41 | 0.41 | 0.40 |
| SRWI | 0.46 | 0.47 | 0.45 |
| MDWI | 0.47 | 0.50 | 0.46 |
| CWI | 0.01 | 0.05 | 0.03 |
| LWI | 0.45 | 0.46 | 0.44 |
| NDWSI | 0.59 | 0.61 | 0.58 |
| NIDI | 0.33 | 0.38 | 0.30 |
| FWBI1 | 0.56 | 0.56 | 0.52 |
| FWBI2 | 0.53 | 0.54 | 0.50 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kong, W.; Huang, W.; Ma, L.; Tang, L.; Li, C.; Zhou, X.; Casa, R. Estimating Vertical Distribution of Leaf Water Content within Wheat Canopies after Head Emergence. Remote Sens. 2021, 13, 4125. https://doi.org/10.3390/rs13204125
Kong W, Huang W, Ma L, Tang L, Li C, Zhou X, Casa R. Estimating Vertical Distribution of Leaf Water Content within Wheat Canopies after Head Emergence. Remote Sensing. 2021; 13(20):4125. https://doi.org/10.3390/rs13204125
Chicago/Turabian StyleKong, Weiping, Wenjiang Huang, Lingling Ma, Lingli Tang, Chuanrong Li, Xianfeng Zhou, and Raffaele Casa. 2021. "Estimating Vertical Distribution of Leaf Water Content within Wheat Canopies after Head Emergence" Remote Sensing 13, no. 20: 4125. https://doi.org/10.3390/rs13204125
APA StyleKong, W., Huang, W., Ma, L., Tang, L., Li, C., Zhou, X., & Casa, R. (2021). Estimating Vertical Distribution of Leaf Water Content within Wheat Canopies after Head Emergence. Remote Sensing, 13(20), 4125. https://doi.org/10.3390/rs13204125