Retrieval of Leaf Area Index by Linking the PROSAIL and Ross-Li BRDF Models Using MODIS BRDF Data
Abstract
:1. Introduction
2. Data
2.1. Canopy BRDF Simulations with the PROSAIL Model
2.2. 500-m MODIS BRDF Parameter Product
2.3. LAI Measurements at the 500-m Plot Level and with 30-m LAI Maps
3. Methods
3.1. Sensitivity Analysis of the BRDF to Vegetation Parameters
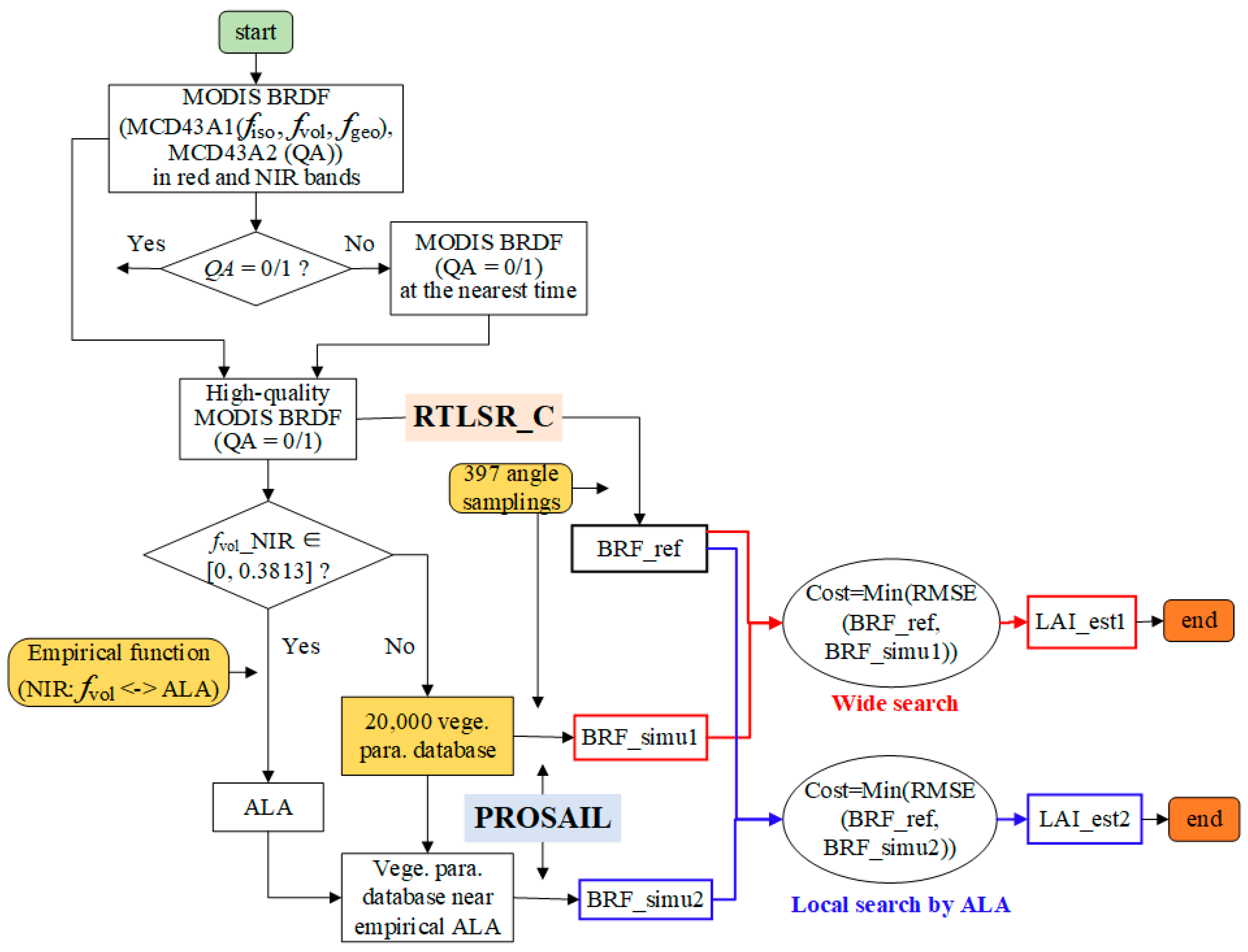
3.2. LAI Estimation from MODIS BRDF Data by Linking the PROSAIL and Ross-Li Models
3.3. LAI Validation and Error Analysis
4. Results and Analysis
4.1. Sensitivity of the BRDF to Vegetation Parameters
4.1.1. Analysis Based on EFAST
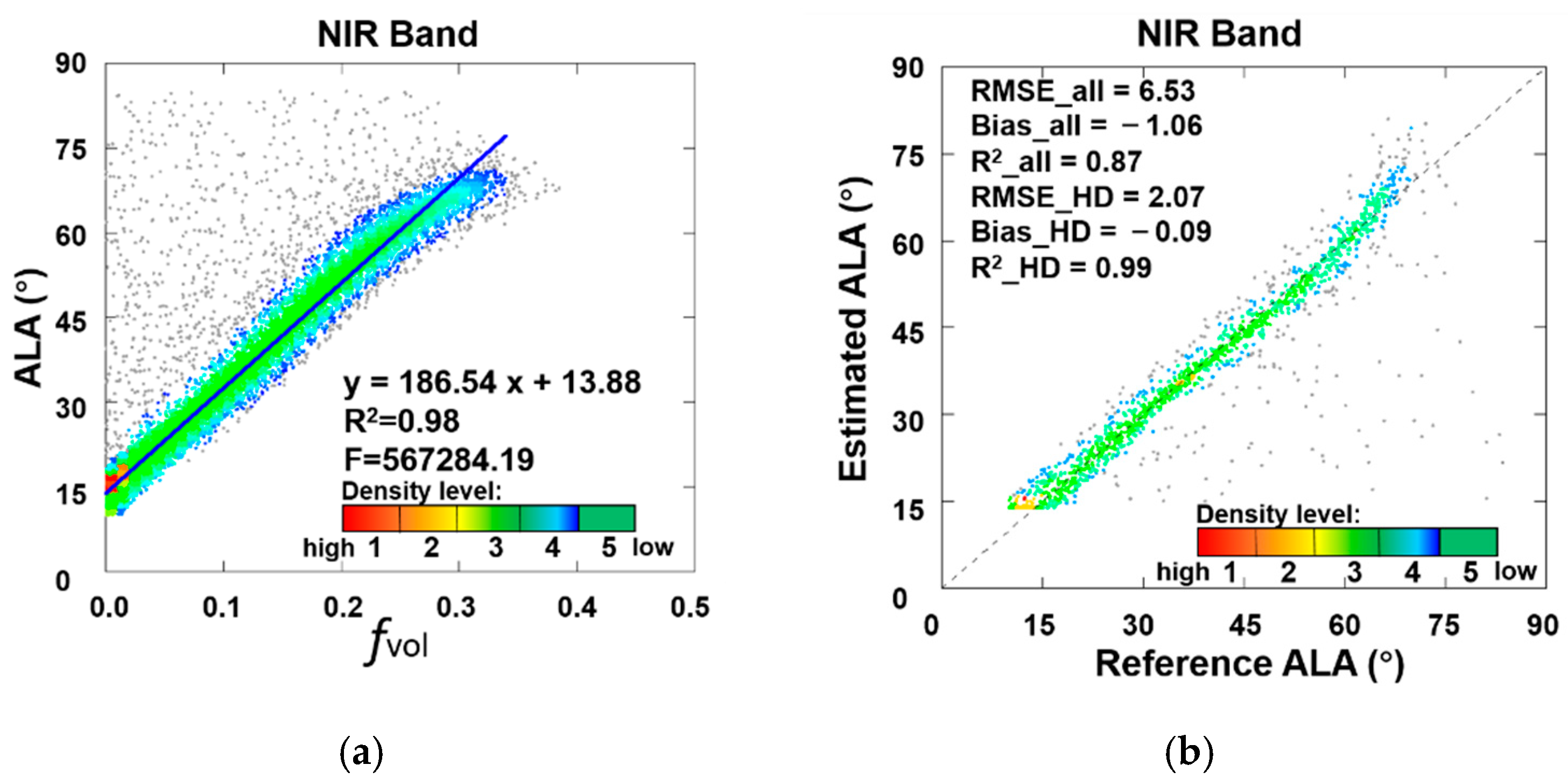
4.1.2. Modelling and Evaluation of Linear Relationships
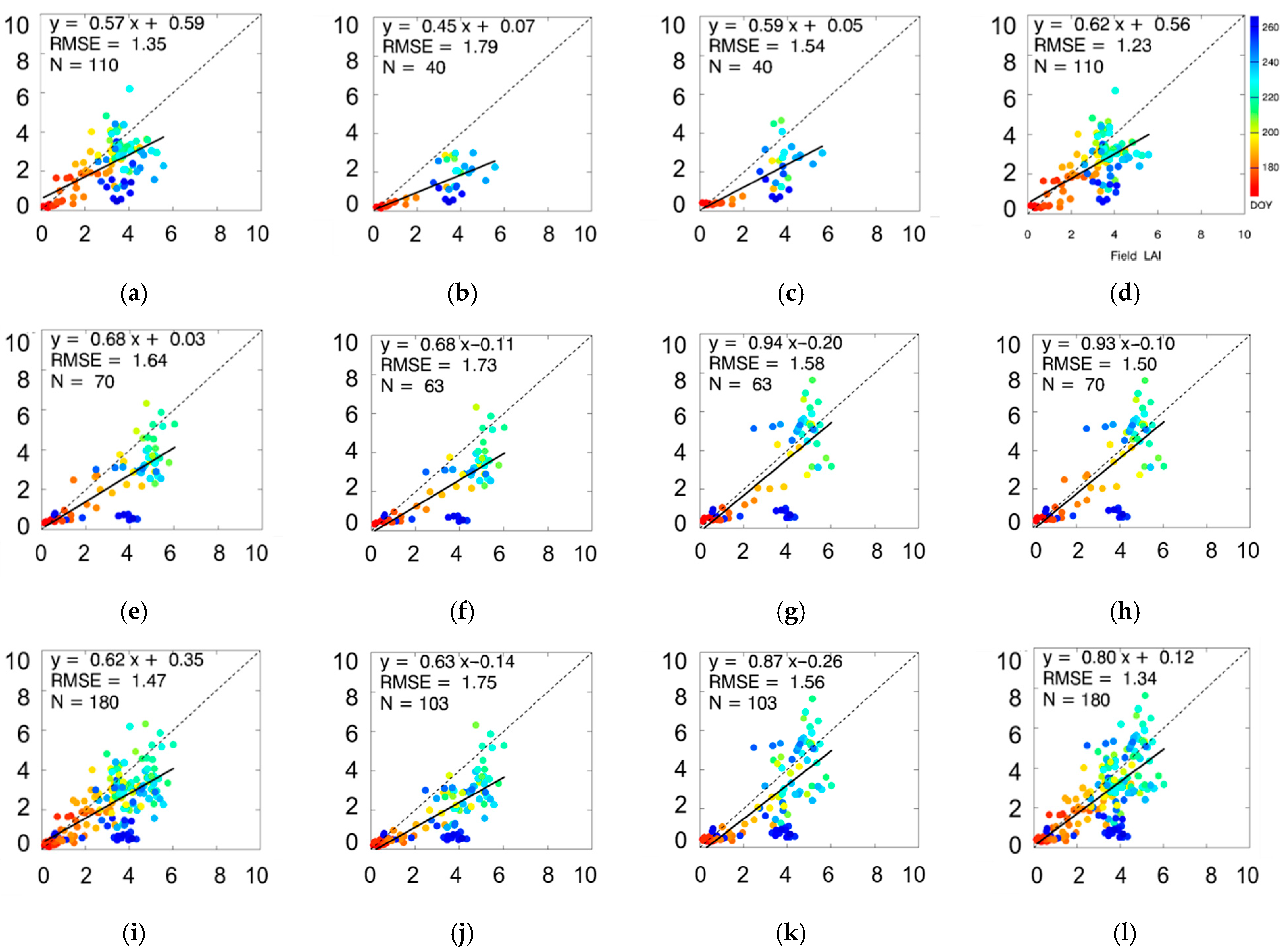
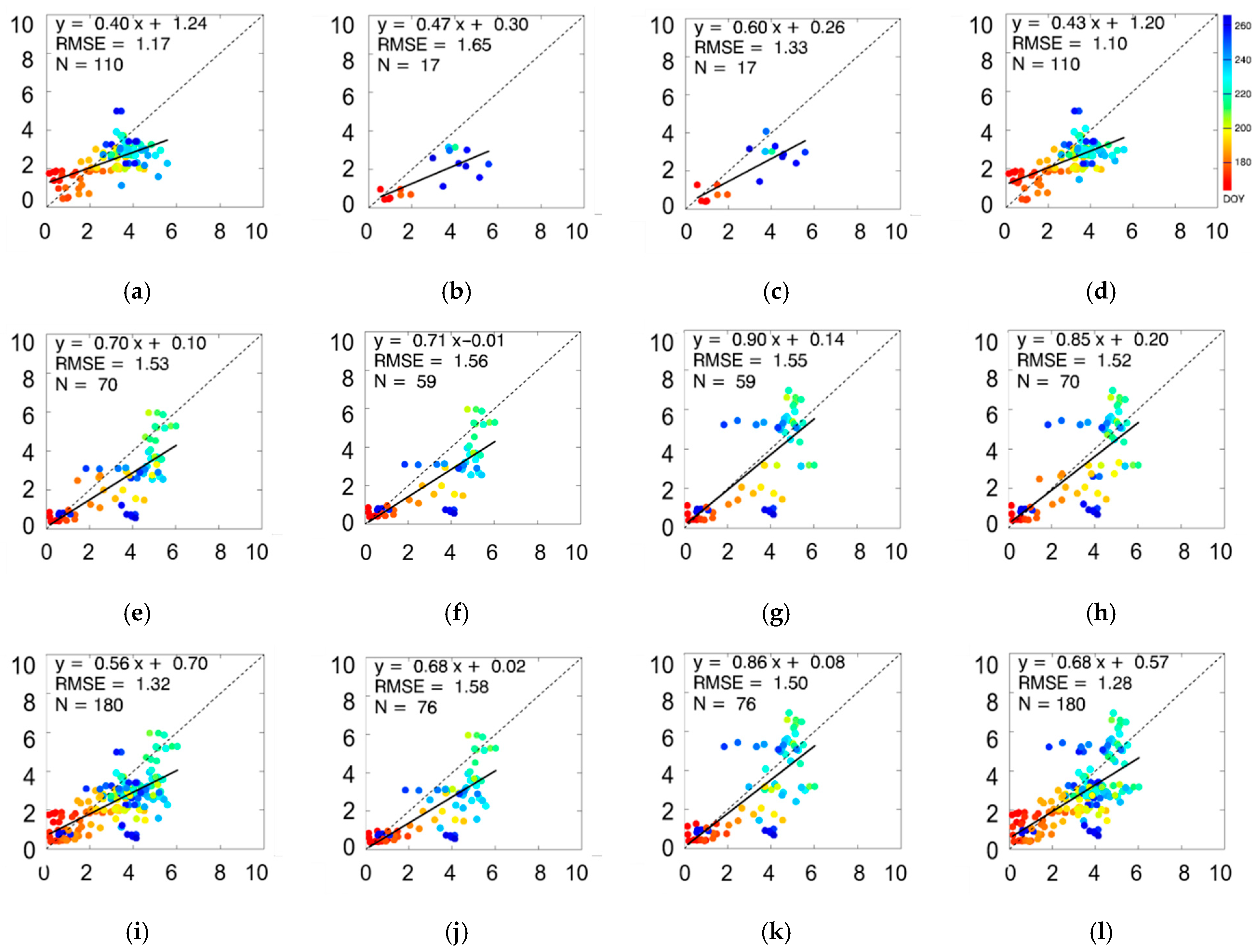
4.2. Validation of the LAI Estimations Based on Field Measurements
4.3. Error Analysis and Method Improvement
4.4. General Flowchart for LAI Estimation and Validation Based on LAI Maps
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jiang, L.; Guli, J.; Bao, A.; Guo, H.; Ndayisaba, F. Vegetation Dynamics and Responses to Climate Change and Human Activities in Central Asia. Sci. Total. Environ. 2017, 599–600, 967–980. [Google Scholar] [CrossRef]
- Privette, J.L.; Emery, W.J.; Schimel, D.S. Inversion of a Vegetation Reflectance Model with NOAA AVHRR Data. Remote Sens. Environ. 1996, 58, 187–200. [Google Scholar] [CrossRef]
- Sellers, P.J.; Dickinson, R.E.; Randall, D.A.; Betts, A.K.; Hall, F.G.; Berry, J.A.; Collatz, G.J.; Denning, A.S.; Mooney, H.A.; Nobre, C.A.; et al. Modeling the Exchanges of Energy, Water, and Carbon Between Continents and the Atmosphere. Science 1997, 275, 502–509. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Verger, A.; Baret, F.; Weiss, M. Near Real-Time Vegetation Monitoring at Global Scale. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 3473–3481. [Google Scholar] [CrossRef]
- Xiao, Z.; Liang, S.; Wang, J.; Chen, P.; Yin, X.; Zhang, L.; Song, J. Use of General Regression Neural Networks for Generating the GLASS Leaf Area Index Product from Time-Series MODIS Surface Reflectance. IEEE Trans. Geosci. Remote Sens. 2014, 52, 209–223. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, R.; Chen, J.M. Retrospective Retrieval of Long-Term Consistent Global Leaf Area Index (1981–2011) from Combined AVHRR and MODIS Data. J. Geophys. Res. Biogeosci. 2012, 117, G04003. [Google Scholar] [CrossRef]
- Yan, K.; Park, T.; Yan, G.; Chen, C.; Yang, B.; Liu, Z.; Nemani, R.R.; Knyazikhin, Y.; Myneni, R.B. Evaluation of MODIS LAI/FPAR Product Collection 6. Part 1: Consistency and Improvements. Remote Sens. 2016, 8, 359. [Google Scholar] [CrossRef] [Green Version]
- Yan, K.; Park, T.; Yan, G.; Liu, Z.; Yang, B.; Chen, C.; Nemani, R.R.; Knyazikhin, Y.; Myneni, R.B. Evaluation of MODIS LAI/FPAR Product Collection 6. Part 2: Validation and Intercomparison. Remote Sens. 2016, 8, 460. [Google Scholar] [CrossRef] [Green Version]
- Baret, F.; Weiss, M.; Verger, A.; Smets, B. ATBD for LAI, FAPAR and FCOVER from PROBA-V Products at 300M Resolution (Geov3). In IMAGINES_RP2.1_ATBD-LAI300m; Implementing Multi-scale AGricultural INdicators Exploiting Sentinels (ImagineS): INRA, France, 2016; pp. 1–61. [Google Scholar]
- Yan, K.; Park, T.; Chen, C.; Xu, B.; Song, W.; Yang, B.; Zeng, Y.; Liu, Z.; Yan, G.; Knyazikhin, Y.; et al. Generating Global Products of LAI and FPAR from SNPP-VIIRS Data: Theoretical Background and Implementation. IEEE Trans. Geosci. Remote Sens. 2018, 56, 2119–2137. [Google Scholar] [CrossRef]
- Zhou, H.M.; Wang, J.D.; Liang, S.L.; Xiao, Z.Q. Extended Data-Based Mechanistic Method for Improving Leaf Area Index Time Series Estimation with Satellite Data. Remote Sens. 2017, 9, 533. [Google Scholar] [CrossRef] [Green Version]
- Xiao, Z.Q.; Liang, S.L.; Wang, J.D.; Xie, D.H.; Song, J.L.; Fensholt, R. A Framework for Consistent Estimation of Leaf Area Index, Fraction of Absorbed Photosynthetically Active Radiation, and Surface Albedo from MODIS Time-Series Data. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3178–3197. [Google Scholar] [CrossRef]
- Roujean, J.L.; Leroy, M.M.; Deschamps, P.Y. A Bidirectional Reflectance Model of the Earth’s Surface for the Correction of Remote Sensing Data. J. Geophys. Res. Atmos. 1992, 97, 20455–20468. [Google Scholar] [CrossRef]
- Roosjen, P.P.J.; Brede, B.; Suomalainen, J.M.; Bartholomeus, H.M.; Kooistra, L.; Clevers, J.G.P.W. Improved Estimation of Leaf Area Index and Leaf Chlorophyll Content of a Potato Crop Using Multi-Angle Spectral Data-Potential of Unmanned Aerial Vehicle Imagery. Int. J. Appl. Earth Obs. 2018, 66, 14–26. [Google Scholar] [CrossRef]
- Barnsley, M.J.; Strahler, A.H.; Morris, K.P.; Muller, J.P. Sampling the Surface Bidirectional Reflectance Distribution Function (BRDF): 1. Evaluation of Current and Future Satellite Sensors. Remote Sens. Rev. 1994, 8, 271–311. [Google Scholar] [CrossRef]
- Lucht, W.W.; Lewis, P.E. Theoretical Noise Sensitivity of BRDF and Albedo Retrieval from the EOS-MODIS and MISR Sensors with Respect to Angular Sampling. Int. J. Remote Sens. 2000, 21, 81–98. [Google Scholar] [CrossRef]
- Chen, A.; Bian, L.; Liu, Y. Deriving Albedo over Cloudy Areas with Composite Inversion. In Proceedings of the SPIE-The International Society for Optical Engineering, Nanjing, China, 25 May 2007; Volume 6753, pp. 1–11. [Google Scholar]
- Wanner, W.; Li, X.W.; Strahler, A.H. On the Derivation of Kernels for Kernel-Driven Models of Bidirectional Reflectance. J. Geophys. Res. Atmos. 1995, 100, 21077–21089. [Google Scholar] [CrossRef]
- Nicodemus, F.E.; Richmond, J.C.; Hsia, J.J.; Ginsberg, I.W.; Limperis, T. Geometrical Considerations and Nomenclature for Reflectance; National Bureau of Standards: Washington, DC, USA, 1977. [Google Scholar]
- Schaaf, C.B.; Liu, J.C.; Gao, F.; Strahler, A.H. Aqua and Terra MODIS Albedo and Reflectance Anisotropy Products. In Land Remote Sensing and Global Environmental Change: NASA’s Earth Observing System and the Science of ASTER and MODIS; Ramachandran, B., Justice, C.O., Abrams, M.J., Eds.; Springer: New York, NY, USA, 2011; Volume 11, pp. 549–561. [Google Scholar]
- Schaaf, C.B.; Gao, F.; Strahler, A.H.; Lucht, W.W.; Li, X.W.; Tsang, T.; Strugnell, N.C.; Zhang, X.Y.; Jin, Y.F.; Muller, J.P.; et al. First Operational BRDF, Albedo Nadir Reflectance Products from MODIS. Remote Sens. Environ. 2002, 83, 135–148. [Google Scholar] [CrossRef] [Green Version]
- Bréon, F.M.; Maignan, F. A BRDF–BPDF Database for the Analysis of Earth Target Reflectances. Earth Syst. Sci. Data. 2017, 9, 31–45. [Google Scholar] [CrossRef] [Green Version]
- Bacour, C.; Breon, F.M. Variability of Biome Reflectance Directional Signatures as Seen by POLDER. Remote Sens. Environ. 2005, 98, 80–95. [Google Scholar] [CrossRef]
- He, T.; Liang, S.L.; Wang, D.D.; Cao, Y.F.; Gao, F.; Yu, Y.Y.; Feng, M. Evaluating Land Surface Albedo Estimation from Landsat MSS, TM, ETM Plus, and OLI Data Based on the Unified Direct Estimation Approach. Remote Sens. Environ. 2018, 204, 181–196. [Google Scholar] [CrossRef]
- Qu, Y.; Liu, Q.; Liang, S.L.; Wang, L.Z.; Liu, N.F.; Liu, S.H. Direct-Estimation Algorithm for Mapping Daily Land-Surface Broadband Albedo from MODIS Data. IEEE Trans. Geosci. Remote Sens. 2014, 52, 907–919. [Google Scholar] [CrossRef]
- Liang, S.L. A Direct Algorithm for Estimating Land Surface Broadband Albedos from MODIS Imagery. IEEE Trans. Geosci. Remote Sens. 2003, 41, 136–145. [Google Scholar] [CrossRef]
- Zhang, X.; Jiao, Z.; Dong, Y.; He, T.; Ding, A.; Yin, S.; Zhang, H.; Cui, L.; Chang, Y.; Guo, J.; et al. Development of the Direct-Estimation Albedo Algorithm for Snow-Free Landsat TM Albedo Retrievals Using Field Flux Measurements. IEEE Trans. Geosci. Remote Sens. 2020, 58, 1550–1567. [Google Scholar] [CrossRef]
- Jiao, Z.T.; Zhang, H.; Dong, Y.D.; Liu, Q.; Xiao, Q.; Li, X.W. An Algorithm for Retrieval of Surface Albedo from Small View-Angle Airborne Observations through the Use of BRDF Archetypes as Prior Knowledge. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 3279–3293. [Google Scholar] [CrossRef]
- Jiao, Z.T.; Dong, Y.D.; Schaaf, C.B.; Chen, J.M.; Román, M.; Wang, Z.S.; Zhang, H.; Ding, A.X.; Erb, A.; Hill, M.J.; et al. An Algorithm for the Retrieval of the Clumping Index (CI) from the MODIS BRDF Product Using an Adjusted Version of the Kernel-Driven BRDF Model. Remote Sens. Environ. 2018, 209, 594–611. [Google Scholar] [CrossRef]
- Chen, J.M.; Menges, C.H.; Leblanc, S.G. Global Mapping of Foliage Clumping Index Using Multi-Angular Satellite Data. Remote Sens. Environ. 2005, 97, 447–457. [Google Scholar] [CrossRef]
- He, L.M.; Chen, J.M.; Pisek, J.; Schaaf, C.B.; Strahler, A.H. Global Clumping Index Map Derived from the MODIS BRDF Product. Remote Sens. Environ. 2012, 119, 118–130. [Google Scholar] [CrossRef]
- Pisek, J.; Govind, A.; Arndt, S.K.; Hocking, D.; Wardlaw, T.J.; Fang, H.; Matteucci, G.; Longdoz, B. Intercomparison of Clumping Index Estimates from POLDER, MODIS, and MISR Satellite Data over Reference Sites. ISPRS J. Photogramm. 2015, 101, 47–56. [Google Scholar] [CrossRef]
- Wei, S.; Fang, H. Estimation of Canopy Clumping Index from MISR and MODIS Sensors Using the Normalized Difference Hotspot and Darkspot (NDHD) Method: The Influence of BRDF Models and Solar Zenith Angle. Remote Sens. Environ. 2016, 187, 476–491. [Google Scholar] [CrossRef]
- Zhu, G.L.; Ju, W.M.; Chen, J.M.; Gong, P.; Xing, B.L.; Zhu, J.F. Foliage Clumping Index over China’s Landmass Retrieved from the MODIS BRDF Parameters Product. IEEE Trans. Geosci. Remote Sens. 2012, 50, 2122–2137. [Google Scholar] [CrossRef]
- Wang, Z.S.; Schaaf, C.B.; Lewis, P.E.; Knyazikhin, Y.; Schull, M.A.; Strahler, A.H.; Yao, T.; Myneni, R.B.; Chopping, M.J.; Blair, B.J. Retrieval of Canopy Height Using Moderate-Resolution Imaging Spectroradiometer (MODIS) Data. Remote Sens. Environ. 2011, 115, 1595–1601. [Google Scholar] [CrossRef] [Green Version]
- Cui, L.; Jiao, Z.; Dong, Y.; Sun, M.; Zhang, X.; Yin, S.; Ding, A.; Chang, Y.; Guo, J.; Xie, R. Estimating Forest Canopy Height Using MODIS BRDF Data Emphasizing Typical-Angle Reflectances. Remote Sens. 2019, 11, 2239. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Li, G.; Ding, J.; Guo, Z.; Tang, S.; Wang, C.; Huang, Q.; Liu, R.; Chen, J.M. A Combined GLAS and MODIS Estimation of the Global Distribution of Mean Forest Canopy Height. Remote Sens. Environ. 2016, 174, 24–43. [Google Scholar] [CrossRef]
- Mu, X.; Song, W.; Gao, Z.; McVicar, T.R.; Donohue, R.J.; Yan, G. Fractional Vegetation Cover Estimation by Using Multi-Angle Vegetation Index. Remote Sens. Environ. 2018, 216, 44–56. [Google Scholar] [CrossRef]
- Dong, Y.; Jiao, Z.; Cui, L.; Zhang, H.; Zhang, X.; Yin, S.; Ding, A.; Chang, Y.; Xie, R.; Guo, J. Assessment of the Hotspot Effect for the PROSAIL Model with POLDER Hotspot Observations Based on the Hotspot-Enhanced Kernel-Driven BRDF Model. IEEE Trans. Geosci. Remote Sens. 2019, 57, 8048–8064. [Google Scholar] [CrossRef]
- Jiao, Z.T.; Schaaf, C.B.; Dong, Y.D.; Roman, M.O.; Hill, M.J.; Chen, J.M.; Wang, Z.S.; Zhang, H.; Saenz, E.; Poudyal, R.; et al. A Method for Improving Hotspot Directional Signatures in BRDF Models Used for MODIS. Remote Sens. Environ. 2016, 186, 135–151. [Google Scholar] [CrossRef] [Green Version]
- Javier Garcia-Haro, F.; Campos-Taberner, M.; Munoz-Mari, J.; Laparra, V.; Camacho, F.; Sanchez-Zapero, J.; Camps-Valls, G. Derivation of Global Vegetation Biophysical Parameters from Eumetsat Polar System. ISPRS J. Photogramm. 2018, 139, 57–74. [Google Scholar] [CrossRef]
- Zhang, X.; Jiao, Z.; Dong, Y.; Zhang, H.; Li, Y.; He, D.; Ding, A.; Yin, S.; Cui, L.; Chang, Y. Potential Investigation of Linking PROSAIL with the Ross-Li BRDF Model for Vegetation Characterization. Remote Sens. 2018, 10, 437. [Google Scholar] [CrossRef] [Green Version]
- Feret, J.B.; François, C.; Asner, G.P.; Gitelson, A.A.; Martin, R.E.; Bidel, L.P.R.; Ustin, S.L.; le Maire, G.; Jacquemoud, S. PROSPECT-4 and 5: Advances in the Leaf Optical Properties Model Separating Photosynthetic Pigments. Remote Sens. Environ. 2008, 112, 3030–3043. [Google Scholar] [CrossRef]
- Verhoef, W.; Jia, L.; Xiao, Q.; Su, Z. Unified Optical-Thermal Four-Stream Radiative Transfer Theory for Homogeneous Vegetation Canopies. IEEE Trans. Geosci. Remote Sens. 2007, 45, 1808–1822. [Google Scholar] [CrossRef]
- Jacquemoud, S.; Verhoef, W.; Baret, F.; Bacour, C.; Zarco Tejada, P.J.; Asner, G.P.; François, C.; Ustin, S.L. PROSPECT+SAIL Models: A Review of Use for Vegetation Characterization. Remote Sens. Environ. 2009, 113, 56–66. [Google Scholar] [CrossRef]
- Wang, L.J.; Dong, T.F.; Zhang, G.M.; Niu, Z. LAI Retrieval Using PROSAIL Model and Optimal Angle Combination of Multi-Angular Data in Wheat. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 1730–1736. [Google Scholar] [CrossRef]
- Yi, Y.H.; Yang, D.W.; Huang, J.F.; Chen, D.Y. Evaluation of MODIS Surface Reflectance Products for Wheat Leaf Area Index (LAI) Retrieval. ISPRS J. Photogramm. 2008, 63, 661–677. [Google Scholar] [CrossRef]
- Zarco-Tejada, P.J.; Miller, J.R.; Noland, T.L.; Mohammed, G.H.; Sampson, P.H. Scaling-Up and Model Inversion Methods with Narrowband Optical Indices for Chlorophyll Content Estimation in Closed Forest Canopies with Hyperspectral Data. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1491–1507. [Google Scholar] [CrossRef] [Green Version]
- Knyazikhin, Y.; Martonchik, J.V.; Diner, D.J.; Myneni, R.B.; Verstraete, M.; Pinty, B.; Gobron, N. Estimation of Vegetation Canopy Leaf Area Index and Fraction of Absorbed Photosynthetically Active Radiation from Atmosphere-Corrected MISR Data. J. Geophys. Res. Atmos. 1998, 103, 32239–32256. [Google Scholar] [CrossRef] [Green Version]
- Jacquemoud, S.; Ustin, S.L.; Verdebout, J.; Schmuck, G.; Andreoli, G.; Hosgood, B. Estimating Leaf Biochemistry Using the PROSPECT Leaf Optical Properties Model. Remote Sens. Environ. 1996, 56, 194–202. [Google Scholar] [CrossRef]
- Saltelli, A.; Tarantola, S.; Chan, K.P.S. A Quantitative Model-Independent Method for Global Sensitivity Analysis of Model Output. Technometrics 1999, 41, 39–56. [Google Scholar] [CrossRef]
- Xiao, Y.F.; Zhao, W.J.; Zhou, D.M.; Gong, H.L.; Du, P.P. Sensitivity Analysis of Vegetation Reflectance to Biochemical and Biophysical Variables at Leaf, Canopy, and Regional Scales. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4014–4024. [Google Scholar] [CrossRef]
- Bacour, C.; Jacquemoud, S.; Tourbier, Y.; Dechambre, M.; Frangi, J.P. Design and Analysis of Numerical Experiments to Compare Four Canopy Reflectance Models. Remote Sens. Environ. 2002, 79, 72–83. [Google Scholar] [CrossRef]
- Schaepman-Strub, G.; Schaepman, M.E.; Painter, T.H.; Dangel, S.; Martonchik, J.V. Reflectance Quantities in Optical Remote Sensing-Definitions and Case Studies. Remote Sens. Environ. 2006, 103, 27–42. [Google Scholar] [CrossRef]
- Fang, H.; Zhang, Y.; Wei, S.; Li, W.; Ye, Y.; Sun, T.; Liu, W. Validation of Global Moderate Resolution Leaf Area Index (LAI) Products Over Croplands in Northeastern China. Remote Sens. Environ. 2019, 233, 111377. [Google Scholar] [CrossRef]
- Sandmeier, S.R.; Strahler, A.H. BRDF Laboratory Measurements. Remote. Sens. Rev. 2000, 18, 481–502. [Google Scholar] [CrossRef]
- Huang, X.Y.; Jiao, Z.T.; Dong, Y.D.; Zhang, H.; Li, X.W. Analysis of BRDF and Albedo Retrieved by Kernel-Driven Models Using Field Measurements. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 149–161. [Google Scholar] [CrossRef]
- Shuai, Y.M.; Schaaf, C.B.; Strahler, A.H.; Liu, J.C.; Jiao, Z.T. Quality Assessment of BRDF/Albedo Retrievals in MODIS Operational System. Geophys. Res. Lett. 2008, 35, 1–5. [Google Scholar] [CrossRef]
- Jin, Y.F.; Schaaf, C.B.; Woodcock, C.E.; Gao, F.; Li, X.W.; Strahler, A.H.; Lucht, W.W.; Liang, S.L. Consistency of MODIS Surface Bidirectional Reflectance Distribution Function and Albedo Retrievals: 2. Validation. J. Geophys. Res. Atmos. 2003, 108, 4159. [Google Scholar] [CrossRef] [Green Version]
- Hu, B.X.; Lucht, W.; Li, X.W.; Strahler, A.H. Validation of Kernel-Driven Semiempirical Models for the Surface Bidirectional Reflectance Distribution Function of Land Surfaces. Remote Sens. Environ. 1997, 62, 201–214. [Google Scholar] [CrossRef]
- Wang, Z.S.; Schaaf, C.B.; Strahler, A.H.; Chopping, M.J.; Roman, M.O.; Shuai, Y.M.; Woodcock, C.E.; Hollinger, D.Y.; Fitzjarrald, D.R. Evaluation of MODIS Albedo Product (MCD43A) over Grassland, Agriculture and Forest Surface Types During Dormant and Snow-Covered Periods. Remote Sens. Environ. 2014, 140, 60–77. [Google Scholar] [CrossRef] [Green Version]
- Jin, Y.F.; Schaaf, C.B.; Gao, F.; Li, X.W.; Strahler, A.H.; Lucht, W.; Liang, S.L. Consistency of MODIS Surface Bidirectional Reflectance Distribution Function and Albedo Retrievals: 1. Algorithm Performance. J. Geophys. Res. Atmos. 2003, 108, 4158. [Google Scholar] [CrossRef]
- Fang, H.; Ye, Y.; Liu, W.; Wei, S.; Ma, L. Continuous Estimation of Canopy Leaf Area Index (LAI) and Clumping Index over Broadleaf Crop Fields: An Investigation of the PASTIS-57 Instrument and Smartphone Applications. Agr. Forest Meteorol. 2018, 253, 48–61. [Google Scholar] [CrossRef]
- Fang, H.; Li, W.; Wei, S.; Jiang, C. Seasonal Variation of Leaf Area Index (LAI) Over Paddy Rice Fields in NE China: Intercomparison of Destructive Sampling, LAI-2200, Digital Hemispherical Photography (DHP), and AccuPAR Methods. Agr. Forest Meteorol. 2014, 198, 126–141. [Google Scholar] [CrossRef]
- Jiao, Z.T.; Hill, M.J.; Schaaf, C.B.; Zhang, H.; Wang, Z.S.; Li, X.W. An Anisotropic Flat Index (AFX) to Derive BRDF Archetypes from MODIS. Remote Sens. Environ. 2014, 141, 168–187. [Google Scholar] [CrossRef]
- Weiss, M.; Baret, F.; Myneni, R.B.; Pragnere, A.; Knyazikhin, Y. Investigation of a Model Inversion Technique to Estimate Canopy Biophysical Variables from Spectral and Directional Reflectance Data. Agronomie 2000, 20, 3–22. [Google Scholar] [CrossRef]
- Jacquemoud, S.; Bacour, C.; Poilve, H.; Frangi, J.P. Comparison of Four Radiative Transfer Models to Simulate Plant Canopies Reflectance: Direct and Inverse Mode. Remote Sens. Environ. 2000, 74, 471–481. [Google Scholar] [CrossRef]
- Saltelli, A. Sensitivity Analysis: Could Better Methods be Used? J. Geophys. Res. Atmos. 1999, 104, 3789–3793. [Google Scholar] [CrossRef]
- Chen, J.M.; Cihlar, J. A Hotspot Function in a Simple Bidirectional Reflectance Model for Satellite Applications. J. Geophys. Res. Atmosph. 1997, 102, 25907–25913. [Google Scholar] [CrossRef]
- Chappell, A.; Zobeck, T.M.; Brunner, G. Using Bi-Directional Soil Spectral Reflectance to Model Soil Surface Changes Induced by Rainfall and Wind-Tunnel Abrasion. Remote Sens. Environ. 2006, 102, 328–343. [Google Scholar] [CrossRef]
- Liu, J.C.; Schaaf, C.B.; Strahler, A.H.; Jiao, Z.T.; Shuai, Y.M.; Zhang, Q.L.; Roman, M.O.; Augustine, J.A.; Dutton, E.G. Validation of Moderate Resolution Imaging Spectroradiometer (MODIS) Albedo Retrieval Algorithm: Dependence of Albedo on Solar Zenith Angle. J. Geophys. Res. Atmos. 2009, 114, 1–11. [Google Scholar] [CrossRef]
- Chang, Y.X.; Jiao, Z.T.; Zhang, X.N.; Mei, L.L.; Dong, Y.D.; Yin, S.Y.; Cui, L.; Ding, A.X.; Guo, J.; Xie, R.; et al. Assessment of Improved Ross-Li BRDF Models Emphasizing Albedo Estimates at Large Solar Angles Using POLDER Data. IEEE Trans. Geosci. Remote Sens. 2021, 59, 9968–9986. [Google Scholar] [CrossRef]
- Widlowski, J.L.; Mio, C.; Disney, M.; Adams, J.; Andredakis, I.; Atzberger, C.; Brennan, J.; Busetto, L.; Chelle, M.; Ceccherini, G.; et al. The Fourth Phase of the Radiative Transfer Model Intercomparison (RAMI) Exercise: Actual Canopy Scenarios and Conformity Testing. Remote Sens. Environ. 2015, 169, 418–437. [Google Scholar] [CrossRef]
- Kuusk, A. A Two-Layer Canopy Reflectance Model. J. Quant. Spectrosc. Ra. 2001, 71, 1–9. [Google Scholar] [CrossRef]
- Leblanc, S.G.; Chen, J.M. A Windows Graphic User Interface (GUI) for the Five-Scale Model for Fast BRDF Simulations. Remote. Sens. Rev. 2000, 19, 293–305. [Google Scholar] [CrossRef]
- Gastellu-Etchegorry, J.P.; Lauret, N.; Yin, T.G.; Landier, L.; Kallel, A.; Malenovsky, Z.; Al Bitar, A.; Aval, J.; Benhmida, S.; Qi, J.B.; et al. DART: Recent Advances in Remote Sensing Data Modeling with Atmosphere, Polarization, and Chlorophyll Fluorescence. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 2640–2649. [Google Scholar] [CrossRef]
- Qi, J.; Xie, D.; Yin, T.; Yan, G.; Gastellu-Etchegorry, J.; Li, L.; Zhang, W.; Mu, X.; Norford, L.K. LESS: Large-Scale Remote Sensing Data and Image Simulation Framework over Heterogeneous 3D Scenes. Remote Sens. Environ. 2019, 221, 695–706. [Google Scholar] [CrossRef]
- Rahman, H.; Verstraete, M.M.; Pinty, B. Coupled Surface-Atmosphere Reflectance (CSAR) Model. 1. Model Description and Inversion on Synthetic Data. J. Geophys. Res. Atmosph. 1993, 98, 20779–20789. [Google Scholar] [CrossRef]
- Li, X.W.; Strahler, A.H.; Friedl, M.A. A Conceptual Model for Effective Directional Emissivity from Nonisothermal Surfaces. IEEE Trans. Geosci. Remote Sens. 1999, 37, 2508–2517. [Google Scholar]
- Huang, H.; Qin, W.; Liu, Q. Rapid: A Radiosity Applicable to Porous Individual Objects for Directional Reflectance over Complex Vegetated Scenes. Remote Sens. Environ. 2013, 132, 221–237. [Google Scholar] [CrossRef]
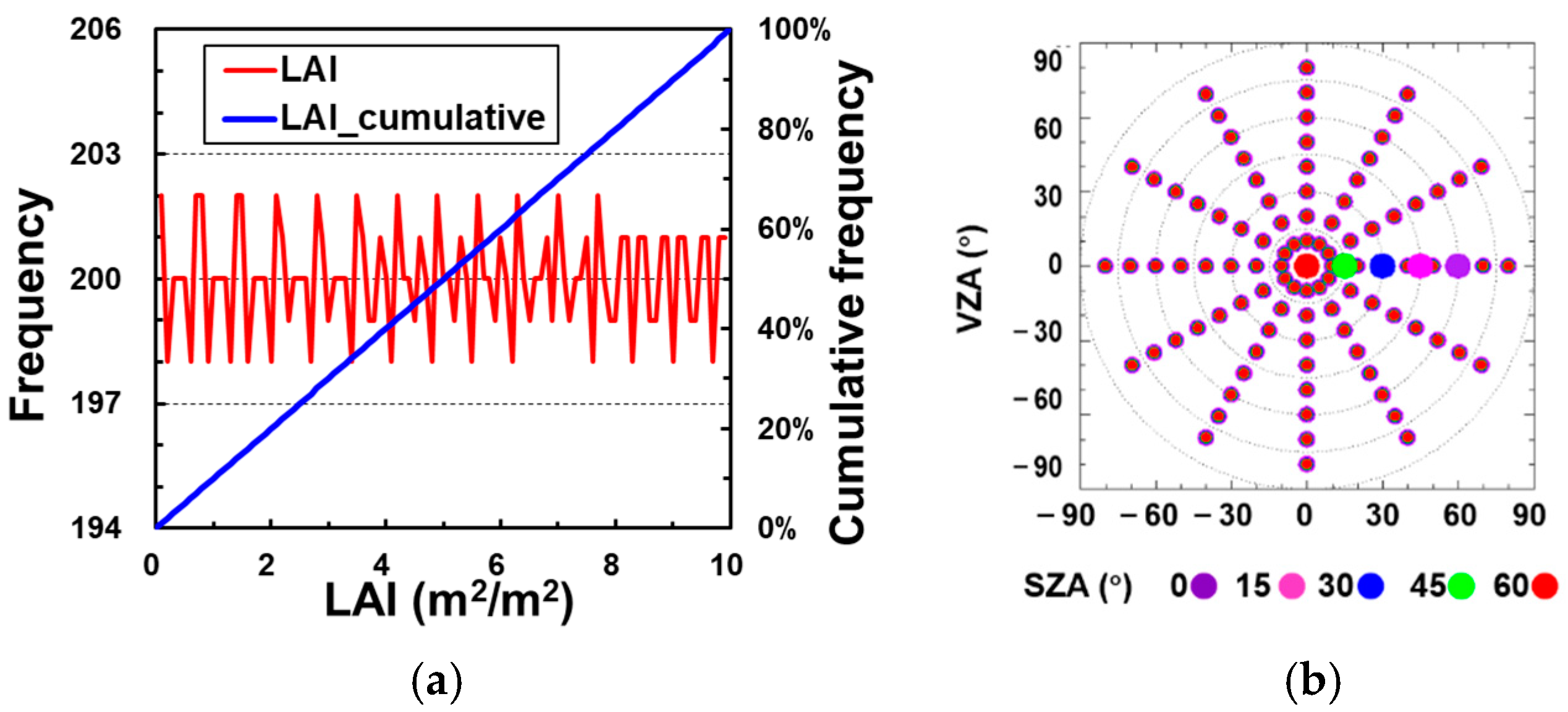

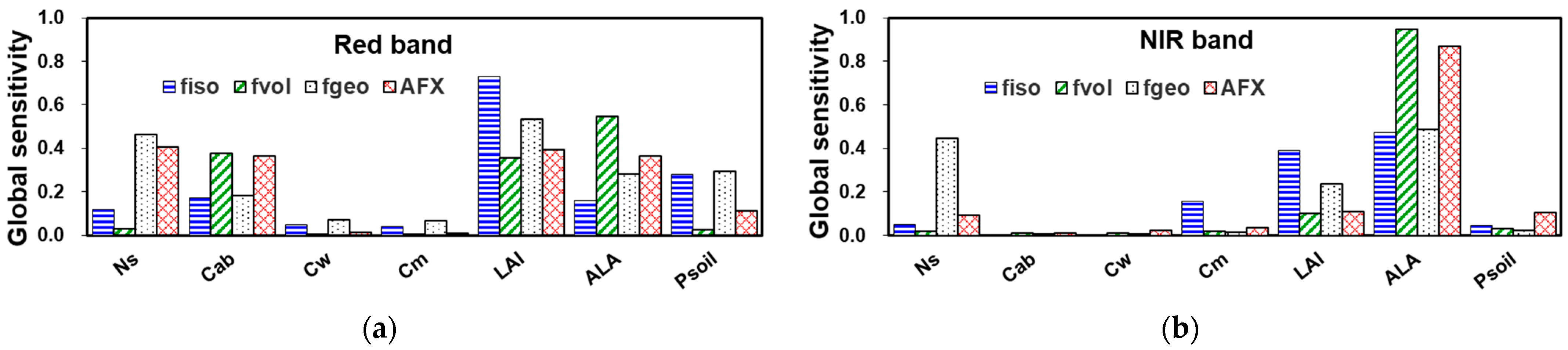


| Parameters | Unit | Common Value | Search Range (Step) |
|---|---|---|---|
| Leaf scale | |||
| leaf structure parameter (Ns) | -- | 1.5 | 1–3 |
| chlorophyll a and b content (Cab) | μg/cm2 | 50 | 20–80 |
| carotenoids content (Car) | μg/cm2 | 12 | |
| brown pigment content (Cbrown) | -- | 0 | |
| Equivalent water thickness (Cw) | cm | 0.015 | 0.004–0.04 |
| leaf mass per unit leaf area (Cm) | g/cm2 | 0.009 | 0.0019–0.0165 |
| Canopy scale | |||
| leaf area index (LAI) | m2/m2 | 3.5 | 0–10 |
| average leaf angle (ALA) | degrees (°) | 50 | 10–85 |
| hot spot (Hspot) | -- | 0.2 | |
| soil coefficient (Psoil) | -- | 0.1 [0,1] | 0–1 |
| diffuse/direct radiation (SKYL) | % | 0 | |
| Observation geometry | |||
| solar zenith angle (SZA) | degrees (°) | 30 | 0–60 (15) |
| view zenith angle (VZA) | degrees (°) | 0 | 0–80 (10) |
| relative azimuth angle (RAA (φ)) | degrees (°) | 0 | 0–330 (30) |
| Band (nm) | 645 | 858 | 469 | 555 | 1240 | 1640 | 2130 |
|---|---|---|---|---|---|---|---|
| C1 | 0.5 | 0.5 | 0.4 | 0.5 | 0.4 | 0.4 | 0.4 |
| C2 (°) | 3.4 | 3.0 | 3.8 | 3.1 | 4.5 | 4.5 | 4.5 |
| Data for Linear Modelling (90%, ALA = a × fvol_NIR + b) | Data for Evaluation (10%) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Group | a | b | R2 | F | RMSE_All | Bias_All | R2_All | RMSE_HD | Bias_HD | R2_HD |
| 1 | 186.66 | 13.87 | 0.98 | 565,079 | 7.35 | −1.18 | 0.83 | 2.27 | 0.00 | 0.98 |
| 2 | 186.69 | 13.85 | 0.98 | 584,873 | 6.68 | −1.18 | 0.86 | 2.43 | −0.10 | 0.98 |
| 3 | 186.78 | 13.85 | 0.98 | 584,443 | 6.83 | −1.08 | 0.85 | 2.96 | −0.10 | 0.97 |
| 4 | 186.54 | 13.88 | 0.98 | 567,284 | 6.53 | −1.06 | 0.87 | 2.07 | −0.09 | 0.99 |
| 5 | 186.68 | 13.85 | 0.98 | 585,602 | 6.75 | −1.05 | 0.85 | 2.95 | −0.19 | 0.97 |
| 6 | 186.54 | 13.87 | 0.98 | 568,940 | 6.05 | −1.07 | 0.88 | 2.22 | −0.13 | 0.98 |
| 7 | 186.64 | 13.85 | 0.98 | 587,354 | 6.36 | −1.00 | 0.87 | 2.29 | −0.15 | 0.98 |
| 8 | 186.59 | 13.86 | 0.98 | 586,356 | 7.10 | −1.25 | 0.84 | 1.98 | −0.10 | 0.99 |
| 9 | 186.66 | 13.85 | 0.98 | 586,247 | 6.92 | −1.17 | 0.85 | 2.10 | −0.19 | 0.98 |
| 10 | 186.69 | 13.85 | 0.98 | 585,865 | 6.80 | −1.07 | 0.86 | 2.30 | −0.08 | 0.98 |
| average | -- | -- | 0.98 | 580,204 | 6.74 | −1.11 | 0.86 | 2.36 | −0.11 | 0.98 |
| Dataset | Method | Data Number | RMSE | BIAS | R2 | RRMSE(%) |
|---|---|---|---|---|---|---|
| Honghe | MODIS | 110 | 1.55 | −0.28 | 0.13 | 50.2 |
| wide search | 110 | 1.35 | −0.75 | 0.34 | 43.7 | |
| wide search of local search data | 40 | 1.79 | −1.45 | 0.55 | 65.0 | |
| local search by the ALA | 40 | 1.54 | −1.09 | 0.52 | 55.9 | |
| fused results | 110 | 1.23 | −0.62 | 0.40 | 39.8 | |
| Hailun | MODIS | 70 | 1.59 | −0.10 | 0.35 | 45.4 |
| wide search | 70 | 1.64 | −1.09 | 0.53 | 46.9 | |
| wide search of local search data | 63 | 1.73 | −1.24 | 0.57 | 49.1 | |
| local search by the ALA | 63 | 1.58 | −0.42 | 0.55 | 44.9 | |
| fused results | 70 | 1.50 | −0.36 | 0.55 | 42.9 | |
| All crops | MODIS | 180 | 1.57 | −0.21 | 0.24 | 48.3 |
| wide search | 180 | 1.47 | −0.89 | 0.44 | 45.3 | |
| wide search of local search data | 103 | 1.75 | −1.32 | 0.57 | 54.4 | |
| local search by the ALA | 103 | 1.56 | −0.68 | 0.54 | 48.5 | |
| fused results | 180 | 1.34 | −0.52 | 0.49 | 41.3 |
| Dataset | Method | Data Number | RMSE | BIAS | R2 | RRMSE(%) |
|---|---|---|---|---|---|---|
| Honghe | wide search | 110 | 1.17 | −0.60 | 0.36 | 37.8 |
| wide search of local search data | 17 | 1.65 | −1.25 | 0.58 | 55.7 | |
| local search by the ALA | 17 | 1.33 | −0.94 | 0.66 | 45.1 | |
| fused results | 110 | 1.10 | −0.55 | 0.41 | 35.8 | |
| Hailun | wide search | 70 | 1.53 | −0.97 | 0.57 | 43.5 |
| wide search of local search data | 59 | 1.56 | −1.00 | 0.59 | 45.0 | |
| local search by the ALA | 59 | 1.55 | −0.22 | 0.53 | 44.8 | |
| fused results | 70 | 1.52 | −0.32 | 0.50 | 43.4 | |
| All crops | wide search | 180 | 1.32 | −0.74 | 0.47 | 40.6 |
| wide search of local search data | 76 | 1.58 | −1.05 | 0.58 | 47.2 | |
| local search by the ALA | 76 | 1.50 | −0.38 | 0.54 | 45.0 | |
| fused results | 180 | 1.28 | −0.46 | 0.45 | 39.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Jiao, Z.; Zhao, C.; Yin, S.; Cui, L.; Dong, Y.; Zhang, H.; Guo, J.; Xie, R.; Li, S.; et al. Retrieval of Leaf Area Index by Linking the PROSAIL and Ross-Li BRDF Models Using MODIS BRDF Data. Remote Sens. 2021, 13, 4911. https://doi.org/10.3390/rs13234911
Zhang X, Jiao Z, Zhao C, Yin S, Cui L, Dong Y, Zhang H, Guo J, Xie R, Li S, et al. Retrieval of Leaf Area Index by Linking the PROSAIL and Ross-Li BRDF Models Using MODIS BRDF Data. Remote Sensing. 2021; 13(23):4911. https://doi.org/10.3390/rs13234911
Chicago/Turabian StyleZhang, Xiaoning, Ziti Jiao, Changsen Zhao, Siyang Yin, Lei Cui, Yadong Dong, Hu Zhang, Jing Guo, Rui Xie, Sijie Li, and et al. 2021. "Retrieval of Leaf Area Index by Linking the PROSAIL and Ross-Li BRDF Models Using MODIS BRDF Data" Remote Sensing 13, no. 23: 4911. https://doi.org/10.3390/rs13234911
APA StyleZhang, X., Jiao, Z., Zhao, C., Yin, S., Cui, L., Dong, Y., Zhang, H., Guo, J., Xie, R., Li, S., Zhu, Z., & Tong, Y. (2021). Retrieval of Leaf Area Index by Linking the PROSAIL and Ross-Li BRDF Models Using MODIS BRDF Data. Remote Sensing, 13(23), 4911. https://doi.org/10.3390/rs13234911








