Abstract
It is of great significance for the validation of remotely sensed evapotranspiration (ET) products to solve the spatial-scale mismatch between site observations and remote sensing estimations. To overcome this challenge, this paper proposes a comprehensive framework for obtaining the ground truth ET at the satellite pixel scale (1 × 1 km resolution in MODIS satellite imagery). The main idea of this framework is to first quantitatively evaluate the spatial heterogeneity of the land surface, then combine the eddy covariance (EC)-observed ET (ET_EC) to be able to compare and optimize the upscaling methods (among five data-driven and three mechanism-driven methods) through direct validation and cross-validation, and finally use the optimal method to obtain the ground truth ET at the satellite pixel scale. The results showed that the ET_EC was superior over homogeneous underlying surfaces with a root mean square error (RMSE) of 0.34 mm/d. Over moderately and highly heterogeneous underlying surfaces, the Gaussian process regression (GPR) method performed better (the RMSEs were 0.51 mm/d and 0.60 mm/d, respectively). Finally, an integrated method (namely, using the ET_EC for homogeneous surfaces and the GPR method for moderately and highly heterogeneous underlying surfaces) was proposed to obtain the ground truth ET over fifteen typical underlying surfaces in the Heihe River Basin. Furthermore, the uncertainty of ground truth ET was quantitatively evaluated. The results showed that the ground truth ET at the satellite pixel scale is relatively reliable with an uncertainty of 0.02–0.41 mm/d. The upscaling framework proposed in this paper can be used to obtain the ground truth ET at the satellite pixel scale and its uncertainty, and it has great potential to be applied in more regions around the globe for remotely sensed ET products’ validation.
1. Introduction
The evapotranspiration (ET) of the land surface is a significant part of the global hydrologic cycle and plays an important role among climate systems, energy balance processes, and carbon cycles [1]. Accurate monitoring and estimations of ET are critical not only for water resource management but also for modeling regional and global climate and hydrological cycles [2]. Remote sensing technology is effective for monitoring ET [3], and a variety of remotely sensed ET products have been produced and available, such as the Moderate Resolution Imaging Spectroradiometer (MODIS) Global Evapotranspiration Project (MOD16) [4], Global Land Evaporation Amsterdam Model (GLEAM) [5], Global LAnd Surface Satellite (GLASS) [6], ETMonitor [7], and Breathing Earth System Simulator (BESS) [8] products. However, remotely sensed ET products have various sources of uncertainties [9,10], resulting in different accuracies, with mean absolute percentage errors (MAPEs) at instantaneous (15–30%), daily (14–44%), monthly (10–36%), and annual scales (5–21%) [11,12,13,14]. Thus, it is significant to validate remotely sensed ET products before being used in practical applications.
The most popular method for remotely sensed ET validation is directly using site observation data derived from eddy covariance (EC) and large aperture scintillometer (LAS) [15,16]. In contrast to the single point observations obtained for the leaf area index (LAI), land surface temperature (LST), and soil moisture, the EC and LAS measurements represent the footprint scale. Their spatial representations (flux source area) vary with wind speed/direction, atmospheric stability, surface roughness, and instrument height. In addition, due to the ubiquity of land surface spatial heterogeneity, the problem of spatial-scale mismatches between site observation values and remote sensing estimation values inevitably arises. The introduction of the flux footprint and source area helps solve the problem of spatial-scale mismatches to some extent [9]. However, the fact that the given source area cannot always completely cover one or several satellite pixels will bring some uncertainty to the validation results. Therefore, it is necessary to study how to upscale ET from the footprint scale to the satellite pixel scale through upscaling methods to reduce the uncertainty caused by spatial-scale mismatches.
Upscaling is defined as the process of transforming data or information from a fine scale to a coarse scale in the spatial dimension or from a short scale to a long scale in the temporal dimension [17]. Upscaling is the most effective and most commonly used approach for obtaining ground truth data at the satellite pixel scale. Current studies on upscaling ET can be divided into these studies using data-driven methods and those using mechanism-driven methods. Among them, data-driven methods can be divided into probability-based methods, regression model-based methods, and machine learning-based methods, while mechanism-driven methods can be divided into the fusion of prior information-based methods and process model-based methods [17,18,19,20,21,22].
Probability-based methods include the arithmetic average [18], area-weighted (AW) average [23,24,25], and footprint-weighted [18] methods. Based on the multi-site measurement datasets and a high-resolution landcover map in the downstream of the Heihe River Basin (HRB) in 2014, Xu et al. [25] used the AW method to upscale the sensible heat (H) flux from multi-site to the LAS scale. Regression model-based methods include the multiple linear regression, ordinary least squares, Bayesian linear regression (BLR), and ridge regression methods [26,27,28,29]. Based on the flux observation matrix and a high-resolution landcover map in the midstream of the HRB in 2012, Xu et al. [24] upscaled the H flux from multi-site to the LAS scale using footprint analysis and multiple linear regression, and the results were validated by LAS observations. Machine learning model-based methods include artificial neural network (ANN) [30,31], regression tree [20,32], support vector machine [20,33], random forest (RF) [19,34], Gaussian process regression (GPR) [35], deep belief network (DBN) [19], etc. Based on observation data obtained from FLUXNET, Bodesheim et al. [34] trained an RF model on different underlying surfaces, fed the regional grid data into the trained model, and finally obtained latent heat (LE) and H fluxes with a spatial resolution of 0.5° and a temporal resolution of half an hour over a global range. The fusion of prior information-based methods includes the kriging framework (kriging interpolation and its derivatives) [36,37] and Bayesian framework (Bayesian method in information entropy theory) methods [38,39]. Supported by the flux observation matrix datasets (multiple ECs), Ge et al. [37] obtained the H flux at the LAS footprint scale upscaled from the EC scale by using the area-to-area regression kriging estimation equation combined with auxiliary information. Process model-based methods include physics-based models [18,40] and data assimilation methods [41,42]. These two methods incorporate site data to determine model parameters or relationships, and they combine surface flux observation data, meteorological data, and remote sensing data to obtain surface water and heat fluxes at a pixel scale. Based on a dataset from the flux observation matrix of the midstream in the HRB, Liu et al. [18] fitted a linear regression relationship between the Priestley–Taylor coefficient and the difference between the surface temperature and air temperature, combined with auxiliary information, and estimated ET value at the satellite pixel scale using the Priestley–Taylor equation.
In summary, although some progress has been made in the study of ET upscaling, the current research on upscaling ET still faces the following challenges. First, the aforementioned upscaling methods focus mainly on multiple EC observation towers, such as flux observation matrices and global- or watershed-scale observation networks [19,20]. However, most site observations are based on a single EC system, lysimeter, scintillometer, etc. For example, the FLUXNET only has one EC flux observation tower per site and is widely utilized in the validation of remotely sensed ET products or ET estimation models at a regional or global scale [12]. Second, most upscaling methods do not fully address the effect of the spatial heterogeneity of the land surface hydrothermal conditions (LSHCs) on the upscaled results [43]. However, land surface heterogeneity is ubiquitous and is the key to scaling effects and upscaling methods. Therefore, upscaling methods considering spatial heterogeneity can be more universal than other methods that do not consider spatial heterogeneity. Moreover, the ground truth values at the pixel scale obtained by the upscaling method are not “true values” in the absolute sense, and the uncertainty mainly arises from ET observational errors, upscaling method errors, and auxiliary information errors [44], all of which directly affect the accuracy and reliability of the validation results of remote sensing products [43,45]. Therefore, the uncertainties arising in the upscaled results need to be quantitatively analyzed. In addition, considering that different upscaling methods have different advantages, disadvantages, and applicabilities, it is necessary to comprehensively compare and optimize different types of upscaling methods. Therefore, upscaling ET based on a single site while considering the effects of the heterogeneity of the LSHCs and quantitatively evaluating the uncertainty derived in the upscaled results is still challenging.
In this paper, we propose a comprehensive framework for acquiring ground truth ET at the satellite pixel scale to solve the spatial-scale mismatch issue during remotely sensed ET validation. The objectives of this paper are to (1) compare the performances of eight upscaling methods (including five data-driven and three mechanism-driven methods) combined with EC-observed ET (ET_EC) and discuss the different performances of these methods; (2) acquire the ground truth ET data at the satellite pixel scale on fifteen typical surface types in the HRB; and (3) analyze the uncertainties of the ground truth ET at the satellite pixel scale.
2. Study Area and Datasets
2.1. Study Area
The study area is located in the HRB (37.7°–42.7°N, 97.1°–102.0°E), which is the second-largest endorheic basin in the arid and semiarid regions of Northwest China and has a typical continental arid climate, with an area of approximately 143,000 km2 (Figure 1). The HRB includes the upstream, midstream, and downstream areas with different kinds of underlying surfaces, and the air temperature and precipitation show obvious zonal characteristics with the change in elevation from the upstream to downstream regions. The landscape zonality of the HRB is also obvious; more specifically, it forms a “snow/ice/frozen soil–forest–grassland–oasis–desert/Gobi–tail-end lake” pattern of diverse natural landscapes, using water as a link from the upstream to the midstream and downstream regions [46]. These unique characteristics make the HRB an ideal region for upscaling research based on the different climate and land surface types.
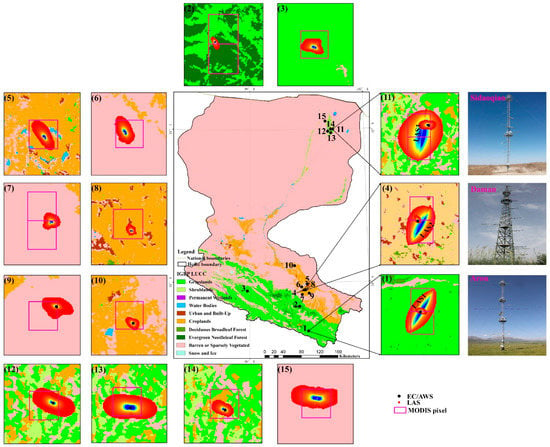
Figure 1.
The spatial location of the HRB and the locations of the Arou superstation (1), Guantan station (2), and Dashalong (3) station in the upstream; the Daman superstation (4), Wetland (5), Bajitan Gobi (6), Huazhaizi Desert Steppe (7), Yingke (8), Shenshawo (9), and Linze (10) stations in the midstream; the Sidaoqiao superstation (11), the Populus euphratica (12), Mixed Forest (13), Barren Land (14), and Desert (15) stations in the downstream; and the filled ovals represent the flux source areas of the EC (at all stations) and LAS (at superstations) (corresponding to approximately 90% of the source area contribution), and the squares represent the corresponding 1 × 1 or 2 × 1 MODIS pixels.
To enhance the observation ability of the land surface processes in the HRB, the Heihe integrated observatory network was established; this network is characterized by being multielement, multiscale, and distributed, and it incorporates satellite–airborne–ground-based observations [46,47]. The Heihe integrated observatory network was developed from two successive observation experiments: the first part of the network was established in 2007 during the Watershed Allied Telemetry Experimental Research (WATER) experiment (2007–2011) [48], and the second part was completed in 2013 during the HiWATER experiment (2012–2015) [49]. There are three superstations and twenty ordinary stations in the HRB. In 2016, the number of stations was reduced to eleven carrying out refined observations. These stations cover the primary surface types of the HRB [46,49,50,51]. The three superstations were selected for the comparison and optimization of the upscaling methods, and ordinary stations representing typical surface types in the HRB were also selected to obtain the ground truth ET at the satellite pixel scale. Among them, the superstations include flux towers with heights of 30–40 m equipped with multiscale and multielement observation systems. Each observation system consists of a lysimeter/thermal dissipation probe (TDP)–EC–LAS, an in situ soil temperature/moisture profile–cosmic-ray probe–soil moisture/temperature sensor network, and a multilayer meteorological gradient observation system. At each ordinary station, there is an EC system and an automatic weather station (AWS) to monitor the H, LE, and meteorological elements. Specifications of the superstations and ordinary stations are given in Figure 1 and Table 1. More detailed information can be found in [46,49]. Three superstations and eleven ordinary stations from the Heihe Integrated Observatory Network and one other researcher’s site (Linze station [52]) were selected for the study of ground truth ET at the satellite pixel-scale acquisition.

Table 1.
Specifications of the stations in the HRB used in this study.
2.2. Datasets
2.2.1. Station Observation Data
The original EC data were processed with the raw 10 Hz data, and the 30-min average EC data values were obtained by the EddyPro software (http://www.licor.com/env/products/eddy_covariance/software.html, accessed on 10 March 2019). To force the energy balance closure, the Bowen ratio closure method was used. The daily ET was calculated using the continuous 30-min data, and the nonlinear regression method was used if the 30-min data were missing. In addition, if the absence rate of the 30-min data was greater than 50% in one day, then the data on this day were not used. More information about EC data processing and quality control can be found in [53].
For the LAS data, first, the raw LAS data were averaged to 30-min intervals. The daily LAS-LE was calculated by the energy balance equation (). The net radiation ( and surface soil heat were measured by a four-component radiometer and three soil heat flux plates, respectively. When advection occurs, namely, H was less than 10 W/m2 in the daytime, and the relationship between LAS-LE and under non-advection conditions was used to obtain LAS-LE directly from the linear interpolation [18]. Finally, the daily ET was obtained using the continuous 30-min data. Moreover, if the absence rate of the 30-min data was over 50% in one day, then the day was regarded as a missing day, and the data were not selected.
The AWS data obtained at each station included the wind speed/direction, air temperature and humidity, precipitation, atmospheric pressure, downward (upward) shortwave (longwave) radiation, soil heat flux, soil temperature/moisture profile, etc. The processing and quality control steps were necessary and included processing the data to 30-min averages, rejecting data during processing that were beyond the physical normal values, and so on. The LST data were obtained from the downward and upward longwave radiation observed using the AWSs and the surface emissivity observed using the FT-IR (Fourier-transform infrared spectroscopy) spectrometer [54]. The site measurement datasets used in this study can be accessed via the National Tibetan Plateau Data Center (http://data.tpdc.ac.cn/en/, accessed on 10 March 2019).
2.2.2. Remote Sensing and Atmospheric Forcing Data
To obtain remote sensing data with a high spatiotemporal resolution through the fusion of multisource remote sensing data obtained in the study area, 286 ETM+ images (path/row: 133/33, 133/34, 134/33, 134/31) from 2010 to 2016 were fused with the MODIS data using the Enhanced Spatial and Temporal Adaptive Reflectance Fusion Model (ESTARFM) [55]. The ETM+ images and MODIS data were derived from the Land Processes Distributed Active Archive Center (LP DAAC) (http://glovis.usgs.gov/, accessed on 15 May 2019) and the United States Geological Survey (USGS) (https://landsat.usgs.gov/, accessed on 15 May 2019), respectively. Before data fusion, these data are preprocessed, including geometric correction, atmospheric correction, etc. Then, the fused data were used to calculate the remote sensing land surface parameters (e.g., , LST, normalized difference vegetation index (NDVI), Albedo, and LAI) [56] and were finally resampled using the bilinear resampling method from a 100 m to a 30 m resolution. Land use/land cover data obtained in the study area at a 30 m resolution [57] were used. In addition, to reduce the influence of the error derived from the remote sensing data on the upscaled results, according to the current retrieval error of the LST and [58,59], 3 K for LST and 10% for were used as the error thresholds in data filtering.
In this study, atmospheric pressure, air temperature, relative humidity, precipitation, and other atmospheric forcing data at a spatial resolution of 100 m were generated by Ma et al. [56]. We used the bilinear resampling method to resample these data to a 30 m resolution. In addition, the high-resolution ET data (resampled to 30 m) were used in this paper to evaluate the spatial heterogeneity of the LSHCs in these sites with sparse vegetation. First, surface parameters for estimating daily ET were obtained through the fusion algorithm (ESTARFM). Then, the surface parameters were imported into the revised Surface Energy Balance System (SEBS) model. Finally, the high-resolution ET data at a spatial resolution of 100 m were obtained [56] and can be downloaded from the National Tibetan Plateau Data Center (http://data.tpdc.ac.cn/en/, accessed on 7 January 2021).
2.2.3. Flux Source Area Data
To better determine the spatial representative range of the observed flux, it is essential to calculate the flux source areas of the EC and LAS. In this paper, an Eulerian analytical flux footprint model [60] was used to determine the source area of the EC at a 30 m resolution. By combining the path-weighting function with the footprint model for the point fluxes, the source area of the LAS was computed [61] with a 30 m resolution. In addition, the flux contribution of the chosen total source area was set to 90%. In this paper, we selected the MODIS pixel corresponding to each station according to the size and location of the flux source area, as illustrated in Figure 1 and Table 1, and obtained the ground truth ET of these MODIS pixels.
3. Methodology
A universal framework for obtaining the ground truth ET at the pixel scale should consider different underlying surface types. The HRB has multiple natural landscapes and diverse land cover types, which provides an ideal observation area for obtaining the ground truth ET at the pixel scale. To improve the capability of the framework for obtaining the ground truth ET at the pixel scale, we selected the stations in the typical underlying surface in the HRB to test the upscaling method, including three superstations and twelve ordinary stations. The underlying surface types of the Arou, Daman, and Sidaoqiao superstations are subalpine meadow, maize, and Tamarix, respectively. The underlying surface types of the ordinary stations include Qinghai spring (GT) and marsh alpine meadow (DSL) in the upstream area; wetland (Wetland), Reaumuria desert (BJT), Kalidium foliatum desert (HZZ), maize (YK and LZ), and sandy desert (SSW) in the midstream; and Populus euphratica (P.E), Populus euphratica and Tamarix (HHL), bare land (LD), and Reaumuria desert (Desert) in the downstream (see Table 1). The primary framework of acquiring the ground truth ET at the satellite pixel scale is to quantitatively evaluate the spatial heterogeneity of the LSHCs firstly and then to compare the data-driven and mechanism-driven upscaling methods taking LAS measurements as the reference value. Finally, the optimal upscaling method is used to obtain the ground truth ET at the satellite pixel scale, and the uncertainty of ground truth ET is estimated using uncertainty quantification methods. The framework of this approach is divided into three steps (Figure 2). (1) Based on the flux source area data, the corresponding MODIS pixels are selected, and the heterogeneity evaluation scheme is used to quantitatively evaluate the spatial heterogeneity of the LSHCs in these pixels [62]; the pixels can be divided into the homogeneous, moderately heterogeneous, and highly heterogeneous underlying surfaces. (2) Based on the quantitative evaluation result of spatial heterogeneity, a comprehensive validation method is adopted; this validation method includes a direct validation taking LAS measurements as the reference value and cross-validation based on the three-cornered hat (TCH) method to compare and analyze several upscaling methods, including data-driven and mechanism-driven methods as well as the eddy covariance (EC)-observed ET (ET_EC). (3) Finally, according to the optimal upscaling method, the ground truth ET at the satellite pixel scale is obtained at these sites over the typical underlying surface in the HRB, and the uncertainty of the ground truth ET is evaluated quantitatively to verify the effectiveness and universality of the framework.
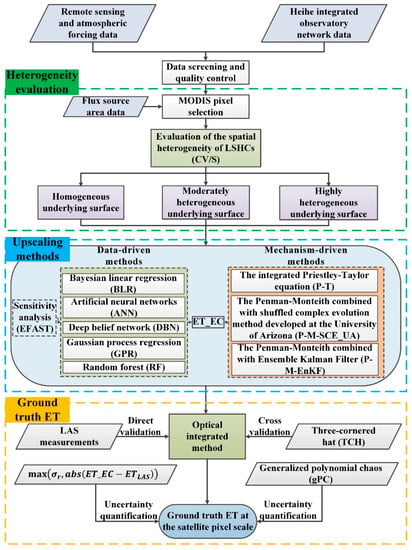
Figure 2.
The framework of acquiring the ground truth ET at the satellite pixel scale.
3.1. Evaluation Method of Spatial Heterogeneity
Spatial heterogeneity is an important property of natural landscapes on earth, and the spatial distribution of the LSHCs is complex and ubiquitous. Considering that the degree of heterogeneity of the LSHCs is diverse and the accuracies and applicability of the various upscaling methods are also different, it is necessary to analyze the spatial heterogeneity of the LSHCs before selecting the appropriate upscaling method to acquire the ground truth ET at the satellite pixel scale. An evaluation scheme was applied to estimate the spatial heterogeneity of the LSHCs [62] in this study. In this scheme, two heterogeneity evaluation indicators (the coefficient of variation (CV) and normalized information entropy (S)) are combined with remotely sensed LAI data to assess the spatial heterogeneity of the LSHCs. In addition, the criteria used to define the classification of the degree of heterogeneity is the following: if S is less than or equal to 0.5, then the underlying surface is defined as a homogeneous underlying surface; if S is greater than 0.5 and the CV is less than or equal to 0.3, then the underlying surface is defined as a moderately heterogeneous underlying surface; and if S is greater than 0.5 and the CV is greater than 0.3, then the underlying surface is defined as a highly heterogeneous underlying surface [62].
3.2. Upscaling Methods
As introduced in Section 1, different upscaling methods have pros and cons in various aspects that influence their applications. In this paper, eight upscaling methods (including the two categories of data-driven and mechanism-driven methods, which can be subdivided into five subcategories) are selected for comparison and optimization to obtain ground truth ET at the satellite pixel scale. Specifically, there are four machine learning-based methods (e.g., ANN, DBN, GPR, and RF), three process model-based methods (e.g., the integrated Priestley–Taylor equation (P-T), the Penman–Monteith equation combined with shuffled complex evolution (P-M-SCE_UA) method, and Penman–Monteith equation combined with Ensemble Kalman Filter (P-M-EnKF) method) and one regression model-based method (e.g., BLR). In addition, the probability-based methods themselves require multiple observation stations, and the fusion of prior information-based methods usually requires more station data to provide more useful prior auxiliary information, so they are not suitable for the upscaling of single-station data and are not selected in this paper. For P-M-SCE_UA and P-M-EnKF, two data assimilation methods (DA) were used in the Penman–Monteith equation to improve the model estimates. For the data used in the upscaling method in this paper, the time periods for data used are shown in Table 1. In this paper, we divide the above data into a training set, validation set, and testing set, and the allocation proportion is 60%, 20%, and 20%, respectively.
For the P-T method, in brief, firstly, the Priestley–Taylor coefficient, , is determined by using the observation data obtained at a given site; secondly, the relationship between and the difference between the land surface temperature and air temperature is created; finally, the ground truth ET at the satellite pixel scale is calculated by using remote sensing data and observation data combined with the Priestley–Taylor formula [18]. For the DA methods (P-M-EnKF and P-M-SCE_UA), in simple terms, the EnKF algorithm and SCE_UA algorithm are used to calibrate the two parameters ( and , see Appendix A) and six parameters (, ,, , and , see Appendix A) in the corresponding Penman–Monteith formula based on the observation data of a given site, respectively, and then, the ground truth ET at the satellite pixel scale is calculated by combining the remote sensing data and the observation data of the site with the corresponding Penman–Monteith formula [63,64,65,66]. For the data-driven methods (i.e., ANN, BLR, DBN, GPR, and RF), firstly, by inputting the EC observation data and related influencing factors (e.g., LST, , and NDVI) at a single site, these models are trained; secondly, through the debugging and constant updating of model parameter, the optimal model is determined; and finally, the corresponding remote sensing data are input to the trained model to estimate the ground truth ET at the pixel scale and achieve the upscaling of ET [67,68,69,70,71]. In addition, the LAS measurements were selected as the satellite pixel reference values in the comparison processes of the upscaling methods. More specific details about the methods used in this study to obtain ground truth ET at the satellite pixel scale are given in Appendix A.
3.3. Cross-Validation Method
The cross-validation method can validate the relative precision and the rationality of the spatiotemporal distributions of diverse products and intercompare products. The TC (triple collocation) method can be used to calculate the relative error between various products. However, the TC method has a hypothesis that the errors of the three products involved in the calculation are independent. When the number of datasets is greater than three groups, assuming that the datasets are independent of each other, the variance may be negative. At this time, the TCH (three-cornered hat) method can be used to analyze the relative error between more than three groups of data. This method is effective for characterizing the relative error of more than three products [44,72]. Therefore, in this study, in addition to the direct validation with LAS observations, the TCH method is also used to perform cross-validation for an intercomparison of the eight upscaling methods. More details about the TCH method are given in Appendix B.
3.4. Sensitivity Analysis Method
The Fourier amplitude sensitivity test (FAST) is a variance-based method that can quantify the main and interactive effects derived from the input parameters. Saltelli et al. [73] developed a method called the extended FAST (EFAST) method, which is based on the classical FAST method. The EFAST method partitions the whole variance in the model output and quantifies the contribution of each input parameter to the variance. The EFAST method combines the optimized efficiency of FAST with the capacity of Sobol’s method to compute the total effects. The EFAST method can qualitatively rank the importance of each input parameter by calculating the contribution of each parameter to variation in the model’s output. In this paper, the EFAST method is mainly used to filter the sensitive factors that are used as the input parameters for the construction of the data-driven upscaling methods (i.e., ANN, BLR, DBN, GPR, and RF). More details about the EFAST method are given in Appendix C.
3.5. Uncertainty Quantification Method
The ground truth ET at the satellite pixel scale obtained by the upscaling method is not a “true value” in the absolute sense, and it contains uncertainty. It is necessary to use a method to evaluate the uncertainty quantitatively. The Monte Carlo (MC) method is widely used for quantifying uncertainty. However, the MC method has a slow convergence speed and high computational overhead and requires a large number of sampling point calculations to obtain results with satisfactory accuracy. Therefore, its application in high-dimensional and multivariable uncertainty quantization problems is limited. The generalized polynomial chaos (gPC) method is a more efficient method for quantifying uncertainty [74,75]; it has the advantages of a small calculation load and high precision, and it has developed into a significant method of uncertainty research. In this method, the correspondence between the probability density function of a random variable and the gPC basis function is found, such that the gPC method can be used for uncertainty analysis of common types of random variables. An important tool for uncertainty quantifications, the gPC method can be used to quantify the uncertainty of the ground truth ET at the satellite pixel scale obtained by a given upscaling method. When ET_EC is used to represent the ground truth ET at the satellite pixel scale over the homogeneous underlying surface, the method of Beyrich et al. [23] is used to quantify the uncertainty of the ground truth ET. More details about the uncertainty quantification methods are given in Appendix D.
4. Results and Discussion
4.1. Analysis of the Spatial Heterogeneity of the LSHCs
The spatial heterogeneities of the superstations and the major ordinary stations were evaluated using this evaluation scheme in 2015 as an example (Figure 3). In addition, the heterogeneity evaluation scheme is also not applicable to sites with sparse vegetation, such as the BJT, HZZ, SSW, LD, and Desert stations. According to the S of the high-resolution ET derived from [56], the S values of the five stations were lower than 0.5 over the whole year, and thus, the five stations were defined as having homogeneous underlying surfaces (Figure 3f,g,i,n,o)). For the Arou (Figure 3a) and DSL (Figure 3c) stations, S was lower than 0.5 over the whole year, and thus, these stations can be defined as having homogeneous underlying surfaces. For the Wetland station (Figure 3e), S was greater than 0.5, and the CV was less than 0.3 over the whole year; thus, it could be defined as having moderately heterogeneous underlying surfaces. For the HHL (Figure 3m), Sidaoqiao (Figure 3k), and P.E (Figure 3l) stations, the days from the beginning of March to the middle of April could be defined as having moderately heterogeneous underlying surfaces, and the remaining days could be defined as having highly heterogeneous underlying surfaces. For the Daman superstation (Figure 3d), the days from 10 June to 10 July and from 3 September to 15 September were defined as a moderately heterogeneous underlying surface, and the other days could be defined as a homogeneous underlying surface. For the GT station (Figure 3b), the days from the middle of June to the end of July could be defined as a homogeneous underlying surface, and the remaining days could be defined as a moderately heterogeneous underlying surface. For the LZ station (Figure 3j), the days from the middle of June to the end of July could be defined as a moderately heterogeneous underlying surface, and the remaining days could be defined as a homogeneous underlying surface. For the YK station (Figure 3h), the days from the middle of June to the beginning of July and from the beginning of September to the middle of September could be defined as a moderately heterogeneous underlying surface, and the remaining days could be defined as a homogeneous underlying surface.
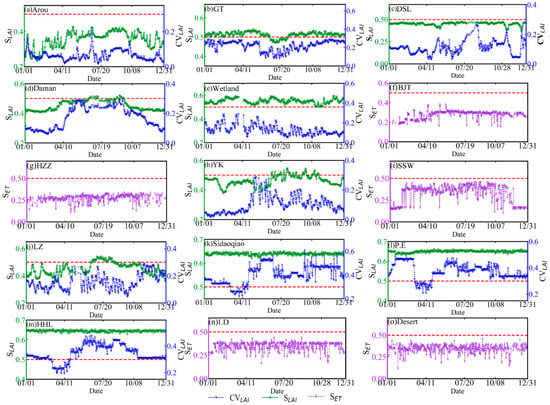
Figure 3.
The assessment results of the spatial heterogeneity of the LSHCs. (a–o) correspond to the Arou, GT, DSL, Daman, Wetland, BJT, HZZ, YK, SSW, LZ, Sidaoqiao, P.E, HHL, LD, and Desert stations, respectively. The red horizontal line represents the threshold line of the evaluation scheme.
4.2. Sensitivity Analysis of Input Variables
ET is mainly affected by the available energy (e.g., , Albedo) and water conditions (e.g., LST) and the vegetation status (e.g., LAI and NDVI) [76,77]. For the ANN, BLR, RF, DBN, and GPR models, the results could be significantly affected by the input variables. Thus, the LST, NDVI, , Albedo, and LAI factors were selected for a sensitivity analysis; then, the important factors were selected for the model construction (ANN, BLR, RF, DBN, and GPR). Through the sensitivity analysis involving determining the contribution rate of each variable to the output result, we obtained the important influence input variables and then performed quality control of input variables to reduce their influence on the model results. The sensitivity analysis was performed using EFAST on the input variables (LST, NDVI, , Albedo, and LAI) at three superstations (Figure 4). For the three superstations in the upstream, midstream, and downstream regions, the ANN, RF, DBN, GPR, and BLR models were more sensitive (relatively higher total effects index) to , LST, and NDVI than to Albedo or LAI. Therefore, , LST, and NDVI were taken as input variables in the ANN, BLR, RF, DBN, and GPR upscaling methods.
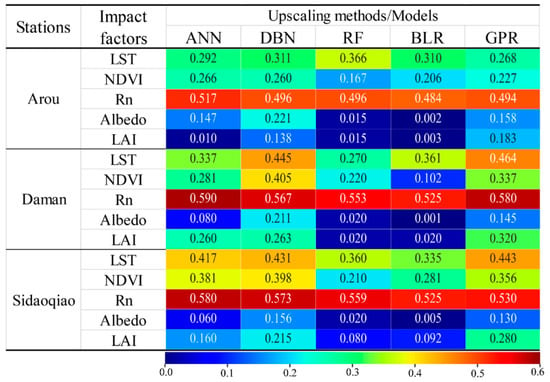
Figure 4.
Sensitivity analysis at the Arou, Daman, and Sidaoqiao superstations in 2015. (The colors from green to red represent the index of the total effects from small to large).
4.3. Optimization of Upscaling Methods
4.3.1. Comparison with LAS Measurements
Compared with the 100 m scale of EC observations, LAS has a larger observation scale in kilometers. The scintillometer can observe the average water and heat flux along the light path of 1–5 km; these measurements can be well-matched with the remote sensing pixel scales. It can be used as the reference value and has been broadly applied in the validation of remotely sensed or modeled ET [9,78]. As shown in Figure 1—(1,4,11), the proportion of the daytime-averaged LAS source areas accounted for approximately 80% of the 2 × 1 MODIS pixels at the Arou superstation in the upstream region and Daman superstation in the midstream region in 2015. This proportion was more than 95% at the Sidaoqiao superstation in the downstream region in 2015. The source area covered the corresponding MODIS pixels located in the central area. Thus, it could be supposed that the LAS measurements can represent the measurements at the 2 × 1 MODIS pixel scale in the Arou, Daman, and Sidaoqiao superstations. As a result, the LAS measurements could be taken as the reference of the 2 × 1 MODIS pixel for evaluating the upscaled ET derived from the upscaling methods at three superstations.
Based on the ET observation data and the fused high-resolution remote sensing data at the Arou superstation from January 2013 to December 2016, the Daman superstation from June 2012 to December 2016, and the Sidaoqiao superstation from April 2015 to December 2016, the upscaled ET derived from the eight upscaling methods was compared with the LAS measurements (Figure 5 and Table 2). In addition, the effect of using ET_EC as ground truth ET at the satellite pixel scale is also evaluated. Over homogeneous underlying surfaces, ET_EC had the highest accuracy, with the root mean square error (RMSE), mean relative error (MRE), and correlation coefficient (R) of 0.34 mm/d, 1.57%, and 0.98, respectively, which were immediately followed by the P-M-EnKF, P-M-SCE_UA, and P-T mechanism-driven methods with RMSEs (MRE, R) of 0.36 mm/d (−1.68%, 0.98), 0.39 mm/d (1.87%, 0.98), and 0.44 mm/d (2.24%, 0.97), and then, followed by the GPR, RF, ANN, and DBN data-driven methods, with RMSEs (MRE, R) of 0.46 mm/d (2.59%, 0.96), 0.51 mm/d (2.81%, 0.96), 0.54 mm/d (9.07%, 0.95), and 0.57 mm/d (−10.97%, 0.95), respectively. The accuracy of the BLR method was relatively lower, with an RMSE (MRE, R) of 0.62 mm/d (12.45%, 0.94) (Figure 5a,b and Table 2). Over moderately heterogeneous underlying surfaces, the GPR, RF data-driven methods, and the P-M-EnKF mechanism-driven method performed better compared with the other methods with RMSEs (MRE, R) of 0.51 mm/d (3.23%, 0.97), 0.57 mm/d (3.42%, 0.96), and 0.54 mm/d (3.37%, 0.97), respectively; then, these were followed by the P-M-SCE_UA, ANN, P-T, and DBN methods with RMSEs (MRE, R) of 0.60 mm/d (−4.39%, 0.96), 0.64 mm/d (10.95%, 0.96), 0.66 mm/d (−11.03%, 0.96), and 0.68 mm/d (11.86%, 0.95), respectively. Similarly, the BLR method performed relatively poorly under these conditions, with an RMSE (MRE, R) of 0.70 mm/d (−13.44%, 0.95) (Figure 5c,d and Table 2). Over highly heterogeneous underlying surfaces, the GPR and RF data-driven methods performed better compared with the other methods with RMSEs (MRE, R) of 0.60 mm/d (4.59%, 0.91) and 0.67 mm/d (−4.94%, 0.87), which were followed by the ANN method with an RMSE (MRE, R) of 0.71 mm/d (−11.74%, 0.85); the P-T mechanism-driven method performed worse than the others, with an RMSE (MRE, R) of 0.89 mm/d (−20.13%, 0.87) (Figure 5e,f and Table 2). Therefore, these results also indicated that it was necessary and reasonable to optimize the upscaling method based on a quantitative evaluation result of the spatial heterogeneity of the underlying surfaces.
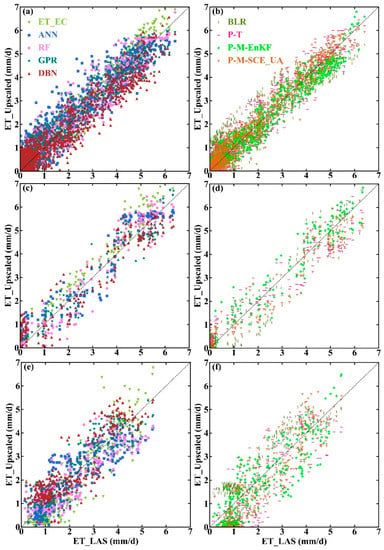
Figure 5.
Comparison of upscaled ET obtained from eight upscaling methods and ET_EC with LAS measurements (a,b). Homogeneous underlying surfaces (c,d). Moderately heterogeneous underlying surfaces; (e,f). Highly heterogeneous underlying surfaces).

Table 2.
Statistics for comparison among the upscaled ET of eight upscaling methods, ET_EC, and LAS measurements.
The ET_EC represents the ground truth ET at the satellite pixel scale with good accuracy over homogeneous underlying surfaces, but with an increase in the spatial heterogeneity of the underlying surface, the accuracy of ET_EC decreased over moderately and highly heterogeneous underlying surfaces. This is because in the case of heterogeneous underlying surfaces, the uncertainty of the ET derived from EC at a given station representing the ground truth ET data at the satellite pixel scale will increase as the spatial heterogeneity increases, so its accuracy will decrease with an increase in the spatial heterogeneity of the underlying surface [18]. In addition, some studies have shown that if the pixels where the site is located are homogeneous and the size of the flux source area is the same or similar to the satellite pixel scale, the flux observation value can be used to validate these remote sensing products [78,79]. This is also consistent with the result in this paper. In addition, the P-M-EnKF and P-M-SCE_UA mechanism-driven methods performed better than the other mechanism-driven method for homogeneous and moderately heterogeneous underlying surfaces. The reasons for this result are as follows. For the P-M-EnKF method, first, EnKF can effectively combine two kinds of information (here, the fitting model and the observation data), introduce new observation data into the process model, continuously reduce or filter the noise in the process model, and make the model simulation trajectory closer to the real state of nature [80]. Second, as an effective data assimilation method, P-M-EnKF is an optimization method used to estimate target parameters by combining model simulation with external observations. It is a sequential assimilation algorithm used to estimate the covariance of the forecasting error by MC’s set prediction method; this algorithm can effectively decrease the error of the estimation process and enhance the prediction accuracy. It can directly use the nonlinear model operator and the observation operator, thus maintaining all of the dynamic characteristics of the model. The advantage of P-M-EnKF is that it does not require the tangent linear model or the adjoint model of the prediction operator; it also performs good simulations for dynamic models with strong nonlinearity and discontinuity, and it has achieved great success in applications of land and atmospheric data assimilation [80]. For the P-M-SCE-UA method, SCE-UA is a global optimization algorithm, which combines the advantages of the random search algorithm, simplex method, cluster analysis, biological competitive evolution, etc. It can effectively solve the rough, insensitive area and non-convex problems of the reflection surface of the objective function and avoid the interference of local minimum points. This method can optimize multiple parameters in the model at the same time and is an effective method for parameter optimization [66]. In addition, we found that the P-M-EnKF method was slightly superior to the P-M-SCE_UA method for different heterogeneous underlying surfaces. The reason could be that although both data assimilation methods obtain optimal parameters by incorporating observed data, the P-M-SCE_UA method is optimized for six parameters (,,, , and , see Appendix A). The inaccuracy of some parameters will make the P-M-SCE_UA method perform worse, while the P-M-EnKF method is optimized for two parameters ( and ). At the same time, we found that the accuracy of the P-M-EnKF and P-M-SCE_UA methods decreased with increased heterogeneity. The reason for this result is that in these upscaling methods, we used DA to predict and update the adjustment parameters ( and in P-M-EnKF; ,,, , and in P-M-SCE_UA) in the P-M equation, and we assumed that these parameters are suitable for the whole region. For homogeneous underlying surfaces, such as that of the Arou superstation, these parameters are well represented in the whole 2 × 1 MODIS region. Therefore, P-M-EnKF and P-M-SCE_UA methods also have a higher accuracy and perform better than the other upscaling methods. However, with the increasing heterogeneity of the underlying surface, the representativeness of these parameters in the region gradually decreases. For example, from the Daman superstation with moderate heterogeneity in the midstream region to the Sidaoqiao superstation with high heterogeneity in the downstream region, the accuracy of the P-M-EnKF and P-M-SCE_UA methods gradually decreased.
It can be found that compared with other data-driven methods, the GPR and RF methods have a better performance over moderately and highly heterogeneous underlying surfaces. For the GPR method, this can be mainly attributed to the advantage of the GPR model over other models; this advantage lies in its clear probability formula, which provides probabilistic predictions and can also deduce model parameters, such as parameters that adjust the shape or noise level of the kernel. First, compared to the additive model, the GPR method contains a more flexible nonadditive covariance function. Second, with the support of the kernel trick, infinite basis function expansion can be used. In addition, GPR can perform Bayesian inference in another dimension of space, namely, the latent function space [69]. Additionally, the RF method performs relatively well. This is mainly because, as an integrated learning method, the RF contains a lot of regression trees, which can determine complex relationships presented in the data and use the adaptive nature of decision rules to explain the nonlinear relationship between predictors and response variables. In addition, the RF uses bagging technology to introduce randomness to the regression tree and averages a large number of unrelated individual trees to decrease the generalization error. On the one hand, these factors can minimize the risk of the model fit, with greater stability. On the other hand, these factors also make the model fit more robust in the face of slight changes in the input data [70]. In addition, data-driven methods (e.g., GPR) calculate the global (whole area) characteristics in the application; i.e., they consider the features of the overall pixel extraction in the area, and they can also better capture the LSHCs because they break the land surface into very fragmented structures for learning and training. Therefore, even with an increase in the heterogeneity, although the accuracy of data-driven methods also decreases, their accuracy is still slightly better than that of mechanism-driven methods (e.g., P-M-EnKF, P-M-SCE_UA methods). In other words, with the increase in surface heterogeneity, the two data-driven methods (GPR and RF) have more obvious advantages than the mechanism-driven methods. The DBN method is relatively poor in performance. Although DBN is a deep learning method, its capability is higher for complicated functions when there is a large amount of data available for the model training. Therefore, for small data volumes, DBN does not perform as well as other algorithms, even simple algorithms [68].
To compare the accuracy of the five data-driven methods, we evaluated these models with repeated ten-fold cross-validation (ten repeats) using the EC observation data in three superstations. The workflow partitions the original sample into ten disjoint subsets, uses nine of those subsets in the training process, and then makes predictions about the remaining subset (Figure 6). Over the homogeneous underlying surface, the R (RMSE) values were 0.96, 0.95, 0.95, 0.96, and 0.97 (0.49, 0.55, 0.51, 0.45, and 0.47 mm/d) for the ANN, BLR, DBN, GPR, and RF models, respectively. Over the moderately heterogeneous underlying surface, the R (RMSE) values were 0.94, 0.92, 0.93, 0.95, and 0.94 (0.54, 0.60, 0.56, 0.49, and 0.52 mm/d) for the ANN, BLR, DBN, GPR, and RF models, respectively. Over the highly heterogeneous underlying surface, the R (RMSE) values were 0.94, 0.94, 0.94, 0.95, and 0.95 (0.63, 0.68, 0.65, 0.57, and 0.60 mm/d) for the ANN, BLR, DBN, GPR, and RF models, respectively. Overall, the performance of the GRP method is the best in the five methods, followed by the RF method, which is consistent with the results in Figure 5 and Table 2.
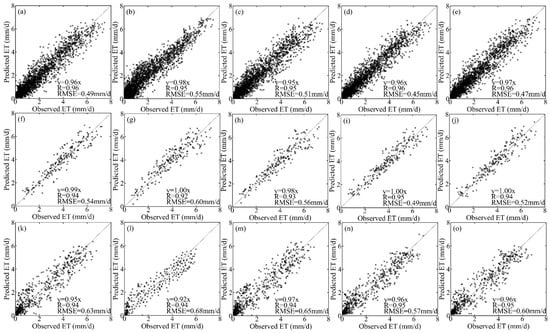
Figure 6.
Ten-fold cross-validation results of methods (from left to right are ANN, BLR, DBN, GPR, and RF) over the homogeneous underlying surface (a–e), the moderately heterogeneous underlying surface (f–j), and the highly heterogeneous underlying surface (k–o) at three superstations.
To quantify the effects of the observed LAS, input variables (LST, , and NDVI), and the heterogeneity of LSHCs (NDVI and the heterogeneity of LSHCs are expressed by ) on the upscaled ET obtained using eight methods at three superstations, an analysis of the residual errors (upscaled ET—LAS observed ET) was performed (Figure 7). The residual error was distributed over the entire range, and there was a relatively large error in the observed ET between approximately 2 and 4 mm/d, except for in the BLR and DBN methods. The residual errors of P-M-EnKF and P-M-SCE_UA were smaller than those of the other methods over homogeneous underlying surfaces. The retrieval accuracy of and LST was obtained by comparing these with ground observation values. In addition, when the retrieval accuracy of and LST was relatively high ( < 13 W/m2, LST < 1.8 K), the effect of the retrieval error on the results was not significant. When the retrieval errors of and LST were greater than 13 W/m2 and 1.8 K, respectively, the retrieval errors had an obvious influence on the results; in other words, the errors in the upscaled ET increased with increased retrieval errors. In addition, overall, the impact of the retrieval error was slightly greater than that of the LST inversion error. This finding may result from the fact that is more sensitive than the LST to changes in ET; this can also be seen in the sensitivity analysis shown in Figure 4. As described in Section 4.1, can reflect the degree of heterogeneity of the LSHCs. Figure 7 shows that with an increasing , the degree of heterogeneity increases. The upscaled ET’s error appeared to have a slight increase, and especially when the was greater than 0.4, the error of the upscaled results became more obvious with an increasing degree of heterogeneity. This result is also consistent with the results of [18,19]. Therefore, for the upscaling methods, in addition to the significant influence of the input variables on the upscaled results, the influence of the heterogeneity of the LSHCs on the upscaled results should not be ignored.
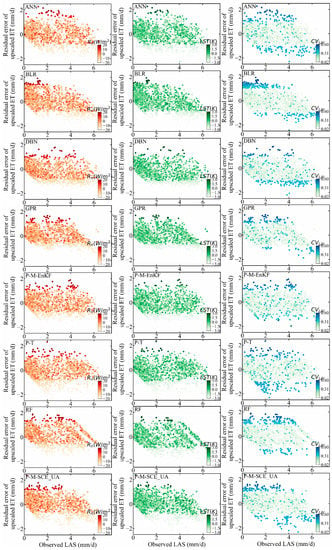
Figure 7.
Relationships of the residual error in the upscaled ET derived from the eight upscaling methods with the observed LAS, and the retrieval accuracy of , LST, and at three superstations (the color ramp represents the retrieval error and heterogeneity).
4.3.2. Cross-Validation with the Three-Cornered Hat Method
A cross-validation method, the three-cornered hat (TCH) method, was used for an intercomparison of the different upscaling methods at three superstations in the period from 2012 to 2016 (Figure 8). In Figure 8, the magnitude of the relative error (square root of variance divided by average) varies depending on the spatial heterogeneity of the LSHCs. As shown in Figure 8, on the whole, the relative error over homogeneous underlying surfaces was smaller than that over moderately heterogeneous underlying surfaces, and the relative error over highly heterogeneous underlying surfaces was the largest. Over homogeneous underlying surfaces, ET_EC represents the ground truth ET at the satellite pixel scale with the smallest relative error, 4.74%, which was immediately followed by those of the P-M-EnKF and P-M-SCE_UA mechanism-driven methods and then followed by the GPR, RF, ANN, and DBN data-driven methods with relative errors of approximately 7–9%. In addition, the BLR method had a relative error greater than 11%. Over moderately heterogeneous underlying surfaces, the GPR data-driven method had the smallest relative error, 11.07%, which was followed by those of the P-M-EnKF and RF methods, with relative errors of 12.57% and 14.15%, respectively, and then followed by P-M-SCE_UA, ANN, P-T, and DBN, with relative errors of approximately 15–20%. Similarly, the BLR method had a relative error of 21.10%. Over highly heterogeneous underlying surfaces, the GPR and RF data-driven methods performed well, with the slight relative error of 14.89% and 17.24%, which was followed by the ANN methods, and the P-T method performed relatively poorly compared to the others, with a relatively large relative error of 34.66%.
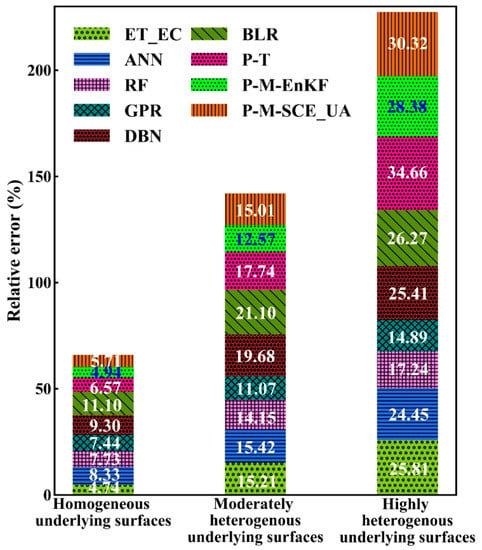
Figure 8.
Intercomparison of eight upscaling methods and ET_EC based on the TCH method.
Before conducting further analysis of the results of the TCH method, a comparison was made between the relative error from the TCH method and RMSE results obtained by direct validation (compared with the LAS measurements) (Figure 9). As can be seen from Figure 9, the results of the TCH method for ET_EC and different upscaling methods were consistent with the results obtained when taking the LAS measurements as the references. In addition, the results also corresponded to the spatial heterogeneity discussed in Section 4.1; in other words, overall, when the heterogeneity was small, the relative error was also small, and when the direct validation errors in the upscaling methods were large (small), the relative errors in the cross-validation were also large (small). Therefore, this also indicated that both the direct validation (compared with the LAS measurements) and cross-validation (with the TCH method) can optimize the upscaling method more comprehensively and can further explain the reliability of the preferred upscaling method.
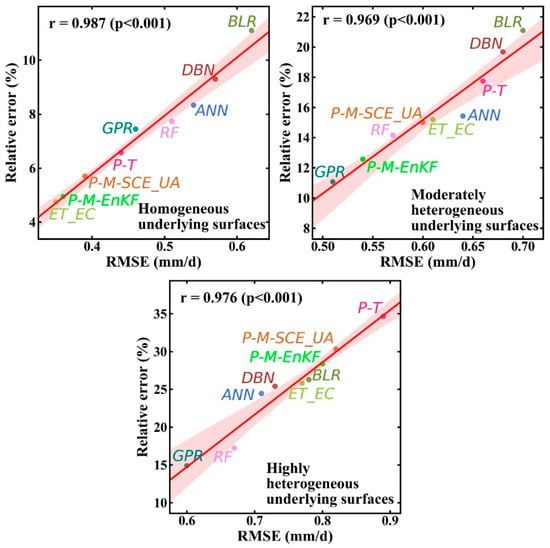
Figure 9.
Comparison of relative error derived from the TCH method and RMSE derived from the comparison among LAS measurements, ET_EC, and eight upscaling methods over homogeneous, moderately heterogeneous, and highly heterogeneous underlying surfaces. The r, p, and red shaded area represent correlation coefficient, confidence level, and 95% confidence interval, respectively.
To further analyze the characteristics of the relative errors in upscaled ET from the perspective of their spatial distributions (Figure 10), at the Arou superstation (homogeneous underlying surface), the underlying surface (subalpine meadow) in the area was relatively single and uniform, and the relative error distributions of the various upscaling methods were also relatively uniform (Figure 10a). Additionally, the relative error of the P-M-EnKF method was the smallest, while the relative error of the BLR method was the largest over the underlying surface of the subalpine meadow. The possible reason is that the factors and in P-M-EnKF had good representativeness over the homogeneous underlying surface. At the Daman superstation, the relative error difference between the GPR method and the P-M-EnKF method was small over the cropland underlying surface, while in the relatively fragmented underlying surface of villages (i.e., ellipse areas in Figure 10b), the relative error of the P-M-EnKF method was significantly greater than that of the GPR method. The possible reason is that on the one hand, the GPR method considered the regional distribution characteristics, to a certain extent, thus reducing the error of the area, and on the other hand, EC was installed on the cropland underlying surface, while in the village area, the representativeness of the factors and in P-M-EnKF were significantly affected, increasing the relative error of the method in this area. At the Sidaoqiao superstation, the underlying surface was cracked, and its relative error distribution was also relatively messy. Thus, the distribution of the relative error had a good relationship with the distribution of the underlying surface types. The relative errors of various upscaling methods on the Tamarix underlying surface were smaller than those on the other underlying surfaces, and the relative error of each method was larger on the bare land underlying surface (i.e., rectangular regions in Figure 10c) than on other surfaces. This is because these upscaling methods were mainly based on flux observation stations, which represent small areas and covered single surface types, and the upscaling method applied based on the observed data over this underlying surface had better applicability, while the prediction effects for other surface types were naturally worse. This was also consistent with the previous analysis result, further demonstrating the importance of heterogeneity in influencing the accuracy of upscaled results.
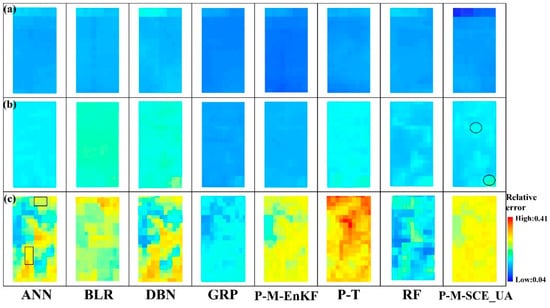
Figure 10.
Distribution of relative errors derived from the TCH method with a 30 m resolution at three superstations. (a–c) represent homogeneous underlying surfaces in the upstream region (Arou), moderately heterogeneous underlying surfaces in the midstream region (Daman), and highly heterogeneous underlying surfaces in the downstream region (Sidaoqiao), respectively. The ellipse areas in Figure 10b represent village areas, and the rectangular regions in Figure 10c represent bare land areas.
Combining the results in this paper with the research in the literature [18,19,24,25,36,37], it can be seen that if the pixel where the site is located is homogeneous, the ET observed value can be used as the ground truth ET at the pixel scale. If the pixel where the site is located is heterogeneous, it is required to obtain the ground truth ET at the pixel scale by using the upscaling method that takes the LSHCs into account. Over moderately heterogeneous surfaces, the data-driven methods, such as GPR and RF, and the mechanism-driven methods, such as P-M-EnKF and P-M-SCE_UA, can be used to obtain the ground truth ET at the pixel scale. Over highly heterogeneous surfaces, data-driven methods such as GPR and RF can be used to obtain the ground truth ET at the pixel scale.
4.4. Acquisition of ET at the Pixel Scale over the Main Surface Types in the HRB
Based on the analysis results in this paper, the comprehensive method for obtaining daily ground truth ET data at the satellite pixel scale over typical underlying surfaces in the HRB is as follows: for homogeneous underlying surfaces, the daily ground truth ET data at the satellite pixel scale were obtained by the ET_EC; for moderately and highly heterogeneous underlying surfaces, the daily ground truth ET data at the satellite pixel scale were obtained using the GPR data-driven methods. Figure 11 shows the daily ground truth ET data at three superstations, and we used the bar to represent the maximum and minimum of the ground truth ET. It can be found that the ET value and variation trend are relatively consistent with those of the LAS observations, while, with an increase in the surface heterogeneity, the consistency slightly decreases from the Arou to the Daman to the Sidaoqiao superstations. From the precipitation data of the three superstations shown in Figure 11, the annual precipitation varies greatly in the HRB, and the precipitation totals from the upstream to the midstream to the downstream region are approximately 400–500 mm, 100–160 mm, and 30–40 mm, respectively. The water sources of ET differ among the three superstations. The Arou superstation is located in the runoff generation area, and abundant precipitation provides the main water source for ET. The Daman and Sidaoqiao superstations are located in water consumption areas; irrigation and groundwater recharge provide the main water source for ET, respectively. For example, during the irrigation period, there was a significant increase in ET. At the Sidaoqiao superstation, changes in the groundwater table were also related to changes in ET. The groundwater table dropped from 1 m at the beginning of the vegetation growth period to 3 m at the end of the vegetation growth period. In general, the annual average ET at the Daman superstation was higher than those of the Arou and Sidaoqiao superstations. There was no significant difference in the seasonal changes in ET among the three superstations, with high values appearing in summer (July or August) and low values appearing in winter. There was no significant variation in the interannual variation in ET at the Arou superstation. In addition, the ET at the Daman superstation showed a slight decline in 2016, which may be due to the changes in the irrigation method that occurred in this area from flooding irrigation to drip irrigation [46]. Moreover, the ET at the Sidaoqiao superstation rose slightly during 2015–2016, which could have something to do with the rising groundwater table.
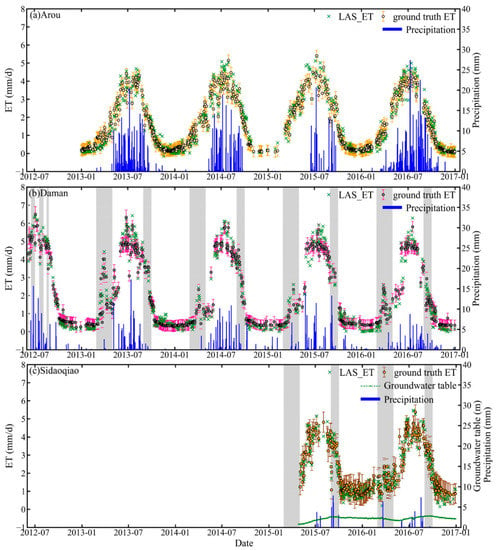
Figure 11.
Daily ground truth ET at the satellite pixel scale (2 × 1 MODIS pixel) at the Arou (a), Daman (b), and Sidaoqiao (c) superstations (the error bar indicates the maximum and minimum value in the ground truth ET at the satellite pixel scale; the gray shadows represent irrigation periods).
Based on the above methods, we calculated the ground truth ET at the satellite pixel scale over twelve typical underlying surfaces in the HRB (Figure 12). In Figure 12a, on the one hand, it can be found that the trend of the ground truth ET at the satellite pixel scale can be captured well over time at every surface type, and the seasonal and interannual variations of ET among all surface types are generally consistent. The high values of ground truth ET appear in summer, and lower values appear in winter. On the other hand, due to the different types of underlying surfaces, the variation ranges in the ground truth ET were also different among the stations. For example, at the DSL station with a marsh alpine meadow, the lowest and highest ET values were 0.14 mm/d and 5.50 mm/d, respectively. At the LZ and YK stations with maize, the lowest and highest ET values were 0.07 mm/d and 9.23 mm/d, respectively. At the HHL station with Populus euphratica and Tamarix, the lowest and highest ET values were 0.03 mm/d and 6.49 mm/d, respectively. As shown in Figure 12b, overall, the seasonal variation in ET over different underlying surface types is generally consistent, showing a single peak distribution trend that first increased and then decreased. The larger ET values were mainly concentrated from May to September, with the smallest ET in January and December and the largest ET in July. After April, the ET values over different underlying surfaces began to rise rapidly, among which the ET values over the maize underlying surface rose the fastest and reached a maximum in July; then, they began to decline, with no significant change from November to February of the following year. The ET over the wetland underlying surface was higher than those of the other underlying surfaces almost every month. The seasonal variation range in the maize underlying surface was larger than those of the other surfaces, while that of the Reaumuria desert underlying surface was the smallest. From May to September, there were significant differences in ET among different underlying surface types due to large differences in plant transpiration and soil evaporation during the growing period, but no significant differences were observed from October of a given year to March of the following year. This mainly results from the fact that from May to September is the growing season for various types of vegetation, with relatively high temperature, sufficient sunshine, and abundant rain, all of which provide sufficient conditions for ET, especially plant transpiration; thus, ET increased and the difference was significant; after September, the plants withered, precipitation decreased, the conditions changed and were not conducive to ET, and the difference decreased. Figure 12c shows that the multiyear average ET values were closely related to the underlying surface types, and there were great differences observed among different underlying surface types. Among them, the multiyear average daily ET was the largest over the wetland underlying surface (3.41 mm/d); this value greatly exceeded those of the other underlying surface types, which was followed by the maize underlying surface (2.56 mm/d), and the smallest ET was found over the Reaumuria desert underlying surface (0.21 mm/d).
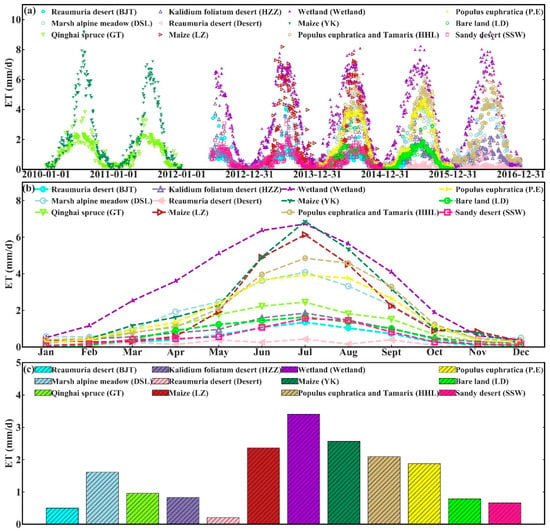
Figure 12.
The statistics of the ground truth ET at the pixel scale over twelve surface types in the HRB during the period from 2010 to 2016. (a) Daily variation, (b) monthly average daily value, and (c) multiyear average daily value.
In addition to accuracy validation of the ET at the satellite pixel scale, it is also important to quantify the uncertainty of the upscaled ET for the validation of remotely sensed ET products. To characterize the uncertainty of the ground truth ET at the satellite pixel scale, the method of Beyrich et al. [23] was used to quantitatively evaluate the ground truth ET derived from ET_EC over a homogeneous underlying surface, and the gPC method was used to quantitatively evaluate the ground truth ET derived from the upscaling method over moderately and highly heterogeneous underlying surfaces (Figure 13). Violin plots are an effective method for reflecting data dispersion. Figure 13 shows the uncertainty of the ground truth ET at three superstations and twelve ordinary stations with typical surface types. For the three superstations, the uncertainties ranged from 0.10 to 0.14 mm/d, 0.19 to 0.36 mm/d, and 0.31 to 0.49 mm/d, and the average uncertainties were 0.11 mm/d, 0.24 mm/d, and 0.39 mm/d, respectively. From the Arou to Daman to Sidaoqiao superstation, it can be found that the uncertainty of the ground truth ET gradually increased, which is the same trend as that seen in the comparison with the LAS observations and the intercomparison with the TCH method among the relative errors in Section 4.3. The relative accuracy (RA) (see Appendix D) at the Arou, Daman, and Sidaoqiao superstations were 93.23%, 89.23 %, and 82.18%, respectively. For the ordinary stations, the Populus euphratica and Tamarix underlying surface at the HHL station had the largest uncertainty (approximately 0.41 mm/d), and the Reaumuria desert underlying surface at the Desert station had the smallest uncertainty (approximately 0.02 mm/d). In addition, the uncertainty distribution of the marsh alpine meadow underlying surface at the DSL station was relatively scattered, while the uncertainty distribution of the Qinghai spruce underlying surface at the GT station was relatively concentrated. Combined with the analysis in Figure 13, generally speaking, it can be found that with an increase in the heterogeneity of the surface, the uncertainty of the ground truth ET also increases. The average uncertainties of the ground truth ET at stations with homogeneous surfaces, such as the Arou, BJT, Desert, and HZZ stations, were 0.11 mm/d, 0.04 mm/d, 0.02 mm/d, and 0.06 mm/d, respectively, and the RA was 93.23%, 92.57%, 90.57%, and 92.62%, respectively. At moderately heterogeneous surface stations, such as the Wetland station, the average uncertainty was 0.32 mm/d, and the RA was 90.58%. At the stations with highly heterogeneous surfaces, such as the HHL, P.E and Sidaoqiao stations, the average uncertainty was 0.41 mm/d, 0.38 mm/d, and 0.39 mm/d, and the RA was 81.12%, 82.18%, and 81.25%. This may be related to the heterogeneity of the underlying surface. Heterogeneity has a significant effect on the ground observation ET and the accuracy of input variables retrieval by remote sensing data. In addition, heterogeneity will also make the atmospheric forcing data more uncertain and reduce the applicability of parameters in the model. Therefore, an increase in heterogeneity may contribute to greater uncertainties in the ground truth ET at the satellite pixel scale. Based on the above analysis, it can be concluded that the accuracy of the daily ground truth ET at the satellite pixel scale obtained in this paper was relatively reliable and therefore could meet the requirements of validating the remotely sensed ET products.
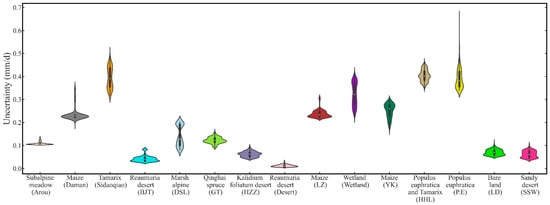
Figure 13.
Violin plots (the length and width represent the range and frequency, respectively, and the black bar shows the third quartile, median, and first quartile from top to bottom) for the uncertainty of the ground truth ET at the pixel scale at fifteen typical surface type sites in the HRB during the period from 2010 to 2016.
5. Conclusions
The validation of remotely sensed ET products is challenging due to the spatial-scale mismatch issue between site observations and remote sensing pixels over heterogeneous underlying surfaces. Therefore, in response to this challenge, this paper proposes a comprehensive framework for obtaining ground truth ET at the satellite pixel scale to resolve the spatial-scale mismatch issue. Based on the dataset from the Heihe integrated observatory network and high-resolution satellite remote sensing data in the HRB, eight upscaling methods were compared and combined with ET_EC. Then, the ground truth ET at the satellite pixel scale over fifteen typical underlying surfaces in the HRB was obtained by an integrated method, and the uncertainty of the ground truth ET was analyzed.
A comparison with LAS measurements showed that over homogeneous underlying surfaces, the ET_EC was slightly superior with an RMSE of 0.34 mm/d, which was followed by the P-M-EnKF method. Over moderately heterogeneous underlying surfaces, the GPR data-driven method and P-M-EnKF mechanism-driven method performed slightly better than the other methods, with small RMSEs of 0.51 mm/d and 0.54 mm/d, respectively. Over highly heterogeneous underlying surfaces, the GPR and RF data-driven methods performed slightly better than the other methods, with small RMSEs of 0.60 mm/d and 0.67 mm/d, respectively. The results of the cross-validation were consistent with the results of comparison with LAS measurements and showed that the relative error increased with an increase in the heterogeneity of the underlying surface. In addition, the results also indicated the retrieval accuracies of LST and , and the heterogeneity of the underlying surface was the predominant influencing factor for all of the upscaling methods.
The ground truth ET at the satellite pixel scale was obtained by the proposed integrated method (namely, using the ET_EC for homogeneous underlying surfaces and the GPR method for moderately and highly heterogeneous underlying surfaces) over fifteen typical underlying surfaces, and the results showed that the ground truth ET at the satellite pixel scale had good accuracy and could capture the variation trend in the ET data over time well; this also indicated the universality of the framework proposed in this paper to a certain extent. The ground truth ET at the wetland underlying surface (Wetland station) had the largest value, and the multiyear average daily value is 3.41 mm/d. Meanwhile, that of the Reaumuria desert (Desert station) had the smallest value, and the average daily value is 0.21 mm/d. The ground truth ET for maize (YK station) had a large variation range, from 0.07 to 9.23 mm/d, while that at the Reaumuria desert (Desert station) had a small variation range, from 0.01 to 3.46 mm/d. The uncertainties in the ground truth ET at the satellite pixel scale were calculated, and the results showed that the Populus euphratica and Tamarix underlying surface at the HHL station had the largest uncertainty (approximately 0.41 mm/d), and the Reaumuria desert underlying surface at the Desert station had the smallest uncertainty (approximately 0.02 mm/d). In addition, with an increase in the heterogeneity of the underlying surface, the uncertainty of the ground truth ET obtained by the upscaling method also increased from 0.02 to 0.41 mm/d. In addition, on the whole, the RA of the ground truth ET at the satellite pixel scale over the homogeneous underlying surface was relatively larger, about 90–93%, and it was relatively smaller over the moderately and highly heterogeneous underlying surfaces, about 81–92%, which is relatively reliable.
The above results demonstrated that the framework of acquiring the ground truth ET at the satellite pixel scale (Figure 2) is necessary, reasonable, and effective. In this paper, based on the results of this study and previous research results, an integrated method was proposed; that is, over the homogeneous underlying surface, the ET_EC can be used to obtain the ground truth ET. Over the heterogeneous underlying surfaces, the ground truth ET should be obtained by upscaling methods. Specifically, over moderately heterogeneous surfaces, the data-driven methods and the mechanism-driven methods can be used to obtain the ground truth ET at the pixel scale; over highly heterogeneous surfaces, data-driven methods can be used to obtain the ground truth ET at the pixel scale. In the future, the framework of acquiring the ground truth ET at the satellite pixel scale needs to be further validated in other climates and other land surface type regions.
Author Contributions
Conceptualization, X.L. and S.L.; methodology, X.L., S.L., X.Y., T.X., Y.Z., X.H. (Xiao Hu) and Q.J.; validation, Y.Z.; formal analysis, X.L., S.L. and X.Y.; investigation, X.L., S.L. and Z.X.; resources, S.L., Y.M. and Z.X.; data curation, S.L., Y.M. and Z.X.; writing—original draft preparation, X.L.; writing—review and editing, X.L., S.L., X.Y., X.H. (Xinlei He), T.X., Z.X., L.S., Y.Z. and X.Z.; visualization, X.L. and S.L.; supervision, S.L.; project administration, S.L.; funding acquisition, S.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Strategic Priority Research Program of the Chinese Academy of Sciences (XDA20100101) and the National Natural Science Foundation of China (41531174).
Data Availability Statement
The data presented in this study were provided by the National Tibetan Plateau Data Center (http://data.tpdc.ac.cn/en/, accessed on 10 March 2019).
Acknowledgments
The authors would like to thank all the scientists, engineers, and students who participated in WATER and HiWATER field campaigns. We appreciate all reviewers and editors for their comments on this paper.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Appendix A shows the details of the eight upscaling methods used in this study.
Artificial neural network (ANN) method:
Artificial neural network (ANN) is a type of algorithm model that imitates the behavioral characteristics of the human brain or biological neural networks and performs distributed parallel information processing. Among them, the backpropagation (BP) artificial neural network is a multilayer feedforward network trained by an error backpropagation algorithm and is a popular neural network model. The neural network topology includes the input layer, hidden layer, and output layer [67]. The neurons between the layers are connected, and the connection between every two neurons can be called a weight, here representing the strength of the connection between the auxiliary variable and ET. Through the weight adjustment process of the forward propagation of signals and backward propagation of errors, the weights are continuously adjusted until the output error of the network is reduced to an acceptable range. In this paper, the input layer includes three neurons, namely, , LST, and NDVI; there are three hidden layers in the network, each layer contains 10 neurons, and the ReLU activation function is used; and the output layer includes only one neuron, namely, ET, which is obtained using a linear activation function.
Bayesian linear regression (BLR) method:
Bayesian linear regression (BLR) is mainly used in the maximum likelihood estimation process, and it is difficult to estimate the complexity of some models. A regression model can be approximated as the addition of the prior distribution of the model parameters based on ordinary linear regression so that the model becomes the maximum a posteriori estimation obtained from the maximum likelihood estimation. The Bayesian linear regression method introduces the prior distribution of the parameters and . The conjugate prior distribution of the parameter ω is the normal distribution with mean and variance . Knowing the model , the posterior distribution of the parameters is as follows:
Since the prior distribution and the posterior distribution of the parameters are conjugated and the prior distribution obeys a normal distribution, the posterior distribution also obeys the normal distribution. The specific form is as follows:
where μ is the mean of the posterior distribution and is the variance of the posterior distribution.
For the convenience of calculation, the prior distribution of the parameter ω is defined as an isotropic normal distribution of a function with a mean of 0 and a variance of α. The mean and variance are as follows:. Substituting these values into the mean and variance values of the posterior distribution yields the following equations:
The optimal solution of the parameter is the mean of the posterior distribution. The required mathematical expression can be used to obtain the required . The values of α and β must be obtained first. The values of α and β are iteratively obtained by the Markov chain Monte Carlo algorithm.
More details of BLR can be found in [71].
Deep belief network (DBN) method:
The deep belief network (DBN) was originally proposed by [68]. Its essence is to learn more essential features by building a neural network learning model, which has some hidden layers and a large amount of training data, thereby improving the accuracy of the network. From a structural point of view, a DBN is composed of several layers of an unsupervised restricted Boltzmann machine (RBM) network and a layer of a supervised BP network. The learning process of DBN can be divided into two stages: pretraining and fine tuning [68]. In the pretraining stage, the RBM output of the lower layer is used as the RBM input of the upper layer to complete the unsupervised training of the RBM layer by layer. In the fine-tuning phase, the error between the actual output and the expected output is back-propagated, and the top-level BP network is trained using supervised learning to tune the model parameters initialized in the pretraining phase. Therefore, the pretraining process of RBM can be considered as the initialization of the weight parameters of a deep BP network, which allows the DBN to overcome the shortcomings that the BP network is prone to fall into involving the local optimization and training time due to the random initialization of the weight parameters. More details regarding the DBN can be found in [68].
Gaussian process regression (GPR) method:
Gaussian process regression (GPR) is used to combine data, the sampling and non-sampling variance in the data, and other information in terms of model parameters into a single final set of estimates. It is based on the Bayesian framework, and it is efficient for hyperparameter optimizations; namely, GPR is a nonparametric kernel-based probabilistic model [69]. The Gaussian process (GP) can be defined as a distribution over function , where is a mapping function, which can map the input space to . The GP consists of its mean function and covariance function such that the following condition is satisfied:
where rows of the design matrix are input vectors, is a vector of the function values, and indicates the -by- matrix of covariance such that .
In GPR, a GP was introduced prior to the target function value. The relationship between the function and the observed with Gaussian noise is specified as follows:
The joint distribution of and with a zero-mean function is as follows:
where and denote design matrices for the training data and test data; and are the training and test outputs; Conditioning on the observed , the predictive distribution can be calculated as follows:
The prior mean was assumed to be zero (in the normalized data), and the kernel function used was the squared exponential, as follows:
where and are two input points and the parameters and are the variance and characteristic length scale, respectively. Thus, the unknown parameters (i.e.,, , and can be solved through the maximum a posteriori estimation (MAP) method. The marginal likelihood can be represented by the following expression:
Given the likelihood and the prior GP over the function , this integral can be analytically solved, which is caused by the log marginal likelihood as follows:
where is the unknown parameter, and the optimal solution can be estimated using a gradient descent algorithm. More details regarding GPR can be found in [69].
The integrated Priestley–Taylor equation (P-T) method:
The potential ET can be determined by the following Priestley–Taylor equation [81]:
where is the LE for saturated surfaces; is the Priestley–Taylor parameter; is the slope of the saturation vapor pressure to the air temperature; and is the psychrometer constant.
In this paper, the P-T method can be divided into three steps. First, the was computed through the Priestley–Taylor equation using the observation data obtained at a given station. Second, the equation between and the difference between the land surface temperature and air temperature (Ts-Ta) was built, and it was assumed that this equation was suitable for the relatively small area (1 × 1 or 2 × 1 MODIS pixel area). Third, the ET at the corresponding pixel was computed by the Priestley–Taylor equation combined with the Ts-Ta derived from the satellite data and atmospheric forcing data. More details can be found in [18,19].
Random forest (RF) method:
The basic classification unit of the random forest algorithm is the decision tree. The essence of the method is a classifier that contains many decision trees, and its output category is determined by the mode of the output category of the decision tree. The algorithm requires few mediation parameters and has high computational efficiency and the ability to process high-dimensional (multi-feature variables) data. The training speed is fast without overfitting. The random forest algorithm has good robustness to feature selection and high accuracy without feature screening; thus, it is suitable for an ultrahigh-dimensional eigenvector space. At the same time, the random forest algorithm has high tolerances for outliers and noise and has good data generalization and generalization ability. More details can be found in [70].
The Penman–Monteith equation combined with shuffled complex evolution method developed at the University of Arizona (P-M-SCE_UA) method:
The Penman model combines the energy balance term with the principle of mass transfer and proposes a formula for calculating the evapotranspiration of saturated underlying surfaces (such as open water surfaces and wet grasslands). Then, considering the Penman formula, Monteith [64] introduced the surface impedance to calculate the actual evapotranspiration. The P-M equation is defined as follows:
where E is the actual evapotranspiration; is the latent heat of vaporization; is the slope of the relationship between the saturated water vapor pressure and the temperature; is the air density; is the specific heat of air at a constant pressure; is the psychometric constant; is the saturated water vapor pressure difference at the reference height ( and are the saturation and actual vapor pressures); and A is the available energy, where ; and are the aerodynamic and surface conductances, respectively.
According to [65], the formula for calculating surface evapotranspiration is defined as follows:
where and are the energy absorbed by the canopy and soil, and , , , and is the transmittance of the canopy; is the attenuation coefficient of the available radiation; is the canopy conductivity; and is the soil evapotranspiration coefficient. The degree of soil moisture can be determined by model calibration.
The parameterization scheme of the canopy conductance was calculated based on the maximum stomatal conductance above the canopy and the LAI, which was proposed by [65] as follows:
where are the attenuation coefficients of the shortwave radiation and available radiation, is the visible radiation flux above the canopy (= 0.8 A), and and are the visible radiation flux and water vapor pressure difference, respectively, when the maximum stomatal conductance ( is the maximum value of ).
The aerodynamic conductance is calculated by the aerodynamic impedance . For , the formula is as follows:
where is the Von Karman constant (0.4); is the wind speed at a given altitude; is the zero plane displacement, ; is the vegetation height; is the Monin–Obukhov length; and and are the correction functions of the heat transfer and momentum exchange stability, respectively. Here, and are the dynamic roughness and thermodynamic roughness, respectively. According to previous studies, the parameterization schemes used for the reference are as follows: = 0.13 h and . For a bare underground cushion surface, , where B = 0.13, is the Reynolds number for the roughness, is the frictional wind speed, and is the coefficient of viscosity of air. For a vegetation underlying surface, , and is the characteristic height of the canopy, which can be fitted based on the observed data; and for a mixed underlying surface, ,, = 0.7.
There are six parameters,, ,,, that must be optimized by the model parameters. Using meteorological data and remote sensing data, evapotranspiration can be estimated according to the formula shown in A18. In this paper, the six key parameters of the model are optimized by using the SCE_UA algorithm [66], and the parameter range is set by referring to the method of [65].
The Penman–Monteith equation combined with Ensemble Kalman Filter (P-M-EnKF) method:
The Penman–Monteith equation has a solid physical foundation and is currently recognized as a method for estimating evapotranspiration with strong adaptability, high calculation accuracy, and reliability. Studies have shown that evapotranspiration predictions are sensitive to the canopy resistance and aerodynamic resistance values and radiation in the Penman–Monteith formula [82,83,84]. Therefore, this data assimilation method can add the adjustment factors and before the energy balance term and the vegetation impedance term ( and are the aerodynamic resistance and canopy resistance, respectively) and improve the prediction of the Penman–Monteith formula by optimizing these two factors. Therefore, ET can be expressed using the following formula based on the Penman–Monteith formula:
where and are adjustment factors used to adjust the energy distribution term and the vegetation canopy impedance term. The assimilated evapotranspiration observations are EC data.
We define the model parameter matrix as follows:
(1) Model initialization
First, the initial values of the model parameters and the background field error covariance matrix are defined according to prior knowledge. Then, the parameter vector in the ith set at the initial moment is expressed as follows:
where is the noise of the background field, which corresponds to a Gaussian distribution with a mean of zero and a standard deviation.
(2) State update
As the model continues to integrate forward, the model’s predicted value at is updated to the following state:
where is the model operator, namely, the Penman–Monteith formula; the superscripts ‘’ and ‘’ refer to the analytical and predicted values of ET, respectively. is the predicted value of the ET of the model in the ith collection at time ; and is the meteorological data and vegetation data variables at time . Here, is the model error vector, which complies with a Gaussian distribution with a mean of zero and a standard deviation.
(3) Measurement update
In the assimilation algorithm, the observation operator can be defined as follows:
where is the observation operator, and the model state variables can be projected onto the observation variables through the observation operator. In this paper, the model’s observation operator is the identity matrix. The term is the observation value at time in the ith ensemble member. is the observation error covariance, and is the observation error vector, which complies with the Gaussian distribution with a mean of zero and an standard deviation. When new observations are added, the predicted values in the ensemble member are updated by the following formulas:
where is the Kalman gain matrix at time ; is the predicted background error covariance matrix at time ; is the predicted state variable mean of ensemble members at time ; and is the observation value at time , namely, the EC observation value. More detailed information about the EnKF method can be found in [63].
In this paper, the ensemble Kalman filter algorithm is used to adjust the two factors and in the assimilation method to optimize the energy balance term and the surface impedance term. Since the sources of model errors are diverse and change with time and space, this article mainly determines the average model error by the following formula:
where is the model error; and are the simulated value and observed value, respectively; and is the number of samples in the time series.
When new observation data are added, the model continuously uses the observation data to modify the model prediction. After using the EnKF to determine the two factors and , it is assumed that the two factors are also applicable to the corresponding MODIS pixel area; then, the meteorological raster data and remote sensing data are input into the P-M formula, and finally, the ground truth ET at the satellite pixel scale is acquired.
Appendix B
In the TCH method, it is assumed that the products to be evaluated can be expressed as the sum of the true values and , as follows.
A reference dataset is randomly selected from the datasets to be evaluated, and the remaining datasets are subjected to a different operation from that used for the reference dataset. Assuming that the time series length of these datasets is , one matrix of size can be obtained to accommodate these difference sequences.
Based on these difference sequences, the corresponding covariance matrix can be calculated. An unknown matrix of size is introduced here to represent the covariance matrix in the random error sequence matrix of the different datasets. The diagonal elements of the matrix are the variance of the random error sequence of the dataset, in other words, the variable to be sought. To calculate these unknown variables, and are related by the following expression:
where is an identity matrix of size , and is a vector of size . Thus far, the number of equations is less than the number of quantities to be calculated. Based on formula (A33), the target quantity still cannot be calculated. To add more constraint expressions, the constrained minimization issue using the Kuhn–Tucker theorem in such a way that the objective function is minimized was introduced to obtain a set of free parameter solutions.
Combining formula (A33) to calculate other unknown elements in , the main diagonal elements of the matrix are the error variances that correspond to the surface evapotranspiration products. We square the result of the error variance and divide the result by the average value of each product to obtain the relative error among each product. More details regarding the TCH method can be found in [72].
Appendix C
We assume a model that can be written as follows: , where is a model input parameter, and is the model output. Then, the total variance in can be obtained by performing a Fourier analysis:
where and are the Fourier coefficients on the integer frequencies, and .
The variance in the unique frequency of parameter (and the harmonics of this frequency ) can be estimated as follows.
We decompose the model sensitivity into a first-order index (representing the individual impact of each model parameter when considering changes in the model output) and a total order index (representing the overall impact of each parameter when considering changes in the model output), including the interactions between this parameter and all of the other parameters.
Then, the first-order effects index and the index of the total effect are calculated as shown in the following equations:
where is the sum of all of the variance terms except for i.
Appendix D
To evaluate the uncertainty of ET_EC as the ground truth ET at the satellite pixel scale over a homogeneous underlying surface, the following formula is used to calculate the uncertainty of the ground truth ET according to the method of Beyrich et al. [23]:
where represents the uncertainty of the ground truth ET, represents the ET observed by EC, represents the LAS observed value, and represents the error of the EC observation, which can be calculated according to the EC data processing software (EddyPro).
For the ground truth ET at the satellite pixel scale obtained by the upscaling method, the gPC method is used to quantitatively evaluate its uncertainty. The gPC method is described in detail below. For the original model with independent random variables, according to the polynomial chaos expansion theory, can be expanded with the orthogonal polynomial chaos corresponding to the input variables in the following form:
where represents the n-order polynomial chaos, which is a function of multidimensional random variables and and are the gPC expansion coefficient and the orthogonal polynomial basis function, respectively, which correspond to and in the formula.
Generalized polynomial chaos is composed of tensor products of univariate orthogonal polynomials that satisfy the following orthogonal relation:
where is the Kronecker operator and is the mathematical expectation. The selection of orthogonal polynomial basis functions is related to the distribution of random variables . When the random variable types are different, different types of Askey orthogonal polynomials should be selected as the basis functions, such as Gaussian distribution for Hermite orthogonal polynomials or uniform distribution corresponding to Legendre orthogonal polynomials. The basic functions corresponding to other typical variable types are detailed in [74].
The coefficients of the polynomial chaotic expansion can be determined by the orthogonal relationship as the following expression:
When performing actual numerical calculations, it is essential to use a polynomial chaos of an order no higher than p for the truncated approximation:
The polynomial chaos retained by the truncation approximation has a P term, which can be determined by the following formula:
After the polynomial chaos expansion model is constructed, the coefficients of the polynomial chaos expansion term are calculated; these coefficients generally include the stochastic Galerkin method (SGM) for intrusive algorithms and the stochastic collocation method (SCM) for nonintrusive algorithms. The SCM treats the original model as a black box and finally obtains the coefficients of the polynomial chaotic expansion term by repeatedly solving the selected collocation points in the input variable; this method has the characteristics of a simple principle and fast solving speed. In this paper, the SCM is used to solve the coefficients of the polynomial chaotic expansion term.
Finally, the mean value and variance of the model can be directly calculated from the expansion coefficient in the following form:
In addition, to facilitate the evaluation of the accuracy of the ground truth ET, the relative accuracy (RA) index is defined to evaluate the accuracy of the ground truth ET, which can be determined by the following formula:
where represents the uncertainty of the ground truth ET obtained by the uncertainty quantization methods, and represents the average value of the ground truth ET.
References
- Jung, M.; Reichstein, M.; Ciais, P.; Seneviratne, S.I.; Sheffield, J.; Goulden, M.L.; Bonan, G.; Cescatti, A.; Chen, J.; De Jeu, R.; et al. Recent decline in the global land evapotranspiration trend due to limited moisture supply. Nature 2010, 467, 951–954. [Google Scholar] [CrossRef]
- Fisher, J.B.; Melton, F.; Middleton, E.; Hain, C.; Anderson, M.; Allen, R.; McCabe, M.F.; Hook, S.; Baldocchi, D.; Townsend, P.A.; et al. The future of evapotranspiration: Global requirements for ecosystem functioning, carbon and climate feedbacks, agricultural management, and water resources. Water Resour. Res. 2017, 53, 2618–2626. [Google Scholar] [CrossRef]
- Li, Z.L.; Tang, R.; Wan, Z.; Bi, Y.; Zhou, C.; Tang, B.; Yan, G.; Zhang, X. A review of current methodologies for regional Evapotranspiration estimation from remotely sensed data. Sensors 2009, 9, 3801–3853. [Google Scholar] [CrossRef] [Green Version]
- Mu, Q.; Zhao, M.; Running, S.W. Improvements to a MODIS global terrestrial evapotranspiration algorithm. Remote Sens. Environ. 2011, 115, 1781–1800. [Google Scholar] [CrossRef]
- Miralles, D.G.; Holmes, T.R.H.; De Jeu, R.A.M.; Gash, J.H.; Meesters, A.G.C.A.; Dolman, A.J. Global land-surface evaporation estimated from satellite-based observations. Hydrol. Earth Syst. Sci. 2011, 15, 453–469. [Google Scholar] [CrossRef] [Green Version]
- Yao, Y.; Liang, S.; Li, X.; Hong, Y.; Fisher, J.B.; Zhang, N.; Chen, J.; Cheng, J.; Zhao, S.; Zhang, X.; et al. Bayesian multimodel estimation of global terrestrial latent heat flux from eddy covariance, meteorological, and satellite observations. J. Geophys. Res. Atmos. 2014, 119, 4521–4545. [Google Scholar] [CrossRef]
- Hu, G.; Jia, L. Monitoring of evapotranspiration in a semi-arid inland river basin by combining microwave and optical remote sensing observations. Remote Sens. 2015, 7, 3056–3087. [Google Scholar] [CrossRef] [Green Version]
- Jiang, C.; Ryu, Y. Multi-scale evaluation of global gross primary productivity and evapotranspiration products derived from Breathing Earth System Simulator (BESS). Remote Sens. Environ. 2016, 186, 528–547. [Google Scholar] [CrossRef]
- Jia, Z.; Liu, S.; Xu, Z.; Chen, Y.; Zhu, M. Validation of remotely sensed evapotranspiration over the Hai River Basin, China. J. Geophys. Res. Atmos. 2012, 117. [Google Scholar] [CrossRef]
- Nearing, G.S.; Mocko, D.M.; Peters-Lidard, C.D.; Kumar, S.V.; Xia, Y. Benchmarking NLDAS-2 soil moisture and evapotranspiration to separate uncertainty contributions. J. Hydrometeorol. 2016, 17, 745–759. [Google Scholar] [CrossRef]
- Kalma, J.D.; McVicar, T.R.; McCabe, M.F. Estimating land surface evaporation: A review of methods using remotely sensed surface temperature data. Surv. Geophys. 2008, 29, 421–469. [Google Scholar] [CrossRef]
- Ershadi, A.; McCabe, M.F.; Evans, J.P.; Chaney, N.W.; Wood, E.F. Multi-site evaluation of terrestrial evaporation models using FLUXNET data. Agric. For. Meteorol. 2014, 187, 46–61. [Google Scholar] [CrossRef]
- Yao, Y.; Liang, S.; Li, X.; Chen, J.; Wang, K.; Jia, K.; Cheng, J.; Jiang, B.; Fisher, J.B.; Mu, Q.; et al. A satellite-based hybrid algorithm to determine the Priestley-Taylor parameter for global terrestrial latent heat flux estimation across multiple biomes. Remote Sens. Environ. 2015, 165, 216–233. [Google Scholar] [CrossRef] [Green Version]
- Michel, D.; Jiménez, C.; Miralles, D.G.; Jung, M.; Hirschi, M.; Ershadi, A.; Martens, B.; Mccabe, M.F.; Fisher, J.B.; Mu, Q.; et al. The WACMOS-ET project—Part 1: Tower-scale evaluation of four remote-sensing-based evapotranspiration algorithms. Hydrol. Earth Syst. Sci. 2016, 20, 803–822. [Google Scholar] [CrossRef] [Green Version]
- Brunsell, N.A.; Ham, J.M.; Arnold, K.A. Validating remotely sensed land surface fluxes in heterogeneous terrain with large aperture scintillometry. Int. J. Remote Sens. 2011, 32, 6295–6314. [Google Scholar] [CrossRef]
- Senay, G.B.; Friedrichs, M.; Singh, R.K.; Velpuri, N.M. Evaluating Landsat 8 evapotranspiration for water use mapping in the Colorado River Basin. Remote Sens. Environ. 2016, 185, 171–185. [Google Scholar] [CrossRef] [Green Version]
- Ge, Y.; Jin, Y.; Stein, A.; Chen, Y.; Wang, J.; Wang, J.; Cheng, Q.; Bai, H.; Liu, M.; Atkinson, P.M. Principles and methods of scaling geospatial Earth science data. Earth-Sci. Rev. 2019, 197, 102897. [Google Scholar] [CrossRef]
- Liu, S.; Xu, Z.; Song, L.; Zhao, Q.; Ge, Y.; Xu, T.; Ma, Y.; Zhu, Z.; Jia, Z.; Zhang, F. Upscaling evapotranspiration measurements from multi-site to the satellite pixel scale over heterogeneous land surfaces. Agric. For. Meteorol. 2016, 230–231, 97–113. [Google Scholar] [CrossRef]
- Li, X.; Liu, S.; Li, H.; Ma, Y.; Wang, J.; Zhang, Y.; Xu, Z.; Xu, T.; Song, L.; Yang, X.; et al. Intercomparison of Six Upscaling Evapotranspiration Methods: From Site to the Satellite Pixel. J. Geophys. Res. Atmos. 2018, 123, 6777–6803. [Google Scholar] [CrossRef]
- Xu, T.; Guo, Z.; Liu, S.; He, X.; Meng, Y.; Xu, Z.; Xia, Y.; Xiao, J.; Zhang, Y.; Ma, Y.; et al. Evaluating different machine learning methods for upscaling evapotranspiration from flux towers to the regional scale. J. Geophys. Res. Atmos. 2018, 123, 8674–8690. [Google Scholar] [CrossRef]
- Li, X.; Jin, R.; Liu, S.; Ge, Y.; Xiao, Q.; Liu, Q.; Ma, M.; Ran, Y. Upscaling research in HiWATER: Progress and prospects. J. Remote Sens. 2016, 20, 921–932. (In Chinese) [Google Scholar]
- Hao, D.; Xiao, Q.; Wen, J.; You, D.; Wu, X.; Lin, X.; Wu, S. Advances in upscaling methods of quantitative remote sensing. Journal of Remote Sensing. J. Remote Sens. 2018, 22, 408–423. (In Chinese) [Google Scholar]
- Beyrich, F.; Leps, J.P.; Mauder, M.; Bange, J.; Foken, T.; Huneke, S.; Lohse, H.; Lüdi, A.; Meijninger, W.M.L.; Mironov, D.; et al. Area-averaged surface fluxes over the litfass region based on eddy-covariance measurements. Bound. -Layer Meteorol. 2006, 121, 33–65. [Google Scholar] [CrossRef]
- Xu, F.; Wang, W.; Wang, J.; Xu, Z.; Qi, Y.; Wu, Y. Area-averaged evapotranspiration over a heterogeneous land surface: Aggregation of multi-point EC flux measurements with a high-resolution land-cover map and footprint analysis. Hydrol. Earth Syst. Sci. 2017, 21, 4037–4051. [Google Scholar] [CrossRef] [Green Version]
- Xu, F.; Wang, W.; Wang, J.; Huang, C.; Qi, Y.; Li, Y.; Ren, Z. Aggregation of area-averaged evapotranspiration over the Ejina Oasis based on a flux matrix and footprint analysis. J. Hydrol. 2019, 575, 17–30. [Google Scholar] [CrossRef]
- Dold, C.; Heitman, J.; Giese, G.; Howard, A.; Havlin, J.; Sauer, T. Upscaling evapotranspiration with parsimonious models in a North Carolina vineyard. Agronomy 2019, 9, 152. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.; Yang, J.; Myint, S.W.; Wang, Z.H.; Tong, B. Empirical modeling and spatio-temporal patterns of urban evapotranspiration for the Phoenix metropolitan area, Arizona. GISci. Remote Sens. 2016, 53, 778–792. [Google Scholar] [CrossRef]
- Khoshravesh, M.; Sefidkouhi, M.A.G.; Valipour, M. Estimation of reference evapotranspiration using multivariate fractional polynomial, Bayesian regression, and robust regression models in three arid environments. Appl. Water Sci. 2017, 7, 1911–1922. [Google Scholar] [CrossRef] [Green Version]
- Carter, C.; Liang, S. Evaluation of ten machine learning methods for estimating terrestrial evapotranspiration from remote sensing. Int. J. Appl. Earth Obs. Geoinf. 2019, 78, 86–92. [Google Scholar] [CrossRef]
- Landeras, G.; Ortiz-Barredo, A.; López, J.J. Comparison of artificial neural network models and empirical and semi-empirical equations for daily reference evapotranspiration estimation in the Basque Country (Northern Spain). Agric. Water Manag. 2008, 95, 553–565. [Google Scholar] [CrossRef]
- Rahimikhoob, A. Comparison between M5 model tree and neural networks for estimating reference evapotranspiration in an arid environment. Water Resour. Manag. 2014, 28, 657–669. [Google Scholar] [CrossRef]
- Jung, M.; Reichstein, M.; Margolis, H.A.; Cescatti, A.; Richardson, A.D.; Arain, M.A.; Arneth, A.; Bernhofer, C.; Bonal, D.; Chen, J.; et al. Global patterns of land-atmosphere fluxes of carbon dioxide, latent heat, and sensible heat derived from eddy covariance, satellite, and meteorological observations. J. Geophys. Res. Biogeosci. 2011, 116, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Yang, F.; White, M.A.; Michaelis, A.R.; Ichii, K.; Hashimoto, H.; Votava, P.; Zhu, A.X.; Nemani, R.R. Prediction of continental-scale evapotranspiration by combining MODIS and AmeriFlux data through support vector machine. IEEE Trans. Geosci. Remote Sens. 2006, 44, 3452–3461. [Google Scholar] [CrossRef]
- Bodesheim, P.; Jung, M.; Gans, F.; Mahecha, M.D.; Reichstein, M. Upscaled diurnal cycles of land-Atmosphere fluxes: A new global half-hourly data product. Earth Syst. Sci. Data 2018, 10, 1327–1365. [Google Scholar] [CrossRef] [Green Version]
- Karbasi, M. Forecasting of multi-step ahead reference evapotranspiration using wavelet-Gaussian process regression model. Water Resour. Manag. 2018, 32, 1035–1052. [Google Scholar] [CrossRef]
- Hu, M.; Wang, J.; Ge, Y.; Liu, M.; Liu, S.; Xu, Z.; Xu, T. Scaling flux tower observations of sensible heat flux using weighted area-to-area regression kriging. Atmosphere 2015, 6, 1032–1044. [Google Scholar] [CrossRef] [Green Version]
- Ge, Y.; Liang, Y.; Wang, J.; Zhao, Q.; Liu, S. Upscaling sensible heat fluxes with area-to-area regression kriging. IEEE Geosci. Remote Sens. Lett. 2015, 12, 656–660. [Google Scholar]
- Xu, D.; Agee, E.; Wang, J.; Ivanov, V.Y. Estimation of Evapotranspiration of Amazon Rainforest Using the Maximum Entropy Production Method. Geophys. Res. Lett. 2019, 46, 1402–1412. [Google Scholar] [CrossRef]
- Hajji, I.; Nadeau, D.F.; Music, B.; Anctil, F.; Wang, J. Application of the maximum entropy production model of evapotranspiration over partially vegetated water-limited land surfaces. J. Hydrometeorol. 2018, 19, 989–1005. [Google Scholar] [CrossRef]
- Heinemann, G.; Kerschgens, M. Comparison of methods for area-averaging surface energy fluxes over heterogenous land surfaces using high-resolution non-hydrostatic simulations. Int. J. Climatol. 2005, 25, 379–403. [Google Scholar] [CrossRef]
- Ruehr, S.; Lee, X.; Smith, R.; Li, X.; Xu, Z.; Liu, S.; Yang, X.; Zhou, Y. A mechanistic investigation of the oasis effect in the Zhangye cropland in semiarid western China. J. Arid Environ. 2020, 176, 104120. [Google Scholar] [CrossRef]
- He, X.; Xu, T.; Bateni, S.M.; Ek, M.; Liu, S.; Chen, F. Mapping regional evapotranspiration in cloudy skies via variational assimilation of all-weather land surface temperature observations. J. Hydrol. 2020, 585, 124790. [Google Scholar] [CrossRef]
- Wu, X.; Xiao, Q.; Wen, J.; You, D.; Hueni, A. Advances in quantitative remote sensing product validation: Overview and current status. Earth-Sci. Rev. 2019, 196, 102875. [Google Scholar] [CrossRef]
- Zhang, Y.; Jia, Z.; Liu, S.; Xu, Z.; Xu, T.; Yao, Y.; Ma, Y.; Song, L.; Li, X.; Hu, X.; et al. Advances in validation of remotely sensed land surface evapotranspiration. J. Remote Sens. 2020, 24, 975–999. (In Chinese) [Google Scholar]
- Wu, X.; Xiao, Q.; Wen, J.; You, D. Direct comparison and triple collocation: Which is more reliable in the validation of coarse-scale satellite surface albedo products. J. Geophys. Res. Atmos. 2019, 124, 5198–5213. [Google Scholar] [CrossRef]
- Liu, S.; Li, X.; Xu, Z.; Che, T.; Xiao, Q.; Liu, Q.; Jin, R.; Guo, J.; Wang, L.; Wang, W.; et al. The Heihe Integrated Observatory Network: A basin-scale land surface processes observatory in China. Vadose Zone J. 2018, 17, 1–21. [Google Scholar] [CrossRef]
- Xu, Z.; Liu, S.; Zhu, Z.; Zhou, J.; Shi, W.; Xu, T.; Yang, X.; Zhang, Y.; He, X. Exploring evapotranspiration changes in a typical endorheic basin through the integrated observatory network. Agric. For. Meteorol. 2020, 290, 108010. [Google Scholar] [CrossRef]
- Li, X.; Li, X.; Li, Z.; Ma, M.; Wang, J.; Xiao, Q.; Liu, Q.; Che, T.; Chen, E.; Yan, G.; et al. Watershed allied telemetry experimental research. J. Geophys. Res. Atmos. 2009, 114, D22103. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Cheng, G.; Liu, S.; Xiao, Q.; Ma, M.; Jin, R.; Che, T.; Liu, Q.; Wang, W.; Qi, Y.; et al. Heihe watershed allied telemetry experimental research (HiWater) scientific objectives and experimental design. Bull. Am. Meteorol. Soc. 2013, 94, 1145–1160. [Google Scholar] [CrossRef]
- Liu, S.; Xu, Z.; Wang, W.; Jia, Z.; Zhu, M.; Bai, J.; Wang, J. A comparison of eddy-covariance and large aperture scintillometer measurements with respect to the energy balance closure problem. Hydrol. Earth Syst. Sci. 2011, 15, 1291–1306. [Google Scholar] [CrossRef] [Green Version]
- Liu, S.; Xu, Z. Micrometeorological methods to determine evapotranspiration. In Observation and Measurement of Ecohydrological Processes; Li, X., Vereecken, H., Eds.; Springer: Berlin/Heidelberg, Germeny, 2018; pp. 201–239. [Google Scholar]
- Ji, X.; Zhao, W.; Kang, E.; Zhang, Z.; Jin, B.; Zhao, L. Carbon dioxide exchange in an irrigated agricultural field within an oasis, Northwest China. J. Appl. Meteorol. Climatol. 2011, 50, 2298–2308. [Google Scholar] [CrossRef]
- Xu, Z.; Liu, S.; Li, X.; Shi, S.; Wang, J.; Zhu, Z.; Xu, T.; Wang, W.; Ma, M. Intercomparison of surface energy flux measurement systems used during the HiWATER-MUSOEXE. J. Geophys. Res. Atmos. 2013, 118, 13140–13157. [Google Scholar] [CrossRef]
- Mu, X.; Hu, R.; Huang, S.; Chen, Y. HiWATER: Dataset of emissivity in the middle reaches of the Heihe River Basin in 2012. Beijing normal university; cold and arid regions environmental and engineering research institute. Chinese Acad. Sci. 2012. [Google Scholar]
- Zhu, X.; Chen, J.; Gao, F.; Chen, X.; Masek, J.G. An enhanced spatial and temporal adaptive reflectance fusion model for complex heterogeneous regions. Remote Sens. Environ. 2010, 114, 2610–2623. [Google Scholar] [CrossRef]
- Ma, Y.; Liu, S.; Song, L.; Xu, Z.; Liu, Y.; Xu, T.; Zhu, Z. Estimation of daily evapotranspiration and irrigation water efficiency at a Landsat-like scale for an arid irrigation area using multi-source remote sensing data. Remote Sens. Environ. 2018, 216, 715–734. [Google Scholar] [CrossRef]
- Zhong, B.; Ma, P.; Nie, A.H.; Yang, A.X.; Yao, Y.J.; Lü, W.B.; Zhang, H.; Liu, Q.H. Land cover mapping using time series HJ-1/CCD data. Sci. China Earth Sci. 2014, 57, 1790–1799. [Google Scholar] [CrossRef]
- Guillevic, P.C.; Biard, J.C.; Hulley, G.C.; Privette, J.L.; Hook, S.J.; Olioso, A.; Göttsche, F.M.; Radocinski, R.; Román, M.O.; Yu, Y.; et al. Validation of Land Surface Temperature products derived from the Visible Infrared Imaging Radiometer Suite (VIIRS) using ground-based and heritage satellite measurements. Remote Sens. Environ. 2014, 154, 19–37. [Google Scholar] [CrossRef]
- Huang, G.; Li, X.; Ma, M.; Li, H.; Huang, C. High resolution surface radiation products for studies of regional energy, hydrologic and ecological processes over Heihe river basin, northwest China. Agric. For. Meteorol. 2016, 230–231, 67–78. [Google Scholar] [CrossRef]
- Kormann, R.; Meixner, F.X. An analytical footprint model for non-neutral stratification. Bound. -Layer Meteorol. 2001, 99, 207–224. [Google Scholar] [CrossRef]
- Meijninger, W.M.L.; Hartogensis, O.K.; Kohsiek, W.; Hoedjes, J.C.B.; Zuurbier, R.M.; De Bruin, H.A.R. Determination of area-averaged sensible heat fluxes with a large aperture scintillometer over a heterogeneous surface–Flevoland field experiment. Bound. -Layer Meteorol. 2002, 105, 37–62. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, S.; Hu, X.; Wang, J.; Li, X.; Xu, Z.; Ma, Y.; Liu, R.; Xu, T.; Yang, X. Evaluating Spatial Heterogeneity of Land Surface Hydrothermal Conditions in the Heihe River Basin. Chin. Geogr. Sci. 2020, 30, 855–875. [Google Scholar] [CrossRef]
- Huang, C.; Li, X.; Lu, L. Retrieving soil temperature profile by assimilating MODIS LST products with ensemble Kalman filter. Remote Sens. Environ. 2008, 112, 1320–1336. [Google Scholar] [CrossRef]
- Monteith, J.L. Evaporation and environment. Symp. Soc. Exp. Biol. 1965, 19, 205–234. [Google Scholar] [PubMed]
- Leuning, R.; Zhang, Y.Q.; Rajaud, A.; Cleugh, H.; Tu, K. A simple surface conductance model to estimate regional evaporation using MODIS leaf area index and the Penman-Monteith equation. Water Resour. Res. 2008, 44, W10419. [Google Scholar] [CrossRef]
- Duan, Q.; Gupta, V. Effective and efficient global optimization for conceptual rainfall-runoff models. Water Resour. Res. 1992, 28, 1015–1031. [Google Scholar] [CrossRef]
- Kumar, M.; Raghuwanshi, N.S.; Singh, R. Artificial neural networks approach in evapotranspiration modeling: A review. Irrig. Sci. 2011, 29, 11–25. [Google Scholar] [CrossRef]
- Hinton, G.E.; Osindero, S.; Teh, Y.W. A fast learning algorithm for deep belief nets. Neural Comput. 2006, 18, 1527–1554. [Google Scholar] [CrossRef] [PubMed]
- Williams, C.K.; Rasmussen, C.E. Gaussian Processes for Machine Learning; MIT Press: Cambridge, MA, USA, 2006. [Google Scholar]
- Tyralis, H.; Papacharalampous, G.; Langousis, A. A brief review of random forests for water scientists and practitioners and their recent history in water resources. Water 2019, 11, 910. [Google Scholar] [CrossRef] [Green Version]
- Ilangakoon, N.T.; Gorsevski, P.V.; Simic Milas, A. Estimating leaf area index by bayesian linear regression using terrestrial Lidar, LAI-2200 plant canopy analyzer, and landsat tm spectral indices. Can. J. Remote Sens. 2015, 41, 315–333. [Google Scholar] [CrossRef]
- Xu, T.; Guo, Z.; Xia, Y.; Ferreira, V.G.; Liu, S.; Wang, K.; Yao, Y.; Zhang, X.; Zhao, C. Evaluation of twelve evapotranspiration products from machine learning, remote sensing and land surface models over conterminous United States. J. Hydrol. 2019, 578, 124105. [Google Scholar] [CrossRef]
- Saltelli, A.; Tarantola, S.; Chan, K.S.P.S.; Saltelli, A.; Tarantoal, S.; Chan, K.S.P.S. A quantitative model-independent method for global sensitivity analysis of model output. Technometrics 1999, 41, 39–56. [Google Scholar] [CrossRef]
- Xiu, D.; Karniadakis, G.E. Modeling uncertainty in flow simulations via generalized polynomial chaos. J. Comput. Phys. 2003, 187, 137–167. [Google Scholar] [CrossRef]
- Najm, H.N. Uncertainty quantification and polynomial chaos techniques in computational fluid dynamics. Annu. Rev. Fluid Mech. 2009, 41, 35–52. [Google Scholar] [CrossRef]
- Yao, Y.; Liang, S.; Fisher, J.B.; Zhang, Y.; Cheng, J.; Chen, J.; Jia, K.; Zhang, X.; Bei, X.; Shang, K.; et al. A Novel NIR-Red Spectral Domain Evapotranspiration Model from the Chinese GF-1 Satellite: Application to the Huailai Agricultural Region of China. IEEE Trans. Geosci. Remote Sens. 2020, 59, 4105–4119. [Google Scholar] [CrossRef]
- Zhang, T.; Jin, S. Evapotranspiration Variations in the Mississippi River Basin Estimated from GPS Observations. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4694–4701. [Google Scholar] [CrossRef]
- Song, L.; Liu, S.; Kustas, W.P.; Nieto, H.; Sun, L.; Xu, Z.; Skaggs, T.H.; Yang, Y.; Ma, M.; Xu, T.; et al. Monitoring and validating spatially and temporally continuous daily evaporation and transpiration at river basin scale. Remote Sens. Environ. 2018, 219, 72–88. [Google Scholar] [CrossRef]
- Velpuri, N.M.; Senay, G.B.; Singh, R.K.; Bohms, S.; Verdin, J.P. A comprehensive evaluation of two MODIS evapotranspiration products over the conterminous United States: Using point and gridded FLUXNET and water balance ET. Remote Sens. Environ. 2013, 139, 35–49. [Google Scholar] [CrossRef]
- Evensen, G. The ensemble Kalman filter: Theoretical formulation and practical implementation. Ocean Dyn. 2003, 53, 343–367. [Google Scholar] [CrossRef]
- Priestley, C.H.B.; Taylor, R.J. On the assessment of surface heat flux and evaporation using large-scale parameters. Mon. Weather Rev. 1972, 100, 81–92. [Google Scholar] [CrossRef]
- Yin, Y.; Wu, S.; Zheng, D.; Yang, Q. Radiation calibration of FAO56 Penman–Monteith model to estimate reference crop evapotranspiration in China. Agric. Water Manag. 2008, 95, 77–84. [Google Scholar] [CrossRef]
- Lindroth, A.; Halldin, S. Numerical analysis of pine forest evaporation and surface resistance. Agric. For. Meteorol. 1986, 38, 59–79. [Google Scholar] [CrossRef]
- Beven, K. A sensitivity analysis of the Penman-Monteith actual evapotranspiration estimates. J. Hydrol. 1979, 44, 169–190. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).