BeiDou-Based Passive Radar Vessel Target Detection: Method and Experiment via Long-Time Optimized Integration

Abstract

The BeiDou navigation satellite system shows its potential for passive radar vessel target detection owing to its global-scale coverage. However, the restrained power budget from BeiDou satellite hampers the detection performance. To solve this limitation, this paper proposes a long-time optimized integration method to obtain an adequate signal-to-noise ratio (SNR). During the long observation time, the range migration, intricate Doppler migration, and noncoherence characteristic bring challenges to the integration processing. In this paper, first, the keystone transform is applied to correct the range walk. Then, considering the noncoherence of the entire echo, the hybrid integration strategy is adopted. To remove the Doppler migration and correct the residual range migration, the long-time integration is modeled as an optimization problem. Finally, the particle swarm optimization (PSO) algorithm is applied to solve the optimization problem, after which the target echo over the long observation time is well concentrated, providing a reliable detection performance for the BeiDou-based passive radar. Its effectiveness is shown by the simulated and experimental results.

1. Introduction

Unlike the conventional active radar system, passive radar system capitalizes on the signals of opportunity already existing in the environment. The absence of a dedicated transmitter makes it low-cost and contributes to its anti-jamming capability [1,2]. Besides, the remarkable advantage of no electromagnetic pollution leads to its extensive applications. In recent years, with the increasing quantity and variety of opportunistic sources, there is a significant growth of interest in passive radar system [3].

Many types of terrestrial sources of opportunity have been investigated in passive radar, such as FM radio, digital audio/video broadcast, and Wi-Fi [4,5,6]. However, owing to the confined transmitter positions and their original intentions, the coverages of terrestrial sources are restrained, which limits their application scenarios of the passive radar system.

Compared with the sources above, the utilization of global navigation satellite system (GNSS) availably extends the signal coverage to global scale for the passive radar system. Thus, GNSS-based passive radar shows its potential for the monitoring of sea areas which are not fully covered by the terrestrial sources [7]. In addition, GNSS provides a relatively large signal bandwidth, which is beneficial for the target detection capability [8,9,10]. Moreover, the most unique feature of GNSS is that any point on the Earth is assured to be simultaneously illuminated by 4–8 satellites in a single GNSS constellation from different angles. The number can be up to 32 if the four GNSS constellations (i.e., GPS, GLONASS, Galileo, and BeiDou) are fully in service, providing a large selection of opportunistic transmitters for passive radar system [11].

Due to the limited emitting power and the greatly long irradiation distance, the most intractable obstruction for the GNSS-based passive radar is its exceedingly low-power density near the Earth’s surface (as low as −135 dBW/m² [12]). In order to increase the signal-to-noise ratio (SNR) for a reliable target detection performance, an effective approach is to integrate the target energy over a long time. With respect to the GNSS-based passive radar, the integration time usually needs to be lengthened to several tens of seconds [13], especially in the case of an extreme SNR such as a low radar cross section (RCS) target or a large radar detection range. However, this paper focuses on the GNSS-based passive radar vessel target detection under the condition of such extreme SNR. The target motion leads to two severe problems that impede the long-time integration. First, the aspect angle of the target varies with time, which causes the decorrelation throughout a long dwell time. Thus, the entire long-time echo is no longer coherent. Furthermore, the conspicuous range and Doppler migrations occur in the echo due to the translation motions of the vessel target and the satellite transmitter. Particularly, when the integration time is in the order of several tens of seconds, the migrations become more intricate. In addition, the oscillation and rotation motions of the vessel target in practice introduce an additional Doppler migration [14]. Usually, the detected vessel target is noncooperative. The inaccessible motion parameters increase the difficulty in the accurate compensation of the migrations.

With respect to the vessel target detection, currently, many researchers focus on the artificial intelligence (AI)-based detection methods [15,16,17,18,19]. The vessel detection is performed on synthetic aperture radar (SAR) or optical remote sensing imagery, and the vessel target is recognized and classified via a deep learning algorithm. In the field of radar target detection, there are also several literatures on the detection of vessel using the GNSS-based passive radar, which try to achieve the long-time integration of target echo after properly handling the aforementioned problems. First, to cope with the noncoherence characteristic of the entire echo, an effective approach is to adopt the hybrid integration strategy, which is commonly used in the pre-existing literature and in this paper. That is, the entire echo is segmented into temporal frames with frame duration in the order of 2–3 s [13]. The signal inside each frame is regard as correlated, thus coherent integration can be performed, followed by the noncoherent integration of multiple frames. 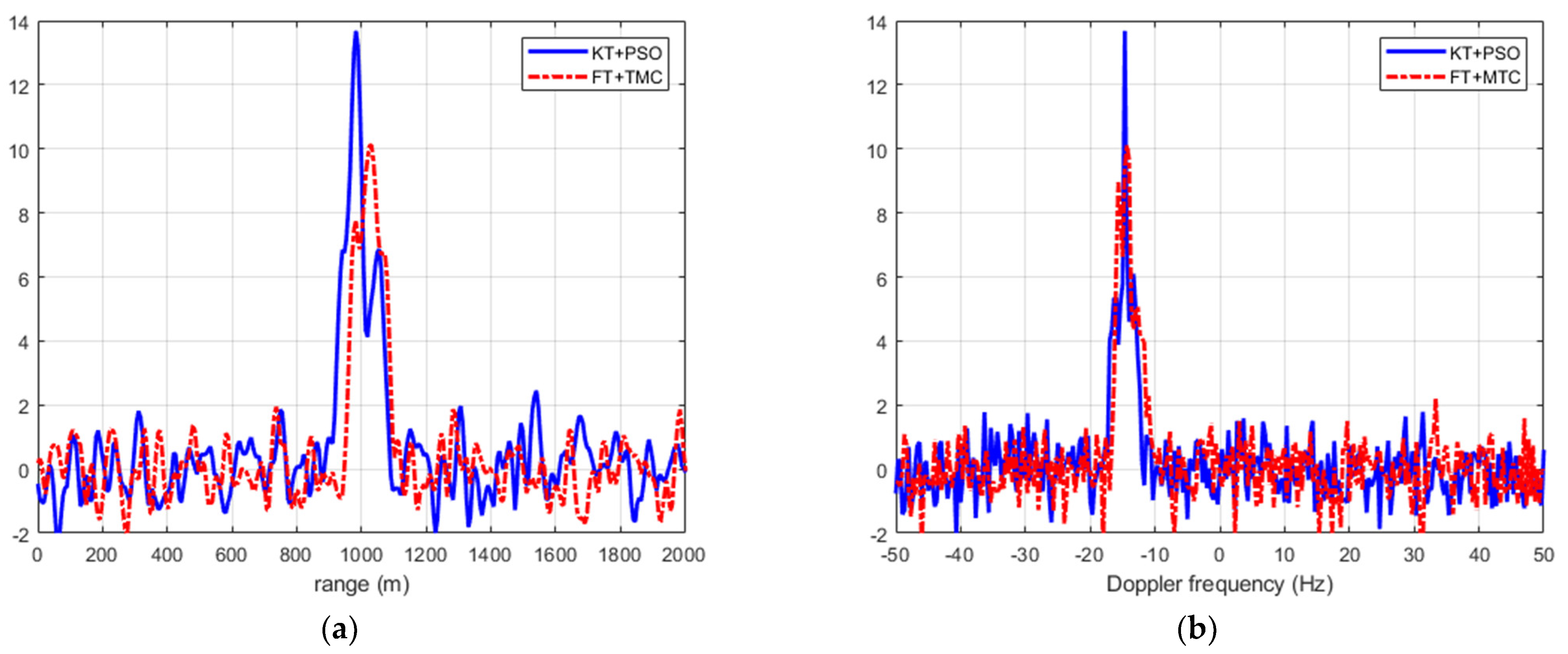In reference [20], a long-time integration method based on the keystone transform and the fractional Fourier transform (FrFT) is proposed for the target moving with a constant velocity. However, only the linear range migration and linear Doppler migration over the entire echo can be well compensated by means of these two transforms. In reference [21], the coherent integration of each frame is performed by means of the Fourier transform along the azimuth direction. After compensation of the range and Doppler migrations with a tested Doppler frequency rate (DFR) value, the noncoherent integration of the multiple frames is performed. Nevertheless, the range and Doppler migrations are regarded as negligible inside frame duration, and only the linear Doppler migration is considered over the entire integration time. Therefore, the integration effectiveness of this method is possibly unsatisfactory. In reference [22], the coherent integration performed in the same way with [21]. In addition, the compensation of range and Doppler migrations between different frames is achieved in the local plane with a tested target velocity. However, this method suffers for an ambiguity problem between the target’s position and velocity.

In this paper, we focus on the vessel target detection using BeiDou-based passive radar consisting of a BeiDou satellite of opportunity and a fixed receiver. The hybrid constellation of BeiDou system provides more options on opportunistic illuminator for the passive radar system [23]. It is observed that in the pre-existing integration methods, only the low-order range and Doppler migrations can be corrected, which constrains the integration time of the target echo and limits the target detection application. By contrast, this paper proposes a long-time optimized integration method for BeiDou-based passive radar vessel target detection, which aims at accurately compensating the high-order migrations and maximizing the SNR. First, the keystone transform is applied to eliminate the range walk. To cope with the noncoherence of entire target, the range migration-corrected data are then segmented into temporal frames and the hybrid integration strategy is adopted. In order to remove the residual range migration, and simultaneously correct the Doppler migration inside each frame and compensate for the Doppler shift at different frames, the long-time integration is modeled as an optimization problem, where the decision variables are the corresponding Doppler centroids (DCs) and DFRs of multiple frames. Finally, the optimization problem is solved by the particle swarm optimization (PSO) algorithm. After that, the final integrated result provides a reliable vessel target detection performance.

The remaining parts of the paper are organized as follows. The echo model of the vessel target is deduced in Section 2. The proposed method is presented in Section 3. The effectiveness of the method is demonstrated via the simulated and experimental results in Section 4. Finally, in Section 5, we draw our conclusions.

2. Echo Model and Characteristic Analysis

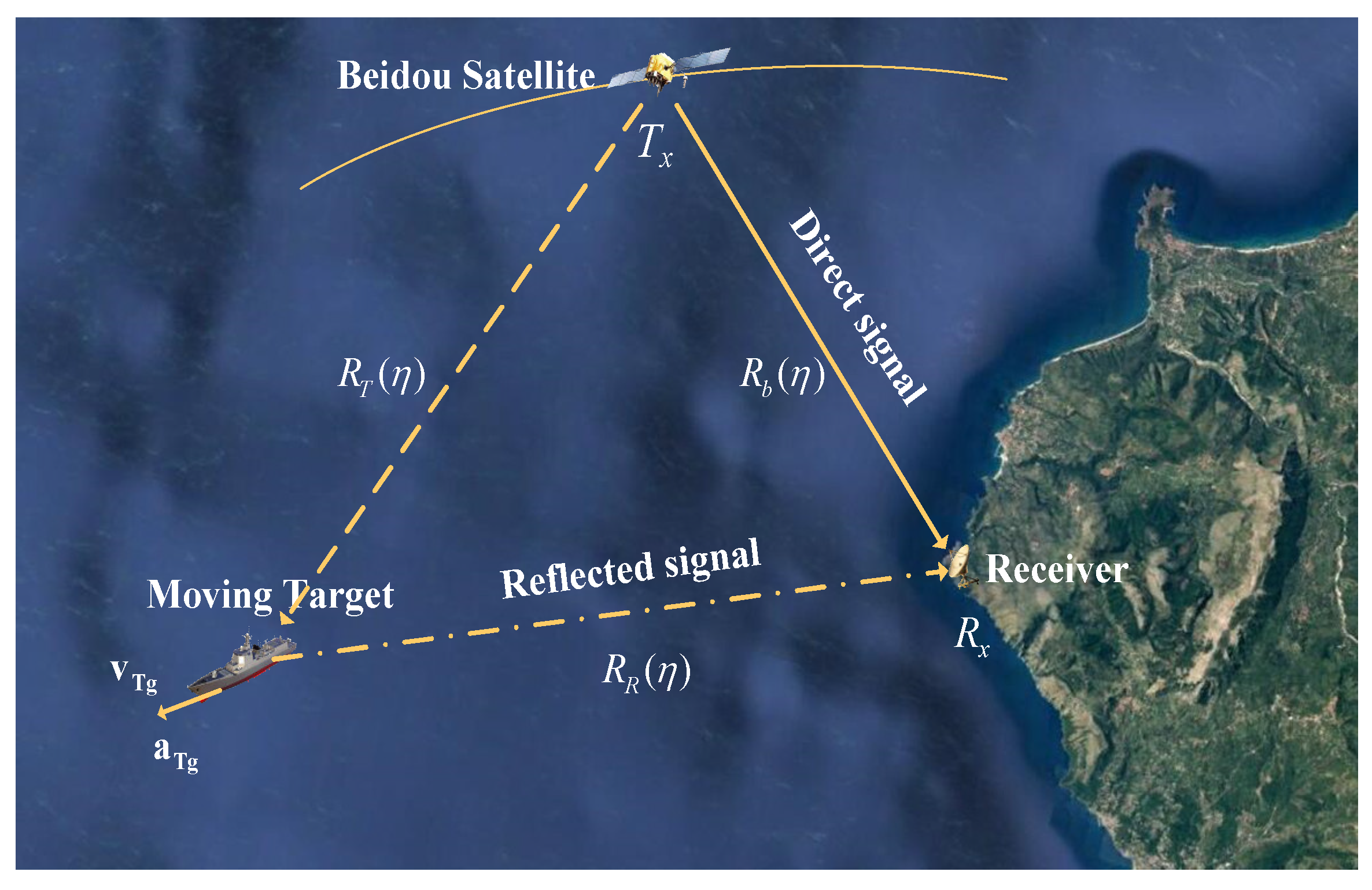
The geometry of the BeiDou-based passive radar is shown in Figure 1 with reference to the vessel target detection. The system is composed of a BeiDou satellite of opportunity and a fixed receiver. T_x is the satellite transmitter of opportunity, and R_x is the fixed receiver on the coast. R_b is the baseline between T_x and R_x. R_T and R_R are the distances from the vessel target to T_x and R_x, respectively.

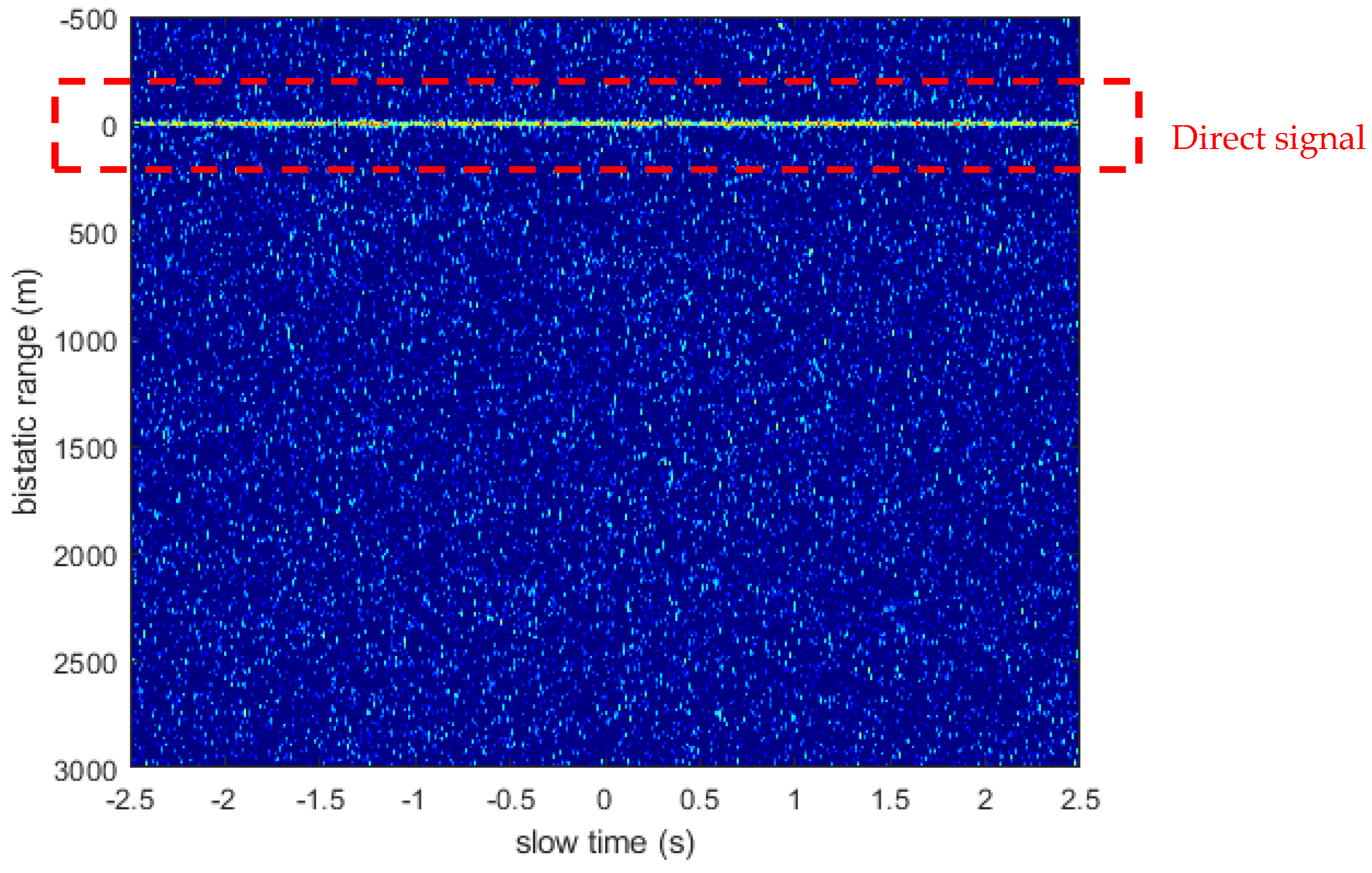
The receiver is equipped with two antennas, i.e., the reference antenna and the surveillance antenna. The former is steered toward the BeiDou satellite to acquire the direct signal, while the latter is utilized to collect the reflected signal from the detection area. Despite the fact that these signals are continuous in time, they can be formatted into two-dimensional fast-time and slow-time domain according to an equivalent pulse repetition interval (PRI) $T_{PRI}$. $\tau \in [-T_{PRI}/2,T_{PRI}/2]$ denotes the fast-time, and $\eta \in [-T_a/2,T_a/2]$ denotes the slow-time, where $T_a$ is the entire dwell time. The equivalent PRI is selected as long as the duration of the transmitted ranging code from the BeiDou satellite, where the typical value is 1 ms.

By the cross-correlation of reflect signal and the reference signal (which can be generated from the direct signal [21]), the range compression as well as the synchronization can be accomplished. The range-compressed data in fast-time and slow-time domain are modeled as [20]:

$$s\left(\tau ,\eta \right)={\sigma }_{\eta }\rho \left[\tau -\frac{R(\eta )}{c}\right]rect\left(\frac{\eta }{T_a}\right)\cdot \exp \left\{-j\frac{2\pi }{\lambda }R(\eta )\right\},$$

(1)

where $j$ denotes the imaginary number, and the operator $rect(\cdot )$ denotes the rectangular window, $\rho (\cdot )$ is the cross-correlation function, $c$ is the light speed, $\lambda$ is the wave length, ${\sigma }_{\eta }$ is the complex reflectivity of the target which changes with slow-time, and $R(\eta )$ is the bistatic range expressed as:

$$R(\eta )=R_T(\eta )+R_R(\eta )-R_b(\eta ),$$

(2)

The corresponding Doppler frequency is obtained as the derivative of the bistatic range with respect to the slow-time variable, i.e.,

$$f_d(\eta )=-\frac{1}{\lambda }\frac{\partial R(\eta )}{\partial \eta },$$

(3)

Then the bistatic range is precisely expanded into Taylor series as:

$$R(\eta )={\displaystyle \sum _{n=0}^N{\alpha }_n{\eta }^n},$$

(4)

where ${\alpha }_n$ is the expansion coefficient. In addition, the echo model in (1) can be rewritten as:

$$s\left(\tau ,\eta \right)={\sigma }_{\eta }\rho \left[\tau -\left({\displaystyle \sum _{n=0}^N{\alpha }_n{\eta }^n}\right)/c\right]rect\left(\frac{\eta }{T_a}\right)\cdot \exp \left\{-j\frac{2\pi }{\lambda }{\displaystyle \sum _{n=0}^N{\alpha }_n{\eta }^n}\right\},$$

(5)

The range and Doppler migrations are intuitively exhibited in (2) and (3). Despite the fact that the vessel target is generally not maneuvering, a long dwell time in the order of tens of seconds still leads to the complicated migrations. In order to analyze the compositions of the range and Doppler migrations, a simulation is conducted with the target motion parameters listed in

Table 1. Motion parameters.

Parameters	Value
Target position	(1000, 0, 0) m
Target velocity	(3.08, 5.35, 0) m/s
Target acceleration	(0.028, 0, 0) m/s2
Dwell time	105 s

, where these values conform with a typical vessel. It is noted that the all the parameters are described inside the east-north-up (ENU) coordinate system, where a fixed receiver is its origin. In response to the case of an extremely low SNR, the dwell time on the target is set to 105 s.

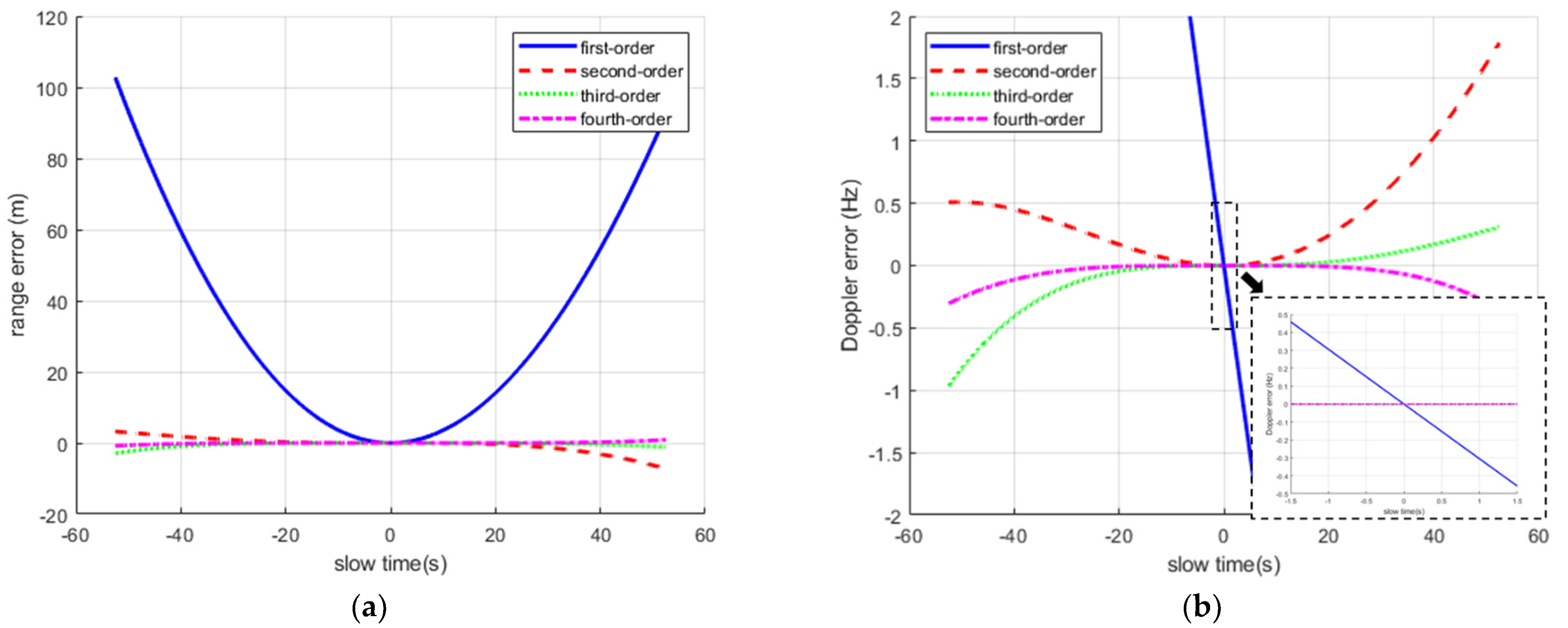
The bistatic range history is expanded into Taylor series with different orders. The fitting errors concerning the bistatic range and the Doppler frequency are presented in Figure 2. First, considering the BeiDou signal with the largest bandwidth (i.e., B3I), the passive radar provides a range resolution of 15 m [21]. Thus, it can be observed from Figure 2a that second-order expansion is sufficient for the bistatic range since the fitting error is smaller than the range resolution even the dwell time is lengthened into 105 s. Then, with respect to the Doppler error presented in Figure 2b, the Doppler resolution is associated with the coherent processing interval $T_{CPI}$, and its value is $1/T_{CPI}$. The $T_{CPI}$ for a typical vessel target is in the order of 2–3 s [13], and hereinafter the value is set equal to 3 s as a rigorous premise. It is seen from the curves in the figure that the fourth-order Taylor expansion cannot fulfill the model precision of the Doppler frequency. A high-order expansion is prerequisite under the condition of such a long dwell time, which goes to indicate an intricate Doppler migration. Moreover, the oscillation and rotation motions of the vessel target in practice can make the Doppler migration more complicated [14]. Finally, the corresponding Doppler error inside the coherent processing interval is shown in the bottom box of Figure 2b. It can be deduced that only the linear Doppler migration is considerable within the $T_{CPI}$ while the high-order components can be neglected.

3. Long-Time Optimized Integration for Vessel Target Detection

It is known that the scattering mechanism of a target is related to its aspect angle [24]. Owing to the motion of the vessel target, the variation of aspect angle causes the spatial decorrelation within the entire dwell time in the order of several tens of seconds. Thus, the long-time echo is no longer coherent. In addition, the range and Doppler migrations detailed in Section 2 increase the difficulty of the long-time integration. In order to obtain an adequate SNR for a reliable BeiDou-base passive radar vessel target detection performance, an optimized long-time integration method via the keystone transform and iterative optimization is proposed in this section.

Transforming the range-compressed signal in (5) into the fast-frequency domain, we have:

$$S_{pc}(f_{\tau },\eta )={\sigma }_{\eta }P(f_{\tau })rect\left(\frac{\eta }{T_a}\right)\exp \left\{-j2\pi \frac{f_{\tau }+f_c}{c}\left({\displaystyle \sum _{n=0}^N{\alpha }_n{\eta }^n}\right)\right\},$$

(6)

where $f_c$ is the carrier frequency, $P(\cdot )$ is the Fourier transform of $\rho (\cdot )$, and $f_{\tau }$ is the fast-frequency. The couplings between $f_{\tau }$ and $\eta$ in the exponent imply the range migration.

In order to correct the range walk, first, the keystone transform expressed as $\eta =f_c/\left(f_{\tau }+f_c\right){\eta }_m$ is applied to (6), where ${\eta }_m$ is the new slow-time variable. Replace ${\eta }_m$ with $\eta$, and the signal becomes:

$$S_{KT}(f_{\tau },\eta )={\sigma }_{\eta }P(f_{\tau })rect\left(\frac{\eta }{T_a}\right)\exp \left\{-j2\pi \frac{1}{c}\left({\displaystyle \sum _{n=0}^N{\alpha }_n\frac{f_c^n}{{\left(f_{\tau }+f_c\right)}^{n-1}}{\eta }^n}\right)\right\},$$

(7)

For the BeiDou-based passive radar, since $f_{\tau }\ll f_c$, the following approximation is valid:

$${\left(\frac{1}{f_{\tau }+f_c}\right)}^{n-1}\approx {\left(\frac{1}{f_c}\right)}^{n-1}-\left(n-1\right){\left(\frac{1}{f_c}\right)}^n{f}_{\tau },$$

(8)

Substituting (8) into (7), the signal becomes:

$$S_{KT}(f_{\tau },\eta )={\sigma }_{\eta }P(f_{\tau })rect\left(\frac{\eta }{T_a}\right)\exp \left\{-j2\pi \left({\displaystyle \sum _{n=0}^N\frac{f_c}{c}{\alpha }_n{\eta }^n-{\displaystyle \sum _{n=0}^N(n-1)\frac{f_{\tau }}{c}{\alpha }_n{\eta }^n}}\right)\right\},$$

(9)

It is concluded from Section 2 that the high-order (higher than second-order) couplings between $f_{\tau }$ and $\eta$ can be neglected as the introduced range migration is smaller than a range resolution. Then, the inverse Fourier transform is applied to (9). For the sake of intuitiveness, ${\alpha }_0$ is replaced with $R_0$, which denotes the bistatic range at the reference instant. In addition, we obtain:

$$s_{KT}\left(\tau ,\eta \right)={\sigma }_{\eta }\rho \left[\tau -\left(R_0-{\alpha }_2{\eta }^2\right)/c\right]rect\left(\frac{\eta }{T_a}\right)\cdot \exp \left\{-j\frac{2\pi }{\lambda }{\displaystyle \sum _{n=0}^N{\alpha }_n{\eta }^n}\right\},$$

(10)

It is observed that the undesired range curvature as well as the intricate Doppler migration still retains in (10), which need to be well handled by the subsequent steps.

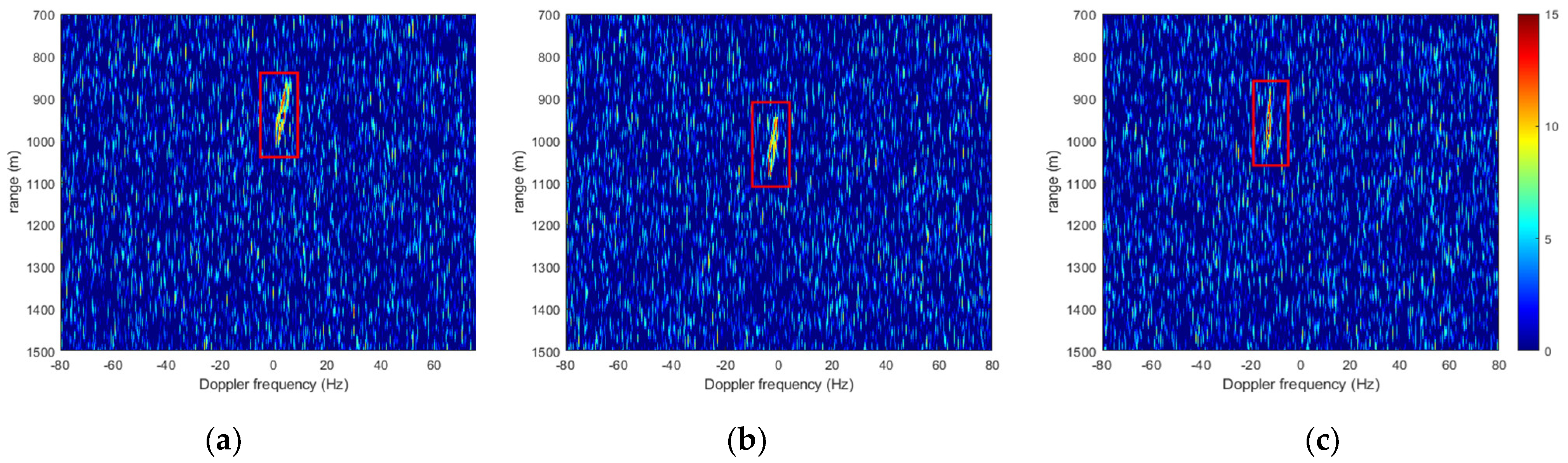
To cope with the noncoherence of the long-time echo, as the previous works [20,21,22], the hybrid integration strategy is performed. The entire echo is segmented into consecutive frames with the duration of $T_{CPI}$. The target’s reflectivity can be reasonably regarded as constant within the $T_{CPI}$. Thus, the coherent integration of each frame is achieved, followed by the noncoherent summation of the multiple frames. After the azimuth segmentation of the data in (10), the m-th ($m=-(M-1)/2,\dots ,(M-1)/2$,$M=T_a/T_{CPI}$) frame can be written as:

$$s_m\left(\tau ,\eta \right)={\sigma }_m\rho \left[\tau -\left(R_0-{\alpha }_2{\eta }^2\right)/c\right]rect\left(\frac{\eta -m{T}_{CPI}}{T_{CPI}}\right)\cdot \exp \left\{-j\frac{2\pi }{\lambda }{\displaystyle \sum _{n=0}^N{\alpha }_n{\eta }^n}\right\},$$

(11)

where ${\sigma }_m$ is the constant complex reflectivity inside the m-th frame.

Define a new slow-time variable as ${\eta }^{\prime }=\eta -m{T}_{CPI}$, and (11) can be rewritten as:

$$\begin{array}{ll}{s}_m\left(\tau ,{\eta }^{\prime }\right)=& {\sigma }_m\rho \left[\tau -\left(R_0-{\alpha }_2{\left({\eta }^{\prime }+m{T}_{CPI}\right)}^2\right)/c\right]\\ & rect\left(\frac{{\eta }^{\prime }}{T_{CPI}}\right)\exp \left\{-j\frac{2\pi }{\lambda }{\displaystyle \sum _{n=0}^N{\displaystyle \sum _{k=0}^n{\alpha }_n{C}_n^k}{\left({\eta }^{\prime }\right)}^{n-k}{\left(m{T}_{CPI}\right)}^k}\right\}\end{array},$$

(12)

where $C_n^k=\frac{n!}{k!(n-k)!}$ denotes the combination number.

Owing to the short frame duration, the range curvature inside each frame can be neglected. Besides, as analyzed in Section 2, only the linear Doppler migration is considered within such short frame duration. Thus, the m-th frame is approximated as:

$$\begin{array}{ll}{s}_m\left(\tau ,{\eta }^{\prime }\right)=& {\sigma }_m\rho \left[\tau -\left(R_0-{\alpha }_{2,0}{\left(m{T}_{CPI}\right)}^2\right)/c\right]\\ & rect\left(\frac{{\eta }^{\prime }}{T_{CPI}}\right)\exp \left\{-j\frac{2\pi }{\lambda }\left({\alpha }_{0,m}+{\alpha }_{1,m}{\eta }^{\prime }+{\alpha }_{2,m}{{\eta }^{\prime }}^2\right)\right\}\end{array},$$

(13)

where

$${\alpha }_{0,m}={\displaystyle \sum _{n=0}^N{\alpha }_n{\left(m{T}_{CPI}\right)}^n, {\alpha }_{1,m}={\displaystyle \sum _{n=1}^N{\alpha }_n{C}_n^1{\left(m{T}_{CPI}\right)}^{n-1}},} {\alpha }_{2,m}={\displaystyle \sum _{n=2}^N{\alpha }_n{C}_n^2{\left(m{T}_{CPI}\right)}^{n-2}},$$

(14)

denote the expansion coefficients pertaining to the m-th frame. Then the DC and DFR parameters of the m-th frame can be expressed as ${\overline{f}}_{dc,m}=-{\alpha }_{1,m}/\lambda$, ${\overline{f}}_{dr,m}=-2{\alpha }_{1,m}/\lambda$. Apparently, the Doppler parameters vary with the frame index m.

Then, to implement the coherent integration of the intraframe signal, the dechirp Fourier transform with a specific DFR value $f_{dr,m}$ expressed as

$$S_m\left(\tau ,f_{\eta };f_{dr,m}\right)={\displaystyle {\int }_{-\infty }^{+\infty }{s}_m\left(\tau ,\eta \right)\exp \left\{-j2\pi f_{\eta }\eta \right\}\exp \left\{-j\pi f_{dr,m}{\eta }^2\right\}}d\eta ,$$

(15)

is applied to (13), where $f_{\eta }$ is the Doppler frequency. The corresponding coherent integration result of (15) can be derived based on the principle of stationary phase (POSP) [25]. Converting the fast-time variable into bistatic range variable as $R=\tau \cdot c$, the result in range and Doppler (RD) domain is given as:

$$\begin{array}{ll}{S}_m(R,f_{\eta };f_{dr,m})=& {\sigma }_m\rho \left[R-\left(R_0+\frac{\lambda }{2}{f}_{dr,0}{\left(m{T}_{CPI}\right)}^2\right)\right]rect\left[\frac{f_{\eta }-{\overline{f}}_{dc,m}}{\left|{\overline{f}}_{dr,m}-f_{dr,m}\right|T_{CPI}}\right]\\ & \cdot \frac{1}{\sqrt{\left|{\overline{f}}_{dr,m}-f_{dr,m}\right|}}\exp \left\{-j\pi \frac{{\left(f_{\eta }-{\overline{f}}_{dc,m}\right)}^2}{{\overline{f}}_{dr,m}-f_{dr,m}}-j\frac{2\pi }{\lambda }{R}_{0,m}\right\}\end{array}$$

(16)

The Doppler migration inside frame is well corrected if the estimated DFR value exactly equals the actual value, i.e., $f_{dr,m}={\overline{f}}_{dr,m}$. With respect to this opportune DFR value, it is observed from (16) that the intraframe signal can be coherently integrated at the specific position $\left(R_0+\frac{\lambda }{2}{f}_{dr,0}{\left(m{T}_{CPI}\right)}^2,{\overline{f}}_{dc,m}\right)$ in the m-th RD plane.

Next, a noncoherent integration of multiple frames is performed to increase the integration time. Due to the fluctuant DC values and the residual range curvature, the coherent integrated peaks of multiple frames are located at different positions, which indicates that a compensation operation is indispensable. We take the central frame as the reference, and after range and Doppler shifts compensation, the multi-frame summation can be expressed as:

$$S(R,f_{\eta })=\frac{1}{M}{\displaystyle \sum _m\left|S_m\left(R+\frac{\lambda }{2}{f}_{dr,0}{\left(m{T}_{CPI}\right)}^2,f_{\eta }-\left({\overline{f}}_{dc,m}-{\overline{f}}_{dc,0}\right);f_{dr,m}\right)\right|},$$

(17)

The target echo is well concentrated after the above processes. However, since the vessel target is usually noncooperative, the multiple DC and DFR values are inaccessible. Thereby the coherent integration in (16) and the noncoherent integration in (17) cannot be simply implemented. Here, we achieve the long-time integration by transforming it into an optimization problem. To correct the Doppler migration of M frames, the DFR values of consecutive M frames are required. In addition, the DFR value of the central frame can be used to correct the residual range curvature in parallel. To compensate for the Doppler shifts, M − 1 decision variables representing the Doppler shift values are required. Therefore, we define the decision vector with 2M − 1 variables as:

$$f_p=\left({\widehat{f}}_{dr,-(M-1)/2},\dots ,{\widehat{f}}_{dr,(M-1)/2},\Delta {\widehat{f}}_{dc,-(M-1)/2},\dots ,\Delta {\widehat{f}}_{dc,-1},\Delta {\widehat{f}}_{dc,1},\dots ,\Delta {\widehat{f}}_{dc,(M-1)/2}\right),$$

(18)

where the ${\widehat{f}}_{dr,m}$ and $\Delta {\widehat{f}}_{dc,m}$ are the estimated DFR value and Doppler shift of the m-th frame. In addition, the corresponding integration result is:

$$S(R,f_{\eta };f_p)=\frac{1}{M}\left\{{\displaystyle \sum _{m\ne 0}^{}\left|S_m\left(R+\frac{\lambda }{2}{\widehat{f}}_{dr,0}{\left(m{T}_{CPI}\right)}^2,f_{\eta }-\Delta {\widehat{f}}_{dc,m};{\widehat{f}}_{dr,m}\right)\right|}+\left|S_0\left(R,f_{\eta };{\widehat{f}}_{dr,0}\right)\right|\right\},$$

(19)

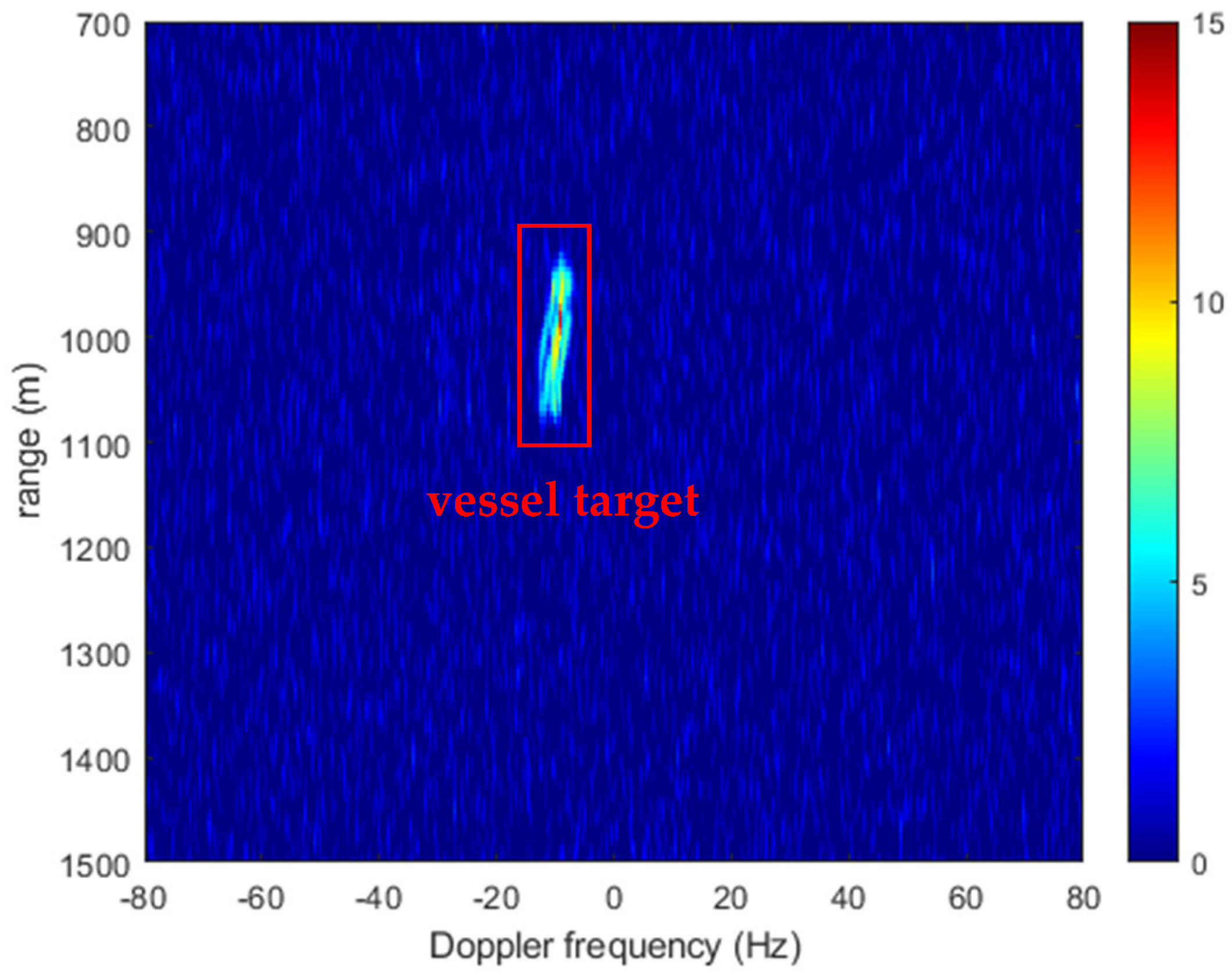
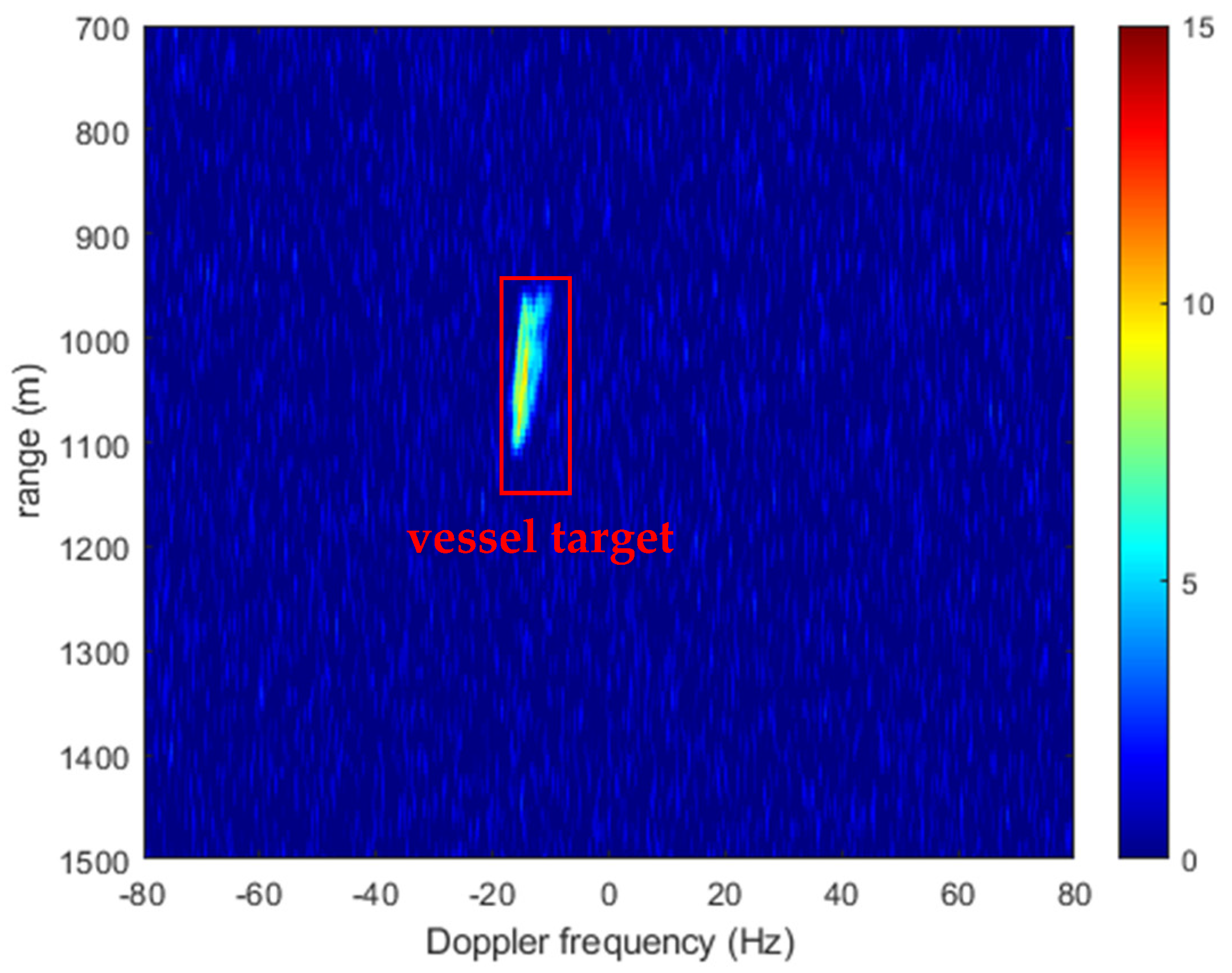
Taking the SNR as the objective function, the maximization optimization problem is expressed as:

$$\max F(f_p)=P_{signal}(f_p)/P_{noise}(f_p),$$

(20)

where $P_{signal}$ and $P_{noise}$ are the signal power and noise power of the integration result presented in (19). In practice, the signal power is estimated as the peak power contributed by the vessel target of the integrated result, and the noise power is evaluated by the mean power of the region containing the noise contribution only.

To solve this optimization problem, an evolutionary algorithm named particle swarm optimization (PSO) [26] is employed. It is a population-based stochastic optimization algorithm, which is inspired by the behavior of bird flocking. The PSO population with particles intends to search for the optimized solution by updating their positions. After the random population initialization, each particle will fly toward the direction guided by its personal best (pBest) and the global best (gBest). As a result, all the particles will converge to a specific point, whose position represents the optimized solution. The procedure of the PSO-based long-time integration is given in Algorithm 1. In theory, the components of optimized solution are the actual Doppler shift and DFR values. Thus, the echo energy can be completely gathered, which is able to provide an integration result in RD domain with maximum SNR.

Algorithm 1 Long-time optimized integration method
Input:	M signal frames after keystone transform
Output:	Actual Doppler shift and DFR values of the M frames
1.	Model the optimization problem as given in (20).
2.	Initialize the population size I, generation number G, search space $S^{2M-1}$.
3.	Randomly initialize ${\mathrm{f}}_{\mathrm{p},i}$ of the i-th particle in $S^{2M-1}$.
4.	Evaluate the initial objective value of the function $F_i({\mathrm{f}}_{\mathrm{p},i})$.
5.	Initialize the personal archive and global archive.
6.	For g = 1 to G
7.	Select gBest from global archive.
8.	Adjust iteration parameters.
9.	For i = 1 to I
10.	Select pBest from personal archive.
11.	Update velocity and position of the i-th particle.
12.	Evaluate the objective value $F_i({\mathrm{f}}_{\mathrm{p},i})$.
13.	Update personal archive.
14.	Update global archive.
15.	End For
16.	End For
17.	Return particle position.

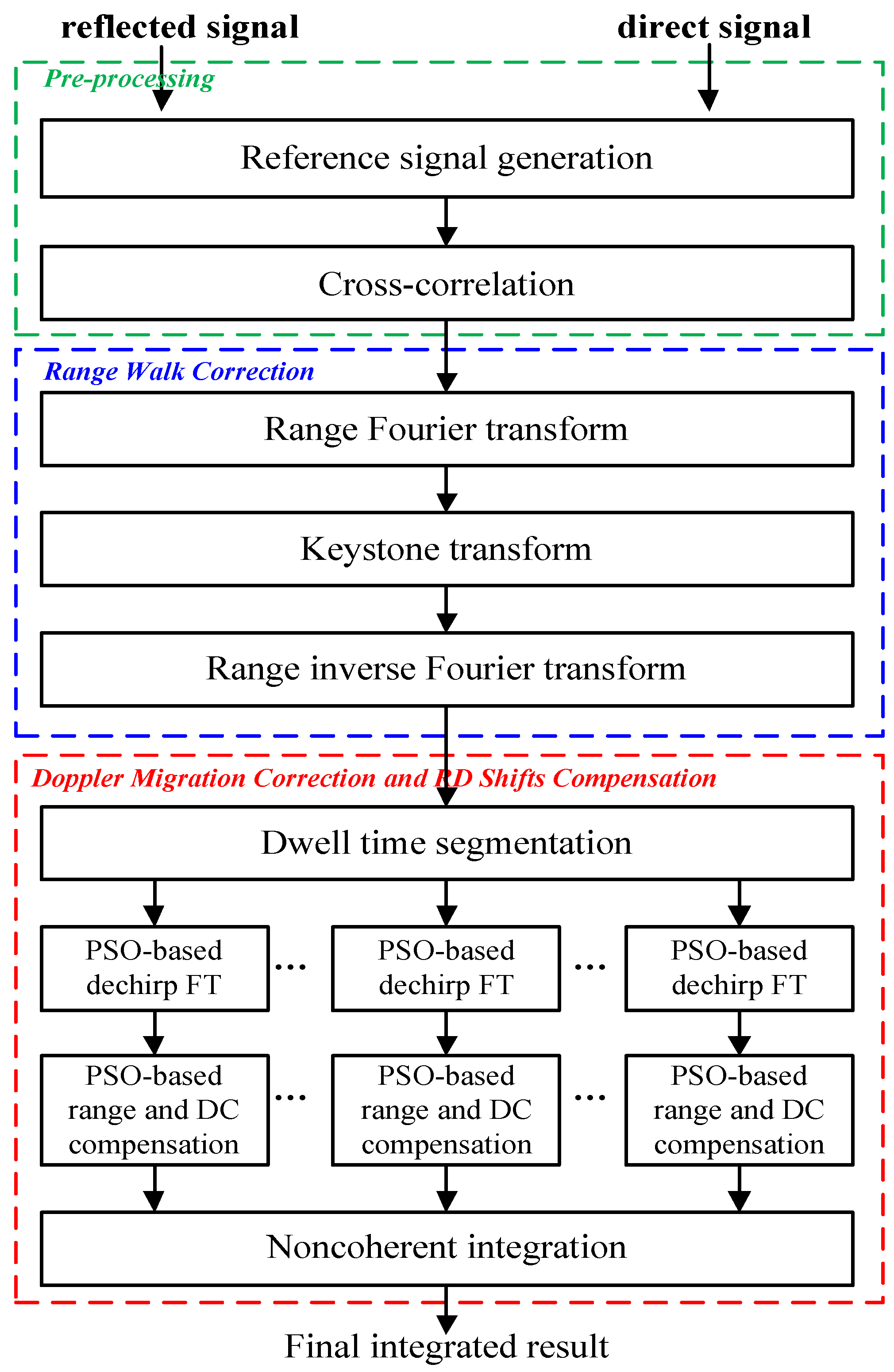
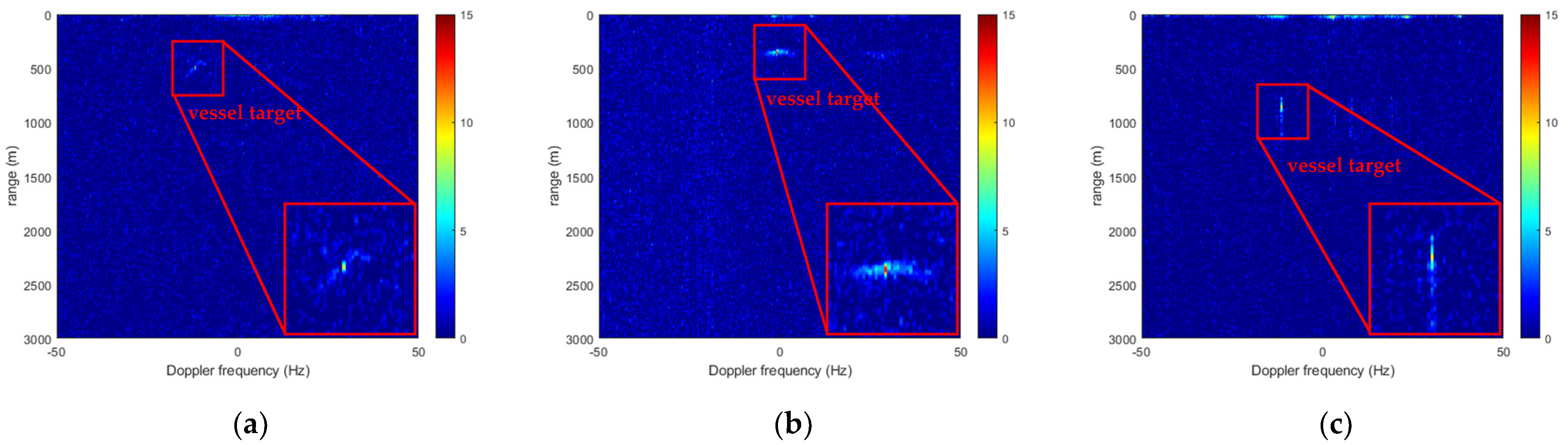
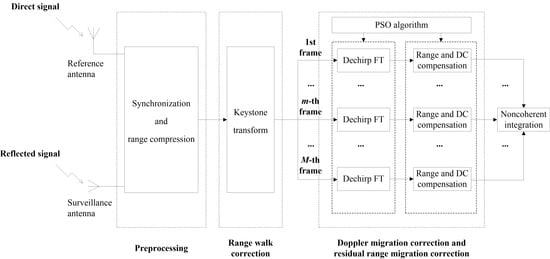
In summary, the mentioned problems are well solved after the procedures, providing an effective target echo integration result for the BeiDou-based passive radar vessel target detection. The flowchart of the proposed integration method is shown in Figure 3.

4. Results

In this section, simulated and experimental results are presented to illustrate the proposed optimized long-time integration method and verify its effectiveness on the BeiDou-based passive radar vessel target detection.

4.1. Simulated Results

In the simulation, a point-like vessel target is considered in the surveillance area. As shown in Figure 4, the target consists of twenty point scatterers, where two adjacent point scatterers are 10 m apart. The receiver is fixed at origin of the Cartesian reference system, and the motion parameters of the vessel target stay the same as those in Table 1. With respect to the opportunistic transmitter, the corresponding parameters are in agreement with those in the experiment presented in the next subsection. The BeiDou signal with chip-rate of 10.23 MHz is considered to be recorded by the fixed receiver. The trajectory of the satellite transmitter is generated according to the actual ephemeris parameters of the BeiDou satellite C41 in medium Earth orbit (MEO). The dwell time on the target is set to be 105 s in the simulation as an extreme condition, and the sampling rate is 50 MHz. An adaptive Gaussian noise occupying in the useful signal bandwidth is considered as the disturbance background. In order to illustrate the overall process of the proposed method, the SNR after the range compression is about −22 dB, where the target detection is still a challenging task.

After the range compression and the keystone transform, the entire echo is segmented into consecutive 35 frames with the coherent processing interval of 3 s. Figure 5 gives the coherent integration results of the first, central, and last frames when the dechirp Fourier transform is performed with their actual DFR values. Hereinafter, the color scale is in dB, where 0 dB represents mean noise power. In the three maps, the vessel target is highlighted by the red rectangles. It can be observed that the target energy over a single frame cannot provide a credible detection performance. It implies the necessity of the subsequent combination of the multiple frames, which helps to reduce the noise fluctuation. In addition, the target is located at different bistatic ranges in these RD maps as a result of the residual range curvature after the keystone transform. In addition, the difference in Doppler frequency between different frames is also evident from the maps. Thus, the range and Doppler compensations are requisite before multi-frame integration, which squares with the analyses in Section 2 and Section 3.

Then, the long-time integration based on PSO is performed. After iterative optimization, the DFR values of multiple frames are obtained, implementing the well coherent integration of frames. The DFR value of the central frame is simultaneously used to correct the residual range curvature. In addition, the Doppler shifts are obtained concurrently, effectively realizing the Doppler compensation and the subsequent noncoherent integration. The final integrated RD map is presented in Figure 6. The strong peak shows that the signal energy is well gathered via the proposed procedure and offers a reliable vessel target detection capability for the BeiDou-based passive radar.

Then, the comparison of the target detection performance between the proposed method and the existing method is carried out. The main steps of the existing method in [21] comprise the Fourier transform (FT) and the target motion compensation (TMC). After performing the existing method on the same simulated data, the corresponding result in the RD domain is shown in Figure 7. Owing to the relatively large SNR of the original target echo, the vessel is also visible in this RD map. To compare the two integrated results intuitively, the range and Doppler cross-sections of the two RD maps in Figure 6 and Figure 7 around their peaks are given in Figure 8. The legend ‘KT+PSO’ denotes the proposed method, and ‘FT+TMC’ denotes the existing method. It is observed that the final SNR provided by the proposed method is larger than that obtained by the existing method (more than 3 dB). That is because only the low-order range and Doppler migrations can be corrected via the existing method, whereas the intricate migrations (including the high-order terms) are able to be compensated by means of the proposed method. Thus, the proposed method provides a better vessel detection performance than the existing method.

Finally, the vessel detection performance of the proposed method is evaluated via the Monte Carlo simulations. The false alarm probability is set as ${10}^{-4}$. The tested SNRs of the range-compressed data are set as [−50:1:−10] dB, and the other parameters stay the same as above. After the Monte Carlo simulations, the detection probability via the proposed method is shown in Figure 9 (see the red curve). Meanwhile, the target detection is also performed via the existing method in [21]. The detection curve is simultaneously shown in Figure 9 (see the blue curve). Apparently, the proposed method shows a superior detection probability owing to its ability to compensate for the intricate range and Doppler migrations. Thus, it provides the capability to detect a vessel target with a smaller RCS or a larger detection distance.

4.2. Experimental Results

A maritime experiment using BeiDou satellite as opportunistic transmitter was conducted at Lianyungang Port in China. As the authors know, this is the world’s first BeiDou-based passive radar vessel target detection experiment. As shown in Figure 10a, during the data acquisition, the passive receiver was placed in the coastal area. The receiver is equipped with two antennas (i.e., reference antenna and surveillance antenna), severally recording the direct signal and the reflected signal from the BeiDou satellites. Both of the antennas provide the gain of 5 dB. For the verification purpose, a large container vessel [see Figure 10b] was designedly treated as the target of opportunity.

As presented in the introduction, the signals from multiple BeiDou in view can simultaneously be collected by the receiver. The signal from a specific satellite can be extracted via the matched filter since the code division multiple access (CDMA) technique is employed in BeiDou system. Hereinafter, the B3I signals transmitted from BeiDou satellite C41 are extracted and processed, and the corresponding experimental parameters are listed in

Table 2. Experimental parameters.

Parameters	Value
Satellite number	C41
Satellite orbit	Medium Earth orbit
Signal type	B3I
Carrier frequency	1268.520 MHz
Signal chip rate	10.23 MHz
Sampling rate	50 MHz
Equivalent PRI	1 ms

.

In order to demonstrate the long-time integration method, a data stream of 105 s is chosen from the entire acquisition, which is in keeping with the long dwell time in the simulation After the range compression, the data of the first 5 s in bistatic range and slow-time domain are presented in Figure 11. The visible peak along the zero bistatic range line is the compressed direct signal recorded in the surveillance antenna. By contrast, it is observed that the vessel target is still invisible after the range compression due to the extremely low SNR, illustrating the necessity of long-time integration processing.

To maximum the SNR, the long-time integration based on PSO is performed on the range-compressed data. The entire signal is still segmented into 35 frames with frame duration of 3 s. It should be pointed out here that, since the direct signal simultaneously exists in the surveillance antenna, if the PSO-based integration processing is directly performed, the obtained decision vector after PSO will correspond to the Doppler parameters of the direct signal. It can be observed that the direct signal is certainly located at zero bistatic range line, and it should be a single-frequency signal along the azimuth direction. Thus, the direct signal will be integrated at (0 m, 0 Hz) in the RD domain if the proposed method is directly performed, where the obtained decision vector is the zero vector. By contrast, the target energy is still diffused with this decision vector. In order to suppress the interference from the direct signal on the vessel target detection, in this paper, we take advantage of the certain position of the direct signal in the RD domain. During the data processing, the direct signal along the zero bistatic range line and zero Doppler frequency line in the RD domain is firstly filtered out to remove its influence. In addition, then the integrating processing is performed on the data without the direct signal. As a result, the obtained peak in the integrated map is completely contributed by the moving vessel target, which conduces to provide a reliable target detection performance.

After iterative optimization, the long-time integration result in RD domain is shown in Figure 12. The visible points located at the zero range line are generated by the direct signal, which is retained to show the difference between the vessel and the direct signal. More importantly, the vessel target can be apparently observed in the red rectangle. For sake of better visualization, the zoom of the region containing the target is presented in the bottom box. The strong peak demonstrates the effectiveness of the proposed long-time integration method. The final SNR of the vessel target reaches 14.4 dB, which provides a reliable target detection performance. Finally, the range profile around the peak of Figure 12 is depicted in Figure 13. To intuitively demonstrate the superiority of the PSO-based integration, the integration is also performed by the conventional method based on the Fourier transform and directly noncoherent summation without any compensation, and the corresponding range profile is also presented in Figure 13. It is observed that the PSO operation provides a conspicuous SNR improvement, proving the necessity of the PSO-based dechirp Fourier transform and the PSO-based RD compensation.

In order to make full use of the experimental data and verify the proposed method as comprehensively as possible, the signals pertaining to different BeiDou satellites have been processed. During the maritime experiment, the transmitted signals from the other BeiDou satellites C27, C38, and C40 have simultaneously been recorded by the receiver. It is pointed out that the BeiDou system is a hybrid constellation. The satellites C27 and C41 are in MEO, while C38 and C40 are in inclined geosynchronous orbit (IGSO). After the matched filtering, the signal pertaining to the specific satellite can be extracted, followed with the proposed long-time integration processing. The corresponding integration results in RD domain referring to the other satellites are presented in Figure 14. It is observed from these maps that the target echoes are all well integrated, illustrating the effectiveness of the proposed method. The different amplitudes of the same vessel are also observed in Figure 12 and Figure 14, which is due to the variant target RCS by different bistatic geometries. In addition, the vessel is located at different positions in these maps. The different range and Doppler parameters pertaining to the multiple satellite transmitters can be utilized to obtain more information of the vessel. However, this is beyond the scope of this paper, and it will be the subject of our future investigations.

5. Discussion

According to Figure 9, the vessel target with SNR higher than −32 dB (after range compression) can be reliably detected by the BeiDou-based passive radar via the method proposed in this paper. Under the same circumstance, the existing method only ensures an effective vessel detection with target SNR higher than −29 dB. This is owing to the fact that the existing method only enables the accurate corrections of the first- and second-order range migration and the first-order Doppler migration over the entire integration time. The integration time in effect is limited. By contrast, the high-order migrations are considered and can be corrected via the proposed method. Thus, if the integration time is further lengthened, the superiority of the proposed method can be more remarkable. The proposed method is more meaningful for the condition where a vessel target with a small RCS or a large distance is intended to be detected. However, the improved detection performance of the proposed method is realized at the expense of a heavy computational burden. Therefore, the real-time processing of the BeiDou-based passive via the proposed method can be hardly achieved.

In addition, this paper only focuses on the bistatic geometry of the BeiDou-based passive radar, where only a satellite is considered as the transmitter of opportunity. Since any point on the Earth is assured to be simultaneously illustrated by multiple BeiDou satellites from different angles, the BeiDou-based passive radar is inherently a multistatic system. The multistatic geometry can be utilized to obtain more target information (such as its position, velocity, etc.). In addition, the combination of the multistatic echoes conduces to improve the vessel target detection performance. This will be the subject of the future investigations.

6. Conclusions

The paper proposes a vessel target detection method for BeiDou-based passive radar. The extremely low power density reaching the Earth from the BeiDou satellite makes the long-time integration of target echo essential. To cope with the range walk caused by target motion, the keystone transform is applied. Then, to integrate the signal along the azimuth direction, the residual range curvature, intricate Doppler migration, and noncoherent characteristic need to be properly handled. The noncoherence issue is solved by the hybrid integration strategy, while the migrations are corrected via the PSO-based long-time integration with multiple DC and DFR values as the decision variables. With the optimized DFR values, the Doppler migration inside frame is corrected and the coherent integration of each frame is effectively achieved in RD domain. The range curvature can be simultaneously removed in the step. With the optimized DC shifts, the Doppler migrations between frames are compensated, implementing the alignment of multiple frames. The noncoherent summation of compensated RD maps provides a higher SNR and allows an effective target detection performance. Simulated and experimental results demonstrate the capability of the proposed method.