Retrieval of Water Quality from UAV-Borne Hyperspectral Imagery: A Comparative Study of Machine Learning Algorithms
Abstract
:1. Introduction
2. Materials and Methods
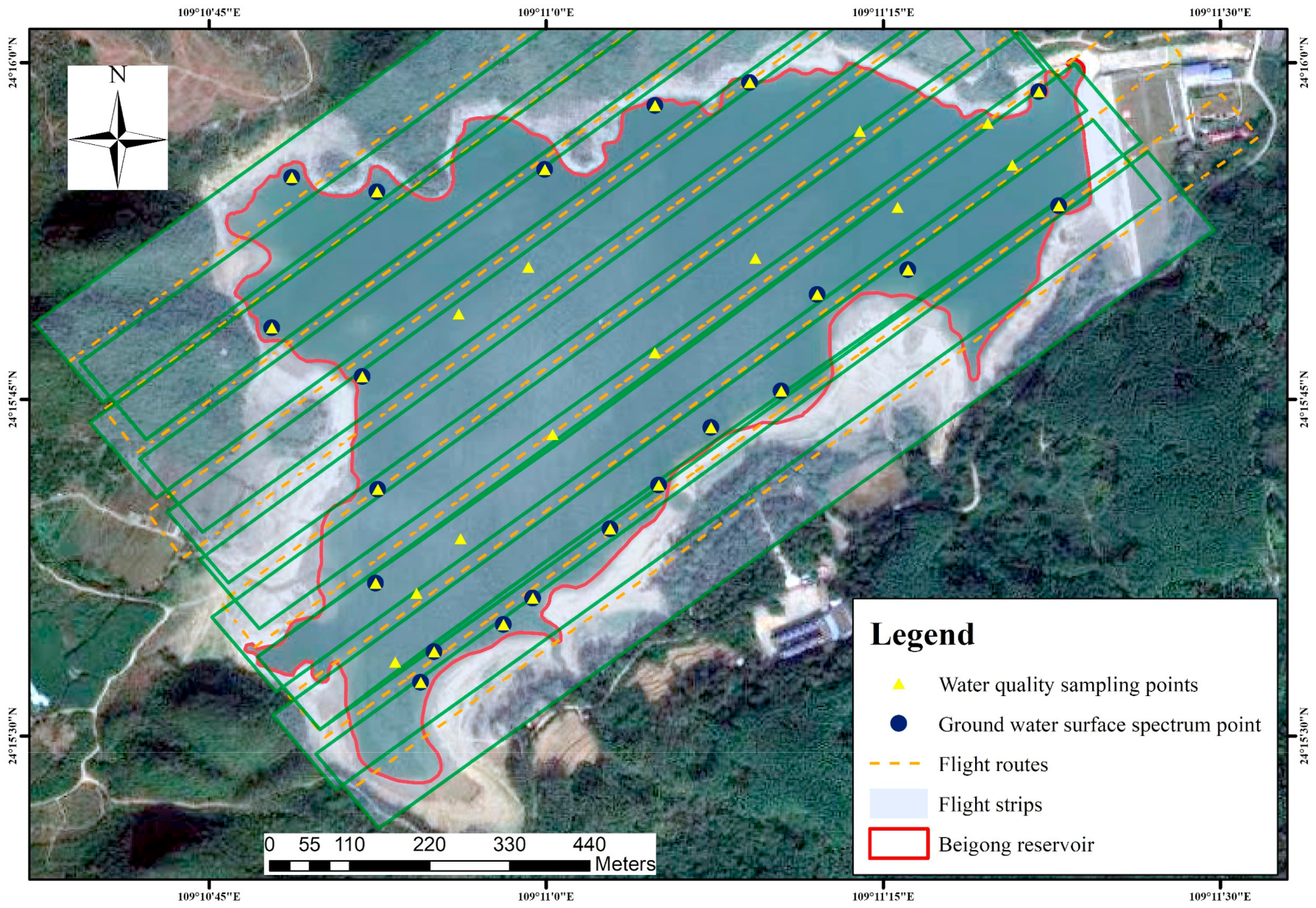
2.1. Study Area
2.2. Data Collection
2.3. Method
2.3.1. Machine Learning Algorithms Used for the Estimation of Water Quality Parameters
Adaboost Regression (ABR)
Gradient Boost Regression tree (GBRT)
Extreme Gradient Boosting Regression (XGBR)
Catboost Regression (CBR)
Random Forest (RF)
Extremely Randomized Trees (ERT)
Support Vector Machine (SVM)
Multi-Layer Perceptron Regression (MLPR)
Elastic Net (EN)
2.3.2. Model Evaluation
3. Results
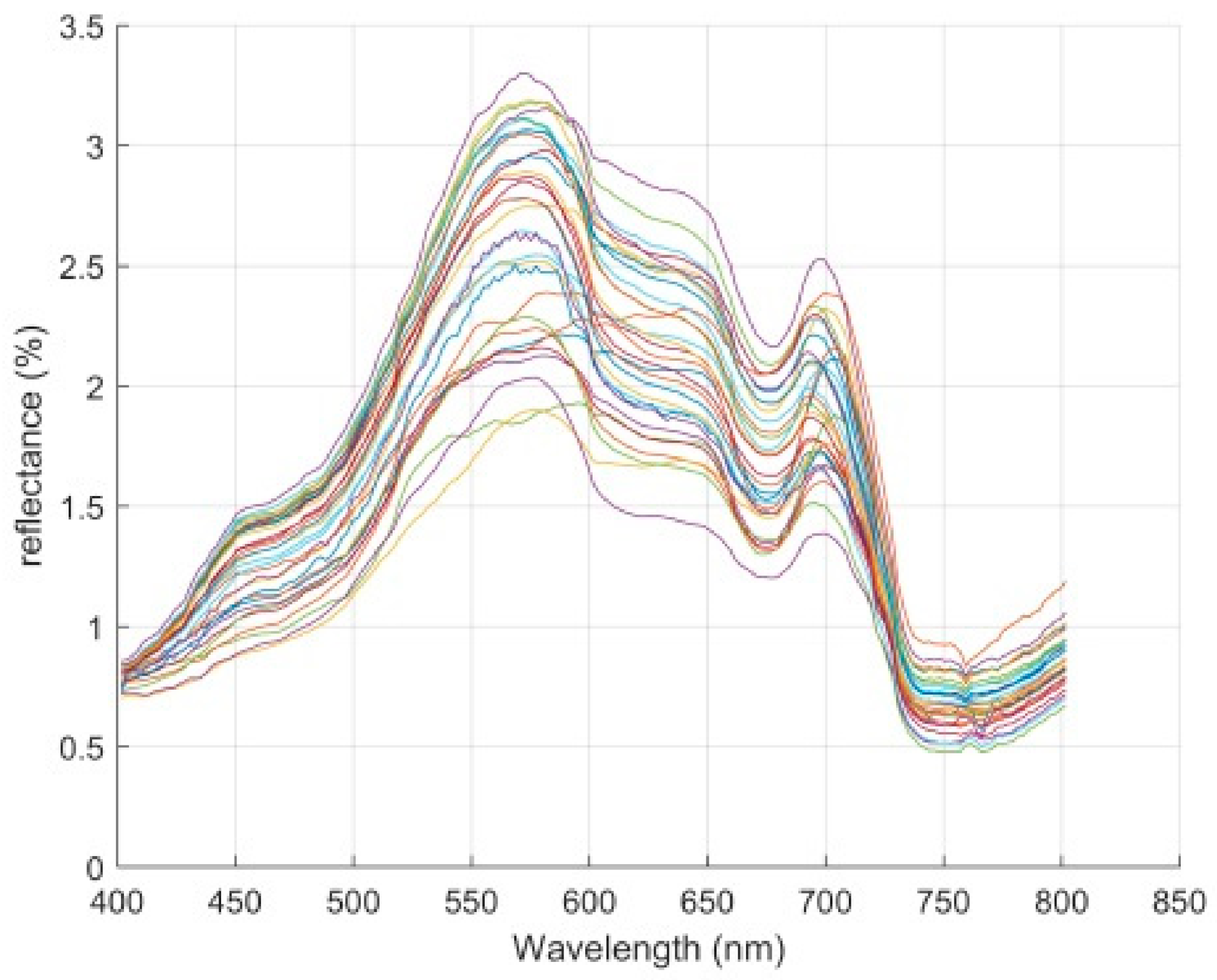
3.1. Spectral Analysis
3.2. Hyperparameters for the Machine Learning Algorithms
3.3. Retrieval Results for Different Water Quality
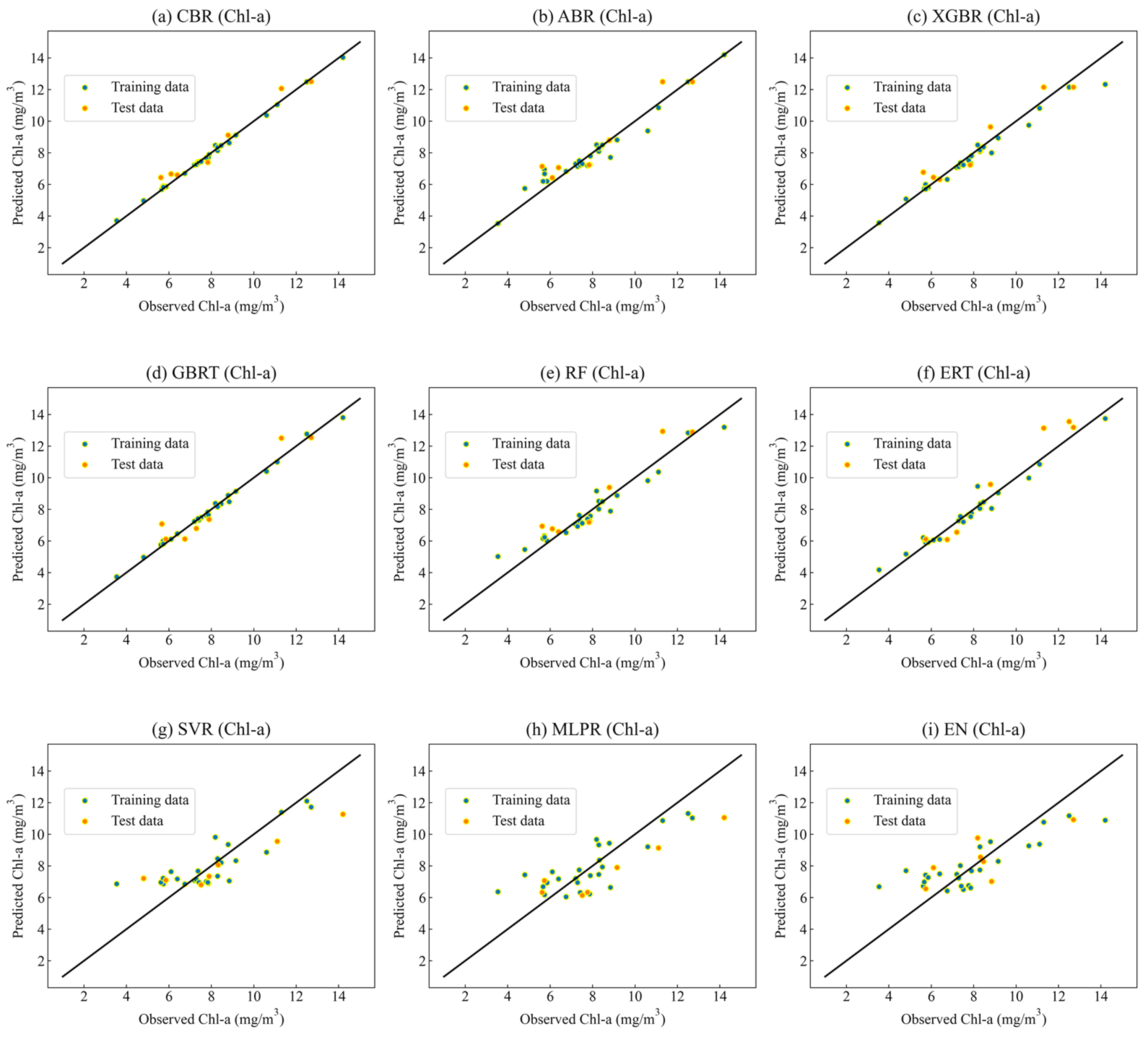
3.3.1. Retrieval Results for Chl-a
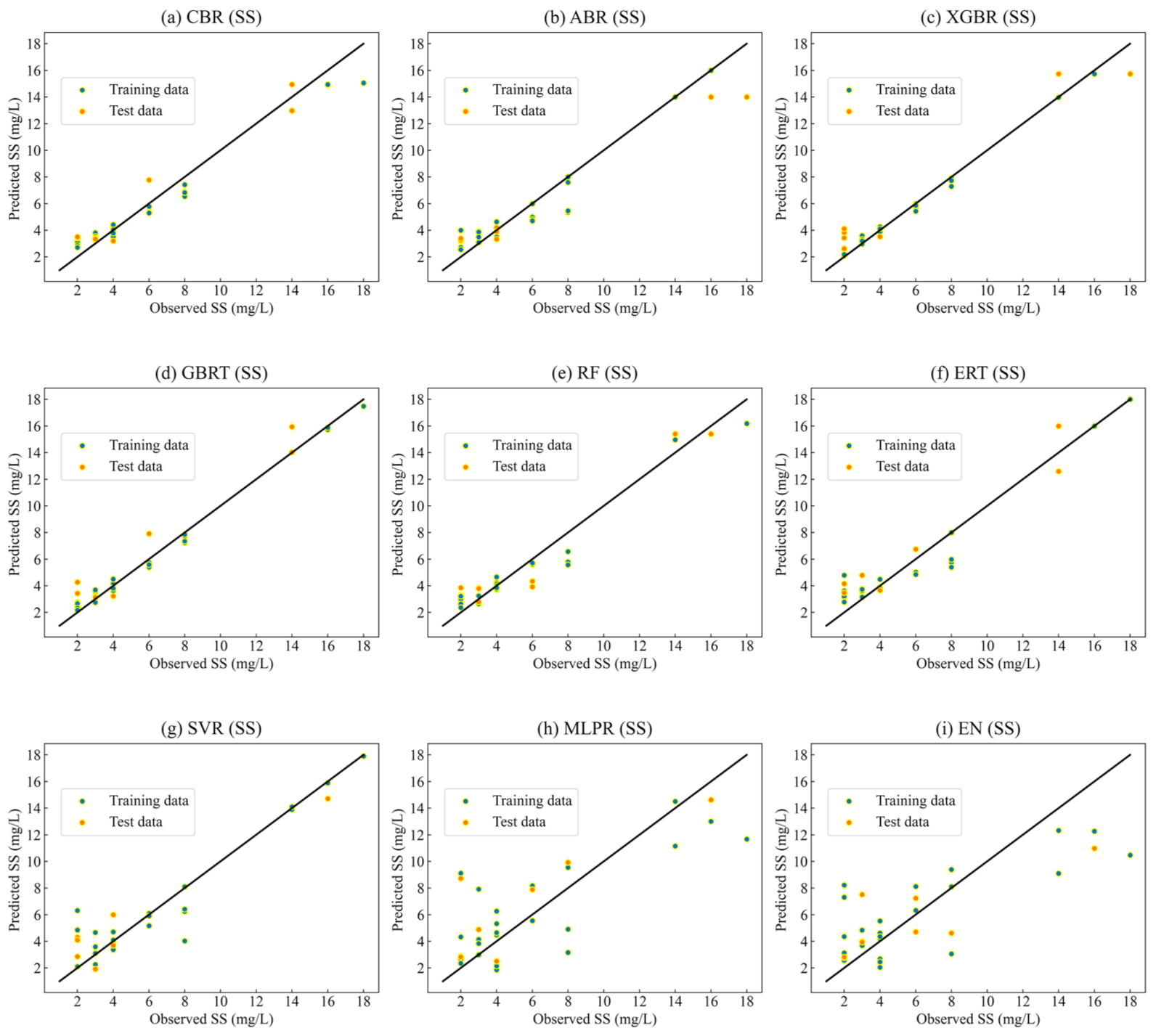
3.3.2. Retrieval Results for SS
4. Discussion
5. Conclusions
- The prediction performance of different machine learning algorithms, including CBR, XGBR, GBRT, ABR, ERT, RF, SVR, MLPR, and EN, in predicting water quality were compared. The overall prediction accuracy of the tree-based models were higher than that of the other three traditional machine learning models.
- Two water quality parameters, including Chl-a and SS, were analyzed with different machine learning models. For the prediction of Chl-a, the R2 values of several models ranged from 0.58 to 0.96; the RMSE ranged from 0.53 to 1.75 mg/m3; and the MAE value ranged from 0.47 to 1.6 mg/m3. Among them, the CBR model had the highest prediction accuracy and the XGBR model had the second-highest prediction accuracy. For the prediction of SS, the R2 values of the nine models ranged from 0.59 to 0.94; the RMSE ranged from 1.2 to 2.97 mg/L; and the MAE value ranged from 1.11 to 2.46 mg/L. The prediction accuracy of the CBR model was the highest and the prediction accuracies of the XGBR and RF models were lower than that of the CBR. Notably, the CBR model showed stable and satisfactory performance for predicting water quality parameters, including Chl-a and SS.
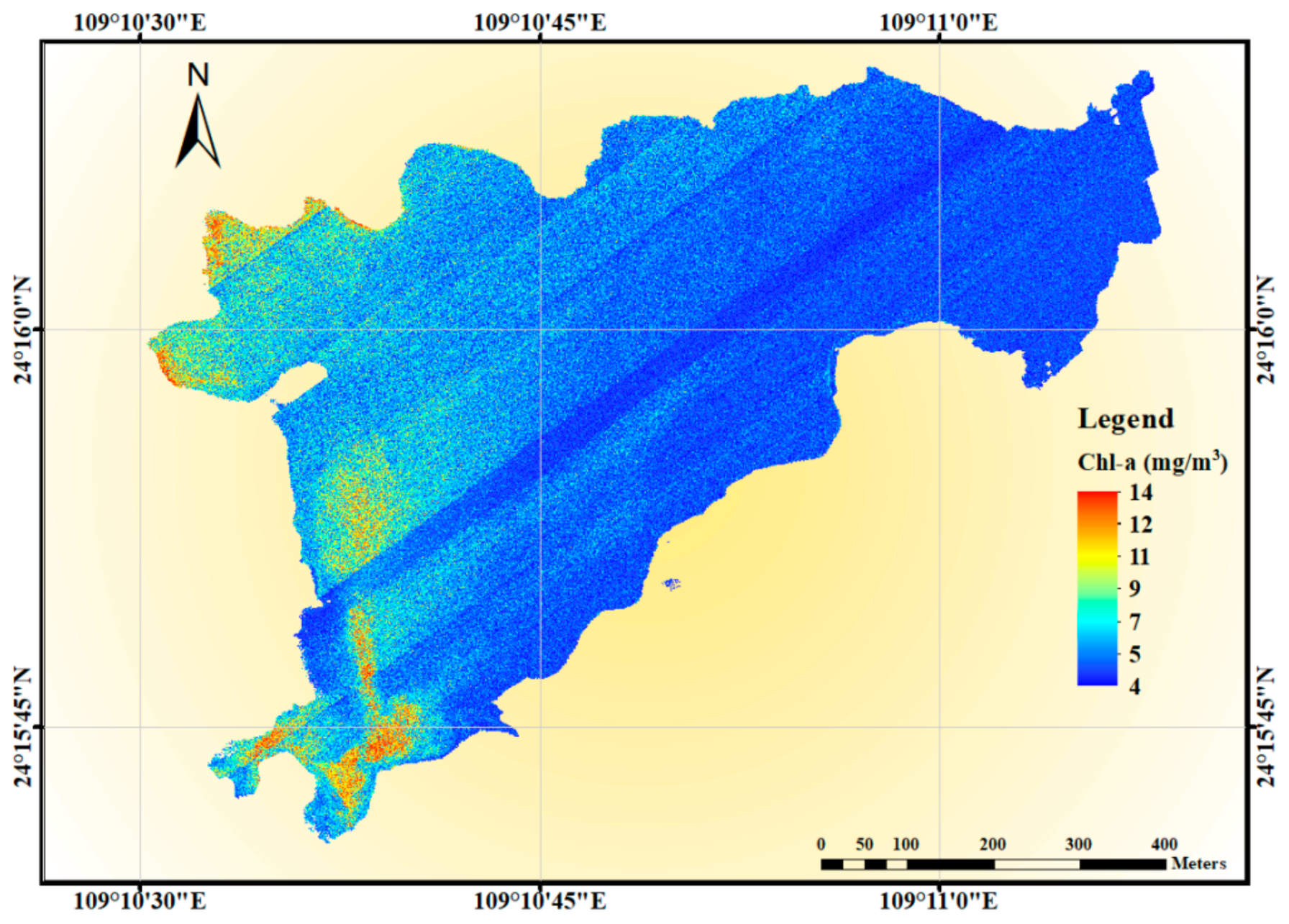
- The water quality distribution map was generated based on the UAV-borne hyperspectral data and machine learning algorithms, which can be used for large-scale and continuous inland water quality monitoring. From the water quality parameter inversion map, we observed that the pollution degree of SS in the west part of Beigong Reservoir was much higher than that in the east part. The areas with the highest Chl-a concentration mainly existed in the southern part of Beigong Reservoir and near the shore area. The management can monitor the water quality from the inversion map, improving the efficiency of water quality maintenance and saving management costs.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, Y.; Liu, D.; Xiao, W.; Zhou, P.; Tian, C.; Zhang, C.; Du, J.; Guo, H.; Wang, B. Coastal Eutrophication in China: Trend, Sources, and Ecological Effects. Harmful Algae 2021, 107, 102058. [Google Scholar] [CrossRef] [PubMed]
- Ding, Y.; Zhao, J.; Peng, W.; Zhang, J.; Chen, Q.; Fu, Y.; Duan, M. Stochastic Trophic Level Index Model: A New Method for Evaluating Eutrophication State. J. Environ. Manag. 2021, 280, 111826. [Google Scholar] [CrossRef] [PubMed]
- Sun, F.; Mu, Y.; Leung, K.M.Y.; Su, H.; Wu, F.; Chang, H. China Is Establishing Its Water Quality Standards for Enhancing Protection of Aquatic Life in Freshwater Ecosystems. Environ. Sci. Policy 2021, 124, 413–422. [Google Scholar] [CrossRef]
- Moses, W.J.; Gitelson, A.A.; Perk, R.L.; Gurlin, D.; Rundquist, D.C.; Leavitt, B.C.; Barrow, T.M.; Brakhage, P. Estimation of Chlorophyll-a Concentration in Turbid Productive Waters Using Airborne Hyperspectral Data. Water Res. 2012, 46, 993–1004. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Birtwell, I.K.; Farrell, M.; Jonsson, A. The Validity of Including Turbidity Criteria For Aquatic Resource Protection in Land Development Guideline (Pacific and Yukon Region). In Canadian Manuscript Report of Fisheries and Aquatic Sciences; Fisheries and Oceans Canada: Ottawa, ON, Canada, 2008. [Google Scholar]
- Bierman, P.; Lewis, M.; Ostendorf, B.; Tanner, J. A Review of Methods for Analysing Spatial and Temporal Patterns in Coastal Water Quality. Ecol. Indic. 2011, 11, 103–114. [Google Scholar] [CrossRef]
- Huang, W.; Chen, S.; Yang, X.; Johnson, E. Assessment of Chlorophyll-a Variations in High- and Low-Flow Seasons in Apalachicola Bay by MODIS 250-m Remote Sensing. Environ. Monit. Assess. 2014, 186, 8329–8342. [Google Scholar] [CrossRef]
- Doña, C.; Chang, N.-B.; Caselles, V.; Sánchez, J.M.; Camacho, A.; Delegido, J.; Vannah, B.W. Integrated Satellite Data Fusion and Mining for Monitoring Lake Water Quality Status of the Albufera de Valencia in Spain. J. Environ. Manag. 2015, 151, 416–426. [Google Scholar] [CrossRef] [Green Version]
- Du, C.; Li, Y.; Wang, Q.; Liu, G.; Zheng, Z.; Mu, M.; Li, Y. Tempo-Spatial Dynamics of Water Quality and Its Response to River Flow in Estuary of Taihu Lake Based on GOCI Imagery. Environ. Sci. Pollut. Res. 2017, 24, 28079–28101. [Google Scholar] [CrossRef]
- Syariz, M.A.; Lin, C.-H.; Nguyen, M.V.; Jaelani, L.M.; Blanco, A.C. WaterNet: A Convolutional Neural Network for Chlorophyll-a Concentration Retrieval. Remote Sens. 2020, 12, 1966. [Google Scholar] [CrossRef]
- Rajesh, A.; Jiji, G.W.; Raj, J.D. Estimating the Pollution Level Based on Heavy Metal Concentration in Water Bodies of Tiruppur District. J. Indian Soc. Remote Sens. 2020, 48, 47–57. [Google Scholar] [CrossRef]
- Rostom, N.G.; Shalaby, A.A.; Issa, Y.M.; Afifi, A.A. Evaluation of Mariut Lake Water Quality Using Hyperspectral Remote Sensing and Laboratory Works. Egypt. J. Remote. Sens. Space Sci. 2017, 20, S39–S48. [Google Scholar] [CrossRef] [Green Version]
- Quan, Q.; Hao, Z.; Xifeng, H.; Jingchun, L. Research on Water Temperature Prediction Based on Improved Support Vector Regression. Neural Comput. Appl. 2020. [Google Scholar] [CrossRef]
- Leong, W.C.; Bahadori, A.; Zhang, J.; Ahmad, Z. Prediction of Water Quality Index (WQI) Using Support Vector Machine (SVM) and Least Square-Support Vector Machine (LS-SVM). Int. J. River Basin Manag. 2021, 19, 149–156. [Google Scholar] [CrossRef]
- Lu, H.; Ma, X. Hybrid Decision Tree-Based Machine Learning Models for Short-Term Water Quality Prediction. Chemosphere 2020, 249, 126169. [Google Scholar] [CrossRef]
- Najah Ahmed, A.; Binti Othman, F.; Abdulmohsin Afan, H.; Khaleel Ibrahim, R.; Ming Fai, C.; Shabbir Hossain, M.; Ehteram, M.; Elshafie, A. Machine Learning Methods for Better Water Quality Prediction. J. Hydrol. 2019, 578, 124084. [Google Scholar] [CrossRef]
- Sharafati, A.; Asadollah, S.B.H.S.; Hosseinzadeh, M. The Potential of New Ensemble Machine Learning Models for Effluent Quality Parameters Prediction and Related Uncertainty. Process. Saf. Environ. Prot. 2020, 140, 68–78. [Google Scholar] [CrossRef]
- Parsimehr, M.; Shayesteh, K.; Godini, K.; Bayat Varkeshi, M. Using Multilayer Perceptron Artificial Neural Network for Predicting and Modeling the Chemical Oxygen Demand of the Gamasiab River. Avicenna J. Environ. Health Eng. 2018, 5, 15–20. [Google Scholar] [CrossRef]
- Xiaojuan, L.; Mutao, H.; Jianbao, L. Remote Sensing Inversion of Lake Water Quality Parameters Based on Ensemble Modelling. E3S Web Conf. 2020, 143, 02007. [Google Scholar] [CrossRef]
- Tang, J.W.; Tian, G.L.; Wang, X.Y.; Wang, X.M.; Song, Q.J. The Methods of Water Spectra Measurement and Analysis I: Above-Water Method. J. Remote. Sens. 2004, 8, 37–44. [Google Scholar]
- Mobley, C.D. Estimation of the Remote-Sensing Reflectance from above-Surface Measurements. Appl. Opt. AO 1999, 38, 7442–7455. [Google Scholar] [CrossRef] [PubMed]
- Kelcey, J.; Lucieer, A. Sensor Correction of a 6-Band Multispectral Imaging Sensor for UAV Remote Sensing. Remote. Sens. 2012, 4, 1462–1493. [Google Scholar] [CrossRef] [Green Version]
- Qun’ou, J.; Lidan, X.; Siyang, S.; Meilin, W.; Huijie, X. Retrieval Model for Total Nitrogen Concentration Based on UAV Hyper Spectral Remote Sensing Data and Machine Learning Algorithms—A Case Study in the Miyun Reservoir, China. Ecol. Indic. 2021, 124, 107356. [Google Scholar] [CrossRef]
- He, J.; Lin, J.; Ma, M.; Liao, X. Mapping Topo-Bathymetry of Transparent Tufa Lakes Using UAV-Based Photogrammetry and RGB Imagery. Geomorphology 2021, 389, 107832. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, L.; Ren, H.; Liu, Y.; Zheng, Y.; Liu, Y.; Dong, J. Mapping Water Quality Parameters in Urban Rivers from Hyperspectral Images Using a New Self-Adapting Selection of Multiple Artificial Neural Networks. Remote Sens. 2020, 12, 336. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Xie, S.; Zhang, X.; Chen, C.; Guo, H.; Du, J.; Duan, Z. A Robust Multi-Band Water Index (MBWI) for Automated Extraction of Surface Water from Landsat 8 OLI Imagery. Int. J. Appl. Earth Obs. Geoinf. 2018, 68, 73–91. [Google Scholar] [CrossRef]
- Campos, J.C.; Sillero, N.; Brito, J.C. Normalized Difference Water Indexes Have Dissimilar Performances in Detecting Seasonal and Permanent Water in the Sahara–Sahel Transition Zone. J. Hydrol. 2012, 464–465, 438–446. [Google Scholar] [CrossRef]
- Ying, H.; Xia, K.; Huang, X.; Feng, H.; Yang, Y.; Du, X.; Huang, L. Evaluation of Water Quality Based on UAV Images and the IMP-MPP Algorithm. Ecol. Inform. 2021, 61, 101239. [Google Scholar] [CrossRef]
- Wei, L.; Huang, C.; Zhong, Y.; Wang, Z.; Hu, X.; Lin, L. Inland Waters Suspended Solids Concentration Retrieval Based on PSO-LSSVM for UAV-Borne Hyperspectral Remote Sensing Imagery. Remote Sens. 2019, 11, 1455. [Google Scholar] [CrossRef] [Green Version]
- Freund, Y. Boosting a Weak Learning Algorithm by Majority; AT&T Laboratories: Murray Hill, NJ, USA, 1995. [Google Scholar]
- Freund, Y.; Schapire, R.E. A Decision-Theoretic Generalization of On-Line Learning and an Application to Boosting. J. Comput. Syst. Sci. 1997, 55, 119–139. [Google Scholar] [CrossRef] [Green Version]
- Friedman, J.H. Greedy Function Approximation: A Gradient Boosting Machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Association for Computing Machinery. New York, NY, USA, 13 August 2016; pp. 785–794. [Google Scholar]
- Dong, W.; Huang, Y.; Lehane, B.; Ma, G. XGBoost Algorithm-Based Prediction of Concrete Electrical Resistivity for Structural Health Monitoring. Autom. Constr. 2020, 114, 103155. [Google Scholar] [CrossRef]
- Dorogush, A.V.; Ershov, V.; Gulin, A. CatBoost: Gradient Boosting with Categorical Features Support. arXiv 2018, arXiv:1810.11363. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Geurts, P.; Ernst, D.; Wehenkel, L. Extremely Randomized Trees. Mach. Learn 2006, 63, 3–42. [Google Scholar] [CrossRef] [Green Version]
- Cheng, H.; Shi, Y.; Wu, L.; Guo, Y.; Xiong, N. An Intelligent Scheme for Big Data Recovery in Internet of Things Based on Multi-Attribute Assistance and Extremely Randomized Trees. Inf. Sci. 2021, 557, 66–83. [Google Scholar] [CrossRef]
- Raghavendra, N.S.; Deka, P.C. Support Vector Machine Applications in the Field of Hydrology: A Review. Appl. Soft Comput. 2014, 19, 372–386. [Google Scholar] [CrossRef]
- Günther, F.; Fritsch, S. Neuralnet: Training of Neural Networks. R J. 2010, 2, 30. [Google Scholar] [CrossRef] [Green Version]
- Zou, H.; Hastie, T. Regression Shrinkage and Selection via the Elastic Net, with Applications to Microarrays. JR Stat. Soc. Ser. B 2004, 67, 301–320. [Google Scholar] [CrossRef] [Green Version]
- He, J.; Chen, Y.; Wu, J.; Stow, D.A.; Christakos, G. Space-Time Chlorophyll-a Retrieval in Optically Complex Waters That Accounts for Remote Sensing and Modeling Uncertainties and Improves Remote Estimation Accuracy. Water Res. 2020, 171, 115403. [Google Scholar] [CrossRef] [PubMed]
- Beck, R.; Zhan, S.; Liu, H.; Tong, S.; Yang, B.; Xu, M.; Ye, Z.; Huang, Y.; Shu, S.; Wu, Q.; et al. Comparison of Satellite Reflectance Algorithms for Estimating Chlorophyll-a in a Temperate Reservoir Using Coincident Hyperspectral Aircraft Imagery and Dense Coincident Surface Observations. Remote. Sens. Environ. 2016, 178, 15–30. [Google Scholar] [CrossRef] [Green Version]
- Soomets, T.; Uudeberg, K.; Jakovels, D.; Brauns, A.; Zagars, M.; Kutser, T. Validation and Comparison of Water Quality Products in Baltic Lakes Using Sentinel-2 MSI and Sentinel-3 OLCI Data. Sensors 2020, 20, 742. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Buma, W.G.; Lee, S.-I. Evaluation of Sentinel-2 and Landsat 8 Images for Estimating Chlorophyll-a Concentrations in Lake Chad, Africa. Remote Sens. 2020, 12, 2437. [Google Scholar] [CrossRef]
- Gholizadeh, M.H.; Melesse, A.M.; Reddi, L. A Comprehensive Review on Water Quality Parameters Estimation Using Remote Sensing Techniques. Sensors 2016, 16, 1298. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Huang, M.; Kim, M.S.; Delwiche, S.R.; Chao, K.; Qin, J.; Mo, C.; Esquerre, C.; Zhu, Q. Quantitative Analysis of Melamine in Milk Powders Using Near-Infrared Hyperspectral Imaging and Band Ratio. J. Food Eng. 2016, 181, 10–19. [Google Scholar] [CrossRef] [Green Version]

| Water Quality Parameters | Range | Average Value | Standard Deviation |
|---|---|---|---|
| Chl-a (n = 33) | 3.54~14.2 (mg/m3) | 8.03 | 2.32 |
| SS (n = 33) | 2~18 (mg/L) | 5.86 | 4.54 |
| Models | Hyperparameters | Meanings | Search Ranges | Optimal Values |
|---|---|---|---|---|
| CBR | Learning rate | Shrinkage coefficient of each tree | (0.01,1) | 0.26 |
| Max depth | Maximum depth of a tree | (1,10) | 4 | |
| Estimators | Number of trees | (100,1000) | 140 | |
| L2_leaf_reg | L2 regularization | (1,10) | 7 | |
| ABR | Learning rate | Shrinkage coefficient of each tree | (0.01,0.1) | 0.1 |
| Estimators | Number of trees | (0,200) | 90 | |
| XGBR | Learning rate | Shrinkage coefficient of each tree | (0.01,1) | 0.1 |
| Max depth | Maximum depth of a tree | (1,10) | 5 | |
| Estimators | Number of trees | (10,100) | 40 | |
| Subsample | Subsample ratio of training samples | (0.1,0.9) | 0.8 | |
| GBRT | Learning rate | Shrinkage coefficient of each tree | (0.010.1) | 0.05 |
| Estimators | Number of trees | (10,200) | 150 | |
| Subsample | Subsample ratio of training samples | (0.5,0.8) | 0.5 | |
| RF | Estimators | Number of trees | (1,100) | 70 |
| Min samples split | Minimum number of samples for nodes’ split | (1,10) | 2 | |
| ERT | Max depth | Maximum depth of a tree | (1,10) | 6 |
| Estimators | Number of trees | (0,300) | 200 | |
| SVR | C | Regularization parameter | (10,200) | 10 |
| Gamma | Kernel coefficient | (0.001,0.1) | 1 | |
| MLPR | Hidden layer size | The number of neurons in the ith hidden layer and the number of hidden layers | (21), (210) | (22) |
| EN | Alpha | The constant of the mixed penalty term | (0.0001,0.001,0.01,0.1,1,10) | 0.1 |
| Models | Hyperparameters | Meanings | Search Ranges | Optimal Values |
|---|---|---|---|---|
| CBR | Learning rate | Shrinkage coefficient of each tree | (0.01,1) | 0.1 |
| Max depth | Maximum depth of a tree | (1,10) | 7 | |
| Estimators | Number of trees | (100,1000) | 190 | |
| L2_leaf_reg | L2 regularization | (1,30) | 26 | |
| ABR | Learning rate | Shrinkage coefficient of each tree | (0.01,0.1) | 0.02 |
| Estimators | Number of trees | (0,200) | 120 | |
| XGBR | Learning rate | Shrinkage coefficient of each tree | (0.01,1) | 0.05 |
| Max depth | Maximum depth of a tree | (1,10) | 2 | |
| Estimators | Number of trees | (100,1000) | 200 | |
| GBRT | Learning rate | Shrinkage coefficient of each tree | (0.01,0.1) | 0.04 |
| Estimators | Number of trees | (10,200) | 100 | |
| Subsample | Subsample ratio of training samples | (0.5,0.9) | 0.8 | |
| RF | Estimators | Number of trees | (1,100) | 7 |
| Min samples split | Minimum number of samples for nodes’ split | (1,10) | 3 | |
| ERT | Max depth | Maximum depth of a tree | (1,10) | 4 |
| Estimators | Number of trees | (10,100) | 20 | |
| SVR | C | Regularization parameter | (10,200) | 100 |
| Gamma | Kernel coefficient | (0.001,10) | 1 | |
| MLPR | Hidden layer size | The number of neurons in the ith hidden layer and the number of hidden layers | (21,21), (28,28) | (23,23) |
| EN | Alpha | The constant of the mixed penalty term | (0.0001,0.001,0.01,0.1,1,10) | 0.1 |
| Models | Running Time (s) | Training Data Set | Test Data Set | ||||
|---|---|---|---|---|---|---|---|
| MAE (mg/m3) | RMSE (mg/m3) | R2 | MAE (mg/m3) | RMSE (mg/m3) | R2 | ||
| CBR | 0.46 | 0.09 | 0.12 | 1.00 | 0.47 | 0.53 | 0.96 |
| ABR | 0.15 | 0.37 | 0.54 | 0.94 | 0.65 | 0.82 | 0.89 |
| XGBR | 0.47 | 0.31 | 0.49 | 0.95 | 0.63 | 0.71 | 0.92 |
| GBRT | 0.06 | 0.13 | 0.16 | 0.99 | 0.67 | 0.80 | 0.90 |
| RF | 0.11 | 0.48 | 0.58 | 0.93 | 0.75 | 0.91 | 0.87 |
| ERT | 0.17 | 0.30 | 0.41 | 0.96 | 0.84 | 0.95 | 0.87 |
| SVR | 0.01 | 0.92 | 1.17 | 0.69 | 1.38 | 1.65 | 0.69 |
| MLPR | 0.66 | 1.08 | 1.29 | 0.63 | 1.60 | 1.75 | 0.62 |
| EN | 0.01 | 1.18 | 1.43 | 0.63 | 1.17 | 1.36 | 0.58 |
| Models | Running Time (s) | Training Data Set | Test Data Set | ||||
|---|---|---|---|---|---|---|---|
| MAE (mg/L) | RMSE (mg/L) | R2 | MAE (mg/L) | RMSE (mg/L) | R2 | ||
| CBR | 0.31 | 0.81 | 1.00 | 0.95 | 1.11 | 1.20 | 0.94 |
| ABR | 0.15 | 0.81 | 1.10 | 0.92 | 1.37 | 1.85 | 0.91 |
| XGBR | 0.51 | 0.22 | 0.29 | 0.99 | 1.50 | 1.64 | 0.93 |
| GBRT | 0.06 | 0.39 | 0.44 | 0.99 | 1.22 | 1.48 | 0.91 |
| RF | 0.02 | 0.86 | 1.11 | 0.93 | 1.23 | 1.39 | 0.93 |
| ERT | 0.03 | 0.85 | 1.17 | 0.93 | 1.41 | 1.54 | 0.90 |
| SVR | 0.12 | 0.84 | 1.44 | 0.90 | 1.42 | 1.57 | 0.89 |
| MLPR | 1.80 | 2.09 | 2.78 | 0.63 | 2.31 | 2.95 | 0.59 |
| EN | 0.01 | 2.12 | 2.91 | 0.60 | 2.46 | 2.97 | 0.55 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, Q.; Si, W.; Wei, L.; Li, Z.; Xia, Z.; Ye, S.; Xia, Y. Retrieval of Water Quality from UAV-Borne Hyperspectral Imagery: A Comparative Study of Machine Learning Algorithms. Remote Sens. 2021, 13, 3928. https://doi.org/10.3390/rs13193928
Lu Q, Si W, Wei L, Li Z, Xia Z, Ye S, Xia Y. Retrieval of Water Quality from UAV-Borne Hyperspectral Imagery: A Comparative Study of Machine Learning Algorithms. Remote Sensing. 2021; 13(19):3928. https://doi.org/10.3390/rs13193928
Chicago/Turabian StyleLu, Qikai, Wei Si, Lifei Wei, Zhongqiang Li, Zhihong Xia, Song Ye, and Yu Xia. 2021. "Retrieval of Water Quality from UAV-Borne Hyperspectral Imagery: A Comparative Study of Machine Learning Algorithms" Remote Sensing 13, no. 19: 3928. https://doi.org/10.3390/rs13193928
APA StyleLu, Q., Si, W., Wei, L., Li, Z., Xia, Z., Ye, S., & Xia, Y. (2021). Retrieval of Water Quality from UAV-Borne Hyperspectral Imagery: A Comparative Study of Machine Learning Algorithms. Remote Sensing, 13(19), 3928. https://doi.org/10.3390/rs13193928








