Automatic Detection of Impervious Surfaces from Remotely Sensed Data Using Deep Learning

Abstract

The large scale quantification of impervious surfaces provides valuable information for urban planning and socioeconomic development. Remote sensing and GIS techniques provide spatial and temporal information of land surfaces and are widely used for modeling impervious surfaces. Traditionally, these surfaces are predicted by computing statistical indices derived from different bands available in remotely sensed data, such as the Landsat and Sentinel series. More recently, researchers have explored classification and regression techniques to model impervious surfaces. However, these modeling efforts are limited due to lack of labeled data for training and evaluation. This in turn requires significant effort for manual labeling of data and visual interpretation of results. In this paper, we train deep learning neural networks using TensorFlow to predict impervious surfaces from Landsat 8 images. We used OpenStreetMap (OSM), a crowd-sourced map of the world with manually interpreted impervious surfaces such as roads and buildings, to programmatically generate large amounts of training and evaluation data, thus overcoming the need for manual labeling. We conducted extensive experimentation to compare the performance of different deep learning neural network architectures, optimization methods, and the set of features used to train the networks. The four model configurations labeled U-Net_SGD_Bands, U-Net_Adam_Bands, U-Net_Adam_Bands+SI, and VGG-19_Adam_Bands+SI resulted in a root mean squared error (RMSE) of 0.1582, 0.1358, 0.1375, and 0.1582 and an accuracy of 90.87%, 92.28%, 92.46%, and 90.11%, respectively, on the test set. The U-Net_Adam_Bands+SI Model, similar to the others mentioned above, is a deep learning neural network that combines Landsat 8 bands with statistical indices. This model performs the best among all four on statistical accuracy and produces qualitatively sharper and brighter predictions of impervious surfaces as compared to the other models.

1. Introduction

The last five decades have seen a dramatic increase in urbanization, with over 3.5 billion people migrating to urban areas [1]. According to the United Nations, the rate of urbanization is expected to continue, with 68% of the world’s population predicted to live in urban areas by 2050 [2]. The rate of urbanization is growing due to the direct impact to protected areas [3], habitat reduction and degradation, loss of biodiversity [4], increase in the urban heat island effect [5], and impacted hydrology [6]. Globally, the rate of urbanization is increasing at an estimated rate of 1.56% to 3.89% of the global urban land areas of 2000 [7,8]. Evaluating the current country and city/local level rate of urbanization is challenging [8]. However, broadly speaking, the number of cities with a significant population greater than 1 million has dramatically increased in the past 50 years, and half of the world’s population lives in urban settlements [9,10]. Specifically, developing nations have observed the most recent dramatic increase in urbanization, with the majority of current urbanization taking place primarily in Asia, most evident in China and India, with a large percentage of urbanization occurring in coastal areas [7,8].

Rapid urbanization has contributed to an increase in impervious surfaces. The United States Geological Survey (USGS) defines impervious surfaces as hard areas that do not allow water to seep into the ground. Examples include artificial structures such as cement and asphalt roads, pavement surfaces such as parking lots and sidewalks, and building roofs covered with water-resistant material. The increase in impervious surfaces has severely altered the ecological balance in metropolitan areas, impacting hydrologic regimes and leading to a reduction in adjacent pervious spaces. Impervious surfaces also trap heat, resulting in a phenomenon known as the “urban heat island effect,” where urban areas are becoming significantly hotter than their surrounding rural areas [11]. For instance, according to a 2009 American Meteorological Study, temperatures can be as much as 14 degrees Fahrenheit hotter in New York City than in rural areas 60 miles away [12]. The high concentration of rainwater runoff from storm drains to nearby creeks and rivers increases stream velocity and therefore the risk of flooding, soil erosion, and natural habitat loss [13]. Pollutants deposited by vehicles and from the atmosphere onto impervious surfaces are carried to local water sources by the runoff, thereby degrading the water quality [14,15,16]. Accurate quantification of impervious surfaces is an important planning tool for urban land use development. Careful planning can mitigate the adverse effects of urban heat islands, water quality degradation, and natural habitat loss caused by the increase in impervious surfaces [17].

Remote sensing and geographic information system (GIS) techniques provide spatial and temporal information of land surfaces from the energy reflected by the Earth that is measured using satellites such as Landsat 8 (e.g., [18,19,20,21]). Satellites typically carry several sensors that measure different ranges of frequencies of the electromagnetic spectrum, known as bands. Effectively, every observation recorded by satellites with optical sensors such as Landsat 8 are images where each pixel is represented by N numbers, one for each of the N bands recorded by the sensors. Landsat 8 measures 11 bands, including nine bands [18] measured by the Operational Land Imager (OLI) sensor and two measured by the Thermal Infrared Sensor (TIRS) sensor [18], which are widely used for modeling impervious surfaces [22]. Remote sensing techniques provide the benefits of relatively low-cost imagery, global coverage, and short refresh cycles that makes them attractive to informing sustainable urban development [23]. Cloud computing and machine learning technologies have demonstrated to be very effective in processing large amounts of satellite imagery (e.g., [24,25,26,27]).

Remote sensing has been extensively utilized for the detection of impervious surfaces. (see e.g., [28,29,30,31,32,33]). Historical scientific research in this domain has focused on computing statistical indices from different bands of remotely sensed data. A statistical index is computed from two or more bands and is designed to enhance specific spectral features of areas such as vegetation, water bodies, or impervious surfaces while minimizing effects of illumination, shadows, and cloud covers. Statistical indices such as the normalized difference vegetation index (NDVI) [34], normalized difference built-up index (NDBI) [35], normalized difference impervious surface index (NDISI) [36], modified NDISI (MNDISI) [37], biophysical composition index (BCI) [38], and perpendicular impervious surface index (PISI) [39] are commonly used to model impervious surfaces.

More recently, researchers have explored classification and regression approaches such as maximum likelihood [40], support vector machines [41], artificial neural networks [42], random forests [43], and regression analysis [44] to model impervious surfaces.

This paper proposes a deep learning convolutional neural network (CNN)-based regression model to predict impervious surfaces from Landsat 8 images. The novelty of our approach is threefold: 1. Using OpenStreetMap [45] data representing roads and buildings, we systematically generate large volumes of training and evaluation data representing different terrains sampled across the globe without the need for manual labeling. 2. CNNs can effectively use spatial information in addition to individual pixel data to improve learning and hence the prediction of impervious surfaces. 3. The deep learning neural network model allows us to effectively combine data from the Landsat 8 bands with the derived statistical indices, resulting in significantly accurate images of predicted impervious surfaces.

2. Related Work

2.1. Statistical Indices

Statistical indices such as NDVI [34], NDBI [35], NDISI [36], MNDISI [37], and PISI [39] have been studied in the literature for modeling impervious surfaces. The following subsections describe these indices in more detail.

2.1.1. NDVI

The normalized difference vegetation index (NDVI) [34] is a standardized index that generates a derived image that displays the “greenness” or relative biomass. NDVI is computed as the normalized difference of the near-infrared and red bands and ranges between the values of −1 and +1 [34]. Healthy vegetation (chlorophyll) reflects more near-infrared and green wavelengths and absorbs red and blue. NDVI is designed to enhance healthy vegetation, giving it values closer to +1, while water bodies and barren surfaces give values closer to −1. Conversely, NDVI also provides valuable insight into detecting or identifying areas with limited vegetation, such as impervious surfaces.

$$NDVI=\frac{NIR-R}{NIR+R}$$

(1)

$NIR$ represents the pixel values extracted from the near-infrared band. R represents the pixel values extracted from the red band.

2.1.2. NDBI

The normalized difference built-up index (NDBI) [35] uses pixel values from the near-infrared (NIR) and the short-wave infrared (SWIR) bands to emphasize human-made built-up areas such as roads and buildings. NDBI attempts to mitigate the effects of terrain illumination differences and atmospheric effects. The index outputs values between −1.0 and +1.0.

$$NDBI=\frac{SWIR1-NIR}{SWIR1+NIR}$$

(2)

$SWIR1$ represents the pixel values extracted from the first shortwave-infrared band. $NIR$ represents the pixel values extracted from the near-infrared band.

2.1.3. NDISI

The normalized difference impervious surface index (NDISI) [36] is used to enhance impervious surfaces and suppress land covers such as soil, sand, and water bodies.

$$MNDWI=\frac{G-SWIR1}{G+SWIR1}$$

(3)

$MNDWI$ represents the modified normalized difference water index, used to calculate the $NDISI$, while G represents the pixel values extracted from the green band. $SWIR1$ represents the pixel values extracted from the $SWIR1$ band.

$$NDISI=\frac{T_b-(MNDWI+NIR+SWIR1)/3}{T_b+(MNDWI+NIR+SWIR1)/3}$$

(4)

The equation to calculate the NDISI index references the MNDWI, whose equation is provided above. $T_b$ refers to the brightness temperature of the $TIRS1$ thermal band. $NIR$ refers to the pixel values extracted from the near-infrared band. $SWIR1$ refers to the pixel values extracted from the first shortwave infrared band.

2.1.4. PISI

The perpendicular impervious surface index (PISI) [39] attempts to overcome the shortcomings of the NDISI and its successor, the modified normalized difference impervious surface index (MNDISI). Specifically, since the NDISI depends on the brightness temperature of the thermal band TIRS1, it performs poorly in geographical areas with a weak heat island effect. MNDISI improves upon NDISI by introducing nighttime light luminosity but is more complicated to compute and unavailable in some of the sensors. The PISI leverages more widely available sensor data from the blue and near-infrared bands and has shown to perform better than other indices.

$$PISI=0.8192\ast B-0.5735\ast NIR+0.075$$

(5)

B represents the pixel values extracted from the blue band. $NIR$ represents the pixel values extracted from the near-infrared band.

2.1.5. Analysis

While the statistical index based methods are intuitive and easily implementable, they have the following limitations. NDBI, which uses the shortwave infrared (SWIR) and near-infrared (NIR) bands, performs poorly in geographical areas with large soil composition because it is unable to distinguish the differences between urban land and vegetation. The NDISI depends on land-surface temperature data and can fail to detect impervious surfaces in geographical areas with a weaker heat island effect. Indices such as MNDISI have limited availability, as some of the remotely sensed datasets do not measure the required bands and transformations. Another challenge for all statistical indices is the determination of the optimal threshold to classify each pixel as either impervious or pervious. Extensive analysis of the statistical indices is needed to compute the threshold, and the threshold can be adjusted for different needs (for example, terrains in various geographical areas) to give different accuracies [39].

2.2. Classification and Regression Methods

Extensive research has been conducted on the application of classification and regression techniques to predict impervious surfaces. The maximum likelihood classifier using NDVI differencing was used for establishing urban change in the Washington D.C. area [40]. Support vector machines (SVM) were trained to classify Landsat images into three classes, vegetation, soil, and impervious surfaces, in Wuhan, China [41]. The classification and regression trees (CART) algorithm was used to predict impervious surfaces in Chicago, Venice, and Guangzhou [46]. A random forest model was explored for combining optical data from Landsat with the synthetic aperture radar (SAR) data [47] for predicting impervious surfaces. Multiple linear regression was employed to relate the percentage of impervious surface to Landsat tasseled cap greenness responses in Minnesota [44].

Classification and regression methods need large volumes of labeled training and evaluation data. The approaches described in the literature use visual interpretation to create labeled data [41]. The need for manual labeling makes it difficult to collect large volumes of data. As a result, these approaches typically focus on predicting impervious surfaces in specific geographic regions. An additional challenge for these approaches is deciphering mixed pixels representing a combination of impervious surfaces and other land cover types [48].

2.3. Deep Learning Neural Networks

Artificial neural networks have been used successfully to solve classification and regression problems. In early work, artificial neural networks such as self organizing maps (SOM) and multi-layer perceptrons (MLP) were trained to predict impervious surfaces in Marion County, Indiana [42].

Recent years have seen the emergence of deep learning neural networks (DNNs) [49]. DNNs are artificial neural networks composed of multiple processing layers that learn representations of underlying data at multiple levels of abstraction. CNNs [50] were the first neural networks that brought the area of deep learning into prominence. CNNs are characterized by the use of the convolution operator whose purpose is to extract relevant features from the input data while preserving spatial and temporal relationships. Deep networks are characterized by their large number (typically, tens or hundreds) of layers as opposed to traditional neural networks such as MLPs, which only have a few (typically, two to three) layers. The multiple layers enable learning progressively richer sets of features from the input training data. Deep learning networks have been successfully applied to computer vision, text transcription, and speech understanding tasks where large amounts of training data are widely available [51].

Semantic image segmentation [52] involves partitioning the input image into different human interpretative segments or objects [53]. Semantic image segmentation is well suited to the task of impervious surface detection from images. It involves classifying each pixel as belonging to one or more classes (e.g., the different land cover classes) or predicting a continuous value. More recently, deep learning networks have been successfully used for semantic image segmentation, yielding remarkable performance improvements compared to more traditional approaches [54]. The DNN architectures for image segmentation are based on a fundamental concept of the encoder-decoder network [55]. The encoder section is a deep neural network that takes the input image and learns discriminative features at progressively higher levels of abstraction. A mirror network called the decoder takes the coarse representation of the input images and applies upsampling [56] to create progressively fine-grained representations until the last layer reconstructs an image of the same size as the input image.

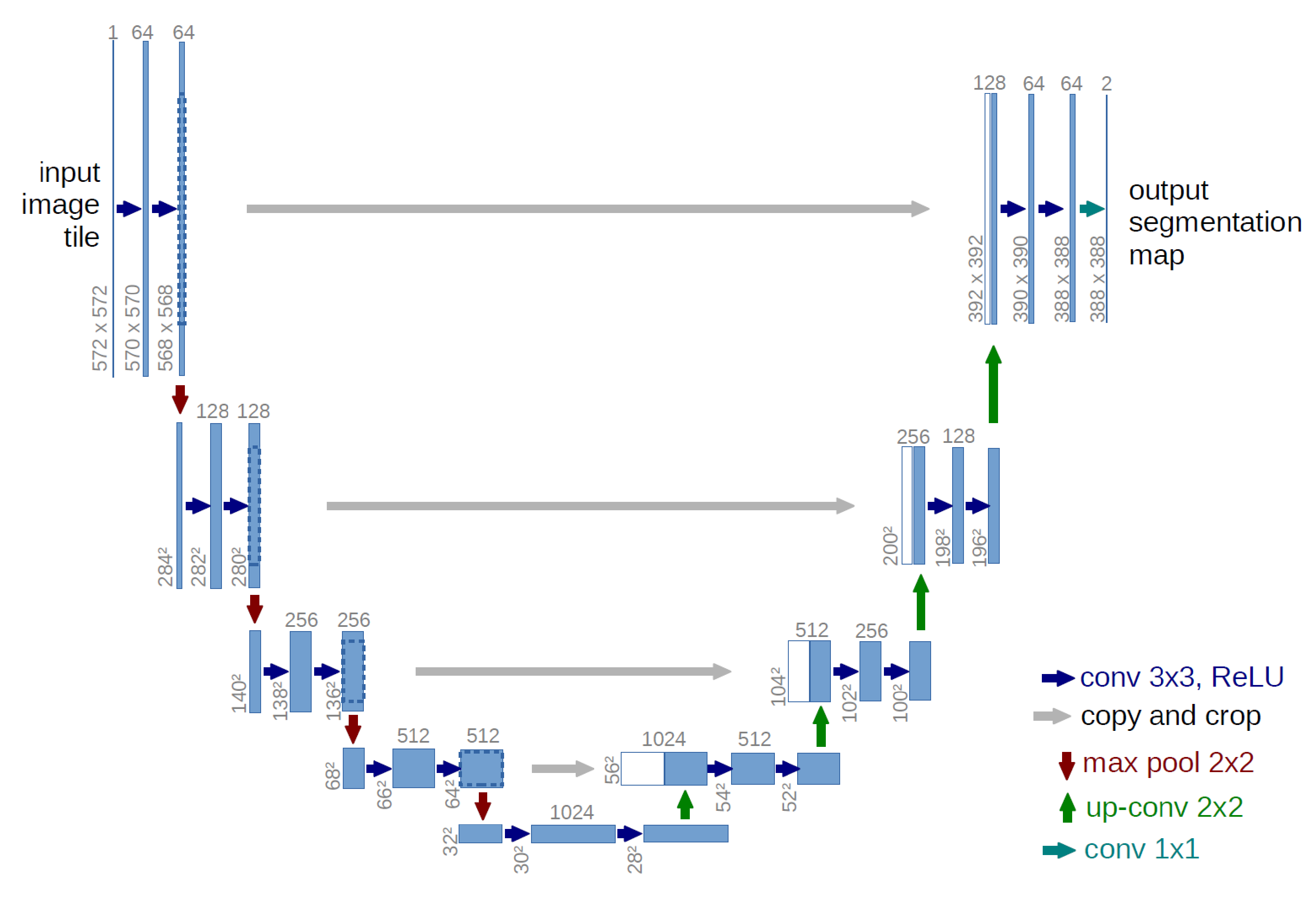
A commonly used deep learning model for semantic image segmentation is the U-Net architecture. The U-Net architecture is a U-shaped neural network with the encoder and decoder layers represented side-by-side. U-Net was originally developed for biomedical image segmentation [56]. Specifically, for the U-Net model architecture, which looks to increase the feature space and reduce the image resolution, our team leveraged the analysis consisting of five multiple convolution layer encoding blocks with a distinct max pooling layer at the end of each block. Figure 1 shows an example of the U-Net architecture.

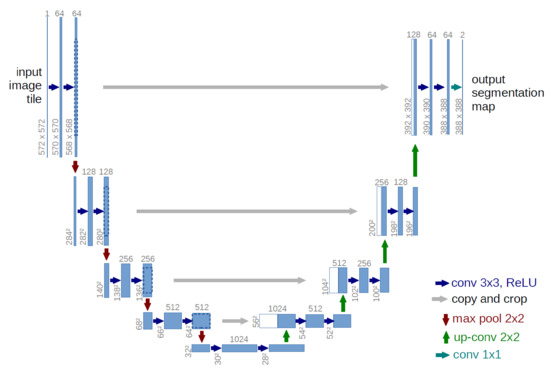
Figure 1. U-Net deep learning neural network architecture (courtesy [56]).

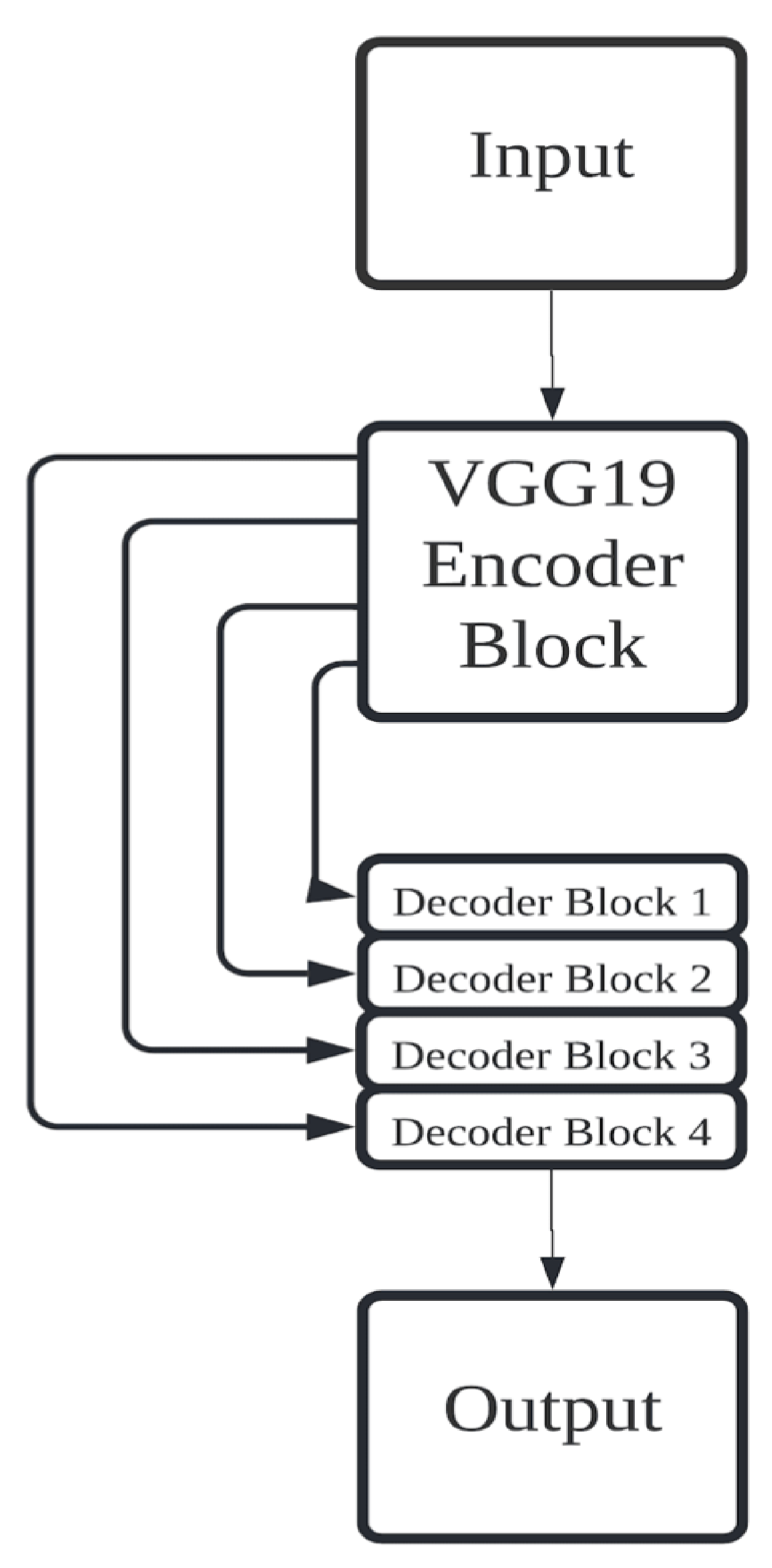
A different image segmentation approach is to use pre-trained deep learning convolutional networks that have historically performed well on the ImageNet [57] challenge problems as the encoder. The idea behind using a pre-trained network is to use the features learned on the ImageNet dataset and transfer them to the image segmentation task. VGG-19 (a neural network architecture designed by the Visual Geometry Group at the University of Oxford) [58], GoogLeNet (a neural network architecture designed by researchers at Google) [59], and ResNet (a residual neural network architecture designed by researchers at Microsoft) [60] are pre-trained neural networks commonly used as the encoder. The rest of the model is comprised of a decoder network just as in the regular U-Net architecture. Figure 2 shows a conceptual model of a VGG-19-based encoder-decoder network for image segmentation.

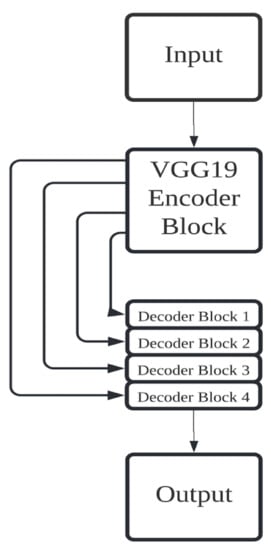
Figure 2. VGG-19-based encoder-decoder network.

For the VGG modeling approach, our team utilized the U-Net Architecture and applied a custom decoder which consists of five blocks utilizing bilinear upsampling layers, followed by convolution layers, and lastly regularization layers. Additionally, each convolution layer in the decoder was initialized using a He normal initialization [61] and was followed by a batch normalization layer [62] and rectified linear unit (ReLU) activation function [63]. Finally, the decoder process utilizes an exit branch consisting of a 2D spatial dropout [64] and a final 1 × 1 convolution employing a softmax activation function.

Regularization techniques were incorporated as part of the decoder architecture to reduce overfitting. Specifically, L2 regularization, with a rate of ${10}^{-3}$, was applied to the parameters of each convolution layer. Additionally, Gaussian noise was added as part of the decoder block to speed up convergence, increase generalization, and reduce the over-fitting [65]. Lastly, a dropout layer [66] was included after the first convolution within each decoder block. Incorporating dropout layers promotes model generalization [66].

2.4. Gradient Descent Optimization

DNNs are trained to minimize a loss function such as mean squared error (MSE) on the training data [67]. The loss minimization is typically performed using one of the popular gradient descent algorithms such as stochastic gradient descent (SGD) [68] or adaptive moment estimation (Adam) [69]. Gradient descent minimizes the loss function by updating the weights of the DNNs in a direction opposite to the gradient of the loss function with respect to the weights. The learning rate ($\mathsf{\eta }$) determines the size of the step taken while updating the weight. Stochastic gradient descent (SGD) performs the update for each training example, which speeds up training and enables the training algorithm to escape local minima [70]. Unlike SGD, which maintains a single learning rate, the Adam optimizer computes individual adaptive learning rates for each weight from the gradients’ first and second moments. Adam is empirically shown to converge to the minimum of the loss function faster [57].

3. Methodology

This section describes our methodology of training DNNs to predict impervious surfaces from Landsat 8 images. We modeled the prediction as a regression task, where the DNN is trained to predict the fraction of the area represented by each pixel of an input image that is covered with impervious surfaces.

3.1. Input Features

Landsat 8 bands blue (B1), green (B2), red (B3), near-infrared (B4), shortwave infrared 1 (B5), and shortwave infrared 2 (B6) were used as input features to train the deep learning models. We experimented with adding statistical indices NDVI, NDBI, and PISI as additional features and trained separate models.

3.2. Impervious Surface Labels

A significant challenge in building deep learning models to predict impervious surfaces is the scarcity of labeled data. In our formulation, these labels represent the percentage of impervious surface per pixel.

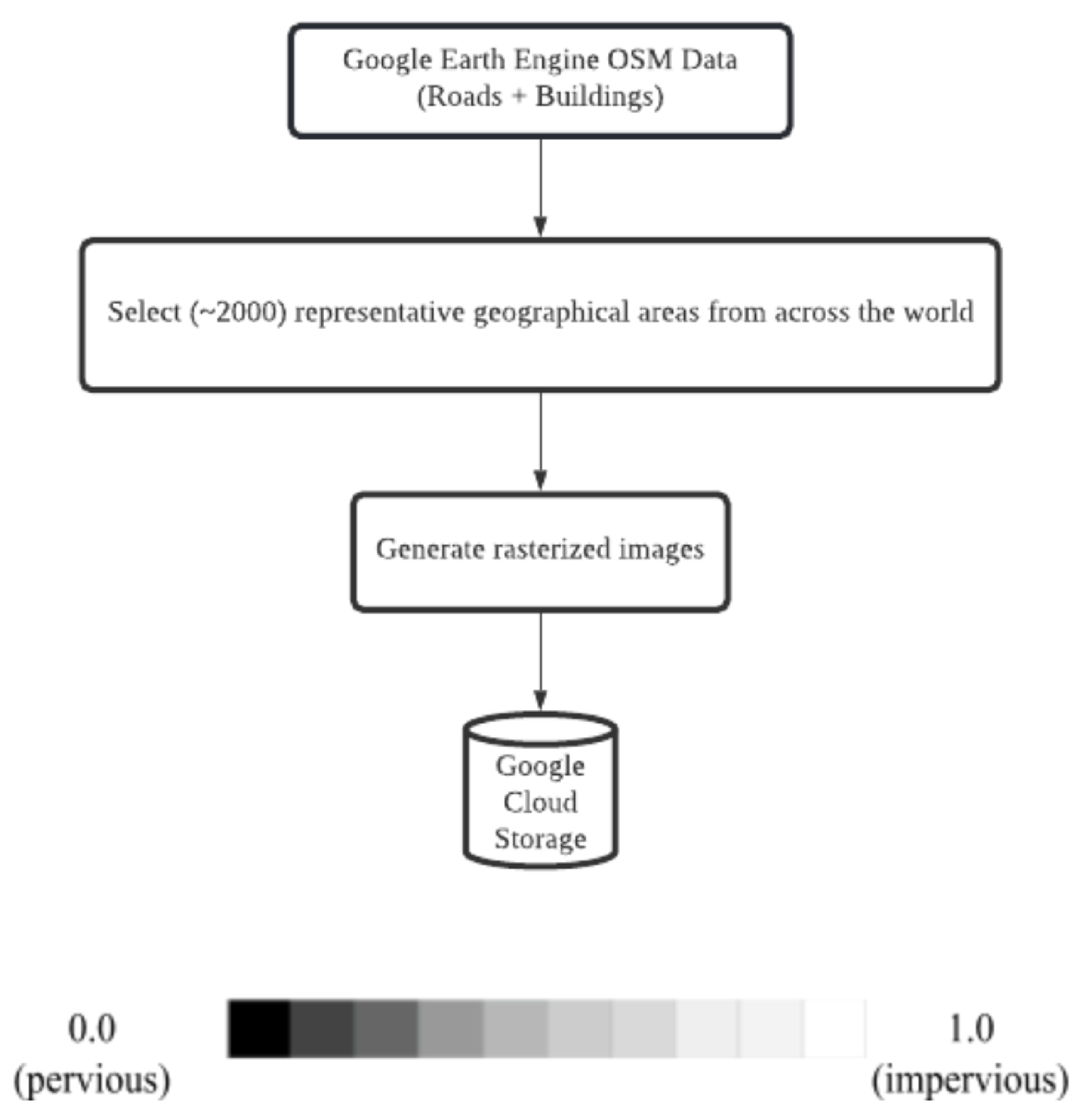
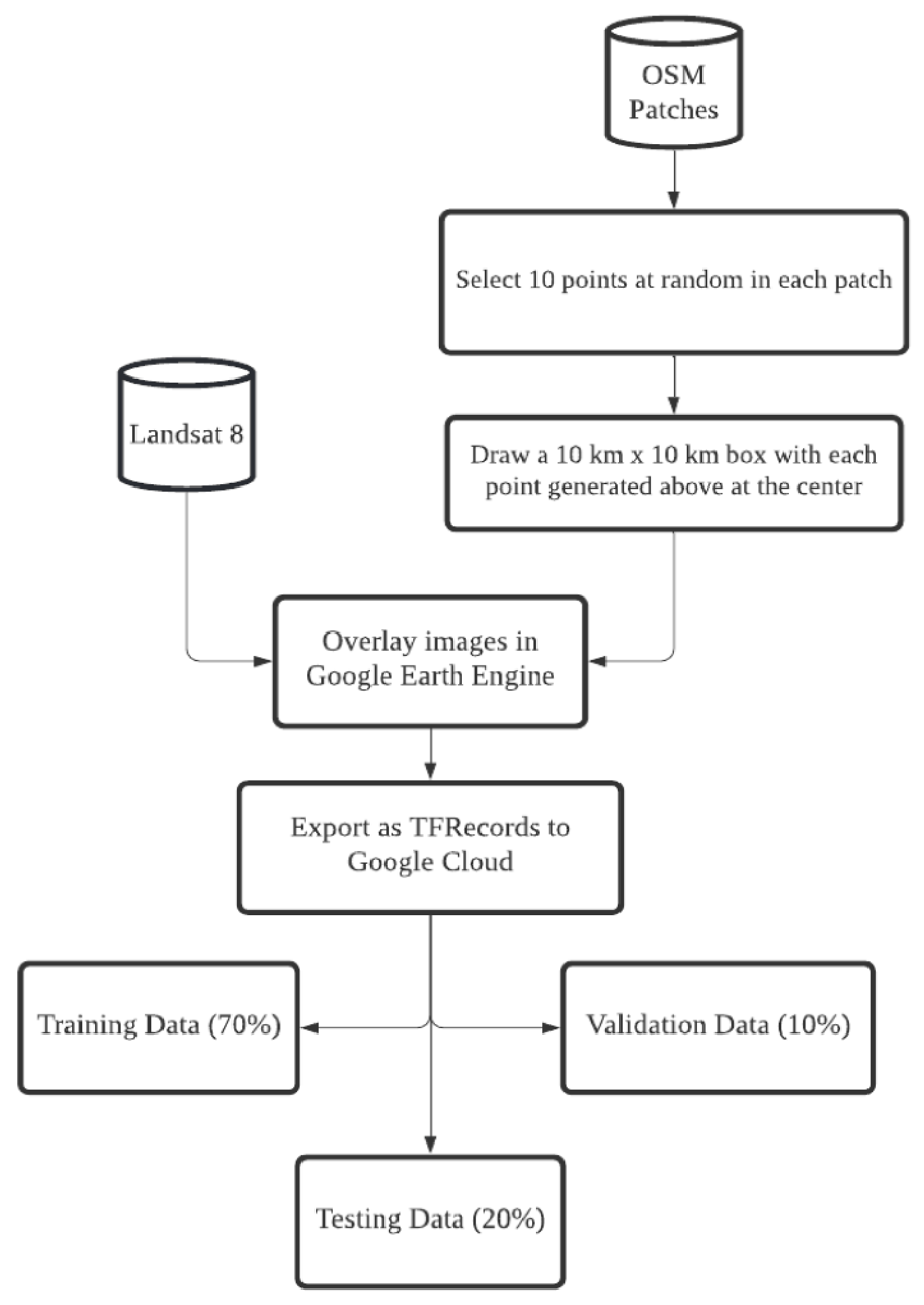
We used OSM data to identify impervious surfaces. OSM relies on volunteers to draw various features like roads, bridges, pavements, and buildings and renders this information on the map [45]. Figure 3 summarizes the process of creating the OSM patches, capturing the percentage of the area of each pixel that is covered by impervious surfaces. The impervious surface label is a value ranging from 0.0 to 1.0, represented as a grayscale image as shown by the legend in Figure 3, where 0.0 (black) represents pervious surfaces (e.g., water bodies, soil, vegetation), and 1.0 (white) denotes a completely impervious surface such as a road or rooftop. This process of generating the impervious surface labels is executed in Google Earth Engine [71], and the resulting images are stored in Google Cloud Storage.

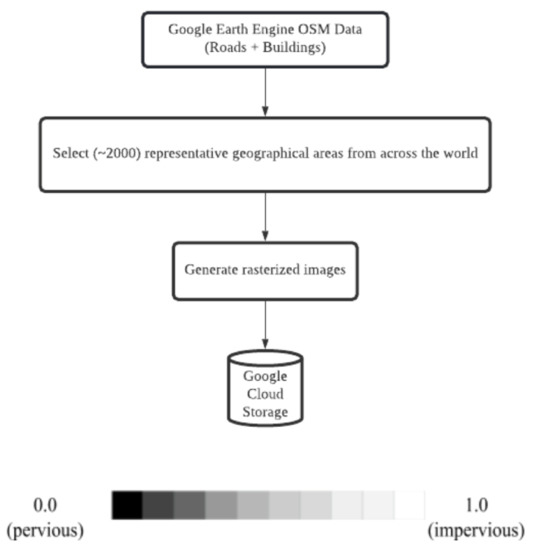
Figure 3. Process for generating OSM patches representing impervious surfaces. Each pixel in the rasterized OSM patch takes a value between 0 and 100, representing the percentage of impervious surface.

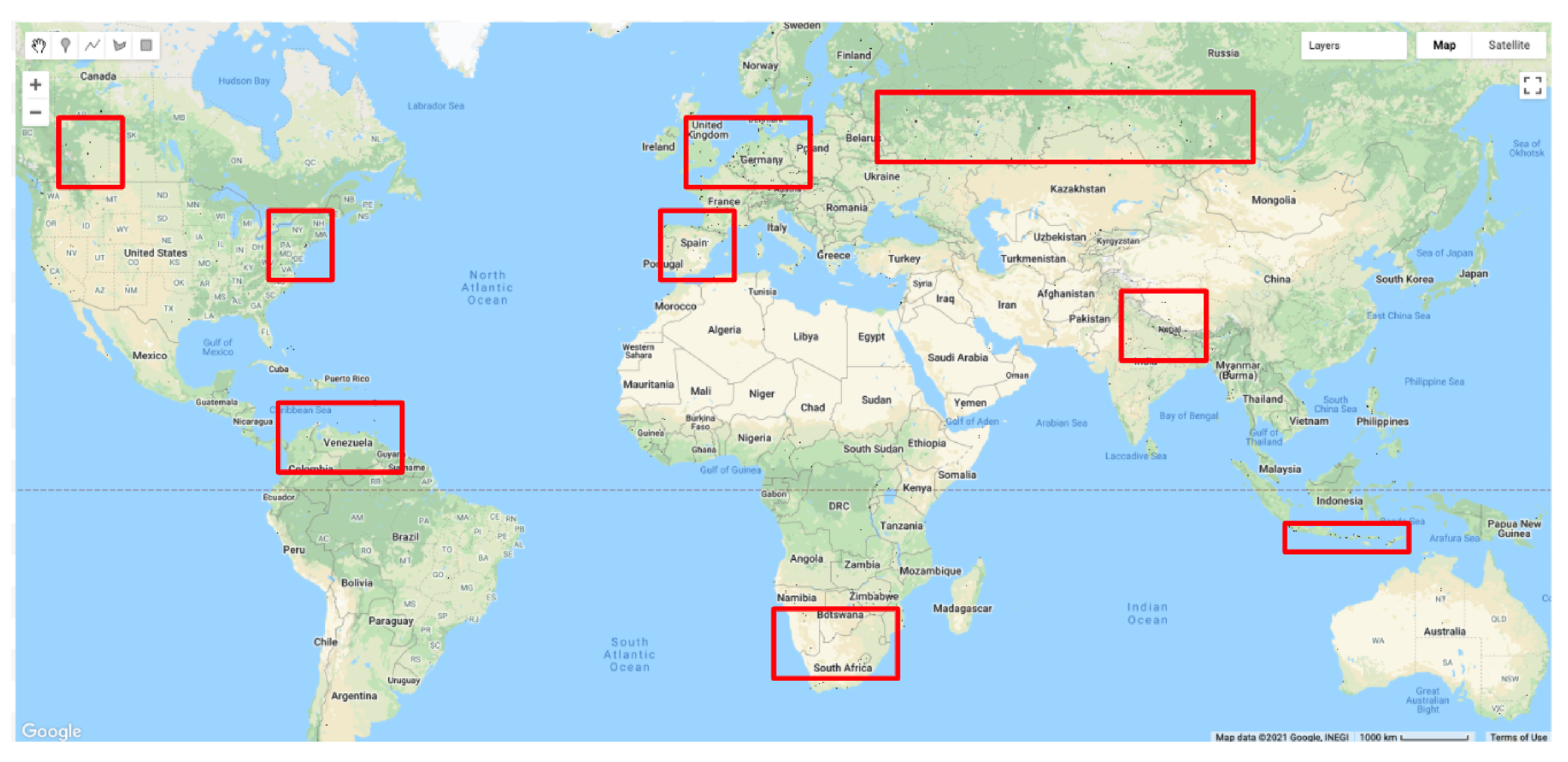
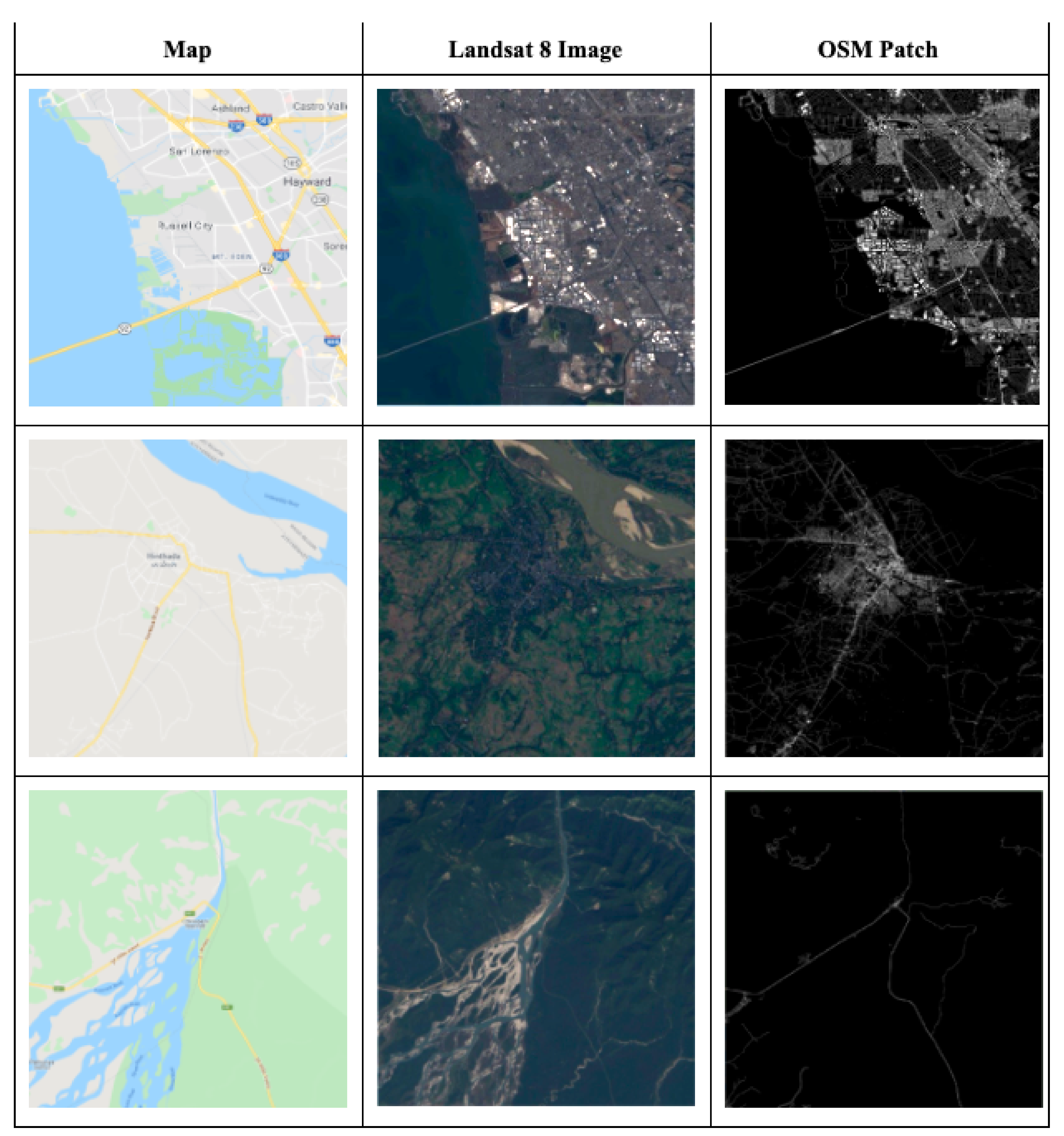
Each OSM patch is a grayscale image representing the impervious surfaces in that geographical region. Figure 4, below, shows where all patches used during the experiments have been sampled from. Patches that appear in clusters have been identified using red boxes. Some countries where patches appear the most include France, Germany, Italy, Myanmar, India, Zimbabwe, Mozambique, the Caribbean Islands, Venezuela, and the United States, to name a few. Figure 5 shows three example images from different parts of the world. The data from the OSM patch will be used as labels for training the deep learning models, as described below.

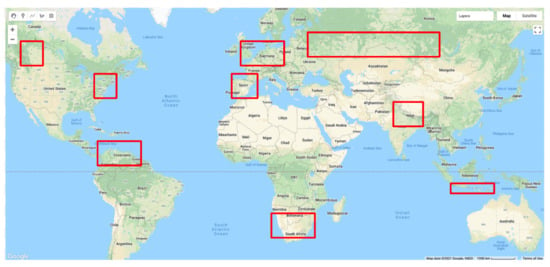
Figure 4. Map indicating 1958 patches sampled across various sites for model training.

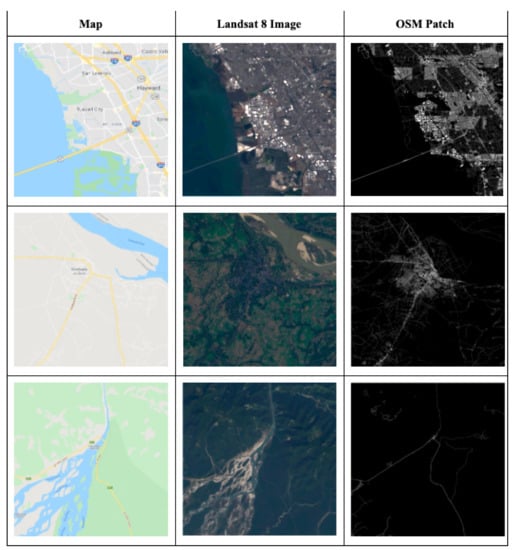
Figure 5. Example OSM patches generated for three different geographical areas (urban, semi-urban, and rural). Column 1 shows the image from Google Maps, column 2 shows the Landsat 8 true color image, and column 3 is the OSM patch.

3.3. Dataset Generation

The labeled training, evaluation, and test datasets were generated using Google Earth Engine. We started with 1958 representative OSM patches selected from different parts of the world. For each OSM patch, we picked k (k = 10 for these experiments) randomly generated points within the patch and marked a 10 km × 10 km area with each point as the centroid. The aforementioned bands were selected for each 10 km × 10 km area, and the impervious surface label representing the percentage of impervious surface was attached. The resulting data were exported as 256 × 256 images in the TensorFlow Record Format [72] to the Google Cloud platform. The flowchart in Figure 6 depicts the process of generating labeled training, evaluation, and testing data.

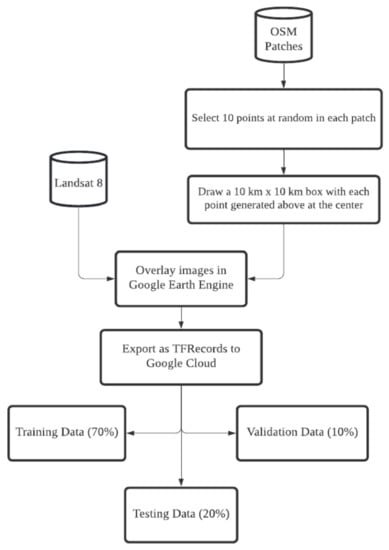
Figure 6. Impervious surfaces labeled data generation.

3.4. Models

We trained deep learning neural network models using Google Colab [73] to predict impervious surfaces. Our experiments involved training four models with different neural network architectures (U-Net and VGG-19), different gradient descent algorithms (SGD and Adam), and different sets of features (Landsat 8 bands and statistical indices).

• U-Net_SGD_Bands: U-Net trained with Landsat 8 bands as features using the stochastic gradient descent (SGD) optimizer.
• U-Net_Adam_Bands: U-Net trained with Landsat 8 bands as features using the Adam optimizer.
• U-Net_Adam_Bands+SI: U-Net trained with Landsat 8 bands and four computed statistical indices as features using the Adam optimizer.
• VGG-19_Adam_Bands+SI: VGG-19-based encoder-decoder trained with Landsat 8 bands and computed statistical indices as features using the Adam optimizer.

The models were set up as regression tasks to predict the percentage of impervious surface per pixel. The root mean squared error (RMSE) was measured on both the training and evaluation data after each training epoch. We employed early stopping, wherein training was stopped if the maximum evaluation RMSE decline was lower than 0.05 over 10 epochs.

3.5. Metrics

We evaluated model performance using two metrics computed over the test data: root mean squared error (RMSE) and accuracy. The accuracy was measured by thresholding both the target image and the predicted image. Pixel values more than or equal to the threshold value are set to 1 (impervious), and those below the threshold are set to 0 (pervious). Accuracy is measured using the percentage of pixels that are classified the same in both images. For the purpose of these experiments, we set the threshold to 0.5. This threshold value was selected by analyzing the pixel values across the training dataset that comprises images from urban, semi-urban, and rural areas. This analysis showed the median pixel value to be approximately 0.5.

While metrics such as RMSE and accuracy give a macro-level view of the model’s performance, we also visually inspected multiple test set images to obtain a qualitative view of each model’s strengths and weaknesses.

4. Results

4.1. Test Set Metrics

Table 1 summarizes the test set metrics for the four different deep learning models we trained.

Table 1. Model performance on testing data as measured by RMSE and test accuracy.

Model Names	Evaluation RMSE	Test RMSE	Test Accuracy
U-Net_SGD_Bands	0.1587	0.1582	90.87%
U-Net_Adam_Bands	0.1356	0.1358	92.28%
U-Net_Adam_Bands+SI	0.1360	0.1375	92.46%
VGG19_Adam_Bands+SI	0.1525	0.1582	90.11%

4.2. Test Set Image Observations

In this section, we qualitatively analyze the performance of the four models on different test images. These images are chosen to represent urban (Figure 7 and Figure 8), semi-urban (Figure 9), and rural areas (Figure 10). The test set predictions for the U-Net_Adam_Bands+SI model are sharper and better able to capture individual rooftops and roads compared to the other models.

Figure 7. Impervious surface predictions from the four deep learning models on an image representing an urban area.

Figure 8. Impervious surface predictions from the four deep learning models on another image representing an urban area.

Figure 9. Impervious surface predictions from the four deep learning models on an image representing a semi-urban area.

Figure 10. Impervious surface predictions from the four deep learning models on an image representing a rural area.

The following figures show the differences in predictions between the OSM patch and the four different predictions. Green boxes have been drawn around specific areas on the OSM patch, corresponding to the ground truth. On the predictions, green boxes represent areas over 93% in accuracy, yellow boxes represent areas between 75% and 93% in accuracy, and red boxes represent areas below 75% in accuracy.

5. Discussion

As indicated by the test set metrics used, whose results are shown in Table 1, the U-Net_Adam_Bands performs better than U-Net_SGD_Bands on both RMSE and test accuracy scores. The U-Net_Adam_Bands+SI has the highest accuracy, while the U-Net_Adam_Bands has the best evaluation and test RMSE. In contrast, both the U-Net_SGD_ Bands and VGG19_Adam_Bands+SI perform with lesser test accuracy and RMSE scores. Furthermore, in Figure 7c, Figure 8c, Figure 9c, and Figure 10c, the U-Net_SGD_Bands model shows significant blurring and an inability to capture individual rooftops and narrow roads. We decided to use the Adam optimizer for the other experiments.

As shown in Table 1, the U-Net_Adam_Bands and U-Net_Adam_Bands+SI are similar in performance on the quantitative metrics. Studying Figure 7e, Figure 8e, Figure 9e, and Figure 10e shows that the predicted U-Net_Adam_Bands+SI images are sharper and able to represent brighter surfaces such as lighter colored rooftops better. This highlights the benefit of using statistical indices as higher level features to better discriminate impervious surfaces in addition to the Landsat 8 bands.

The VGG-19_Adam_Bands+SI underperformed in comparison to the other models, both on test set metrics and when visually inspecting specific test set images. We hypothesize that since the VGG-19 encoder was trained on ImageNet data [57], which only contain household objects and animals, it was not able to effectively discriminate impervious surfaces from the data we provided.

An objective comparison of our models’ results with the statistical indices-based approach and other classification and regression techniques proposed in related literature is difficult because the methods proposed in the literature were based on data constructed at vastly different time periods and focused on specific geographical regions, and threshold calculation in these methods was optimized for specific needs.

The average classification accuracies reported for impervious surfaces computed using NDBI, BCI, MNDISI, and PISI are 64.6%, 83.27%, 87%, and 93.4%, respectively. While we cannot directly compare these accuracies to the average accuracy of the U-Net_SGD_Bands+SI model (92.46%) due to the above reasons, the advantage of our approach is that the model was trained using representative OSM patches from all over the world, and its performance generalizes well to different terrains worldwide.

6. Conclusions and Future Work

Accurately quantifying impervious surfaces is crucial for urban planning, sustainable development, and understanding the environmental impacts of impervious surface land cover. Historically, impervious surface modeling is based on statistical indices computed to accentuate the impervious surfaces in satellite imagery. The past few years have seen tremendous advances in deep learning. In this paper, we have demonstrated how deep learning can be effectively used to predict impervious surfaces. The advantages of our approach are the ability to programmatically generate large volumes of globally representative labeled training data from OpenStreetMap, the ability to use CNNs to harness spatial properties of Landsat 8 images in addition to the individual pixel values, and the effectiveness of combining statistical indices together with Landsat 8 bands as features in training to build models that can better predict impervious surfaces. In summary, we found that the U-Net_Adam_Bands+SI model performed best, both taking into account quantitative metrics (RMSE and accuracy) and visual inspection of predictions on test set images representing urban, semi-urban, and rural areas around the world.

We identified a few areas that merit further research. The brightness of the model’s predicted impervious surfaces is lower than the labeled data from the OSM patches. It will be interesting to explore if a post-processing brightness filter can better accentuate impervious surfaces, resulting in improved model performance. The thresholding approach used to compute test accuracy in our experiments is simplistic. More sophisticated thresholding approaches have been proposed in related literature [39]. Exploring these approaches and comparing our models’ resulting accuracy in the same geographical areas as used in other research will enable obtaining a more objective comparison of the different approaches. In a follow up study, we intend to study the urban–rural interfaces in the context of land cover mapping with impervious surfaces as one class among others.

An interesting application of our DNN model to predict impervious surfaces is in identifying missing roads and buildings in maps such as OSM. Since OSM is manually curated by volunteers, it is conceivable that newer constructions, including buildings and roads, may not yet be represented on the map. Applying the impervious surface model to the most recent Landsat 8 imagery and comparing the prediction to the impervious surfaces appearing on the map will identify geographical areas where the impervious surfaces are not yet represented on the map. This approach can therefore complement existing maps and ground-based data to potentially be used for filling gaps such as missing roads and buildings on the map and tasking OSM volunteers to focus their attention on these missing structures. The data used in this product can be kept up-to-date using the newest satellite imagery provided. This product has the power to globally transform infrastructure mapping.