Abstract
Compact multi-spectral sensors that can be mounted on lightweight drones are now widely available and applied within the geo- and environmental sciences. However; the spatial consistency and radiometric quality of data from such sensors is relatively poorly explored beyond the lab; in operational settings and against other sensors. This study explores the extent to which accurate hemispherical-conical reflectance factors (HCRF) and vegetation indices (specifically: normalised difference vegetation index (NDVI) and chlorophyll red-edge index (CHL)) can be derived from a low-cost multispectral drone-mounted sensor (Parrot Sequoia). The drone datasets were assessed using reference panels and a high quality 1 m resolution reference dataset collected near-simultaneously by an airborne imaging spectrometer (HyPlant). Relative errors relating to the radiometric calibration to HCRF values were in the 4 to 15% range whereas deviations assessed for a maize field case study were larger (5 to 28%). Drone-derived vegetation indices showed relatively good agreement for NDVI with both HyPlant and Sentinel 2 products (R2 = 0.91). The HCRF; NDVI and CHL products from the Sequoia showed bias for high and low reflective surfaces. The spatial consistency of the products was high with minimal view angle effects in visible bands. In summary; compact multi-spectral sensors such as the Parrot Sequoia show good potential for use in index-based vegetation monitoring studies across scales but care must be taken when assuming derived HCRF to represent the true optical properties of the imaged surface.
Keywords:
UAV; drone; multispectral; calibration; reflectance; NDVI; chlorophyll; vegetation; maize; Parrot Sequoia 1. Introduction
Spectral information and derived vegetation indices are at the core of a wide array of methodologies for the monitoring of vegetation. How vegetation reflects light at different wavelengths is indicative of its structure, biochemical composition as well as status and function in terms of photosynthesis and carbon dioxide assimilation [1,2,3]. Deriving spectral information at fine spatial and temporal resolutions was identified as being critical for relating processes measured at local scale to coarser spatial resolution global measurements, for example, to bridge the scaling gap between flux-tower based eddy-covariance measurements and satellite observations [4]. The practicalities of sampling detailed ecosystem optical properties at fine scales previously relied on elaborate and financially costly infrastructure such as in situ spectral measurement tramways [5] or motorised flux-tower mounted cameras [6].
Recently, the use of drones as proximal acquisition platforms has revolutionised the way in which these finely resolved datasets can be collected [7,8,9]. Lightweight drones have the further benefit of low financial cost, flexibility and enable deployment also in remote and harsh environments [10,11]. In tandem with the development and production of compact and lightweight turnkey multispectral sensors, there has been a surge in drone-based multispectral data applications during recent years which make use of the fine spatial resolution or frequent revisit capabilities [12,13,14,15]. Popular sensor solutions are multi-camera array (MCA) systems such as the Parrot Sequoia (Parrot SA, France) and Micasense RedEdge (Micasense, US) which consist of individual cameras with different band-pass filters to record reflected light at specific narrow (10–40 nm) wavelength intervals. The individual camera images are then co-registered to provide a single image with multiple spectral bands. Designed primarily for applications in precision agriculture, these sensors exhibit a number of qualities which have also made them attractive to the scientific community, primarily their low financial cost, simple integration into lightweight drone systems and accompanying software options.
However, data from lightweight MCAs are susceptible to a considerable amount of geometric and radiometric effects that require an extensive workflow of corrections such as dark current, lens distortion and vignetting compensation, as detailed by [16]. These corrections are increasingly handled by commercial, mostly black-box software packages (e.g., Pix4D and Agisoft Metashape) which generate fully mosaicked, orthorectified outputs and include the option of radiometrically calibrating orthomosaics to provide surface reflectance and vegetation index (VI) maps.
The impact of correction and calibration methodologies as well as viewing-angle effects for non-gimbaled acquisitions on the final surface reflectance and derived VI maps can be considerable [17,18] and is relatively poorly explored beyond the lab, in comparison against other optical remote sensing instruments (e.g., onboard satellites or in airplanes) in operational settings. These effects have potential implications for the spatial consistency and sensitivity of the products to the desired plant trait to be monitored [19]. Yet, these uncertainties are not reported to the end-user by the software and the direct integration of products in further processing workflows without critical assessment can potentially lead to bias in the results. Understanding the extent to which these uncertainties influence outputs is important in a precision agriculture context where VIs serve as indicators of local vegetation status. Ensuring that there is sufficient consistency between datasets is also crucial when integrating drone-based data with other remote sensing and in situ data sources, for improved temporal monitoring [20,21,22]. For scaling studies, surface reflectance values should further be traceable and comparable between sensors [23].
Due to the large interest from a diverse user base and the many potential applications of low-cost MCA systems, there is now a need for rigorous data assessments in an applied context. This can determine whether the sensors are able to deliver physical quantities (e.g., surface reflectance) with the required accuracy for scientific research and whether derived VIs are sufficiently consistent to provide useful relative information as sought after for agricultural applications. To this end, we planned a field campaign based on a section of heterogeneous maize field with multi-sensor acquisitions and accompanying spectroscopy field-measurements and sampling of biophysical parameters. The presented study sought to provide a thorough assessment of MCA-derived surface reflectance and derived VI products and to answer the following research questions:
- What is the performance of MCA sensors with regards to measuring surface reflectance?
- (a)
- What is the accuracy of MCA derived hemispherical-conical reflectance factors? (hemispherical-conical reflectance factors (HCRF), following the terminology by [24])
- (b)
- How is HCRF accuracy influenced by the type of calibration procedure followed?
- (c)
- How consistent are HCRF products spatially and over varying vegetation cover?
- What is the performance of MCA sensors with regards to deriving vegetation indices?
- (a)
- How consistent are VI products spatially and over varying vegetation cover?
- (b)
- Are the MCA derived VIs comparable to VIs derived from similar bands of coarser spatial resolution data captured close in time (HyPlant, Sentinel 2)?
Questions 1 (a) and (b) were addressed by a calibration–validation experiment using reference panels imaged in-flight. Both software (Pix4D) implemented proximal panel calibration and empirical line models based on in-flight imagery are compared in their ability to deliver accurate HCRFs. For question 1 (c), a spatially contiguous, pixel-wise HCRF comparison over a heterogeneous maize field (leaf area index (LAI) ranging from 0 to 4) was performed utilising a reference dataset from a simultaneous airborne hyperspectral imager acquisition (HyPlant). Question 2 was answered using field-measured LAI values and vegetation indices derived from comparable acquisitions by drone-based, airborne (HyPlant) and spaceborne (Sentinel 2 multi-spectral satellite) instruments over the same study area.
2. Materials and Methods
The object of study, datasets and comparisons performed are presented in the following sections. An overview of the study highlighting the different scales and the datasets compared is presented in Figure 1.
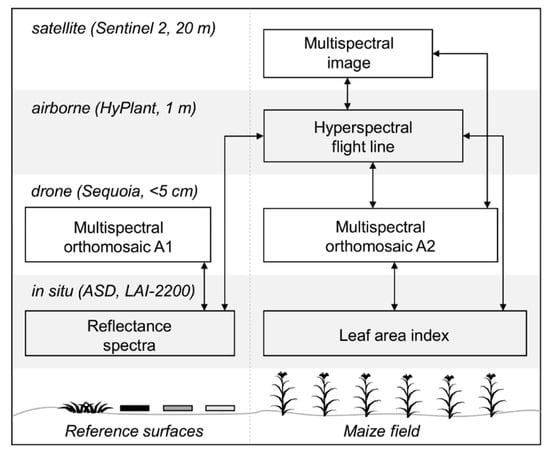
Figure 1.
Overview of the multisource datasets, including details on spatial resolution, and comparison experiments performed. Arrows indicate which datasets are compared within this study.
2.1. Study Site
The study was carried out over a maize field in the vicinity of Braccagni, a province of Grosseto, Italy (N 42°49′7.06″, E 11°3′39.98″, 3 m a.s.l.) (Figure 2). This region has a temperate climate according to the Köppen–Geiger classification (Csa) [25] and experiences dry and hot summers. The maize was planted on clay soil in north-south oriented rows and was drip irrigated. At the time of the study in early July 2018, the majority of the crop was in the tasselling stage. The field showed considerable heterogeneity and variability in plant density, likely due to soil characteristics and some irrigation issues. The region of interest covered parts of two fields with the same sowing date with a spatial extent of 3.4 hectares, limited by drone flying height restrictions and battery capacity.
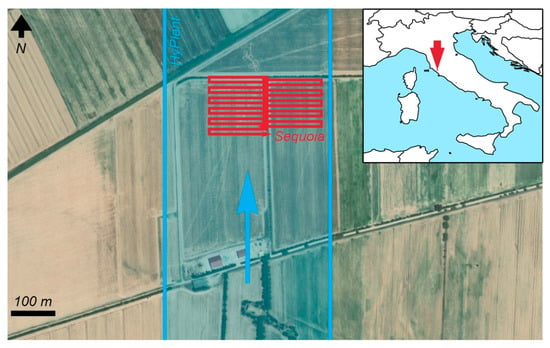
Figure 2.
The studied maize field in the province of Grosseto, Italy is depicted along with its location (inset map). The flight lines and coverage of the drone (Sequoia, red) and airborne (HyPlant, blue) datasets are also shown. Image data licensed by ESRI, © DigitalGlobe.
2.2. Image Data
Multi-source remote sensing data were used for this study and are described in Table 1.

Table 1.
Description of image datasets used within this study, including sensor, acquisition time, ground sampling distance (spatial resolution) and spectral bandwidths (spectral resolution).
Drone image data were acquired using the Parrot Sequoia (Parrot, France) MCA mounted on a 3DR Solo quadcopter. The Sequoia sensor has four monochrome cameras with band-pass filters to record light in different wavelength regions (sensor response depicted in Figure 3, centre wavelengths: 550, 660, 735 and 790 nm, bandwidths: 40, 40, 10 and 40 nm). The mount was custom-designed to fix the camera at a 3-degree angle to offset average in-flight forward tilt. The flying altitude for the drone acquisitions was 45 and 50 m above ground, resulting in a ground sampling distance of 4.15 cm and 4.71 cm respectively. The flying speed was constant at 4 m/s and the camera was triggered every 1.5 s by intervalometer, guaranteeing 85% forward image overlap. The lawnmower-pattern flight plan (Figure 2) was designed with a distance between flight lines resulting in 80% lateral image overlap. Initial georeferencing of the images with a camera internal GPS was refined using six ground control point markers clearly visible within the imagery and surveyed using a high accuracy DGPS system (Topcon HiPer Pro, Japan).
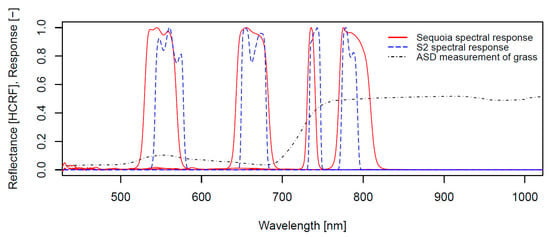
Figure 3.
Relative spectral responses of the four Parrot Sequoia cameras as well as the most closely corresponding Sentinel 2A bands (bands 3, 4, 6 and 7), overlaid on a measured grass reflectance spectrum.
Acquisition 1 (A1) (Table 1) denotes an acquisition for the validation of drone derived surface reflectance factors for panels and natural targets.
Acquisition 2 (A2) consisted of two subsequent flights (F2A and F2B) to cover the entire region of interest (Figure 2), each with a duration of approximately 10 min and 10 min intermission between flights.
Hyperspectral image data over the same area was acquired by the HyPlant airborne imaging spectrometer [26]. The HyPlant instrument consists of two modules (the FLUO and DUAL module) and was mounted on an aircraft flying at 680 m height resulting in a ground sampling distance of 1 m and a swath of 390 m. Data were geometrically and radiometrically corrected. The georeferencing accuracy of the images is 1 pixel, i.e., 1 m. For this study, only data of the DUAL module, which covers the spectral range of 380–2500 nm, was used. Top-of-canopy radiances and relative reflectance was calculated using the laboratory calibration with the GalliGeo software package (SPECIM, Oulu, Finland) and radiative transfer modelling using MODTRAN 5 (for details on the processing of HyPlant imagery see [27]).
Both drone and airborne data were acquired during cloud-free conditions over the study site, though isolated cumulus clouds were passing in the vicinity.
The study site was imaged by Sentinel-2A (S2) during cloud-free conditions at noon the following day. The Level 2A atmospherically corrected surface reflectance data were downloaded from the Copernicus Open Access Hub (https://scihub.copernicus.eu/). Due to the lower resolution of the red edge bands, all bands used were resampled to 20 m pixel resolution. S2 bands 3, 4, 6 and 7 show the best correspondence with the Sequoia bands (Figure 3, centre wavelengths: 560, 665, 740 and 780 nm, bandwidths: 36, 31, 15 and 20 nm).
2.3. Field Measurements
2.3.1. Field Spectral Measurements for Calibration and Validation
Concurrently with A1, five reference panels of varying reflectance as well as a dry bare soil and a grass target were measured using an ASD FieldSpec Pro spectrometer and calibrated to HCRF using a 99% Spectralon® white panel as a reference. The brightest and darkest panel of 50 × 50 cm dimensions and 2% and 44% nominal reflectance across bands were manufactured by MosaicMill (Finland), consisting of a fabric applied to plywood. Three 40 × 60 cm panels of intermediate reflectance (means of 8%, 21% and 39% across Sequoia bands) were manufactured using RustOleum® matte primer and paint on plywood. The target sizes were selected based on targets used in similar studies [23].
For the validation of the HyPlant DUAL derived hyperspectral HCRF product, three tarps of different reflectance (approx. 5%, 40% and 70% average reflectance in the 400 to 1000 nm wavelength range) made of PVC-coated canvas material (Kayospruce Ltd., UK) were measured using the ASD. It should be noted that these tarps were imaged in a different flight line acquired approx. 20 min prior to the one used further within this study, however, the atmospheric conditions are assumed to remain similar and, therefore, the HCRF resulting from atmospheric correction are comparable.
2.3.2. Leaf Area Index Measurements
In the associated field campaign carried out on the same date as the overflights, LAI was estimated using a LAI-2200 (LI-COR, US) instrument. LAI-2200 measurements are a good proxy of real LAI data in maize [28]. Measurements were taken within 20 10 × 10 m plots corresponding to elementary sampling units (ESU) as suggested by the VALERI protocol [29] (Figure 4a). Each ESU was selected to be approximately spatially homogenous in terms of LAI. The LAI measurement protocol for the LAI-2200 device consisted of two Above canopy (A) and six Below canopy (B) readings acquired along a transect that crossed maize crop rows (ABBBBBBA sequence, Figure 4b). A 270° cap was used to restrict the azimuthal field of view, so that the operator was not in view and the open portion of the sensor was pointed north-west along the rows. The spatial subset analysed for this study contains 20 ESUs with mean LAI values ranging from 0.85 to 3.83 m2/m2.
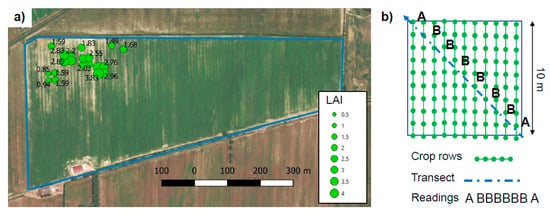
Figure 4.
Position and values of LAI measurements available for the analysis (a), acquired along a transect on 10 × 10 m plots (b).
2.4. Image Data Processing
2.4.1. Surface Reflectance from Drone Image Data
Image processing from individual images for each of the four bands to multispectral HCRF orthomosaics was performed in Pix4D (Pix4D, Switzerland). This included the geometric correction and stitching of images, which employs photogrammetric algorithms as well as the radiometric calibration to surface reflectance. The precise methodology employed in both workflows is not disseminated due to the black-box nature of the proprietary software, however, the radiometric calibration procedure for Sequoia imagery has been shared in application notes by the manufacturer [30], and is documented here.
For each spectral band (individual camera), the digital number (P) recorded within Sequoia image data can be converted to a pseudo-radiance in arbitrary units R homogeneous to W sr−1 m−1 according to Equation (1), where ɛ is the exposure time in seconds, γ is the ISO, f is the f-number (f = 2.2) and A, B and C are camera-specific calibration coefficients which model the non-linear behaviour of the CMOS sensor and are measured in production for each camera [31].
There are several options for deriving HCRF (ρ) from the measured pseudo-radiance R. One commonly applied to drone-based data is the use of a single reference target with a known reflectance factor, imaged proximally before or after the acquisition. This is essentially a one-point simplified empirical line method (ELM) [32] with zero intercept where the band-specific calibration coefficient for converting R to ρ is the ratio of known HCRF of the target () and the spatially averaged R over the target () (Equation (2)). This simplified correction procedure is part of the default workflow for reflectance map generations in photogrammetry softwares such as Pix4D and Agisoft Metashape. Irradiance information which is recorded by the upward-facing sunshine sensor is not used here and the irradiance assumed constant throughout the acquisition.
White (100% reflective) reference targets are unsuited for use with many current drone-based sensors, as the integration times needed to achieve a satisfactory signal-to-noise ratio in the rest of the scene lead to oversaturation over very bright surfaces [13,33]. The reference panel used in this study was a Kodak grey-card, an inexpensive reference panel common in photography, with an approximate 20% reflectance across bands. In a previous study, the difference between the use of a grey card reference and an assumed Lambertian Spectralon® panel of higher (40%) reflectance was shown to be minimal within this calibration procedure [34].
An alternative to the proximal panel calibration is the use of the ELM using reference targets imaged in-flight. A linear model formed by ordinary least squares regression against multiple reference targets or merely one dark and bright target is used to relate to . Adjacency effects, due to diffuse scattering, have previously been observed influencing the reflectance of dark reference panels and leading to erroneous negative values in shaded or dense canopy areas [35], which was also found in a preliminary analysis for this study. Therefore, two alternate versions of the ELM approach were tested using (1) one bright reference panel and the intercept set to zero, (2) one bright reference panel with the intercept set to zero and the lowest value occurring within the vegetated scene subtracted from the data, following recommendations by [35].
2.4.2. Vegetation Index Products
The four bands of the Sequoia sensor allow the calculation of several VIs which are indicative of vegetation vigour and status. Two commonly employed indices were selected for this analysis, the normalised difference vegetation index (NDVI) (Equation (3)) and the red-edge chlorophyll index (CHL) (Equation (4)). The NDVI has been used successfully as an indicator of LAI in crops [36], while CHL is sensitive to canopy chlorophyll content [1].
2.4.3. Multi-Scale HCRF and VI Intercomparison
In order to compare HCRF measurements between data sources, they must be resampled to common spectral and spatial resolutions. To derive panel validation HCRF corresponding to the Sequoia bands, the ASD measured HCRF values were convolved with the Sequoia relative sensor spectral response functions (SRF) (Figure 3). In A1 at a ground sampling distance of 4.15 cm, approximately 140 pixels per reference panel were resolved in the stitched orthomosaic. However, due to concerns of adjacency effects/stray light influencing the values towards the panel edges, only the mean of the central 16 pixels per panel were used and very small inter-pixel differences verified by analysing their standard deviation. If canvas targets are used, a larger number of pixels would be required to account for variability due to surface unevenness.
For an intercomparison of Sequoia derived HCRF values with HyPlant HCRF, the drone derived HCRF orthomosaic was spatially resampled to 1 m spatial resolution. The hyperspectral reflectance values were convolved with the Sequoia SRF, following the basic procedure described by [37] to yield HCRF comparable with the Sequoia bands.
Relative offsets between the image datasets were reduced by updating the georeferencing of the HyPlant image with a 2D polynomial in ArcMap (ESRI, US) using clearly identifiable tie-points between datasets and nearest-neighbour resampling. After spectral resampling, Sequoia comparable VIs were derived from the HyPlant dataset. The resampled HCRF and VI datasets were compared pixel-wise for the entire extent of A2. NDVI values over the sampled ESUs (see Section 2.3.2) were also compared, and a non-linear regression of the NDVI mean values versus estimated LAI was performed.
VIs were further compared to those derived from S2 data (utilising bands 4 and 7 for NDVI, bands 6 and 7 for CHL). For this comparison, Sequoia and HyPlant data were spatially resampled to 20 m resolution and HyPlant bands spectrally resampled to the target S2 bands.
Deviations between datasets are assessed using the mean absolute deviation (MAD) and relative error metrics. MAD was selected as an unambiguous metric that weighs all differences between the datasets equally.
3. Results
3.1. HCRF Products
The HCRF products were derived from the Sequoia, HyPlant and S2 image data and georeferenced and clipped to the extent of the drone dataset. The georeferencing root mean squared error for the Sequoia A2 orthomosaic was 0.007 m. A visual comparison of false-colour infrared composites (Figure 5a), as well as representative spectra, are presented (Figure 5b). It is evident that the drone data can resolve the row structure of the crop and small patches of bare ground. The detailed information on the spatial heterogeneity of the field is partially lost at the comparatively coarse resolution of S2. At this resolution, it was furthermore impossible to extract pure spectral information on soil due to mixed pixels. The HyPlant dataset was able to well-represent the variability of vegetation cover while the reflectance spectra provide an additional wealth of information, particularly by finely resolving the green-peak (550 nm), the chlorophyll absorption in the red wavelength regions (600–700 nm), as well as the sharp red-edge increase in reflectance of healthy vegetation (730 nm). These wavelength regions were all covered by the Sequoia and S2 sensors resolving the same features but at a much coarser spectral resolution.
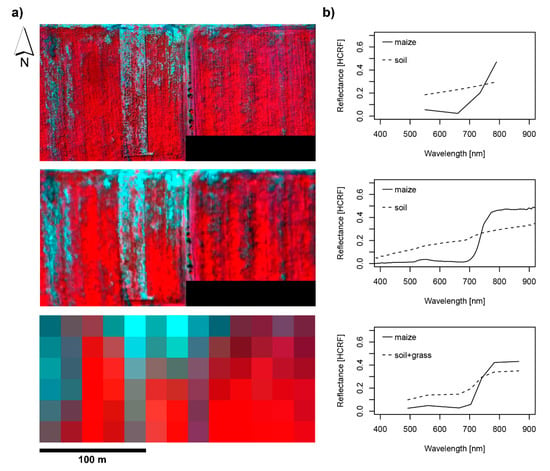
Figure 5.
False-colour infrared representations (a) and representative hemispherical-conical reflectance factors (HCRF) spectra (b) of the Sequoia (top), HyPlant (middle) and S2 (bottom) surface reflectance products over the maize field study site (no pure soil pixel for S2). The subsets shown are the extents analysed. Aerosol and water vapour bands of S2 were omitted.
3.1.1. Reference Target Validation of Drone Derived HCRF
The Sequoia derived HCRF values extracted from the mean of the central pixels of the reference panels imaged in-flight, as well as for a grass and soil target, were compared against in situ ASD-measured HCRF using MAD (Figure 6, Table 2). For the green band, the two brightest panels (>39% reflectance) were saturated and therefore excluded from the analysis. This sensor-inherent issue for the visible bands has been verified by previous studies [35,38] and limits its applicability to surfaces of intermediate brightness.
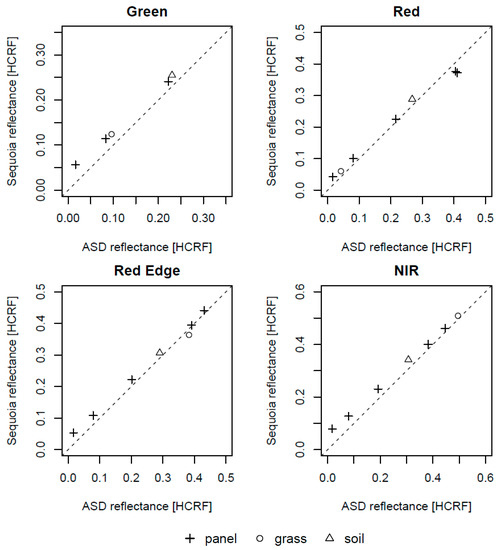
Figure 6.
Sequoia multispectral image data-derived HCRF of validation targets compared to ASD measurements.

Table 2.
Mean absolute deviation (MAD) of Sequoia derived HCRF values per band for the three calibration approaches, estimated from the comparison with field measured reference panels and surfaces.
The standard deviations between the individual pixel values of the panels, assessed for the single panel approach, were small (green: 0.0015, red: 0.0023, red edge: 0.0028, NIR: 0.0020).
Overall, errors per band are in the 2–4% reflectance range which equals 4–15% relative error (Table 2). The largest errors are most apparent for the lower reflective panels in the NIR band, while there is a general over-estimation of reflectance values across all bands. The only exceptions are the grass target which is underestimated in the red edge band as well as the brightest reference panels imaged in the red band. The performance of the single panel calibration and the 0 intercept ELM is similar, while the subtraction of the minimum value within the image leads to considerably smaller errors for the green band, but the largest errors within the NIR band. Therefore, the error does not appear to be a simple offset but shows a wavelength-dependent behaviour, as well as being related to the magnitude of the target reflectance, which is clearly visible for the NIR band (Figure 6).
3.1.2. Spatial Comparison between Airborne and Drone Derived Surface Reflectance
The spatial comparison of the HCRF values was performed for all three reflectance calibration approaches by computing MAD between Sequoia and HyPlant HCRF (Table 3). The HCRFs from the proximal panel approach are visualised as scatterplots per band (Figure 7), as well as difference images between the HCRF values (Figure 8). The relative errors for HyPlant HCRF over the Sequoia band ranges for the three validation tarps were also computed (Table 4).

Table 3.
MAD of Sequoia derived HCRF values per band for the three calibration approaches, estimated from the comparison with HyPlant HCRF values.
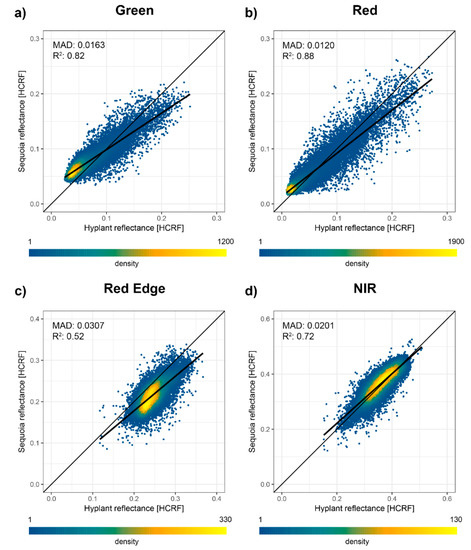
Figure 7.
Scatterplot comparisons of Sequoia and HyPlant based HCRF values for the four bands analysed over the region of interest with an ordinary least squares regression line (bold), the R2 and the MAD.

Figure 8.
Difference images (Sequoia A2 minus HyPlant) of the HCRF values of the four analysed bands over the studied maize fields.

Table 4.
Bias and relative errors of the HyPlant HCRF for the Sequoia band spectral ranges over three differently reflective validation surfaces (tarps).
It is apparent that for the visible bands, pixels which contain dense vegetation are over-estimated in terms of HCRF by the Sequoia by approximately 0.03 while the higher reflective bare-ground pixels are underestimated by a similar amount (Figure 7 and Figure 8). For more mixed pixels, the differences compensate each other and the reflectance is much closer to the HyPlant derived values. As observed for the panel validation experiment, the single panel calibration and 0 intercept ELM based on in-field panels result in similar deviations. The minimum subtraction method greatly increases deviations for the infrared bands.
The difference images (Figure 8) do not exhibit strong surface cover independent spatial bias, except for some spatial variation in the red-edge and NIR bands. For the red-edge, the area covered by F2B (eastern field) is closer to the HyPlant HCRF (mean bias: −0.0135) while the area covered by F2A (western field) is significantly lower (mean bias: −0.0417). This also explains the larger variation of Sequoia red-edge HCRF as opposed to HyPlant values in the scatterplot (Figure 7).
Possible view-angle related effects are visible in the difference image of the NIR band (Figure 8) as faint horizontal striping parallel to the drone flight path and perpendicular to the vertical striping from variable vegetation cover.
3.2. Vegetation indices
VIs derived from Sequoia and HyPlant data, as well as S2 data were compared pixel-wise across the same extent as HCRF (Figure 9 and Figure 10) and the MADs for different calibration methods reported (Table 5). Finally, Histograms of Sequoia and HyPlant NDVI values and their model fits were compared for 10 x 10 m ESUs of varying LAI (Figure 11).
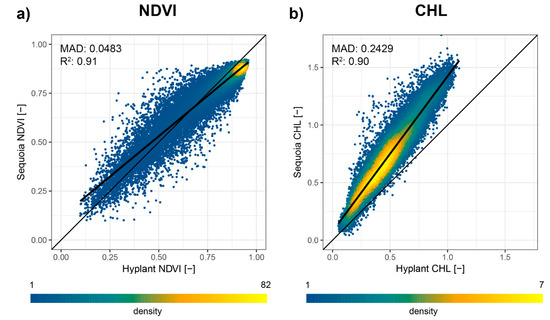
Figure 9.
Scatterplot comparisons of Sequoia and HyPlant based normalised difference vegetation index (NDVI) (a) and chlorophyll index (CHL) (b) values for the region of interest with an ordinary least squares regression line (bold) and the MAD.
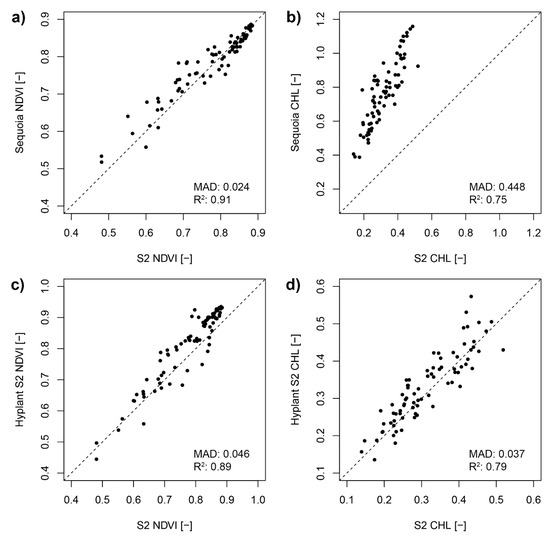
Figure 10.
Top: Scatterplots of NDVI (a) and CHL values (b) derived from S2 and Sequoia imagery (resampled to 20 m spatial resolution). Bottom: Scatterplots of NDVI (c) and CHL values (d) derived from S2 and HyPlant imagery (resampled to 20 m spatial resolution).

Table 5.
MAD of Sequoia derived vegetation index (VI) values (NDVI and CHL) for the three calibration approaches, estimated from the comparison with HyPlant derived index values.
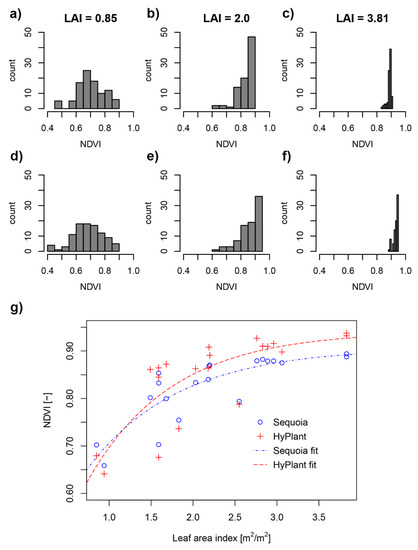
Figure 11.
Histograms of Sequoia (a–c) and HyPlant (d–f) NDVI values for three 10 × 10 m ESUs of varying LAI. (g) NDVI values averaged over ESU extents and the corresponding LAI value measured in the field. Non-linear model fits are provided for illustrative purposes.
While NDVI appears in relatively good agreement across the range for all datasets (Figure 9a and Figure 10a,c), it is evident from the scatterplots, histograms and LAI models (Figure 11) that lower NDVI values due to low vegetation fraction and higher soil contribution are overestimated by the Sequoia data while high NDVI values stemming from purely vegetated pixels are slightly underestimated.
For the CHL index, there is a good linear relationship between the datasets but a very clear offset which increases with higher values of CHL (Figure 9b and Figure 10b). For the Sequoia comparison with S2 (Figure 10b), this is to be expected due to a slight difference in red-edge band positions (Figure A1) but does not explain the offset in comparison to HyPlant (Figure 9b). The impact of HyPlant band spacing was tested using simulated data, the methodology and results of which can be found in the Appendix A. Mean estimated errors for all bands were very small across a variation of LAI and chlorophyll content values, the largest of which were found for the red-edge band (0.00037 for LAI 0.5 to 10 m2/m2 and 0.00018 for chlorophyll from 0 to 100 µg/cm2, Table A1).
4. Discussion
4.1. HCRF Accuracy
The reference panel validation analysis of HCRF factors showed that Sequoia values tended to overestimate panel reflectance by 4–15% (Figure 6, Table 1), and that this effect was most severe for lower reflective panels. The magnitude of deviations from field measurements were comparable to those of other vegetation-focused studies using an identical or similar sensor [23,39]. Going further, this study allowed an assessment of HCRF over varied maize canopy cover at high spatial resolutions (1 m) using the HyPlant dataset, where the same trend of overestimated HCRF in the visible bands was observed for densely vegetated pixels (Figure 7). The HyPlant dataset itself was shown to be sufficiently accurate to serve as reference for the purpose of this comparison (Table 4).
The reason for the overestimation of HCRF for the low reflective panels was likely due to the influence of diffuse scattering and adjacency effects, as pointed out by [35]. Additional spatial smoothing, also affecting the vegetated scene, is caused by projection and stitching which represents an aggregation of pixel values from multiple images during orthomosaic generation. This reduces detector noise but may also lead to bias in measured HCRF. Compensation of this effect could involve kernel-based sharpening/deblurring [40] but restoring original pure spectral responses is not trivial and there have been no studies investigating methods to be used at centimetre scale spatial resolutions where contamination of multiple neighbouring pixels prevails. For panel-based comparisons and calibration, these forms of adjacency effects can be avoided by resolving a greater amount of pure pixels per target which means flying at lower altitude or deploying larger targets relative to the sensor GSD [39].
In addition to adjacency effects, increased temperatures during operation lead to a considerable influence of dark current on measurements [41]. Insufficient compensation of this effect, as well as the non-linearity of the CMOS sensor during software internal calibration to pseudo-radiance (Equation (1)) are further sources of uncertainty [31,35] which may have led to the zero-intercept and modified ELM calibration not yielding overall improvements. Nevertheless, the strong linear relationships observed for the visible bands in comparison with HyPlant HCRF (green R2: 0.82, red R2: 0.88, Figure 7) highlight the potential for improvements of the ELM calibration procedure.
The largest deviations between the image datasets of Sequoia and HyPlant HCRF were found over the red-edge band (Figure 7 and Figure 8) and an offset was also observed for the ASD-measured grass target in the field (Figure 6). As vegetation reflectance increases sharply within the red-edge spectral region, uncertainties within the SRF and the spectral resampling between HCRF products can be expected to have a large impact on derived Sequoia HCRF. The approximated Sequoia SRF for the red-edge band derived from manufacturer information on filter transmission and CMOS sensitivity may be insufficient. This would explain why no strong offsets were observed for the validation panels with spectrally flatter reflectance responses across the measured wavelength range (Figure 6).
Overall, the observed errors are large in an imaging spectroscopy context, indicating that there is still progress to be made in terms of calibration and the implementation of drone MCA data processing and correction procedures within commercial software such as Agisoft Metashape and Pix4D as well as the radiometric calibration reliant on manufacturer calibration coefficients (A, B and C in Equation (1)) which result from high-throughput processes [31]. This software implemented workflow is not currently designed with the goal of delivering reproducible scientific data as there is a lack of transparency considering some key processing steps due to commercially sensitive information. The sensor itself is designed for out-of-the box operation in an agricultural context. In order to guarantee robust HCRF from drones, full lab-based characterisation of sensors and absolute radiometric calibration methodology remains a necessity [42], which however comes at considerable financial cost.
The applications of accurate HCRF data from drone platforms are only beginning to be explored. Opportunities include the evaluation of satellite HCRF products and the performance of atmospheric correction [23], commonly reliant on point-based measurements of uniform surfaces [43] which drone-based measurements can extend to larger, more varied systems. Work towards accurate band-specific HCRFs is further motivated by the ability to provide more information in the context of vegetation biophysical parameter retrieval for the identification of best-suited models e.g., by means of Gaussian process regressions [44].
While this work showed the current limitations of accurate drone-based HCRF retrieval using compact MCA sensors, potential applications motivate the further characterisation of sensor uncertainties and identification of optimal calibration procedures.
4.2. Multi-Scale VI Consistency and Sensitivity
Comparisons with the spatially consistent HyPlant product could provide an assessment of orthomosaic product consistency at unprecedented spatial resolution. Spatial variabilities related to acquisition artefacts have been known to influence stitched orthomosaic drone data products [45], but have previously only been evaluated with repeat measurements at different viewing or solar angles [39,46]. Our findings based on near-simultaneous reference data show that a high level of consistency can be expected even from non-gimbaled drone multispectral measurements which are the default for low-cost practical implementations, e.g., in precision agriculture. However, as directional effects vary greatly depending on plant structural type [47], there is a further need for assessing the impacts on drone-derived VIs over different crops.
The analysis over field-sampled 10 × 10 m ESU plots showed that uncertainties in calibration and radiometry express themselves in a reduced sensitivity of Sequoia NDVI to LAI, assessed against HyPlant NDVI values (Figure 11). This demonstrates that efforts towards reliable calibration are important and can yield improvements even for studies only seeking to derive empirical relationships between VIs and biophysical parameters or where relative VI information is used, such as in guided fertiliser application [48].
Despite these observed biases, there was a strong correspondence between drone-derived VIs and the coarser-grained HyPlant and S2 datasets (NDVI R2 = 0.91, CHL R2 = 0.75–0.9, Figure 9 and Figure 10), indicating that the drone VIs can reflect variations within maize canopy cover and can be compared across scales. This highlights the potential for integrating drone-based VI measurements within or as an alternative to coarser resolution workflows either as validation or additional measurements at desired time steps for monitoring purposes, such as identifying water limitation or phenology of vegetation canopies [22,49]. This remains feasible and cost-effective for study areas <5 ha [50]. However, for multi-temporal monitoring, the stability of derived indices to slightly different acquisition conditions (solar angles, atmospheric composition) is of similar importance to spatial consistency and warrants further investigation as particularly solar angle variations have been shown to have a potentially large effect [39]. This was highlighted by results for the red-edge band in this study, where these temporal changes were visible even between the two drone acquisitions needed to cover the study area (Figure 8c). The long duration of acquisitions during changing illumination conditions represents a major shortcoming of drone-based monitoring [51]. The results presented in this study represent an ideal case based on almost-concurrent acquisitions during constant illumination conditions.
Current developments in drone sensor technology will aid in improving within-product consistency and comparability between drone and satellite measurements. Introducing band-pass filters for MCA sensors that closely match those of satellite sensors, such as the MAIA camera with S2 equivalent bands [44] will reduce band-position based offset effects. Efforts towards fully gimbaled integrations of cameras and irradiance sensors even on lightweight drones may further remove viewing angle and illumination effects and lead to improved product consistency.
5. Conclusions
This study focused on the assessment of accuracy and spatial consistency of drone-based HCRF acquired during ideal illumination conditions, as well as the accuracy of vegetation indices and their comparability to products from other sensors which included a fine-resolution HCRF comparison with simulated spectral bands using the HyPlant DUAL hyperspectral imaging sensor.
MCA derived individual band HCRF values exhibited bias when compared to ASD in situ measurements, particularly over lower reflective surfaces with HCRF < 20% and none of the assessed simple calibration procedures (proximal panel calibration, 0 intercept ELM and minimum subtracted 0 intercept ELM) performed consistently better over all spectral bands. HCRF outputs from simplified calibration procedures should, therefore, be used with caution and independent assessments using high-quality HCRF measurements over large reference targets are encouraged for studies seeking to identify optical properties from drones. Thorough lab-based sensor calibration remains a requirement for reliable physical measurements.
Conversely, the good level of spatial consistency of the drone-mounted MCA-derived products and comparability of NDVI values to those of airborne and spaceborne sensors found in this study mean that drone derived VIs show promise for vegetation monitoring at high spatial resolutions as well as improving temporal resolutions of time series for dedicated study sites (e.g., flux tower footprints), in addition to satellite datasets.
While this study mainly assessed HCRF and VIs from drone MCAs in context of coarser spatial resolutions (1 and 20 m GSD), the ability of drone sensors to resolve individual canopies and even leaves, separating them from background and shading effects, harbours great potential for mapping biochemical plant traits at high resolutions. Once reliable solutions for operational calibration of drone MCA HCRF have been found, the investigation of methods and uncertainties in linking HCRF at the centimetre pixel scale to field measured optical properties of individual leaves and canopies is anticipated to be at the forefront of drone-based vegetation research.
Author Contributions
D.F. wrote the manuscript with significant inputs from all co-authors. D.F., C.P., M.B. and K.A. conceptualised parts of the study. Fieldwork was carried out by D.F., C.P., M.B., G.T., M.C., A.E., K.B. and R.C. with R.C., M.C., C.P., M.B., U.R. and F.M. administering the field campaign. HyPlant datasets and specific inputs were shared by U.R. and D.F. processed the drone data and performed the analysis. All authors have read and agreed to the published version of the manuscript.
Funding
K.A. and D.F. received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie Grant Agreement No 721995. HyPlant data acquisition and processing was funded by the European Space Agency (ESA) in the frame of the FLEXSense campaign (ESA Contract No. ESA RFP/3-15477/18/NL/NA).
Acknowledgments
We thank Jean-Philippe Mevy (IMBE, Aix-Marseille Université) for supporting the field spectroscopy measurements as well as Fondazione per il Clima e la Sostenibilità (FCS), Martina Anelli, Monica Pepe and Gabriele Candiani for general field work support. We also thank “Fattoria Poggetti Vecchi” for hosting the field experiments.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Simulations
In order to investigate the sensitivity of the Sequoia derivable indices NDVI and CHL to the variables of interest as well as the effect of band position differences and its implications for the comparability of Sequoia and S2 derived products in isolation of other influencing factors (e.g., differences due to atmospheric correction, Sequoia data calibration and viewing geometry), a range of vegetation reflectance spectra were simulated using the PROSAIL model which couples the leaf reflectance model PROSPECT with the canopy geometry model SAIL [52]. All parameters besides the LAI and Chlorophyll a+b content were fixed following [53] to values typical for maize, though they do acknowledge that the model is not ideally suited for simulating the geometric properties of a row crop.
The simulations were also used to evaluate the uncertainty due to the HyPlant band spacing when resampled to Sequoia spectral bands.
For the first series, LAI was varied between values of 1 and 10 m2/m2 (10 steps) while Chlorophyll a+b content was set to 50 µg/cm2. For the second series, LAI was kept constant at a value of 3 while Chlorophyll a + b content was varied between 0 and 100 µg/cm2 (10 steps).
Results revealed that for varying LAI, NDVI values derived from Sequoia bands should match those from the equivalent S2 bands despite SRF differences. CHL values, on the other hand, were found, via PROSAIL, to be not directly comparable due to slight band position differences (Figure A1).
Mean estimated errors due to the HyPlant spectral sampling interval for all bands were very small across a variation of LAI and chlorophyll content values (Table A1).
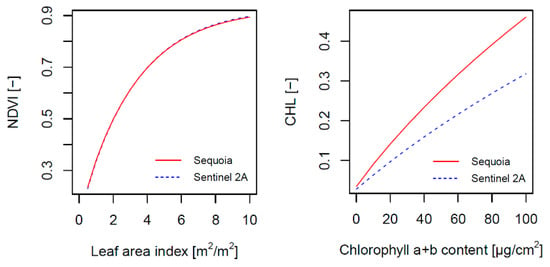
Figure A1.
Simulated Sequoia and Sentinel 2A derived NDVI and CHL values for simulations of varying LAI and Chlorophyll a + b content respectively.

Table A1.
Errors due to spectral sampling interval of the HyPlant bands spectrally resampled to simulate Sequoia data, assessed per band for a PROSAIL simulated series of leaf area index (LAI) and chlorophyll content of a maize-like canopy.
Table A1.
Errors due to spectral sampling interval of the HyPlant bands spectrally resampled to simulate Sequoia data, assessed per band for a PROSAIL simulated series of leaf area index (LAI) and chlorophyll content of a maize-like canopy.
| MAD between Sequoia Band Resampled Values and HyPlant to Sequoia Band Resampled Values | LAI Series (0.5–10) | Chlorophyll Content Series (0–100 µg/cm2) |
|---|---|---|
| Green | 0.0002 | 0.0001 |
| Red | 5.2631 × 10−6 | 1.6583 × 10−6 |
| Red edge | 0.0001 | 6.4832 × 10−5 |
| NIR | 5.7975 × 10−5 | 2.0239 × 10−5 |
References
- Gitelson, A.A.; Viña, A.; Ciganda, V.; Rundquist, D.C.; Arkebauer, T.J. Remote estimation of canopy chlorophyll content in crops. Geophys. Res. Lett. 2005, 32, 1–4. [Google Scholar] [CrossRef]
- Tucker, C.J.; Vanpraet, C.L.; Sharman, M.J.; Van Ittersum, G. Satellite remote sensing of total herbaceous biomass production in the senegalese sahel: 1980–1984. Remote Sens. Environ. 1985, 17, 233–249. [Google Scholar] [CrossRef]
- Gamon, J.A.; Somers, B.; Malenovský, Z.; Middleton, E.M.; Rascher, U.; Schaepman, M.E. Assessing Vegetation Function with Imaging Spectroscopy. Surv. Geophys. 2019, 40, 489–513. [Google Scholar] [CrossRef]
- Gamon, J.A. Reviews and Syntheses: Optical sampling of the flux tower footprint. Biogeosciences 2015, 12, 4509–4523. [Google Scholar] [CrossRef]
- Gamon, J.A.; Cheng, Y.; Claudio, H.; MacKinney, L.; Sims, D.A. A mobile tram system for systematic sampling of ecosystem optical properties. Remote Sens. Environ. 2006, 103, 246–254. [Google Scholar] [CrossRef]
- Hilker, T.; Coops, N.C.; Nesic, Z.; Wulder, M.A.; Black, A.T. Instrumentation and approach for unattended year round tower based measurements of spectral reflectance. Comput. Electron. Agric. 2007, 56, 72–84. [Google Scholar] [CrossRef]
- Anderson, K.; Gaston, K.J. Lightweight unmanned aerial vehicles will revolutionize spatial ecology. Front. Ecol. Environ. 2013, 11, 138–146. [Google Scholar] [CrossRef]
- Berni, J.A.J.; Zarco-Tejada, P.J.; Suárez, L.; Fereres, E. Thermal and narrowband multispectral remote sensing for vegetation monitoring from an unmanned aerial vehicle. IEEE Trans. Geosci. Remote Sens. 2009, 47, 722–738. [Google Scholar] [CrossRef]
- Garzonio, R.; di Mauro, B.; Colombo, R.; Cogliati, S. Surface reflectance and sun-induced fluorescence spectroscopy measurements using a small hyperspectral UAS. Remote Sens. 2017, 9, 472. [Google Scholar]
- Duffy, J.P.; Cunliffe, A.M.; DeBell, L.; Sandbrook, C.; Wich, S.A.; Shutler, J.D.; Myers-Smith, I.H.; Varela, M.R.; Anderson, K. Location, location, location: Considerations when using lightweight drones in challenging environments. Remote Sens. Ecol. Conserv. 2017, 4, 7–19. [Google Scholar] [CrossRef]
- Assmann, J.J.; Kerby, J.T.; Cunliffe, A.M.; Myers-smith, I.H. Vegetation monitoring using multispectral sensors—Best practices and lessons learned from high latitudes. J. Unmanned Veh. Syst. 2019, 7, 54–75. [Google Scholar] [CrossRef]
- Johansen, K.; Raharjo, T.; McCabe, M.F. Using multi-spectral UAV imagery to extract tree crop structural properties and assess pruning effects. Remote Sens. 2018, 10, 854. [Google Scholar] [CrossRef]
- Manuel Fernández-Guisuraga, J.; Sanz-Ablanedo, E.; Suárez-Seoane, S.; Calvo, L. Using Unmanned Aerial Vehicles in Postfire Vegetation Survey Campaigns through Large and Heterogeneous Areas: Opportunities and Challenges. Sensors 2018, 18, 586. [Google Scholar] [CrossRef] [PubMed]
- Nebiker, S.; Lack, N.; Abächerli, M.; Läderach, S. Light-weight multispectral uav sensors and their capabilities for predicting grain yield and detecting plant diseases. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. ISPRS Arch. 2016, 2016, 963–970. [Google Scholar] [CrossRef]
- Wang, S.; Garcia, M.; Ibrom, A.; Bauer-gottwein, P. Temporal interpolation of land surface fluxes derived from remote sensing—Results with an Unmanned Aerial System. Hydrol. Earth Syst. Sci. 2019, 1–27. [Google Scholar] [CrossRef]
- Kelcey, J.; Lucieer, A. Sensor correction of a 6-band multispectral imaging sensor for UAV remote sensing. Remote Sens. 2012, 4, 1462–1493. [Google Scholar] [CrossRef]
- Damm, A.; Guanter, L.; Verhoef, W.; Schläpfer, D.; Garbari, S.; Schaepman, M.E. Impact of varying irradiance on vegetation indices and chlorophyll fluorescence derived from spectroscopy data. Remote Sens. Environ. 2015, 156, 202–215. [Google Scholar] [CrossRef]
- Bendig, J.; Yu, K.; Aasen, H.; Bolten, A.; Bennertz, S.; Broscheit, J.; Gnyp, M.L.; Bareth, G. Combining UAV-based plant height from crop surface models, visible, and near infrared vegetation indices for biomass monitoring in barley. Int. J. Appl. Earth Obs. Geoinf. 2015, 39, 79–87. [Google Scholar] [CrossRef]
- Miura, T.; Huete, A.R.; Yoshioka, H. Evaluation of sensor calibration uncertainties on vegetation indices for MODIS. IEEE Trans. Geosci. Remote Sens. 2000, 38, 1399–1409. [Google Scholar] [CrossRef]
- Gevaert, C.M.; Suomalainen, J.; Tang, J.; Kooistra, L. Generation of Spectral-Temporal Response Surfaces by Combining Multispectral Satellite and Hyperspectral UAV Imagery for Precision Agriculture Applications. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 3140–3146. [Google Scholar] [CrossRef]
- Van Leeuwen, W.J.D.; Orr, B.J.; Marsh, S.E.; Herrmann, S.M. Multi-sensor NDVI data continuity: Uncertainties and implications for vegetation monitoring applications. Remote Sens. Environ. 2006, 100, 67–81. [Google Scholar] [CrossRef]
- Easterday, K.; Kislik, C.; Dawson, T.; Hogan, S.; Kelly, M. Remotely Sensed Water Limitation in Vegetation: Insights from an Experiment with Unmanned Aerial Vehicles (UAVs). Remote Sens. 2019, 11, 1853. [Google Scholar] [CrossRef]
- Padró, J.C.; Muñoz, F.J.; Ávila, L.Á.; Pesquer, L.; Pons, X. Radiometric correction of Landsat-8 and Sentinel-2A scenes using drone imagery in synergy with field spectroradiometry. Remote Sens. 2018, 10, 1687. [Google Scholar] [CrossRef]
- Schaepman-Strub, G.; Schaepman, M.E.; Painter, T.H.; Dangel, S.; Martonchik, J.V. Reflectance quantities in optical remote sensing-definitions and case studies. Remote Sens. Environ. 2006, 103, 27–42. [Google Scholar] [CrossRef]
- Beck, H.E.; Zimmermann, N.E.; McVicar, T.R.; Vergopolan, N.; Berg, A.; Wood, E.F. Present and future köppen-geiger climate classification maps at 1-km resolution. Sci. Data 2018, 5, 1–12. [Google Scholar] [CrossRef]
- Rascher, U.; Alonso, L.; Burkart, A.; Cilia, C.; Cogliati, S.; Colombo, R.; Damm, A.; Drusch, M.; Guanter, L.; Hanus, J.; et al. Sun-induced fluorescence—A new probe of photosynthesis: First maps from the imaging spectrometer HyPlant. Glob. Chang. Biol. 2015, 21, 4673–4684. [Google Scholar] [CrossRef]
- Siegmann, B.; Alonso, L.; Celesti, M.; Cogliati, S.; Colombo, R.; Damm, A.; Douglas, S.; Guanter, L.; Hanuš, J.; Kataja, K.; et al. The high-performance airborne imaging spectrometer HyPlant—From raw images to top-of-canopy reflectance and fluorescence products: Introduction of an automatized processing chain. Remote Sens. 2019, 11, 2760. [Google Scholar] [CrossRef]
- Facchi, A.; Baroni, G.; Boschetti, M.; Gandolfi, C. Comparing Optical and Direct Methods for Leafarea Index Determination in a Maize Crop. J. Agric. Eng. 2010, 41, 33. [Google Scholar]
- Baret, F.; Weiss, M.; Allard, D.; Garrigues, S.; Leroy, M.; Jeanjean, H.; Fernandes, R.; Myneni, R.; Privette, J.; Morisette, J. VALERI: A network of sites and a methodology for the validation of medium spatial resolution land satellite products. Remote Sens. Environ. 2005, 76, 36–39. [Google Scholar]
- Parrot Parrot Sequoia Application Notes. Available online: https://forum.developer.parrot.com/t/parrot-announcement-release-of-application-notes/5455 (accessed on 2 February 2020).
- Fallet, C.; Domenzain, L.M. Necessary Steps for the Systematic Calibration of A Multispectral Imaging System to Achieve A Targetless Workflow in Reflectance Estimation: A Study of Parrot SEQUOIA for Precision Agriculture. In Proceedings of the Algorithms and Technologies for Multispectral, Hyperspectral, and Ultraspectral Imagery XXIV, Orlando, FL, USA, 17–19 April 2018; p. 42. [Google Scholar]
- Smith, G.M.; Milton, E.J. The use of the empirical line method to calibrate remotely sensed data to reflectance. Int. J. Remote Sens. 1999, 20, 2653–2662. [Google Scholar] [CrossRef]
- Jakob, S.; Zimmermann, R.; Gloaguen, R. The Need for Accurate Geometric and Radiometric Corrections of Drone-Borne Hyperspectral Data for Mineral Exploration: MEPHySTo—A Toolbox for Pre-Processing Drone-Borne Hyperspectral Data. Remote Sens. 2017, 9, 88. [Google Scholar] [CrossRef]
- Fawcett, D.; Anderson, K. Investigating Impacts of Calibration Methodology and Irradiance Variations on Lightweight Drone-Based Sensor Derived Surface Reflectance Products. In Proceedings of the Remote Sensing for Agriculture, Ecosystems, and Hydrology XXI, Strasbourg, France, 9–11 September 2019. [Google Scholar]
- Tu, Y.-H.; Phinn, S.; Johansen, K.; Robson, A. Assessing Radiometric Correction Approaches for Multi-Spectral UAS Imagery for Horticultural Applications. Remote Sens. 2018, 10, 1684. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Wardlow, B.D.; Keydan, G.P.; Leavitt, B. An evaluation of MODIS 250-m data for green LAI estimation in crops. Geophys. Res. Lett. 2007, 34, 2–5. [Google Scholar] [CrossRef]
- D’Odorico, P.; Gonsamo, A.; Damm, A.; Schaepman, M.E. Experimental evaluation of sentinel-2 spectral response functions for NDVI time-series continuity. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1336–1348. [Google Scholar] [CrossRef]
- Gilliot, J.-M.; Michelin, J.; Faroux, R.; Domenzain, L.M.; Fallet, C. Correction of in-flight luminosity variations in multispectral UAS images, using a luminosity sensor and camera pair for improved biomass estimation in precision agriculture. Proc. SPIE Int. Soc. Opt. Eng. 2018, 10664, 1066405. [Google Scholar]
- Stow, D.; Nichol, C.J.; Wade, T.; Assmann, J.J.; Simpson, G.; Helfter, C. Illumination Geometry and Flying Height Influence Surface Reflectance and NDVI Derived from Multispectral UAS Imagery. Drones 2019, 3, 55. [Google Scholar] [CrossRef]
- Ji, H.; Wang, K. Robust image deblurring with an inaccurate blur kernel. IEEE Trans. Image Process. 2012, 21, 1624–1634. [Google Scholar] [CrossRef]
- Adler, K. Radiometric Correction of Multispectral Images Collected by A UAV for Phenology Studies; Lund University: Lund, Sweden, 2018. [Google Scholar]
- Hakala, T.; Markelin, L.; Honkavaara, E.; Scott, B.; Theocharous, T.; Nevalainen, O.; Näsi, R.; Suomalainen, J.; Viljanen, N.; Greenwell, C.; et al. Direct reflectance measurements from drones: Sensor absolute radiometric calibration and system tests for forest reflectance characterization. Sensors 2018, 18, 1417. [Google Scholar] [CrossRef]
- Thome, K.; Smith, N.; Scott, K. Vicarious Calibration of MODIS Using Railroad Valley Playa. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS), IEEE, Yokohama, Japan, 9–13 July 2001; Volume 3, pp. 1209–1211. [Google Scholar]
- Revill, A.; Florence, A.; MacArthur, A.; Hoad, S.; Rees, R.; Williams, M. The Value of Sentinel-2 Spectral Bands for the Assessment of Winter Wheat Growth and Development. Remote Sens. 2019, 11, 2050. [Google Scholar] [CrossRef]
- Aasen, H.; Bolten, A. Multi-temporal high-resolution imaging spectroscopy with hyperspectral 2D imagers – From theory to application. Remote Sens. Environ. 2018, 205, 374–389. [Google Scholar] [CrossRef]
- Hakala, T.; Suomalainen, J.; Peltoniemi, J.I. Acquisition of bidirectional reflectance factor dataset using a micro unmanned aerial vehicle and a consumer camera. Remote Sens. 2010, 2, 819–832. [Google Scholar] [CrossRef]
- Román, M.O.; Gatebe, C.K.; Schaaf, C.B.; Poudyal, R.; Wang, Z.; King, M.D. Variability in surface BRDF at different spatial scales (30 m–500 m) over a mixed agricultural landscape as retrieved from airborne and satellite spectral measurements. Remote Sens. Environ. 2011, 115, 2184–2203. [Google Scholar] [CrossRef]
- Toulios, L.; Dercas, N.; Psomiadis, E.; Kavvadias, A.; Chanioti, M.; Tsitouras, A. Unmanned Aerial Vehicle (UAV) Data Analysis for Fertilization Dose Assessment. In Proceedings of the Remote Sensing for Agriculture, Ecosystems, and Hydrology XIX, Warsaw, Poland, 12–14 September 2017; Volume 1042121, p. 78. [Google Scholar]
- Berra, E.F.; Gaulton, R.; Barr, S. Assessing spring phenology of a temperate woodland: A multiscale comparison of ground, unmanned aerial vehicle and Landsat satellite observations. Remote Sens. Environ. 2019, 223, 229–242. [Google Scholar] [CrossRef]
- Matese, A.; Toscano, P.; Di Gennaro, S.F.; Genesio, L.; Vaccari, F.P.; Primicerio, J.; Belli, C.; Zaldei, A.; Bianconi, R.; Gioli, B. Intercomparison of UAV, aircraft and satellite remote sensing platforms for precision viticulture. Remote Sens. 2015, 7, 2971–2990. [Google Scholar] [CrossRef]
- Hakala, T.; Honkavaara, E.; Saari, H.; Mäkynen, J.; Kaivosoja, J.; Pesonen, L.; Pölönen, I. Spectral Imaging From Uavs Under Varying Illumination Conditions. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2013, XL-1/W2, 189–194. [Google Scholar] [CrossRef]
- Jacquemoud, S.; Verhoef, W.; Baret, F.; Bacour, C.; Zarco-Tejada, P.J.; Asner, G.P.; François, C.; Ustin, S.L. PROSPECT + SAIL models: A review of use for vegetation characterization. Remote Sens. Environ. 2009, 113, S56–S66. [Google Scholar] [CrossRef]
- Atzberger, C.; Richter, K. Spatially constrained inversion of radiative transfer models for improved LAI mapping from future Sentinel-2 imagery. Remote Sens. Environ. 2012, 120, 208–218. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).