About the Pitfall of Erroneous Validation Data in the Estimation of Confusion Matrices

Abstract

Accuracy assessment of maps relies on the collection of validation data, i.e., a set of trusted points or spatial objects collected independently from the classified map. However, collecting spatially and thematically accurate dataset is often tedious and expensive. Despite good practices, those datasets are rarely error-prone. Errors in the reference dataset propagate to the probabilities estimated in the confusion matrices. Consequently, the estimates of the quality are biased: accuracy indices are overestimated if the errors are correlated and underestimated if the errors are conditionally independent. The first findings of our study highlight the fact that this bias could invalidate statistical tests of map accuracy assessment. Furthermore, correlated errors in the reference dataset induce unfair comparison of classifiers. A maximum entropy method is thus proposed to mitigate the propagation of errors from imperfect reference datasets. The proposed method is based on a theoretical framework which considers a trivariate probability table that links the observed confusion matrix, the confusion matrix of the reference dataset and the “real” confusion matrix. The method was tested with simulated thematic and geo-reference errors. It proved to reduce the bias to the level of the sampling uncertainty. The method was very efficient with geolocation errors because conditional independence of errors can reasonably be assumed. Thematic errors are more difficult to mitigate because they require the estimation of an additional parameter related to the amount of spatial correlation. In any case, while collecting additional trusted labels is usually expensive, our result show that the benefits for accuracy assessment are much larger than collecting a larger number of questionable reference data.

1. Introduction

Providing a confusion matrix together with a geolocationmap is a prevailing good practice in remote sensing data analysis [1,2]. The confusion matrix indeed yields a complete summary about the matching between geographic data product and reference data. The entries of the confusion matrix allow map users to derive numerous summary measures of the class accuracy, that can be used to compare different classifiers in scientific studies or to inform end users about the quality of the map. The confusion matrix is also used to achieve a better estimate of the area covered by each class.

The reference datasets used to build the confusion matrix are often assumed to be error-free, but even ground data often include some errors [3]. Confusion matrices and associated quality indices are, therefore, likely to yield biased quality assessment of the maps. The negative impact of those errors on the apparent accuracy of maps has been highlighted in previous studies [4,5]. This impact on accuracy indices has been quantified in situations of correlated and non correlated errors. For instance, a case study showed that $10\%$ errors in a reference dataset lead to $18.5\%$ underestimation of the producer accuracy if errors were independent and $12.5\%$ overestimation if they were correlated [6].

The sources of errors in the collection of ground reference data are well documented, and some recent studies aimed at assessing their contribution depending on whether the errors are thematic or positional. Thematic errors consist in assigning the wrong label to a sample unit because of erroneous classification, (uncertainties of the response design [7], temporal mismatch, transitional classes, class interpretation errors, careless error [8]). Positional errors (also called geolocation errors) may result in incorrect matching of reference and map labels because the geographic position of the sampling unit is shifted with respect to the map (mislocation of testing sites, mislocation of the map or uncertain definition of boundaries) [2,9,10].

A range of approaches have been developed to deal with imperfect reference data. In medical science, Enøe et al. [11] used maximum likelihood methods to handle unknown reference information in a binary case, while Espeland and Handelman [12] used latent class models to obtain consensual confusion matrix among several observers. Those methods help to validate datasets without gold standard [13], but they do not adjust for poor quality reference datasets. In remote sensing, Sarmento et al. [14] integrated information from a second label in the reference dataset to build a confidence value on the accuracy estimates. Foody [6] proposed a method to correct sensitivity and specificity estimates when conditional independence holds and the quality of the reference classification is known. Carlotto [3] proposed a method to retrieve the actual overall accuracy based on the apparent accuracy and the errors between the reference and the “ground truth”. However, this method is assuming that errors are equally distributed amongst classes.

Sub-optimal reference data is a reflection of the costs of acquiring high quality data [6]. Instead of correcting the reference dataset, our method therefore proposes to manage its uncertainty globally in order to obtain a corrected confusion matrix, i.e., a confusion matrix that reflects the matching between the map and the trusted labels. This would be particularly useful to manage the diversity of data sources that are now used for validation ( ground survey or aerial surveys; crowdsourced or expert-based). The major difference with previous studies is that we rebuild at best the full confusion matrix and not only some of the indices that can be derived from it. Furthermore, the proposed method does not assume that errors are equally distributed amongst classes nor that the errors are conditionally independent.

This paper is presenting the theoretical developments for recovering the trusted confusion matrix based on the observed confusion matrix and a confusion matrix between the reference dataset and the trusted labels. These theoretical development are then implemented to illustrate the method based on two synthetic case studies. The first case study addresses thematic errors while the second one focuses on geolocation errors.

2. Theoretical Framework

The confusion matrix is usually assumed to represent the overlay between a map and the “ground truth”. In practice the reference data used to estimate it is not perfect, therefore calling it “ground truth” is improper. In this study, we are referring to a map where a set of m classes are considered, where labels from the classification are indexed with i, while the trusted (ground truth) labels are indexed with j. In parallel, we assume that a reference dataset containing errors has been collected, with labels indexed with k. Typically, the correspondence between the classification and the reference is assessed through a confusion matrix (i.e., the table of the joint counts $n(i,k)$ of pixels classified in class i but referenced in class k), from which the $m\times m$ table of the joint probability estimates $\widehat{p}(i,k)=n(i,k)/n$ is computed, where n refers to the sample size. In parallel, let us consider similarly that the $m\times m$ table of the joint counts $n(j,k)$ is at hand (but not necessarily estimated from the same sample), so that the probability estimates $\widehat{p}(j,k)=n(j,k)/n$ assess the correspondence between the trusted and the reference classes over the study area. There are thus two known confusion matrices: the classified map vs the reference and the reference vs the trusted labels.

What is sought for are estimates for the unknown joint $p(i,j)$ probabilities that assess the correspondence between the classification and the ground truth. Instead of the $p(i,k)$ that only quantifies the quality of the map with respect to a reference—that might differ from the ground truth and whose choice might also differ between users—the $p(i,j)$’s are truly assessing the accuracy of the map. The question is how to estimate at best these probabilities when the only knowledge at hand are the sets of $\widehat{p}(i,k)$’s and $\widehat{p}(j,k)$’s while possibly considering an additional conditional independence hypothesis if relevant. We will show hereafter that this problem can be handled using a maximum entropy (MaxEnt) approach (see, e.g., [15,16] for a presentation of the rationale of the method and its panel of applications).

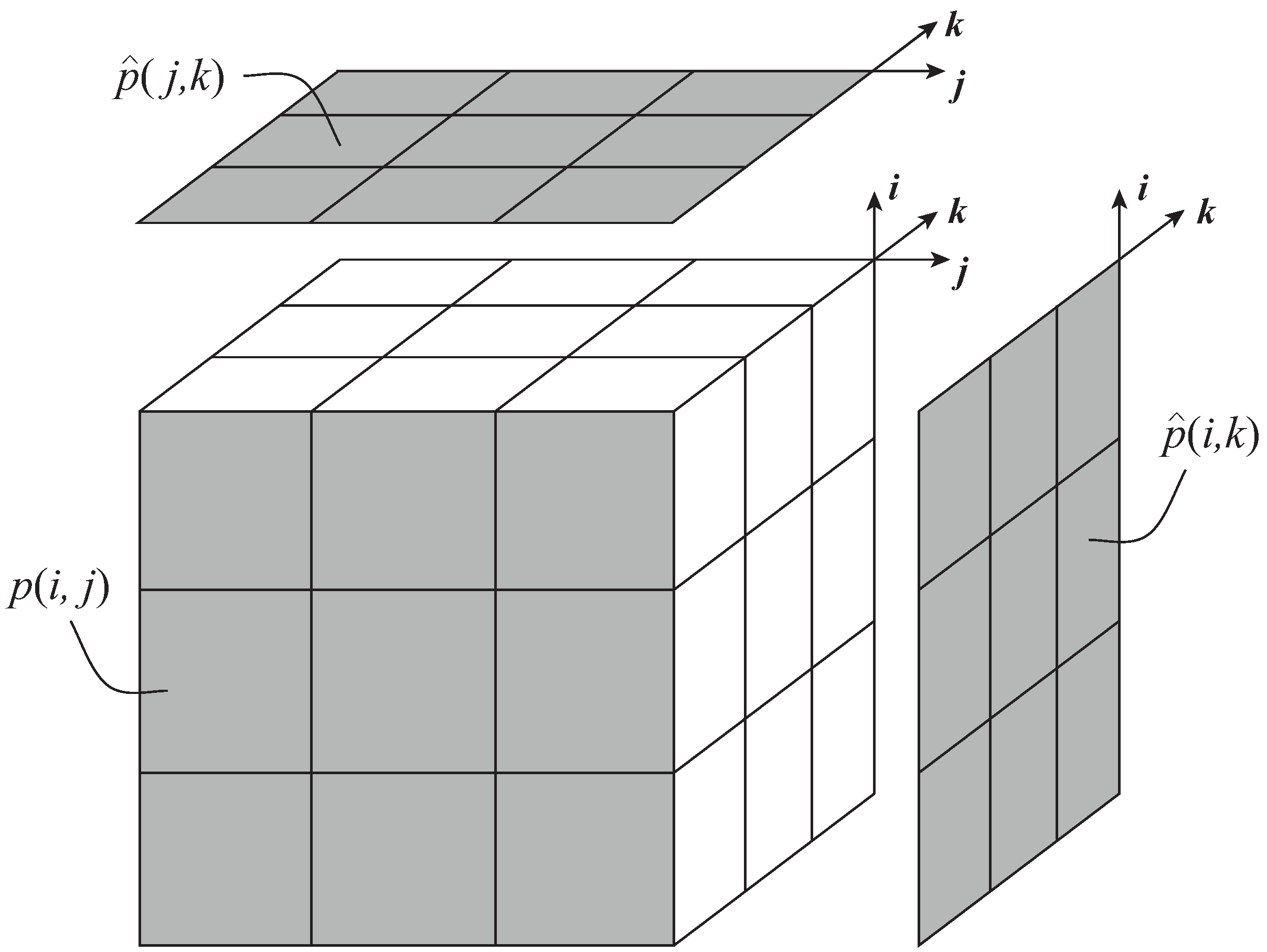
2.1. Joint Probability Table

In order to ease the discussion, let us consider the set of unknown joint probabilities $p(i,j,k)$ that can be organised in a 3D probability table, as shown in Figure 1. By definition, all bivariate probabilities $p(i,j)$, $p(i,k)$ and $p(j,k)$ are marginal probabilities from this table, so that equalling the marginal probabilities with their estimates leads to

$$\sum _{i=1}^{m}p(i,j,k)\stackrel{\Delta }{=}p(j,k)=\widehat{p}(j,k)\forall j,k$$

(1a)

$$\sum _{j=1}^{m}p(i,j,k)\stackrel{\Delta }{=}p(i,k)=\widehat{p}(i,k)\forall i,k$$

(1b)

$$\sum _{k=1}^{m}p(i,j,k)\stackrel{\Delta }{=}p(i,j)\forall i,j$$

(1c)

where the unknown $p(i,j,k)$’s are thus subject to the two constraints given in Equations (1a) and (1b), while Equation (1c) allows us to compute the required $p(i,j)$’s. Furthermore, because ${\sum }_{k}p(j,k)\stackrel{\Delta }{=}p\left(j\right)$, we can further derive from Equation (1a) that $p\left(j\right)=\widehat{p}\left(j\right)$.

When the classification is conducted independently from the selection of the reference, it is reasonable to consider that, for a given “ground truth”, the classification errors are independent from the reference errors. Stated otherwise, we can assume independence between classification and reference errors conditionally to the “ground truth” class. Stated in probability terms, we thus have under this conditional independence the result

$$p(i,k|j)=p(i\left|j\right)p\left(k\right|j)\forall i,j,k$$

(2)

or equivalently (see details in Appendix A)

$$\begin{array}{ccc}\hfill & \hfill & \hfill {\displaystyle p(i,j,k)=\frac{p(i,j)p(j,k)}{p\left(j\right)}\forall i,j,k}\\ \\ \hfill & \hfill ⟺& \hfill {\displaystyle \frac{p(i,j,k)}{p(i,j)}\stackrel{\Delta }{=}p\left(k\right|i,j)=\frac{p(j,k)}{p\left(j\right)}\forall i,j,k}\end{array}$$

(3)

Finally, attention should also be paid to the fact that $\widehat{p}(j,k)$ and $\widehat{p}(i,k)$ cannot be arbitrarily chosen, because summing again over i or j must lead to the same results for $\widehat{p}\left(k\right)$, with

$$\widehat{p}\left(k\right)\stackrel{\Delta }{=}\left\{\begin{array}{c}{\displaystyle \sum _i\widehat{p}(i,k)}\hfill \\ \\ {\displaystyle \sum _j\widehat{p}(j,k)}\hfill \end{array}\right.$$

(4)

However, the usual sum-to-one constraint ${\sum }_{i,j,k}p(i,j,k)=1$ does not need to be explicitly accounted for, as it is automatically enforced from Equations (1a) and (1b) as long as these bivariate probability estimates sum to one, as required.

2.2. Maximum Entropy Estimation

An elegant solution to the estimation of the set of unknown probabilities $\mathbf{p}=\left\{p\right(i,j,k\left)\right\}$ is given by the MaxEnt approach, that aims at looking for $\mathbf{p}$ such that its entropy $H\left(\mathbf{p}\right)$ is maximized, with

$$H\left(\mathbf{p}\right)=E[-ln\mathbf{p}]=-\sum _{i,j,k}p(i,j,k)lnp(i,j,k)$$

(5)

where again $\mathbf{p}$ is subject to the constraints in Equations (1a), (1b) and (3). Using the Lagrangian formalism, it is thus possible to look for $\mathbf{p}$ that maximizes $H\left(\mathbf{p}\right)$ subject to these constraints by maximizing the objective function

$$O\left(\mathbf{p}\right)=H\left(\mathbf{p}\right)+\sum _{i,j}{\lambda }_{ik}\left(p(i,k)-\widehat{p}(i,k)\right)+\sum _{j,k}{\mu }_{jk}\left(p(j,k)-\widehat{p}(j,k)\right)+\sum _{i,j,k}{\kappa }_{ijk}\left(p\left(k\right|i,j)-\frac{\widehat{p}(j,k)}{\widehat{p}\left(j\right)}\right)$$

(6)

where ${\lambda }_{ik}$, ${\mu }_{jk}$ and ${\kappa }_{ijk}$ are Lagrange multipliers and where the last term (i.e., the constraint derived from Equation (3)) is only needed if the conditional independence hypothesis is accounted for. As $H\left(\mathbf{p}\right)$ is convex everywhere, the maximum of Equation (6) can be numerically found using classical constrained convex optimization methods. However, it can be remembered too that maximizing entropy under expectation constraints is equivalent to maximize likelihood (ML) under structural constraints, as each problem is the convex dual of the other. The MaxEnt solution will thus correspond to the ML estimation of $\mathbf{p}$ subject to the conditional independence hypothesis and the $\widehat{p}(i,k)$’s and $\widehat{p}(j,k)$’s estimates. This also means that numerical algorithms used in a ML context are relevant too for finding the MaxEnt solution. In particular, the easy-to-implement iterative proportional fitting algorithm [17] will be used here. For this, let us rewrite $p(i,j,k)$ by accounting for the various constraints in Equations (1a), (1b) and (3), with

$$p(i,j,k)=p(j,k)p\left(i\right|j,k)=\widehat{p}(j,k)\frac{p(i,j,k)}{{\sum }_{i}p(i,j,k)}\forall i,j,k$$

(7a)

$$p(i,j,k)=p(i,k)p\left(j\right|i,k)=\widehat{p}(i,k)\frac{p(i,j,k)}{{\sum }_{j}p(i,j,k)}\forall i,j,k$$

(7b)

$$p(i,j,k)=p\left(k\right|i,j)p(i,j)=\frac{p(j,k)}{p\left(j\right)}p(i,j)=\frac{\widehat{p}(j,k)}{\widehat{p}\left(j\right)}\sum _{k}p(i,j,k)\forall i,j,k$$

(7c)

Starting from initial guesses $p{(i,j,k)}^{\left[0\right]}$, it is then possible to iteratively correct these probabilities by enforcing the constraints, with

$$p{(i,j,k)}^{[\ell +1]}=\widehat{p}(j,k)\frac{p{(i,j,k)}^{[\ell ]}}{{\sum }_{i}p{(i,j,k)}^{[\ell ]}}\forall i,j,k$$

(8a)

$$p{(i,j,k)}^{[\ell +2]}=\widehat{p}(i,k)\frac{p{(i,j,k)}^{[\ell +1]}}{{\sum }_{j}p{(i,j,k)}^{[\ell +1]}}\forall i,j,k$$

(8b)

$$p{(i,j,k)}^{[\ell +3]}=\frac{\widehat{p}(j,k)}{\widehat{p}\left(j\right)}\sum _{k}p{(i,j,k)}^{[\ell +2]}\forall i,j,k$$

(8c)

as it is clear that each constraint is fulfilled at the end of the corresponding step in Equations (8a)–(8c), with

$$p{(j,k)}^{[\ell +1]}=\sum _{i}p{(i,j,k)}^{[\ell +1]}=\widehat{p}(j,k)\forall i,j,k$$

(9a)

$$p{(i,k)}^{[\ell +2]}=\sum _{j}p{(i,j,k)}^{[\ell +2]}=\widehat{p}(i,k)\forall i,j,k$$

(9b)

$${\displaystyle p{\left(k\right|i,j)}^{[\ell +3]}=\frac{p{(i,j,k)}^{[\ell +3]}}{{\sum }_{k}p{(i,j,k)}^{[\ell +3]}}=\frac{\widehat{p}(j,k)}{\widehat{p}\left(j\right)}\forall i,j,k}$$

(9c)

By iterating steps (8a)–(8c) until convergence to the final results ${\mathbf{p}}^{[\infty ]}{=\{p(i,j,k)}^{[\infty ]}$}, the MaxEnt estimates of $p(i,j)$ are then given by $p{(i,j)}^{[\infty ]}={\sum }_k{\mathbf{p}}^{[\infty ]}$.

If the conditional independence is not assumed, Equations (7c), (8c) and (9c) can then simply be omitted from the previous equations and the final corresponding MaxEnt estimates ${\mathbf{p}}^{[\infty ]}$ will be different. The initial guesses ${\mathbf{p}}^{\left[0\right]}$ can be arbitrarily chosen as long as they sum up to one and do not include null values. A convenient choice is ${\mathbf{p}}^{\left[0\right]}=\frac{1}{m^3}$$\forall i,j,k$, that also corresponds to the MaxEnt estimate when no constraints need to be accounted for. Matlab codes are available upon request. The reader may also refer to more generic packages, with R code available in the MIPFP package [18] and Python code available in the IPFN package [19].

2.3. Assessing the Conditional Independence

As previously mentioned, the MaxEnt procedure will lead to two distinct sets of ${\mathbf{p}}^{[\infty ]}$ depending on the fact that the conditional independence hypothesis is or is not accounted for. Conditional independence is a realistic hypothesis when the classification is conducted independently from the selection of the reference, but this is not always the case and errors that can be correlated to various (but in general unknown) extents. The user is thus facing the difficult choice of selecting one of these two distinct MaxEnt estimates. When a subset of $n_{sub}$ data of the reference dataset is consolidated with the highest possible accuracy (e.g., ground survey), it becomes possible to directly obtain estimates $\widehat{\mathbf{p}}=\left\{\widehat{p}(i,j,k)\right\}$, with $\widehat{p}(i,j,k)=n(i,j,k)/n_{sub}$. However, the size $n_{sub}$ for such a sample is typically much lower than the size n of the samples for computing $\widehat{p}(i,k)$ that is used in the MaxEnt estimation procedure. Nevertheless, having at hand $\widehat{\mathbf{p}}$ allows the user to balance the two MaxEnt estimates. Indeed, let us consider the Kullback-Leibler divergence $KL(.||.)$ between the direct frequency estimates $\widehat{\mathbf{p}}$ and one of the MaxEnt estimates ${\mathbf{p}}^{[\infty ]}$ (i.e., with or without conditional independence), with

$$KL(\widehat{\mathbf{p}}\left|\right|{\mathbf{p}}^{[\infty ]})=\sum _{i,j,k}\widehat{\mathbf{p}}ln\frac{\widehat{\mathbf{p}}}{{\mathbf{p}}^{[\infty ]}}$$

(10)

so that the MaxEnt estimate to be favoured is the estimate associated with the smallest divergence. Let us denote ${\mathbf{p}}^{[\infty ,\mathrm{a}+\mathrm{b}]}$ and ${\mathbf{p}}^{[\infty ,\mathrm{a}+\mathrm{b}+\mathrm{c}]}$ as the MaxEnt estimates without and with the conditional independence hypothesis, respectively (where superscripts a, b and c are referencing to Equations (7)–(9)). We proposed here to simply combine these MaxEnt estimates by finding the linear combination

$${\mathbf{p}}^{[\infty ]}\left(\alpha \right)=\alpha ·{\mathbf{p}}^{[\infty ,\mathrm{a}+\mathrm{b}]}+(1-\alpha )·{\mathbf{p}}^{[\infty ,\mathrm{a}+\mathrm{b}+\mathrm{c}]}$$

(11)

that minimizes the divergence $KL\left(\widehat{\mathbf{p}}\right|\left|{\mathbf{p}}^{[\infty ]}\left(\alpha \right)\right)$ between $\widehat{\mathbf{p}}$ and this linear combination, where $\alpha$ and $1-\alpha$ are the weights associated with the MaxEnt estimates without or with this conditional independence hypothesis, respectively. Minimizing $KL\left(\widehat{\mathbf{p}}\right|\left|{\mathbf{p}}^{[\infty ]}\left(\alpha \right)\right)$ with respect to $\alpha$ allows us to combine at best both MaxEnt estimates based on the information brought by $\widehat{\mathbf{p}}$. The final estimates of the $p(i,j)$’s are then given by $p{(i,j)}^{[\infty ]}\left(\alpha \right)={\sum }_k{\mathbf{p}}^{[\infty ]}\left(\alpha \right)$.

3. Synthetic Case Studies

While it is not possible to exhaustively test the proposed methodology for all possible cases that could occur, a variety of quantitative tests were designed for this task. As this request a complete control of the errors in the reference data set and in the classification results, we used a set of synthetic maps, reference and “truth”.

3.1. Virtual Truth

For the sake of simplicity and without loss of generality, we assumed that an existing map (Figure 2) was perfect and we used it as our trusted map (j index). A two-meters resolution land cover map produced by the Lifewatch project [20] was selected for this goal. It covers the Walloon region (South of Belgium) and includes approximately 4 billion pixels. The landscape of the Walloon Region is quite fragmented and was described using 8 main land cover classes, namely croplands, broadleaved forests, needleleaved forests, herbaceous covers, shrublands, bare soils, water bodies and artificial impervious areas.

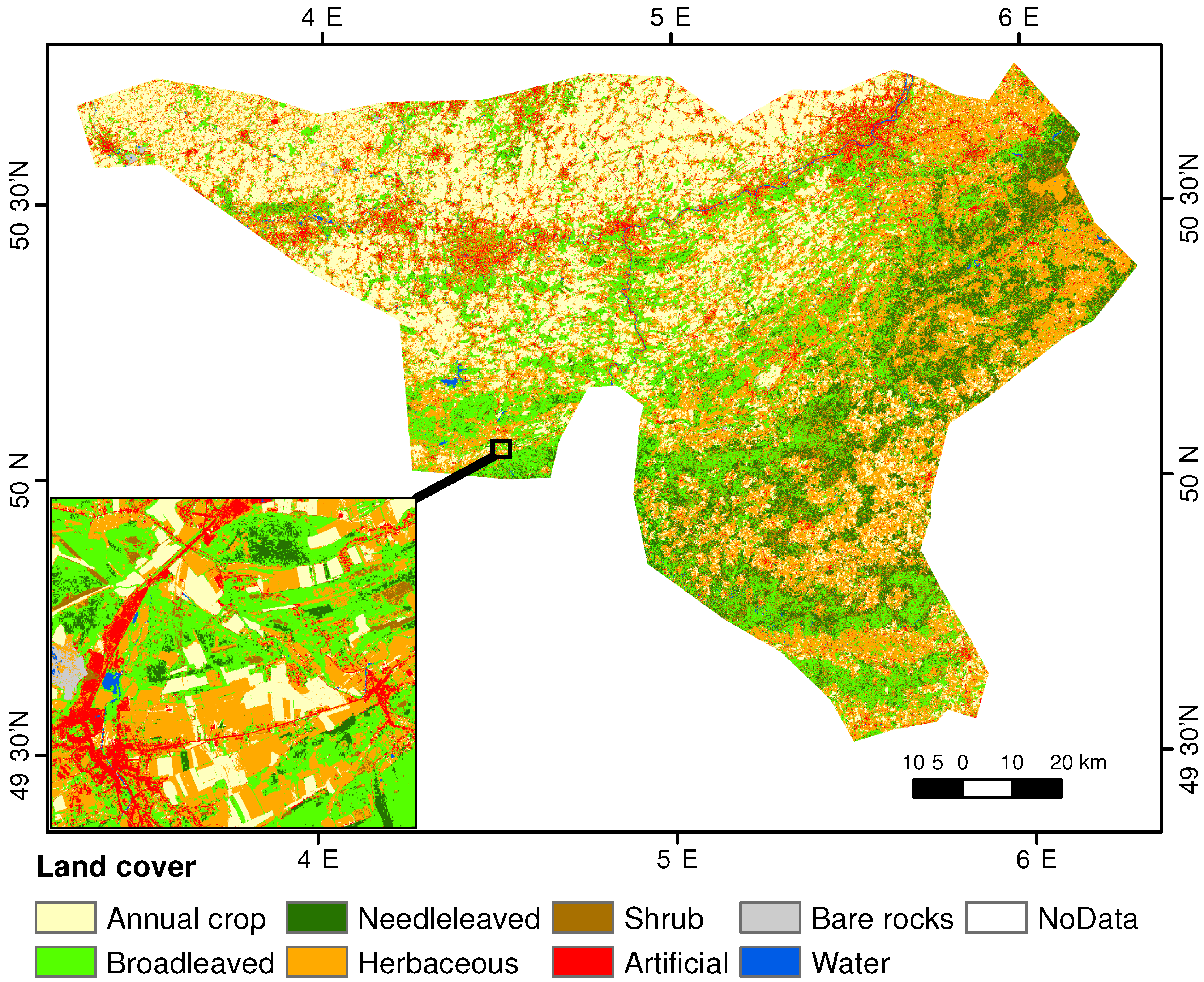
3.2. Classified Maps

The “virtual truth” was used to generate classified maps (i index) by inverting a set of confusion matrices. The classification process was mimicked by using the conditional probabilities. For a pixel with true class j, the classified value was randomly assigned to class i based on the conditional probabilities $p\left(i\right|j)$. The confusion matrices that we used differed by their overall accuracy (a high (H) overall accuracy of about $90\%$ and a low (L) overall accuracy of about $80\%$) and by three distinct patterns for the classification errors:

• An error pattern that reuses the observed confusions that occur in practice, i.e., with many errors between poorly separable classes (e.g., herbaceous cover vs cropland) and few errors between highly separable classes (e.g., a water body vs a tree). An empirical confusion matrix $p(i,j)$ based on quality controlled reference data collection with field survey over the area was used for this. This pattern was selected because classification algorithms often meet the same discrimination issues, therefore they are likely to have a similar pattern despite their different performances. This pattern will be referred to as Obs.
• A class-independent error pattern, where all off-diagonal $p(i,j)$ values are equal to the same constant. The values of the diagonal $p(i,j)$ were set according to the frequency of each class in the virtual truth. This pattern was selected because it was used in a previous study [3]. It will be referred to as Const.
• A random error pattern, where all off-diagonal $p(i,j)$ values are independently selected from a uniform distribution. This pattern was selected for its lack of arbitrary structure, contrary to the constant errors of Const and the more symmetrical errors of Obs. This pattern will be referred to as Rand.

The six resulting confusion matrices are given in Appendix B.

3.3. Reference Datasets

References datasets (k index) were simulated using the trusted map and, in some cases, the classified maps. The two types of errors in the reference data were addressed separately in this study, namely geolocation errors and thematic errors.

3.3.1. Thematic Interpretation Errors

The collection of reference datasets often relies on photo-interpretation, either by experts or by crowdsourcing. The overall accuracy of various reference datasets has been assessed in a few studies, with results ranging from $11\%$ to $100\%$ with a mode at $80\%$ [8]. In practice, estimating the quality of the reference dataset would ideally require a field survey or the consensus between several experts and/or high quality ancillary data. Achieving the highest possible quality on a reference dataset is however very costly, hence rarely applicable on a large number of samples.

Like in the case of the synthetic maps, different OA and different patterns of thematic errors in the reference datasets are tested with synthetic data. The various matrices of $p(j,k)$’s that have been considered are described below (see Appendix C for numerical values):

• A field-based error pattern, with $p(j,k)$ based on the assessment of operators in the study area. A high accuracy $p(j,k)$ confusion matrix was obtained by comparing a consensual point-based photo-interpretation (from 25-cm visible and infra-red orthophotos at two dates, combined with 1-m resolution LIDAR) with a field survey. The corresponding error rate in this dataset is about $3\%$. This pattern will be referred to as Field.
• A class-independent error pattern, where the probability of errors is constant for all classes. Three levels of errors were considered: $10\%$, $5\%$ and $2\%$. This pattern will be referred to as Unif.
• A proportional error pattern, where the probability of errors is proportional to the “virtual truth” class frequency. Two levels of errors were considered: $10\%$, $5\%$ and $2\%$. This pattern will be referred to as Prop.
• A conditional error pattern which is specific to each classified map. Contrary to the other methods, knowledge about i and j classes of the pixel are used to simulate a correlation between the reference and the classification results. For doing this, $50\%$ of the points that were misclassified were labelled with the same incorrect label in the reference dataset (while all other labels remained correct). This pattern will be referred to as Cor, with a mention of the map from which it is derived.

As done previously, the theoretical probabilities $p(j,k)$ were defined according to these 8 patterns. The $p\left(k\right|j)$ were used together with the extracted true class value j to simulate the reference class k for each sample point.

Simulated validations ($n=200$) of the 6 synthetic maps described in Section 3.2 were performed for each of the 8 types of imperfect reference data set. This yielded a total of 48 combinations of classified maps and reference data sets.

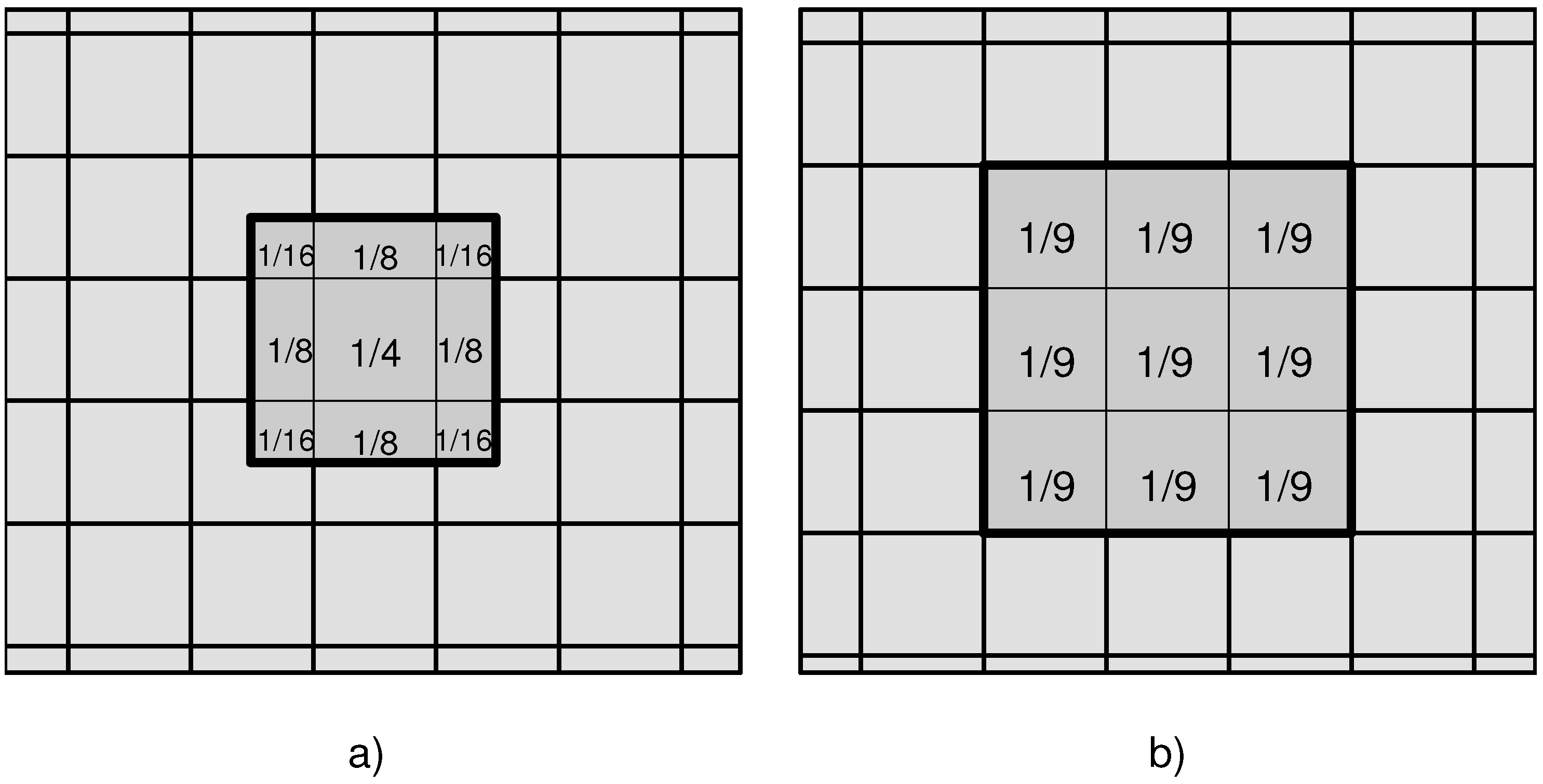
3.3.2. Geolocation Errors

The contamination of thematic accuracy indices by geolocation errors is a current issue in accuracy assessment, even if it has less impact in the case of object-based accuracy assessment [21]. Geolocation errors concern the position of the sampling units (e.g., uncertainty of the GNSS receiver on the ground) as well as the position of the pixels (e.g., uncertainty of the orthorectification). These combined errors yield a relative position error between the classified image and the reference dataset, also called co-registration error. Co-registration errors in turn lead to incorrect labelling when the geolocated sampling unit is not matching the correct pixel anymore.

In order to simulate co-registration errors, the X and Y coordinates of the point samples were randomly shifted based on a uniform distribution. The value of the virtual truth under the point before the shift is compared with the value of the classified map after the shift. Two amplitudes of maximum shifts have been considered: 1 and 1.5 pixel.

The theoretical confusion matrix $p(j,k)$ could be obtained by measuring the frequencies of the class pairs before and after the shift, for all possible multiple of the pixel size and in all directions. These frequencies are weighted by the probability to be located at each position. This probability is computed as the integral of the probability density function (pdf) over each pixel of the neighborhood. Because we used a uniform distribution, the integral of the pdf over a pixel simplifies here to the proportion of the pixel that will be covered by the shift, as illustrated in Figure 3. Of course, more complex (non uniformly distributed) random shifts could be considered, thus requiring to evaluate the integral of the pdf that was used over each pixel (as it is done for computing the contribution of an object to the signal in [22]). For the 1.5 pixel shift, the central pixel and its eight direct neighbours have the same probability of being sampled, that is $1/9$. For the 1 pixel shift, the most likely pixel is the central one (i.e., no impact of the coregistration error) while the neighbouring pixels do not have the same probability of being selected. These probabilities are equal to 1/4 for the central pixel, 1/8 for each of the two vertically and two horizontally neighbouring pixels and 1/16 for each of the four diagonally neighbouring pixels.

3.4. Impact of Erroneous Reference Data

Different methods are tested to estimate the cell values of the $\widehat{p}(i,j)$ confusion matrix in case of errors in the reference dataset. Those estimates are compared with the theoretical $p(i,j)$ confusion matrix. The quantitative comparison is based on the primary accuracy indices used for the accuracy assessment of a map, namely the overall accuracy (OA), the producer accuracies (PA) and the user accuracies (UA). The root mean square error (RMSE) and the bias of the OA are used as main indicator. More specific information is also provided with the average RMSE of UAs and PAs.

These statistics are computed between sets of 200 estimated matrices for each method and the $p(i,j)$ measured with all pixels of the study area. All methods use points that are sampled according to a simple probabilistic sampling design. These points samples provide, as in standard accuracy assessment method, n joints observation of the reference (k) and classified (i) labels.

As described in the following sections, additional information about the trusted (j) label is obtained in a different way when the errors are caused by thematic or by geolocation errors.

3.4.1. Thematic Errors

Thematic errors in the reference dataset are addressed by collecting trusted (j) label information on top of an existing reference (k). We consider that the trusted label is only available for a subset of the points, because of the cost of such information. Obviously, the proposed method would be useless if trusted labels were available for all points. In this study, the quality assessment dataset is made of a 800 points sample with pairs of classified and reference labels, inside which a 100 points subsample is enriched with trusted labels.

The confusion matrix of the reference dataset versus the trusted labels can be estimated from the subsample based on the frequencies of the $(i,j)$ pairs. This 100-points $\widehat{p}(j,k)$ matrix is then combined with the 800-points $\widehat{p}(i,k)$ matrix to reconstruct $p{(i,j)}^{[\infty ]}\left(\alpha \right)$ with the linear combination of MaxEnt estimates that minimize the KL divergence from $\widehat{p}(i,j,k)$, as presented in Section 2.3. These results are compared with the 100-points $\widehat{p}(i,j)$ (an unbiased estimator only based on the trusted labels) and with the 800-points $\widehat{p}(i,k)$ (the confusion matrix commonly used). In order to test the MaxEnt method under ideal conditions, $p{(i,j)}^{[\infty ]}\left(\alpha \right)$ is also computed with the theoretical $p(j,k)$ values instead of their $\widehat{p}(i,k)$ estimates.

3.4.2. Geolocation Errors

In the case of geolocation errors, the $\widehat{p}(j,k)$ matrix is estimated with a high precision, as explained in Section 3.3.2. However, the $\widehat{p}(i,j,k)$’s cannot be estimated because it is not possible to build $(i,j,k)$ triplets without knowing the precise position of each point (only the distribution of the geolocation errors is known). Fortunately, because of the distinct causes associated with thematic and geolocation errors, it is reasonable to assume that the errors in the maps are not correlated with the geolocation mismatches in the reference dataset. The conditional independence is therefore assumed in all cases, so that the trusted confidence matrix is given by $p{(i,j)}^{[\infty ,\mathrm{a}+\mathrm{b}+\mathrm{c}]}={\sum }_k{\mathbf{p}}^{[\infty ,\mathrm{a}+\mathrm{b}+\mathrm{c}]}$. For the sake of comparison with thematic errors, the $\widehat{p}(i,k)$ is based on the frequencies of $(i,k)$ observations in the 800-points sample.

4. Results

The results are presented separately for the thematic and geolocation errors. In each case, we first assess the discrepancies between the trusted confusion matrix (i.e., the simulated $p(i,j)$’s) and the confusion matrix estimated from an imperfect reference dataset (i.e., the $\widehat{p}(i,k)$’s). The results then focus on the potential use of limited information about trusted labels in order to mitigate the impact of errors in the reference dataset using the MaxEnt approach.

4.1. Uncertainty from Thematic Errors

4.1.1. Impact of Imperfect Reference Dataset

Table 1. Overall accuracies (OA) derived from the synthetic maps validated using reference datasets with conditionally independent errors. The first line refers to $p(j,k)$, the first column refers to $p(i,j)$ and the other cells refer to $p(i,k)$. Maximum values for each type of reference dataset are in bold. The maps are sorted based on their OA with trusted reference. Const refers to constant errors on the off-diagonal cells, Rand refers to randomly selected errors, and Obs refers to errors rates that are based on a real case study. For the reference datasets, Unif correspond to uniformly distributed errors, Prop to errors rates proportional to the class frequency, and Field to errors observed in a real case study. The letters L and H refers to low and high quality, respectively.

	References	Trusted	${\mathit{Unif}}_{\mathit{L}}$	${\mathit{Unif}}_{\mathit{H}}$	${\mathit{Prop}}_{\mathit{L}}$	${\mathit{Prop}}_{\mathit{H}}$	$\mathit{Field}$
Maps
Trusted		100	90.1	95.1	90.0	94.9	97.2
$Cons{t}_L$		79.8	72.2	76.0	72.1	75.9	77.5
$Ran{d}_L$		80.8	73.1	77.0	73.0	76.9	78.5
$Ob{s}_L$		83.2	75.3	79.3	75.3	79.2	81.4
$Ran{d}_H$		92.0	83.1	87.6	82.9	87.5	89.5
$Cons{t}_H$		92.4	83.4	87.9	83.2	87.8	89.8
$Ob{s}_H$		93.3	84.2	88.8	84.1	88.7	90.9

and

Table 2. Overall accuracies (OA) derived from the validation of synthetic maps with reference datasets correlated with the errors on the map. The first line refers to $p(j,k)$, the first column refers to $p(i,j)$ and the other cells refer to $p(i,k)$. Maximum values for each type of imperfect reference dataset are in bold. The maps are sorted based on their OA with trusted reference. Const refers to constant errors on the off-diagonal cells, Rand refers to randomly selected errors, and Obs refers to errors rates that are based on a real case study. The letters L and H refer to low and high quality, respectively. For the reference datasets, $50\%$ of the errors are copied from the corresponding classification indicated by the subscript.

	References	Trusted	${\mathit{Cor}}_{{\mathit{Const}}_{\mathit{L}}}$	${\mathit{Cor}}_{{\mathit{Rand}}_{\mathit{L}}}$	${\mathit{Cor}}_{{\mathit{Obs}}_{\mathit{L}}}$	${\mathit{Cor}}_{{\mathit{Rand}}_{\mathit{H}}}$	${\mathit{Cor}}_{{\mathit{Const}}_{\mathit{H}}}$	${\mathit{Cor}}_{{\mathit{Obs}}_{\mathit{H}}}$
Maps
Trusted		100	89.9	90.4	91.5	96.0	96.2	96.6
$Cons{t}_L$		79.8	89.8	73.2	73.4	77.2	77.4	77.3
$Ran{d}_L$		80.8	73.9	90.4	74.4	78.2	78.3	78.3
$Ob{s}_L$		83.2	75.3	75.6	91.7	80.1	80.2	81.0
$Ran{d}_H$		92.0	83.3	83.8	84.4	96.0	89.0	89.1
$Cons{t}_H$		92.4	83.7	84.1	84.7	89.1	96.2	89.4
$Ob{s}_H$		93.3	84.2	84.6	86.0	89.7	89.9	96.7

summarize the results of the simulated validation with different reference datasets (as described in Section 3.3.1) and different maps (as described in Section 3.2). The first column of each table displays the mean of the trusted overall accuracy $O{A}_{(i,j)}$ of each set of simulated maps, i.e., the OA of $p(i,j)$ obtained from a reference dataset without thematic or geolocation errors. The first line of each table shows the $O{A}_{(j,k)}$ for the different reference datasets, i.e., the OA of $p(j,k)$. The other cells contain the $O{A}_{(i,k)}$ obtained by the comparison between each set of simulated map and 10,000 points extracted from each reference dataset, i.e., the OA of $p(i,k)$. These $p(i,k)$ matrices reflect those that are observed (and most of the time published) in scientific papers. When the errors in the reference dataset are independent of the errors in the classified image (see Table 1), the $O{A}_{(i,k)}$ obtained with any of the imperfect reference dataset is always underestimated with respect to the $O{A}_{(i,j)}$ obtained with the trusted labels (first column of the table). The value of the bias (difference between observed and trusted OA) is primarily linked with the OA of the imperfect reference dataset. For our case studies, the underestimation ranges from $-1.5\%$ to $-1.9\%$ using a $98\%$ accurate reference dataset, from $-3.9\%$ to $-4.7\%$ using a $\approx 95\%$ accurate reference dataset, and from $-7.4\%$ to $-9.3\%$ using a $\approx 90\%$ accurate reference dataset. Values for biases are also linked to values of the trusted OA of the maps, as for a given imperfect sample, the bias is larger when the map is more accurate. The distribution of the errors in the imperfect reference datasets has a minor impact on the bias. The results for UAs and PAs (not detailed here) are consistent with the results summarized by OAs. The average RMSE for UA and PA are large on the observed confusion matrices, especially for UA (up to $8.1\%$ for PA and up to $34.8\%$ for UA). The errors are more related to the quality of the reference datasets than to the quality of the map that is being validated.

In the framework of a comparison between different classifiers, accuracy assessment aims at determining the most accurate classifier out of a set of benchmarked approaches. It is therefore interesting to note that conditionally independent errors in the reference dataset did not alter the ranking of the classified maps in terms of OA. In other words, the relative quality of the various classified maps is not modified by the presence of conditionally independent errors in the reference dataset. As shown in Table 1, the most accurate map ($Ob{s}_H$) has the largest observed OA whatever the reference dataset, despite a bias of about $9\%$ in the worst case. This ranking is also preserved between $Cons{t}_H$ and $Ran{d}_H$ (the observed OA of $Cons{t}_H$ remains $0.3\%$ larger than the observed OA of $Ran{d}_H$ with all samples).

On the other hand, when the errors of the reference datasets are correlated with the errors of the classification (see Table 2), the bias is always positive (i.e., the $O{A}_{(i,k)}$ overestimates the $O{A}_{(i,j)}$). When the same errors occur concurrently on a point of reference and its underlying pixel, they are counted as a correct classification in the confusion matrix. The overestimation is thus equal to the amount of co-occurring errors introduced in the dataset (half of the errors of the map, by design in this study). This also has a marked impact on UAs and PAs (not detailed in a table), with average RMSE increased by $40\%$ in several cases.

From the perspective of a comparison between several classifiers, the impact of correlated errors is different than for conditionally independent errors. By construction, the errors in each reference dataset are only correlated to one of the map. Table 2 clearly shows that the largest $O{A}_{(i,k)}$ (in bold characters) is always observed for the map for which the errors in the reference dataset are correlated. Indeed, the difference between (i) the positive bias of the map with errors correlated to the reference dataset and (ii) the negative bias for the other maps where errors are not correlated to the reference dataset, was always larger than the difference between the theoretical OA’s of the case studies. This systematically alters the ranking of the methods. This incorrect ranking was consistently observed for all sets, even when the best ($Ob{s}_H$) and the worst ($Ran{d}_L$) maps (with ${\Delta }_{O{A}_{(i,j)}}=12.5$) are validated with the reference dataset correlated to the $Ran{d}_L$ map.

4.1.2. Maximum Entropy Correction

In order to mitigate the effect of imperfect reference datasets on the estimation of the confusion matrix, the use of the MaxEnt approach has been investigated along with other practical solutions.

Table 3. Comparison between the different methods for estimating the confusion matrix of a map. Each simulated map (first column) is validated with each reference dataset (second column) with conditionally independent errors, as well as with the reference dataset correlated to it by design (named $Cor{r}_{MapName}$). The RMSE ($n=200$) on the estimated ${\widehat{OA}}_{(i,j)}$ compared with the theoretical $O{A}_{(i,j)}$ are provided in columns 3 to 6. In addition, the last two columns show the bias of the MaxEnt and the $p(i,k)$ approaches.

Maps	References	RMSE $\mathit{p}{(\mathit{i},\mathit{j})}^{[\infty ]}\left(\mathit{\alpha }\right)$ with $\widehat{\mathit{p}}(\mathit{j},\mathit{k})$	RMSE $\mathit{p}{(\mathit{i},\mathit{j})}^{[\infty ]}\left(\mathit{\alpha }\right)$ with $\mathit{p}(\mathit{j},\mathit{k})$	RMSE $\widehat{\mathit{p}}(\mathit{i},{j})$ ($\mathit{n}=\mathbf{100}$)	RMSE $\widehat{\mathit{p}}(\mathit{i},\mathit{k})$ ($\mathit{n}=\mathbf{800}$)	Bias $\mathit{p}{(\mathit{i},\mathit{j})}^{[\infty ]}\left(\mathit{\alpha }\right)$ with $\widehat{\mathit{p}}(\mathit{j},\mathit{k})$	Bias $\widehat{\mathit{p}}(\mathit{i},\mathit{k})$
$Cons{t}_H$	$Co{r}_{Cons{t}_H}$	1.82	0.74	2.58	3.81	0.34	3.08
$Cons{t}_H$	Uni $90\%$	5.71	2.04	2.7	9.05	−1.69	−8.92
$Cons{t}_H$	Uni $95\%$	3.25	1.87	2.73	4.66	−1.46	−4.29
$Cons{t}_H$	Uni $98\%$	1.79	1.68	2.68	2.15	−1.25	−0.46
$Cons{t}_H$	Prop $90\%$	5.11	2.16	2.69	9.31	−1.75	−8.54
$Cons{t}_H$	Prop $95\%$	2.96	1.65	2.71	4.51	−1.12	−3.92
$Cons{t}_H$	Prop $98\%$	1.73	1.57	2.63	2.15	−0.95	−2.17
$Cons{t}_H$	Field	1.52	1.46	2.63	2.83	−0.42	−3.79
$Cons{t}_L$	$Co{r}_{Cons{t}_L}$	2.96	1.78	4	10.11	1.52	10.62
$Cons{t}_L$	Uni $90\%$	3.93	1.99	4.01	7.72	−0.74	−6.51
$Cons{t}_L$	Uni $95\%$	2.63	1.91	3.9	4.19	−0.85	−4.13
$Cons{t}_L$	Uni $98\%$	1.86	1.8	4.03	2.21	−0.79	−1.13
$Cons{t}_L$	Prop $90\%$	3.33	1.81	4.06	7.9	−0.6	−9.63
$Cons{t}_L$	Prop $95\%$	2.37	1.86	4.01	4.12	−0.48	−7.63
$Cons{t}_L$	Prop $98\%$	1.73	1.72	4.02	2.15	−0.54	−3.88
$Cons{t}_L$	Field	1.8	1.77	3.95	2.74	−0.32	−1.76
$Ran{d}_H$	$Co{r}_{Ran{d}_H}$	1.83	0.79	2.78	4.05	0.43	3.84
$Ran{d}_H$	Uni $90\%$	5.65	1.92	2.69	9.08	−1.52	−8.79
$Ran{d}_H$	Uni $95\%$	3.28	1.71	2.78	4.72	−1.26	−3.54
$Ran{d}_H$	Uni $98\%$	1.8	1.61	2.71	2.19	−1.07	−2.41
$Ran{d}_H$	Prop $90\%$	5.09	1.86	2.63	9.17	−1.41	−9.91
$Ran{d}_H$	Prop $95\%$	3.05	1.7	2.8	4.6	−0.97	−4.29
$Ran{d}_H$	Prop $98\%$	1.77	1.56	2.64	2.08	−0.81	−2.04
$Ran{d}_H$	Field	1.54	1.4	2.68	2.75	−0.4	−2.66
$Ran{d}_L$	$Co{r}_{Ran{d}_L}$	2.8	1.65	3.91	9.58	1.39	11.05
$Ran{d}_L$	Uni $90\%$	3.85	1.89	3.87	7.85	−0.53	−6.2
$Ran{d}_L$	Uni $95\%$	2.61	1.91	3.92	4.21	−0.74	−3.07
$Ran{d}_L$	Uni $98\%$	1.73	1.71	3.69	2.13	−0.68	−1.82
$Ran{d}_L$	Prop $90\%$	3.18	1.7	3.94	7.95	−0.33	−10.45
$Ran{d}_L$	Prop $95\%$	2.23	1.73	3.82	4.07	−0.32	−4.95
$Ran{d}_L$	Prop $98\%$	1.75	1.75	4.01	2.13	−0.5	−3.07
$Ran{d}_L$	Field	1.77	1.73	3.86	2.67	−0.24	−3.57
$Ob{s}_H$	$Co{r}_{Ob{s}_H}$	1.85	0.69	2.49	3.44	0.21	3.69
$Ob{s}_H$	Uni $90\%$	6.29	3.31	2.35	9.23	−3.1	−10.18
$Ob{s}_H$	Uni $95\%$	3.77	2.81	2.54	4.75	−2.58	−3.93
$Ob{s}_H$	Uni $98\%$	2.08	2.18	2.46	2.16	−1.89	−2.68
$Ob{s}_H$	Prop $90\%$	5.61	3	2.43	9.29	−2.75	−11.18
$Ob{s}_H$	Prop $95\%$	3.57	2.38	2.41	4.61	−2.05	−3.68
$Ob{s}_H$	Prop $98\%$	2.05	1.86	2.56	2.09	−1.47	−1.81
$Ob{s}_H$	Field	1.68	1.52	2.51	2.62	−0.37	−4.56
$Ob{s}_L$	$Co{r}_{Ob{s}_L}$	2.66	1.42	3.67	8.54	1.13	6.42
$Ob{s}_L$	Uni $90\%$	5.23	2.79	3.78	8.16	−2.39	−5.95
$Ob{s}_L$	Uni $95\%$	3.32	2.46	3.74	4.31	−1.96	−4.33
$Ob{s}_L$	Uni $98\%$	2.15	2.08	3.65	2.14	−1.51	−2.33
$Ob{s}_L$	Prop $90\%$	4.68	2.55	3.76	8.02	−2	−7.33
$Ob{s}_L$	Prop $95\%$	3.03	2.13	3.69	4.09	−1.51	−1.2
$Ob{s}_L$	Prop $98\%$	2	1.89	3.78	2.06	−1.15	−0.58
$Ob{s}_L$	Field	2.02	1.89	3.87	2.28	−0.55	−2.33

provides a comparison between the tested estimators of the $\widehat{p}(i,j)$ matrix, namely the MaxEnt approach estimate $p{(i,j)}^{[\infty ]}\left(\alpha \right)$ with a known (theoretical) $p(j,k)$ matrix, the MaxEnt approach where the $\widehat{p}(j,k)$ matrix is estimated from a subsample of 100 points, and the direct estimate of $\widehat{p}(i,j)$ based on a subsample of 100 points with trusted label. The $\widehat{p}(i,k)$ values estimated from a sample of 800 points are also considered, as it is currently used instead of the $p(i,j)$ matrix in most scientific papers. This has been done for all synthetic maps validated by all of the imperfect reference datasets. On average and for all case studies, the lowest RMSE is achieved by the MaxEnt approach estimate $p{(i,j)}^{[\infty ]}\left(\alpha \right)$ with a known (theoretical) $p(j,k)$ matrix (mean RMSE = 1.86). In increasing order of RMSE values, one can then identify the MaxEnt approach when estimating $\widehat{p}(j,k)$ from a subsample of 100 points (mean RMSE = 2.92), followed by estimating $\widehat{p}(i,j)$ from a subsample of 100 points (mean RMSE = 3.27) and, finally, substituting $\widehat{p}(i,j)$ with $\widehat{p}(i,k)$ based on a sample of 800 points (mean RMSE = 4.94). Each method has however its own advantages and weaknesses, as described below.

The MaxEnt approach $p{(i,j)}^{[\infty ]}\left(\alpha \right)$ with known $p(j,k)$, along with a sample of 800 points with i and k values, yields OA estimates with a RMSE ranging from $0.69$ to $3.31$ (second column of Table 3). It outperforms other methods in all cases except when $Ob{s}_H$ (OA = $93.3\%$) is validated with reference samples of low quality (OA ≈ 90%). In those two cases, the direct estimate of the confusion matrix based on a small ($n=100$) sample of trusted labels is better. The RMSE values for UAs and PAs (results not shown) are also significantly improved after applying the corrections on the confusion matrices, but the results are better for PA than for UA. The largest RMSE after correction was $6.1\%$ for UA and $1\%$ for PA.

When the $p(j,k)$ values are estimated from a sample of 100 points, the RMSE of the MaxEnt approach increase, with a bias of approximately $-2\%$ for the case of the $90\%$ accurate reference (to be compared with $-0.5\%$ for the correct $p(j,k)$). Nevertheless, combining a large sample from an inaccurate reference dataset with a small sample from a trusted reference proved to be a good compromise between the cost and the efficiency of the validation process. The MaxEnt approach with estimated $\widehat{p}(j,k)$ systematically yielded a smaller RMSE than when using $\widehat{p}(i,k)$. However, the $\widehat{p}(i,j)$ estimates based on 100 points have a lower RMSE than the MaxEnt approach when the accuracy of the synthetic map is large and the accuracy of the reference dataset is small. For our synthetic study, it occurred 12 times out of the 48 cases (Table 3).

The $\widehat{p}(i,j)$ based on a subsample of points with trusted label is unbiased. As seen from the theoretical variance of OA estimates which is given by

$$Var\left[\widehat{OA}\right]=OA·(1-OA)/n$$

(12)

their RMSEs will increase when the OA of the map gets closer to $50\%$ or when the sample size n decreases. This is corroborated by the RMSEs of Table 3 (biases not shown as they are theoretically equal to zero). RMSEs with $n=100$ points ranges from $2.4$ to $4\%$ depending on the OA of the maps (RSME is smaller when the OA of the map is larger).

4.2. Uncertainty from Geolocation Errors

4.2.1. Impact of Imperfect Reference Dataset

Table 4. Example of confusion matrix for a 1.5 pixel shift along the vertical Y-axis.

	Shifted	Crop	BroadL	NeedleL	Herbac	Shrub	Artif	Bare	Water	Tot
Original
Crop		27.01	0.13	0.03	0.79	0.01	0.12	0.00	0.01
BroadL		0.12	17.68	0.37	1.02	0.67	0.21	0.00	0.01
NeeldleL		0.02	0.39	8.21	0.47	0.34	0.08	0.00	0.00
Herb.		0.81	0.95	0.48	26.94	0.63	0.91	0.02	0.01
Shrub		0.01	0.70	0.34	0.59	3.26	0.05	0.00	0.00
Artif		0.12	0.22	0.09	0.90	0.04	4.58	0.00	0.01
Bare		0.00	0.00	0.00	0.02	0.00	0.00	0.13	0.00
Water		0.01	0.01	0.00	0.01	0.00	0.01	0.00	0.50
Accuracy		0.96	0.88	0.86	0.88	0.66	0.77	0.87	0.95	88.30

and

Table 5. Example of confusion matrix for a 1.5 pixel shift along the diagonal of the X,Y axes.

	Shifted	Crop	BroadL	NeedleL	Herbac	Shrub	Artif	Bare	Water	Tot
Original
Crop		26.82	0.16	0.04	0.92	0.02	0.14	0.00	0.01
BroadL		0.15	17.17	0.55	1.15	0.77	0.26	0.00	0.01
NeedleL		0.03	0.57	7.92	0.52	0.38	0.10	0.00	0.00
Herb		0.92	1.13	0.53	26.44	0.65	1.05	0.02	0.01
Shrub		0.02	0.79	0.38	0.63	3.09	0.05	0.00	0.00
Artif		0.15	0.25	0.10	1.05	0.05	4.35	0.00	0.01
Bare		0.00	0.00	0.00	0.02	0.00	0.00	0.13	0.00
Water		0.01	0.01	0.00	0.01	0.00	0.01	0.00	0.49
Accuracy		0.95	0.86	0.83	0.86	0.62	0.73	0.85	0.93	86.41

give the joint frequencies of labels observed at the accurate position of the sample and at their shifted position (by 1.5 pixel). Those matrices are almost symmetrical, showing no difference between a positive and a negative shift. Furthermore, the matrices with vertically and horizontally shifted pixels are similar to each other (with less than $0.1\%$ difference for their OAs), and the same similarity is observed for the matrices with diagonally shifted pixels. This leads to the conclusion that the landscape in the study area is isotropic, i.e., the probability of error does not depend on the direction of the shift. The difference between the horizontal (Table 4) and the diagonal (Table 5) shifts are due to the larger distances to the centers of the pixels along the diagonals.

As explained in Section 3.3.2, the four median, the four diagonal and the central confusion matrices are then combined to compute the $p(j,k)$ confusion matrices of geolocation for 1 pixel and 1.5 pixel shifts. Results for the 1.5 pixel shifts is illustrated in

Table 6. Total weighted confusion matrix for a maximum shift of 1.5 pixel.

	Shifted	Crop	BroadL	NeedleL	Herbac	Shrub	Artif	Bare	Water	Tot
Original
Crop		27.03	0.13	0.03	0.76	0.01	0.11	0	0.01
BroadL		0.12	17.73	0.4	0.98	0.62	0.2	0	0.01
NeedleL		0.02	0.43	8.23	0.44	0.31	0.08	0	0
Herbac		0.78	0.9	0.45	27.13	0.58	0.88	0.01	0.01
Shrub		0.01	0.66	0.32	0.54	3.38	0.05	0	0
Artif		0.12	0.21	0.08	0.86	0.04	4.63	0	0.01
Bare		0	0	0	0.01	0	0	0.13	0
Water		0.01	0.01	0	0.01	0	0.01	0	0.5
Accuracy		0.96	0.88	0.86	0.88	0.68	0.78	0.87	0.94	88.76
geo. errors		0.04	0.12	0.14	0.12	0.32	0.22	0.13	0.06	11.24

. The OAs of these matrices represent the probability that a randomly shifted point falls in the land cover category where it is supposed to be. As expected, the OA is smaller for the maximum shift of 1.5 ($O{A}_{(j,k)}=88.76\%$) than for the maximum shift of 1 pixel ($O{A}_{(j,k)}=90.76\%$).

The probability to fall on another label than the label under the exact location of the sampling point (that we call geolocation errors) varies across classes, as it can be seen on the last line of Table 6. Those differences are mainly linked to the landscape structure associated with these classes rather than to the total area covered by the class. Land cover classes that occur in large patches are indeed less affected than sparsely distributed ones. For instance, crop fields and herbaceous patches cover approximately the same area, but the geolocation errors for crop fields ($4\%$) is much lower than for herbaceous patches ($12\%$), as the latter are much smaller and more dispersed. On the other hand, and despite the presence of hundreds of small ponds, most of the water pixels are grouped inside a few big lakes. The water class is therefore little affected by geolocation errors even if it covers a small area (≈1%) by comparison with, e.g., trees or herbaceous covers.

The geolocation mismatch observed with the geolocation confusion matrices contaminate the thematic confusion matrix. For a simulated classification with an overall accuracy of $93.3\%$ according to the $p(i,j)$ matrix, the bias due to the geolocation error cannot be neglected. This bias is equal to $7.6$% and $9.7\%$ with 1 and 1.5 maximum pixel shifts, respectively.

4.2.2. Maximum Entropy Correction

In the case of geolocation mismatch, a point sample would not provide joint $(i,j)$ information because the value and the orientation of the shift are unknown for a specific location. It is therefore not possible to directly obtain $\widehat{p}(i,j)$ estimates in this situation. The MaxEnt estimates ${\mathbf{p}}^{[\infty ,\mathrm{a}+\mathrm{b}+\mathrm{c}]}$ can however be obtained by taking advantage of the $p(j,k)$ matrix. Table 6 illustrates one of the matrices which are used as $\widehat{p}(j,k)$ by the MaxEnt approach. The test is performed here in the worst conditions for the MaxEnt approach, i.e., with a high OA of the synthetic map ($Ob{s}_H$) and with OAs of approximately 89 and 91 % as derived from the $p(j,k)$ values.

The bias for the OAs derived from the $p{(i,j)}^{[\infty ,\mathrm{a}+\mathrm{b}+\mathrm{c}]}$ matrix is equal to 0.26% and 0.35% for 2 and 3 pixels neighborhoods, respectively. These values are close to the usually accepted uncertainty and are better than the residual bias observed in the case of thematic errors on the same synthetic map. The RMSE for UAs and PAs also strongly decreases. For UAs, it drops from $18.0\%$ to $2.4\%$ and from $13.3\%$ to $1.8\%$ on the 3 and 2 pixels neighborhood, respectively. Similarly, for PAs, it drops from $12.4\%$ to $2.0\%$ and from $9.9\%$ to $1.6\%$ on the 3 and 2 pixels neighborhoods, respectively.

5. Discussion

This paper highlighted the substantial misestimation of primary quality indices (i.e., overall accuracy, user’s and producer’s accuracies) when the reference dataset is not error-free. Errors in the reference dataset lead to an underestimation of the map quality when these errors are conditionally independent, and to an overestimation otherwise. The absolute value of the bias is often significantly larger than the confidence interval on the estimated indices, which means that the quantity and the quality of the reference samples are equally important to build a reliable confusion matrix. The MaxEnt approach that was proposed in this paper allowed us to reduce the estimation bias in both cases (correlated and conditionally independent errors) for all maps. However, it requires some knowledge about the actual quality of the reference dataset in order to be optimal.

Considering the cost of collecting high quality reference dataset, a pragmatic approach is often recommended [1]. With this goal in mind, Section 5.1 focuses on the selection of the best classification algorithm while Section 5.2 discusses the ways to evaluate the absolute quality of maps and improve area estimates. Accordingly, the sampling strategy should be optimized for these two main usages of the confusion matrix. The contamination by geolocation errors is also discussed in Section 5.3.

5.1. Comparing Classification Outputs

When it comes to assess the performance of a new classifier by comparison with state-of-the-art classifiers, the focus is mainly on the comparison of the classification outputs, typically based on their respective overall accuracies. In parallel, methods for determining the optimal sample size focus on the statistical significance of a difference in the proportion of correctly allocated cases [23].

In this context, our results highlight the risk to invalidate the conclusion of these statistical tests due to the presence of biases in the estimated confusion matrices. Indeed, if the errors in the reference dataset are correlated with the errors of one of the classification algorithms, this algorithm will be systematically favoured by comparison with the other ones, due to an overestimation of its overall accuracy. This should be kept in mind, especially in the case of classification methods that make use of correlated calibration and validation datasets.

The MaxEnt approach is able to reduce the absolute value of the bias for the validation of all classifiers (either with correlated or conditionally independent errors), hence making the comparison more fair. However, there is no theoretical expression for the variance of the prediction with the MaxEnt method, and the bias is not completely removed by the corrections. Consequently, a rigorous test of the statistical significance of differences between OA remains unpractical.

Fortunately, a ranking of the classification algorithms is reliable when using $\widehat{p}(i,k)$ estimates built from a large (yet uncertain) reference dataset that offer some guarantee about the conditional independence of errors. In other words, it is possible to determine the best classifier if and only if the (potential) errors in the validation data are conditionally independent with the errors of all classifiers. Under this assumption, the statistical significance of the superiority of one classifier can be tested with the OA derived from $\widehat{p}(i,k)$, and the MaxEnt approach additionally provides the unbiased value of this OA.

5.2. Map Quality Assessment and Area Estimates

Quality indices derived from the confusion matrix aim to decide if the quality requirements of the map for end users are fulfilled. Clearly, the presence of a bias that would be larger than the confidence interval on these quality indices invalidates the use of statistical tests for deciding if the map can be considered as agreeable to users. Our results have shown, on one hand, that the bias is a function of the amount of errors in the reference dataset and, on the other hand, that this bias is often larger than the recommended confidence interval on overall accuracies. The $p(i,k)$’s should therefore not be used a a substitute for the $p(i,j)$’s in general. As illustrated in Section 4, using this substitution can lead to strong underestimation of overestimation of the quality indices.

Two methods that can be considered to estimate the $p(i,j)$’s are (i) a direct frequency estimate using a small reference dataset of the highest possible reliability, or (ii) the MaxEnt approach that combines a large but imperfect reference dataset with information about the quality of this dataset. In both cases, it is necessary to collect costly high quality reference data, but the first method puts all the efforts on the high quality reference while the second takes advantage of cheaper material such as, e.g., crowdsourcing or even existing maps. It is not possible to decide in advance which method will be the most efficient, because it depends on the accuracy of the reference dataset and the distribution of the classes in the map. On average, ours results showed that the MaxEnt method should prevail, but $\widehat{p}(i,j)$’s could be used when the accuracy of the map is very large while the accuracy of the reference dataset is very low.

Another use of the confusion matrix is the estimation of the area of each class based on pixel counting adjusted by the UA [24], which is considered as the state-of-the-art correction [1]. The correction of the area estimates is also directly impacted by the presence of errors in the confusion matrix. The uncertainty about the UA’s is then of paramount importance. When the errors of the map are correlated with the errors of reference dataset, these errors are synergizing instead of cancelling. When errors are conditionally independent, the consequences of the state-of-the-art correction of the area estimates are usually not predictable, although our results showed that there are more geolocation errors on small and sparsely distributed classes compared with large and compact classes. In this case, the area of the small and dispersed patches is therefore likely to be even more underestimated after applying the area correction. Considering the cost that such errors on areas can have for decision making (e.g., ecosystem service assessment [25]), a correction of the confusion matrix is therefore strongly recommended in this case. Again, the MaxEnt approach would be interesting in this situation has it positively impacts the UA’s estimation.

5.3. Geolocation Error

Mitigating the effect of geolocation errors is the most promising use of the proposed MaxEnt approach, as the conditional independence of these errors is typically fulfilled and the error associated with various positioning tools is usually well known. A good understanding of these geolocation errors is however necessary in order to achieve appropriate corrections, and the results depend on the spatial resolution and the sources of errors. A uniform spatial distribution of these errors was chosen in this study for the sake of simplicity, though it is not necessarily a realistic choice. In real case studies, it is thus necessary to rigorously describe the distribution of those geolocation errors in order to estimate at best the $p(j,k)$’s.

For this goal, the classified map or an existing map with high spatial precision can be used as long as the spatial structure of the landscape is preserved (e.g., no salt-and-pepper effect induced by the classification itself). Those maps are indeed likely to preserve the size of the patches and the neighbouring information around each class. Directional effects could also be taken into account, as the orientation of edges with respect to sun and viewing angles can lead to various geolocation errors for vertical objects (trees, buildings, etc.) [26]. In parallel, RMSE of the orthorectification model and/or of the GPS receiver on the field can provide information about the distribution of the geolocation errors around each point.

5.4. Practical Recommendation

Despite the fact that the proposed MaxEnt method successfully managed to provide sound estimates for the $p(i,j)$’s, limiting the presence of errors in the reference dataset should be the priority. The consequences of correlated errors in the validation process are more detrimental than conditionally independent errors. As explained before, these correlated errors can lead to misleading conclusions when comparing the performance of various classification algorithms, as they amplify the errors for area estimates and they yield over-optimistic results about the quality of a map.

The risks of correlated errors is largely reduced if good practices in geographic data accuracy assessment are properly accounted for. The validation dataset should not be a subset of the training/calibration dataset, as this will automatically create correlated errors. Spatial auto-correlation should also be avoided, such as systematically selecting validation points inside polygons that are used for the calibration or in the neighborhood of calibration points. This is particularly important with convolutional neural networks and other context-based classifiers. Indeed, because of their use of neighbourhoods (by design), spatially correlated errors are likely to be correlated in the classification. If possible, using a completely different source of validation is recommended too, like e.g., ground data, higher resolution images, images at different dates, etc.

Finally, it is worth noting that the best way to provide information about the quality of the reference dataset is by using a set of $(i,j,k)$ triplets, as it allows the user to test whether errors are correlated or not. However, providing the $\widehat{p}(j,k)$’s remains useful if the conditional independence of the errors can be assumed, like in the case of geolocation errors. The MaxEnt method can then be applied to reduce the bias of the $\widehat{p}(i,j)$ estimates, hence improving the reliability of the accuracy assessment.

6. Conclusions

In this study, we provide quantitative results about the key role that accurate reference datasets play for the validation of maps. The need for such accurate reference datasets is often forgotten when the focus is on the precision of the accuracy assessment. However, the presence of a bias on the overal accuracy invalidates the conclusions of statistical tests comparing the differences of correctly classified pixels. In particular, we show why it is not possible to conclude about the superiority of a classifier when the independence between the validation dataset and the calibration dataset is not guaranteed.

A maximum entropy method is thus proposed to mitigate the impact of erroneous reference dataset of the confusion matrix. Based on a variety of simulated cases, our results emphasize the benefit and the efficiency of this approach, both in the case of thematic errors in the reference dataset and in the case of geolocation errors inducing label mismatches. This method relies on the collection of a relatively smaller number of trusted labels in addition to usual large reference dataset. While collecting additional trusted labels is usually expensive, the benefits for accuracy assessment are much larger than collecting a larger number of questionable reference data.

Although we combined jointly in this study a large variety of synthetic situations for the sources of errors (i.e., various error patterns, absolute errors, thematic and geolocation errors), it remains true that the superiority of the MaxEnt approach has not been proven for all possible cases and based on theoretical grounds. However, using information theory opens new perspectives for map validation with imperfect samples at a reasonable cost.