Irrigation Events Detection over Intensively Irrigated Grassland Plots Using Sentinel-1 Data
Abstract
1. Introduction
2. Materials
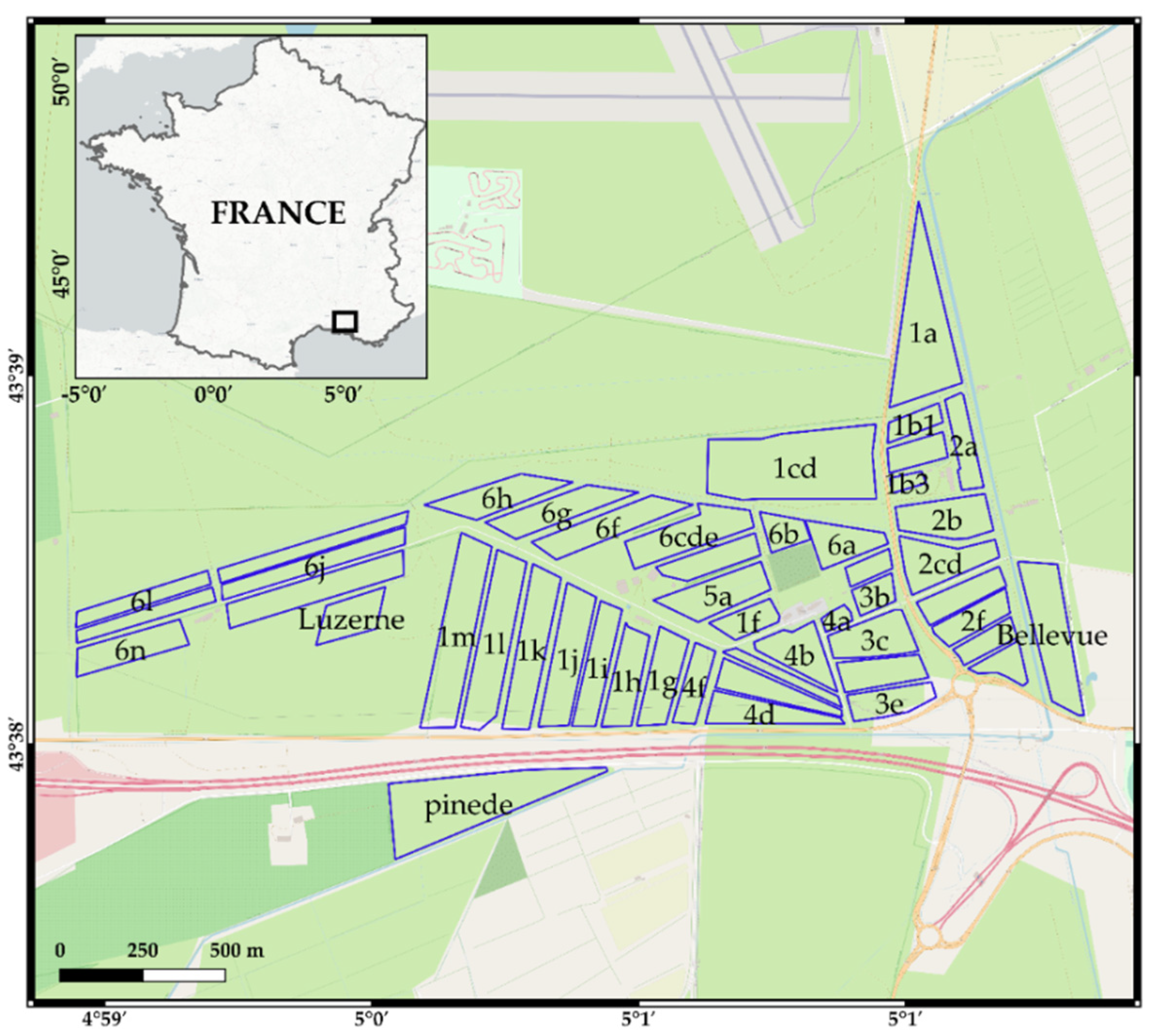
2.1. Study Site
2.2. Reference Data
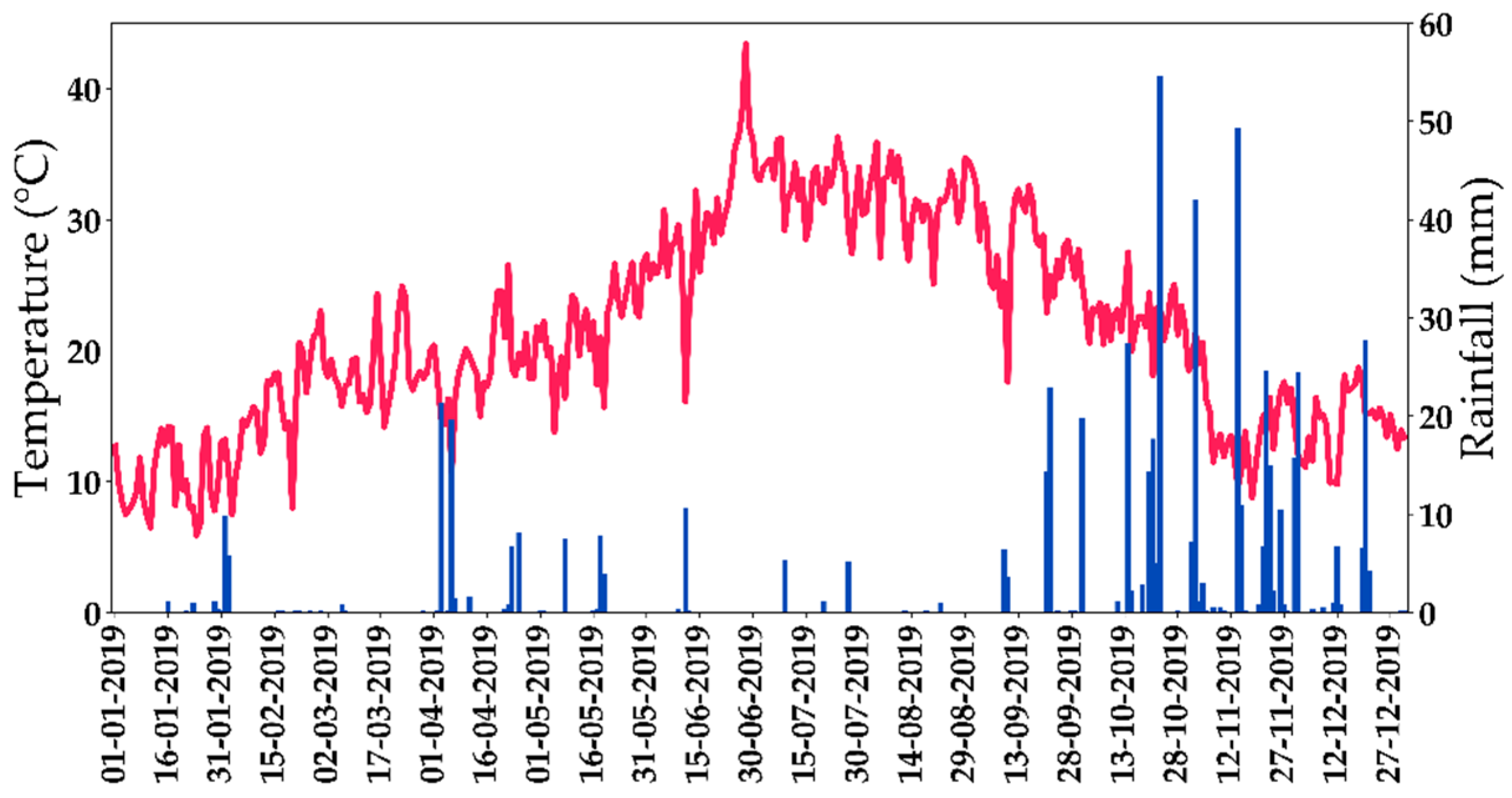
2.3. Sentinel-1 SAR Data
2.4. Sentinel-2 Optical Data
3. Methods
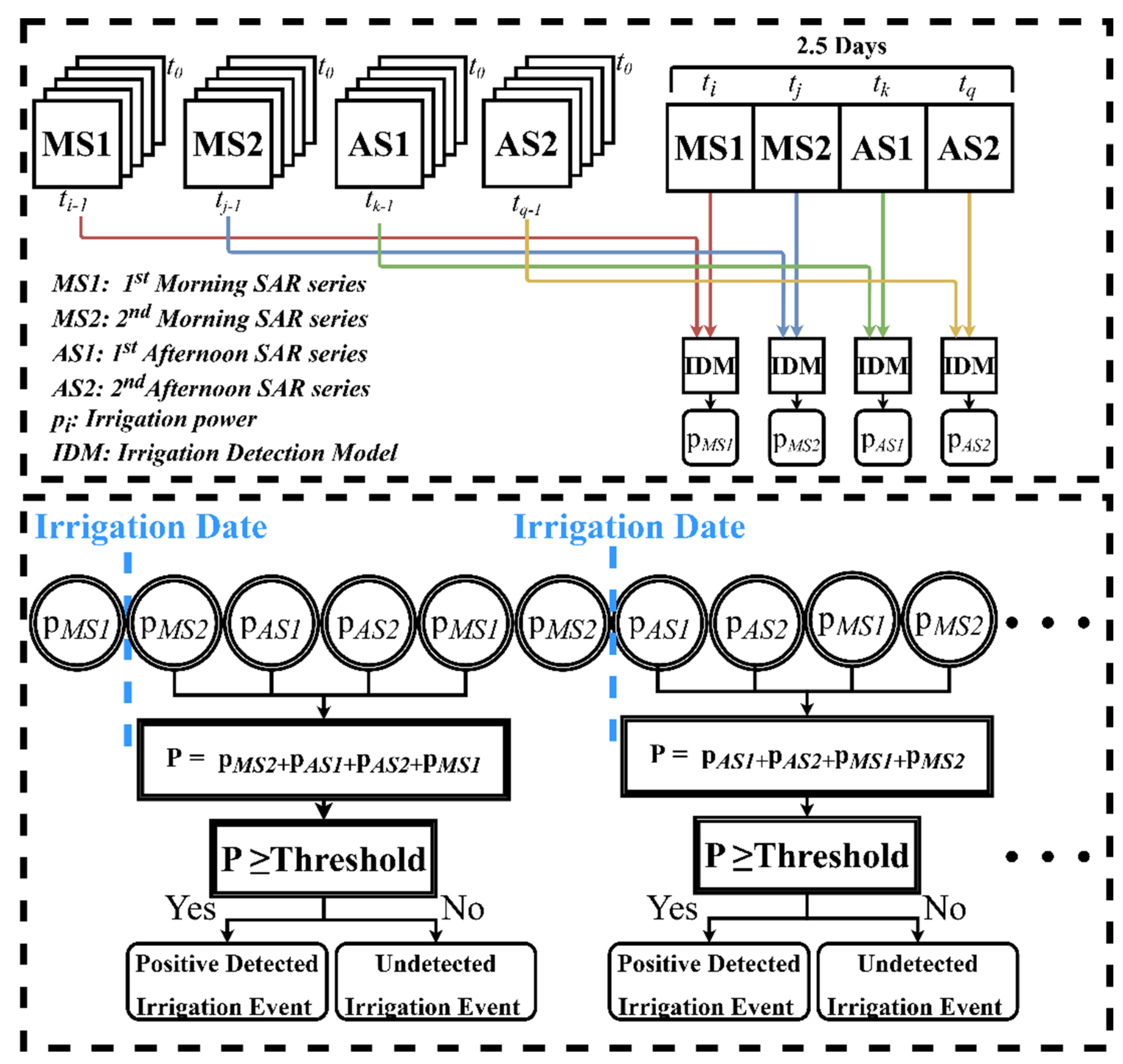
3.1. Irrigation Detection Model
- The SAR backscattering signal at plot and grid scales;
- Surface Soil Moisture at plot and grid scales;
- The NDVI value at plot scale.
3.1.1. σ° SAR Backscattering at Plot Scale
3.1.2. σ° SAR Backscattering at Grid Scale
3.1.3. NDVI Values
3.1.4. Surface Soil Moisture Estimation
3.2. Application and Assessment of the IDM
4. Results
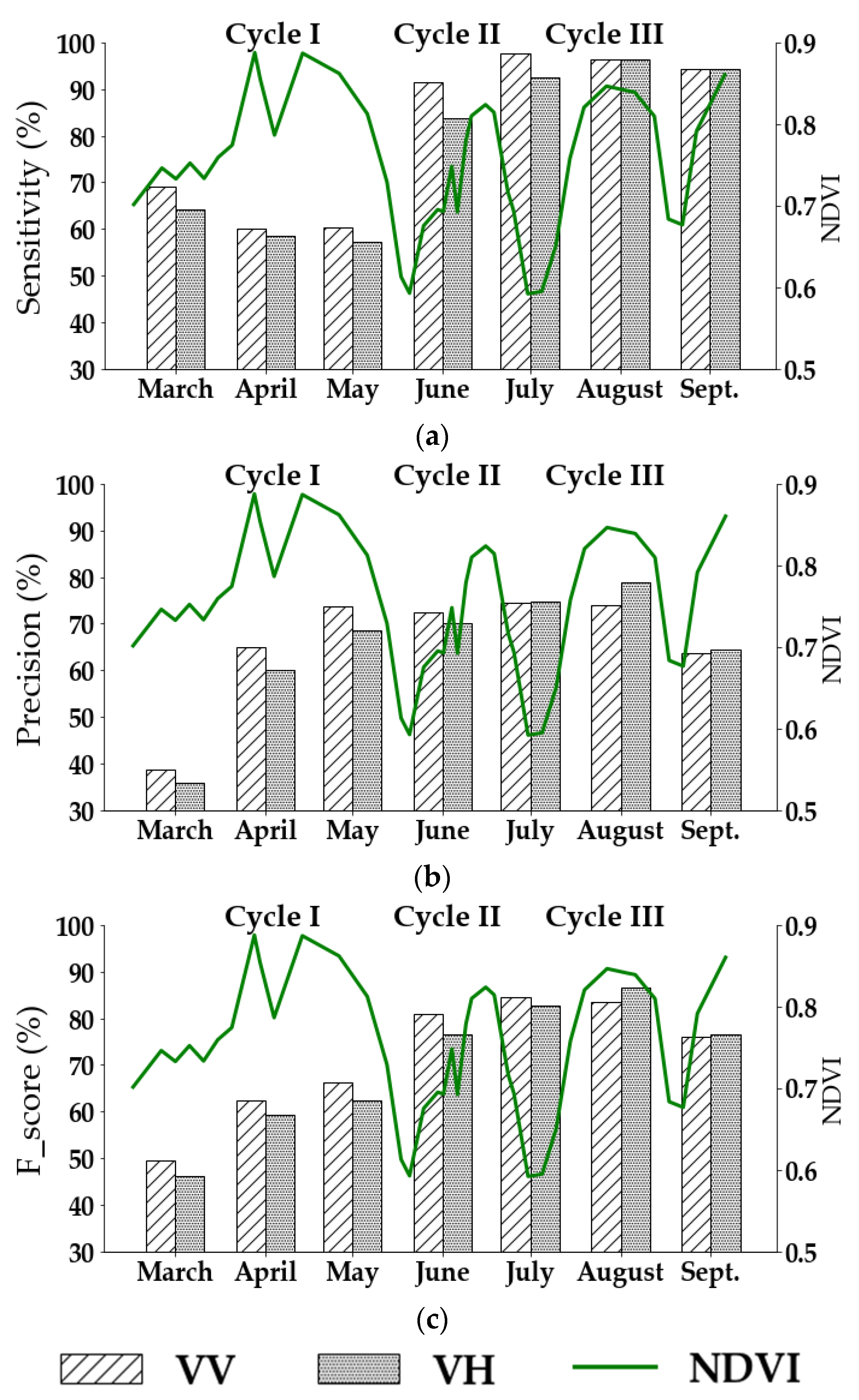
4.1. Irrigation Detection Using VV and VH Separately
4.2. Irrigation Detection Using Combined VV and VH
5. Discussion
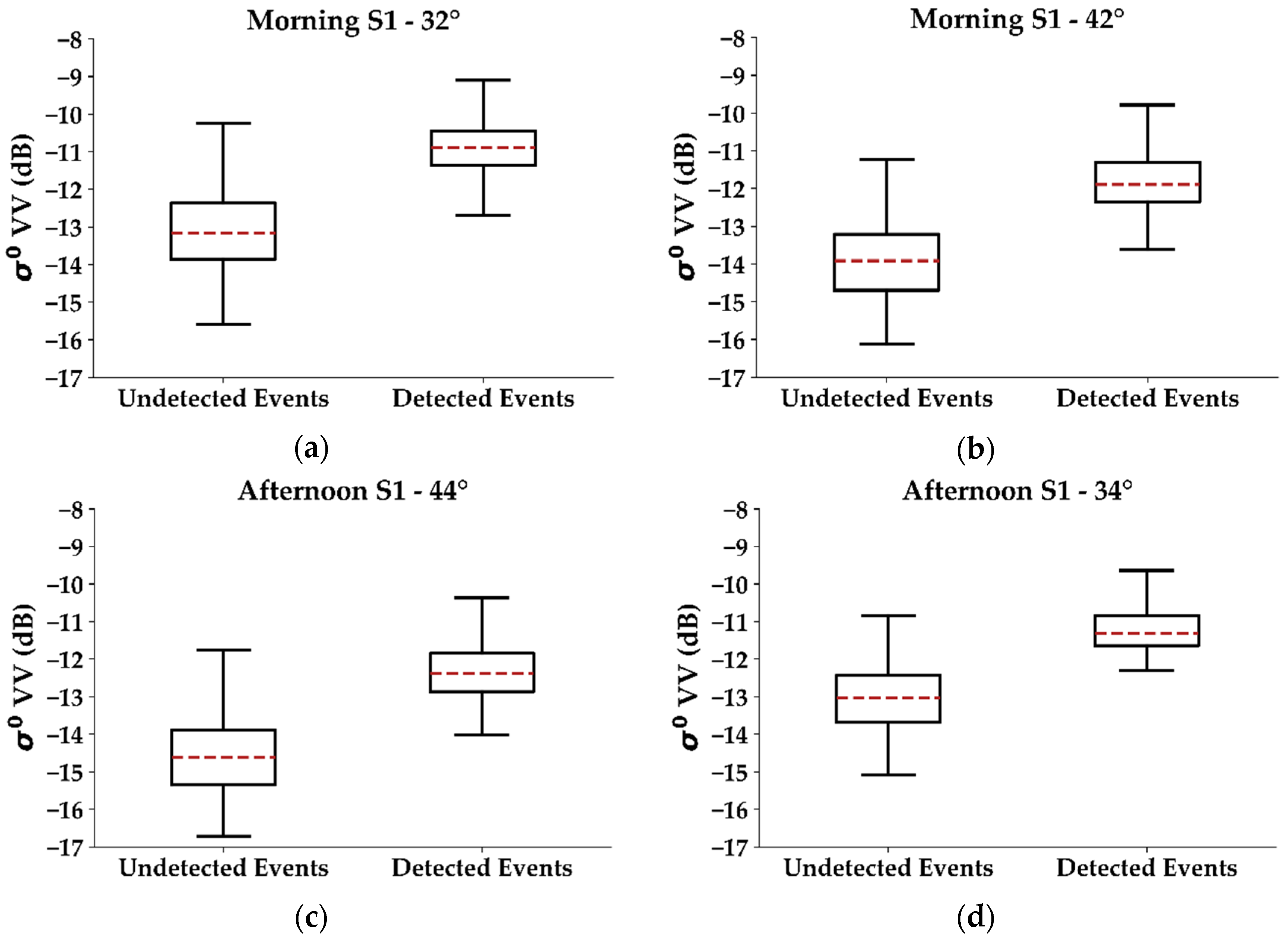
5.1. Effect of the Geometrical Structure of the Plots
5.2. Effect of the Vegetation Cover
5.3. Effect of Precipitation and Harvesting
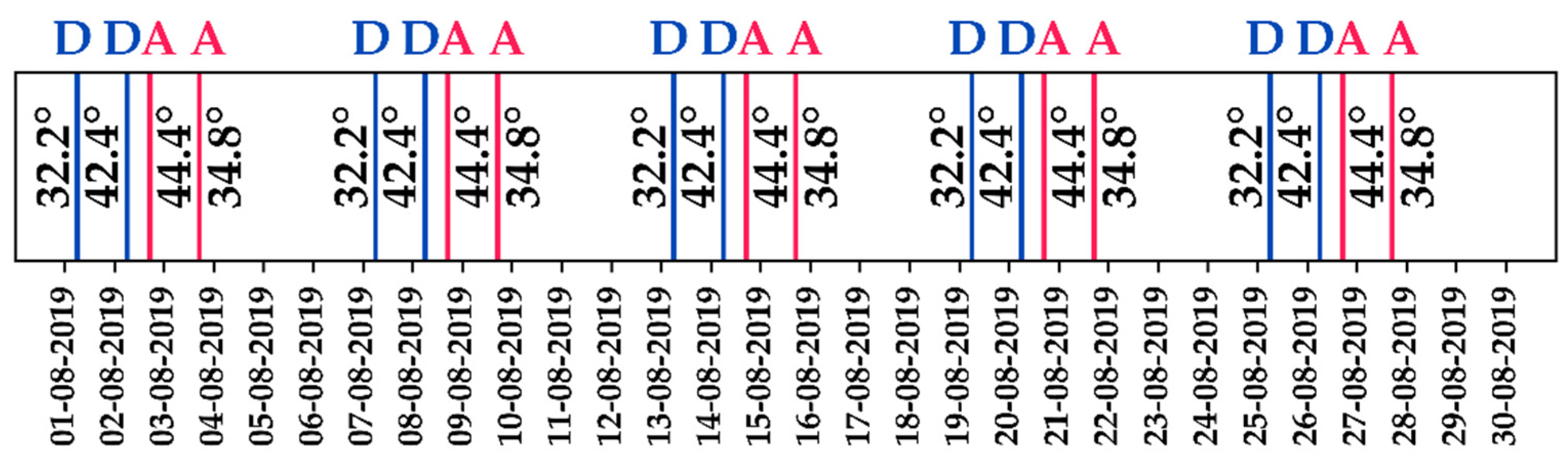
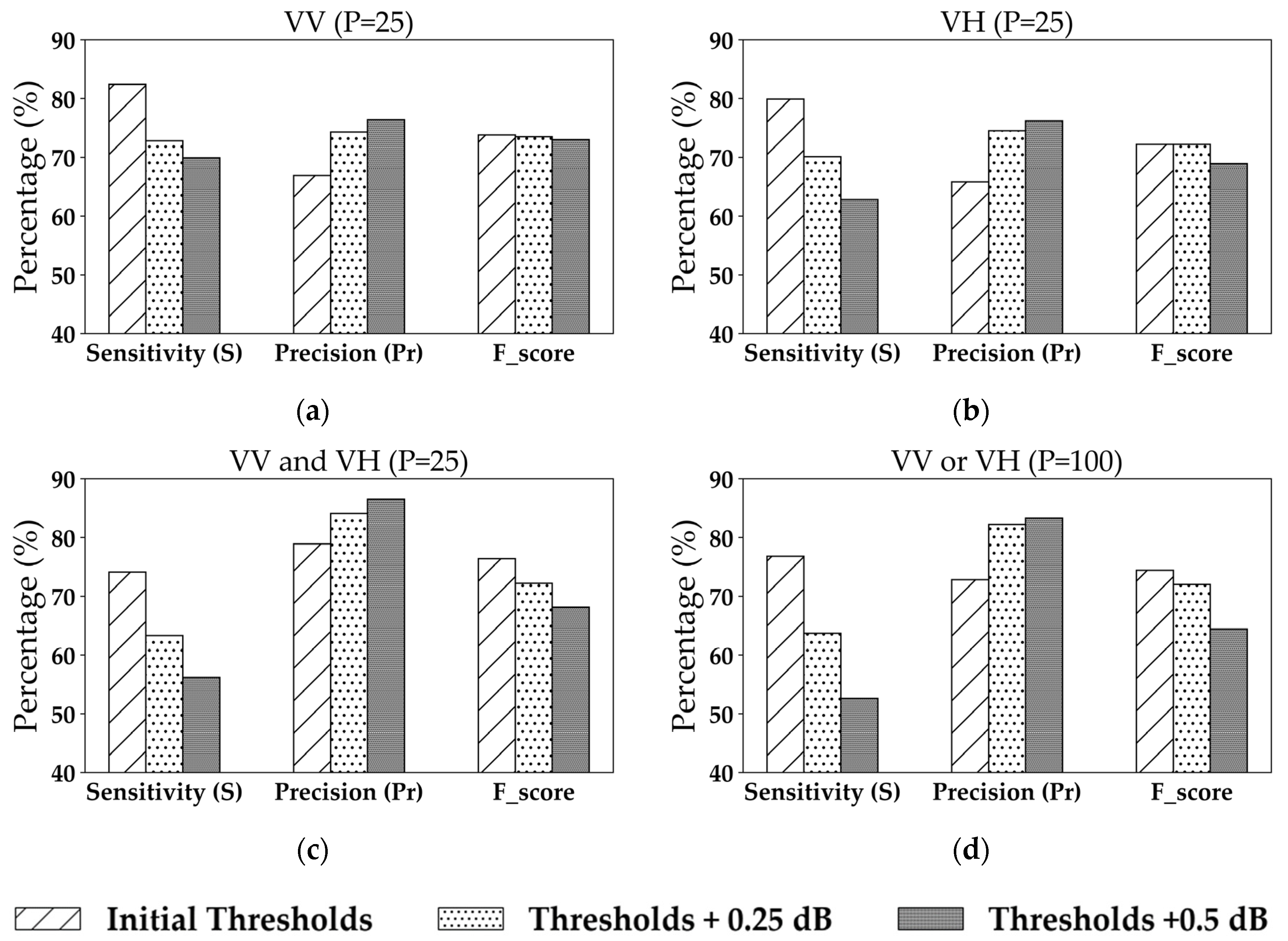
5.4. Sensitivity Analysis of the IDM Threshold Values
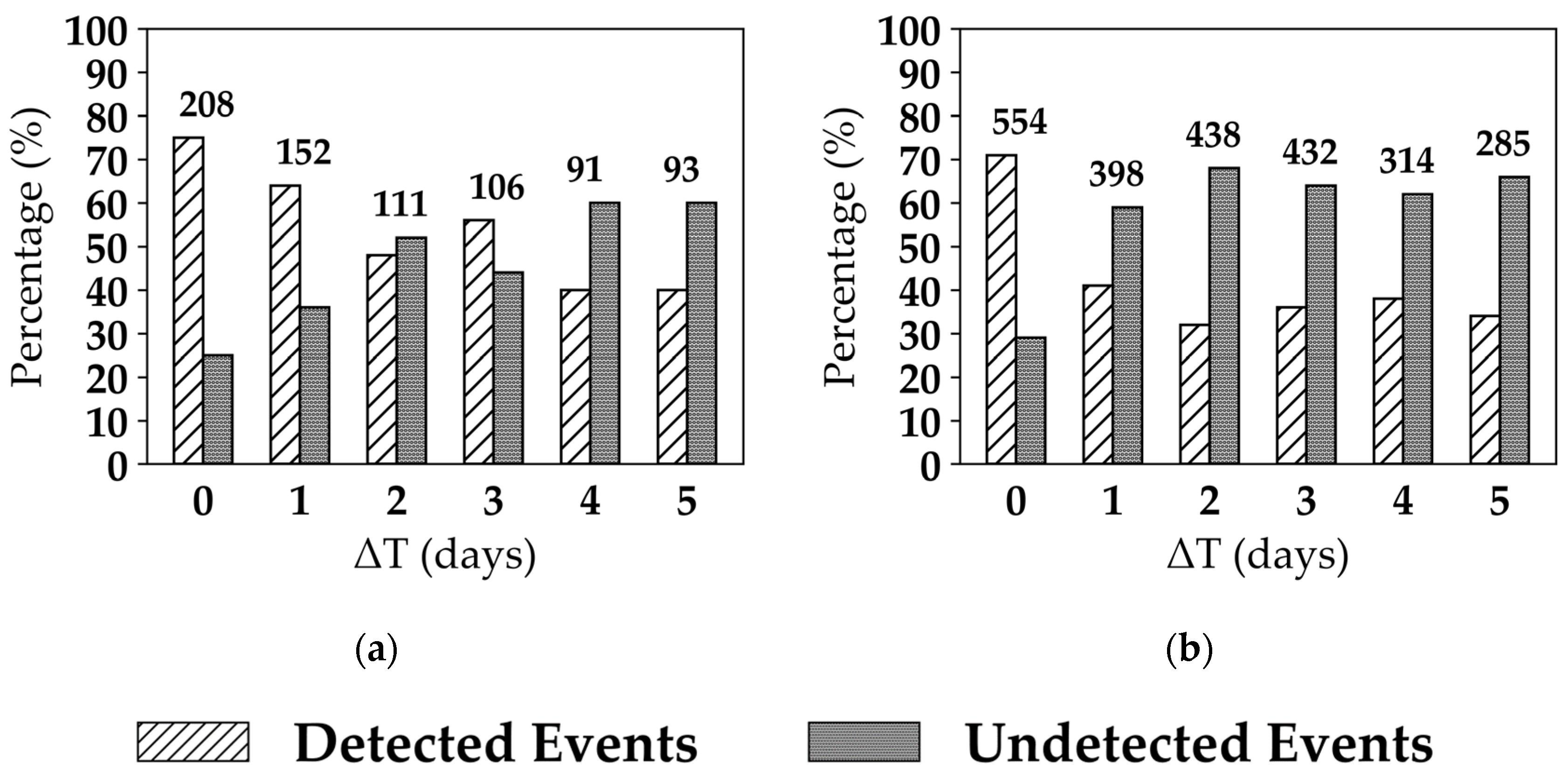
5.5. Effect of the S1 Revisit Time on the Irrigation Detection
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Tilman, D.; Clark, M. Food, agriculture & the environment: Can we feed the world & save the earth? Daedalus 2015, 144, 8–23. [Google Scholar] [CrossRef]
- Tilman, D.; Balzer, C.; Hill, J.; Befort, B.L. Global food demand and the sustainable intensification of agriculture. Proc. Natl. Acad. Sci. USA 2011, 108, 20260–20264. [Google Scholar] [CrossRef] [PubMed]
- Godfray, H.C.J.; Beddington, J.R.; Crute, I.R.; Haddad, L.; Lawrence, D.; Muir, J.F.; Pretty, J.; Robinson, S.; Thomas, S.M.; Toulmin, C. Food security: The challenge of feeding 9 billion people. Science 2010, 327, 812–818. [Google Scholar] [CrossRef] [PubMed]
- Pokhrel, Y.N.; Hanasaki, N.; Wada, Y.; Kim, H. Recent progresses in incorporating human land-water management into global land surface models toward their integration into Earth system models: Recent progresses in incorporating human land-water management into global land surface models. WIREs Water 2016, 3, 548–574. [Google Scholar] [CrossRef]
- Ozdogan, M. Exploring the potential contribution of irrigation to global agricultural primary productivity: Irrigation and Primary Productivity. Glob. Biogeochem. Cycles 2011, 25. [Google Scholar] [CrossRef]
- Burney, J.; Woltering, L.; Burke, M.; Naylor, R.; Pasternak, D. Solar-powered drip irrigation enhances food security in the Sudano–Sahel. Proc. Natl. Acad. Sci. USA 2010, 107, 1848–1853. [Google Scholar] [CrossRef]
- Paredes, P.; Rodrigues, G.C.; Alves, I.; Pereira, L.S. Partitioning evapotranspiration, yield prediction and economic returns of maize under various irrigation management strategies. Agric. Water Manag. 2014, 135, 27–39. [Google Scholar] [CrossRef]
- Thenkabail, P.S.; Schull, M.; Turral, H. Ganges and Indus river basin land use/land cover (LULC) and irrigated area mapping using continuous streams of MODIS data. Remote Sens. Environ. 2005, 95, 317–341. [Google Scholar] [CrossRef]
- Thenkabail, P.S.; Biradar, C.M.; Noojipady, P.; Dheeravath, V.; Li, Y.; Velpuri, M.; Gumma, M.; Gangalakunta, O.R.P.; Turral, H.; Cai, X.; et al. Global irrigated area map (GIAM), derived from remote sensing, for the end of the last millennium. Int. J. Remote Sens. 2009, 30, 3679–3733. [Google Scholar] [CrossRef]
- Thenkabail, P.; Dheeravath, V.; Biradar, C.; Gangalakunta, O.R.; Noojipady, P.; Gurappa, C.; Velpuri, M.; Gumma, M.; Li, Y. Irrigated area maps and statistics of India using remote sensing and national statistics. Remote Sens. 2009, 1, 50–67. [Google Scholar] [CrossRef]
- Dheeravath, V.; Thenkabail, P.S.; Chandrakantha, G.; Noojipady, P.; Reddy, G.P.O.; Biradar, C.M.; Gumma, M.K.; Velpuri, M. Irrigated areas of India derived using MODIS 500 m time series for the years 2001–2003. ISPRS J. Photogramm. Remote Sens. 2010, 65, 42–59. [Google Scholar] [CrossRef]
- Gumma, M.K.; Thenkabail, P.S.; Hideto, F.; Nelson, A.; Dheeravath, V.; Busia, D.; Rala, A. Mapping irrigated areas of Ghana using fusion of 30 m and 250 m resolution remote-sensing data. Remote Sens. 2011, 3, 816–835. [Google Scholar] [CrossRef]
- Xiang, K.; Ma, M.; Liu, W.; Dong, J.; Zhu, X.; Yuan, W. Mapping irrigated areas of northeast China in comparison to natural vegetation. Remote Sens. 2019, 11, 825. [Google Scholar] [CrossRef]
- Gao, Q.; Zribi, M.; Escorihuela, M.; Baghdadi, N.; Segui, P. Irrigation mapping using sentinel-1 time series at field scale. Remote Sens. 2018, 10, 1495. [Google Scholar] [CrossRef]
- Bousbih, S.; Zribi, M.; El Hajj, M.; Baghdadi, N.; Lili-Chabaane, Z.; Gao, Q.; Fanise, P. Soil moisture and irrigation mapping in a semi-arid region, based on the synergetic use of sentinel-1 and sentinel-2 data. Remote Sens. 2018, 10, 1953. [Google Scholar] [CrossRef]
- Bazzi, H.; Baghdadi, N.; Ienco, D.; El Hajj, M.; Zribi, M.; Belhouchette, H.; Escorihuela, M.J.; Demarez, V. Mapping irrigated areas using sentinel-1 time series in Catalonia, Spain. Remote Sens. 2019, 11, 1836. [Google Scholar] [CrossRef]
- Pervez, M.S.; Brown, J.F. Mapping irrigated lands at 250-m scale by merging MODIS data and national agricultural statistics. Remote Sens. 2010, 2, 2388–2412. [Google Scholar] [CrossRef]
- Chen, Y.; Lu, D.; Luo, L.; Pokhrel, Y.; Deb, K.; Huang, J.; Ran, Y. Detecting irrigation extent, frequency, and timing in a heterogeneous arid agricultural region using MODIS time series, Landsat imagery, and ancillary data. Remote Sens. Environ. 2018, 204, 197–211. [Google Scholar] [CrossRef]
- Bazzi, H.; Baghdadi, N.; El Hajj, M.; Zribi, M.; Minh, D.H.T.; Ndikumana, E.; Courault, D.; Belhouchette, H. Mapping paddy rice using sentinel-1 SAR time series in Camargue, France. Remote Sens. 2019, 11, 887. [Google Scholar] [CrossRef]
- Fieuzal, R.; Duchemin, B.; Jarlan, L.; Zribi, M.; Baup, F.; Merlin, O.; Hagolle, O.; Garatuza-Payan, J. Combined use of optical and radar satellite data for the monitoring of irrigation and soil moisture of wheat crops. Hydrol. Earth Syst. Sci. 2011, 15, 1117. [Google Scholar] [CrossRef]
- Baghdadi, N.; Choker, M.; Zribi, M.; Hajj, M.E.; Paloscia, S.; Verhoest, N.E.; Lievens, H.; Baup, F.; Mattia, F. A new empirical model for radar scattering from bare soil surfaces. Remote Sens. 2016, 8, 920. [Google Scholar] [CrossRef]
- Aubert, M.; Baghdadi, N.N.; Zribi, M.; Ose, K.; El Hajj, M.; Vaudour, E.; Gonzalez-Sosa, E. Toward an operational bare soil moisture mapping using TerraSAR-X data acquired over agricultural areas. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 6, 900–916. [Google Scholar] [CrossRef]
- Baghdadi, N.; Camus, P.; Beaugendre, N.; Issa, O.M.; Zribi, M.; Desprats, J.F.; Rajot, J.L.; Abdallah, C.; Sannier, C. Estimating surface soil moisture from TerraSAR-X data over two small catchments in the Sahelian Part of Western Niger. Remote Sens. 2011, 3, 1266–1283. [Google Scholar] [CrossRef]
- El Hajj, M.; Baghdadi, N.; Zribi, M.; Bazzi, H. Synergic use of sentinel-1 and sentinel-2 Images for operational soil moisture mapping at high spatial resolution over agricultural areas. Remote Sens. 2017, 9, 1292. [Google Scholar] [CrossRef]
- Bousbih, S.; Zribi, M.; Lili-Chabaane, Z.; Baghdadi, N.; El Hajj, M.; Gao, Q.; Mougenot, B. Potential of sentinel-1 radar data for the assessment of soil and cereal cover parameters. Sensors 2017, 17, 2617. [Google Scholar] [CrossRef] [PubMed]
- Hajj, M.; Baghdadi, N.; Belaud, G.; Zribi, M.; Cheviron, B.; Courault, D.; Hagolle, O.; Charron, F. Irrigated grassland monitoring using a time series of TerraSAR-X and COSMO-SkyMed X-Band SAR data. Remote Sens. 2014, 6, 10002–10032. [Google Scholar] [CrossRef]
- El Hajj, M.; Baghdadi, N.; Bazzi, H.; Zribi, M. Penetration analysis of SAR signals in the C and L bands for wheat, maize, and grasslands. Remote Sens. 2018, 11, 31. [Google Scholar] [CrossRef]
- Nasrallah, A.; Baghdadi, N.; El Hajj, M.; Darwish, T.; Belhouchette, H.; Faour, G.; Darwich, S.; Mhawej, M. Sentinel-1 data for winter wheat phenology monitoring and mapping. Remote Sens. 2019, 11, 2228. [Google Scholar] [CrossRef]
- Bazzi, H.; Baghdadi, N.; Fayad, I.; Zribi, M.; Belhouchette, H.; Demarez, V. Near real-time irrigation detection at plot scale using sentinel-1 data. Remote Sens. 2020, 12, 1456. [Google Scholar] [CrossRef]
- Bazzi, H.; Baghdadi, N.; El Hajj, M.; Zribi, M. Potential of sentinel-1 surface soil moisture product for detecting heavy rainfall in the south of France. Sensors 2019, 19, 802. [Google Scholar] [CrossRef]
- Le Page, M.; Jarlan, L.; El Hajj, M.M.; Zribi, M.; Baghdadi, N.; Boone, A. Potential for the detection of irrigation events on maize plots using sentinel-1 soil moisture products. Remote Sens. 2020, 12, 1621. [Google Scholar] [CrossRef]
- Bazzi, H.; Baghdadi, N.; El Hajj, M.; Zribi, M.; Belhouchette, H. A Comparison of two soil moisture products S 2 MP and Copernicus-SSM over southern France. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 3366–3375. [Google Scholar] [CrossRef]
- Tiercelin, J.-R. Traité D’irrigation; Tec & Doc: Paris, France, 2006; ISBN 978-2-7430-0910-6. [Google Scholar]
- Baghdadi, N.N.; El Hajj, M.; Zribi, M.; Fayad, I. Coupling SAR C-band and optical data for soil moisture and leaf area index retrieval over irrigated grasslands. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 1229–1243. [Google Scholar] [CrossRef]
- El Hajj, M.; Baghdadi, N.; Zribi, M.; Belaud, G.; Cheviron, B.; Courault, D.; Charron, F. Soil moisture retrieval over irrigated grassland using X-band SAR data. Remote Sens. Environ. 2016, 176, 202–218. [Google Scholar] [CrossRef]
- Mérot, A. Analyse et Modélisation du Fonctionnement Biophysique et Décisionnel d’un Système Prairial Irrigué-Application aux Prairies Plurispécifiques de Crau En Vue de l’élaboration d’un Outil d’aide à la Décision. Ph.D. Thesis, Ecole Nationale Superieure Agronomique de Montpellier, Montpellier, France, September 2007. [Google Scholar]
- Inglada, J.; Vincent, A.; Arias, M.; Tardy, B.; Morin, D.; Rodes, I. Operational high resolution land cover map production at the country scale using satellite image time series. Remote Sens. 2017, 9, 95. [Google Scholar] [CrossRef]
- Cookmartin, G.; Saich, P.; Quegan, S.; Cordey, R.; Burgess-Allen, P.; Sowter, A. Modeling microwave interactions with crops and comparison with ERS-2 SAR observations. IEEE Trans. Geosci. Remote Sens. 2000, 38, 658–670. [Google Scholar] [CrossRef]
- Mattia, F.; le Toan, T.; Picard, G.; Posa, F.I.; D’Alessio, A.; Notarnicola, C.; Gatti, A.M.; Rinaldi, M.; Satalino, G.; Pasquariello, G. Multitemporal c-band radar measurements on wheat fields. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1551–1560. [Google Scholar] [CrossRef]
- Del Frate, F.; Ferrazzoli, P.; Guerriero, L.; Strozzi, T.; Wegmuller, U.; Cookmartin, G.; Quegan, S. Wheat cycle monitoring using radar data and a neural network trained by a model. IEEE Trans. Geosci. Remote Sens. 2004, 42, 35–44. [Google Scholar] [CrossRef]
- Baghdadi, N.; El Hajj, M.; Choker, M.; Zribi, M.; Bazzi, H.; Vaudour, E.; Gilliot, J.-M.; Ebengo, D. Potential of sentinel-1 images for estimating the soil roughness over bare agricultural soils. Water 2018, 10, 131. [Google Scholar] [CrossRef]
- Baghdadi, N.; Zribi, M.; Loumagne, C.; Ansart, P.; Anguela, T. Analysis of TerraSAR-X data and their sensitivity to soil surface parameters over bare agricultural fields. Remote Sens. Environ. 2008, 112, 4370–4379. [Google Scholar] [CrossRef]



| Configuration | Metric | Thresholds | |||
|---|---|---|---|---|---|
| VV | S (%) | 82.4 | 66.5 | 44.6 | 32.3 |
| Pr (%) | 66.9 | 81.6 | 91.8 | 93.7 | |
| F_score (%) | 73.8 | 73.3 | 60.0 | 48.0 | |
| VH | S (%) | 79.9 | 60.10 | 29.7 | 18.0 |
| Pr (%) | 65.8 | 76.8 | 86.6 | 85.44 | |
| F_score (%) | 72.2 | 67.4 | 44.2 | 29.7 | |
| Configuration | Metric | Thresholds | |||
|---|---|---|---|---|---|
| VV or VH | S (%) | 88.2 | 76.8 | 51.6 | 38.0 |
| Pr (%) | 58.5 | 72.8 | 87.4 | 89.5 | |
| F_score (%) | 70.3 | 74.7 | 64.9 | 53.3 | |
| VV and VH | S (%) | 74.1 | 50.0 | 22.7 | 12.1 |
| Pr (%) | 78.9 | 91.8 | 95.2 | 94.1 | |
| F_score (%) | 76.4 | 64.7 | 36.7 | 21.4 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bazzi, H.; Baghdadi, N.; Fayad, I.; Charron, F.; Zribi, M.; Belhouchette, H. Irrigation Events Detection over Intensively Irrigated Grassland Plots Using Sentinel-1 Data. Remote Sens. 2020, 12, 4058. https://doi.org/10.3390/rs12244058
Bazzi H, Baghdadi N, Fayad I, Charron F, Zribi M, Belhouchette H. Irrigation Events Detection over Intensively Irrigated Grassland Plots Using Sentinel-1 Data. Remote Sensing. 2020; 12(24):4058. https://doi.org/10.3390/rs12244058
Chicago/Turabian StyleBazzi, Hassan, Nicolas Baghdadi, Ibrahim Fayad, François Charron, Mehrez Zribi, and Hatem Belhouchette. 2020. "Irrigation Events Detection over Intensively Irrigated Grassland Plots Using Sentinel-1 Data" Remote Sensing 12, no. 24: 4058. https://doi.org/10.3390/rs12244058
APA StyleBazzi, H., Baghdadi, N., Fayad, I., Charron, F., Zribi, M., & Belhouchette, H. (2020). Irrigation Events Detection over Intensively Irrigated Grassland Plots Using Sentinel-1 Data. Remote Sensing, 12(24), 4058. https://doi.org/10.3390/rs12244058








