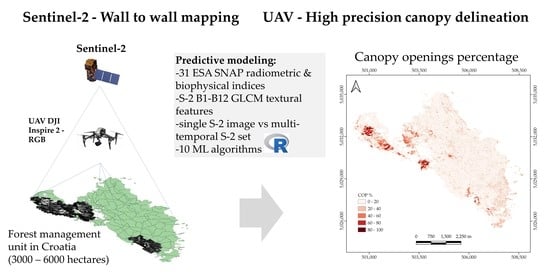
Mapping of the Canopy Openings in Mixed Beech–Fir Forest at Sentinel-2 Subpixel Level Using UAV and Machine Learning Approach
Abstract
1. Introduction
2. Materials and Methods
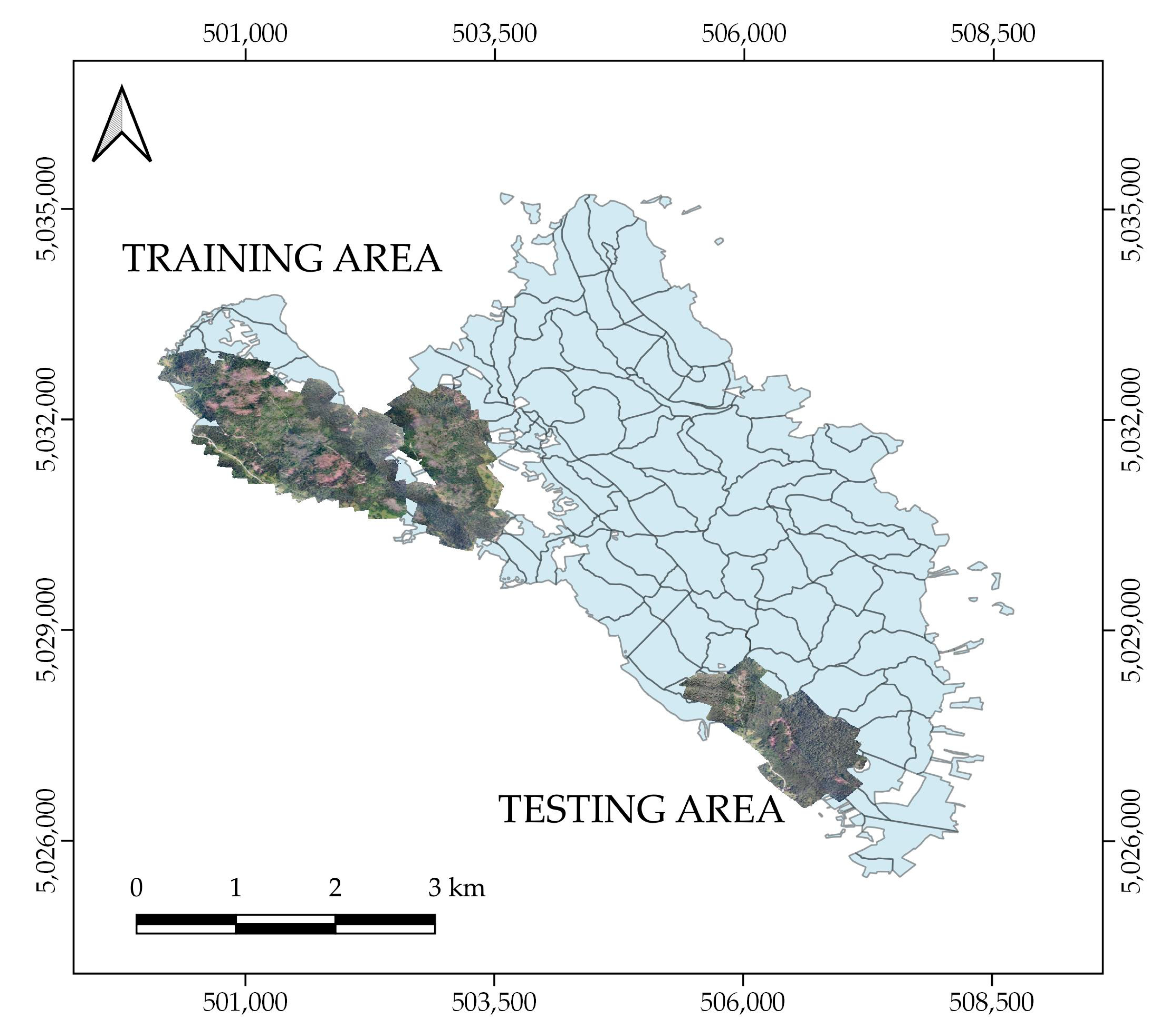
2.1. Study Area
2.2. UAV Survey of the Training and the Testing Area
2.3. Satellite Image Processing and Index Extraction
2.4. Integration of Sentinel 2 and UAV Data
2.5. Model Building and Validation
2.5.1. Ordinary Least Squares (OLS) Linear Regression
2.5.2. Partial Least Squares (PLS)
2.5.3. Ridge Regression (RR)
2.5.4. Elastic Net (ENET)
2.5.5. Feed-Forward Neural Networks (NNET)
2.5.6. Support Vector Machine (SVM)
2.5.7. Random Forest (RF)
2.5.8. Boosting (GBM, XGBoost, Catboost)
3. Results
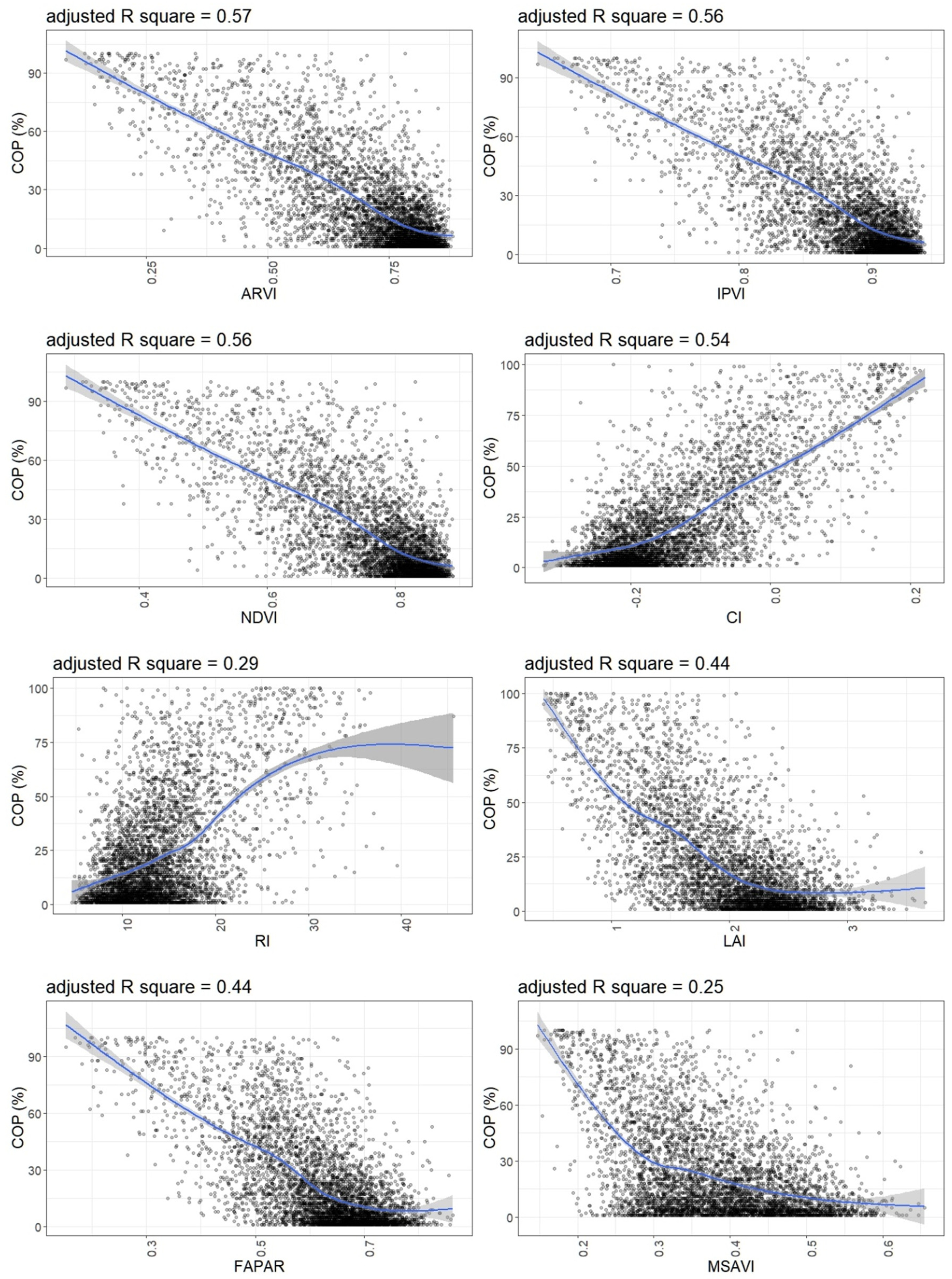
3.1. Relationship of UAV Canopy Openings Percentage (COP) and Individual Sentinel-2 Indices
3.2. Training and Validation of Predictive Models
3.3. The Importance of Satellite Indices in Prediction
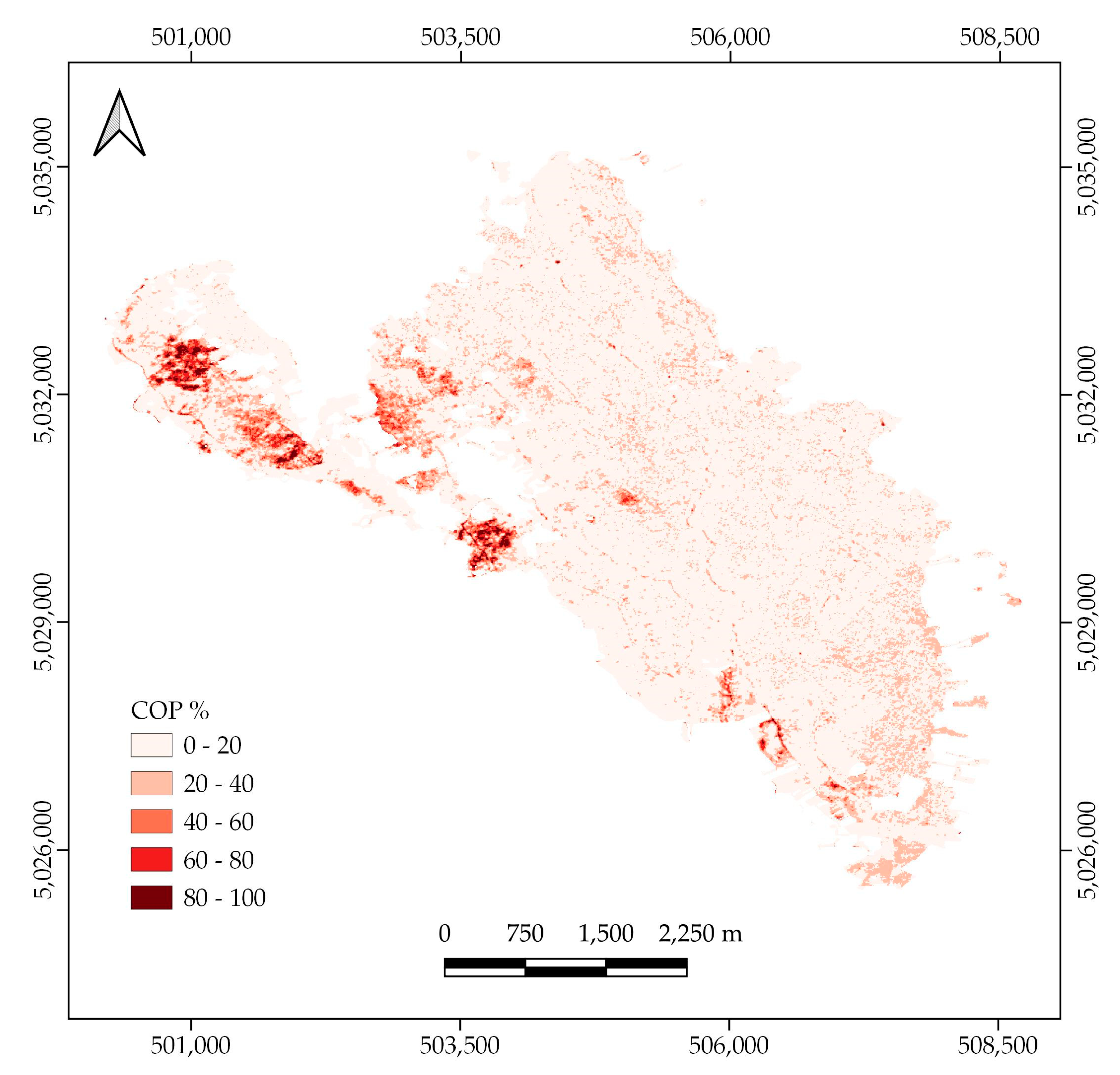
3.4. Final Model Building and COP Map Production
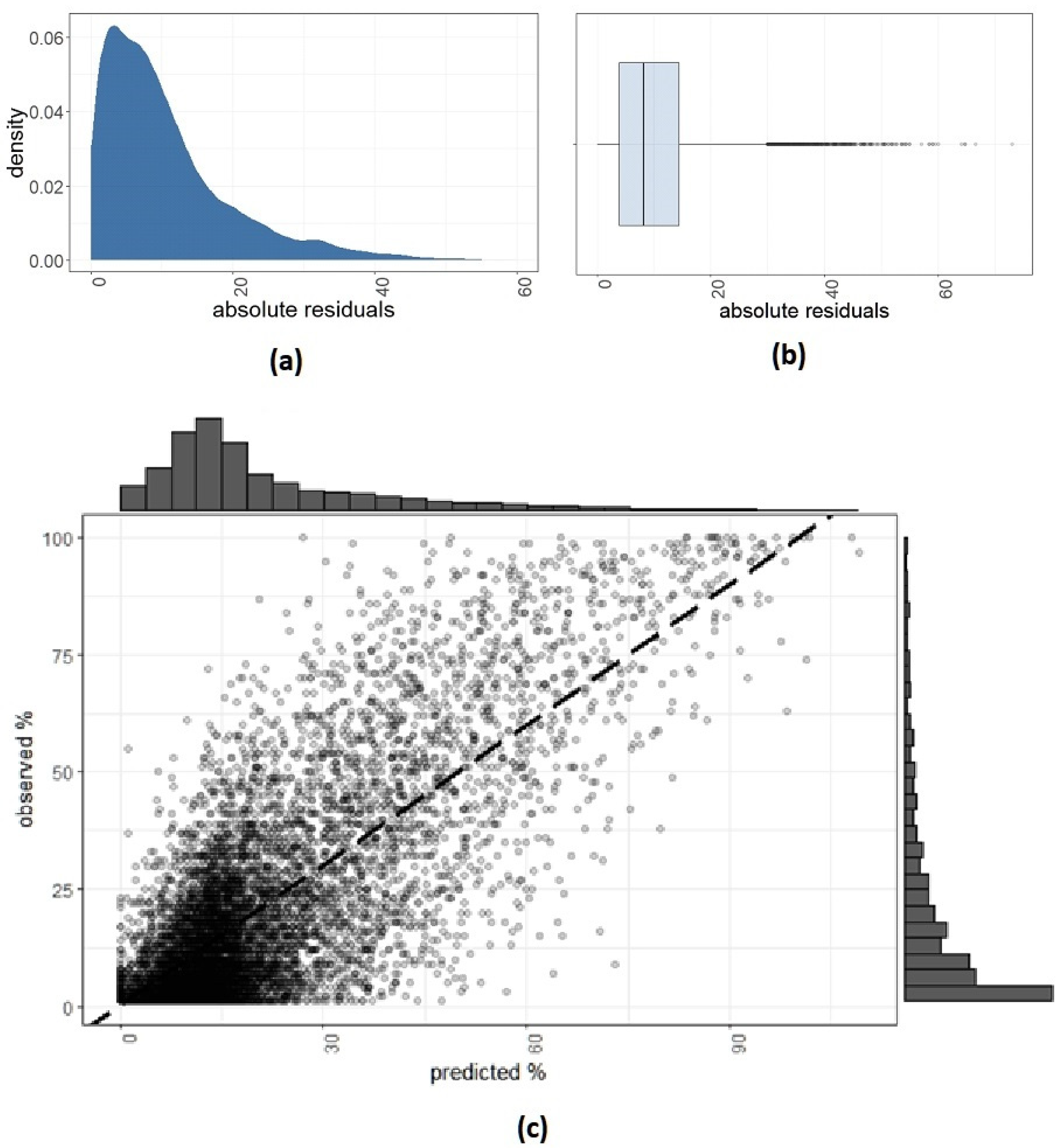
3.5. Analysis of Residuals and Observed Shortcomings of the Model
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Čater, M.; Diaci, J.; Roženbergar, D. Gap size and position influence variable response of Fagus sylvatica L. and Abies alba Mill. For. Ecol. Manag. 2014, 325, 128–135. [Google Scholar] [CrossRef]
- Dobrowolska, D.; Veblen, T.T. Treefall-gap structure and regeneration in mixed Abies alba stands in central Poland. For. Ecol. Manag. 2008, 255, 3469–3476. [Google Scholar] [CrossRef]
- Ugarković, D.; Tikvić, I.; Popić, K.; Malnar, J.; Stankić, I. Microclimate and natural regeneration of forest gaps as a consequence of silver fir (Abies alba Mill.) dieback. J. For. 2018, 5–6, 235–245. [Google Scholar]
- Muscolo, A.; Sidari, M.; Mercurio, R. Variations in soil chemical properties and microbial biomass in artificial gaps in silver fir stands. Eur. J. For. Res. 2007, 126, 59–65. [Google Scholar] [CrossRef]
- Muscolo, A.; Sidari, M.; Bagnato, S.; Mallamaci, C.; Mercurio, R. Gap size effects on above and below-ground processes in a silver fir stand. Eur. J. For. Res. 2010, 129, 355–365. [Google Scholar] [CrossRef]
- Albanesi, E.; Gugliotta, O.I.; Mercurio, I.; Mercurio, R. Effects of gap size and within-gap position on seedlings establishment in silver fir stands. Forest 2005, 2, 358–366. [Google Scholar] [CrossRef]
- Nagel, T.A.; Svoboda, M. Gap disturbance regime in an old-growth Fagus-Abies forest in the Dinaric Mountains, Bosnia-Hercegovina. Can. J. For. Res. 2008, 38, 2728–2737. [Google Scholar] [CrossRef]
- Nagel, T.A.; Svoboda, M.; Diaci, J. Regeneration patterns after intermediate wind disturbance in an old-growth Fagus-Abies forest in Southeastern Slovenia. For. Ecol. Manag. 2006, 226, 268–278. [Google Scholar] [CrossRef]
- Diaci, J.; Pisek, R.; Boncina, A. Regeneration in experimental gaps of subalpine Picea abies forest in Slovenian Alps. Eur. J. For. Res. 2005, 124, 29–36. [Google Scholar] [CrossRef]
- Malcolm, D.C.; Mason, W.I.; Clarke, G.C. The transformation of conifer forests in Britain—Regeneration, gap size and silvicultural systems. For. Ecol. Manag. 2001, 151, 7–23. [Google Scholar] [CrossRef]
- Navarro-Cerrillo, R.M.; Camarero, J.J.; Menzanedo, R.D.; Sánchez-Cuesta, R.; Quintanilla, J.L.; Sánchez, S. Regeneration of Abies pinsapo within gaps created by Heterobasidion annosuminduced tree mortality in southern Spain. iForest 2014, 7, 209–215. [Google Scholar] [CrossRef]
- Vilhar, U.; Roženbergar, D.; Simončić, P.; Diaci, J. Variation in irradiance, soil features and regeneration patterns in experimental forest canopy gaps. Ann. For. Sci. 2015, 72, 253–266. [Google Scholar] [CrossRef]
- Streit, K.; Wunder, K.; Brang, P. Slit-shaped gaps are a successful silvicultural technique to promote Picea abies regeneration in mountain forests of the Swiss Alps. For. Ecol. Manag. 2009, 257, 1902–1909. [Google Scholar] [CrossRef]
- Thurnher, C.; Klopf, M.; Hasenauer, H. Forest in Transition: A Harvesting Model for Uneven-aged Mixed Species Forest in Austria. Forestry 2011, 84, 517–526. [Google Scholar] [CrossRef]
- Abdollahnejad, A.; Panagiotidis, D.; Surový, P. Forest canopy density assessment using different approaches—Review. J. For. Sci. 2017, 63, 106–115. [Google Scholar] [CrossRef]
- Paletto, A.; Tosi, V. Forest canopy cover and canopy closure: Comparison of assessment techniques. Eur. J. For. Res. 2009, 128, 265–272. [Google Scholar] [CrossRef]
- Karhonen, L.; Karhonen, K.T.; Rautiainen, M.; Stenberg, P. Estimation of forest canopy cover: A Comparison of Field Measurement Techniques. Silva Fenn. 2006, 40, 577–588. [Google Scholar] [CrossRef]
- Arumäe, T.; Lang, M. Estimation of canopy cover in dense mixed-species forests using airborne lidar data. Eur. J. Remote Sens. 2017, 51, 132–141. [Google Scholar] [CrossRef]
- Wu, X.; Shen, X.; Cao, L.; Wang, G.; Cao, F. Assessment of Individual Tree Detection and Canopy Cover Estimation using Unmanned Aerial Vehicle based Light Detection and Ranging (UAV-LiDAR) Data in Planted Forests. Remote Sens. 2019, 11, 908. [Google Scholar] [CrossRef]
- Deutcher, J.; Granica, K.; Steinegger, M.; Hirschmugl, M.; Perko, R.; Schardt, M. Updating Lidar-derived Crown Cover Density Products with Sentinel-2. IGARSS 2017, 2867–2870. [Google Scholar] [CrossRef]
- Karna, K.Y.; Penman, T.D.; Aponte, C.; Bennett, L.T. Assessing Legacy Effects of Wildfires on the Crown Structure of Fire-Tolerant Eucalypt Trees Using Airborne LiDAR Data. Remote Sens. 2019, 11, 2433. [Google Scholar] [CrossRef]
- Huang, C.; Yang, L.; Wylie, B.; Homer, C. A strategy for estimating tree canopy density using Landsat 7 ETM+ and high resolution images over large areas. In Proceedings of the Third International Conference on Geospatial Information in Agriculture and Forestry, Denver, CO, USA, 5–7 November 2001. [Google Scholar]
- Mon, M.S.; Mizoue, N.; Htun, N.Z.; Kajisa, T.; Yoshida, S. Estimating forest canopy density of tropical mixed deciduous vegetation using Landsat data; a comparison of three classification approaches. Int. J. Remote Sens. 2012, 33, 1042–1057. [Google Scholar] [CrossRef]
- Baynes, J. Assessing forest canopy density in a highly variable landscape using Landsat data and FCD Mapper software. Aust. For. 2004, 67, 247–253. [Google Scholar] [CrossRef]
- Joshi, C.; De Leeuw, J.; Skidmore, A.K.; van Duren, I.C.; van Oosten, H. Remote sensed estimation of forest canopy density: A comparison of the performance of four methods. Int. J. Appl. Earth Obs. Geoinf. 2006, 8, 84–95. [Google Scholar] [CrossRef]
- Korhonen, L.; Hadi Packalen, P.; Rautiainen, M. Comparison of Sentinel-2 and Landsat 8 in the estimation of boreal forest canopy cover and leaf area index. Remote Sens. Environ. 2017, 195, 259–274. [Google Scholar] [CrossRef]
- Mulatu, K.A.; Decuyper, M.; Brede, B.; Kooistra, L.; Reiche, J.; Mora, B.; Herold, M. Linking terrestrial LiDAR scanner and conventional forest structure measurements with multi-modal satellite data. Forests 2019, 10, 291. [Google Scholar] [CrossRef]
- Revill, A.; Florence, A.; MacArthur, A.; Hoad, S.; Rees, R.; Williams, M. Quantifying uncertainity and bridging the scaling ga pin the retrieval of leaf area indeks by coupling Sentinel-2 and UAV observations. Remote Sens. 2020, 12, 1843. [Google Scholar] [CrossRef]
- Copernicus Land Monitoring Service. Available online: https://land.copernicus.eu/ (accessed on 15 August 2020).
- Sentinel 2 User Handbook; Rev 2; European Space Agency: Paris, France, 2015; p. 64. Available online: https://sentinel.esa.int/documents/247904/685211/Sentinel-2_User_Handbook (accessed on 18 August 2020).
- Lima, T.A.; Beuchle, R.; Langner, A.; Grecchi, R.C.; Griess, V.C.; Achard, F. Comparing Sentinel-2 MSI and Landsat 8 OLI imagery for monitoring selective logging in the Brazilian Amazon. Remote Sens. 2019, 11, 961. [Google Scholar] [CrossRef]
- Masiliūnas, D. Evaluating the potential of Sentinel-2 and Landsat image time series for detecting selective logging in the Amazon. In Geo-Information Science and Remote Sensing; Thesis Report GIRS-2017-27; Wageningen University and Research Centre: Wageningen, The Netherlands, 2017; p. 54. [Google Scholar]
- Barton, I.; Király, G.; Czimber, K.; Hollaus, M.; Pfeifer, N. Treefall gap mapping using Sentinel-2 images. Forests 2017, 8, 426. [Google Scholar] [CrossRef]
- Šimić Milas, A.; Rupasinghe, P.; Balenović, I.; Grosevski, P. Assessment of Forest Damage in Croatia using Landsat-8 OLI Images. SEEFOR 2015, 6, 159–169. [Google Scholar] [CrossRef]
- Navarro, J.A.; Algeet, N.; Fernández-Landa, A.; Esteban, J.; Rodríguez-Noriega, P.; Guillén-Climent, M.L. Integration of UAV, Sentinel-1, and Sentinel-2 Data for Mangrove Plantation Aboveground Biomass Monitoring in Senegal. Remote Sens. 2019, 11, 77. [Google Scholar] [CrossRef]
- Pla, M.; Bota, G.; Duane, A.; Balagué, J.; Curcó, A.; Gutiérrez, R.; Brotons, L. Calibrating Sentinel-2 imagery with multispectral UAV derived information to quantify damages in Mediterranean rice crops caused by Western Swamphen (Porphyrio porphyrio). Drones 2019, 3, 45. [Google Scholar] [CrossRef]
- Castro, C.C.; Gómez, J.A.D.; Martin, J.D.; Sánchez, B.A.H.; Arango, J.L.C.; Tuya, F.A.C.; Diaz-Varela, R. An UAV and satellite multispectral data approach to monitor water quality in small reservoirs. Remote Sens. 2020, 12, 1514. [Google Scholar] [CrossRef]
- Copernicus Open Access Hub. Available online: https://scihub.copernicus.eu/ (accessed on 12 February 2020).
- Xue, J.; Su, B. Significant Remote Sensing Vegetation Indices: A Review of Developments and Applications. J. Sens. 2017, 17. [Google Scholar] [CrossRef]
- Bannari, A.; Morin, D.; Bonn, F. A Review of vegetation indices. Remote Sens. Rev. 1995, 13, 95–120. [Google Scholar] [CrossRef]
- Silleos, N.G.; Alexandridis, T.K.; Gitas, I.Z.; Perakis, K. Vegetation Indices: Advances Made in Biomass Estimation and Vegetation Monitoring in the Last 30 Years. Geocarto Int. 2006, 21, 21–28. [Google Scholar] [CrossRef]
- Escadafal, R.; Girard, M.C.; Courault, D. Munsell soil color and soil reflectance in the visible spectral bands of landsat MSS and TM data. Remote Sens. Environ. 1989, 27, 37–46. [Google Scholar] [CrossRef]
- Djamai, N.; Zhong, D.; Fernandes, R.; Zhou, F. Evaluation of Vegetation Biophysical variables Time Series Derived from Synthetic Sentinel-2 Images. Remote Sens. 2019, 11, 1547. [Google Scholar] [CrossRef]
- Godinho, S.; Guiomar, N.; Gil, A. Estimating tree canopy cover percentage in a mediterranean silvopastoral systems using Sentinel-2A imagery and the stochastic gradient boosting algorithm. Int. J. Remote Sens. 2018, 39, 4640–4662. [Google Scholar] [CrossRef]
- Haralick, R.; Shanmugam, K.; Dinstein, I. Textural Features for Image Classification. IEEE Trans. Syst. Man Cybern. 1973, 3, 610–621. [Google Scholar] [CrossRef]
- Wickham, H. Tidy data. J. Stat. Softw. 2014, 59, 1–23. [Google Scholar] [CrossRef]
- Gašparović, M.; Seletković, A.; Berta, A.; Balenović, I. The evaluation of photogrammetry-based DSM from low-cost UAV by LiDAR-based DSM. SEEFOR 2017, 8, 117–125. [Google Scholar] [CrossRef]
- Gašparović, M.; Zrinjski, M.; Barković, Đ.; Radočaj, D. An automatic method for weed mapping in oat fields based on UAV imagery. Comput Electron. Agric. 2020, 173, 105385. [Google Scholar] [CrossRef]
- Mathieu, R.; Pouget, M.; Cervelle, B.; Escadafal, R. Relationships between satellite-based radiometric indices simulated using laboratory reflectance data and typic soil color of an arid environment. Remote Sens. Environ. 1998, 66, 17–28. [Google Scholar] [CrossRef]
- Madeira, J.; Bedidi, A.; Cervelle, B.; Pouget, M.; Flay, N. Visible spectrometric indices of hematite (Hm) and goethite (Gt) content in lateritic soils: The application of a Thematic Mapper (TM) image for soil-mapping in Brasilia, Brazil. Int. J. Remote Sens. 1997, 18, 2835–2852. [Google Scholar] [CrossRef]
- Escadafal, R.; Huete, A. Etude des propriétés spectrales des sols arides appliquée à l’amélioration des indices de végétation obtenus par télédétection. In Comptes Rendus de l’Académie des Sciences. Série 2, Mécanique, Physique, Chimie, Sciences de l’univers, Sciences de la Terre; Gauthier-Villars: Paris, France, 1991; Volume 312, pp. 1385–1391. [Google Scholar]
- Louhaichi, M.; Borman, M.M.; Johnson, D.E. Spatially located platform and aerial photography for documentation of grazing impacts on wheat. Geocarto Int. 2001, 16, 65–70. [Google Scholar] [CrossRef]
- Tucker, C.J. Red and photographic infrared linear combinations for monitoring vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Kaufman, Y.J.; Stark, R.; Rundquist, D. Novel algorithms for remote estimation of vegetation fraction. Remote Sens. Environ. 2002, 80, 76–87. [Google Scholar] [CrossRef]
- Kuhn, M.; Johnson, K. Applied Predictive Modeling; Springer: New York, NY, USA, 2013; p. 615. [Google Scholar]
- The Caret Package. Available online: http://topepo.github.io/caret/index.html (accessed on 18 May 2020).
- Wittke, S.; Yu, X.; Karjalainen, M.; Hyyppä, J.; Puttonen, E. Comparison of two-dimensional multitemporal Sentinel-2 data with three dimensional remote sensing data sources for forest inventory parameter estimation over a boreal forest. Int. J. Appl. Earth Obs. Geoinf. 2019, 76, 167–178. [Google Scholar] [CrossRef]
- Macintyre, P.; van Niekerk, A.; Mucina, L. Efficacy of multi-season Sentinel-2 imagery for compositional vegetation classification. Int. J. Appl. Earth. Obs. Geoinf. 2020, 85, 101980. [Google Scholar] [CrossRef]




| Platform ID | Year | Month | Day | Time of Acquisition | Relative Orbit Number | Tile Number Field |
|---|---|---|---|---|---|---|
| S2A | 2018 | 7 | 25 | 10:00 a.m. | R122 | T33TVL |
| S2B | 2018 | 8 | 1 | 10:00 a.m. | R122 | T33TVL |
| S2B | 2018 | 8 | 29 | 10:00 a.m. | R122 | T33TVL |
| S2B | 2018 | 9 | 28 | 10:00 a.m. | R122 | T33TVL |
| Satellite Index | Spectral Bands | Sentinel 2 Bands |
|---|---|---|
| Soil radiometric indices | ||
| BI—Brightness Index | red, green | B4, B3 |
| BI2—The Second Brightness Index | red, green, NIR(near infrared) | B4, B3, B8 |
| RI—Redness Index | red, green | B4, B3 |
| CI—Color Index | red, green | B4, B3 |
| Vegetation radiometric indices | ||
| SAVI—Soil-Adjusted Vegetation Index | red, NIR | B4, B8 |
| NDVI—Normalized Difference Vegetation Index | red, NIR | B4, B8 |
| TSAVI—Transformed Soil-Adjusted Vegetation Index | red, NIR | B4, B8 |
| MSAVI—Modified Soil-Adjusted Vegetation Index | red, NIR | B4, B8 |
| MSAVI2—The Second Modified Soil-Adjusted Vegetation Index | red, NIR | B4, B8 |
| DVI—Difference Vegetation Index | red, NIR | B4, B8 |
| RVI—Ratio Vegetation Index | red, NIR | B4, B8 |
| PVI—Perpendicular Vegetation Index | red, NIR | B4, B8 |
| IPVI—Infrared Percentage Vegetation Index | red, NIR | B4, B8 |
| WDVI—Weighted Difference Vegetation Index | red, NIR | B4, B8 |
| TNDVI—Transformed Normalized Difference Vegetation Index | red, NIR | B4, B8 |
| GNDVI—Green Normalized Difference Vegetation Index | green, NIR | B3, B7 |
| GEMI—Global Environmental Monitoring Index | red, NIR | B4, B8A |
| ARVI—Atmospherically Resistant Vegetation Index | red, blue, NIR | B4, B2, B8 |
| NDI45—Normalized Difference Index | red, red edge | B4, B5 |
| MTCI—Meris Terrestrial Chlorophyll Index | red, red edge, NIR | B4, B5, B6 |
| MCARI—Modified Chlorophyll Absorption Ratio Index | red, red edge, green | B4, B5, B3 |
| REIP—Red-Edge Inflection Point Index | red, red edge, red edge, NIR | B4, B5, B6, B7 |
| S2REP—Red-Edge Position Index | red, red edge, red edge, NIR | B4, B5, B6, B7 |
| IRECI—Inverted Red-Edge Chlorophyll Index | red, red edge, red edge, NIR | B4, B5, B6, B7 |
| PSSRa—Pigment-Specific Simple Ratio Index | red, NIR | B4, B7 |
| Water Radiometric Indices | ||
| NDWI—Normalized Difference Water Index | NIR, MIR(mid-infrared) | B8, B12 |
| NDWI2—Second Normalized Difference Water Index | green, NIR | B3, B8 |
| MNDWI—Modified Normalized Difference Water Index | green, MIR | B3, B12 |
| NDPI—Normalized Difference Pond Index | green, MIR | B3, B12 |
| NDTI—Normalized Difference Turbidity Index | red, green | B4, B3 |
| Biophysical indices | ||
| LAI—Leaf Area Index | B3, B4, B5, B6, B7, B8a, B11, B12, cos(viewing_zenith), cos(sun_zenith), cos(sun_zenith), cos(relative_azimuth_angle) | |
| FAPAR—Fraction of Absorbed Photosynthetically Active Radiation | ||
| FVC—Fraction of Vegetation Cover | ||
| CAB—Chlorophyll Content in the Leaf | ||
| CWC—Canopy Water Content | ||
| Texture (Gray-Level Co-occurrence Matrix, GLCM) | ||
| Contrast | ||
| Dissimilarity | ||
| Homogeneity | ||
| Angular Second Moment | ||
| Energy | ||
| Maximum Probability | ||
| Entropy | ||
| GLCM Mean | ||
| GLCM Variance | ||
| GLCM Correlation | ||
| 10-Fold CV Training Set: Single Sentinel-2 Image (S2 25 July 2018) | |||||
|---|---|---|---|---|---|
| Model | RMSE | R2 | MAE | Tuning Parameters | |
| Multiple regression (Ordinary Least Squares)—OLS | 15.684 | 0.603 | 11.366 | ||
| Multiple regression (Ordinary Least Squares) with PCA pre-processing—OLS with PCA | 16.301 | 0.571 | 11.909 | ||
| Partial Least Squares—PLS | 15.618 | 0.604 | 11.397 | ncomp = 20 | |
| Ridge Regression RR | 15.611 | 0.606 | 11.305 | lambda = 0.007142857 | |
| Elastic Net—ENET | 15.629 | 0.605 | 11.314 | fraction = 1 lambda = 0.01 | |
| Model Averaged Neural Network—NNET | 15.864 | 0.591 | 11.531 | size = 5 decay = 0.01 | |
| Support Vector Machines with Radial Basis Function Kernel—SVM | 15.344 | 0.622 | 10.784 | sigma = 0.007735318 C = 2 | |
| Random Forest—RF | 15.394 | 0.616 | 11.374 | mtry = 10 | |
| Stochastic Gradient Boosting—GBM | 15.376 | 0.616 | 11.206 | n.trees = 910 interaction.depth = 7 | |
| shrinkage = 0.01 n.minobsinnode = 20 | |||||
| Extreme Gradient Boosting—XGBoost | 15.148 | 0.624 | 11.070 | nrounds = 550 | max_depth = 5 |
| eta = 0.025 | |||||
| Catboost—Cboost | 15.308 | 0.619 | 11.197 | depth = 8 | learning_rate = 0.1 |
| leaf_reg = 0.001 | rsm = 0.95 | ||||
| 10-Fold CV Training Set: Sentinel 2 Multitemporal (S2 25 July 2018; S2 1 August 2018; S2 29 August 2018; S2 28 September 2018) | |||||
|---|---|---|---|---|---|
| Model | RMSE | R2 | MAE | Tuning Parameters | |
| Multiple regression (Ordinary Least Squares)—OLS | 87.413 | 0.593 | 14.458 | ||
| Partial Least Squares—PLS | 15.020 | 0.650 | 10.770 | ncomp = 10 | |
| Ridge Regression—RR | 41.520 | 0.611 | 11.890 | lambda = 0.1 | |
| Elastic Net—ENET | 14.360 | 0.669 | 10.543 | fraction = 0.2 lambda = 0.01 | |
| Model Averaged Neural Network—NNET | 14.230 | 0.680 | 10.520 | size = 11 decay = 0.1 | |
| Support Vector Machines with Radial Basis Function Kernel—SVM | 13.756 | 0.697 | 9.872 | sigma = 0.001703831 C = 2 | |
| Random Forest—RF | 14.265 | 0.673 | 10.732 | mtry = 213 | |
| Stochastic Gradient Boosting—GBM | 13.952 | 0.685 | 10.369 | n.trees = 910 interaction.depth = 7 | |
| shrinkage = 0.01 n.minobsinnode = 30 | |||||
| Extreme Gradient Boosting—XGBoost | 13.991 | 0.683 | 10.348 | nrounds = 650 | max_depth = 4 |
| eta = 0.05 | |||||
| Catboost—Cboost | 14.195 | 0.676 | 10.460 | depth = 6 | learning_rate = 0.1 |
| leaf_reg = 0.001 | rsm = 0.95 | ||||
| Test Set: Single Sentinel-2 Image (S2 25 July 2018) | |||
|---|---|---|---|
| Model | RMSE | R2 | MAE |
| Multiple regression (Ordinary Least Squares)—OLS | 15.264 | 0.406 | 11.655 |
| Partial Least Squares—PLS | 15.220 | 0.410 | 11.450 |
| Ridge Regression—RR | 15.110 | 0.420 | 11.230 |
| Elastic Net—ENET | 15.090 | 0.420 | 11.190 |
| Model Averaged Neural Network—NNET | 15.360 | 0.410 | 11.090 |
| Support Vector Machines with Radial Basis Function Kernel—SVM | 16.110 | 0.380 | 11.390 |
| Random Forest—RF | 15.290 | 0.410 | 11.240 |
| Stochastic Gradient Boosting—GBM | 15.580 | 0.400 | 11.150 |
| Extreme Gradient Boosting—XGBoost | 15.645 | 0.387 | 11.233 |
| Catboost—Cboost | 15.488 | 0.403 | 11.171 |
| Test Set—Sentinel-2 Multitemporal (S2 25 July 2018; S2 1 August 2018; S2 29 August 2018; S2 28 September 2018) | |||
|---|---|---|---|
| Model | RMSE | R2 | MAE |
| Multiple regression (Ordinary Least Squares)—OLS | 15.264 | 0.406 | 11.655 |
| Partial Least Squares—PLS | 15.303 | 0.425 | 11.190 |
| Ridge Regression—RR | 15.359 | 0.440 | 11.140 |
| Elastic Net—ENET | 14.999 | 0.445 | 10.916 |
| Model Averaged Neural Network—NNET | 15.846 | 0.402 | 11.447 |
| Support Vector Machines with Radial Basis Function Kernel—SVM | 16.020 | 0.410 | 11.240 |
| Random Forest—RF | 14.900 | 0.440 | 10.935 |
| Stochastic Gradient Boosting—GBM | 14.940 | 0.440 | 10.730 |
| Extreme Gradient Boosting—XGBoost | 15.102 | 0.428 | 10.874 |
| Catboost—Cboost | 14.951 | 0.441 | 10.793 |
| CBoost | S-2 | Score | GBM | S-2 | Score | XGBoost | S-2 | Score |
| IPVI | I | 100.00 | CI | I | 100.00 | CI | I | 100.00 |
| NDTI | I | 92.57 | ARVI | I | 36.53 | ARVI | I | 33.58 |
| TNDVI | I | 75.02 | NDI45 | III | 32.07 | IPVI | I | 33.48 |
| NDI45 | IV | 71.79 | PSSRA | I | 29.16 | NDI45 | III | 19.74 |
| NDI45 | II | 54.44 | NDI45 | II | 26.5 | PSSRA | II | 13.47 |
| NDTI | II | 49.79 | IPVI | I | 22.65 | NDI45 | I | 11.85 |
| NDVI | IV | 41.68 | NDI45 | IV | 16.43 | NDI45 | IV | 11.73 |
| MCARI | I | 40.58 | CI | II | 15.6 | CI | II | 10.79 |
| ARVI | I | 37.70 | NDI45 | I | 15.02 | IPVI | IV | 5.63 |
| RI | II | 36.04 | CI | IV | 10.75 | CI | IV | 5.61 |
| TNDVI | IV | 34.42 | IPVI | IV | 7.27 | NDI45 | I | 5.50 |
| NDWI2 | IV | 32.80 | ARVI | II | 7.22 | RI | II | 4.62 |
| CI | II | 32.24 | RI | II | 7.08 | MCARI | IV | 4.18 |
| PSSRA | I | 31.53 | PSSRA | II | 6.04 | MCARI | I | 3.8 |
| NDTI | IV | 30.57 | CI | III | 5.99 | ARVI | II | 3.48 |
| NDTI | III | 29.08 | MCARI | IV | 5.65 | CI | III | 3.24 |
| GLCM_VAR_B1 | IV | 28.21 | MCARI | I | 4.66 | GLCM_VAR_B1 | IV | 2.54 |
| ARVI | IV | 27.97 | PSSRA | II | 4.61 | ARVI | IV | 2.46 |
| CI | III | 27.32 | NDWI2 | IV | 4.08 | NDWI2 | IV | 2.46 |
| NDVI | I | 26.11 | ARVI | IV | 3.64 | PSSRA | II | 1.78 |
| ENET | S-2 | Score | RF | S-2 | Score | SVM | S-2 | Score |
| ARVI | I | 100 | NDI45 | IV | 100 | ARVI | I | 100 |
| TNDVI | I | 98.85 | ARVI | I | 80.22 | TNDVI | I | 98.85 |
| IPVI | I | 98.85 | MCARI | IV | 79.45 | IPVI | I | 98.85 |
| NDVI | I | 98.85 | RI | II | 75.48 | NDVI | I | 98.85 |
| RVI | IV | 98.45 | IPVI | IV | 73 | RVI | IV | 98.45 |
| RVI | I | 98.45 | PSSRA | I | 71.2 | RVI | I | 98.45 |
| ARVI | II | 97.85 | MCARI | I | 69.72 | ARVI | II | 97.85 |
| CI | I | 97.73 | CI | IV | 69.61 | NDTI | I | 97.73 |
| NDTI | I | 97.73 | CI | II | 65.47 | CI | I | 97.73 |
| PSSRA | I | 97.46 | CI | I | 65.11 | PSSRA | I | 97.46 |
| CI | II | 96.73 | NDVI | IV | 63.8 | NDTI | II | 96.73 |
| NDTI | II | 96.73 | NDTI | I | 63.28 | CI | II | 96.73 |
| IPVI | II | 96.4 | TNDVI | IV | 62.23 | IPVI | II | 96.4 |
| NDVI | II | 96.4 | NDTI | IV | 59.98 | NDVI | II | 96.4 |
| TNDVI | II | 96.4 | RVI | IV | 59.08 | TNDVI | II | 96.4 |
| PSSRA | II | 96.28 | NDTI | II | 57.78 | PSSRA | II | 96.28 |
| RVI | II | 95.78 | RVI | I | 56.28 | RVI | II | 95.78 |
| PSSRA | III | 93.33 | ARVI | IV | 55.73 | PSSRA | III | 93.33 |
| ARVI | III | 92.24 | NDVI | I | 55.57 | ARVI | IV | 92.24 |
| NDVI | III | 91.45 | TNDVI | I | 54.88 | NDVI | IV | 91.45 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pilaš, I.; Gašparović, M.; Novkinić, A.; Klobučar, D. Mapping of the Canopy Openings in Mixed Beech–Fir Forest at Sentinel-2 Subpixel Level Using UAV and Machine Learning Approach. Remote Sens. 2020, 12, 3925. https://doi.org/10.3390/rs12233925
Pilaš I, Gašparović M, Novkinić A, Klobučar D. Mapping of the Canopy Openings in Mixed Beech–Fir Forest at Sentinel-2 Subpixel Level Using UAV and Machine Learning Approach. Remote Sensing. 2020; 12(23):3925. https://doi.org/10.3390/rs12233925
Chicago/Turabian StylePilaš, Ivan, Mateo Gašparović, Alan Novkinić, and Damir Klobučar. 2020. "Mapping of the Canopy Openings in Mixed Beech–Fir Forest at Sentinel-2 Subpixel Level Using UAV and Machine Learning Approach" Remote Sensing 12, no. 23: 3925. https://doi.org/10.3390/rs12233925
APA StylePilaš, I., Gašparović, M., Novkinić, A., & Klobučar, D. (2020). Mapping of the Canopy Openings in Mixed Beech–Fir Forest at Sentinel-2 Subpixel Level Using UAV and Machine Learning Approach. Remote Sensing, 12(23), 3925. https://doi.org/10.3390/rs12233925