Estimating Structure and Biomass of a Secondary Atlantic Forest in Brazil Using Fourier Transforms of Vertical Profiles Derived from UAV Photogrammetry Point Clouds
Abstract
1. Introduction
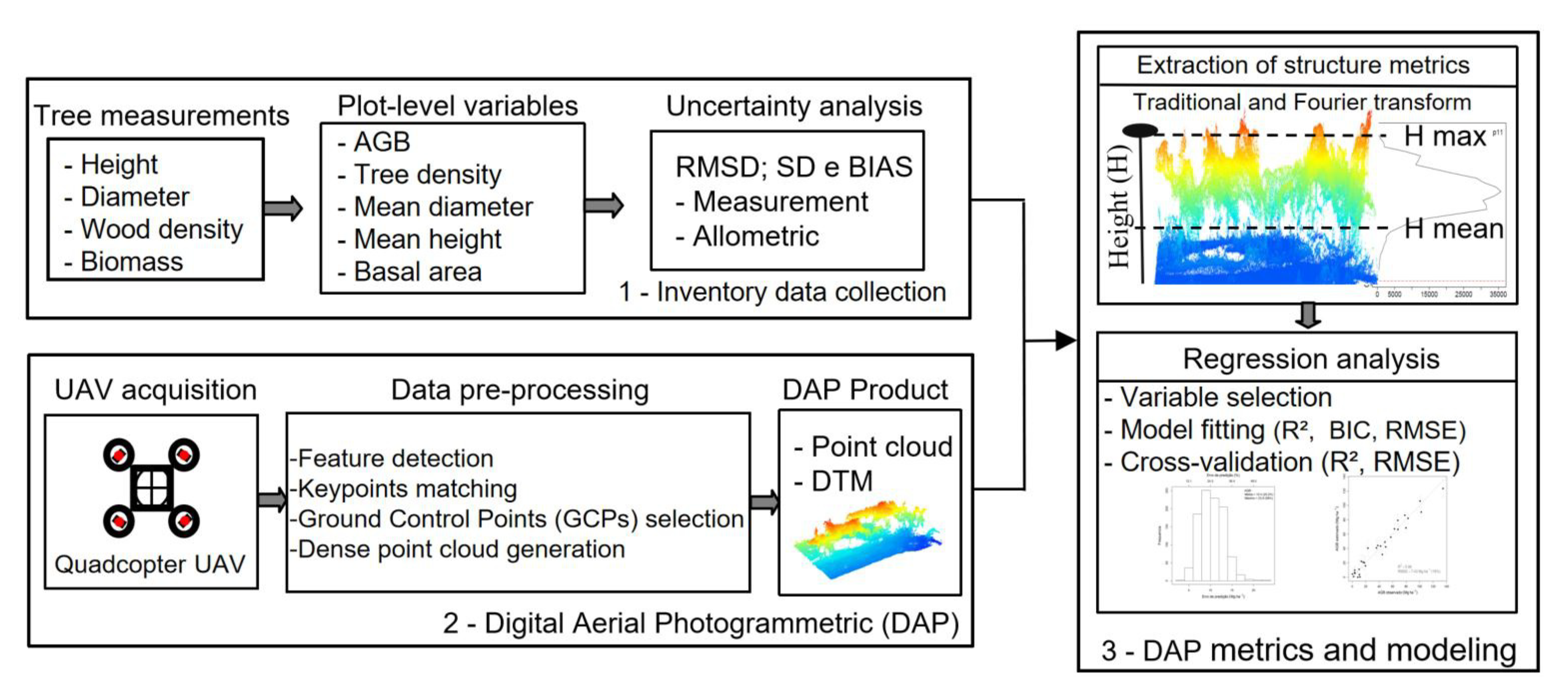
2. Materials and Methods
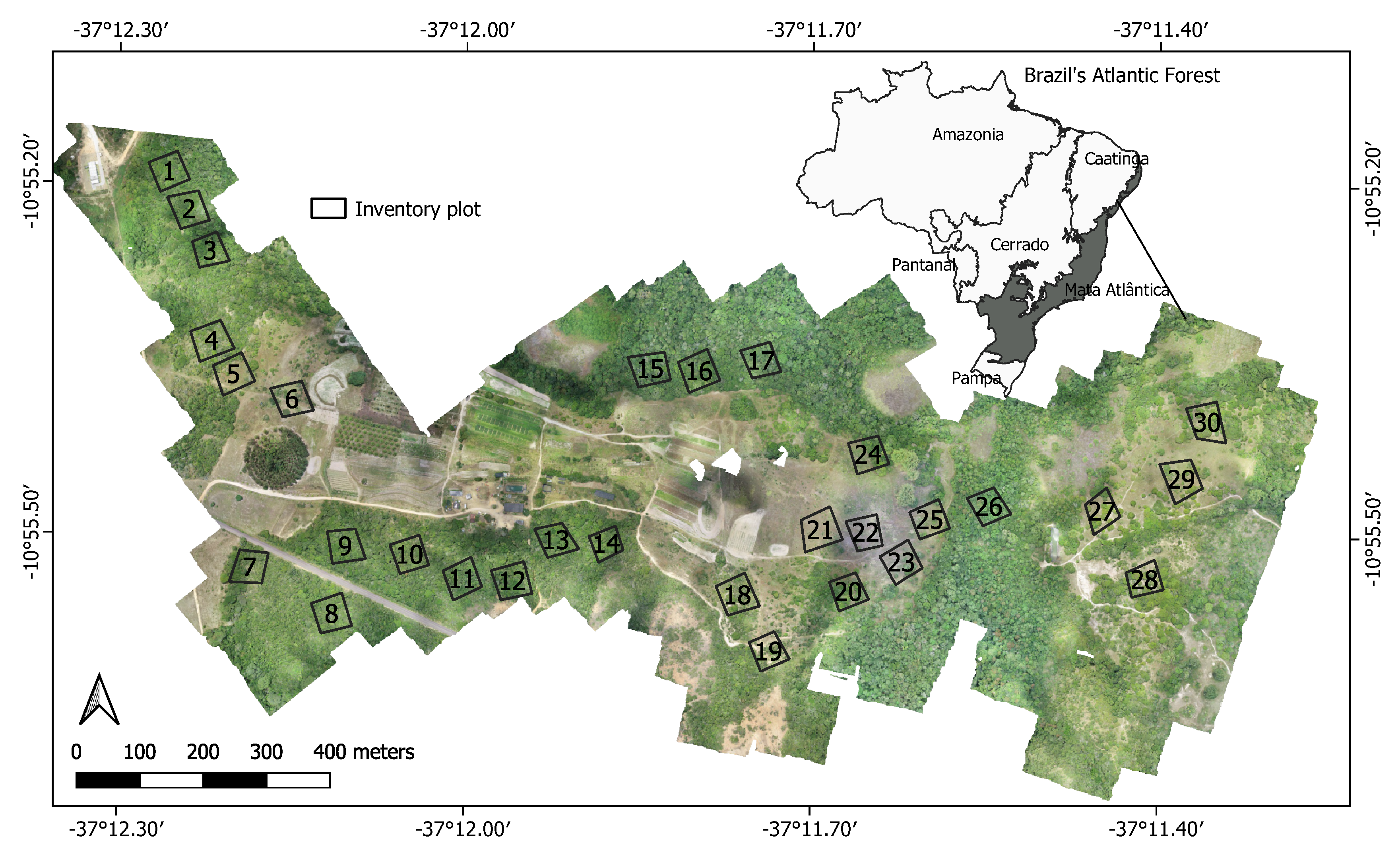
2.1. Characterization of the Study Site
2.2. Methods
2.2.1. Collection of Forest Inventory Data
2.2.2. Estimation of Biomass and the Associated Uncertainty
2.2.3. Digital Aerial Photogrammetry (DAP)
UAV Data
Photogrammetric Processing of UAV Imagery
DAP Assessment
2.2.4. Structural Metrics
Traditional Metrics
Fourier Metrics
2.2.5. Statistical Methods
3. Results
3.1. Forest Inventory
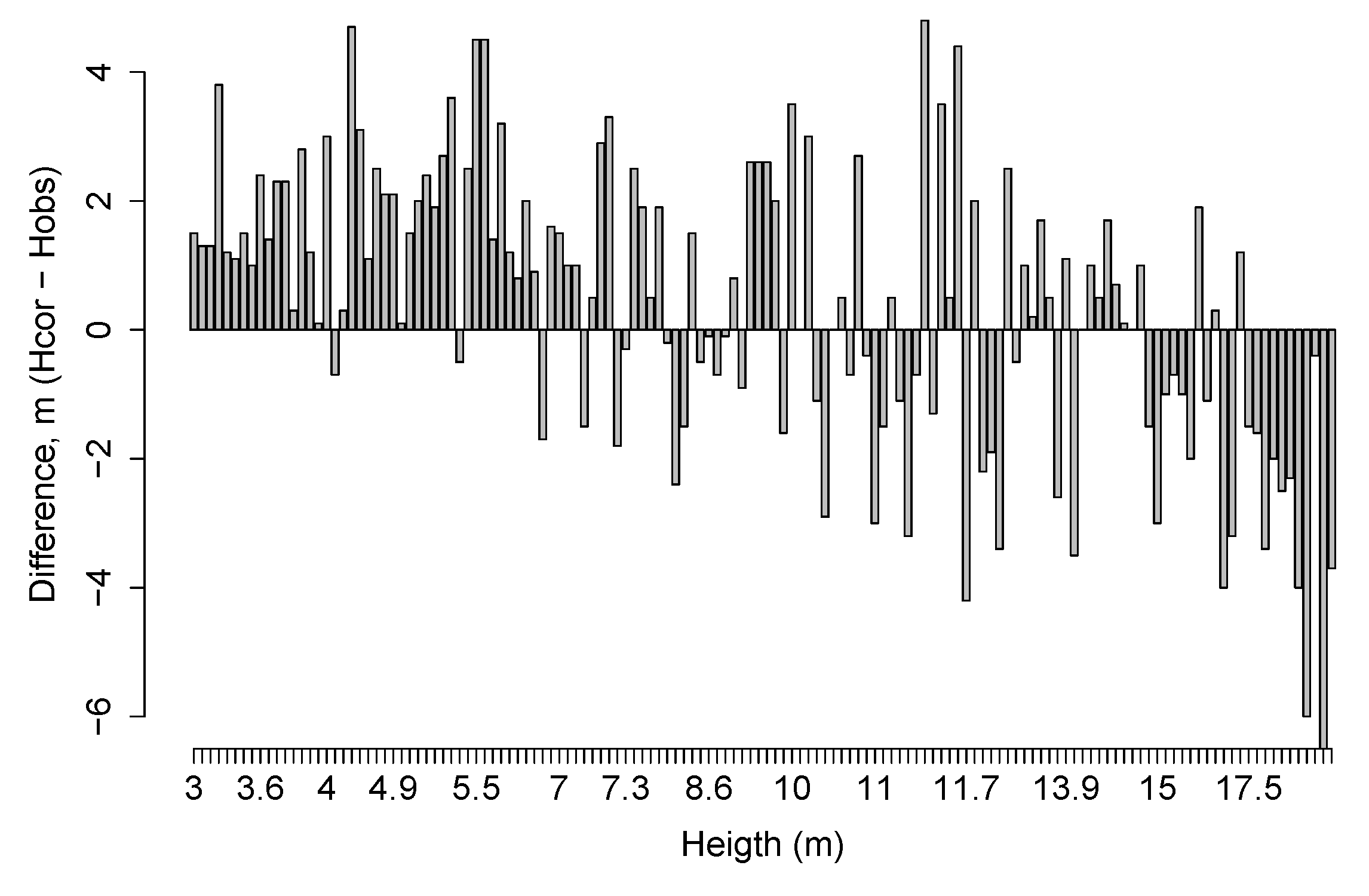
3.2. Biomass Uncertainty
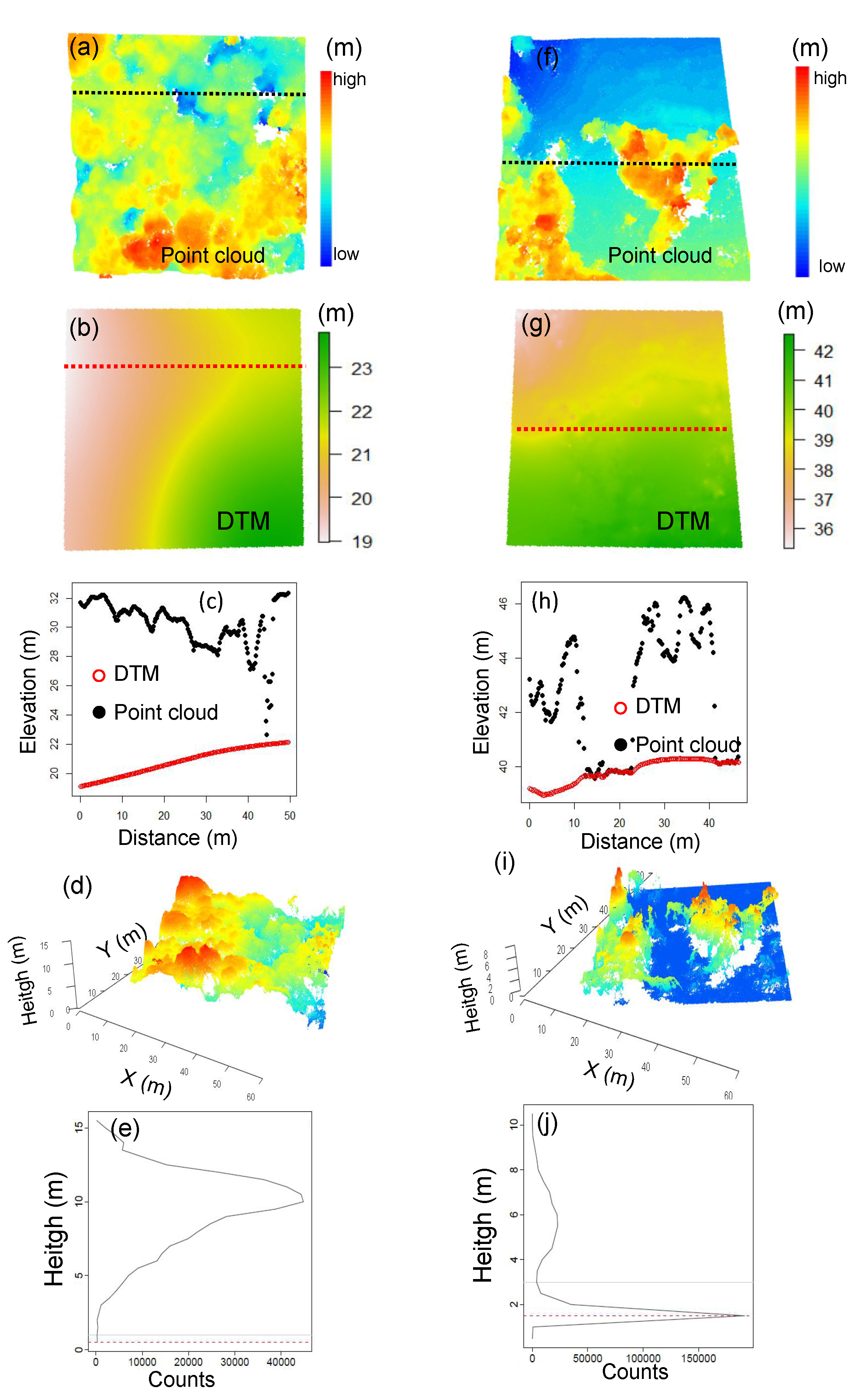
3.3. Dap Assessment
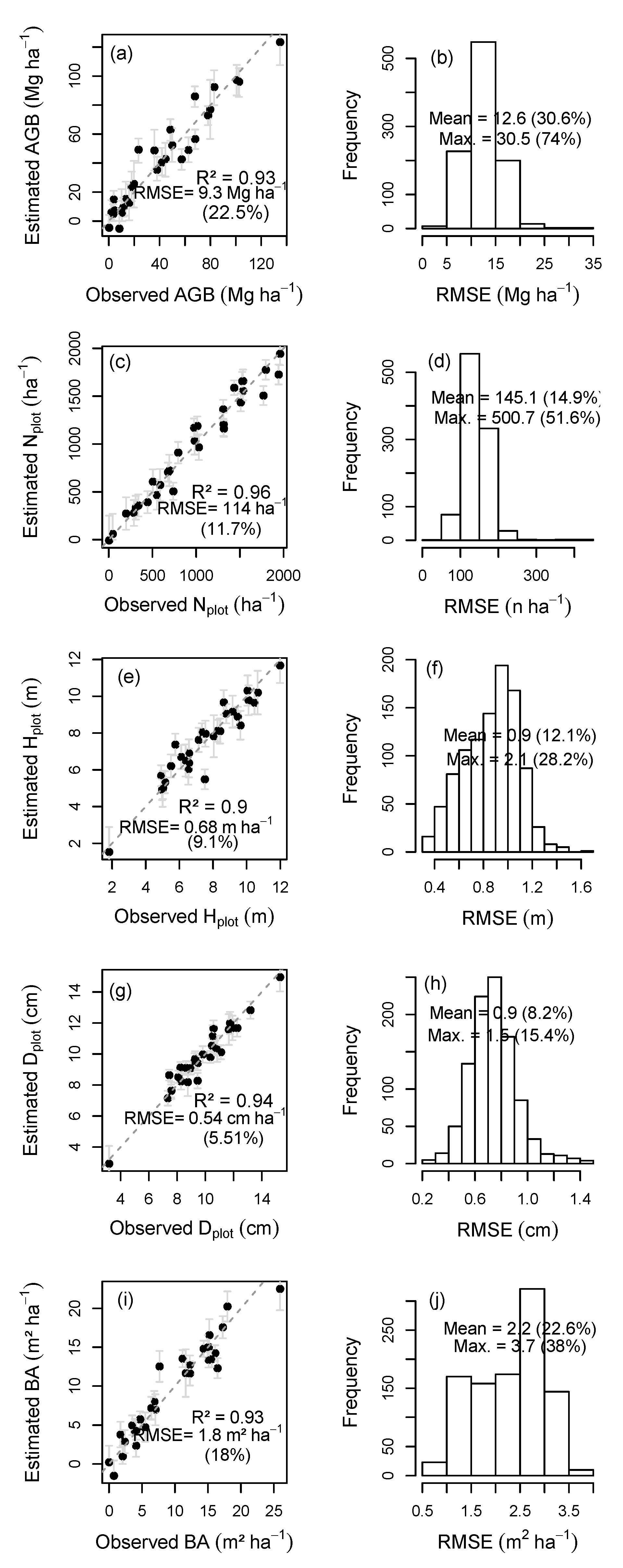
3.4. Statistical Models
4. Discussion
4.1. Uncertainties in the Estimation of Field AGB
4.2. Reconstruction of the 3D Forest Structure Using DAP
4.3. DAP for Biomass Estimation
4.4. DAP for Estimation of Basal Area, Diameter, Height and Density
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| 3D | Three dimensions |
| AGB | Aboveground Biomass |
| AGL | Above Ground Level |
| amp | Fourier amplitude |
| BA | Basal area |
| BIC | Bayesian Information Criterion |
| CF | Correction Factor |
| D | Diameter at breast height |
| DAP | Digital Aerial Photogrammetry |
| Mean plot diameter | |
| DTM | Digital Terrain Model |
| EMBRAPA | Brazilian Agricultural Research Corporation |
| GCPs | Ground Control Points |
| GNSS | Global Navigation Satellite System |
| H | Tree height |
| Corrected tree height | |
| Visually estimated tree height | |
| Mean plot height | |
| IPCC | Intergovernmental Panel on Climate Change |
| InSAR | Interferometric Synthetic Aperture Radar |
| LiDAR | Light Detection and Ranging |
| First measurement D or Hobs | |
| Second measurement D or Hobs | |
| Dry aboveground biomass of palm species | |
| Dry aboveground biomass of tree species | |
| N | Number of trees per hectare |
| REDD+ | Reducing Emissions from Deforestation and Forest Degradation |
| RMSD | Root Mean Square Deviation |
| RMSE | Root Mean Square Error |
| RTK | Real-Time Kinematic |
| SD | Standard Deviation |
| SfM | Structure from Motion |
| SIRGAS | Geocentric Reference System for the Americas |
| UAV | Unmanned Aerial Vehicle |
| UFS | Federal University of Sergipe |
| UTM | Universal Transverse Mercator |
| VLOS | Visual Line of Sight |
| w(z) | The number of points found in the bin centered at height z |
| X | X coordinate |
| Y | Y coordinate |
| Fourier transform | |
| Z | Z coordinate |
| Uncertainty associated with the residuals of the allometric model | |
| Total uncertainty of the AGB estimate | |
| Measurement errors in diameter at breast height | |
| Measurement errors in tree height | |
| Uncertainty in the biomass estimate of each tree | |
| Measurement error in wood density | |
| Uncertainty associated with the allometric model selection | |
| Wood density |
References
- Andersen, H.E.; Reutebuch, S.E.; McGaughey, R.J. A rigorous assessment of tree height measurements obtained using airborne lidar and conventional field methods. Can. J. Remote Sens. 2006, 32, 355–366. [Google Scholar] [CrossRef]
- Houghton, R.; Greenglass, N.; Baccini, A.; Cattaneo, A.; Goetz, S.; Kellndorfer, J.; Laporte, N.; Walker, W. The role of science in Reducing Emissions from Deforestation and Forest Degradation (REDD). Carbon Manag. 2010, 1, 253–259. [Google Scholar] [CrossRef]
- Boisvenue, C.; Running, S.W. Impacts of climate change on natural forest productivity - evidence since the middle of the 20th century. Glob. Chang. Biol. 2006, 12, 862–882. [Google Scholar] [CrossRef]
- Noss, R.F. Beyond Kyoto: Forest Management in a Time of Rapid Climate Change. Conserv. Biol. 2001, 15, 578–590. [Google Scholar] [CrossRef]
- Stas, S. Above-Ground Biomass and Carbon Stocks in a Secondary Forest in Comparison with Adjacent Primary Forest on Limestone in Seram, the Moluccas, Indonesia; Working Paper 145; CIFOR: Bogor, Indonesia, 2014. [Google Scholar] [CrossRef]
- Houghton, R.A.; Hall, F.; Goetz, S.J. Importance of biomass in the global carbon cycle. J. Geophys. Res. Biogeosci. 2009, 114. [Google Scholar] [CrossRef]
- IPCC. IPCC—Task Force on National Greenhouse Gas Inventories; IPCC: Hong Kong, China, 2006.
- Foody, G.M. Remote sensing of tropical forest environments: Towards the monitoring of environmental resources for sustainable development. Int. J. Remote Sens. 2003, 24. [Google Scholar] [CrossRef]
- McRoberts, R.; Tomppo, E. Remote sensing support for national forest inventories. Remote Sens. Environ. 2007, 110, 412–419. [Google Scholar] [CrossRef]
- Su, Y.; Guo, Q.; Xue, B.; Hu, T.; Alvarez, O.; Tao, S.; Fang, J. Spatial distribution of forest aboveground biomass in China: Estimation through combination of spaceborne lidar, optical imagery, and forest inventory data. Remote Sens. Environ. 2016, 173, 187–199. [Google Scholar] [CrossRef]
- Dube, T.; Mutanga, O. Evaluating the utility of the medium-spatial resolution Landsat 8 multispectral sensor in quantifying aboveground biomass in uMgeni catchment, South Africa. ISPRS J. Photogramm. Remote Sens. 2015, 101, 36–46. [Google Scholar] [CrossRef]
- Pandit, S.; Tsuyuki, S.; Dube, T. Landscape-Scale Aboveground Biomass Estimation in Buffer Zone Community Forests of Central Nepal: Coupling In Situ Measurements with Landsat 8 Satellite Data. Remote Sens. 2018, 10, 1848. [Google Scholar] [CrossRef]
- Wulder, M.; Skakun, R.; Kurz, W.; White, J. Estimating time since forest harvest using segmented Landsat ETM+ imagery. Remote Sens. Environ. 2004, 93, 179–187. [Google Scholar] [CrossRef]
- Nguyen, T.H.; Jones, S.D.; Soto-Berelov, M.; Haywood, A.; Hislop, S. Monitoring aboveground forest biomass dynamics over three decades using Landsat time-series and single-date inventory data. Int. J. Appl. Earth Obs. Geoinf. 2020, 84, 101952. [Google Scholar] [CrossRef]
- Rana, P.; Korhonen, L.; Gautam, B.; Tokola, T. Effect of field plot location on estimating tropical forest above-ground biomass in Nepal using airborne laser scanning data. ISPRS J. Photogramm. Remote Sens. 2014, 94, 55–62. [Google Scholar] [CrossRef]
- Clark, M.L.; Roberts, D.A.; Ewel, J.J.; Clark, D.B. Estimation of tropical rain forest aboveground biomass with small-footprint lidar and hyperspectral sensors. Remote Sens. Environ. 2011, 115, 2931–2942. [Google Scholar] [CrossRef]
- Margolis, H.A.; Nelson, R.F.; Montesano, P.M.; Beaudoin, A.; Sun, G.; Andersen, H.E.; Wulder, M.A. Combining satellite lidar, airborne lidar, and ground plots to estimate the amount and distribution of aboveground biomass in the boreal forest of North America. Can. J. For. Res. 2015, 45, 838–855. [Google Scholar] [CrossRef]
- González-Ferreiro, E.; Diéguez-Aranda, U.; Miranda, D. Estimation of stand variables in Pinus radiata D. Don plantations using different LiDAR pulse densities. For. Int. J. For. Res. 2012, 85, 281–292. [Google Scholar] [CrossRef]
- Kachamba, D.; Ørka, H.; Næsset, E.; Eid, T.; Gobakken, T. Influence of Plot Size on Efficiency of Biomass Estimates in Inventories of Dry Tropical Forests Assisted by Photogrammetric Data from an Unmanned Aircraft System. Remote Sens. 2017, 9, 610. [Google Scholar] [CrossRef]
- Zarco-Tejada, P.; Diaz-Varela, R.; Angileri, V.; Loudjani, P. Tree height quantification using very high resolution imagery acquired from an unmanned aerial vehicle (UAV) and automatic 3D photo-reconstruction methods. Eur. J. Agron. 2014, 55, 89–99. [Google Scholar] [CrossRef]
- Goodbody, T.R.H.; Coops, N.C.; White, J.C. Digital Aerial Photogrammetry for Updating Area-Based Forest Inventories: A Review of Opportunities, Challenges, and Future Directions. Curr. For. Rep. 2019, 5, 55–75. [Google Scholar] [CrossRef]
- Iglhaut, J.; Cabo, C.; Puliti, S.; Piermattei, L.; O’Connor, J.; Rosette, J. Structure from Motion Photogrammetry in Forestry: A Review. Curr. For. Rep. 2019, 5, 155–168. [Google Scholar] [CrossRef]
- Díaz-Varela, R.; de la Rosa, R.; León, L.; Zarco-Tejada, P. High-Resolution Airborne UAV Imagery to Assess Olive Tree Crown Parameters Using 3D Photo Reconstruction: Application in Breeding Trials. Remote Sens. 2015, 7, 4213–4232. [Google Scholar] [CrossRef]
- Tang, L.; Shao, G. Drone remote sensing for forestry research and practices. J. For. Res. 2015, 26, 791–797. [Google Scholar] [CrossRef]
- Tomasi, C.; Kanade, T. Shape and motion from image streams under orthography: A factorization method. Int. J. Comput. Vis. 1992, 9, 137–154. [Google Scholar] [CrossRef]
- Lin, J.; Wang, M.; Ma, M.; Lin, Y. Aboveground Tree Biomass Estimation of Sparse Subalpine Coniferous Forest with UAV Oblique Photography. Remote Sens. 2018, 10, 1849. [Google Scholar] [CrossRef]
- Ota, T.; Ogawa, M.; Shimizu, K.; Kajisa, T.; Mizoue, N.; Yoshida, S.; Takao, G.; Hirata, Y.; Furuya, N.; Sano, T.; et al. Aboveground Biomass Estimation Using Structure from Motion Approach with Aerial Photographs in a Seasonal Tropical Forest. Forests 2015, 6, 3882–3898. [Google Scholar] [CrossRef]
- Puliti, S.; Ørka, H.; Gobakken, T.; Næsset, E. Inventory of Small Forest Areas Using an Unmanned Aerial System. Remote Sens. 2015, 7, 9632–9654. [Google Scholar] [CrossRef]
- Shen, X.; Cao, L.; Yang, B.; Xu, Z.; Wang, G. Estimation of Forest Structural Attributes Using Spectral Indices and Point Clouds from UAS-Based Multispectral and RGB Imageries. Remote Sens. 2019, 11, 800. [Google Scholar] [CrossRef]
- Fankhauser, K.; Strigul, N.; Gatziolis, D. Augmentation of Traditional Forest Inventory and Airborne Laser Scanning with Unmanned Aerial Systems and Photogrammetry for Forest Monitoring. Remote Sens. 2018, 10, 1562. [Google Scholar] [CrossRef]
- Baltsavias, E.P. A comparison between photogrammetry and laser scanning. ISPRS J. Photogramm. Remote Sens. 1999, 54, 83–94. [Google Scholar] [CrossRef]
- Gobakken, T.; Bollandsås, O.M.; Næsset, E. Comparing biophysical forest characteristics estimated from photogrammetric matching of aerial images and airborne laser scanning data. Scand. J. For. Res. 2014, 30, 73–86. [Google Scholar] [CrossRef]
- Cao, L.; Liu, H.; Fu, X.; Zhang, Z.; Shen, X.; Ruan, H. Comparison of UAV LiDAR and Digital Aerial Photogrammetry Point Clouds for Estimating Forest Structural Attributes in Subtropical Planted Forests. Forests 2019, 10, 145. [Google Scholar] [CrossRef]
- Puliti, S.; Solberg, S.; Granhus, A. Use of UAV Photogrammetric Data for Estimation of Biophysical Properties in Forest Stands Under Regeneration. Remote Sens. 2019, 11, 233. [Google Scholar] [CrossRef]
- Goodbody, T.R.H.; Coops, N.C.; Tompalski, P.; Crawford, P.; Day, K.J.K. Updating residual stem volume estimates using ALS- and UAV-acquired stereo-photogrammetric point clouds. Int. J. Remote Sens. 2016, 38, 2938–2953. [Google Scholar] [CrossRef]
- Hobi, M.L.; Ginzler, C.; Commarmot, B.; Bugmann, H. Gap pattern of the largest primeval beech forest of Europe revealed by remote sensing. Ecosphere 2015, 6, art76. [Google Scholar] [CrossRef]
- Wang, Z.; Ginzler, C.; Waser, L.T. A novel method to assess short-term forest cover changes based on digital surface models from image-based point clouds. For. Int. J. For. Res. 2015, 88, 429–440. [Google Scholar] [CrossRef]
- Zielewska-Büttner, K.; Adler, P.; Ehmann, M.; Braunisch, V. Automated Detection of Forest Gaps in Spruce Dominated Stands Using Canopy Height Models Derived from Stereo Aerial Imagery. Remote Sens. 2016, 8, 175. [Google Scholar] [CrossRef]
- White, J.C.; Tompalski, P.; Coops, N.C.; Wulder, M.A. Comparison of airborne laser scanning and digital stereo imagery for characterizing forest canopy gaps in coastal temperate rainforests. Remote Sens. Environ. 2018, 208, 1–14. [Google Scholar] [CrossRef]
- Dietmaier, A.; McDermid, G.J.; Rahman, M.M.; Linke, J.; Ludwig, R. Comparison of LiDAR and Digital Aerial Photogrammetry for Characterizing Canopy Openings in the Boreal Forest of Northern Alberta. Remote Sens. 2019, 11, 1919. [Google Scholar] [CrossRef]
- Zahawi, R.A.; Dandois, J.P.; Holl, K.D.; Nadwodny, D.; Reid, J.L.; Ellis, E.C. Using lightweight unmanned aerial vehicles to monitor tropical forest recovery. Biol. Conserv. 2015, 186, 287–295. [Google Scholar] [CrossRef]
- Kachamba, D.; Ørka, H.; Gobakken, T.; Eid, T.; Mwase, W. Biomass Estimation Using 3D Data from Unmanned Aerial Vehicle Imagery in a Tropical Woodland. Remote Sens. 2016, 8, 968. [Google Scholar] [CrossRef]
- McGaughey, R.J. FUSION/LDV: Software for LiDAR Data Analysis and Visualization; Version 3.30; U.S. Department of Agriculture Forest Service, Pacific Northwest Research Station, University of Washington: Seattle, WA, USA, 2018; Available online: http://forsys.cfr.washington.edu/fusion/fusionlatest.html (accessed on 13 February 2019).
- Treuhaft, R.N.; Chapman, B.D.; dos Santos, J.R.; Gonçalves, F.G.; Dutra, L.V.; Graça, P.M.L.A.; Drake, J.B. Vegetation profiles in tropical forests from multibaseline interferometric synthetic aperture radar, field, and lidar measurements. J. Geophys. Res. 2009, 114. [Google Scholar] [CrossRef]
- Treuhaft, R.N.; Gonçalves, F.G.; Drake, J.B.; Chapman, B.D.; dos Santos, J.R.; Dutra, L.V.; Graça, P.M.L.A.; Purcell, G.H. Biomass estimation in a tropical wet forest using Fourier transforms of profiles from lidar or interferometric SAR. Geophys. Res. Lett. 2010, 37. [Google Scholar] [CrossRef]
- Aes Gonçalves, F.G. Vertical Structure and Aboveground Biomass of Tropical Forests from Lidar Remote Sensing. Ph.D. Thesis, Oregon State University, Corvallis, OR, USA, 2014. [Google Scholar]
- Chazdon, R.L.; Broadbent, E.N.; Rozendaal, D.M.A.; Bongers, F.; Zambrano, A.M.A.; Aide, T.M.; Balvanera, P.; Becknell, J.M.; Boukili, V.; Brancalion, P.H.S.; et al. Carbon sequestration potential of second-growth forest regeneration in the Latin American tropics. Sci. Adv. 2016, 2, e1501639. [Google Scholar] [CrossRef] [PubMed]
- Silveira, E.M.; Cunha, L.I.F.; Galvão, L.S.; Withey, K.D.; Júnior, F.W.A.; Scolforo, J.R.S. Modelling aboveground biomass in forest remnants of the Brazilian Atlantic Forest using remote sensing, environmental and terrain-related data. Geocarto Int. 2019, 1–18. [Google Scholar] [CrossRef]
- Silveira, E.M.; Silva, S.H.G.; Acerbi-Junior, F.W.; Carvalho, M.C.; Carvalho, L.M.T.; Scolforo, J.R.S.; Wulder, M.A. Object-based random forest modelling of aboveground forest biomass outperforms a pixel-based approach in a heterogeneous and mountain tropical environment. Int. J. Appl. Earth Obs. Geoinf. 2019, 78, 175–188. [Google Scholar] [CrossRef]
- Longo, M.; Keller, M.; dos Santos, M.N.; Leitold, V.; Pinagé, E.R.; Baccini, A.; Saatchi, S.; Nogueira, E.M.; Batistella, M.; Morton, D.C. Aboveground biomass variability across intact and degraded forests in the Brazilian Amazon. Glob. Biogeochem. Cycles 2016, 30, 1639–1660. [Google Scholar] [CrossRef]
- Santos, E.G.D.; Shimabukuro, Y.E.; Moura, Y.M.D.; Gonçalves, F.G.; Jorge, A.; Gasparini, K.A.; Arai, E.; Duarte, V.; Ometto, J.P. Multi-scale approach to estimating aboveground biomass in the Brazilian Amazon using Landsat and LiDAR data. Int. J. Remote Sens. 2019, 40, 8635–8645. [Google Scholar] [CrossRef]
- Lefsky, M.A.; Harding, D.J.; Keller, M.; Cohen, W.B.; Carabajal, C.C.; Espirito-Santo, F.D.B.; Hunter, M.O.; de Oliveira, R. Estimates of forest canopy height and aboveground biomass using ICESat. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]
- Lei, Y.; Treuhaft, R.; Keller, M.; dos Santos, M.; Gonçalves, F.; Neumann, M. Quantification of selective logging in tropical forest with spaceborne SAR interferometry. Remote Sens. Environ. 2018, 211, 167–183. [Google Scholar] [CrossRef]
- Treuhaft, R.; Lei, Y.; Gonçalves, F.; Keller, M.; Santos, J.; Neumann, M.; Almeida, A. Tropical-Forest Structure and Biomass Dynamics from TanDEM-X Radar Interferometry. Forests 2017, 8, 277. [Google Scholar] [CrossRef]
- Neeff, T.; Dutra, L.V.; dos Santos, R.; Freitas, C.d.C.; Araujo, L.S. Tropical Forest Measurement by Interferometric Height Modeling and P-Band Radar Backscatter. For. Sci. 2005, 51, 585–594. [Google Scholar] [CrossRef]
- da Silva, J.M.C.; Tabarelli, M. Tree species impoverishment and the future flora of the Atlantic forest of northeast Brazil. Nature 2000, 404, 72–74. [Google Scholar] [CrossRef] [PubMed]
- Ribeiro, M.C.; Metzger, J.P.; Martensen, A.C.; Ponzoni, F.J.; Hirota, M.M. The Brazilian Atlantic Forest: How much is left, and how is the remaining forest distributed? Implications for conservation. Biol. Conserv. 2009, 142, 1141–1153. [Google Scholar] [CrossRef]
- Becknell, J.M.; Keller, M.; Piotto, D.; Longo, M.; dos Santos, M.N.; Scaranello, M.A.; de Oliveira Cavalcante, R.B.; Porder, S. Landscape-scale lidar analysis of aboveground biomass distribution in secondary Brazilian Atlantic Forest. Biotropica 2018, 50, 520–530. [Google Scholar] [CrossRef]
- David, H.C.; de Araújo, E.J.G.; Morais, V.A.; Scolforo, J.R.S.; Marques, J.M.; Netto, S.P.; MacFarlane, D.W. Carbon stock classification for tropical forests in Brazil: Understanding the effect of stand and climate variables. For. Ecol. Manag. 2017, 404, 241–250. [Google Scholar] [CrossRef]
- Erb, K.H.; Kastner, T.; Plutzar, C.; Bais, A.L.S.; Carvalhais, N.; Fetzel, T.; Gingrich, S.; Haberl, H.; Lauk, C.; Niedertscheider, M.; et al. Unexpectedly large impact of forest management and grazing on global vegetation biomass. Nature 2017, 553, 73–76. [Google Scholar] [CrossRef]
- Millar, C.I.; Stephenson, N.L.; Stephens, S.L. Climate change and forests of the future: Managing in the face of uncertainty. Ecol. Appl. 2007, 17, 2145–2151. [Google Scholar] [CrossRef]
- Veloso, H.P.; Rangel-Filho, A.L.R.; Lima, J.C.A. Classificação da vegetação brasileira, adaptada a um sistema universal; IBGE: Rio de Janeiro, Brazil, 1991.
- Koeppen, W. Climatologia: Con un estudio de los climas de la tierra; Fondo de Cultura Económica: México City, Mexico, 1948; 478p. [Google Scholar]
- Chave, J.; Condit, R.; Aguilar, S.; Hernandez, A.; Lao, S.; Perez, R. Error propagation and scaling for tropical forest biomass estimates. Philos. Trans. R. Soc. London. Ser. B Biol. Sci. 2004, 359, 409–420. [Google Scholar] [CrossRef]
- Chave, J.; Muller-Landau, H.C.; Baker, T.R.; Easdale, T.A.; ter Steege, H.; Webb, C.O. Regional and phylogenetic variation of wood density across 2456 neotropical tree species. Ecol. Appl. 2006, 16, 2356–2367. [Google Scholar] [CrossRef]
- Saldarriaga, J.G.; West, D.C.; Tharp, M.L.; Uhl, C. Long-Term Chronosequence of Forest Succession in the Upper Rio Negro of Colombia and Venezuela. J. Ecol. 1988, 76, 938. [Google Scholar] [CrossRef]
- Chambers, J.Q.; dos Santos, J.; Ribeiro, R.J.; Higuchi, N. Tree damage, allometric relationships, and above-ground net primary production in central Amazon forest. For. Ecol. Manag. 2001, 152, 73–84. [Google Scholar] [CrossRef]
- Brown, S.; Gillespie, A.J.R.; Lugo, A.E. Biomass Estimation Methods for Tropical Forests with Applications to Forest Inventory Data. For. Sci. 1989, 35, 881–902. [Google Scholar] [CrossRef]
- Brown, S. Estimating Biomass and Biomass Change of Tropical Forests: A Primer; Food & Agriculture Organization: Rome, Italy, 1997; Volume 134, p. 55. [Google Scholar]
- Chave, J.; Andalo, C.; Brown, S.; Cairns, M.A.; Chambers, J.Q.; Eamus, D.; Fölster, H.; Fromard, F.; Higuchi, N.; Kira, T.; et al. Tree allometry and improved estimation of carbon stocks and balance in tropical forests. Oecologia 2005, 145, 87–99. [Google Scholar] [CrossRef]
- Gonçalves, F.; Treuhaft, R.; Law, B.; Almeida, A.; Walker, W.; Baccini, A.; dos Santos, J.; Graça, P. Estimating Aboveground Biomass in Tropical Forests: Field Methods and Error Analysis for the Calibration of Remote Sensing Observations. Remote Sens. 2017, 9, 47. [Google Scholar] [CrossRef]
- Chave, J.; Réjou-Méchain, M.; Búrquez, A.; Chidumayo, E.; Colgan, M.S.; Delitti, W.B.; Duque, A.; Eid, T.; Fearnside, P.M.; Goodman, R.C.; et al. Improved allometric models to estimate the aboveground biomass of tropical trees. Glob. Chang. Biol. 2014, 20, 3177–3190. [Google Scholar] [CrossRef] [PubMed]
- Baskerville, G.L. Use of Logarithmic Regression in the Estimation of Plant Biomass. Can. J. For. Res. 1972, 2, 49–53. [Google Scholar] [CrossRef]
- Agisoft LLC, S.P. Agisoft Metashape Professional Edition v.1.6. 2019. Available online: http://www.agisoft.com/pdf/metashape-pro_1_5_en.pdf (accessed on 20 February 2020).
- Remondino, F.; Spera, M.G.; Nocerino, E.; Menna, F.; Nex, F. State of the art in high density image matching. Photogramm. Rec. 2014, 29, 144–166. [Google Scholar] [CrossRef]
- Verhoeven, G.; Doneus, M.; Briese, C.; Vermeulen, F. Mapping by matching: A computer vision-based approach to fast and accurate georeferencing of archaeological aerial photographs. J. Archaeol. Sci. 2012, 39, 2060–2070. [Google Scholar] [CrossRef]
- Domingo, D.; Ørka, H.O.; Næsset, E.; Kachamba, D.; Gobakken, T. Effects of UAV Image Resolution, Camera Type, and Image Overlap on Accuracy of Biomass Predictions in a Tropical Woodland. Remote Sens. 2019, 11, 948. [Google Scholar] [CrossRef]
- Axelsson, P. Processing of laser scanner data—algorithms and applications. ISPRS J. Photogramm. Remote Sens. 1999, 54, 138–147. [Google Scholar] [CrossRef]
- Dandois, J.P.; Ellis, E.C. Remote Sensing of Vegetation Structure Using Computer Vision. Remote Sens. 2010, 2, 1157–1176. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2020. [Google Scholar]
- Jayathunga, S.; Owari, T.; Tsuyuki, S. Digital Aerial Photogrammetry for Uneven-Aged Forest Management: Assessing the Potential to Reconstruct Canopy Structure and Estimate Living Biomass. Remote Sens. 2019, 11, 338. [Google Scholar] [CrossRef]
- Dandois, J.P.; Ellis, E.C. High spatial resolution three-dimensional mapping of vegetation spectral dynamics using computer vision. Remote Sens. Environ. 2013, 136, 259–276. [Google Scholar] [CrossRef]
- Messinger, M.; Asner, G.P.; Silman, M. Rapid Assessments of Amazon Forest Structure and Biomass Using Small Unmanned Aerial Systems. Remote Sens. 2016, 8, 615. [Google Scholar] [CrossRef]
- Swinfield, T.; Lindsell, J.A.; Williams, J.V.; Harrison, R.D.; Agustiono, H.; Gemita, E.; Schönlieb, C.B.; Coomes, D.A. Accurate Measurement of Tropical Forest Canopy Heights and Aboveground Carbon Using Structure From Motion. Remote Sens. 2019, 11, 928. [Google Scholar] [CrossRef]
- Dandois, J.P.; Olano, M.; Ellis, E.C. Optimal Altitude, Overlap, and Weather Conditions for Computer Vision UAV Estimates of Forest Structure. Remote Sens. 2015, 7, 13895–13920. [Google Scholar] [CrossRef]
- Shen, X.; Cao, L. Tree-Species Classification in Subtropical Forests Using Airborne Hyperspectral and LiDAR Data. Remote Sens. 2017, 9, 1180. [Google Scholar] [CrossRef]
- White, J.C.; Stepper, C.; Tompalski, P.; Coops, N.C.; Wulder, M.A. Comparing ALS and Image-Based Point Cloud Metrics and Modelled Forest Inventory Attributes in a Complex Coastal Forest Environment. Forests 2015, 6, 3704–3732. [Google Scholar] [CrossRef]
- Goodbody, T.R.; Coops, N.C.; Marshall, P.L.; Tompalski, P.; Crawford, P. Unmanned aerial systems for precision forest inventory purposes: A review and case study. For. Chron. 2017, 93, 71–81. [Google Scholar] [CrossRef]
- Barrett, F.; McRoberts, R.E.; Tomppo, E.; Cienciala, E.; Waser, L.T. A questionnaire-based review of the operational use of remotely sensed data by national forest inventories. Remote Sens. Environ. 2016, 174, 279–289. [Google Scholar] [CrossRef]
- Caccamo, G.; Iqbal, I.A.; Osborn, J.; Bi, H.; Arkley, K.; Melville, G.; Aurik, D.; Stone, C. Comparing yield estimates derived from LiDAR and aerial photogrammetric point-cloud data with cut-to-length harvester data in a Pinus radiata plantation in Tasmania. Aust. For. 2018, 81, 131–141. [Google Scholar] [CrossRef]
- Iqbal, I.A.; Musk, R.A.; Osborn, J.; Stone, C.; Lucieer, A. A comparison of area-based forest attributes derived from airborne laser scanner, small-format and medium-format digital aerial photography. Int. J. Appl. Earth Obs. Geoinf. 2019, 76, 231–241. [Google Scholar] [CrossRef]
- Navarro, J.A.; Fernández-Landa, A.; Tomé, J.L.; Guillén-Climent, M.L.; Ojeda, J.C. Testing the quality of forest variable estimation using dense image matching: A comparison with airborne laser scanning in a Mediterranean pine forest. Int. J. Remote Sens. 2018, 39, 4744–4760. [Google Scholar] [CrossRef]
- Strunk, J.L.; Gould, P.J.; Packalen, P.; Gatziolis, D.; Greblowska, D.; Maki, C.; McGaughey, R.J. Evaluation of pushbroom DAP relative to frame camera DAP and lidar for forest modeling. Remote Sens. Environ. 2020, 237, 111535. [Google Scholar] [CrossRef]
- Nurminen, K.; Karjalainen, M.; Yu, X.; Hyyppä, J.; Honkavaara, E. Performance of dense digital surface models based on image matching in the estimation of plot-level forest variables. ISPRS J. Photogramm. Remote Sens. 2013, 83, 104–115. [Google Scholar] [CrossRef]
- Ota, T.; Ogawa, M.; Mizoue, N.; Fukumoto, K.; Yoshida, S. Forest Structure Estimation from a UAV-Based Photogrammetric Point Cloud in Managed Temperate Coniferous Forests. Forests 2017, 8, 343. [Google Scholar] [CrossRef]
- Krause, S.; Sanders, T.G.M.; Mund, J.P.; Greve, K. UAV-Based Photogrammetric Tree Height Measurement for Intensive Forest Monitoring. Remote Sens. 2019, 11, 758. [Google Scholar] [CrossRef]
- Straub, C.; Stepper, C.; Seitz, R.; Waser, L.T. Potential of UltraCamX stereo images for estimating timber volume and basal area at the plot level in mixed European forests. Can. J. For. Res. 2013, 43, 731–741. [Google Scholar] [CrossRef]
| Equations | Source |
|---|---|
| [70] | |
| [66] | |
| Alternative equations | |
| [69] | |
| [70] | |
| [67] | |
| [68] |
| Parameter | |
|---|---|
| Coverage area (ha) | 52 (flight 1)/45 (flight 2) |
| Flight height (m) | 120 |
| Flight speed (m/s) | 10 |
| Flight time (min) | 15 |
| Forward overlap (%) | 75 |
| Lateral overlap (%) | 70 |
| Sensor | 1” CMOS 20M pixel |
| Spectral bands | Red, Green, Blue |
| Ground sample distance (cm) | 3.2 |
| Number of images | 221 (flight 1)/213(flight 2) |
| Image format | JPG |
| Task | Parameters |
|---|---|
| (i) Image alignment | Accuracy: high |
| Pair selection: reference | |
| Key points: 40,000 | |
| Tie points: 4000 | |
| (ii) Guided marker positioning | Manual relocation of markers on the 31 |
| control points and 10 check points | |
| (iii) Building dense point clouds | Quality: medium |
| Depth filtering: mild |
| Type of Metric | Name | Description |
|---|---|---|
| (i) Height | Minimum | |
| Maximum | ||
| Mean | ||
| Mode | ||
| Coefficient of variation | ||
| Standard deviation | ||
| Variance | ||
| Interquartile distance | ||
| Skewness | ||
| Kurtosis | ||
| (H01, H05, H10, H20, H25, H30, H40, H50, H60, H70, H75, H80, H90, H95, H99) | Percentiles values (1st, 5th, 10th, 20th, 25th, 30th, 40th, 50th, 60th, 70th, 75th, 80th, 90th, 95th, 99th) | |
| Generalized mean for the 2nd power | ||
| Generalized mean for the 3rd power | ||
| HAAD | Average absolute deviation | |
| Median of the absolute deviations from the overall median | ||
| Mode of the absolute deviations from the overall mode | ||
| HL1, HL2, HL3 and HL4 | Linear moments | |
| L-moment skewness | ||
| L-moment kurtosis | ||
| HCRR | Canopy relief ratio ( − )/( − ) | |
| (ii) Canopy cover | CCH | # of points above 3.0 m |
| # of points above the mean height | ||
| # of points above the mode height | ||
| # of points above 3.0 m/total # of points × 100 | ||
| # of points above the mean height/total # of points × 100 | ||
| # of points above the mode height/total # of points × 100 |
| Variable | Range | RMSD | Bias | Standard Deviation |
|---|---|---|---|---|
| Diameter (cm) | 16.0–95.8 | 1.0 (2.8%) | −0.008 (0.02%) | 1.0 (2.8%) |
| Height (m) | 3.1–21.5 | 2.5 (24.2%) | −0.3 (3.4%) | 2.5 (24.9%) |
| Variable | Symbol | Mean | Range | Standard Deviation |
|---|---|---|---|---|
| Tree density (ha) | N | 970.7 | 3.3–1959.5 | 581.8 |
| Diameter (cm) | 9.7 | 0.5–149.2 | 5.9 | |
| Height (m) | 7.0 | 1.0–23.5 | 3.3 | |
| Basal area (m ha) | BA | 9.7 | 0.002–25.9 | 6.4 |
| Biomass (Mg ha) | AGB | 43.1 | 0.2–134.78 | 36.7 |
| Error Source | Mean Error (Minimum–Maximum) |
|---|---|
| Measurement () | 6.7% (2.6–33.4%) |
| Allometry (model selection, ) | 6.5% (0.8–10.0%) |
| Allometry (model residuals, ) | 2.6% (1.0–13.6%) |
| Total () | 9.7% (2.9–37.5%) |
| Variable | Equation * | R | RMSE | BIC | R | RMSE |
|---|---|---|---|---|---|---|
| AGB (Mg ha) | amp.12,amp.13,amp.14,amp.15,H20, CC%H | 0.93 | 9.3 (22.5%) | −60.9 | 0.87 | 12.6 (30.6%) |
| N (trees.ha) | amp.06,H,HMAD,H60,HCRR, CC%H | 0.96 | 113.8 (12.0%) | −73.1 | 0.94 | 145.1 (14.9%) |
| (m) | amp.08,amp.25,HL,H01,H05,H10 | 0.90 | 0.67 (9.1%) | −60.0 | 0.84 | 0.9 (12.0%) |
| (cm) | amp.06,HL3,HL4,HL,H01,CC%H | 0.94 | 0.53 (5.5%) | −60.2 | 0.88 | 0.8 (8.2%) |
| BA (cm) | amp.21,H,H50,CC%H | 0.93 | 1.75 (18.0%) | −59.2 | 0.89 | 2.2 (22.6%) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Almeida, A.; Gonçalves, F.; Silva, G.; Souza, R.; Treuhaft, R.; Santos, W.; Loureiro, D.; Fernandes, M. Estimating Structure and Biomass of a Secondary Atlantic Forest in Brazil Using Fourier Transforms of Vertical Profiles Derived from UAV Photogrammetry Point Clouds. Remote Sens. 2020, 12, 3560. https://doi.org/10.3390/rs12213560
Almeida A, Gonçalves F, Silva G, Souza R, Treuhaft R, Santos W, Loureiro D, Fernandes M. Estimating Structure and Biomass of a Secondary Atlantic Forest in Brazil Using Fourier Transforms of Vertical Profiles Derived from UAV Photogrammetry Point Clouds. Remote Sensing. 2020; 12(21):3560. https://doi.org/10.3390/rs12213560
Chicago/Turabian StyleAlmeida, André, Fabio Gonçalves, Gilson Silva, Rodolfo Souza, Robert Treuhaft, Weslei Santos, Diego Loureiro, and Márcia Fernandes. 2020. "Estimating Structure and Biomass of a Secondary Atlantic Forest in Brazil Using Fourier Transforms of Vertical Profiles Derived from UAV Photogrammetry Point Clouds" Remote Sensing 12, no. 21: 3560. https://doi.org/10.3390/rs12213560
APA StyleAlmeida, A., Gonçalves, F., Silva, G., Souza, R., Treuhaft, R., Santos, W., Loureiro, D., & Fernandes, M. (2020). Estimating Structure and Biomass of a Secondary Atlantic Forest in Brazil Using Fourier Transforms of Vertical Profiles Derived from UAV Photogrammetry Point Clouds. Remote Sensing, 12(21), 3560. https://doi.org/10.3390/rs12213560










