Assessment of Temporal Variations of Orthometric/Normal Heights Induced by Hydrological Mass Variations over Large River Basins Using GRACE Mission Data
Abstract
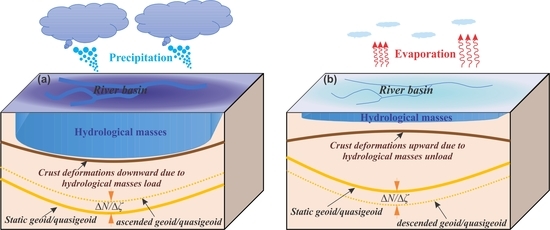
1. Introduction
2. Data and Methods Used
3. Results
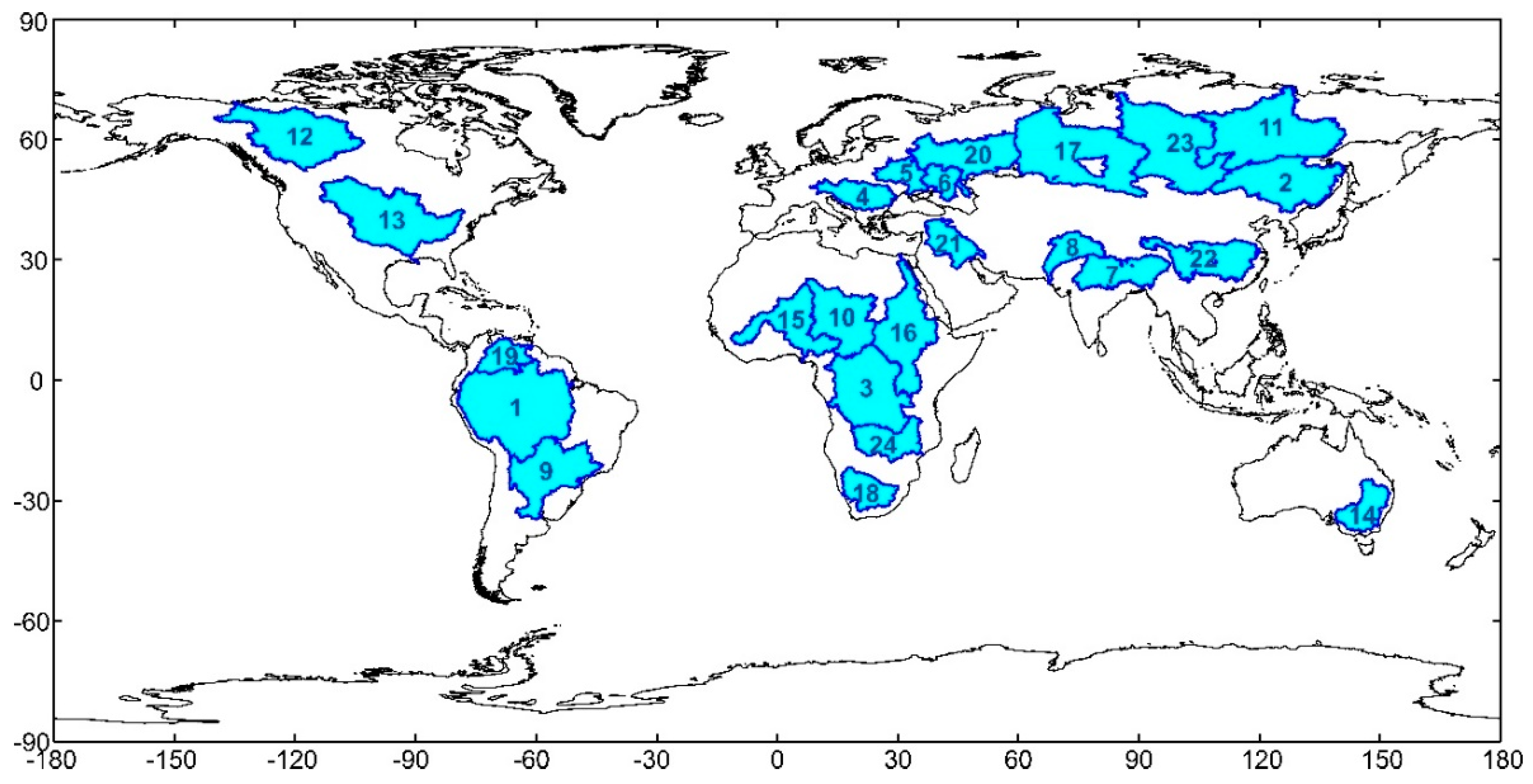
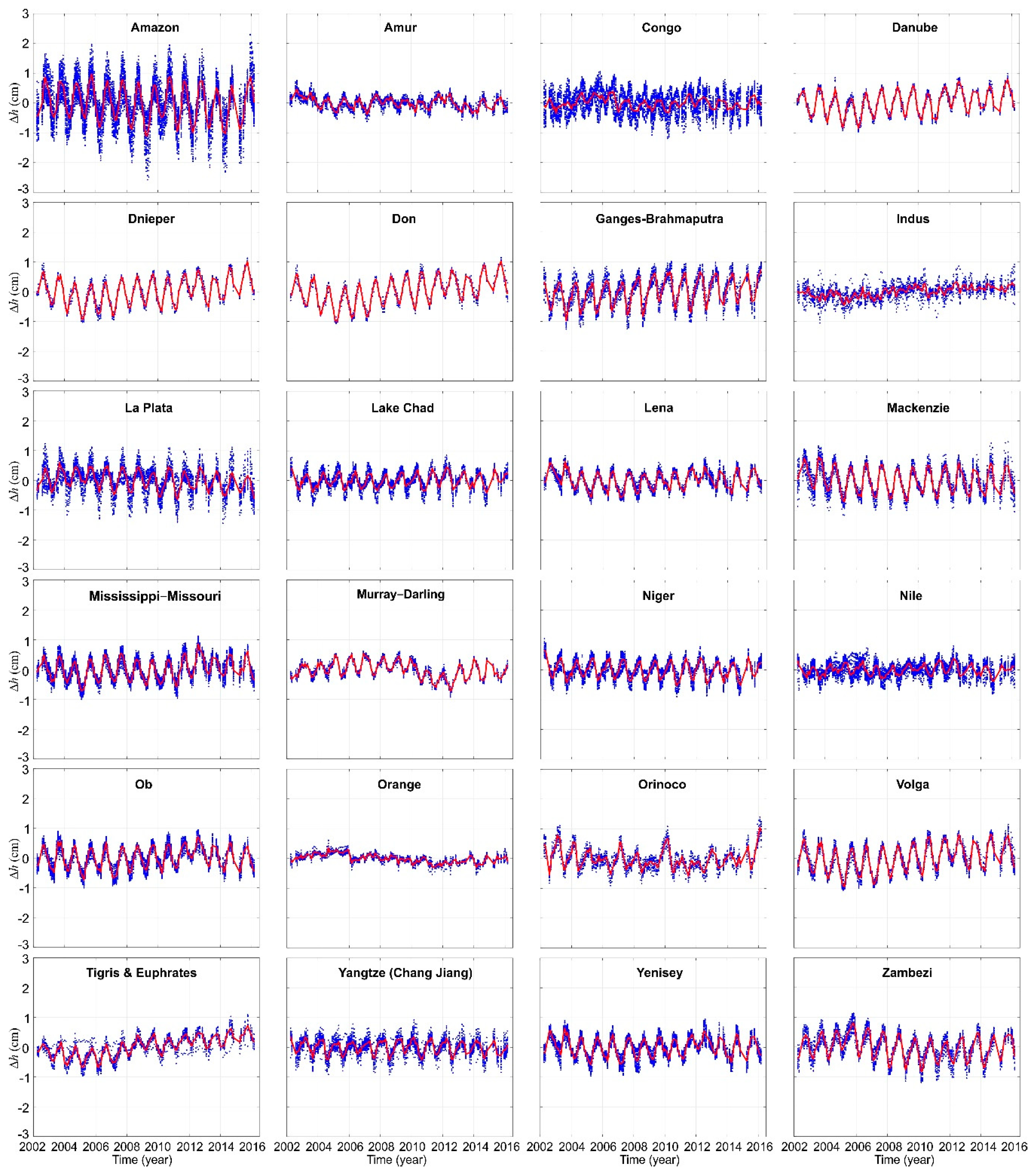
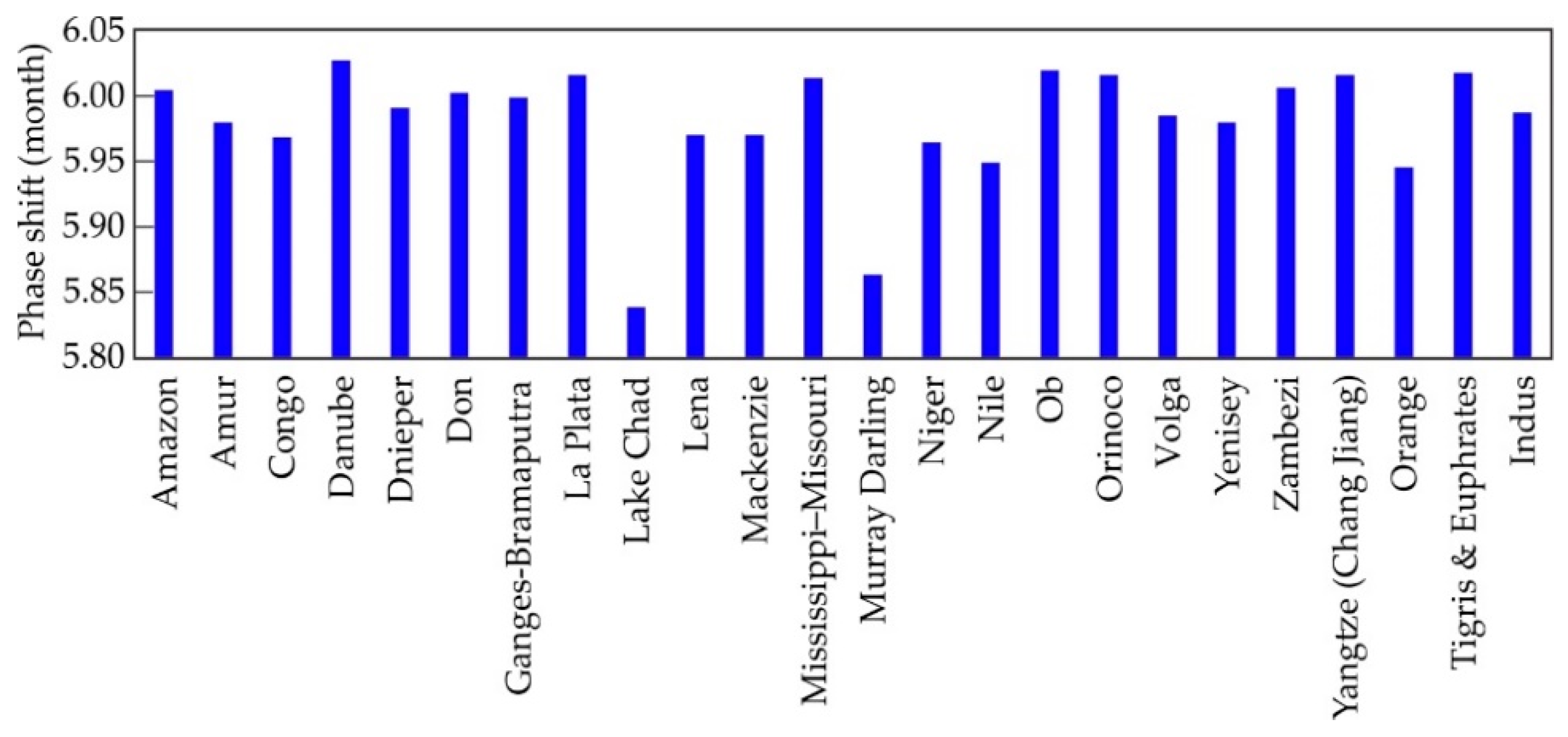
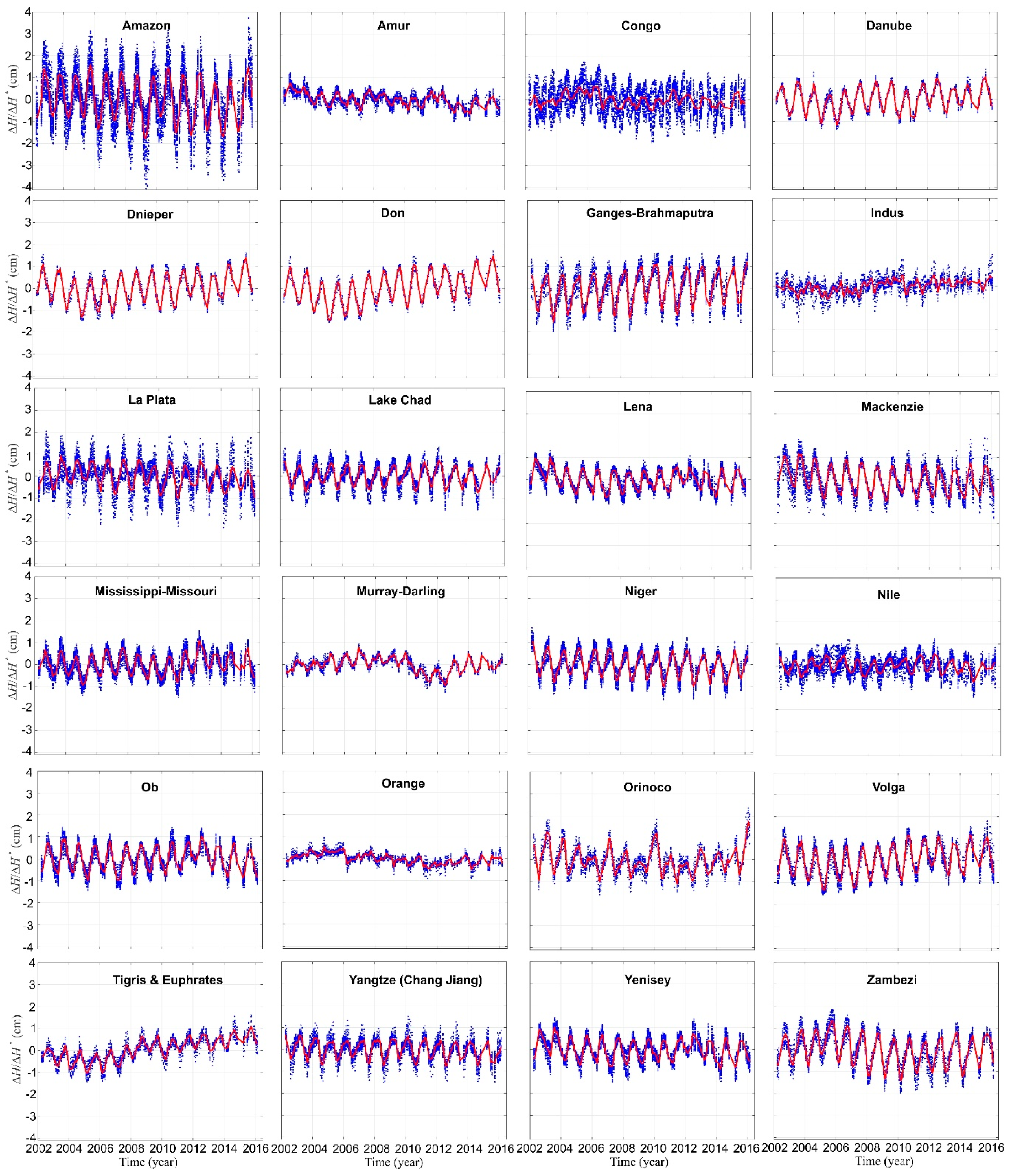
3.1. Orthometric/Normal Height Changes in the Time Domain
3.2. Orthometric/Normal Height Changes in the Space-Time Domain
4. Discussion and Conclusions
- Amplitudes of ΔH/ΔH* significantly differ from each other between large river basins investigated. The largest amplitudes were obtained for river basins located over tropical rainforests, whilst the lowest ones were observed over desert areas. This is due to the fact that hydrological mass changes within large river basins located in the tropical rain forest are substantially larger than the ones over desert areas. For example, the range of ΔH/ΔH* for the same subarea at different epochs reaches 8 cm over the Amazon basin and only ca. 2 cm for the Orange basin.
- For some large river basins ΔH/ΔH* time series obtained for particular subareas of the river basin are similar and close to each other, e.g., Danube, Dnieper and Don basins. This is because the hydrological mass changes patterns over the entire large river basins are consistent. However, in many cases differences between ΔH/ΔH* obtained at subareas within the same river basin are significant, sometimes exceeding three times the amplitude of the average of ΔH/ΔH* over the whole river basin, e.g., for the Congo basin. This is due to the fact that hydrological mass changes patterns substantially differ among subareas located in the same large river basin.
- For 88% of river basins subareas negative correlations between detrended ΔH/ΔH* and detrended ∆EWT were observed, whereas they are strong for 48% of those subareas. This is because the increase of hydrological masses results in decrease of ΔH/ΔH*, and vice versa, the decrease of hydrological masses results in increase of ΔH/ΔH*. For the remaining 12% of river basins subareas there are no correlations between detrended ∆H/ΔH* and detrended ∆EWT. The main reason for observing no correlations can be ascribed to the fact that the majority of those subareas are located in regions of a very weak hydrological signal (e.g., southern Sahara). However, further investigations concerning the correlation between ∆H/ΔH* from GRACE satellite mission data and ∆EWT from the WGHM for some subareas such as the ones located in Lena, Mackenzie and Ganges–Brahmaputra river basins are recommended.
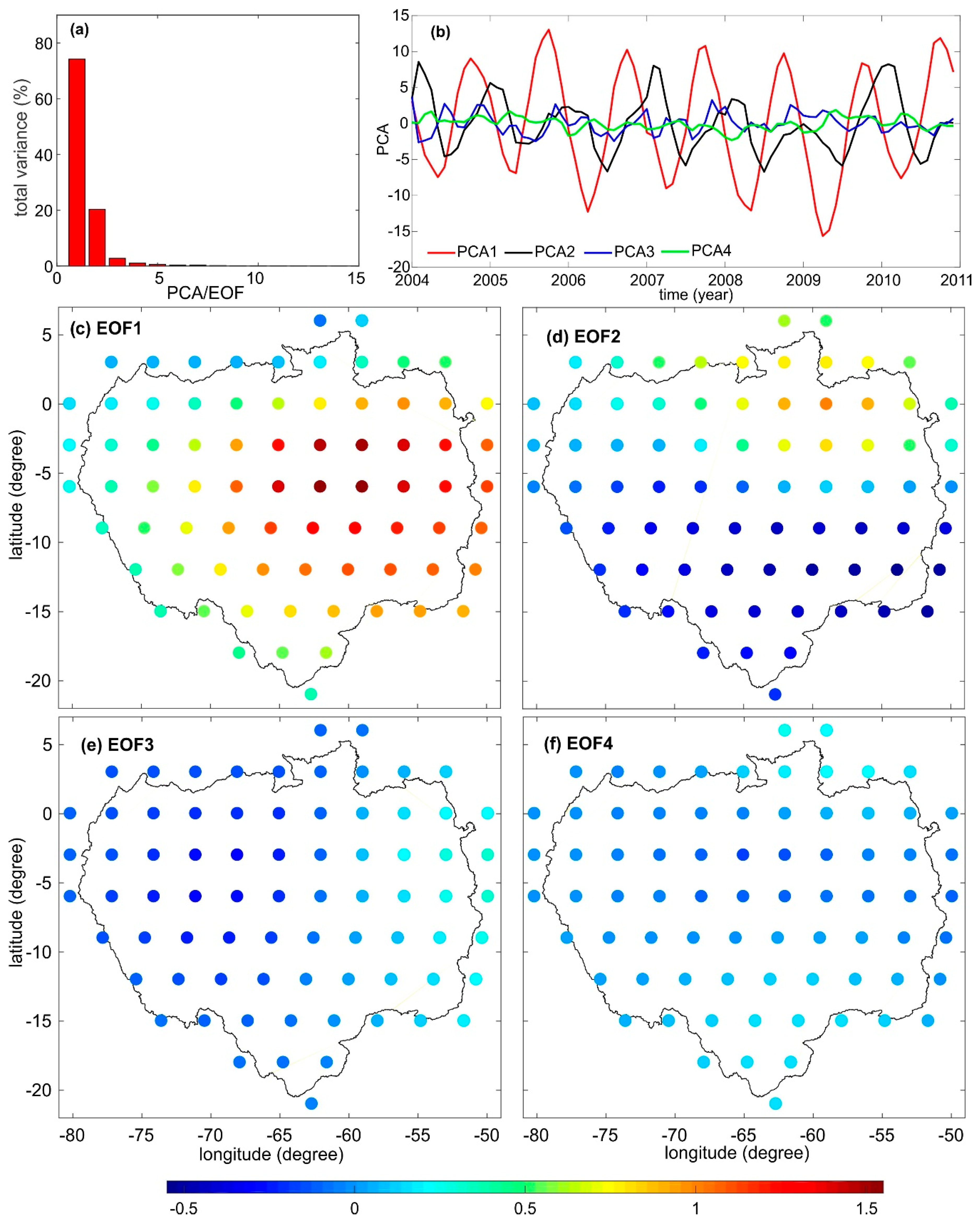
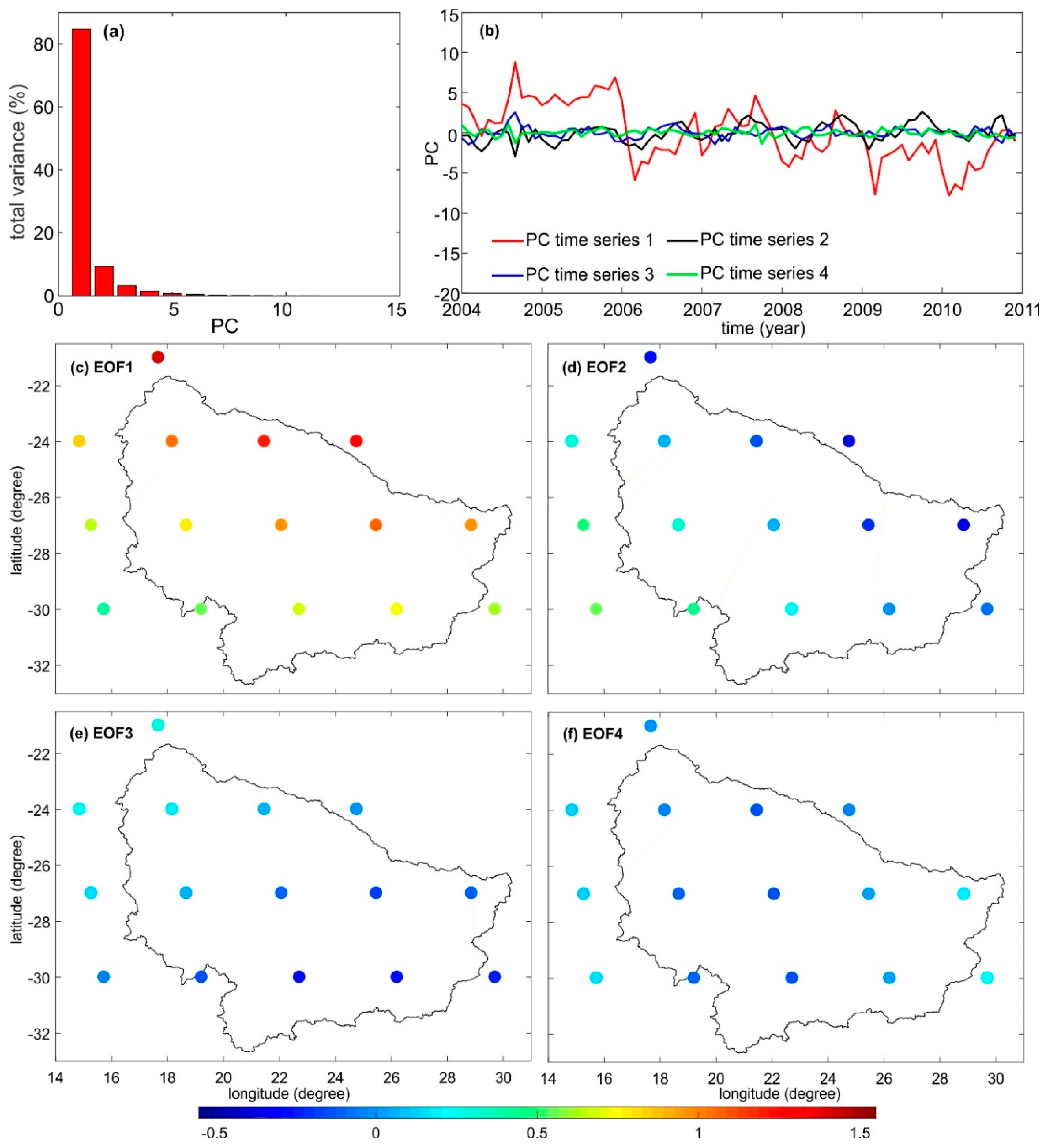
- For Amazon and Orange basins, the 1st and 2nd PCs time series reflect together 95%, and 94% of a total variance of ΔH/ΔH* signal, respectively. Although, these percentages are close to each other, the contribution of the first and second PCs time series is different in the case of both river basins, i.e., the first and second PCs time series are 77%, and 20%, respectively, for the Amazon basin, and the first and second PCs time series are 85% and 9%, respectively, for the Orange basin. The first and second PCs time series exhibit that ∆H/∆H* are not an artefact, but are a consequence of the processes inducing hydrological mass transport. These temporal variations of orthometric/normal heights are strongly associated to different spatio–temporal patterns of the entire river basins. They can be associated with the extreme drought, the unusual flood, the location of the upstream and downstream areas of the river basin, the rainfall seasonality induced by the seasonal migration of the Intertropical Convergence Zone (ITC) and other climatic conditions, the spatial distribution of the water storage of the entire river basin and the geological structure of the river basin.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Farahani, H.H.; Klees, R.; Slobbe, C. Data requirements for a 5–mm quasi–geoid in The Netherlands. Stud. Geophys. Geod. 2017, 61, 675–702. [Google Scholar] [CrossRef]
- Foroughi, I.; Vaníček, P.; Kingdon, R.W.; Goli, M.; Sheng, M.; Afrasteh, Y.; Novák, P.; Santos, M.C. Sub-centimetre geoid. J. Geod. 2019, 93, 849–868. [Google Scholar] [CrossRef]
- Ellmann, A.; Märdla, S.; Oja, T. The 5 mm geoid model for Estonia computed by the least squares modified Stokes’s formula. Surv. Rev. 2019, 52, 352–372. [Google Scholar] [CrossRef]
- Drewes, H.; Kuglitsch, F.; Adám, J.; Rózsa, S. The Geodesist’s handbook 2016. J. Geod. 2016, 90, 907–1205. [Google Scholar] [CrossRef]
- Li, X.; Zhang, X.; Ren, X.; Fritsche, M.; Wickert, J.; Schuh, H. Precise positioning with current multi-constellation Global Navigation Satellite Systems: GPS, GLONASS, Galileo and BeiDou. Sci. Rep. 2015, 5, 8328. [Google Scholar] [CrossRef] [PubMed]
- Heiskanen, W.; Moritz, H. Physical Geodesy; WH Freeman: San Francisco, CA, USA, 1967. [Google Scholar]
- Godah, W.; Szelachowska, M.; Krynski, J. Investigation of geoid height variations and vertical displacements of the Earth surface in the context of the realization of the modern vertical reference system —A case study for Poland. Int. Assoc. Geod. Symp. 2019, 148, 135–141. [Google Scholar] [CrossRef]
- Godah, W.; Szelachowska, M.; Krynski, J. Application of the PCA/EOF method for the analysis and modelling of temporal variations of geoid heights over Poland. Acta Geod. Geophys. 2018, 53, 93–105. [Google Scholar] [CrossRef]
- Godah, W. IGiK–TVGMF: A MATLAB package for computing and analysing temporal variations of gravity/mass functionals from GRACE satellite based global geopotential models. Comput. Geosci. 2019, 123, 47–58. [Google Scholar] [CrossRef]
- Zeray Öztürk, E.; Godah, W.; Abbak, R.A. Estimation of Physical Height Changes from GRACE Satellite Mission Data and WGHM over Turkey. Acta Geod. Geophys. 2020, 55, 301–317. [Google Scholar] [CrossRef]
- Tapley, B.D.; Bettadpur, S.; Watkins, M.; Reigber, C. The gravity recovery and climate experiment: Mission overview and early results. Geophys. Res. Lett. 2004, 31, L09607. [Google Scholar] [CrossRef]
- Kornfeld, R.P.; Arnold, B.W.; Gross, M.A.; Dahya, N.T.; Klipstein, W.M.; Gath, P.F.; Bettadpur, S. GRACE-FO: The Gravity Recovery and Climate Experiment Follow-On Mission. J. Spacecr. Rocket. 2019, 56, 931–951. [Google Scholar] [CrossRef]
- Tapley, B.D.; Bettadpur, S.; Ries, S.C.; Thompson, P.F.; Watkins, M.M. GRACE Measurements of Mass Variability in the Earth System. Science 2004, 305, 503–505. [Google Scholar] [CrossRef] [PubMed]
- Rangelova, E. A Dynamic Geoid Model for Canada. PhD. Thesis, Department of Geomatics Engineering, University of Calgary, Calgary, AB, Canada, 2007. [Google Scholar]
- Rangelova, E.; Fotopoulos, G.; Sideris, M.G. Implementing a dynamic geoid as a vertical datum for orthometric heights in Canada. Int. Assoc. Geod. Symp. 2010, 135, 295–302. [Google Scholar] [CrossRef]
- Rangelova, E.; Sideris, M.G. Contributions of terrestrial and GRACE data to the study of the secular geoid changes in North America. J. Geodyn. 2008, 46, 131–143. [Google Scholar] [CrossRef]
- Krynski, J.; Kloch-Główka, G.; Szelachowska, M. Analysis of time variations of the gravity field over Europe obtained from GRACE data in terms of geoid height and mass variations. Int. Assoc. Geod. Symp. 2014, 139, 365–370. [Google Scholar] [CrossRef]
- Godah, W.; Szelachowska, M.; Krynski, J. On the estimation of physical height changes using GRACE satellite mission data—A case study of Central Europe. Geod. Cartogr. 2017, 66, 211–226. [Google Scholar] [CrossRef][Green Version]
- Godah, W.; Szelachowska, M.; Krynski, J. On the analysis of temporal geoid height variations obtained from GRACE–based GGMs over the area of Poland. Acta Geophys. 2017, 65, 713–725. [Google Scholar] [CrossRef]
- Kusche, J.; Schrama, E. Surface mass redistribution inversion from global GPS deformation and Gravity Recovery and Climate Experiment (GRACE) gravity data. J. Geophys. Res. 2005, 110, B09409. [Google Scholar] [CrossRef]
- Tregoning, P.; Watson, C.; Ramillien, G.; McQueen, H.; Zhang, J. Detecting hydrologic deformation using GRACE and GPS. Geophys. Res. Lett. 2009, 36, L15401. [Google Scholar] [CrossRef]
- Rietbroek, R.; Fritsche, M.; Dahle, C.; Brunnabend, S.E.; Behnisch, M.; Kusche, J.; Flechtner, F.; Schröter, J.; Dietrich, R. Can GPS-Derived Surface Loading Bridge a GRACE Mission Gap? Surv. Geophys. 2014, 35, 1267–1283. [Google Scholar] [CrossRef]
- van Dam, T.; Wahr, J.; Lavallée, D. A comparison of annual vertical crustal displacements from GPS and Gravity Recovery and Climate Experiment (GRACE) over Europe. J. Geophys. Res. 2007, 112, B03404. [Google Scholar] [CrossRef]
- Davis, J.L.; Elósegui, P.; Mitrovica, J.X.; Tamisiea, M.E. Climate-driven deformation of the solid earth from GRACE and GPS. Geophys. Res. Lett. 2004, 31, L24605. [Google Scholar] [CrossRef]
- Bevis, M.; Alsdorf, D.; Kendrick, E.; Fortes, L.P.; Forsberg, B.; Smalley, R., Jr.; Becker, J. Seasonal fluctuations in the mass of the Amazon River system and Earth’s elastic response. Geophys. Res. Lett. 2005, 32, L16308. [Google Scholar] [CrossRef]
- Knowles, L.A.; Bennett, R.A.; Harig, C. Vertical Displacements of the Amazon Basin from GRACE and GPS. J. Geophys. Res. Solid Earth 2020, 125, e2019JB018105. [Google Scholar] [CrossRef]
- Nahmani, S.; Bock, O.; Bouin, M.-N.; Santamaría-Gómez, A.; Boy, J.P.; Collilieux, X.; Métivier, L.; Panet, I.; Genthon, P.; De Linage, C.; et al. Hydrological deformation induced by the West African Monsoon: Comparison of GPS, GRACE and loading models. J. Geophys. Res. Solid Earth 2012, 117, B05409. [Google Scholar] [CrossRef]
- Birhanu, Y.; Bendick, R. Monsoonal loading in Ethiopia and Eritrea from vertical GPS displacement time series. J. Geophys. Res. Solid Earth 2015, 120, 7231–7238. [Google Scholar] [CrossRef]
- Heki, K. Dense GPS array as a new sensor of seasonal changes of surface loads. Geophys. Monogr. Ser. 2004, 150, 177–196. [Google Scholar] [CrossRef]
- Steckler, M.S.; Nooner, S.L.; Akhter, S.H.; Chowdhury, S.K.; Bettadpur, S.; Seeber, L.; Kogan, M.G. Modeling Earth deformation from monsoonal flooding in Bangladesh using hydrographic, GPS, and Gravity Recovery and Climate Experiment (GRACE) data. J. Geophys. Res. Solid Earth 2010, 115, B08407. [Google Scholar] [CrossRef]
- Liu, R.L.; Li, J.; Fok, H.S.; Shum, C.K.; Li, Z. Earth surface deformation in the North China plain detected by joint analysis of GRACE and GPS data. Sensors 2014, 14, 19861–19876. [Google Scholar] [CrossRef]
- Zhang, B.; Yao, Y.; Fok, H.S.; Hu, Y.; Chen, Q. Potential seasonal terrestrial water storage monitoring from GPS vertical displacements: A case study in the lower three-rivers headwater region, China. Sensors 2016, 16, 1526. [Google Scholar] [CrossRef]
- Jiang, W.; Yuan, P.; Chen, H.; Cai, J.; Li, Z.; Chao, N.; Sneeuw, N. Annual variations of monsoon and drought detected by GPS: A case study in Yunnan, China. Sci. Rep. 2017, 7, 5874. [Google Scholar] [CrossRef] [PubMed]
- Zou, R.; Wang, Q.; Freymueller, J.T.; Poutanen, M.; Cao, X.; Zhang, C.; Yang, S.; He, P. Seasonal hydrological loading in southern Tibet detected by joint analysis of GPS and GRACE. Sensors 2015, 15, 30525–30538. [Google Scholar] [CrossRef] [PubMed]
- Pan, Y.; Shen, W.B.; Hwang, C.; Liao, C.; Zhang, T.; Zhang, G. Seasonal Mass Changes and Crustal Vertical Deformations Constrained by GPS and GRACE in Northeastern Tibet. Sensors 2016, 16, 1211. [Google Scholar] [CrossRef] [PubMed]
- Rajner, M.; Liwosz, T. Studies of crustal deformation due to hydrological loading on GPS height estimates. Geod. Cartogr. 2011, 60, 135–144. [Google Scholar] [CrossRef][Green Version]
- Godah, W.; Szelachowska, M.; Ray, J.D.; Krynski, J. Comparison of vertical deformations of the Earth’s surface obtained using GRACE-based GGMs and GNSS data—A case study of Poland. Acta Geodyn. Geomater. 2020, 17, 169–176. [Google Scholar] [CrossRef]
- Bevis, M.; Wahr, J.; Khan, S.A.; Madsen, F.B.; Brown, A.; Willis, M.; Kendrick, E.; Knudsen, P.; Box, J.E.; van Dam, T.; et al. Bedrock displacements in Greenland manifest ice mass variations, climate cycles and climate change. Proc. Natl. Acad. Sci. USA 2012, 109, 11944–11948. [Google Scholar] [CrossRef]
- Fu, Y.; Freymueller, J.T.; Jensen, T. Seasonal hydrological loading in southern Alaska observed by GPS and GRACE. Geophys. Res. Lett. 2012, 39, L15310. [Google Scholar] [CrossRef]
- Chew, C.C.; Small, E.E. Terrestrial water storage response to the 2012 drought estimated from GPS vertical position anomalies. Geophys. Res. Lett. 2014, 41, 6145–6151. [Google Scholar] [CrossRef]
- Fu, Y.; Argus, D.F.; Landerer, F.W. GPS As an Independent Measurement to Estimate Terrestrial Water Storage Variations in Washington and Oregon. J. Geophys. Res. Solid Earth 2015, 120, 552–566. [Google Scholar] [CrossRef]
- Tan, W.; Dong, D.; Chen, J.; Wu, B. Analysis of systematic differences from GPS-measured and GRACE-modeled deformation in Central Valley, California. Adv. Space Res. 2016, 57, 19–29. [Google Scholar] [CrossRef]
- Eriksson, D.; MacMillan, D.S. Continental hydrology loading observed by VLBI measurements. J. Geod. 2014, 88, 675–690. [Google Scholar] [CrossRef]
- Öztürk, E.Z.; Abbak, R.A. PHCSOFT: A Software package for computing physical height changes from GRACE based global geopotential models. Earth Sci. Inform. 2020, 2, 1–7. [Google Scholar] [CrossRef]
- Fotopoulos, G. An Analysis on the Optimal Combination of Geoid, Orthometric and Ellipsoidal Height Data. PhD Thesis, Department of Geomatics Engineering, University of Calgary, Calgary, AB, Canada, 2003. [CrossRef]
- Fuhrmann, T.; Westerhaus, M.; Zippelt, K.; Heck, B. Vertical displacement rates in the Upper Rhine Graben area derived from precise leveling. J. Geod. 2014, 88, 773–787. [Google Scholar] [CrossRef]
- Mäkinen, J.; Saaranen, V. Determination of post-glacial land uplift from the three precise levellings in Finland. J. Geod. 1998, 72, 516–529. [Google Scholar] [CrossRef]
- Bettadpur, S. Gravity Recovery and Climate Experiment Level–2 Gravity Field Product User Handbook. Center for Space Research at The University of Texas at Austin. Available online: ftp://podaac-ftp.jpl.nasa.gov/allData/grace/docs/L2-UserHandbook_v4.0.pdf (accessed on 18 September 2020).
- Dziewonski, A.M.; Anderson, D.L. Preliminary reference Earth model. Phys. Earth Planet. Inter. 1981, 25, 297–356. [Google Scholar] [CrossRef]
- Sun, Y.; Riva, R.; Ditmar, P. Optimizing estimates of annual variations and trends in geocenter motion and J2 from a combination of GRACE data and geophysical models. J. Geophys. Res. Solid Earth 2016, 121, 8352–8370. [Google Scholar] [CrossRef]
- Cheng, M.K.; Tapley, B.D.; Ries, J.C. Deceleration in the Earth’s oblateness. J. Geophys. Res. Solid Earth 2013, 118, 740–747. [Google Scholar] [CrossRef]
- Kusche, J.; Schmidt, R.; Petrovic, S.; Rietbroek, R. Decorrelated GRACE time–variable gravity solutions by GFZ, and their validation using a hydrological model. J. Geod. 2009, 83, 903–913. [Google Scholar] [CrossRef]
- Göttl, F.; Schmidt, M.; Seitz, F. Mass-related excitation of polar motion: An assessment of the new RL06 GRACE gravity field models. Earth Planets Space 2018, 70, 195. [Google Scholar] [CrossRef]
- Kvas, A.; Behzadpour, S.; Ellmer, M.; Klinger, B.; Strasser, S.; Zehentner, N.; Mayer-Gürr, T. ITSG-Grace2018: Overview and Evaluation of a New GRACE-Only Gravity Field Time Series. J. Geophys. Res. Solid Earth 2019, 124, 9332–9344. [Google Scholar] [CrossRef]
- Adhikari, S.; Ivins, E.R.; Frederikse, T.; Landerer, F.W.; Caron, L. Sea-level fingerprints emergent from GRACE mission data. Earth Syst. Sci. Data 2019, 11, 629–646. [Google Scholar] [CrossRef]
- Barthelmes, F. Definition of Functionals of the Geopotential and their Calculation from Spherical Harmonic Models: Theory and Formulas Used by the Calculation Service of the International Centre for Global Earth Models (ICGEM); Scientific Technical Report STR09/02; GFZ German Research Centre for Geosciences: Potsdam, Germany, 2013; p. 32. Available online: http://icgem.gfz-potsdam.de (accessed on 18 September 2020).
- Zhang, X.; Jin, S.; Lu, X. Global Surface Mass Variations from Continuous GPS Observations and Satellite Altimetry Data. Remote Sens. 2017, 9, 1000. [Google Scholar] [CrossRef]
- Müller Schmied, H. Evaluation, modification and application of a global hydrological model. In Frankfurt Hydrology Paper 16; Institute of Physical Geography, Goethe University Frankfurt: Frankfurt am Main, Germany; Available online: https://www.uni-frankfurt.de/65883413/Mueller_Schmied_2017_evaluation_modification_and_application_of_a_global_hydrological_model.pdf (accessed on 18 September 2020).
- Müller Schmied, H.; Eisner, S.; Franz, D.; Wattenbach, M.; Portmann, F.T.; Flörke, M.; Döll, P. Sensitivity of simulated global-scale freshwater fluxes and storages to input data, hydrological model structure, human water use and calibration. Hydrol. Earth Syst. Sci. 2014, 18, 3511–3538. [Google Scholar] [CrossRef]
- Döll, P.; Hoffmann-Dobrev, H.; Portmann, F.T.; Siebert, S.; Eicker, A.; Rodell, M.; Strassberg, G.; Scanlon, B.R. Impact of water withdrawals from groundwater and surface water on continental water storage variations. J. Geodyn. 2012, 59, 143–156. [Google Scholar] [CrossRef]
- Schmidt, R.; Petrovic, S.; Güntner, A.; Barthelmes, F.; Wünsch, J.; Kusche, J. Periodic components of water storage changes from GRACE and global hydrology models. J. Geophys. Res. Solid Earth 2008, 113, B08419. [Google Scholar] [CrossRef]
- Landerer, F.W.; Dickey, J.O.; Güntner, A. Terrestrial water budget of the Eurasian pan-Arctic from GRACE satellite measurements during 2003–2009. J. Geophys. Res. Atmos. 2010, 115, D23115. [Google Scholar] [CrossRef]
- Döll, P.; Fritsche, M.; Eicker, A.; Müller Schmied, H. Seasonal water storage variations as impacted by water abstractions: Comparing the output of a global hydrological model with GRACE and GPS observations. Surv. Geophys. 2014, 35, 1311–1331. [Google Scholar] [CrossRef]
- Scanlon, B.R.; Zhang, Z.; Save, H.; Sun, A.Y.; Schmied, H.M.; Van Beek, L.P.; Wiese, D.N.; Wada, Y.; Long, D.; Reedy, R.C.; et al. Global models underestimate large decadal declining and rising water storage trends relative to GRACE satellite data. Proc. Natl. Acad. Sci. USA 2018, 115, E1080–E1089. [Google Scholar] [CrossRef]
- Jolliffe, I. Principal Component Analysis; Springer: New York, NY, USA, 2002. [Google Scholar]
- Li, J.; Wang, S.; Zhou, F. Time Series Analysis of Long-term Terrestrial Water Storage over Canada from GRACE Satellites Using Principal Component Analysis. Can. J. Remote Sens. 2016, 42, 161–170. [Google Scholar] [CrossRef]
- Preisendorfer, R.W.; Mobley, C.D. Principal Component Analysis in Meteorology and Oceanography; Elsevier: Amsterdam, The Netherlands, 1988. [Google Scholar]
- Schrama, E.J.O.; Visser, P.N.A.M. Accuracy assessment of the monthly GRACE geoids based upon a simulation. J. Geod. 2007, 81, 67–80. [Google Scholar] [CrossRef]
- Wahr, J.; Molenaar, M.; Bryan, F. Time variability of the Earth’s gravity field: Hydrological and oceanic effects and their possible detection using GRACE. J. Geophys. Res. 1998, 103, 30205–30229. [Google Scholar] [CrossRef]
- Zeng, N. Seasonal cycle and interannual variability in the Amazon hydrologic cycle. J. Geophys. Res. Atmos. 1999, 104, 9097–9106. [Google Scholar] [CrossRef]
- Chen, J.L.; Rodell, M.; Wilson, C.R.; Famiglietti, J.S. Low degree spherical harmonic influences on Gravity Recovery and Climate Experiment (GRACE) water storage estimates. Geophys. Res. Lett. 2005, 32, L14405. [Google Scholar] [CrossRef]
- Güntner, A.; Stuck, J.; Werth, S.; Döll, P.; Verzano, K.; Merz, B. A global analysis of temporal and spatial variations in continental water storage. Water Resour. Res. 2007, 43, W05416. [Google Scholar] [CrossRef]
- Tomasella, J.; Borma, L.S.; Marengo, J.A.; Rodriguez, D.A.; Cuartas, L.A.; ANobre, C.; Prado, M.C. The droughts of 1996–97 and 2004–5 in Amazonia: Hydrological response in the river main-stem. Hydrol. Process. 2011, 25, 1228–1242. [Google Scholar] [CrossRef]
- Chen, J.L.; Wilson, C.R.; Tapley, B.D. The 2009 exceptional Amazon flood and interannual terrestrial water storage change observed by GRACE. Water Resour. Res. 2010, 46, W12526. [Google Scholar] [CrossRef]
- Hasan, E.; Tarhule, A.; Zume, J.T.; Kirstetter, P.-E. +50 Years of Terrestrial Hydroclimatic Variability in Africa’s Transboundary Waters. Sci. Rep. 2019, 9, 12327. [Google Scholar] [CrossRef] [PubMed]
- SADC. Regional Flood Watch No. 1. January 2006. Available online: https://reliefweb.int/report/malawi/regional-flood-watch-no-1-jan-2006 (accessed on 31 July 2020).
- Diederichs, M.; Mander, M.; Caroline Sullivan, C.; dermot O’reagan, D.; mathew Fry, M.; Mckenzie, M. Orange River Basin—Baseline Vulnerability Assessment Report. NeWater. Available online: http://www.newater.uni-osnabrueck.de/intern/sendfile.php?id=1278 (accessed on 18 September 2020). [CrossRef]
- Hughes, D.A.A. Simple approach to estimating channel transmission losses in large South African river basin. J. Hydrol. Reg. Stud. 2019, 25, 100619. [Google Scholar] [CrossRef]
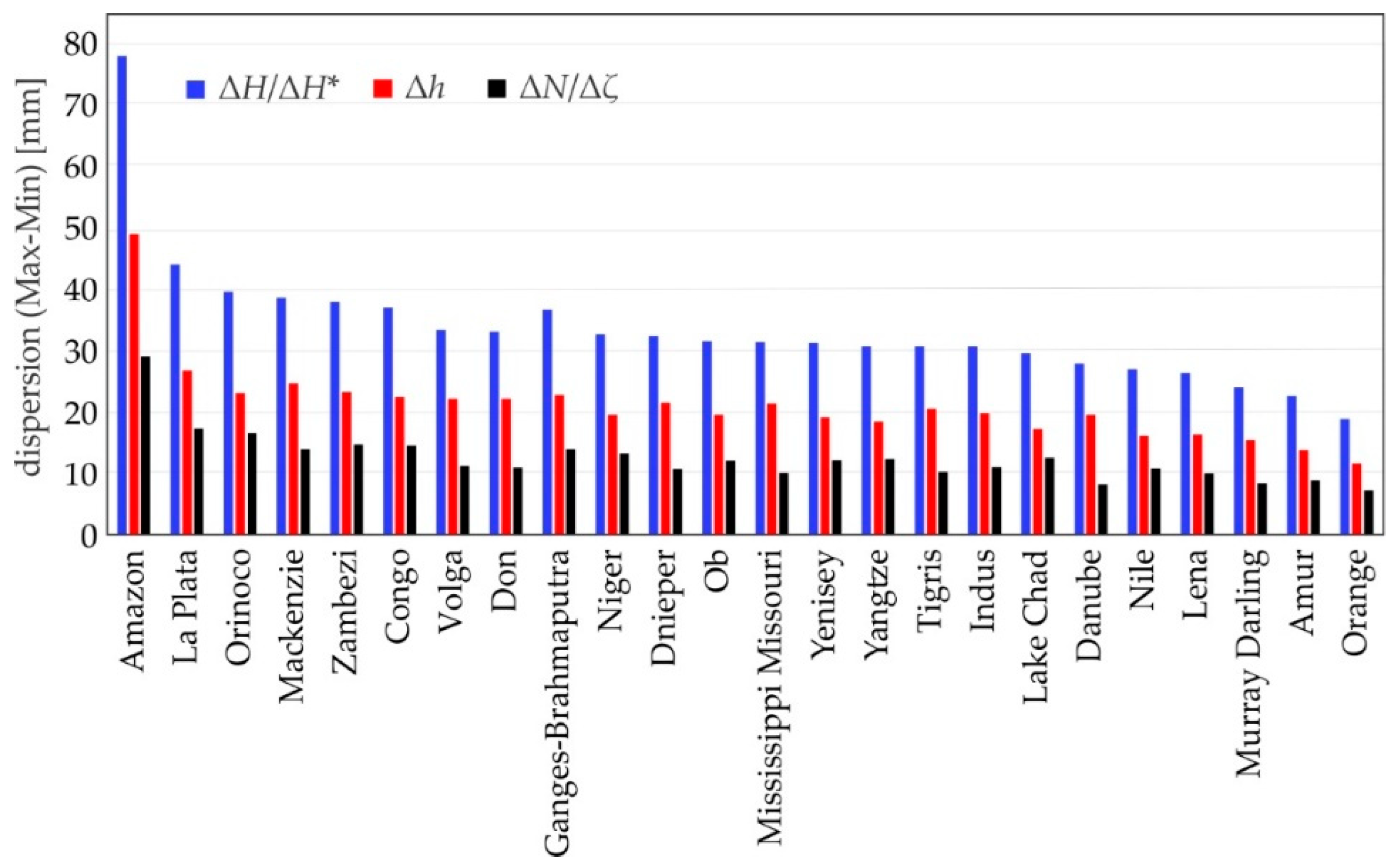

| River Basin | ∆N/∆ζ | ∆h | ∆H/∆H* | |||
|---|---|---|---|---|---|---|
| Max | Min | Max | Min | Max | Min | |
| Amazon | 7.5 | 0.9 | 12.3 | 1.6 | 19.8 | 2.5 |
| Amur | 1.8 | 0.9 | 2.9 | 1.3 | 4.5 | 2.0 |
| Congo | 3.7 | 1.3 | 5.4 | 1.9 | 9.1 | 3.1 |
| Danube | 1.9 | 1.3 | 4.2 | 3.6 | 6.0 | 4.8 |
| Dnieper | 2.3 | 1.7 | 4.8 | 3.8 | 7.0 | 5.4 |
| Don | 2.4 | 2.2 | 4.8 | 4.1 | 7.1 | 6.2 |
| Ganges–Brahmaputra | 4.1 | 1.9 | 6.3 | 3.1 | 10.4 | 5.0 |
| Indus | 2.2 | 0.8 | 3.9 | 1.4 | 6.0 | 2.0 |
| Lake Chad | 3.3 | 1.1 | 4.2 | 1.4 | 7.3 | 2.1 |
| La Plata | 4.9 | 1.1 | 7.3 | 1.8 | 12.2 | 2.1 |
| Lena | 2.2 | 1.2 | 3.9 | 1.7 | 5.9 | 2.7 |
| Mackenzie | 3.1 | 1.3 | 5.8 | 3.6 | 8.5 | 4.8 |
| Mississippi–Missouri | 2.1 | 1.1 | 4.3 | 2.9 | 6.4 | 3.8 |
| Murray Darling | 1.5 | 0.8 | 3.1 | 2.6 | 3.8 | 3.1 |
| Niger | 3.3 | 1.2 | 4.1 | 1.5 | 7.3 | 2.3 |
| Nile | 2.7 | 0.6 | 3.6 | 1.4 | 6.3 | 2.1 |
| Ob | 2.6 | 0.7 | 4.7 | 1.4 | 7.0 | 1.8 |
| Orange | 1.8 | 0.7 | 2.4 | 1.3 | 4.1 | 1.9 |
| Orinoco | 3.6 | 1.7 | 4.7 | 2.1 | 8.2 | 3.7 |
| Tigris | 2.4 | 1.1 | 4.6 | 1.6 | 6.9 | 3.3 |
| Volga | 2.5 | 2.1 | 4.8 | 4.0 | 7.3 | 6.1 |
| Yangtze | 3.6 | 1.0 | 5.2 | 1.4 | 8.7 | 2.4 |
| Yenisey | 2.7 | 1.0 | 4.6 | 1.4 | 7.0 | 2.1 |
| Zambezi | 3.7 | 1.9 | 5.6 | 2.2 | 9.2 | 4.0 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Godah, W.; Szelachowska, M.; Krynski, J.; Ray, J.D. Assessment of Temporal Variations of Orthometric/Normal Heights Induced by Hydrological Mass Variations over Large River Basins Using GRACE Mission Data. Remote Sens. 2020, 12, 3070. https://doi.org/10.3390/rs12183070
Godah W, Szelachowska M, Krynski J, Ray JD. Assessment of Temporal Variations of Orthometric/Normal Heights Induced by Hydrological Mass Variations over Large River Basins Using GRACE Mission Data. Remote Sensing. 2020; 12(18):3070. https://doi.org/10.3390/rs12183070
Chicago/Turabian StyleGodah, Walyeldeen, Malgorzata Szelachowska, Jan Krynski, and Jagat Dwipendra Ray. 2020. "Assessment of Temporal Variations of Orthometric/Normal Heights Induced by Hydrological Mass Variations over Large River Basins Using GRACE Mission Data" Remote Sensing 12, no. 18: 3070. https://doi.org/10.3390/rs12183070
APA StyleGodah, W., Szelachowska, M., Krynski, J., & Ray, J. D. (2020). Assessment of Temporal Variations of Orthometric/Normal Heights Induced by Hydrological Mass Variations over Large River Basins Using GRACE Mission Data. Remote Sensing, 12(18), 3070. https://doi.org/10.3390/rs12183070