SCoBi Multilayer: A Signals of Opportunity Reflectometry Model for Multilayer Dielectric Reflections
Abstract
1. Introduction
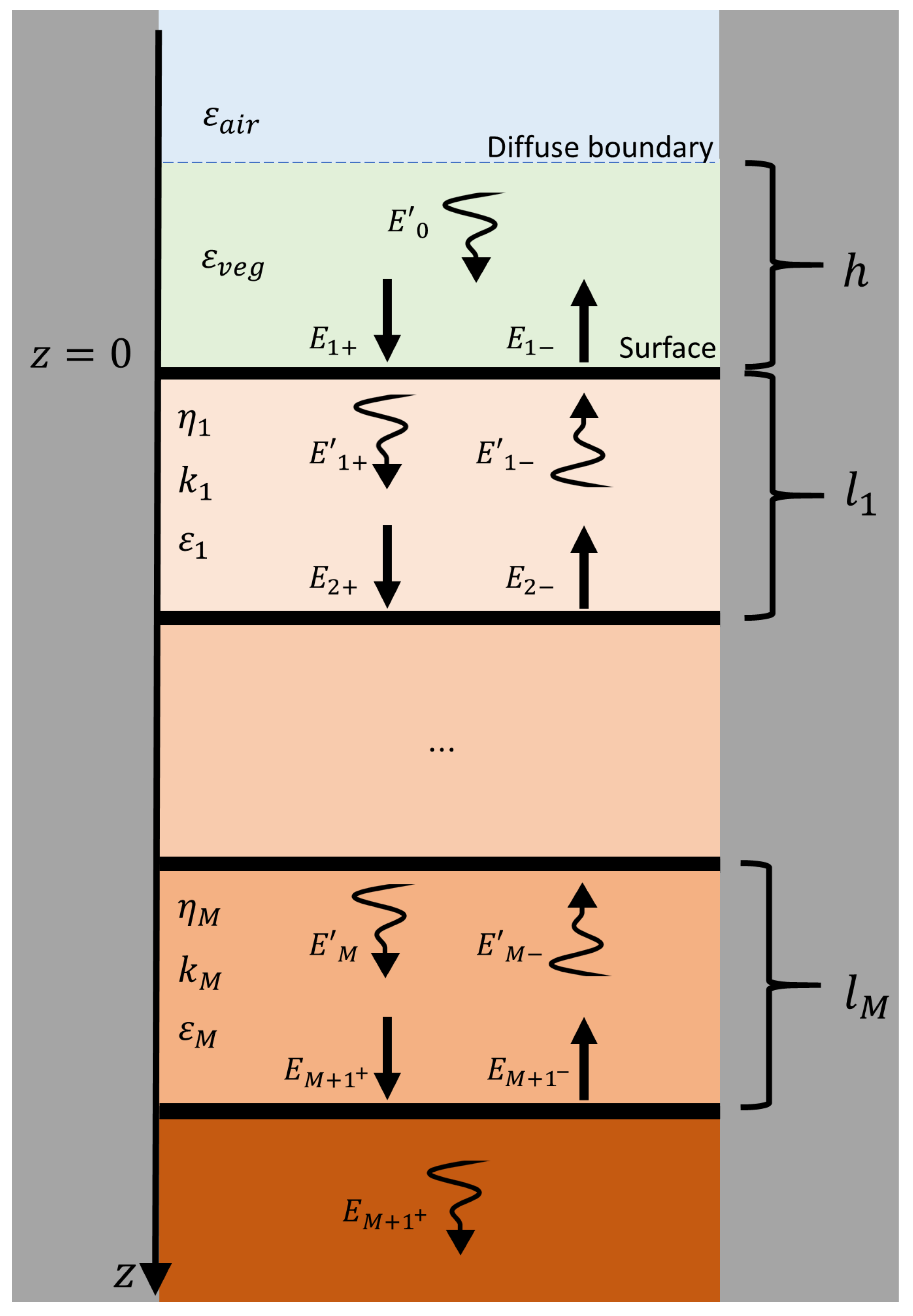
2. Model
2.1. Reflection Processes from a Multilayered Dielectric Slab
2.2. Use of Multilayer Module within SCoBi
2.3. Penetration Depth Calculation
2.4. Simulation Tools and Soil Moisture Profile Representations
3. Methodology
3.1. Single Slab Study
3.2. Dual Slab Study
3.3. Arbitrary Profile Study
4. Results
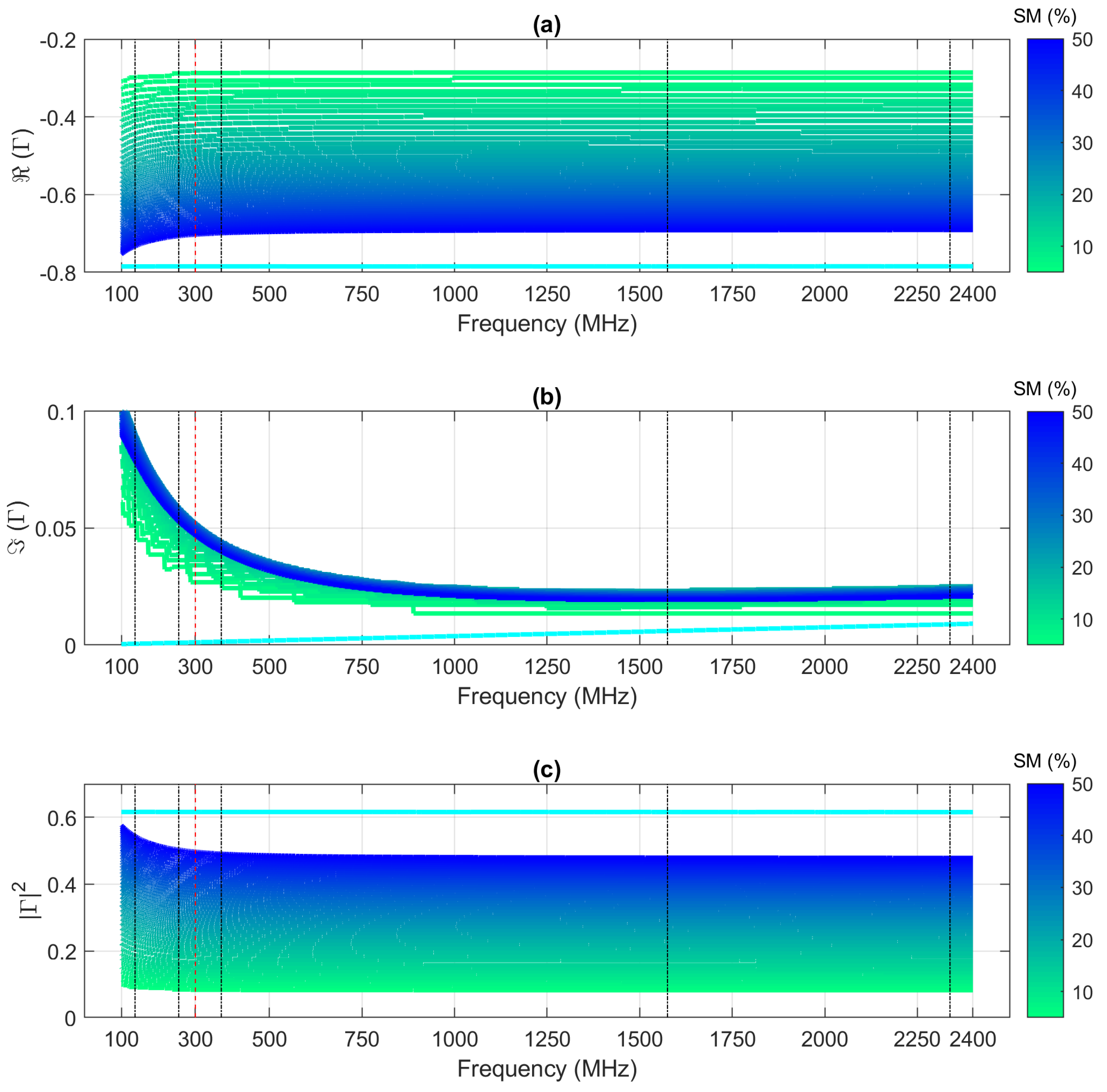
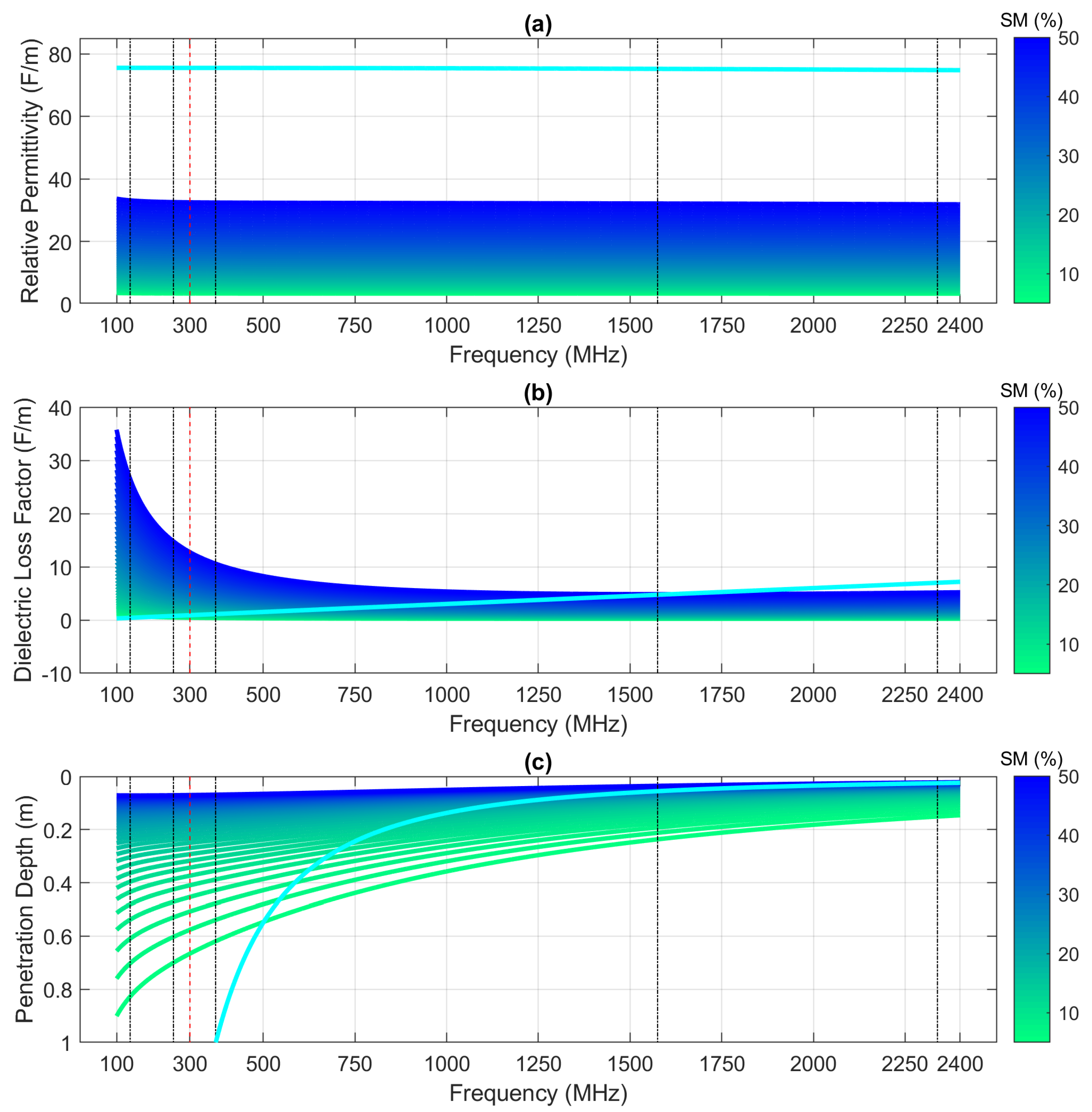
4.1. Single Slab
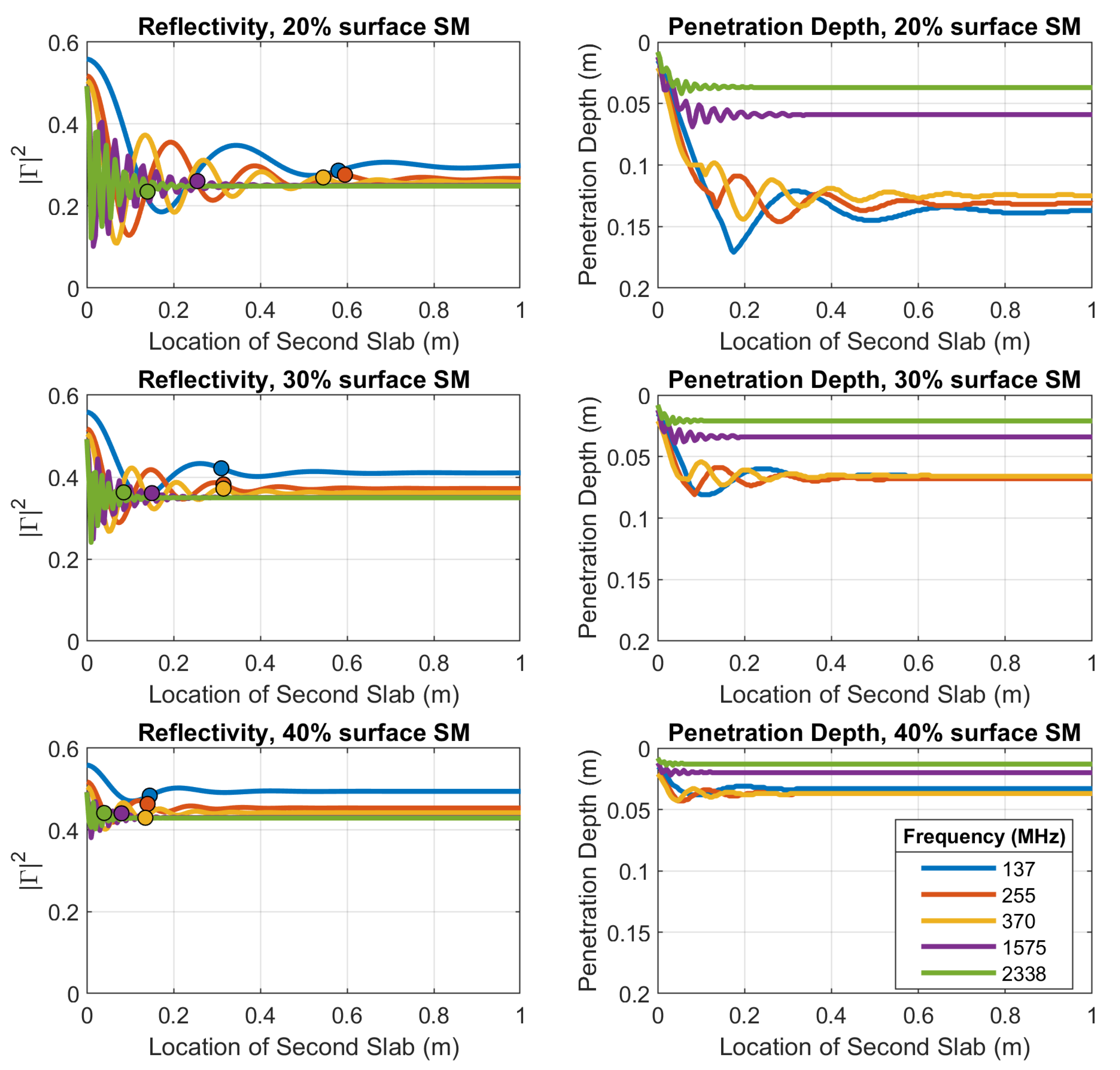
4.2. Dual Slab Study
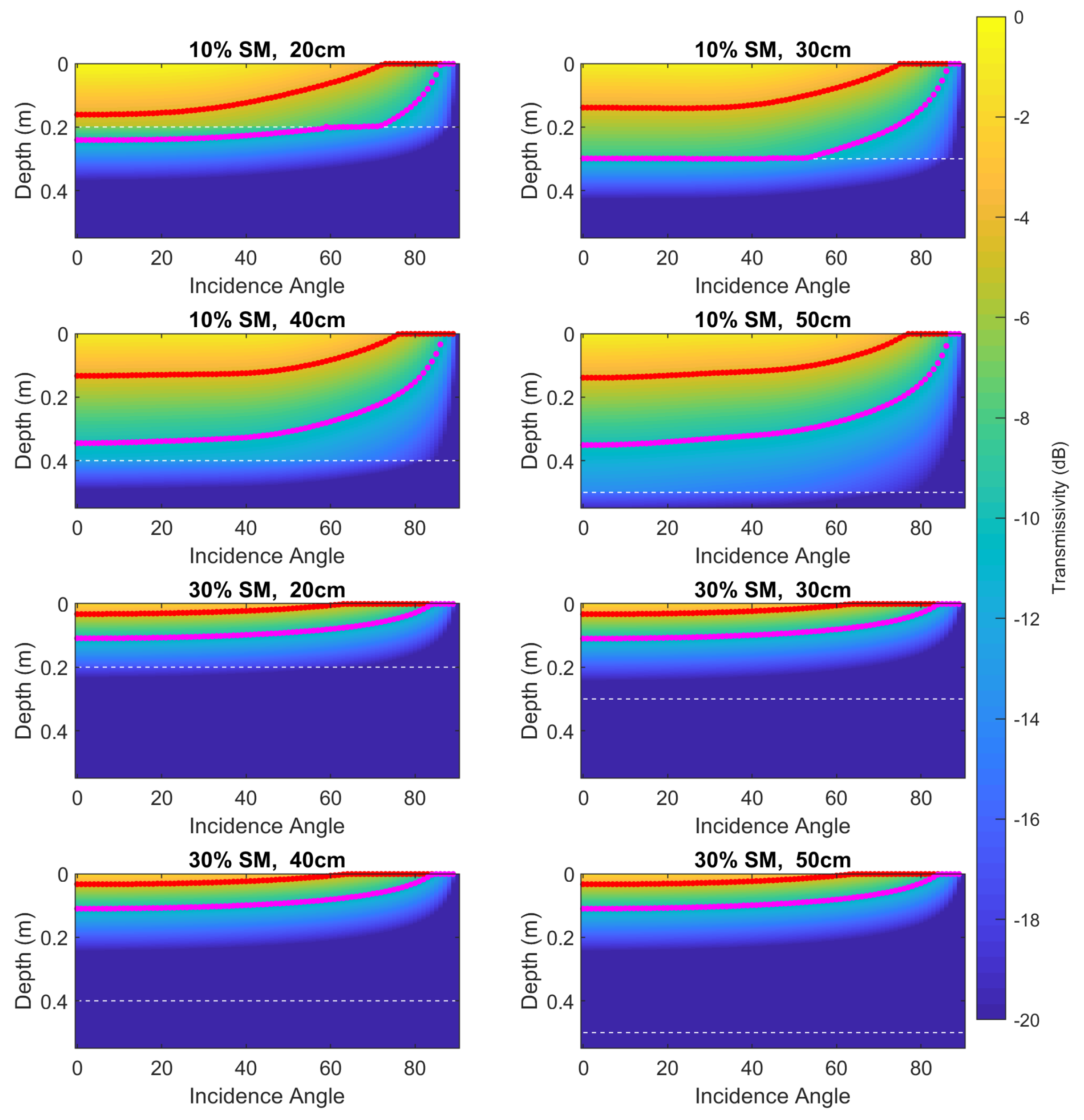
4.2.1. Saturation Depth of Descending Slab
4.2.2. Frequency and Angle Response of Dual Slab Configurations
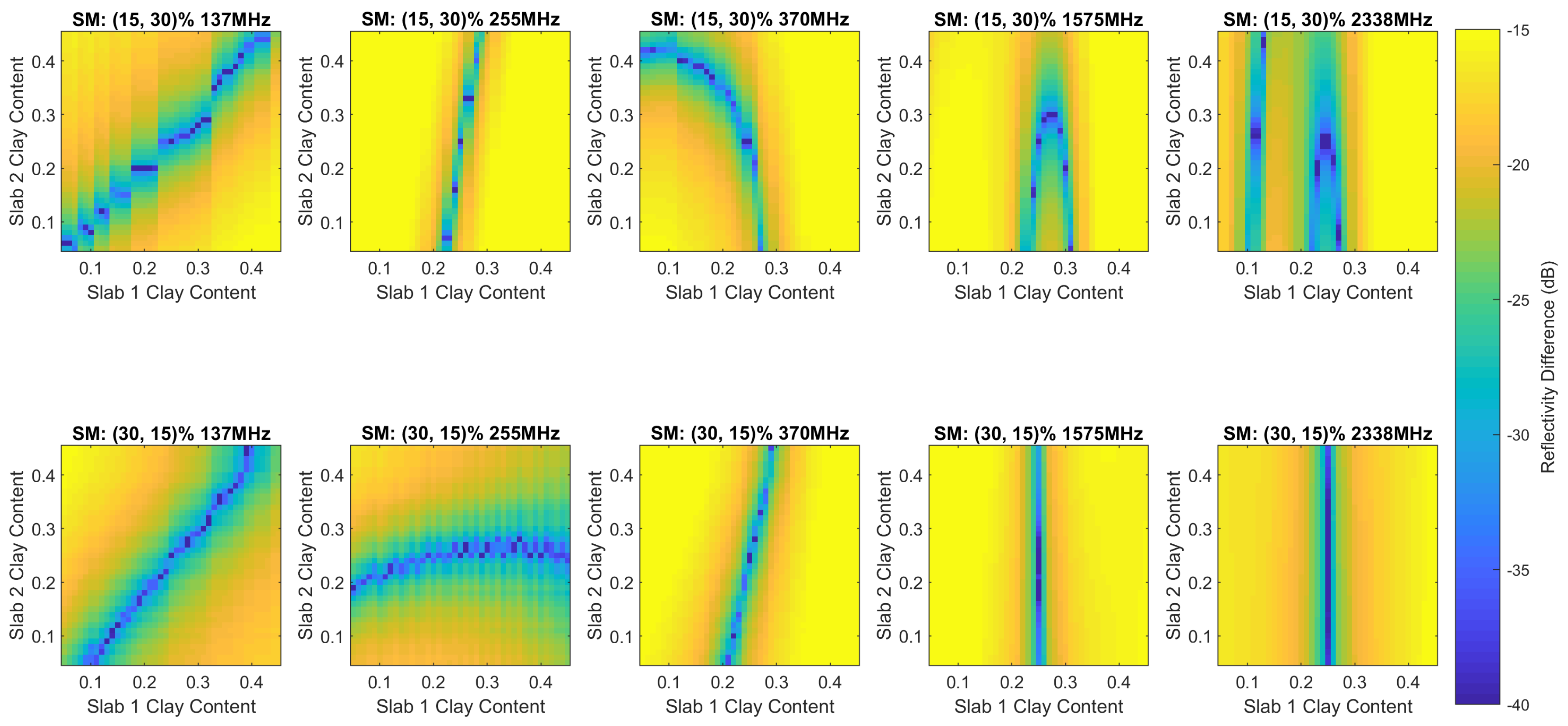
4.2.3. Clay Content Response to Dual Slab Configurations
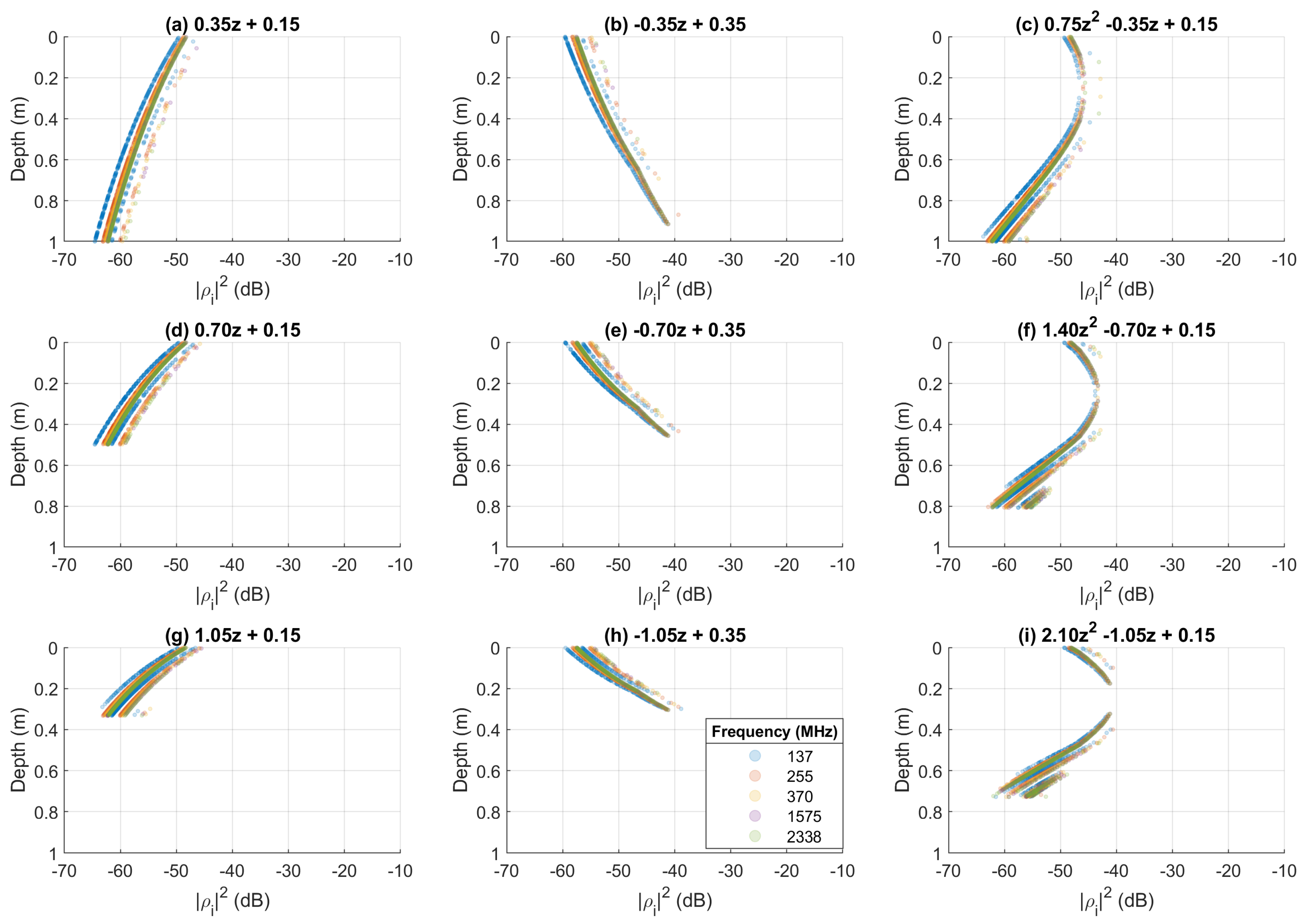
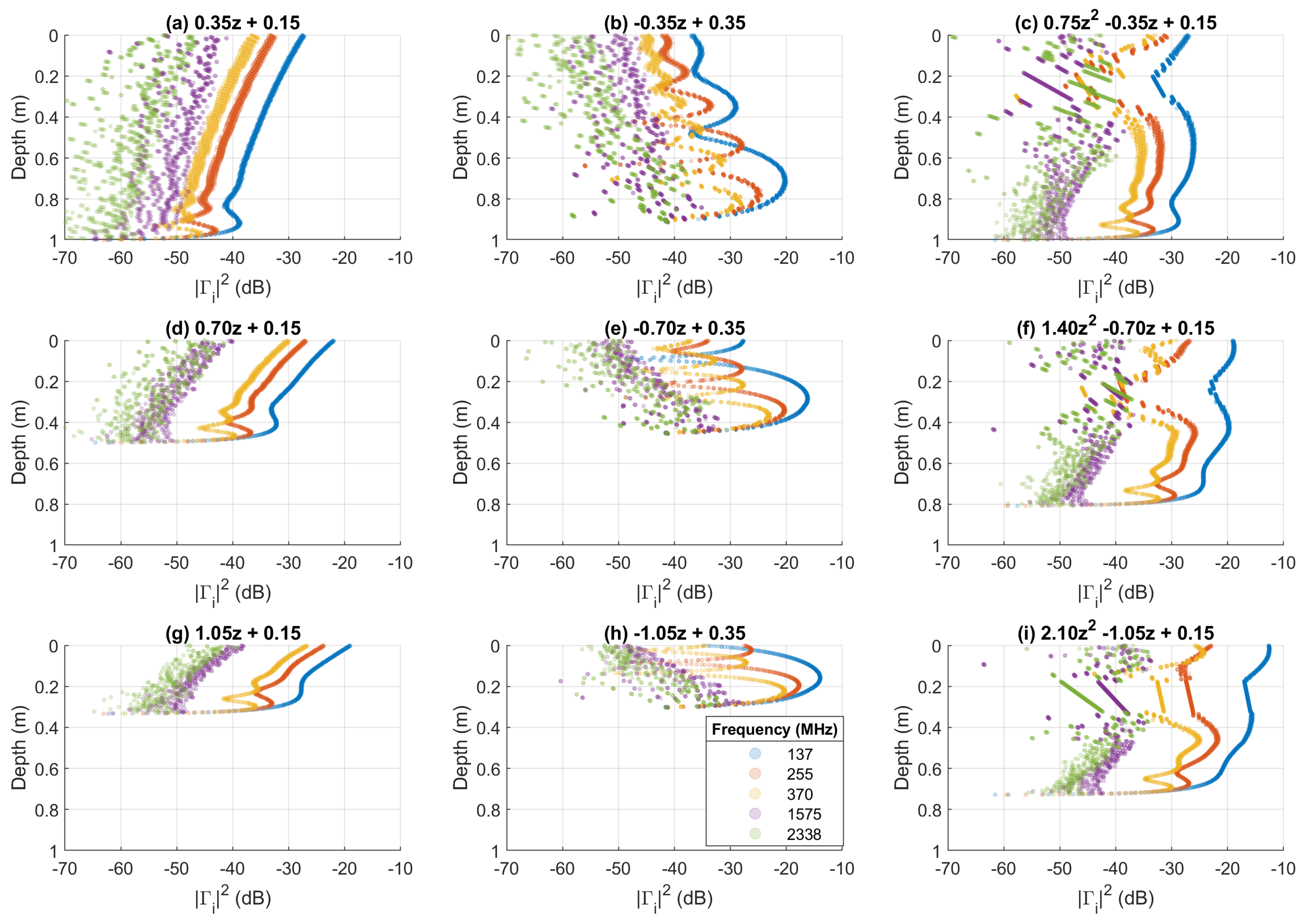
4.3. Arbitrary Profile
5. Discussion
6. Summary and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Gleason, S. Remote Sensing of Ocean, Ice and Land Surfaces Using Bistatically Scattered GNSS Signals from Low Earth Orbit. Ph.D. Thesis, University of Surrey, Guildford, UK, 2006. [Google Scholar] [CrossRef]
- Jales, P. Spaceborne Receiver Design for Scatterometric GNSS Reflectometry. Ph.D. Thesis, University of Surrey, Guildford, UK, 2012. [Google Scholar]
- Ruf, C.S.; Gleason, S.; Jelenak, Z.; Katzberg, S.; Ridley, A.; Rose, R.; Scherrer, J.; Zavorotny, V. The CYGNSS nanosatellite constellation hurricane mission. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; pp. 214–216. [Google Scholar] [CrossRef]
- Chew, C.C.; Small, E.E. Soil Moisture Sensing Using Spaceborne GNSS Reflections: Comparison of CYGNSS Reflectivity to SMAP Soil Moisture. Geophys. Res. Lett. 2018, 45, 4049–4057. [Google Scholar] [CrossRef]
- Clarizia, M.P.; Pierdicca, N.; Costantini, F.; Floury, N. Analysis of CYGNSS data for soil moisture retrieval. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 2227–2235. [Google Scholar] [CrossRef]
- Eroglu, O.; Kurum, M.; Boyd, D.; Gurbuz, A.C. High Spatio-Temporal Resolution CYGNSS Soil Moisture Estimates Using Artificial Neural Networks. Remote Sens. 2019, 11, 2272. [Google Scholar] [CrossRef]
- Garrison, J.; Piepmeier, J.; Shah, R.; Vega, M.; Spencer, D.; Banting, R.; Firman, C.; Nold, B.; Larsen, K.; Bindlish, R. SNOOPI: A Technology Validation Mission for P-band Reflectometry using Signals of Opportunity. In Proceedings of the IGARSS 2019—2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 5082–5085. [Google Scholar]
- Chew, C.C.; Small, E.E.; Larson, K.M.; Zavorotny, V.U. Effects of near-surface soil moisture on GPS SNR data: Development of a retrieval algorithm for soil moisture. IEEE Trans. Geosci. Remote Sens. 2014, 52, 537–543. [Google Scholar] [CrossRef]
- Pierdicca, N.; Guerriero, L.; Egido, A.; Paloscia, S.; Floury, N. Exploiting GNSS signals for soil moisture and vegetation biomass retrieval. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 5119–5122. [Google Scholar] [CrossRef]
- Knuble, J.; Piepmeier, J.; Deshpande, M.; Toit, C.D.; Garrison, J.; Lin, Y.C.; Stienne, G.; Katzberg, S.; Alikakos, G. Airborne P-band Signal of Opportunity (SoOP) demonstrator instrument; Status update. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 5638–5641. [Google Scholar] [CrossRef]
- Garrison, J.; Lin, Y.C.; Nold, B.; Piepmeier, J.R.; Vega, M.A.; Fritts, M.; Toit, C.F.; Knuble, J. Remote sensing of soil moisture using P-band signals of opportunity (SoOp): Initial results. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 4158–4161. [Google Scholar] [CrossRef]
- Garrison, J.L.; Kurum, M.; Nold, B.; Piepmeier, J.; Vega, M.A.; Bindlish, R.; Pignotti, G.; Lafayette, W. Remote Sensing of Root-Zone Soil Moisture Using I- and P-band Signals of Opportunity: Instrument Validation Studies. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 8305–8308. [Google Scholar]
- Yueh, S.; Shah, R.; Xu, X.; Elder, K.; Starr, B. Experimental Demonstration of Soil Moisture Remote Sensing Using P-Band Satellite Signals of Opportunity. IEEE Geosci. Remote Sens. Lett. 2019, 17, 207–211. [Google Scholar] [CrossRef]
- Ulaby, F.T.; Long, D.G. Microwave Radar and Radiometric Remote Sensing, 1st ed.; University of Michigan Press: Ann Arbor, MI, USA, 2014. [Google Scholar] [CrossRef]
- Kurum, M.; Deshpande, M.; Joseph, A.T.; O’Neill, P.E.; Lang, R.H.; Eroglu, O. SCoBi-Veg: A generalized bistatic scattering model of reflectometry from vegetation for signals of opportunity applications. IEEE Trans. Geosci. Remote Sens. 2018, 57, 1049–1068. [Google Scholar] [CrossRef]
- Eroglu, O.; Boyd, D.R.; Kurum, M. The Signals of Opportunity Coherent Bistatic Scattering Simulator: A Free, Open Source Simulator Framework. IEEE Geosci. Remote Sens. Mag. 2020. [Google Scholar] [CrossRef]
- Ulaby, F.; Moore, R.; Fung, A. Microwave Remote Sensing: Microwave Remote Sensing Fundamentals and Radiometry; Artech House: London, UK, 1981. [Google Scholar]
- Orfanidis, S. Waves and Antennas Electromagnetic, 2nd ed.; 2016; p. 1413. Available online: http://eceweb1.rutgers.edu/~orfanidi/ewa/ (accessed on 21 October 2020).
- Lang, R.H.; Sighu, J.S. Electromagnetic backscattering from a layer of vegetation: A discrete approach. IEEE Trans. Geosci. Remote. Sens. 1983, GE-21, 62–71. [Google Scholar] [CrossRef]
- Eroglu, O.; Boyd, D.R.; Kurum, M. SCoBi User’s Manual; 2018; Available online: https://github.com/impresslab/SCoBi/tree/master/docs/manuals (accessed on 21 October 2020).
- Ulaby, F.; Moore, R.; Fung, A. Microwave Remote Sensing: Active and Passive. Volume 2—Radar Remote Sensing and Surface Scattering and Emission Theory; Addison-Wesley Publishing: Boston, MA, USA, 1982. [Google Scholar]
- Bruckler, L.; Witono, H.; Stengel, P. Near surface soil moisture estimation from microwave measurements. Remote Sens. Environ. 1988, 26, 101–121. [Google Scholar] [CrossRef]
- Boisvert, J.; Gwyn, Q.; Brisco, B.; Major, D.; Brown, R. Evaluation of soil moisture estimation techniques and microwave penetration depth for radar applications. Can. J. Remote Sens. 1995, 21, 110–123. [Google Scholar] [CrossRef]
- Wang, J.R.; Schmugge, T.J. An empirical model for the complex dielectric permittivity of soils as a function of water content. IEEE Trans. Geosci. Remote Sens. 1980, GE-18, 288–295. [Google Scholar] [CrossRef]
- Dobson, M.C.; Ulaby, F.F.; Hallikainen, M.T.; El-Rayes, M.A. Microwave dielectric behavior of wet soil—Part II: Dielectric mixing models. IEEE Trans. Geosci. Remote Sens. 1985, 23, 35–46. [Google Scholar] [CrossRef]
- Peplinski, N.R.; Ulaby, F.T.; Dobson, M.C. Dielectric properties of soils in the 0.3–1.3-GHz range. IEEE Trans. Geosci. Remote Sens. 1995, 33, 1340. [Google Scholar] [CrossRef]
- Mironov, V.L.; Fomin, S.V. Temperature and Mineralogy Dependable Model for Microwave Dielectric Spectra of Moist Soils. PIERS Online 2009, 5, 411–415. [Google Scholar] [CrossRef]
- Mironov, V.L.; De Roo, R.D.; Savin, I.V. Temperature-dependable microwave dielectric model for an arctic soil. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2544–2556. [Google Scholar] [CrossRef]
- Yayong, S.; Jianwei, M.; Jie, P.; Shifeng, H.; Kun, Y.; Peng, Z.; He, Z. Preliminary Applicability Analysis of Soil Dielectric Constant Model of the Different Soil Texture Condition. In Proceedings of the IGARSS 2019—2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 7148–7151. [Google Scholar]
- Mialon, A.; Richaume, P.; Leroux, D.; Bircher, S.; Bitar, A.A.; Pellarin, T.; Wigneron, J.P.; Kerr, Y.H. Comparison of Dobson and Mironov dielectric models in the SMOS soil moisture retrieval algorithm. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3084–3094. [Google Scholar] [CrossRef]
- Hosmer, D.W., Jr.; Lemeshow, S.; Sturdivant, R.X. Applied Logistic Regression; John Wiley & Sons: Hoboken, NJ, USA, 2013; Volume 398. [Google Scholar]
- Ulaby, F.T. Radar Measurement of Soil Moisture Content. IEEE Trans. Antennas Propag. 1974, 11, 257–265. [Google Scholar] [CrossRef]
- Champion, I.; Faivre, R. Sensitivity of the radar signal to soil moisture: Variation with incidence angle, frequency, and polarization. IEEE Trans. Geosci. Remote Sens. 1997, 35, 781–783. [Google Scholar] [CrossRef]
- Oh, Y. Radar measurement of soil moisture: From professor Fawwaz Ulaby’s pioneering works in the early 1970s to its current status. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; pp. 1258–1261. [Google Scholar] [CrossRef]
- Kurum, M.; Lang, R.H.; O’Neill, P.E.; Joseph, A.T.; Cosh, M.; Jackson, T. Forest canopy effects on the estimation of soil moisture at L-band. In Proceedings of the IGARSS 2008—2008 IEEE International Geoscience and Remote Sensing Symposium, Boston, MA, USA, 7–11 July 2008; Volume 1, pp. I-33–I-36. [Google Scholar] [CrossRef]
- Tabatabaeenejad, A.; Burgin, M.; Duan, X.; Moghaddam, M. P-band radar retrieval of subsurface soil moisture profile as a second-order polynomial: First AirMOSS results. IEEE Trans. Geosci. Remote Sens. 2015, 53, 645–658. [Google Scholar] [CrossRef]
- Sadeghi, M.; Tabatabaeenejad, A.; Tuller, M.; Moghaddam, M.; Jones, S.B. Advancing NASA’s AirMOSS P-band Radar Root-zone Soil Moisture Retrieval Algorithm via Incorporation of Richards’ Equation. Remote Sens. 2017, 9, 17. [Google Scholar] [CrossRef]
- Zribi, M.; Gorrab, A.; Baghdadi, N.; Lili-Chabaane, Z.; Mougenot, B. Influence of radar frequency on the relationship between bare surface soil moisture vertical profile and radar backscatter. IEEE Geosci. Remote Sens. Lett. 2014, 11, 848–852. [Google Scholar] [CrossRef]
- Boyd, D.R.; Kurum, M.; Eroglu, O.; Gurbuz, A.C.; Garrison, J.; Nold, B.; Piepmeier, J.; Vega, M.; Bindlish, R. Investigation of Root-Zone Soil Moisture Profile Sensitivity to Multiple Signals of Opportunity Sources. In Proceedings of the 2019 USNC-URSI National Radio Science Meeting, Boulder, CO, USA, 9–12 January 2019; p. 170. [Google Scholar]
- Park, H.; Camps, A.; Castellvi, J.; Muro, J. Generic Performance Simulator of Spaceborne GNSS-Reflectometer for Land Applications. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 3179–3191. [Google Scholar] [CrossRef]
- Dente, L.; Guerriero, L.; Comite, D.; Pierdicca, N. Space-Borne GNSS-R Signal over a Complex Topography: Modeling and Validation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 1218–1233. [Google Scholar] [CrossRef]
- Tabatabaeenejad, A.; Duan, X.; Moghaddam, M. Coherent scattering of electromagnetic waves from two-layer rough surfaces within the kirchhoff regime. IEEE Trans. Geosci. Remote Sens. 2013, 51, 3943–3953. [Google Scholar] [CrossRef]
- Duan, X.; Moghaddam, M. Bistatic vector 3-D scattering from layered rough surfaces using stabilized extended boundary condition method. IEEE Trans. Geosci. Remote Sens. 2013, 51, 2722–2733. [Google Scholar] [CrossRef]
- Kuo, C.H.; Moghaddam, M. Electromagnetic scattering from multilayer rough surfaces with arbitrary dielectric profiles for remote sensing of subsurface soil moisture. IEEE Antennas Propag. Soc. APS Int. Symp. 2007, 45, 4797–4800. [Google Scholar] [CrossRef]



| Depth (cm) | Soil Moisture | Sand Ratio | Clay Ratio | Soil Bulk Density (g/cm3) |
|---|---|---|---|---|
| 5 | 10% | 10% | 31% | 1.4 |
| 10 | 30% | 10% | 31% | 1.4 |
| 20 | 20% | 10% | 31% | 1.4 |
| 40 | 40% | 10% | 31% | 1.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Boyd, D.; Kurum, M.; Eroglu, O.; Gurbuz, A.C.; Garrison, J.L.; Nold, B.R.; Vega, M.A.; Piepmeier, J.R.; Bindlish, R. SCoBi Multilayer: A Signals of Opportunity Reflectometry Model for Multilayer Dielectric Reflections. Remote Sens. 2020, 12, 3480. https://doi.org/10.3390/rs12213480
Boyd D, Kurum M, Eroglu O, Gurbuz AC, Garrison JL, Nold BR, Vega MA, Piepmeier JR, Bindlish R. SCoBi Multilayer: A Signals of Opportunity Reflectometry Model for Multilayer Dielectric Reflections. Remote Sensing. 2020; 12(21):3480. https://doi.org/10.3390/rs12213480
Chicago/Turabian StyleBoyd, Dylan, Mehmet Kurum, Orhan Eroglu, Ali Cafer Gurbuz, James L. Garrison, Benjamin R. Nold, Manuel A. Vega, Jeffrey R. Piepmeier, and Rajat Bindlish. 2020. "SCoBi Multilayer: A Signals of Opportunity Reflectometry Model for Multilayer Dielectric Reflections" Remote Sensing 12, no. 21: 3480. https://doi.org/10.3390/rs12213480
APA StyleBoyd, D., Kurum, M., Eroglu, O., Gurbuz, A. C., Garrison, J. L., Nold, B. R., Vega, M. A., Piepmeier, J. R., & Bindlish, R. (2020). SCoBi Multilayer: A Signals of Opportunity Reflectometry Model for Multilayer Dielectric Reflections. Remote Sensing, 12(21), 3480. https://doi.org/10.3390/rs12213480







