A New Approach for Understanding Urban Microclimate by Integrating Complementary Predictors at Different Scales in Regression and Machine Learning Models
Abstract
1. Introduction
2. Materials and Methods
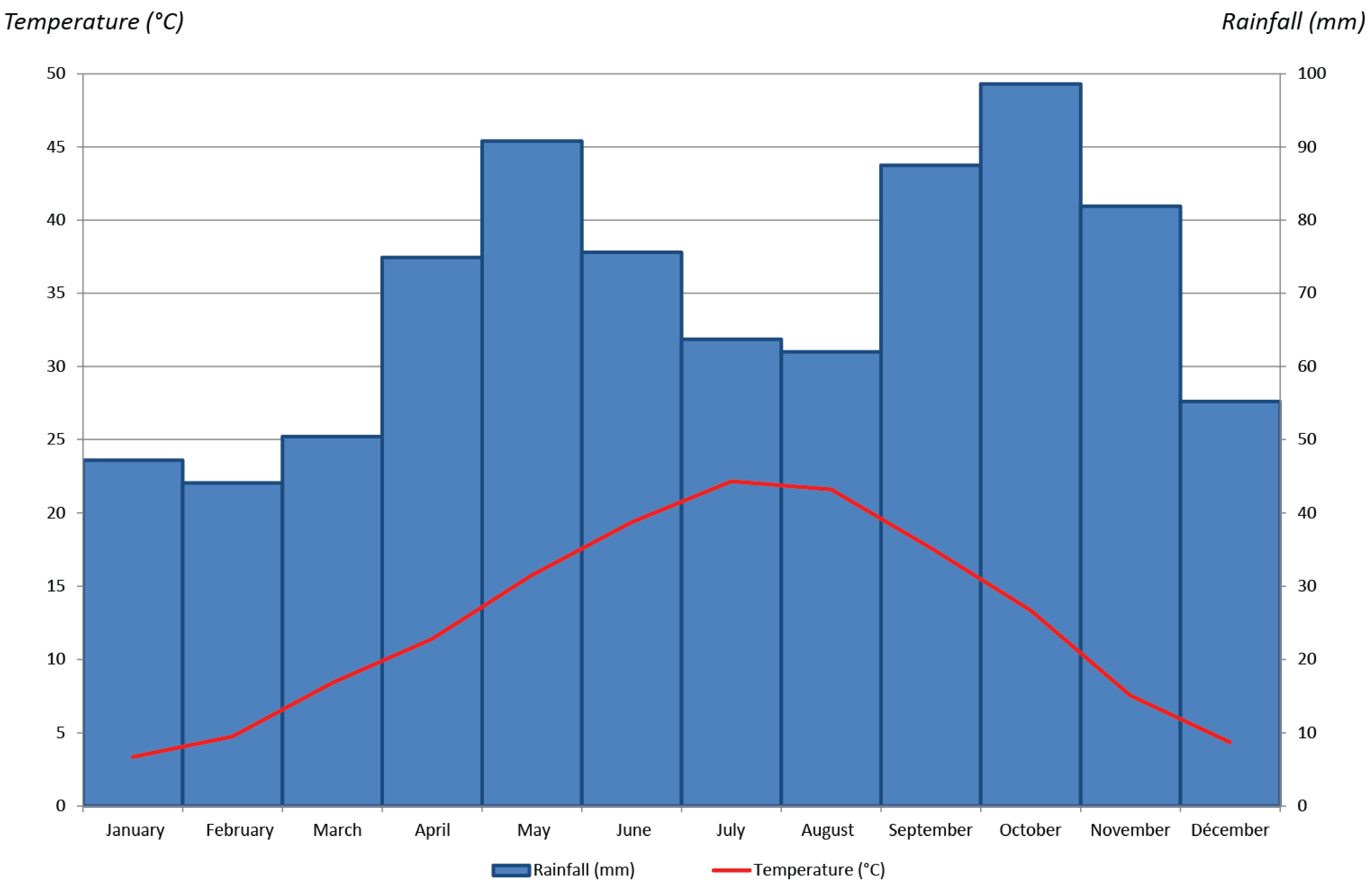
2.1. Lyon: A Study Area Characterized by a Considerable Urban Morphological Diversity
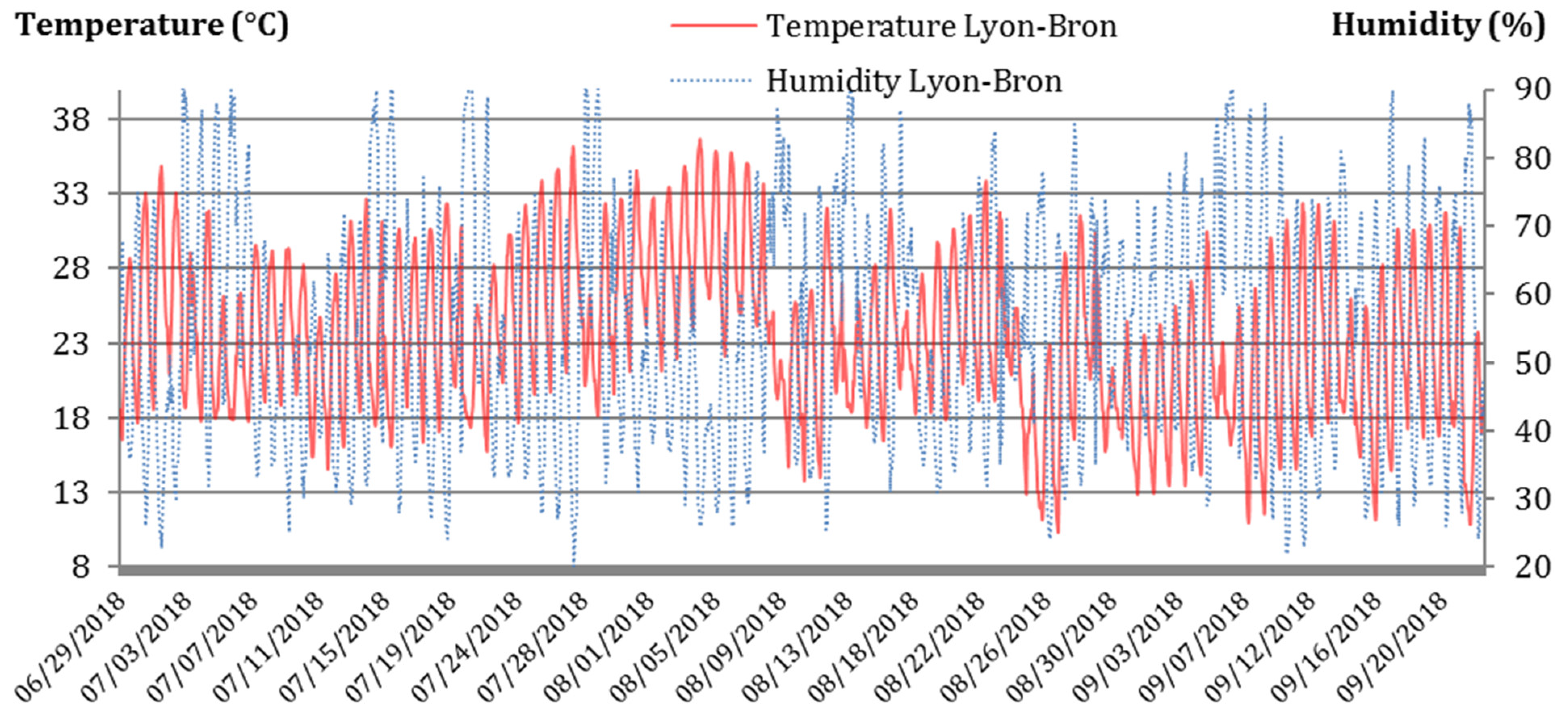
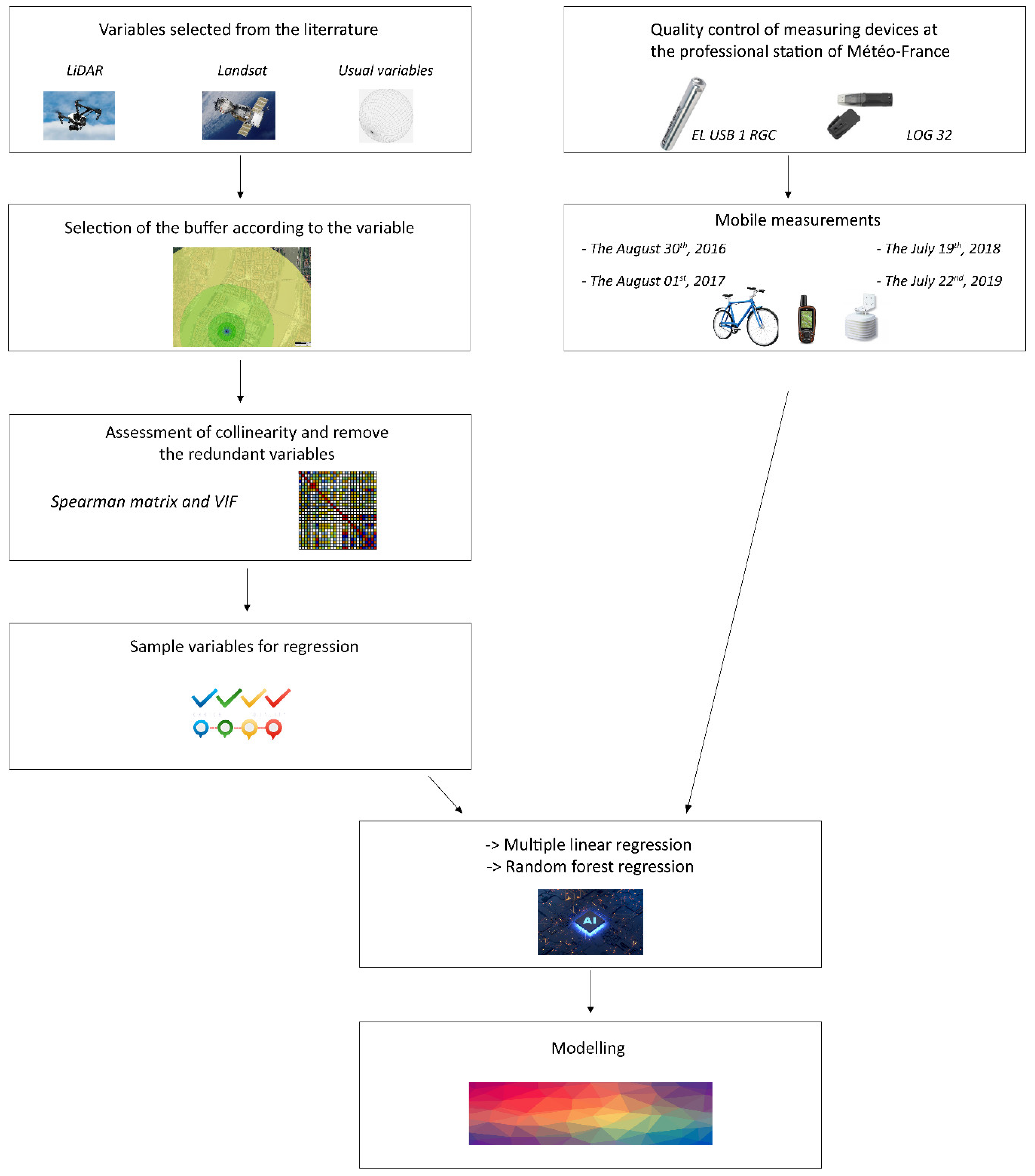
2.2. Data Acquired by the Measuring Instruments and Selected Days
2.3. Morphological Descriptors Relevant to Air Temperature Estimation
2.4. The Statistical Procedure Followed
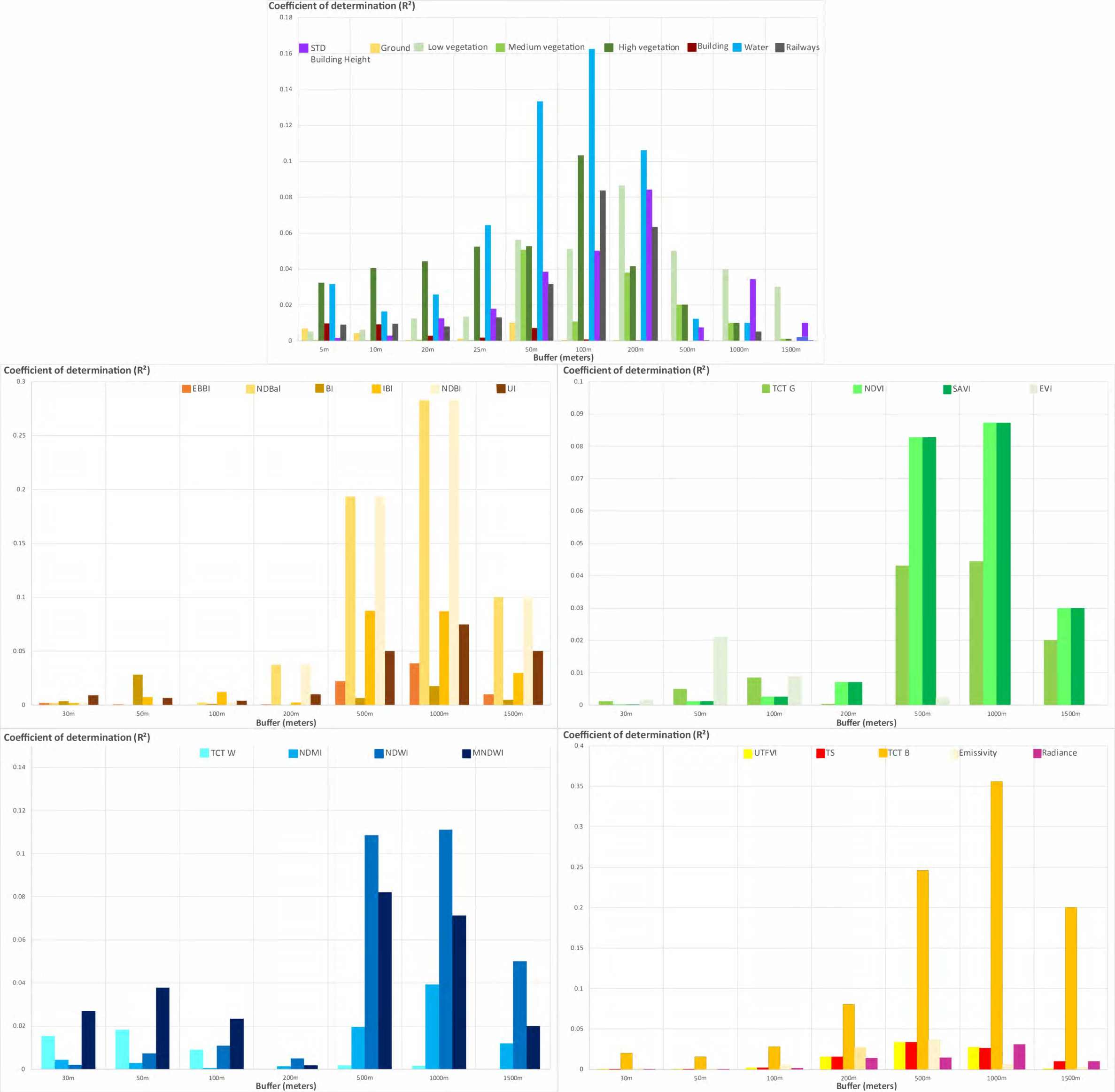
2.4.1. An Explanatory Buffer Zone, Which Varies According to the Indicator
2.4.2. Three Complementary Regression Methods in Modelling Use
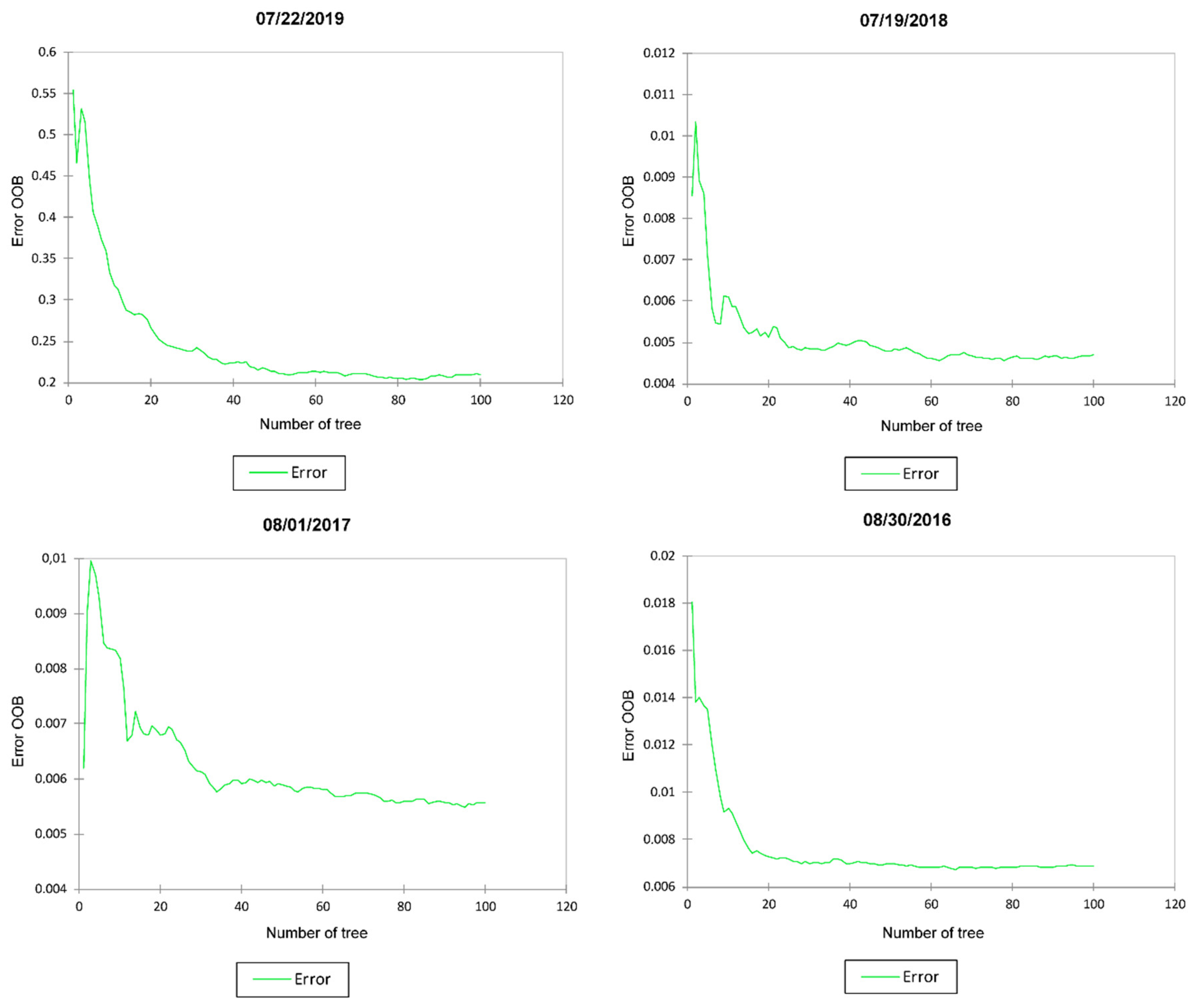
2.4.3. Quality Control on Modeling by Spatial Identification of Error Clusters
3. Results
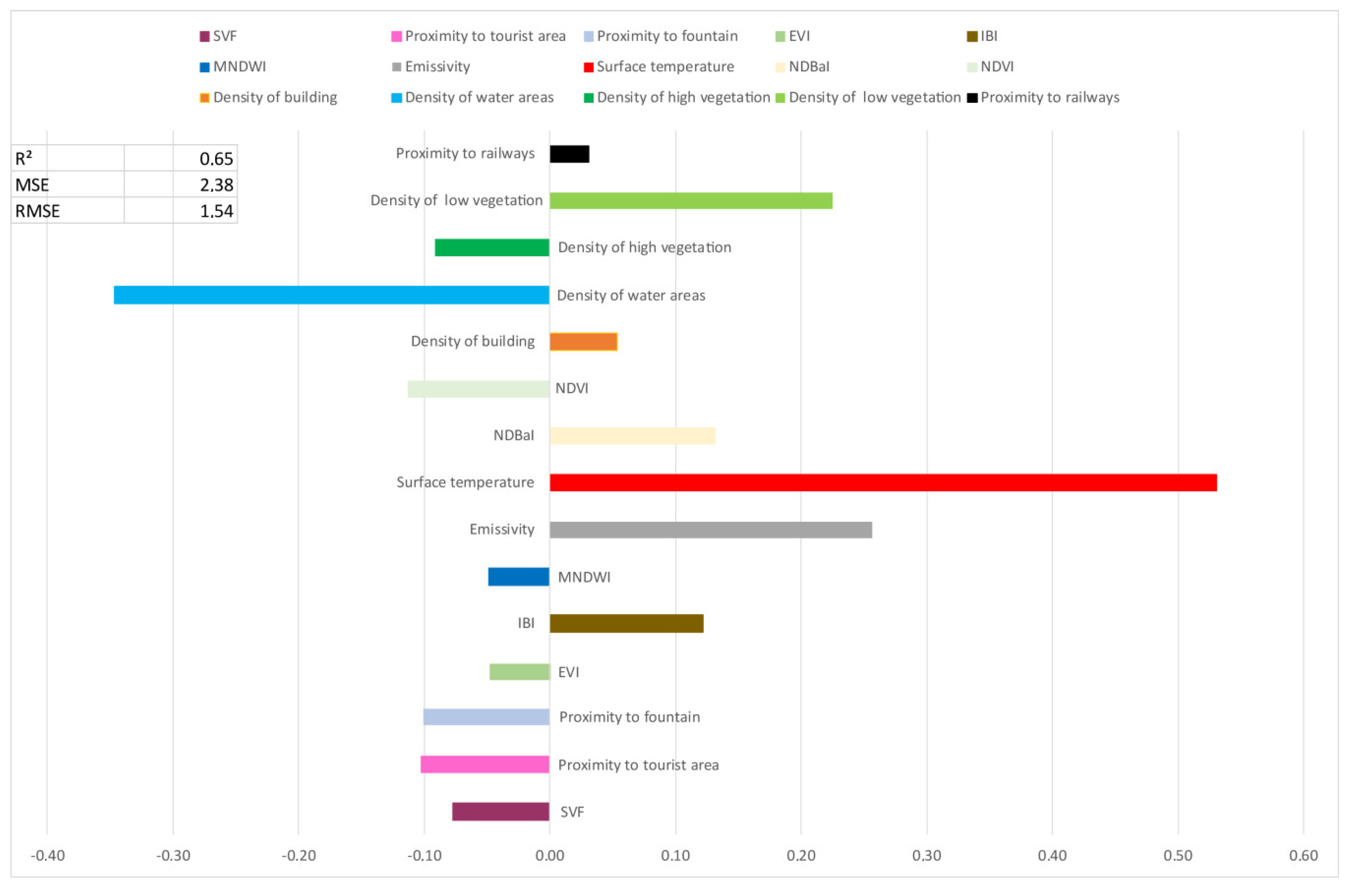
3.1. Multiple Linear Regression Modeling
3.2. Partial Least Square Regression Modeling
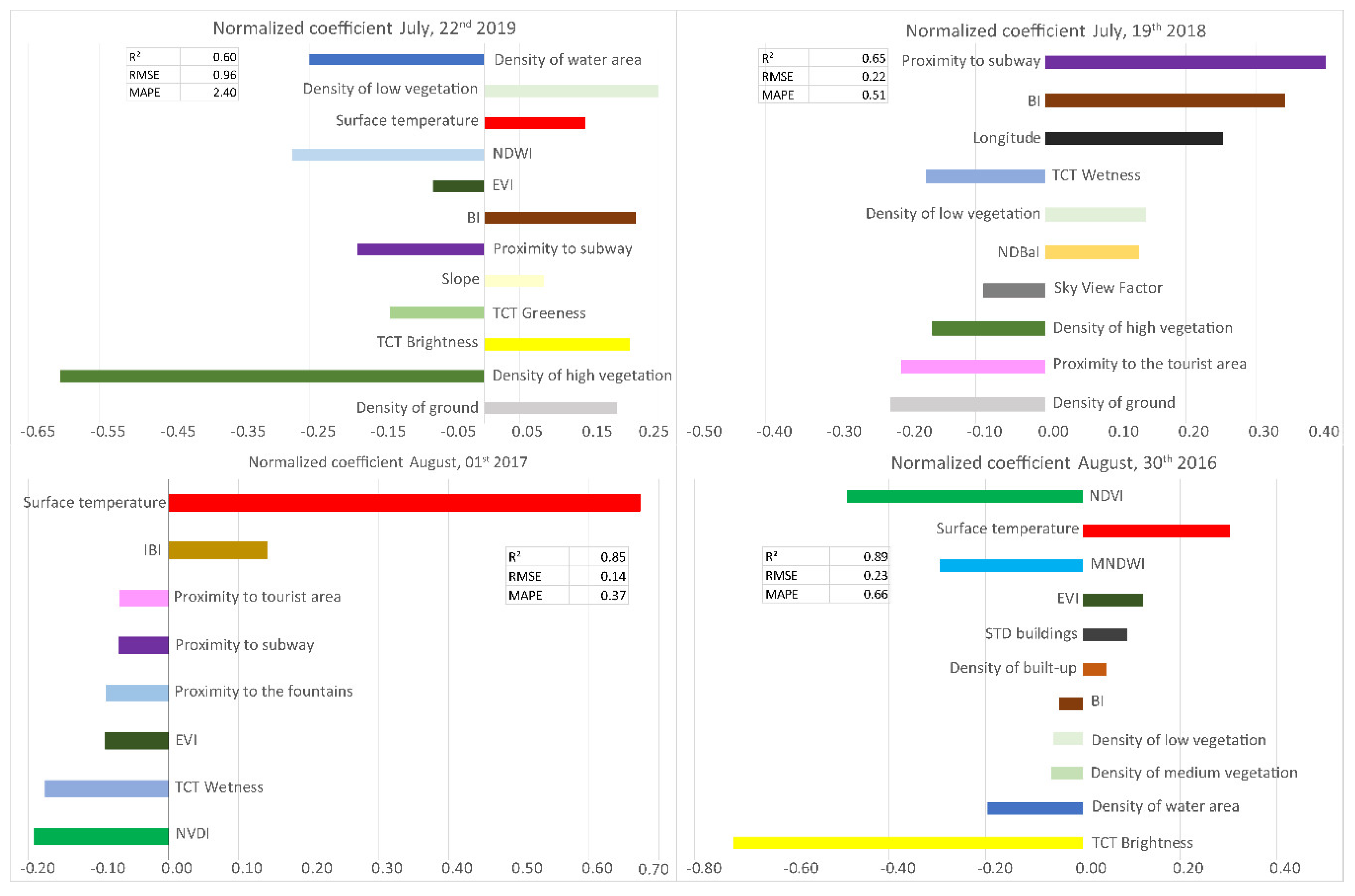
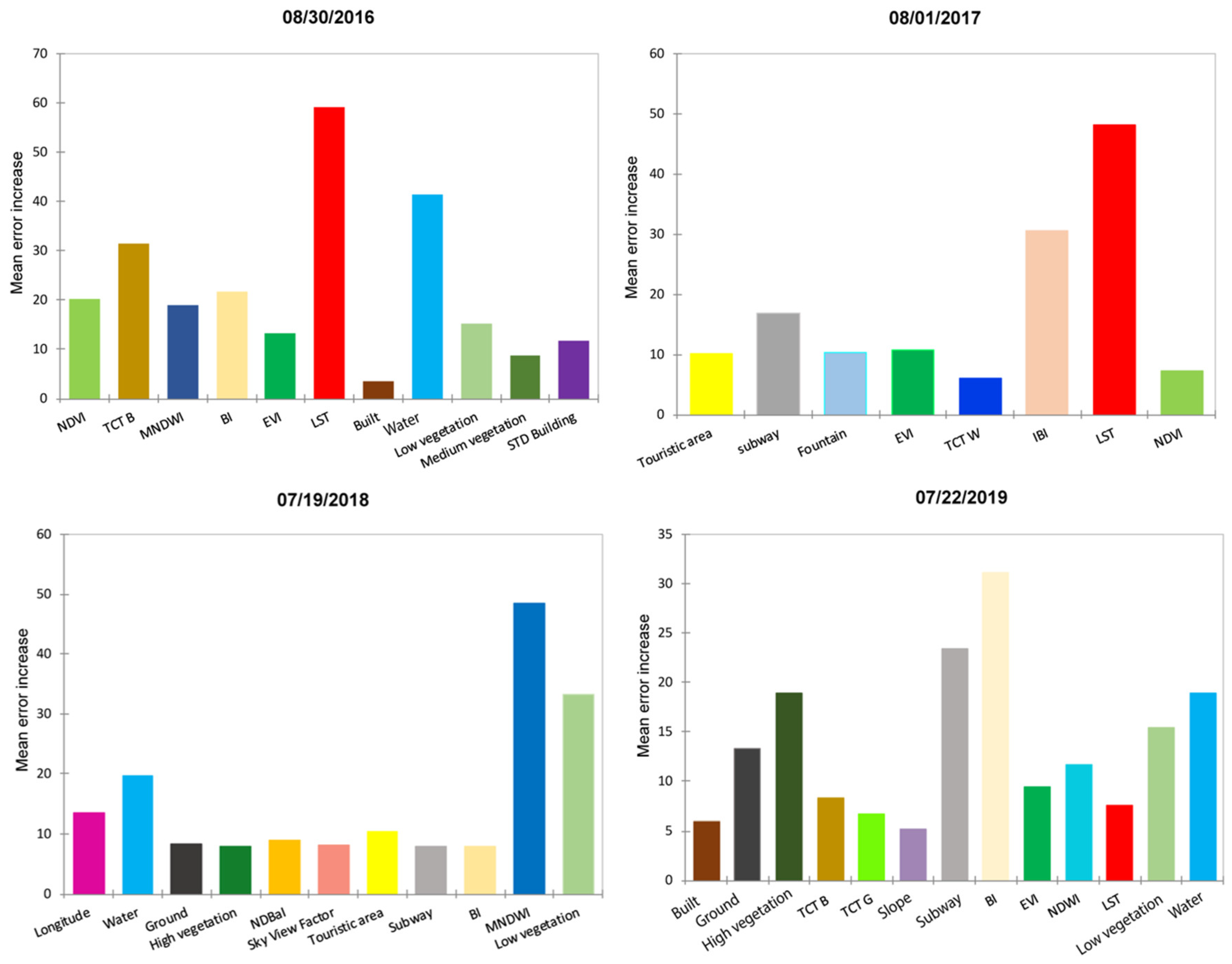
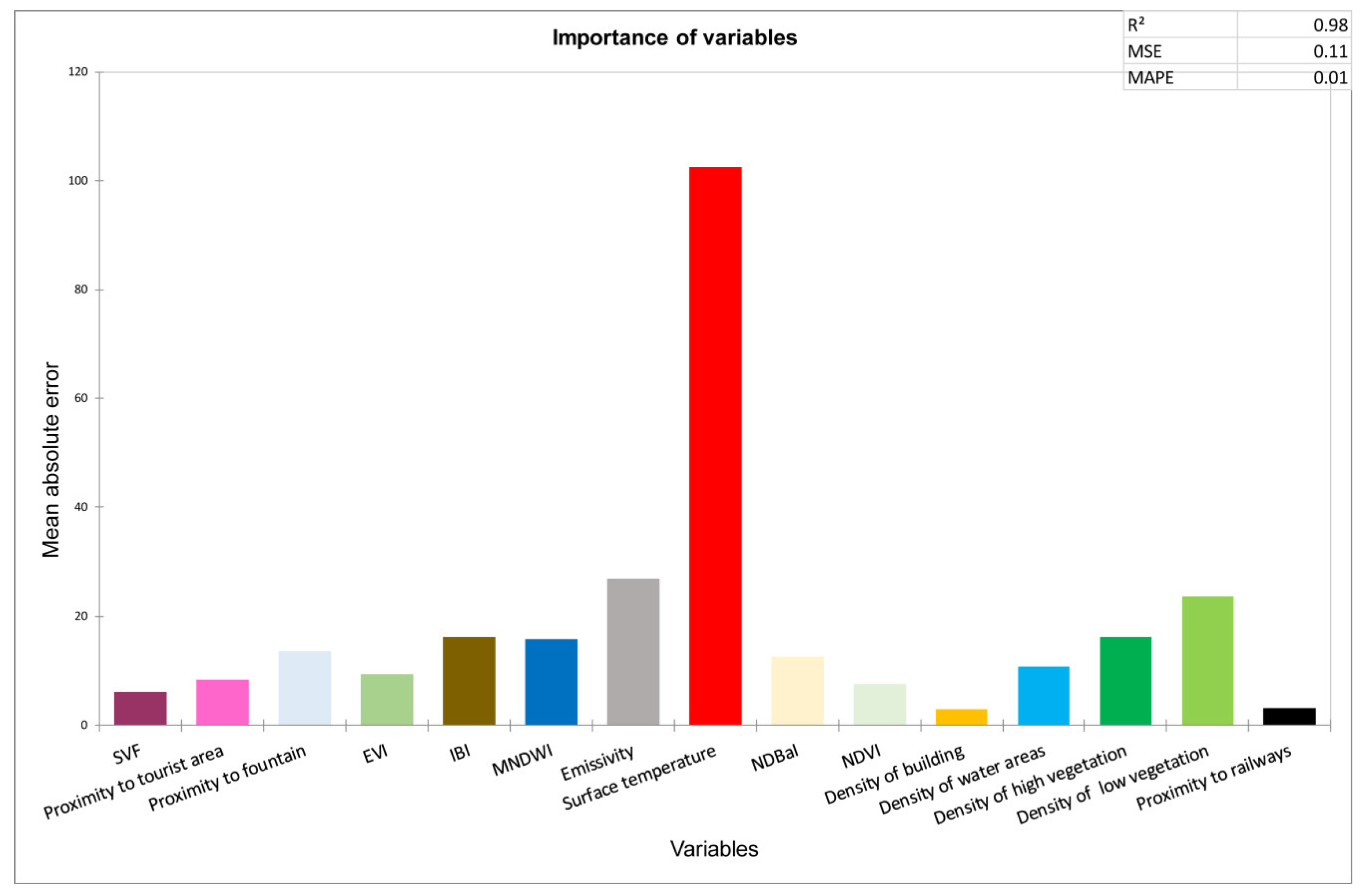
3.3. Random Forest Regression Modeling
4. Discussion
4.1. Implication of Important Predictors in Urban Air Temperature Modeling
4.2. Spatialization of Error
4.3. Grouping of Similar Errors
4.4. Limits and Future Research Outlooks
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Explanatory Variables Selected to Estimate Fine-Scale Air Temperature
| Data Category | Variables Used for the Input (Units) | Expected Effect of the Variable on the Model | Calculation Method | Reference |
| Climatic data from remote sensing | Surface temperature (°C) | Positive | Single channel algorithm | [49,89,121,122] |
| UTFVI Urban Thermal Field Variation Index) | Positive | [87,123] | ||
| Brightness temperatures (°C) | Positive | [124,125] | ||
| Vegetation index | NDVI Normalized Difference Vegetation Index | Negative | [85,126,127] | |
| SAVI Soil Adjusted Vegetation Index | Negative | [126] | ||
| EVI Enhanced Vegetation Index | Negative | [126] | ||
| Tasseled Cap greenness or GVI | Negative | [128] | ||
| Density of low vegetation | Positive | LasTool Software (LasTool: http://lastools.org/) Vegetation quantity according to different buffer size | [46,97] | |
| Density of medium vegetation | Negative | LasTool Software Vegetation quantity according to different buffer size | [46,97] | |
| Density of high vegetation | Negative | LasTool Software Vegetation quantity according to different buffer size | [110] | |
| Water presence index | NDWI Normalized Difference Water Index | Negative | [85,126] | |
| MNDWI Modified Normalized Difference Water Index | Negative | [126] | ||
| Moisture index | Tasseled Cap Wetness | Negative | [128] | |
| NDMI Normalized Difference Moisture Index | Negative | [86,88] | ||
| Bare soil index | NDBaI Normalized Difference Bareness Index | Positive | [85,126] | |
| BI Bare Soil Index | Positive | [126] | ||
| EBBI Enhanced Built-Up and Bareness Index | Positive | [126] | ||
| Building index | NDBI Normalized Difference Built-Up Index | Positive | [85,126] | |
| UI Urban Index | Positive | [126] | ||
| IBI Index-based Built-Up Index | Positive | [126] | ||
| Building density | Positive | LasTool Software Building quantity according to different buffer size | [46,97] | |
| Topographic | Slope (%) | Depending on the context | From the DEM (RVT 1.3 Software (RVT 1.3: https://iaps.zrc-sazu.si/en/rvt#v)) | [129,130] |
| Exposure (°N) | Depending on the context | From the DEM (RVT 1.3 Software) | [131] | |
| Curvature | Depending on the context | From the DEM (RVT 1.3 Software) | [132,133] | |
| Proximity to land occupations | Water area | Negative | Water area according to different buffer size | [134,135] |
| Distance to fountains | Negative | Euclidean distance to nearest fountain | ||
| Distance to subway entrances | Depending on the context | Euclidean distance to the nearest subway entrance | ||
| Distance to points of tourist interest | Negative | Euclidean distance to the nearest tourist point | ||
| Distance to railway tracks | Positive | Length of the railways according to different buffer size | ||
| Radiation index | Spectral Radiance | Negative | [136] | |
| Emissivity | Negative | [137] | ||
| Tasseled Cap Brightness | Positive | [128] | ||
| Urban morphology | Sky View Factor | Depending on the context | RVT 1.3 Software | [16,111,138] |
| Variation in building height | Negative | Standard deviation of the building height | [97,116,139] |
References
- GIEC. Rapport Spécial du GIEC Sur le Réchauffement Planétaire de 1.5 °C. Organisation Météorologique Mondiale. Available online: https://public.wmo.int/fr/ressources/bulletin/rapport-sp%C3%A9cial-du-giec-sur-le-r%C3%A9chauffement-plan%C3%A9taire-de-15-%C2%B0c (accessed on 6 January 2020).
- Oke, T.R. Canyon geometry and the nocturnal urban heat island: Comparison of scale model and field observations. J. Clim. 1981, 1, 237–254. [Google Scholar] [CrossRef]
- Weston, K.J. Boundary layer climates. Q. J. R. Meteorol. Soc. 1988, 114, 1568. [Google Scholar] [CrossRef]
- Oke, T. City size and the urban heat island. Atmos. Environ. 1973, 7, 769–779. [Google Scholar] [CrossRef]
- Comtois, P.; Oke, T.R. Boundary layer climates, londres, methuen, 372 p., 15, 5 × 23, 5 cm, $18, 95. Géo. Phys. Quat. 1978, 32, 290–291. [Google Scholar] [CrossRef][Green Version]
- Aram, F.; García, E.H.; Solgi, E.; Mansournia, S. Urban green space cooling effect in cities. Heliyon 2019, 5, e01339. [Google Scholar] [CrossRef]
- Buyadi, S.N.A.; Naim, W.; Mohd, W.; Misni, A. Quantifying green space cooling effects on the urban microclimate using remote sensing and GIS techniques. In Proceedings of the XXV International Federation of Surveyors, Kuala Lumpur, Malaysia, 16–21 June 2014. [Google Scholar]
- Lahme, E.; Bruse, M. Microclimatic Effects of a Small Urban Park in Densely Built-up Areas: Measurements and Model Simulations; ICUC5: Lodz, Poland, 2003; Volume 5. [Google Scholar]
- Oliveira, S.; Andrade, H.; Vaz, T. The cooling effect of green spaces as a contribution to the mitigation of urban heat: A case study in Lisbon. Build. Environ. 2011, 46, 2186–2194. [Google Scholar] [CrossRef]
- Robitu, M.; Musy, M.; Inard, C.; Groleau, D. Modeling the influence of vegetation and water pond on urban microclimate. Sol. Energy 2006, 80, 435–447. [Google Scholar] [CrossRef]
- Slater, G. The Cooling Ability of Urban Parks; University of Guelph: Guelph, ON, Canada, 2010; Available online: https://www.asla.org/2010studentawards/169.html (accessed on 16 July 2020).
- Spronken-Smith, R.A.; Oke, T.R.; Lowry, W.P. Advection and the surface energy balance across an irrigated urban park. Int. J. Climatol. 2000, 20, 1033–1047. [Google Scholar] [CrossRef]
- Yang, H.; Yang, K.; Miao, Y.; Wang, L.; Ye, C. Comparison of potential contribution of typical pavement materials to heat island effect. Sustainability 2020, 12, 4752. [Google Scholar] [CrossRef]
- Erell, E.; Williamson, T. Intra-urban differences in canopy layer air temperature at a mid-latitude city. Int. J. Clim. 2007, 27, 1243–1255. [Google Scholar] [CrossRef]
- Hodul, M.; Knudby, A.; Ho, H.C. Estimation of continuous urban sky view factor from landsat data using shadow detection. Remote Sens. 2016, 8, 568. [Google Scholar] [CrossRef]
- Svensson, M.K. Sky view factor analysis—Implications for urban air temperature differences. Meteorol. Appl. 2004, 11, 201–211. [Google Scholar] [CrossRef]
- Meng, C.; Dou, Y. Quantifying the anthropogenic footprint in Eastern China. Sci. Rep. 2016, 6, 24337. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Santamouris, M. Urban heat island and mitigation technologies in Asian and Australian Cities—impact and mitigation. Urban Sci. 2018, 2, 74. [Google Scholar] [CrossRef]
- Zhou, D.; Zhao, S.; Zhang, L.; Sun, G.; Liu, Y. The footprint of urban heat island effect in China. Sci. Rep. 2015, 5, 11160. [Google Scholar] [CrossRef]
- Ma, S.; Pitman, A.; Hart, M.; Evans, J.; Haghdadi, N.; MacGill, I. The impact of an urban canopy and anthropogenic heat fluxes on Sydney’s climate. Int. J. Clim. 2017, 37, 255–270. [Google Scholar] [CrossRef]
- United Nations. Climate Change Summit. Available online: https://www.un.org/en/climatechange/cities-pollution.shtml (accessed on 24 June 2020).
- Alonso, L.; Renard, F. A Comparative study of the physiological and socio-economic vulnerabilities to heat waves of the population of the metropolis of Lyon (France) in a climate change context. Int. J. Environ. Res. Public Heal. 2020, 17, 1004. [Google Scholar] [CrossRef]
- Dousset, B.; Gourmelon, F.; Laaidi, K.; Zeghnoun, A.; Giraudet, E.; Bretin, P.; Mauri, E.; Vandentorre, S. Satellite monitoring of summer heat waves in the Paris metropolitan area. Int. J. Clim. 2010, 31, 313–323. [Google Scholar] [CrossRef]
- Dousset, B.; Gourmelon, F. Satellite multi-sensor data analysis of urban surface temperatures and landcover. ISPRS J. Photogramm. Remote Sens. 2003, 58, 43–54. [Google Scholar] [CrossRef]
- Meehl, G.A. More intense, more frequent, and longer lasting heat waves in the 21st Century. Science 2004, 305, 994–997. [Google Scholar] [CrossRef]
- Fallmann, J.; Forkel, R.; Emeis, S. Secondary effects of urban heat island mitigation measures on air quality. Atmos. Environ. 2016, 125, 199–211. [Google Scholar] [CrossRef]
- Benas, N.; Chrysoulakis, N.; Cartalis, C. Trends of urban surface temperature and heat island characteristics in the Mediterranean. Theor. Appl. Clim. 2016, 130, 807–816. [Google Scholar] [CrossRef]
- Chapman, S.; Watson, J.; Salazar, Á.; Thatcher, M.; McAlpine, C.A. The impact of urbanization and climate change on urban temperatures: A systematic review. Landsc. Ecol. 2017, 32, 1921–1935. [Google Scholar] [CrossRef]
- Kukla, G.; Gavin, J.; Karl, T.R. Urban Warming. J. Clim. Appl. Meteorol. 1986, 25, 1265–1270. [Google Scholar] [CrossRef]
- Sun, Y.; Gao, C.; Li, J.; Wang, R.; Liu, J. Quantifying the effects of urban form on land surface temperature in subtropical high-density urban areas using machine learning. Remote Sens. 2019, 11, 959. [Google Scholar] [CrossRef]
- Wang, Y.; Ji, W.; Yu, X.; Xu, X.; Jiang, N.; Wang, Z.; Zhuang, D.-F. The impact of urbanization on the annual average temperature of the past 60 years in Beijing. Adv. Meteorol. 2014, 2014, 374987. [Google Scholar] [CrossRef]
- Bobb, J.F.; Peng, R.D.; Bell, M.L.; Dominici, F. Heat-related mortality and adaptation to heat in the United States. Environ. Heal. Perspect. 2014, 122, 811–816. [Google Scholar] [CrossRef]
- Renard, F.; Alonso, L.; Fitts, Y.; Hadjiosif, A.; Comby, J. Evaluation of the effect of urban redevelopment on surface Urban Heat Islands. Remote Sens. 2019, 11, 299. [Google Scholar] [CrossRef]
- Rosenfeld, A.; Romm, J.; Akbari, H.; Pomerantz, M.; Taha, H. Policies to Reduce Heat Islands: Magnitudes of Benefits and Incentives to Achieve Them; Lawrence Berkeley National Lab.: Berkeley, CA, USA, 1996. [Google Scholar]
- Akbari, H.; Pomerantz, M.; Taha, H. Cool surfaces and shade trees to reduce energy use and improve air quality in urban areas. Sol. Energy 2001, 70, 295–310. [Google Scholar] [CrossRef]
- Santamouris, M.; Cartalis, C.; Synnefa, A.; Kolokotsa, D. On the impact of urban heat island and global warming on the power demand and electricity consumption of buildings—A review. Energy Build. 2015, 98, 119–124. [Google Scholar] [CrossRef]
- Santamouris, M. On the energy impact of urban heat island and global warming on buildings. Energy Build. 2014, 82, 100–113. [Google Scholar] [CrossRef]
- Chen, M.; Ban-Weiss, G.A.; Sanders, K.T. The role of household level electricity data in improving estimates of the impacts of climate on building electricity use. Energy Build. 2018, 180, 146–158. [Google Scholar] [CrossRef]
- McPherson, E.G.; Nowak, D.; Heisler, G.; Grimmond, C.S.B.; Souch, C.; Grant, R.; Rowntree, R. Quantifying urban forest structure, function, and value: The Chicago Urban Forest Climate Project. Urban Ecosyst. 1997, 1, 49–61. [Google Scholar] [CrossRef]
- Cristóbal, J.; Ninyerola, M.; Pons, X. Modeling air temperature through a combination of remote sensing and GIS data. J. Geophys. Res. Space Phys. 2008, 113. [Google Scholar] [CrossRef]
- Kustas, W.P.; Norman, J.M. Use of remote sensing for evapotranspiration monitoring over land surfaces. Hydrol. Sci. J. 1996, 41, 495–516. [Google Scholar] [CrossRef]
- Alonso, L.; Renard, F. Integrating satellite-derived data as spatial predictors in multiple regression models to enhance the knowledge of air temperature patterns. Urban Sci. 2019, 3, 101. [Google Scholar] [CrossRef]
- De Ridder, K.; Maiheu, B.; Lauwaet, D.; Daglis, I.A.; Keramitsoglou, I.; Kourtidis, K.; Manunta, P.; Paganini, M. Urban Heat Island Intensification during Hot Spells—The Case of Paris during the Summer of 2003. Urban Sci. 2017, 1, 3. [Google Scholar] [CrossRef]
- Leconte, F.; Bouyer, J.; Claverie, R.; Pétrissans, M. Analysis of nocturnal air temperature in districts using mobile measurements and a cooling indicator. Theor. Appl. Clim. 2016, 130, 365–376. [Google Scholar] [CrossRef]
- Journal officiel du Sénat. Fermetures de Stations Météo-France et Avenir du Service Public Météorologique Français—Sénat. Available online: https://www.senat.fr/questions/base/2011/qSEQ110317685.html (accessed on 25 April 2019).
- Foissard, X.; Dubreuil, V.; Quénol, H. Defining scales of the land use effect to map the urban heat island in a mid-size European city: Rennes (France). Urban Clim. 2019, 29, 100490. [Google Scholar] [CrossRef]
- Richard, Y.; Emery, J.; Dudek, J.; Pergaud, J.; Chateau-Smith, C.; Zito, S.; Rega, M.; Vairet, T.; Castel, T.; Thévenin, T.; et al. How relevant are local climate zones and urban climate zones for urban climate research? Dijon (France) as a case study. Urban Clim. 2018, 26, 258–274. [Google Scholar] [CrossRef]
- Nichol, J.E.; To, P.H. Temporal characteristics of thermal satellite images for urban heat stress and heat island mapping. ISPRS J. Photogramm. Remote Sens. 2012, 74, 153–162. [Google Scholar] [CrossRef]
- Tsin, P.K.; Knudby, A.; Krayenhoff, E.S.; Ho, H.C.; Brauer, M.; Henderson, S.B. Microscale mobile monitoring of urban air temperature. Urban Clim. 2016, 18, 58–72. [Google Scholar] [CrossRef]
- Mira, M.; Ninyerola, M.; Batalla, M.; Pesquer, L.; Pons, X. Improving mean minimum and maximum month-to-month air temperature surfaces using satellite-derived land surface temperature. Remote Sens. 2017, 9, 1313. [Google Scholar] [CrossRef]
- Boer, E.P.J.; de Beurs, K.M.; Hartkamp, A.D. Kriging and thin plate splines for mapping climate variables. Int. J. Appl. Earth Obs. GeoInf. 2001, 3, 146–154. [Google Scholar] [CrossRef]
- Jarvis, C.H.; Stuart, N. A Comparison among strategies for interpolating maximum and minimum daily air temperatures. Part II: The interaction between number of guiding variables and the type of interpolation method. J. Appl. Meteorol. 2001, 40, 1075–1084. [Google Scholar] [CrossRef]
- Antonić, O.; Križan, J.; Marki, A.; Bukovec, D. Spatio-temporal interpolation of climatic variables over large region of complex terrain using neural networks. Ecol. Model. 2001, 138, 255–263. [Google Scholar] [CrossRef]
- Wang, M.; He, G.; Zhang, Z.; Wang, G.; Zhang, Z.; Cao, X.; Wu, Z.; Liu, X. Comparison of spatial interpolation and regression analysis models for an estimation of monthly near surface air temperature in China. Remote Sens. 2017, 9, 1278. [Google Scholar] [CrossRef]
- Zhang, Z.; Du, Q. A bayesian kriging regression method to estimate air temperature using remote sensing data. Remote Sens. 2019, 11, 767. [Google Scholar] [CrossRef]
- Chen, Y.; Quan, J.; Zhan, W.; Guo, Z. Enhanced statistical estimation of air temperature incorporating nighttime light data. Remote Sens. 2016, 8, 656. [Google Scholar] [CrossRef]
- Cristóbal, J.; Ninyerola, M.; Pons, X.; Pla, M. Improving air temperature modelization by means of remote sensing variables. In Proceedings of the 2006 IEEE International Symposium on Geoscience and Remote Sensing, Denver, CO, USA, 31 July–4 August 2006; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2006; Volume 2006, pp. 2251–2254. [Google Scholar]
- Hengl, T.; Heuvelink, G.B.; Tadić, M.P.; Pebesma, E. Spatio-temporal prediction of daily temperatures using time-series of MODIS LST images. Theor. Appl. Clim. 2011, 107, 265–277. [Google Scholar] [CrossRef]
- Zhu, W.; Lű, A.; Jia, S. Estimation of daily maximum and minimum air temperature using MODIS land surface temperature products. Remote Sens. Environ. 2013, 130, 62–73. [Google Scholar] [CrossRef]
- Lhotellier, R. Spatialisation de la température minimale de l’air à échelle quotidienne sur quatre départements alpins français. Climatologie 2006, 3, 55–69. [Google Scholar] [CrossRef][Green Version]
- Zhou, B.; Erell, E.; Hough, I.; Shtein, A.; Just, A.C.; Novack, V.; Rosenblatt, J.; Kloog, I. Estimation of hourly near surface air temperature across israel using an ensemble model. Remote Sens. 2020, 12, 1741. [Google Scholar] [CrossRef]
- Van Der Schriek, T.; Varotsos, K.V.; Giannakopoulos, C.; Founda, D. projected future temporal trends of two different urban heat islands in Athens (Greece) under three climate change scenarios: A statistical approach. Atmosphere 2020, 11, 637. [Google Scholar] [CrossRef]
- Voelkel, J.; Shandas, V.; Haggerty, B. Developing high-resolution descriptions of urban heat islands: A public health imperative. Prev. Chronic Dis. 2016, 13. [Google Scholar] [CrossRef] [PubMed]
- Leconte, F. Caractérisation des Îlots de Chaleur Urbain par Zonage Climatique et Mesures Mobiles: Cas de Nancy. Available online: http://www.theses.fr/2014LORR0255 (accessed on 24 June 2020).
- Taha, H.; Levinson, R.; Mohegh, A.; Gilbert, H.; Ban-Weiss, G.A.; Chen, S. Air-temperature response to neighborhood-scale variations in albedo and canopy cover in the real world: Fine-resolution meteorological modeling and mobile temperature observations in the los angeles climate archipelago. Climate 2018, 6, 53. [Google Scholar] [CrossRef]
- Fung, W.Y.; Lam, K.S.; Nichol, J.; Wong, M.S. Derivation of nighttime urban air temperatures using a satellite thermal image. J. Appl. Meteorol. Clim. 2009, 48, 863–872. [Google Scholar] [CrossRef]
- Dobrovolný, P.; Krahula, L. The spatial variability of air temperature and nocturnal urban heat island intensity in the city of Brno, Czech Republic. Morav. Geogr. Rep. 2015, 23, 8–16. [Google Scholar] [CrossRef]
- Charfi, S. Le Comportement Spatio-Temporel de la Température Dans L’agglomération de Tunis. Available online: http://www.theses.fr/2012NICE2036 (accessed on 24 June 2020).
- Charfi, S.; Dahech, S. Cartographie des Températures à Tunis par Modélisation Statistique et Télédétection. Mappemonde 2018, 123, 19–30. [Google Scholar] [CrossRef]
- Dahech, S. Evolution de la répartition spatiale des températures de l’air et de surface dans l’agglomération de Sfax entre 1987 et Impact sur la consommation d’énergie en été. (Evolution of the spatial distribution of air and surface temperatures in the agglomeration of Sfax between 1987 and 2010. Impact on energy consumption in summer). Climatologie 2012, 11–32. [Google Scholar] [CrossRef]
- Heusinkveld, B.G.; Van Hove, L.W.A.; Jacobs, C.M.J.; Steeneveld, G.J.; Elbers, J.A.; Moors, E.J.; Holtslag, A.A.M. Use of a mobile platform for assessing urban heat stress in Rotterdam. In Proceedings of the 7th Conference on Biometeorology, Freiburg, Germany, 12–14 April 2010; pp. 433–438. [Google Scholar]
- Liu, L.; Lin, Y.; Wang, D.; Liu, J. An improved temporal correction method for mobile measurement of outdoor thermal climates. Theor. Appl. Clim. 2016, 129, 201–212. [Google Scholar] [CrossRef]
- Rajkovich, N.; Larsen, L. A Bicycle-based field measurement system for the study of thermal exposure in Cuyahoga County, Ohio, USA. Int. J. Environ. Res. Public Heal. 2016, 13, 159. [Google Scholar] [CrossRef] [PubMed]
- Brandsma, T.; Wolters, D. Measurement and statistical modeling of the Urban Heat Island of the City of Utrecht (the Netherlands). J. Appl. Meteorol. Clim. 2012, 51, 1046–1060. [Google Scholar] [CrossRef]
- Joly, D.; Nilsen, L.; Fury, R.; Elvebakk, A.; Brossard, T. Temperature interpolation at a large scale: Test on a small area in Svalbard. Int. J. Clim. 2003, 23, 1637–1654. [Google Scholar] [CrossRef]
- Beltrando, G. La climatologie: Une science géographique. Geo. Inf. 2000, 64, 241–261. [Google Scholar] [CrossRef]
- Siewert, J.; Kroszczynski, K. GIS data as a valuable source of information for increasing resolution of the WRF Model for Warsaw. Remote Sens. 2020, 12, 1881. [Google Scholar] [CrossRef]
- Wu, X.; Xu, Y.; Chen, H. Study on the spatial pattern of an extreme heat event by remote sensing: A case study of the 2013 extreme heat event in the Yangtze River Delta, China. Sustainability 2020, 12, 4415. [Google Scholar] [CrossRef]
- Köppen, W. Versuch einer klassifikation der klimate, vorzugsweise nach ihren beziehungen zur pflanzenwelt. (Schluss). (Attempt to classify the climates, preferably according to their relationship to the flora. (Enough). Geogr. Z. 1900, 6, 657–679. [Google Scholar]
- Kottek, M.; Grieser, J.; Beck, C.; Rudolf, B.; Rubel, F. World Map of the Köppen-Geiger climate classification updated. Meteorol. Z. 2006, 15, 259–263. [Google Scholar] [CrossRef]
- Liu, Y.; Peng, J.; Wang, Y. Efficiency of landscape metrics characterizing urban land surface temperature. Landsc. Urban Plan. 2018, 180, 36–53. [Google Scholar] [CrossRef]
- Miaomiao, X.; Yanglin, W.; Meichen, F. An overview and perspective about causative factors of Surface Urban Heat Island Effects. Prog. Geogr. 2011, 30, 35–41. [Google Scholar] [CrossRef]
- Chen, A.; Sun, R.; Chen, L.-D. Studies on urban heat island from a landscape pattern view: A review. Acta Ecol. Sin. 2012, 32, 4553–4565. [Google Scholar] [CrossRef]
- Yang, Q.; Huang, X.; Li, J. Assessing the relationship between surface urban heat islands and landscape patterns across climatic zones in China. Sci. Rep. 2017, 7, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Zhao, H.-M.; Li, P.-X.; Yin, Z.-Y. Remote sensing image-based analysis of the relationship between urban heat island and land use/cover changes. Remote Sens. Environ. 2006, 104, 133–146. [Google Scholar] [CrossRef]
- Jin, S.; Sader, S.A. Comparison of time series tasseled cap wetness and the normalized difference moisture index in detecting forest disturbances. Remote Sens. Environ. 2005, 94, 364–372. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, Y. Urban Heat Island Analysis Using the Landsat TM Data and ASTER Data: A Case Study in Hong Kong. Remote Sens. 2011, 3, 1535–1552. [Google Scholar] [CrossRef]
- Nguyen, A.K.; Liou, Y.-A.; Li, M.-H.; Tran, T.A. Zoning eco-environmental vulnerability for environmental management and protection. Ecol. Indic. 2016, 69, 100–117. [Google Scholar] [CrossRef]
- Sobrino, J.A.; Jiménez-Muñoz, J.C.; Paolini, L. Land surface temperature retrieval from LANDSAT TM. Remote Sens. Environ. 2004, 90, 434–440. [Google Scholar] [CrossRef]
- Guo, Y.-J.; Han, J.-J.; Zhao, X.; Dai, X.-Y.; Zhang, H. Understanding the role of optimized land use/land cover components in mitigating summertime intra-surface urban heat island effect: A study on downtown Shanghai, China. Energies 2020, 13, 1678. [Google Scholar] [CrossRef]
- Di Paola, F.; Ricciardelli, E.; Cimini, D.; Cersosimo, A.; Di Paola, A.; Gallucci, D.; Gentile, S.; Geraldi, E.; LaRosa, S.; Nilo, S.T.; et al. MiRTaW: An algorithm for atmospheric temperature and water vapor profile estimation from ATMS measurements using a random forests technique. Remote Sens. 2018, 10, 1398. [Google Scholar] [CrossRef]
- Sekulić, A.; Kilibarda, M.; Heuvelink, G.B.M.; Nikolić, M.; Bajat, B. Random forest spatial interpolation. Remote Sens. 2020, 12, 1687. [Google Scholar] [CrossRef]
- Dempster, A.P. Upper and lower probability inferences for families of hypotheses with monotone density ratios. Ann. Math. Stat. 1969, 40, 953–969. [Google Scholar] [CrossRef]
- Shapiro, S.S.; Wilk, M.B. An analysis of variance test for normality (complete samples). Biometrika 1965, 52, 591–611. [Google Scholar] [CrossRef]
- Dormann, C.F.; Elith, J.; Bacher, S.; Buchmann, C.; Carl, G.; Carré, G.; Márquez, J.R.G.; Gruber, B.; Lafourcade, B.; Leitão, P.J.; et al. Collinearity: A review of methods to deal with it and a simulation study evaluating their performance. Ecography 2012, 36, 27–46. [Google Scholar] [CrossRef]
- Joint Research Centre—European Commission. Handbook on Constructing Composite Indicators: Methodology and User Guide; OCDE: Paris, France, 2008. [Google Scholar]
- Shandas, V.; Voelkel, J.; Williams, J.; Hoffman, J.S. Integrating satellite and ground measurements for predicting locations of extreme urban heat. Climate 2019, 7, 5. [Google Scholar] [CrossRef]
- Dempster, A.P. Elements of Continuous Multivariate Analysis; Addison-Wesley Pub. Co.: Boston, MA, USA, 1969. [Google Scholar]
- Wold, S.; Sjöström, M.; Andersson, P.M.; Linusson, A.; Edman, M.; Lundstedt, T.; Nordén, B.; Sandberg, M.; Uppgård, L.-L. Multivariate Design and Modelling in QSAR, Combinatorial Chemistry, and Bioinformatics. In Molecular Modeling and Prediction of Bioactivity; Gundertofte, K., Jørgensen, F.S., Eds.; Springer: Boston, MA, USA, 2000. [Google Scholar] [CrossRef]
- Tenenhaus, M.; Pagès, J.; Ambroisine, L.; Guinot, C. PLS methodology to study relationships between hedonic judgements and product characteristics. Food Qual. Prefer. 2005, 16, 315–325. [Google Scholar] [CrossRef]
- Breiman, L.; Friedman, J.H.; Olshen, R.; Stone, C.J. Classification and Regression Trees; CRC Press: Boca Raton, FL, USA, 1984. [Google Scholar]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- Gislason, P.O.; Benediktsson, J.A.; Sveinsson, J.R. Random Forests for land cover classification. Pattern Recognition Letters. Available online: https://dl.acm.org/doi/abs/10.1016/j.patrec.2005.08.011 (accessed on 30 May 2020).
- Reid, S.; Tibshirani, R.; Friedman, J. A study of error variance estimation in Lasso regression. Stat. Sin. 2016, 26, 35–67. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. Ser. B Stat. Methodol. 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Anselin, L. Local indicators of spatial association-LISA. Geogr. Anal. 2010, 27, 93–115. [Google Scholar] [CrossRef]
- Getis, A.; Ord, J.K. The analysis of spatial association by use of distance statistics. Geogr. Anal. 2010, 24, 189–206. [Google Scholar] [CrossRef]
- Getis, A.; Ord, J. A research agenda for geographic information science. In Spatial Analysis and Modeling in a GIS Environment; Robert, B., McMaster, E., Lynn, U., Eds.; CRC Press: Boca Raton, FL, USA, 1996; Available online: https://books.google.fr/books?hl=fr&lr=&id=k9x0B3V3op0C&oi=fnd&pg=PA157&ots=cOnYyDRjKL&sig=nW-5WZ7_04hBe-lbgv2MdwBABBM&redir_esc=y#v=onepage&q&f=false (accessed on 3 May 2019).
- Zhao, Q.; Yang, J.; Wang, Z.; Wentz, E.A. Assessing the cooling benefits of tree shade by an outdoor urban physical scale model at Tempe, AZ. Urban Sci. 2018, 2, 4. [Google Scholar] [CrossRef]
- Chen, L.; Ng, E.; An, X.; Ren, C.; Lee, M.; Wang, U.; He, Z. Sky view factor analysis of street canyons and its implications for daytime intra-urban air temperature differentials in high-rise, high-density urban areas of Hong Kong: A GIS-based simulation approach. Int. J. Clim. 2010, 32, 121–136. [Google Scholar] [CrossRef]
- Lin, P.; Lau, S.S.-Y.; Qin, H.; Gou, Z. Effects of urban planning indicators on urban heat island: A case study of pocket parks in high-rise high-density environment. Landsc. Urban Plan. 2017, 168, 48–60. [Google Scholar] [CrossRef]
- Browder, G.; Ozment, S.; Rehberger Besco, I.; Gartner, T.; Lange, G.-M. Integrating Green and Gray: Creating Next Generation Infrastructure; World Bank: Washington, DC, USA; World Resources Institute: Washington, DC, USA, 2019; Available online: https://openknowledge.worldbank.org/handle/10986/31430 (accessed on 30 May 2020).
- Gunawardena, K.; Wells, M.; Kershaw, T. Utilising green and bluespace to mitigate urban heat island intensity. Sci. Total. Environ. 2017, 584, 1040–1055. [Google Scholar] [CrossRef] [PubMed]
- Colaninno, N.; Morello, E. Modelling the impact of green solutions upon the urban heat island phenomenon by means of satellite data. J. Physics Conf. Ser. 2019, 1343, 012010. [Google Scholar] [CrossRef]
- Makido, Y.; Hellman, D.; Shandas, V. Nature-based designs to mitigate urban heat: The efficacy of green infrastructure treatments in Portland, Oregon. Atmosphere 2019, 10, 282. [Google Scholar] [CrossRef]
- Eliasson, I.; Svensson, M.K. Spatial air temperature variations and urban land use—a statistical approach. Meteorol. Appl. 2003, 10, 135–149. [Google Scholar] [CrossRef]
- Suomi, J.; Käyhkö, J. The impact of environmental factors on urban temperature variability in the coastal city of Turku, SW Finland. Int. J. Clim. 2011, 32, 451–463. [Google Scholar] [CrossRef]
- Zhao, C.; Fu, G.; Liu, X.; Fu, F. Urban planning indicators, morphology and climate indicators: A case study for a north-south transect of Beijing, China. Build. Environ. 2011, 46, 1174–1183. [Google Scholar] [CrossRef]
- Voogt, J.A.; Oke, T. Thermal remote sensing of urban climates. Remote Sens. Environ. 2003, 86, 370–384. [Google Scholar] [CrossRef]
- Tran, H.; Uchihama, D.; Ochi, S.; Yasuoka, Y. Assessment with satellite data of the urban heat island effects in Asian mega cities. Int. J. Appl. Earth Obs. GeoInf. 2006, 8, 34–48. [Google Scholar] [CrossRef]
- Gallo, K.; Hale, R.; Tarpley, D.; Yu, Y. Evaluation of the Relationship between Air and Land Surface Temperature under Clear- and Cloudy-Sky Conditions. J. Appl. Meteorol. Clim. 2011, 50, 767–775. [Google Scholar] [CrossRef]
- Alfraihat, R.; Mulugeta, G.; Gala, T.S. Ecological evaluation of Urban Heat Island in Chicago City, USA. J. Atmos. Pollut. 2016, 4, 23–29. [Google Scholar] [CrossRef]
- Pelta, R.; Chudnovsky, A.A.; Schwartz, J. Spatio-temporal behavior of brightness temperature in Tel-Aviv and its application to air temperature monitoring. Environ. Pollut. 2016, 208, 153–160. [Google Scholar] [CrossRef][Green Version]
- Walawender, J.P.; Szymanowski, M.; Hajto, M.J.; Bokwa, A. Land surface temperature patterns in the urban agglomeration of Krakow (Poland) derived from landsat-7/ETM+ data. Pure Appl. Geophys. 2014, 171, 913–940. [Google Scholar] [CrossRef]
- Hasanlou, M.; Mostofi, N. Investigating Urban Heat Island Effects and Relation Between Various Land Cover Indices in Tehran City Using Landsat 8 Imagery. In Proceedings of the 1st International Electronic Conference on Remote Sensing, Basel, Switzerland, 22 May 2015; p. 1. [Google Scholar]
- Roşca, C.F.; Harpa, G.V.; Croitoru, A.-E.; Herbel, I.; Imbroane, A.M.; Burada, D.C. The impact of climatic and non-climatic factors on land surface temperature in southwestern Romania. Theor. Appl. Clim. 2016, 130, 775–790. [Google Scholar] [CrossRef]
- Baig, M.H.A.; Zhang, L.; Shuai, T.; Tong, Q. Derivation of a tasselled cap transformation based on Landsat 8 at-satellite reflectance. Remote Sens. Lett. 2014, 5, 423–431. [Google Scholar] [CrossRef]
- Kim, Y.-H.; Baik, J.-J. Daily maximum urban heat island intensity in large cities of Korea. Theor. Appl. Clim. 2004, 79, 151–164. [Google Scholar] [CrossRef]
- Weng, Q.; Firozjaei, M.K.; Sedighi, A.; Kiavarz, M.; Alavipanah, S.K. Statistical analysis of surface urban heat island intensity variations: A case study of Babol City, Iran. GISci. Remote Sens. 2018, 56, 576–604. [Google Scholar] [CrossRef]
- Ali-Toudert, F.; Mayer, H. Effects of asymmetry, galleries, overhanging façades and vegetation on thermal comfort in urban street canyons. Sol. Energy 2007, 81, 742–754. [Google Scholar] [CrossRef]
- Hafner, J.; Kidder, S.Q. Urban Heat Island modeling in conjunction with satellite-derived surface/soil parameters. J. Appl. Meteorol. 1999, 38, 448–465. [Google Scholar] [CrossRef]
- Weng, Q.; Quattrochi, D.A. Thermal remote sensing of urban areas: An introduction to the special issue. Remote Sens. Environ. 2006, 104, 119–122. [Google Scholar] [CrossRef]
- Shohei, K.; Takeki, I.; Hideo, T. Relationship between Terra/ASTER land surface temperature and ground-observed air temperature. Geogr. Rev. Jpn. Ser. B 2016, 88, 38–44. [Google Scholar] [CrossRef]
- Madelin, M.; Bigot, S.; Duché, S.; Rome, S. Intensité et délimitation de l’îlot de chaleur nocturne de surface sur l’agglomération parisienne. In Archive ouverte en Sciences de l’Homme et de la Société; HAL: Houston, TX, USA, 2017; Volume 9. [Google Scholar]
- Iizawa, I.; Umetani, K.; Ito, A.; Yajima, A.; Ono, K.; Amemura, N.; Onishi, M.; Sakai, S. time evolution of an urban heat island from high-density observations in Kyoto City. SOLA 2016, 12, 51–54. [Google Scholar] [CrossRef]
- Taha, H. Urban climates and heat islands: Albedo, evapotranspiration, and anthropogenic heat. Energy Build. 1997, 25, 99–103. [Google Scholar] [CrossRef]
- Qaid, A.; Ossen, D.R.; Rasidi, M.H.; Bin Lamit, H. Effect of the position of the visible sky in determining the sky view factor on micrometeorological and human thermal comfort conditions in urban street canyons. Theor. Appl. Clim. 2017, 131, 1083–1100. [Google Scholar] [CrossRef]
- Voelkel, J.; Shandas, V. Towards systematic prediction of urban heat islands: Grounding measurements, assessing modeling techniques. Climte 2017, 5, 41. [Google Scholar] [CrossRef]
| Land Use/Land Cover | Covered Surface Area (%) |
|---|---|
| Continuous urban fabric | 50 |
| Industrial, commercial, military, or public units | 19.5 |
| Roads (main and secondary) | 14.3 |
| Vegetation | 8.9 |
| Water | 7.3 |
| LOG 32 n°1 | LOG 32 n°2 | EL-USB-1-RCG n°1 | EL-USB-1-RCG n°2 | |
|---|---|---|---|---|
| Temperature (°C) | MSE: 0.892 | MSE: 0.797 | MSE: 0.516 | MSE: 0.566 |
| RMSE: 0.944 | RMSE: 0.893 | RMSE: 0.718 | RMSE: 0.752 | |
| R2: 0.983 | R2: 0.981 | R2: 0.989 | R2: 0.987 | |
| Humidity (%) | MSE: 12.305 | MSE: 11.970 | ||
| RMSE: 3.507 | RMSE: 3.459 | |||
| R2: 0.977 | R2: 0.978 |
| Temperature (°C) | Humidity (%) | Wind Speed (m/s) | Pressure (hPa) | Wind Direction (degrees) | Start | Finish | |
|---|---|---|---|---|---|---|---|
| 08/30/2016 | 27.7 | 46 | 9 | 1017.8 | 350 | 14:42 | 16:50 |
| 08/01/2017 | 29.4 | 52 | 10 | 1012.2 | 34 | 15:23 | 18:37 |
| 07/19/2018 | 29.8 | 42 | 5 | 1014.2 | 309 | 12:32 | 14:45 |
| 07/22/2019 | 30.1 | 41 | 11 | 1022 | 10 | 12:25 | 16:12 |
| Mean | 29.3 | 45.3 | 8.8 | 1016.6 | 260.8 | ||
| Standard deviation | 0.9 | 4.3 | 2.3 | 3.7 | 132.0 | ||
| Minimum | 27.7 | 41 | 5 | 1012.2 | 34 | ||
| Maximum | 30.1 | 52 | 11 | 1022 | 350 |
| Variables (Units) | Acquisition Source | Variables (Units) | Acquisition Source | ||
|---|---|---|---|---|---|
| Climate data from remote sensing | Surface temperature (°C) | Landsat 8 | Building Index | NDBI Normalized Difference Built-Up Index | Landsat 8 |
| UTFVI Urban Thermal Field Variance Index | Landsat 8 | ||||
| Sunshine duration of the study day (h) | LiDAR data and modelling by ESRI ARCGIS | UI Urban Index | Landsat 8 | ||
| Radiation received for the study day (WH/m2) | LiDAR data and modelling by ESRI ARCGIS | IBI Index-based Built-Up Index | Landsat 8 | ||
| Vegetation index | NDVI Normalized Difference Vegetation Index | Landsat 8 | Building Density | LiDAR | |
| SAVI Soil Adjusted Vegetation Index | Landsat 8 | ||||
| EVI Enhanced Vegetation Index | Landsat 8 | ||||
| Tasseled Cap Transformation greenness (GVI) | Landsat 8 | Topographic | Slope (°) | Data Grand Lyon | |
| Density of low vegetation | LiDAR | ||||
| Density of medium vegetation | LiDAR | Exposure | LiDAR | ||
| Density of high vegetation | LiDAR | Curvature | Data Grand Lyon | ||
| Water presence index | MNDWI Modified Normalized Difference Water Index | Landsat 8 | Urban morphology | Sky View Factor | LiDAR |
| NDWI Normalized Difference Water Index | Landsat 8 | Standard Deviation (STD) of Building Height (building height variation) | Data Grand Lyon | ||
| Moisture index | Tasseled cap Transformation Wetness | Landsat 8 | Land use | Distance to railway tracks | Data Grand Lyon |
| NDMI Normalized Difference Moisture Index | Landsat 8 | Distance to points of tourist interest | Data Grand Lyon | ||
| Bare soil index | NDBaI Normalized Difference Bareness Index | Landsat 8 | Distance to subway entrances | Data Grand Lyon | |
| BI Bare Soil Index | Landsat 8 | Distance to fountains | Data Grand Lyon | ||
| EBBI Enhanced Built-Up and Bareness Index | Landsat 8 | Water area | Data Grand Lyon | ||
| Density of bare soil | LiDAR | ||||
| Radiation Index | Spectral radiance | Landsat 8 | |||
| Emissivity | Landsat 8 | ||||
| Tasseled Cap Transformation Brightness | Landsat 8 | ||||
| Variables (unit) | Buffer Zone (m) | Variables (unit) | Buffer Zone (m) | ||
|---|---|---|---|---|---|
| Climate data from remote sensing | Surface temperature (°C) | 500 | Bare soil index | NDBaI | 1000 |
| UTFVI | 500 | BI | 50 | ||
| Vegetation index | NDVI | 1000 | EBBI | 1000 | |
| SAVI | 1000 | Density of bare soil | 50 | ||
| EVI | 50 | Built index | NDBI | 1000 | |
| Tasseled Cap greenness | 1000 | UI | 1000 | ||
| Density of low vegetation | 200 | IBI | 500 | ||
| Density of medium vegetation | 50 | Density of built-up | 5 | ||
| Density of high vegetation | 100 | Urban morphology | STD Building Height | 100 | |
| Water index | MNDWI | 500 | Radiation Index | Spectral radiance | 1000 |
| NDWI | 500 | Emissivity | 500 | ||
| Moisture index | Tasseled cap Wetness | 50 | Tasseled Cap Brightness | 1000 | |
| NDMI | 1000 | Land use | Density of water area | 100 |
| Variables | After Spearman Correlation Matrix and VIF | |||
|---|---|---|---|---|
| 08/30/2016 | 08/01/2017 | 07/19/2018 | 07/22/2019 | |
| Surface temperature (°C) | X | X | X | X |
| UTFVI | ||||
| Sunshine duration of the study day | ||||
| Radiation received for the study day | X | X | X | |
| NDVI | X | X | X | |
| SAVI | ||||
| EVI | X | X | X | X |
| Tasseled Cap greenness (GVI) | X | |||
| Density of low vegetation | X | X | X | X |
| Density of medium vegetation | X | X | X | X |
| Density of high vegetation | X | X | X | X |
| MNDWI | X | X | X | X |
| NDWI | X | |||
| Tasseled Cap Wetness | X | X | X | X |
| NDMI | X | |||
| NDBaI | X | |||
| BI | X | X | X | X |
| EBBI | ||||
| Density of bare soil | X | X | X | X |
| Spectral radiance | ||||
| Emissivity | X | X | ||
| Tasseled Cap Brightness | X | X | X | |
| NDBI | X | |||
| UI | ||||
| IBI | X | X | ||
| Building Density | X | X | X | X |
| Digital Elevation Model | X | X | X | X |
| Slope (°) | X | X | X | X |
| Longitude | X | |||
| Exposure | X | X | X | |
| Curvature | X | X | X | X |
| Sky View Factor | X | X | X | X |
| STD Building Height | X | X | ||
| Distance to railway tracks | X | X | X | X |
| Distance to points of tourist interest | X | X | X | |
| Distance to subway entrances | X | X | X | |
| Distance to fountains | X | X | X | |
| Water area | X | X | X | X |
| Final Number | 21 | 27 | 22 | 26 |
| Date | R2 | MSE | RMSE | Variables | Model Parameter in Absolute Value | Impact on the Model |
|---|---|---|---|---|---|---|
| 08/30/2016 | 0.79 | 0.11 | 0.33 | LST | 0.0675 | Negative |
| NDVI | 1.71 | Positive | ||||
| MNDWI | 4.53 | Positive | ||||
| 08/01/2017 | 0.77 | 0.03 | 0.18 | BI | 0.58 | Positive |
| NDMI | 0.51 | Negative | ||||
| NDBI | 0.51 | Positive | ||||
| 07/19/2018 | 0.37 | 0.09 | 0.07 | Emissivity | 2.1128 | Negative |
| Longitude | 1.3906 | Positive | ||||
| NDBaI | 1.2262 | Positive | ||||
| 07/22/2019 | 0.,53 | 1.13 | 1.06 | Emissivity | 7.4782 | Positive |
| BI | 3.0472 | Positive | ||||
| NDBaI | 2.5931 | Positive | ||||
| Mean | 0.62 | 0.34 | 0.41 |
| Date | R2 | Out-Of-Bag | RMSE |
|---|---|---|---|
| 08/30/2016 | 0.98 | 0.0071 | 0.08 |
| 08/01/2017 | 0.96 | 0.0045 | 0.07 |
| 07/19/2018 | 0.95 | 0.0071 | 0.08 |
| 07/22/2019 | 0.92 | 0.19 | 0.44 |
| Mean | 0.95 | 0.05 | 0.17 |
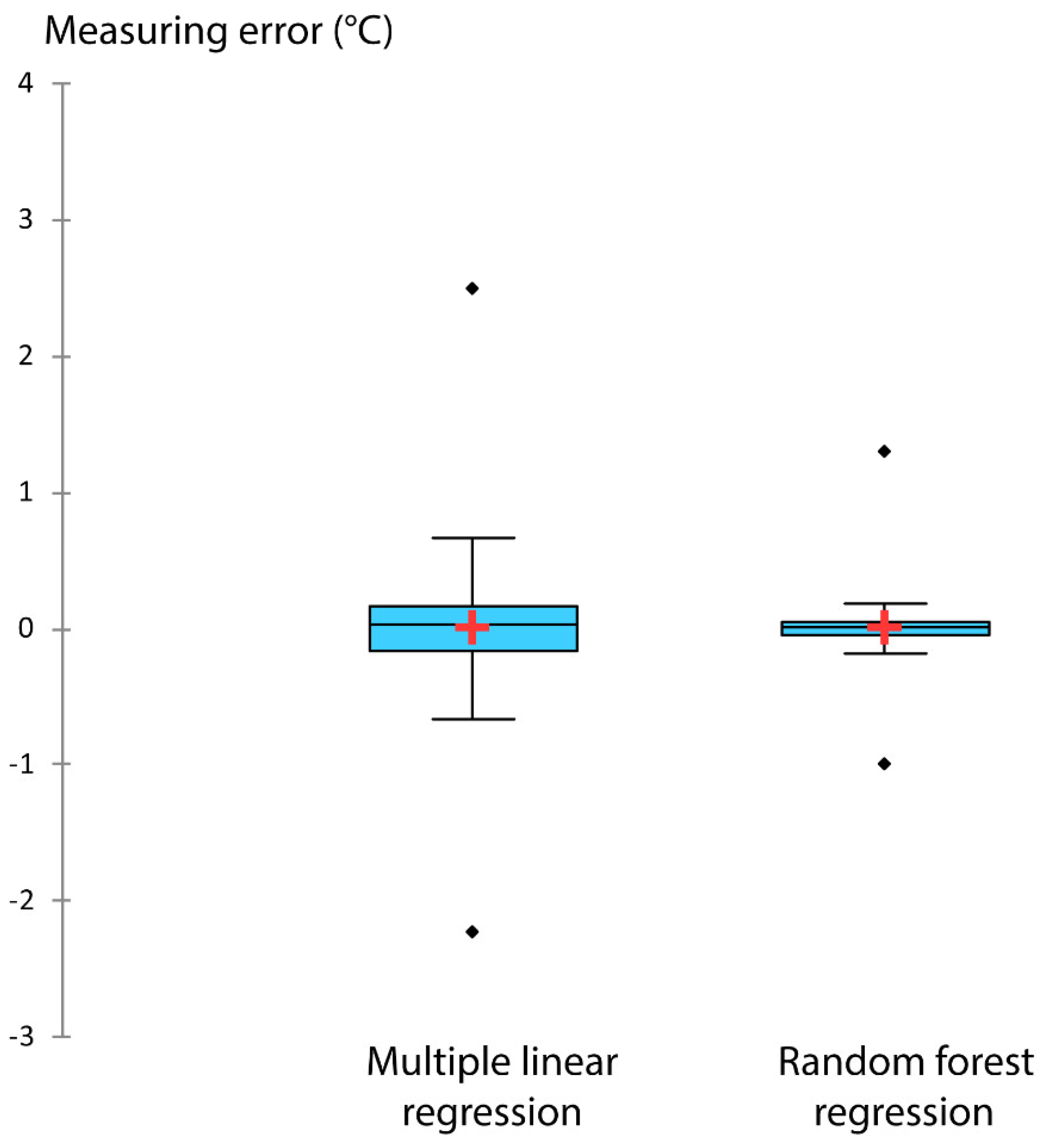
| MLR | RDF | |
|---|---|---|
| Biggest negative error (°C) | −2.23 | −0.99 |
| Biggest maximum error (°C) | 2.50 | 1.29 |
| First Quartile | −0.17 | −0.05 |
| Median | 0.02 | 0.002 |
| Third Quartile | 0.17 | 0.05 |
| Mean | 0.01 | 0.003 |
| Variance | 0.19 | 0.03 |
| Standard deviation | 0.44 | 0.17 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alonso, L.; Renard, F. A New Approach for Understanding Urban Microclimate by Integrating Complementary Predictors at Different Scales in Regression and Machine Learning Models. Remote Sens. 2020, 12, 2434. https://doi.org/10.3390/rs12152434
Alonso L, Renard F. A New Approach for Understanding Urban Microclimate by Integrating Complementary Predictors at Different Scales in Regression and Machine Learning Models. Remote Sensing. 2020; 12(15):2434. https://doi.org/10.3390/rs12152434
Chicago/Turabian StyleAlonso, Lucille, and Florent Renard. 2020. "A New Approach for Understanding Urban Microclimate by Integrating Complementary Predictors at Different Scales in Regression and Machine Learning Models" Remote Sensing 12, no. 15: 2434. https://doi.org/10.3390/rs12152434
APA StyleAlonso, L., & Renard, F. (2020). A New Approach for Understanding Urban Microclimate by Integrating Complementary Predictors at Different Scales in Regression and Machine Learning Models. Remote Sensing, 12(15), 2434. https://doi.org/10.3390/rs12152434






