Positional Accuracy Assessment of Lidar Point Cloud from NAIP/3DEP Pilot Project
Abstract
:1. Introduction
1.1. Lidar Point Cloud Accuracy
1.2. NAIP/3DEP Pilot Project
- Determine if data meeting both NAIP imagery specifications and 3DEP LBS can be acquired in a cost-effective way on the same platform.
- Determine if this approach to acquisition has any strengths or weaknesses for various purposes of the NAIP and 3DEP stakeholder communities.
- Potentially increase the frequency of repeat data collection for lidar data nationally.
- Encourage the innovation of more sustainable approaches to acquiring these and other national datasets as technology improves.
- Explore the unique applications of co-collected imagery and lidar data.
- Consider whether this technology and potential partnership between the imagery and lidar communities could support statewide lidar collections where requirements exist for both data products.
2. Methods
2.1. Ground Truth Survey
2.1.1. Conventional Surveying Methodology
2.1.2. Terrestrial Laser Scanner Methodology
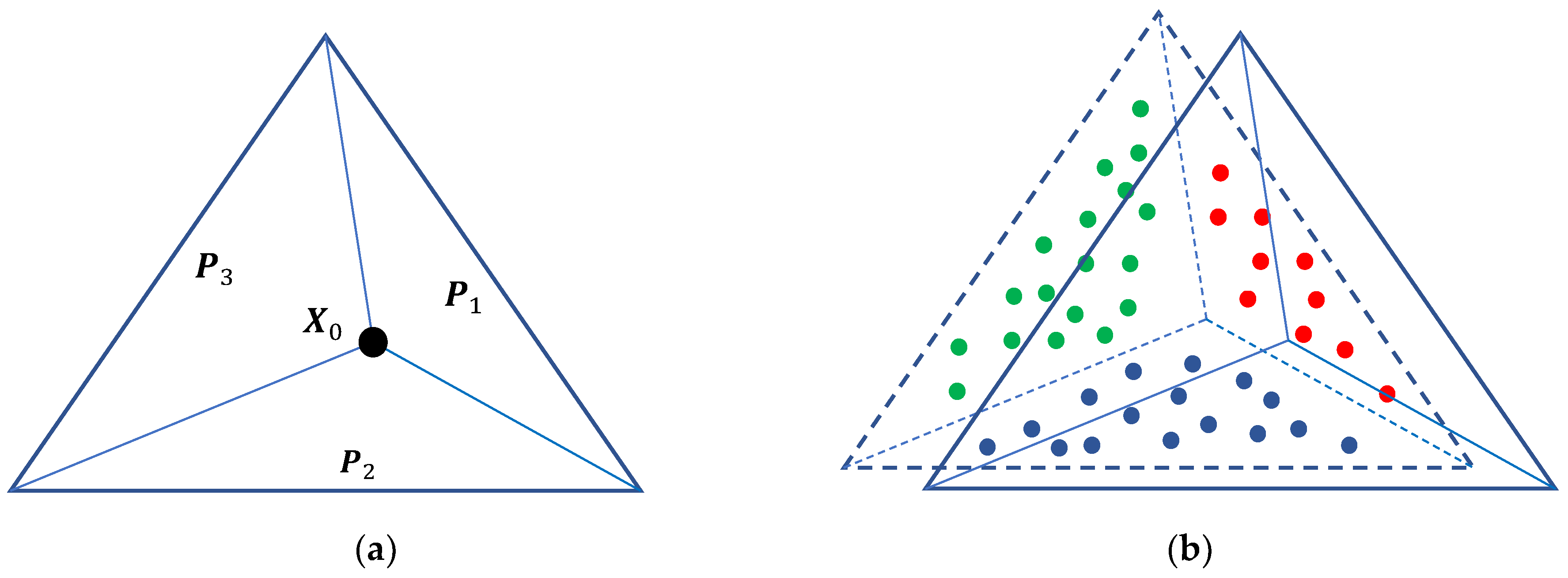
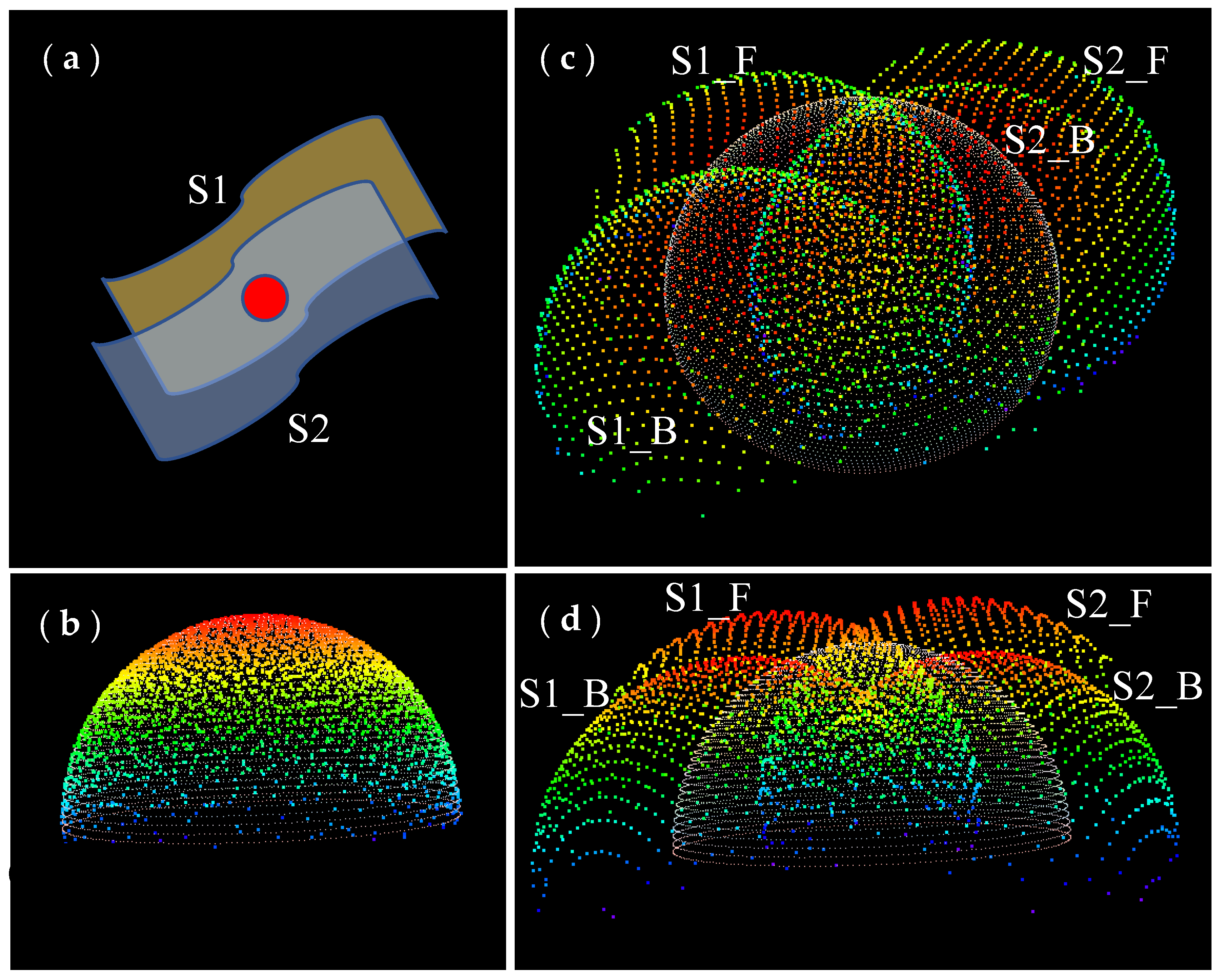
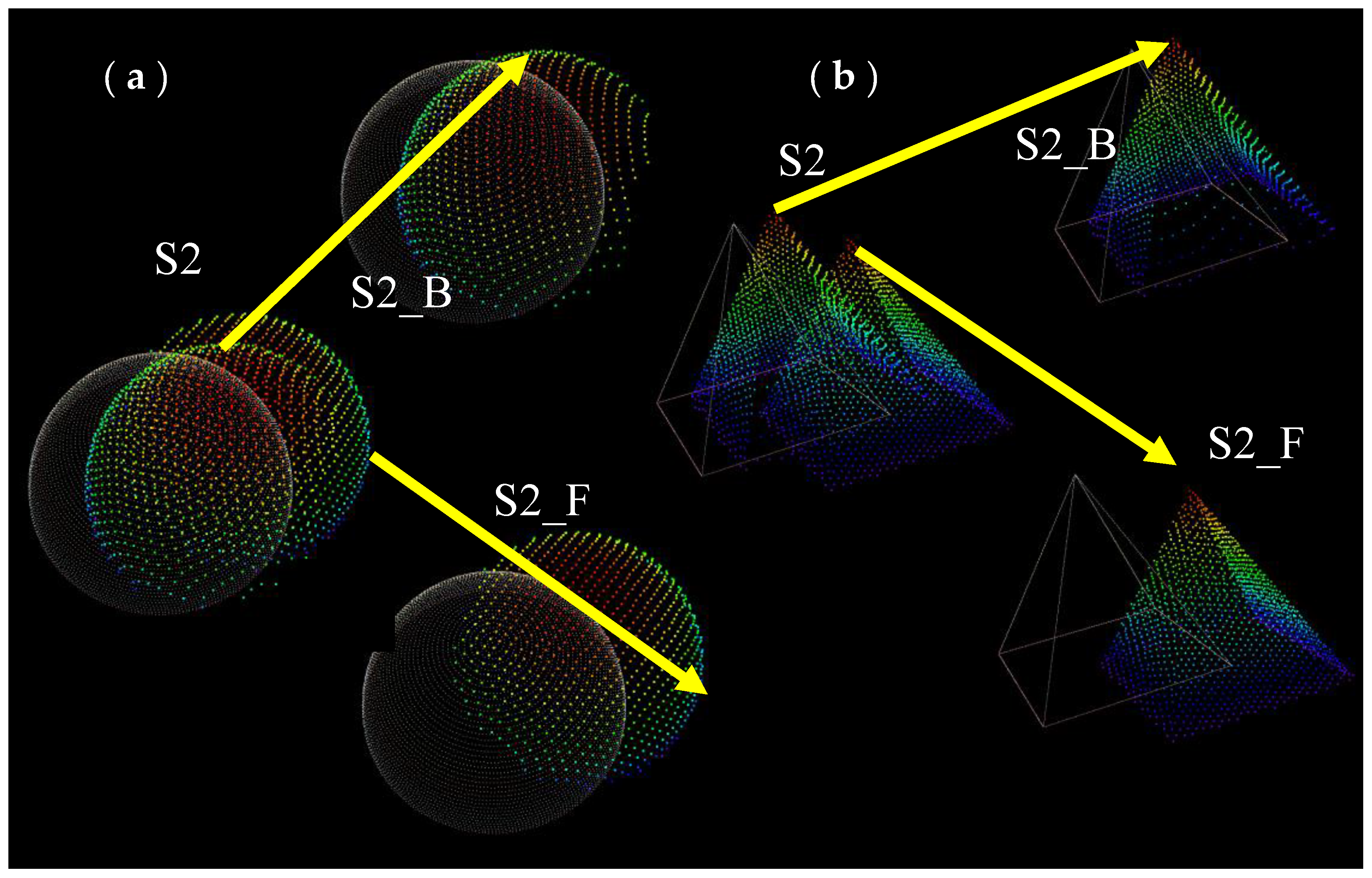
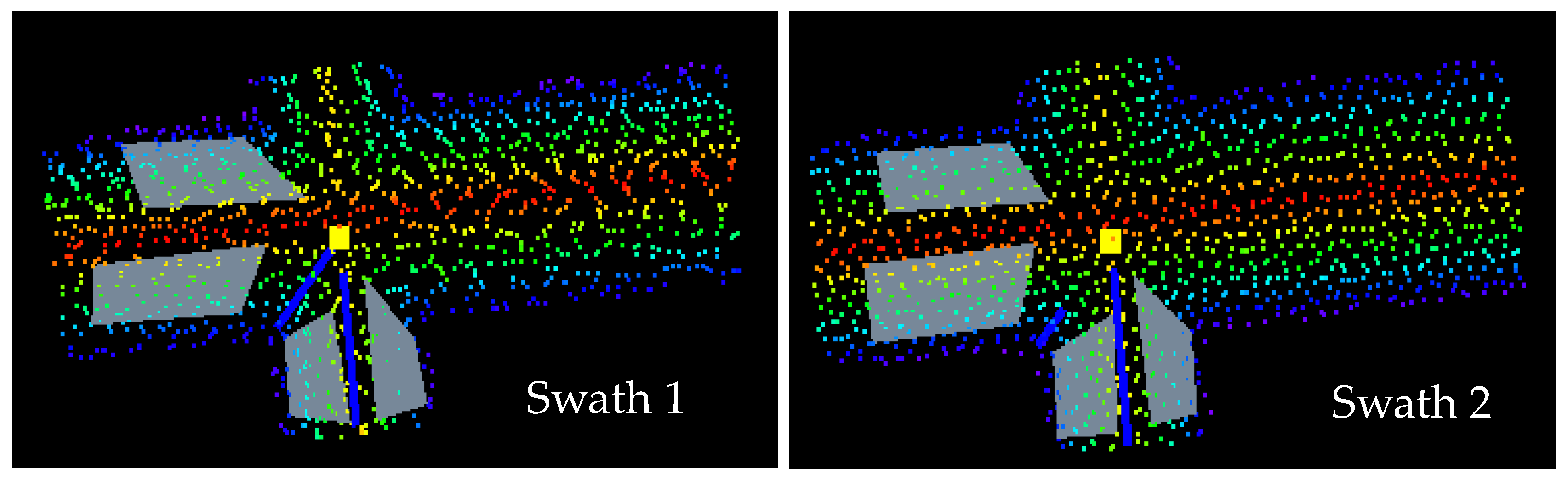
2.2. Three-Plane Intersection and 3D Accuracy Assessment
2.3. Intraswath and Interswath Analysis
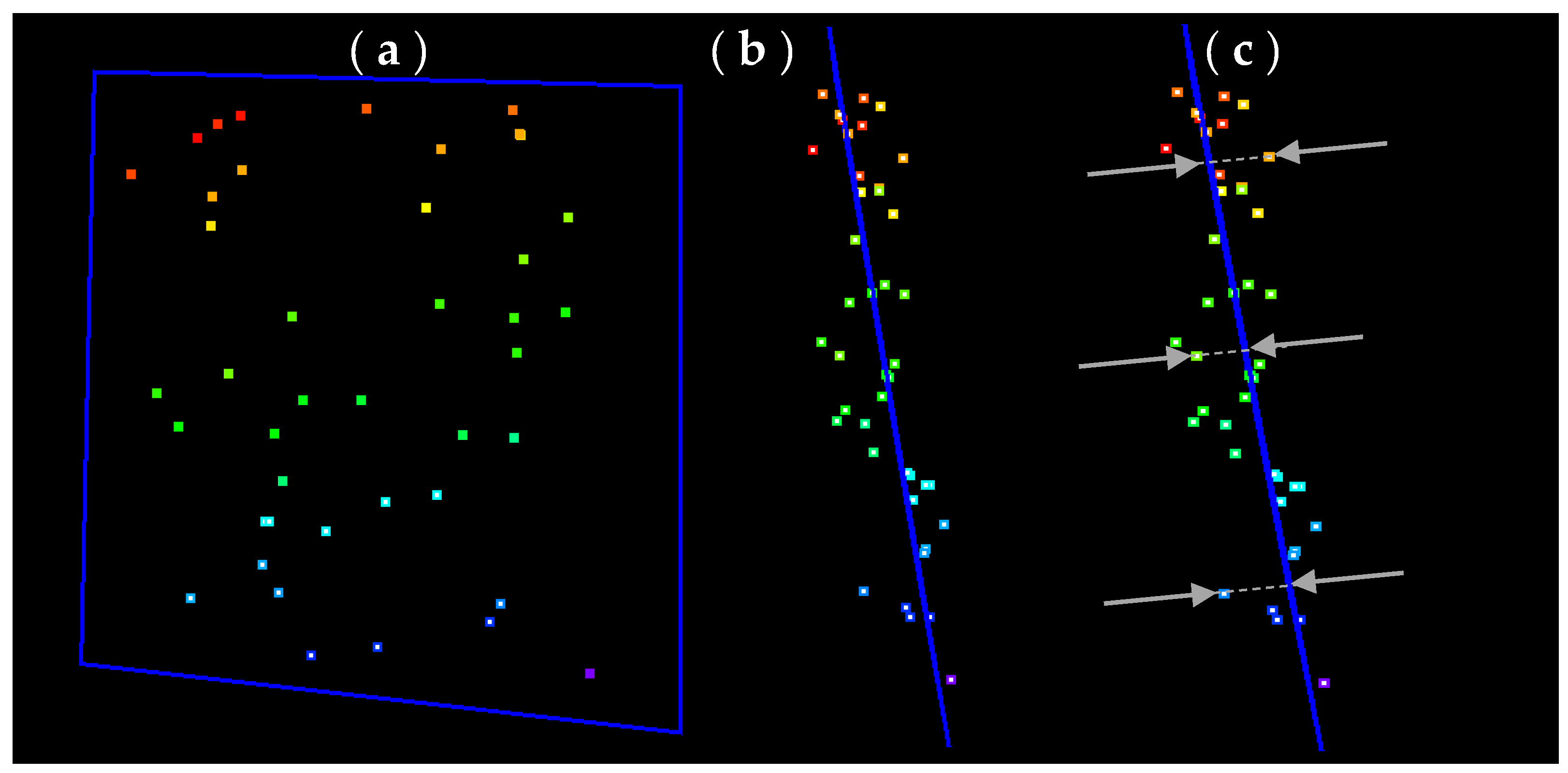
2.3.1. Intraswath Smooth Surface Precision
2.3.2. Intraswath Scan Direction Registration
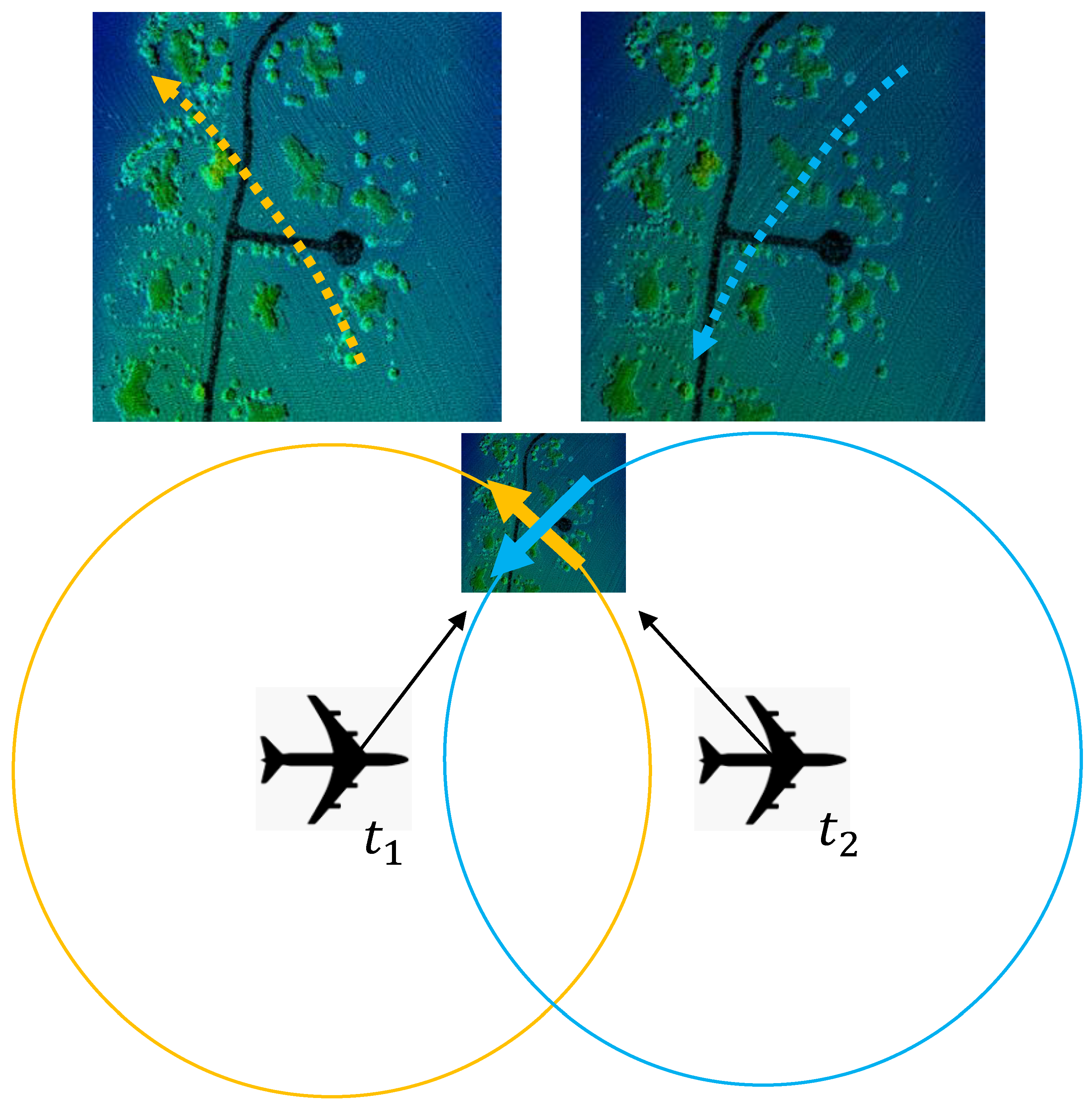
2.3.3. Interswath Consistency
2.4. Absolute Vertical Accuracy
3. Results
3.1. Intraswath Smooth Surface Precision
3.2. Intraswath Difference between Opposite Scan Direction
3.3. Interswath Consistency
3.4. Absolute Vertical Accuracy
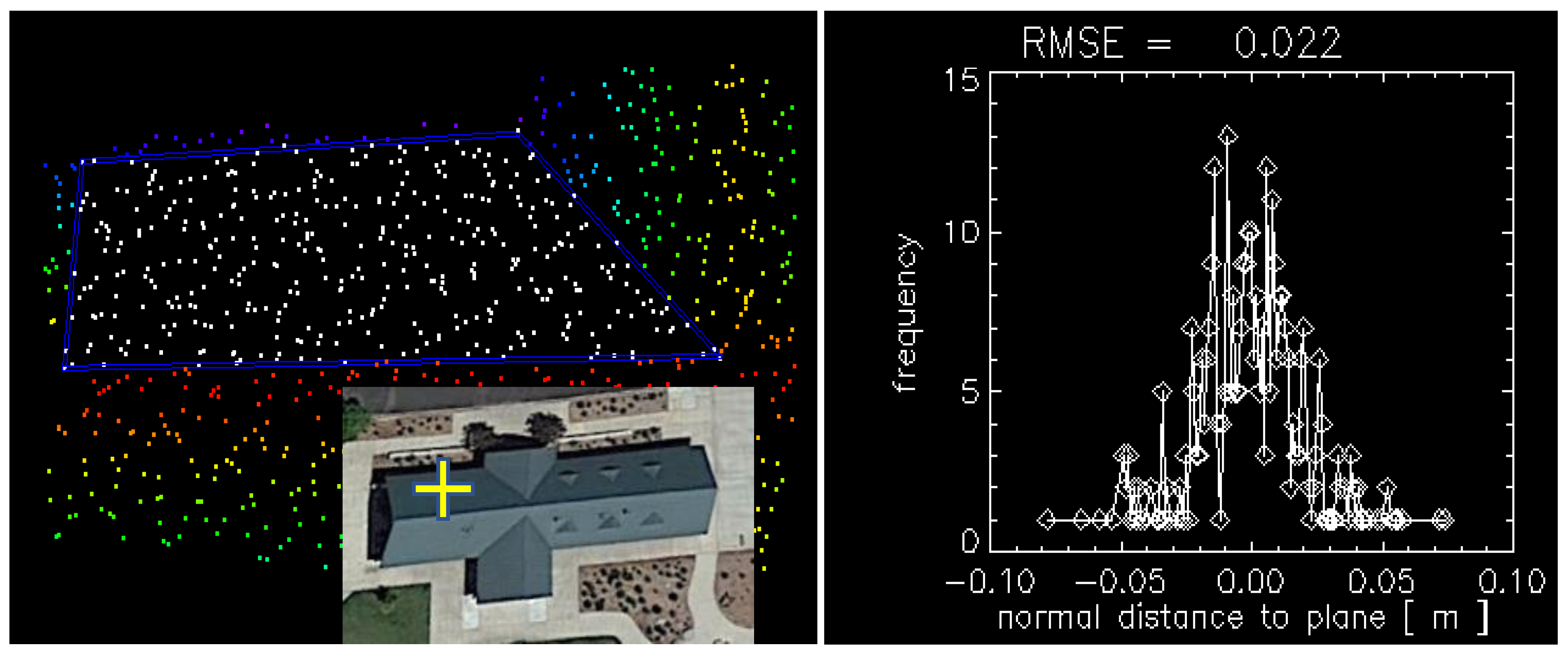
3.4.1. Nonvegetated Vertical Accuracy
3.4.2. Vegetated Vertical Accuracy
3.5. D Absolute Accuracy Analysis
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- ASPRS. ASPRS Positional Accuracy Standards for Digital Geospatial Data. Photogramm. Eng. Remote Sens. 2015, 81, A1–A26. [Google Scholar] [CrossRef]
- Heidemann, H.K. Lidar Base Specification; (Version 1.3, February 2018); Book 11; Chapter B4; U.S. Geological Survey Standards: Reston, VA, USA, 2018; p. 101. [Google Scholar] [CrossRef] [Green Version]
- NDEP (National Digital Elevation Program). National Digital Elevation Program, Guidelines for Digital Elevation Data; Version 1.0.; ASPRS: Bethesda, MD, USA, 2004. [Google Scholar]
- FGDC (Federal Geographic Data Committee). Geospatial Positioning Accuracy Standards. Part 3: National Standard for Spatial Data Accuracy; FGDC-STD-007.3-1998; USGS: Reston, VA, USA, 1998. [Google Scholar]
- FEMA. Guidelines and Standards for Flood Hazard Mapping Partners; FEMA: Washington, DC, USA, 2003.
- Habib, A.; Bang, K.I.; Kersting, A.P.; Lee, D.C. Error budget of LiDAR systems and quality control of the derived data. Photogramm. Eng. Remote Sens. 2009, 75, 1093–1108. [Google Scholar] [CrossRef]
- Tulldahl, M.; Bissmarck, F.; Larsson, H.; Grönwall, C.; Tolt, G. Accuracy evaluation of 3D lidar data from small UAV. In Proceedings of the SPIE 9649, Electro-Optical Remote Sensing, Photonic Technologies, and Applications IX, Auditorium Antoine de Saint-Exupery, Toulouse, France, 21–22 September 2015; p. 964903. [Google Scholar]
- Borrmann, D.; Elseberg, J.; Kai, L.; Nüchter, A. The 3D Hough Transform for plane detection in point clouds: A review and a new accumulator design. 3D Res. 2011, 2, 1–13. [Google Scholar] [CrossRef]
- Georgiev, K.; Creed, R.T.; Lakaemper, R. Fast plane extraction in 3d range data based on line segments. In Proceedings of the Intelligent Robots and Systems (IROS), IEEE/RSJ International Conference, San Francisco, CA, USA, 25–30 September 2011; pp. 3808–3815. [Google Scholar]
- Vosselman, G.; Gorte, B.G.; Sithole, G.; Rabbani, T. Recognising structure in laser scanner point clouds. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2004, 46, 339–344. [Google Scholar]
- Rabbani, T.; van den Heuvel, F.A.; Vosselman, G. Segmentation of point clouds using smoothness constraint. In Proceedings of the International Archives of Photogrammetry, Remote Sensing & Spatial Information Sciences, Goa, India, 25–30 September 2006. [Google Scholar]
- Tarsha-Kurdi, F.; Landes, T.; Grussenmeyer, P.; Koehl, M. Model-driven and data-driven approaches using LIDAR data: Analysis and comparison. In Proceedings of the Photogrammetric Image Analysis, Munich, Germany, 19–21 September 2007; pp. 87–92. [Google Scholar]
- Chen, L.; Zhao, S. Building detection in an urban area using LiDAR data and quickbird imagery. Int. J. Remote Sens. 2012, 33, 5135–5148. [Google Scholar] [CrossRef]
- Li, Y.; Wu, H.; An, R.; Xu, H.; He, Q.; Xu, J. An improved building boundary extraction algorithm based on fusion of optical imagery and LIDAR data. Optik 2013, 124, 5357–5362. [Google Scholar] [CrossRef]
- Zhou, G.; Zhou, X. Seamless Fusion of LiDAR and Aerial Imagery for Building Extraction. IEEE Trans. Geosci. Remote Sens. 2014, 52, 7393–7407. [Google Scholar] [CrossRef]
- Zarea, A.; Mohammadzadeh, A. A Novel Building and Tree Detection Method from LiDAR Data and Aerial Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 1864–1875. [Google Scholar] [CrossRef]
- Krishnamachari, S.; Chellappa, R. Delineating buildings by grouping lines with MRFs. IEEE Trans. Image Process. 1996, 5, 164–168. [Google Scholar] [CrossRef] [PubMed]
- Kim, M.; Park, S.; Danielson, J.; Irwin, J.; Stensaas, G.; Stoker, J.; Nimetz, J. General External Uncertainty Models of Three-Plane Intersection Point for 3D Absolute Accuracy Assessment of Lidar Point Cloud. Remote Sens. 2019, 11, 2737. [Google Scholar] [CrossRef] [Green Version]
- Trimble Navigation Limited. Trimble R8 GNSS and R6/5800 GPS Receivers User Guide (Revision A); Trimble Navigation Limited: Dayton, OH, USA, 2008. [Google Scholar]
- Trimble Navigation Limited. Trimble S6 Total Station Datasheet; Trimble Navigation Limited: Dayton, OH, USA, 2013. [Google Scholar]
- Irwin, J.R.; Sampath, A.; Kim, M.; Bauer, M.A.; Burgess, M.A.; Park, S.; Danielson, J.J. Country Mapper Sensor Validation Survey Data: U.S. Geological Survey Data Release. 2020. Available online: https://usgs.ornl.gov/metadata/catalog/html/Earth_Resources_Observation_and_Science_%28EROS%29_Center/5e5d679ae4b01d50924f2d23.html (accessed on 17 May 2020). [CrossRef]
- Optech Incorporated. Optech ILRIS-3D; Optech Inc.: Toronto, ON, Canada, 2006. [Google Scholar]
- Gexel. JRC 3D Reconstructor Software Manual; Gexel: Brescia, Italy, 2017. [Google Scholar]
- Gellert, W.; Gottwald, S.; Hellwich, M.; Kästner, H.; Künstner, H. VNR Concise Encyclopedia of Mathematics, 2nd ed.; Van Nostrand Reinhold: New York, NY, USA, 1989. [Google Scholar]
- Wilkinson, B.; Lassiter, H.A.; Abd-Elrahman, A.; Carthy, R.R.; Ifju, P.; Broadbent, E.; Grimes, N. Geometric Targets for UAS Lidar. Remote Sens. 2019, 11, 3019. [Google Scholar] [CrossRef] [Green Version]
- Kim, M. Airborne Waveform Lidar Simulator Using the Radiative Transfer of a Laser Pulse. Appl. Sci. 2019, 9, 2452. [Google Scholar] [CrossRef] [Green Version]
- U.S. Geological Survey. USGS Lidar Point Cloud ID KootenaiRiver 2017 KRTH 0031: U.S. Geological Survey; USGS: Reston, VA, USA, 2020.
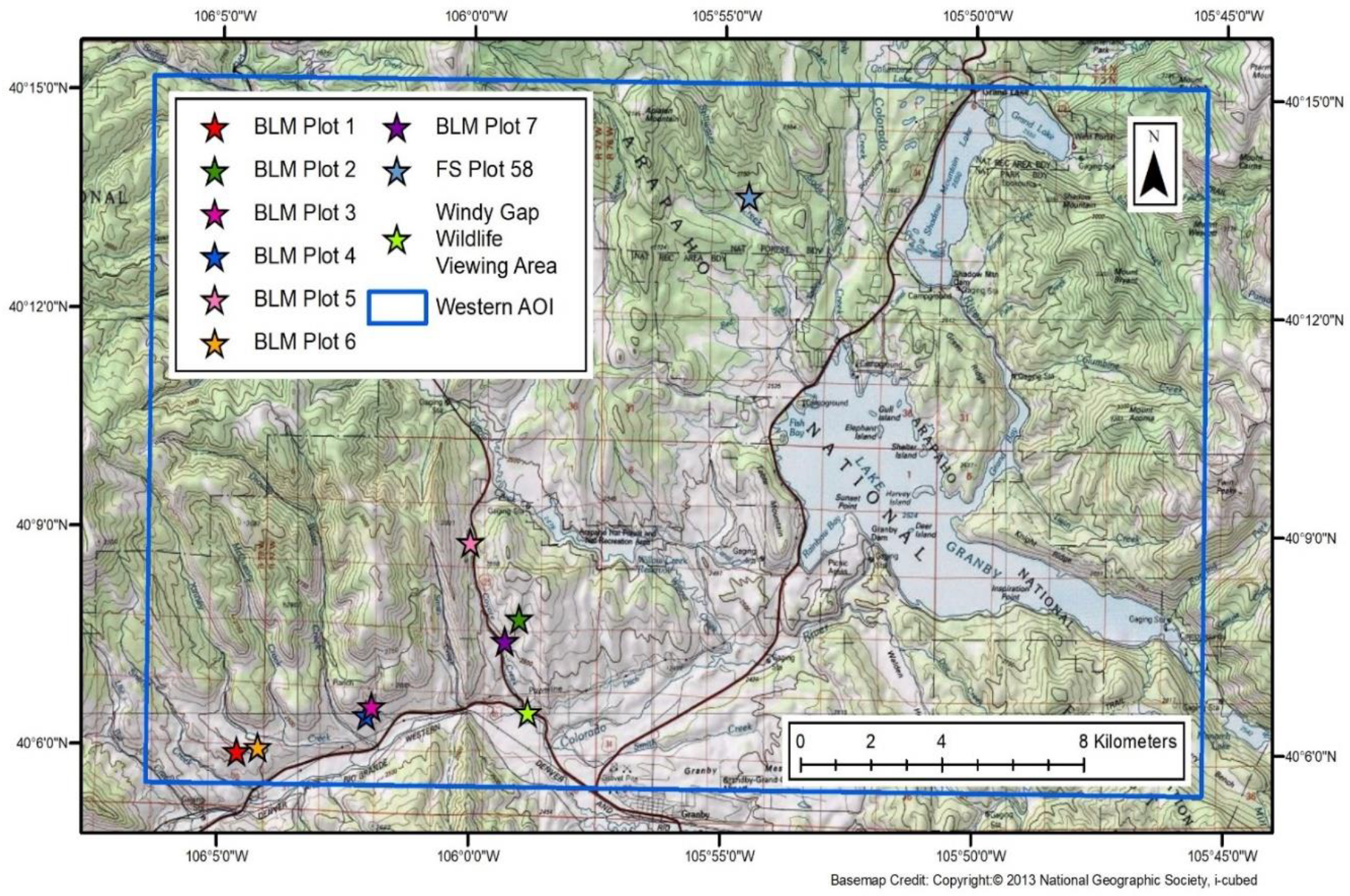
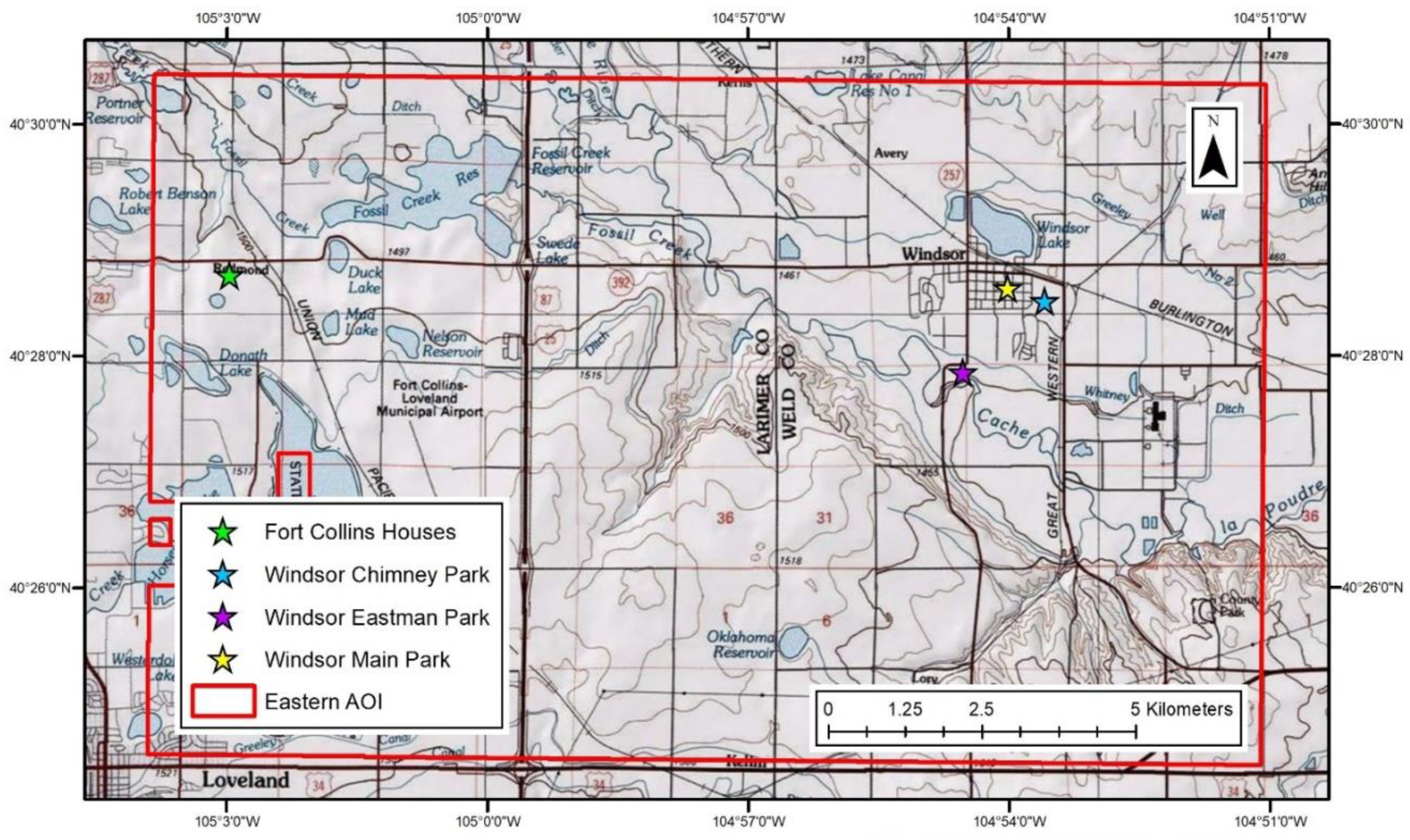




| Granby Area | Fort Collins Houses | Main and Chimney Parks | Eastman Park | All Areas | |
|---|---|---|---|---|---|
| Min PDOP | 1.214 | 1.028 | 1.153 | 1.349 | 1.028 |
| Max PDOP | 2.729 | 2.290 | 1.826 | 2.093 | 2.729 |
| Mean PDOP | 1.653 | 1.468 | 1.361 | 1.556 | 1.611 |
| Min Hor. Precision (95%) | 0.012 | 0.011 | 0.012 | 0.014 | 0.011 |
| Max Hor. Precision (95%) | 0.032 | 0.023 | 0.024 | 0.022 | 0.032 |
| Mean Hor. Precision (95%) | 0.016 | 0.016 | 0.015 | 0.016 | 0.016 |
| Min Vert. Precision (95%) | 0.015 | 0.014 | 0.014 | 0.017 | 0.014 |
| Max Vert. Precision (95%) | 0.048 | 0.030 | 0.029 | 0.028 | 0.048 |
| Mean Vert. Precision (95%) | 0.023 | 0.018 | 0.019 | 0.020 | 0.022 |
| Sites | Rover–Lidar | |
|---|---|---|
| Mean | RMSE(z) | |
| Eastman Park | 0.0209 | 0.0245 |
| Ft Collins Houses | 0.0238 | 0.0287 |
| Windsor Park & Chimney Park | 0.0221 | 0.0135 |
| Sites | Rover–Lidar | Rover–UAS Lidar | Rover–SfM | |||
|---|---|---|---|---|---|---|
| Mean | RMSE(z) | Mean | RMSE(z) | Mean | RMSE(z) | |
| BLM1 | −0.0375 | 0.0315 | −0.0264 | 0.0222 | −0.2912 | 0.0854 |
| BLM3 | −0.0850 | 0.0434 | −0.0688 | 0.0301 | −0.1471 | 0.0512 |
| BLM4 | −0.0633 | 0.0306 | −0.0845 | 0.0309 | −0.1290 | 0.0562 |
| BLM5 | −0.0433 | 0.0518 | −0.0453 | 0.0269 | −0.1333 | 0.0737 |
| BLM6 | −0.0298 | 0.0284 | −0.0027 | 0.0212 | −0.1602 | 0.0794 |
| BLM7 | −0.0495 | 0.0448 | −0.0111 | 0.0215 | −0.2226 | 0.0693 |
| Method 1: Generic Three-Plane | Method 2: Translation Only | |||||
|---|---|---|---|---|---|---|
| Dx | Dy | Dz | Dx | Dy | Dz | |
| Eastman Park 1-Point 1 | 0.263 | 0.133 | 0.058 | 0.256 | 0.118 | 0.039 |
| Eastman Park 1-Point 2 | 0.227 | 0.158 | 0.029 | 0.246 | 0.154 | 0.039 |
| Eastman Park 2-Point 1 | 0.268 | 0.097 | 0.086 | 0.230 | 0.159 | 0.013 |
| Eastman Park 2-Point 2 | 0.278 | 0.109 | 0.081 | 0.222 | 0.148 | 0.017 |
| Ft Collins House 1-Point 1 | 0.227 | 0.201 | 0.094 | 0.240 | 0.155 | 0.022 |
| Ft Collins House 1-Point 2 | 0.245 | 0.104 | 0.098 | 0.238 | 0.171 | 0.022 |
| Ft Collins House 1-Point 3 | 0.215 | 0.135 | 0.064 | 0.235 | 0.160 | 0.025 |
| Ft Collins House 1-Point 4 | 0.229 | 0.099 | 0.065 | 0.242 | 0.109 | 0.025 |
| Ft Collins House 1-Point 5 | 0.236 | 0.080 | 0.028 | 0.231 | 0.118 | 0.033 |
| Ft Collins House 1-Point 6 | 0.187 | 0.241 | 0.061 | 0.232 | 0.083 | 0.032 |
| Ft Collins House 1-Point 7 | 0.225 | 0.042 | 0.052 | 0.228 | 0.114 | 0.032 |
| Ft Collins House 1-Point 8 | 0.246 | 0.156 | 0.076 | 0.219 | 0.094 | 0.017 |
| Ft Collins House 2-Point 1 | 0.229 | 0.096 | 0.060 | 0.218 | 0.058 | 0.051 |
| Ft Collins House 2-Point 2 | 0.181 | 0.009 | 0.049 | 0.254 | 0.167 | 0.067 |
| Ft Collins House 2-Point 3 | 0.116 | −0.081 | 0.075 | 0.237 | −0.067 | 0.061 |
| Chimney Park 1-Point 1 | 0.166 | −0.042 | 0.070 | 0.159 | −0.117 | 0.022 |
| Chimney Park 1-Point 2 | 0.089 | −0.012 | 0.079 | 0.134 | −0.120 | 0.022 |
| Chimney Park 2-Point 1 | 0.257 | 0.092 | 0.061 | 0.203 | 0.000 | 0.036 |
| Chimney Park 2-Point 2 | 0.258 | 0.011 | 0.061 | 0.203 | 0.002 | 0.036 |
| Windsor Park 1-Point 1 | 0.118 | −0.034 | 0.063 | 0.160 | −0.028 | 0.060 |
| Method 1: Generic Three-Plane | Method 2: Translation Only | |||||
|---|---|---|---|---|---|---|
| Dx | Dy | Dz | Dx | Dy | Dz | |
| Mean | 0.213 | 0.080 | 0.066 | 0.219 | 0.074 | 0.034 |
| RMSE | 0.054 | 0.084 | 0.018 | 0.033 | 0.096 | 0.016 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, M.; Park, S.; Irwin, J.; McCormick, C.; Danielson, J.; Stensaas, G.; Sampath, A.; Bauer, M.; Burgess, M. Positional Accuracy Assessment of Lidar Point Cloud from NAIP/3DEP Pilot Project. Remote Sens. 2020, 12, 1974. https://doi.org/10.3390/rs12121974
Kim M, Park S, Irwin J, McCormick C, Danielson J, Stensaas G, Sampath A, Bauer M, Burgess M. Positional Accuracy Assessment of Lidar Point Cloud from NAIP/3DEP Pilot Project. Remote Sensing. 2020; 12(12):1974. https://doi.org/10.3390/rs12121974
Chicago/Turabian StyleKim, Minsu, Seonkyung Park, Jeffrey Irwin, Collin McCormick, Jeffrey Danielson, Gregory Stensaas, Aparajithan Sampath, Mark Bauer, and Matthew Burgess. 2020. "Positional Accuracy Assessment of Lidar Point Cloud from NAIP/3DEP Pilot Project" Remote Sensing 12, no. 12: 1974. https://doi.org/10.3390/rs12121974
APA StyleKim, M., Park, S., Irwin, J., McCormick, C., Danielson, J., Stensaas, G., Sampath, A., Bauer, M., & Burgess, M. (2020). Positional Accuracy Assessment of Lidar Point Cloud from NAIP/3DEP Pilot Project. Remote Sensing, 12(12), 1974. https://doi.org/10.3390/rs12121974






