Adaptive Modeling of the Global Ionosphere Vertical Total Electron Content

Abstract

The Kalman filter (KF) is widely applied in (ultra) rapid and (near) real-time ionosphere modeling to meet the demand on ionosphere products required in many applications extending from navigation and positioning to monitoring space weather events and naturals disasters. The requirement of a prior definition of the stochastic models attached to the measurements and the dynamic models of the KF is a drawback associated with its standard implementation since model uncertainties can exhibit temporal variations or the time span of a given test data set would not be large enough. Adaptive methods can mitigate these problems by tuning the stochastic model parameters during the filter run-time. Accordingly, one of the primary objectives of our study is to apply an adaptive KF based on variance component estimation to compute the global Vertical Total Electron Content (VTEC) of the ionosphere by assimilating different ionospheric GNSS measurements. Secondly, the derived VTEC representation is based on a series expansion in terms of compactly supported B-spline functions. We highlight the morphological similarity of the spatial distributions and the magnitudes between VTEC values and the corresponding estimated B-spline coefficients. This similarity allows for deducing physical interpretations from the coefficients. In this context, an empirical adaptive model to account for the dynamic model uncertainties, representing the temporal variations of VTEC errors, is developed in this work according to the structure of B-spline coefficients. For the validation, the differential slant total electron content (dSTEC) analysis and a comparison with Jason-2/3 altimetry data are performed. Assessments show that the quality of the VTEC products derived by the presented algorithm is in good agreement, or even more accurate, with the products provided by IGS ionosphere analysis centers within the selected periods in 2015 and 2017. Furthermore, we show that the presented approach can be applied to different ionosphere conditions ranging from very high to low solar activity without concerning time-variable model uncertainties, including measurement error and process noise of the KF because the associated covariance matrices are computed in a self-adaptive manner during run-time.

1. Introduction

The selection of an appropriate parameter estimation strategy, which allows for handling of the large data sets from various space geodetic observation techniques, e.g., the continuously operating IGS network of GNSS receivers, is vital for (ultra) rapid and (near) real-time VTEC modeling. Recursive filtering methods, e.g., the Kalman Filter [1] and the Ensemble Kalman Filter [2], provide mathematical tools in terms of assimilating new data immediately once they are available [3,4]. These conventional filters are generally extended by adaptive approaches to cope with time-varying model uncertainties in many applications. In this sense, the focus of this paper is on the application of the adaptive discrete Kalman Filter (KF) to ultra-rapid VTEC modeling based on B-splines. The presented approach is a comprehensive extension to the study by Erdogan et al. [5] employing a conventional KF.

The discrete Kalman filter (KF) relies on consecutively performed steps, namely the time update and the measurement update; the former represents the propagation of the unknown parameters with time and the latter step is responsible for the incorporation of new allocated measurements into the filter [3]. A stochastic model attached to the deterministic models describes the corresponding covariance matrices of process and measurement noise. The conventional KF is very sensitive to these matrices which are required to be introduced beforehand. The common practice to manually define the parameters of these matrices is to perform multiple tests by executing the filter for different values of the parameters; for further details, we refer to Maybeck [6]. However, the data used in tests may not be appropriate to define these matrices. Furthermore, the covariance matrices may change with time. An inappropriate definition of these matrices can lead to an estimation of poor quality, or even worse, the filter may diverge. A self-learning filter which is capable of adapting itself to changes during run-time can cope with such situations [4]. Accordingly, several approaches, classified under the name of adaptive modeling, were proposed after Kalman’s seminal study from 1960 to tune the parameters in run-time for achieving optimal results and avoiding a filter divergence.

According to Hide et al. [7], the approaches for adaptive modeling can be categorized as (1) covariance scaling, (2) multiple-model adaptive estimation (MMAE) and (3) stochastic modeling. The first method means a simple and effective algorithm in which the predicted or process noise covariance matrix of the KF is multiplied by a factor which can be deduced from the innovations or the residuals of the filter [8,9,10]. The MMAE was introduced by Magill [11] and relies on the combination of multiple outputs derived from multiple KF instances running in parallel with different values of measurement and process noise parameters. High computational cost is the drawback of the MMAE method. Furthermore, methods based on a stochastic modeling attempt to estimate the overall covariance matrices using the innovation or residual sequences collected and stored at previous steps of the filter, see e.g., [12]. This approach makes use of data sequences collected in a time window of past epochs and suffer mostly from the fact that the size of innovations, residuals or state vectors of the filter at the consecutive epochs can change over time [13]. Furthermore, the method of variance component estimation (VCE), which goes back to the study by Helmert [14], was extensively investigated using different types of estimators to obtain a realistic stochastic model of measurement uncertainties in the sense of batch parameter estimation. We refer to, e.g., [15,16,17,18] and references therein for a comprehensive review. In recent decades, many studies were carried out in an attempt to incorporate the VCE approach into the KF to achieve a recursive and an adaptive estimator. A VCE-based adaptive KF does not require the storage of data from previous epochs of the filter and may be categorized as a covariance scaling approach. For example, Yang and Xu [13] introduced an adaptive robust Kalman filter resisting to outliers as well as determining an adaptive factor using the ratio of variance components between the measurements and the predicted state vector computed by referring to the study by [19]. Hu et al. [9] developed an adaptive estimator derived from innovations. Gao et al. [20] presented an adaptive KF based on the Helmert VCE method for the positioning and the attitude determination by integrating measurements from the Multi-Constellation GNSS and the Inertial Navigation System. Chang et al. [21] incorporated the least-squares VCE approach into a KF to estimate the epoch differenced ionospheric delay for repairing cycle slips of GNSS signals. In the framework of GNSS meteorology, Yang et al. [22] presented an adaptive KF algorithm to tune the process noise in real time by inserting the least-squares VCE method into the filter to compute precipitable water vapor content derived from estimated zenith tropospheric delays of GNSS signals.

VCE allows for the determination of proper weights for different types of observation groups with varying model uncertainties, which can exhibit limited knowledge of noise characteristics [23]. A covariance matrix of an observation type can generally be decomposed into two parts, namely a known co-factor matrix and an unknown scaling factor, i.e., the variance component. The known matrix refers to a weighting matrix determining the contributions of observations according to pre-defined quality criteria. For instance, in this study it is defined according to the elevation angle of GNSS observations. Run-time computations of the unknown variance components in a Kalman filter for each observation group allows the implementation of a computationally efficient adaptive filtering approach. When the VCE approach is chosen, it decreases the number of unknown parameters compared to the stochastic modeling approach attempting to estimate an entire covariance matrix which generally leads to a less stable filter implementation due to an increased number of unknowns as well as lack of enough observations. In this paper, we use the VCE approach for the adaptive Kalman filtering implementation to separately handle different observation groups. The estimation of variance components for each type of observations acquired from GPS and GLONASS is iteratively carried out and can be driven according to the Maximum-Likelihood method or Förstner’s iterative method, see, e.g., [16,18,23,24,25].

Contrary to physical models, empirical models are mostly data driven approaches and do not rely on physical equations and quantities. The selection of a proper empirical model which allows analyzing local structures and deducing physical interpretations from the model parameters is crucial. Ionosphere models relying on localized basis functions have been increasingly gaining popularity, for instance, applications of B-spline functions [26,27,28,29] and Slepian functions [30]. The B-spline representation of VTEC provides an empirical approximation for evaluating temporal and spatial variations. Whereas the VTEC products provided by the Ionosphere Associated Analysis Centers (IAAC) of the International GNSS Service (IGS) are mostly based on spherical harmonics (SH), i.e., basis function of global support, DGFI-TUM aims at VTEC representations using series expansions in terms of B-spline functions. B-splines are an appropriate mathematical tool for handling the heterogeneous input data distribution including data gaps [31] due to their compact support. Moreover, they allow the generation of a multi-scale signal analysis of VTEC [26,32,33,34] and can easily be extended for multi-dimensional model definitions, e.g., for 3D/4D electron density modeling [27,35,36].

By exploiting the advantages of B-splines, we show that the estimated B-spline coefficients resemble the global VTEC structure in terms of shape and magnitude, which paves the way of assigning a physical meaning to the B-spline coefficients. For instance, we found a very high correlation between a time series of mean B-spline coefficients and corresponding mean VTEC values providing a valuable indicator about temporal VTEC activity as well as space weather events. The physical interpretation of the coefficients leads to extending the definition of the stochastic model attached to the dynamic model, which is also called the prediction model of the KF. In this context, an exponential empirical model taking the mean value of the B-spline coefficients and their relative variations into account is introduced to define the uncertainty of the prediction model. Moreover, the compact support property of the B-spline representation provides additional flexibility to locally tune the sensitivity of the filter to observations without causing a global effect. This is unlikely for models making use of globally defined basis functions e.g., spherical harmonics. The empirical model is extended to consider the number of observations to keep the filter more sensitive to the observations at regions including very high data density.

In summary, the main goal of the present study is to introduce an adaptive KF for VTEC modeling using a B-splines series expansion. The measurement covariance matrices of the GNSS observations are adaptively obtained using the VCE approach. We highlight structural similarities between the spatial distributions of VTEC over the globe and the estimated B-spline coefficients that allow for deducing physical interpretations from the coefficients. Accordingly, we introduce an adaptive empirical model for the process noise covariance matrix of the B-spline coefficients regarding the temporal and spatial variation of VTEC. The presented adaptive filtering approach can significantly reduce the efforts to define or to set up the model uncertainties. Moreover, exploiting the localizing property of the B-spline basis functions allows for tuning the filter sensitivity to observations in the vicinity of a point without causing a significant global effect, which means a huge advantage w.r.t. methods relying on globally defined basis functions such as spherical harmonics. The approach is applied to ultra-rapid VTEC modeling by assimilating carrier phase and pseudo-range observations from GPS and GLONASS, which can be extended for additional GNSS constellations such as GALILEO or measurement techniques such as the DORIS (Doppler Orbitography and Radiopositioning Integrated by Satellite) technique. The presented adaptive algorithm was recently employed in [37] to generate high-resolution VTEC maps of Europe by means of a series expansion in B-spline functions.

The paper is outlined as follows. The first section shows the B-spline representation for global VTEC modeling and the definition of the selected coordinate system. In Section 3, the extraction of ionosphere observations from raw hourly GNSS data is explained. Section 4 gives the background for the sequential estimation algorithm using the adaptive KF. This section comprises the introduction of the measurement and prediction models of the filter, the fundamentals of the adaptive Kalman filtering using variance components, and the handling of the model constraints in the filter. Section 5 explains the validation techniques, accuracy of the presented approach, and discussions. Finally, Section 6 provides the conclusion and future work.

2. Global VTEC Representation Based On B-Splines

In this study, the B-spline representation of the global VTEC distribution reads

$$VTEC(\phi ,\lambda ,t)={\displaystyle \sum _{k_1=0}^{K_{J_1}-1}}{\displaystyle \sum _{k_2=0}^{K_{J_2}-1}}{d}_{k_1,k_2}^{J_1,J_2}(t)N_{J_1,k_1}^2(\phi )T_{J_2,k_2}^3(\lambda ),$$

(1)

where $d_{k_1,k_2}^{J_1,J_2}(t)$ are the time-dependent unknown B-spline coefficients, $N_{J_1,k_1}^2(\phi )$ are the polynomial B-spline functions of degree 2 depending on the latitude $\phi$, and $T_{J_2,k_2}^3(\lambda )$ are the trigonometric B-splines of order 3 depending on the longitude $\lambda$ [26,31,32]. The geometrical positions of the two-dimensional (2-D) basis functions $N_{J_1,k_1}^2(\phi )·T_{J_2,k_2}^3(\lambda )$ on the sphere are described by the values $k_1$ and $k_2$. $K_{J_1}$ stands for the number of polynomial B-spline functions according to the associated level $J_1$ and, similarly, the number of trigonometric B-spline functions for the level $J_2$ is given by $K_{J_2}$. Accordingly, the numerical values of $K_{J_1}$ for the level $J_1$ and $K_{J_2}$ for the level $J_2$ are given as $K_{J_1}=2^{J_1}+2$ and $K_{J_2}=3·2^{J_2}$.

For the implementation of the B-spline functions, we refer to the approach introduced by [29] and applied to ionosphere modeling by [26,31,34]. Compared to the global representation given by [28] and employed e.g., by [5] for VTEC modeling, the advantage of the implemented approach is that the continuity at the longitudinal boundaries are satisfied by definition. This leads to setting up a smaller number of trigonometric B-spline functions and no additional constraints have to be formulated. However, the global representation requires introducing constraints to handle the spherical geometry, since the 2-D B-spline model represents a function defined on a sphere [28]. Two sets of constraint equations, namely the pole equality and the pole continuity have to be taken into account.

The criteria which are considered to select the resolution levels $J_1$ and $J_2$ for the B-spline representation in the Kalman filter implementation depend, e.g., on the distribution of the input data, the computational burden and the desired level of smoothness [5]. Increasing the number of basis functions leads to a B-spline definition enabling the representation of high resolution details on VTEC maps, but the computational load of the Kalman filter increases in return. Contrarily, the levels chosen too low can cause an undesired smoothing on VTEC variations, which may lead to a loss of information.

A representation quality comparable to the IGS final products can be obtained by setting, e.g., $J_1=4$ and $J_2=3$ which correspond to the maximum SH degrees of about 17 and 12 in latitude and longitude, respectively [32]. These levels of resolution were employed by [5] in a Kalman filter setting using B-spline basis functions. Considering an increasing number of IGS GNSS receiver sites, providing hourly measurements with improved geographical distribution, the resolution level can be increased further. A higher resolution B-spline representation with level values $J_1=5$ and $J_2=3$ in comparison to a spherical harmonic representation and the VTEC products of the IGS analysis centers (CODE and UPC) were studied by [32]. By taking into account the trade-off between the resolution level and the computational burden when running the filter in an operational mode, B-spline level values of $J_1=5$ and $J_2=3$ were selected in this study.

Coordinate System

The Earth’s magnetic field plays a crucial role on dynamics, structure and formation of the upper atmosphere and space weather phenomena such as ionospheric plasma motion, polar lights, the electron density distribution and the equatorial ionization anomaly. A proper selection of the coordinate system can become significant in terms of the strength of a dominating driver. For instance, at the altitudes close to the Earth’s surface, the geomagnetic field is stronger than the magnetic disturbances derived by solar winds, so that, a coordinate system aligned with the Earth’s magnetic dipole axis would be more appropriate for ionospheric phenomena [38]. Solar magnetic coordinates, which take into account the shift of the dipole axis from the Earth’s rotation axis, are usually adapted for ionospheric electron content modeling (e.g., Mannucci et al. [39]). In opposite to this simple dipole approximation, a better representation of the Earth’s magnetic field can be obtained by considering the non-dipole features of the field which can show significant deviation from the center dipole approximation at the ionospheric altitudes. Corrected geomagnetic coordinates [40,41], modified apex coordinates and quasi-dipole (QD) coordinates [42] are some examples which come at the expense of, e.g., a high computational load, complexity and non-orthogonality. For example, the apex coordinates are employed in physics-based models simulating the thermospheric and ionospheric behavior, such as the Thermosphere Ionosphere Electrodynamics General Circulation Model (TIEGCM) [43,44,45]. Among the ionosphere modeling community, the modified dip latitude (MODIP) coordinates [46], which takes the Earth’s magnetic field into account to compute the latitude of a given point in terms of the dip latitude, are also in use. Azpilicueta et al. [47] applied the MODIP coordinates to the VTEC representation using spherical harmonics and declared a significant improvement in their solutions compared to the VTEC solution obtained using geographic latitude.

Since the Sun is the primary driver of the photo-ionization process, it causes spatio-temporal variations in the ionosphere. In VTEC modeling, keeping the VTEC structure aligned with the position of the Sun leads to a Sun-fixed coordinate system definition. This mitigates the effect of the Earth’s diurnal motion that leads to a much slower temporal variation of ionospheric VTEC (see e.g., Mannucci et al. [39], Komjathy and Langley [48]).

In this study, in order to consider the effects of the magnetic field and the Sun on the formation of VTEC structure, a solar magnetic coordinate system (GSM) (e.g., [49]) is used. The z-axis of the GSM coordinates aligns with the centered dipole axis and points to the Northern Hemisphere. The x-axis is defined such that the x-z plane contains the Sun–Earth line and the y-axis is perpendicular to the Sun–Earth line.

3. GNSS Ionospheric Observables

Due to the dispersive characteristics of the ionosphere, electromagnetic signals transmitted by the GNSS satellites are refracted while traveling through the medium. The rate of the ionospheric refraction varies with respect to the frequencies of the transmitted signals. The geometry-free linear combination of the code pseudo-ranges observations $P_{r,f_1}^s$ and $P_{r,f_2}^s$ as well as the carrier-phases observations ${\mathsf{\Phi }}_{r,f_1}^s$ and ${\mathsf{\Phi }}_{r,f_2}^s$, acquired from GPS and GLONASS signals at the distinct carrier frequencies $f_1$ and $f_2$, lead to the ionospheric observables

$$\begin{array}{cc}\hfill P_{\mathrm{I},r}^s& =P_{r,f_2}^{\mathrm{s}}-P_{r,f_1}^{\mathrm{s}}={\alpha }_r^s·\mathrm{STEC}+b_{\mathrm{r}}+b^{\mathrm{s}}+e_{P_{\mathrm{I},r}^s},\hfill \end{array}$$

(2a)

$$\begin{array}{cc}\hfill L_{\mathrm{I},r}^s& ={\mathsf{\Phi }}_{r,f_1}^s-{\mathsf{\Phi }}_{r,f_2}^{\mathrm{s}}={\alpha }_r^s·\mathrm{STEC}+B_{\mathrm{r}}+B^{\mathrm{s}}+B_{\mathrm{A},r}^s+e_{L_{\mathrm{I},r}^s}\hfill \end{array}$$

(2b)

where $P_{\mathrm{I},r}^s$ and $L_{\mathrm{I},r}^s$ are the pseudo-range and the carrier-phase ionosphere combinations, respectively [50]. $B_{\mathrm{r}}$ and $B^{\mathrm{s}}$ refer to the receiver and the satellite inter-frequency biases (IFB) of the carrier phase observations, $b_{\mathrm{r}}$ and $b^{\mathrm{s}}$ are the pseudo-range IFB of the receiver and the satellite, respectively, which are also commonly called differential code biases (DCB). The combined ambiguity bias of the carrier-phase observations is denoted by $B_{\mathrm{A},r}^s$. The terms $e_{P_{\mathrm{I},r}^s}$ and $e_{L_{\mathrm{I},r}^s}$ stand for the measurement errors. Furthermore, considering $P_{\mathrm{I},r}^s$ and $L_{\mathrm{I},r}^s$ are given in units of meters, ${\alpha }_r^s$ is a frequency-dependent factor defined as ${\alpha }_r^s=40.3\frac{(f_1^2-f_2^2)}{(f_1^2{f}_2^2)}{10}^{16}$.

The pseudo-range ionosphere combination (2a) is rather noisy but unambiguous. Although the carrier-phase ionosphere combination is around two orders of magnitude more precise, it is biased by an unknown integer number of cycles [50,51]. A widely common approach for mitigating the ambiguity and exploiting the precision of the carrier-phase observation is the so-called leveling bias computation [39,52]. The leveling bias $C_r^s$ includes the IFBs and the carrier-phase ambiguity term. It can be determined by the weighted averaging of the epoch-wise differencing of $L_{\mathrm{I},r}^s$ and $P_{\mathrm{I},r}^s$ and reads

$$\begin{array}{cc}\hfill C_r^s& \approx \frac{{\displaystyle \sum _i}{w}_i\left(L_{\mathrm{I},r,i}^s-P_{\mathrm{I},r,i}^s\right)}{{\displaystyle \sum _i}{w}_i}+e_{C_r^s}\hfill \\ \hfill & \approx {〈B_{\mathrm{r}}+B^{\mathrm{s}}+B_{\mathrm{A},r}^s-b_{\mathrm{r}}-b^{\mathrm{s}}〉}_w\hfill \end{array}$$

(3)

where $w_i$ is the weight of the $i^{\mathrm{th}}$ observation referring to the precision of the differenced observations on a phase continuous arc (see e.g., [39]). The term $e_{C_r^s}$ is the error of the leveling bias. The value for the weight $w_i$ can be determined by taking into account, e.g., the elevation angle of the observations, the receiver tracking modes and the signal power. Prior to the computation of the leveling bias, a two step cycle slip detection method, which is composed of a double differences of ionospheric phase observations and the Melbourne-Wübbena combination, is applied for the detection of jumps and the construction of phase continuous arcs between receivers and satellite pairs [53,54,55].

Once the leveling bias is obtained, the leveled carrier-phase ionospheric observations ${\tilde{L}}_{\mathrm{I},r}^s$ along a continuous arc are computed by

$$\begin{array}{cc}\hfill y_r^s={\tilde{L}}_{\mathrm{I},r}^s& =L_{\mathrm{I},r}^{\mathrm{s}}-C_r^s\hfill \\ \hfill & ={\alpha }_r^s·\mathrm{STEC}+b_{\mathrm{r}}+b^{\mathrm{s}}+e_{{\tilde{L}}_{\mathrm{I},r}^s}\hfill \end{array}$$

(4)

where $e_{{\tilde{L}}_{\mathrm{I},r}^s}$ refer to the error of the leveled carrier-phase ionosphere combination which is dominated by the error $e_{C_r^s}$ of the leveling bias.

The accuracy and the precision of the leveling bias in Equation (3) depends on different factors which are primarily measurement noise and multipath effects. The measurement noise on carrier-phase measurements can be neglected, since those effects are much smaller compared to the ones on the code measurements. Ciraolo et al. [50] showed that the multipath effect on code measurements is a primary error source that cannot totally be removed in Equation (3) by the averaging procedure and can vary for different receivers and antennas types. Besides, depending on the environmental conditions around the receivers, the IFBs of code measurements can present intra-day variations that violate the long term stability assumption on the IFBs, and consequently result in a systematic error in the leveling bias.

To reduce the effects of the systematic errors, the following measures are considered in the computation of the leveled carrier-phase observable:

• Observations with an elevation angle of less than 10${}^{\circ }$ were rejected from the data to avoid contributions from likely very noisy measurements.
• Since the quality of the averaging procedure in Equation (3) relies on the length of a given phase continuous arc [39], a minimum threshold of 30 min arc length is applied to mitigate the pseudo-range noise.
• To mitigate the errors due to multi-path effects on pseudo-range measurements, which are generally inversely proportional to the satellite elevation angle, only the observations with elevation angles larger than 20${}^{\circ }$ are included in the determination of the leveling bias (3).
• Moreover, an elevation dependent weighting function, e.g., $w_i=\sin (e_i)$, is introduced to leverage the influence of more precise observations. $e_i$ means the elevation angle of the $i\mathrm{th}$ observation along the arc.
• A pre-processing algorithm was developed for the recursive processing of GNSS data acquired as hourly data blocks broadcasted, e.g., by the IGS global data centers. To reach a maximum number of observations and a high pre-processing quality, data blocks with a moving window of 3 h length are considered. For instance, to apply the pre-processing procedures to a new acquired data set between $t_k$ and $t_k+1h$, a data set with a window length of 3 h extending from $t_k-2h$ to $t_k+1h$ is considered for a more accurate computation of the leveling bias.

Assuming that the code and carrier-phase ionosphere observations are uncorrelated throughout a continuous arc, the variance of the leveled carrier-phase observations can be derived by applying the law of error propagation to Equation (4). Consequently, the variance ${\sigma }_{{\tilde{L}}_{\mathrm{I},r}^s,k}^2$ reads

$$\begin{array}{c}\hfill {\sigma }_{{\tilde{L}}_{\mathrm{I},r}^s,k}^2=\left\{\begin{array}{c}{\sigma }_{L_{\mathrm{I},r}^s}^2\frac{{(W_T-w_k)}^2}{W_T^2}+\frac{{\sigma }_{L_{\mathrm{I},r}^s}^2}{W_T^2}{\displaystyle \sum _{l=l_b}^{l_e}}{w}_l^2(1-{\delta }_{lk})+\frac{{\sigma }_{P_{\mathrm{I},r}^s}^2}{W_T^2}{\displaystyle \sum _{l=l_b}^{l_e}}{w}_l^2,\mathrm{if}{l}_b\le k\le l_e\hfill \\ {\sigma }_{L_{\mathrm{I},r}^s}^2+\frac{{\sigma }_{L_{\mathrm{I},r}^s}^2}{W_T^2}{\displaystyle \sum _{l=l_b}^{l_e}}{w}_l^2+\frac{{\sigma }_{P_{\mathrm{I},r}^s}^2}{W_T^2}{\displaystyle \sum _{l=l_b}^{l_e}}{w}_l^2,\mathrm{otherwise}\hfill \end{array}\right.\end{array}$$

(5)

where $k=1,\cdots ,N$ is the time index of the observations along an arc with a total number of N observations. $l_b$ and $l_e$, respectively, refer to the beginning and the end points on the arc that bind the data used for the determination of the leveling bias in Equation (3) and ${\delta }_{lk}$ is the Kronecker delta symbol. Herein the total weight is $W_T={\displaystyle \sum _{l=l_b}^{l_e}}{w}_l$. Following the Equations (2a) and (2b), the variances ${\sigma }_{P_{\mathrm{I},r}^s}^2$ and ${\sigma }_{L_{\mathrm{I},r}^s}^2$ of pseudo-range and carrier phase ionosphere combinations approximately read ${\sigma }_{P_{\mathrm{I},r}^s}^2\approx {\sigma }_{P_{r,f_1}^s}^2+{\sigma }_{P_{r,f_2}^s}^2$ and ${\sigma }_{L_{\mathrm{I},r}^s}^2\approx {\sigma }_{{\mathsf{\Phi }}_{r,f_1}^s}^2+{\sigma }_{{\mathsf{\Phi }}_{r,f_2}^s}^2$.

4. Adaptive Estimation of Global Ionospheric VTEC

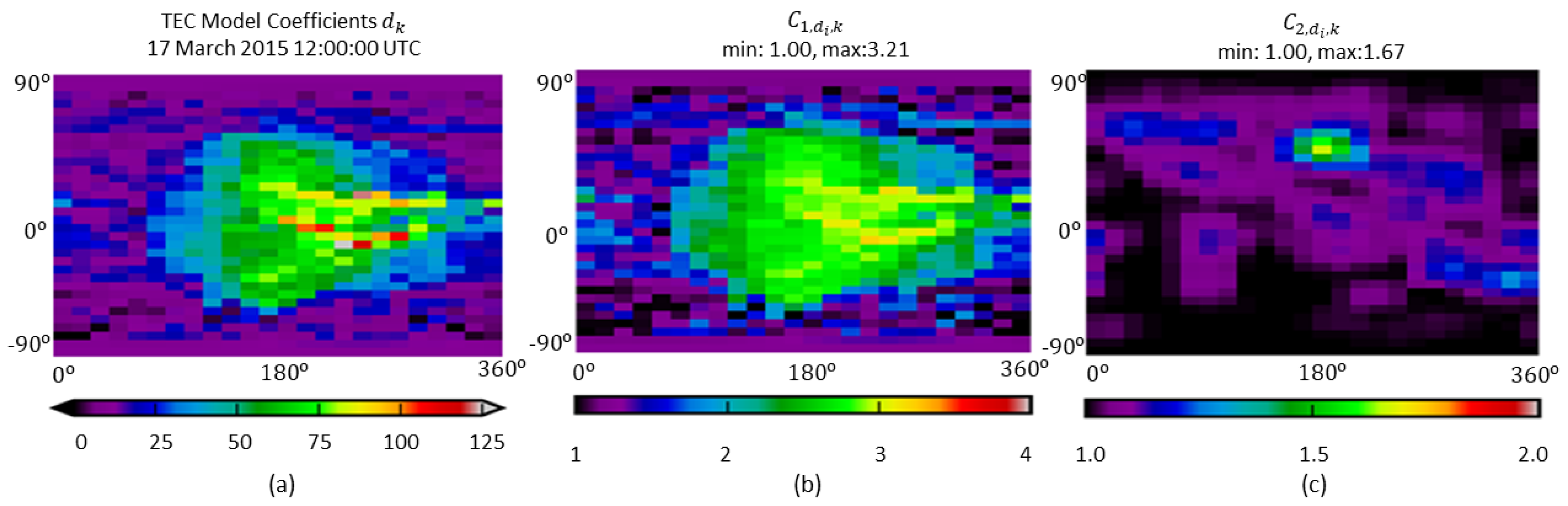
4.1. Model Definition

The discrete linear system of equations describing a dynamical process is given by

$$\begin{array}{ccc}\hfill {\mathit{\beta }}_k& =& {\mathbf{F}}_k{\mathit{\beta }}_{k-1}+{\mathit{w}}_{k-1}\hfill \end{array}$$

(6)

$$\begin{array}{ccc}\hfill {\mathit{y}}_k& =& {\mathbf{X}}_k{\mathit{\beta }}_k+{\mathit{e}}_k\hfill \end{array}$$

(7)

where k is the time stamp, ${\mathbf{F}}_k$ is the transition matrix, ${\mathit{\beta }}_k$ the vector of the unknown parameters, ${\mathit{y}}_k$ is the vector of the observations and ${\mathbf{X}}_k$ is the corresponding design matrix. The measurement error vector ${\mathit{e}}_k$ and the vector of the process noise ${\mathit{w}}_k$ are normal distributed, i.e., ${\mathit{w}}_k\sim N(\mathbf{0},{\mathsf{\Sigma }}_{w,k})$ and ${\mathit{e}}_k\sim N(\mathbf{0},{\mathsf{\Sigma }}_{y,k})$ and fulfill the assumptions

$$E\left[{\mathit{w}}_k{\mathit{w}}_l^T\right]={\mathsf{\Sigma }}_w{\delta }_{kl},E\left[{\mathit{e}}_k{\mathit{e}}_l^T\right]={\mathsf{\Sigma }}_y{\delta }_{kl}$$

(8)

and

$$E\left[{\mathit{w}}_k{\mathit{e}}_l^T\right]=\mathbf{0}\mathrm{for}\mathrm{all}k,l$$

(9)

The covariance matrices referring to the vectors ${\mathit{e}}_k$ and ${\mathit{w}}_k$ are automatically computed by the introduced algorithms in a self-learning manner. Accordingly, the adaptive algorithm defining the covariance matrix of the measurement error vector is explained in Section 4.4. The developed time-varying adaptive model of the process noise covariance matrix for the ionospheric target parameters is presented and discussed in Section 4.3.

4.2. Measurement Model

The measurement equations following from Equation (4) are re-written as

$$\begin{array}{cc}\hfill y_{{\mathrm{GPS}}_r^s,k}& =m(z_{r,k}^s)·VTE{C}_k+\frac{c·{10}^{-9}}{{\alpha }_r^s}\left(b_{r,\mathrm{GPS}}+b_{\mathrm{GPS}}^s\right)+e_{\mathrm{GPS},k},\hfill \\ \hfill y_{{\mathrm{GLO}}_r^s,k}& =m(z_{r,k}^s)·VTE{C}_k+\frac{c·{10}^{-9}}{{\alpha }_r^s}\left(b_{r,\mathrm{GLO}}+b_{\mathrm{GLO}}^s\right)+e_{\mathrm{GLO},k}\hfill \end{array}$$

(10)

where $y_{{\mathrm{GPS}}_r^s,k}$ and $y_{{\mathrm{GLO}}_r^s,k}$ are the leveled ionospheric observations in TECU at time stamp k for the GPS and GLONASS constellations. The quantity $STEC$ in Equation (4) at time $t_k$ is represented by the so-called Single Layer Model (SLM) (see e.g., [56]) as $STE{C}_k=m(z_{r,k}^s)·VTE{C}_k$ where $m(·)$ stands for the Modified Single Layer Mapping Function depending on the satellite elevation angle $z_{r,k}^s$ [56,57]. Moreover, $VTE{C}_k$ at time $t_k$ is given by Equation (1). The values $b_{r,\mathrm{GPS}}$, $b_{r,\mathrm{GLO}}$ and $b_{\mathrm{GPS}}^s$, $b_{\mathrm{GLO}}^s$ stand for the receiver and the satellite DCBs in nanosecond for GPS and GLONASS. The speed of light is denoted as c in m/s.

The state vector ${\mathit{\beta }}_k$ of the linear models given by the Equations (6) and (7) consists of the sub-vector ${\mathit{d}}_k=(d_{k_1,k_2}^{J_1,J_2}(t_k))$ of the unknown B-spline coefficients $d_{k_1,k_2}^{J_1,J_2}(t_k)$, the sub-vectors ${\mathit{b}}_{\mathrm{GPS},k}$ and ${\mathit{b}}_{\mathrm{GLO},k}$ referring to the receiver DCBs and ${\mathit{b}}_k^{\mathrm{GPS}}$ and ${\mathit{b}}_k^{\mathrm{GLO}}$ standing for the satellite DCBs. Thus, the vectors ${\mathit{\beta }}_k$ and ${\mathit{y}}_k$ read

$${\mathit{\beta }}_k=\left[\begin{array}{c}{\mathit{d}}_k\\ {\mathit{b}}_{\mathrm{GPS},k}\\ {\mathit{b}}_k^{\mathrm{GPS}}\\ {\mathit{b}}_{\mathrm{GLO}.k}\\ {\mathit{b}}_k^{\mathrm{GLO}}\end{array}\right],{\mathit{y}}_k=\left[\begin{array}{c}{\mathit{y}}_{\mathrm{GPS},k}\\ {\mathit{y}}_{\mathrm{GLO},k}\end{array}\right].$$

(11)

Consequently, the design matrix ${\mathbf{X}}_k$ is given as

$${\mathbf{X}}_k=\left[\begin{array}{ccccc}{\mathbf{X}}_{d_{\mathrm{GPS}},k}& {\mathbf{X}}_{b_{\mathrm{GPS}},k}& {\mathbf{X}}_{b^{\mathrm{GPS}},k}& \mathbf{0}& \mathbf{0}\\ {\mathbf{X}}_{d_{\mathrm{GLO}},k}& \mathbf{0}& \mathbf{0}& {\mathbf{X}}_{b_{\mathrm{GLO}},k}& {\mathbf{X}}_{b^{\mathrm{GLO}},k}\end{array}\right].$$

(12)

Herein, ${\mathbf{X}}_{d_{\mathrm{GPS}},k}$ and ${\mathbf{X}}_{d_{\mathrm{GLO}},k}$ are the design sub-matrices of GPS and GLONASS observations in connection with the vector ${\mathit{d}}_k$ of unknown B-spline coefficients. The design sub-matrices for the GPS and GLONASS receiver DCBs are ${\mathbf{X}}_{b_{\mathrm{GPS}},k}$ and ${\mathbf{X}}_{b_{\mathrm{GLO}},k}$. In the same way, the sub-matrices ${\mathbf{X}}_{b^{\mathrm{GPS}},k}$ and ${\mathbf{X}}_{b^{\mathrm{GLO}},k}$ refer to the design matrices of the satellite DCBs.

Assuming the vectors ${\mathit{y}}_{\mathrm{GPS},k}$, and ${\mathit{y}}_{\mathrm{GLO},k}$ are uncorrelated, the measurement covariance matrix ${\mathsf{\Sigma }}_{y,k}$ consisting of the covariance matrices ${\mathsf{\Sigma }}_{y_{GPS},k}$ and ${\mathsf{\Sigma }}_{y_{GLO},k}$ for GPS and GLONASS reads

$${\mathsf{\Sigma }}_{y,k}=\left[\begin{array}{cc}{\mathsf{\Sigma }}_{y_{\mathrm{GPS}},k}& \mathbf{0}\\ \mathbf{0}& {\mathsf{\Sigma }}_{y_{\mathrm{GLO}},k}\end{array}\right].$$

(13)

This study aims on the computation of the measurement covariance matrix ${\mathsf{\Sigma }}_{y,k}$ in run-time by employing an appropriate adaptive estimation method. For problems with a large number of unknowns and/or measurements, the computation of each component in the measurement covariance matrix results in very high complexity and computational burden. Additionally, an unstable filter implementation would emerge due to a lack of a sufficient number of observations. To cope with these problems, a common simplified approach is to assume that the covariance matrix is known up to a scaling factor. Taking VCE into account, this factor can be handled as an unknown variance component. Accordingly, the measurement covariance matrix ${\mathsf{\Sigma }}_{y_j,k}$ for each observation technique $j\in \{1,\dots ,p\}$ with the associated variance component ${\sigma }_{y_j,k}^2$ is expressed by (see [19] )

$${\mathsf{\Sigma }}_{y_j,k}={\sigma }_{y_j,k}^2{\mathbf{P}}_{y_j,k}^{-1}$$

(14)

where ${\mathbf{P}}_{y_j,k}$ is the appropriate weight matrix. Consequently, considering that $y_1=y_{\mathrm{GPS}},{\sigma }_{y_1,k}^2={\sigma }_{y_{GPS},k}^2$ and $y_2=y_{\mathrm{GLO}},{\sigma }_{y_2,k}^2={\sigma }_{y_{GLO},k}^2$, Equation (13) can be written as

$${\mathsf{\Sigma }}_{y,k}=\left[\begin{array}{cc}{\sigma }_{y_{\mathrm{GPS}},k}^2{\mathbf{P}}_{y_{\mathrm{GPS}},k}^{-1}& \mathbf{0}\\ \mathbf{0}& {\sigma }_{y_{\mathrm{GLO}},k}^2{\mathbf{P}}_{y_{\mathrm{GLO}},k}^{-1}\end{array}\right],$$

(15)

where ${\sigma }_{y_{\mathrm{GPS}},k}^2$ and ${\sigma }_{y_{\mathrm{GLO}},k}^2$ are the unknown variance components for GPS and GLONASS. The matrices ${\mathbf{P}}_{y_{\mathrm{GPS}},k}$ and ${\mathbf{P}}_{y_{\mathrm{GLO},k}}$ are given positive definite matrices which can be determined to ensure more contributions from the precise observations by introducing high relative weights. In this sense, the weight matrix can refer to numerous quality factors for GNSS observations, such as the satellite elevation angle, the receiver-antenna configuration and the signal strength. A common and simple strategy is to adapt an elevation-dependent weighting scheme for each individual observation. Assuming that the observations are uncorrelated, the weight matrix ${\mathbf{P}}_{y_j,k}$ becomes a diagonal matrix and its diagonal element $p_{nn}$ can be defined by

$$p_{nn}=\frac{1}{{\sigma }_{{\tilde{L}}_{\mathrm{I},r}^s,k}^2(1+{sin}^2(z_m))}$$

(16)

where $z_m$ is the zenith angle of the mth measurement. The term ${\sigma }_{{\tilde{L}}_{\mathrm{I},r}^s,k}^2$ refers to the prior observation variance described by Equation (5).

4.3. Prediction Model

Since VTEC is a time varying phenomenon, a proper model is required to represent its propagation between consecutive epochs $t_{k-1}$ and $t_k$ in accordance with Equation (6).

In the current implementation of the approach, VTEC is represented in the GSM, and thus, leading to slow temporal variations in the corresponding B-spline coefficients. Accordingly, a simple model based on a random walk process is set to represent the temporal variations. Moreover, it should be noted that the unknown system biases, precisely the GNSS DCBs are also quite stable over the course of time, which allows the use of simple prediction models, too. Consequently, a random walk process is introduced as a prediction model for these biases. The entire prediction model with ${\mathbf{F}}_k=\mathbf{I}$ of the state vector reads, therefore, following from Equation (6)

$${\mathit{\beta }}_k={\mathit{\beta }}_{k-1}+{\mathit{w}}_k$$

(17)

where ${\mathit{w}}_k$ is the process noise vector with the covariance matrix ${\mathsf{\Sigma }}_{w,k}$ defined as

$${\mathsf{\Sigma }}_{w,k}=\left[\begin{array}{ccccc}{\mathsf{\Sigma }}_{w_d,k}& \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}\\ \mathbf{0}& {\sigma }_{b_{r,\mathrm{GPS}}}^2{\mathbf{I}}_{m_1}& \mathbf{0}& \mathbf{0}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}& {\sigma }_{b_{\mathrm{GPS}}^s}^2{\mathbf{I}}_{m_2}& \mathbf{0}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}& \mathbf{0}& {\sigma }_{b_{r,\mathrm{GLO}}}^2{\mathbf{I}}_{m_3}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}& {\sigma }_{b_{\mathrm{GLO}}^s}^2{\mathbf{I}}_{m_4}\end{array}\right]$$

(18)

where ${\mathsf{\Sigma }}_{w_d,k}$ is the diagonal matrix consisting of the components ${\sigma }_{d_i,k}^2$ with $i=\{1,\dots ,K_{J_1}·K_{J_2}\}$ corresponding to the variance of the random walk process for each B-spline coefficients. The quantities ${\sigma }_{b_{r,\mathrm{GPS}}}^2$, ${\sigma }_{b_{r,\mathrm{GLO}}}^2$, ${\sigma }_{b_{\mathrm{GPS}}^s}^2$, and ${\sigma }_{b_{\mathrm{GLO}}^s}^2$ are the variance components of the receiver and satellite DCBs for GPS and GLONASS, respectively. Moreover, ${\mathbf{I}}_{m_l}$ with $l=\{1,\dots ,4\}$ are identity matrices of different sizes for each type of DCB. Process noise variances should be set properly, since these values effect the filter performance. The improper selection of the process noise could lead to a divergence of the filter. Moreover, the process noise plays an important role to tune the sensitivity of the filter to the measurements. The higher the value of the process noise the more sensitive is the filter not only to the measurements but also to, e.g., outliers and undetected biases in the measurements. For instance, increasing the process noise results in larger values of the predicted covariance matrix ${\mathsf{\Sigma }}_{\beta ,k}^{-}$ in Equation (31) which leads to a relatively high weighting of the measurements.

Considering the changing environmental conditions, such as seasonal solar activity or solar storms, the error of the prediction model for the B-spline coefficients is time dependent. Therefore, each process noise variance component ${\sigma }_{d_i,k}^2$ of ${\mathsf{\Sigma }}_{w_d,k}$ in Equation (18) changes with time. The difficulty in assigning a proper process noise to the B-spline coefficients arises from the fact that the coefficients do not have a physical meaning. However, fortunately, the structure of B-spline coefficients resembles the VTEC signal. For instance, VTEC maps derived from the IGS final GIM product for 17 March 2015 are illustrated in the top row of Figure 1 and the coefficients of the corresponding B-spline representation are depicted in the bottom row. The coefficients are estimated by fitting the B-spline model (1) to the VTEC values given on a regular grid obtained from the IGS product. The spatial resolution of the grid is of 5${}^{\circ }$ × 2.5${}^{\circ }$ in longitude and latitude and the corresponding VTEC values are given in an Earth-fixed geographic coordinate system. The similarity of the structures between the VTEC values and the B-spline coefficients paves the way of deducing physical information from B-spline coefficients.

In this regard, the mean VTEC value at a given time provides an appropriate indicator representing the overall VTEC activity sensitive to seasonal, monthly and daily variations (see e.g., [56]). Moreover, abnormal variations due to high solar activities can be detected from the mean VTEC value (see e.g., [58] in case of coronal mass ejections). The global mean VTEC values of the IGS final GIMs during the year 2015 with a temporal sampling of 2 h are plotted (red dots) in Figure 2. In the same figure, the corresponding mean values of the B-spline coefficients are illustrated by blue dots. There is a very high correlation between the mean VTEC values and the corresponding mean B-spline coefficients, namely $\rho =0.999$.

In the general case, the variance of a random walk process can be defined as

$${\sigma }_{d_i,k}^2={\dot{q}}_{d_i,k}·\Delta t$$

(19)

where $\Delta t$ is the length of the time step between two consecutive epochs (i.e., $\Delta t=t_k-t_{k-1}$) and $\dot{q_k}$ is the variance rate referring to the change of the variance with time [39,59]. Considering that the B-spline coefficients resemble the structure of the VTEC signal, the variance rate ${\dot{q}}_{d_i,k}$ of the process noise ${\sigma }_{d_i,k}^2$ for the coefficient $d_{i,k}$ is defined by the product

$${\dot{q}}_{d_i,k}=C_{0,k}·C_{1,d_{i,k}}·C_{2,d_{i,k}}.$$

(20)

The coefficient $C_{0,k}$ is given as

$$C_{0,k}=m_s·{\overline{d}}_k$$

(21)

where $m_s$ is a constant value determined experimentally. The mean absolute value ${\overline{d}}_k$ of the absolute value of the B-spline coefficients for global VTEC modeling is given as

$${\overline{d}}_k=\frac{1}{K_1{K}_2}{\displaystyle \sum _{k_1=0}^{K_1-1}}{\displaystyle \sum _{k_2=0}^{K_2-1}}\left|d_{k_1,k_2}^{J_1,J_2}(t_k)\right|.$$

(22)

$C_{1,d_{i,k}}$ and $C_{2,d_{i,k}}$ are coefficients to tune the filter sensitivity according to spatial variations of the B-spline coefficients and data distribution. The model error of the random walk approach for a B-spline coefficient is proportional to the ionospheric activity, since the higher the VTEC values, the larger the associated B-spline coefficients as well as the higher is the ionospheric activity. In this context, the coefficients $C_{1,d_{i,k}}$ are introduced to represent the relative variations of the process noise in magnitude between the B-spline coefficients. The coefficients $C_{1,d_{i,k}}$ are defined by using an exponential empirical model as

$$C_{1,d_{i,k}}=1+{\mathrm{e}}^{\left(1-\frac{{\overline{d}}_k}{\left|d_{i,k}\right|}\right)}$$

(23)

where the e-function allows the generation of bounded values approaching to a limit value. From the Equations (19), (20) and (23), a relatively high process noise is assigned to a coefficient which has a large absolute value. Additionally, a further control on the filter behavior with respect to the data distribution can locally be accomplished using the B-spline representation. The sensitivity of the filter to ionosphere observations can be tuned regionally. For instance, the European and the North American regions have a very dense data distribution. By a proper setting of the process noise of the B-spline coefficients corresponding to these regions, the filter can be forced to be more sensitive to these observations without causing a global effect. To this end, the coefficient $C_{2,d_{i,k}}$ is introduced and defined by

$$C_{2,d_{i,k}}={\mathrm{e}}^{\left(m_w·\frac{N_{d_i,k}}{N_{d_{total},k}}\right)}$$

(24)

where $m_w$ is a constant value determined experimentally. The term $N_{d_i,k}$ stands for the number of measurements supporting the B-spline coefficient $d_i$ and it can be obtained, e.g., by counting the total number of non-zero elements through the corresponding column of the design matrix in Equation (12). Furthermore, the term $N_{d_{total},k}$ is the total number of observations at the epoch $t_k$. Exemplary illustrations for the maps of the coefficients, $C_{1,d_i,k}$ and $C_{2,d_i,k}$ with $C_{0,k}=0.0006$ are shown in Figure 3 referring to the time epoch 12:00 UTC, 17 March 2015 (see Section 5.3.1 for the corresponding VTEC map).

The process noise variance components ${\sigma }_{b_{r,\mathrm{GPS}}}^2$, ${\sigma }_{b_{r,\mathrm{GLO}}}^2$, ${\sigma }_{b_{\mathrm{GPS}}^s}^2$, and ${\sigma }_{b_{\mathrm{GLO}}^s}^2$ for the DCBs in the Equation (18) are set to constant values defined as

$$\begin{array}{cc}\hfill & {\sigma }_{b_{r,\mathrm{GPS}}}^2=C_{b_{r,\mathrm{GPS}}},{\sigma }_{b_{r,\mathrm{GLO}}}^2=C_{b_{r,\mathrm{GLO}}},\hfill \\ \hfill & {\sigma }_{b_{\mathrm{GPS}}^s}^2=C_{b_{\mathrm{GPS}}^s},{\sigma }_{b_{\mathrm{GLO}}^s}^2=C_{b_{\mathrm{GLO}}^s}\hfill \end{array}$$

(25)

where the constants $C_{b_{r,\mathrm{GPS}}}$, $C_{b_{r,\mathrm{GLO}}}$, $C_{b_{\mathrm{GPS}}^s}$ and $C_{b_{\mathrm{GLO}}^s}$ are defined by conducting tests.

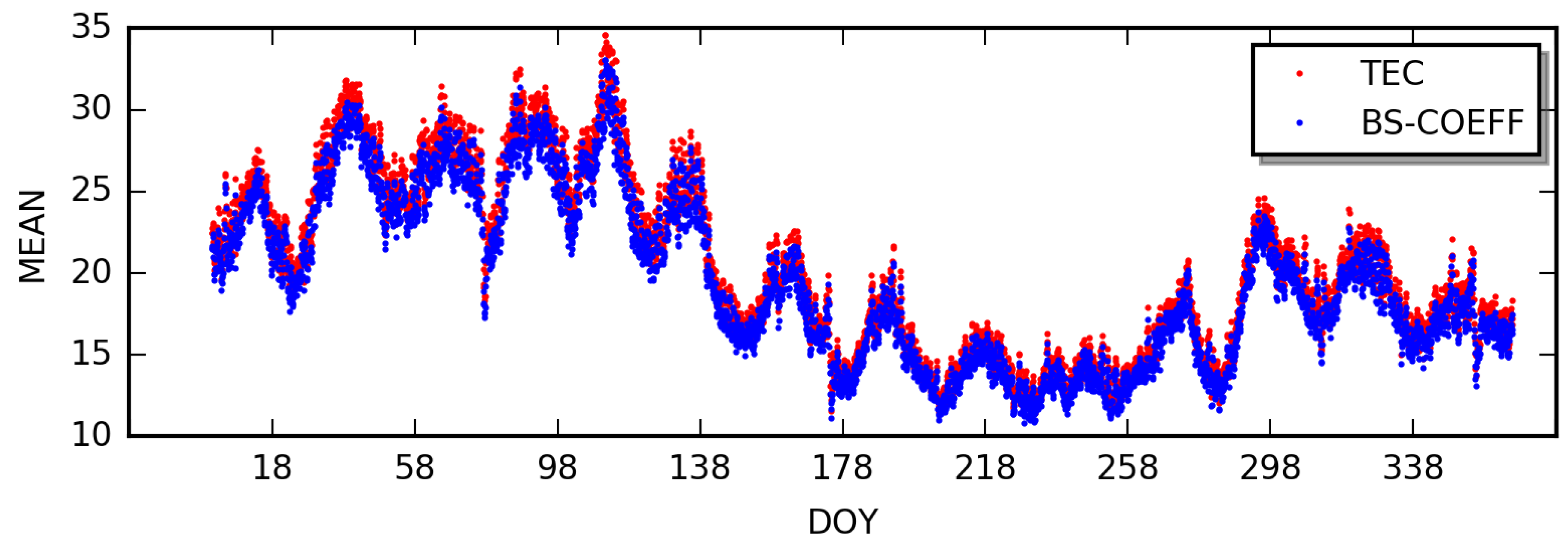
4.4. Adaptive Filtering Using Method of Variance-Components (VC) Estimation

Kalman [1] proposed a recursive solution to the problem defined in the Equations (6) and (7). Following this pioneering study, various authors have re-interpreted the filtering problem from different perspectives leading to the same set of KF equations, for instance, the maximum likelihood estimation [60], as a sub-class of the Bayesian estimation [61] and the minimum variance estimation (e.g., Jazwinski [62]). The prediction and correction equations that are solutions of the filtering problem read

$$\begin{array}{cc}\hfill {\mathit{\beta }}_k^{-}& ={\mathbf{F}}_k{\widehat{\mathit{\beta }}}_{k-1},\hfill \end{array}$$

(26)

$$\begin{array}{cc}\hfill {\mathsf{\Sigma }}_{\beta ,k}^{-}& ={\mathbf{F}}_k{\widehat{\mathsf{\Sigma }}}_{\beta ,k-1}{\mathbf{F}}_k^T+{\mathsf{\Sigma }}_{w,k},\hfill \end{array}$$

(27)

$$\begin{array}{cc}\hfill {\widehat{\mathit{\beta }}}_k& ={\mathit{\beta }}_k^{-}+{\mathbf{K}}_k({\mathit{y}}_k-{\mathbf{X}}_k{\mathit{\beta }}_k^{-}),\hfill \end{array}$$

(28)

$$\begin{array}{cc}\hfill {\widehat{\mathsf{\Sigma }}}_{\beta ,k}& =(\mathbf{I}-{\mathbf{K}}_k{\mathbf{X}}_k){\mathsf{\Sigma }}_{\beta ,k}^{-},\hfill \end{array}$$

(29)

$$\begin{array}{cc}\hfill {\mathbf{K}}_k& ={\mathsf{\Sigma }}_{\beta ,k}^{-}{\mathbf{X}}_k^T{({\mathbf{X}}_k{\mathsf{\Sigma }}_{\beta ,k}^{-}{\mathbf{X}}_k^T+{\mathsf{\Sigma }}_{y,k})}^{-1}\hfill \end{array}$$

(30)

where ${\mathbf{K}}_k$ is the gain matrix and the index “${·}^{-}$” refers to “predicted” whereas “ $\widehat{·}$ “ stands for “estimated” [3,59,62]. The Equations (28) and (29) of the measurement update step can be re-written as

$$\begin{array}{cc}\hfill & {\widehat{\mathit{\beta }}}_k={\widehat{\mathsf{\Sigma }}}_{\beta ,k}·({\mathbf{X}}_k^T{\mathsf{\Sigma }}_{y,k}^{-1}{\mathbf{y}}_k+{({\mathsf{\Sigma }}_{\beta ,k}^{-})}^{-1}{\mathit{\beta }}_k^{-}),\hfill \end{array}$$

(31)

$$\begin{array}{cc}\hfill & {\widehat{\mathsf{\Sigma }}}_{\beta ,k}={\left({\mathbf{X}}_k^T{\mathsf{\Sigma }}_{y,k}^{-1}{\mathbf{X}}_k+{({\mathsf{\Sigma }}_{\beta ,k}^{-})}^{-1}\right)}^{-1}\hfill \end{array}$$

(32)

by taking into account the matrix identities ${\mathbf{D}}^{-1}\mathbf{C}{(\mathbf{A}-\mathbf{B}{\mathbf{D}}^{-1}\mathbf{C})}^{-1}={(\mathbf{D}-\mathbf{C}{\mathbf{A}}^{-1}\mathbf{B})}^{-1}\mathbf{C}{\mathbf{A}}^{-1}$ and ${(\mathbf{A}-\mathbf{B}{\mathbf{D}}^{-1}\mathbf{C})}^{-1}={\mathbf{A}}^{-1}+{\mathbf{A}}^{-1}\mathbf{B}{(\mathbf{D}-\mathbf{C}{\mathbf{A}}^{-1}\mathbf{B})}^{-1}\mathbf{C}{\mathbf{A}}^{-1}$ (see e.g., Koch [17], Koch [18] and Jazwinski [62]). Observations from different techniques generally exhibit different characteristics in terms of precision and accuracy. Therefore, the determination of the measurement covariance matrix should be handled carefully to provide a reliable estimation of the unknown parameters. Assuming that intra-technique observations are uncorrelated, Equation (7) can be partitioned into blocks for each of the related techniques (see e.g., [23,26]). This leads to the solution

$${\widehat{\mathit{\beta }}}_k={\widehat{\mathsf{\Sigma }}}_{\beta ,k}·\left({\displaystyle \sum _{j=1}^p}{\mathbf{X}}_{y_j,k}^T{\mathsf{\Sigma }}_{y_j,k}^{-1}{\mathit{y}}_{y_j,k}+{({\mathsf{\Sigma }}_{\beta ,k}^{-})}^{-1}{\mathit{\beta }}_k^{-}\right)$$

(33)

with

$${\widehat{\mathsf{\Sigma }}}_{\beta ,k}={\left({\displaystyle \sum _{j=1}^p}{\mathbf{X}}_{y_j,k}^T{\mathsf{\Sigma }}_{y_j,k}^{-1}{\mathbf{X}}_{y_j,k}+{({\mathsf{\Sigma }}_{\beta ,k}^{-})}^{-1}\right)}^{-1}$$

(34)

where each group of observation vector ${\mathit{y}}_{y_j,k}$ (GPS and GLONASS observations in this study) is defined by the index $j\in \{1,\dots ,p\}$. Each covariance matrix ${\mathsf{\Sigma }}_{y_j,k}$ of observations of the group j is replaced by the expression given in Equation (14) to estimate the associated variance components. Accordingly, the overall set of adaptive filtering equations is given by

$${\widehat{\mathit{\beta }}}_k={\widehat{\mathsf{\Sigma }}}_{\beta ,k}·\left({\displaystyle \sum _{j=1}^p}\frac{1}{{\sigma }_{y_j,k}^2}{\mathbf{X}}_{y_j,k}^T{\mathbf{P}}_{y_j,k}{\mathit{y}}_{y_j,k}+{({\mathsf{\Sigma }}_{\beta ,k}^{-})}^{-1}{\mathit{\beta }}_k^{-}\right)$$

(35)

with

$${\widehat{\mathsf{\Sigma }}}_{\beta ,k}={\left({\displaystyle \sum _{j=1}^p}\frac{1}{{\sigma }_{y_j,k}^2}{\mathbf{X}}_{y_j,k}^T{\mathbf{P}}_{y_j,k}{\mathbf{X}}_{y_j,k}+{({\mathsf{\Sigma }}_{\beta ,k}^{-})}^{-1}\right)}^{-1}.$$

(36)

Herein the unknown variance component ${\sigma }_{y_j,k}^2$ for each group j is determined via VCE as

$${\widehat{\sigma }}_{y_j,k}^2=\frac{{\widehat{\mathit{e}}}_{y_j,k}^T{\mathbf{P}}_{y_j,k}{\widehat{\mathit{e}}}_{y_j,k}}{r_{y_j,k}}$$

(37)

where ${\widehat{\mathit{e}}}_{y_j,k}={\mathit{y}}_{j,k}-{\mathbf{X}}_{{\mathit{y}}_{j,k}}{\widehat{\mathit{\beta }}}_k$ is the residual vector for the observation group j and $r_{y_j,k}$ is the corresponding partial redundancy defined as

$$r_{y_j,k}=n_j-\mathrm{trace}\left({\mathbf{N}}_{y_j,k}{\mathbf{N}}_k^{-1}\right)$$

(38)

where ${\mathbf{N}}_k$ is the overall normal equation matrix, i.e., ${\mathbf{N}}_k^{-1}={\widehat{\mathsf{\Sigma }}}_{\beta ,k}$ and $n_j$ is the total number of observations of group j. The normal equation matrix ${\mathbf{N}}_{y_j,k}$ for the observation group j is given by

$${\mathbf{N}}_{y_j,k}=\frac{1}{{\widehat{\sigma }}_{y_j,k}^2}{\mathbf{X}}_{y_j,ks}^T{\mathbf{P}}_{y_j,k}{\mathbf{X}}_{y_j,k}.$$

(39)

An iterative estimation of the unknown variance components ${\sigma }_{y_j,k}^2$ is carried out until a point of convergence is reached. The iteration starts from the approximate values ${\sigma }_{y_j,k}^{2,o}$ of the variance components. The estimated variance components at the previous epoch $t_{k-1}$ of the filter are used as initial values at the current epoch $t_k$, i.e., ${\sigma }_{y_j,k}^{2,o}={\widehat{\sigma }}_{y_j,k-1}^2$. At each iteration step, the Equations (35)–(37) are re-executed for the updated values of the variance components.

4.5. Constrained Filtering

Numerous ways to incorporate constraints into the KF have been studied. For a comprehensive review the reader is referred to [63] and references therein. Here, the focus is on perfect measurements and the estimate projection methods. The main distinction between the two methods is that the former one is performed during the measurement update step of the filter whereas the second method uses the constraints following the measurement update step. The estimate projection method was employed by [5] in the context of ionosphere VTEC modeling relying on a standard KF implementation referring to the Equations (28) and (29). Contrarily, in this study, the “perfect measurement” method is carried out to ensure a more stable KF implementation.

Although the alternative implementation of KF given by the Equations (35) and (36) offers a faster execution time and a lower memory consumption via the normal equation representation for large problems, i.e., for a design matrix ${\mathbf{X}}_{mn}$ with $m\gg n$, the filter becomes more vulnerable to numerical problems such as ill-conditioning and rank deficiency. For instance, data gaps and an inhomogeneous GNSS data distribution result in unobserved unknown parameters. Moreover, the observation equations have a linear dependency problem due to the terms including satellite DCBs. However, the perfect measurement method increases the numerical stability of the filter, since the method considers the constraints as additional information exploited during the measurement update step of the filter. It threats constraints as fictitious observations and augments the measurement model as

$${\mathit{y}}_{\mathrm{aug},k}={\mathbf{X}}_{\mathrm{aug},k}{\mathit{\beta }}_k+{\mathit{e}}_{\mathrm{aug},k}$$

(40)

where the augmented measurement vector, the design matrix and the error vector are, respectively, given by

$${\mathit{y}}_{\mathrm{aug},k}=\left[\begin{array}{c}{\mathit{y}}_k\\ {\mathit{y}}_{c,k}\end{array}\right],{\mathbf{X}}_{\mathrm{aug},k}=\left[\begin{array}{c}{\mathbf{X}}_k\\ {\mathbf{X}}_{y_c,k}\end{array}\right],{\mathit{e}}_{\mathrm{aug},k}=\left[\begin{array}{c}{\mathit{e}}_k\\ \mathbf{0}\end{array}\right];$$

(41)

the new augmented measurement covariance matrix reads

$${\mathsf{\Sigma }}_{{\mathit{y}}_{\mathrm{aug}},k}=\left[\begin{array}{cc}{\mathsf{\Sigma }}_{\mathit{y},k}& \mathbf{0}\\ \mathbf{0}& {\mathsf{\Sigma }}_{{\mathit{y}}_{\mathrm{c}},k}\end{array}\right]$$

(42)

where ${\mathsf{\Sigma }}_{{\mathit{y}}_{\mathrm{c}},k}$ is a zero matrix by definition, since the constraints are handled as perfect measurements. However, in order to avoid singularity in practice, ${\mathsf{\Sigma }}_{{\mathit{y}}_{\mathrm{c}},k}$ is generally replaced by a matrix of very small numbers, i.e., ${\mathsf{\Sigma }}_{y_c,k}={\sigma }_{\mathrm{c}}^2\mathbf{I}$ [64]. In this study, ${\sigma }_{\mathrm{c}}^2$ is set to ${10}^{-8}$ which is defined as small as possible by considering the computational precision. The equality constraint equations can be handled in the measurement model described by the Equations (35) and (36) via considering them as a block of measurements with a known covariance matrix (see, e.g., [17,65]). In the scope of this study, the constraint equations introduced for preserving the spherical geometry read

$${\mathbf{X}}_{c_d,k}{\mathit{d}}_k=\mathbf{0}$$

(43)

where ${\mathbf{X}}_{c_d,k}$ is a known matrix [28]. Furthermore, a zero mean constraint, which is usually adapted in the parameter estimation methods employed by the IAACs, is introduced for the DCBs to vanish the linear dependency in the observation equations. It is given as

$$\begin{array}{c}\hfill {\mathbf{X}}_{c_{b^{\mathrm{GPS}}},k}{\mathit{b}}_k^{\mathrm{GPS}}=0\\ \hfill {\mathbf{X}}_{c_{b^{\mathrm{GLO}},k}}{\mathit{b}}_k^{\mathrm{GLO}}=0\end{array}$$

(44)

where ${\mathbf{X}}_{c_{b^{\mathrm{GPS}}},k}$ and ${\mathbf{X}}_{c_{b^{\mathrm{GLO}}},k}$ are known matrices. A simplified notation for a general definition of the equality constrained equations is defined as

$${\mathbf{X}}_{y_c,k}{\mathit{\beta }}_k={\mathit{y}}_{c,k}.$$

(45)

From the Equations (43) and (44) the design matrix ${\mathbf{X}}_{y_c,k}$ of the constraint equations for the current problem reads

$${\mathbf{X}}_{y_c,k}=\left[\begin{array}{ccccc}{\mathbf{X}}_{c_d,k}& \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}& {\mathbf{X}}_{c_{b^{\mathrm{GPS}}},k}& \mathbf{0}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}& {\mathbf{X}}_{c_{b^{\mathrm{GLO}}},k}\end{array}\right]$$

(46)

and the vector ${\mathit{y}}_{c,k}$ is given by ${\mathit{y}}_{c,k}=\mathbf{0}$.

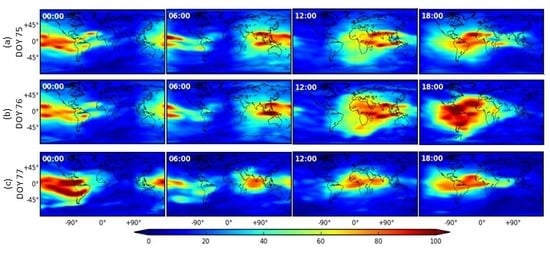
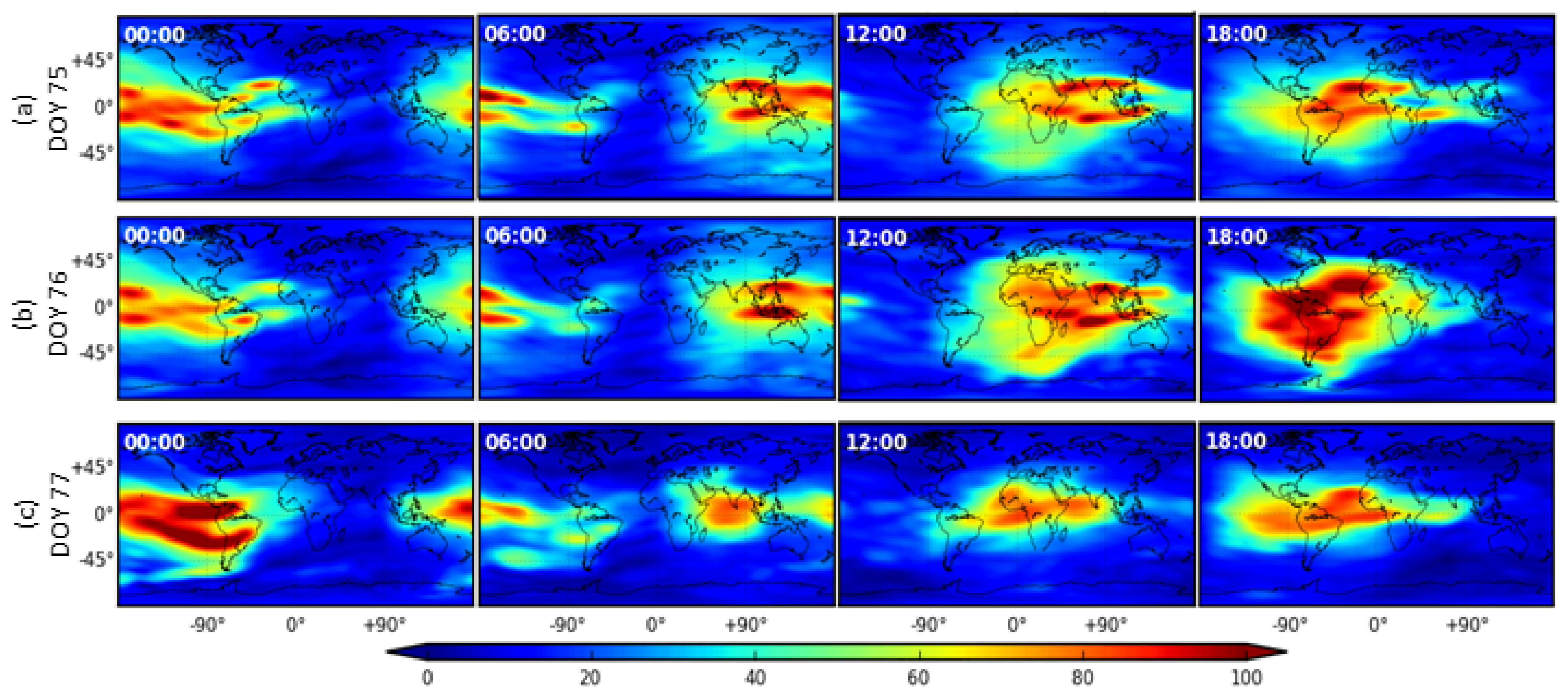
5. Results and Discussions

5.1. Filter Settings

Analysis centers rely on different sets of GNSS stations selected according to the requirements for their modeling approaches and the chosen performance criteria. In the presented approach, the list of available GNSS stations is downloaded and updated every hour. The selected stations are mostly from the IGS network, which is extended by a few additional stations from the UNAVCO and the EUREF network to obtain a better geographical coverage.

Data from the GNSS receivers is based on the hourly data blocks provided from GNSS data centers with a latency of about 1 h. The temporal sampling of the GNSS data is mostly 30 s or less. This allows for running the filter theoretically with a step size of 30 s. However, high temporal sampling of the filter results in an increased computational burden and a storage requirement, which can lead to difficulties for efficiently managing the resources when the model runs in operational mode. Moreover, VTEC varies slowly in time in a Sun-fixed coordinate system during low and moderate ionospheric activity. However, a very long filter step size should also be avoided since the filter prediction error generally grows in line with the filter step size. Accordingly, the filter step size is set to 5 min by taking the computational load and the Kalman Filter prediction error into account. The estimated target parameters, related auxiliary data, and the VTEC products generated from the estimated parameters are stored every 10 min by considering the storage requirements.

The convergence rate of the filter depends on the accuracy of the initial values of the unknown ionospheric target parameters, their initial covariance matrix and the size of the filter state vector. The initial values of the B-spline coefficients are computed using the IGS analysis center products to decrease the convergence rate. The analysis of the estimated covariance matrices and the residuals over time shows that the filter state vector is stabilized around 1 h (12 epochs with a filter step size of 5 min) after the initialization of the filter.

5.2. Validation Methods and Data Sets

The quality of the VTEC products derived by executing the developed adaptive filtering approach is assessed using (1) the dSTEC analysis and (2) altimeter VTEC comparisons. The dSTEC analysis is a very precise and appropriate method for the validation of VTEC products on areas including GNSS receivers. The method has been widely preferred for assessments of ionospheric product quality, for example, see [66,67,68,69].

The comparison of the results with altimeter data acquired from the Jason-2/3 missions allows for a validation of the VTEC maps over oceans. Although the VTEC values obtained from the altimetry missions are noisy and biased, the method provides an appropriate external validation approach for qualifying VTEC values over the oceans, and it is one of the fundamental approaches for the comparison of VTEC products provided by the IGS analysis centers, see e.g., [70,71].

The VTEC products in IONEX format with the labels “igsg”, “uqrg”, “esag”, “jplg” and “codg” provided by the IAACs, which are respectively IGS, UPC, ESA, JPL and CODE, are used for the validation of the results. The VTEC maps of IGS, ESA and JPL refer to their final products with a temporal sampling of 2 h, whereas the product of CODE has a sampling interval of 1 h. Although UPC has final VTEC products, we consider their rapid solution labeled “uqrg” which has a very high accuracy and a temporal resolution of 15 min and is one of the best products within the IGS analysis centers (see, e.g., [70]). The estimated VTEC maps generated using the developed method will be labeled “othg” in the remainder of the paper. The letters “o”, “t”, “h” and “g” stands for the following expressions; project "O"PTIMAP, temporal resolution of 10 (“t”en) minutes, “h”igh resolution with $J_1=5$, $J_2=3$ and “G”lobal VTEC Maps, respectively. For further information on product generation at different resolution levels and the corresponding label definitions, we refer to [32,37].

Two data sets referring to different time intervals are selected for the VTEC product generation and validation. The first data set comprises GNSS data collected during a considerably high ionospheric activity between 10 February 2015 and 20 April 2015 including the St. Patrick geomagnetic storm of 17 March 2015. The second set consists of data obtained between 10 August 2017 and 20 October 2017 which show a lower ionosphere activity compared to the data set of 2015 but includes powerful solar flares and two consecutive Coronal Mass Ejection arrivals disturbing the Earth’s ionosphere significantly during 6–10 September 2017.

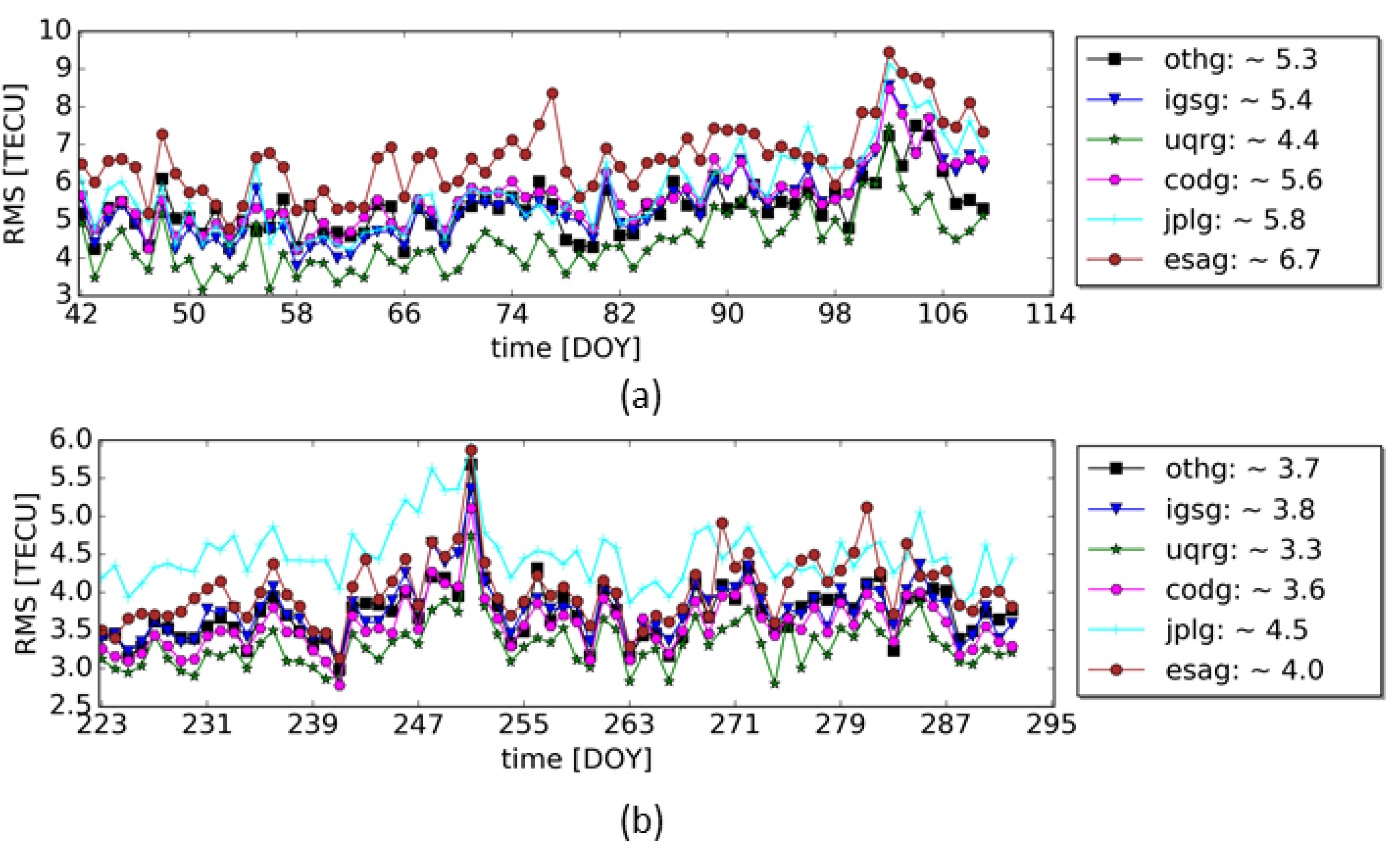
5.3. Comparisons to IGS and IAACs

5.3.1. dSTEC Analysis

The results of the dSTEC analysis are shown in Figure 4 to reveal the performance of the products according to the varying VTEC activity in different geographical regions. The geographical distribution of the selected GNSS receivers is illustrated in the panel (a) of Figure 4. The stations used for validation were selected amongst those which exist in both the 2015 and the 2017 time periods. Moreover, we searched in all VTEC products of the analysis centers for a set of geographically well-distributed common stations. Next, we selected GNSS stations either used by all IAACs or are in a very close distance to a used one. The mean RMS values of the dSTEC variations covering the test periods are separately computed for each of the sites and the analysis centers and depicted in the panels (b) and (c) of Figure 4 corresponding to the data sets of 2015 and 2017, respectively. The numbers within the brackets given in the legends show the average values of the RMS deviations computed from all GPS receivers for each analysis center; for further information on the computations, we refer to [5].

The average RMS values of “othg” for 2015 and 2017 are 1.62 and 0.85 for the dSTEC analysis, respectively, whereas the RMS values of the IAACs are varying between 1.64 and 2.33 TECU for 2015 and 0.74 and 1.17 TECU for 2017. The RMS values indicate that the quality of the VTEC product “othg” is consistent with those from the other analysis centers. In particular, the average RMS values of “othg” are in very close agreement with the values of “uqrg” product which has a high temporal resolution.

The RMS values of the dSTEC deviations are considerably larger for the GNSS receivers located around the geomagnetic equator as expected since those regions suffer from poor data coverage as well as magnitudes of VTEC variations which are very large at regions close to the geomagnetic equator. Furthermore, the average RMS values for the 2015 data set are almost 2 times larger than for the data set of 2017. The RMS values clearly reveal the quality degradation of the VTEC products in response to the higher ionosphere activity. For instance, “othg” has an RMS value of 1.62 TECU for the data set of 2015 whereas the value drops to 0.85 TECU in 2017. In addition to the high ionospheric activity, the impact of the geomagnetic storm on 17 March 2015, on VTEC variations can be seen in Figure 5. The maps cover the days 16–18 March 2015. For instance, VTEC reaches peak values at 18:00 UTC on 17 September compared to the VTEC values at the same time the day before and the day after.

5.3.2. Altimetry Comparisons

The VTEC measurements acquired from the Jason-2 and Jason-3 missions equipped with dual frequency altimeters were used to assess the quality of the “othg” solution in comparison with the products of the other analysis centers. Prior to the performing analysis, the VTEC data from the altimeter missions were pre-processed to remove outliers and to reduce noise by applying filtering and smoothing steps. Furthermore, VTEC maps of the analysis centers were interpolated to obtain VTEC values at points of altimeter observations as explained by [5]. In the comparisons, data from Jason-2 were used to evaluate the data set of 2015 whereas VTEC data from the Jason-3 mission was considered for the year 2017.

The RMS deviations with respect to altimeter VTEC values are shown in the panels (a) and (b) of Figure 6 for the data sets of 2015 and 2017, respectively. The RMS values of the analysis centers range from 4.4 to 6.7 TECU for the year of 2015 and from 3.3 to 4.5 TECU in 2017. The RMS values of “othg” solution for the corresponding data sets have values 5.3 and 3.7 TECU. These RMS values are in line with the results of the other analysis centers. In panel (b), significant increases in the values of RMS deviations covering DOY 249–251 of September 2017 clearly show the effect of space weather events, including CMEs and powerful solar flares.

5.4. Evaluation of the Proposed Approach

This section is devoted to scrutinizing individual contributions of each developed method, including the VCE-based adaptation and the process noise definition, to the performance of the overall KF algorithm. The data set of 2015, which comes with challenging ionosphere conditions, is considered in the evaluations. Several test cases with different filter settings, summarized in

Table 1. Test cases with different KF settings used in the model evaluations.

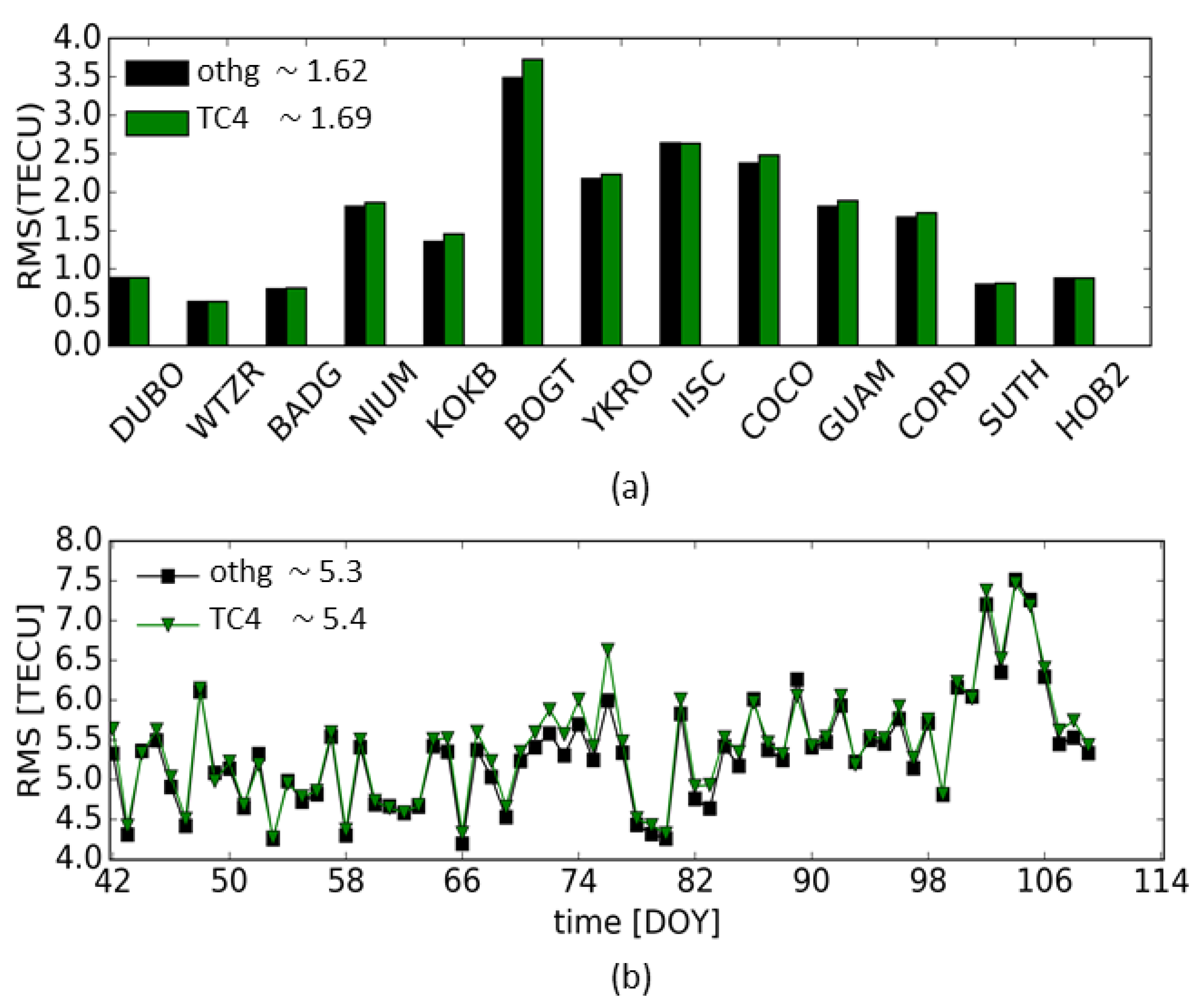
Product Label	VCE	Process Noise Model	Test Definition	Product Quality (in TECU)
othg	Enabled	Enabled	presented approach	${\mathrm{RMS}}_{\mathrm{dSTEC},\mathrm{OTHG}}=1.62$, ${\mathrm{RMS}}_{\mathrm{ALT},\mathrm{OTHG}}=5.3$
TC1	Disabled	Disabled	${\sigma }_{y_{\mathrm{GPS}},k}^2={\sigma }_{y_{\mathrm{GPS},\mathrm{NOM}}}^2$, ${\sigma }_{y_{\mathrm{GLO}}}^2={\sigma }_{y_{\mathrm{GLO},\mathrm{NOM}}}^2$, ${\sigma }_{d_i,k}^2={\sigma }_{d_{\mathrm{NOM}}}^2$	${\mathrm{RMS}}_{\mathrm{dSTEC},\mathrm{TC}1}=1.66$, ${\mathrm{RMS}}_{\mathrm{ALT},\mathrm{TC}1}=5.4$
TC2	Disabled	Enabled	${\sigma }_{y_{\mathrm{GPS}},k}^2={\sigma }_{y_{\mathrm{GPS},\mathrm{NOM}}}^2$, ${\sigma }_{y_{\mathrm{GLO}},k}^2={\sigma }_{y_{\mathrm{GLO},\mathrm{NOM}}}^2$, ${\mathbf{P}}_{y_{\mathrm{GPS}},k}={\mathbf{P}}_{y_{\mathrm{GLO}},k}=\mathbf{I}$	${\mathrm{RMS}}_{\mathrm{dSTEC},\mathrm{TC}2}=1.94$, ${\mathrm{RMS}}_{\mathrm{ALT},\mathrm{TC}2}=5.9$
TC3	Disabled	Enabled	${\sigma }_{y_{\mathrm{GPS}},k}^2={\sigma }_{y_{\mathrm{GLO},\mathrm{NOM}}}^2$, ${\sigma }_{y_{\mathrm{GLO}},k}^2={\sigma }_{y_{\mathrm{GLO},\mathrm{NOM}}}^2$	${\mathrm{RMS}}_{\mathrm{dSTEC},\mathrm{TC}3}=1.75$, ${\mathrm{RMS}}_{\mathrm{ALT},\mathrm{TC}3}=5.5$
TC4	Enabled	Disabled	${\sigma }_{d_i,k}^2={\sigma }_{d_{\mathrm{NOM}}}^2$	${\mathrm{RMS}}_{\mathrm{dSTEC},\mathrm{TC}4}=1.69$, ${\mathrm{RMS}}_{\mathrm{ALT},\mathrm{TC}4}=5.4$
TC5	Enabled	Enabled	$C_{1,k}=C_{2,k}=1$ in Equation (20)	${\mathrm{RMS}}_{\mathrm{dSTEC},\mathrm{TC}5}=1.76$, ${\mathrm{RMS}}_{\mathrm{ALT},\mathrm{TC}5}=5.6$

, were designed and the KF was carried out for each case to reveal the model performance. The test case with the label “othg” in Table 1 refers to the final version of the presented adaptive approach.

Firstly, one drawback of the standard KF is the requirement for the prior knowledge of the process noise and the measurement error covariance matrices. In common practice, these matrices are defined by conducting multiple test runs of the filter with different candidate values of the variances defining the covariance matrices. To simulate this situation, the nominal values ${\sigma }_{y_{\mathrm{GPS},\mathrm{NOM}}}^2$, ${\sigma }_{y_{\mathrm{GLO},\mathrm{NOM}}}^2$ for the corresponding variance components in Equation (15) and the constant nominal value ${\sigma }_{d_{\mathrm{NOM}}}^2$ for the process noise variance of the B-spline coefficients in Equation (19) were manually selected. As it is expected, the results of the altimetry and the dSTEC comparisons for the products derived by the proposed approach with label “othg” and the nominal solution, labeled “TC1” in Table 1, are approximately in line. The RMS values for the altimetry and the dSTEC comparisons of the nominal solution are respectively ${\mathrm{RMS}}_{\mathrm{ALT},\mathrm{TC}1}=5.4$ and ${\mathrm{RMS}}_{\mathrm{dSTEC},\mathrm{TC}1}=1.66$ TECU. These results show that the “othg” solution exhibits about 2% better performance compared to the nominal solution “TC1”. The manual computation procedure, which is what the nominal solution relies on, is time-consuming since it requires executing the filter multiple times to find out the optimal values defining the measurement and process noise covariance matrices. Moreover, it is not guaranteed that the nominal values are valid for any given time since they are computed using a small data set in 2015. However, the presented approach “othg” takes the variances into account in an adaptive way by computing them during the filter run-time. This assures that the values of the variances are always up-to date and sensitive to the changes in errors of GNSS measurements as well as temporal ionospheric variations. For example, the nominal values of the GPS and GLONASS variance components computed using the data set of 2015 are approximately two times larger than the ones computed using the data set of 2017. The data set of 2015 includes considerably larger VTEC variations in magnitude due to high VTEC activity which can significantly degrade the quality of GNSS measurements. The adaptive filter approach successfully handles this issue by assigning larger values to the error covariance matrix of GNSS measurements for the data set of 2015 compared to those computed for the data set of 2017.

Adaptive filters generally allow flexible updates of the underlying model parameters. For instance, in case that the computation of the weight matrices in Equation (15) defined by (16) is replaced by another model, the corresponding value of the nominal variances have to be re-computed in a standard KF. However, the adaptive filtering approach does not require such a time consuming effort. The effect of an inappropriate variance definition to the filter performance is simulated in the test scenario labeled “TC2” in Table 1. The weight matrices ${\mathbf{P}}_{y_{\mathrm{GPS}},k}$ and ${\mathbf{P}}_{y_{\mathrm{GLO},k}}$ in Equation (15) were set to identity matrices but the nominal values of the corresponding variance components are kept as they were computed in “TC1”. The RMS values for the altimetry and dSTEC comparisons for the test case “TC2” are ${\mathrm{RMS}}_{\mathrm{ALT},\mathrm{TC}2}=5.9$ TECU and ${\mathrm{RMS}}_{\mathrm{dSTEC},\mathrm{TC}2}=1.94$ TECU. The values respectively exhibit about 11% and 17% performance degradation compared to those of the “othg”.

To compute ionosphere target parameters reliably, data sets from different sources (e.g., GPS and GLONASS in this study) are required to be handled carefully by means of an appropriate selection of relative weights. The presented adaptive approach deals with this issue by computing different variance components for the observations from each of the constellations. The test case labeled “TC3” is designed to show a performance degradation in case of improper assignment of weights to the observation groups. A unique value, ${\sigma }_{y_{\mathrm{GLO},\mathrm{NOM}}}^2$ obtained from the test case “TC1”, was assigned to the variance components of GPS and GLONASS observations to conduct the simulation labeled “TC3” in Table 1. The RMS values for the altimetry and dSTEC comparisons for the test case are ${\mathrm{RMS}}_{\mathrm{ALT},\mathrm{TC}3}=5.5$ TECU and ${\mathrm{RMS}}_{\mathrm{dSTEC},\mathrm{TC}3}=1.75$ TECU. The RMS values show about 4% and 8% performance degradation compared to the corresponding RMS values of the “othg” solution.

The final evaluations are dedicated to assess the effectiveness of the process noise definition given by the Equations (19) and (20) for the B-spline coefficients. In this context, the test case labeled “TC4” in Table 1 is considered. The test scenario refers to the constant nominal value ${\sigma }_{d_{\mathrm{NOM}}}^2$ definition for the process noise variances of the B-spline coefficients. The RMS values of the dSTEC analysis and the altimetry comparisons for the test case are illustrated in the panels (a) and (b) of Figure 7, respectively. The average RMS values shown in the legend of the figure refer to ${\mathrm{RMS}}_{\mathrm{dSTEC},\mathrm{TC}4}=1.69$ TECU and ${\mathrm{RMS}}_{\mathrm{ALT},\mathrm{TC}4}=5.4$ TECU for the test case “TC4”. The RMS values exhibit about 4% and 2% performance degradation compared to those of the “othg” solution. The RMS values of the dSTEC analysis at the test stations depicted in Figure 7a clearly show that the “othg” solution relying on the signal and data-adaptive process noise definition outperforms the nominal solution over the continental area. A closer look at the RMS values of the dSTEC analysis reveals that the improvements are considerably larger for the receivers at the sites NIUM, KOKB, BOGT, YKRO, COCO, GUAM which are located at low latitudes closer to the geomagnetic equator. These regions generally exhibit very high VTEC activity during the day due to the Equatorial Ionization Anomaly (EIA). The daily RMS values of the altimetry analysis illustrated in Figure 7b indicate that the “othg” solution performs slightly better than the nominal solution for the entire test period of 2015 over oceanic areas. Notable differences between the RMS values of the two solutions can be observed for the days ranging from DOY-72 to DOY-76, which are characterized by very high VTEC activity. During these days, especially the Saint Patrick storm day (DOY-76), the “othg” solution significantly outperforms the nominal solution.

Furthermore, in order to test the sub-parameters of the empirical model defining the process noise variances, a test run of the filter, which is labeled “TC5” in Table 1, was conducted by only considering the $C_{0,k}$ coefficient in Equation (20). The coefficients $C_{1,k}$ and $C_{2,k}$ are set to 1, which means omitting the assumption that the temporal uncertainties of the B-spline coefficients are correlated to their relative variations. The RMS values for the altimetry and dSTEC comparisons are ${\mathrm{RMS}}_{\mathrm{ALT},\mathrm{TC}5}=5.6$ TECU and ${\mathrm{RMS}}_{\mathrm{dSTEC},\mathrm{TC}5}=1.76$ TECU, where the values show about 6% and 9% performance degradation, respectively, compared to the RMS values of the “othg” solution. Considering that the process noise variance behaves like a weighting factor, the results indicate that the performance of the estimator is significantly sensitive to the relative variations of the B-spline coefficients, which are effectively taken into account by the “othg” solution.

6. Conclusions

Adaptive approaches allowing for tuning of model uncertainties in run-time are introduced into the Kalman Filter for global VTEC modeling relying on the B-spline representation. The representation of the global VTEC signal using a series expansion of B-spline functions allows proper handling of regional signal variations as well as the heterogeneous data distribution. Incorporating B-splines into a recursive filter results in a very powerful data assimilation framework for ultra-rapid and (near)real-time VTEC modeling. In this regard, the study by [5], which includes the basic recursive algorithms for VTEC product generation using B-splines, was comprehensively extended for adaptive estimation of the unknown ionospheric target parameters.

The adaptive algorithm, incorporated into the KF implementation, makes use of the VCE estimation approach to tune the quality of GPS and GLONASS observations by estimating proper scaling factors (variance components) for each type of observation group during the filter run-time. The adaptive KF approach leads to the construction of the measurement covariance matrix automatically, whereas the standard KF requires manually conducting multiple tests for the identification of the covariance matrix. The equality constraint equations, which are introduced to preserve the spherical geometry of the global VTEC distribution and DCB related restrictions, were inserted into the filter by considering the constraints as perfect measurements.

We also showed that there are very high morphological similarities between the global VTEC distribution and the corresponding B-spline coefficients, which allows deducing physical interpretation directly from the magnitude and the distribution of B-spline coefficients. By exploiting this advantage of the B-spline representation, an empirical model to define the process noise of the filter was developed. The process noise represents the uncertainty of the KF time update (prediction) step; therefore, it plays an essential role in the performance of the filter. In this way, value of the process noise for each coefficient is tuned in an adaptive manner during the course of time according to the structure of the B-spline coefficients.

Furthermore, the hourly block of raw measurements acquired from GPS and GLONASS receivers are provided by IGS’s data centers with a latency of 1 h. The ionosphere measurements are obtained from the combination of raw GNSS pseudorange and carrier-phase measurements by applying the method of geometry-free linear combinations.

The performance of the implemented algorithms on VTEC modeling is verified by carrying out the dSTEC analysis and altimetry VTEC comparisons, which shows the generated VTEC products are consistent and in good agreement with the products of the other analysis centers.

The proposed adaptive KF is applied to groups of measurements from the GPS and GLONASS constellations. The approach as well as the data pre-processing module will be extended in the near future to handle the additional constellations, including, e.g., GALILEO and BeiDou. VTEC maps with label “othg”, derived using the presented approach, are referred to as ultra-rapid products due to latency in the acquisition of GNSS hourly data from the IGS data centers. However, the adaptive filtering algorithm can be directly used in a real-time modeling study. Therefore, the modeling approach including the data pre-processing will be extended to compute real-time global VTEC as a further step. Moreover, the VCE approach was applied to the measurement covariance matrix. Further studies will be conducted to extend the algorithm for self-tuning of the predicted covariance matrix of the unknown state vector in the sense of VCE.