1. Introduction
The upcoming Surface Water and Ocean Topography (SWOT, [
1,
2]) and Coastal and Ocean Measurement with Precise and Innovative Radar Altimeter (COMPIRA, [
3]) missions are planned to deliver high resolution maps of ocean surface topography using radar interfereometers. In order to achieve the target sea surface height (SSH) accuracy of a few cm at kilometer resolutions, the new remote sensing technology requires taking into the account multiple spatially correlated errors. In recent years, the SWOT error covariance model [
2], developed by the Jet Propulsion Laboratory (JPL), has served as a basis for numerous experiments (e.g., [
4,
5,
6]) assessing the added value of the mission in monitoring the global ocean.
SSH errors caused by the uncertainties in the interferometer geometry and orientation (hereinafter referred to as geometric and orientation errors, GOEs) provide one of the two major contributions to the overall error budget. Recently, attempts have been made to remove these errors in data assimilation experiments using simulated SWOT data [
7,
8]. Success of the approach largely depends on the accuracy of the projection of the SSH innovations on the range of GOE covariance matrix as well as on the relative contribution of other types of errors to this projection. In a more general perspective, the problem of introducing non-local observation error covariances into data assimilation systems requires an efficient algorithm for statistically consistent normalization of the innovations (multiplication of the innovations by the inverse square root of the respective observational error covariance). Regarding SWOT altimetry, some progress has been made in this direction in recent years [
5,
9].
In this note, we consider an approximation to the GOE model which facilitates the accuracy of the above mentioned projection and provides a computationally efficient algorithm for the pseudo-inversion of the respective error covariance matrix and its symmetric square root.
2. The Goe Model for Swot Altimetry
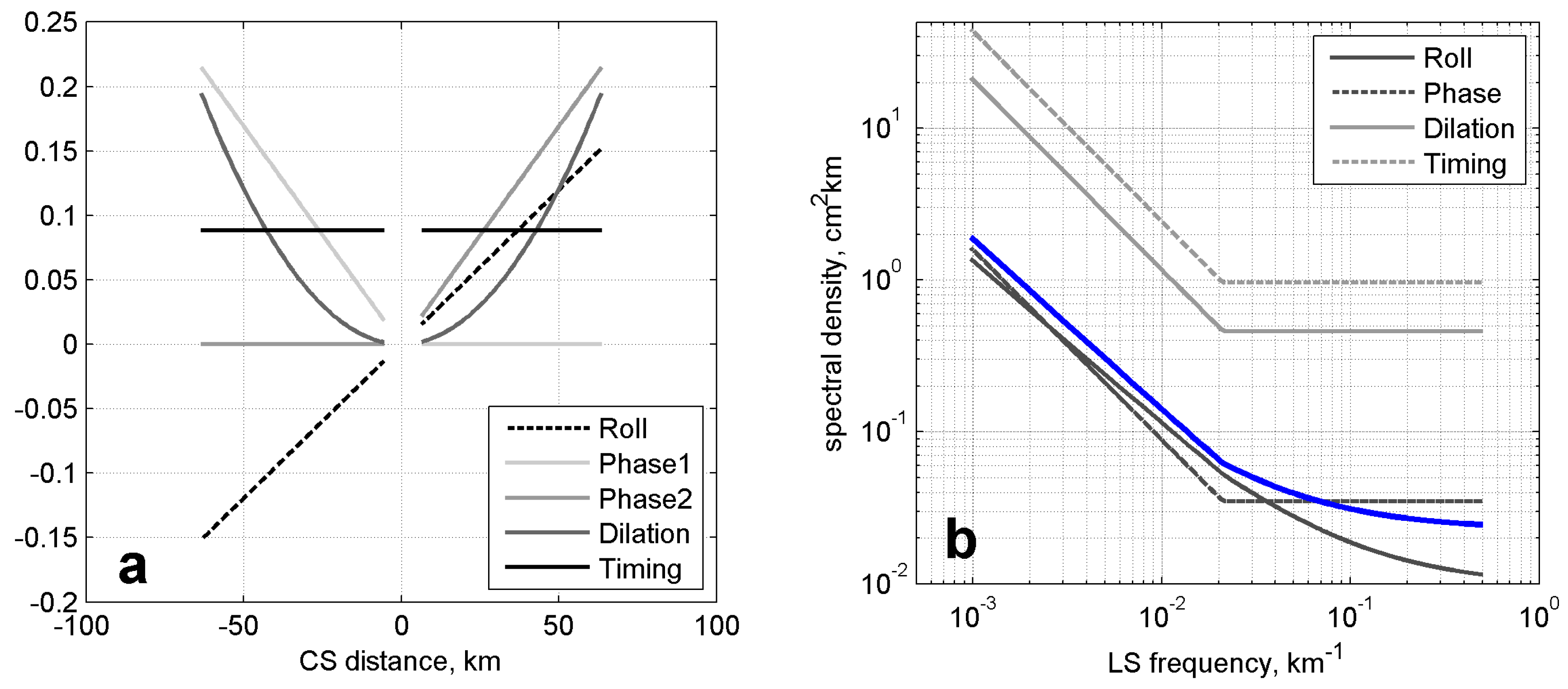
In the following, we denote the cross-swath (CS) direction by x and the along-swath (LS) direction by y, assume that SWOT observations are already projected on a regular grid, and enumerate CS grid points by the indices and along-track grid points by the indices . Matrices and vectors are denoted by bold capital and lowercase letters, respectively. To distinguish between matrices (vectors) defined on the swath and matrices (vectors) defined on either across- or along-swath directions, we italisize the latter.
2.1. Formulation
The JPL error model [
2,
10] takes into account the following four GOE components
,
caused by the uncertainties in: (a) satellite roll angle (roll error
), (b) relative postioning of the two interferometer antennas (phase error
); (c) thermal expansion of the antennas (dilation error
), and (d) orbit height (timing error
). A realization of the GOE field
is given by the sum of the four error components:
where
are the elements of the square root of the along-track covariance matrix of the
qth error component,
is the respective vector of normal noise in the LS direction, and
are the CS structure functions (
Figure 1a) for each of the four components (roll, phase, dilation and timing). The LS square root GOE covariance matrices
are assumed to have a diagonal represention in terms of the along-track Fourier components:
where
is the matrix of the along-track Fourier transform and
are the positive-definite diagonal marices with the square roots of the LS GOE power spectra shown in
Figure 1b.
Similar to [
7,
8], we consider regional applications involving finite pieces of the satellite swath and, therefore, utilize the LS Fourier transform representation by the
unitary matrix
.
Note that in practice one has to deal with GOE noise realizations in the form of 2d normal error fields
defined on a regular grid of the SWOT swath [
10]. Therefore, it is convenient to rewrite Equation (
1) in the equivalent form involving four 2d noise realizations
. To do this, we supplement the structure functions with the operators
which perform summation of
in the CS direction and keep the unit variance of the output. As a result, the vectors
are converted into
matrices
whose elements
are given by
or in the matrix/vector notation,
where ⊗ denotes the Kronecker product. Using this notation, Equation (
1) can be rewritten in the form
At this point it is necessary to note that representation (
5) can be treated in a more general way as if the matrices
were operating in the entire subspace spanned by the structure functions
, and not by the individual ones implied by the definition (
4). In the particular case of SWOT, the CS constituent of the phase error covariance involves two orthogonal structure functions shown by gray lines in
Figure 1b, whereas the structure function of the roll error is defined by their difference (dashed line in
Figure 1b). Hereinafter we shall imply that
are known
a priori and have this general form.
The
GOE covariance matrix
is given by
In deriving (7) we used the expression for the normal noise covariance:
where
is the Kronecker delta,
denote the ensemble average and
are the identity matrices in the across- and along-track directions.
2.2. Modification of the Goe Covariance Model
Although the GOE covariance model given by (
6) exhibits a lot of symmetries, one cannot take advantage of exposed factorizations when computing the pseudo-inverse matrix
, which is a necessary prerequisite for projecting the innovation field
onto the subspace spanned by the eigenmodes of
:
This type of projection was used in [
7,
8] to remove GOEs from simulated SWOT observations under a rather restrictive assumption that the GOE field does not change along the track.
The above restriction, however, can be removed by a slight (several percent) modification of the GOE covariance model. The modification is likely to be within the uncertainty limits of the model’s formulation and it is based on the similarity of the LS spectra shown in
Figure 1b. In particular, JPL documentation [
2,
10] implies that for swath lengths less than 3000 km the along section spectra have similar forms, so that they can be approximated by some universal spectrum
within the above mentioned degree of accuracy. In this case, the projection can be further simplified by employing the symmetric square root
of the above approximation to the GOE covariance matrix. Introducing the notations
and
for the square root of
, the expression for the projector
takes the form
Here we took into account that
. Furthermore, since by the definition
the rhs of (
11) is a
matrix of rank 4, so its svd decomposition
(where
is the
matrix with orthonormal columns and
is the diagonal
matrix of the respective eigenvalues) can be easily computed. As a consequence, the symmetric square root of
is given by
and can be readily used to compute the approximate projector
Keeping in mind that the simplified expression (
13) is valid within the accuracy of the approximation (
9), we examine it in the next section.
2.3. Approximation Errors
To find the best approximation of the symmetric square root of the GOE covariance
(Equation (
12)), adopt the notations
and consider the following optimization problem
where
is the Frobenius norm.
Setting the derivatives of (
15) with respect to
,
to zero, using Parceval’s identity and properties of the Kronecker product yields the following equations with respect to
unknowns
and diag
:
where
is the
positive-definite matrix.
Multiplying Equation (
16) by
, Equations (
16) and (
17) can be further simplified to
The system of Equations (
18) and (
19) is non-linear and has multiple solutions (
is one of those). To avoid this ambiguity, a good first guess for the control vector
can be prepared by first rescaling the spectral components
to minimize the distance between them by choosing a suboptimal
, and then averaging the resulting scaled approximations of
in order to get a plausible first guess for
. In the simple case when the along-track spectra can be rescaled with zero error (
), Equations (
16) and (
17) are reduced to identities.
Since the exact expressions for the cost function (
15) and gradients (
16) and (
17) are available, minimization of (
15) can be done at relatively low expense by a quasi-Newtonian algorithm. The above expressions depend only on the four structure functions
and four along-track spectra
, that are easy to manipulate.
After optimization of the the GOE model parameters
the approximation error can be estimated as
. The results of the optimization are shown in
Table 1 for four different resolutions
of a 1024 kilometer long piece of swath.
As it is seen, the optimal rescaling parameters weakly depend on swath resolution, but the value of the approximation error is roughly proportional to the inverse of the grid step.
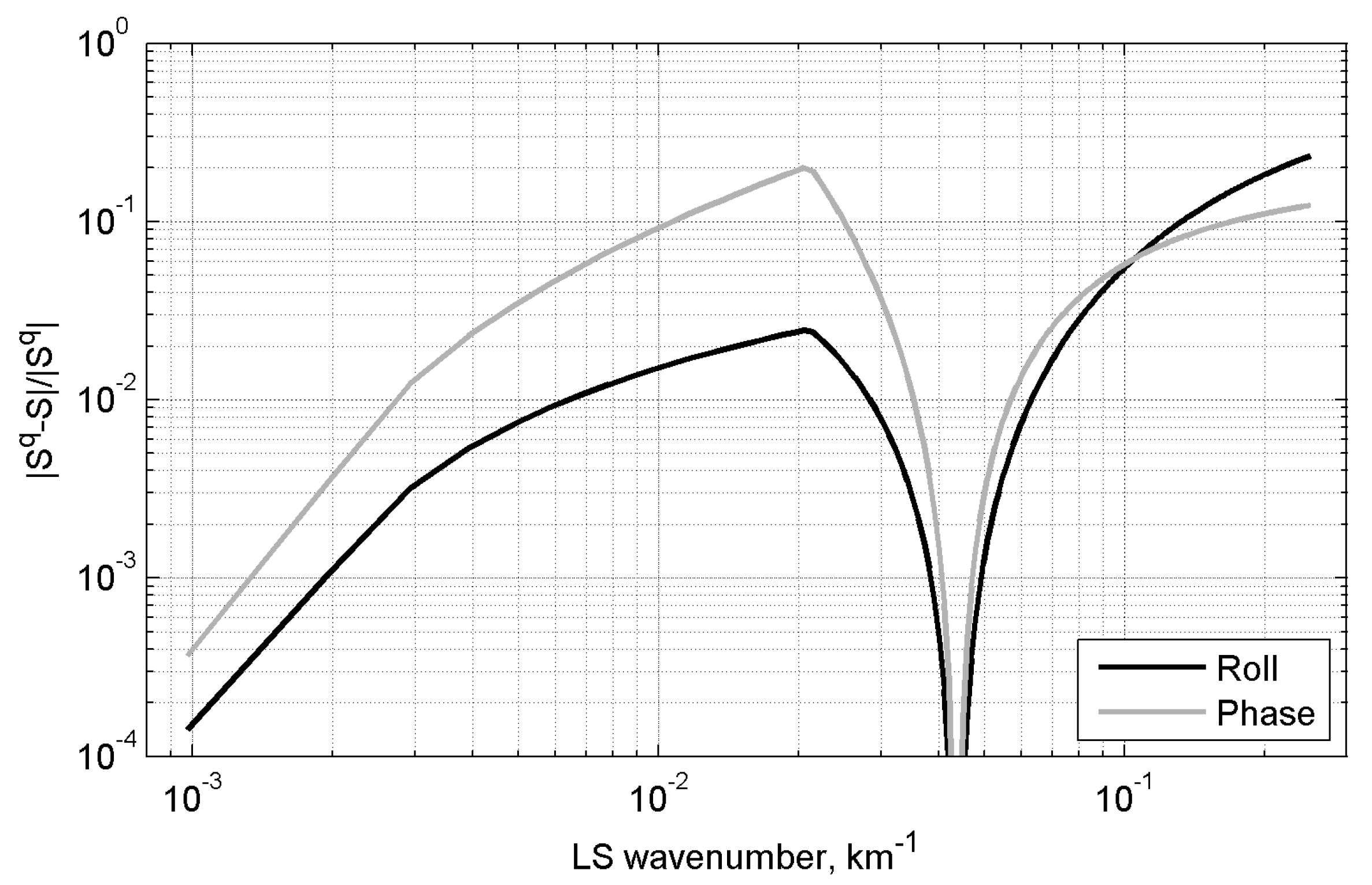
Figure 2 demonstrates the relative approximation errors
of the roll and phase components of GOE spectra as a function of the wavenumber
k. For the dominant spectral components with
(cf.
Figure 1) the errors are generally less than a few percent and yield the mean approximation errors
of 2–7% depending on the grid resolution (
Table 1). We assume that these values are small enough to be comparable with the modelling uncertainties of the LS error spectra.
In that respect it might be useful to take into account the similarities of the LS GOE spectra at the stage of their estimation from the basic principles [
2], because the respective “universal” LS GOE model (
12) provides much better computational efficiency of the pseudo-inversion and projection matrices.
2.4. Computational Savings
Computation of is a costly task because it involves a singular value decomposition of a large matrix (e.g., at 1 km swath resolution and 1000 km long piece of swath, the matrix size is ). However, this task is not insurmountable because we need to find only 4000 eigenvectors corresponding to all non-zero eigenvalues. After they are found offline, the entire projection of requires approximately floating point multiplications (FPMs), which may still appear computationally expensive.
On the other hand, Equation (
13) shows that the approximate projection corresponding to the GOE model (
12) with universal LS error spectrum can be obtained at the expense of only
FPMs, i.e.
times faster.
Similarity of the LS GOE spectra also provides a small parameter
that can be employed to improve the accuracy of the projector via Taylor expansion in the vicinity of
(Equation (
13)). In particular, adopting the notation
, we get
where
and
. As we have already seen (Equation (
10)), application of
is reduced to projecting SWOT observations on the GOE eigenmodes in every point in the along-track direction. Furthermore, since
the matrix
is symmetric, and, as it can be seen from the rhs of (
21), its action on a vector is performed in four sweeps, each containing the following two steps:
perform spectral transform in the along-track direction times (for every along-track section) using the qth diagonal matrix at the expense of FPMs.
project the result using on the qth column of times (for every across-track section) which is approximately equivalent to N multiplications.
After that, perform summation of the results over all four cross-track GOE components q. The computational complexity of the above described first-order correction is estimated as , still a considerable ( times) saving compared to the exact projection.
3. Discussion
In this study we observed that similarity of the LS GOE spectra can potentially bring considerable computational savings in assimilating wide-swath altimetry data into numerical models. These savings are due to the possibility of accurately approximating the symmetric square root of the GOE covariance matrix by factorizing it as a Kronecker product of two smaller ( and ) matrices operating in the CS and LS directions. As a consequence, (pseudo)inversion operations on are reduced to (pseudo)inversions of the respective factors in the Kronecker product. The spectral similarity also provides a small parameter that can be used to improve the accuracy of the above approximations via Taylor expansions of the exact GOE covariance matrix in the vicinity of its computationally efficient estimate.
In view of the above, the GOE covariance model [
2] derived from the first principles, could be supplemented by a version featuring the universal LS spectrum. This development may bring extra practical benefits to the data assimilation community.
An ultimate goal of incorporation of the wide-swath altimetry into the data assimilation systems is providing a computationally efficient algorithm of statistically consistent rescaling of the innovations. Conventionally, it was done under the assumption of spatially uncorrelated observation errors whose covariance matrix is diagonal and is easily inverted. That is not the case for the wide-swath altimetry characterized by substantial error correlations at distances larger than the sampling scale, making the inversion of
a cahllenging task. A few attempts have been made to do so [
5,
9] using purely heuristic assumptions on the sparsity pattern of
. In the presented study, we explicitly use information on the structure of the GOE part of the SWOT error covariance matrix to derive computationally efficient approximations to its pseudo-inverse and the respective projection operator
.
The presented effort sheds more light on the structure of
and provides an opportunity to go beyond the simple assumptions used in [
7,
8] for filtering of the GOEs from innovations. It is necessary to note that the success of the filtering technique largely depends on the relative magnitudes of other types of errors (such as KaRIN noise, wet/dry atmosphere and model error) that contribute to the innovations. In practice, GOEs are often dominated by other error components, and in this case the “LS longwave approximation” of the type used in [
7,
8] and additional ensemble information on the model errors may improve the filter quality. An alternative filtering approach [
11] has demonstrated a certain superiority of a two-parameter family of isotropic smoothing kernels generated by quadratic polynomial of the Laplacian operator
over the kernel generated by
.
Numerical assimilation experiments with simulated SWOT data demonstrate that wide-swath SSH observations are especially useful for monitoring oceanic small scale phenomena at wavelengths below 50 km [
12,
13]. At these scales, the KaRIN noise, whose error covariance is diagonal, dominates over all other SWOT error components [
10], thus providing an efficient rescaling algorithm for the submesoscale innovations. In this case, GOE and wet atmosphere error covariances can be treated as small perturbations to the KaRIN noise covariance matrix, so the rescaling matrix can be well approximated by the expansion of the inverse square root of the KaRIN noise in the respective perturbations. Equations (
12), (
20) and (
21) provide numerically efficient GOE contributions to this expansion. At the same time, the obtained low-rank approximation of the square root of the GOE covariance (
12) provides an efficient way of computing the joint impact of KaRIN noise and GOEs using the approach of [
14].
In a more general perspective, we assume that obtaining a universal and numerically efficient algorithm for rescaling the wide-swath altimetry observations is a challenging problem that could be solved by jointly analyzing real data from the forthcoming missions and ensemble simulations of the ocean surface topography by state-of-the-art numerical models. Highly structured observation error covariances of the wide-swath altimetry provide an opportunity to apply deep learning techniques (e.g., [
15,
16]) for retrieval of both more realistic estimates of the covariance matrices and their inverses. Extensive literature (e.g., [
17,
18,
19,
20]) also exists on other methods of approximating the inverse covariances. These methods are more general, as they do not take into account the specific structure of the covariance model, as it was done in the present study. Of particular interest are applications of the modified Cholesky decomposition [
18], under the sparsifying assumption of conditional independence of the observation errors beyond a given localization scale. This approach is suitable for efficient parallelization [
19] and guarantees the positive definite property of the inverse covariance.
In the SWOT application, one may think of combining the above mentioned methods with the specific information on the correlation structure of the swath altimetry to produce an accurate and computationally efficient inverse covariance approximation. The presented study could be treated as a step towards this ultimate goal.