Evaluation of UAV LiDAR for Mapping Coastal Environments
Abstract
1. Introduction
2. Related Work
3. UAV-Based Mobile Mapping System Integration and System Calibration
4. Study Sites and Data Acquisition
4.1. Dana Island, Turkey
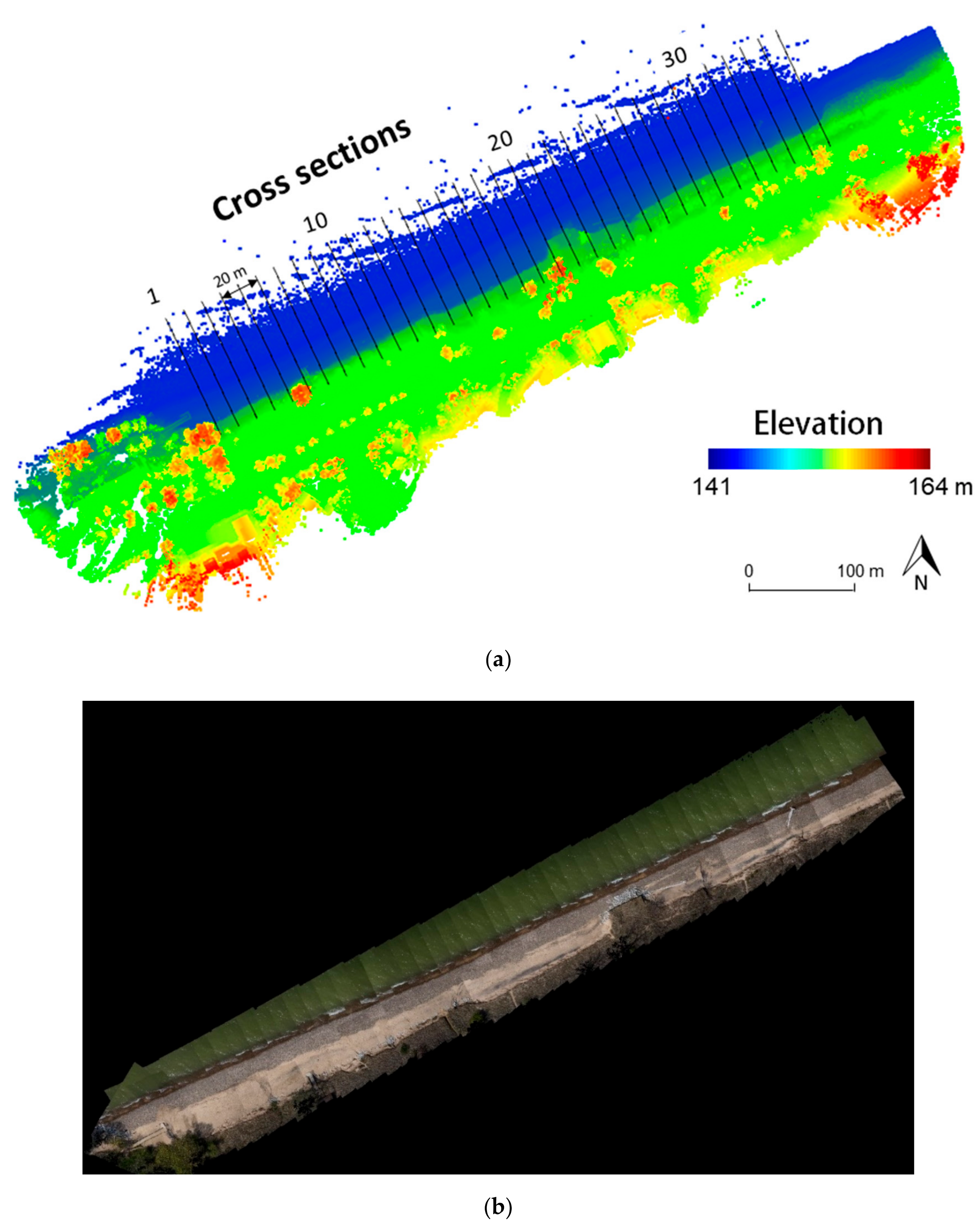
4.2. Indiana Shoreline of Southern Lake Michigan, USA
5. Methodology
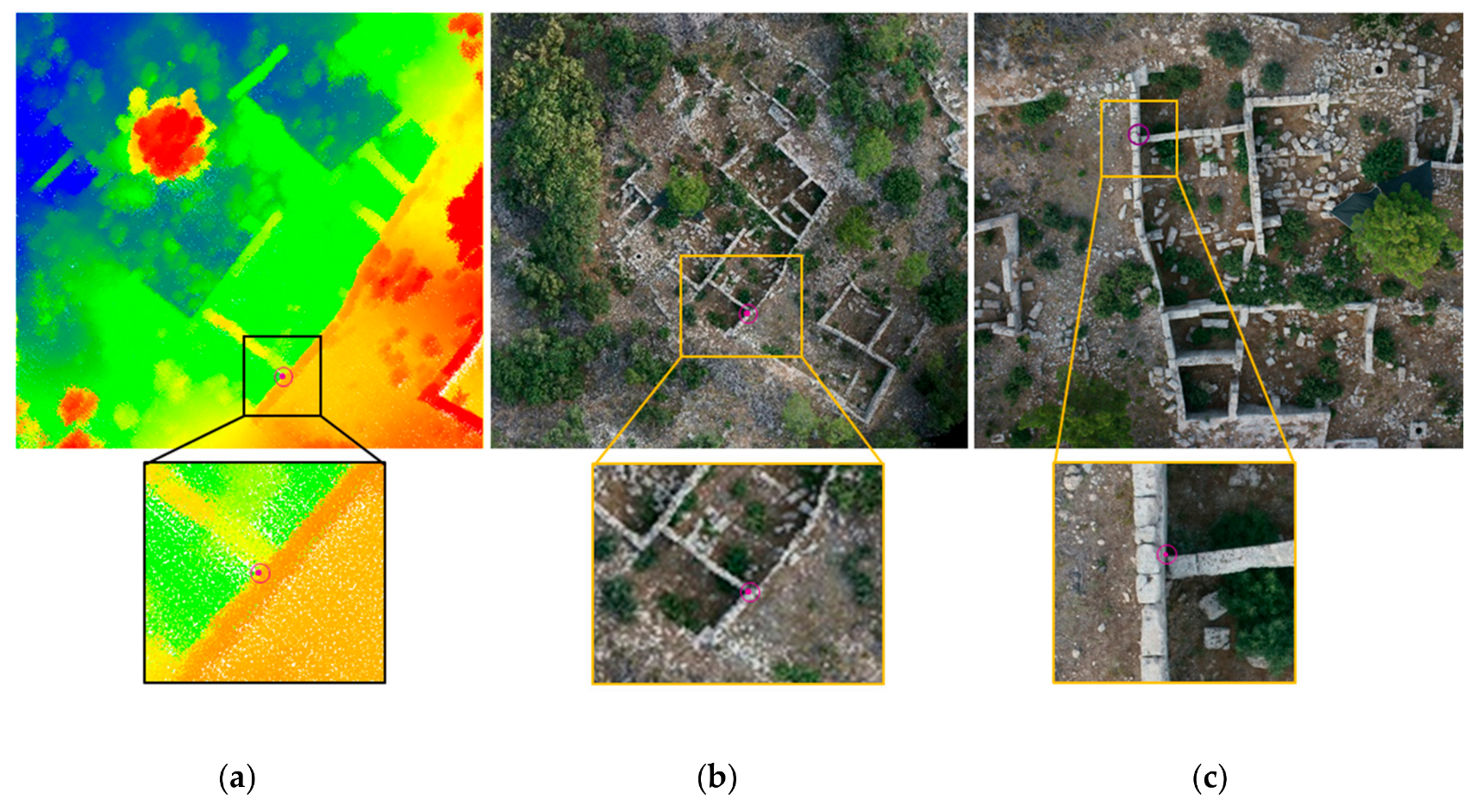
5.1. LiDAR Point Cloud Reconstruction
5.2. Image-Based 3D Reconstruction
5.3. Point Cloud Quality Assessment and Comparison
5.4. DSM, Orthophoto, and Color-Coded Point Cloud Generation
5.5. Shoreline Change Quantification
6. Experimental Results
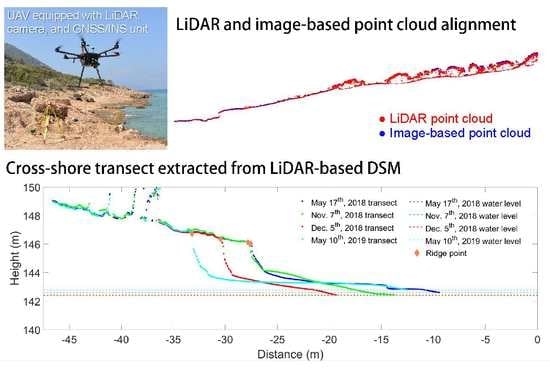
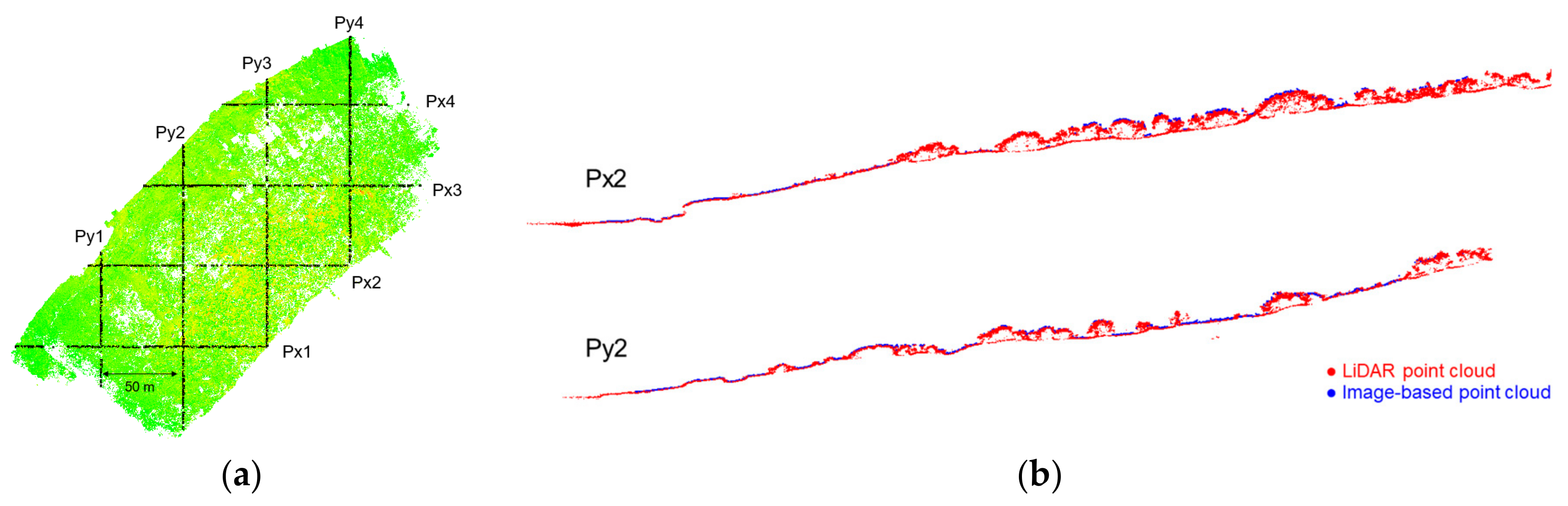
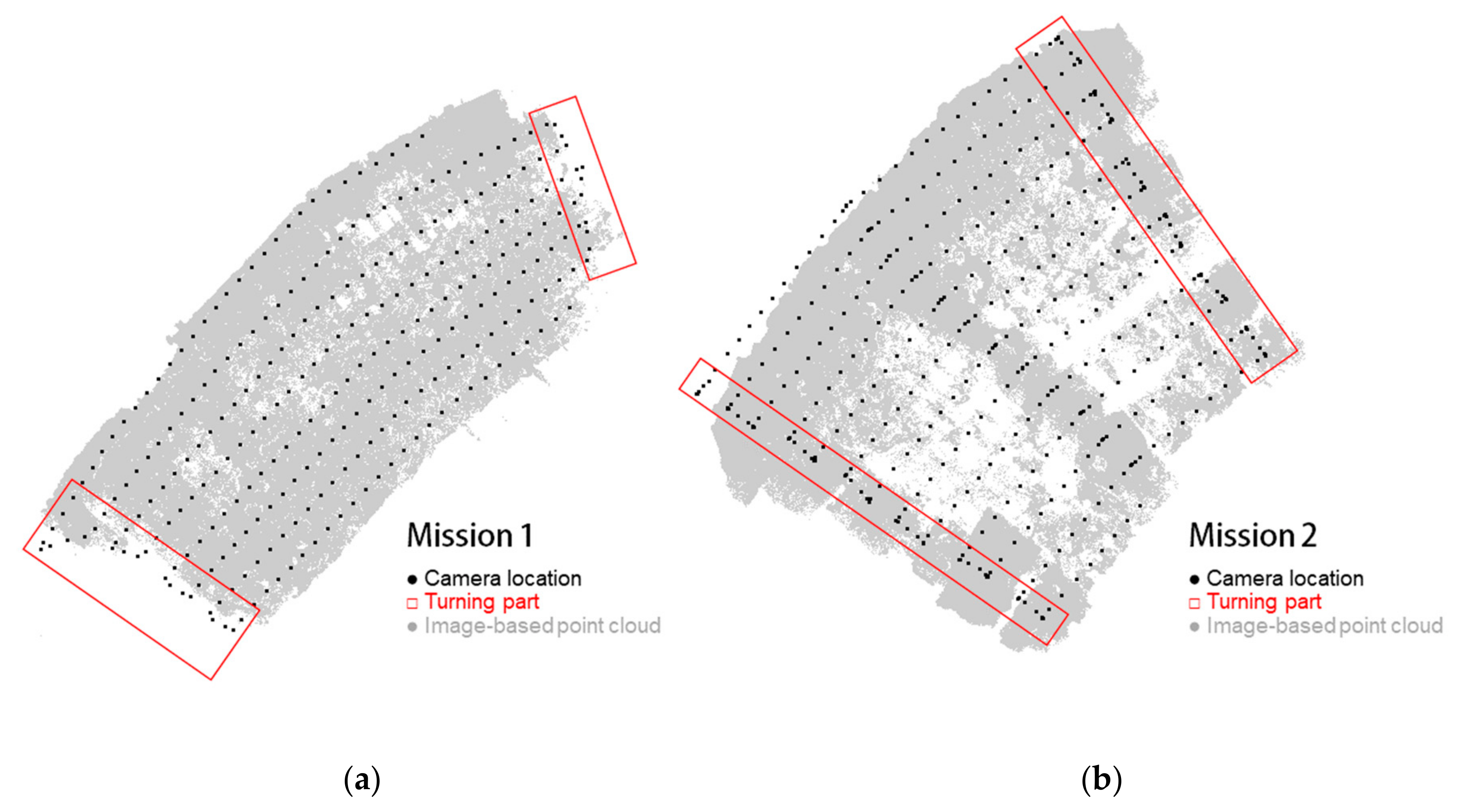
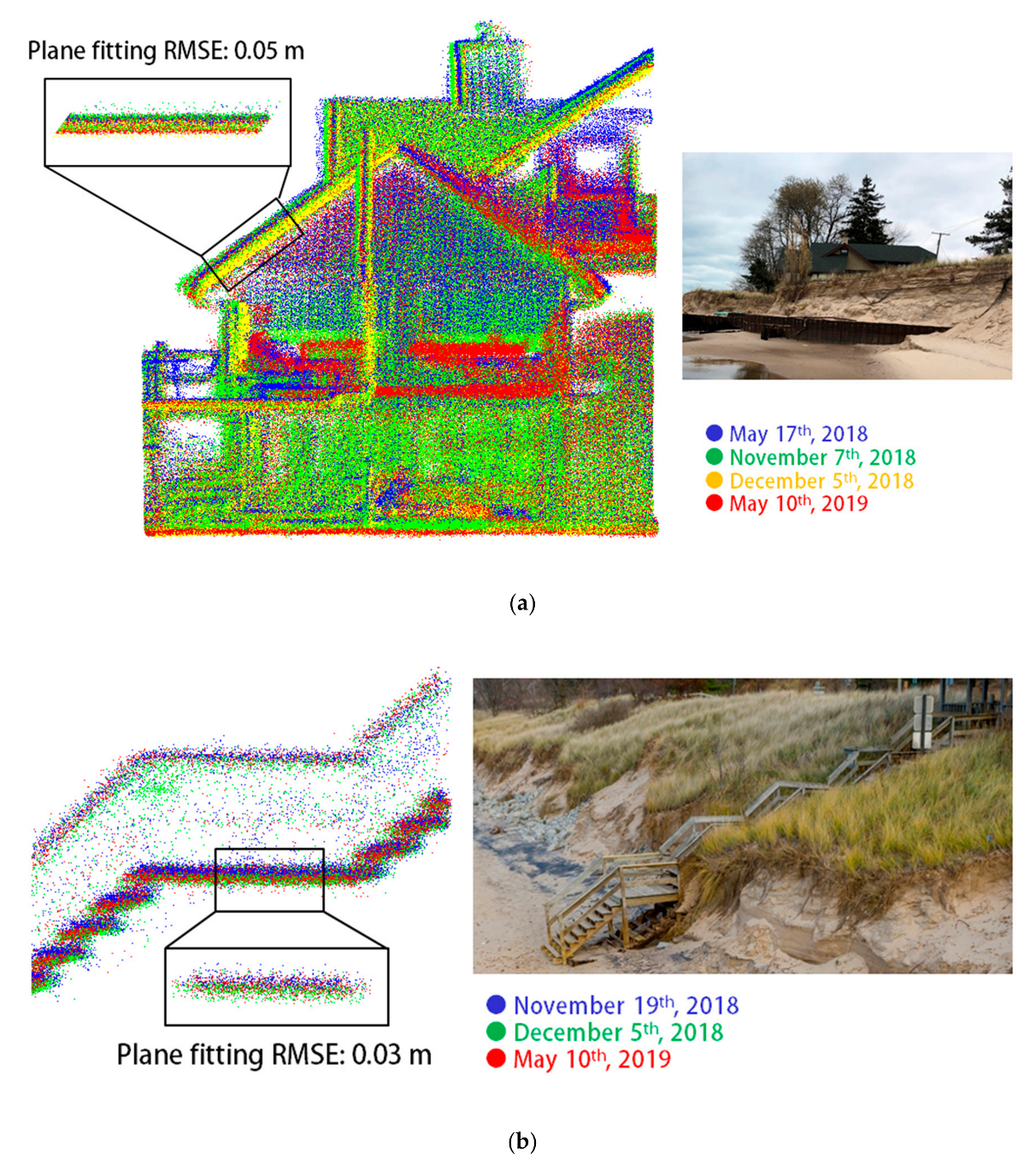
6.1. LiDAR Point Cloud Alignment
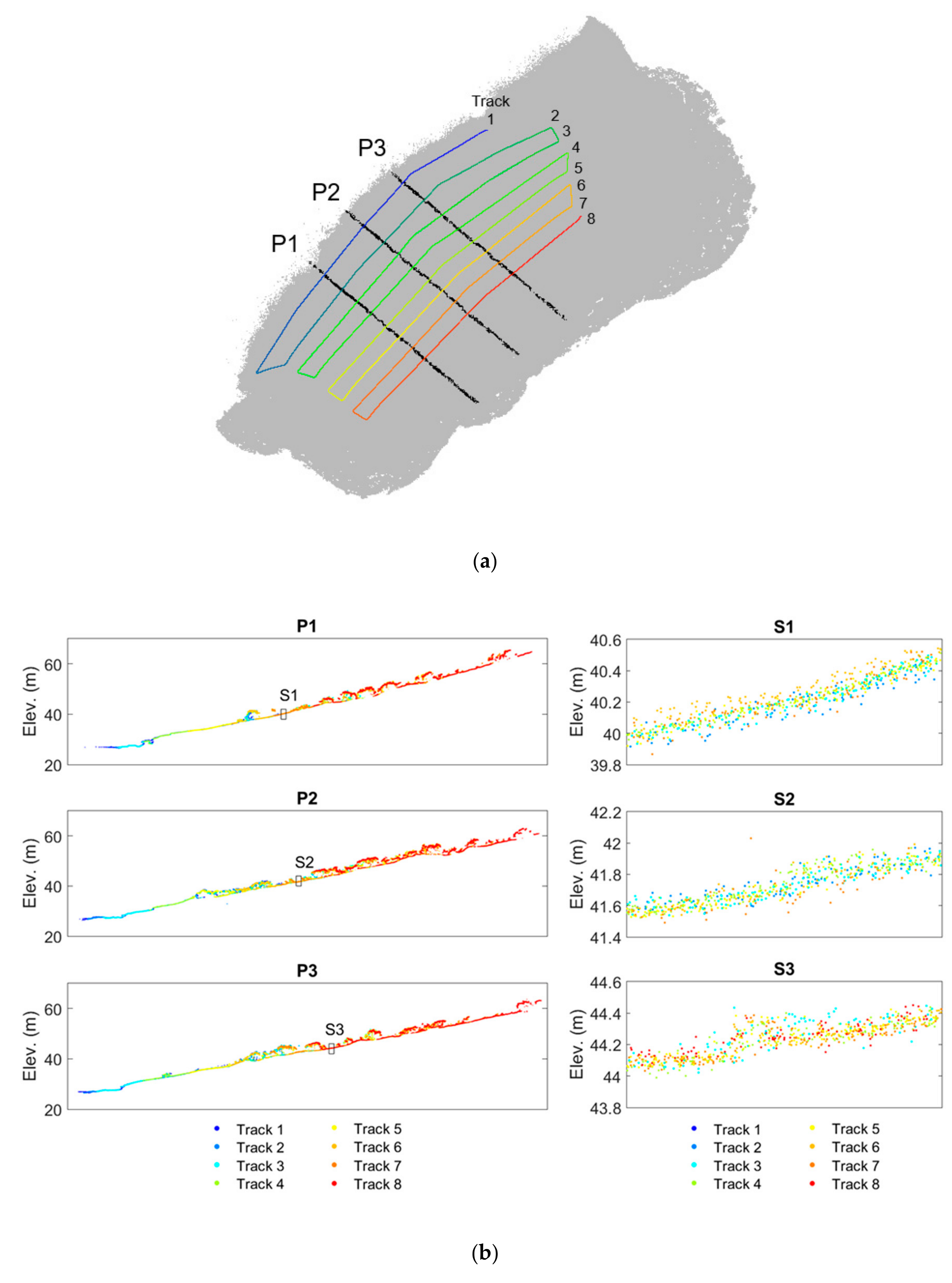
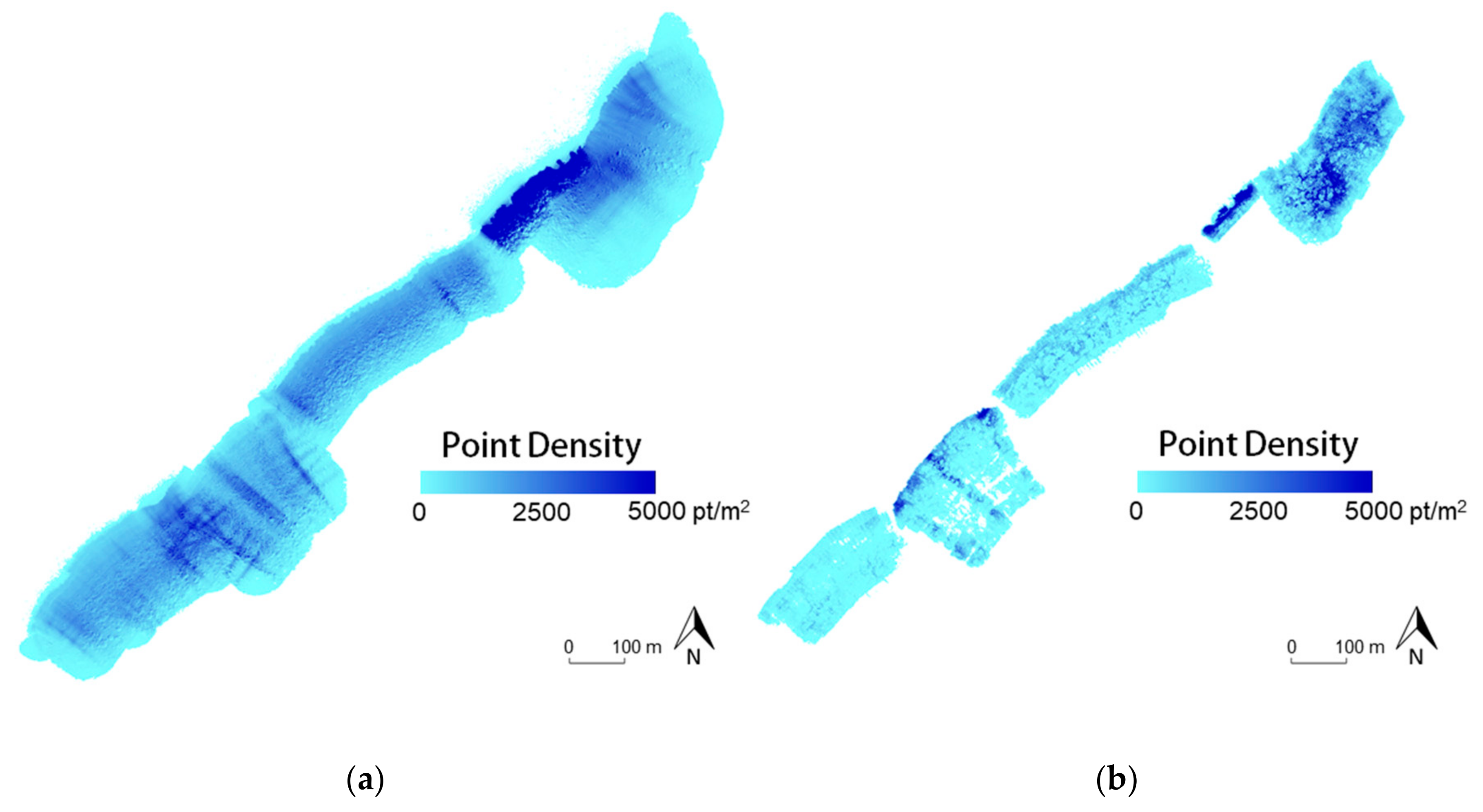
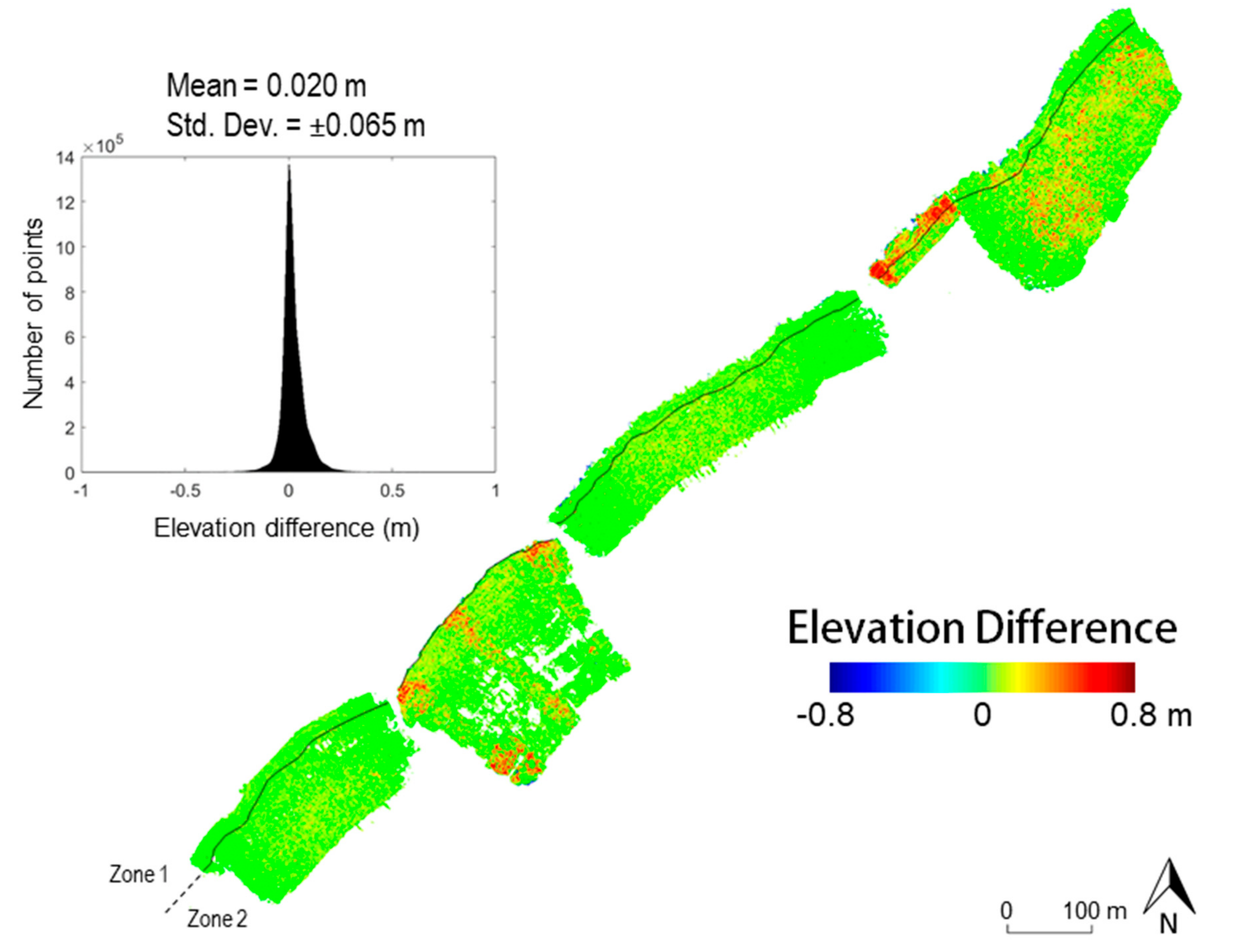
6.2. Comparative Quality Assessment of LiDAR and Image-Based Point Clouds
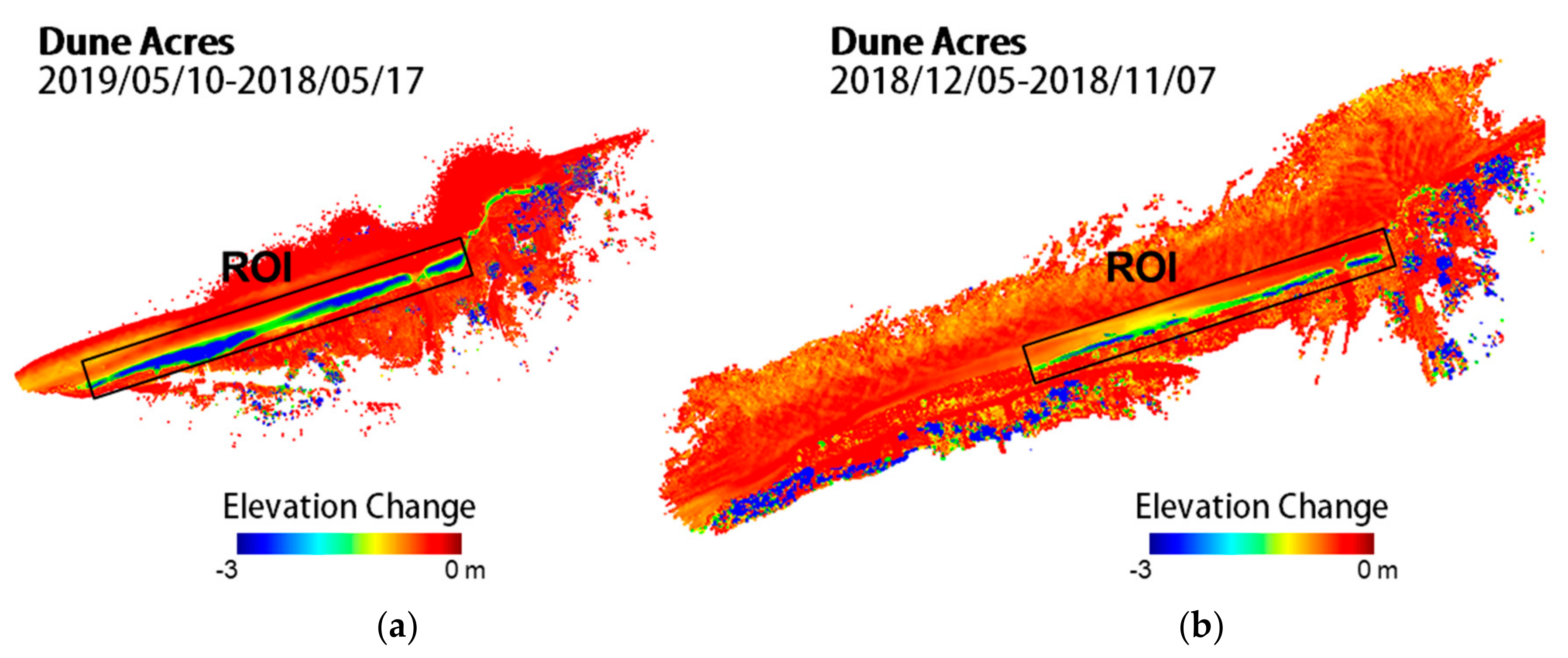
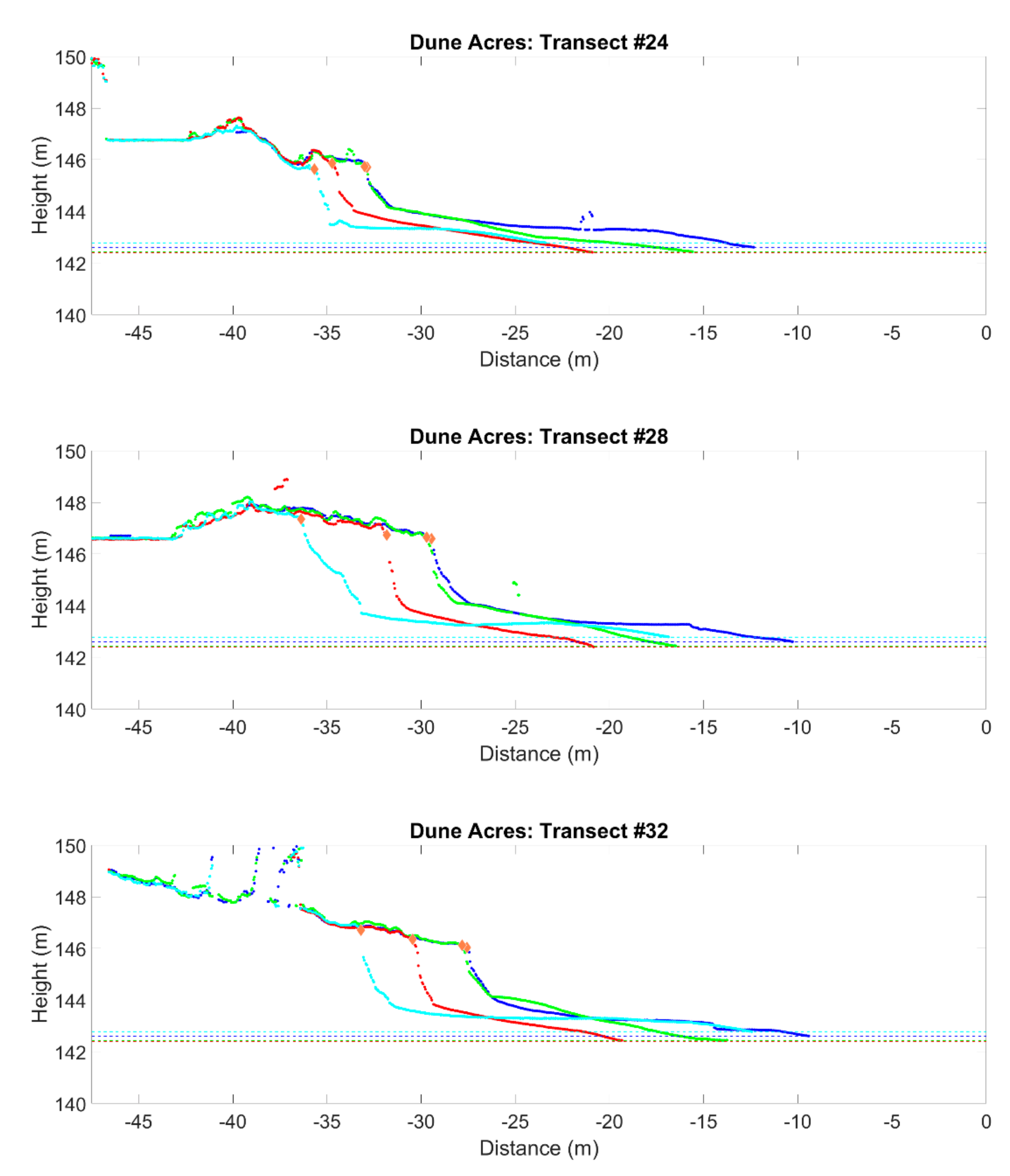
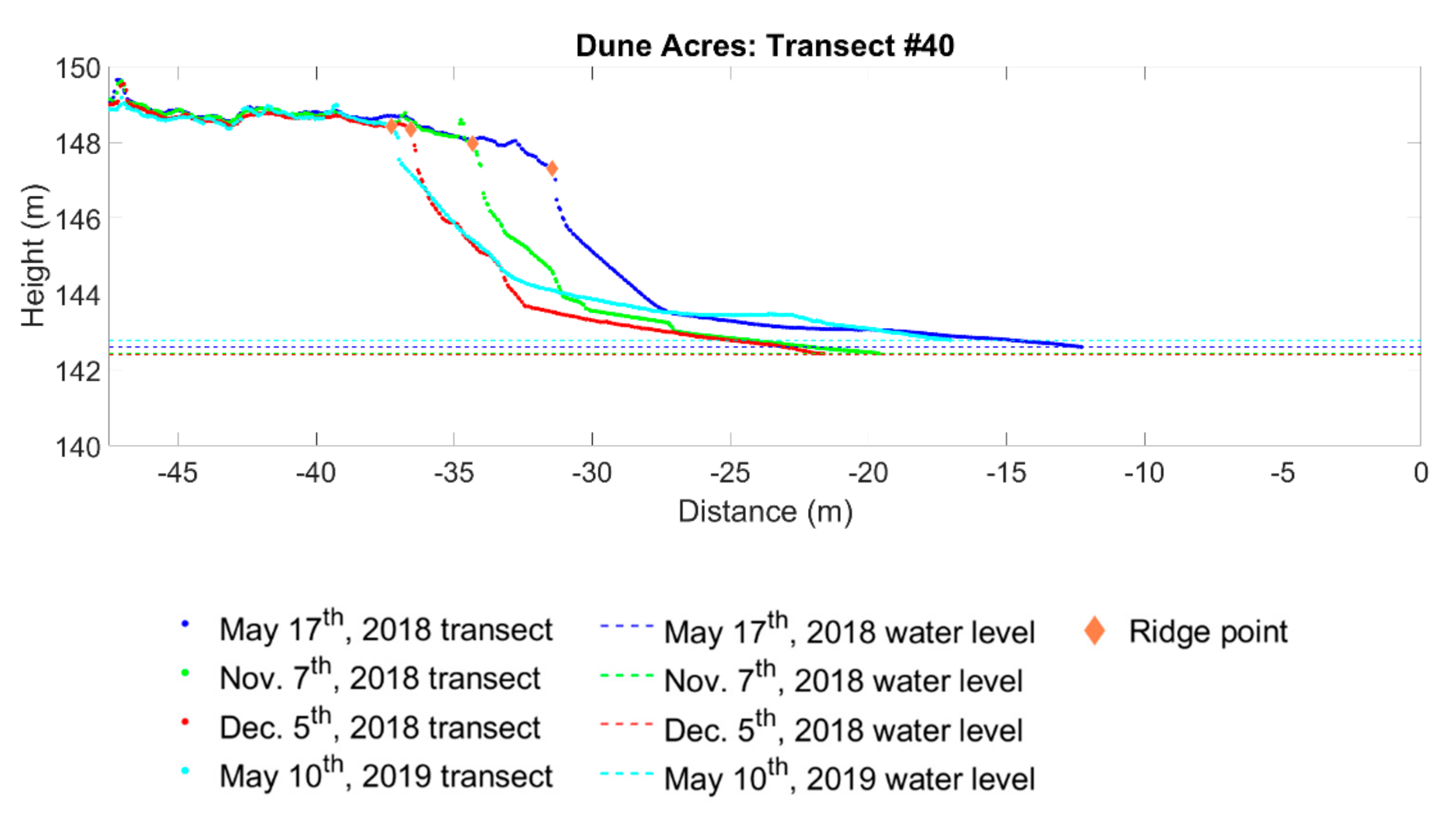
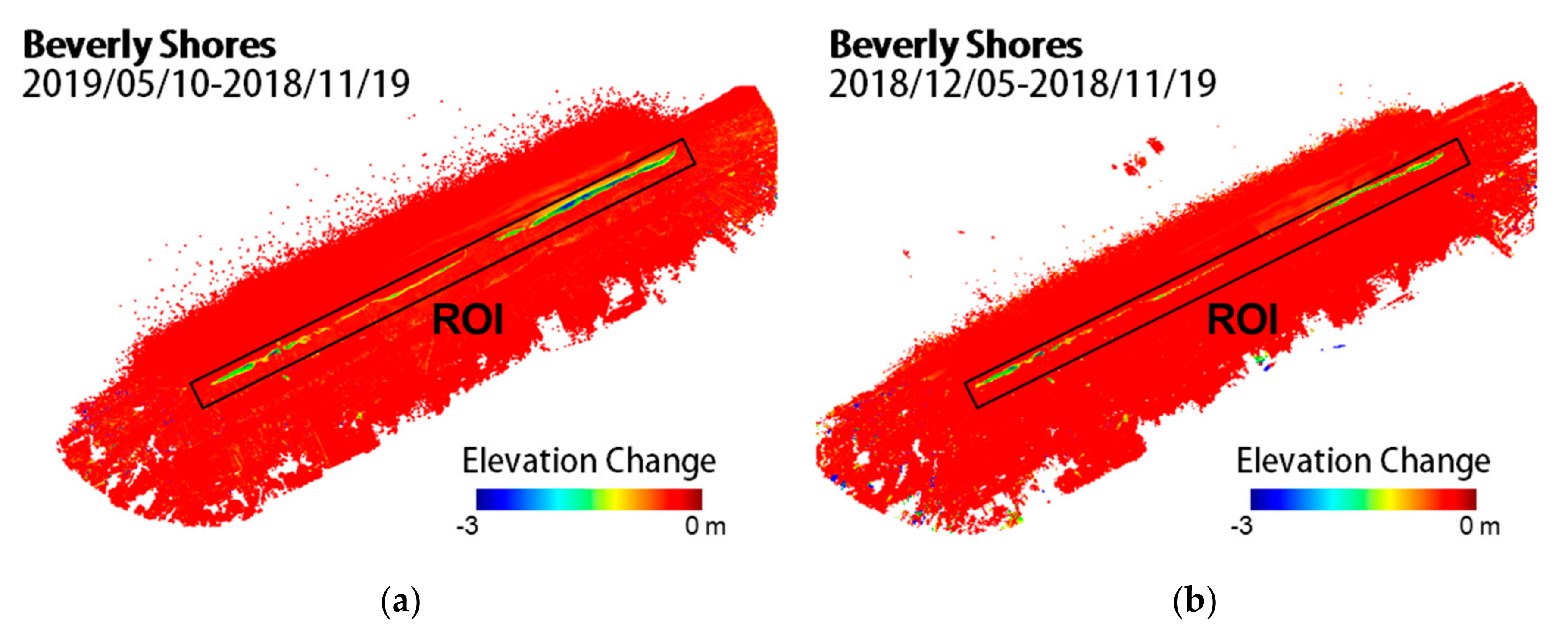
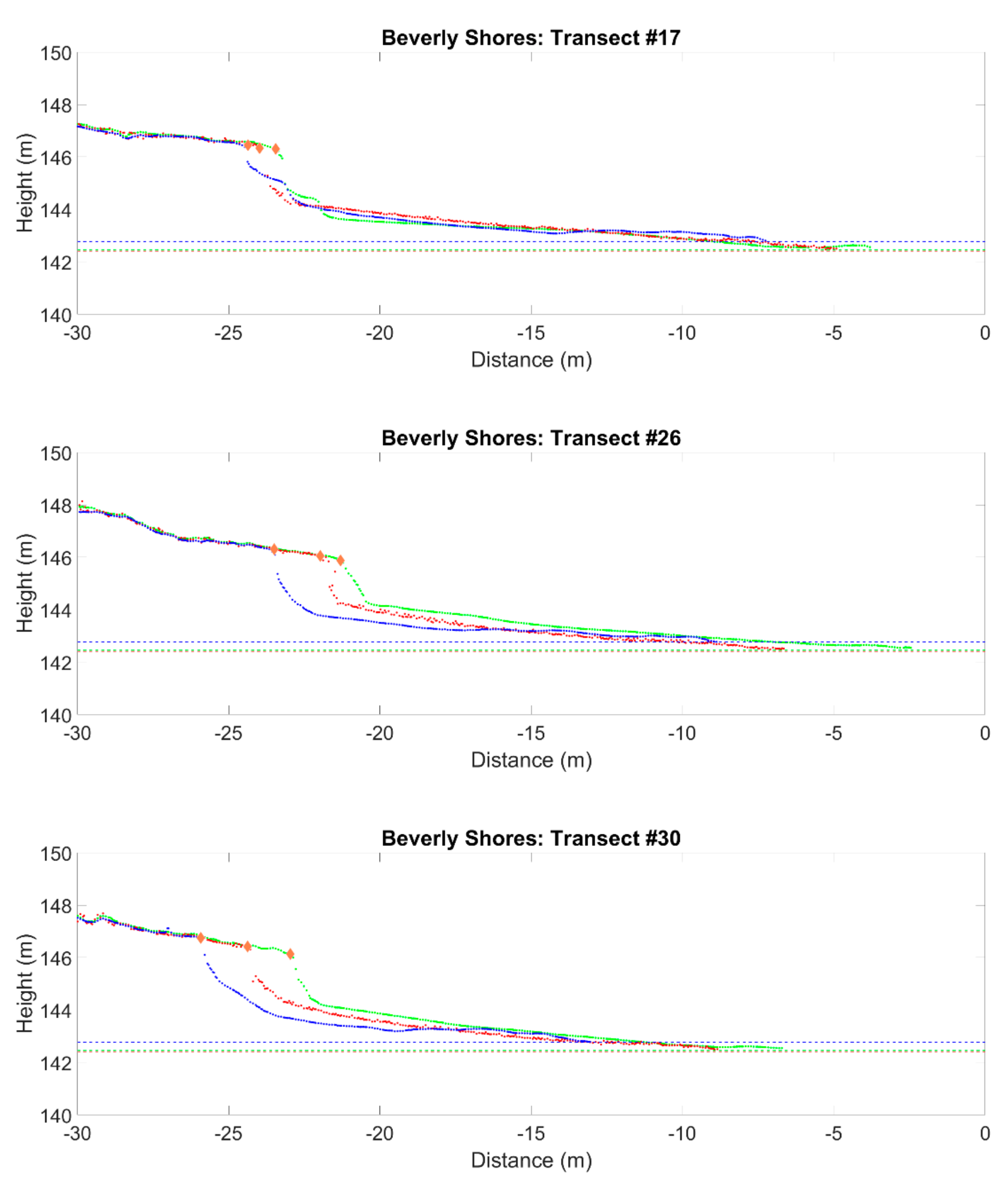
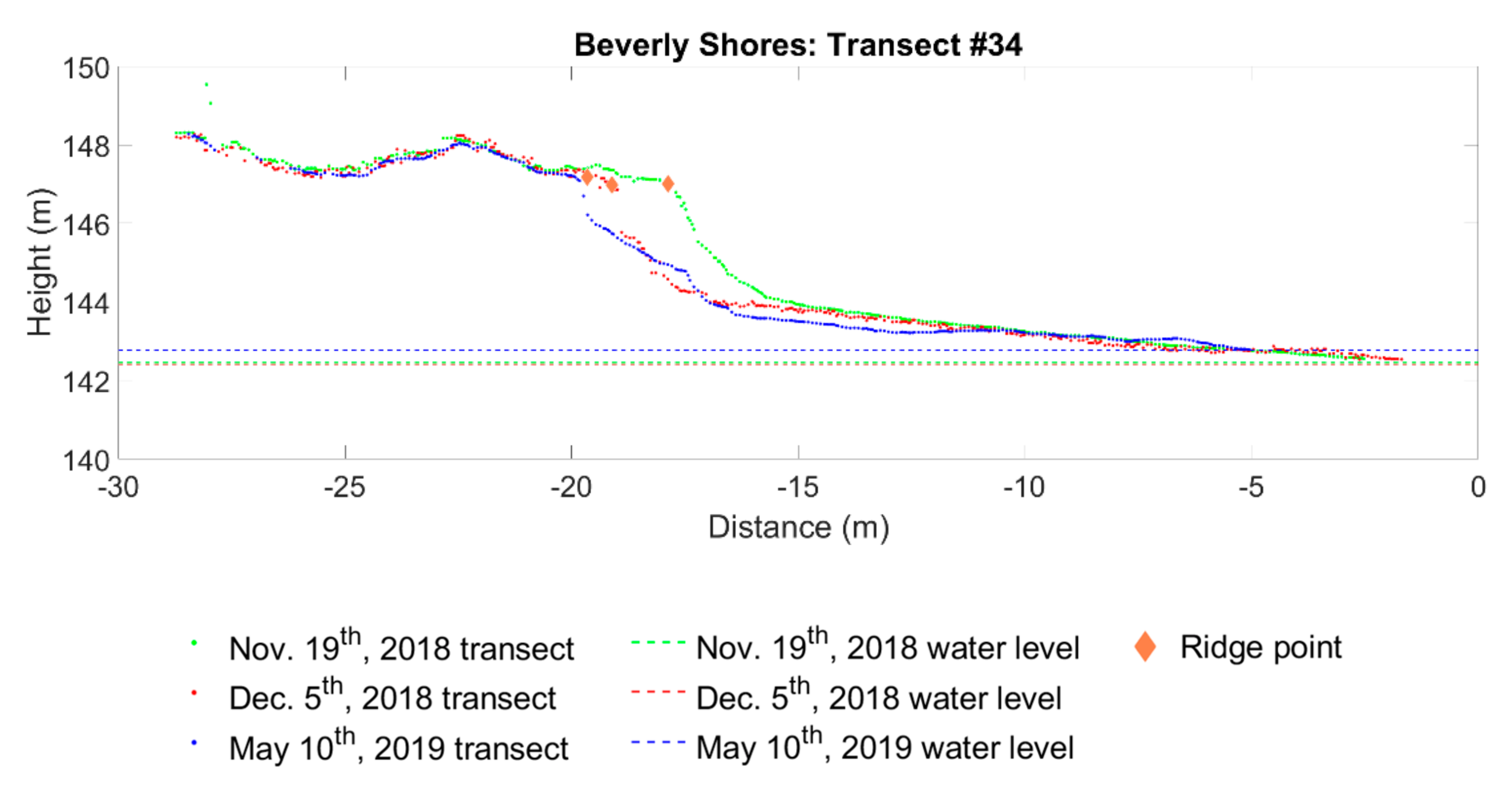
6.3. Shoreline Change Estimation
7. Discussion
7.1. Comparative Performance of UAV LiDAR and UAV Photogrammetry
- The point cloud alignment between different LiDAR strips is good (within the noise level of the point cloud) and the overall precision of the derived point cloud is ±0.10 m.
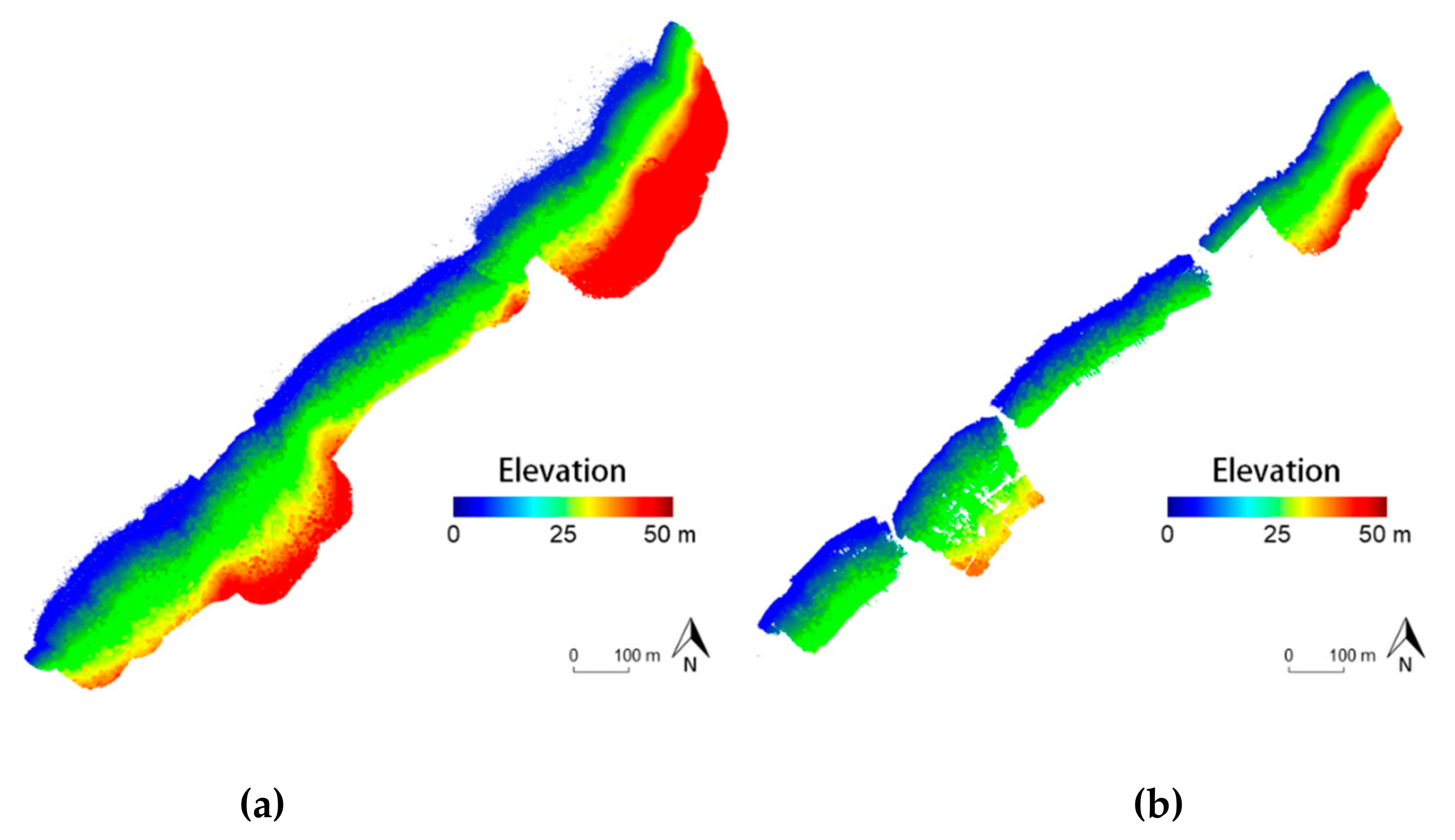
- LiDAR provides a considerable larger spatial coverage when compared to photogrammetric products.
- Profiles along X and Y directions show that the overall discrepancies along the X and Y directions between LiDAR and image-based point clouds are 0.2 cm and 0.1 cm, respectively. The discrepancy along Z direction ranges from 8.9 cm to 8.6 cm, with an average of 0.2 cm, suggesting that the image-based surface is slightly higher than the LiDAR-based surface.
- The elevation difference between LiDAR and image-based point clouds is 0.020 ± 0.065 m. In this study, technical factors (e.g., the narrow baseline problem for image reconstruction when UAV slowed down to make turns) has a major impact on the discrepancy between LiDAR and image-based point clouds, and environmental factors have a minor impact. Overall, the point clouds generated by both techniques are compatible within a 5 to 10 cm range.
7.2. UAV LiDAR for Shoreline Change Quantification
- The compatibility of the point clouds collected over the one-year period is evaluated quantitatively and qualitatively. The result shows that the point clouds are compatible within a 0.05 m range.
- Substantial shoreline erosion is observed both over the one-year period (May 2018 to May 2019) and from the storm-induced period (November 2018 to December 2018).
- The storm-induced coastal change captured by the UAV system highlights the ability to resolve coastal changes over episodic timescales, at a low cost.
- Foredune ridge recession at Dune Acres and Beverly Shores ranges from 2 m to 9 m and 0 m to 4 m, respectively.
- Volume loss at Dune Acres is 3998.6 m3 (equating an average volume loss of 18.2 cubic meters per meter of beach shoreline) within the one-year period and 2673.9 m3 (equating an average volume loss of 12.2 cubic meters per meter of beach shoreline) within the storm-induced period. Volume loss at Beverly Shores is 938.4 m3 (equating an average volume loss of 2.8 cubic meters per meter of beach shoreline) within the survey period and 883.8 m3 (equating an average volume loss of 2.6 cubic meters per meter of beach shoreline) within the storm-induced period.
8. Conclusions and Recommendations for Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Eltner, A.; Kaiser, A.; Castillo, C.; Rock, G.; Neugirg, F.; Abellán, A. Image-based surface reconstruction in geomorphometry–merits, limits and developments. Earth Surf. Dyn. 2016, 4, 359–389. [Google Scholar] [CrossRef]
- Moloney, J.G.; Hilton, M.J.; Sirguey, P.; Simons-Smith, T. Coastal Dune Surveying Using a Low-Cost Remotely Piloted Aerial System (RPAS). J. Coast. Res. 2017, 34, 1244–1255. [Google Scholar] [CrossRef]
- Mancini, F.; Dubbini, M.; Gattelli, M.; Stecchi, F.; Fabbri, S.; Gabbianelli, G. Using unmanned aerial vehicles (UAV) for high-resolution reconstruction of topography: The structure from motion approach on coastal environments. Remote Sens. 2013, 5, 6880–6898. [Google Scholar] [CrossRef]
- Guisado-Pintado, E.; Jackson, D.W.; Rogers, D. 3D mapping efficacy of a drone and terrestrial laser scanner over a temperate beach-dune zone. Geomorphology 2019, 328, 157–172. [Google Scholar] [CrossRef]
- Deis, D.R.; Mendelssohn, I.A.; Fleeger, J.W.; Bourgoin, S.M.; Lin, Q. Legacy effects of Hurricane Katrina influenced marsh shoreline erosion following the Deepwater Horizon oil spill. Sci. Total Environ. 2019, 672, 456–467. [Google Scholar] [CrossRef]
- Eulie, D.O.; Corbett, D.R.; Walsh, J.P. Shoreline erosion and decadal sediment accumulation in the Tar-Pamlico estuary, North Carolina, USA: A source-to-sink analysis. Estuar. Coast. Shelf Sci. 2018, 202, 246–258. [Google Scholar] [CrossRef]
- Rangel-Buitrago, N.G.; Anfuso, G.; Williams, A.T. Coastal erosion along the Caribbean coast of Colombia: Magnitudes, causes and management. Ocean Coast. Manag. 2015, 114, 129–144. [Google Scholar] [CrossRef]
- Hancock, G.R. The impact of different gridding methods on catchment geomorphology and soil erosion over long timescales using a landscape evolution model. Earth Surf. Process. Landf. 2006, 31, 1035–1050. [Google Scholar] [CrossRef]
- Bater, C.W.; Coops, N.C. Evaluating error associated with lidar-derived DEM interpolation. Comput. Geosci. 2009, 35, 289–300. [Google Scholar] [CrossRef]
- Obu, J.; Lantuit, H.; Grosse, G.; Günther, F.; Sachs, T.; Helm, V.; Fritz, M. Coastal erosion and mass wasting along the Canadian Beaufort Sea based on annual airborne LiDAR elevation data. Geomorphology 2017, 293, 331–346. [Google Scholar] [CrossRef]
- Tamura, T.; Oliver, T.S.N.; Cunningham, A.C.; Woodroffe, C.D. Recurrence of extreme coastal erosion in SE Australia beyond historical timescales inferred from beach ridge morphostratigraphy. Geophys. Res. Lett. 2019, 46, 4705–4714. [Google Scholar] [CrossRef]
- Elaksher, A.F. Fusion of hyperspectral images and lidar-based dems for coastal mapping. Opt. Lasers Eng. 2008, 46, 493–498. [Google Scholar] [CrossRef]
- Awad, M.M. Toward robust segmentation results based on fusion methods for very high resolution optical image and lidar data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 2067–2076. [Google Scholar] [CrossRef]
- Launeau, P.; Giraud, M.; Robin, M.; Baltzer, A. Full-Waveform LiDAR Fast Analysis of a Moderately Turbid Bay in Western France. Remote Sens. 2019, 11, 117. [Google Scholar] [CrossRef]
- Reif, M.K.; Wozencraft, J.M.; Dunkin, L.M.; Sylvester, C.S.; Macon, C.L. A review of US Army Corps of Engineers airborne coastal mapping in the Great Lakes. J. Great Lakes Res. 2013, 39, 194–204. [Google Scholar] [CrossRef]
- Klemas, V. Beach profiling and LIDAR bathymetry: An overview with case studies. J. Coast. Res. 2011, 27, 1019–1028. [Google Scholar] [CrossRef]
- Hapke, C.J.; Himmelstoss, E.A.; Kratzmann, M.G.; List, J.H.; Thieler, E.R. National Assessment of Shoreline Change: Historical Shoreline Change Along the New England and Mid-Atlantic Coasts. US. Geological Survey Open-File Report; 2010. Available online: https://pubs.usgs.gov/of/2010/1118/ (accessed on 4 December 2019).
- Fletcher, C.H.; Romine, B.M.; Genz, A.S.; Barbee, M.M.; Dyer, M.; Anderson, T.R.; Lim, S.C.; Vitousek, S.; Bochicchio, C.; Richmond, B.M. National Assessment of Shoreline Change: Historical Shoreline Change in the Hawaiian Islands. U.S. Geological Survey Open-File Report; 2011. Available online: https://pubs.usgs.gov/of/2011/1051 (accessed on 4 December 2019).
- Ruggerio, P.; Kratzmann, M.G.; Himmelstoss, E.A.; Reid, D.; Allan, J.; Kaminsky, G. National Assessment of Shoreline Change: Historical Shoreline Change along the Pacific Northwest Coast. No. 2012-1007; U.S. Geological Survey Open-File Report; 2012. Available online: http://dx.doi.org/10.3133/ofr20121007 (accessed on 4 December 2019).
- Parrish, C.E.; Magruder, L.A.; Neuenschwander, A.L.; Forfinski-Sarkozi, N.; Alonzo, M.; Jasinski, M. Validation of ICESat-2 ATLAS Bathymetry and Analysis of ATLAS’s Bathymetric Mapping Performance. Remote Sens. 2019, 11, 1634. [Google Scholar] [CrossRef]
- Smith, A.; Gares, P.A.; Wasklewicz, T.; Hesp, P.A.; Walker, I.J. Three years of morphologic changes at a bowl blowout, Cape Cod, USA. Geomorphology 2017, 295, 452–466. [Google Scholar] [CrossRef]
- Montreuil, A.L.; Bullard, J.E.; Chandler, J.H.; Millett, J. Decadal and seasonal development of embryo dunes on an accreting macrotidal beach: North Lincolnshire, UK. Earth Surf. Process. Landf. 2013, 38, 1851–1868. [Google Scholar] [CrossRef]
- Guillot, B.; Pouget, F. UAV application in coastal environment, example of the Oleron island for dunes and dikes survey. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, XL-3/W3, 321–326. [Google Scholar] [CrossRef]
- Gonçalves, J.A.; Henriques, R. UAV photogrammetry for topographic monitoring of coastal areas. ISPRS J. Photogramm. Remote Sens. 2015, 104, 101–111. [Google Scholar] [CrossRef]
- Turner, I.L.; Harley, M.D.; Drummond, C.D. UAVs for coastal surveying. Coast. Eng. 2016, 114, 19–24. [Google Scholar] [CrossRef]
- Papakonstantinou, A.; Topouzelis, K.; Pavlogeorgatos, G. Coastline zones identification and 3D coastal mapping using UAV spatial data. ISPRS Int. J. Geo Inf. 2016, 5, 75. [Google Scholar] [CrossRef]
- Scarelli, F.M.; Cantelli, L.; Barboza, E.G.; Rosa, M.L.C.; Gabbianelli, G. Natural and Anthropogenic coastal system comparison using DSM from a low cost UAV survey (Capão Novo, RS/Brazil). J. Coast. Res. 2016, 75, 1232–1237. [Google Scholar] [CrossRef]
- Mateos, R.M.; Azañón, J.M.; Roldán, F.J.; Notti, D.; Pérez-Peña, V.; Galve, J.P.; Pérez-García, J.L.; Colomo, C.M.; Gómez-López, J.M.; Montserrat, O.; et al. The combined use of PSInSAR and UAV photogrammetry techniques for the analysis of the kinematics of a coastal landslide affecting an urban area (SE Spain). Landslides 2017, 14, 743–754. [Google Scholar] [CrossRef]
- Nahon, A.; Molina, P.; Blázquez, M.; Simeon, J.; Capo, S.; Ferrero, C. Corridor Mapping of Sandy Coastal Foredunes with UAS Photogrammetry and Mobile Laser Scanning. Remote Sens. 2019, 11, 1352. [Google Scholar] [CrossRef]
- Westoby, M.J.; Lim, M.; Hogg, M.; Pound, M.J.; Dunlop, L.; Woodward, J. Cost-effective erosion monitoring of coastal cliffs. Coast. Eng. 2018, 138, 152–164. [Google Scholar] [CrossRef]
- Elsner, P.; Dornbusch, U.; Thomas, I.; Amos, D.; Bovington, J.; Horn, D. Coincident beach surveys using UAS, vehicle mounted and airborne laser scanner: Point cloud inter-comparison and effects of surface type heterogeneity on elevation accuracies. Remote Sens. Environ. 2018, 208, 15–26. [Google Scholar] [CrossRef]
- Shaw, L.; Helmholz, P.; Belton, D.; Addy, N. Comparison of UAV LiDAR and imagery for beach monitoring. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, XLII-2/W13, 589–596. [Google Scholar] [CrossRef]
- Aguilar, M.A.; del Mar Saldana, M.; Aguilar, F.J. Assessing geometric accuracy of the orthorectification process from GeoEye-1 and WorldView-2 panchromatic images. Int. J. Appl. Earth Obs. 2013, 21, 427–435. [Google Scholar] [CrossRef]
- WorldView-2 Satellite Sensor. (n.d.) Available online: https://www.satimagingcorp.com/satellite-sensors/worldview-2/ (accessed on 21 November 2019).
- National Agriculture Imagery Program. (n.d.). Available online: https://www.fsa.usda.gov/programs-and-services/aerial-photography/imagery-programs/naip-imagery/ (accessed on 21 November 2019).
- Sankey, T.; Donager, J.; McVay, J.; Sankey, J.B. UAV lidar and hyperspectral fusion for forest monitoring in the southwestern USA. Remote Sens. Environ. 2017, 195, 30–43. [Google Scholar] [CrossRef]
- Zhu, X.; Hou, Y.; Weng, Q.; Chen, L. Integrating UAV optical imagery and LiDAR data for assessing the spatial relationship between mangrove and inundation across a subtropical estuarine wetland. ISPRS J. Photogramm. Remote Sens. 2019, 149, 146–156. [Google Scholar] [CrossRef]
- Miura, N.; Yokota, S.; Koyanagi, T.F.; Yamada, S. Herbaceous Vegetation Height Map on Riverdike Derived from UAV LiDAR Data. In Proceedings of the IGARSS 2018–2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 5469–5472. [Google Scholar]
- Khan, S.; Aragão, L.; Iriarte, J. A UAV–lidar system to map Amazonian rainforest and its ancient landscape transformations. Int. J. Remote Sens. 2017, 38, 2313–2330. [Google Scholar] [CrossRef]
- Pu, S.; Xie, L.; Ji, M.; Zhao, Y.; Liu, W.; Wang, L.; Zhao, Y.; Yang, F.; Qiu, D. Real-time powerline corridor inspection by edge computing of UAV Lidar data. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, 4213, 547–551. [Google Scholar] [CrossRef]
- Velodyne. UltraPuck Data Sheet. Available online: https://hypertech.co.il/wp-content/uploads/2016/05/ULTRA-Puck_VLP-32C_Datasheet.pdf (accessed on 10 October 2019).
- He, F.; Habib, A. Target-based and Feature-based Calibration of Low-cost Digital Cameras with Large Field-of-view. In Proceedings of the ASPRS 2015 Annual Conference, Tampa, FL, USA, 4–8 May 2015. [Google Scholar]
- Ravi, R.; Lin, Y.J.; Elbahnasawy, M.; Shamseldin, T.; Habib, A. Simultaneous System Calibration of a Multi-LiDAR Multicamera Mobile Mapping Platform. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 1694–1714. [Google Scholar] [CrossRef]
- Ravi, R.; Shamseldin, T.; Elbahnasawy, M.; Lin, Y.J.; Habib, A. Bias Impact Analysis and Calibration of UAV-Based Mobile LiDAR System with Spinning Multi-Beam Laser Scanner. Appl. Sci. 2018, 8, 297. [Google Scholar] [CrossRef]
- Varinlioğlu, G.; Kaye, N.; Jones, M.R.; Ingram, R.; Rauh, N.K. The 2016 Dana Island Survey: Investigation of an Island Harbor in Ancient Rough Cilicia by the Boğsak Archaeological Survey. Near East. Archaeol. 2017, 80, 50–59. [Google Scholar] [CrossRef]
- NOAA. Calumet Harbor, IL—Station ID: 9087044. (n.d.). Available online: https://tidesandcurrents.noaa.gov/stationhome.html?id=9087044 (accessed on 21 November 2019).
- Habib, A.; Lay, J.; Wong, C. Specifications for the quality assurance and quality control of lidar systems. Submitted to the Base Mapping and Geomatic Services of British Columbia. 2006. Available online: https://engineering.purdue.edu/CE/Academics/Groups/Geomatics/DPRG/files/LIDARErrorPropagation.zip (accessed on 1 December 2019).
- He, F.; Zhou, T.; Xiong, W.; Hasheminnasab, S.; Habib, A. Automated aerial triangulation for UAV-based mapping. Remote Sens. 2018, 10, 1952. [Google Scholar] [CrossRef]
- Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vision 2004, 60, 91–110. [Google Scholar] [CrossRef]
- He, F.; Habib, A. Automated relative orientation of UAV-based imagery in the presence of prior information for the flight trajectory. Photogramm. Eng. Remote Sens. 2016, 82, 879–891. [Google Scholar] [CrossRef]
- Furukawa, Y.; Ponce, J. Accurate, dense, and robust multiview stereopsis. IEEE Trans. Pattern Anal. Mach. Intell. 2009, 32, 1362–1376. [Google Scholar] [CrossRef]
- Besl, P.J.; McKay, N.D. Method for registration of 3-D shapes. In Sensor Fusion IV: Control Paradigms and Data Structures; International Society for Optics and Photonics: Bellingham, WA, USA, 1992; Volume 1611, pp. 586–606. [Google Scholar]
- Gharibi, H.; Habib, A. True Orthophoto Generation from Aerial Frame Images and LiDAR Data: An Update. Remote Sens. 2018, 10, 581. [Google Scholar] [CrossRef]
- Gatziolis, D.; Lienard, J.F.; Vogs, A.; Strigul, N.S. 3D tree dimensionality assessment using photogrammetry and small unmanned aerial vehicles. PLoS ONE 2015, 10, e0137765. [Google Scholar] [CrossRef]
- Zarco-Tejada, P.J.; Diaz-Varela, R.; Angileri, V.; Loudjani, P. Tree height quantification using very high resolution imagery acquired from an unmanned aerial vehicle (UAV) and automatic 3D photo-reconstruction methods. Eur. J. Agron. 2014, 55, 89–99. [Google Scholar] [CrossRef]
- Koch, T.; Körner, M.; Fraundorfer, F. Automatic and Semantically—Aware 3D UAV Flight Planning for Image-Based 3D Reconstruction. Remote Sens. 2019, 11, 1550. [Google Scholar] [CrossRef]





| Technique | Pros | Cons | Spatial Resolution | Accuracy | Example References |
|---|---|---|---|---|---|
| Satellite imagery |
|
| 0.46 m 2 | 2 m 2 | [7,20] |
| Aerial photography |
|
| 1 m 3 | 6 m 3 | [5,6,12,13] |
| Airborne LiDAR |
|
| 1 m 4 | Horizontal 0.50 m Vertical 0.15 m 4 | [10,11,12,13,14,15,16,17,18,19] |
| Terrestrial LiDAR |
|
| Higher than 0.1 m 5 | Centimeter-level 0.02–0.05 m | [21,22] |
| UAV photogrammetry |
|
| Higher than 0.1 m 5 | Centimeter-level 0.02–0.05 m | [23,24,25,26,27,28,29,30,31,32] |
| Mission 1 | Mission 2 | Mission 3 | Mission 4 | Mission 5 | |
|---|---|---|---|---|---|
| Date | 28 July 2019 | 26 July 2019 | 27 July 2019 | 29 July 2019 | 29 July 2019 |
| Number of images | 590 | 514 | 597 | 663 | 587 |
| Flying height (m) | 45–50 | 45–65 | 45 | 22/40 | 50–90 |
| Average speed (m/s) | 5.5 | 6.0 | 5.0 | 3.0 | 5.0 |
| Overlap (%) | 73 | 80 | 75 | 70 | 78–88 |
| Sidelap (%) | 67 | 73 | 75 | 74 | 75–86 |
| GSD 1 (cm) | 0.63 | 0.77 | 0.63 | 0.30 | 0.70–1.20 |
| Flight time (min) | 15 | 13 | 15 | 17 | 15 |
| Profiles along X Direction | Profiles along Y Direction | ||||||
|---|---|---|---|---|---|---|---|
| ID | Horizontal Shift (m) | Vertical Shift (m) | Rotation (deg) | ID | Horizontal Shift (m) | Vertical Shift (m) | Rotation (deg) |
| Px1 | 0.0143 | 0.0590 | 0.0464 | Py1 | 0.0114 | 0.0347 | 0.0623 |
| Px2 | 0.0052 | 0.0353 | 0.0192 | Py2 | 0.0103 | 0.0182 | 0.0112 |
| Px3 | 0.0067 | 0.0472 | 0.0101 | Py3 | 0.0080 | 0.0866 | 0.0127 |
| Px4 | 0.0055 | 0.0533 | 0.0414 | Py4 | 0.0130 | 0.0550 | 0.0447 |
| Px5 | 0.0008 | 0.0072 | 0.0110 | Py5 | 0.0107 | 0.0054 | 0.0144 |
| Px6 | 0.0011 | 0.0041 | 0.0050 | Py6 | 0.0025 | 0.0133 | 0.0091 |
| Px7 | 0.0048 | 0.0503 | 0.0097 | Py7 | 0.0026 | 0.0086 | 0.0009 |
| Px8 | 0.0121 | 0.0384 | 0.0058 | Py8 | 0.0069 | 0.0328 | 0.0127 |
| Px9 | 0.0146 | 0.0590 | 0.0394 | Py9 | 0.0008 | 0.0092 | 0.0141 |
| Px10 | 0.0280 | 0.0894 | 0.0590 | Py10 | 0.0024 | 0.0522 | 0.0300 |
| Px11 | 0.0075 | 0.0124 | 0.0302 | Py11 | 0.0059 | 0.0348 | 0.0007 |
| Px12 | 0.0086 | 0.0515 | 0.0020 | Py12 | 0.0121 | 0.0658 | 0.0141 |
| Px13 | 0.0023 | 0.0525 | 0.0048 | Py13 | 0.0041 | 0.0833 | 0.0272 |
| Px14 | 0.0091 | 0.0661 | 0.0812 | Py14 | 0.0002 | 0.0498 | 0.0186 |
| Px15 | 0.0115 | 0.0146 | 0.1119 | Py15 | 0.0114 | 0.0325 | 0.0367 |
| Px16 | 0.0002 | 0.0001 | 0.0059 | Py16 | 0.0199 | 0.0173 | 0.0588 |
| Px17 | 0.0019 | 0.0107 | 0.0281 | Py17 | 0.0015 | 0.0120 | 0.0194 |
| Px18 | 0.0000 | 0.0002 | 0.0001 | Py18 | 0.0046 | 0.0012 | 0.0109 |
| Px19 | 0.0024 | 0.0110 | 0.0041 | Py19 | 0.0010 | 0.0008 | 0.0011 |
| Px20 | 0.0093 | 0.0124 | 0.0008 | Py20 | 0.0052 | 0.0292 | 0.0175 |
| Px21 | 0.0009 | 0.0102 | 0.0017 | Py21 | 0.0015 | 0.0030 | 0.0007 |
| Px22 | 0.0017 | 0.0082 | 0.0050 | Py22 | 0.0031 | 0.0179 | 0.0098 |
| Avg. | 0.0019 | 0.0139 | 0.0050 | Avg. | 0.0009 | 0.0195 | 0.0051 |
| Mission 1 | Mission 2 | Mission 3 | Mission 4 | Mission 5 | All Missions | ||
|---|---|---|---|---|---|---|---|
| Zone 1 | Mean (m) | 0.006 | n/a | 0.006 | 0.031 | 0.014 | 0.014 |
| Std. Dev. (m) | 0.055 | n/a | 0.053 | 0.072 | 0.045 | 0.056 | |
| Zone 2 | Mean (m) | 0.027 | 0.019 | 0.026 | 0.030 | 0.019 | 0.021 |
| Std. Dev. (m) | 0.055 | 0.101 | 0.063 | 0.069 | 0.053 | 0.066 | |
| Overall | Mean (m) | 0.022 | 0.019 | 0.020 | 0.030 | 0.019 | 0.020 |
| Std. Dev. (m) | 0.056 | 0.101 | 0.061 | 0.070 | 0.052 | 0.065 |
| Foredune Ridge Recession (m) | Eroded Volume per m Shoreline (m3/m) | Total Eroded Volume (m3) | |||
|---|---|---|---|---|---|
| Average | Min. | Max. | |||
| May 2018November 2018 | 1.2 | 2.5 | 4.2 | 10.2 | 2243.2 |
| November 2018December 2018 | 1.2 | 0.2 | 5.6 | 12.2 | 2673.9 |
| December 2018May 2019 | 1.1 | 0.6 | 6.2 | 4.2 | 925.7 |
| Total | 5.1 | 1.6 | 8.9 | 18.2 | 3998.6 |
| Foredune Ridge Recession (m) | Eroded Volume per m Shoreline (m3/m) | Total Eroded Volume (m3) | |||
|---|---|---|---|---|---|
| Average | Min. | Max. | |||
| November 2018December 2018 | 0.8 | 0.2 | 3.4 | 2.6 | 883.8 |
| December 2018May 2019 | 0.7 | 0.2 | 2.5 | 0.2 | 80.5 |
| Total | 1.6 | 0.2 | 4.0 | 2.8 | 938.4 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, Y.-C.; Cheng, Y.-T.; Zhou, T.; Ravi, R.; Hasheminasab, S.M.; Flatt, J.E.; Troy, C.; Habib, A. Evaluation of UAV LiDAR for Mapping Coastal Environments. Remote Sens. 2019, 11, 2893. https://doi.org/10.3390/rs11242893
Lin Y-C, Cheng Y-T, Zhou T, Ravi R, Hasheminasab SM, Flatt JE, Troy C, Habib A. Evaluation of UAV LiDAR for Mapping Coastal Environments. Remote Sensing. 2019; 11(24):2893. https://doi.org/10.3390/rs11242893
Chicago/Turabian StyleLin, Yi-Chun, Yi-Ting Cheng, Tian Zhou, Radhika Ravi, Seyyed Meghdad Hasheminasab, John Evan Flatt, Cary Troy, and Ayman Habib. 2019. "Evaluation of UAV LiDAR for Mapping Coastal Environments" Remote Sensing 11, no. 24: 2893. https://doi.org/10.3390/rs11242893
APA StyleLin, Y.-C., Cheng, Y.-T., Zhou, T., Ravi, R., Hasheminasab, S. M., Flatt, J. E., Troy, C., & Habib, A. (2019). Evaluation of UAV LiDAR for Mapping Coastal Environments. Remote Sensing, 11(24), 2893. https://doi.org/10.3390/rs11242893