Combining InSAR and GNSS to Track Magma Transport at Basaltic Volcanoes
Abstract
1. Introduction
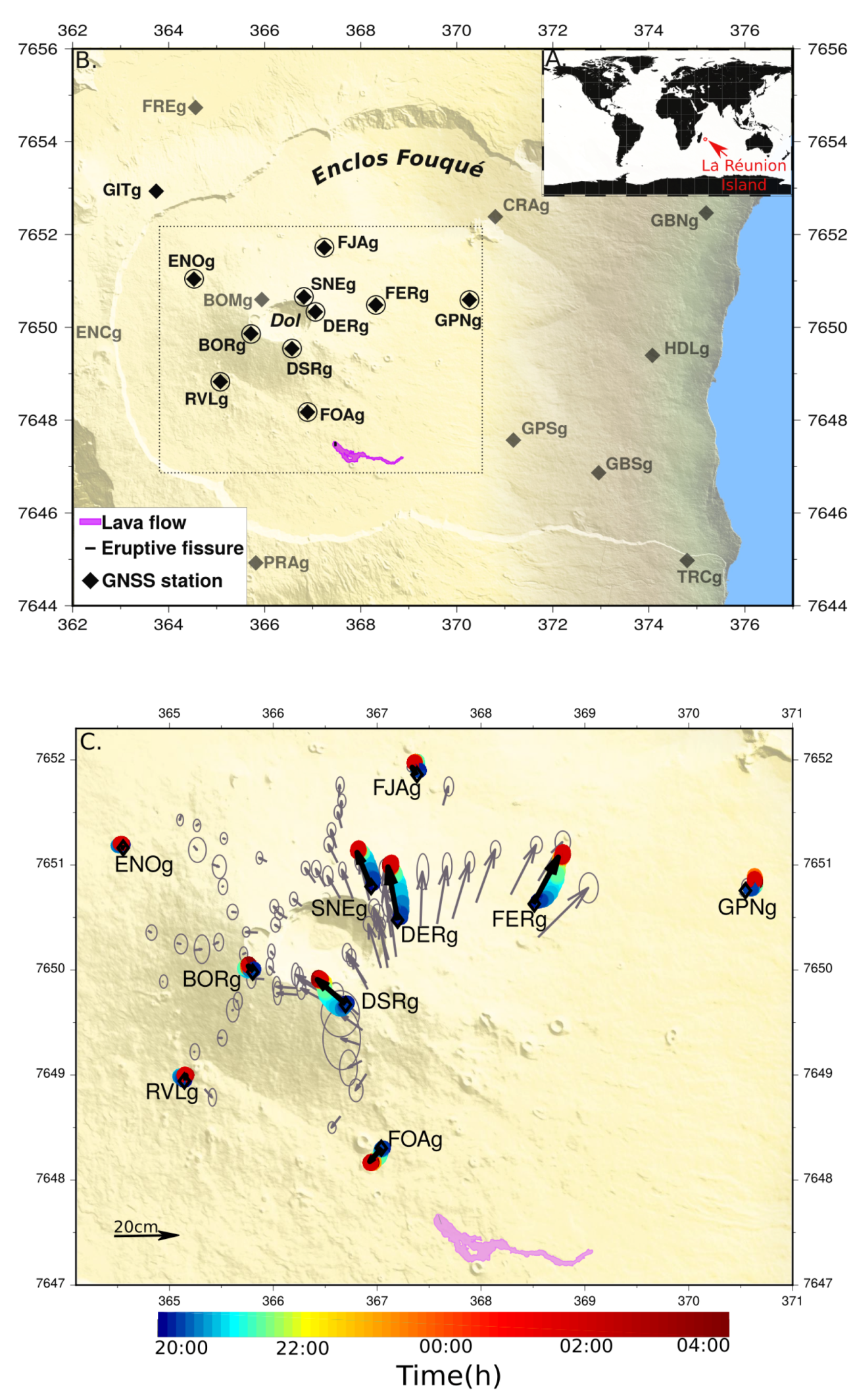
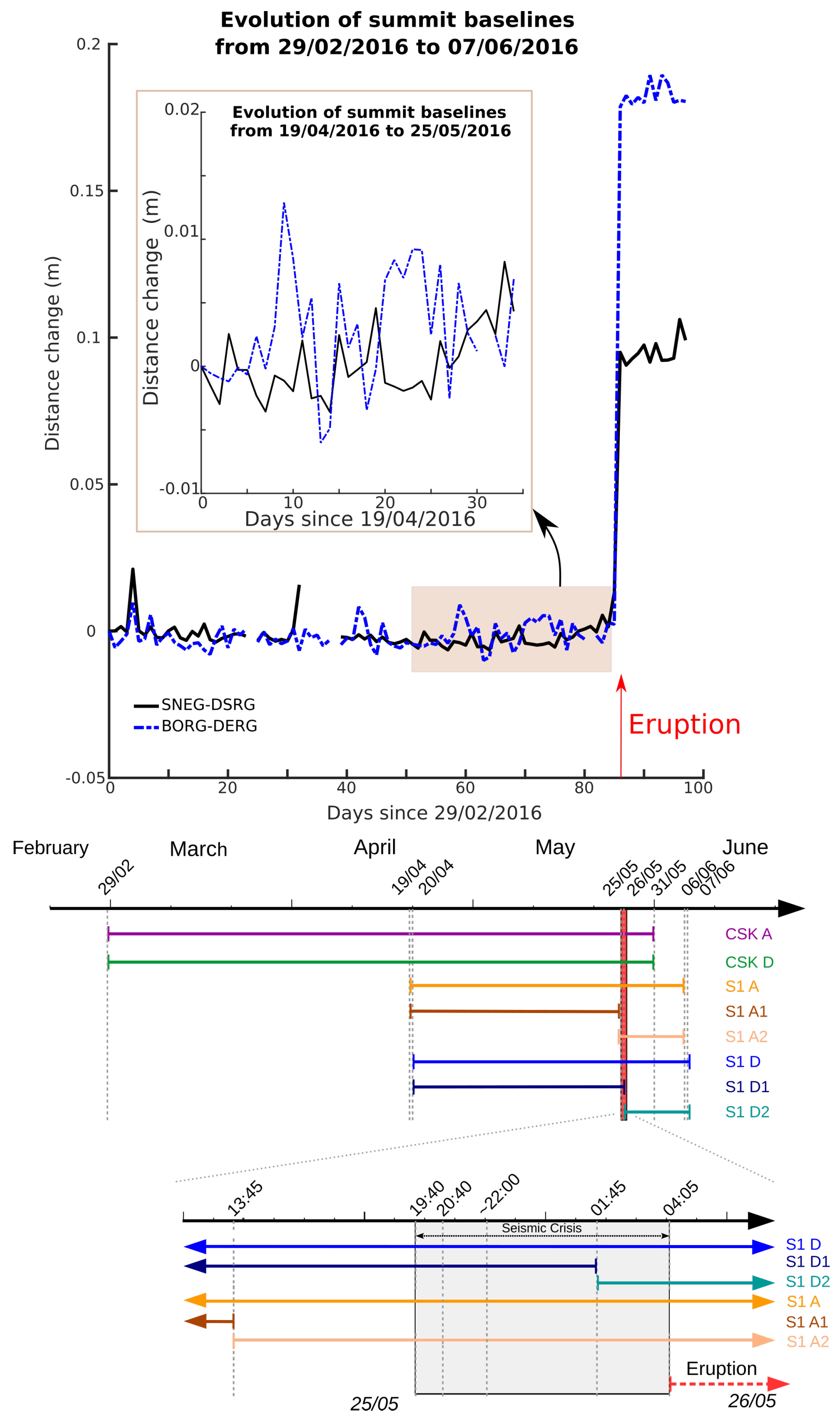
2. The 26 May 2016 Eruption of Piton De La Fournaise Volcano
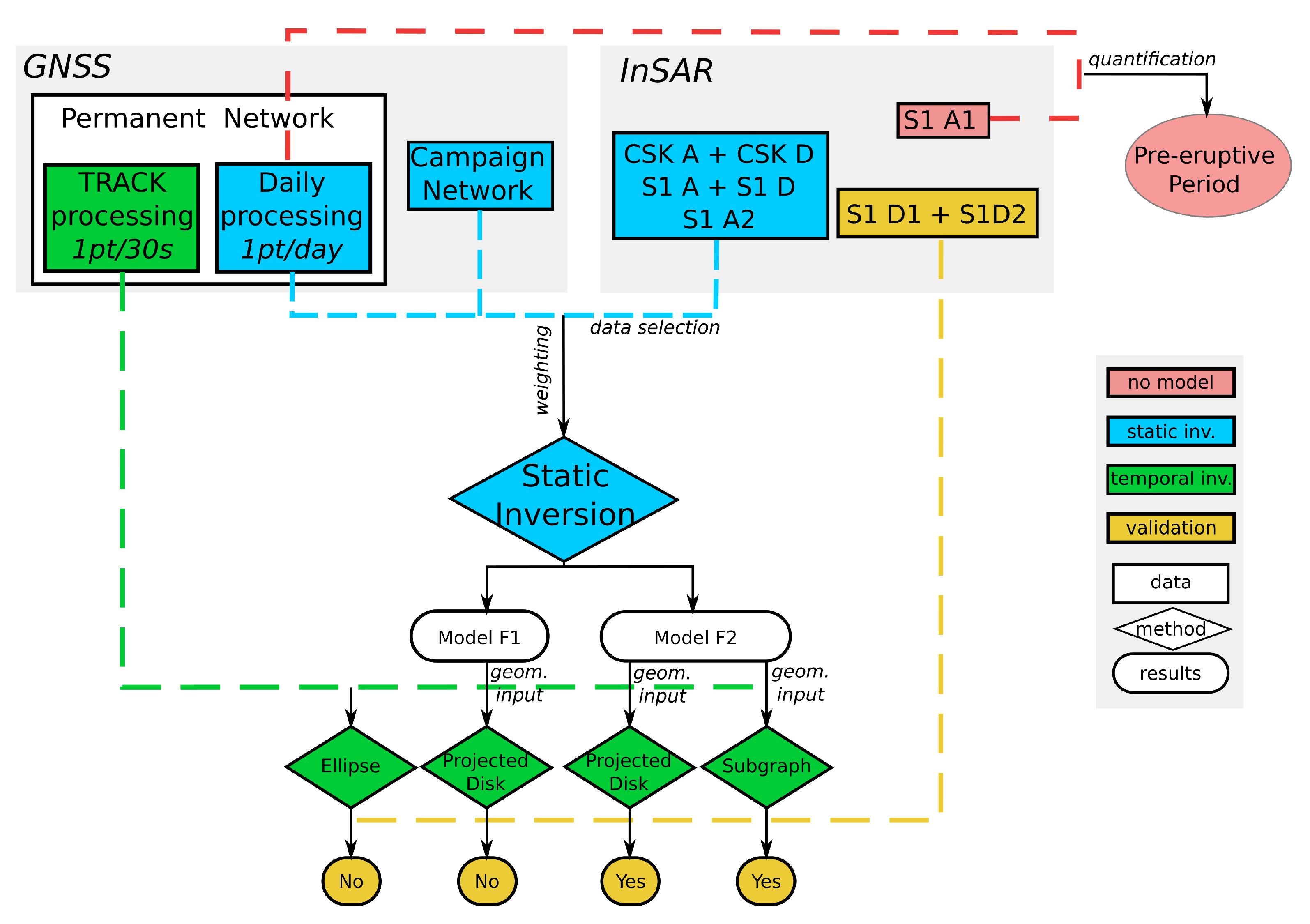
3. Geodetic Measurement Description
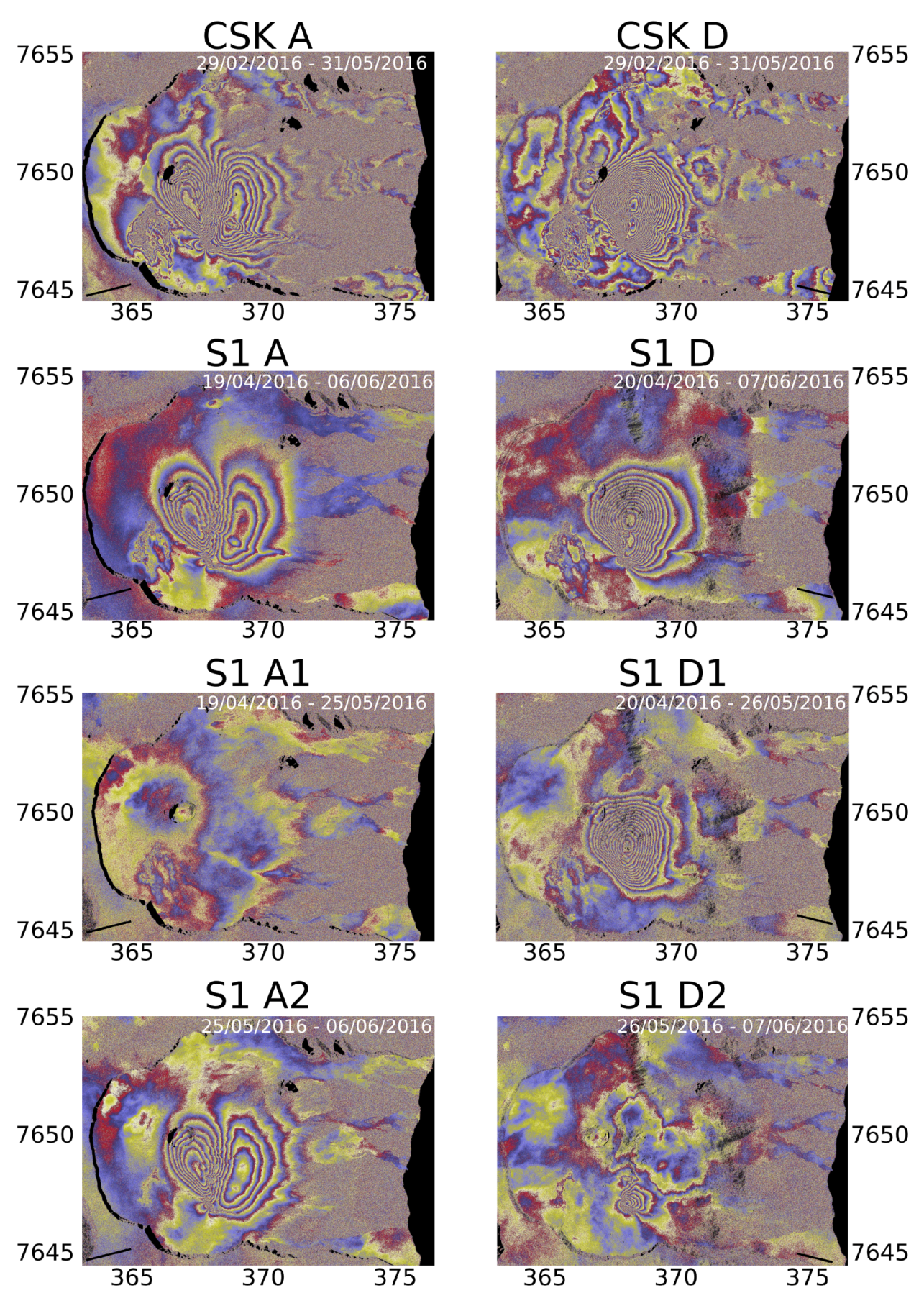
3.1. InSAR Data
3.2. GNSS Data
4. Inverse Models
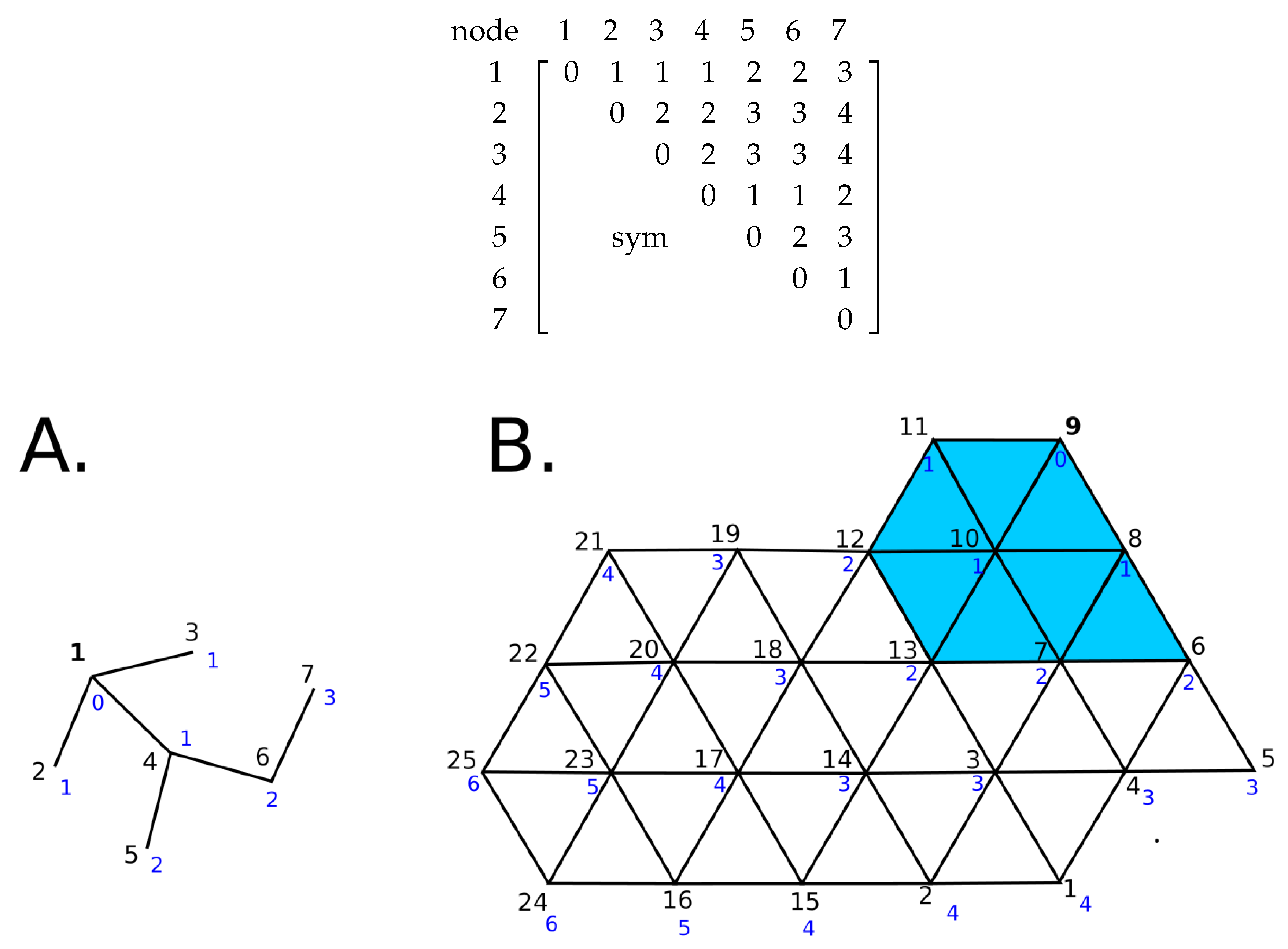
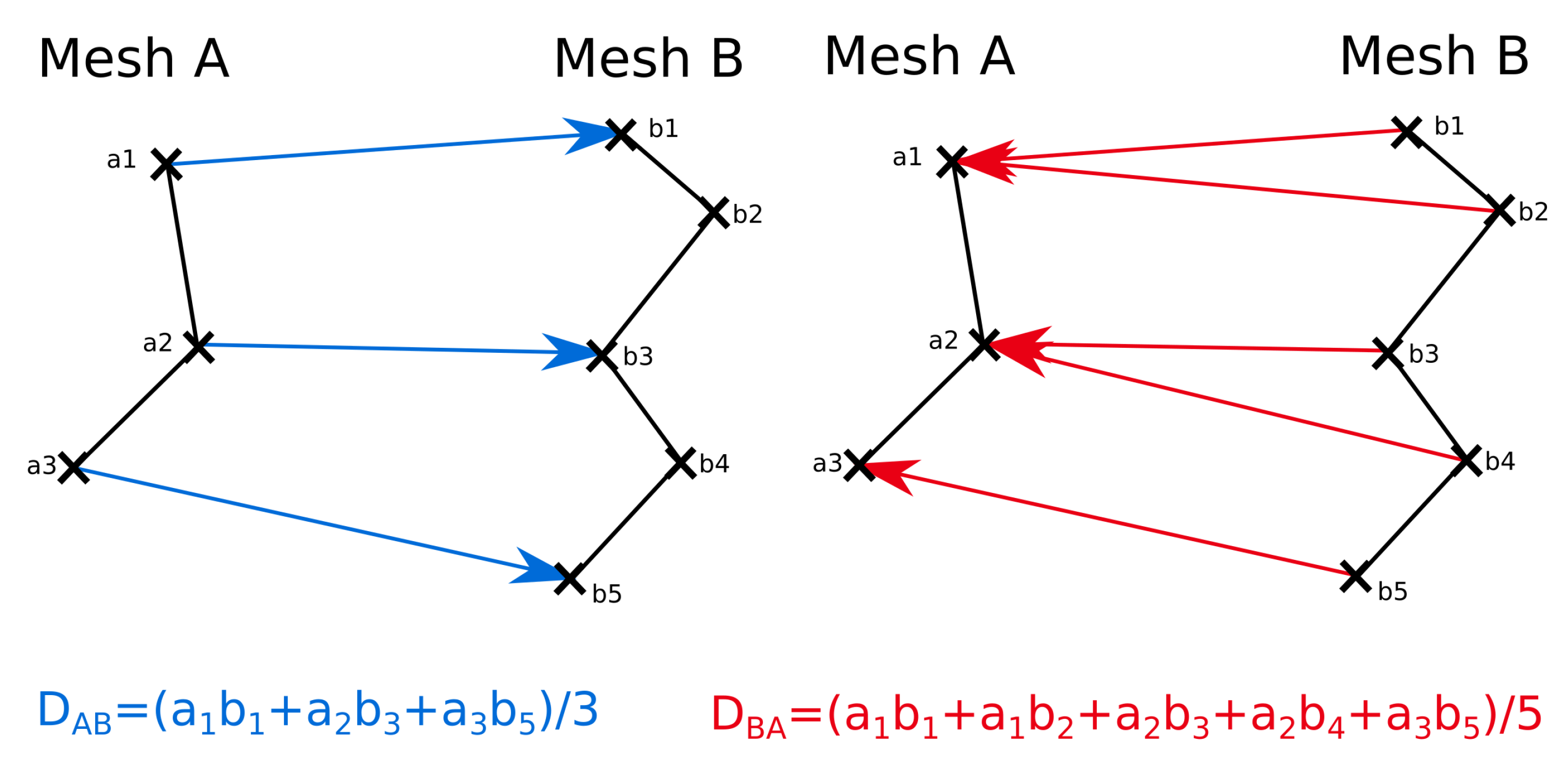
4.1. Inversion and Data Weighting Through the Covariance Matrix
4.2. Static Inversion
4.3. Temporal Inversion
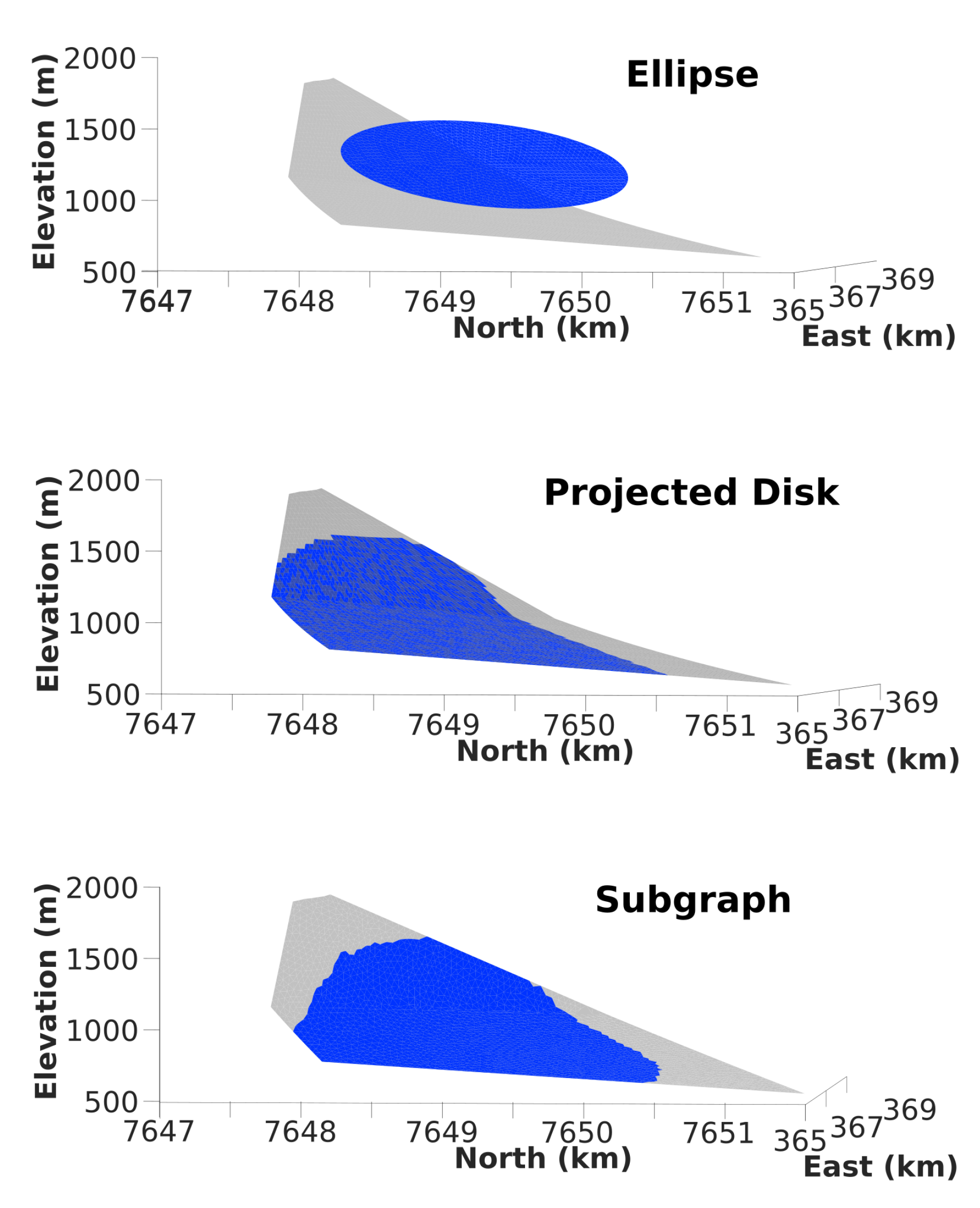
4.3.1. A Method without Any Geometric a Priori from the Static Inversion: The Ellipse Method
4.3.2. A First Method with a Geometric a Priori: The Projected Disk Method
4.3.3. A Second Method with a Geometric a Priori: The Subgraph Method
5. Results
5.1. Static Inversion
5.1.1. Two Model Families Which Explain the Data Equally Well
5.1.2. Importance of Consistency between Time Periods Covered
5.1.3. Relative Weights of Ascending Versus Descending Interferograms
5.1.4. Relative Weights of InSAR Versus GNSS Data
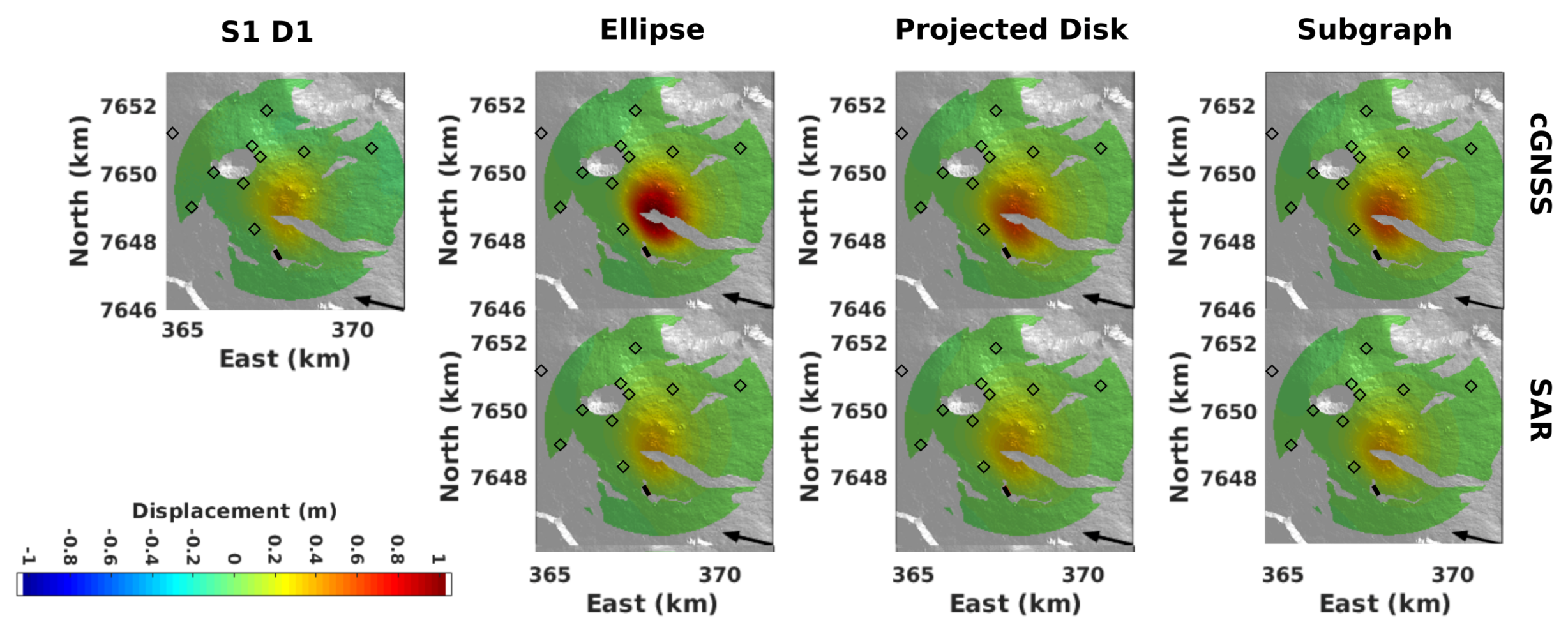
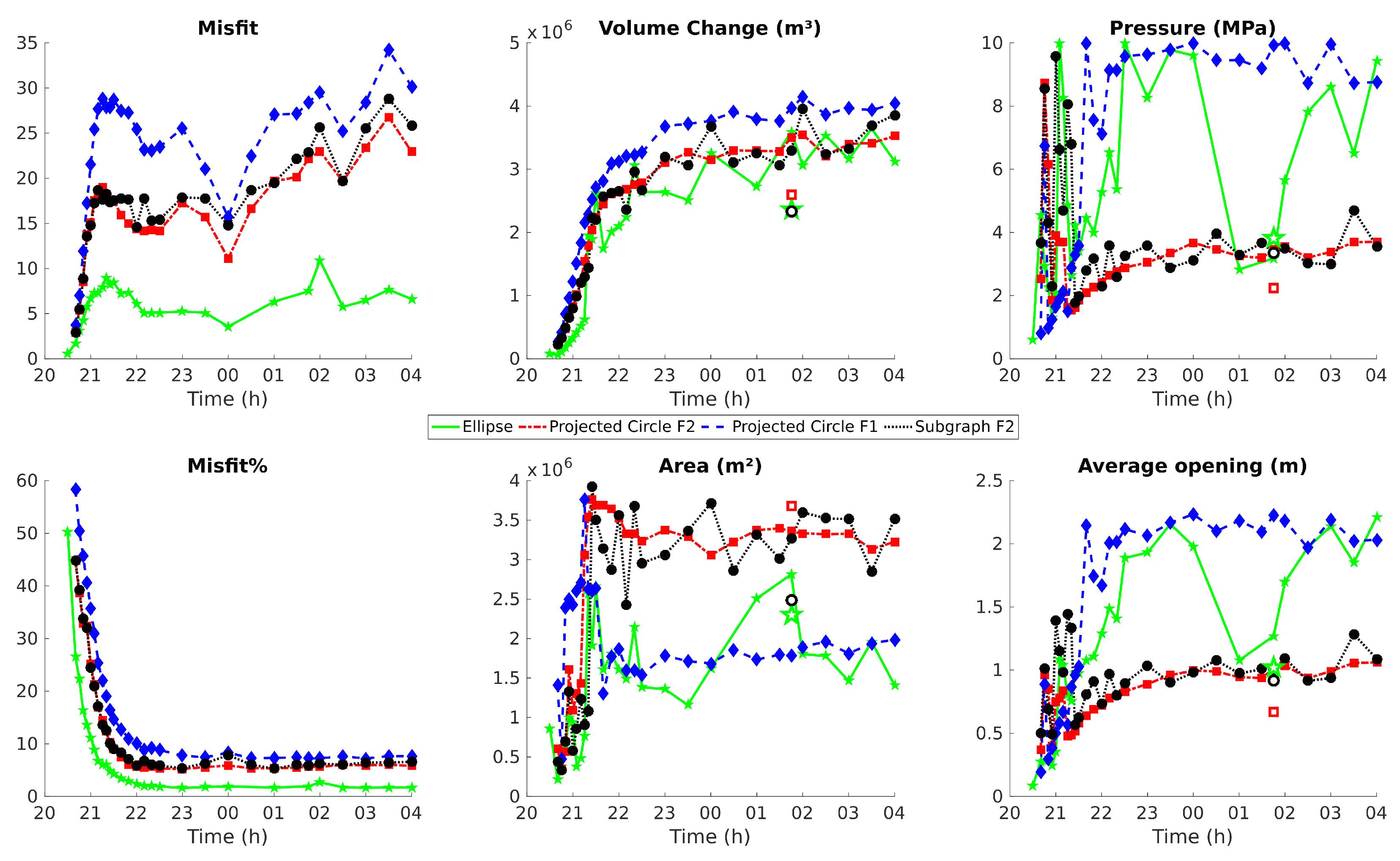
5.2. Temporal Inversion
5.2.1. A Need for Geometrical a Priori to Invert for the GNSS Time Series
5.2.2. Inversion of GNSS Time Series to Improve Discrimination between Families of Intrusion Geometry
6. Discussion
6.1. Discrepancies between Independent Datasets Reveal Hidden Processes
6.1.1. Discrepancies in the Covered Time Periods Reveal Pre-Eruptive Displacement
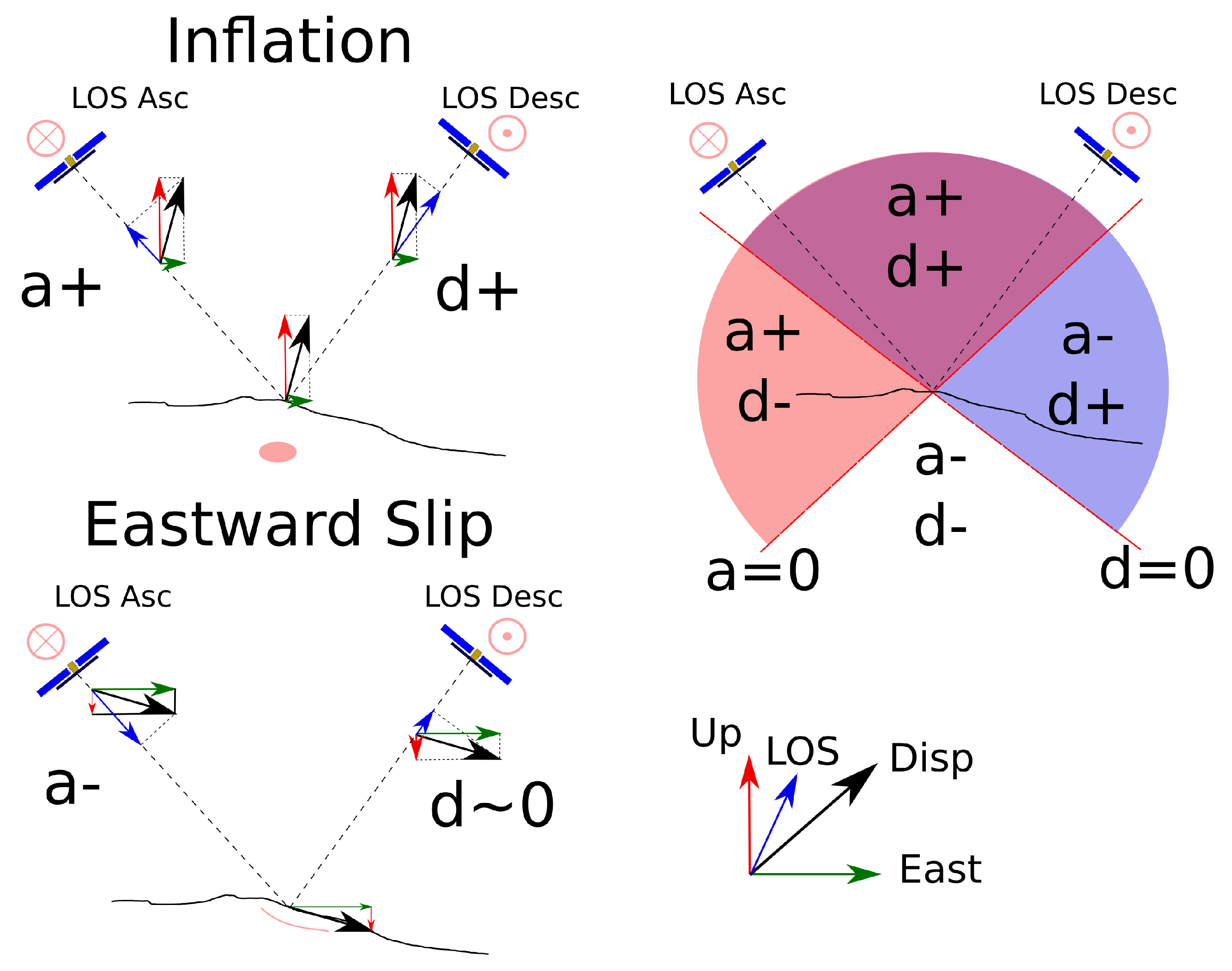
6.1.2. Discrepancies in Amplitude Along the Different Los Reveal Flank Displacement
6.2. Combining InSAR and GNSS for Complementary Spatial and Temporal Information
6.2.1. InSAR Static Inversion Constrains the Temporal Inversion
6.2.2. Advantages of the Subgraph Method for Temporal Inversions
6.2.3. GNSS Temporal Inversion Solves the Conundrum of Non Unique Static Inversion
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| ANR | Agence Nationale de la Recherche |
| GNSS | Global Navigation Satellite System |
| InSAR | Interferometric Synthetic Aperture Radar |
| LOS | Line of Sight |
| OVPF | Observatoire volcanologique du Piton de la Fournaise (Piton de la Fournaise Volcanological Observatory) |
| Piton de la Fournaise | |
| PCA | Principal Component Analysis |
| SAR | Synthetic Aperture Radar |
References
- Lu, Z.; Dzurisin, D. InSAR imaging of Aleutian volcanoes. In InSAR Imaging of Aleutian Volcanoes; Springer: Berlin/Heidelberg, Germany, 2014; pp. 87–345. [Google Scholar]
- Pinel, V.; Poland, M.P.; Hooper, A. Volcanology: Lessons learned from synthetic aperture radar imagery. J. Volcanol. Geotherm. Res. 2014, 289, 81–113. [Google Scholar] [CrossRef]
- Biggs, J.; Pritchard, M.E. Global volcano monitoring: What does it mean when volcanoes deform? Elements 2017, 13, 17–22. [Google Scholar] [CrossRef]
- Fialko, Y.; Simons, M. Evidence for on-going inflation of the Socorro magma body, New Mexico, from interferometric synthetic aperture radar imaging. Geophys. Res. Lett. 2001, 28, 3549–3552. [Google Scholar] [CrossRef]
- Baker, S.; Amelung, F. Top-down inflation and deflation at the summit of Kīlauea Volcano, Hawai ‘i observed with InSAR. J. Geophys. Res. Solid Earth 2012, 117. [Google Scholar] [CrossRef]
- Ebmeier, S.K.; ANdrews, B.J.; Araya, M.C.; Arnold, D.W.D.; Biggs, J.; Cooper, C.; Cottrell, E.; Furtney, M.; Hickey, J.; Jay, J.; et al. Synthesis of global satellite observations of magmatic and volcanic deformation: Implications for volcano monitoring and the lateral extent of magmatic domains. J. Appl. Volcanol. 2018. [Google Scholar] [CrossRef]
- Pritchard, M.; Simons, M. An InSAR-based survey of volcanic deformation in the central Andes. Geochem. Geophys. Geosyst. 2004, 5. [Google Scholar] [CrossRef]
- Roult, G.; Peltier, A.; Taisne, B.; Staudacher, T.; Ferrazzini, V.; Di Muro, A.; The OVPF Team. A new comprehensive classification of the Piton de la Fournaise activity spanning the 1985–2010 period. Search and analysis of short-term precursors from a broad-band seismological station. J. Volcanol. Geotherm. Res. 2012, 241, 78–104. [Google Scholar] [CrossRef]
- Sigmundsson, F.; Hooper, A.; Hreinsdóttir, S.; Vogfjörd, K.S.; Ófeigsson, B.G.; Heimisson, E.R.; Dumont, S.; Parks, M.; Spaans, K.; Gudmundsson, G.B.; et al. Segmented lateral dyke growth in a rifting event at Bárðarbunga volcanic system, Iceland. Nature 2015, 517, 191. [Google Scholar] [CrossRef] [PubMed]
- Pedersen, R.; Sigmundsson, F. Temporal development of the 1999 intrusive episode in the Eyjafjallajökull volcano, Iceland, derived from InSAR images. Bull. Volcanol. 2006, 68, 377–393. [Google Scholar] [CrossRef]
- Jónsson, S.; Zebker, H.; Cervelli, P.; Segall, P.; Garbeil, H.; Mouginis-Mark, P.; Rowland, S. A shallow-dipping dike fed the 1995 flank eruption at Fernandina Volcano, Galápagos, observed by satellite radar interferometry. Geophys. Res. Lett. 1999, 26, 1077–1080. [Google Scholar] [CrossRef]
- Bagnardi, M.; Amelung, F. Space-geodetic evidence for multiple magma reservoirs and subvolcanic lateral intrusions at Fernandina Volcano, Galápagos Islands. J. Geophys. Res. Solid Earth 2012, 117. [Google Scholar] [CrossRef]
- Aoki, Y.; Segall, P.; Kato, T.; Cervelli, P.; Shimada, S. Imaging magma transport during the 1997 seismic swarm off the Izu Peninsula, Japan. Science 1999, 286, 927–930. [Google Scholar] [CrossRef] [PubMed]
- Montgomery-Brown, E.K.; Sinnett, D.; Poland, M.; Segall, P.; Orr, T.; Zebker, H.; Miklius, A. Geodetic evidence for en echelon dike emplacement and concurrent slow slip during the June 2007 intrusion and eruption at Kīlauea volcano, Hawaii. J. Geophys. Res. Solid Earth 2010, 115. [Google Scholar] [CrossRef]
- Grandin, R.; Jacques, E.; Nercessian, A.; Ayele, A.; Doubre, C.; Socquet, A.; Keir, D.; Kassim, M.; Lemarchand, A.; King, G. Seismicity during lateral dike propagation: Insights from new data in the recent Manda Hararo–Dabbahu rifting episode (Afar, Ethiopia). Geochem. Geophys. Geosyst. 2011, 12. [Google Scholar] [CrossRef]
- Smittarello, D.; Cayol, V.; Pinel, V.; Peltier, A.; Froger, J.L.; Ferrazzini, V. Magma Propagation at Piton de la Fournaise From Joint Inversion of InSAR and GNSS. J. Geophys. Res. Solid Earth 2019, 124, 1361–1387. [Google Scholar] [CrossRef]
- Duputel, Z.; Lengliné, O.; Ferrazzini, V. Constraining Spatiotemporal Characteristics of Magma Migration at Piton De La Fournaise Volcano From Pre-eruptive Seismicity. Geophys. Res. Lett. 2019, 46, 119–127. [Google Scholar] [CrossRef]
- Bagnardi, M.; Amelung, F.; Poland, M.P. A new model for the growth of basaltic shields based on deformation of Fernandina volcano, Galápagos Islands. Earth Planet. Sci. Lett. 2013, 377, 358–366. [Google Scholar] [CrossRef]
- Massonnet, D.; Feigl, K.L. Radar interferometry and its application to changes in the Earth’s surface. Rev. Geophys. 1998, 36, 441–500. [Google Scholar] [CrossRef]
- Masterlark, T.; Lu, Z. Transient volcano deformation sources imaged with interferometric synthetic aperture radar: Application to Seguam Island, Alaska. J. Geophys. Res. Solid Earth 2004, 109. [Google Scholar] [CrossRef]
- Parks, M.M.; Moore, J.D.; Papanikolaou, X.; Biggs, J.; Mather, T.A.; Pyle, D.M.; Raptakis, C.; Paradissis, D.; Hooper, A.; Parsons, B.; et al. From quiescence to unrest: 20 years of satellite geodetic measurements at Santorini volcano, Greece. J. Geophys. Res. Solid Earth 2015, 120, 1309–1328. [Google Scholar] [CrossRef]
- Biggs, J.; Amelung, F.; Gourmelen, N.; Dixon, T.H.; Kim, S.W. InSAR observations of 2007 Tanzania rifting episode reveal mixed fault and dyke extension in an immature continental rift. Geophys. J. Int. 2009, 179, 549–558. [Google Scholar] [CrossRef]
- Dieterich, J.H.; Decker, R.W. Finite element modeling of surface deformation associated with volcanism. J. Geophys. Res. 1975, 80, 4094–4102. [Google Scholar] [CrossRef]
- Montgomery-Brown, E.K.; Segall, P.; Miklius, A. Kilauea slow slip events: Identification, source inversions, and relation to seismicity. J. Geophys. Res. Solid Earth 2009, 114. [Google Scholar] [CrossRef]
- Got, J.L.; Peltier, A.; Staudacher, T.; Kowalski, P.; Boissier, P. Edifice strength and magma transfer modulation at Piton de la Fournaise volcano. J. Geophys. Res. Solid Earth 2013, 118, 5040–5057. [Google Scholar] [CrossRef]
- Biggs, J.; Lu, Z.; Fournier, T.; Freymueller, J.T. Magma flux at Okmok Volcano, Alaska, from a joint inversion of continuous GPS, campaign GPS, and interferometric synthetic aperture radar. J. Geophys. Res. Solid Earth 2010, 115. [Google Scholar] [CrossRef]
- Montgomery-Brown, E.K.; Sinnett, D.; Larson, K.; Poland, M.P.; Segall, P.; Miklius, A. Spatiotemporal evolution of dike opening and décollement slip at Kīlauea Volcano, Hawai’i. J. Geophys. Res. Solid Earth 2011, 116. [Google Scholar] [CrossRef]
- Grandin, R.; Socquet, A.; Binet, R.; Klinger, Y.; Jacques, E.; de Chabalier, J.B.; King, G.; Lasserre, C.; Tait, S.; Tapponnier, P.; et al. September 2005 Manda Hararo-Dabbahu rifting event, Afar (Ethiopia): constraints provided by geodetic data. J. Geophys. Res. Solid Earth 2009, 114. [Google Scholar] [CrossRef]
- Okada, Y. Surface deformation due to shear and tensile faults in a half-space. Bull. Seismol. Soc. Am. 1985, 75, 1135–1154. [Google Scholar]
- Tridon, M.; Cayol, V.; Froger, J.L.; Augier, A.; Bachèlery, P. Inversion of coeval shear and normal stress of Piton de la Fournaise flank displacement. J. Geophys. Res. Solid Earth 2016, 121, 7846–7866. [Google Scholar] [CrossRef]
- Zeller, S.S.; Pollard, D.D. Boundary conditions for rock fracture analysis using the boundary element method. J. Geophys. Res. Solid Earth 1992, 97, 1991–1997. [Google Scholar] [CrossRef]
- Froger, J.L.; Famin, V.; Cayol, V.; Augier, A.; Michon, L.; Lénat, J.F. Time-dependent displacements during and after the April 2007 eruption of Piton de la Fournaise, revealed by interferometric data. J. Volcanol. Geotherm. Res. 2015, 296, 55–68. [Google Scholar] [CrossRef]
- Michon, L.; Staudacher, T.; Ferrazzini, V.; Bachèlery, P.; Marti, J. April 2007 collapse of Piton de la Fournaise: A new example of caldera formation. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
- Peltier, A.; Staudacher, T.; Bachèlery, P.; Cayol, V. Formation of the April 2007 caldera collapse at Piton de La Fournaise volcano: Insights from GPS data. J. Volcanol. Geotherm. Res. 2009, 184, 152–163. [Google Scholar] [CrossRef]
- Chen, Y.; Remy, D.; Froger, J.L.; Peltier, A.; Villeneuve, N.; Darrozes, J.; Perfettini, H.; Bonvalot, S. Long-term ground displacement observations using InSAR and GNSS at Piton de la Fournaise volcano between 2009 and 2014. Remote Sens. Environ. 2017, 194, 230–247. [Google Scholar] [CrossRef]
- Lengliné, O.; Duputel, Z.; Ferrazzini, V. Uncovering the hidden signature of a magmatic recharge at Piton de la Fournaise volcano using small earthquakes. Geophys. Res. Lett. 2016, 43, 4255–4262. [Google Scholar] [CrossRef]
- Vlastélic, I.; Di Muro, A.; Bachèlery, P.; Gurioli, L.; Auclair, D.; Gannoun, A. Control of source fertility on the eruptive activity of Piton de la Fournaise volcano, La Réunion. Sci. Rep. 2018, 8, 14478. [Google Scholar] [CrossRef] [PubMed]
- Peltier, A.; Froger, J.L.; Villeneuve, N.; Catry, T. Assessing the reliability and consistency of InSAR and GNSS data for retrieving 3D-displacement rapid changes, the example of the 2015 Piton de la Fournaise eruptions. J. Volcanol. Geotherm. Res. 2017, 344, 106–120. [Google Scholar] [CrossRef]
- CNES. Philosophy and Instructions for the Use of the DIAPASON Interferometry Software System Developed at CNES; CNES: Paris, France, 1996. [Google Scholar]
- Chen, C.W.; Zebker, H.A. Phase unwrapping for large SAR interferograms: Statistical segmentation and generalized network models. IEEE Trans. Geosci. Remote Sens. 2002, 40, 1709–1719. [Google Scholar] [CrossRef]
- Welstead, S.T. Fractal and Wavelet Image Compression Techniques; SPIE Optical Engineering Press Bellingham: Washington, DC, USA, 1999. [Google Scholar]
- Jónsson, S.; Zebker, H.; Segall, P.; Amelung, F. Fault slip distribution of the 1999 Mw 7.1 Hector Mine, California, earthquake, estimated from satellite radar and GPS measurements. Bull. Seismol. Soc. Am. 2002, 92, 1377–1389. [Google Scholar] [CrossRef]
- Herring, T.; King, R.; McClusky, S. Introduction to Gamit/Globk; Massachusetts Institute of Technology: Cambridge, MA, USA, 2010. [Google Scholar]
- Wright, T.J.; Parsons, B.E.; Lu, Z. Toward mapping surface deformation in three dimensions using InSAR. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef]
- Cayol, V.; Cornet, F. 3D mixed boundary elements for elastostatic deformation field analysis. Int. J. Rock Mech. Min. Sci. 1997, 34, 275–287. [Google Scholar] [CrossRef]
- Cayol, V.; Cornet, F.H. Three-dimensional modeling of the 1983–1984 eruption at Piton de la Fournaise Volcano, Réunion Island. J. Geophys. Res. Solid Earth 1998, 103, 18025–18037. [Google Scholar] [CrossRef]
- Cayol, V.; Cornet, F.H. Effects of topography on the interpretation of the deformation field of prominent volcanoes–Application to Etna. Geophys. Res. Lett. 1998, 25, 1979–1982. [Google Scholar] [CrossRef]
- Fukushima, Y.; Cayol, V.; Durand, P. Finding realistic dike models from interferometric synthetic aperture radar data: The February 2000 eruption at Piton de la Fournaise. J. Geophys. Res. Solid Earth 2005, 110. [Google Scholar] [CrossRef]
- Masterlark, T. Magma intrusion and deformation predictions: Sensitivities to the Mogi assumptions. J. Geophys. Res. Solid Earth 2007, 112. [Google Scholar] [CrossRef]
- Tarantola, A. Inverse Problem Theory: Method for Data Fitting and Model Parameter Estimation; Elsevier: Amsterdam, The Netherlands, 1987; Volume 613. [Google Scholar]
- Fukushima, Y.; Cayol, V.; Durand, P.; Massonnet, D. Evolution of magma conduits during the 1998–2000 eruptions of Piton de la Fournaise volcano, Réunion Island. J. Geophys. Res. Solid Earth 2010, 115. [Google Scholar] [CrossRef]
- Sambridge, M. Geophysical inversion with a neighbourhood algorithm -I. Searching a parameter space. Geophys. J. Int. 1999, 138, 479–494. [Google Scholar] [CrossRef]
- Sambridge, M. Geophysical inversion with a neighbourhood algorithm -II. Appraising the ensemble. Geophys. J. Int. 1999, 138, 727–746. [Google Scholar] [CrossRef]
- Fournier, T.; Freymueller, J.; Cervelli, P. Tracking magma volume recovery at Okmok volcano using GPS and an unscented Kalman filter. J. Geophys. Res. Solid Earth 2009, 114. [Google Scholar] [CrossRef]
- Cannavò, F.; Camacho, A.G.; González, P.J.; Mattia, M.; Puglisi, G.; Fernández, J. Real time tracking of magmatic intrusions by means of ground deformation modeling during volcanic crises. Sci. Rep. 2015, 5, 10970. [Google Scholar] [CrossRef]
- Taisne, B.; Jaupart, C. Dike propagation through layered rocks. J. Geophys. Res. Solid Earth 2009, 114. [Google Scholar] [CrossRef]
- Tarantola, A. Inverse Problem Theory and Methods for Model Parameter Estimation; SIAM: Philadelphia, PA, USA, 2005; Volume 89. [Google Scholar]
- Peltier, A.; Ferrazzini, V.; Staudacher, T.; Bachèlery, P. Imaging the dynamics of dyke propagation prior to the 2000–2003 flank eruptions at Piton de La Fournaise, Reunion Island. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]


| Model | Covariance Weighting | Family | GNSS | InSAR | |||||
|---|---|---|---|---|---|---|---|---|---|
| S1D | S1 A | S1 A2 | CSKD | CSKA | Total | ||||
| Inv01 | No | F1 | 78 | 97 | 81 | 75 | 97 | 83 | 93.5 |
| Inv02a* | No | F2 | 73 | 95 | 82 | 72 | 95 | 82 | 92.5 |
| Inv02b | No | F2 | 75 | 96 | 83 | 76 | 95 | 83 | 93.0 |
| Inv03 | F2 | 73 | 96 | 86 | 77 | 96 | 87 | 94.1 | |
| Inv04a | F1 | 77 | 95 | 82 | 74 | 95 | 87 | 93.5 | |
| Inv04b | F2 | 71 | 96 | 83 | 72 | 96 | 85 | 93.5 | |
| Inv05 | No | F1 | 83 | 94 | 67 | 57 | 95 | 75 | 90.3 |
| Inversion | Inv01 | Inv02a | Inv02b | Inv03 | Inv04a | Inv04b | Inv05 | |
|---|---|---|---|---|---|---|---|---|
| Family | F1 | F2 | F2 | F2 | F1 | F2 | F1 | |
| Inv01 | F1 | X | 129 | 124 | 109 | 90 | 139 | 132 |
| Inv02a * | F2 | 121 | X | 107 | 167 | 150 | 169 | 177 |
| Inv2b | F2 | 105 | 110 | X | 80 | 153 | 78 | 194 |
| Inv03 | F2 | 104 | 153 | 72 | X | 157 | 51 | 202 |
| Inv04a | F1 | 85 | 141 | 168 | 167 | X | 185 | 63 |
| Inv04b | F2 | 116 | 144 | 61 | 46 | 164 | X | 209 |
| Inv05 | F1 | 132 | 168 | 216 | 209 | 62 | 214 | X |
| GNSS | S1 D | S1 A | CSKD | CSKA | Total | |
|---|---|---|---|---|---|---|
| X | 1100 | 500 | 1000 | 470 | 3070 | |
| % | X | 36% | 16% | 33% | 15% | 100% |
| after weighting | X | 25% | 25% | 25% | 25% | 100% |
| 4800 | 1100 | 500 | 1000 | 470 | 7870 | |
| % | 61% | 14% | 6% | 13% | 6% | 100% |
| after weighting | 20% | 20% | 20% | 20% | 20% | 100% |
| Method Data | Ellipse | Projected Disk | Subgraph | ||||
|---|---|---|---|---|---|---|---|
| GNSS | InSAR | GNSS | InSAR | GNSS | InSAR | ||
| Overpressure (MPa) | 3.2 | 7.0 | 3.5 | 1.9 | 3.4 | 2.5 | |
| Average opening (m) | 1.3 | 1.3 | 1.0 | 0.6 | 1.0 | 0.7 | |
| Area (10 m) | 2.8 | 1.6 | 3.4 | 3.9 | 3.3 | 3.1 | |
| Volume (10 m) | 3.6 | 2.1 | 3.5 | 2.4 | 3.3 | 2.2 | |
| GNSS | 96 | 85 | 84 | 83 | 83 | 84 | |
| InSAR S1 D1 | 22 | 95 | 77 | 96 | 83 | 94 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Smittarello, D.; Cayol, V.; Pinel, V.; Froger, J.-L.; Peltier, A.; Dumont, Q. Combining InSAR and GNSS to Track Magma Transport at Basaltic Volcanoes. Remote Sens. 2019, 11, 2236. https://doi.org/10.3390/rs11192236
Smittarello D, Cayol V, Pinel V, Froger J-L, Peltier A, Dumont Q. Combining InSAR and GNSS to Track Magma Transport at Basaltic Volcanoes. Remote Sensing. 2019; 11(19):2236. https://doi.org/10.3390/rs11192236
Chicago/Turabian StyleSmittarello, Delphine, Valérie Cayol, Virginie Pinel, Jean-Luc Froger, Aline Peltier, and Quentin Dumont. 2019. "Combining InSAR and GNSS to Track Magma Transport at Basaltic Volcanoes" Remote Sensing 11, no. 19: 2236. https://doi.org/10.3390/rs11192236
APA StyleSmittarello, D., Cayol, V., Pinel, V., Froger, J.-L., Peltier, A., & Dumont, Q. (2019). Combining InSAR and GNSS to Track Magma Transport at Basaltic Volcanoes. Remote Sensing, 11(19), 2236. https://doi.org/10.3390/rs11192236





