What Rainfall Does Not Tell Us—Enhancing Financial Instruments with Satellite-Derived Soil Moisture and Evaporative Stress
Abstract
1. Introduction
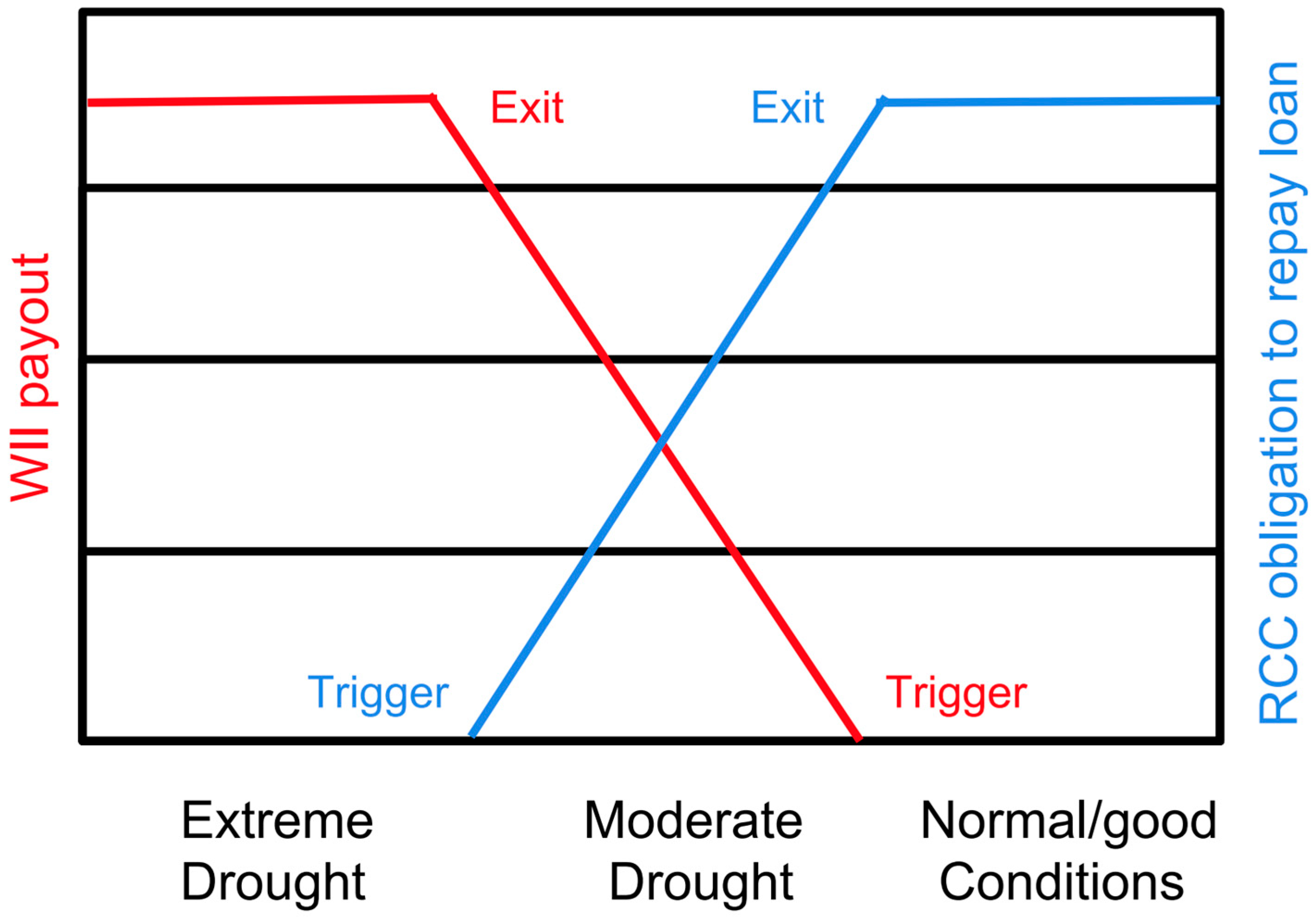
2. Role of Soil Moisture and Evapotranspiration for Parametric Insurance
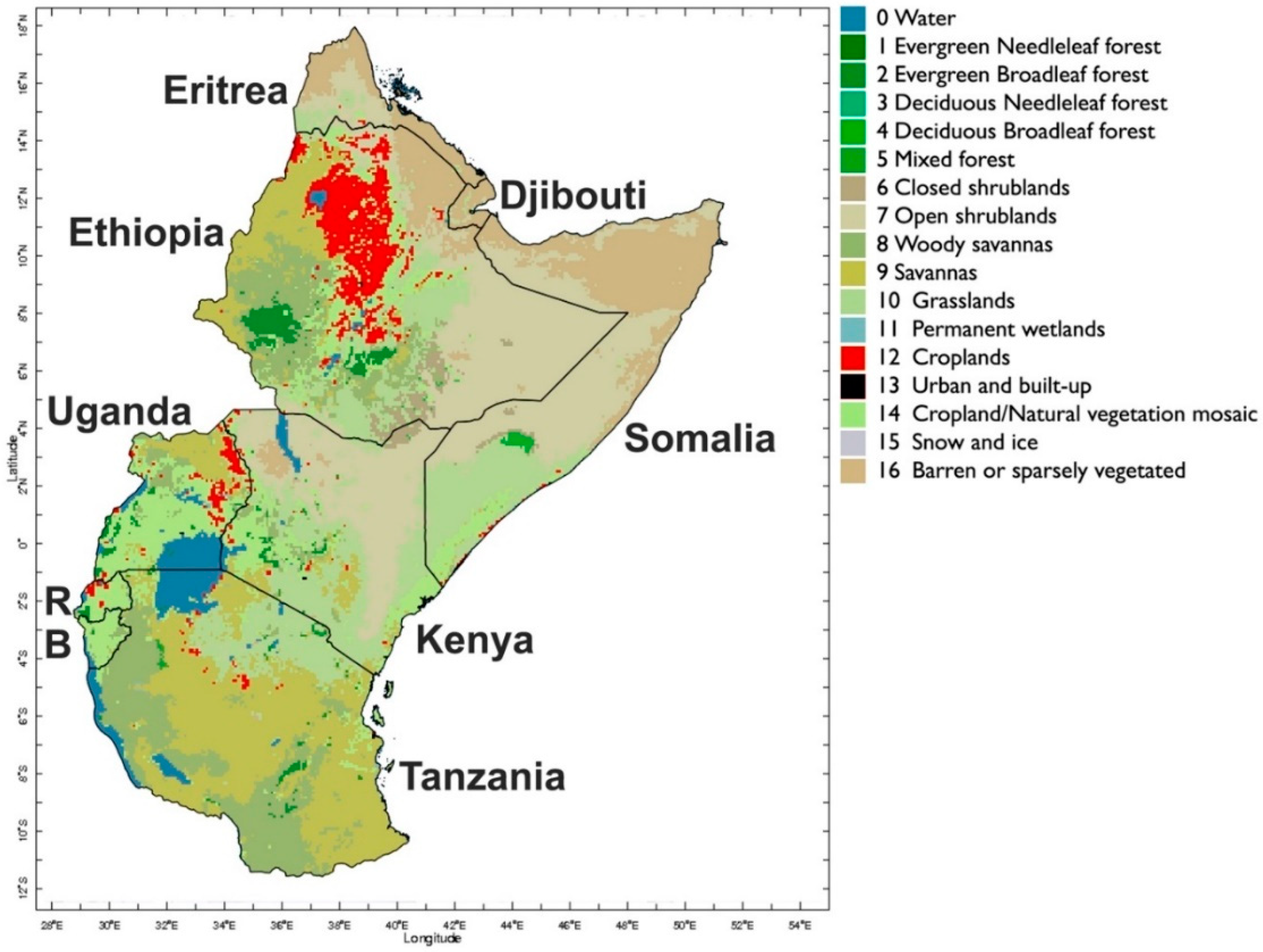
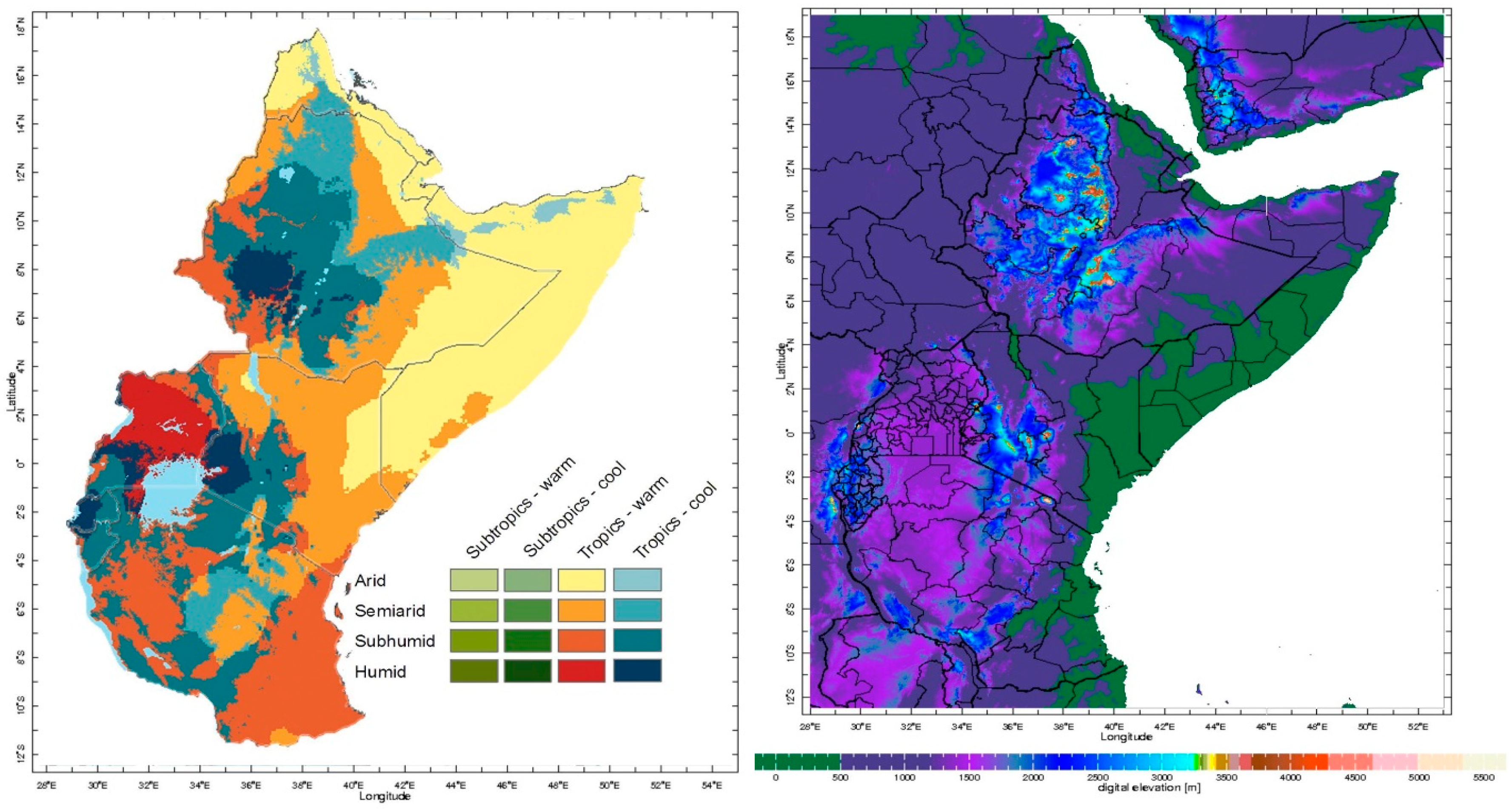
3. Region of Interest
4. Datasets and Methods
4.1. Satellite Data
4.1.1. Satellite-Derived Soil Moisture
4.1.2. ESI
4.1.3. CHIRPS
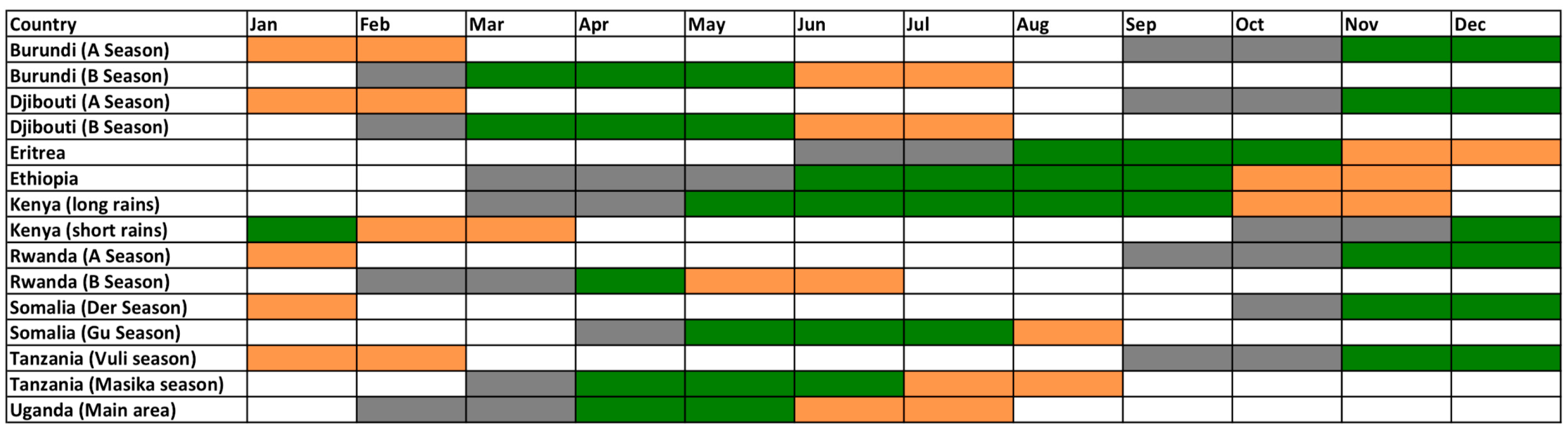
4.2. Maize Yield Estimates and Agricultural Calendar
4.3. Methods
4.3.1. Satellite Data Processing and Spatiotemporal Analyses
4.3.2. Regression Analysis
5. Results
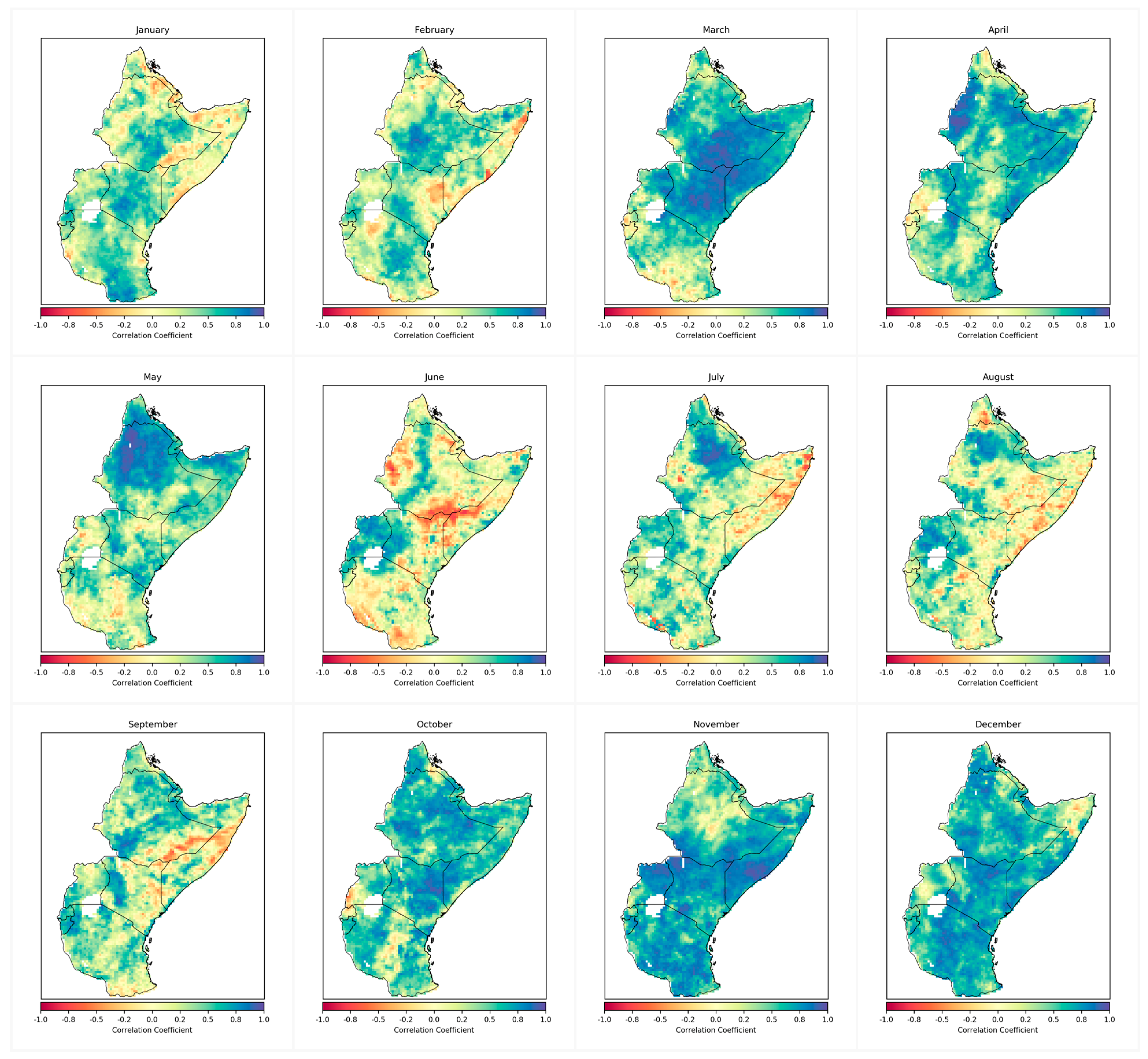
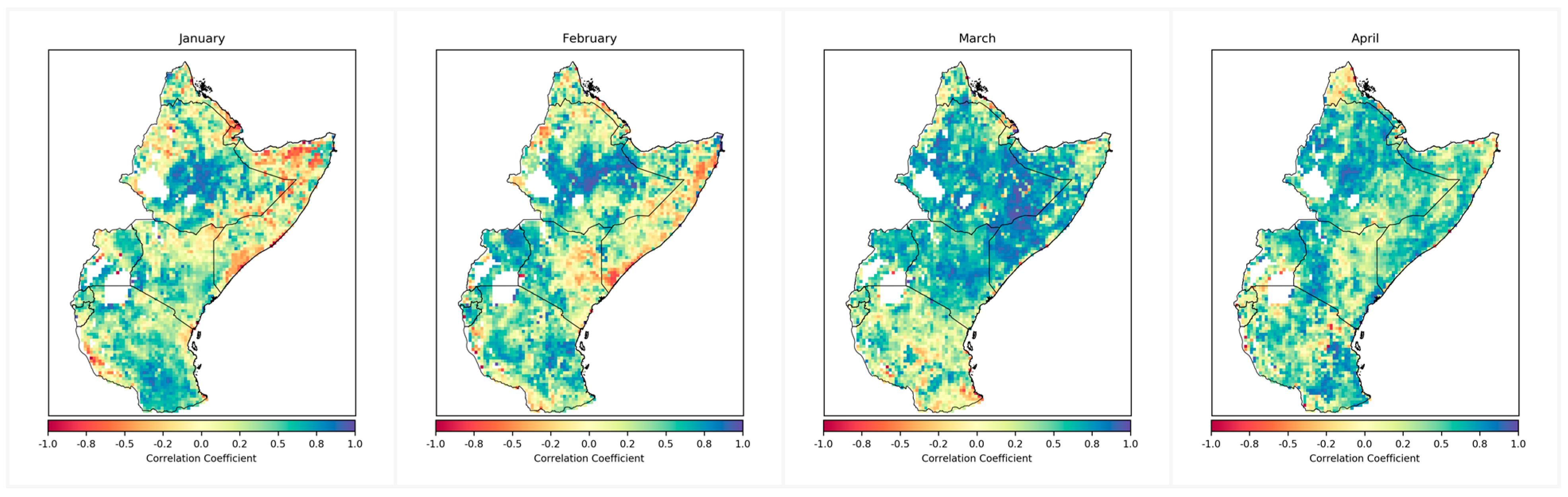
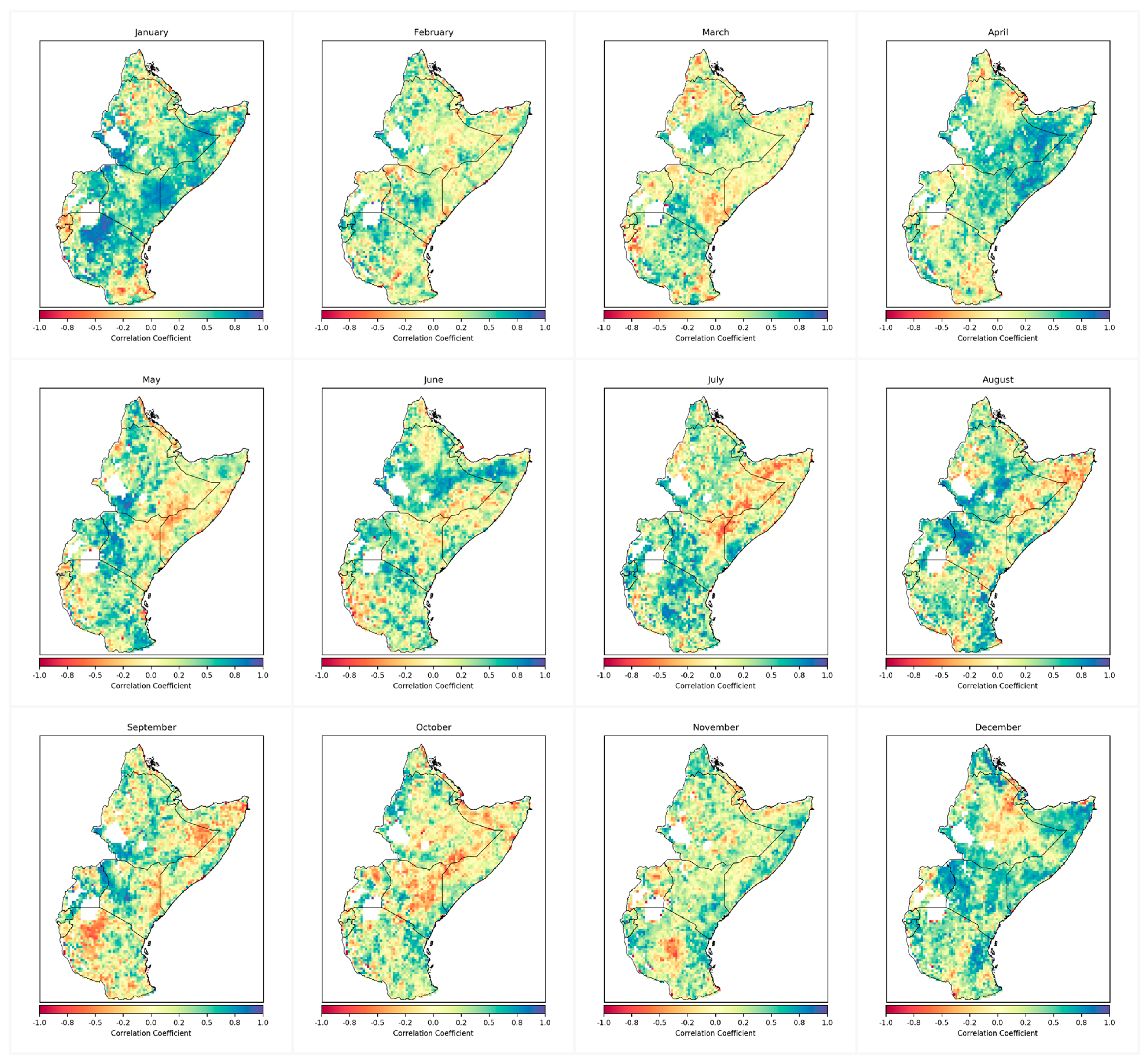
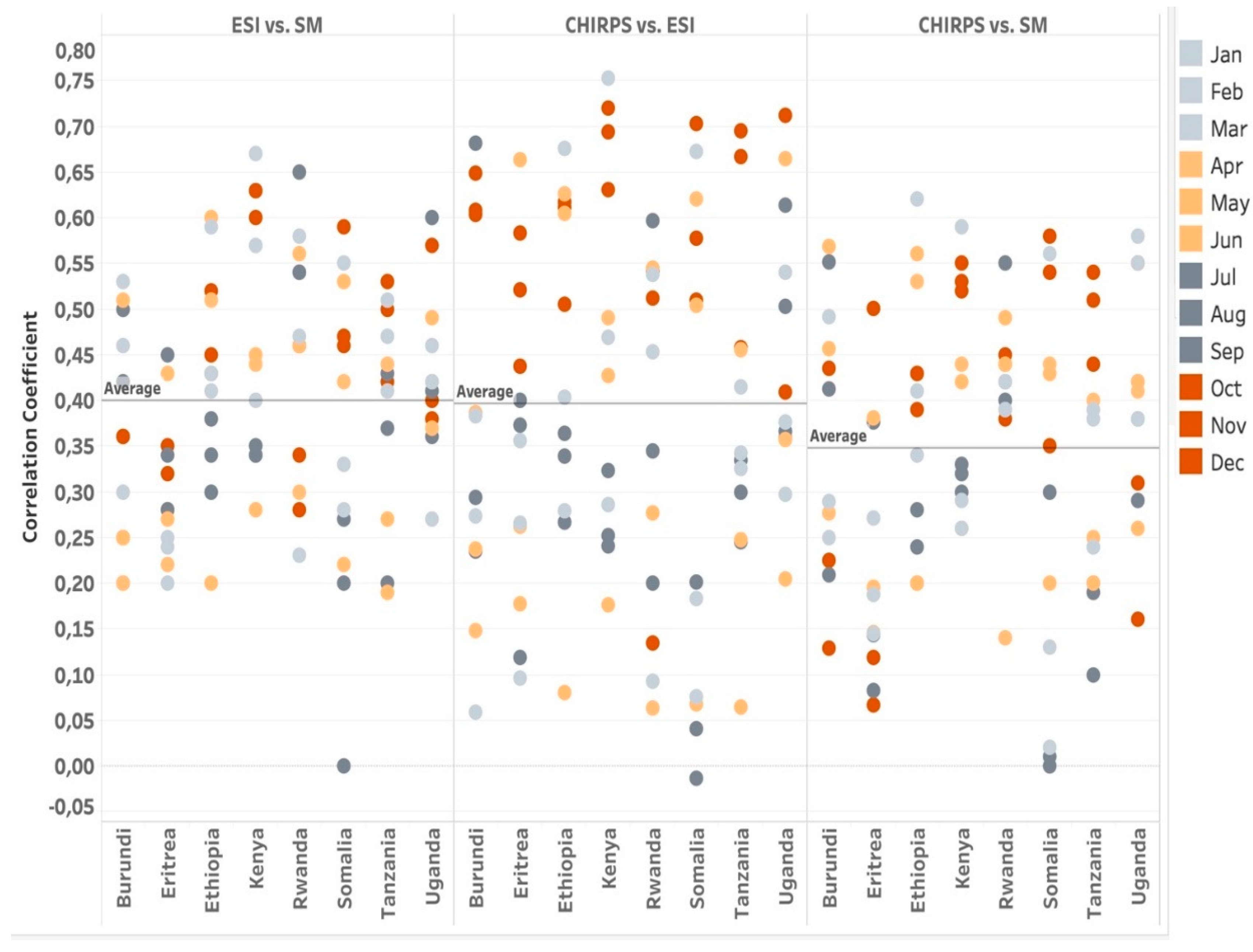
5.1. Spatial Correlation Analysis
5.2. Regression Analysis
5.2.1. Results Based on Annual Satellite-Derived Variables
5.2.2. Results Based on (Sub)seasonal Satellite-Derived Estimates
6. Summary and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A




References
- IFAD and UN FAO. Smallholders, Food Security and the Environment. Available online: https://www.ifad.org/documents/10180/666cac24-14b6-43c2-876d-9c2d1f01d5dd (accessed on 20 May 2018).
- Barrett, C.B. Covariate Catastrophic Risk Management in the Developing World: Discussion. Am. J. Agric. Econ. 2011, 93, 512–513. [Google Scholar] [CrossRef]
- Hellmuth, M.E.; Osgood, D.E.; Hess, U.; Moorhead, A.; Bhojwani, H. Index Insurance and Climate Risk: Prospects for Development and Disaster Management; International Research Institute for Climate and Society: Palisades, NY, USA, 2009. [Google Scholar]
- Madajewicz, M.; Tsegay, A.H.; Norton, M. Managing Risks to agricultural Livelihoods: Impact evaluation of the Harita Program in Tigray, Ethiopia, 2009–2012. Available online: https://www.oxfamamerica.org/static/media/file/Oxfam_America_Impact_Evaluation_of_HARITA_2009-2012_English.pdf (accessed on 13 April 2018).
- Dinku, T.; Hailemariam, K.; Maidment, R.; Tarnavsky, E.; Connor, S. Combined use of satellite estimates and rain gauge observations to generate high-quality historical rainfall time series over Ethiopia: Combining satellite and ground observations. Int. J. Climatol. 2014, 34, 2489–2504. [Google Scholar] [CrossRef]
- Dorigo, W.; de Jeu, R. Satellite soil moisture for advancing our understanding of earth system processes and climate change. Int. J. Appl. Earth Obs. Geoinf. 2016, 48, 1–4. [Google Scholar] [CrossRef]
- Anderson, M.C.; Kustas, W.P.; Norman, J.M.; Hain, C.R.; Mecikalski, J.R.; Schultz, L.; González-Dugo, M.P.; Cammalleri, C.; d’Urso, G.; Pimstein, A.; et al. Mapping daily evapotranspiration at field to continental scales using geostationary and polar orbiting satellite imagery. Hydrol. Earth Syst. Sci. 2011, 15, 223–239. [Google Scholar] [CrossRef]
- Ciabatta, L.; Massari, C.; Moramarco, T.; Hahn, S.; Hasenauer, S.; Kidd, R.; Dorigo, W.; Wagner, W.; Levizzani, V.; Wagner, W. Soil as a natural rain gauge: Estimating global rainfall from satellite soil moisture data. J. Geophys. Res. Atmos. 2014, 119, JD021489. [Google Scholar]
- Svoboda, M.; Fuchs, B. Handbook of Drought Indicators and Indices; World Meteorological Organization: Geneva, Switzerland, 2016. [Google Scholar]
- De Leeuw, J.; Vrieling, A.; Shee, A.; Atzberger, C.; Hadgu, K.M.; Biradar, C.M.; Keah, H.; Turvey, C. The Potential and Uptake of Remote Sensing in Insurance: A Review. Remote Sens. 2014, 6, 10888–10912. [Google Scholar] [CrossRef]
- Tarnavsky, E.; Maidment, R.; Greatrex, H.; Mookerjee, A.; Quaife, T.; Brown, M. The Use of Remotely Sensed Rainfall for Managing Drought Risk: A Case Study of Weather Index Insurance in Zambia. Remote Sens. 2016, 8, 342. [Google Scholar]
- Shee, A.; Turvey, C.G. Collateral-free lending with risk-contingent credit for agricultural development: Indemnifying loans against pulse crop price risk in India. Agric. Econ. 2012, 43, 561–574. [Google Scholar] [CrossRef]
- Western, A.W.; Zhou, S.-L.; Grayson, R.B.; McMahon, T.A.; Blöschl, G.; Wilson, D.J. Spatial correlation of soil moisture in small catchments and its relationship to dominant spatial hydrological processes. J. Hydrol. 2004, 286, 113–134. [Google Scholar] [CrossRef]
- Yang, L.; Sun, G.; Zhi, L.; Zhao, J. Negative soil moisture-precipitation feedback in dry and wet regions. Sci. Rep. 2018, 8, 4026. [Google Scholar] [CrossRef] [PubMed]
- Koster, R.D.; Dirmeyer, P.A.; Guo, Z.; Bonan, G.; Chan, E.; Cox, P.; Liu, P. Regions of Strong Coupling Between Soil Moisture and Precipitation. Science 2004, 305, 1138–1140. [Google Scholar] [CrossRef] [PubMed]
- Trenberth, K.E.; Fasullo, J.T.; Kiehl, J. Earth’s Global Energy Budget. Bull. Am. Meteorol. Soc. 2009, 90, 311–324. [Google Scholar] [CrossRef]
- Jung, M.; Reichstein, M.; Ciais, P.; Seneviratne, S.I.; Sheffield, J.; Goulden, M.L.; Dolman, A.J. Recent decline in the global land evapotranspiration trend due to limited moisture supply. Nature 2010, 467, 951–954. [Google Scholar] [CrossRef] [PubMed]
- Verstraeten, W.; Veroustraete, F.; Feyen, J. Assessment of Evapotranspiration and Soil Moisture Content Across Different Scales of Observation. Sensors 2008, 8, 70–117. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Li, P.; Yang, J. Soil Moisture Retrieval and Spatiotemporal Pattern Analysis Using Sentinel-1 Data of Dahra, Senegal. Remote Sens. 2017, 9, 1197. [Google Scholar] [CrossRef]
- Naeimi, V.; Bartalis, Z.; Wagner, W. ASCAT Soil Moisture: An Assessment of the Data Quality and Consistency with the ERS Scatterometer Heritage. J. Hydrometeorol. 2009, 10, 555–563. [Google Scholar] [CrossRef]
- Hain, C.R.; Crow, W.T.; Mecikalski, J.R.; Anderson, M.C.; Holmes, T. An intercomparison of available soil moisture estimates from thermal infrared and passive microwave remote sensing and land surface modeling. J. Geophys. Res. Atmos. 2011, 116. [Google Scholar] [CrossRef]
- Enenkel, M.; Osgood, D.; Anderson, M.; Powell, B.; McCarty, J.; Neigh, C.; Carroll, M.; Wooten, M.; Husak, G.; Hain, C.; et al. Exploiting the convergence of evidence in satellite data for advanced weather index insurance design. Weather Clim. Soc. 2018. in review. [Google Scholar] [CrossRef]
- Anderson, M.C.; Zolin, C.A.; Sentelhas, P.C.; Hain, C.R.; Semmens, K.; Yilmaz, M.T.; Gao, F.; Otkin, J.A.; Tetraulth, R. The Evaporative Stress Index as an indicator of agricultural drought in Brazil: An assessment based on crop yield impacts. Remote Sens. Environ. 2016, 174, 82–99. [Google Scholar] [CrossRef]
- Friedl, M.A.; Sulla-Menashe, D.; Tan, B.; Schneider, A.; Ramankutty, N.; Sibley, A.; Huang, X. MODIS Collection 5 global land cover: Algorithm refinements and characterization of new datasets. Remote Sens. Environ. 2010, 114, 168–182. [Google Scholar] [CrossRef]
- Sebastian, K. Agroecological Zones; International Food Policy Research Institute: Washington, DC, USA, 2014. [Google Scholar]
- Wagner, W.; Dorigo, W.; de Jeu, R.; Fernandez, D.; Benveniste, J.; Haas, E.; Ertl, M. Fusion of active and passive microwave observations to create an essential climate variable data record on soil moisture. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, I–7, 315–321. [Google Scholar]
- Liu, Y.; Parinussa, R.M.; Dorigo, W.A.; de Jeu, R.A.M.; Wagner, W.; van Dijk, A.I.J.M.; McCabe, M.F.; Evans, J.P. Developing an improved soil moisture dataset by blending passive and active microwave satellite-based retrievals. Hydrol. Earth Syst. Sci. 2011, 15, 425–436. [Google Scholar] [CrossRef]
- Liu, Y.Y.; Dorigo, W.A.; Parinussa, R.M.; de Jeu, R.A.; Wagner, W.; McCabe, M.F.; Van Dijk, A.I.J.M. Trend-preserving blending of passive and active microwave soil moisture retrievals. Remote Sens. Environ. 2012, 123, 280–297. [Google Scholar] [CrossRef]
- Anderson, M.C.; Zolin, C.A.; Hain, C.R.; Semmens, K.; Yilmaz, M.T.; Gao, F. Comparison of satellite-derived LAI and precipitation anomalies over Brazil with a thermal infrared-based Evaporative Stress Index for 2003–2013. J. Hydrol. 2015, 526, 287–302. [Google Scholar] [CrossRef]
- Anderson, M.C.; Norman, J.M.; Mecikalski, J.R.; Otkin, J.A.; Kustas, W.P. A climatological study of evapotranspiration and moisture stress across the continental United States based on thermal remote sensing: 1. Model formulation. J. Geophys. Res. 2007, 112, D10117. [Google Scholar] [CrossRef]
- Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Shukla, S.; Michaelsen, J. The climate hazards infrared precipitation with stations—A new environmental record for monitoring extremes. Sci. Data 2015, 2, 150066. [Google Scholar] [CrossRef] [PubMed]
- Dorigo, W.; Wagner, W.; Albergel, C.; Albrecht, F.; Balsamo, G.; Brocca, L.; Haas, E. ESA CCI Soil Moisture for improved Earth system understanding: State-of-the art and future directions. Remote Sens. Environ. 2017, 203, 185–215. [Google Scholar] [CrossRef]
- Yilmaz, M.T.; Crow, W.T.; Anderson, M.C.; Hain, C. An objective methodology for merging satellite- and model-based soil moisture products. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Qiu, J.; Crow, W.T.; Nearing, G.S.; Mo, X.; Liu, S. The impact of vertical measurement depth on the information content of soil moisture times series data. Geophys. Res. Lett. 2014, 2014, GL060017. [Google Scholar] [CrossRef]
- Wagner, W.; Lemoine, G.; Rott, H. A Method for Estimating Soil Moisture from ERS Scatterometer and Soil Data. Remote Sens. Environ. 1999, 70, 191–207. [Google Scholar] [CrossRef]
- Dorigo, W.; de Jeu, R.; Chung, D.; Parinussa, R.; Liu, Y.; Wagner, W.; Fernández-Prieto, D. Evaluating global trends (1988–2010) in harmonized multi-satellite surface soil moisture. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
- McNally, A.; Shukla, S.; Arsenault, K.R.; Wang, S.; Peters-Lidard, C.D.; Verdin, J.P. Evaluating ESA CCI soil moisture in East Africa. Int. J. Appl. Earth Obs. Geoinf. 2016, 48, 96–109. [Google Scholar] [CrossRef] [PubMed]
- Anderson, M.C.; Norman, J.M.; Diak, G.R.; Kustas, W.P.; Micikalski, J.R. A two-source time-integrated model for estimating surface fluxes using thermal infrared remote sensing. Remote Sens. Environ. 1997, 60, 195–216. [Google Scholar] [CrossRef]
- Ji, X.B.; Chen, J.M.; Zhao, W.Z.; Kang, E.S.; Jin, B.W.; Xu, S.Q. Comparison of hourly and daily Penman-Monteith grass- and alfalfa-reference evapotranspiration equations and crop coefficients for maize under arid climatic conditions. Agric. Water Manag. 2017, 192, 1–11. [Google Scholar] [CrossRef]
- Otkin, J.A.; Anderson, M.C.; Hain, C.; Svoboda, M. Using Temporal Changes in Drought Indices to Generate Probabilistic Drought Intensification Forecasts. J. Hydrometeorol. 2015, 16, 88–105. [Google Scholar] [CrossRef]
- Otkin, J.A.; Anderson, M.C.; Hain, C.; Mladenova, I.E.; Basara, J.B.; Svoboda, M. Examining Rapid Onset Drought Development Using the Thermal Infrared–Based Evaporative Stress Index. J. Hydrometeorol. 2013, 14, 1057–1074. [Google Scholar] [CrossRef]
- Hain, C.R.; Crow, W.T.; Anderson, M.C.; Mecikalski, J.R. An ensemble Kalman filter dual assimilation of thermal infrared and microwave satellite observations of soil moisture into the Noah land surface model: Assimilation of tir and microwave soil moisture. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Hain, C.R.; Anderson, M.C. Estimating morning change in land surface temperature from MODIS day/night observations: Applications for surface energy balance modeling: Estimating Morning ΔLST From MODIS. Geophys. Res. Lett. 2017, 44, 9723–9733. [Google Scholar] [CrossRef] [PubMed]
- Claverie, M.; Vermote, E.; NOAA CDR Program. NOAA Climate Data Record (CDR) of Leaf Area Index (LAI) and Fraction of Absorbed Photosynthetically Active Radiation (FAPAR), Version 4; NOAA National Climatic Data Center: Asheville, NC, USA, 2014. [Google Scholar]
- Saha, S.; Moorthi, S.; Pan, H.L.; Wu, X.; Wang, J.; Nadiga, S.; Liu, H. The NCEP Climate Forecast System Reanalysis. Bull. Am. Meteorol. Soc. 2010, 91, 1015–1057. [Google Scholar] [CrossRef]
- Anderson, W.B.; Zaitchik, B.F.; Hain, C.R.; Anderson, M.C.; Yilmaz, M.T.; Mecikalski, J.; Schultz, L. Towards an integrated soil moisture drought monitor for East Africa. Hydrol. Earth Syst. Sci. 2012, 16, 2893–2913. [Google Scholar] [CrossRef]
- Yilmaz, M.T.; Anderson, M.C.; Zaitchik, B.; Hain, C.R.; Crow, W.T.; Ozdogan, M.; Chun, J.A.; Evans, J. Comparison of prognostic and diagnostic surface flux modeling approaches over the Nile River basin: Prognostic and diagnostic modeling over nile. Water Resour. Res. 2014, 50, 386–408. [Google Scholar] [CrossRef]
- Holmes, T.R.H.; Hain, C.R.; Crow, W.T.; Anderson, M.C.; Kustas, W.P. Microwave implementation of two-source energy balance approach for estimating evapotranspiration. Hydrol. Earth Syst. Sci. 2018, 22, 1351–1369. [Google Scholar] [CrossRef]
- Hessels, T.M. Comparison and Validation of Several Open Access Remotely Sensed Rainfall Products for the Nile Basin. Master’s Thesis, Geoscience & Engineering, Delft University of Technology, Delft, The Netherlands, 2015. [Google Scholar]
- Katsanos, D.; Retalis, A.; Michaelides, S. Validation of a high-resolution precipitation database (CHIRPS) over Cyprus for a 30-year period. Atmos. Res. 2016, 169, 459–464. [Google Scholar] [CrossRef]
- Rivera, J.A.; Marianetti, G.; Hinrichs, S. Validation of CHIRPS precipitation dataset along the Central Andes of Argentina. Atmos. Res. 2018, 213, 437–449. [Google Scholar] [CrossRef]
- Kimani, M.; Hoedjes, J.; Su, Z. An Assessment of Satellite-Derived Rainfall Products Relative to Ground Observations over East Africa. Remote Sens. 2017, 9, 430. [Google Scholar] [CrossRef]
- US AID. FEWS Tanzania Food Security Report 22 Dec 2003–Drought relief needs only partly met. Available online: https://reliefweb.int/report/united-republic-tanzania/fews-tanzania-food-security-report-22-dec-2003-drought-relief-needs (accessed on 22 June 2018).
- Schlenker, W.; Lobell, D.B. Robust negative impacts of climate change on African agriculture. Environ. Res. Lett. 2010, 5, 014010. [Google Scholar] [CrossRef]
- Davenport, F.; Funk, C.; Galu, G. How will East African maize yields respond to climate change and can agricultural development mitigate this response? Clim. Chang. 2018, 147, 491–506. [Google Scholar] [CrossRef]
- Wagner, W.; Hahn, S.; Kidd, R.; Melzer, T.; Bartalis, Z.; Hasenauer, S.; Komma, J. The ASCAT Soil Moisture Product: A Review of its Specifications, Validation Results, and Emerging Applications. Meteorol. Z. 2013, 22, 5–33. [Google Scholar] [CrossRef]
- Dinku, T.; Funk, C.; Peterson, P.; Maidment, R.; Tadesse, T.; Gadain, H.; Ceccato, P. Validation of the CHIRPS satellite rainfall estimates over eastern Africa. Q. J. R. Meteorol. Soc. 2018. [Google Scholar] [CrossRef]
- Lopresti, M.F.; di Bella, C.M.; Degioanni, A.J. Relationship between MODIS-NDVI data and wheat yield: A case study in Northern Buenos Aires province, Argentina. Inf. Process. Agric. 2015, 2, 73–84. [Google Scholar] [CrossRef]


| Annual | |||||||
|---|---|---|---|---|---|---|---|
| DEP VARIABLE | Maize Yield | ||||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | |
| CHIRPS | 463.50 | −996.10 | −514.20 | −1054 | |||
| (1359) | (1357) | (1375) | (1368) | ||||
| SM | 6227 *** | 5477 ** | 6688 *** | 5842 ** | |||
| (1867) | (2601) | (1974) | (2650) | ||||
| ESI | 1380 ** | 306.6 | 1439 ** | 356.4 | |||
| (540.9) | (735.9) | (566.1) | (740.4) | ||||
| Constant | 11,696 *** | 12,200 *** | 13,180 *** | 12,480 *** | 12,014 *** | 13,129 *** | 12,328 *** |
| (1389) | (1290) | (1448) | (1460) | (1318) | (1462) | (1476) | |
| Observations | 112 | 112 | 112 | 112 | 112 | 112 | 112 |
| R-squared | 0.35 | 0.43 | 0.40 | 0.43 | 0.43 | 0.40 | 0.43 |
| Number of Country | 8 | 8 | 8 | 8 | 8 | 8 | 8 |
| Annual | |||||||
|---|---|---|---|---|---|---|---|
| DEP VARIABLE | Bad Year | ||||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | |
| CHIRPS | −0.164 | −0.125 | −0.0801 | −0.0530 | |||
| (0.232) | (0.422) | (0.254) | (0.477) | ||||
| SM | −0.152 | −0.0772 | −0.0472 | −0.0321 | |||
| (0.232) | (0.255) | (0.421) | (0.479) | ||||
| ESI | −0.897 *** | −0.892 *** | −0.890 *** | −0.890 *** | |||
| (0.255) | (0.256) | (0.256) | (0.256) | ||||
| Constant | −1.307 *** | −1.306 *** | −1.505 *** | −1.510 *** | −1.307 *** | −1.508 *** | −1.509 *** |
| (0.232) | (0.232) | (0.270) | (0.271) | (0.232) | (0.270) | (0.271) | |
| Observations | 112 | 112 | 112 | 112 | 112 | 112 | 112 |
| Pseudo R2 | 0.00433 | 0.00368 | 0.122 | 0.122 | 0.00444 | 0.122 | 0.122 |
| Growing Season | |||||||
|---|---|---|---|---|---|---|---|
| DEP VARIABLE | Maize Yield | ||||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | |
| CHIRPS | −1294 | −3487 *** | −2391 * | −3384 ** | |||
| (1203) | (1280) | (1324) | (1309) | ||||
| SM | 3236 ** | 4391 ** | 5000 *** | 5588 *** | |||
| (1255) | (1845) | (1375) | (1847) | ||||
| ESI | 609.4 | −585.4 | 1024 * | −324.7 | |||
| (485.1) | (689.6) | (531.2) | (675.9) | ||||
| Constant | 11,535 *** | 11,804 *** | 12,109 *** | 11,740 *** | 11,778 *** | 12,198 *** | 11,766 *** |
| (1346) | (1309) | (1478) | (1449) | (1264) | (1460) | (1404) | |
| Observations | 112 | 112 | 111 | 111 | 112 | 111 | 111 |
| R-squared | 0.36 | 0.40 | 0.36 | 0.40 | 0.44 | 0.38 | 0.44 |
| Number of Country | 8 | 8 | 8 | 8 | 8 | 8 | 8 |
| Growing Season | |||||||
|---|---|---|---|---|---|---|---|
| DEP VARIABLE | Bad Year | ||||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | |
| CHIRPS | −0.0271 | 0.333 | 0.0523 | 0.330 | |||
| (0.231) | (0.397) | (0.247) | (0.415) | ||||
| SM | −0.174 | −0.0810 | −0.446 | −0.348 | |||
| (0.233) | (0.248) | (0.402) | (0.419) | ||||
| ESI | −0.570 ** | −0.559 ** | −0.576 ** | −0.561 ** | |||
| (0.241) | (0.243) | (0.242) | (0.243) | ||||
| Constant | 1.299 *** | 1.308 *** | 1.429 *** | 1.432 *** | 1.319 *** | 1.429 *** | 1.443 *** |
| (0.230) | (0.232) | (0.251) | (0.251) | (0.234) | (0.251) | (0.254) | |
| Observations | 112 | 112 | 111 | 111 | 112 | 111 | 111 |
| Pseudo R2 | 0.000118 | 0.00484 | 0.0522 | 0.0531 | 0.0109 | 0.0526 | 0.0587 |
| Harvesting Season | |||||||
|---|---|---|---|---|---|---|---|
| DEP VARIABLE | Maize Yield | ||||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | |
| CHIRPS | 545.50 | −124.50 | −1009 | −1108 | |||
| (914.4) | (964.3) | (980.0) | (989.1) | ||||
| SM | 2611 ** | 1110 | 2675 * | 1326 | |||
| (1278) | (1585) | (1376) | (1595) | ||||
| ESI | 1104 *** | 889.4 * | 1310 *** | 1074 ** | |||
| (385.4) | (493.3) | (434.2) | (519.4) | ||||
| Constant | 11,697 *** | 11,826 *** | 13,722 *** | 13,715 *** | 11,807 *** | 13,728 *** | 13,721 *** |
| (1363) | (1328) | (1513) | (1518) | (1344) | (1513) | (1515) | |
| Observations | 112 | 112 | 110 | 110 | 112 | 110 | 110 |
| R-squared | 0.36 | 0.38 | 0.39 | 0.40 | 0.38 | 0.40 | 0.41 |
| Number of Country | 8 | 8 | 8 | 8 | 8 | 8 | 8 |
| Harvest Season | |||||||
|---|---|---|---|---|---|---|---|
| DEP VARIABLE | Bad Year | ||||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | |
| CHIRPS | −0.108 | −0.00145 | 0.334 | 0.448 | |||
| (0.231) | (0.330) | (0.317) | (0.411) | ||||
| SM | −0.149 | 0.117 | −0.148 | −0.166 | |||
| (0.231) | (0.280) | (0.336) | (0.392) | ||||
| ESI | −1.022 *** | −1.063 *** | −1.153 *** | −1.142 *** | |||
| (0.296) | (0.315) | (0.333) | (0.334) | ||||
| Constant | −1.303 *** | −1.306 *** | −1.662 *** | −1.672 *** | −1.306 *** | −1.715 *** | −1.720 *** |
| (0.231) | (0.232) | (0.295) | (0.297) | (0.232) | (0.307) | (0.308) | |
| Observations | 112 | 112 | 110 | 110 | 112 | 110 | 110 |
| Pseudo R2 | 0.00190 | 0.00359 | 0.132 | 0.134 | 0.00359 | 0.143 | 0.144 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Enenkel, M.; Farah, C.; Hain, C.; White, A.; Anderson, M.; You, L.; Wagner, W.; Osgood, D. What Rainfall Does Not Tell Us—Enhancing Financial Instruments with Satellite-Derived Soil Moisture and Evaporative Stress. Remote Sens. 2018, 10, 1819. https://doi.org/10.3390/rs10111819
Enenkel M, Farah C, Hain C, White A, Anderson M, You L, Wagner W, Osgood D. What Rainfall Does Not Tell Us—Enhancing Financial Instruments with Satellite-Derived Soil Moisture and Evaporative Stress. Remote Sensing. 2018; 10(11):1819. https://doi.org/10.3390/rs10111819
Chicago/Turabian StyleEnenkel, Markus, Carlos Farah, Christopher Hain, Andrew White, Martha Anderson, Liangzhi You, Wolfgang Wagner, and Daniel Osgood. 2018. "What Rainfall Does Not Tell Us—Enhancing Financial Instruments with Satellite-Derived Soil Moisture and Evaporative Stress" Remote Sensing 10, no. 11: 1819. https://doi.org/10.3390/rs10111819
APA StyleEnenkel, M., Farah, C., Hain, C., White, A., Anderson, M., You, L., Wagner, W., & Osgood, D. (2018). What Rainfall Does Not Tell Us—Enhancing Financial Instruments with Satellite-Derived Soil Moisture and Evaporative Stress. Remote Sensing, 10(11), 1819. https://doi.org/10.3390/rs10111819





