Stability Analysis and Treatment of Pebble Soil Slopes Under Rainfall and Earthquake Conditions
Abstract
1. Introduction
2. Overview and Methods of the Study Area
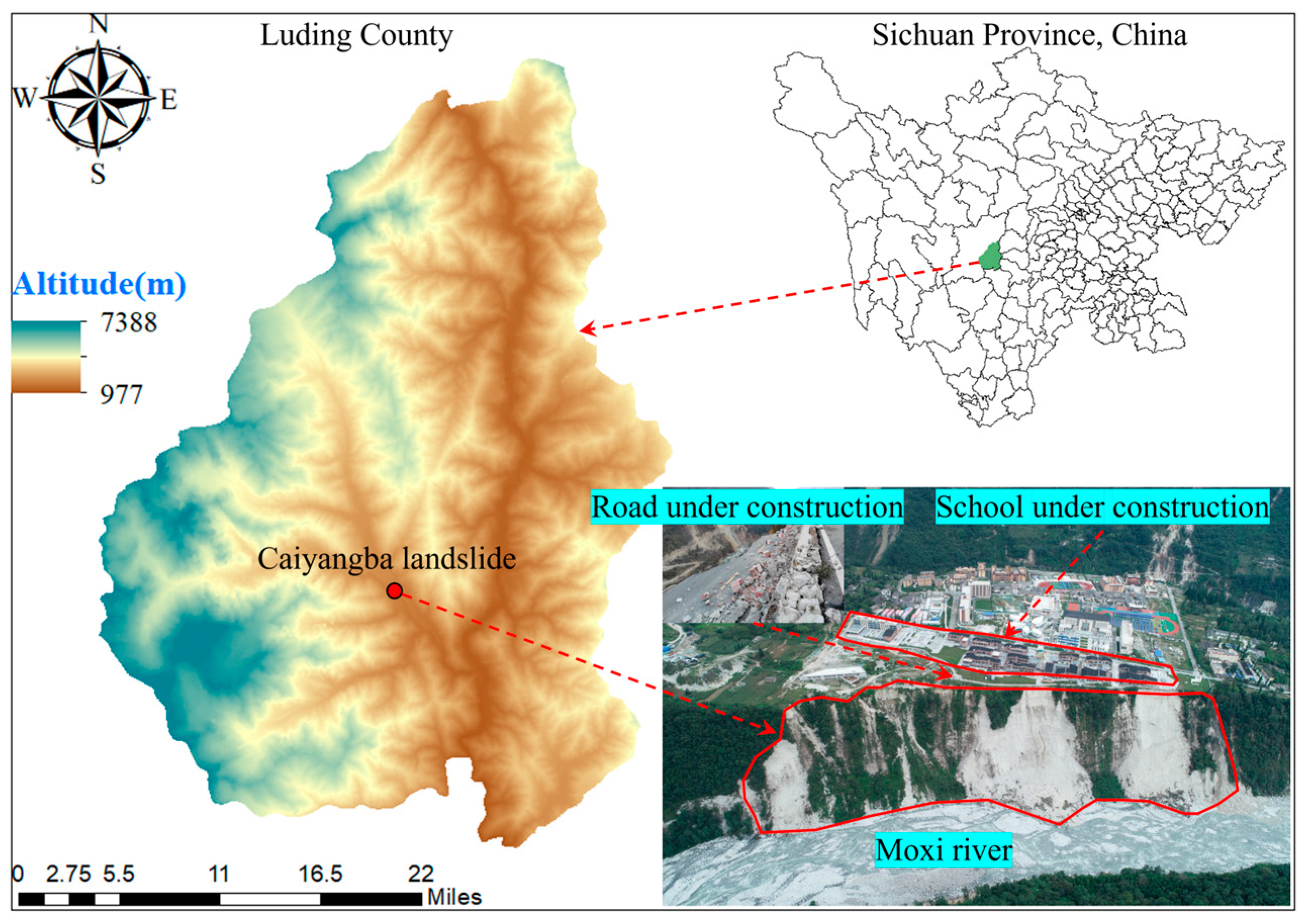
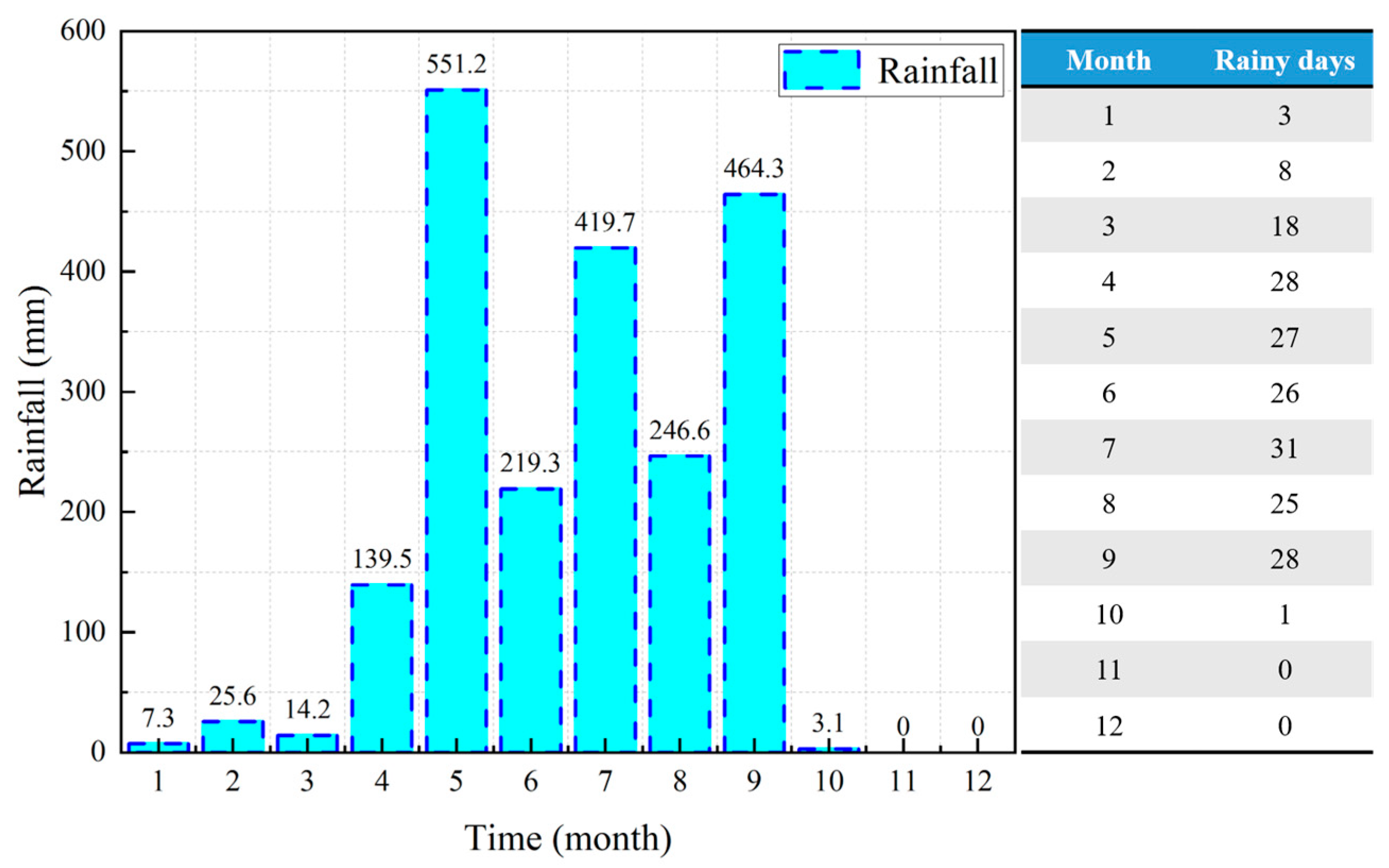
2.1. Overview of the Study Area
2.2. Stratum Composition and Parameters
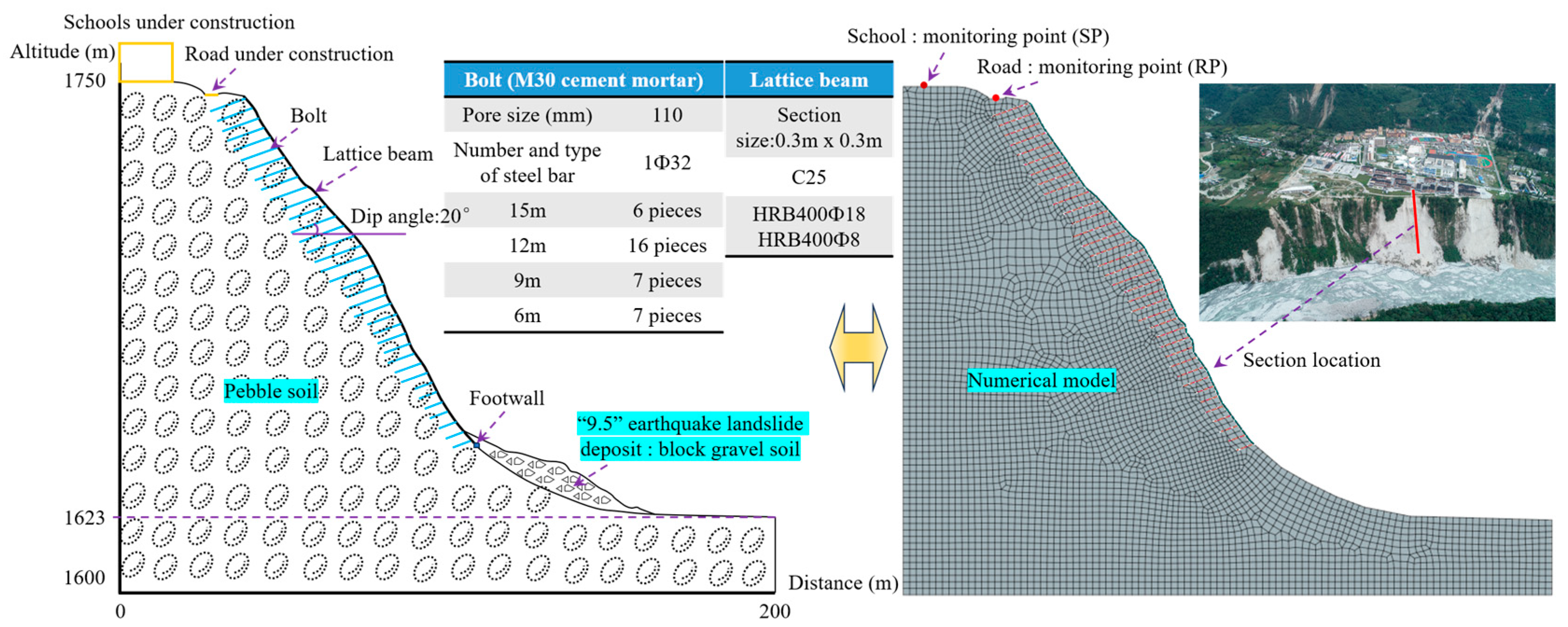
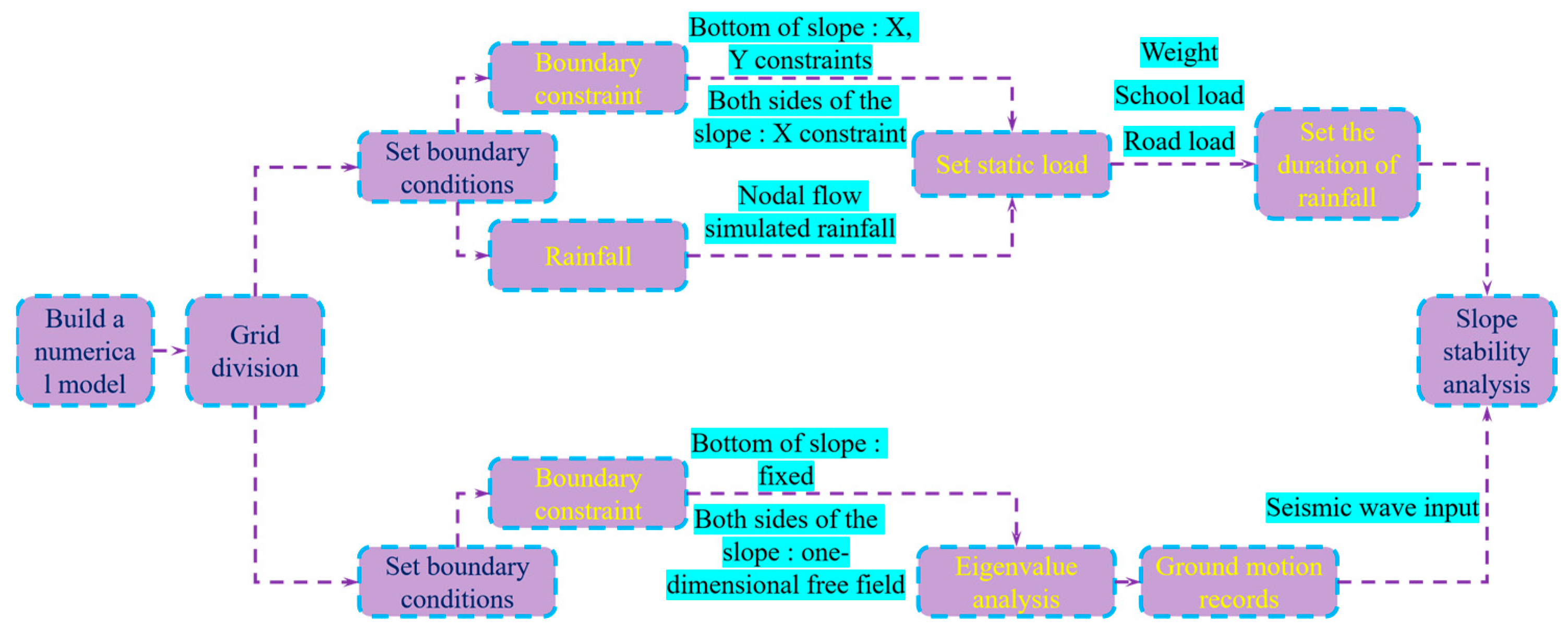
2.3. Study Method
3. Results and Discussions
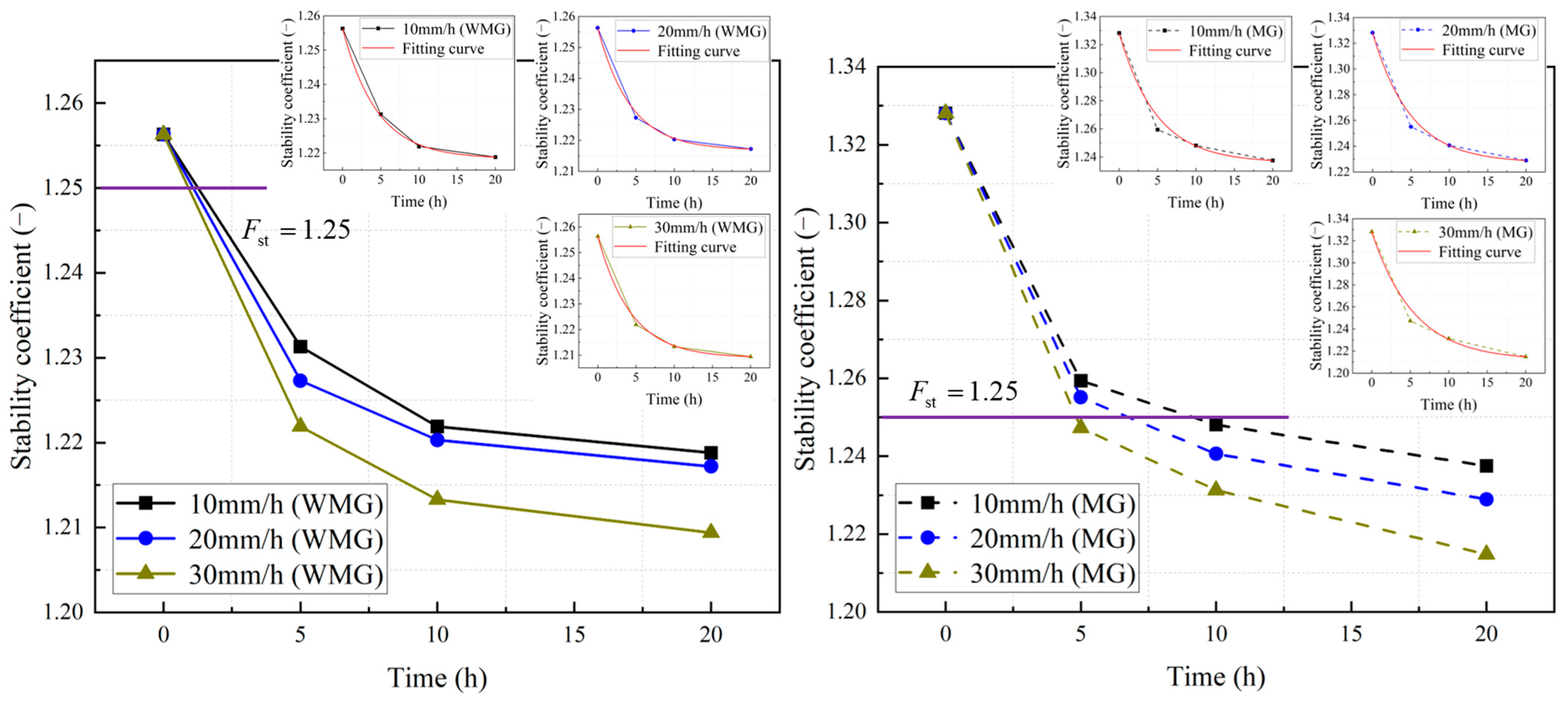
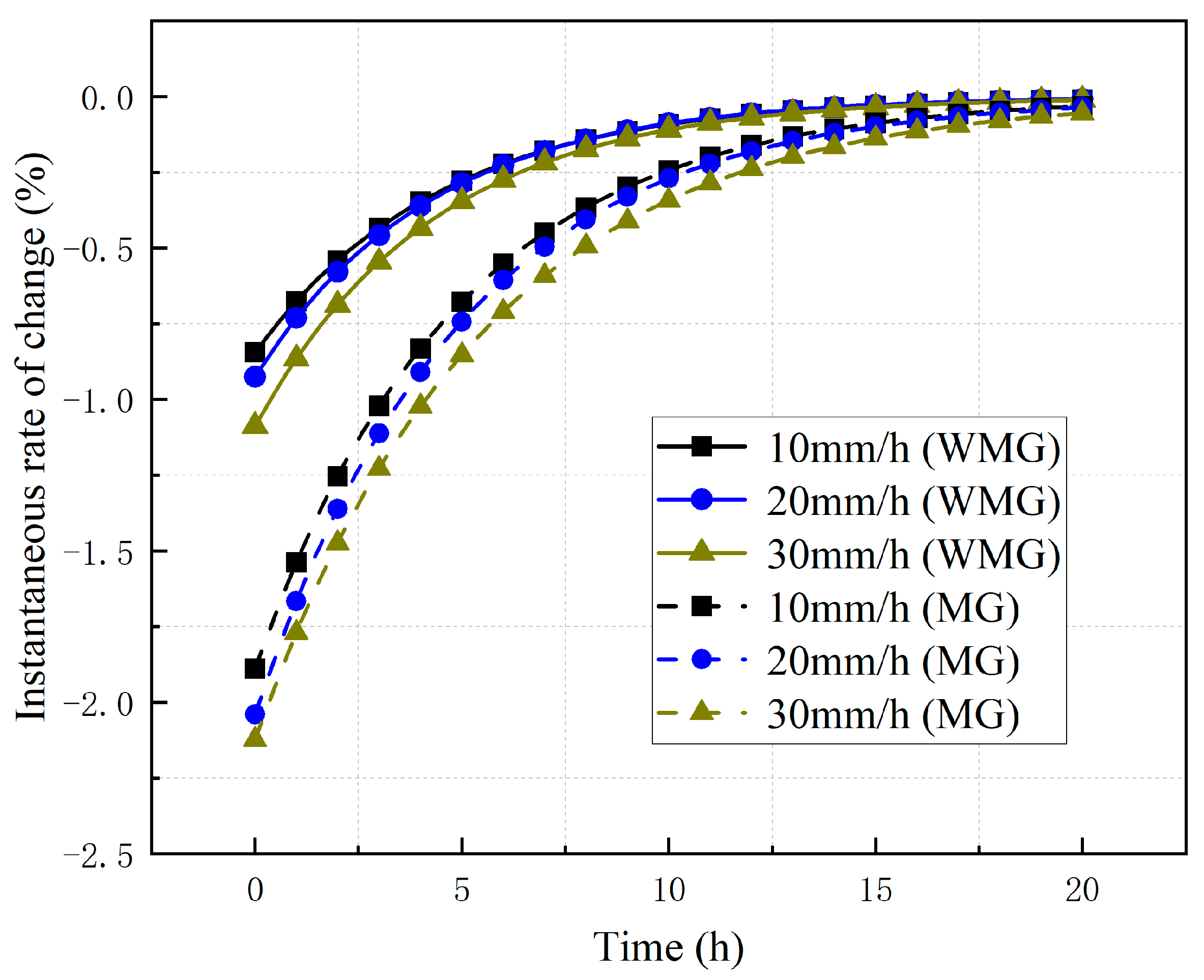
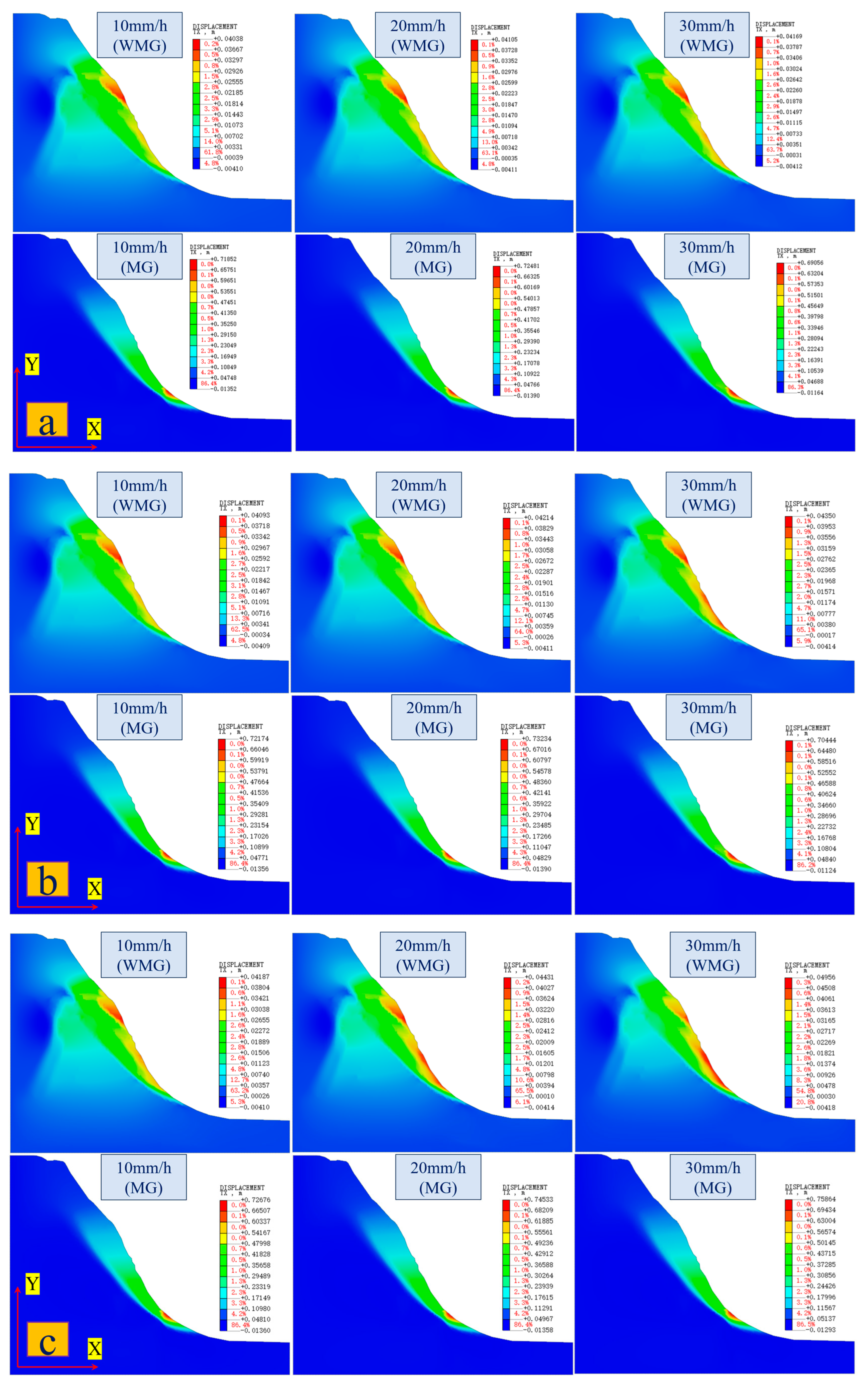
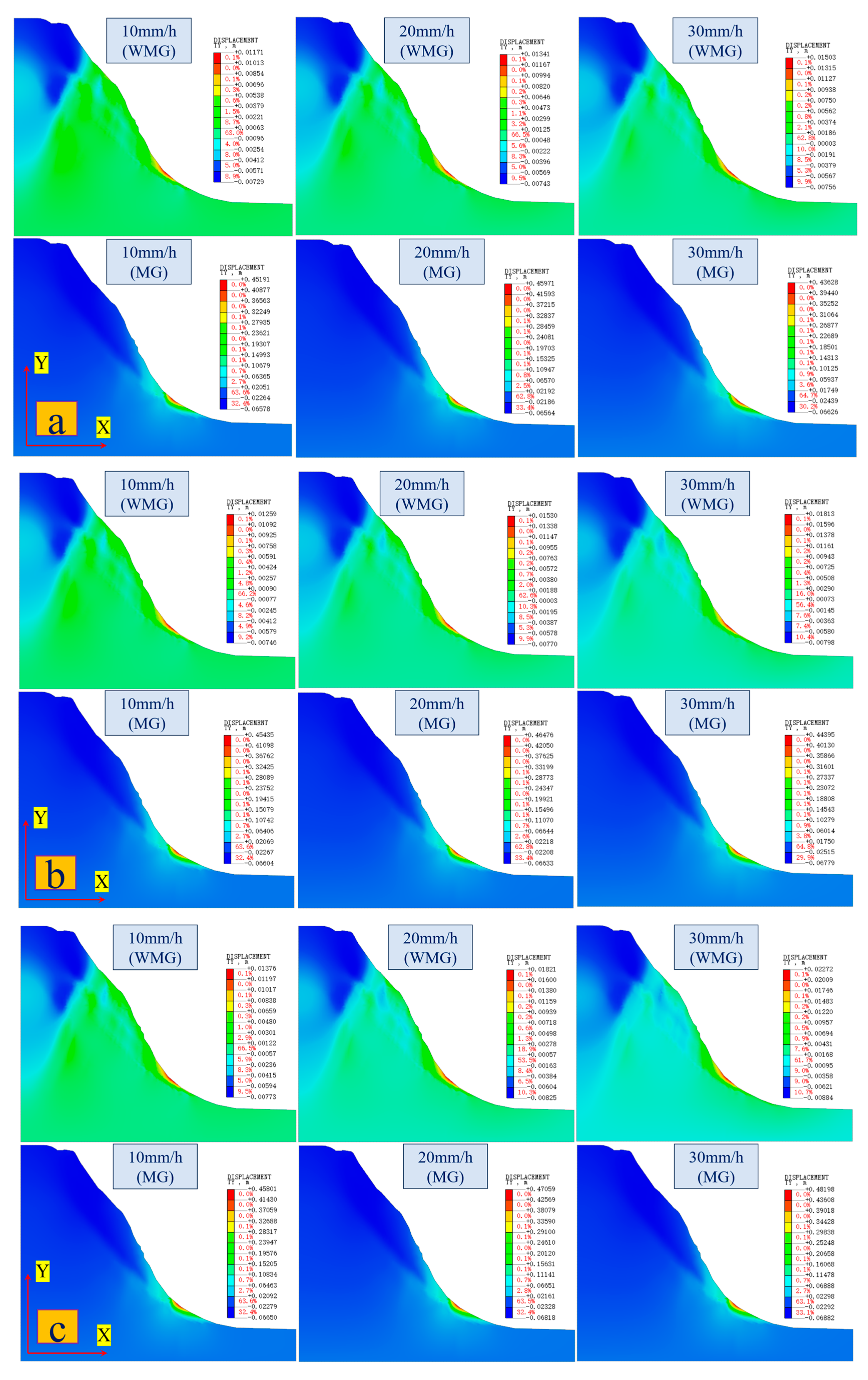
3.1. Slope Stability Analysis Under Different Rainfall Conditions
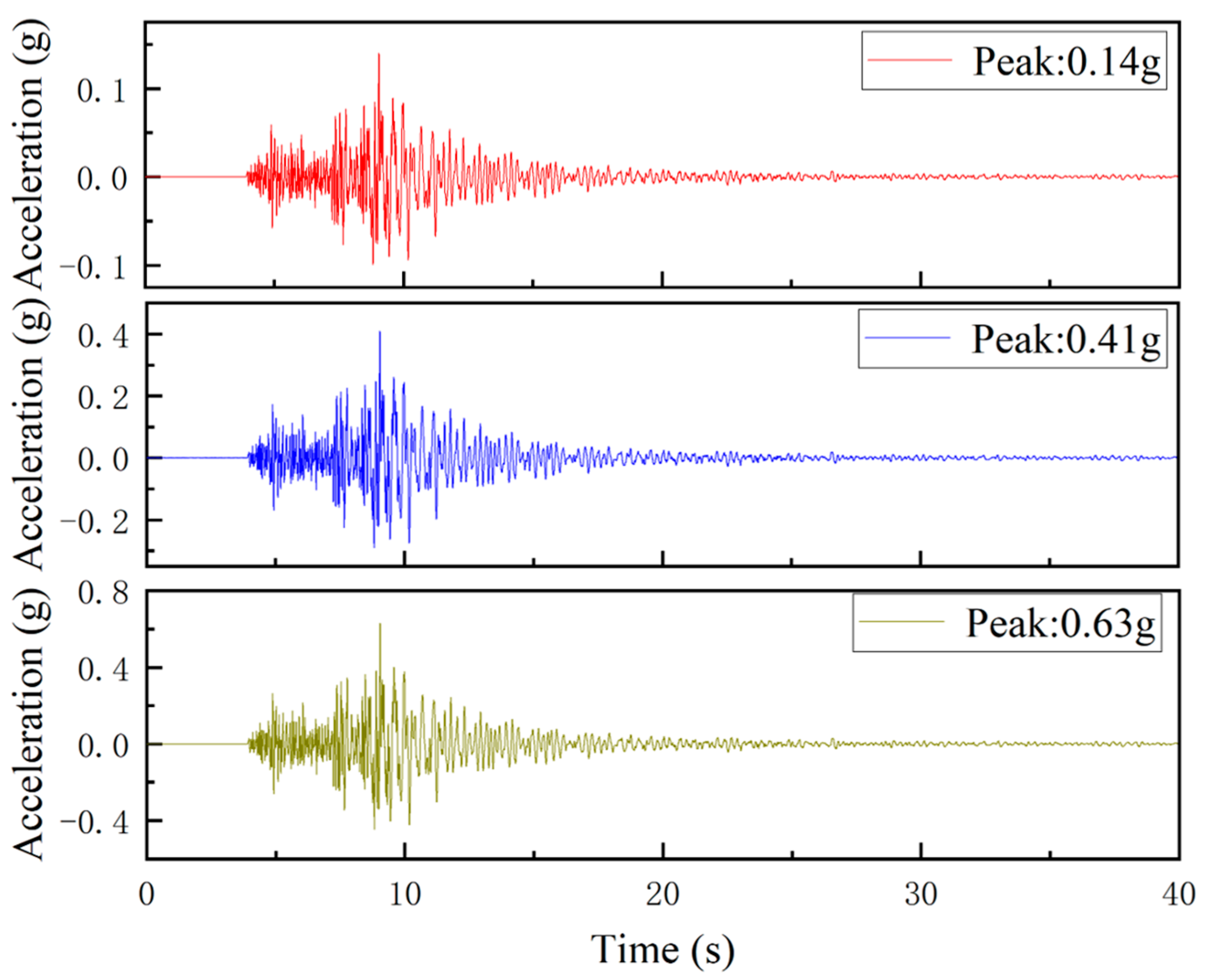
3.2. Slope Stability Analysis Under Different Seismic Conditions
4. Conclusions
- The “anchor lattice treatment method” can effectively improve the stability of the Caiyangba landslide. The improvement effect of slope stability decreases with the increase in rainfall duration and the rainfall itself. Under the influence of rainfall, the development law of slope stability coefficient in WMG condition and MG condition with rainfall duration conforms to the development law of the exponential function (). At the same time, the expression () of the instantaneous change rate of the slope stability coefficient is derived. It is found that the slope stability coefficient will not always decrease under the influence of rainfall, but will gradually approach a limit value. When the curve of the slope is close to zero and tends to be stable, the dynamic development of the slope should be monitored to prevent the sudden instability of the slope.
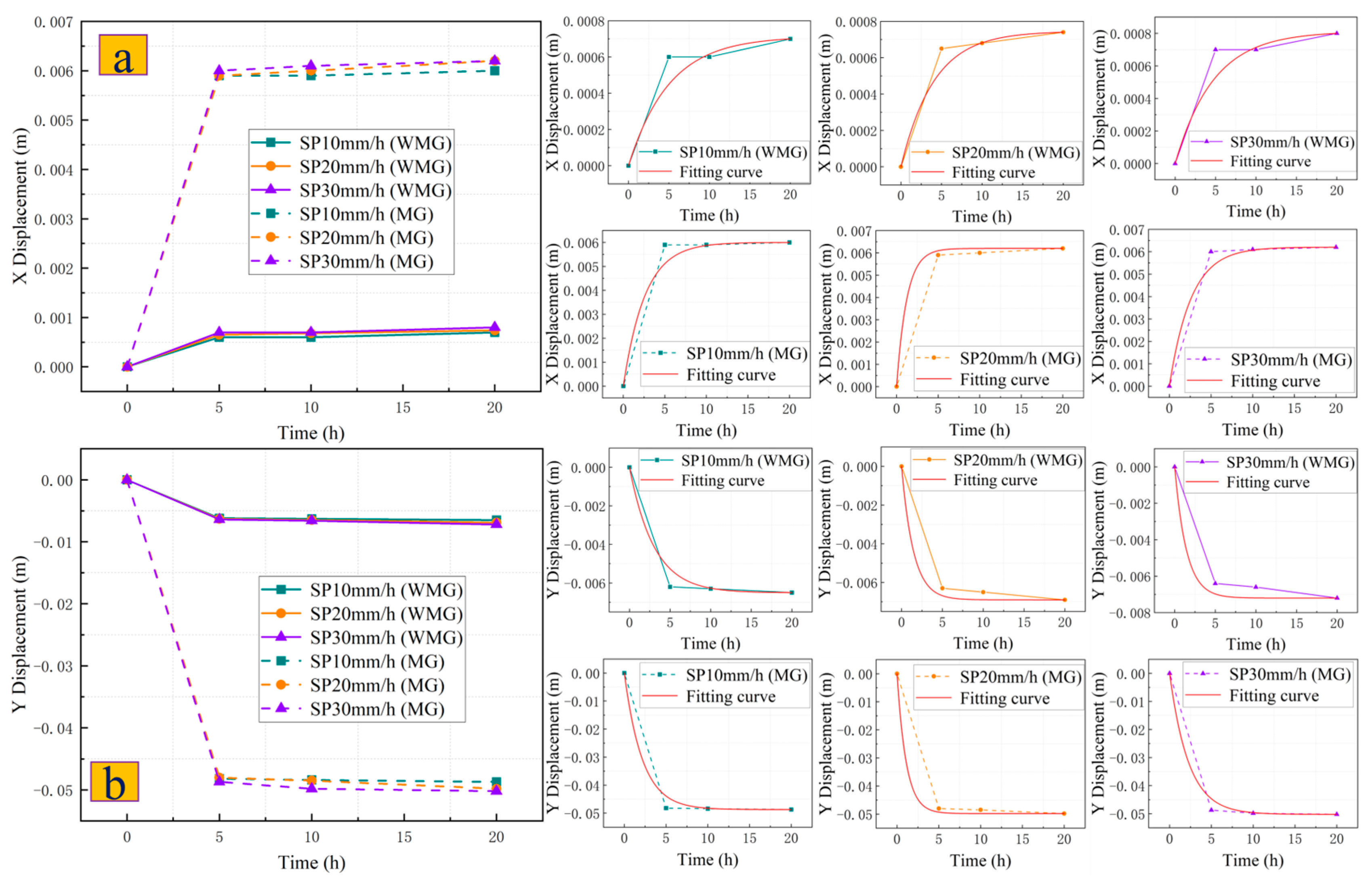
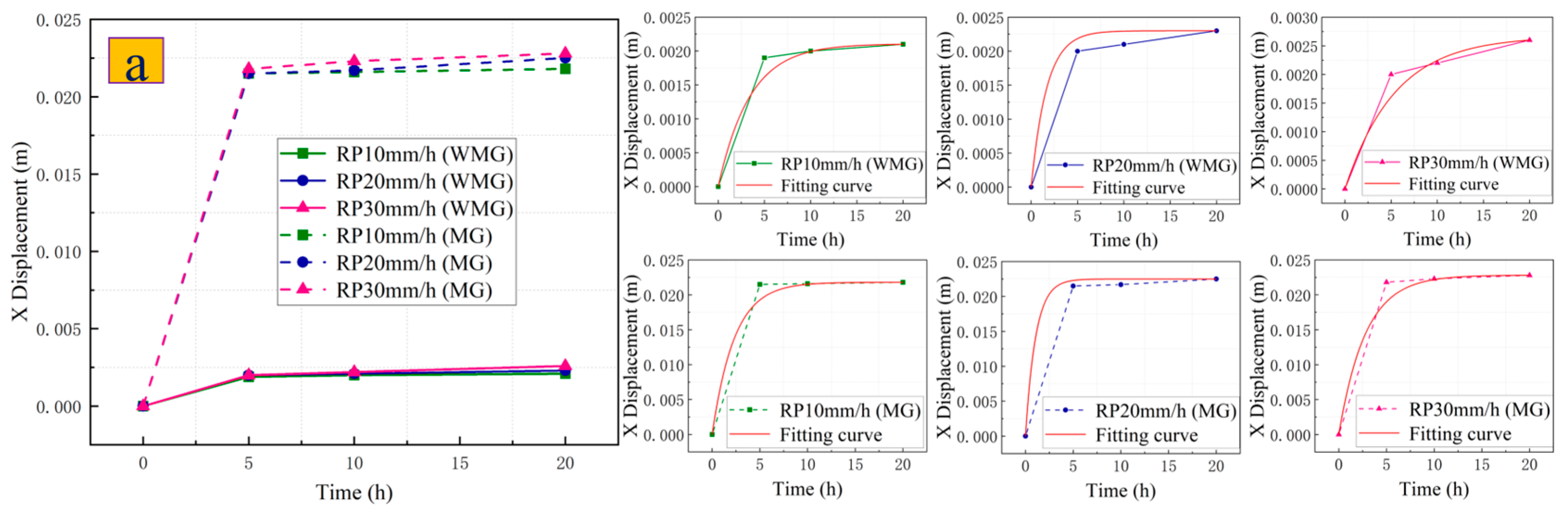
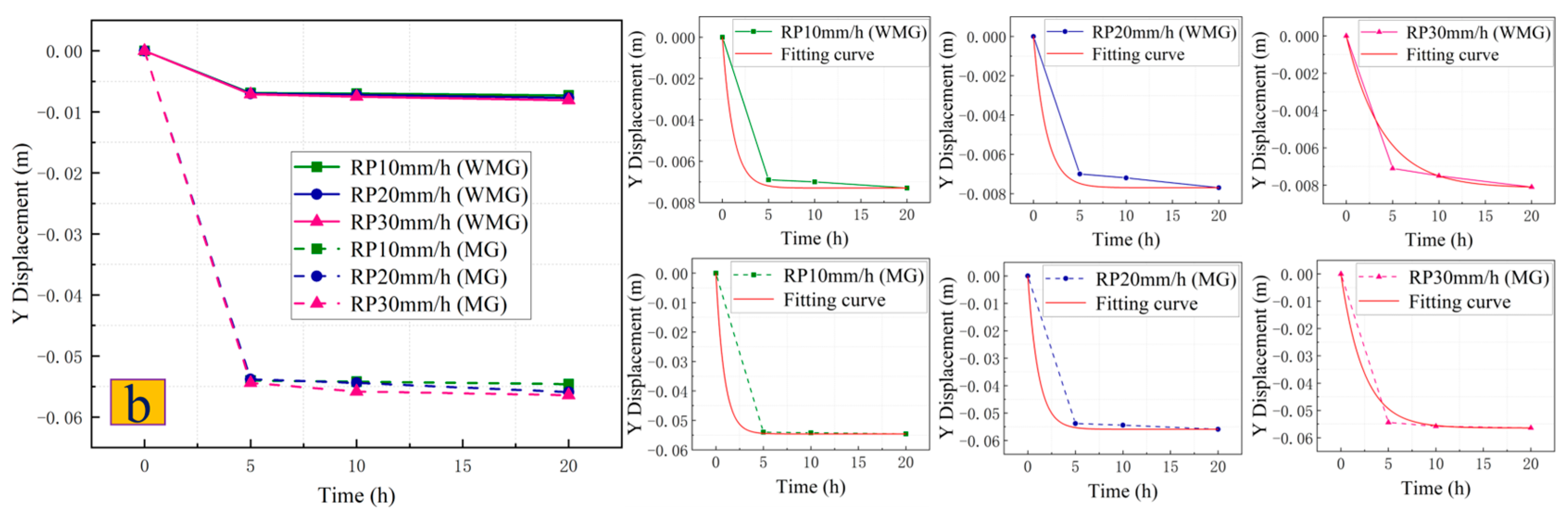
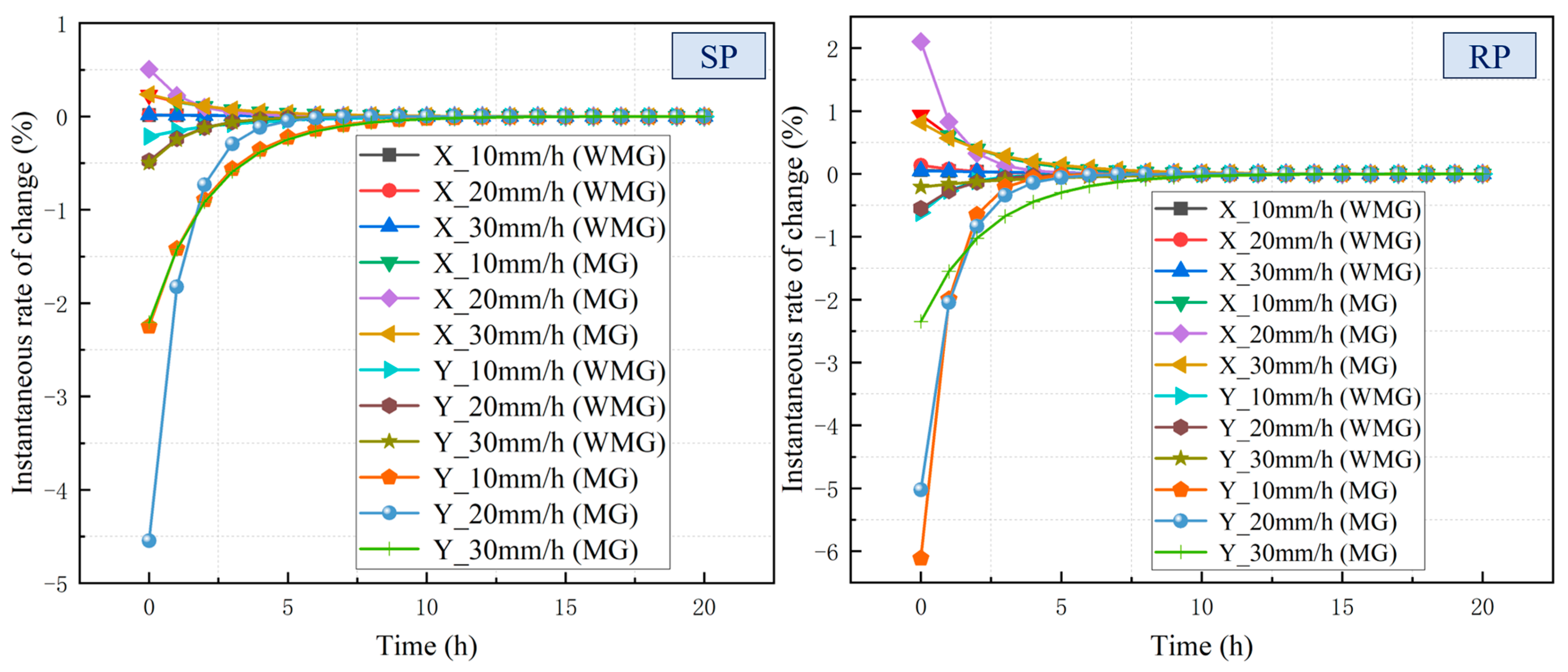
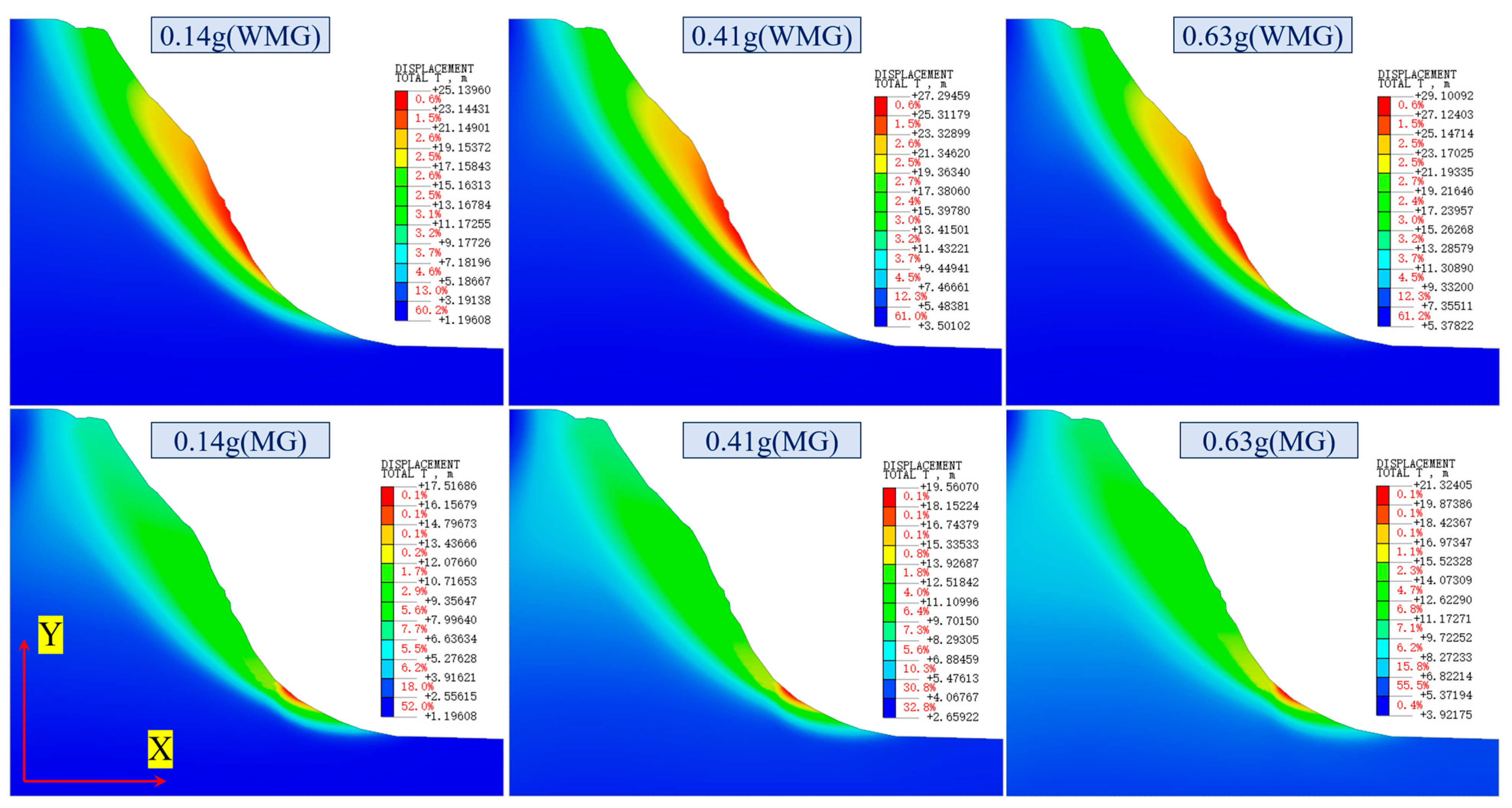
- After adopting the “anchor lattice treatment method”, the potential sliding surface of the Caiyangba landslide is reinforced, which greatly increases the integrity of the Caiyangba landslide, so that the X-direction displacement of the slope is mainly concentrated at the toe of the slope. At the same time, the extrusion phenomenon of the slope has also been greatly alleviated, so that the local uplift of the slope is mainly concentrated at the foot of the slope. Therefore, after adopting the “anchor lattice treatment method”, a gravity retaining wall should also be added to the slope toe to reduce the displacement deformation of the slope toe. And the development law of X-direction displacement and Y-direction displacement of SP and RP conforms to the development law of the exponential function (). The development law of the instantaneous change rate of the SP and RP displacements also conforms to the development law of the expression (). And after adopting the “anchor lattice treatment method”, the Caiyangba landslide can withstand greater displacement deformation and increase the usability of the slope.
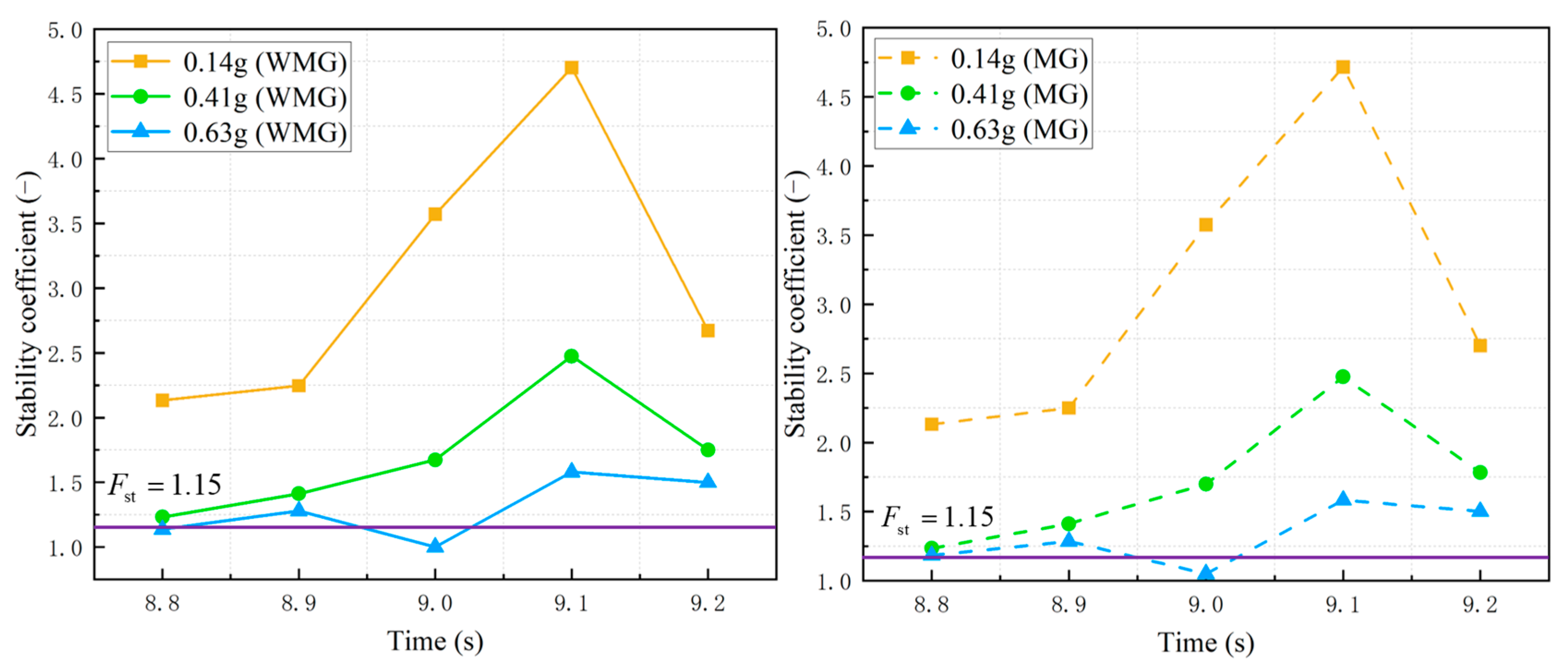
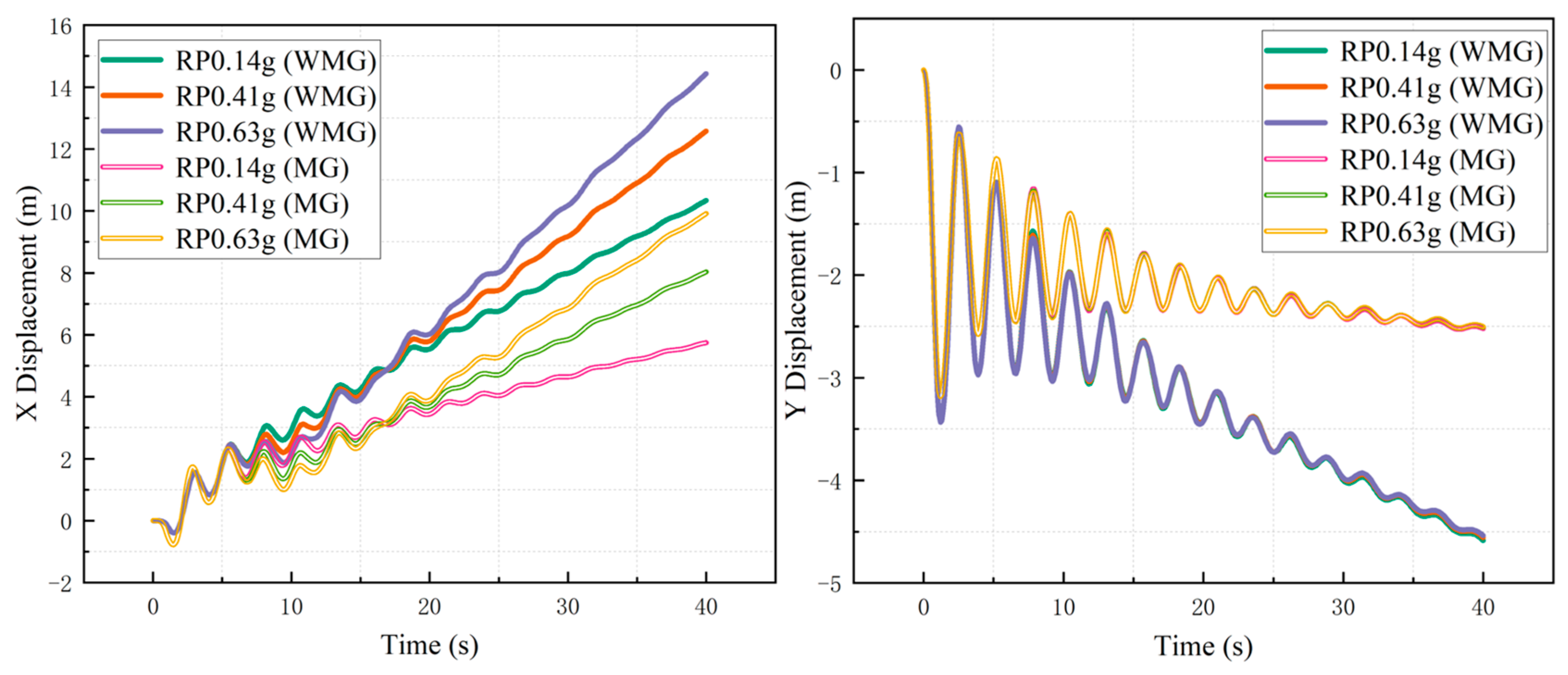
- With the increase in seismic intensity, the probability of instability and failure of the Caiyangba landslide also increases. Under the influence of ground motion, the effect of the “anchor lattice treatment method” on the improvement of the slope stability coefficient is limited. However, the improvement effect of slope stability increases with the increase in seismic intensity. Under the influence of ground motion, the variation in slope stability coefficient with time shows obvious fluctuation. The displacement of SP and RP shows obvious fluctuation with the development of ground motion duration, and its fluctuation law is similar to that of ground motion records. In the WMG condition, the large deformation position of the slope is mainly located at the midsection and toe of the slope. In the MG condition, the large deformation position of the slope is mainly located at the toe of the slope. Therefore, the displacement of the slope toe can be reduced by adding a gravity retaining wall at the slope toe. At the same time, it is also suggested that school buildings near the slope should reduce the load of the building on the foundation by reducing the number of floors, and the number of pile foundations should be increased to enhance the anti-settlement ability of the building. Roads should restrict the passage of heavier vehicles, such as cars. And the road should also be carefully stacked items to reduce the load of the road on the roadbed.
- At present, the treatment of the Caiyangba landslide is in progress. The research results of this paper fill the research gap of slope stability and displacement characteristics of the Caiyangba landslide under rainfall and earthquake conditions. It provides some suggestions and references for the follow-up treatment of the Caiyangba landslide. This paper mainly studies the pebble soil slope in Luding County. In the follow-up study, the Caiyangba landslide will be the core object of the study. The geotechnical mechanism research and verification research of pebble soil slope are carried out by collecting perfect actual data. Improve the treatment of Caiyangba landslide, explore the mechanical mechanism and economic effect of different treatment methods, and provide a perfect theoretical basis for the treatment of pebble soil slope in Luding County.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ministry of Emergency Management of the People’s Republic of China. Available online: https://www.mem.gov.cn/index.shtml (accessed on 30 July 2025).
- Asteris, P.G.; Rizal, F.I.M.; Koopialipoor, M.; Roussis, P.C.; Ferentinou, M.; Armaghani, D.J.; Gordan, B. Slope Stability Classification under Seismic Conditions Using Several Tree-Based Intelligent Techniques. Appl. Sci. 2022, 12, 1753. [Google Scholar] [CrossRef]
- Deng, D.-p. Novel Model for Limit-Equilibrium Analysis of Slope Stability with a Nonlinear Strength Criterion. Int. J. Geomech. 2021, 21, 06021021. [Google Scholar] [CrossRef]
- Shi, C.; Ma, J.; Zhou, Y.; Zhang, Y.; Pian, J. Three-dimensional slope stability analysis method based on perturbation displacement isosurface. Nat. Hazards 2023, 116, 2157–2171. [Google Scholar] [CrossRef]
- Du, C.; Ye, J. Decision-making strategy for slope stability using similarity measures between interval-valued fuzzy credibility sets. Soft Comput. 2022, 26, 5105–5114. [Google Scholar] [CrossRef]
- Xiong, X.; Shi, Z.; Xiong, Y.; Peng, M.; Ma, X.; Zhang, F. Unsaturated slope stability around the Three Gorges Reservoir under various combinations of rainfall and water level fluctuation. Eng. Geol. 2019, 261, 105231. [Google Scholar] [CrossRef]
- Xu, W.; Kang, Y.; Chen, L.; Wang, L.; Qin, C.; Zhang, L.; Liang, D.; Wu, C.; Zhang, W. Dynamic assessment of slope stability based on multi-source monitoring data and ensemble learning approaches: A case study of Jiuxianping landslide. Geol. J. 2023, 58, 2353–2371. [Google Scholar] [CrossRef]
- Jia, L.; Wang, J.; Fang, L.; Cui, Y.; Chen, J.; Cao, L. Study on numerical simulation of groundwater flow field and slope stability in multi-aquifer open pit mine. Sci. Rep. 2024, 14, 31088. [Google Scholar] [CrossRef]
- Liu, W.; Sheng, G.; Kang, X.; Yang, M.; Li, D.; Wu, S. Slope Stability Analysis of Open-Pit Mine Considering Weathering Effects. Appl. Sci. 2024, 14, 8449. [Google Scholar] [CrossRef]
- Mikroutsikos, A.; Theocharis, A.I.; Koukouzas, N.C.; Zevgolis, I.E. Slope stability of deep surface coal mines in the presence of a weak zone. Geomech. Geophys. Geo-Energy Geo-Resour. 2021, 7, 66. [Google Scholar] [CrossRef]
- Huang, S.; Huang, M.; Lyu, Y. An Improved KNN-Based Slope Stability Prediction Model. Adv. Civ. Eng. 2020, 2020, 1–16. [Google Scholar] [CrossRef]
- Zhu, Z.; Wang, D.; Zhang, W. Catastrophic submarine landslides with non-shallow shear band propagation. Comput. Geotech. 2023, 163, 105751. [Google Scholar] [CrossRef]
- Moradi, S.; Heinze, T.; Budler, J.; Gunatilake, T.; Kemna, A.; Huisman, J.A. Combining Site Characterization, Monitoring and Hydromechanical Modeling for Assessing Slope Stability. Land 2021, 10, 423. [Google Scholar] [CrossRef]
- Pei, H.; Zhang, S.; Borana, L.; Zhao, Y.; Yin, J. Slope stability analysis based on real-time displacement measurements. Measurement 2019, 131, 686–693. [Google Scholar] [CrossRef]
- Lamens, P.; Askarinejad, A. Pile driving and submarine slope stability: A hybrid engineering approach. Landslides 2021, 18, 1351–1367. [Google Scholar] [CrossRef]
- Wang, X.; Wu, S.; Han, L.; Wang, J.; Cui, J.; Shen, Y. Slope stability prediction based on GSOEM-SV: A mobile application practicably deploy in engineering verification. Adv. Eng. Softw. 2024, 192. [Google Scholar] [CrossRef]
- Zhang, L.; Guo, D.; Wu, J. Rocky Slope Stability Prediction Model and Its Engineering Application Based on the VIKOR and Binary Semantics. Korean Soc. Civ. Eng. J. Civ. Eng. 2023, 27, 3300–3312. [Google Scholar] [CrossRef]
- Deng, D.-p.; Zhao, L.-h.; Li, L. Limit equilibrium method for slope stability based on assumed stress on slip surface. J. Cent. South Univ. 2016, 23, 2972–2983. [Google Scholar] [CrossRef]
- Zhu, D.Y.; Lee, C.F.; Jiang, H.D. Generalised framework of limit equilibrium methods for slope stability analysis. Geotechnique 2003, 53, 377–395. [Google Scholar] [CrossRef]
- Dyson, A.P.; Griffiths, D.V. An efficient strength reduction method for finite element slope stability analysis. Comput. Geotech. 2024, 174, 106593. [Google Scholar] [CrossRef]
- Sun, W.; Wang, G.; Zhang, L. Slope stability analysis by strength reduction method based on average residual displacement increment criterion. Bull. Eng. Geol. Environ. 2021, 80, 4367–4378. [Google Scholar] [CrossRef]
- Rajan, K.C.; Aryal, M.; Sharma, K.; Bhandary, N.P.; Pokhrel, R.; Acharya, I.P. Development of a framework for the prediction of slope stability using machine learning paradigms. Nat. Hazards 2025, 121, 83–107. [Google Scholar] [CrossRef]
- Yadav, D.K.; Chattopadhyay, S.; Tripathy, D.P.; Mishra, P.; Singh, P. Enhanced slope stability prediction using ensemble machine learning techniques. Sci. Rep. 2025, 15, 7302. [Google Scholar] [CrossRef]
- Baghbani, A.; Faradonbeh, R.S.; Lu, Y.; Soltani, A.; Kiany, K.; Baghbani, H.; Abuel-Naga, H.; Samui, P. Enhancing earth dam slope stability prediction with integrated AI and statistical models. Appl. Soft Comput. 2024, 164, 111999. [Google Scholar] [CrossRef]
- Mao, Y.; Chen, L.; Nanehkaran, Y.A.; Azarafza, M.; Derakhshani, R. Fuzzy-Based Intelligent Model for Rapid Rock Slope Stability Analysis Using Qslope. Water 2023, 15, 2949. [Google Scholar] [CrossRef]
- Cai, J.-S.; Yeh, T.-C.J.; Yan, E.C.; Tang, R.-X.; Hao, Y.-H.; Huang, S.-Y.; Wen, J.-C. Importance of variability in initial soil moisture and rainfalls on slope stability. J. Hydrol. 2019, 571, 265–278. [Google Scholar] [CrossRef]
- Wang, J.; Wang, Z.; Sun, G.; Luo, H. Analysis of three-dimensional slope stability combined with rainfall and earthquake. Nat. Hazards Earth Syst. Sci. 2024, 24, 1741–1756. [Google Scholar] [CrossRef]
- Pan, Y.; Wu, G.; Zhao, Z.; He, L. Analysis of rock slope stability under rainfall conditions considering the water-induced weakening of rock. Comput. Geotech. 2020, 128, 103806. [Google Scholar] [CrossRef]
- Han, T.; Liu, L.; Li, G. The Influence of Horizontal Variability of Hydraulic Conductivity on Slope Stability under Heavy Rainfall. Water 2020, 12, 2567. [Google Scholar] [CrossRef]
- Naidu, S.; Sajinkumar, K.S.; Oommen, T.; Anuja, V.J.; Samuel, R.A.; Muraleedharan, C. Early warning system for shallow landslides using rainfall threshold and slope stability analysis. Geosci. Front. 2018, 9, 1871–1882. [Google Scholar] [CrossRef]
- Gu, X.; Song, L.; Xia, X.; Yu, C. Finite Element Method-Peridynamics Coupled Analysis of Slope Stability Affected by Rainfall Erosion. Water 2024, 16, 2210. [Google Scholar] [CrossRef]
- Chen, B.; Shui, W.; Liu, Y.; Deng, R. Analysis of Slope Stability with Different Vegetation Types under the Influence of Rainfall. Forests 2023, 14, 1865. [Google Scholar] [CrossRef]
- Zhou, L.; Su, L.; Wang, Z.; Zhu, D.; Shi, W.; Ling, X. Slope Stability and Effectiveness of Treatment Measures during Earthquake. Sustainability 2023, 15, 5309. [Google Scholar] [CrossRef]
- Ma, Z.; Liao, H.; Dang, F.; Cheng, Y. Seismic slope stability and failure process analysis using explicit finite element method. Bull. Eng. Geol. Environ. 2021, 80, 1287–1301. [Google Scholar] [CrossRef]
- Ma, N.; Zhang, Y.; Yao, Z. Slope stability prediction under seismic loading based on the EO-LightGBM algorithm. Front. Earth Sci. 2025, 13, 1591219. [Google Scholar] [CrossRef]
- Xu, J.-s.; Yang, X.-l. Effects of Seismic Force and Pore Water Pressure on Three Dimensional Slope Stability in Nonhomogeneous and Anisotropic Soil. Korean Soc. Civ. Eng. J. Civ. Eng. 2018, 22, 1720–1729. [Google Scholar] [CrossRef]
- Zhang, W.-g.; Meng, F.-s.; Chen, F.-y.; Liu, H.-l. Effects of spatial variability of weak layer and seismic randomness on rock slope stability and reliability analysis. Soil Dyn. Earthq. Eng. 2021, 146, 106735. [Google Scholar] [CrossRef]
- Zhou, J.; Qin, C. Finite-element upper-bound analysis of seismic slope stability considering pseudo-dynamic approach. Comput. Geotech. 2020, 122, 103530. [Google Scholar] [CrossRef]
- Chen, C.-Y.; Chen, H.-W.; Wu, W.-C. Numerical modeling of interactions of rainfall and earthquakes on slope stability analysis. Environ. Earth Sci. 2021, 80, 524. [Google Scholar] [CrossRef]
- GB/T 28592-2012; Grade of Precipitation. Standards Press of China: Beijing, China, 2012.
- China Meteorological Administration. Available online: https://www.cma.gov.cn/ (accessed on 20 July 2025).
- Lu Ding Xian Zhi. Available online: https://www.scfzg.cn/#/ (accessed on 20 July 2025).
- IRIS. Available online: https://ds.iris.edu/wilber3/find_stations/11595065 (accessed on 20 July 2025).
- GB/T 17742-2020; The Chinese Seismic Intensity Scale. China Earthquake Administration: Beijing, China, 2020.
- GB 50011-2010; Code for Seismic Design of Buildings. China Architecture & Building Press: Beijing, China, 2010.
- GB/T 38509-2020; Code for the Design of Landslide Stabilization. Standards Press of China: Beijing, China, 2020.
- GB 50009-2012; Load Code for the Design of Building Structures. China Architecture & Building Press: Beijing, China, 2012.
- JTG B01-2014; Technical Standard of Highway Engineering. People’s Communications Publishing House Co., Ltd.: Beijing, China, 2014.
- Kadlícek, T.; Masín, D. The Strength Reduction Method in Clay Hypoplasticity. Comput. Geotech. 2020, 126, 103687. [Google Scholar] [CrossRef]
- GB 50330-2013; Technical Code for Building Slope Engineering. China Architecture & Building Press: Beijing, China, 2013.

| Magnitude | 2 | 3 | 4 | 5 | 6 | 7 | 8 | >8 |
| Epicentral intensity | 1~2 | 3 | 4~5 | 6~7 | 7~8 | 9~10 | 11 | 12 |
| Seismic Intensity | Frequent Earth-quake | Design Basis Earthquake | Maximum Considered Earthquake |
|---|---|---|---|
| 9 degree | 140 cm/s2 | 400 cm/s2 | 620 cm/s2 |
| 0.14 g | 0.41 g | 0.63 g |
| Particle Size (mm) | Proportion (%) | Average Value | ||
|---|---|---|---|---|
| Sample 1 | Sample 2 | Sample 3 | ||
| >200 | 37.42 | 28.83 | 37.50 | 34.58 |
| 200~60 | 31.25 | 29.62 | 26.27 | 29.05 |
| 60~40 | 8.58 | 12.88 | 11.08 | 10.85 |
| 40~20 | 4.09 | 6.20 | 5.62 | 5.30 |
| 20~10 | 2.04 | 4.41 | 3.45 | 3.30 |
| 10~5 | 2.37 | 3.10 | 2.52 | 2.66 |
| 5~2 | 5.70 | 4.89 | 3.02 | 4.54 |
| 2~1 | 2.85 | 3.86 | 3.80 | 3.50 |
| 1~0.5 | 1.64 | 2.23 | 1.74 | 1.87 |
| 0.5~0.25 | 1.97 | 1.47 | 2.91 | 2.12 |
| 0.25~0.075 | 1.31 | 1.55 | 1.32 | 1.39 |
| <0.075 | 0.77 | 0.95 | 0.77 | 0.83 |
| (mm) | 178.25 | 135.59 | 182.46 | 165.43 |
| (mm) | 57.66 | 43.76 | 49.78 | 50.40 |
| (mm) | 2.59 | 1.95 | 1.98 | 2.17 |
| Uniformity coefficient | 68.82 | 69.53 | 92.15 | 76.83 |
| Curvature coefficient | 7.20 | 7.24 | 6.86 | 7.10 |
| Soil | Elastic Modulus (MPa) | Poisson Ratio | Volume Weight (kN/m3) | Saturated Volume Weight (kN/m3) | Initial Void Ratio | Permeability Coefficient (m/s) | Cohesion (kPa) | Internal Friction Angle (°) |
|---|---|---|---|---|---|---|---|---|
| pebble soil | 90.60 | 0.28 | 19.91 | 20.31 | 0.50 | 0.000205 | 36.00 | 38.00 |
| Condition | Rainfall (mm/h) | Rainfall Duration (h) |
|---|---|---|
| JY1-1 | 10 | 5 |
| JY1-2 | 10 | 10 |
| JY1-3 | 10 | 20 |
| JY2-1 | 20 | 5 |
| JY2-2 | 20 | 10 |
| JY2-3 | 20 | 20 |
| JY3-1 | 30 | 5 |
| JY3-2 | 30 | 10 |
| JY3-3 | 30 | 20 |
| Condition | Seismic Intensity | PGA (g) | Direction |
|---|---|---|---|
| DZ-1 | 9-degree frequent earthquake | 0.14 | X |
| DZ-2 | 9-degree design basis earthquake | 0.41 | X |
| DZ-3 | 9-degree maximum considered earthquake | 0.63 | X |
| Condition | |
|---|---|
| Weight | 1.30 |
| Weight + Rainfall | 1.25 |
| Weight + Earthquake | 1.15 |
| Stability coefficient | ||||
| State | Instability | Under stability | Basic stability | Stability |
| Rainfall | Working Condition | 0 (h) | 5 (h) | 10 (h) | 20 (h) |
|---|---|---|---|---|---|
| 10 mm/h | WMG () | 1.2563 | 1.2313 | 1.2219 | 1.2188 |
| MG () | 1.3281 | 1.2594 | 1.2481 | 1.2375 | |
| MG ()-WMG () | 0.0718 | 0.0281 | 0.0262 | 0.0187 | |
| 20 mm/h | WMG () | 1.2563 | 1.2273 | 1.2203 | 1.2172 |
| MG () | 1.3281 | 1.2551 | 1.2406 | 1.2289 | |
| MG ()-WMG () | 0.0718 | 0.0278 | 0.0203 | 0.0117 | |
| 30 mm/h | WMG () | 1.2563 | 1.2219 | 1.2133 | 1.2094 |
| MG () | 1.3281 | 1.2473 | 1.2313 | 1.2148 | |
| MG ()-WMG () | 0.0718 | 0.0254 | 0.0180 | 0.0054 |
| Condition | (Coefficient of Determination) | |||
|---|---|---|---|---|
| 10 mm/h (WMG) | 1.21836 | 0.03794 | 4.49540 | 0.99939 |
| 20 mm/h (WMG) | 1.21684 | 0.03946 | 4.26761 | 0.99663 |
| 30 mm/h (WMG) | 1.20892 | 0.04738 | 4.35506 | 0.99680 |
| 10 mm/h (MG) | 1.23597 | 0.09213 | 4.87892 | 0.98147 |
| 20 mm/h (MG) | 1.22712 | 0.10098 | 4.95242 | 0.98698 |
| 30 mm/h (MG) | 1.21178 | 0.11632 | 5.47822 | 0.98345 |
| Condition | (Coefficient of Determination) | |||
|---|---|---|---|---|
| SP10 mm/h (WMG) | 0.00071 | −0.00071 | 5.03037 | 0.92540 |
| SP20 mm/h (WMG) | 0.00075 | −0.00075 | 4.06402 | 0.95853 |
| SP30 mm/h (WMG) | 0.00081 | −0.00081 | 4.73654 | 0.92855 |
| SP10 mm/h (MG) | 0.00600 | −0.00600 | 2.62017 | 0.97648 |
| SP20 mm/h (MG) | 0.00620 | −0.00620 | 1.22623 | 0.99717 |
| SP30 mm/h (MG) | 0.00620 | −0.00620 | 2.61097 | 0.98186 |
| RP10 mm/h (WMG) | 0.00211 | −0.00211 | 3.43634 | 0.97302 |
| RP20 mm/h (WMG) | 0.00230 | −0.00230 | 1.66904 | 0.97920 |
| RP30 mm/h (WMG) | 0.00267 | −0.00267 | 5.42868 | 0.96094 |
| RP10 mm/h (MG) | 0.02180 | −0.02180 | 2.32747 | 0.98568 |
| RP20 mm/h (MG) | 0.02250 | −0.02250 | 1.06895 | 0.99650 |
| RP30 mm/h (MG) | 0.02282 | −0.02282 | 2.79754 | 0.97894 |
| Condition | (Coefficient of Determination) | |||
|---|---|---|---|---|
| SP10 mm/h (WMG) | −0.00651 | 0.00651 | 3.02874 | 0.97063 |
| SP20 mm/h (WMG) | −0.00690 | 0.00690 | 1.44928 | 0.99079 |
| SP30 mm/h (WMG) | −0.00720 | 0.00720 | 1.44270 | 0.98014 |
| SP10 mm/h (MG) | −0.04870 | 0.04870 | 2.16545 | 0.98930 |
| SP20 mm/h (MG) | −0.04980 | 0.04980 | 1.09545 | 0.99814 |
| SP30 mm/h (MG) | −0.05021 | 0.05021 | 2.27475 | 0.99101 |
| RP10 mm/h (WMG) | −0.00730 | 0.00730 | 1.18089 | 0.99532 |
| RP20 mm/h (WMG) | −0.00770 | 0.00770 | 1.40633 | 0.98821 |
| RP30 mm/h (WMG) | −0.00815 | 0.00815 | 3.95061 | 0.96417 |
| RP10 mm/h (MG) | −0.05460 | 0.05460 | 0.89311 | 0.99986 |
| RP20 mm/h (MG) | −0.05590 | 0.05590 | 1.11208 | 0.99804 |
| RP30 mm/h (MG) | −0.05641 | 0.05641 | 2.40369 | 0.98903 |
| Time (s) | ||||||
|---|---|---|---|---|---|---|
| 0.14 g (WMG) | 0.14 g (MG) | 0.41 g (WMG) | 0.41 g (MG) | 0.63 g (WMG) | 0.63 g (MG) | |
| 8.8 | 2.1344 | 2.1313 | 1.2328 | 1.2344 | 1.1375 | 1.1844 |
| 8.9 | 2.2457 | 2.2500 | 1.4129 | 1.4125 | 1.2793 | 1.2856 |
| 9.0 | 3.5707 | 3.5750 | 1.6738 | 1.7000 | 1.0000 | 1.0500 |
| 9.1 | 4.7035 | 4.7156 | 2.4750 | 2.4750 | 1.5797 | 1.5828 |
| 9.2 | 2.6719 | 2.7000 | 1.7504 | 1.7836 | 1.4992 | 1.5012 |
| Average value | 2.7638 | 2.7833 | 1.6335 | 1.6556 | 1.2920 | 1.3220 |
| MG-WMG | 0.0195 | 0.0221 | 0.0300 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, B.; Liu, T.; Li, Y. Stability Analysis and Treatment of Pebble Soil Slopes Under Rainfall and Earthquake Conditions. Sustainability 2025, 17, 10754. https://doi.org/10.3390/su172310754
Wang B, Liu T, Li Y. Stability Analysis and Treatment of Pebble Soil Slopes Under Rainfall and Earthquake Conditions. Sustainability. 2025; 17(23):10754. https://doi.org/10.3390/su172310754
Chicago/Turabian StyleWang, Bing, Taian Liu, and Yuanyi Li. 2025. "Stability Analysis and Treatment of Pebble Soil Slopes Under Rainfall and Earthquake Conditions" Sustainability 17, no. 23: 10754. https://doi.org/10.3390/su172310754
APA StyleWang, B., Liu, T., & Li, Y. (2025). Stability Analysis and Treatment of Pebble Soil Slopes Under Rainfall and Earthquake Conditions. Sustainability, 17(23), 10754. https://doi.org/10.3390/su172310754






