Data-Driven Coordinated Voltage Control Strategy for Distribution Networks with High Proportion of Renewable Energy Based on Voltage–Power Sensitivity
Abstract
:1. Introduction
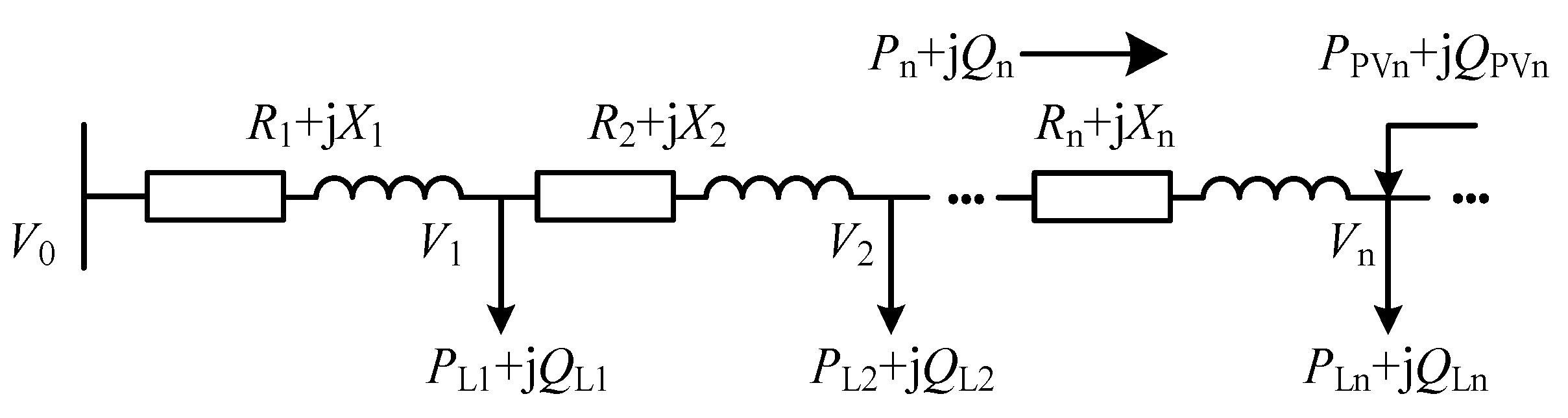
2. Voltage–Power Sensitivity
2.1. Traditional Algorithm
2.1.1. Inverse of Power Flow Calculation
2.1.2. Approximate Sensitivity Calculation
2.2. Artificial Intelligence Algorithm Prediction
- (1)
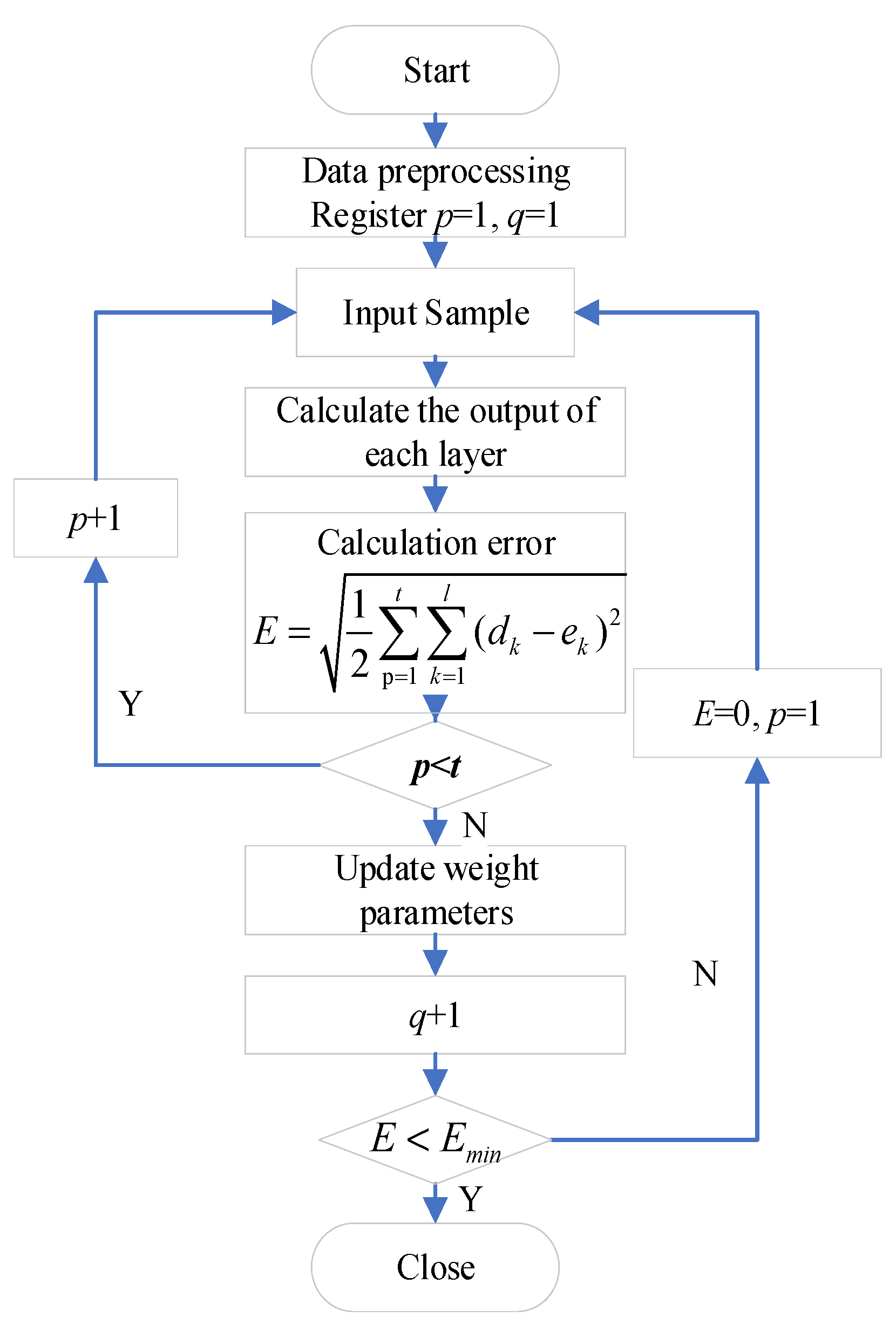
- A data set comprising input features and target values is constructed, and normalization processing is performed.
- (2)
- The BP neural network regression prediction model is then established, requiring the selection of the appropriate number of hidden layers, network weights, and bias parameters. Multiple experiments were conducted using Bayesian optimization [22], and the optimal parameters and structure of the BP neural network were determined, as shown in Table 1: the number of iterations is 1000, the optimizer selects Tainlm, the learning rate is 0.001, and the dynamic increase and decrease factors mu_dec = 0.1 and mu_inc = 10 and the maximum allowable value of the learning rate mu_max = 10 are set.
- (3)
- The mean square error is calculated to ascertain the extent of the prediction error made by the network.
- (4)
- The gradient of each weight bias parameter to the loss is calculated, and the corresponding parameter is updated.
- (5)
- Steps 3 to 4 are repeated until the loss function converges.
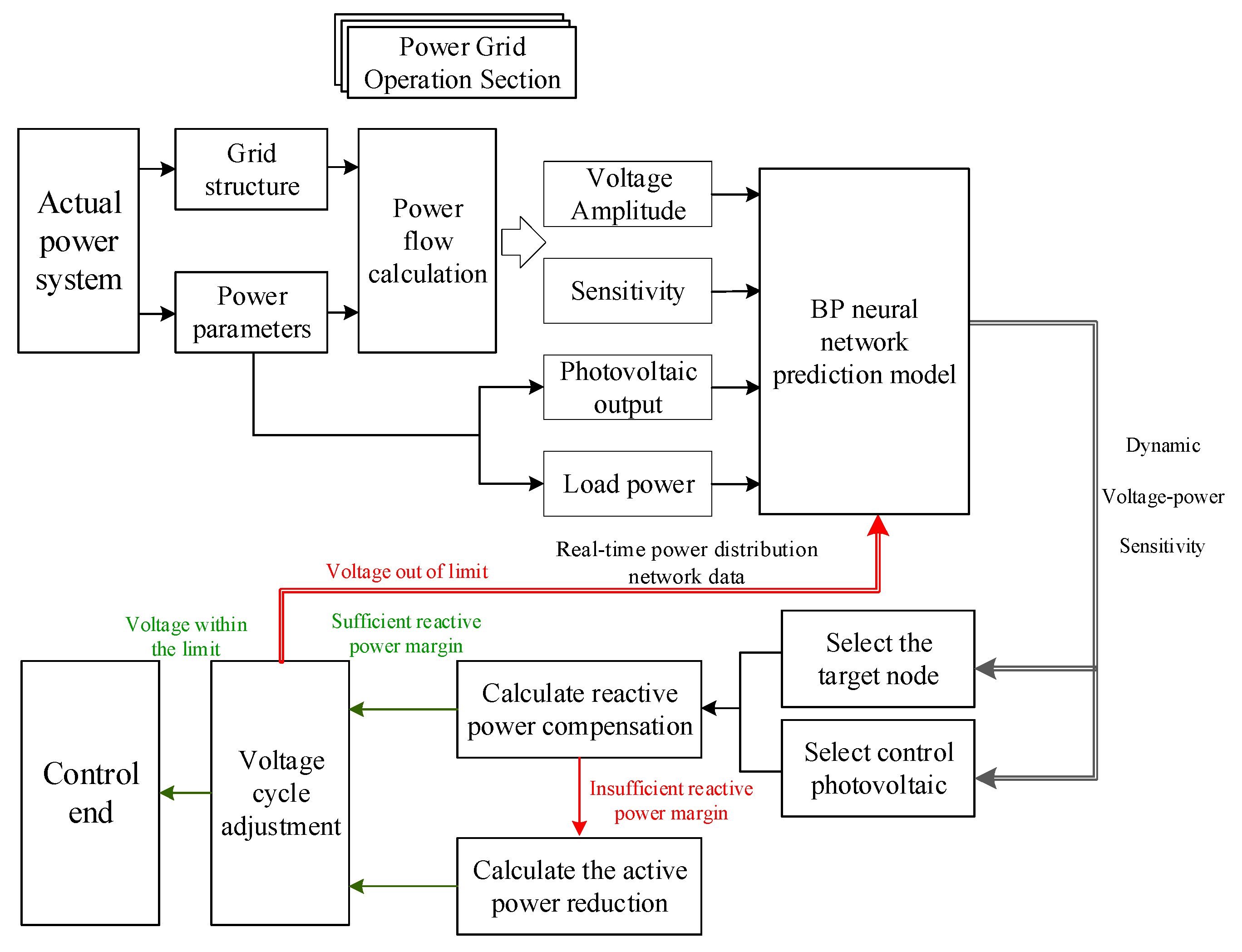
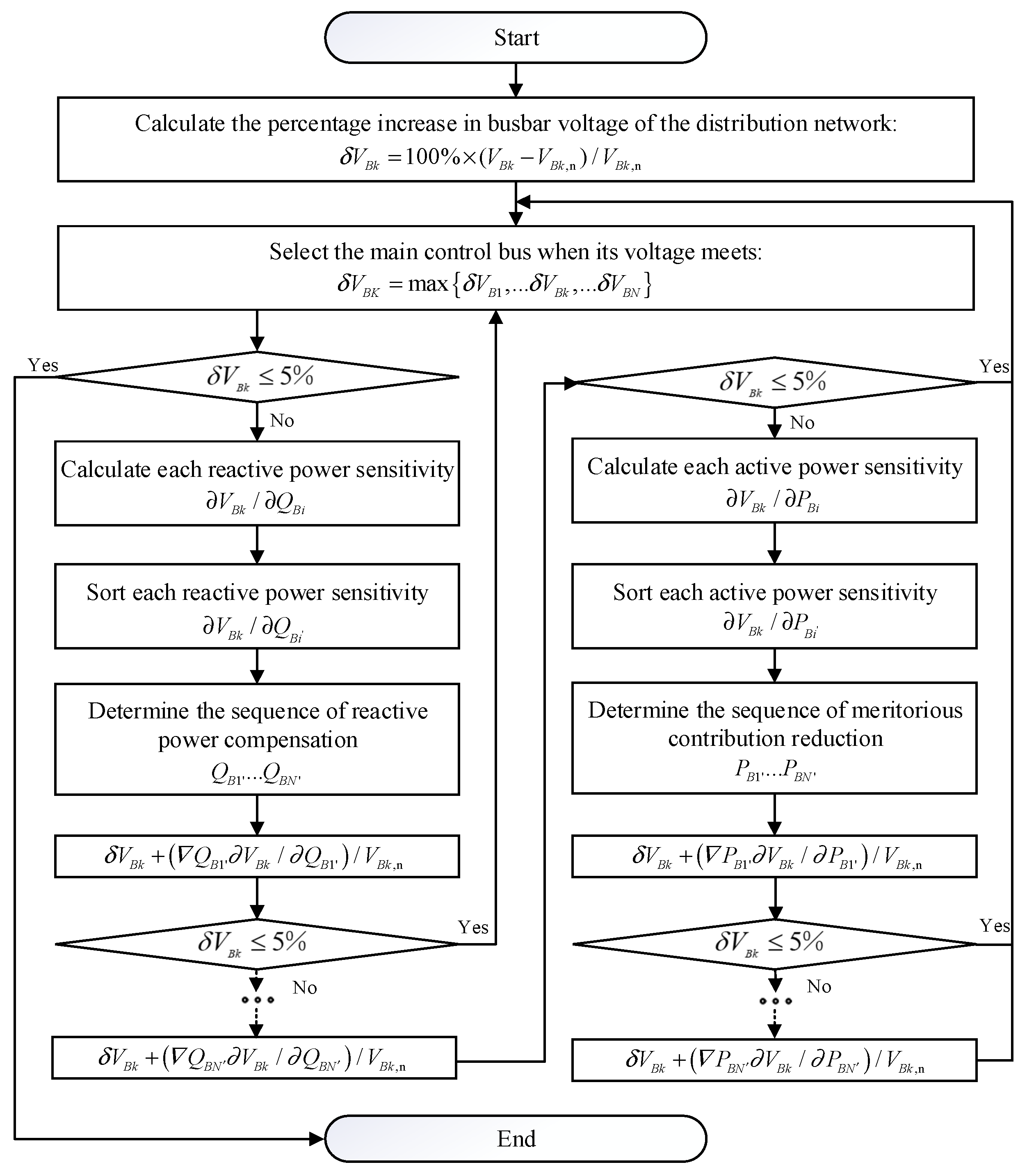
3. A Strategy for the Voltage Coordination Control
- (1)
- The target node should be selected. The distribution network’s node voltage is evaluated to identify the node with the greatest degree of exceedance as the target.
- (2)
- The PV power supply should be selected and controlled. Dependent on the above voltage–power sensitivity, the PV power supply with the largest value is preferentially regulated.
- (3)
- The power adjustment is calculated. The theoretical output power is calculated using the voltage–power sensitivity and voltage over-limit, and the actual output power is compared with the current power margin of the PV power supply.
- (4)
- Cycle control is implemented. The reactive power compensation and active power reduction of each node are performed successively, and the node voltage is iteratively regulated until the voltage of all nodes returns to the normal state.
3.1. Reactive Power Compensation
3.2. Active Power Reduction
- (1)
- When the power factor of the PV power supply is higher than the threshold, the power of the PV power supply is adjusted in turn according to the relationship between the active power reduction and the corresponding power factor, and the reactive power margin is released to participate in voltage regulation.
- (2)
- When the power factor of the PV power supply falls below the threshold, the maximum reduction is 5% of the active power output of the current PV power supply, with voltage regulation implemented sequentially.
4. Numerical Simulation Result
4.1. IEEE 33-Node Distribution System
4.2. IEEE 141-Node Distribution System
5. Conclusions
- (1)
- A BP neural network regression prediction model for voltage–power sensitivity was established, achieving a nonlinear and rapid mapping from power/node voltage to node voltage sensitivity.
- (2)
- The voltage regulation principle of the distribution network based on the descending order arrangement of the voltage–power sensitivity of the target node was constructed, and a two-stage voltage regulation mode of the distribution network combining reactive power compensation and active power reduction was proposed, which overcame the shortcomings of the traditional voltage regulation methods of the distribution network in terms of regulation speed and accuracy.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| PV | Photovoltaic |
| HEM | Holomorphic Embedding Metho |
| GRNN | Generalized Regression Neural Network |
| SVM | Support vector machine |
| ADN | Active distribution network |
References
- Zhao, Y.; Zhang, G.; Hu, W.; Huang, Q.; Chen, Z.; Blaabjerg, F. Meta-Learning Based Voltage Control for Renewable Energy Integrated Active Distribution Network Against Topology Change. IEEE Trans. Power Syst. 2023, 38, 5937–5940. [Google Scholar] [CrossRef]
- Pierrou, G.; Wang, X. An Online Network Model-Free Wide-Area Voltage Control Method Using PMUs. IEEE Trans. Power Syst. 2023, 36, 4672–4682. [Google Scholar] [CrossRef]
- Pappalardo, D.; Calderaro, V.; Galdi, V. Microgrids-Based Approach for Voltage Control in Distribution Systems by an Efficient Sensitivity Analysis Method. IEEE Syst. J. 2022, 16, 4210–4221. [Google Scholar] [CrossRef]
- Gao, H.; Chen, J.; Diao, R.; Zhang, J. A HEM-Based Sensitivity Analysis Method for Fast Voltage Stability Assessment in Distribution Power Network. IEEE Access 2021, 9, 13344–13353. [Google Scholar] [CrossRef]
- Nazir, F.U.; Pal, B.C.; Jabr, R.A. Affinely Adjustable Robust Volt/Var Control Without. Centralized Computations. IEEE Trans. Power Syst. 2023, 38, 656–667. [Google Scholar] [CrossRef]
- Banfield, B.; Robinson, D.A.; Agalgaonkar, A.P. Distributed MPC of Residential Energy Storage for Voltage Regulation and Peak Shaving Along Radial Distribution Feeders. IEEE Trans. Energy Convers. 2021, 36, 1413–1424. [Google Scholar] [CrossRef]
- Li, S.; Wu, W. Data-Driven Linear-Time-Variant MPC Method for Voltage and Power Regulation in Active Distribution Networks. IEEE Trans. Smart Grid. 2024, 15, 2625–2638. [Google Scholar] [CrossRef]
- Cao, D.; Zhao, J.; Hu, W.; Ding, F.; Huang, Q.; Chen, Z.; Blaabjerg, F. Data-Driven Multi-Agent Deep Reinforcement Learning for Distribution System Decentralized Voltage Control With High Penetration of PVs. IEEE Trans. Smart Grid 2021, 12, 4137–4150. [Google Scholar] [CrossRef]
- Bassett, D.L. Update of the status of IEEE 1547.8, expanding on IEEE Standard 1547. In Proceedings of the Transmission & Distribution Conference & Exposition, Orlando, FL, USA, 7–10 May 2012. [Google Scholar] [CrossRef]
- Shailendra, S.; Vijay, B.P.; Amit, K.T.; Singh, S.P.; Hoay, B.G. Profit Maximization in ADN Through Voltage Control and DR Management With Networked Community Micro-Grids. IEEE Trans. Ind. Appl. 2023, 59, 2706–2719. [Google Scholar]
- Pierrou, G.; Lai, H.; Hug, G.; Wang, X. A Decentralized Wide-Area Voltage Control Scheme for Coordinated Secondary Voltage Regulation Using PMUs. IEEE Trans. Power Syst. 2024, 39, 7153–7165. [Google Scholar] [CrossRef]
- Fazio, A.; Risi, C.; Russo, M.; Santis, M. Coordinated Optimization for Zone-Based Voltage Control in Distribution Grids. IEEE Trans. Ind. Appl. 2022, 58, 173–184. [Google Scholar] [CrossRef]
- Zhang, Z.; Mishra, Y.; Dou, C.; Yue, D.; Zhang, B.; Tian, Y.-C. Steady-State Voltage Regulation with Reduced Photovoltaic Power Curtailment. IEEE J. Photovolt. 2020, 10, 1853–1863. [Google Scholar] [CrossRef]
- Pacheco, C.; David, S.; Mayo, M.; Jonathan, C.; Escobar, G.; Guillen, D.; Soto, J. Decentralised Data-Driven Voltage Control for Clustered PV Inverters with Local Deviation Priority. IEEE Access 2025, 13, 67136–67148. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, J.; Zhu, X.; Li, X.; Guo, L.; Bai, L.; Wang, C. Model-Free Distributed Voltage Control for Distribution Networks Based on State Space Mapping and Super-Linear Feedback. IEEE Trans. Power Syst. 2024, 39, 6290–6304. [Google Scholar] [CrossRef]
- Sun, X.; Qiu, J.; Tao, Y.; Zhao, J. Data-Driven Combined Central and Distributed Volt/Var Control in Active Distribution Networks. IEEE Trans. Smart Grid 2022, 14, 1855–1867. [Google Scholar] [CrossRef]
- Feng, X.; Peng, Z.; Chen, Q.; Chen, Y.; Xie, H.; Liang, S. Data-Physical Hybrid-Driven Adaptive Voltage Control of Active Distribution Network. Proc. CSU-EPSA 2023, 35, 80–88. [Google Scholar]
- Zhang B, K.; Kong, L.; Zhang, Q.; Zhang, Y.; Zhao, C. Coordinated Power Control Strategy of PV Inverters and VSCs in DC-Interconnected Low-Voltage Distribution Networks. IEEE Trans. Ind. Appl. 2025, 1–13. [Google Scholar] [CrossRef]
- Li, R.; Wong, P.; Wang, K.; Li, B.; Yuan, F. Power Quality Enhancement and Engineering Application with High Permeability Distributed Photovoltaic Access to Low-Voltage Distribution Networks in Australia. Prot. Control Mod. Power Syst. 2020, 5, 18. [Google Scholar] [CrossRef]
- Harold, R.C.; Adrian, G.; Eun-Jin, K.; Francisco, G.; Álvaro, O.; Wilmar, M. Information Length Quantification and Forecasting of Power Systems Kinetic Energy. IEEE Trans. Power Syst. 2022, 37, 4473–4484. [Google Scholar]
- Wei, X.; Zhang, X.; Wang, G.; Hu, Z.; Zhu, Z.; Chan, K. Online Voltage Control Strategy: Multi-Mode Based Data-Driven Approach for Active Distribution Networks. IEEE Trans. Ind. Appl. 2025, 61, 1569–1580. [Google Scholar] [CrossRef]
- Masum, M.; Shahriar, H.; Haddad, H.; Faruk, M.J.H.; Valero, M.; Khan, M.A.; Rahman, M.A.; Adnan, M.I.; Cuzzocrea, A.; Wu, F. Bayesian Hyperparameter Optimization for Deep Neural Network-Based Network Intrusion Detection. In Proceedings of the 2021 IEEE International Conference on Big Data, Orlando, FL, USA, 15–18 December 2021; pp. 5413–5419. [Google Scholar]
- Huang, W.; Zhao, C. Deep-Learning-Aided Voltage-Stability-Enhancing Stochastic Distribution Network Reconfiguration. IEEE Trans. Power Syst. 2023, 39, 2827–2836. [Google Scholar] [CrossRef]
- Sun, X.; Qiu, J.; Zhao, J. Real-Time Volt/Var Control in Active Distribution Networks With Data-Driven Partition Method. IEEE Trans. Power Syst. 2021, 36, 2448–2461. [Google Scholar] [CrossRef]
- Song, Y.; Zheng, Y.; Liu, T.; Lei, S.; Hillm, D.J. A New Formulation of Distribution Network Reconfiguration for Reducing the Voltage Volatility Induced by Distributed Generation. IEEE Trans. Power Syst. 2020, 35, 496–507. [Google Scholar] [CrossRef]
- Tang, H.; He, Y.; Wang, X.; Zheng, H.; Xu, B.; Zhao, W.; Wu, H. Two-Stage Multi-Mode Voltage Control for Distribution Networks: A Deep Reinforcement Learning Approach Based on Multiple Intelligences. IEEE Trans. Ind. Appl. 2024, 60, 5681–5691. [Google Scholar] [CrossRef]
- Huo, Y.; Li, P.; Ji, H.; Yu, H.; Yan, J.; Wu, J.; Wang, C. Data-Driven Coordinated Voltage Control Method of Distribution Networks With High DG Penetration. IEEE Trans. Power Syst. 2023, 38, 1543–1557. [Google Scholar] [CrossRef]
- ANSI C84.1-2020; American National Standard for Electric Power Systems and Equipment-Voltage Ratings (60 Hz). American National Standards Institute: Washington, DC, USA, 2020.
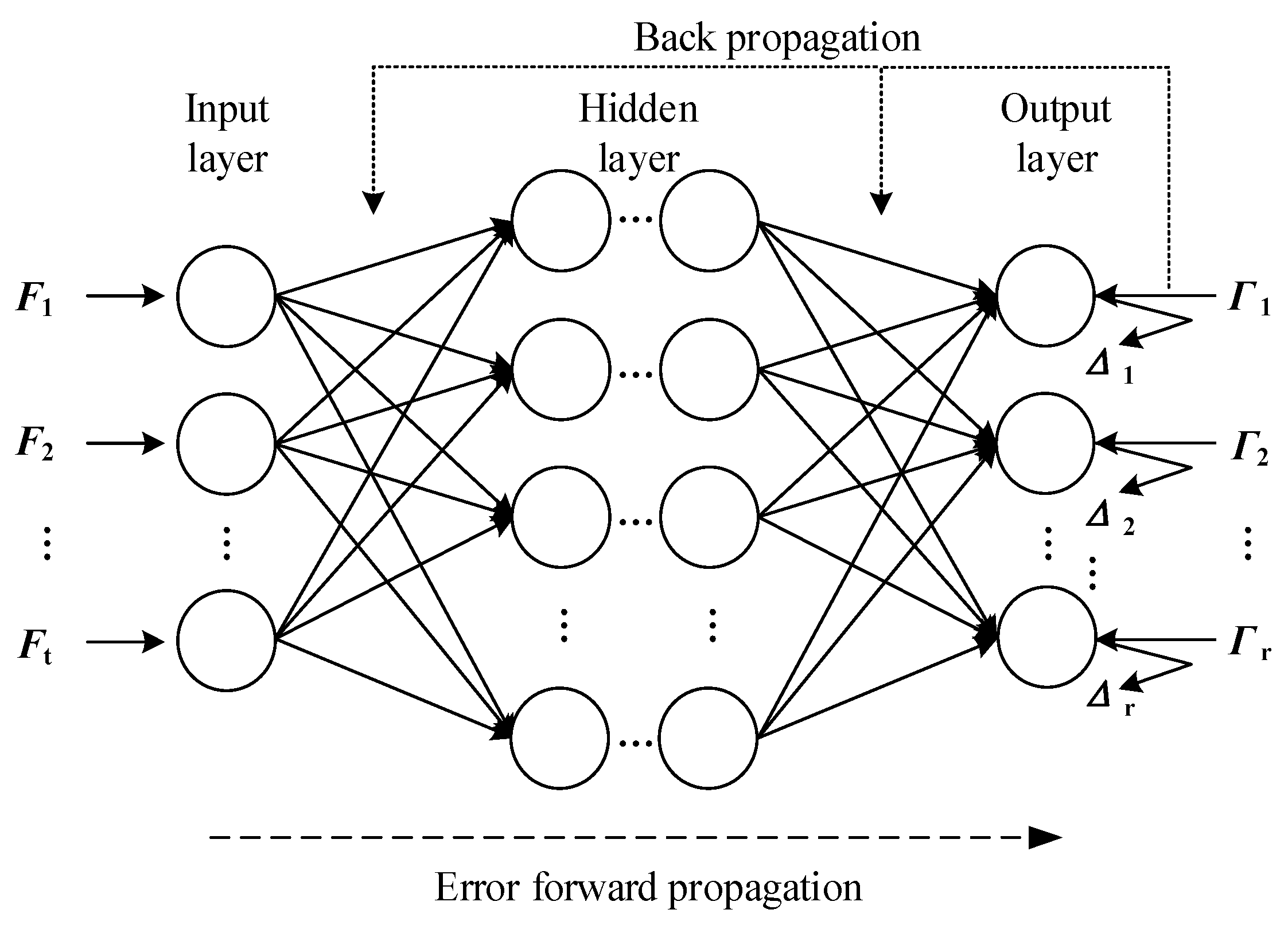














| Type | Nerve Cell | Activation Function |
|---|---|---|
| Input layer | 111 | / |
| Hidden layer | 5 | Tansing |
| Output layer | 224 | Purelin |
| Parameters | Values |
|---|---|
| Voltage/kV | 10 |
| Limited voltage/p.u. | 0.95~1.05 |
| PV capacity/MVA | 0.38, 0.76, 0.38, 0.76, 0.98, 0.66, 0.75, 0.99, 0.56, 1.08, 0.91, 0.76, 0.57, 1.14, 0.91, 0.39, 0.39, 1.16, 1.93, 1.93, 0.79, 0.59, 0.95, 0.92, 0.9 |
| Power factor threshold | 0.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, Z.; Wang, L.; Su, C.; Zhang, R.; Li, X.; Zhang, B. Data-Driven Coordinated Voltage Control Strategy for Distribution Networks with High Proportion of Renewable Energy Based on Voltage–Power Sensitivity. Sustainability 2025, 17, 4955. https://doi.org/10.3390/su17114955
Cheng Z, Wang L, Su C, Zhang R, Li X, Zhang B. Data-Driven Coordinated Voltage Control Strategy for Distribution Networks with High Proportion of Renewable Energy Based on Voltage–Power Sensitivity. Sustainability. 2025; 17(11):4955. https://doi.org/10.3390/su17114955
Chicago/Turabian StyleCheng, Ziwei, Lei Wang, Can Su, Runtao Zhang, Xiaocong Li, and Bo Zhang. 2025. "Data-Driven Coordinated Voltage Control Strategy for Distribution Networks with High Proportion of Renewable Energy Based on Voltage–Power Sensitivity" Sustainability 17, no. 11: 4955. https://doi.org/10.3390/su17114955
APA StyleCheng, Z., Wang, L., Su, C., Zhang, R., Li, X., & Zhang, B. (2025). Data-Driven Coordinated Voltage Control Strategy for Distribution Networks with High Proportion of Renewable Energy Based on Voltage–Power Sensitivity. Sustainability, 17(11), 4955. https://doi.org/10.3390/su17114955







