Evaluation of Urban-Scale Building Energy-Use Models and Tools—Application for the City of Fribourg, Switzerland
Abstract
1. Introduction
- CitySim is a large-scale building energy simulation tool developed at EPFL (Ecole Polytechnique Fédérale de Lausanne) that includes a solver module (CitySim Solver) and a graphical interface (CitySim Pro) [23]. The simulation is based on a simplified thermal-electrical analogy and the aim is to support the more sustainable planning of urban environment [32,33].
Research Objectives and Originality
- -
- To quantify the simulation error against calibrated space heating consumption data. For privacy concerns, the measured consumption data could not be disclosed, and was therefore used to calibrate a CitySim simulation. The calibration was based on annual heat demand data, for which measurements were available on a per-building basis. The shares of this energy used for space heating and domestic hot water were estimated with the methodology contained in the Swiss norms, which consider the number of occupants. Buildings were grouped into clusters according to their normalized space heating demand and occupancy type, and a search algorithm was used to find the optimal value of the unintended air infiltration rate (ach) within each cluster, with which the buildings were finally simulated. The data obtained in this way retains quantitative information about the heating consumption while losing all information on user-specific dynamic behavior.
- -
- To understand how the most important parameters affect the simulation through a sensitivity analysis carried out for the EN model, in order to improve accuracy of the tested models.
- -
- To evaluate the strengths and weaknesses of the investigated models and to identify an accurate, flexible and easily applicable methodology to simulate energy consumption patterns in different urban contexts on a city scale.
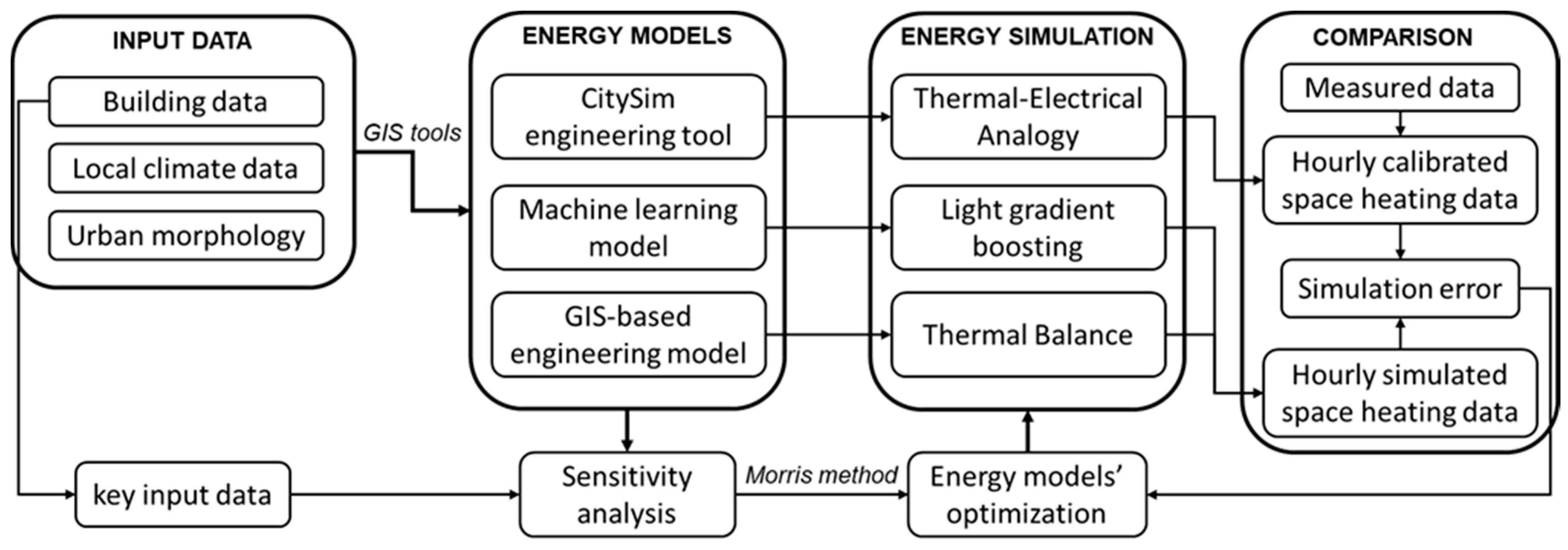
2. Materials and Methods
- A machine learning (ML) model based on the light gradient boosting machine algorithm [40] which makes an estimation of the hourly energy consumption of each building. Gradient boosting was chosen over other ML algorithms as it is usually among the top performers on energy load prediction comparisons [41,42] and because it provides a good balance between performance and training times.
- A GIS-based engineering (EN) model uses a bottom-up approach and it is based on a thermal balance of buildings at urban scale in order to predict space heating energy consumption and greenhouse gas emissions of groups of buildings in built-up context.
- CitySim (CS), an open source simulation software that can be used to estimate the energy demand and energy-use for heating and cooling of multiple buildings, up to district scale, also taking into account the urban context. The simulation solver is based on the thermal-electrical analogy.
| Models and Tools | Method | Technique | Ref. |
|---|---|---|---|
| Machine learning (ML) model | Black box | Artificial Intelligence, light gradient boosting | [40,41,43,44] |
| GIS-based engineering (EN) model | Gray box | Thermal balance, iterative procedure | [45,46,47] |
| CitySim (CS) engineering tool | White box | Thermal-electrical analogy | [32,33,48] |
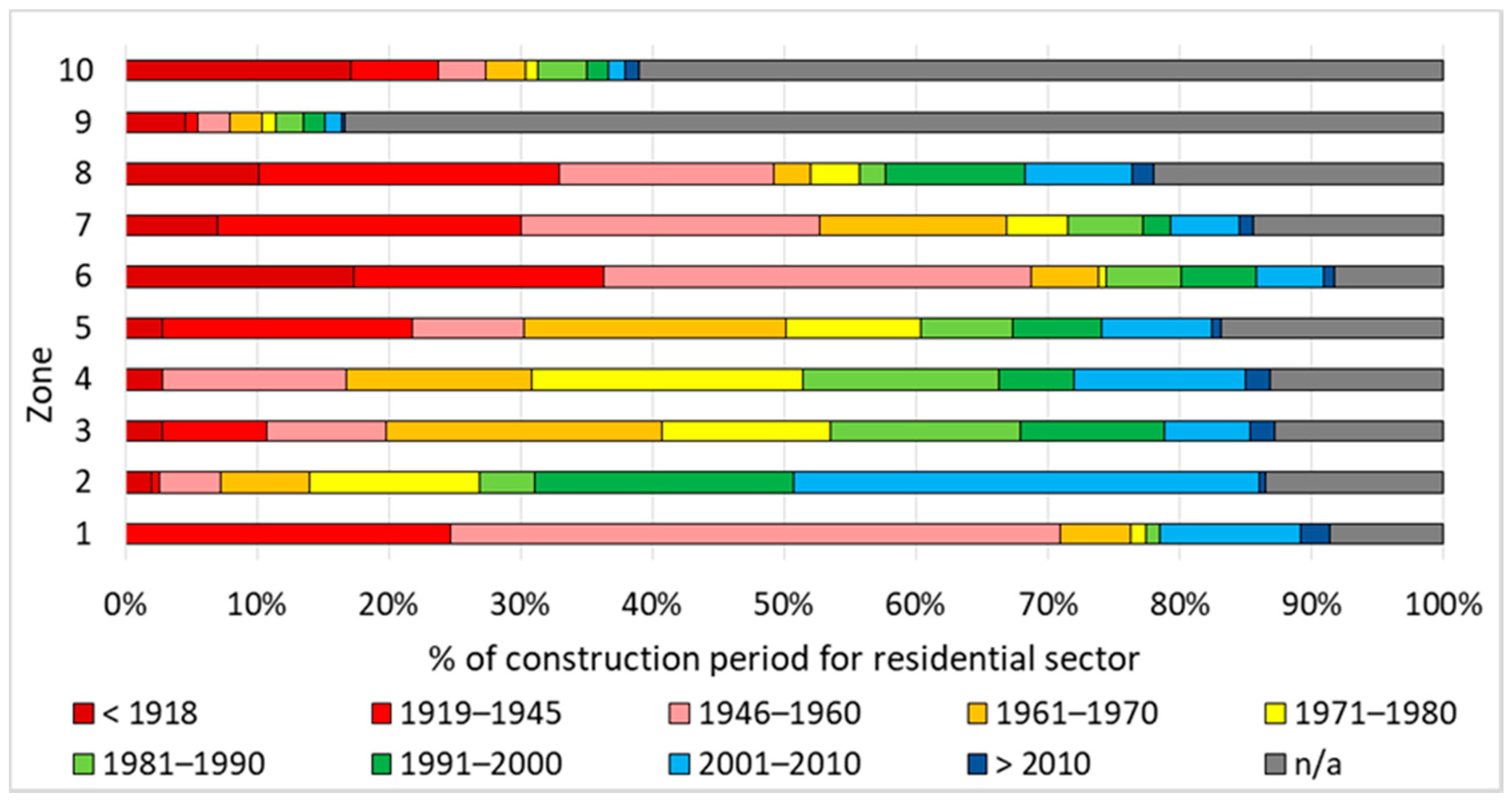
2.1. Case Study
2.2. Input Data
2.3. Application of Energy-Use Models and Tools
2.3.1. Machine Learning (ML) Model
- Building features: footprint surface, height, net volume, heat loss surface, ach, U values of walls, floor, roof and glass, glazing ratio, SVF.
- Climate features: air temperature, surface temperature, relative humidity, wind speed, global direct and diffuse radiation.
2.3.2. GIS-Based Engineering (EN) Model
2.3.3. CitySim (CS) Engineering Tool
2.4. Sensitivity Analysis
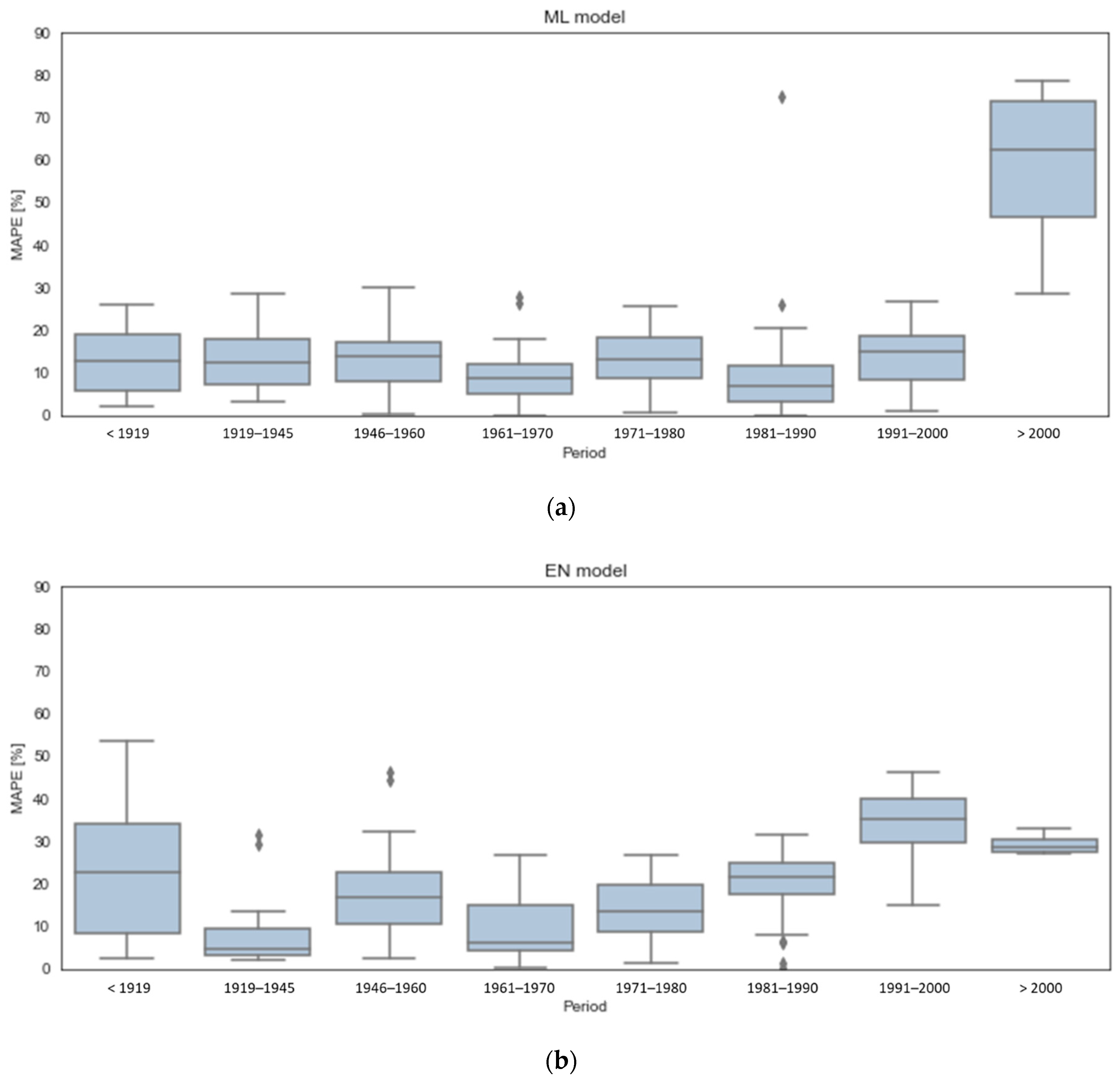
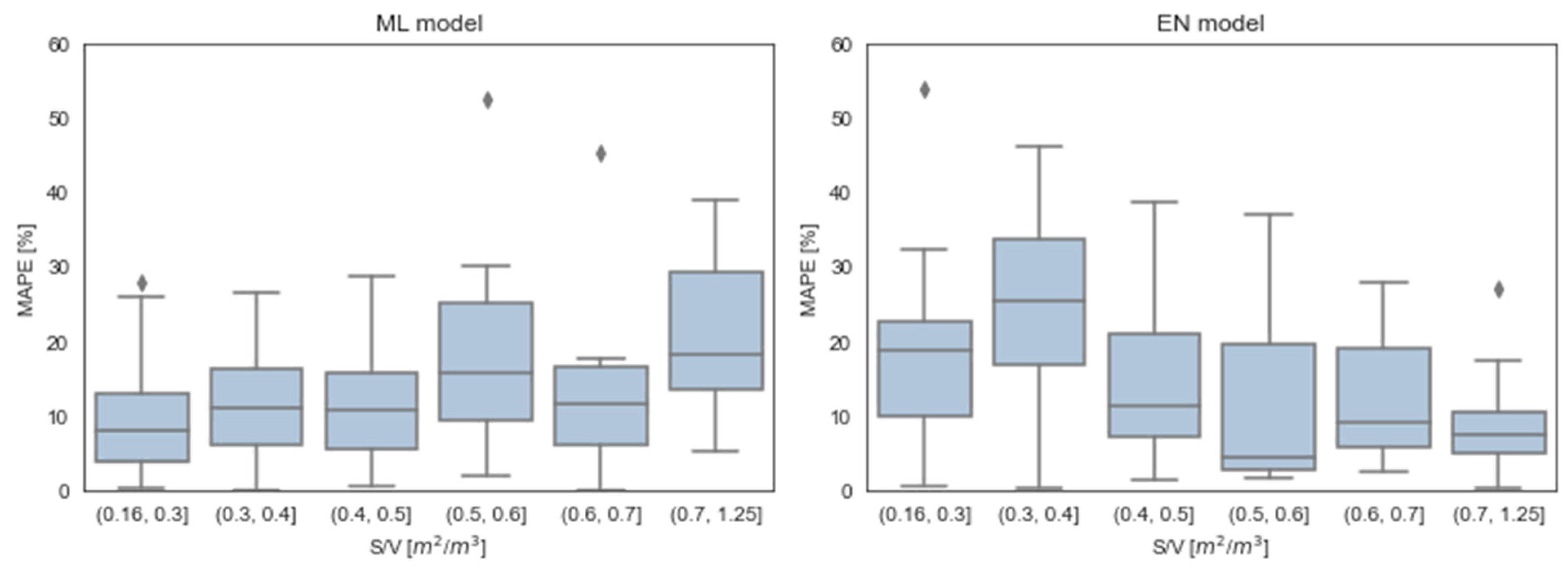
3. Results
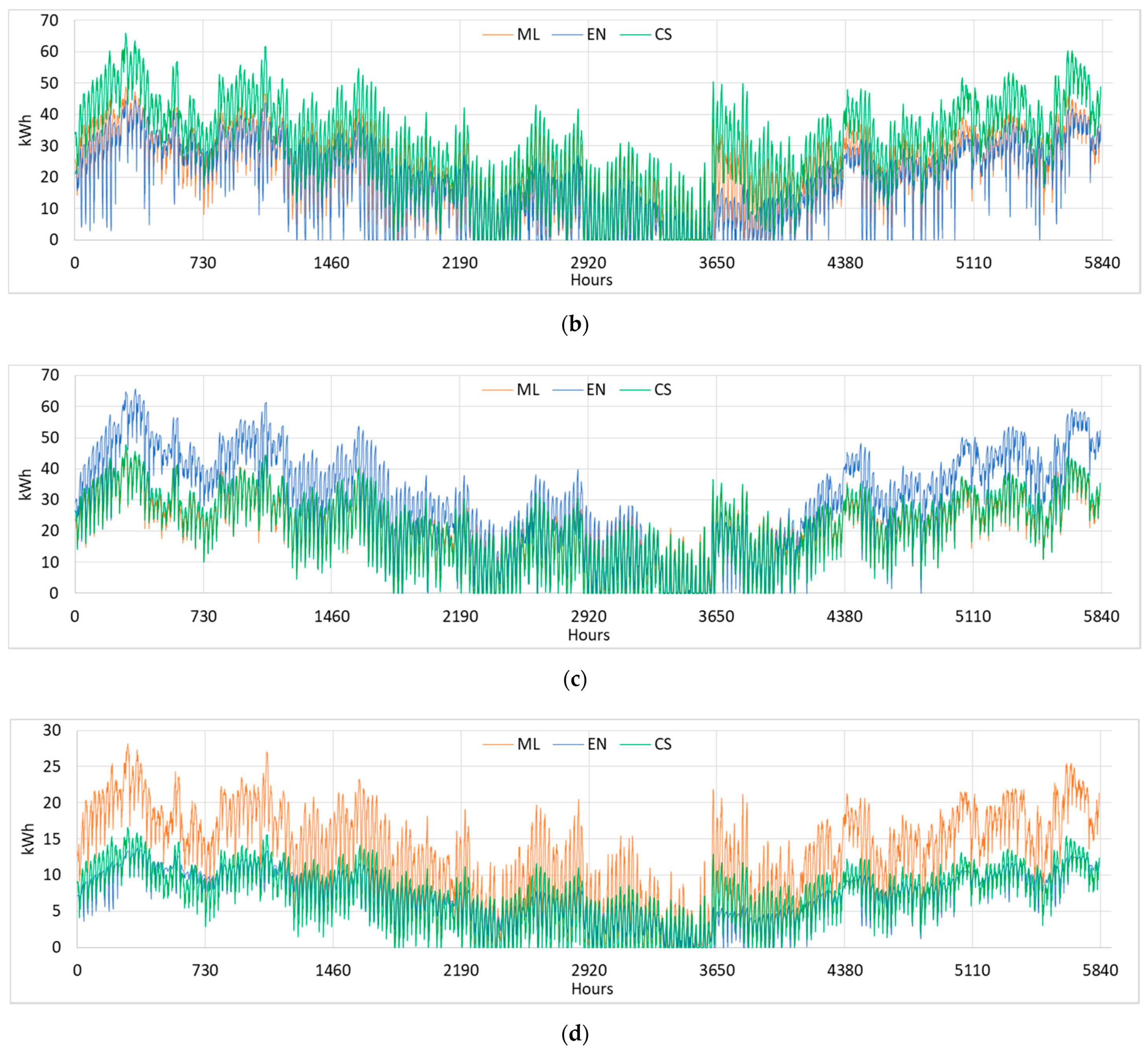
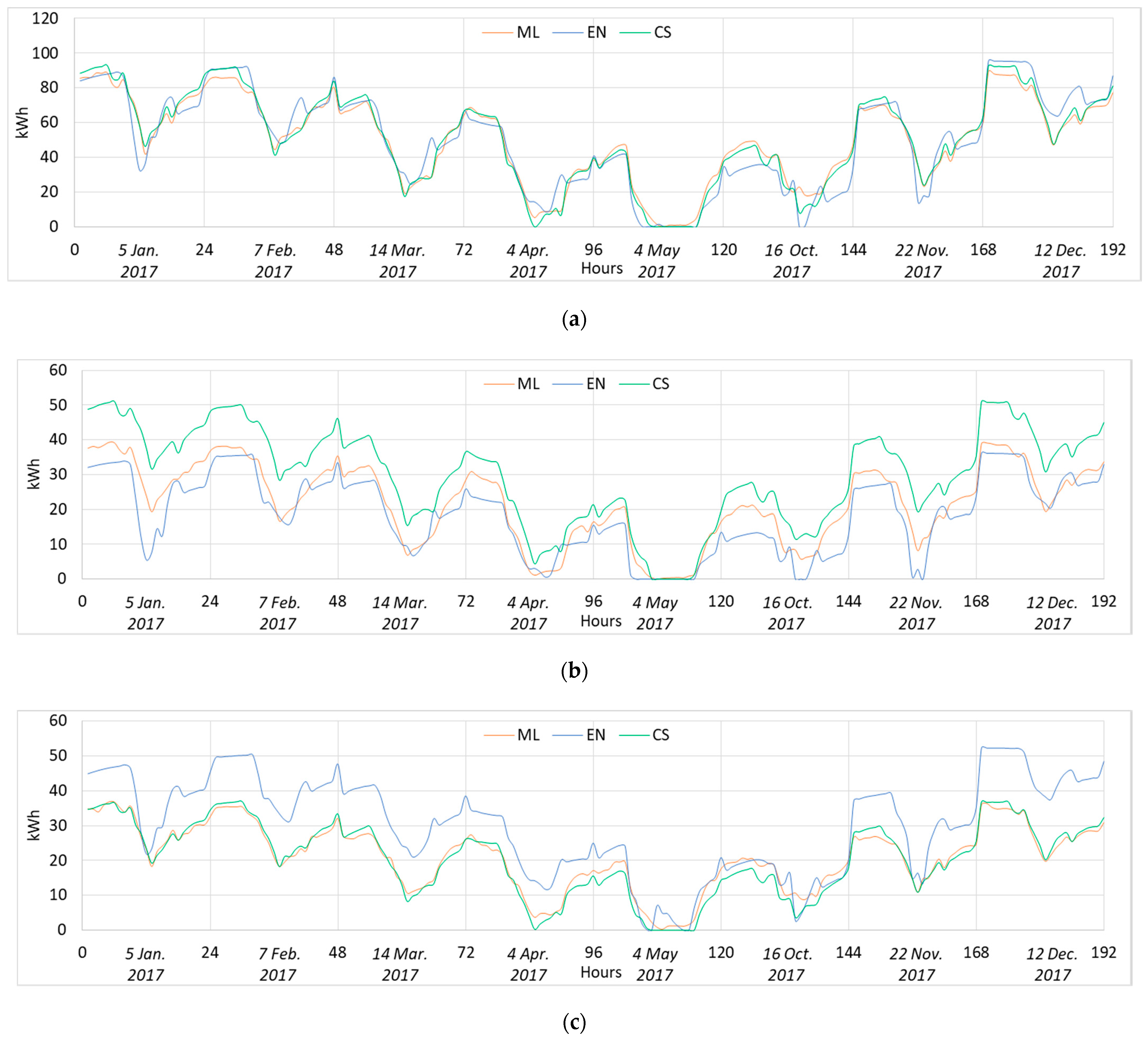
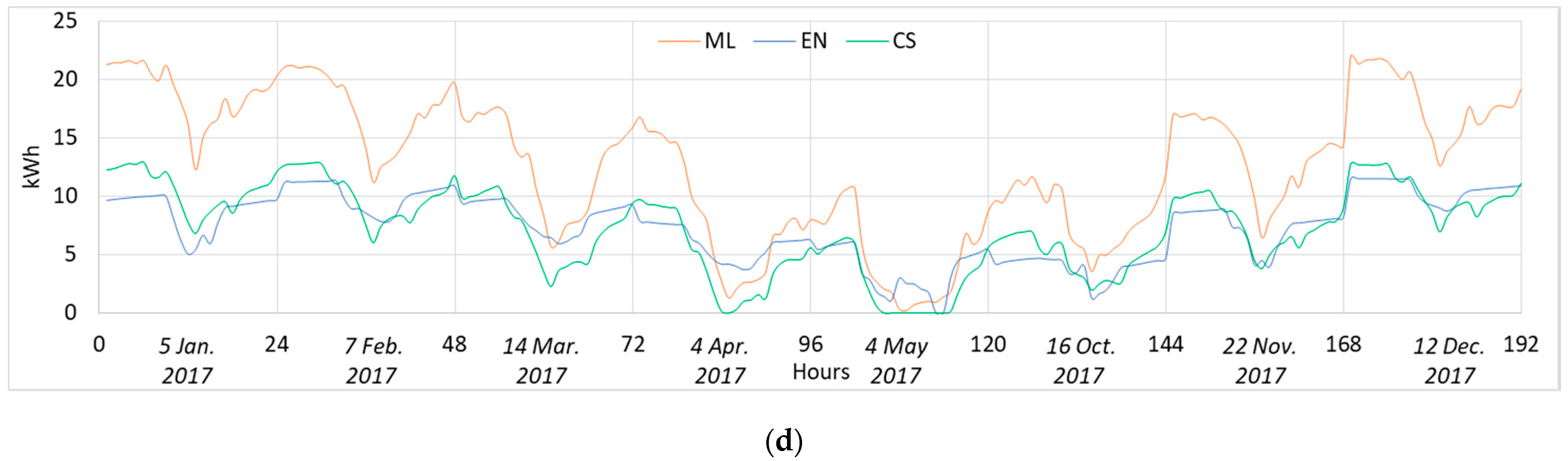
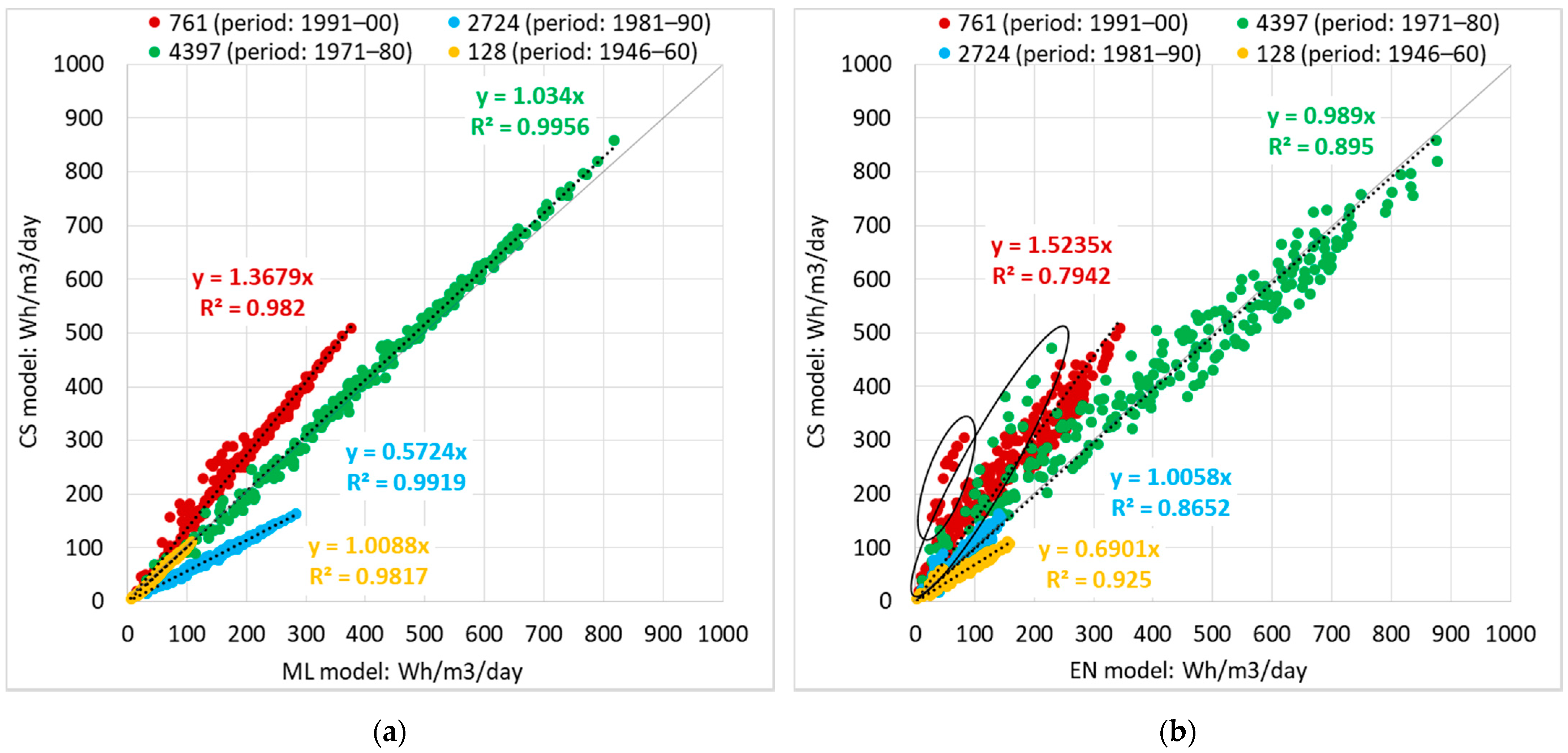
- Building ID 761 (built between 1991 and 2000) was problematic for both models, which tended to underestimate the real heating consumption during the whole heating season. With building ID 4397 (1971–1980), on the other hand, both models showed a good accuracy and were able to approximate the behavior of the building well.
- As had already emerged from the hourly profiles, with regards to building ID 2724 (built between 1981 and 1990), on which the ML model had a much higher error than the EN model, the heating consumption was overestimated. Similar results were obtained by the EN model, which overestimated the heating consumption of building ID 128 (built between 1946 and 1960), on which the ML model showed high precision instead.
4. Discussion
- The ML and EN models, being simplified models, have very short simulation times (a second to simulate a single building) compared to complex simulation software like CS (10 min to simulate a single building). This allows to easily apply the models assuming different urban scenarios in order to select and optimize the most sustainable configuration from an energy, environmental and economic point of view.
- The simulation time partly depends on the number of input data required. The CS tool is a complex model that requires more information than the two models analyzed. So, the ML and EN models are more suitable for doing city-scale energy simulations, for example, in the preliminary planning stages, as they require less detailed data while having sufficient accuracy to describe the distribution of energy consumption at different territorial level.
- An important aspect is that these models mainly used open data, therefore, it is possible to easily apply them to different cities.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Grove-Smith, J.; Aydin, V.; Feist, W.; Schnieders, J.; Thomas, S. Standards and policies for very high energy efficiency in the urban building sector towards reaching the 1.5 °C target. Curr. Opin. Environ. Sustain. 2018, 30, 103–114. [Google Scholar] [CrossRef]
- Sebi, C.; Nadel, S.; Schlomann, B.; Steinbach, J. Policy strategies for achieving large long-term savings from retrofitting existing buildings. Energy Effic. 2018, 12, 89–105. [Google Scholar] [CrossRef]
- Sola, A.; Corchero, C.; Salom, J.; Sanmarti, M. Multi-domain urban-scale energy modelling tools: A review. Sustain. Cities Soc. 2020, 54, 101872. [Google Scholar] [CrossRef]
- Johansson, T.; Olofsson, T.; Mangold, M. Development of an energy atlas for renovation of the multifamily building stock in Sweden. Appl. Energy 2017, 203, 723–736. [Google Scholar] [CrossRef]
- Ben, H.; Steemers, K. Modelling energy retrofit using household archetypes. Energy Build. 2020, 224, 110224. [Google Scholar] [CrossRef]
- Cerezo, C.; Sokol, J.; Alkhaled, S.; Reinhart, C.; Al-Mumin, A.; Hajiah, A. Comparison of four building archetype characterization methods in urban building energy modeling (UBEM): A residential case study in Kuwait City. Energy Build. 2017, 154, 321–334. [Google Scholar] [CrossRef]
- Mutani, G.; Todeschi, V. Space heating models at urban scale for buildings in the city of Turin (Italy). Energy Procedia 2017, 122, 841–846. [Google Scholar] [CrossRef]
- Swan, L.G.; Ugursal, V.I. Modeling of end-use energy consumption in the residential sector: A review of modeling techniques. Renew. Sustain. Energy Rev. 2009, 13, 1819–1835. [Google Scholar] [CrossRef]
- Abbasabadi, N.; Ashayeri, M. Urban energy use modeling methods and tools: A review and an outlook. Build. Environ. 2019, 161, 106270. [Google Scholar] [CrossRef]
- Akbari, K.; Jolai, F.; Ghaderi, S.F. Optimal design of distributed energy system in a neighborhood under uncertainty. Energy 2016, 116, 567–582. [Google Scholar] [CrossRef]
- Ferrari, S.; Zagarella, F.; Caputo, P.; D’Amico, A. Results of a literature review on methods for estimating buildings energy demand at district level. Energy 2019, 175, 1130–1137. [Google Scholar] [CrossRef]
- Al-Shammari, E.T.; Keivani, A.; Shamshirband, S.; Mostafaeipour, A.; Yee, P.L.; Petković, D.; Ch, S. Prediction of heat load in district heating systems by Support Vector Machine with Firefly searching algorithm. Energy 2016, 95, 266–273. [Google Scholar] [CrossRef]
- Li, W.; Zhou, Y.; Cetin, K.; Eom, J.; Wang, Y.; Chen, G.; Zhang, X. Modeling urban building energy use: A review of modeling approaches and procedures. Energy 2017, 141, 2445–2457. [Google Scholar] [CrossRef]
- Foucquier, A.; Robert, S.; Suard, F.; Stéphan, L.; Jay, A. State of the art in building modelling and energy performances prediction: A review. Renew. Sustain. Energy Rev. 2013, 23, 272–288. [Google Scholar] [CrossRef]
- Koulamas, C.; Kalogeras, A.; Pacheco-Torres, R.; Casillas, J.; Ferrarini, L. Suitability analysis of modeling and assessment approaches in energy efficiency in buildings. Energy Build. 2018, 158, 1662–1682. [Google Scholar] [CrossRef]
- Wei, Y.; Zhang, X.; Shi, Y.; Xia, L.; Pan, S.; Wu, J.; Han, M.; Zhao, X. A review of data-driven approaches for prediction and classification of building energy consumption. Renew. Sustain. Energy Rev. 2018, 82, 1027–1047. [Google Scholar] [CrossRef]
- Goy, S.; Maréchal, F.; Finn, D. Data for Urban Scale Building Energy Modelling: Assessing Impacts and Overcoming Availability Challenges. Energies 2020, 13, 4244. [Google Scholar] [CrossRef]
- Dochev, I.; Gorzalka, P.; Weiler, V.; Schmiedt, J.E.; Linkiewicz, M.; Eicker, U.; Hoffschmidt, B.; Peters, I.; Schröter, B. Calculating urban heat demands: An analysis of two modelling approaches and remote sensing for input data and validation. Energy Build. 2020, 226, 110378. [Google Scholar] [CrossRef]
- Rodríguez, L.R.; Duminil, E.; Ramos, J.S.; Eicker, U. Assessment of the photovoltaic potential at urban level based on 3D city models: A case study and new methodological approach. Sol. Energy 2017, 146, 264–275. [Google Scholar] [CrossRef]
- Kaden, R.; Kolbe, T.H. Simulation-Based Total Energy Demand Estimation of Buildings using Semantic 3D City Models. Int. J. 3-D Inf. Model. 2014, 3, 35–53. [Google Scholar] [CrossRef]
- Rosser, J.F.; Long, G.; Zakhary, S.; Boyd, D.S.; Mao, Y.; Robinson, D. Modelling Urban Housing Stocks for Building Energy Simulation using CityGML EnergyADE. ISPRS Int. J. Geo-Inf. 2019, 8, 163. [Google Scholar] [CrossRef]
- Wate, P.; Coors, V. 3D Data Models for Urban Energy Simulation. Energy Procedia 2015, 78, 3372–3377. [Google Scholar] [CrossRef]
- Mutani, G.; Todeschi, V.; Kampf, J.; Coors, V.; Fitzky, M. Building energy consumption modeling at urban scale: Three case studies in Europe for residential buildings. In Proceedings of the 2018 IEEE International Telecommunications Energy Conference (INTELEC), Turin, Italy, 7–11 October 2018; pp. 1–8. [Google Scholar]
- Li, C. 2.09-GIS for Urban Energy Analysis. In Earth Systems and Environmental Sciences; Elsevier: Oxford, UK, 2018; pp. 187–195. ISBN 978-0-12-804793-4. [Google Scholar]
- Groppi, D.; De Santoli, L.; Cumo, F.; Garcia, D.A. A GIS-based model to assess buildings energy consumption and usable solar energy potential in urban areas. Sustain. Cities Soc. 2018, 40, 546–558. [Google Scholar] [CrossRef]
- Nageler, P.; Zahrer, G.; Heimrath, R.; Mach, T.; Mauthner, F.; Leusbrock, I.; Schranzhofer, H.; Hochenauer, C. Novel validated method for GIS based automated dynamic urban building energy simulations. Energy 2017, 139, 142–154. [Google Scholar] [CrossRef]
- Alhamwi, A.; Medjroubi, W.; Vogt, T.; Agert, C. GIS-based urban energy systems models and tools: Introducing a model for the optimisation of flexibilisation technologies in urban areas. Appl. Energy 2017, 191, 1–9. [Google Scholar] [CrossRef]
- Chen, Y.; Hong, T.; Piette, M.A. Automatic generation and simulation of urban building energy models based on city datasets for city-scale building retrofit analysis. Appl. Energy 2017, 205, 323–335. [Google Scholar] [CrossRef]
- Luo, X.; Hong, T.; Tang, Y.-H. Modeling Thermal Interactions between Buildings in an Urban Context. Energies 2020, 13, 2382. [Google Scholar] [CrossRef]
- Sola, A.; Corchero, C.; Salom, J.; Sanmarti, M. Simulation Tools to Build Urban-Scale Energy Models: A Review. Energies 2018, 11, 3269. [Google Scholar] [CrossRef]
- Chen, Y.; Hong, T. Impacts of building geometry modeling methods on the simulation results of urban building energy models. Appl. Energy 2018, 215, 717–735. [Google Scholar] [CrossRef]
- Walter, E.; Kämpf, J.H. A verification of CitySim results using the BESTEST and monitored consumption values. In Proceedings of the 2nd Building Simulation Applications conference, Bozen-Bolzano, Italy, 4–6 February 2015; pp. 215–222. [Google Scholar]
- Robinson, D.; Haldi, F.; Leroux, P.; Perez, D.; Rasheed, A.; Wilke, U. CITYSIM: Comprehensive Micro-Simulation of Resource Flows for Sustainable Urban Planning. In Proceedings of the Eleventh International IBPSA Conference, Glasgow, UK, 27–30 July 2009. [Google Scholar]
- Reinhart, C.; Dogan, T.; Jakubiec, J.; Rakha, T.; Sang, A. Umi-an urban simulation environment for building energy use, daylighting and walkability. In Proceedings of the 13th Conference of International Building Performance Simulation Association, Chambéry, France, 26–28 August 2013; pp. 476–483. [Google Scholar]
- Quan, S.J.; Wu, J.; Wang, Y.; Shi, Z.; Yang, T.; Yang, P.P.-J. Urban Form and Building Energy Performance in Shanghai Neighborhoods. Energy Procedia 2016, 88, 126–132. [Google Scholar] [CrossRef]
- Monsalvete, P.; Robinson, D.; Eicker, U. Dynamic Simulation Methodologies for Urban Energy Demand. Energy Procedia 2015, 78, 3360–3365. [Google Scholar] [CrossRef]
- Nouvel, R.; Zirak, M.; Coors, V.; Eicker, U. The influence of data quality on urban heating demand modeling using 3D city models. Comput. Environ. Urban Syst. 2017, 64, 68–80. [Google Scholar] [CrossRef]
- Nouvel, R.; Brassel, K.H.; Bruse, M.; Duminil, E.; Coors, V.; Eicker, U.; Robinson, D. SimStadt, a new workflow-driven urban energy simulation platform for CityGML city models. In Proceedings of the International Conference CISBAT 2015 Future Buildings and Districts Sustainability from Nano to Urban Scale, Lausanne, Switzerland, 9–11 September 2015; pp. 889–894. [Google Scholar]
- Nutkiewicz, A.; Yang, Z.; Jain, R.K. Data-driven Urban Energy Simulation (DUE-S): A framework for integrating engineering simulation and machine learning methods in a multi-scale urban energy modeling workflow. Appl. Energy 2018, 225, 1176–1189. [Google Scholar] [CrossRef]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.-Y. LightGBM: A Highly Efficient Gradient Boosting Decision Tree; Neural Information Processing Systems (NIPS): Brooklyn, NY, USA, 2017. [Google Scholar]
- Wang, Z.; Hong, T.; Piette, M.A. Building thermal load prediction through shallow machine learning and deep learning. Appl. Energy 2020, 263, 114683. [Google Scholar] [CrossRef]
- Miller, C.; Arjunan, P.; Kathirgamanathan, A.; Fu, C.; Roth, J.; Park, J.Y.; Balbach, C.; Gowri, K.; Nagy, Z.; Fontanini, A.D.; et al. The ASHRAE Great Energy Predictor III competition: Overview and results. Sci. Technol. Built Environ. 2020, 26, 1427–1447. [Google Scholar] [CrossRef]
- Boghetti, R.; Fantozzi, F.; Kämpf, J.H.; Salvadori, G. Understanding the performance gap: A machine learning approach on residential buildings in Turin, Italy. J. Phys. Conf. Ser. 2019, 1343, 012042. [Google Scholar] [CrossRef]
- Boghetti, R.; Fantozzi, F.; Kämpf, J.; Mutani, G.; Salvadori, G.; Todeschi, V. Building energy models with Morphological urban-scale parameters: A case study in Turin. In Proceedings of the 4th Building Simulation Applications Conference—BSA; Free University of Bozen Bolzano: Bolzano, Italy, 2019; pp. 1–8. [Google Scholar]
- Mutani, G.; Todeschi, V. Building energy modeling at neighborhood scale. Energy Effic. 2020, 13, 1353–1386. [Google Scholar] [CrossRef]
- Mutani, G.; Todeschi, V.; Beltramino, S. Energy Consumption Models at Urban Scale to Measure Energy Resilience. Sustainability 2020, 12, 5678. [Google Scholar] [CrossRef]
- Mutani, G.; Todeschi, V.; Pastorelli, M. Thermal-Electrical Analogy for Dynamic Urban-Scale Energy Modeling. Int. J. Heat Technol. 2020, 38, 571–582. [Google Scholar] [CrossRef]
- Kämpf, J.H.; Robinson, D. A simplified thermal model to support analysis of urban resource flows. Energy Build. 2007, 39, 445–453. [Google Scholar] [CrossRef]
- Farrell, W.J.; Cavellin, L.D.; Weichenthal, S.; Goldberg, M.; Hatzopoulou, M. Capturing the urban canyon effect on particle number concentrations across a large road network using spatial analysis tools. Build. Environ. 2015, 92, 328–334. [Google Scholar] [CrossRef]
- Perez, D. A Framework to Model and Simulate the Disaggregated Energy Flows Supplying Buildings in Urban Areas; EPFL: Lausanne, Switzerland, 2014. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-Learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Büchlmann, P.; Yu, B. Analyzing Bagging. Ann. Stat. 2002, 30, 927–961. [Google Scholar]
- Robinson, D.; Stone, A. Solar radiation modelling in the urban context. Sol. Energy 2004, 77, 295–309. [Google Scholar] [CrossRef]
- Herman, J.D.; Usher, W. SALib: An open-source Python library for Sensitivity Analysis. J. Open Source Softw. 2017, 2, 9–10. [Google Scholar] [CrossRef]
- Morris, M.D. Factorial Sampling Plans for Preliminary Computational Experiments. Technometrics 1991, 33, 161–174. [Google Scholar] [CrossRef]
- Calama-González, C.M.; Symonds, P.; Petrou, G.; Suárez, R.; León-Rodríguez, Á.L. Bayesian calibration of building energy models for uncertainty analysis through test cells monitoring. Appl. Energy 2021, 282, 116118. [Google Scholar] [CrossRef]
- Silva, A.S.; Ghisi, E. Estimating the sensitivity of design variables in the thermal and energy performance of buildings through a systematic procedure. J. Clean. Prod. 2020, 244, 118753. [Google Scholar] [CrossRef]
- Campolongo, F.; Cariboni, J.; Saltelli, A. An effective screening design for sensitivity analysis of large models. Environ. Model. Softw. 2007, 22, 1509–1518. [Google Scholar] [CrossRef]
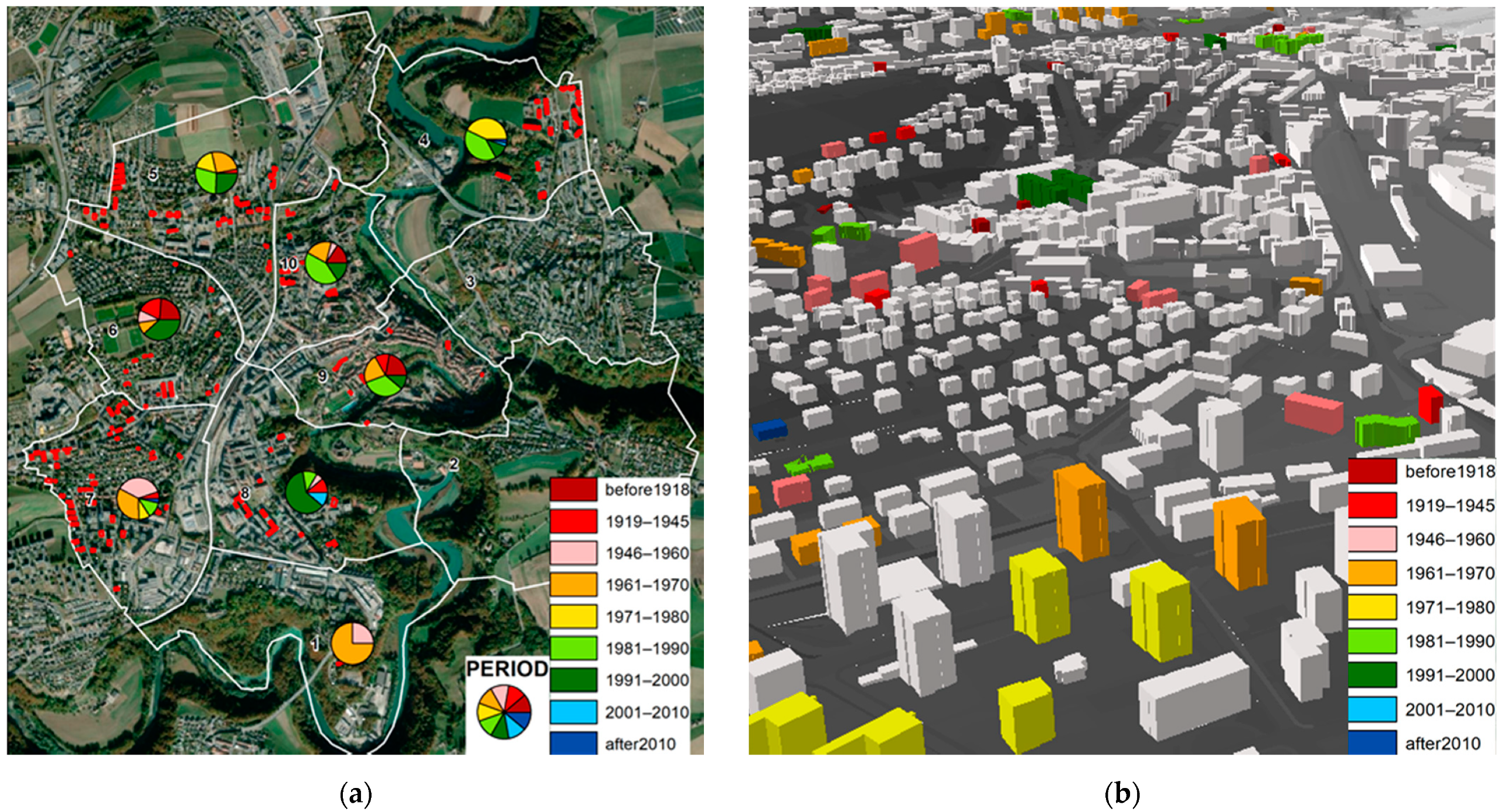
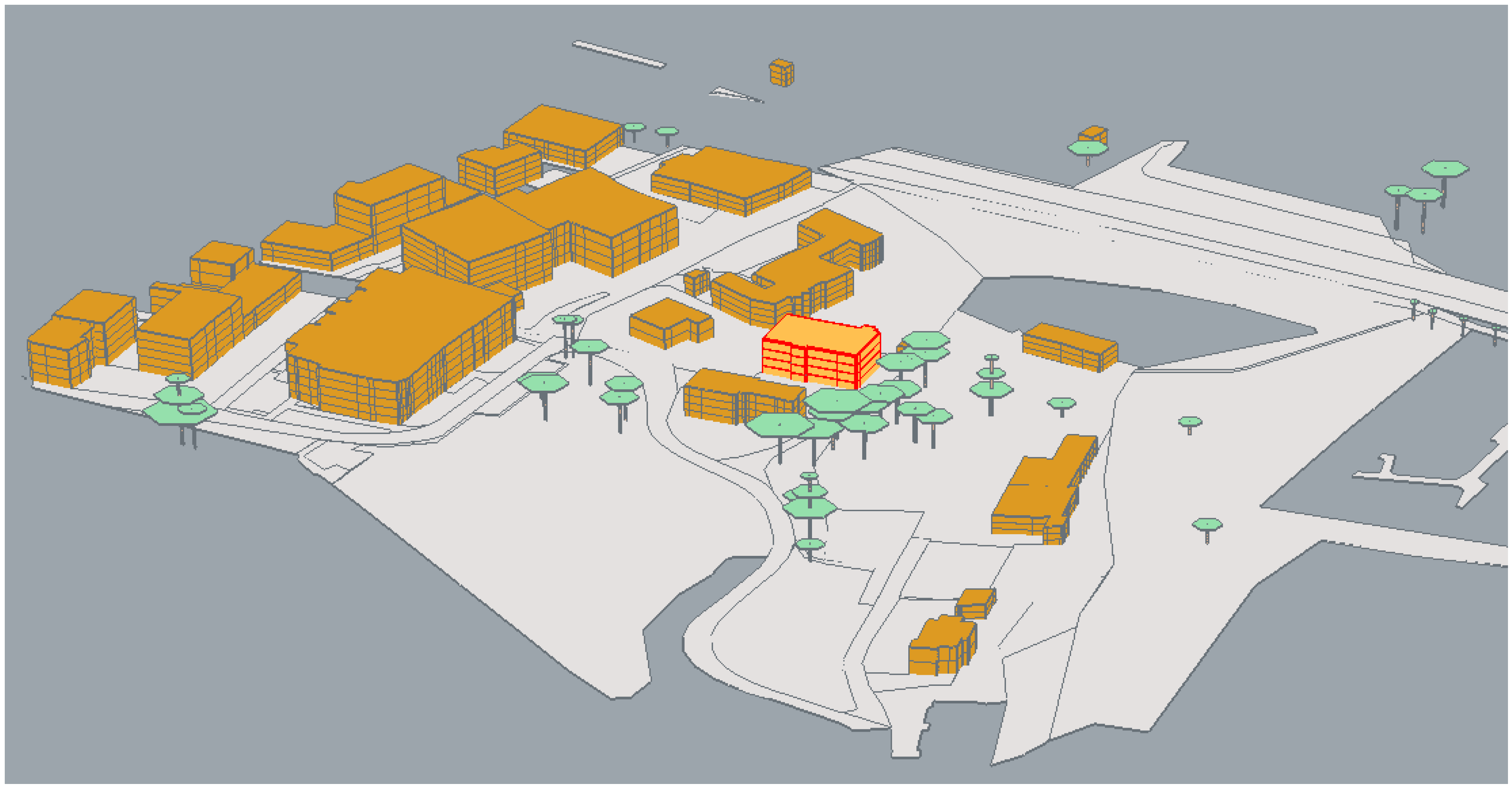



| Input Data | Source | Tools | Scale |
|---|---|---|---|
| Type of users and geometrical characteristics | Cadastral data | GIS | Building |
| Internal air temperature | norm SIA 380/1:2009 | None | |
| Infiltration rate and thermo-physical proprieties | norm SIA 380/1:2009 and [50] | None | |
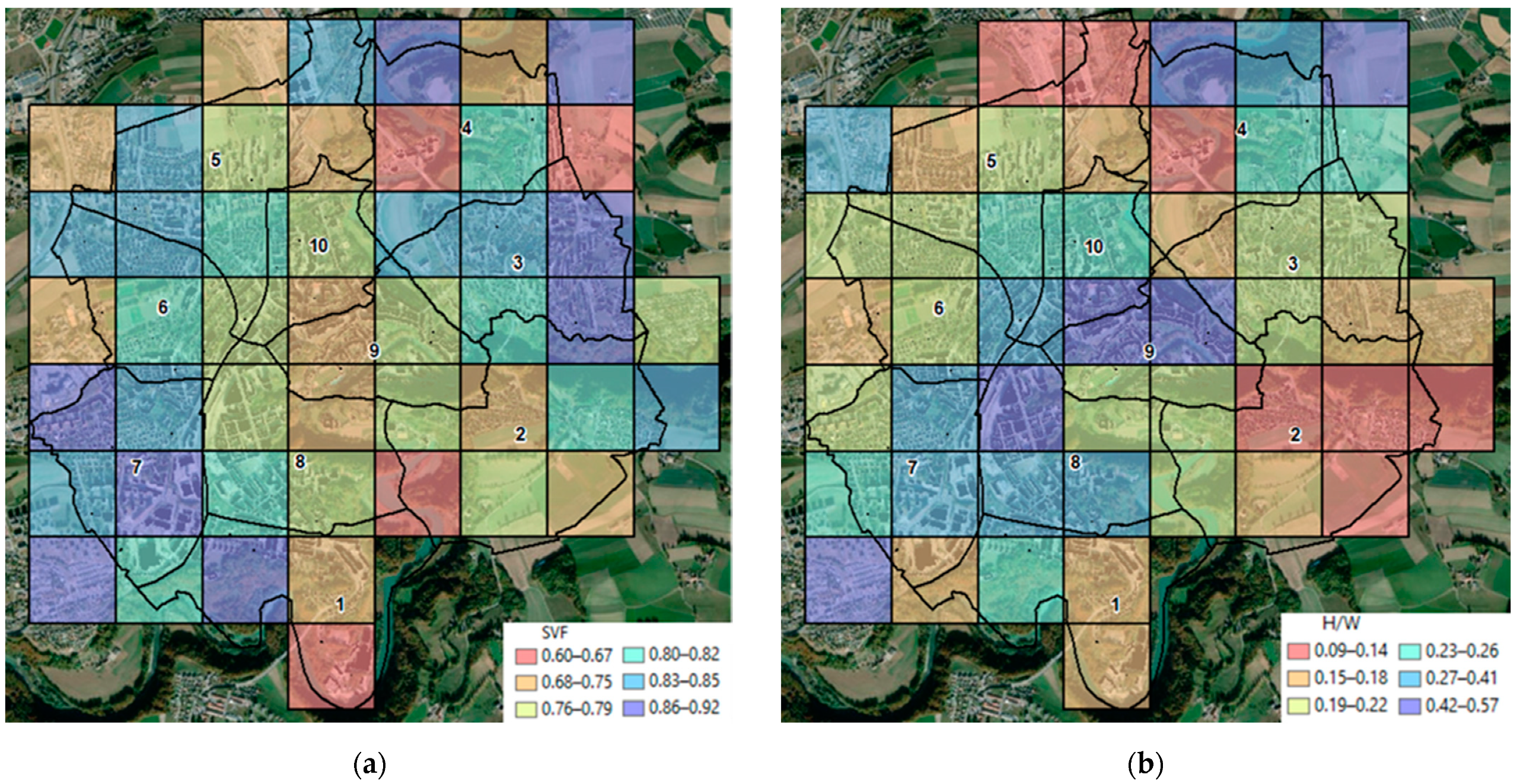
| Sky view factor (SVF) | Cadastral data and digital surface model | Relief Visualization Toolbox software, GIS | Urban |
| Height-to-distance ratio (H/W) | Cadastral data | GIS | |
| Meteorological data | meteonorm.com and www.meteoswiss.ch | Meteonorm software | City |
| Period | ach * | Cwall | dm | Uwall | Uground | Uroof | Uglass | gG | gratio |
|---|---|---|---|---|---|---|---|---|---|
| [-] | [h−1] | [kJm−2·K−1] | [m] | [Wm−2·K−1] ** | [-] | [-] | |||
| Before 1945 | 0.70 | 660 | 0.44 | 0.94 | 1.60 | 0.70 | 2.3 | 0.47 | 0.25 |
| 1946–1960 | 0.60 | 487 | 0.37 | 1.35 | 1.50 | ||||
| 1961–1970 | 0.55 | 355 | 0.27 | 1.03 | 1.30 (0.32) | 0.65 (0.32) | |||
| 1971–1980 | 0.50 | 356 | 0.28 | 0.88 | 1.10 (0.36) | 0.60 (0.34) | |||
| 1981–1990 | 0.40 | 493 | 0.25 | 0.90 | 0.68 (0.33) | 0.43 (0.27) | |||
| 1991–2000 | 0.35 | 494 | 0.27 | 0.69 | 0.49 (0.33) | 0.31 (0.27) | |||
| 2001–2010 | 0.30 | 495 | 0.30 | 0.51 | 0.35 (0.27) | 0.25 (0.20) | 1.7 | 0.49 | 0.35 |
| From 2010 | 507 | 0.37 | 0.25 (0.20) | 0.22 (0.17) | |||||
| Hyperparameter | Value | Tested Range | Hyperparameter | Value | Tested Range |
|---|---|---|---|---|---|
| Bagging fraction | 0.95 | 0.4–1 | Lambda L2 | 0.58 | 0–0.6 |
| Bagging frequency | 9 | 1–10 | Max bin | 300 | 100–2000 |
| Feature fraction | 0.6 | 0.4–1 | Number of estimators * | 1000 | 100–1000 |
| Lambda L1 | 0.59 | 0–0.6 | Number of leaves | 38 | 20–40 |
| Input Data | Unit | Range | Step Size | Standard Dev. |
|---|---|---|---|---|
| Ventilation rate (ach) | h−1 | 0.2–1.5 | 0.43 | 0.40 |
| Thermal transmittances of walls (Uwall) | Wm−2·K−1 | 0.1–3.0 | 0.97 | 1.04 |
| Thermal transmittances of roof (Uroof) | Wm−2·K−1 | 0.1–3.0 | 0.97 | 1.10 |
| Thermal transmittances of ground slab (Uground) | Wm−2·K−1 | 0.1–3.0 | 0.97 | 1.05 |
| Glazing ratio (gratio) | - | 0.1–0.9 | 0.27 | 0.30 |
| Building ID | Period of Construction | S/V m2/m3 | Heated vol. m3 | ach h−1 | ach * h−1 | SVF - | H/W - | Zone | CS kWh/y | MAEML Wh | MAEEN Wh |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 4397 | 1971–1980 | 0.27 | 8185 | 0.50 | 0.99 | 0.84 | 0.41 | 4 | 292,713 | 2784 | 7195 |
| 761 | 1991–2000 | 0.56 | 2802 | 0.35 | 1.025 | 0.88 | 0.25 | 10 | 167,999 | 10,525 | 8465 |
| 128 | 1946–1960 | 0.30 | 3108 | 0.60 | 0.65 | 0.85 | 0.32 | 7 | 118,075 | 1436 | 10,196 |
| 2724 | 1981–1990 | 1.24 | 609 | 0.40 | 0.65 | 0.99 | 0.19 | 5 | 41,014 | 5572 | 1323 |
| Typical Monthly Day | Tae °C | Tae,avg °C | Isol,avg Wh/m2/day | MAEML Wh | MAEEN Wh |
|---|---|---|---|---|---|
| 5 January | 0.0 | 0.2 | 2168 | 7576 | 13,967 |
| 7 February | 1.2 | 1.7 | 2973 | 7887 | 10,883 |
| 14 March | 5.2 | 5.6 | 4899 | 5896 | 9827 |
| 4 April | 9.2 | 9.3 | 5983 | 3897 | 8259 |
| 4 May | 12.9 | 14.3 | 6655 | 2525 | 4233 |
| 16 October | 10.4 | 10.2 | 3438 | 3292 | 9662 |
| 22 November | 5.5 | 4.5 | 2427 | 6299 | 10,206 |
| 12 December | 0.9 | 1.1 | 1570 | 8294 | 10,823 |
| Input Data | μ kWh/y | μ * kWh/y | σ kWh/y | μ *conf kWh/y | ||||
|---|---|---|---|---|---|---|---|---|
| CS | EN | CS | EN | CS | EN | CS | EN | |
| ach | 110,145 | 148,126 | 110,145 | 148,126 | 6623 | 16,981 | 3599 | 9720 |
| Uwall | 49,018 | 188,870 | 49,018 | 188,870 | 37,895 | 23,030 | 19,021 | 12,969 |
| Uroof | 32,159 | 79,088 | 32,159 | 79,088 | 6079 | 5340 | 3639 | 2798 |
| Uground | 53,335 | 72,336 | 53,335 | 72,336 | 7724 | 3872 | 4802 | 2192 |
| gratio | 9790 | −86,846 | 28,175 | 86,846 | 36,555 | 49,263 | 13,828 | 34,248 |
| USEM | Strengths | Weaknesses |
|---|---|---|
| ML model | - Since the model relies on real data, it is more specialized on the considered case study and therefore frequently more precise - During the training phase, it is able to learn aspects deeply related to the case study that affect consumption (i.e., the average behavior of the occupants) - Very short simulation times (almost instantaneous) | - Since the model is trained on a very specific problem space, it lacks the ability to generalize - Real consumption data are needed to train and design the model, possibly on a large number of training samples - Since the model is trained on a sample of buildings, it is less robust (it is reliable in the range of values it has already investigated) |
| EN model | - Real consumption data are only needed to eventually calibrate the model - Since the model is based on the thermal balance equations, it is more robust - Since the mathematical relationships between input and the output are known, it is possible to improve the accuracy of the results adding/updating the input data - Very short simulation times (almost instantaneous) | - Since the model is based on simplified thermal balance, it is less precise, as it fails to consider some aspects such as the variation of the internal ventilation (is set constant), the diffuse component of solar gains (is considered only the direct one), and the geometrical interactions with the surroundings |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Todeschi, V.; Boghetti, R.; Kämpf, J.H.; Mutani, G. Evaluation of Urban-Scale Building Energy-Use Models and Tools—Application for the City of Fribourg, Switzerland. Sustainability 2021, 13, 1595. https://doi.org/10.3390/su13041595
Todeschi V, Boghetti R, Kämpf JH, Mutani G. Evaluation of Urban-Scale Building Energy-Use Models and Tools—Application for the City of Fribourg, Switzerland. Sustainability. 2021; 13(4):1595. https://doi.org/10.3390/su13041595
Chicago/Turabian StyleTodeschi, Valeria, Roberto Boghetti, Jérôme H. Kämpf, and Guglielmina Mutani. 2021. "Evaluation of Urban-Scale Building Energy-Use Models and Tools—Application for the City of Fribourg, Switzerland" Sustainability 13, no. 4: 1595. https://doi.org/10.3390/su13041595
APA StyleTodeschi, V., Boghetti, R., Kämpf, J. H., & Mutani, G. (2021). Evaluation of Urban-Scale Building Energy-Use Models and Tools—Application for the City of Fribourg, Switzerland. Sustainability, 13(4), 1595. https://doi.org/10.3390/su13041595








