A Game-Theoretic Approach to Solve Competition between Multi-Type Electric Vehicle Charging and Parking Facilities
Abstract
1. Introduction
- Planning level: issues such as charging pile deployment, electrical infrastructure construction, and vehicle charging scheduling arrangements have been studied.
- Economic level: the economic benefits of vehicle-to-grid (V2G) technology, the income of electric vehicle parking lots, and government support subsidies are studied.
- The competition and pricing strategy between parking/charging decks is studied with the local charging service platform as the main body to guarantee the optimal pricing strategy at the Nash equilibrium point;
- The paper applies the game theory principles to study the competitive relationship among parking platforms in order to maximize revenues, explains the nature of the problem using a special non-cooperative Bertrand game theory model, and provides an effective solution based on Nikaido–Isoda equations;
- EVs are divided into three groups according to price sensitivity with the quantified responses of different groups of customers through the experimental data, which simulate the customer behavior when the parking decks adopt different pricing strategies, and we obtain the experimental results for verification.
2. Problem Formulation
- The initial conditions of all parking/charging decks in the game theory model are the same, including electricity costs, parking fees, geographical advantages, etc.
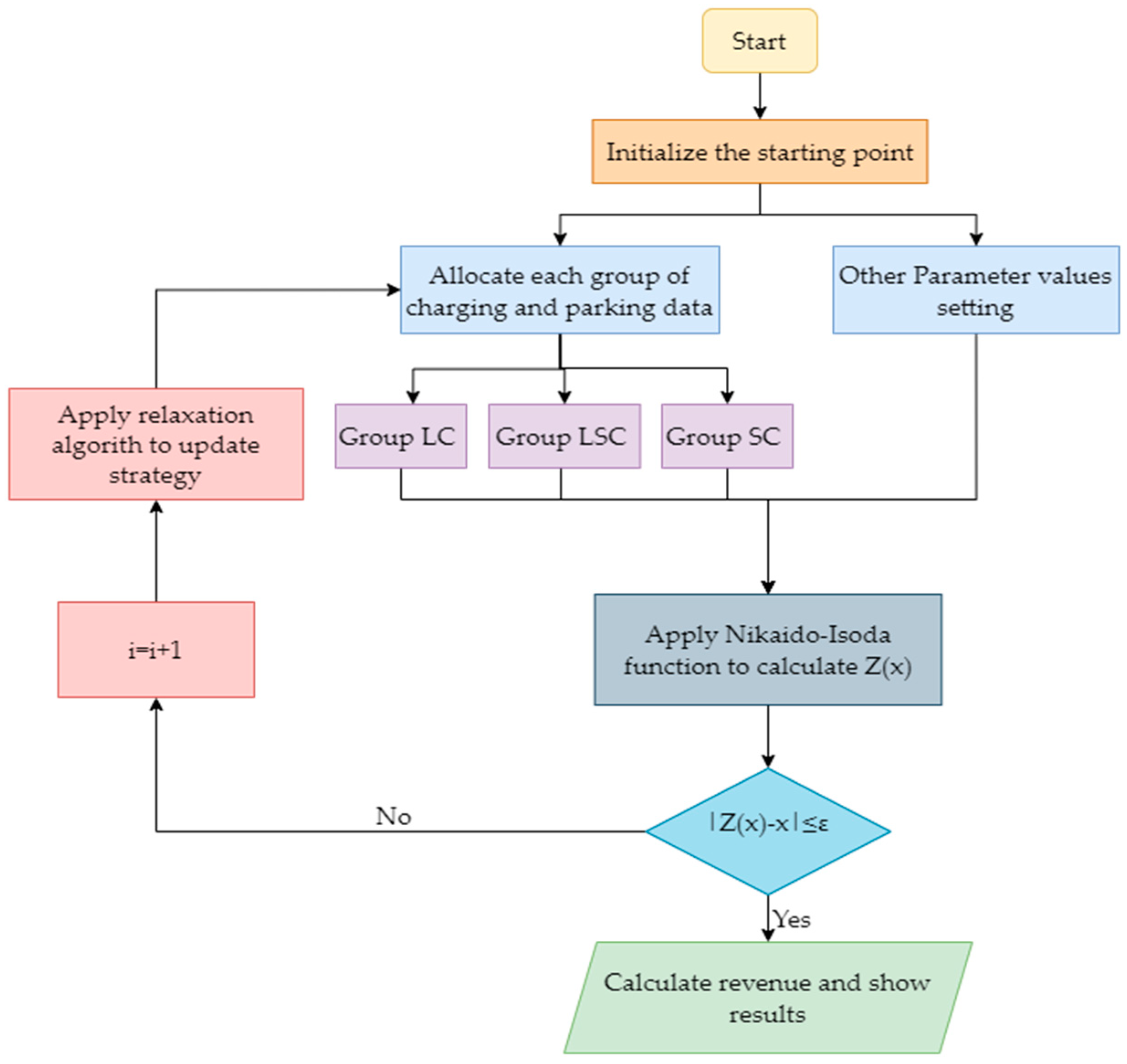
- The game theory model uses the relaxation algorithm and Nikaido–Isoda function in the iterative process. The Nikaido–Isoda function is used to iteratively update the pricing strategy until the conditions are met to end the iterative process.
- The model will eventually reach an equilibrium point. Under the condition that other parking/charging decks keep their pricing strategies unchanged, no matter how this deck changes its strategy, it cannot continue to improve its own revenue.
2.1. Parking
2.2. Charging
2.3. Charging Constraints of Electric Vehicles
2.3.1. Constraint of Charging Demand
2.3.2. Constraint of Dynamic Grid
3. Game Theory and Solution
3.1. Game Theory Definition and Concepts
3.2. Nikaido–Isoda Function
3.3. Relaxation Algorithm
4. Numerical Results
4.1. Experiment Settings and Condition Configuration
4.2. Case Study
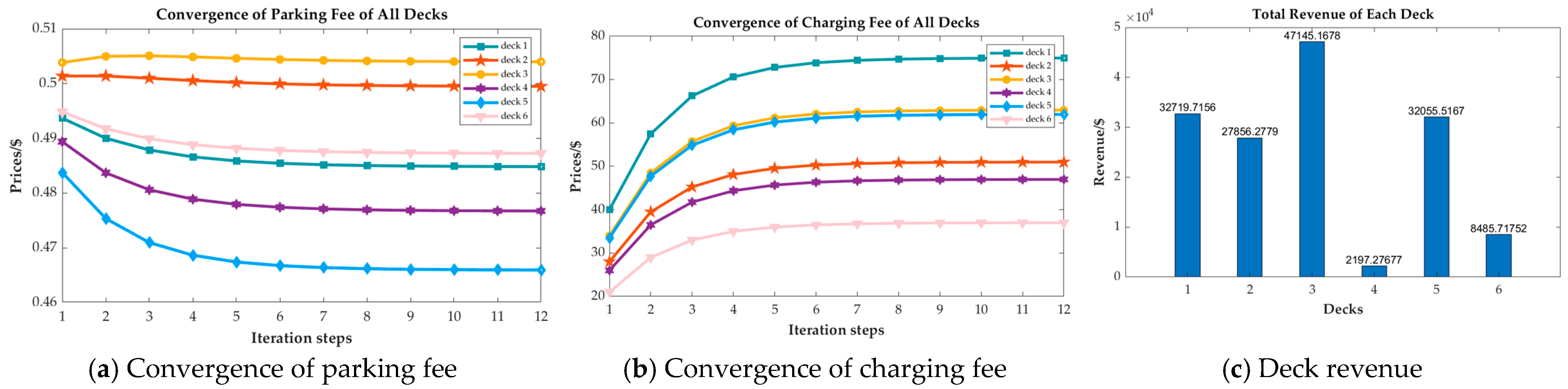
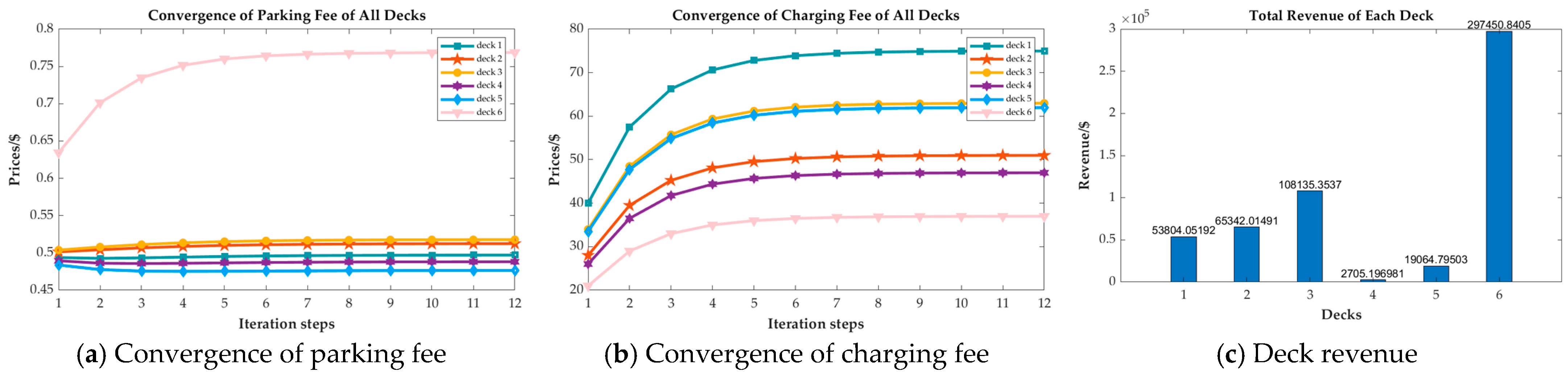
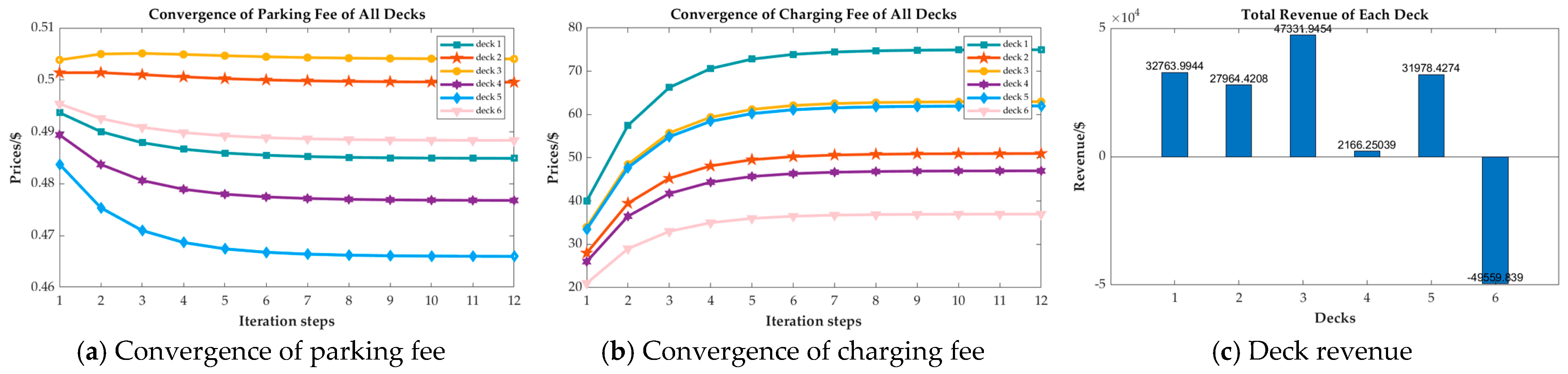
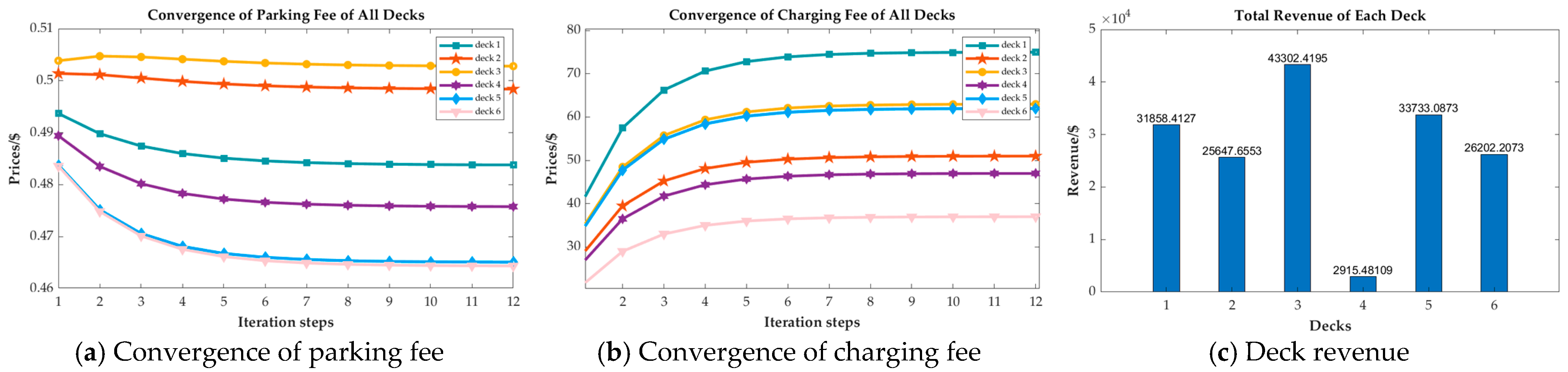
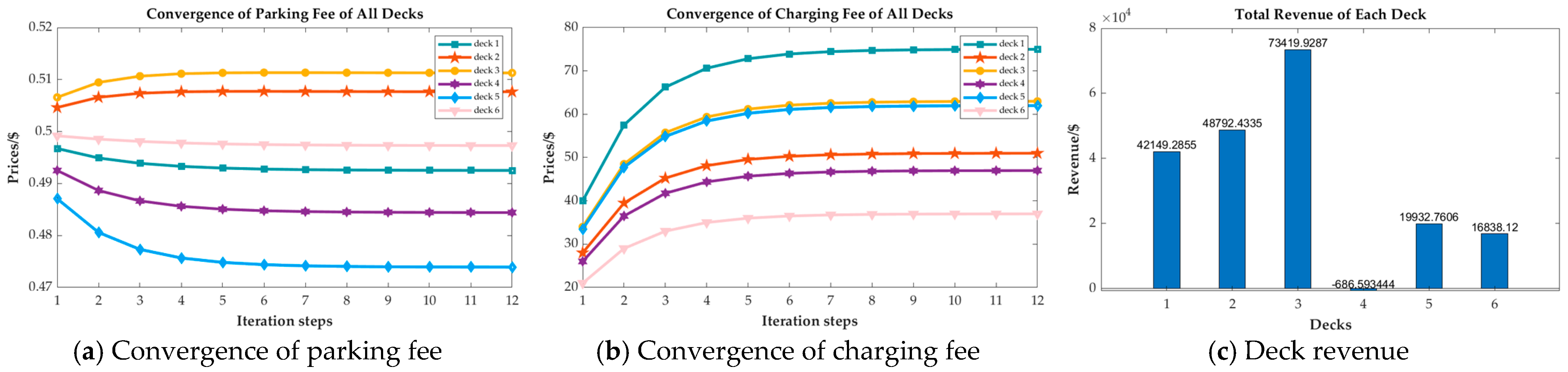
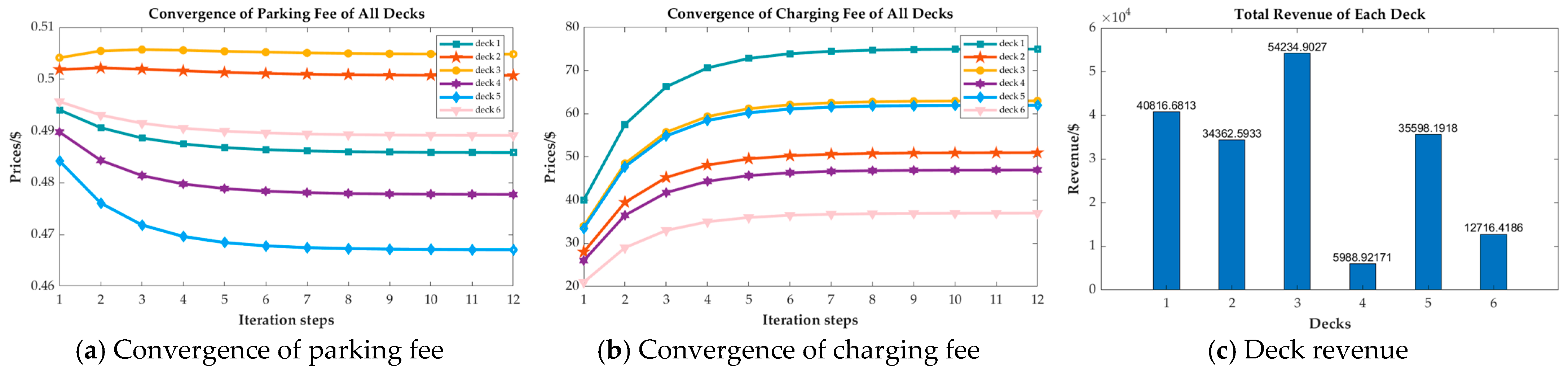
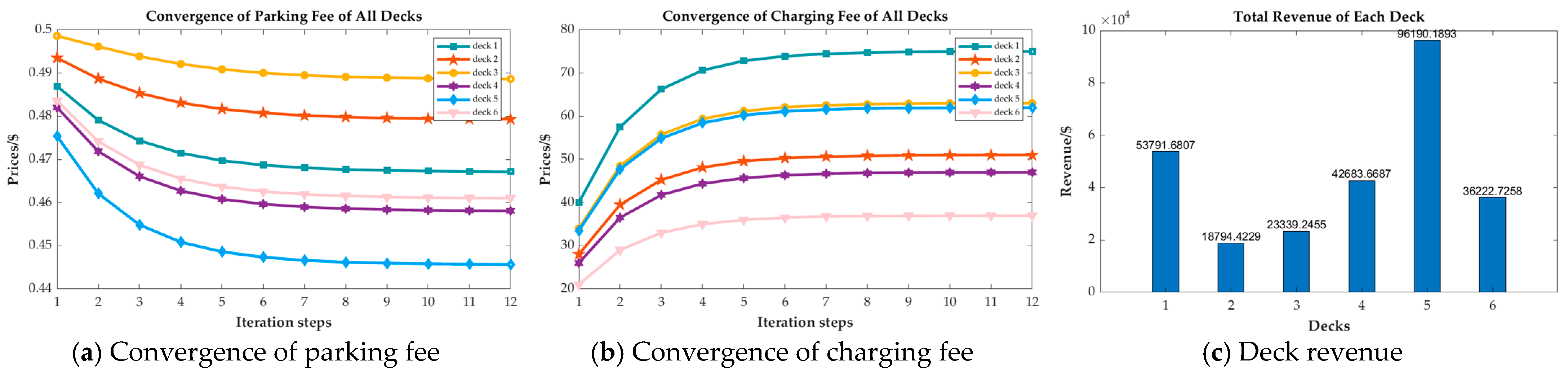
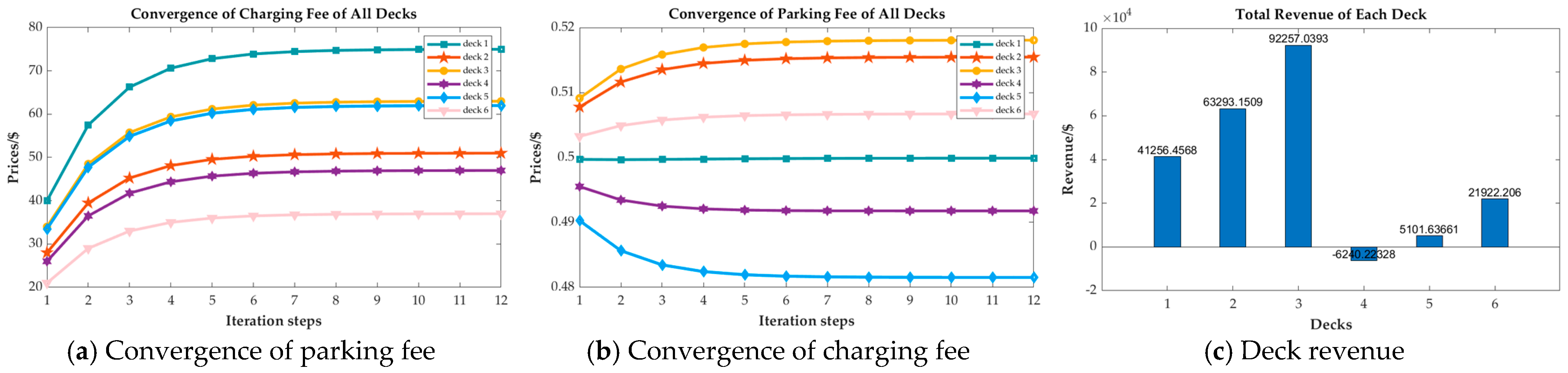
4.2.1. Check of Convergence
4.2.2. Evaluate Customer Influences
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xing, J.; Leard, B.; Li, S. What does an electric vehicle replace. J. Environ. Econ. Manag. 2021, 107, 102432. [Google Scholar] [CrossRef]
- Un-Noor, F.; Padmanaban, S.; Mihet-Popa, L.; Mollah, M.N.; Hossain, E. A Comprehensive Study of Key Electric Vehicle (EV) Components, Technologies, Challenges, Impacts, and Future Direction of Development. Energies 2007, 10, 1217. [Google Scholar] [CrossRef]
- Chen, T.; Zhang, X.P.; Wang, J.; Li, J.; Wu, C.; Hu, M.; Bian, H. A review on electric vehicle charging infrastructure development in the UK. J. Mod. Power Syst. Clean Energy 2020, 8, 193–205. [Google Scholar] [CrossRef]
- Szinai, J.; Sheppard, C.J.; Abhyankar, N.; Gopal, A.R. Reduced grid operating costs and renewable energy curtailment with electric vehicle charge management. Energy Policy 2020, 136, 111051. [Google Scholar] [CrossRef]
- Chen, T.; Zhang, B.; Pourbabak, H.; Kavousi-Fard, A.; Su, W. Optimal Routing and Charging of an Electric Vehicle Fleet for High-Efficiency Dynamic Transit Systems. IEEE Trans. Smart Grid 2016, 9, 3563–3572. [Google Scholar] [CrossRef]
- Lai, K.; Chen, T.; Natarajan, B. Optimal scheduling of electric vehicles car-sharing service with multi-temporal and multi-task operation. Energy 2020, 204, 117929. [Google Scholar] [CrossRef]
- Manríquez, F.; Sauma, E.; Aguado, J.; de la Torre, S.; Contreras, J. The impact of electric vehicle charging schemes in power system expansion planning. Appl. Energy 2020, 262, 114527. [Google Scholar] [CrossRef]
- Wang, C.; Gao, Z.; Yang, P.; Wang, Z.; Li, Z. Electric Vehicle Charging Facility Planning Based on Flow Demand—A Case Study. Sustainability 2021, 13, 4952. [Google Scholar] [CrossRef]
- Ashfaq, M.; Butt, O.; Selvaraj, J.; Rahim, N. Assessment of electric vehicle charging infrastructure and its impact on the electric grid: A review. Int. J. Green Energy 2021, 18, 657–686. [Google Scholar] [CrossRef]
- Cui, Y.; Hu, Z.; Duan, X. Optimal Pricing of Public Electric Vehicle Charging Stations Considering Operations of Coupled Transportation and Power Systems. IEEE Trans. Smart Grid 2021, 12, 3278–3288. [Google Scholar] [CrossRef]
- Su, W.; Chow, M.Y. Performance evaluation of an EDA-based large-scale plug-in hybrid electric vehicle charging algorithm. IEEE Trans. Smart Grid 2021, 3, 308–315. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhou, Y.; Jiang, C.; Wang, Y.; Zhang, R.; Chen, G. Plug-in Electric Vehicle Charging with Multiple Charging Options: A Systematic Analysis of Service Providers’ Pricing Strategies. IEEE Trans. Smart Grid 2021, 12, 524–537. [Google Scholar] [CrossRef]
- Helmus, J.R.; Lees, M.H.; Hoed, R.V.D. A data driven typology of electric vehicle user types and charging sessions. Transp. Res. Part C: Emerg. Technol. 2020, 115, 102637. [Google Scholar] [CrossRef]
- Su, W.; Wang, J.; Zhang, K.; Huang, A.Q. Model predictive control-based power dispatch for distribution system consider-ing plug-in electric vehicle uncertainty. Electr. Power Syst. Res. 2014, 106, 29–35. [Google Scholar] [CrossRef]
- Cao, W.; Wan, Y.; Wang, L.; Wu, Y. Location and capacity determination of charging station based on electric vehicle charging behavior analysis. IEEJ Trans. Electr. Electron. Eng. 2021, 16, 827–834. [Google Scholar] [CrossRef]
- Chen, T.; Pourbabak, H.; Liang, Z.; Su, W. An integrated eVoucher mechanism for flexible loads in real-time retail electricity market. IEEE Access 2017, 5, 2101–2110. [Google Scholar] [CrossRef]
- Zhang, Q.; Sun, T.; Ding, Z.; Li, C. Nodal dynamic charging price formulation for electric vehicle through the Stackelberg game considering grid congestion. IET Smart Grid 2021, 4, 461–473. [Google Scholar] [CrossRef]
- Moschella, M.; Murad, M.A.A.; Crisostomi, E.; Milano, F. Decentralized Charging of Plug-In Electric Vehicles and Impact on Transmission System Dynamics. IEEE Trans. Smart Grid 2020, 12, 1772–1781. [Google Scholar] [CrossRef]
- Zhou, X.; Zou, S.; Wang, P.; Ma, Z. Voltage regulation in constrained distribution networks by coordinating electric vehicle charging based on hierarchical ADMM. IET Gener. Transm. Distrib. 2020, 14, 3444–3457. [Google Scholar] [CrossRef]
- Wei, Z.; Li, Y.; Zhang, Y.; Cai, L. Intelligent parking garage EV charging scheduling considering battery charging characteristic. IEEE Trans. Ind. Electron. 2017, 65, 2806–2816. [Google Scholar] [CrossRef]
- Solanke, T.U.; Ramachandaramurthy, V.K.; Yong, J.Y.; Pasupuleti, J.; Kasinathan, P.; Rajagopalan, A. A review of strategic charging–discharging control of grid-connected electric vehicles. J. Energy Storage 2020, 28, 101193. [Google Scholar] [CrossRef]
- Das, R.; Wang, Y.; Putrus, G. Multi-objective techno-economic-environmental optimization of electric vehicle for energy ser-vices. Appl. Energy 2020, 257, 113965. [Google Scholar] [CrossRef]
- Xiong, Y.; Gan, J.; An, B.; Miao, C.; Bazzan, A.L.C. Optimal Electric Vehicle Fast Charging Station Placement Based on Game Theoretical Framework. IEEE Trans. Intell. Transp. Syst. 2017, 19, 2493–2504. [Google Scholar] [CrossRef]
- Ma, J.; Hou, Y.; Wang, Z.; Yang, W. Pricing strategy and coordination of automobile manufacturers based on government intervention and carbon emission reduction. Energy Policy 2021, 148, 111919. [Google Scholar] [CrossRef]
- Zavvos, E.; Gerding, E.H.; Brede, M. A Comprehensive Game-Theoretic Model for Electric Vehicle Charging Station Competition. IEEE Trans. Intell. Transp. Syst. 2021, 23, 12239–12250. [Google Scholar] [CrossRef]
- Guo, Y.; Xiong, J.; Xu, S.; Su, W. Two-Stage Economic Operation of Microgrid-Like Electric Vehicle Parking Deck. IEEE Trans. Smart Grid 2015, 7, 1703–1712. [Google Scholar] [CrossRef]
- Tu, H.; Feng, H.; Srdic, S.; Lukic, S. Extreme Fast Charging of Electric Vehicles: A Technology Overview. IEEE Trans. Transp. Electrif. 2019, 5, 861–878. [Google Scholar] [CrossRef]
- Qu, X.; Yu, Y.; Zhou, M.; Lin, C.-T.; Wang, X. Jointly dampening traffic oscillations and improving energy consumption with electric, connected and automated vehicles: A reinforcement learning based approach. Appl. Energy 2019, 257, 114030. [Google Scholar] [CrossRef]
- Sun, X.; Li, Z.; Wang, X.; Li, C. Technology Development of Electric Vehicles: A Review. Energies 2019, 13, 90. [Google Scholar] [CrossRef]
- Liu, K.; Li, Y.; Hu, X.; Lucu, M.; Widanage, W.D. Gaussian Process Regression With Automatic Relevance Determination Kernel for Calendar Aging Prediction of Lithium-Ion Batteries. IEEE Trans. Ind. Inform. 2020, 16, 3767–3777. [Google Scholar] [CrossRef]
- Hu, X.; Zhang, K.; Liu, K.; Lin, X.; Dey, S.; Onori, S. Advanced Fault Diagnosis for Lithium-Ion Battery Systems: A Review of Fault Mechanisms, Fault Features, and Diagnosis Procedures. IEEE Ind. Electron. Mag. 2020, 14, 65–91. [Google Scholar] [CrossRef]
- Paraskevas, A.; Aletras, D.; Chrysopoulos, A.; Marinopoulos, A.; Doukas, D.I. Optimal Management for EV Charging Stations: A Win–Win Strategy for Different Stakeholders Using Constrained Deep Q-Learning. Energies 2022, 15, 2323. [Google Scholar] [CrossRef]
- De Hoog, J.; Alpcan, T.; Brazil, M.; Thomas, D.A.; Mareels, I. Optimal charging of electric vehicles taking distribution network constraints into account. IEEE Trans. Power Syst. 2014, 30, 365–375. [Google Scholar] [CrossRef]
- Nikaidô, H.; Isoda, K. Note on non-cooperative convex game. Pac. J. Math. 1955, 5, 807–815. [Google Scholar] [CrossRef]
- Aubin, J.P. Mathematical Methods of Game and Economic Theory; Courier Corporation: Chelmsford, MA, USA, 2007. [Google Scholar]
- Uryas’ ev, S.; Rubinstein, R.Y. On relaxation algorithms in computation of noncooperative equilibria. Autom. Control IEEE Trans. 1994, 39, 1263–1267. [Google Scholar] [CrossRef]
- Krawczyk, J.B.; Uryasev, S. Relaxation algorithms to find Nash equilibria with economic applications. Environ. Model. Assess. 2000, 5, 63–73. [Google Scholar] [CrossRef]
- Saad, W.; Han, Z.; Poor, H.V.; Basar, T. Game-Theoretic Methods for the Smart Grid: An Overview of Microgrid Systems, Demand-Side Management, and Smart Grid Communications. IEEE Signal Process. Mag. 2012, 29, 86–105. [Google Scholar] [CrossRef]

| Customer Categories | Description | Whether Sensitive to Parking Price | Whether Sensitive to Charging Price | Examples |
|---|---|---|---|---|
| Loyalty customers (LC) | Consists of loyal customers who spend the same amount time charging on a fixed deck each day. | No | No | Customers who live or work locally and do not care about financial expenses. |
| Less-sensitive customers (LSC) | Consists of customers who choose the same deck each day, but whose charging duration varies with the charging price. | Yes | No | Customers who live or work locally, care about financial expenses, and care more about convenience between economy and convenience. |
| Sensitive customers (SC) | Consists of customers who use variable charging decks and have variable charging durations whose choices are influenced by both the price of the deck and the average price of all other decks. | Yes | Yes | Passing customers who are willing to spend time on economic planning. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, M.; Chen, T.; Gao, C.; Ma, R.; Su, W.; Kavousi-Fard, A. A Game-Theoretic Approach to Solve Competition between Multi-Type Electric Vehicle Charging and Parking Facilities. World Electr. Veh. J. 2023, 14, 59. https://doi.org/10.3390/wevj14030059
Jiang M, Chen T, Gao C, Ma R, Su W, Kavousi-Fard A. A Game-Theoretic Approach to Solve Competition between Multi-Type Electric Vehicle Charging and Parking Facilities. World Electric Vehicle Journal. 2023; 14(3):59. https://doi.org/10.3390/wevj14030059
Chicago/Turabian StyleJiang, Meihui, Tao Chen, Ciwei Gao, Rui Ma, Wencong Su, and Abdollah Kavousi-Fard. 2023. "A Game-Theoretic Approach to Solve Competition between Multi-Type Electric Vehicle Charging and Parking Facilities" World Electric Vehicle Journal 14, no. 3: 59. https://doi.org/10.3390/wevj14030059
APA StyleJiang, M., Chen, T., Gao, C., Ma, R., Su, W., & Kavousi-Fard, A. (2023). A Game-Theoretic Approach to Solve Competition between Multi-Type Electric Vehicle Charging and Parking Facilities. World Electric Vehicle Journal, 14(3), 59. https://doi.org/10.3390/wevj14030059









