Abstract
With the popularity and promotion of electric vehicles (EVs), virtual power plants (VPPs) provide a new means for the orderly charging management of decentralized EVs. How to set the price of electricity sales for VPP operators to achieve a win–win situation with EV users is a hot topic of current research. Based on this, this paper first proposes a Stackelberg game model in which the VPP participates in the orderly charging management of EVs as a power sales operator, where the operator guides the EV users to charge in an orderly manner by setting a reasonable power sales price and coordinates various distributed resources to jointly participate in the power market. Furthermore, taking into account the impact of wind power output uncertainty on VPP operation, a robust optimization method is used to extend the deterministic Stackelberg game pricing model into a robust optimization model, and a robust adjustment factor is introduced to flexibly adjust the conservativeness of the VPP operator’s bidding scheme in the energy market. The model is then transformed into a robust mixed-integer linear programming (RMILP) problem solved by Karush–Kuhn–Tucker (KKT) conditions and strong dyadic theory. Finally, the effectiveness of the solution method is verified in the calculation example, which gives the optimal pricing strategy for the VPP operator, the optimal charging scheme for EV users, and the remaining internal resources’ contribution plan, providing an important idea for the VPP to centrally manage the charging behavior of EVs and improve its own operating revenue.
1. Introduction
With the accelerated progress of the “double carbon” goal, energy production is accelerated, clean energy consumption is highly electrified, energy allocation is increasingly platform-based, and energy utilization is gradually becoming more efficient [1,2]. The profound adjustment of the energy pattern will definitely bring significant changes to the future development of electric power systems [3,4]. In this process, electric vehicles (EVs) are vigorously promoted, with their advantages of energy savings and zero emissions. The grid connection of a large number of EVs can improve the utilization of resources in our electricity market on the one hand, but on the other hand it may also increase the peak-to-valley difference in grid load due to the disorderly charging behavior of EVs, which brings great challenges to the stable operation and efficient management of the grid [5,6,7].
At present, some scholars in China have conducted research on the orderly charging management of EVs after grid integration. Wei et al. [8] considered that the number of EVs in the jurisdiction is relatively large and requires decentralized management of EVs by means of agents, so the distribution of benefits between cell-charging agents and EVs can be realized based on Stackelberg game theory, but the number of EVs that can be dispatched by agents within it is small, and they do not have the ability to participate in electricity market transactions. Hou et al. [9] managed the orderly charging of EVs in charging stations through price and incentive demand response mechanisms, but they did not take into account that the charging process of EVs is stochastic. Zang et al. [10] determined the optimal EV charging and discharging strategy based on a model-free approach for interior point strategy optimization, but EV users could only participate in grid interactions as price receivers, and the authors did not consider the charging cost of EV users. Zhan et al. [11] established a bidding strategy for charging stations under the electricity retail market based on the non-cooperative game relationship between multiple charging station agents to achieve an orderly interaction between EVs and the grid, but they did not consider the equilibrium relationship between the interests of charging station agents and EVs. Cai et al. [12] proposed that multiple aggregators separately integrate large-scale EVs into the grid to participate in the electricity market bidding and guide EVs to optimize charging and discharging behavior in real time based on the bidding results, but they failed to consider that the basic attribute of EVs is transportation and that off-grid EVs do not have the ability to interact with the grid, which limits the ability of EV aggregators to integrate EV user groups to participate in electricity market transactions.
Because of the limitations of the EV orderly charging optimization theories in the above studies in enabling the effective utilization of multiregional, large-scale EVs in the power market and generating economies of scale in the power market, in this case, the virtual power plant (VPP) [13,14]—as a new type of operator in the power system—is more competitive in the power market because it can manage the charging behavior of massive amounts of EVs through advanced control, metering, and communication technologies, as well as integrating different types of distributed energy sources such as distributed power sources, energy storage, and flexible loads to provide efficient and stable power to the grid; these advantages enable the VPP to be more competitive in the electricity market [15]. Therefore, this paper adopts a VPP as an EV management concept for EV sales and coordinates multiple distributed resources to jointly participate in the power market, which can not only achieve the orderly grid entry of EVs and the coordination and complementation among multiple new energy sources, but also generate the corresponding socioeconomic benefits of making large-scale EVs.
Furthermore, when a VPP produces renewable energy, the VPP must consider the risk that uncertainty in renewable energy output poses to its market bidding decisions and economic operations [16]. Currently, the main methods to deal with the uncertainty of renewable energy are the stochastic programming method, the conditional value-at-risk (CVaR) method, and the robust optimization method. Yang et al. [17] dealt with the uncertainty of renewable energy output using the stochastic programming method, but it did not reflect the actual situation of the variables through only limited scenario simulation. Although Li et al. [18] and Wang et al. [19] used the CVaR method to ensure that the expected return under the corresponding scenario was not lower than the given confidence level, thereby reducing the risk of the system, the scenario analysis method itself led to a less accurate model. Compared with the above methods, the robust optimization method, as an optimization method that replaces the probability distribution of random variables with an uncertainty set [20], can effectively deal with the uncertainty of the power output of wind power or PV units and further improve the robustness of the VPP operator’s decision scheme, which is more suitable for the actual engineering needs [21]. All of the above analyses motivated us to build a Stackelberg game model of a VPP and EVs based on Stackelberg game theory and robust optimization ideas. The main contributions of this work are summarized as follows:
- (1)
- For the problem of orderly charging management of EV customers, based on Stackelberg theory, we propose a Stackelberg game model in which a VPP acts as the electricity sales operator and coordinates resources such as wind turbines, energy storage, and demand response loads to participate in the orderly charging management of EVs. Among them, the VPP guides EVs’ orderly charging by specifying a reasonable pricing strategy, which not only solves the problem of balanced benefit distribution between the VPP and EVs, but also realizes the advantages of multiple distributed resources to complement one another.
- (2)
- Based on the existing electric power communication network resources, this paper integrates multiple kinds of data such as demand response, energy storage management and other business systems, distributed energy, and EV charging station monitoring, and combines communication technologies such as broadband power line carriers, micropower wireless, Wi-Fi Halow, and 5G networks to build a communication structure for VPP–grid interaction. In addition, this paper also proposes a supporting operation model for the VPP to manage EVs’ participation in power market trading, in conjunction with the actual day-ahead market trading process.
- (3)
- Considering the impact of wind power output volatility on VPP operation revenue, this paper extends the deterministic Stackelberg game optimization model into a robust optimization model through a strong pairwise theory and robust optimization method, introduces the robust adjustment coefficient as a measure of risk–return for VPP operators, and compares the impacts of different robust adjustment coefficients on VPP operation revenue under nominal parameters in the calculation example. This can provide an important reference for VPPs to optimize their operation strategies according to their own risk preferences.
- (4)
- The impact of different maximum energy storage capacity on the VPP’s operating revenue is investigated for a given robust regulation factor, and the optimal maximum energy storage capacity for this VPP system is summarized by the analysis.
The rest of this paper is organized as follows: In Section 2, the communication structure of the VPP is built based on the existing power communication network resources, and the operation model of the VPP is given based on the existing market transaction rules. In Section 3, a Stackelberg game pricing model for a VPP with EV determinism is built based on Stackelberg game theory. In Section 4, the Stackelberg game model of the VPP and EVs is transformed into a mixed-integer linear programming (MILP) problem by first linearizing the nonlinear part of the objective function and constraints based on strong dyadic theory and KKT conditions. Then, the original MILP problem is extended to a robust mixed-integer linear programming (RMILP) problem by introducing robust conditioning coefficients in the deterministic bidding model based on the robust optimization idea. Finally, the solution method of the RMILP problem is given. In Section 5, the validity of the solution method is verified by example analysis, and important conclusions such as the optimal pricing strategy for VPP operators and the optimal charging strategy for EV users are presented. Finally, in Section 6, the important contributions and conclusions of this work are highlighted.
2. The Communication Structure of the VPP and Its Operation Mode
2.1. Communication Structure of the VPP
The VPP in this paper consists of four parts: wind turbine, energy storage equipment, demand response load, and EVs. Its communication network architecture is based on the existing electric power communication network resources and incorporates multiple sources and types of data, such as demand response, energy storage equipment management and other business systems, distributed energy, and EV charging station monitoring. In the local communication layer of the VPP, demand response loads, DERs, energy storage, EVs, and other multiple business terminals transmit local data through plug-and-play communication units with multiple communication technologies, such as broadband power line carriers (HPLC) and micropower wireless/Wi-Fi Halow as a backup to one another. The communication band of the VPP can be considered to use 230 MHz [22]—a dedicated frequency band for electricity—and the 40 and 25 kHz frequency points in this band are aggregated by using IF carrier aggregation to meet the minimum 1 MHz communication bandwidth requirement of Wi-Fi Halow. The VPP’s participation in power market transactions and interaction with the grid leads to the gradual extension of control-type services—such as distributed power control and demand response—to the medium- and low-voltage distribution network. The time delay and security of traditional 4G networks no longer meet the basic service requirements of the VPP, so the VPP should adopt 5G networks with the advantages of low time delay and high reliability to realize the communication and data transmission with power trading center. The communication structure of the VPP interacting with the power grid is shown in Figure 1 below.
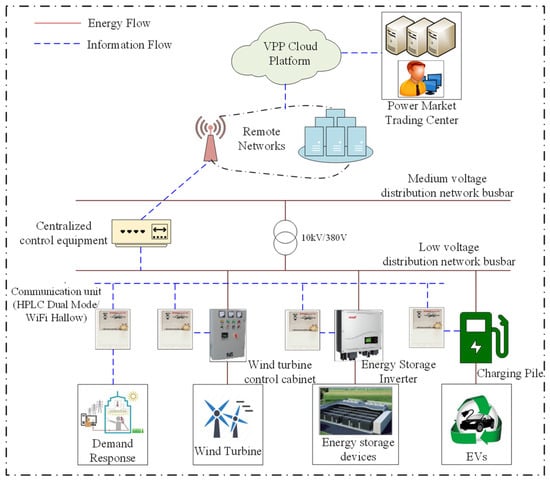
Figure 1.
The communication structure of the VPP interacting with the power grid.
2.2. Operational Model of the VPP
Assuming that the VPP participates in the day-ahead electricity market (DAM) as a price receiver [23], EV users charge according to the charging price and charging slots agreed with the VPP operator, and the rest of the distributed resources purchase and sell electricity according to the basic tariff of the grid; the specific operation model of the VPP is as follows:
- (1)
- Before the end of the energy market transaction on day (D), EV users shall submit to the operator the charging periods and power demand for day (D + 1). Based on the power demand of EV users, the VPP shall coordinate and optimize internal resources to determine the power demand for each period on day (D + 1) and draw up the corresponding power purchase and sale plan.
- (2)
- The VPP operator will promptly release the tariff information for each period on day (D + 1) to EV customers after signing a power purchase and sale contract with the grid in the day-ahead market. In addition, this paper stipulates that the VPP operator’s retail electricity price for selling electricity to EV users shall not be higher than the grid’s benchmark sale price, and that the average daily sale price shall be set to fully guarantee the basic interests of EV customers. For example, if the operator deliberately raises the price of electricity in a certain period, the price of electricity in other periods is required to be lower than the average price of electricity, and then the intelligent terminal will naturally choose the “valley price” period to charge EV users automatically.
- (3)
- After the EV is connected to the charging pile, the intelligent charging terminal on the pile will automatically control the EV’s charging and pay the charging fee for the user instantly. At the same time, the operator can assess the performance of EV users who do not charge at the agreed time.
3. The Stackelberg Game Model of the VPP and EVs
3.1. The Objective Function of the Upper-Level Problem of the Stackelberg Game Model
The upper-level description of the Stackelberg game model in Figure 2 is an optimization problem with the objective of maximizing the daily operating revenue of the VPP operator as the solution, and its objective function is shown in Equation (1) below:
where is the scheduling period of the VPP, taken as 24 h; is the scheduling step, taken as 1 h; is the total number of EVs dispatched by the VPP operator; is the charging power of the -th EV in time period ; is the operation and maintenance cost of energy storage equipment in time period ; is the scheduling cost of demand response load in time period ; and is the transaction cost of the VPP in the DAM in time period .
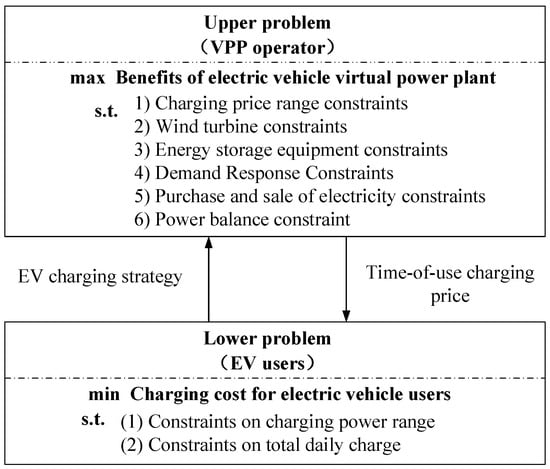
Figure 2.
The Stackelberg game structure of the VPP and EVs.
- (1)
- The cost of the energy storage equipment [24]:
- (2)
- The scheduling costs for demand response loads [7,25]:
- (3)
- The transaction costs of the VPP in the day-ahead market:
3.2. Constraints on the Upper-Level Problem of the Stackelberg Game Model
- (1)
- Constraints related to the price of electricity sold by VPP operators:
- (2)
- Constraints related to wind turbines:
- (3)
- Constraints related to energy storage devices:
- (4)
- Demand-response-related constraints:
In addition, since auxiliary variables are introduced in the process of converting Equation (3) to Equation (4), the corresponding constraints need to be added as follows:
- (5)
- Constraints related to the VPP’s purchase and sale of electricity:
- (6)
- Constraints related to power balance:
3.3. The Objective Function and Constraints of the Lower-Level Problem of the Stackelberg Game Model
The lower layer of the model describes the optimization problem of the EV users’ charging strategy as follows:
where is the ratio of the minimum power required for the -th EV trip to the maximum capacity of the onboard battery, is the maximum capacity of the onboard battery of the -th EV, is the initial power of the onboard battery when the -th EV is on the network, is the maximum charging power of the -th EV, and is the charging period of the EV.
In the above equations, the objective function Equation (21) indicates that the EV users should minimize their charging costs at the tariff given by the VPP operator. Equation (22) indicates that the EV should charge to the travel demand power at the off-grid moment. Equation (23) indicates that the charging power of the EV after going off-grid is 0.
Because in Equations (1)–(24) EV users will actively choose charging periods according to the charging prices provided by the VPP operators for each period, and the VPP operators will also optimize the charging tariffs for each period according to the EV users’ charging periods, the pricing strategy of the VPP operators’ and EV users’ charging strategies form a Stackelberg game relationship. Therefore, and in Equation are both variables. In addition, the VPP will face the influence of many random factors in actual operation; in particular, the prediction accuracy of wind power output is difficult to guarantee, and the VPP scheduling scheme obtained by the deterministic wind power prediction output value will often appear risky, so should be a random variable rather than a deterministic value.
Therefore, the Stackelberg model with random variables established in this section is neither linear nor convex and cannot be solved directly by the solver. The focus of the next section is to transform the two-level nonlinear programming problem with random variables shown in Equations (1)–(24) into a robust mixed-integer linear programming (RMILP) problem that can be solved by using the KKT condition and strong dyadic theory, thereby finding the equilibrium point between the interests of both sides of the Stackelberg game.
4. Solving Method
4.1. Equivalent Nonlinear Programming Transformation of Stackelberg Game Models
For the lower-level problem in the Stackelberg game model, since the EV receives a charging price that is already set by the VPP at the time of decision-making, it is first necessary to replace Equations (21)–(24) by the KKT condition [26] to obtain the constraint relations of variables and . Assuming that the pairwise variables corresponding to Equations (21)–(24) are , , and , respectively, their corresponding KKT conditions are as follows:
The above Equations (30) and (31) represent the complementary relaxation conditions of the original constraint and its dual variables, which need to be linearized in order to be solved because they are nonlinear.
Next is the linearization of the complementary relaxation conditions. Referring to the Big-M method in the literature [27], Equations (30) and (31) can be transformed into the following linear inequalities by introducing the Boolean variable :
After transformation, Equations (32)–(35) are equivalent to the original Equations (30) and (31). Furthermore, the objective function Equation (1) needs to be linearized. Since both and are independent variables in Equation, is a nonlinear composite variable and cannot be solved directly. The strong dyadic theory shows that in the event that the original problem has an optimal solution, the value of the objective function at its optimal solution is equal to that of the dyadic problem, so the following equation holds:
Thus, the nonlinear part of Equation (1) has been linearized by equivalent substitution, and the Stackelberg game model of the VPP and EVs has been reduced to a mixed-integer linear programming (MILP) problem that can be solved directly.
4.2. Robust Transformation of Deterministic Stackelberg Game Models
Furthermore, this paper considers that the predicted values of wind turbine output should be in the uncertainty interval :
where is the maximum deviation of wind turbine output in the VPP in time period .
Thus, the wind power output prediction in the inequality of Equation (8) should be a random variable and no longer a set of definite values. According to the robust optimization principle introduced in the appendix of the literature [28], the original MILP problem can be transformed into the RMILP problem shown in the following equations:
where and are auxiliary decision variables introduced to describe the range of variation of uncertain parameters , and is also an auxiliary variable introduced, but not a decision variable. is the robust adjustment factor, and . When , the VPP operator is not concerned about the impact of wind power output uncertainty on the system’s operation. When , the larger the value of , the more sensitive the VPP operator is to changes in uncertainty, and the more conservative the operation strategy is.
Therefore, the VPP operator can control the risk of system operation due to the deviation of wind power output forecast by adjusting the coefficient to balance the robustness and economy of the VPP’s operation.
5. Case Study
5.1. Basic Parameters of the Algorithm
The calculations in this paper set the EVs after equivalence aggregation into three groups, with 50, 100, and 350 EVs, respectively, for a total of 500 EVs. The charging time slots for each group of EVs are shown in Table 1 (where “1” means that EVs are charged in that time slot, and “0” means that they are not charged in that time slot). According to the driving characteristics and charging behaviors of the EVs, in order to simulate all possible EV charging preferences, Group 1 EVs are set as “early departure and late return”, Group 2 EVs are set as “regular work and rest”, and Group 3 EVs are set as “late night work”. The basic parameters of the three groups of EVs are shown in Table 2. The electricity market purchase prices set in reference [29] are shown in Table 3. To prevent the VPP from arbitrage from the market, the VPP sells electricity to the day-ahead market at the price . The upper limit of retail tariff pricing for EV users , and the lower limit ; the average price = 0.5 (CNY/). The operating parameters of the remaining resources within the VPP system are shown in Table 4. In this paper, the maximum deviation of wind power output fluctuation is considered to be 15% of the predicted value [30], and the predicted values of wind power output are shown in Table 5.

Table 1.
Electric vehicles’ charging time.

Table 2.
Electric vehicle parameters.

Table 3.
Time-of-use period and price parameters.

Table 4.
Operating parameters of the VPP.

Table 5.
Predicted values of wind turbine output.
5.2. Optimal Solution with Standard Parameters
Based on the nominal parameters in Section 5.1, taking , the optimal operating revenue of the VPP operator is CNY 5744.3, and the minimum charging cost to the EV user is CNY 7197.6. The optimal power sales pricing of the VPP, the optimal charging strategy of the EV users, the wind turbine output power, the charging and discharging power of the energy storage devices, the actual and desired power of the demand response load, and the purchased and sold power of the VPP are shown in Figure 3, Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8, respectively.
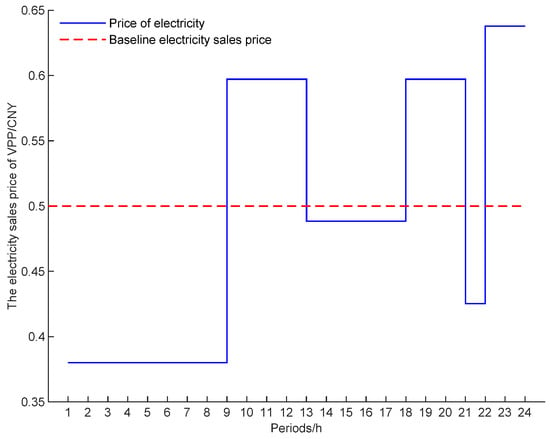
Figure 3.
Optimal pricing strategy of the VPP.
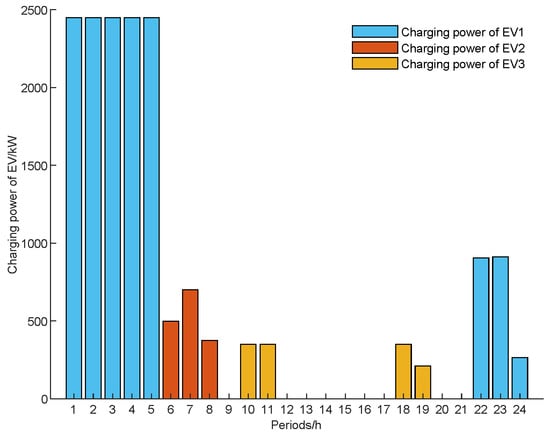
Figure 4.
Optimal charging strategy for the EV users.
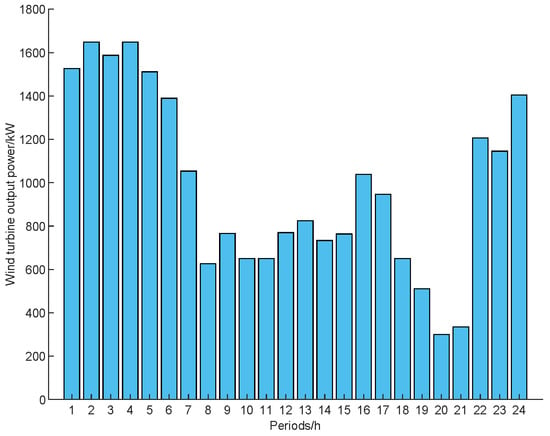
Figure 5.
Wind turbine output power.
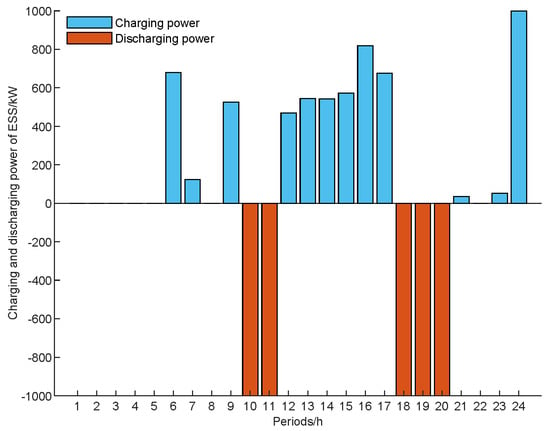
Figure 6.
Charge and discharge power of the energy storage devices.
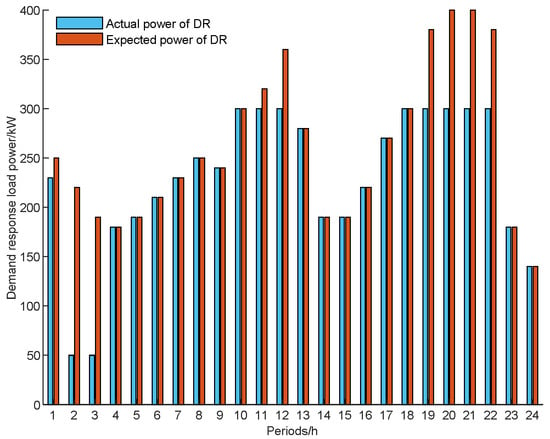
Figure 7.
The actual and expected power of the demand response load.
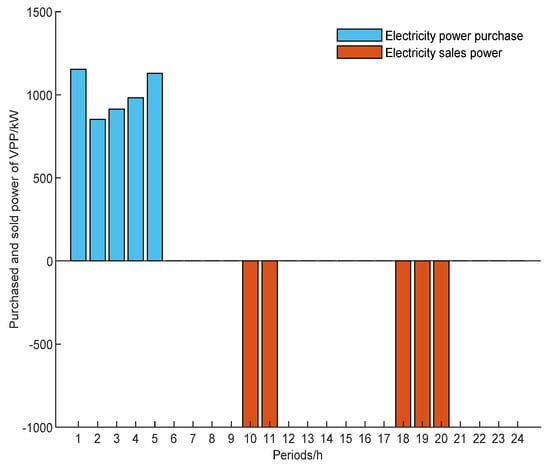
Figure 8.
Power purchased and sold by the VPP.
In Figure 3 and Figure 4, since the number of EVs in the “early departure and late return” group is significantly higher than the other two groups, the VPP operators always set the tariff to the upper limit of the baseline electricity price for that period during the period when Group 1 EVs are charging, and they lower the tariff during the period when Group 1 EVs are not charging, in order to meet the average price constraint for the whole day. In addition, the electricity sales tariff drawn up by the VPP does not theoretically fully satisfy the charging benefit needs of Group 1 EV users; however, from a macro business perspective, this pricing strategy meets the VPP’s benefit needs and minimizes the charging cost for all EV users while meeting the travel electricity demand.
In Figure 5, Figure 6, Figure 7 and Figure 8, the power required to charge EVs and energy storage devices in the VPP from 1:00 to 8:00 mainly comes from clean electricity from wind turbines, and the shortage is purchased uniformly by the VPP from the market. From 9:00 to 12:00, with the increase in the grid’s time-of-use tariff, the VPP operator will arrange for the output of energy storage devices and load shedding through demand response as much as possible, in order to gain additional revenue while meeting the basic charging needs of EVs. Since 13:00 to 17:00 is the “flat tariff” period, the VPP operator will adjust some of the demand response load from the “peak tariff” period to this period so that the actual demand response load is the same as the expected load value. From 18:00 to 20:00 is the “peak tariff” period, where the VPP operator will set a higher charging price to guide the EV users to choose the charging period reasonably, while at the same time releasing the stored power in the energy storage equipment to gain as much revenue as possible. From 21:00 to 24:00 is the “normal tariff” period, and the wind power resources are richer during this period, so the VPP will give priority to selling the electricity generated by wind turbines to EV users, and the surplus electricity will be stored in the energy storage equipment to achieve a balance between supply and demand and avoid the “abandoned wind” phenomenon.
5.3. Influence of EV Proportion on the Optimal Solution
With the total number of EVs and the robust adjustment factor unchanged, the optimal pricing strategy for VPP operators with different EV ratios is obtained by varying the ratio of each type of EV, and the optimal pricing strategy of the VPP operator for different EV ratios is obtained by taking , , , , and (as shown in Figure 9) and the revenue of the VPP operator and the charging cost for the EV users (as shown in Figure 10).
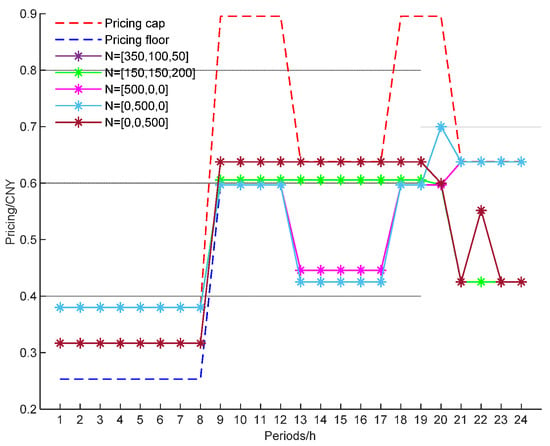
Figure 9.
VPP pricing results under different EV proportions.
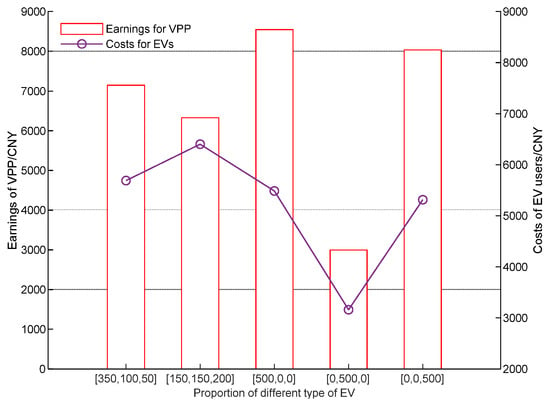
Figure 10.
Optimization results of VPP operating benefits and EV power purchase costs.
In Figure 9, the optimal pricing strategy of the VPP is adjusted when the proportion of EVs changes, subject to a certain total number of EVs, which is mainly influenced by the number of EVs of each charging type. For example, when the ratio of EVs is —i.e., there are more “early morning and late evening” vehicles in the EV group—the nighttime pricing of VPP sales will be relatively higher because of the high demand for nighttime charging of these EVs; when the ratio of EVs is —i.e., there are only “late-night working” vehicles in the EV group—the nighttime pricing of the VPP will be relatively higher. When the proportion of EVs is “late-night working”, the nighttime pricing of the VPP is set to the base price, while the daytime pricing is set to a higher level.
In Figure 10, the operating revenue of the VPP and the charging cost for EV users are higher when or , while the operating revenue and charging cost of the VPP are lowest when . This is mainly determined by the acceptable charging periods for each group of EVs, as Group 2 EVs have more acceptable charging periods and a larger timespan, so they can choose to complete charging during the “valley tariff” hours to avoid excessive charging costs. However, the actual charging cost is still lower than the cost of purchasing electricity directly from the real-time market, and from this point of view all EV users save on charging costs.
Furthermore, the profitability of the VPP operator is slightly lower when the ratio of EVs of the three types is more even. This is because the VPP cannot set the charging price too high for each time slot in order to meet the demand for multiple charging slots, leading in turn to a reduction in total profitability. However, when the EV charging type in the VPP is too homogeneous, the operator will raise the price for that type of EV charging session to maximize profitability.
5.4. Impact of Robust Adjustment Factors on the VPP’s Operating Income
In order to compare the effects of different robust adjustment factors () on the VPP’s operating revenue, Table 6 below shows the variation in the VPP’s operating revenue with different robust adjustment coefficients.

Table 6.
Predicted value of wind turbine output.
In Table 6, as increases, the operator’s use of wind power output becomes gradually more conservative, which then leads to a gradual decrease in the VPP’s operating revenue. When changes from 0 to 1, it indicates that the VPP’s attitude toward wind power usage gradually changes from proactive to pessimistic and conservative. However, the charging cost of EV users does not change during this process. This indicates that when the VPP’s use of wind turbine output changes, the operator will always prioritize the interests of EV users and will not transfer the risk cost to the charging cost of EV users, but will rely on the energy storage within the VPP, the regulated capacity of the demand response load, or the purchase and sale of electricity in the market to maintain the stable operation of the system.
5.5. Influence of Energy Storage Equipment Capacity on the Optimal Solution
For a given robust adjustment coefficient, assuming that the maximum capacity of the energy storage equipment varies from 2000 to 5000 , the change step is 100 , and the corresponding trend of operating revenue of the VPP operators is shown in Figure 11 below.
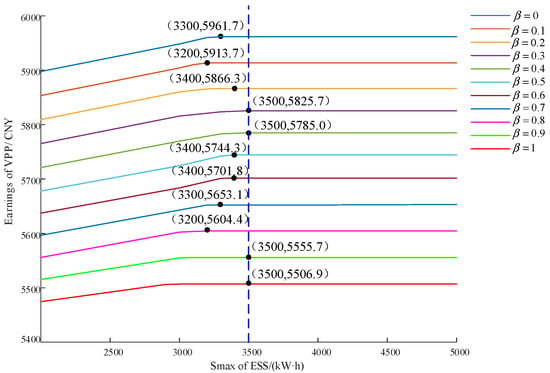
Figure 11.
Income of VPP operators under the maximum capacity of different energy storage equipment.
In Figure 11, regardless of the value of the robust adjustment coefficient () set by the VPP operator, the operating revenue of the VPP gradually increases and then stabilizes as the maximum capacity of energy storage () increases. For example, when , as long as the maximum energy storage capacity () is greater than or equal to 3400 , the VPP operator can obtain a stable operating revenue of CNY 5744.3. This is because the larger the storage capacity, the more power the VPP can store during the “valley tariff” hours, and then the VPP can obtain higher additional revenue from the sale of electricity during the “peak tariff” hours. However, when the capacity increases to a certain level, the capacity may be wasted due to the limitation of the storage power itself, so the revenue of the VPP will eventually stabilize.
In addition, in order for the VPP operators to obtain stable operating revenue with any robust adjustment factor, the above figure shows that the maximum capacity of energy storage should be set at 3500 (kW·h) for the VPP system.
6. Conclusions
- (1)
- In this paper, we propose a Stackelberg game model in which the VPP operator participates in the orderly charging management of EVs as the main objective of electricity market reform in China, with the opening up of the electricity sales side as the background. In the model, the VPP operator does not need to directly intervene in the charging behavior of EV customers but only issues charging tariffs, and EV customers are no longer just passive “price takers” but can freely choose charging periods according to their charging preferences. This optimal management idea takes into account both the response of EV users’ charging strategies to the VPP price and the influence of the pricing scheme on EV users’ charging behavior. The optimization result of the Stackelberg game achieves a win–win situation for both sides of the VPP and EV game.
- (2)
- In this paper, the nonlinear master–slave game model is transformed into a solvable robust mixed-integer linear programming problem by KKT conditions and strong dyadic theory, and the optimal pricing strategy for the VPP operator and the optimal charging scheme for the EV user are accurately derived. Under the nominal parameters, the optimal operating revenue of the VPP operator is CNY 5744.3, and the minimum charging cost to the EV user is CNY 7197.6.
- (3)
- The results of the algorithm can truly and reasonably reflect the change in the VPP operator’s revenue when the robust adjustment factor changes. Therefore, the operator can flexibly measure the relationship between risk and return according to the attitude towards the use of wind power output and the output characteristics of controllable resources in the VPP, while adjusting the robust adjustment factor to maximize its operating return in the energy market.
- (4)
- The results show that increasing the maximum capacity of the energy storage device within a certain range is an important way for the VPP operator to steadily increase their operating profit. By varying the maximum capacity of energy storage with different robust adjustment coefficients, the optimal maximum capacity of energy storage adapted to this VPP system is 3500 .
Author Contributions
Software, J.T.; resources, K.Z.; data curation, Q.Y.; funding acquisition, Q.L. All authors have read and agreed to the published version of the manuscript.
Funding
The State Grid Zhejiang Electric Power Company Key Science and Technology Projects (B311DJ220004).
Data Availability Statement
Not applicable.
Acknowledgments
This research was supported by the State Grid Zhejiang Electric Power Company Key Science and Technology Projects “Construction of a highly resilient power trading system based on source-grid-load-storage interaction and pilot green Asian Games market trading” (B311DJ220004).
Conflicts of Interest
Q.L. and J.T. are employees of Zhejiang Power Exchange Center Company Ltd. K.Z. is an employee of State Grid Ningbo Power Supply Company. Q.Y. is an employee of Zhejiang Huayun Information Technology Co. Ltd. This paper reflects the views of the scientists and not the companies for which they work.
References
- Mansouri, S.A.; Jordehi, A.R.; Marzband, M.; Tostado-Véliz, M.; Jurado, F.; Aguado, J.A. An IoT-enabled hierarchical decentralized framework for multi-energy microgrids market management in the presence of smart prosumers using a deep learning-based forecaster. Appl. Energy 2023, 333, 120560. [Google Scholar] [CrossRef]
- Guo, C.X. Carbon neutrality by 2060 leads to fundamental changes in China’s economic system. J. Beijing Univ. Technol. (Soc. Sci. Ed.) 2021, 21, 64–77. [Google Scholar]
- Mansouri, S.A.; Nematbakhsh, E.; Javadi, M.S.; Jordehi, A.R.; Shafie-khah, M.; Catalão, J.P. Resilience Enhancement via Automatic Switching considering Direct Load Control Program and Energy Storage Systems. In Proceedings of the 2021 IEEE International Conference on Environment and Electrical Engineering and 2021 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Bari, Italy, 7–10 September 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Mansouri, S.A.; Ahmarinejad, A.; Sheidaei, F.; Javadi, M.S.; Jordehi, A.R.; Nezhad, A.E.; Catalao, J.P. A multi-stage joint planning and operation model for energy hubs considering integrated demand response programs. Int. J. Electr. Power Energy Syst. 2022, 140, 108103. [Google Scholar] [CrossRef]
- Mansouri, S.A.; Ahmarinejad, A.; Nematbakhsh, E.; Javadi, M.S.; Jordehi, A.R.; Catalão, J.P. Energy Hub Design in the Presence of P2G System Considering the Variable Efficiencies of Gas-Fired Converters. In Proceedings of the 2021 International Conference on Smart Energy Systems and Technologies (SEST), Vaasa, Finland, 6–8 September 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Zhang, L.; Zhu, L.Z.; Chen, N.; Zhao, D.; Qu, L. Review on generic model for renewable energy generation. Autom. Electr. Power Syst. 2015, 39, 129–138. [Google Scholar]
- Song, J.Q.; Yang, Y.B.; Xu, Q.S.; Liu, Z.Q.; Zhang, X.Y. Robust Bidding Game Method for Multiple Virtual Power Plants to Participate in Day-ahead Power Market. Electr. Power Autom. Equip. 2023, 1–23. [Google Scholar] [CrossRef]
- Mansouri, S.A.; Ahmarinejad, A.; Javadi, M.S.; Nezhad, A.E.; Shafie-Khah, M.; Catalão, J.P. Demand response role for enhancing the flexibility of local energy systems. Distrib. Energy Resour. Local Integr. Energy Syst. 2021, 9, 279–313. [Google Scholar]
- Wei, W.; Chen, Y.; Liu, F.; Mei, S.W.; Tian, F.; Zhang, X. Stackelberg Game Based retailer pricing scheme and EV charging management in smart residential area. Power Syst. Technol. 2015, 39, 939–945. [Google Scholar]
- Hou, H.; Wang, Y.; Zhao, B. Electric Vehicle Aggregator Dispatching Strategy Under Price and Incentive Demand Response. Power Syst. Technol. 2022, 46, 1259–1269. [Google Scholar]
- Zang, H.Z.; Ye, Y.J.; Tang, Y. Constrained Electric Vehicle Charging and Discharging Strategy Based on Safe Reinforcement Learning. Power Syst. Technol. 2023, 1–12. [Google Scholar] [CrossRef]
- Zhan, X.; Yang, J.; Han, S.; Zhou, T.; Wu, F.Z.; Liu, S. Two-stage Market Bidding Strategy of Charging Station Considering Schedulable Potential Capacity of Electric Vehicle. Autom. Electr. Power Syst. 2021, 45, 86–96. [Google Scholar]
- Cai, G.W.; Jiang, Y.Q.; Huang, N.T.; Yang, D.Z.; Pan, X.; Shang, W.Y. Large-scale Electric Vehicles Charging and Discharging Optimization Scheduling Based on Multi-agent Two-level Game Under Electricity Demand Response Mechanism. Proc. CSEE 2023, 43, 85–98. [Google Scholar]
- Bai, X.Y.; Fan, Y.F.; Wang, T.S.; Liu, Y.J.; Nie, X.L.; Yan, C.Y. Dynamic aggregation method of virtual power plants considering reliability of renewable energy. Electr. Power Autom. Equip. 2022, 42, 102–110. [Google Scholar]
- Tian, L.; Cheng, L.; Guo, J.; Wang, X.; Yun, Q.; Gao, W. A Review on the Study of Management and Interaction Mechanism for Distributed Energy in Virtual Power Plants. Power Syst. Technol. 2020, 44, 2097–2108. [Google Scholar]
- Kang, C.Q.; Chen, Q.X.; Su, J.; AI, Q.; Ji, Y.; Pan, W.W.; Gao, H.C.; Wu, M. Scientific Problems and Research Framework of Virtual Power Plant with Enormous Flexible Distributed Energy Resources in New Power System. Autom. Electr. Power Syst. 2022, 46, 3–14. [Google Scholar]
- Zhou, B.; Lv, L.; Gao, H.; Liu, J.; Chen, Q.; Tan, X. Robust Day-Ahead Trading Strategy for Multiple Virtual Power Plants. Power Syst. Technol. 2018, 42, 2694–2703. [Google Scholar]
- Yang, F.; Wang, W.Q.; He, S.; Zhao, H.L.; Cheng, J. Stochastic Planning of Wind-Storage-Vehicle Capacity Based on Multi-Scenario Operation Simulation. High Volt. Eng. 2023, 1–15. [Google Scholar] [CrossRef]
- Li, Q.; Zhu, D.D.; Huang, D.; Wu, S.J.; Yang, Y.B.; Song, J.Q. Pricing strategy of Stackelberg game between virtual power plant operators and electric vehicles users. Electr. Power Eng. Technol. 2022, 41, 183–191. [Google Scholar]
- Wang, H.; Wang, J.; Wang, C.; Zhang, G.; Fan, M. Risk-constrained Energy Management Modeling of Virtual Power Plant. Proc. CSEE 2017, 37, 5942–5950. [Google Scholar]
- Qiu, H.; Gu, W.; Liu, P.; Sun, Q.; Wu, Z.; Lu, X. Application of two-stage robust optimization theory in power system scheduling under uncertainties: A review and perspective. Energy 2022, 251, 123942. [Google Scholar] [CrossRef]
- Liu, Y.X.; Guo, L.; Wang, C.S. Economic Dispatch of Microgrid Based on Two Stage Robust Optimization. Proc. CSEE 2018, 38, 4013–4022. [Google Scholar]
- Wang, W.Q.; Su, J.; Pan, J.; Zhang, H.; Gao, K.Q.; Liu, C. Prospect of Research on Communication Network Architecture and Key Technologies for Virtual Power Plant. Autom. Electr. Power Syst. 2022, 46, 15–25. [Google Scholar]
- Sun, Z.X.; Liu, H.Q.; Zhao, Z.; Ding, J.; Chang, C. Research on economical efficiency of energy storage. Proc. CSEE 2013, 33, 54–58. [Google Scholar]
- Zhou, Y.; Sun, G.; Huang, W.; Xu, Z.; Wei, Z.; Zhang, H.; Chu, Y. Strategic Bidding Model for Virtual Power Plant in Different Electricity Markets Considering Electric Vehicles and Demand Response. Power Syst. Technol. 2017, 41, 1759–1767. [Google Scholar]
- Zhang, B.; Li, Q.; Wang, L.; Feng, W. Robust optimization for energy transactions in multi-microgrids under uncertainty. Appl. Energy 2018, 217, 346–360. [Google Scholar] [CrossRef]
- Fortuny-Ama, J.; Mccarl, B. A representation and economic interpretation of a two-level programming problem. J. Oper. Res. Soc. 1981, 32, 783–792. [Google Scholar] [CrossRef]
- Dominguez, R.; Baringo, L.; Conejo, A.J. Optimal offering strategy for a concentrating solar power plant. Appl. Energy 2012, 98, 316–325. [Google Scholar] [CrossRef]
- Wang, X.Y.; Liu, D.N.; Liu, Q.; Liu, M.G.; Wang, J.N.; Gao, Y.; Wang, X.F.; Song, Y.H. Operation Mechanism and Key Technologies of Virtual Power Plant Under Ubiquitous Internet of Things. Power Syst. Technol. 2019, 43, 3175–3183. [Google Scholar]
- China Electricity Council. NB/T 32011-2013 Technical Requirement of Power Forecasting System for PV Power Station; National Energy Administration of China: Beijing, China, 2013. (In Chinese)
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).