Abstract
For the neutral point clamped (NPC) three-level converter fed permanent magnet synchronous motor (PMSM) system, the performance of the conventional model predictive current control (MPCC) algorithm will be deteriorated if the amplitude of the neutral point potential (NPP) is large. Additionally, the adjustment process of the weighted coefficients of the conventional MPCC algorithm is complex because of numerous control terms in the cost function. To solve the above issues, an improved MPCC algorithm is proposed in this paper. Firstly, Newtonian iteration is used to transfer the stator current into stator voltage in the cost function. Then, the NPP term in the conventional cost function can be eliminated by introducing the partition control of the NP potential, which also eliminates the whole adjustment process of weighting coefficients. Finally, based on the amplitude of the NPP, the amplitude and phase angle of medium and small vectors are modified to improve the control performance of the torque and flux. Experimental results show that the fluctuation of the neutral point potential can be suppressed rapidly. Meanwhile, the performance of the torque, flux and current are also improved compared with the conventional MPCC.
1. Introduction
PMSMs have the advantages of a simple structure, high power density, low operating noise and high efficiency [1,2,3]. Compared with the conventional two-level converter, the NPC three-level converter possesses advantages such as low voltage stress, high output waveform quality and low switching loss [4,5,6]. Thus, the NPC three-level converter fed PMSM system is widely used in high-power medium-voltage motor drive applications such as electric traction and ship propulsion.
For MPCC, the discrete switching characteristic of the converter is considered, and the switching state minimizing the cost function is selected as the input for the next control period. The multi-objective optimization can be easily obtained by MPCC. Moreover, MPCC can be easily implemented and system constraints can be easily handled [7]. Therefore, it has been widely researched in industry and academia.
When MPCC is applied to NPC three-level inverter fed PMSM systems, the NPP term has to be added into the cost function with d-axis and q-axis stator current terms, which can achieve multi-objective optimal control of the current and NPP. In the cost function of the conventional MPCC algorithm, current and NPP terms have different dimensions, so it is necessary to adjust various weighting coefficients, which means the adjustment process is complicated. The weighting coefficient of the stator current term needs to be increased if the stator current ripple is considered as the primary control objective. However, the NPP ripple will rise if the weighting coefficient of the stator current term is much larger than that of the NPP term, which will also affect the control performance of the stator current.
The stator current terms can be transferred into either a torque/flux term [8,9,10,11] or a stator voltage term [12,13,14,15] for simplification. Alternatively, the stator current term can also be unified as the duration of the voltage vector [16]. Although the d-axis and q-axis stator current terms can be unified as one, the neutral point potential term still remains in the cost function. Thus, weighted coefficients still need to be adjusted.
In [17], a two-stage MPCC algorithm is proposed to reduce the NPP ripple of an NPC three-level inverter fed PMSM system. For the first stage, six medium vectors are used to construct the finite control set. For the second stage, large and zero vectors that do not affect the NPP and small vectors that reduce the NPP ripple are adopted to establish the finite control set. Thus, the NPP ripple can be effectively restrained. In [18], the finite control set is composed of basic voltage vectors and virtual voltage vectors that do not affect the NPP, such that an inherent DC-link voltage balancing can be achieved. In [19,20,21,22], the voltage offset is added to the reference voltage in the cost function. Medium vectors and redundant states of small vectors are selected appropriately to construct the finite control set according to the power factor. Then, the NPP ripple can be suppressed. Although the NPP ripple can be reduced by the above algorithms, the amplitude and phase angle of small and medium vectors will be changed when the imbalance of the NPP is large (DC voltage is imbalanced or the capacitance of the upper and lower DC-link capacitor is not equal). If the finite control set is still constructed according to the original basic voltage vectors, the control performance will be deteriorated.
An improved MPCC algorithm is proposed in this paper. The adjusting process of the weighted coefficients is eliminated. Meanwhile, the neutral point potential imbalance can be rapidly suppressed. For the proposed MPCC, the Newton iteration method is used to obtain the predictive model. Then, the neutral point potential partition control is introduced to eliminate the adjusting process of the weighted coefficients in the cost function. The amplitude and phase angle of basic vectors are modified when the amplitude of the neutral point potential is large. Furthermore, the FCS is reconstructed and the alternative vectors in the FCS are brought into the cost function. Then, the optimal vector for the next control period can be obtained.
2. Conventional MPCC
The topology of the NPC three-level converter fed PMSM system is shown in Figure 1. Vdc is the voltage of the DC source. C1 and C2 are DC-link capacitors. Each phase consists of power devices Sx1~Sx4 and clamping diodes Dx1 and Dx2, where x ϵ {A, B, C}.
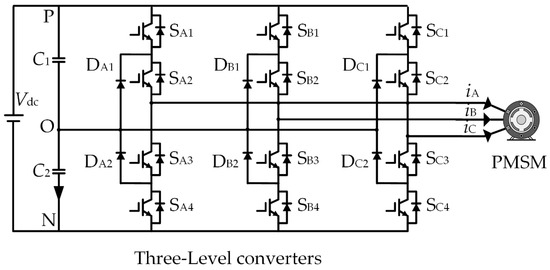
Figure 1.
NPC three-level converter fed PMSM system.
The switching states and output voltages of each phase are shown in Table 1.

Table 1.
Output voltage corresponding to each switching state.
For three-level converters, there are three switching states for each phase. Thus, a total of 33 = 27 switching states can be output for three phases, corresponding to 19 basic voltage vectors in the space vector diagram, as shown in Figure 2. According to the amplitude, they can be divided into: large vectors (V1, V3, V5, V7, V9, V11), medium vectors (V2, V4, V6, V8, V10, V12), small vectors (V13~V18) and zero vectors (V19).
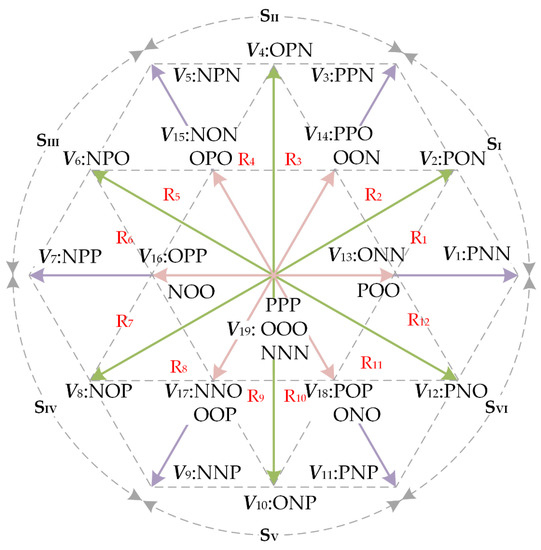
Figure 2.
Space vector diagram of NPC three-level converter.
When the neutral point of the DC-link is directly connected to the load, the charging and discharging of the DC-link capacitor by the load current will cause the fluctuation of the neutral point potential vo.
The relationship between vo and neutral point current io can be expressed as follows:
where C is the value of the DC-link capacitor. The neutral point current can be represented by the three-phase switching state and the load current as
where Sx denotes the switching state of each phase, Sxϵ{1, 0, −1}. Substituting (2) into (1) and discretizing by the forward Euler method, the predictive value of vo at (k + 1)Ts is obtained as
where = [|| || ||], = [|| || ||].
The current predictive model of PMSM in the d-q axis coordinate system is obtained by the forward Euler discretization method as
where Ts is the sample period; k and k + 1 represent the kTs and (k + 1)Ts sample period, respectively; ud and uq are d-axis and q-axis components of the stator voltage, respectively; id and iq are d-axis and q-axis components of the stator current, respectively; Ld and Lq are d-axis and q-axis components of the stator inductance, respectively; Rs is the stator resistance; ψf is the stator flux; and ωr is the rotor electricity angular speed.
For the NPC three-level converter fed PMSM system, the neutral point potential balance needs to be taken into account when designing the cost function. Therefore, the cost function of MPCC generally includes a stator current term and a neutral point potential term, shown as follows
where and are the reference values of id and iq, respectively, and λi and λv denote the weighted coefficients for the stator current term and the neutral point potential term.
The block diagram of MPCC is shown in Figure 3 and the algorithm is executed in the following steps:
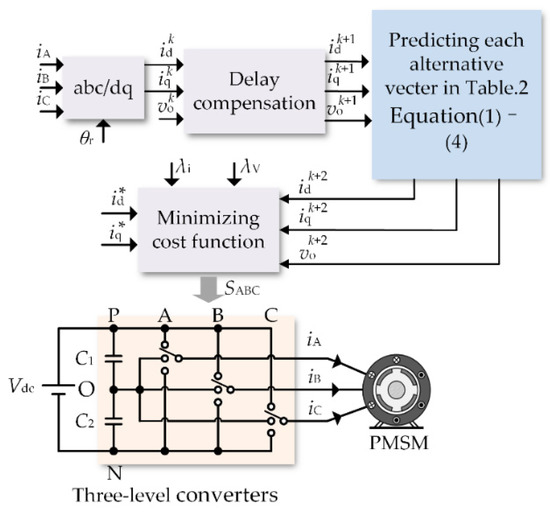
Figure 3.
The block diagram of conventional MPCC.
- (1)
- Stator currents and neutral point potentials are sampled at kTs;
- (2)
- From (3) and (4), , and at (k + 1)Ts are obtained and can be used as the initial values of the algorithm;
- (3)
- The sector in which the optimal vector of the last control period was located is determined, and the alternative vector set can be established as Table 2. The alternative vectors in Table 2 are substituted into (3) and (4) to obtain (n), (n) and (n) at (k + 2)Ts, n = 1, 2,…, m, where m denotes the number of alternative vectors;
 Table 2. Alternative voltage vectors of conventional MPCC.
Table 2. Alternative voltage vectors of conventional MPCC. - (4)
- According to (5), the cost function corresponding to each alternative voltage vector in the FCS is calculated, and the voltage vector corresponding to the minimum value of the cost function is selected to act on the converter.
3. Proposed MPCC
3.1. Newton’s Iterative Algorithm
Conventional MPCC uses a forward Eulerian formula to discretize the predictive model. Due to the truncation errors, the predictive value of the motor at the next control period is inaccurate. In this paper, the predictive accuracy of the algorithm is improved by using Newton’s iteration method to normalize the stator current term in (5) as
where
The MPCC algorithm can be transformed into a quadratic optimization problem of (6) under the constraint (7). In this paper, based on the Hessian matrix, the stator voltage to be controlled at the next period is iterated by the Newton iteration method. The Hessian matrix can be expressed as
where the subscript r corresponds to the rth iterations, and the forward Newton iteration algorithm is
Substituting (7) into (8) yields the following:
where γ (0 < γ ≤ 1) is the control coefficient for the number of iterations. Moreover, the iteration convergence condition ε (0 < ε ≤ 1) is introduced, i.e., the Euclidean norm of the difference between the results of two successive iterations does not exceed the error ε.
3.2. Dynamic Division of Sectors
When the neutral point potential is shifted significantly, the amplitude and phase angle of medium vectors and small vectors in the space vector diagram will change, which in turn affects the control performance of the system. In order to quantify the neutral point potential imbalance, the imbalance coefficients d1 and d2 are defined as follows:
where vc1 and vc2 correspond to the upper and lower voltage of the DC-link capacitor, respectively.
Taking sub-regions R1 and R2 in sector SI as an example, the change of the basic voltage vectors under the imbalanced neutral point potential (d1 = 0.5 and d2 = 1.5) are shown in Figure 4.
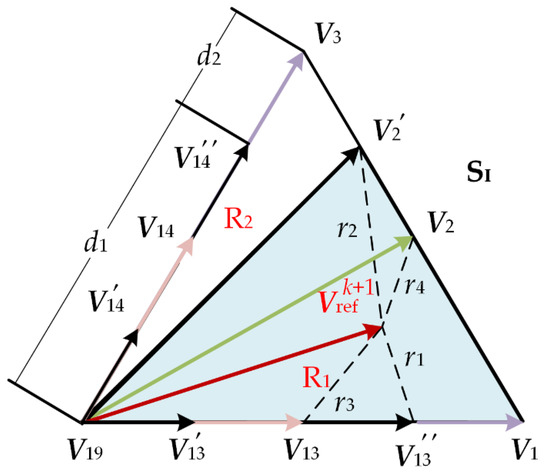
Figure 4.
Medium and small vectors for d1 = 0.5 and d2 = 1.5.
From Figure 4, the amplitude and phase angle of the medium vector change, from V2 to . The phase angle of small vectors remains the same while the amplitude changes, from V13 to (ONN) and (POO), respectively, and from V14 to (ONN) and (PPO), respectively. Assuming the reference vector is located in the position shown in Figure 4, for conventional MPCC, the distance r4 between V2 and is shorter than the distance r3 between V13 and ; thus, V2 is the optimal vector. When the neutral point potential rises, V2 and V13 will become and /, respectively. The distance r2 between and is greater than the distance r1 between and
; thus, is actually the optimal vector.
In summary, it can be seen that the amplitude and the phase angle of basic voltage vectors will be changed when the neutral point potential rises. If the basic vectors shown in Figure 2 are still used as alternative vectors to establish the FCS, it will cause the optimal vector to be selected incorrectly. In this paper, the amplitude and the phase angle of medium and small vectors are modified according to the amplitude of the neutral point potential. The basic voltage vector in the two-phase stationary coordinate system can be calculated as follows:
The amplitude of the small vectors as well as the amplitude and phase angle of the medium vectors can be calculated by (12). After the actual basic vectors of the three-level converter have been calculated, the space vector diagram can be dynamically divided. Figure 5 shows the space vector diagram for the imbalance coefficients d1 = 0.5 and d2 = 1.5.
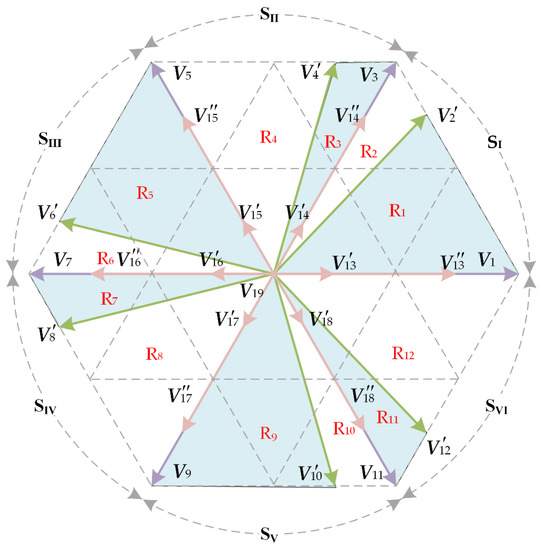
Figure 5.
Space vector diagram of three-level converter for d1 = 0.5 and d2 = 1.5.
3.3. The Partition Control of Neutral Point Potential Imbalance
When the amplitude of the neutral point potential is small, the change of the amplitude and phase angle of basic vectors is not significant. The neutral point potential term in the cost function can be omitted. Only the stator voltage is considered as the control target. When the amplitude of the neutral point potential is large, the change of the amplitude and phase angle of basic vectors cannot be ignored. In such a case, the neutral point potential is taken as the control target, and the stator voltage term is omitted to ensure the rapid balance of the neutral point potential.
From the above analysis, it can be seen that the amplitude of the neutral point potential can be divided into two regions for control. By reasonably designing the threshold, the weighted coefficients are eliminated while ensuring the control performance of the system.
(1) Control strategy of region I
When the neutral point potential amplitude is less than the threshold, the neutral point potential term in (5) is eliminated and the cost function becomes
The amplitude of the neutral point potential is small, and the effect on the amplitude and phase angle of basic voltage vectors can be ignored. The sector is still divided according to Figure 2 and the corresponding alternative vector set is shown in Table 3.

Table 3.
Alternative voltage vector in region I.
(2) Control strategy of region II
When the neutral point potential amplitude is greater than the threshold, the stator current term in (5) is eliminated and the cost function becomes
In such a case, the amplitude of the neutral point potential is large and the amplitude and phase angle of basic vectors need to be modified according to (13). Only medium vectors as well as small vectors are adopted to establish the FCS, as shown in Table 4.

Table 4.
Alternative voltage vector at region II.
The block diagram of the proposed MPCC algorithm is shown in Figure 6. The implementation process of the improved MPCC algorithm is as follows:
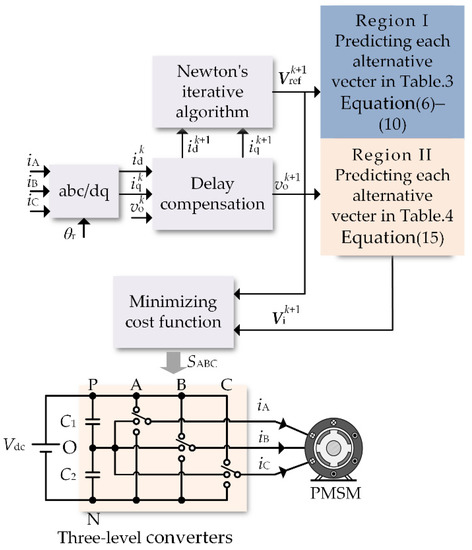
Figure 6.
The block diagram of the proposed MPCC.
- (1)
- The stator current and the neutral point potential are sampled at kTs;
- (2)
- From (3) and (4), , and at (k + 1)Ts are obtained and can be used as the initial values of the algorithm;
- (3)
- The reference voltage vector is calculated by (6) and the FCS is selected according to the amplitude of the neutral point potential;
- (4)
- The alternative vector with the minimum value of the cost function is selected as the optimal vector and applied to the converter.
4. Experimental Results
4.1. Experimental Platform
In this paper, a three-level converter fed PMSM system is set up and the dSPACE rapid control prototyping simulator is used as the controller. The performance of the conventional model predictive current control (MPCC1, with (5) as the cost function and Table 2 as the finite control set), MPCC2 [17] and the proposed improved model predictive current control (MPCC3, with (14) and (15) as the cost function, Table 3 and Table 4 as the finite control set and the neutral point potential threshold set to 20 V) are compared. The experimental prototype is shown in Figure 7, and the experimental parameters are shown in Table 5.

Figure 7.
Experimental prototype.

Table 5.
Rated parameters of PMSM.
4.2. Experimental Analysis
4.2.1. Control Performance of the Neutral Point Potential
The amplitude of the neutral point potential is set to 40 V (vC1 = 140 V, vC2 = 180 V) to verify the neutral point potential balance capability of MPCC1 and MPCC3. Figure 8 shows the variation of the neutral point potential (vo = vC1 − vC2). It can be seen that the amplitude of the neutral point potential returns to zero for both MPCC1 and MPCC3. The settling times for MPCC1 and MPCC3 are 0.96 s and 0.61 s, respectively. The settling time of MPCC3 is shorter than that of MPCC1. The control performance of the neutral point potential is improved by the proposed MPCC.
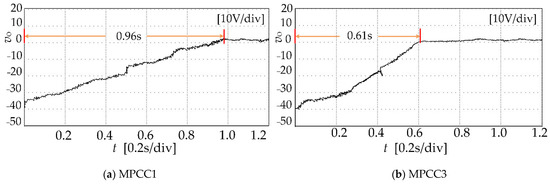
Figure 8.
Neutral point potential balance capability.
4.2.2. Control Performance under Steady State
For different load torque TL and motor speed nr operating conditions (case 1: TL = 5 N·m, nr = 500 r/min, vc1 = 140 V, vc2 = 180 V; case 2: TL =10 N·m, nr = 500 r/min, vc1 = 140 V, vc2 = 180 V), the experimental results of the stator current iA, electromagnetic torque Te (The experimental result of torque is estimated by the stator current, flux linkage and rotator position), amplitude of stator flux |ψs| and neutral point potential vo are shown in Figure 9 and Figure 10. It can be seen that when the amplitude of the neutral point potential is large, the current and torque fluctuation of MPCC3 is lower than that of MPCC1 and MPCC2. As for MPCC3, the change of the amplitude and the phase angle of basic vectors are fully considered and the actual optimal vector is selected.
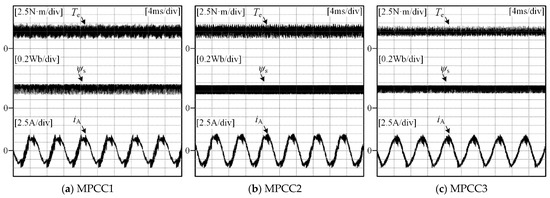
Figure 9.
Experimental results of MPCC1, MPCC2 and MPCC3 (case 1).
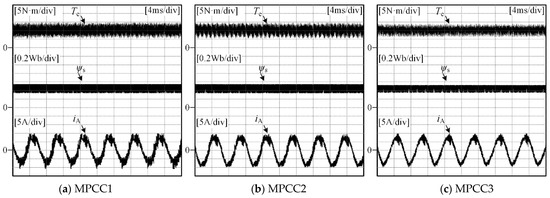
Figure 10.
Experimental results of MPCC1, MPCC2 and MPCC3 (case 2).
The torque fluctuation rate DT and flux fluctuation rate Dψ are used as torque performance and flux performance indicators and are defined as follows:
where Te_max and Te_min represent the maximum and minimum values of electromagnetic torque and |ψs|_max and |ψs|_min represent the maximum and minimum values of stator flux.
The total harmonic distortion of the output current ITHD is used as the current performance evaluation index and is defined as follows.
where I1 denotes the rms value of the fundamental component of the output current and In denotes the rms value of the nth harmonic component. Figure 11 shows the DT, Dψ and ITHD for case 1 and case 2.
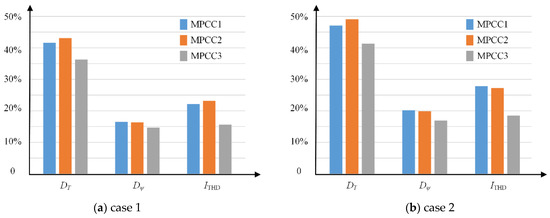
Figure 11.
Performance evaluation indicators for case 1 and case 2.
From Figure 11, under large neutral point potential conditions, the DT, Dψ and ITHD of MPCC3 are all lower than those of MPCC1 and MPCC2, which verifies that the steady state performance of the improved MPCC is superior to that of conventional MPCC.
4.2.3. Control Performance under Dynamic State
Under sudden change conditions (case 3: TL = 0 N·m→5 N·m, nr = 500 r/min), the experimental results of the stator current iA, electromagnetic torque Te, amplitude of stator flux |ψs| and neutral point potential vo are shown in Figure 12.
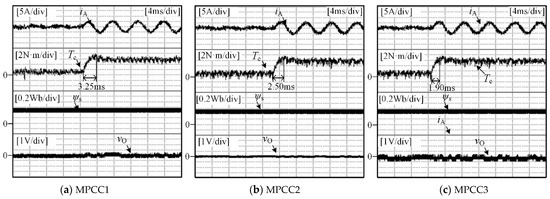
Figure 12.
Experimental results of MPCC1, MPCC2 and MPCC3 (case 3).
It can be seen from Figure 12 that the dynamic processes of MPCC1, MPCC2 and MPCC3 are 3.25 ms, 2.50 ms and 1.90 ms, respectively, for case 3. The dynamic performance of the proposed MPCC is better than that of the conventional MPCC.
Compared with MPCC1 and MPCC2, MPCC3 transfers the stator current term in the cost function into a stator voltage term, and completely eliminates the weight coefficients in the cost function by neutral point potential partition control. The neutral point potential can be balanced rapidly by the modification of the amplitude and the phase angle of basic vectors and reconstruction of the finite control set when the amplitude of the neutral point potential is large. The improved algorithm can effectively improve the dynamic and steady state performance.
5. Conclusions
For the conventional MPCC of the NPC three-level converter fed PMSM system, the adjustment process of the weighted coefficients is complicated. Moreover, the flux and torque performance are deteriorated when there is a large deviation of the neutral point potential. This paper proposes an improved MPCC algorithm to solve the above issue. The improved algorithm has the following advantages:
(1) The proposed MPCC transfers the stator current term in the cost function into a stator voltage term, and completely eliminates the weight coefficients in the cost function by neutral point potential partition control.
(2) The neutral point potential can be balanced rapidly by the modification of the amplitude and the phase angle of basic vectors and reconstruction of the finite control set when the amplitude of neutral point potential is large.
The experimental results show that the improved algorithm can effectively improve the dynamic and steady state performance under the neutral point potential imbalance conditions.
Author Contributions
Conceptualization, G.Z. and X.G; methodology, G.Z. and Q.L.; software, Q.L.; validation, Q.L.; formal analysis, J.W.; investigation, X.G.; resources, J.W.; data curation, J.W.; writing—original draft preparation, Q.L.; writing—review and editing, C.L.; visualization, C.L.; supervision, X.G.; project administration, X.G.; funding acquisition, X.G. and G.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by The National Natural Science Foundation of China, grant number 52177055 and Zhejiang Provincial Basic Public Welfare Research Projects, grant number LGG22E070011.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Cho, Y.; Lee, K.B.; Song, J.H.; Lee, Y., II. Torque-ripple minimization and fast dynamic scheme for torque predictive control of per-manent-magnet synchronous motors. IEEE Trans. Power Electron. 2015, 4, 2182–2190. [Google Scholar] [CrossRef]
- Rodriguez, J.; Bernet, S.; Steimer, P.K.; Lizama, I.E. A survey on neutral-point-clamped inverters. IEEE Trans. Ind. Electron. 2010, 57, 2219–2230. [Google Scholar] [CrossRef]
- Yang, Y.; Wen, H.; Fan, M.; Xie, M.; Chen, R. A fast finite-switching-state model predictive control method without weighting factors for T-type three-level three-phase inverters. IEEE Trans. Power Electron. 2019, 15, 1298–1310. [Google Scholar] [CrossRef]
- Xia, C.; Zhang, G.; Yan, Y.; Gu, X.; Shi, T.; He, X. Discontinuous space vector PWM strategy of neutral-point-clamped three-level inverters for output current ripple reduction. IEEE Trans. Power Electron. 2017, 32, 5109–5121. [Google Scholar] [CrossRef]
- Schweizer, M.; Friedli, T.; Kolar, J.W. Comparative evaluation of advanced three-phase three-level inverter/converter to-pologies against two-level systems. IEEE Trans. Ind. Electron. 2013, 12, 5515–5527. [Google Scholar] [CrossRef]
- Zhang, X.; Hou, B. Double vectors model predictive torque control without weighting factor based on voltage tracking error. IEEE Trans. Power Electron. 2018, 33, 2368–2380. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, X.; Xie, W.; Wang, F.; Dou, M.; Kennel, R.M.; Lorenz, R.D.; Gerling, D. Deadbeat Model-Predictive Torque Control With Discrete Space-Vector Modulation for PMSM Drives. IEEE Trans. Ind. Electron. 2017, 64, 3537–3547. [Google Scholar] [CrossRef]
- Xia, C.; Qiu, X.; Wang, Z.; Shi, T. Predictive torque control based on optimal operating time of vector. Proc. CSEE 2016, 36, 3045–3053. [Google Scholar]
- Xu, Y.; Li, Y.; Zhang, B.; Qin, Z. Three-vector based model predictive torque control of eliminating weighting factor. Trans. China Electrotech. Soc. 2018, 33, 3925–3934. [Google Scholar]
- Zhang, Y.; Yang, H. Generalized two-vector-based model predictive torque control of induction motor drives. IEEE Trans. Power Electron. 2015, 30, 3818–3829. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, H. Model-predictive flux control of induction motor drives with switching instant optimization. IEEE Trans. Energy Convers. 2015, 30, 1113–1122. [Google Scholar] [CrossRef]
- Xia, C.; Zhang, T.; Zhou, Z.; Zhang, G. Model predictive torque control with switching table for neutral point clamped three-level inverter-fed PMSM. Trans. China 12 Electrotech. Soc. 2016, 31, 83–92. [Google Scholar]
- Xie, W.; Wang, X.; Wang, F.; Xu, W.; Kennel, R.M.; Gerling, D.; Lorenz, R.D. Finite-Control-Set Model Predictive Torque Control with a Deadbeat Solution for PMSM Drives. IEEE Trans. Ind. Electron. 2015, 62, 5402–5410. [Google Scholar] [CrossRef]
- Rojas, C.A.; Rodriguez, J.; Villarroel, F.; Espinoza, J.R.; Silva, C.A.; Trincado, M. Predictive torque and flux control without weighting factors. IEEE Trans. Ind. Electron. 2013, 60, 681–690. [Google Scholar] [CrossRef]
- Yang, Y.; Chen, R.; Fan, M.; Xiao, Y.; Zhang, X.; Norambuena, M.; Rodriguez, J. Improved Model Predictive Current Control for Three-Phase Three-Level Converters with Neutral-Point Voltage Ripple and Common Mode Voltage Reduction. IEEE Trans. Energy Convers. 2021, 36, 3053–3062. [Google Scholar] [CrossRef]
- Alhosaini, W.; Diao, F.; Mahmud, M.H.; Wu, Y.; Zhao, Y. A Virtual Space Vector-Based Model Predictive Control for Inherent DC-Link Voltage Balancing of Three-Level T-Type Converters. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 9, 1751–1764. [Google Scholar] [CrossRef]
- Jun, E.-S.; Nguyen, M.H.; Kwak, S.-S. Model Predictive Control Method With NP Voltage Balance by Offset Voltage Injection for Three-Phase Three-Level NPC Inverter. IEEE Access 2020, 8, 172175–172195. [Google Scholar] [CrossRef]
- Pou, J.; Brnovich, D.; Pintado, R. New feedforward space -vector PWM method to obtain balanced AC output voltages in a three-level neutral-point-clamped converter. IEEE Trans. Power Electron. 2002, 49, 1026–1034. [Google Scholar] [CrossRef]
- Lewicki, A.; Krzeminski, Z.; Abu-Rub, H. Space-vector pulse width modulation for three-level NPC converter with the neutral point voltage control. IEEE Trans. Ind. Electron. 2011, 58, 5076–5086. [Google Scholar] [CrossRef]
- Xiang, C.-Q.; Shu, C.; Han, D.; Mao, B.-K.; Wu, X.; Yu, T.-J. Improved Virtual Space Vector Modulation for Three-Level Neutral-Point-Clamped Converter With Feedback of Neutral-Point Voltage. IEEE Trans. Power Electron. 2017, 33, 5452–5464. [Google Scholar] [CrossRef]
- Lopez, I.; Ceballos, S.; Pou, J.; Zaragoza, J.; Andreu, J.; Kortabarria, I.; Agelidis, V.G. Modulation Strategy for Multiphase Neutral-Point-Clamped Converters. IEEE Trans. Power Electron. 2015, 31, 928–941. [Google Scholar] [CrossRef]
- Kakosimos, P.; Abu-Rub, H. Predictive Speed Control with Short Prediction Horizon for Permanent Magnet Synchronous Motor Drives. IEEE Trans. Power Electron. 2017, 33, 2740–2750. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
