State-Feedback Control of Interleaved Buck–Boost DC–DC Power Converter with Continuous Input Current for Fuel Cell Energy Sources: Theoretical Design and Experimental Validation

Abstract

It is well known that the classical topologies of Buck–Boost converters drain pulsating current from the power source. These pulsating currents entail acceleration of the aging rate of the fuel cell. In this paper, we are considering a Buck–Boost DC–DC converter topology featuring continuous input current. The converter interleaved structure ensures the substantial increase in power density compensating power losses related to the converter switching nature. The control objective is to enforce the DC-bus voltage to track its desired value despite load uncertainties and to ensure adequate current sharing between the different parallel modules of the fuel cell interleaved Buck–Boost converter (FC-IBBC). The point is that the internal voltage of the fuel cell is not accessible for measurement. Therefore, the state-feedback control, which consists of nonlinear control laws, is designed on the basis of a nonlinear model of the FC-IBBC system. We formally prove that the proposed controller meets its objectives, i.e., DC-bus voltage regulation and equal current sharing. The theoretical proof relies on the asymptotic stability analysis of the closed-loop system using Lyapunov stability tools. The theoretical results are well confirmed both by simulation, using MATLAB^®/Simulink^®, and by experimental tests using DS 1202 MicroLabBox.

1. Introduction

In the past two decades, clean energy demand has become a worldwide strategic challenge. To meet this challenge, huge financial investments are being made in the technological development of renewable energies, especially fuel cell, solar energy, wind energy, marine energy, and others [1,2,3]. All sources contribute to reducing CO₂ emissions and reducing global warming effects [4]. In this study, fuel cell energy sources are focused on. A fuel cell is an electrochemical generator, whose electrodes are continuously supplied with fuel and oxidant. In electric vehicles, proton exchange membrane fuel cell (PEMFC) technology is used [5]. Accordingly, proton exchange membranes supply hydrogen, while oxygen is obtained from the air. In most applications, the electrical energy produced by fuel cells is not well shaped for immediate use (e.g., the provided voltage is not constant). To be usable with several loads of different nature, a fuel cell needs to be associated with one or more power converters with appropriate topologies. The converters are required to shape the provided electric energy (see Figure 1).

Indeed, the static (current-voltage) characteristic of PEMFC, shown in Figure 2, is nonlinear [6,7] and depends on the thermodynamically predicted fuel cell voltage output and the following three majors losses: activation losses (due to electrochemical reaction), ohmic losses (due to ionic electronic condition), and concentration losses (due to mass transport). Therefore, PEMFC systems need to use the DC–DC power converters to supply regulated and stable power to the different loads and equipment [8,9,10,11,12,13,14,15,16,17,18,19,20,21]. Classical DC–DC power converters of Boost and Buck converters are widely used in the fuel cell system [22,23,24,25]. The electrical loads in fuel cell systems are generally changing; this is particularly the case in electric vehicle applications.

A changing load leads to voltage drops (when the load increases) that need to be compensated for by implementing a step-up converter in the fuel cell systems.

However, this open-loop solution proves only to be satisfactory with small voltage drops. In the presence of wide range variations in the fuel cell voltage, the lowest voltage may become smaller than a third of the nominal open-circuit voltage $E_0$ [6,26,27,28]. Then, the solution is to use a Buck converter in the fuel cell system to cope with voltage regulation. It turns out that a fuel cell system must include both Boost and Buck power converters (see Figure 2). Each converter is operated in turn, according to a well defined control strategy that aims at achieving a satisfactory DC-bus voltage regulation.

According to the previous observations, the DC–DC Buck–Boost power converter would be the best interfacing topology for fuel cells as it combines both the Buck mode and Boost mode. Furthermore, the proposed topology of the Buck–Boost converter requires few components, and hence features good reliability [14]. The point is that classical Buck–Boost converter topologies drain pulsating currents from the input power source [29]. Such currents are likely to accelerate the aging rate of the fuel cell [30,31]. To obtain round pulsating currents, power converters can be augmented with input inductors to smooth currents. In this respect, Sepic and Cuk converters are potential solutions to compensate for the pulsating currents in fuel cells. However, these converters require a large number of components, which increases their cost and reduces their reliability [32]. In this paper, we propose a fuel cell system with a Buck–Boost DC–DC converter that features a continuous input current [33,34]. The proposed topology of interleaved Buck–Boost DC–DC power converter features a structure that ensures much higher power density in the switching converters. The interleaving principle consists of connecting a number of converters connected in parallel with an appropriate switching function between transistors. It is shown in many places (e.g., in [35]); DC–DC power converters based on the interleaving technique offer substantial features. Indeed, when the interleaving N module switches phase shift $\frac{2\pi }{N}$, the frequency of the total current ripple is much smaller than that of the current in the various individual modules; specifically, the ratio between both frequencies is less than $\frac{1 }{N}$. Therefore, for a given net ripple amplitude and electromagnetic interference specification, the parameter values of the input filter can be made smaller by a factor of $\frac{1 }{N}$. On the other hand, for a fixed net frequency f, the switching frequency in the individual modules is reduced to $\frac{f}{N}$, leading to a substantial reduction in the switching losses. Furthermore, splitting the total power on the N paralleled converters entails the division $N$ of the input/output current in each individual module. Accordingly, the current ripple can be reduced N times, and so can the inductance value in each module, consequently, allowing a smaller size converter under current passive component technology. Ensuring a satisfactory energy exchange between the FC-IBBC and the load necessitates the design and implementation of a controller with the following satisfactory performances: stability, reliability, robustness, etc. In this respect, several controllers have been proposed in the literature for the association of the FC and the power converter.

In [9], a (linear/nonlinear/adaptive…) controller was proposed for a multi-device multi-phase interleaved Buck–Boost converter, which meets the constraint of current continuity of the fuel cell. The point with the considered architecture is the high number of the converter components, which entails the high cost and large size of the converter, and greater energy losses.

In [10], a classical interleaved Buck–Boost converter (with N = 6) has been highlighted and a (linear/nonlinear/adaptive…) controller has been proposed. A drawback of the proposed solution is that actuation is performed by transistors with a gap between them, in order to ensure the continuity of the current of the fuel cell.

The authors [15,16,17] present multi-level architectures of Boost-type power converters; these converters are not suitable with the fuel cell as a power source, when one wants a converter output voltage lower than V_{fc_min} (minimum fuel cell voltage). However, they can be used in other applications.

In [33], DC-bus voltage in a mono-module (N = 1) FC-IBBC system was indirectly dealt with by regulating the inductor current at a given reference. The indirect control strategy was motivated by the non-minimum phase nature of the involved Buck–Boost converter. The study emphasized the importance of conveniently sizing the converter components (especially capacitance and inductance) to avoid excessive peaks in current ripples.

The present work is focused on the problem of controlling multiple-module ($N>1$) FC-IBBC systems. We seek the achievement of the following control objectives: (i) tight regulation of the DC-bus voltage, (ii) equal current sharing between different parallel modules of the IBBC, and (iii) asymptotic stability of the closed-loop system. In addition to the (multiple-module) interleaved structure of the converter, the system complexity also lies in the nonlinear non-minimum phase dynamics, and the load variation and uncertainty. The control problem at hand is coped with by developing a nonlinear controller that is designed using the backstepping technique, on the basis of the nonlinear system model. The adaptive feature reflects the controller’s ability to perform an online estimate of load resistance (a part of the system), despite parameter uncertainty. To this end, estimating the load resistance entails the reduction in sensors and, consequently, the increase in control system reliability and the reduction in its size. The effectiveness of the proposed controller is first established by a theoretical analysis of the closed-loop control stability. The outcome of the theoretical analysis is then confirmed both by the simulation results and by experimental tests.

The rest of the paper is organized as follows: the system of interest, including a PEMFC and an interleaved DC–DC Buck–Boost power converter is described, modelled, and analyzed in Section 2; in Section 3, we present an adaptive state-feedback controller; the simulation and experimental results are presented in Section 4. A conclusion and reference list conclude the paper.

2. Modelling and Analysis of Fuel-Cell in Association with Buck–Boost Converter

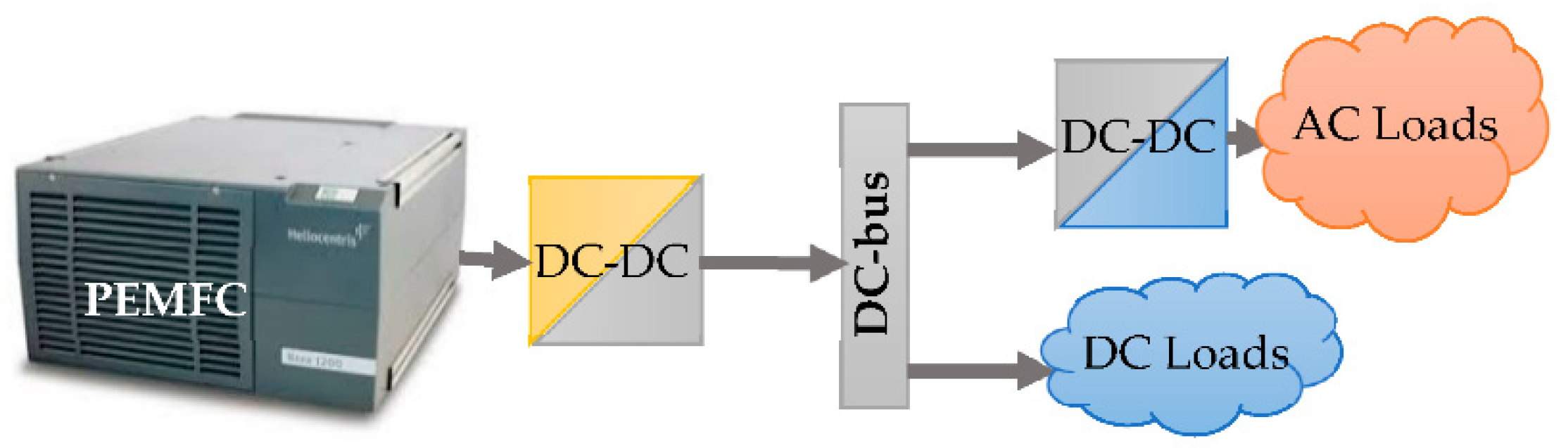
2.1. System Presentation

The FC-IBBC system of interest is depicted in Figure 3. It is constituted of a fuel cell (FC), an interleaved Buck–Boost converter (IBBC), and a load. The FC is represented by its equivalent electric circuit [36,37]. The IBBC contains $N$ modules connected in parallel, operating according to the pulse width modulation (PWM) principal. The parallel modules share a common DC-bus with the load, which is a resistance$R$. The FC is characterized by an open-circuit voltage $E_0$, an ohmic resistance $R_o$, an equivalent electrical capacitance $C_{fc}$, and a series equivalent resistance of activation and concentration resistance $R_{ac}$. Each Buck–Boost module consists of an inductor L_k with its equivalent series resistance $r_k$, a filtering capacitor C in parallel with the switches and diodes, a static switch S_k controlled by the binary input signal u_k, and a diode D_k (k = 1, …, N). Each diode anode is connected to the same point with the load represented by a pure resistance R, according to the input impedance of the DC-bus. This impedance is actually unknown because it depends on the power demand. This uncertainty, together with other parameter uncertainties, will be investigated in the next section.

2.2. System Modelling

Applying Kirchhoff’s laws to the systems of Figure 3, we obtain the following bilinear model:

$$\frac{d{i}_k}{dt}=-\frac{r_k}{L_k}{i}_k-\frac{1}{L_k}\left(1-u_k\right)v_c+\frac{1}{L_k}{v}_{fc}$$

(1)

$$\frac{d{v}_c}{dt}=\frac{1}{C}{\sum }_{k=1}^N\left(1-u_k\right)i_k+\frac{1}{RC}\left(v_{fc}-v_c\right)$$

(2)

$$\frac{d{v}_i}{dt}=-\frac{1}{{\tau }_{fc}}{v}_i+\frac{1}{C_{fc}}{i}_{fc}$$

(3)

$$i_{fc}=\frac{R}{R+R_o}{\sum }_{k=1}^N{i}_k+\frac{1}{R+R_o}\left(E_0-v_c-v_i\right)$$

(4)

$$v_{fc}=E_0-R_o{i}_{fc}-v_i$$

(5)

$$v_{dc}=v_c-v_{fc}$$

(6)

with $k=1,\dots ,N$, where u_k denotes the binary control signal, taking values 1 or 0, N is the number of the parallelly connected Buck–Boost modules composing the IBBC; ${\tau }_{fc}=C_{fc}{R}_{ac}$ is the fuel cell electrical time constant. This model is useful for circuit simulation purposes but is not suitable for the controller design because it involves binary control inputs u_k. For the control design purpose, the following averaged model is obtained using the averaging technique [38], which will prove to be useful:

$$\frac{d{x}_{1k}}{dt}=-\frac{r}{L}{x}_{1k}-\frac{1}{L}\left(1-{\mu }_k\right)x_2+\frac{1}{L}{\overline{v}}_{fc}$$

(7)

$$\frac{d{x}_2}{dt}=\frac{1}{C}{\sum }_{k=1}^N\left(1-{\mu }_k\right)x_{1k}+\frac{1}{RC}\left({\overline{v}}_{fc}-x_2\right)$$

(8)

$$\frac{d{x}_3}{dt}=-\frac{1}{{\tau }_{fc}}{x}_3+\frac{1}{C_{fc}}{\overline{i}}_{fc}$$

(9)

$${\overline{i}}_{fc}=\frac{R}{R+R_o}{\sum }_{k=1}^N{x}_{1k}+\frac{1}{R+R_o}\left(E_0-x_2-x_3\right)$$

(10)

$${\overline{v}}_{fc}=E_0-R_o{\overline{i}}_{fc}-x_3$$

(11)

$${\overline{v}}_{dc}=x_2-{\overline{v}}_{fc}$$

(12)

where the state variables $x_{1k}; \left(k=1,\dots ,N\right)$ designate the average values over the switching period of the inductor current of each module (i_k), x₂ and x₃ designate the average values of the capacitor voltage (v_c) and the FC internal voltage (v_i), respectively. The quantity μ_k ∈ [0, 1], which denotes the duty ratio function of the PWM control signal $u_k$, acts as the control input for each IBBC module. The quantities ${\overline{v}}_{fc}$, ${\overline{i}}_{fc}$ and ${\overline{v}}_{dc}$ respectively denote the average values of the fuel cell voltage $v_{fc}$, the fuel cell current $i_{fc}$, the DC-bus voltage $v_{dc}$. For simplicity, we assumed the IBBC modules to be identical, leading to equal inductances and their ESR in (7), i.e., $L_k=L$ and $r_k=r$, $k=1,\dots ,N$.

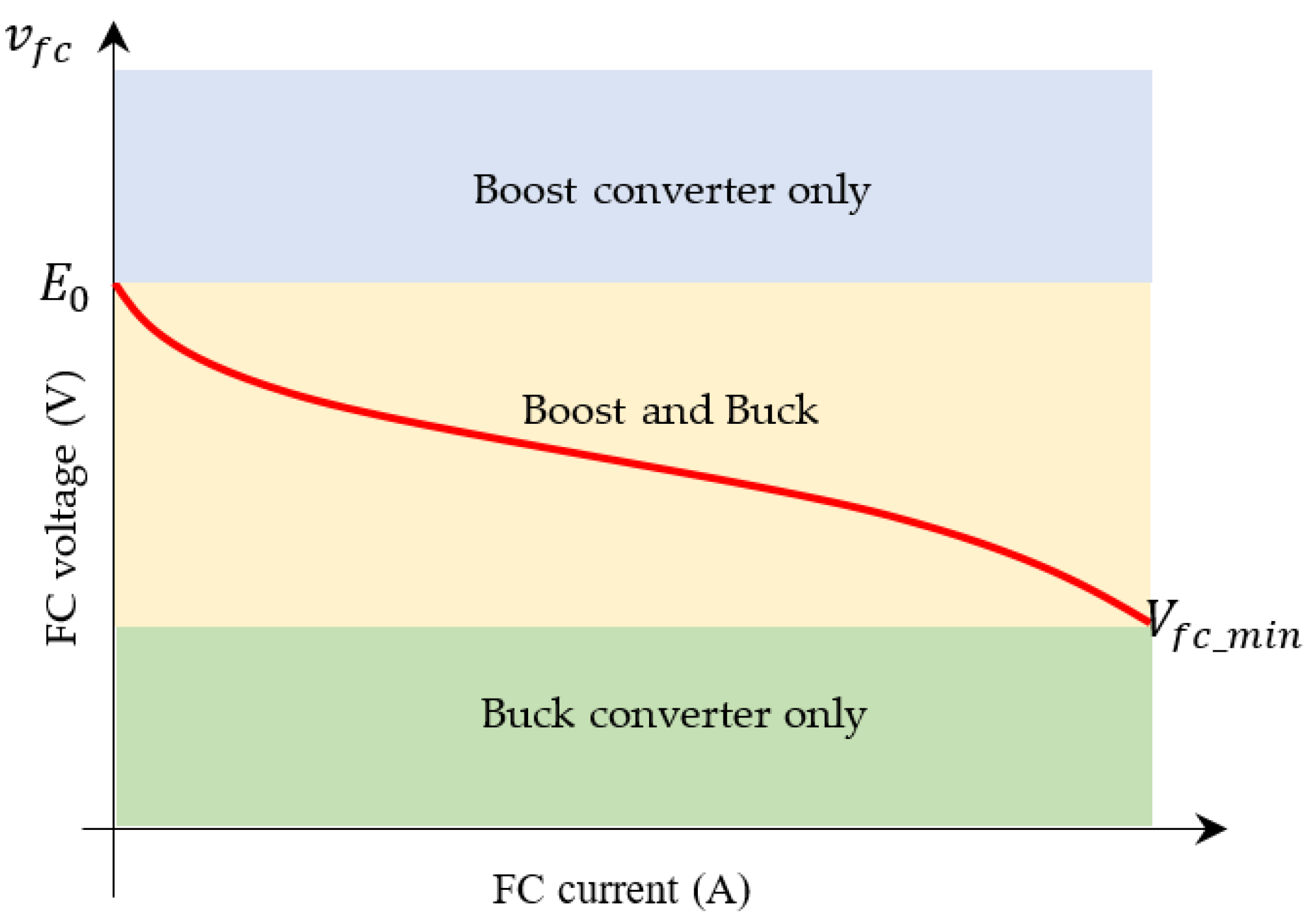
2.3. System Steady State Analysis

$V_d$ denotes the desired output voltage in the steady state. The (average) DC components are obtained by setting to zero all the state variable derivatives in (7–9). Doing so, we obtain the following equations from (9):

$$V_d=\frac{U{E}_0}{1-U}\times \eta$$

(13)

$$I_d=\frac{V_d}{NR\left(1-U\right)}$$

(14)

$$I_{fc}=\frac{V_d}{R}\frac{U}{\left(1-U\right)}$$

(15)

$$V_{fc}=E_0-\left(R_o+R_{ac}\right)I_{fc}$$

(16)

$$V_c=V_d+V_{fc}$$

(17)

$$\mathrm{with} \eta =\frac{R{\left(1-U\right)}^2}{R{\left(1-U\right)}^2+\left(R_o+R_{ac}\right)U^2+\frac{r}{N}}$$

(18)

where $V_c$, $V_{fc}$, $I_d$, $I_{fc}$ and $U$ denote the steady-state values of the various variables, i.e., capacitor voltage, fuel cell voltage, inductor current in each IBBC branch, fuel cell current, the duty ratio of each IBBC module.

From (13), the conversion ratio of the FC-IBBC system is given by

$$G_v\left(U\right)=\frac{V_d}{E_0}=\frac{U}{1-U}\times \eta$$

(19)

Remark 1.

Equation (18) shows that the interleaving nature improves the conversion ratio as the ideality factor$\eta$in (19) increases with$N$. On the other hand, (18) also shows that$\eta$depends on fuel cell parameters ($R_o,R_{ac}$) and the inductance ESR. For$r$, the smaller it is (r,$R_o,R_{ac}$), the larger the conversion ratio.

Remark 2.

In ideal conditions, i.e.,$R_o=R_{ac}=r=0$, one has$\eta =1$, which gives$G_{vi}=\frac{U}{1-U}$. The latter represents the classical conversion ratio for the traditional Buck–Boost converter. When the duty ratio$U$varies between 0 and 1, the output voltage could be smaller or larger than the input voltage$E_0$; this justifies the Buck–Boost designation of the converter. It is worth noting that the main feature of the proposed Buck–Boost is the continuous current provided by the fuel cell.Figure 4illustrates the conversion ratio versus duty ratio in the presence of the variations in the load resistance$R$and parasitic parameters ($R_o, R_{ac}, r$).

The maximum conversion ratio $G_{vmax}$ and its corresponding duty ratio $U_{max}$ are obtained from (18), (19), which is as follows:

$$U_{max}=\frac{-\left(r+N{R}_o-\sqrt{\left(r+NR\right)\left(r+N\left(R_{ac}+R_o\right)\right)}\right)}{N\left(R_{ac}+R_o-R\right)}$$

(20)

$$G_{vmax}=\frac{R{U}_{max}\left(1-U_{max}\right)}{R{\left(1-U_{max}\right)}^2+\left(R_o+R_{ac}\right)U_{max}^2+ \frac{r}{N}}$$

(21)

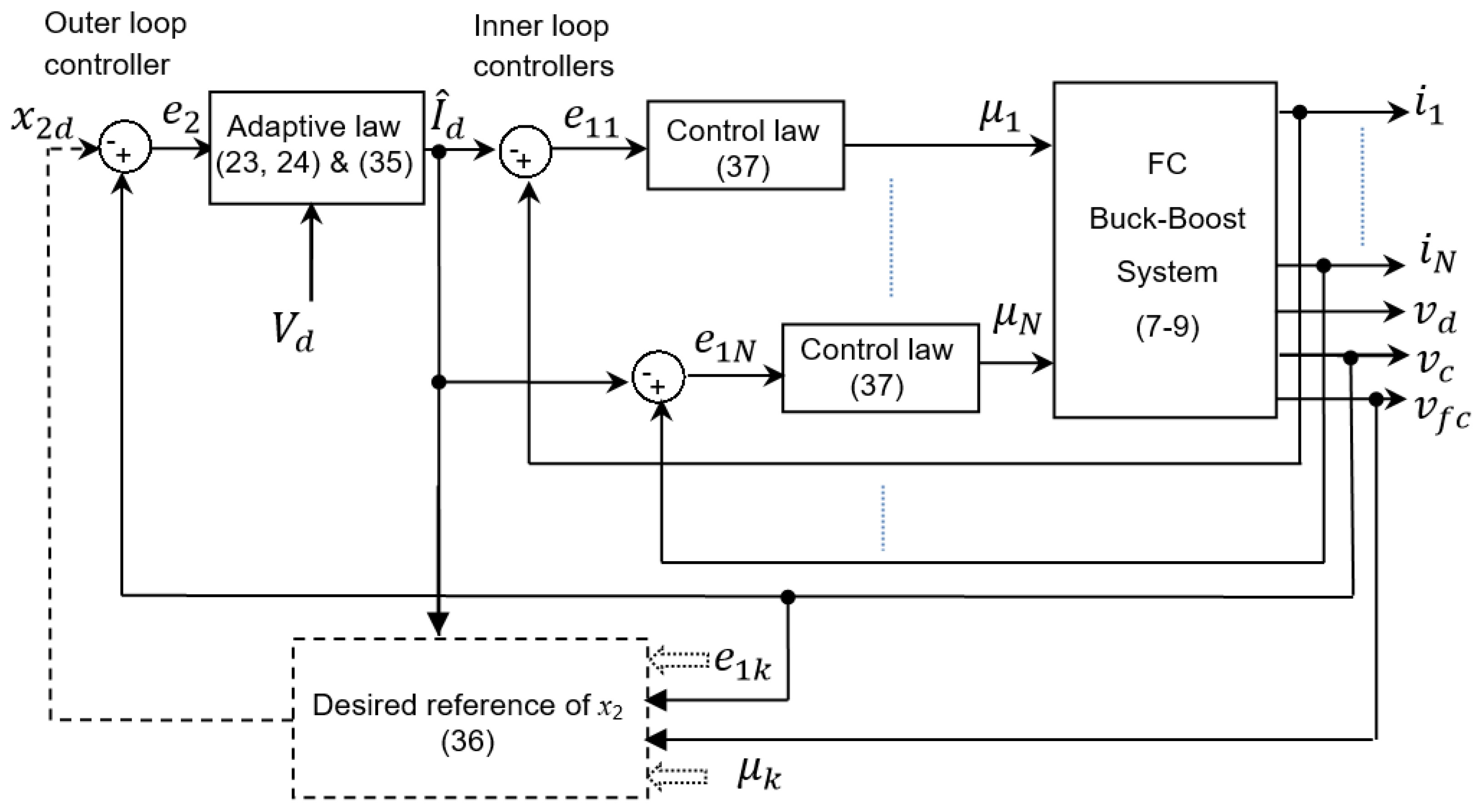
3. Nonlinear State Feedback Controller

In this section, we aim at designing an appropriate controller for the nonlinear system (1–3), on the basis of the nonlinear model (7–9). The model complexity lies in its nonlinearity and the uncertainty of the load resistance. The control objectives are the following:

(i)

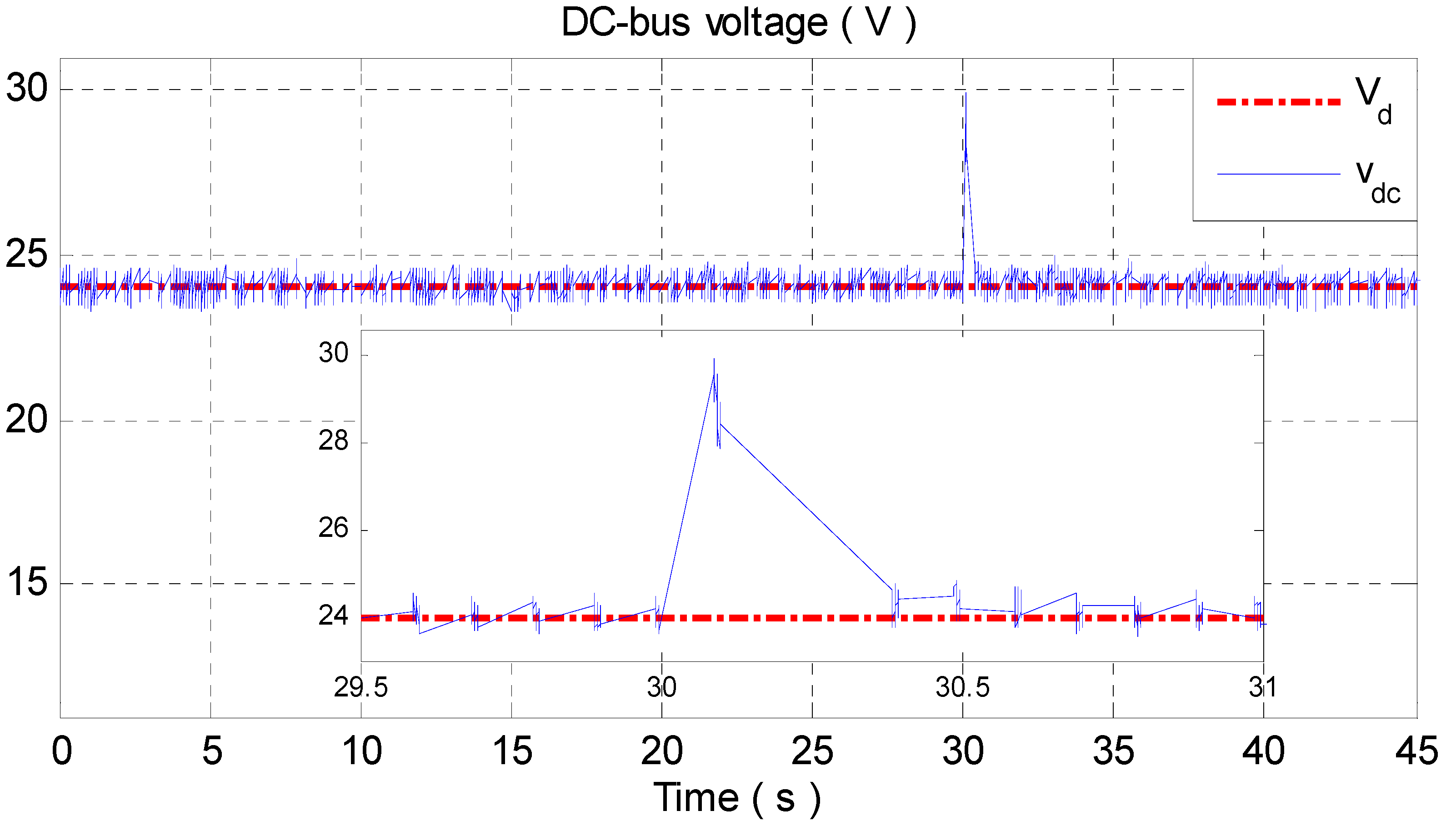
Tight regulation of output DC-bus voltage despite load uncertainty.

(ii)

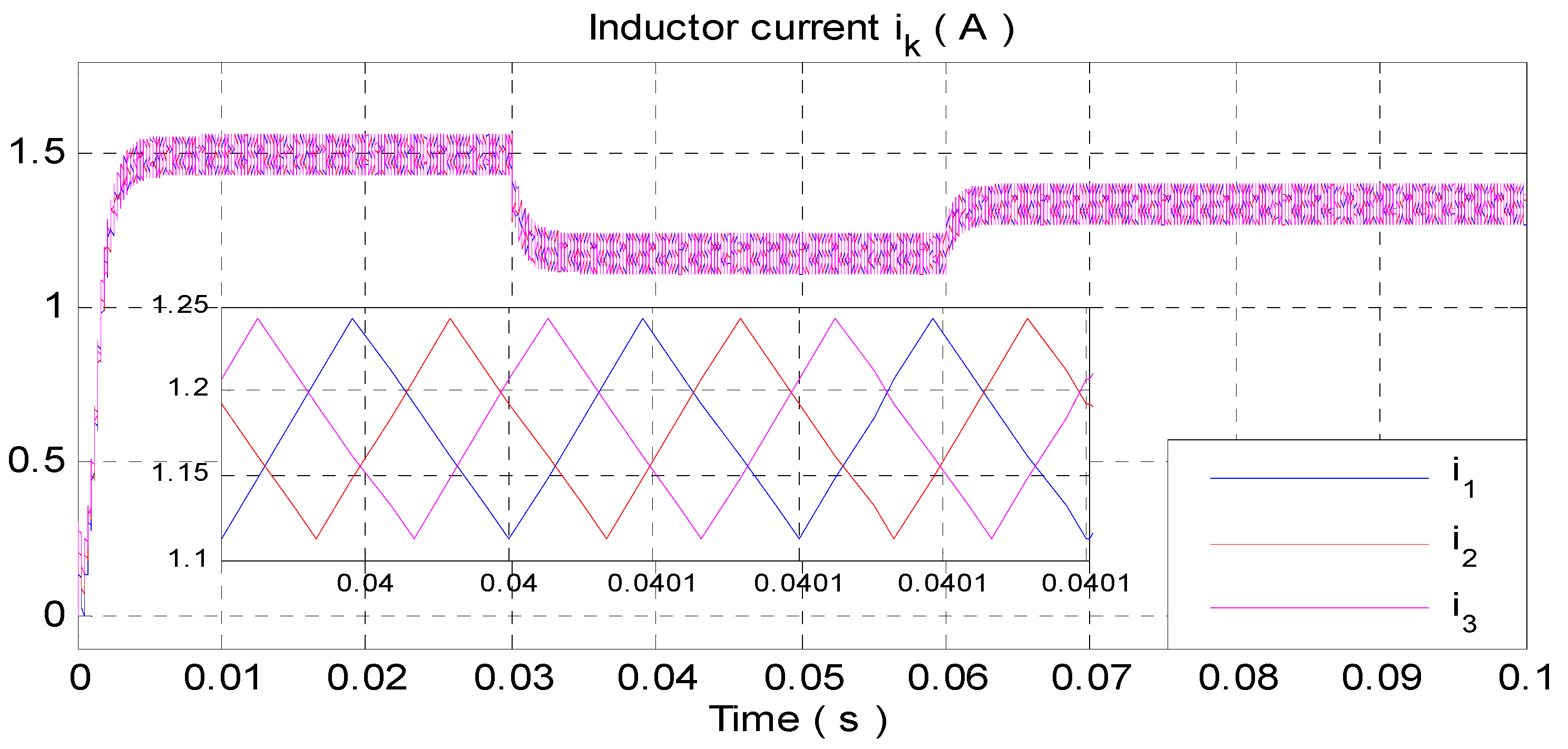
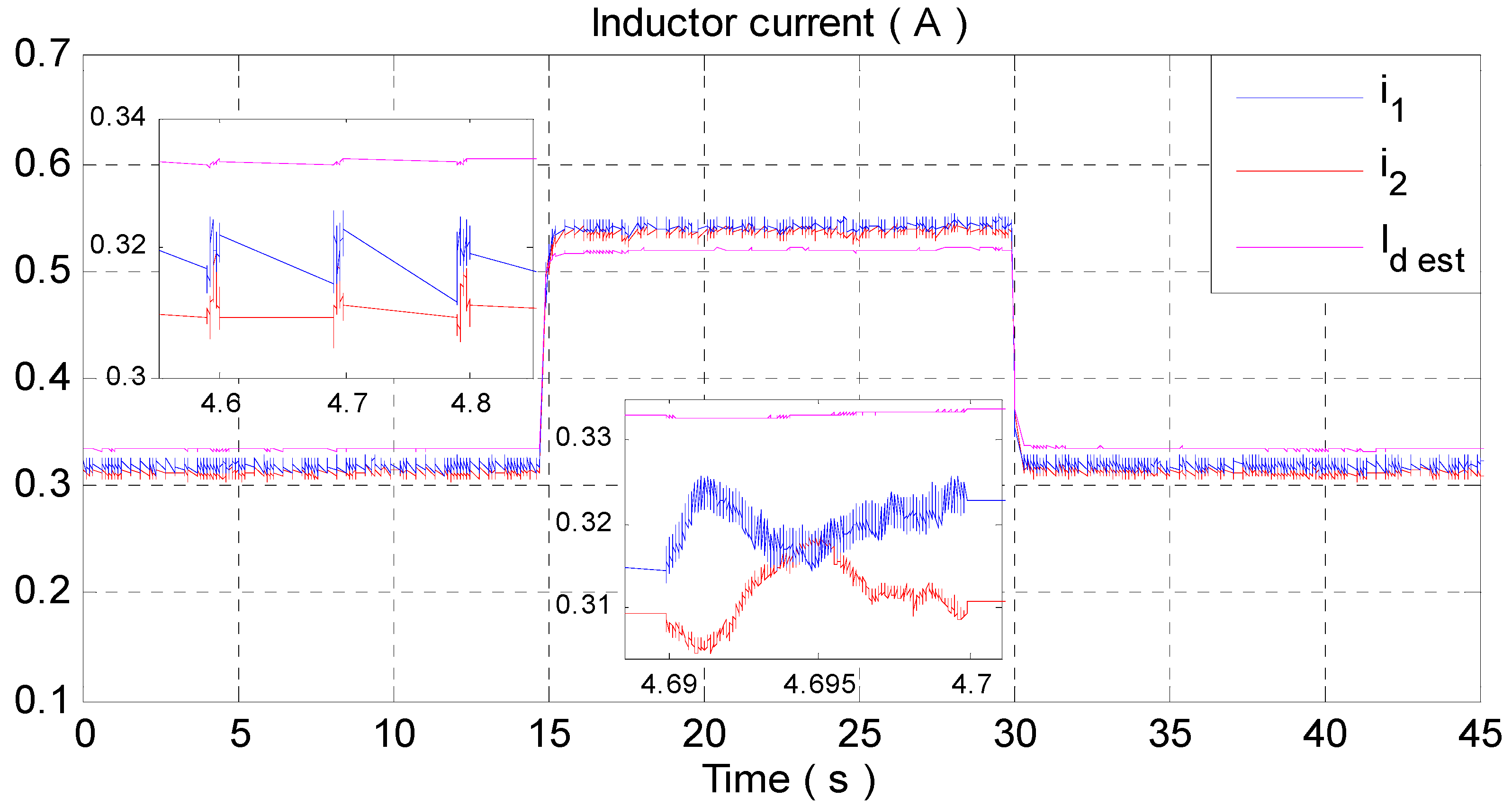
Equal current sharing between IBBC branches, i.e., the inductor currents should be equal to each other in order to avoid overloading one of the modules, especially when supplying heavy loads. This property entails the reduction in the current ripple, which is beneficial for fuel cells.

(iii)

Asymptotic stability of the closed-loop system.

Note that load resistance R uncertainty results from the fact that the load usually varies in practical applications. This model uncertainty will now be solved by providing the controller with adaptive capability. To this end, the controller to be designed will be equipped with a parameter estimator providing online estimates of the unknown parameter $\theta =\frac{1}{R}$.

The first control objective amounts to enforcing the DC-bus voltage v_dc to track its desired value V_d. The point is that the Buck–Boost converter is of a non-minimum phase nature [39] and so perfect tracking of the arbitrary reference signals is not achievable. To avoid this issue, we seek the achievement of the above objective indirectly. Specifically, we consider the inductor currents $x_{1k}$, in IBBC modules, as output signals and aim at enforcing them to track reference signals, denoted I_d. The latter is chosen so that if $x_{1k}=I_d$ then $v_{dc}=V_d$. From (13), (14), we obtain the following relationship between the desired current value $I_d$ and the desired voltage $V_d$:

$$I_d=\frac{V_d}{N}\left({\eta }_0\frac{V_d}{E_0}+1\right)\frac{1}{R}=K\theta$$

(22)

with

$$K=\frac{V_d}{N}\left({\eta }_0\frac{V_d}{E_0}+1\right)$$

(23)

where ${\eta }_0\ge 1$ is an ideality factor introduced to take into account all losses, including switching losses in the converters and the losses in the inductances ESR and the losses in the fuel cell resistance (see Section 2.3). Since $\theta$ is unknown, one must introduce the estimated value of $I_d$.

$${\widehat{I}}_d=K\widehat{\theta }$$

(24)

where $\widehat{\theta }$ is an online estimate of $\theta =\frac{1}{R}$ provided by a parameter estimator yet to be determined. The following state tracking errors are introduced:

$$e_{1k}=x_{1k}-{\widehat{I}}_d; k=1,\dots ,N$$

(25)

Clearly, the objective of regulating the DC-bus voltage $v_{dc}$ to its reference value $V_d$ amounts to regulating the errors $e_k$ to zero. To meet the last requirement, we will apply the backstepping design technique. Accordingly, we first highlight the dynamics of $e_k$ by differentiation (25), with respect to time, and using (7) as follows:

$${\dot{e}}_{1k}=-\frac{r}{L}{x}_{1k}-\frac{1}{L}\left(1-{\mu }_k\right)x_2+\frac{1}{L}{\overline{v}}_{fc}-K\dot{\widehat{\theta }}$$

(26)

To make the errors $e_{1k}$ asymptotically vanish, one can enforce their dynamics to behave as follows:

$${\dot{e}}_{1k}=-c_{1k}{e}_{1k}+e_2$$

(27)

where $c_{1k}>0$are design parameters, and

$$e_2=x_2-x_{2d}$$

(28)

is the error between the capacitor voltage $x_2$ and $x_{2d}$, which is its desired value to be defined later.

Combining (26) with (27), one can obtain the following control laws for the FC-IBBC system:

$${\mu }_k=1+\frac{L}{x_2}\left(-c_{1k}{e}_{1k}+e_2+\frac{r}{L}{x}_{1k}-\frac{1}{L}{\overline{v}}_{fc}+K\dot{\widehat{\theta }}\right)$$

(29)

Using (8) and (28), it is readily checked that the dynamics of $e_2$ are governed by the following equation:

$${\dot{e}}_2=\frac{1}{C}{\sum }_{k=1}^N\left(1-{\mu }_k\right)x_{1k}+\frac{1}{C}\left({\overline{v}}_{fc}-x_2\right)\left(\tilde{\theta }+\widehat{\theta }\right)-{\dot{x}}_{2d}$$

(30)

The third control objective ensures asymptotic stability of the error system with state variables$(e_{1k},e_2)$. This requirement will be enforced by conveniently selecting the still free quantities $x_{2d}$ and $\widehat{\theta }$, in (26) and (29). To this end, we consider the following Lyapunov function candidate [40] for the$(e_{1k},e_2,\tilde{\theta })$system as follows:

$$V_1=\frac{1}{2}\left({\sum }_{k=1}^N{e}_{1k}^2+e_2^2+\frac{1}{\gamma }{\tilde{\theta }}^2\right)$$

(31)

with $\tilde{\theta }=\theta -\widehat{\theta }$ being the estimation error and $\gamma >0$any real scalar, which is called parameter adaptation gain, to be chosen by the designer. The time-derivative of $V_1$ gives the following equation, using (27):

$${\dot{V}}_1=-{\sum }_{k=1}^N{c}_{1k}{e}_{1k}^2+e_2({\sum }_{k=1}^N{e}_{1k}+{\dot{e}}_2)+\frac{1}{\gamma }\tilde{\theta }\dot{\tilde{\theta }}$$

(32)

Using (32), it follows from (32).

$${\dot{V}}_1=-{\sum }_{k=1}^N{c}_{1k}{e}_{1k}^2+e_2\left({\sum }_{k=1}^N{e}_{1k}+\frac{1}{C}{\sum }_{k=1}^N\left(1-{\mu }_k\right)x_{1k}+\frac{\widehat{\theta }}{C}\left({\overline{v}}_{fc}-x_2\right)-{\dot{x}}_{2d}\right)+\left(-\frac{\dot{\widehat{\theta }}}{\gamma }+\frac{1}{C}\left({\overline{v}}_{fc}-x_2\right)e_2\right)\tilde{\theta }$$

(33)

Equation (33) shows that ${\dot{V}}_1$ can be made negative definite, letting ${\dot{x}}_{2d}$ and $\dot{\widehat{\theta }}$ be the following:

$$\{\begin{array}{c}{\sum }_{k=1}^N{e}_{1k}+\frac{1}{C}{\sum }_{k=1}^N\left(1-{\mu }_k\right)x_{1k}+\frac{\widehat{\theta }}{C}\left({\overline{v}}_{fc}-x_2\right)\\ \\ -{\dot{x}}_{2d}=-c_2{e}_2\\ \\ -\frac{\dot{\widehat{\theta }}}{\gamma }+\frac{1}{C}\left({\overline{v}}_{fc}-x_2\right)e_2=0\end{array}$$

(34)

where $c_2>0$is a design parameter. From the second part of (34), we obtain the following parameter adaptive control law:

$$\dot{\widehat{\theta }}=-\dot{\tilde{\theta }}=\frac{\gamma }{C}\left({\overline{v}}_{fc}-x_2\right)e_2$$

(35)

using the fact that $\dot{\tilde{\theta }}=-\dot{\widehat{\theta }}$, assuming that the uncertain parameter $\theta$ is time-invariant or subject to infrequent step changes. In addition, using (28), the first part of (34) implies the following desired value $x_{2d}$:

$$x_{2d}=\frac{1}{s+c_2}\left[{\sum }_{k=1}^N{c}_{1k}{e}_{1k}+c_2{x}_2+\frac{1}{C}{\sum }_{k=1}^N\left(1-{\mu }_k\right)x_{1k}+\frac{\widehat{\theta }}{C}\left({\overline{v}}_{fc}-x_2\right)\right]$$

(36)

with s being the Laplace variable.

Finally, using (36) and (35), the control law (29) becomes the following equation:

$${\mu }_k=1+\frac{L}{x_2}\left(-c_{1k}{e}_{1k}+e_2+\frac{r}{L}{x}_{1k}-\frac{1}{L}{\overline{v}}_{fc}+\frac{K\gamma }{C}\left({\overline{v}}_{fc}-x_2\right)e_2\right)$$

(37)

The main result of this subsection is now summarized in the following Theorem 1.

Theorem 1.

Consider the closed-loop system consisting of a fuel cell interleaved Buck–Boost converter system described by (7)–(9), subject to load resistor uncertainty, and the controller consisting of the adaptive control law (37), the parameter update law (35), and the desired trajectory $x_{2d}$of the capacitor voltage (36). Then, one has the following:

(1) 

The closed-loop system with state variables$(e_{1k},e_2)$is globally asymptotically stable around the origin;

(2) 

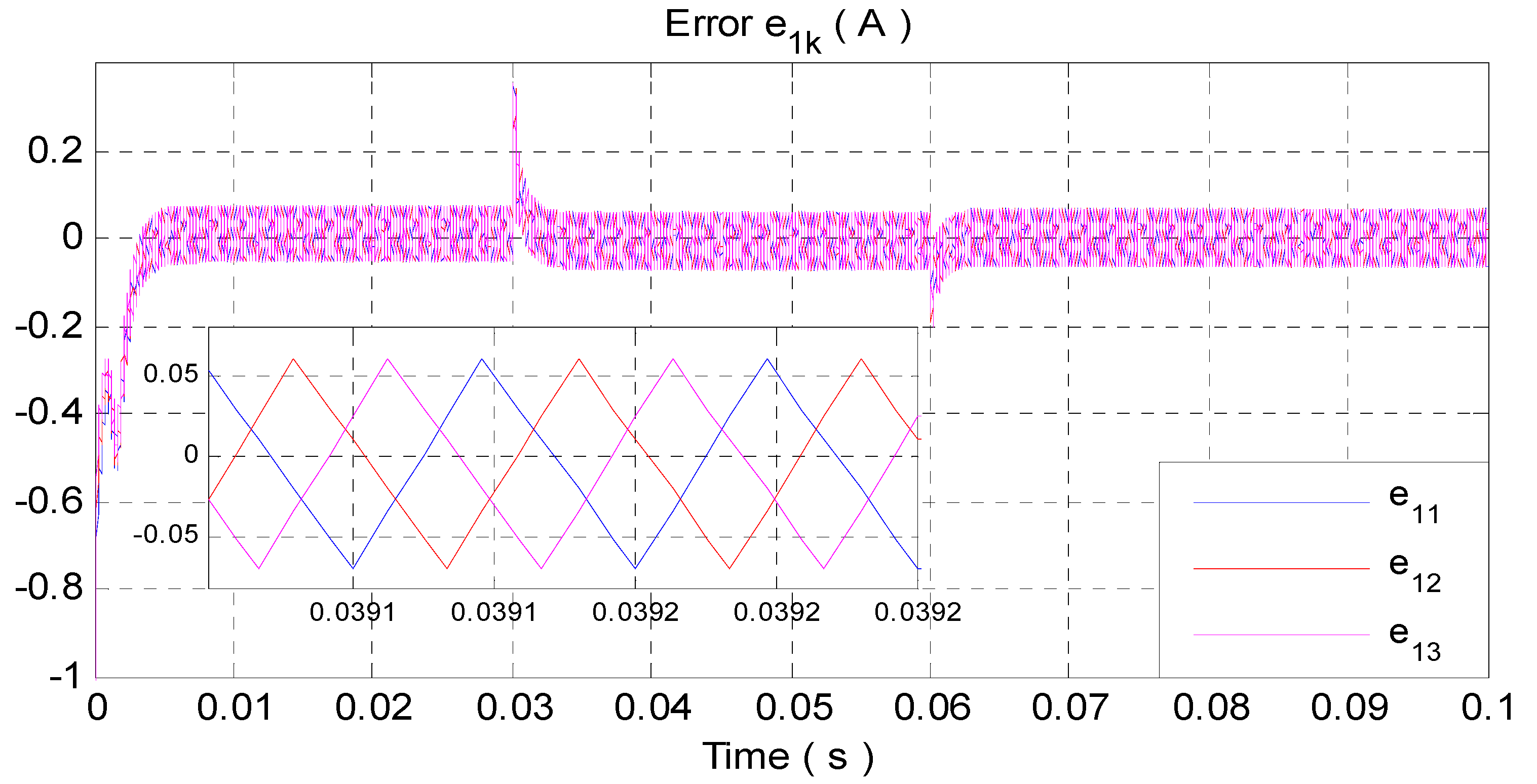
The tracking errors$e_{1k}$converge asymptotically to zero, implying proper current sharing between the modules;

(3) 

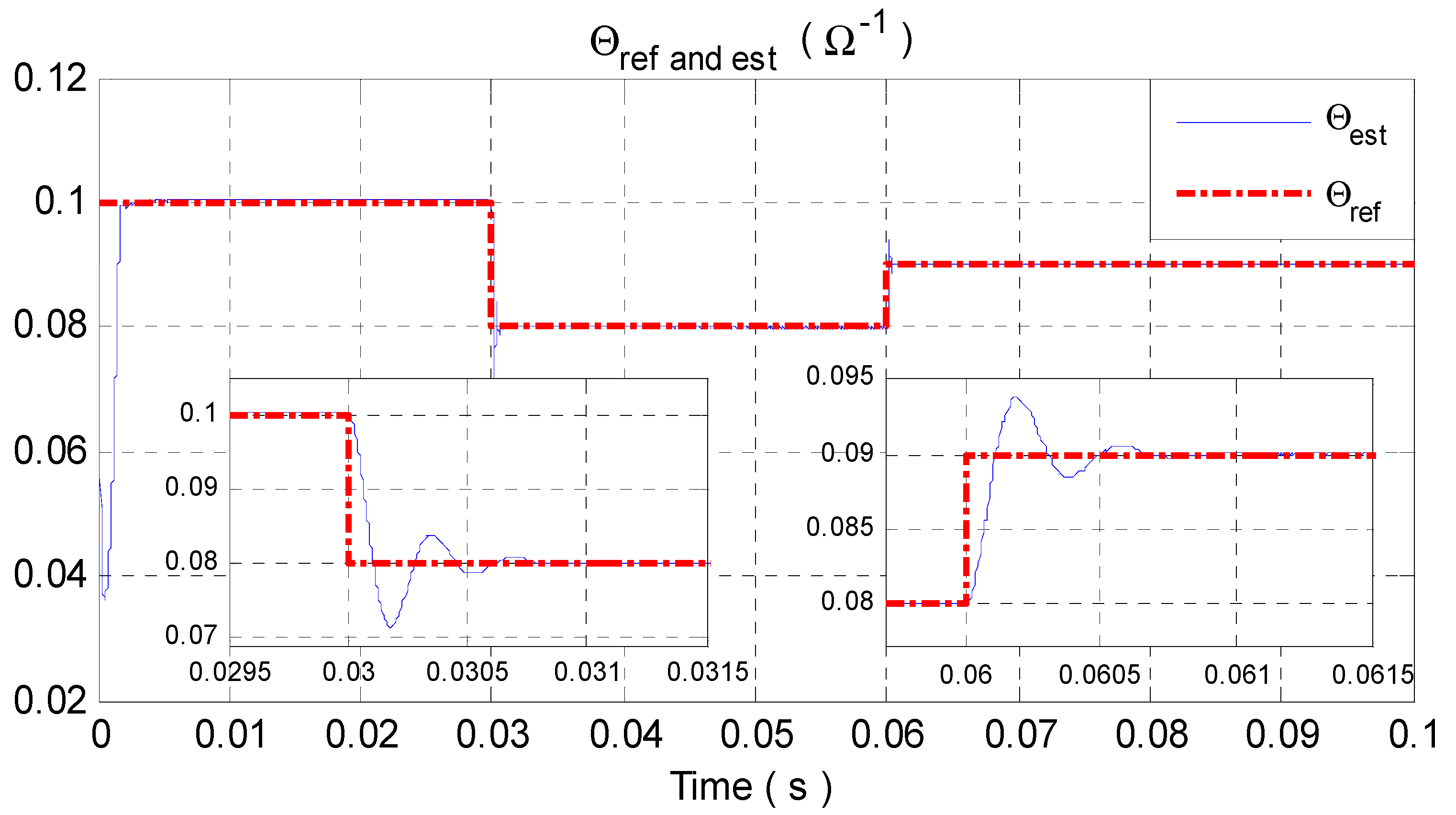
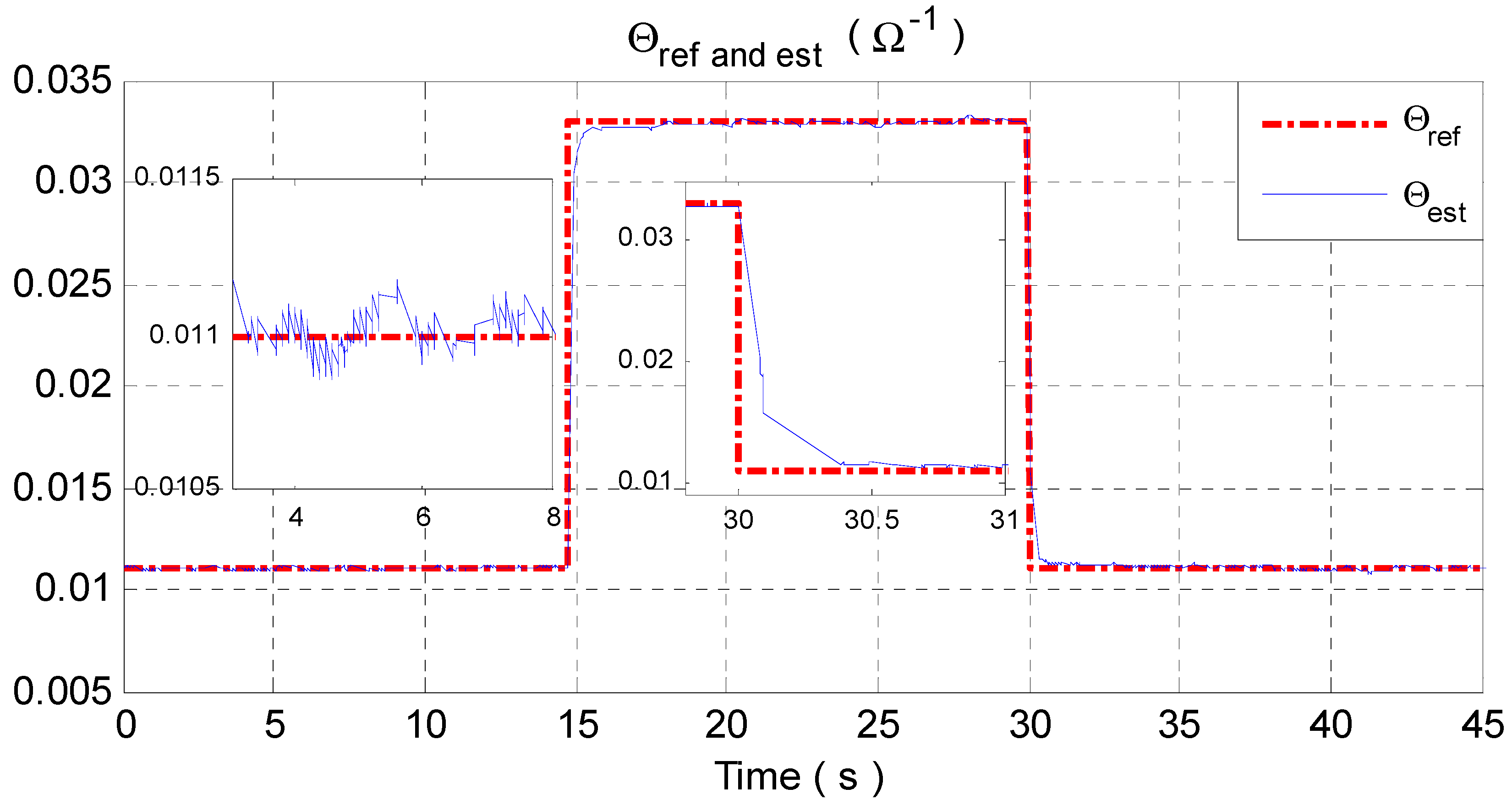
The estimation error$\tilde{\theta }=\theta -\widehat{\theta }$converges to zero and, consequently, the estimated reference current${\widehat{I}}_d$converges to its real value,$I_d$. It turns out that the tracking error$\epsilon =v_{dc}-V_d$converges to zero, ensuring tight regulation of the DC-bus voltage.

Proof. 

First, a state-space representation of the closed-loop system should be obtained, substituting ${\dot{x}}_{2d}$ obtained from (34) in (32) yields.

$${\dot{e}}_2=-c_2{e}_2-{\sum }_{k=1}^N{e}_{1k}+\frac{1}{C}\left({\overline{v}}_{fc}-x_2\right)\tilde{\theta }$$

(38)

This together with (27) and (35) describes the closed-loop system, which is rewritten as follows:

$${\dot{e}}_{1k}=-{\sum }_{k=1}^N{e}_{1k}{c}_{1k}+e_2;k=1,\dots ,N$$

(39)

$${\dot{e}}_2=-c_2{e}_2-{\sum }_{k=1}^N{e}_{1k}+\frac{1}{C}\left({\overline{v}}_{fc}-x_2\right)\tilde{\theta }$$

(40)

$$\dot{\tilde{\theta }}=-\dot{\widehat{\theta }}=-\frac{\gamma }{C}\left({\overline{v}}_{fc}-x_2\right)e_2$$

(41)

Part 1: Now, substituting the right side of (34) in (33), one obtains the following derivative of the Lyapunov function:

$${\dot{V}}_1=-{\sum }_{k=1}^N{c}_{1k}{e}_{1k}^2-c_2{e}_2^2$$

(42)

In view of (30), (38) shows that ${\dot{V}}_1$ is a negative semi-definite function of the state vector$(e_{1k},e_2, \tilde{\theta })$. Therefore, $(e_{1k},e_2,\tilde{\theta })=\left(0, 0, 0\right)$ is globally stable.

Part 2: After applying LaSalle’s invariance theorem [41], it further follows that the state vector $(e_{1k},e_2, \tilde{\theta })$ converges to the largest invariant set of (40–42) contained in the set $\left\{(e_{1k},e_2, \tilde{\theta })\in I{R}^{N+2}/{\dot{V}}_1=0\right\}$. Given (38), the invariant set denoted M is contained in $M_0\stackrel{\scriptscriptstyle\mathrm{def}}{=}\left\{(e_{1k},e_2, \tilde{\theta })\in I{R}^{N+2}/(e_{1k},e_2)=0\right\}$, which shows that

$$\underset{t\to \infty }{\lim }(e_{1k}\left(t\right),e_2\left(t\right))=0$$

(43)

which in turn, using (40) and the fact that$\underset{t\to \infty }{ \lim }({\dot{e}}_{1k}\left(t\right),{\dot{e}}_2\left(t\right))=0$, shows that

$$\underset{t\to \infty }{\lim }\tilde{\theta }\left(t\right)=0$$

(44)

This implies that $\widehat{\theta }$ converges to its true value $\theta$ and, in turn, gives ${\widehat{I}}_d\to I_d$, which also implies, using (25), that

$$\underset{t\to \infty }{\lim }{x}_{1k}\left(t\right)=0=I_d$$

(45)

From Figure 3, in the steady-state, the averaged current in each transistor is

$$I_{Sk}=\underset{t\to \infty }{\mathit{lim}}{\mu }_k{x}_{1k}=U{I}_{d }; k=1,\dots ,N$$

(46)

which, using (14) and (15), gives

$$I_{Sk}=\frac{I_{fc}}{N};k=1,\dots ,N$$

(47)

This clearly shows that the fuel cell current is equally shared between the IBBC branches. This implies that the objective of proper current sharing between the modules is ensured.

Part 3: We have just shown that ${\widehat{I}}_d$ converges towards its true value $I_d$. We will now demonstrate that the DC-bus voltage $v_{dc}$ converges to its desired value $V_d$.

From (8), it follows in the steady-state, using (12), that

$$\underset{t\to \infty }{\lim }{\overline{v}}_{dc}\left(t\right)=R\left(1-U\right)N{I}_d$$

(48)

which implies, using (14), that

$$\underset{t\to \infty }{\lim }{\overline{v}}_{dc}\left(t\right)=V_d$$

(49)

This shows that the objective of tight regulation of the DC-bus voltage is also achieved; the proof of Theorem 1 is then completed. □

Remark 3.

The nonlinear controller composed of the adaptive control law (37) and the parameter update law (35) looks similar to a classic cascade control architecture consisting of an inner current loop and an outer voltage loop. In this case, the control law (37) is considered as an inner loop for each IBBC branch, while (22), (23) and (35) are considered as an outer loop for all branches. Figure 5 illustrates a simplified architecture of the proposed control approach.

For convenience, the FC-IBBC system is summarized, along with the adaptive controller in

Table 1. Nonlinear adaptive controller.

FC-IBBC system	$\frac{d{x}_{1k}}{dt}=-\frac{r}{L}{x}_{1k}-\frac{1}{L}\left(1-{\mu }_k\right)x_2+\frac{1}{L}{\overline{v}}_{fc}$	(7)
	$\frac{d{x}_2}{dt}=\frac{1}{C}{\displaystyle {\displaystyle \sum }_{k=1}^N}\left(1-{\mu }_k\right)x_{1k}+\frac{1}{RC}\left({\overline{v}}_{fc}-x_2\right)$	(8)
	$\frac{d{x}_3}{dt}=-\frac{1}{{\tau }_{fc}}{x}_3+\frac{1}{C_{fc}}{\overline{i}}_{fc}$	(9)
	where $k=1,\dots ,N$;
Adaptive control laws	$K=\frac{V_d}{N}\left({\eta }_0\frac{V_d}{E_0}+1\right)$	(23)
	${\widehat{I}}_d=K\widehat{\theta }$	(24)
	$e_{1k}=x_{1k}-{\widehat{I}}_d$	(25)
	$e_2=x_2-x_{2d}$	(28)
	$x_{2d}=\frac{1}{s+c_2}\left[{\displaystyle {\displaystyle \sum }_{k=1}^N}{c}_{1k}{e}_{1k}+c_2{x}_2+\frac{1}{C}{\displaystyle {\displaystyle \sum }_{k=1}^N}\left(1-{\mu }_k\right)x_{1k}+\frac{\widehat{\theta }}{C}\left({\overline{v}}_{fc}-x_2\right)\right]$	(36)
	${\mu }_k=1+\frac{L}{x_2}\left(-c_{1k}{e}_{1k}+e_2+\frac{r}{L}{x}_{1k}-\frac{1}{L}{\overline{v}}_{fc}+\frac{K\gamma }{C}\left({\overline{v}}_{fc}-x_2\right)e_2\right)$	(37)
Adaptive law	$\dot{\widehat{\theta }}=\frac{\gamma }{C}\left({\overline{v}}_{fc}-x_2\right)e_2$	(35)
Design parameters	${\eta }_0\ge 1$;$V_d>0$; $\gamma >0$; $c_{1k}>0$;$c_2>0$;

.

4. Simulation and Experimental Results

The adaptive nonlinear controller developed in this paper for the FC-IBBC system will now be validated both by simulation and by experiments. Simulation is carried out using the Matlab^®/Simulink^® SimPower toolbox, and the experiments are performed using a laboratory prototype based on the Dspace DS1202 card.

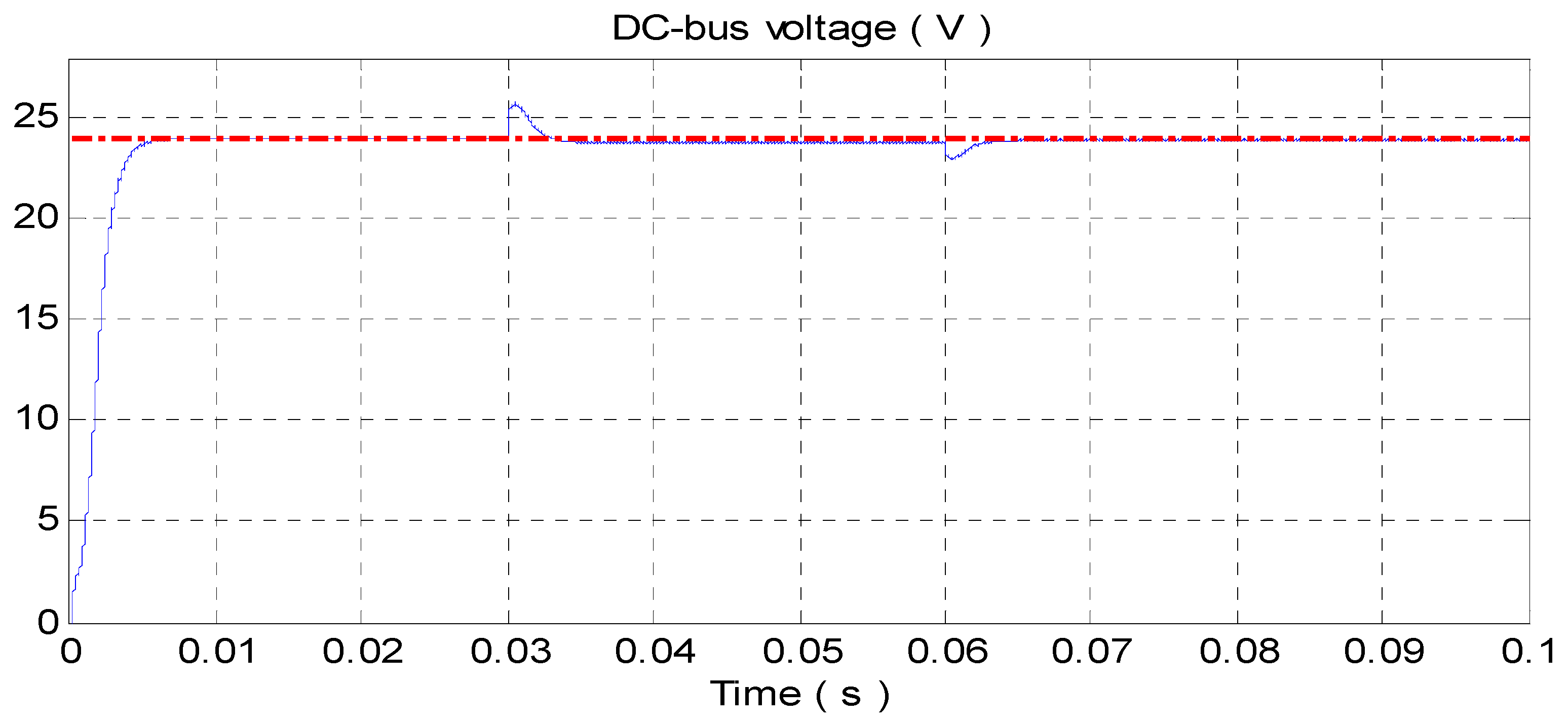
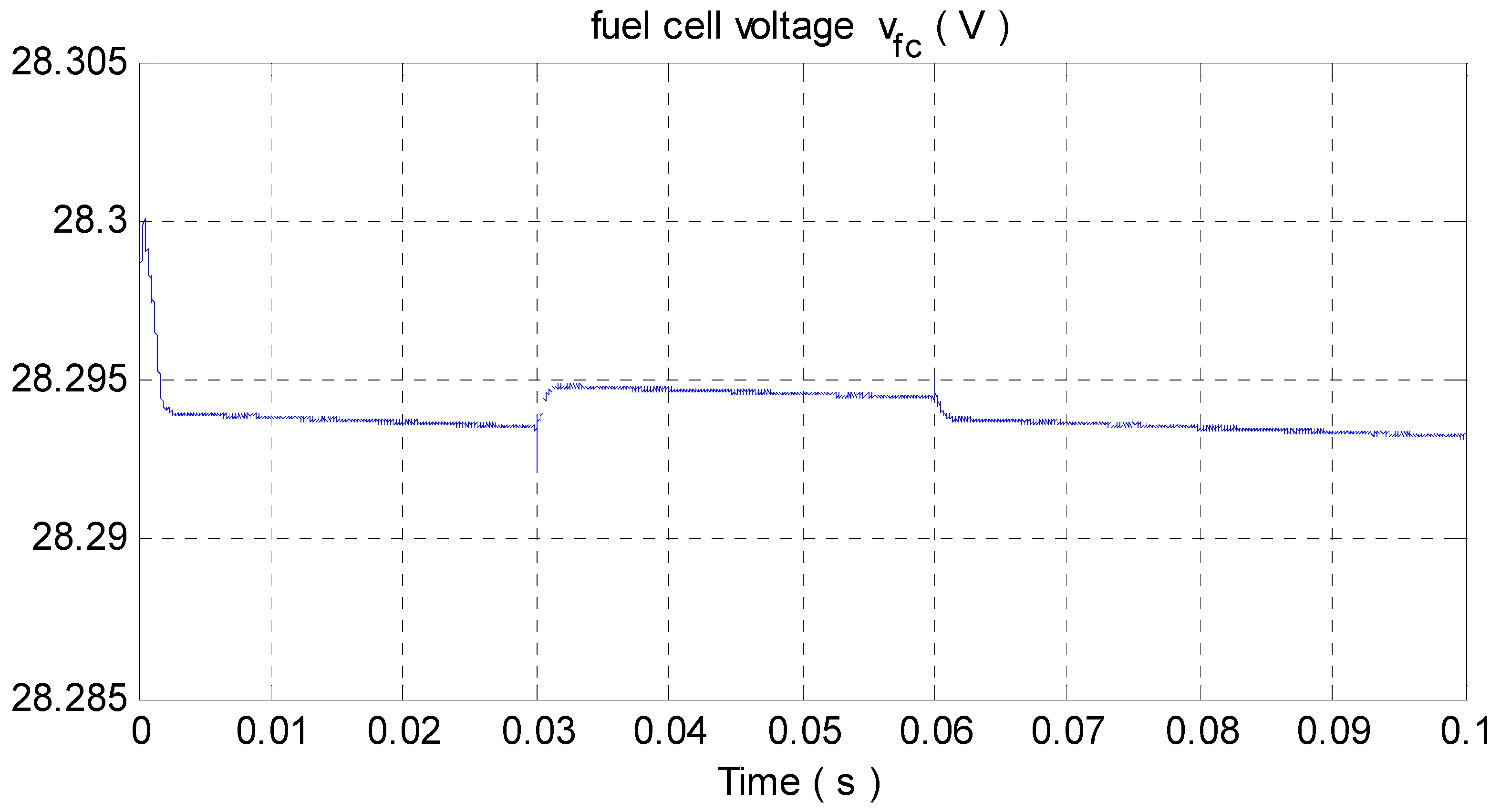
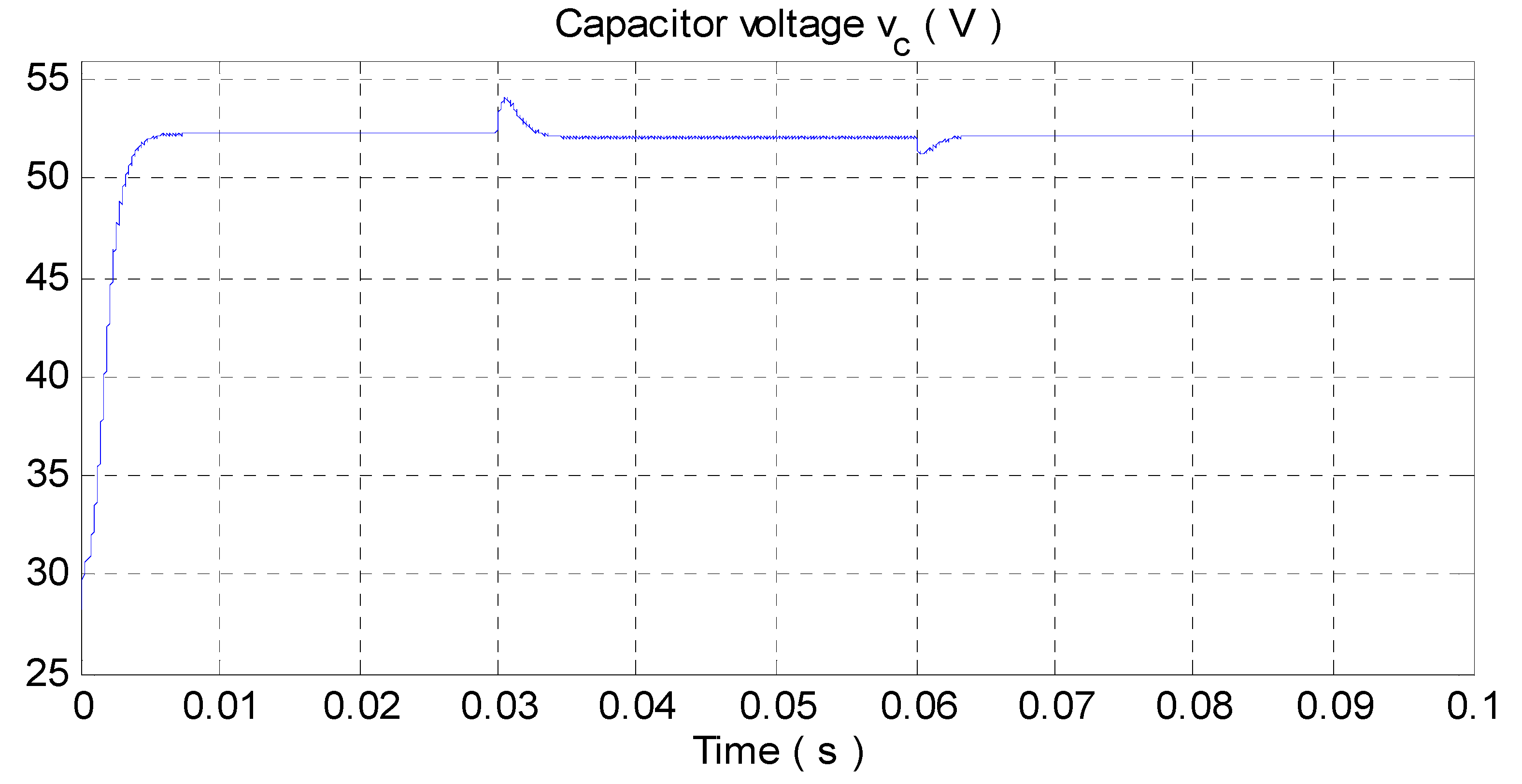
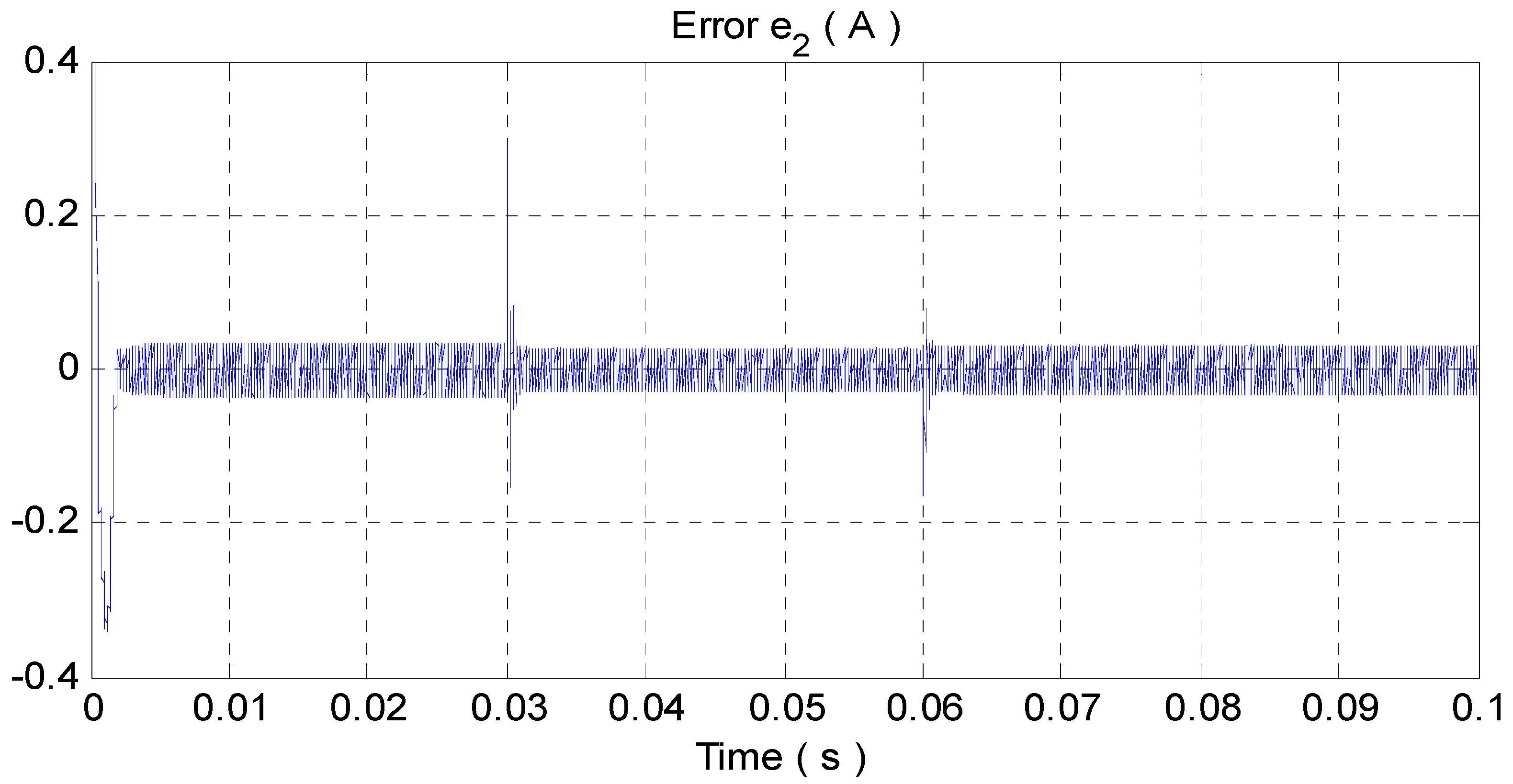
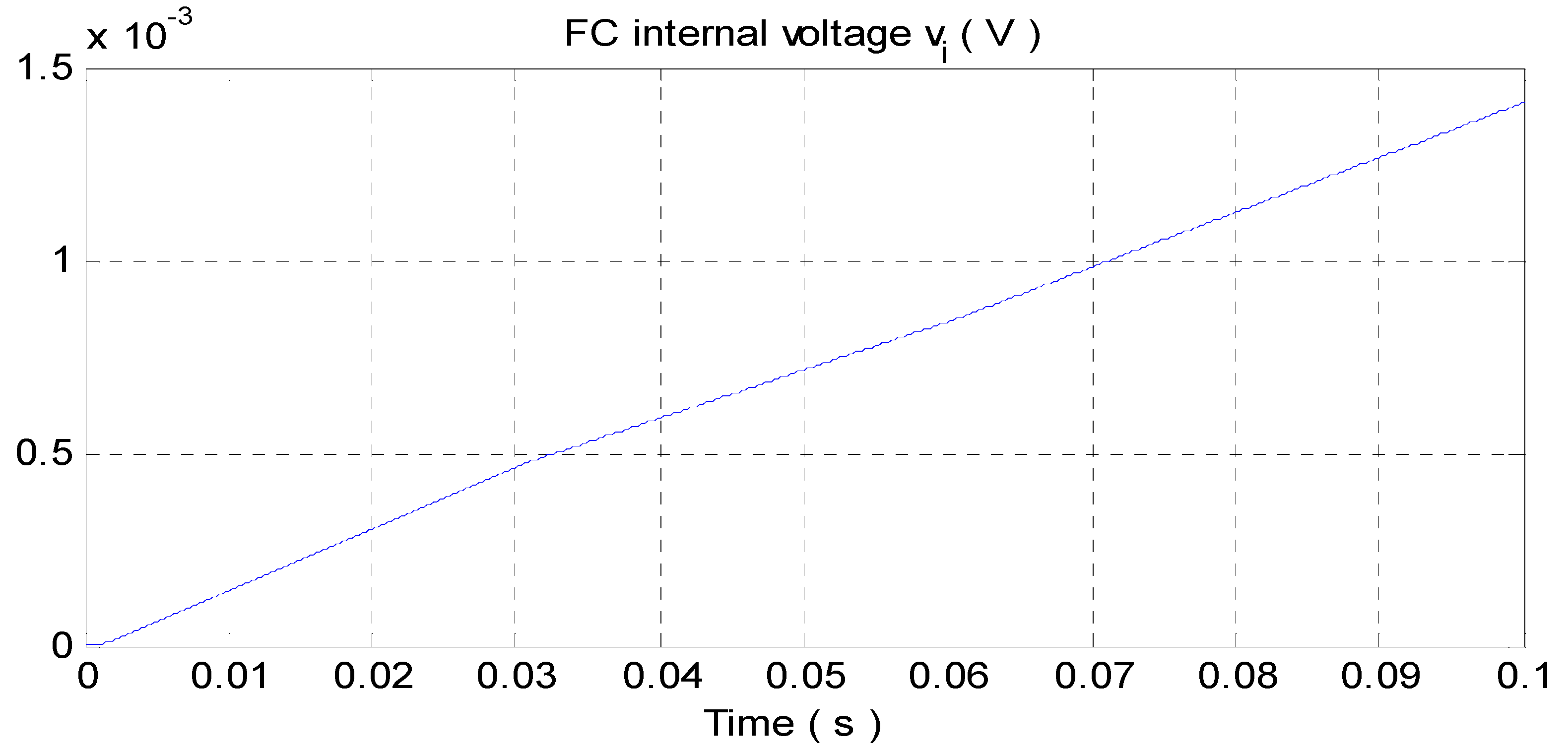
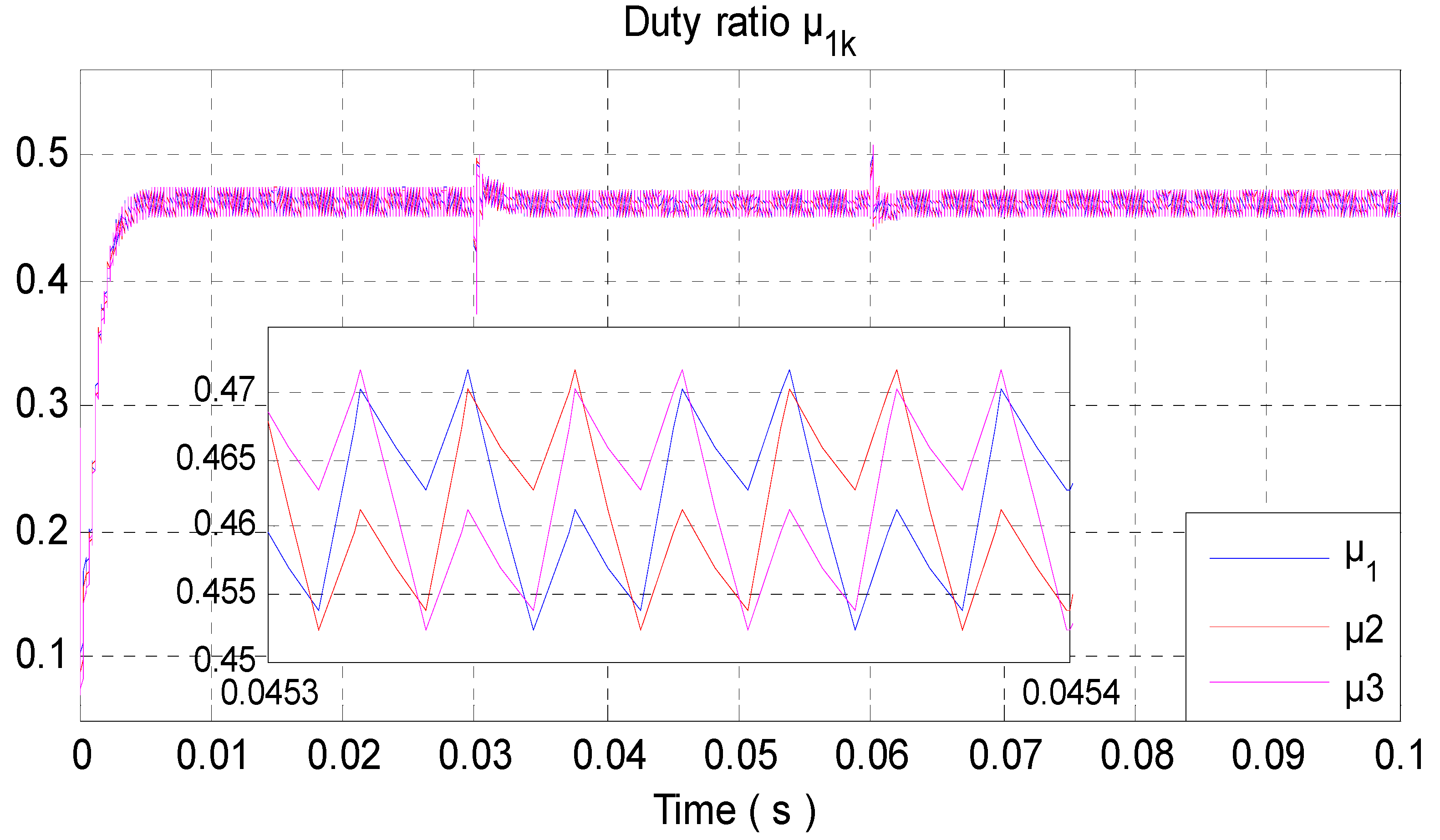
4.1. Simulation Results

The fuel cell parameters are those of the Ballard Nexa 1200 fuel cell module, which has a rated power of 1.2 kW. Figure 5 describes the simulation bench of the controlled system FC-IBBC. The controlled system characteristics are listed in

Table 2. Controlled system parameters.

	Parameter Designation	Value
Fuel Cell	FC open circuit voltage	$E_0=28.3 \mathrm{V}$
	FC internal capacitor	$C_{fc}=130 \mathrm{F}$
	Association of the activation and concentration resistances	$R_{ac}=0.155 \mathsf{\Omega }$
	Ohmic resistance	$R_O=2.89 \mathrm{m}\mathsf{\Omega }$
IBBC	Number of IBBC	$N=3$
	Filtering inductance	$L_1=L_2=L_3=1 \mathrm{mH}$
	Filtering capacitor	$C=68 \mathsf{\mu }\mathrm{F}$
	ESR of the inductance	$r_1=r_2=r_3=0.2 \mathsf{\Omega }$
	Switching frequency	$f_s=20 \mathrm{kHz}$

. The adaptive control design parameters are listed in

Table 3. The design control parameters.

Parameter	Value
C11= C12= C13	6000
C2	10,000
$\gamma$	0.0025
η0	1

.

Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15 and Figure 16 show the resulting control performances of the fuel cell interleaved Buck–Boost converter system.

Figure 6 illustrates the voltage measurement of v_dc and its reference signal V_d. In this figure, one can observe that the controller behavior is satisfactory. Indeed, the DC-bus v_dc perfectly tracks its reference V_d. The overshoot is 0 at t₀ and 5% of V_d at the instant of change in the load, the system response time is less than 5 ms.

Figure 7 shows that the inductance currents are equal to the variation in the load. So, the equal current sharing between the IBBC branches is ensured.

Figure 8 shows the error e_1k between the inductance current in each IBBC branch and its reference. The figure clearly shows that the error e_1k converges to zero, despite load variations. The signal ripple is tolerable, as it is less than 0.12A.

Figure 9 shows that the online estimate of the unknown parameter $\theta$ converges to its true value.

Figure 10 and Figure 11 respectively show the behavior of the voltage v_fc and current i_fc of the fuel cell in the presence of load variations. We can observe that the current of the fuel cell is continuous, which is beneficial for the fuel cell.

Figure 12 illustrates the capacitor voltage v_c.

Figure 13 shows the error e₂ between the capacitor voltage x₂ and its desired value x_2d. Clearly, e₂ is well regulated to zero, despite the variation in the load.

Figure 14 shows the FC internal voltage v_i; one should note that the value of v_i is low because its charge rate is very high. The value of v_i also represents the discharge of hydrogen H₂ in the fuel cell.

Figure 15 and Figure 16 show the control signals µ_1k and the PWM signals, with a switching frequency of 20 kHz.

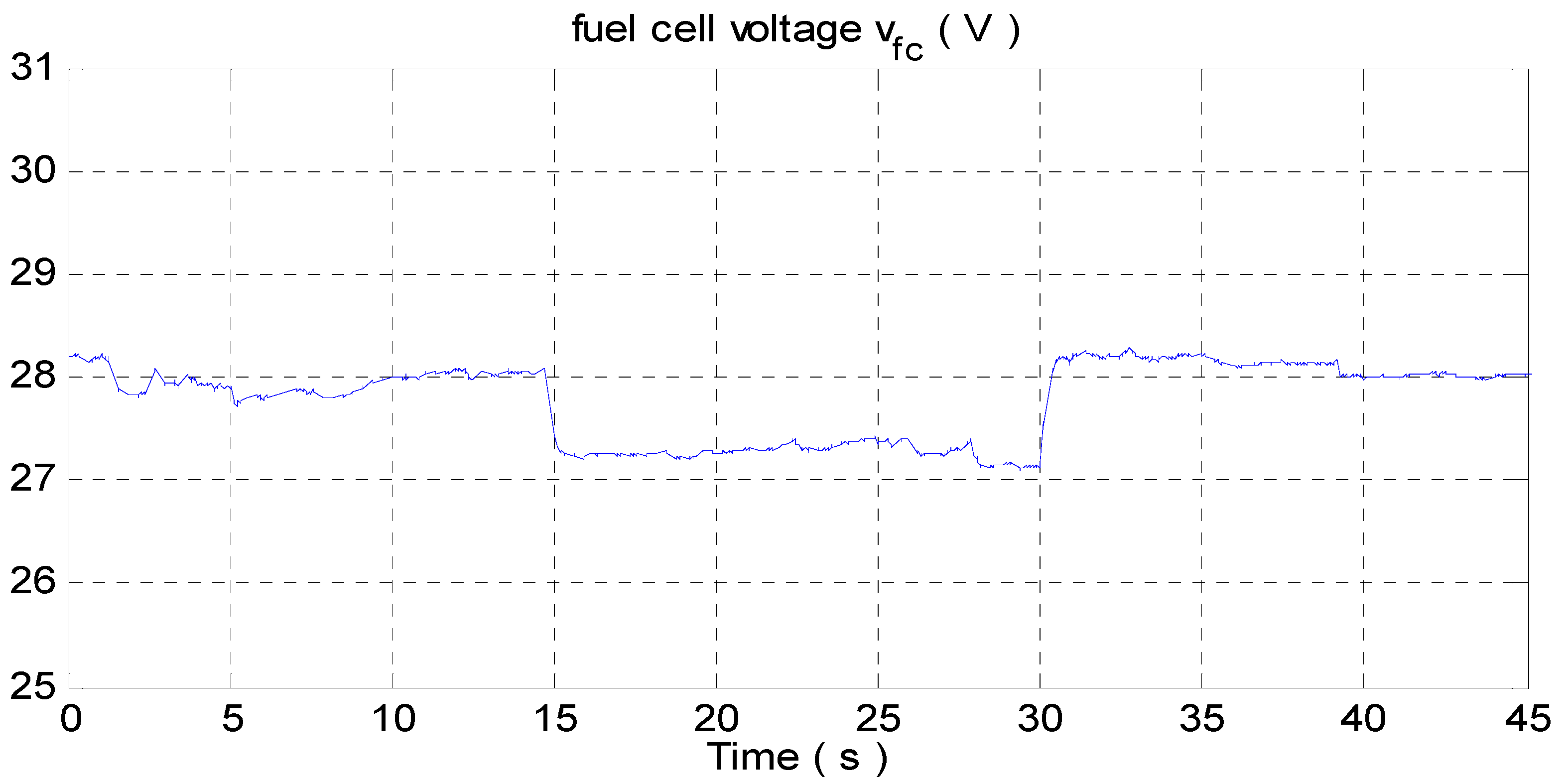
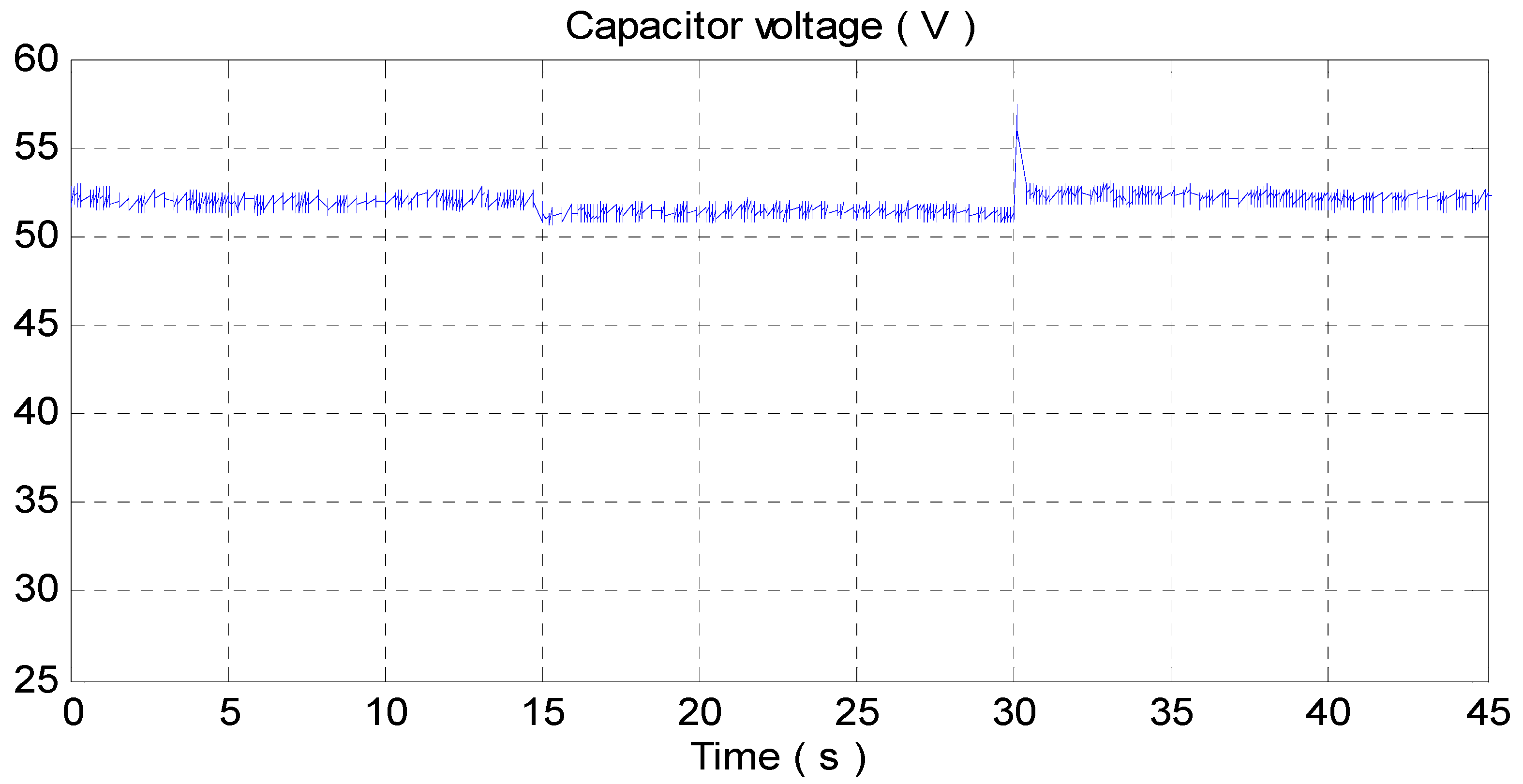
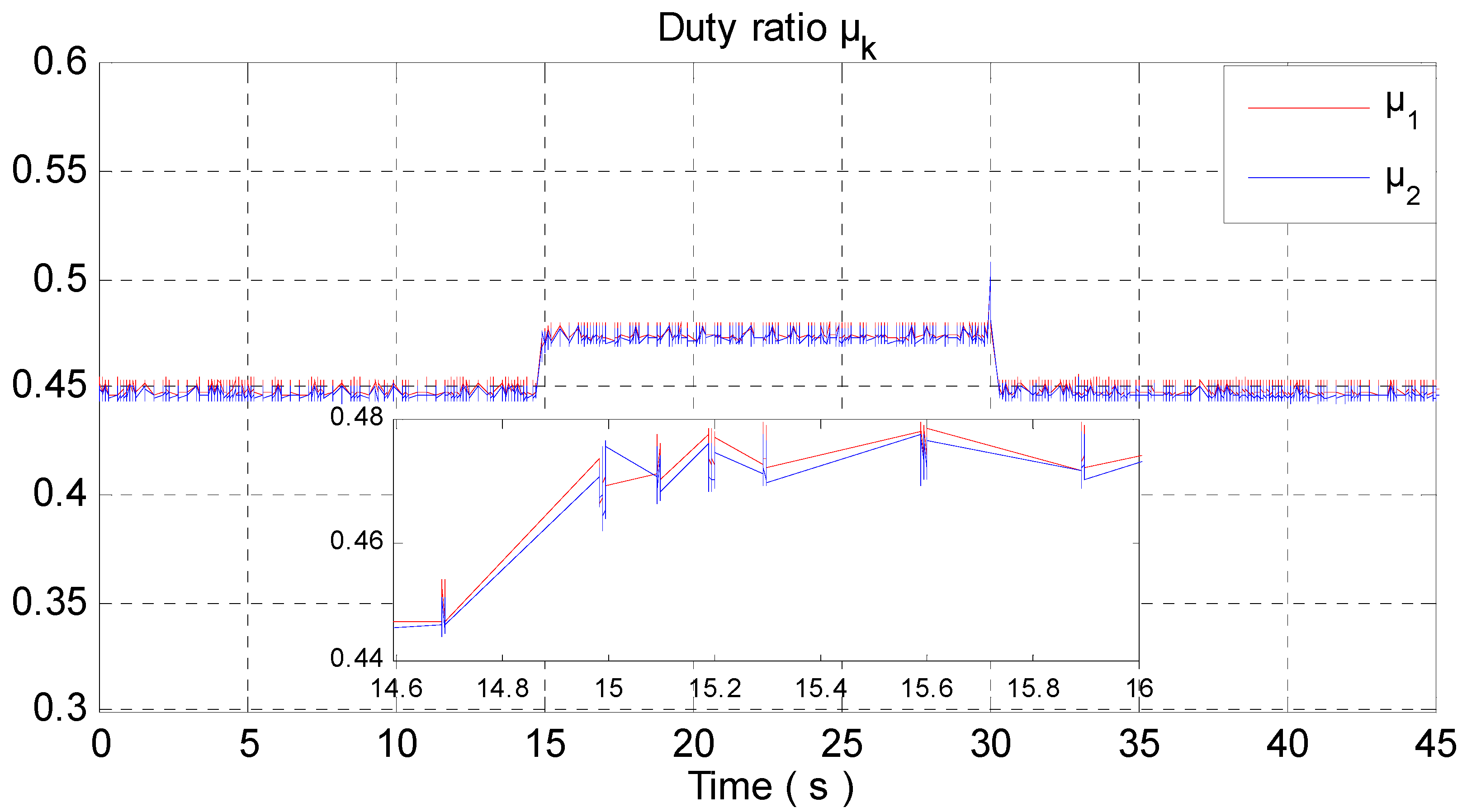
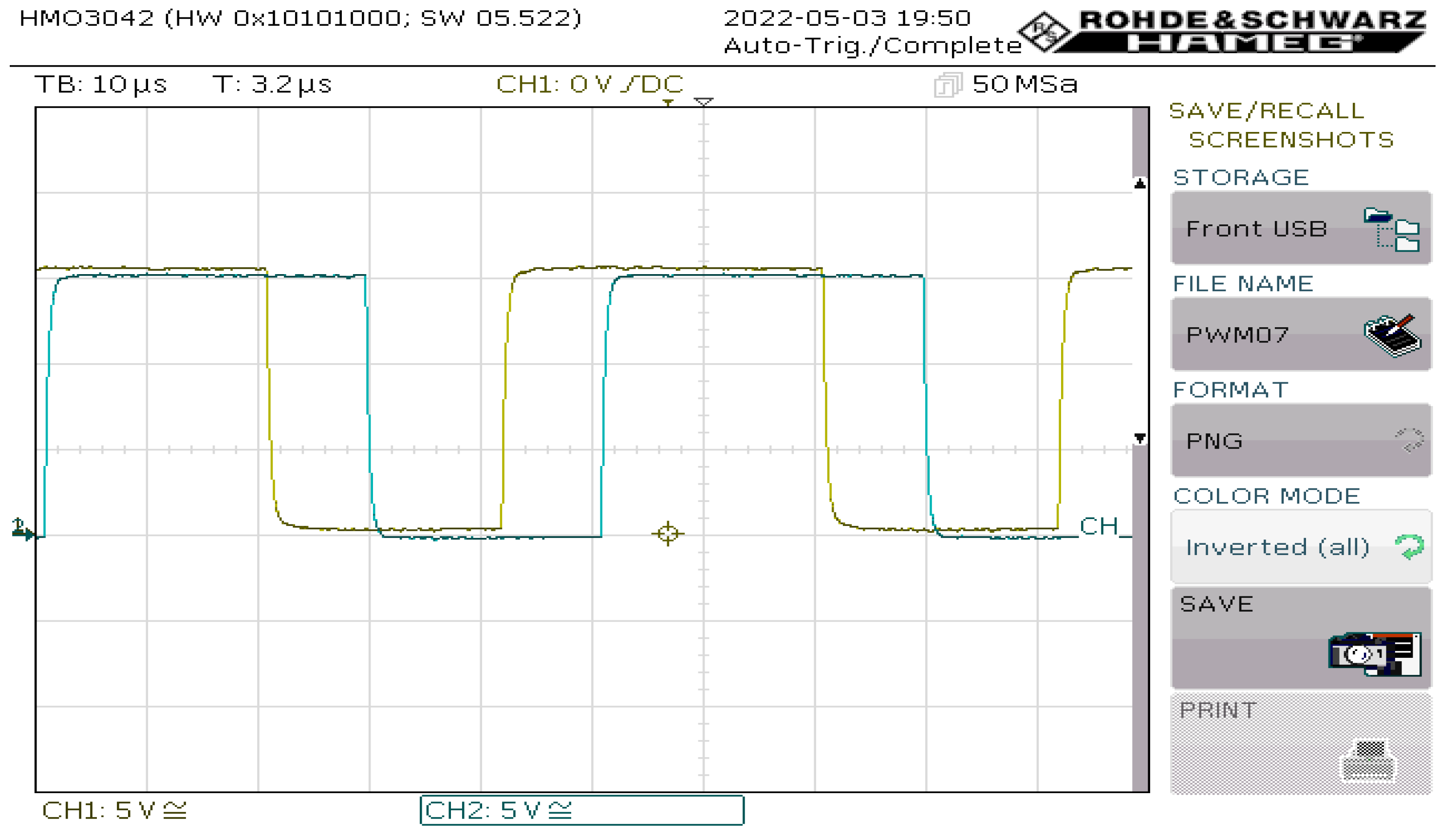
4.2. Experimental Results

The considered experimental test bench of the fuel cell interleaved Buck–Boost converter system is shown by Figure 17. The adaptive state-feedback controller of Table 2 is implemented using dSPACE 1202 and Control Desk^®/software^®. The testbed consists essentially of the following elements:

Ballard Nexa 1200 fuel cell module with its monitoring software.

Three metal hydride canisters from Heliocentris with storage capacities of 800 NL hydrogen.

-

Power supply from BK Precision.

-

Power resistors.

-

Programmable DC electronic load from BK Precision.

-

MicroLabBox-dSPACE DS1202 with Control Desk^®/software^® plugged in a Pentium 4 personal computer.

-

Semikron IGBT module (SEMITEACH).

-

Power card together with measurement card.

-

Two ferrite inductance.

-

Two hall effect current sensors.

-

Two voltage sensors.

-

A digital scope.

The load resistance changes are programmed using the programmable DC electronic load. The controlled system characteristics are summarized in

Table 4. Controlled system parameters.

	Parameter Designation	Value
Fuel Cell	Ballard Nexa 1200 fuel cell module the fuel cell has a rated power of 1.2 kW
IBBC	Number of IBBCs	$N=2$
	Filtering inductance	$L_1=L_2=4 \mathrm{mH}$
	Filtering capacitor	$C=110 \mathsf{\mu }\mathrm{F}$
	ESR of the inductance	$r_1=r_2=0.3 \mathsf{\Omega }$
	Switching frequency	$f_s=20 \mathrm{kHz}$

. The adaptive control design parameters are shown in

Table 5. The design control parameters.

Parameter	Value
C11 = C12	2000
C2	90,000
$\gamma$	0.002
η0	1.077

. The number of parallel branches of the IBBC is N = 2.

The load switches from 90 Ω to 30 Ω and returns to 90 Ω. The reference signal of the DC-bus voltage is set to $V_{dc}=24 \mathrm{V}$.

Figure 18 illustrates the voltage measurement of v_dc and its reference signal V_d. In this figure, one can observe that the controller behavior is satisfactory. Indeed, the DC-bus v_dc perfectly tracks its reference V_d.

Figure 19 shows that the inductance currents are equal to the variation in the load. So, the equal current sharing between IBBC branches is ensured. This figure clearly shows that the desired current I_d was well estimated.

Figure 20 shows that the online estimate of the unknown parameter $\theta$ converges to its true value.

Figure 21 shows the voltage v_fc of the fuel cell in the presence of load variations.

Figure 22 illustrates the capacitor voltage v_c.

Figure 23 and Figure 24 show the control signals µ_1k and the PWM signals, with a switching frequency of 20 kHz.

The experimental results confirm the performances established in the theoretical analysis and simulation. Specifically, the DC-bus voltage regulation and the equal current sharing between modules are well ensured, etc.

5. Conclusions

The problem of controlling an interleaved Buck–Boost converter connected to a fuel cell energy source is dealt with in this paper. The control objectives are as follows: (i) output DC-bus voltage regulation under load uncertainty (this is necessary to maintain the voltage constant in the DC-bus), (ii) equal current sharing between IBBC branches, especially when supplying heavy loads, and (iii) asymptotic stability of the closed-loop system. To meet these objectives, we have developed an adaptive state-feedback controller that consists of nonlinear control laws. Using theoretical analysis, simulation study, and experimental tests, we have shown that the proposed controller indeed meets all the control objectives.