Analysis of the THD and Common-Mode Voltage of the Three-Phase Boost-Buck EV Traction Inverter
Abstract
:1. Introduction
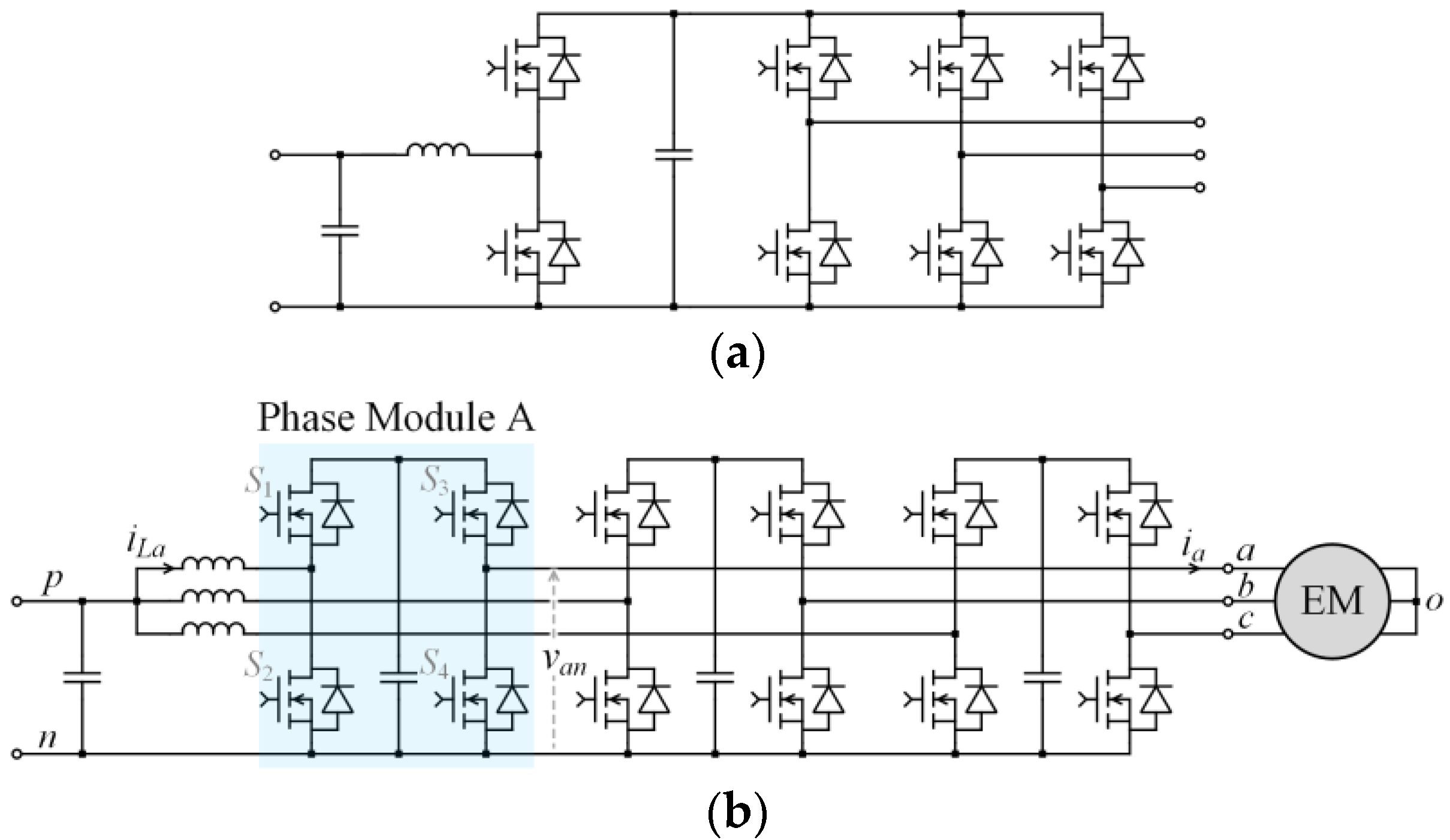
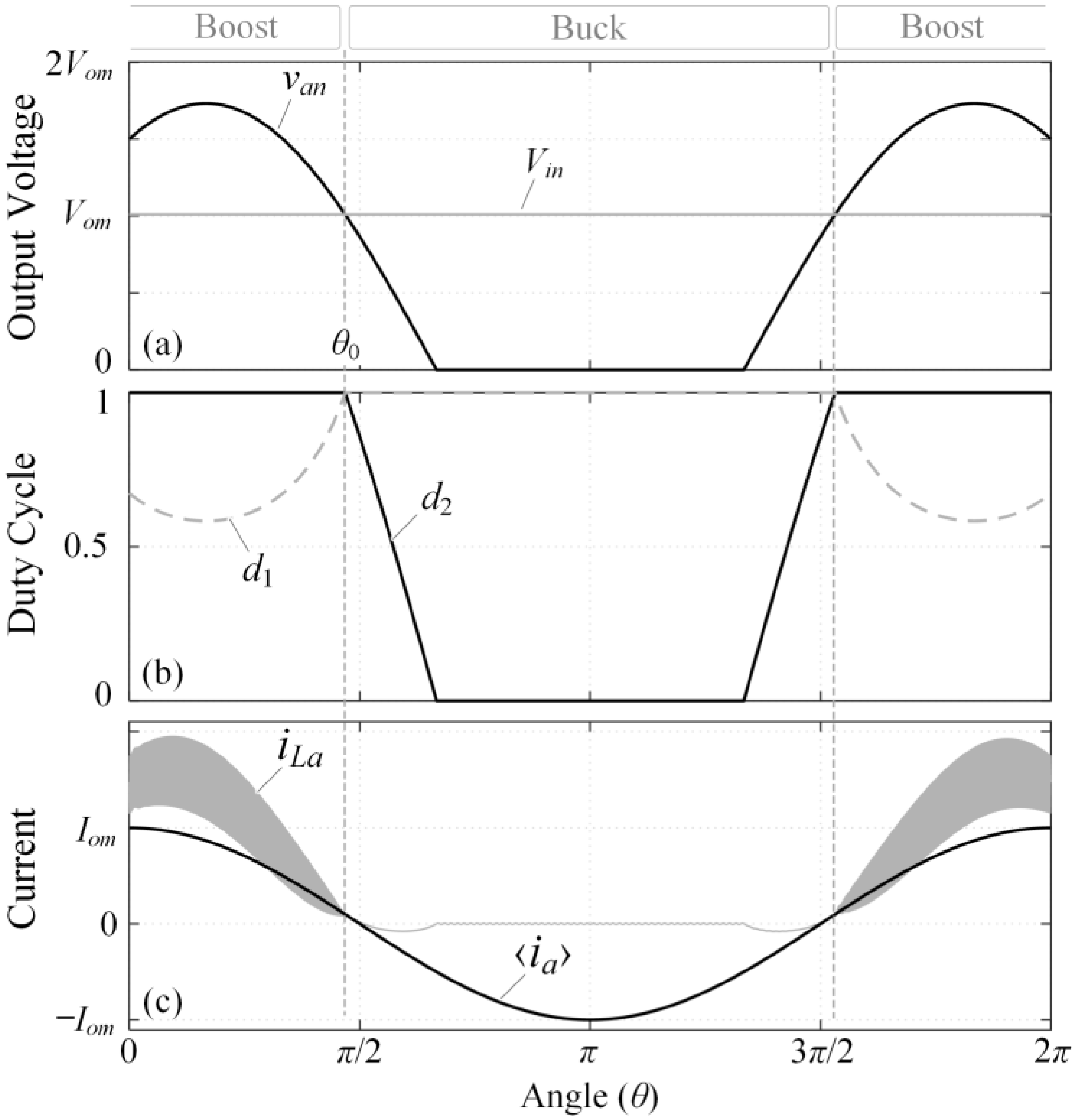
2. Operating Principle
3. CM Voltage, THD, and Interleaving Method
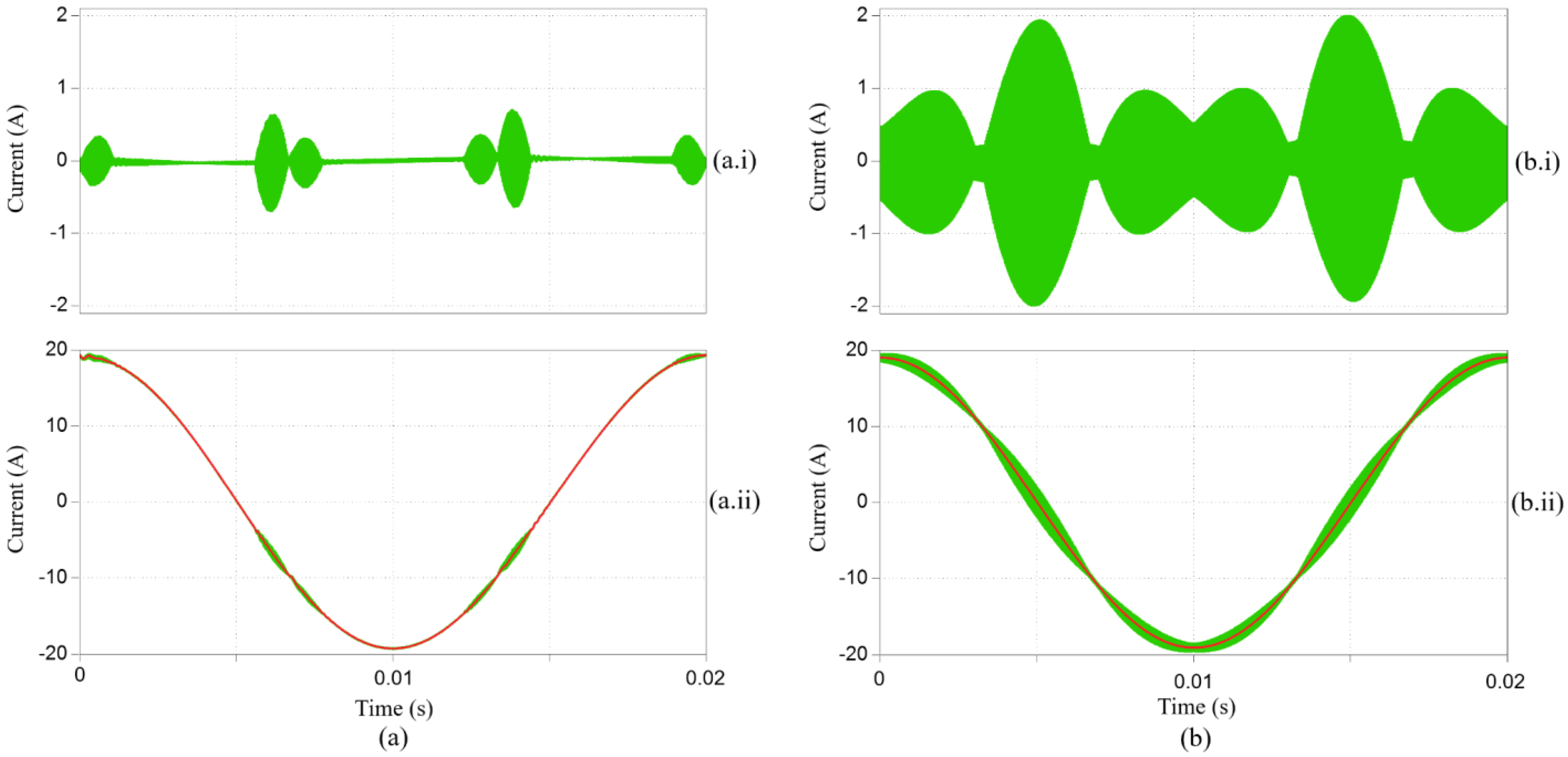
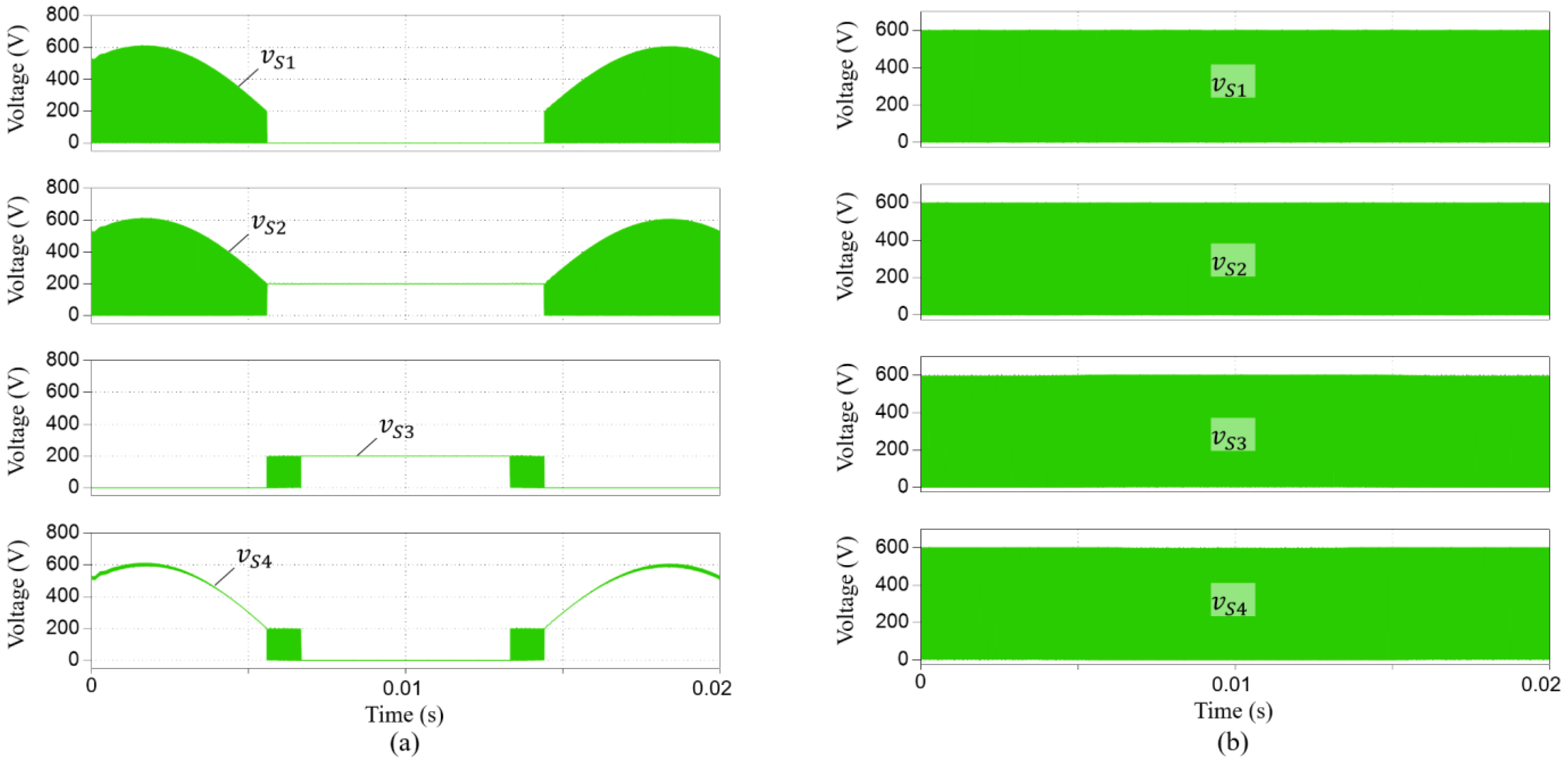
3.1. CM Voltage and Current
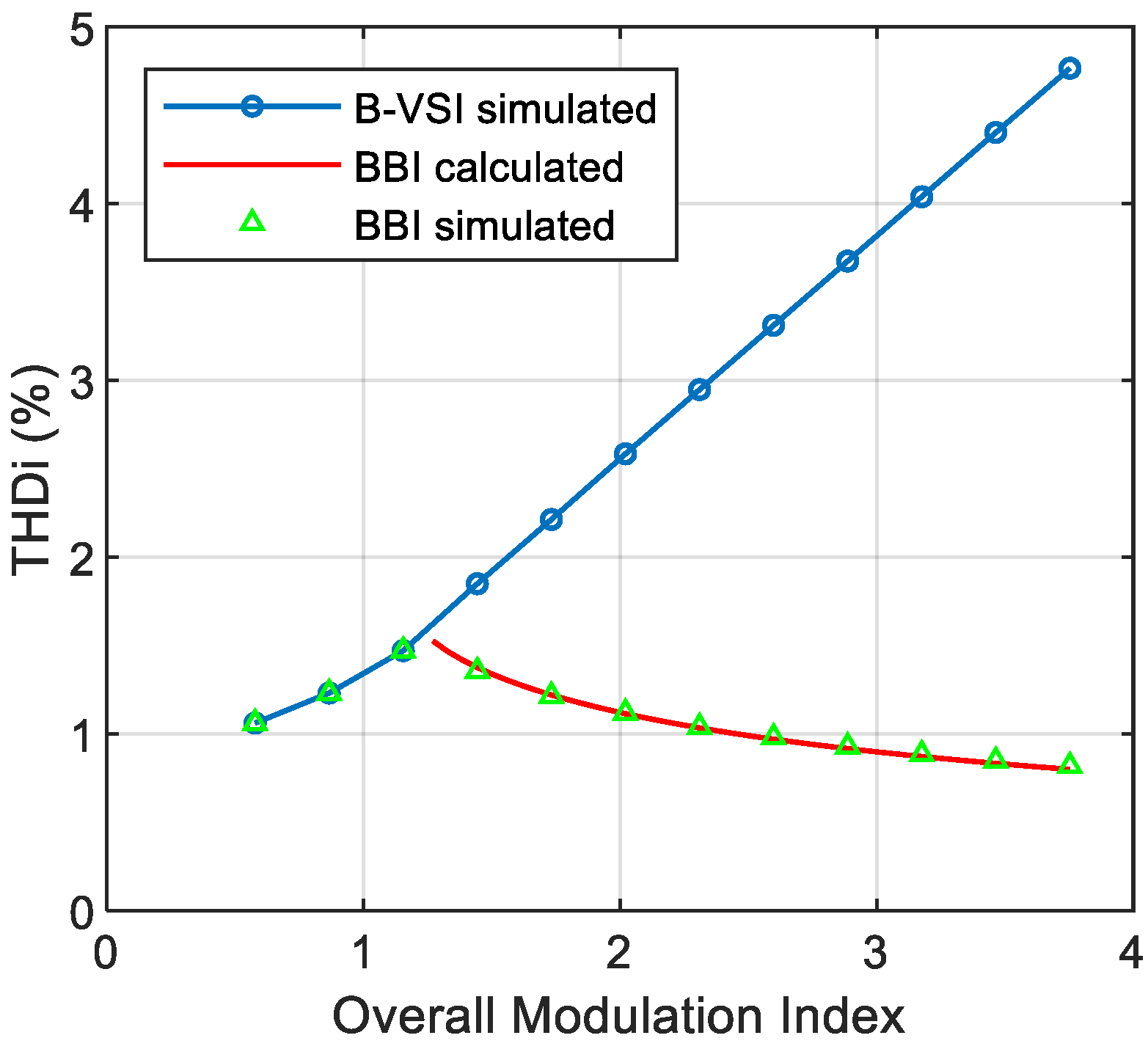
3.2. THD of the Output Current
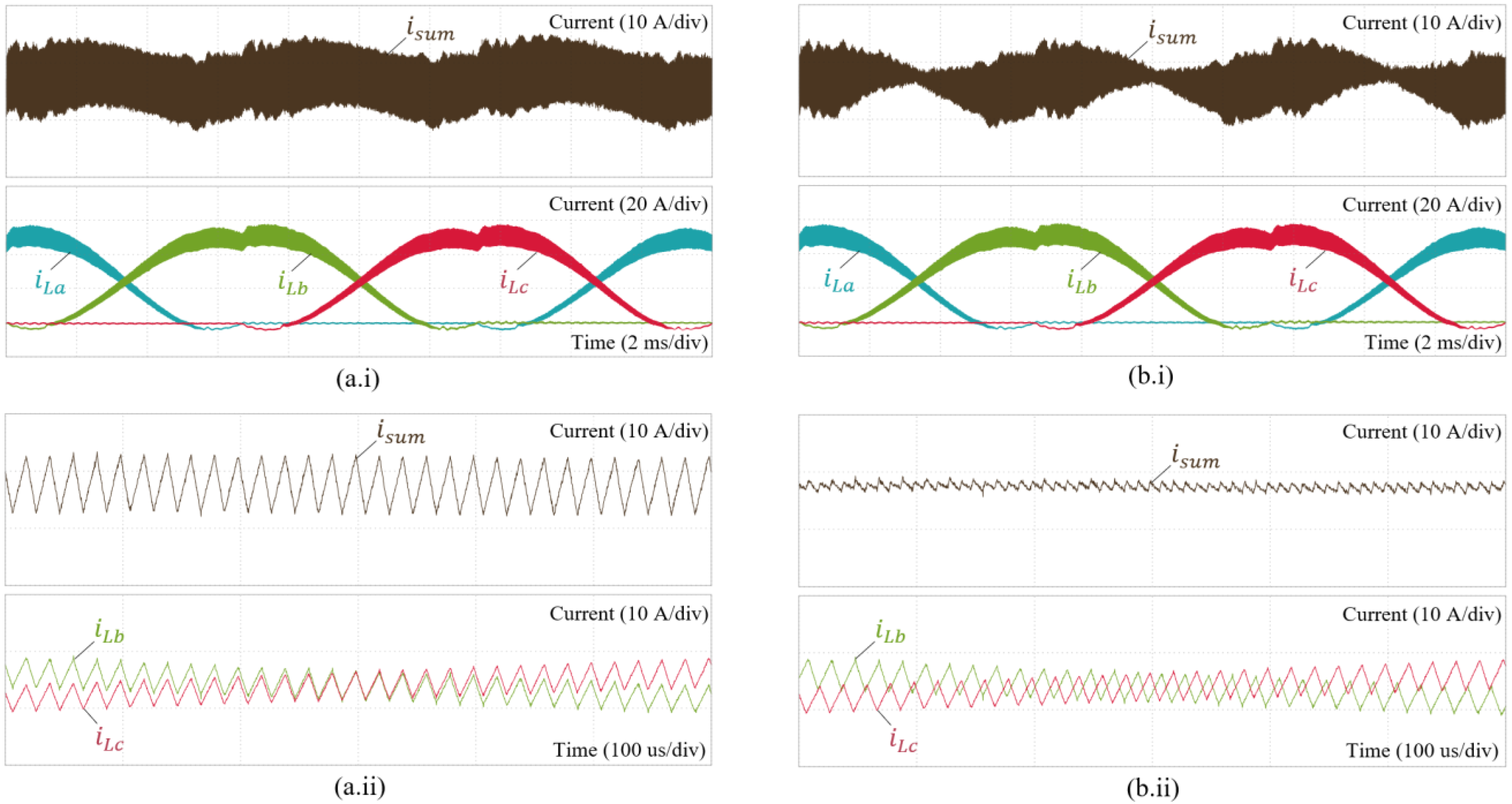
3.3. Phase Swapping Interleaving Method

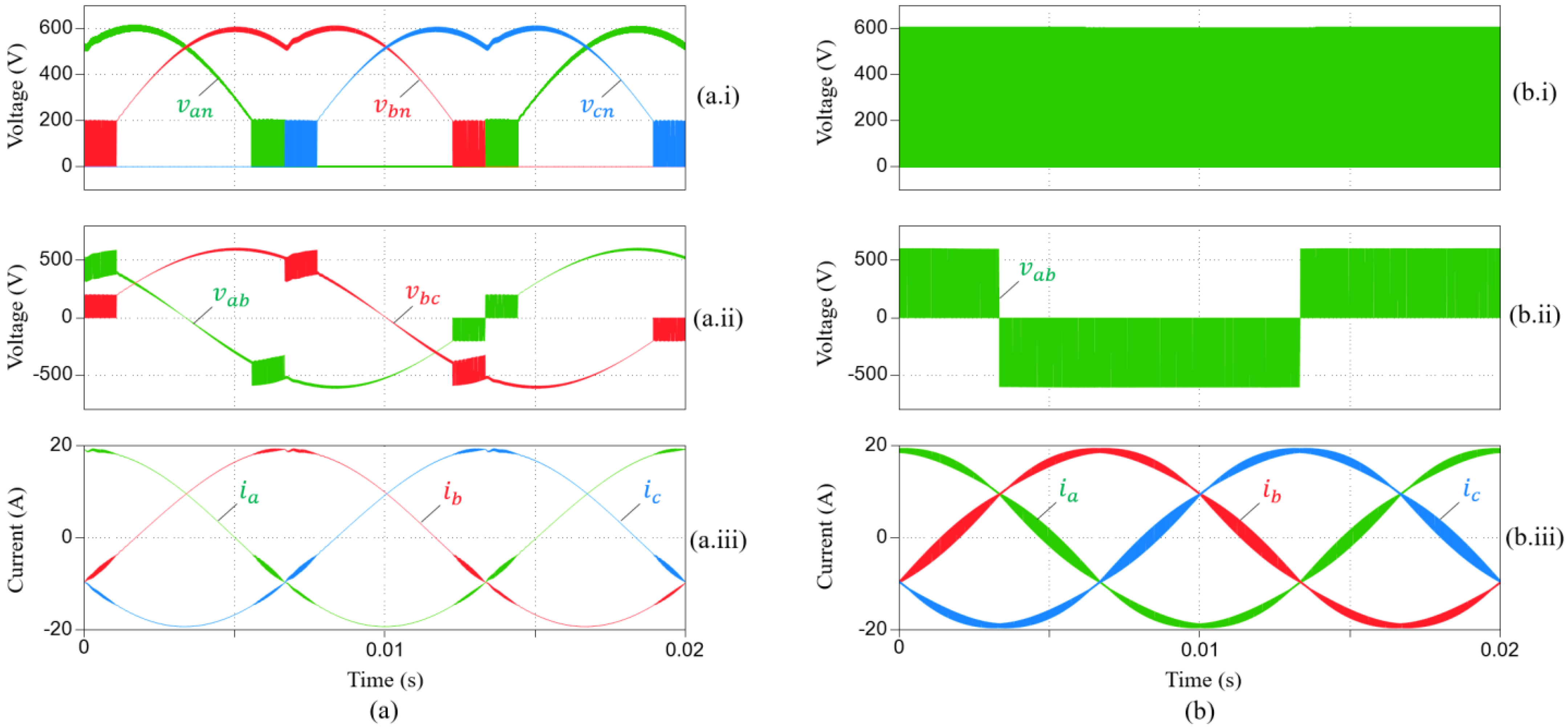
4. Simulation Evaluation
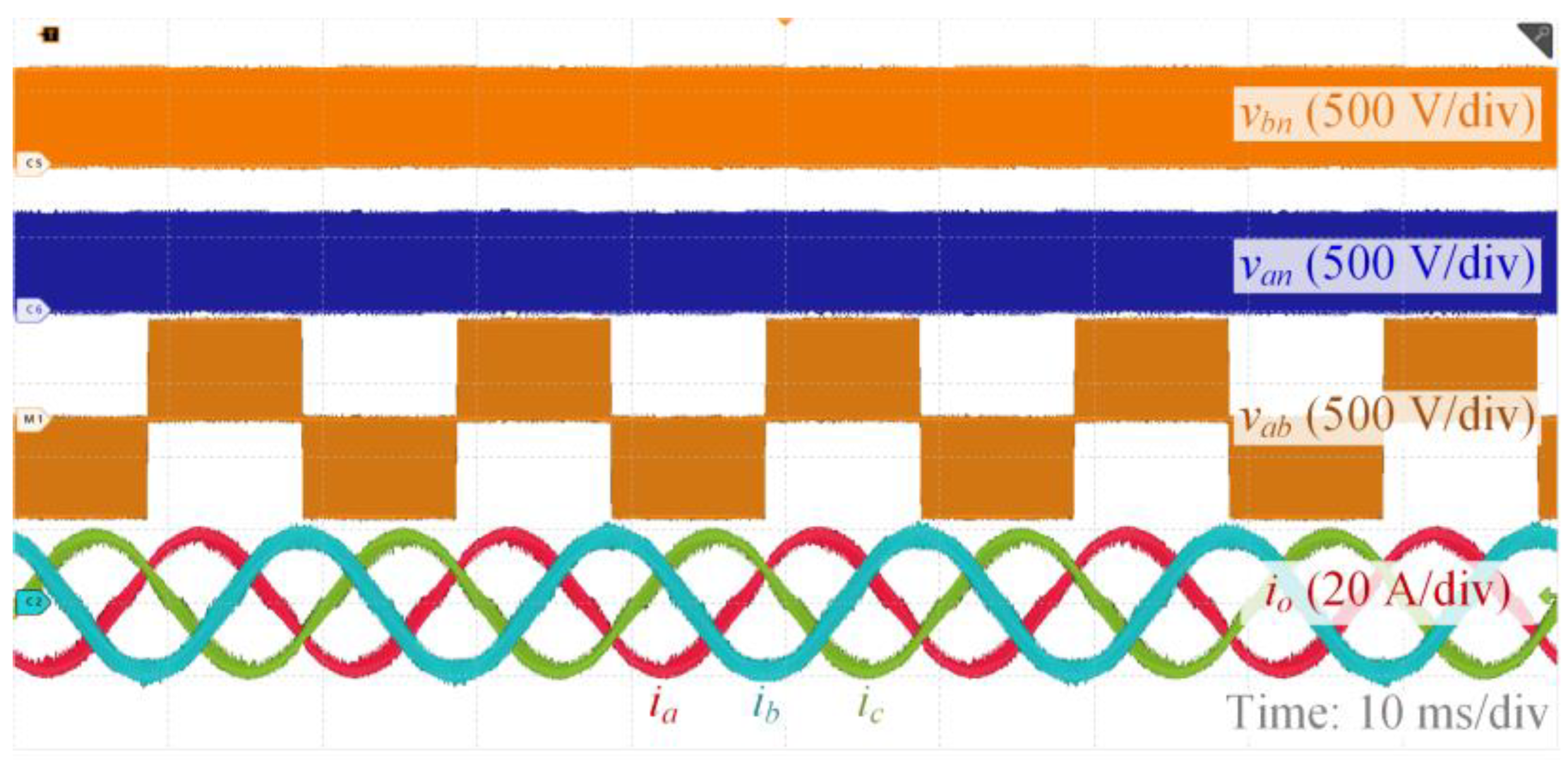
5. Experimental Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lai, J.-S.; Nelson, D. Energy management power converters in hybrid electric and fuel cell vehicles. Proc. IEEE 2007, 95, 766–777. [Google Scholar] [CrossRef]
- Estima, J.; Cardoso, A.M. Efficiency analysis of drive train topologies applied to electric/hybrid vehicles. IEEE Trans. Veh. Technol. 2012, 61, 1021–1031. [Google Scholar] [CrossRef]
- Burress, T.; Campbell, S. Benchmarking EV and HEV power electronics and electric machines. In Proceedings of the 2013 IEEE Transportation Electrification Conference and Expo (ITEC), Detroit, MI, USA, 16–19 June 2013; pp. 1–6. [Google Scholar]
- Anwar, M.; Alam, M.K.; Gleason, S.E.; Setting, J. Traction Power Inverter Design for EV and HEV Applications at General Motors: A Review. In Proceedings of the 2019 IEEE Energy Conversion Congress and Exposition (ECCE), Baltimore, MD, USA, 29 September–3 October 2019; pp. 6346–6351. [Google Scholar]
- Chen, L.; Ge, B. High Power Traction Inverter Design and Comparison for Electric Vehicles. In Proceedings of the 2018 IEEE Transportation Electrification Conference and Expo (ITEC), Long Beach, CA, USA, 13–15 June 2018; pp. 583–588. [Google Scholar]
- Goli, C.S.; Essakiappan, S.; Sahu, P.; Manjrekar, M.; Shah, N. Review of Recent Trends in Design of Traction Inverters for Electric Vehicle Applications. In Proceedings of the 2021 IEEE 12th International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Virtual, 28 June–1 July 2021; pp. 1–6. [Google Scholar]
- Shen, Z.J.; Omura, I. Power Semiconductor Devices for Hybrid, Electric, and Fuel Cell Vehicles. Proc. IEEE 2007, 95, 778–789. [Google Scholar] [CrossRef]
- Graovac, D.; Christmann, A.; Münzer, M. Power semiconductor solutions for hybrid-electric and electric vehicles. In Proceedings of the 2012 15th International Power Electronics and Motion Control Conference (EPE/PEMC), Novi Sad, Serbia, 4–6 September 2012; pp. LS4d.3-1–LS4d.3-8. [Google Scholar]
- Song, C.-H.; Song, I.-S.; Shin, H.-S.; Lee, C.-H.; Kim, K.-C. A Design of IPMSM for High-Power Electric Vehicles with Wide-Field-Weakening Control Region. IEEE Trans. Magn. 2022, 58, 1–5. [Google Scholar] [CrossRef]
- Chen, S.; Ding, S.; Shen, S.; Dai, Y.; Yang, Z.; Zhang, J. Influence of Field Weakening Control on Electromagnetic Force and Electromagnetic Vibration of SPMSMs. In Proceedings of the 2021 IEEE 12th Energy Conversion Congress & Exposition—Asia (ECCE-Asia), Singapore, 24–27 May 2021; pp. 221–225. [Google Scholar]
- Wang, B.; Zhang, J.; Yu, Y.; Zhang, X.; Xu, D. Unified Complex Vector Field-Weakening Control for Induction Motor High-Speed Drives. IEEE Trans. Power Electron. 2020, 36, 7000–7011. [Google Scholar] [CrossRef]
- Muta, K.; Yamazaki, M.; Tokieda, J. Development of New-Generation Hybrid System THS II—Drastic Improvement of Power Performance and Fuel Economy. In Proceedings of the SAE 2004 World Congress & Exhibition, Detroit, MI, USA, 8–11 March 2004. [Google Scholar]
- Burress, T.A.; Campbell, S.L.; Coomer, C.; Ayers, C.W.; A Wereszczak, A.; Cunningham, J.P.; Lin, H.T. Evaluation of the 2010 Toyota Prius Hybrid Synergy Drive System; Oak Ridge National Lab: Oak Ridge, TN, USA, 2011. [Google Scholar]
- Gebregergis, A.; Chowdhury, M.; Islam, M.; Sebastian, T. Modeling of permanent-magnet synchronous machine including torque ripple effects. IEEE Trans. Ind. Appl. 2015, 51, 232–239. [Google Scholar] [CrossRef]
- Mattavelli, P.; Tubiana, L.; Zigliotto, M. Torque-ripple reduction in pm synchronous motor drives using repetitive current control. IEEE Trans. Power Electron. 2005, 20, 1423–1431. [Google Scholar] [CrossRef]
- Feng, G.; Lai, C.; Kar, N.C. Practical Testing Solutions to Optimal Stator Harmonic Current Design for PMSM Torque Ripple Minimization Using Speed Harmonics. IEEE Trans. Power Electron. 2017, 33, 5181–5191. [Google Scholar] [CrossRef]
- Casadei, D.; Serra, G.; Tani, A.; Zarri, L. Theoretical and experimental analysis for the RMS current ripple minimization in induction motor drives controlled by SVM technique. IEEE Trans. Ind. Electron. 2004, 51, 1056–1065. [Google Scholar] [CrossRef]
- Kumar, A.C.B.; Narayanan, G. Variable-Switching Frequency PWM Technique for Induction Motor Drive to Spread Acoustic Noise Spectrum with Reduced Current Ripple. IEEE Trans. Ind. Appl. 2016, 52, 3927–3938. [Google Scholar] [CrossRef]
- Chen, C.; Wang, Y. Analysis of the impact of current ripple on the eddy current loss of axial-flux permanent magnet motor. In Proceedings of the 2014 IEEE Conference and Expo Transportation Electrification Asia-Pacific (ITEC Asia-Pacific), Beijing, China, 31 August–3 September 2014; pp. 1–5. [Google Scholar]
- Jeong, T.C.; Kim, W.H.; Kim, M.J.; Lee, K.D.; Lee, J.J.; Han, J.H.; Sung, T.-H.; Kim, H.-J.; Lee, J. Current Harmonics Loss Analysis of 150-kW Traction Interior Permanent Magnet Synchronous Motor through Co-Analysis of d-q Axis Current Control and Finite Element Method. IEEE Trans. Magn. 2013, 49, 2343–2346. [Google Scholar] [CrossRef]
- Yoshida, Y.; Nakamura, K.; Ichinokura, O. Calculation of eddy current loss in permanent magnet motor caused by carrier harmonics based on reluctance network analysis. In Proceedings of the 2013 15th European Conference on Power Electronics and Applications (EPE), Lille, France, 2–6 September 2013; pp. 1–6. [Google Scholar]
- Yamazaki, K.; Abe, A. Loss Investigation of Interior Permanent-Magnet Motors Considering Carrier Harmonics and Magnet Eddy Currents. IEEE Trans. Ind. Appl. 2009, 45, 659–665. [Google Scholar] [CrossRef]
- Van Do, T.; Trovao, J.P.F.; Li, K.; Boulon, L. Wide-Bandgap Power Semiconductors for Electric Vehicle Systems: Challenges and Trends. IEEE Veh. Technol. Mag. 2021, 16, 89–98. [Google Scholar] [CrossRef]
- Adabi, J.; Zare, F.; Ledwich, G.; Ghosh, A. Leakage current and common mode voltage issues in modern AC drive systems. In Proceedings of the 2007 Australasian Universities Power Engineering Conference, Perth, WA, Australia, 9–12 December 2007; pp. 1–6. [Google Scholar]
- Ogasawara, S.; Akagi, H. Modeling and damping of high-frequency leakage currents in PWM inverter-fed AC motor drive systems. IEEE Trans. Ind. Appl. 1996, 32, 1105–1114. [Google Scholar] [CrossRef] [Green Version]
- Murai, Y.; Kubota, T.; Kawase, Y. Leakage current reduction for a high-frequency carrier inverter feeding an induction motor. IEEE Trans. Ind. Appl. 1992, 28, 858–863. [Google Scholar] [CrossRef]
- Muetze, A.; Binder, A. Calculation of circulating bearing currents in machines of inverter-based drive systems. IEEE Trans. Ind. Electron. 2007, 54, 932–938. [Google Scholar] [CrossRef]
- Sundaresan, A.; Chandorkar, M. Traction Motor Bearing Failures Due to Bearing Currents in Electric Locomotives. In Proceedings of the 2019 IEEE Transportation Electrification Conference and Expo (ITEC), Novi, MI, USA, 19–21 June 2019; pp. 1–6. [Google Scholar]
- Kriese, M.; Wittek, E.; Gattermann, S.; Tischmacher, H.; Poll, G.; Ponick, B. Influence of bearing currents on the bearing lifetime for converter driven machines. In Proceedings of the 2012 XXth International Conference on Electrical Machines, Marseille, France, 2–5 September 2012; pp. 1735–1739. [Google Scholar] [CrossRef]
- Han, Y.; Wu, Z.; Wu, D. Analysis and Design of a Modular Three-Phase Boost-Buck EV Traction Inverter. In Proceedings of the 34th International Electric Vehicle Symposium and Exhibition (EVS34), Nanjing, China, 25–28 June 2021. [Google Scholar]








| Parameter | Value |
|---|---|
| Nominal power (kW) | 10 |
| Input DC voltage (V) | 200 |
| Output voltage, L-L RMS (V) | 400 |
| Input filter inductance (uH) | 240 |
| DC bus Capacitance (uF) | 12 |
| Switching frequency (kHz) | 50 |
| Load inductance (mH) | 0.5 |
| Topology | Efficiency | THDi | CM Current RMS |
|---|---|---|---|
| BBI | 97.7% | 1.74% | 86 mA |
| B-VSI | 96.8% | 12.52% | 776 mA |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, Y.; Zhu, Y.; Wu, D. Analysis of the THD and Common-Mode Voltage of the Three-Phase Boost-Buck EV Traction Inverter. World Electr. Veh. J. 2022, 13, 114. https://doi.org/10.3390/wevj13070114
Han Y, Zhu Y, Wu D. Analysis of the THD and Common-Mode Voltage of the Three-Phase Boost-Buck EV Traction Inverter. World Electric Vehicle Journal. 2022; 13(7):114. https://doi.org/10.3390/wevj13070114
Chicago/Turabian StyleHan, Yongjie, Yuan Zhu, and Deliang Wu. 2022. "Analysis of the THD and Common-Mode Voltage of the Three-Phase Boost-Buck EV Traction Inverter" World Electric Vehicle Journal 13, no. 7: 114. https://doi.org/10.3390/wevj13070114
APA StyleHan, Y., Zhu, Y., & Wu, D. (2022). Analysis of the THD and Common-Mode Voltage of the Three-Phase Boost-Buck EV Traction Inverter. World Electric Vehicle Journal, 13(7), 114. https://doi.org/10.3390/wevj13070114






