A State-of-Charge Estimation Method Based on Multi-Algorithm Fusion

Abstract

Lithium-ion power batteries are widely used in the electric vehicle (EV) industry due to their high working voltage, high energy density, long cycle life, low self-discharge rate, and environmental protection. A multi-algorithm fusion method is proposed in this paper to estimate the battery state of charge (SOC), establishing the Thevenin model and collecting the terminal voltage residuals when the extended Kalman filter (EKF), adaptive extended Kalman filter (AEKF), and H infinite filter (HIF) estimate the SOC separately. The residuals are fused by Bayesian probability and the weight is obtained, and then the SOC estimated value of the fusion algorithm is obtained from the weight. A comparative analysis of the estimation accuracy of a single algorithm and a fusion algorithm under two different working conditions is made. Experimental results show that the fusion algorithm is more robust in the whole process of SOC estimation, and its estimation accuracy is better than the EKF algorithm. The estimation result for the fusion algorithm under a Dynamic Stress Test (DST) is better than that under a Hybrid Pulse Power Characterization (HPPC) test. With the emergence of cloud batteries, the fusion algorithm is expected to realize real vehicle online application.

1. Introduction

Lithium-ion power batteries (hereinafter referred to as lithium batteries) have become the first choice for electric vehicles due to their high working voltage, high energy density, long cycle life, low self-discharge rate, and environmental friendliness [1]. The state of charge (SOC) is one of the important pieces of state information for lithium-ion batteries. An accurate SOC can help the driver make an informed decision as to when to charge the battery and help the battery management system (BMS) avoid overcharge or overdischarge safety problems [2]. Due to the high non-linearity and time-varying characteristics of the battery and the uncertainty of the battery chemical reaction, it is a difficult problem to accurately estimate the battery SOC [3].

Lithium-ion battery SOC estimation methods can be roughly divided into the following four types: the ampere-hour integration method, characterization parameter method, model-based method, and data-drive method [4,5,6,7]. At present, the mainstream SOC estimation method is based on a model to achieve battery SOC estimation, and the filter algorithm based on the equivalent circuit model (ECM) is especially widely used to estimate battery SOC. Compared with the complex electrochemical model, ECM can also use fewer parameters to characterize the dynamic characteristics of the battery, which has the advantage of less computation [8].

SOC estimation methods based on ECM include the Kalman filter (KF) series, sliding mode observer, H infinite filter, particle filter (PF), etc. [9,10,11,12]. However, it is difficult to meet the SOC estimation accuracy requirements for complex driving conditions by using a single algorithm. George S et al. [13] proposed a new and accurate hybrid SOC estimation method. Combining the advantages of different estimation techniques to minimize SOC errors and limit the amount of computation, the proposed solution can ensure the safe operation of the battery within the acceptable SOC limits and extend its life. Li H et al. [14] propose a state charge estimation method for energy storage systems based on the NARX network and filter joint algorithm, and apply the extended Kalman filter (EKF) to the improved nonlinear autoregressive algorithm with an exogenous neural network (NARXNN). The proposed NARX-EKF algorithm proves that it has higher accuracy and robustness than a single algorithm, which is validated by an experiment. Xiong R et al. [15] designed a fusion algorithm of SOC and capacity in a complex application environment. The convergence and anti-noise performance of the fusion algorithm are further discussed. The experimental results showed that the proposed fusion algorithm can achieve high-precision SOC estimation with a relative error of less than 2% when considering different aging degrees for lithium-ion batteries in a wide temperature range. Zhang K et al. [16] developed an adaptive weighted volume particle filter (AWCPF) method to estimate battery SOC. Different initial SOC values under different working conditions have been considered in the process of experimental verification. The results indicated that the proposed SOC estimation method, in view of the AWCPF algorithm, has high estimation accuracy, strong robustness, and fast convergence speed, and the maximum SOC estimation error is less than 1%. Inspired by the above literature, this paper attempts to realize the fusion of multiple algorithms based on a Bayesian formula and compares the estimation results with a single algorithm in DST and HPPC conditions.

The remainder of the paper is constituted as follows: Section 2 describes the modeling process and the battery parameter identification method. Section 3 introduces the individual estimation algorithms and the fusion algorithm. Section 4 verifies the algorithm under two working conditions. Finally, the key conclusions are summarized in Section 5.

2. Modelling and Parameter Identification

2.1. Modelling for Lithium-Ion Batteries

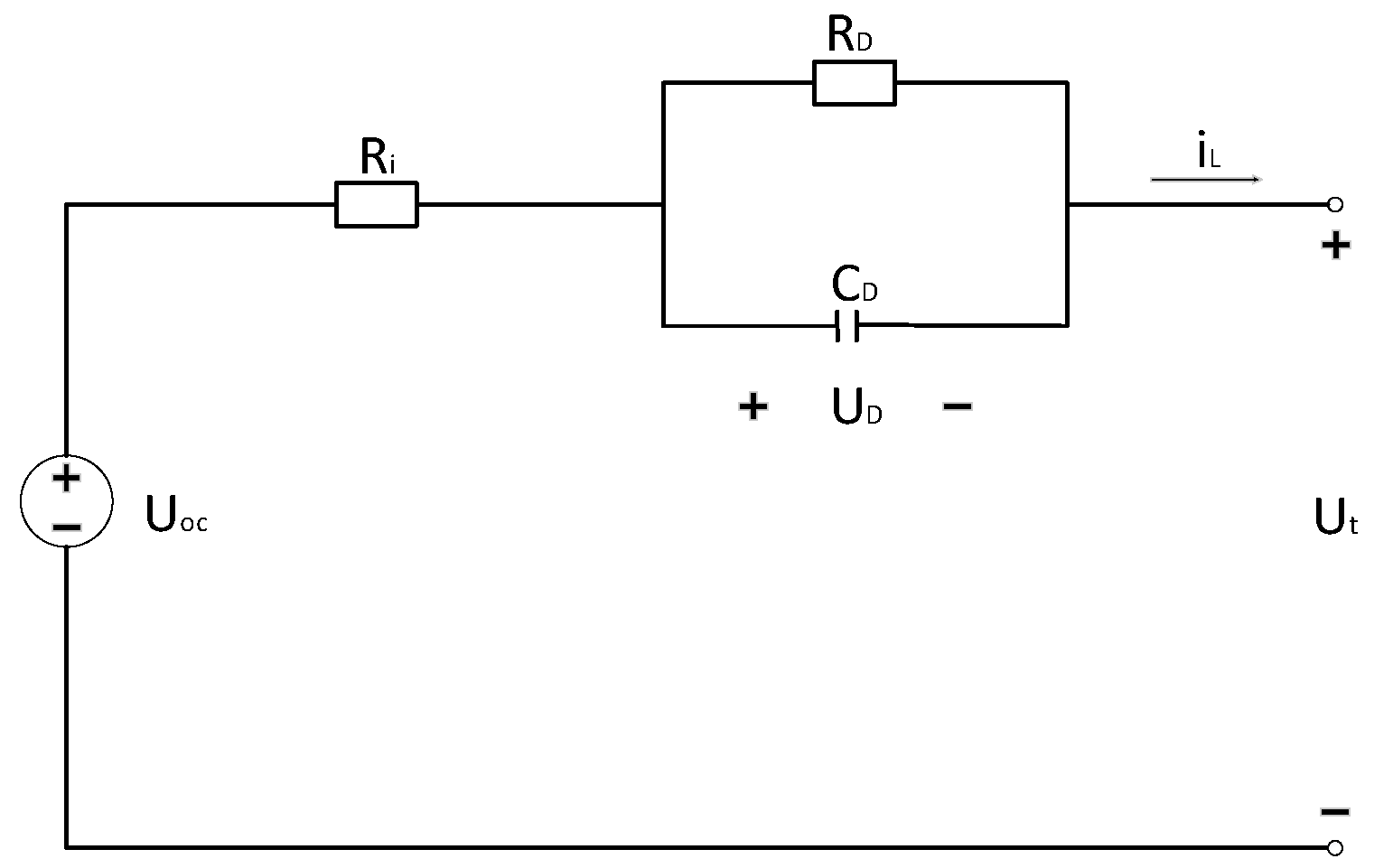
The equivalent circuit model uses traditional resistors, capacitors, constant voltage sources, and other circuit components to form a circuit network to describe the external characteristics of the power batteries. The voltage source represents the thermodynamic equilibrium potential of the power battery, and the RC network is adopted to describe the battery dynamic characteristics. The main advantages of the equivalent circuit model are its simple structure, small calculation amount, and high accuracy. The Rint model, Thevenin model, and Dual Polarization (DP) model are the commonly equivalent circuit models. [17,18]. Previous literature [19] comprehensively considers the accuracy of the models’ parameter identification and the complexity of their structure, and considers the Akaike Information Criterion (AIC) of the first-order RC ECM (Thevenin model) as the smallest compared with other kinds of ECMs, which is the model with the best balance between accuracy and structural complexity. In view of this, this experiment constructs a Thevenin model as the research basis.

The experiments introduced in this paper were all implemented in a Arbin-BT2000 power battery single test equipment. At the same time, a programmable temperature and humidity three-layer test box was used as the environmental simulation equipment, and the temperature was controlled at 25 °C. Lithium battery A (ANR26650M1A) of 3.3 V/2.3 Ah and battery B (SPIM14245190) of 3.7 V/35 Ah were used in the experiment. The maximum usable capacity of the two batteries were recalibrated at a room temperature of 25 °C: 2.22 ah for battery A and 31.80 ah for battery B.

The computer used for this experimental algorithm is an HP 288 Pro G6 microtower PC (HP, Palo Alto, CA, USA), which is configured with a 3.1 GHz Intel (R) core (TM) i5-10500 CPU and 8 GB ram (Intel, Santa Clara, CA, USA). All estimation algorithms are designed and implemented in MATLAB 2020b.

As shown in Figure 1, $U_D$ is the terminal voltage; $U_{OC}$ is the open circuit voltage; $R_D$ and $C_D$ are the polarization internal resistance and polarization capacitance, respectively; $R_i$ is the ohmic resistance; $i_L$ is the circuit current. The battery state space equation can be written as follows:

$$\{\begin{array}{l}{\stackrel{.}{U}}_D=\frac{i_L}{C_D}-\frac{U_D}{C_D{R}_D}\\ U_t=U_{OC}-U_D-i_L{R}_i\end{array}$$

(1)

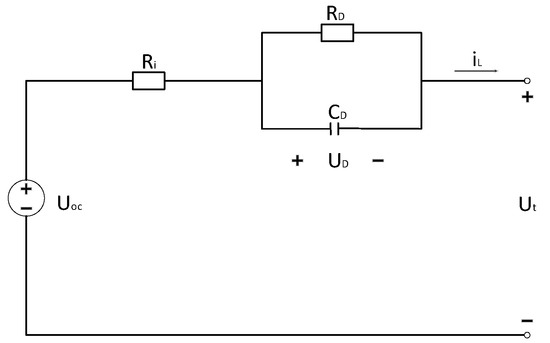
Figure 1. Thevenin mode.

The polarization voltage expression obtained by the model discretization is as follows;

$$U_{\mathrm{D}}[(k+1)\mathsf{\Delta }t]=e^{\frac{-\mathsf{\Delta }t}{\tau }}{U}_{\mathrm{D}}(k\mathsf{\Delta }t)+R_{\mathrm{D}}{i}_{\mathrm{L}}[(k+1)\mathsf{\Delta }t][1-e^{\frac{-\mathsf{\Delta }t}{\tau }}]$$

(2)

among them

$$\tau =R_{\mathrm{D}}\times C_D$$

2.2. OCV-SOC Curve

The open circuit voltage (OCV) test is performed on two batteries at room temperature (25 °C), and the process is as follows:

• The battery is fully charged through the standard constant current and constant voltage (CC-CV) charging method. After standing for 5 h, the terminal voltage was measured. This value is regarded as the open circuit voltage value of SOC = 100%.
• Discharge with standard current and constant current. The cutoff condition is that the discharge capacity reaches 5% of the maximum available capacity, or the battery voltage drops to the discharge cutoff voltage. After standing for 5 h, measure the terminal voltage.
• Repeat step 2 until the power battery reaches the discharge cutoff voltage.

The OCV-SOC relation is fitted as follows:

$$U_{OC}\left(z\right)={\alpha }_0+{\alpha }_{1}z+{\alpha }_2{z}^2+{\alpha }_3{z}^3+{\alpha }_4/z+{\alpha }_5\ln z+{\alpha }_{6}1\mathrm{n}\left(1-z\right)$$

(3)

for battery A, α₀ = 3.04342712, α₁ = 0.69965544, α₂ = −0.70823233, α₃ = 0.31435882, α₄ = −0.014878876, α₅ = −0.10513395, α₆ = −0.01276305.

2.3. Parameter Identification

At present, the main parameter identification methods can be divided into offline and online identification [20,21]. The calculation amount for offline parameter identification is much smaller than that for online parameter identification, and it is more widely used in EVs. The online identification method can calculate the model parameters by measuring the voltage and current in real time. It can achieve performance prediction according to different battery aging levels and operating conditions [22,23,24]. In this experiment, the HPPC test was used for two batteries to perform offline parameter identification of the model, so as to obtain the model parameters under different SOCs.

The process is listed as follows:

• Fully charge the two batteries with the CC-CV charging method.
• Let stand for 5 h.
• Load the mixed pulse current excitation sequence, discharge the battery with constant current for a certain period of time, and then let it stand for 1 h. (Constant current discharge of battery to ensure 10% SOC interval between two times).
• Repeat step 3 until the discharge reaches the cutoff voltage.

Offline parameter identification is carried out by the multiple linear regression method. The identification results for battery A are shown in Table 1.

Table 1. Identification result for battery A.

SOC	Ri	RD	CD
0.9	0.0200678	0.0280174	6005.6549
0.8	0.0198582	0.0295043	5975.013
0.7	0.0198537	0.0291771	6244.846
0.6	0.0198369	0.0250574	6376.551
0.5	0.0198402	0.0272475	6077.899
0.4	0.0201856	0.0312714	45,796.440
0.3	0.0203209	0.0322185	65,557.043
0.2	0.0206306	0.0360988	55,199.546
0.1	0.020996	0.0429594	44,303.6293

3. State of Charge Estimation

3.1. State of Charge Definition

SOC is a value that describes the ratio of the remaining capacity of the battery to the current maximum available capacity:

$$SO{C}_t=SO{C}_0-\frac{1}{C_a}\underset{0}{\overset{t}{{\displaystyle \int }}}{\eta }_i{i}_L\left(\tau \right)\mathrm{d}\tau$$

(4)

where SOC_t is the present SOC; SOC₀ is the SOC’s initial value; i_L is the instantaneous load current (assumed positive for discharge, negative for charge); η_i is the Coulomb efficiency, which is the function of the current and the temperature; and Ca is the present maximum available capacity, which may be different from the rated capacity for the age effect.

Describing (4) with a discrete-time style:

$$SO{C}_k=SO{C}_{k-1}-\frac{{\eta }_i{i}_L\left(k\right)\mathsf{\Delta }t}{C_a}$$

(5)

3.2. Extended Kalman Filter Estimation Method

KF is mainly applicable to linear systems, while a power battery is a highly non-linear system. In order to improve the estimation accuracy of the KF method for power battery SOCs, the EKF method is proposed.

For a nonlinear discrete system, the general form of its state equation and observation equation is as follows:

$$\{\begin{array}{l}{x}_{\mathrm{k}}=f(x_{k-1},u_{k-1})+w_{k-1}\\ y_k=h(x_k,u_k)+v_k\end{array}$$

(6)

in the Equation (6), the subscript k is the time; x is the system state vector; y is the observation vector; u is the system input vector; w is the state white noise with a mean value of 0 and a covariance of Q; v is the state white noise with a mean value of 0 and a covariance of R; w and v do not affect each other.

Expand f($x_k$,$u_k$) and h($x_k$,$u_k$) with the first-order Taylor formula, linearize them, and substitute them back into the equation. Get the following Equation (7):

$$\{\begin{array}{l}{x}_k\approx A_{k-1}{x}_{k-1}+B_{k-1}{u}_{p-1}+w_{k-1}\\ y_k\approx C_k{x}_k+D_k+v_k\end{array}$$

(7)

In the equation: $x={\left[U_D z\right]}^T$ (z means SOC), $u=i_L$, $y=U_t$.

$$A_k=\left[\begin{array}{cc}{e}^{\frac{{}^{-\mathsf{\Delta }t}}{\tau }}& 1\\ 0& 0\end{array}\right] B_k=[(1-e^{\frac{{}^{-\mathsf{\Delta }t}}{\tau }})RD;\frac{ \eta i\mathsf{\Delta }t}{C_a}]$$

$$C_k=\left[-1 \frac{d{U}_{oc}\left(z\right)}{dz}\right] D_k=U_{OC,k}-U_{D,k}-R_i{u}_k-C_k{x}_k$$

3.3. SOC Estimation Algorithm with Adaptive Extended Kalman Filter Method

When the EKF method is employed to estimate the battery SOC, it is necessary to define the initial value of the state white noise covariance Q and the observed white noise covariance R. If the selection of the initial value is not appropriate, it can affect the SOC estimation accuracy or even cause the divergence of the filter. In order to solve this problem, the adaptive extended Kalman filter method is proposed in this study.

The adaptive EKF method updates the Kalman gain matrix and the state estimation error covariance P while iteratively updating Q and R. The specific update method is listed as follows:

$$\{\begin{array}{l}{H}_k=\frac{1}{M}{\displaystyle \sum _{i=k-M+1}^k{e}_i{e}_i{}^T}\\ R_k=H_k-C_k{P}_k{}^{-}{C}_k{}^T\\ Q_k=K_k{H}_k{K}_k{}^T\end{array}$$

(8)

where e is new innovation; H is the real-time estimated covariance function of innovation obtained by the windowed estimation principle; M is the size of the window.

3.4. H Infinity Filter SOC Estimation Algorithm

The Kalman filter is based on the premise that the system model is accurate and the external input characteristics are known, which does not conform to the actual situation. In actual operation, the statistical characteristics of noise are difficult to obtain, and the established model is also different from reality. In order to overcome the insufficiencies of the Kalman filter and the uncertainty in the modeling process and improve the robustness of the estimation, the HIF algorithm came into being.

The calculation process for the HIF algorithm is summarized in Table 2.

Table 2. HIF process.

Establish the Linear Discretization Equation of Thevenin Model.
Initialization	Set the Initial Value of the State Observer: ${\mathit{x}}_0, {\mathit{P}}_0,\mathit{Q},\mathit{R},\mathit{\lambda },\mathit{S}$
① $$\begin{gathered} \mathrm{from}\mathit{k}-{\mathbf{1}}^{+} \\ \mathrm{to}{\left(\mathit{k}\right)}^{-} \end{gathered}$$	System state estimation:            ${\stackrel{\wedge }{x}}_{{}_k}^{-}=f(x_{k-1},u_{k-1})$
	HIF feature matrix estimation:      $P_k^{-}=A_{k-1}{P}_{k-1}{A}_{k-1}{}^T+Q$
② $$\begin{gathered} \mathrm{from}{\left(\mathit{k}\right)}^{-} \\ \mathrm{to}{\left(\mathit{k}\right)}^{+} \end{gathered}$$	Innovation matrix:             $e_k=y_k-h({\stackrel{\wedge }{x}}_{{}_k}^{-},u_k)$
	Gain matrix:     $K_k=A_k{P}_k^{-}{(1-\lambda S{P}_{\mathrm{k}}^{-}+C_k^T{R}^{-1}{C}_k{P}_{\mathrm{k}}^{-})}^{-1}{C}_k^T{R}^{-1}$
	System status correction:             ${\stackrel{\wedge }{x}}_{{}_k}^{+}={\stackrel{\wedge }{x}}_{{}_k}^{-}+K_k{e}_k$
	Feature matrix correction:    $P_k^{+}=P_k^{-}{(1-\lambda S{P}_k^{-}+C_k^T{R}^{-1}{C}_k{P}_k^{-})}^{-1}$
③ Time scale update	Take the state and covariance matrix at time ${\left(k\right)}^{+}$ as the final output, prepare the state estimate at time (k + 1).

where x₀ is the initial value of the state quantity, $P_0$ is the initial state error covariance matrix, $\lambda$ is the performance boundary, S is the emphasis matrix; if there is a high degree of attention to a certain state quantity, the value in the matrix corresponding to the state quantity is greater than the value in the matrix corresponding to another state quantity.

3.5. Multi-Algorithm Fusion SOC Estimation

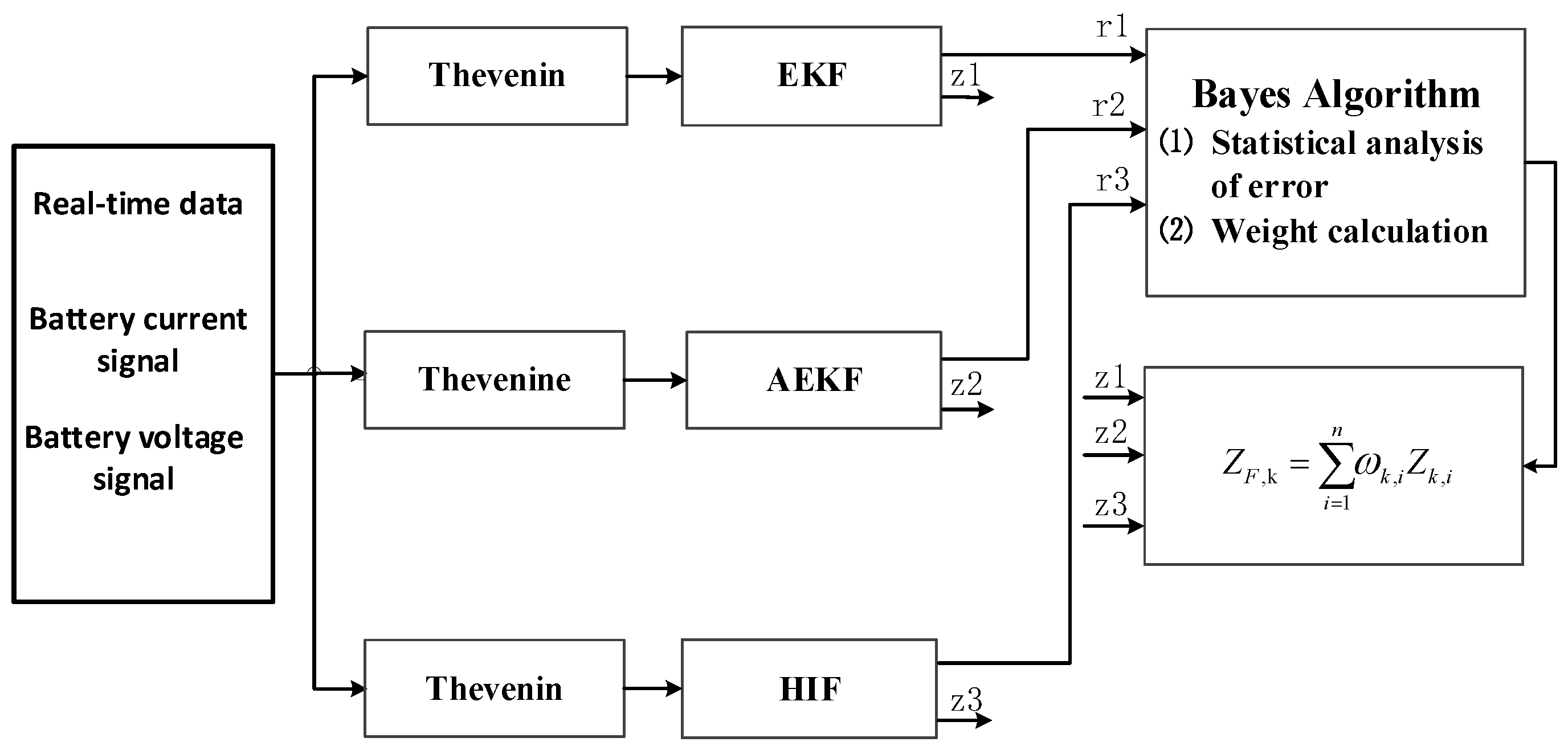
The terminal voltage residual of the algorithm has a certain mapping relationship with the SOC estimation accuracy. Assuming that the residuals obey a normal distribution, the mean and variance of the residuals can be obtained by windowing (M), which can realize the real-time estimation of the probability density, and then the fusion weight values of the three algorithm can be obtained. The algorithm diagram is shown in Figure 2.

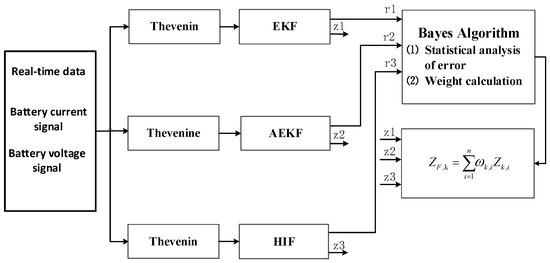
Figure 2. SOC fusion implementation flow chart.

Specific steps are as follows:

1.

Import the terminal voltage residuals of the previous three algorithms.

2.

Calculate the residual mean ${\overline{r}}_{k,i}$ and variance $s_{k,i}$ of each algorithm. ($i$ = 1,2,3, corresponding to the three algorithms).

$$\{\begin{array}{l}{\overline{r}}_{k,i}=\frac{1}{M}{\displaystyle {\displaystyle \sum }_{j=k-M-1}^k}{r}_{j,i}\\ s_{k,i}=\frac{1}{M}{\displaystyle {\displaystyle \sum }_{j=k-M-1}^k}(r_{j,i}-{\overline{r}}_{k,i})\end{array}$$

(9)

3.

Calculate the conditional probability density function at time k for each algorithm.

$$f_{Y_k|{\alpha }_{\mathrm{i}},Y_{k-1}}=\frac{1}{\sqrt{2\pi s_{k,i}}}\exp (-\frac{1}{2}{\overline{r}}_{k,i}{}^T{s}_{k,i}{\overline{r}}_{k,i})$$

(10)

4.

Calculate the weight ${\omega }_k$ of each algorithm at time k, where n is the number of algorithms.

$${\omega }_{k,i}=(1-\frac{f_{Y_k|{\alpha }_{\mathrm{i}},Y_{k-1}}{\mathrm{s}}_{k,i}}{{\displaystyle {\displaystyle \sum }_{i=1}^n}{f}_{Y_k|{\alpha }_{\mathrm{i}},Y_{k-1}}{\mathrm{s}}_{k,i}})/(n-1)$$

(11)

5.

Obtain the SOC estimated value of the fusion algorithm according to the weight.

$$Z_{F,\mathrm{k}}={\displaystyle \sum }_{i=1}^n{\omega }_{k,i}{Z}_{k,i}$$

(12)

4. Results and Discussion

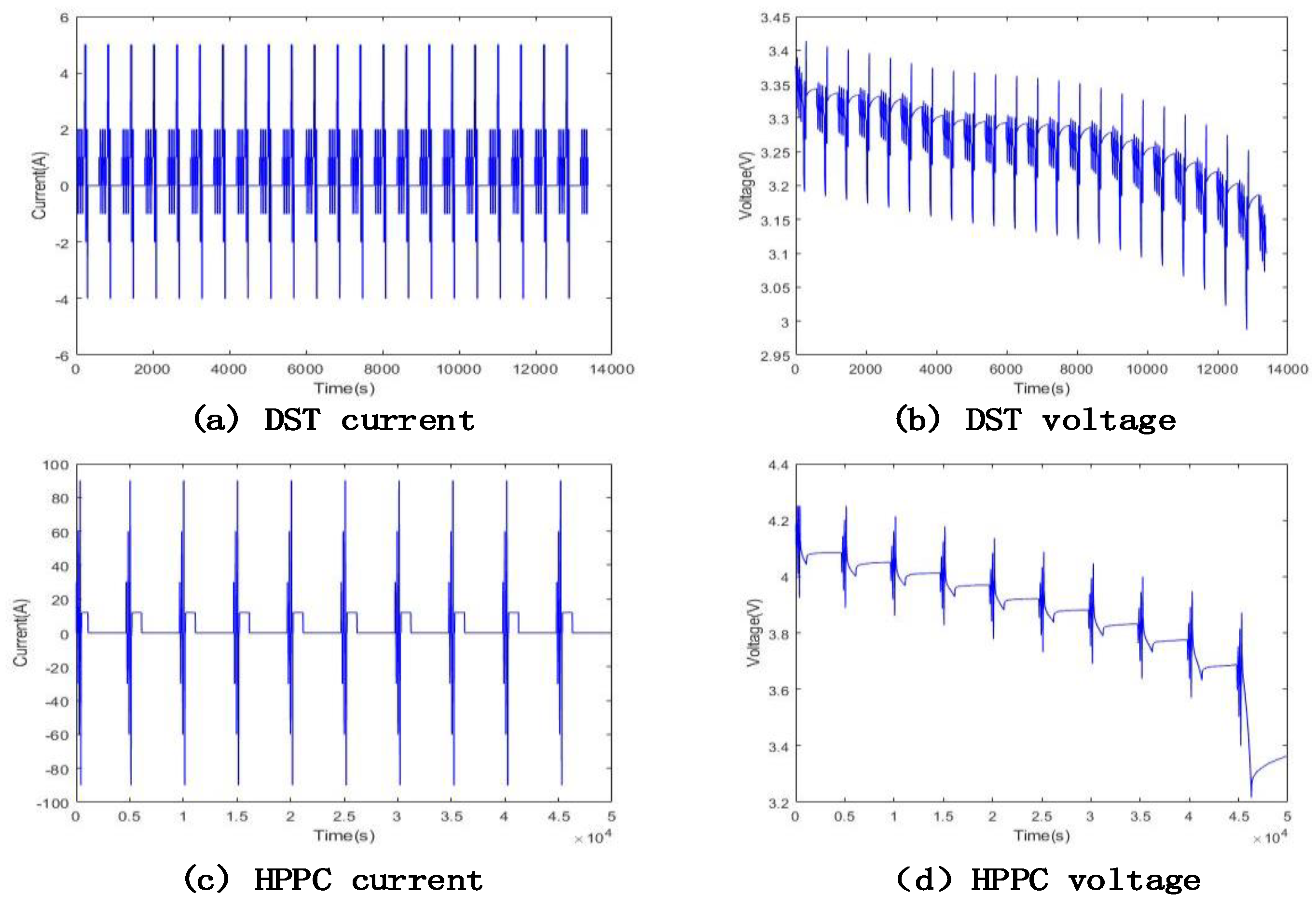
Battery A is verified under DST using the three EKF, AEKF, and HIF algorithms to fuse it, and the terminal voltage residuals and SOC estimated by the three algorithms are imported into the fusion algorithm. The working condition current and voltage are shown in Figure 3a,b. Battery B is verified under HPPC conditions using the three EKF, AEKF, and HIF algorithms to fuse it, and the terminal voltage residuals and SOC estimated by the three algorithms are imported into the fusion algorithm. The working condition current and voltage are shown in Figure 3c,d.

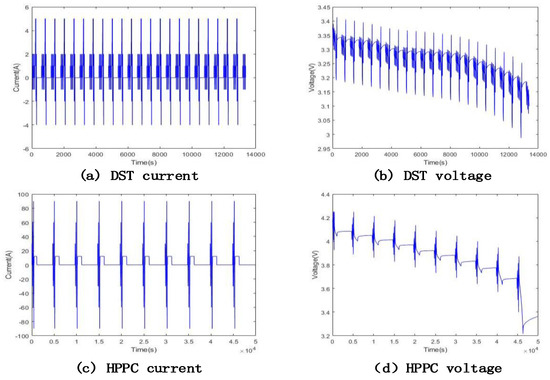
Figure 3. Testing.

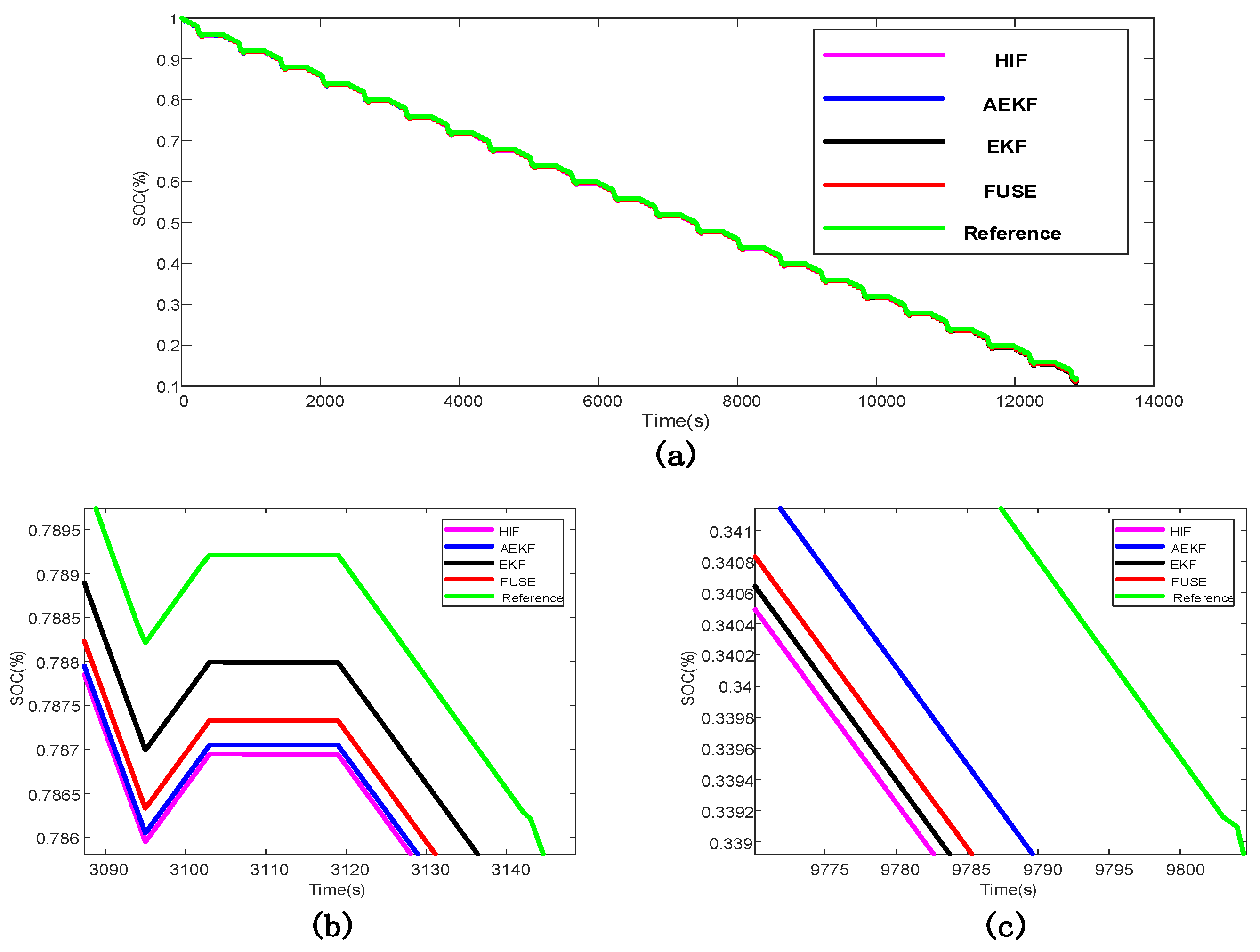
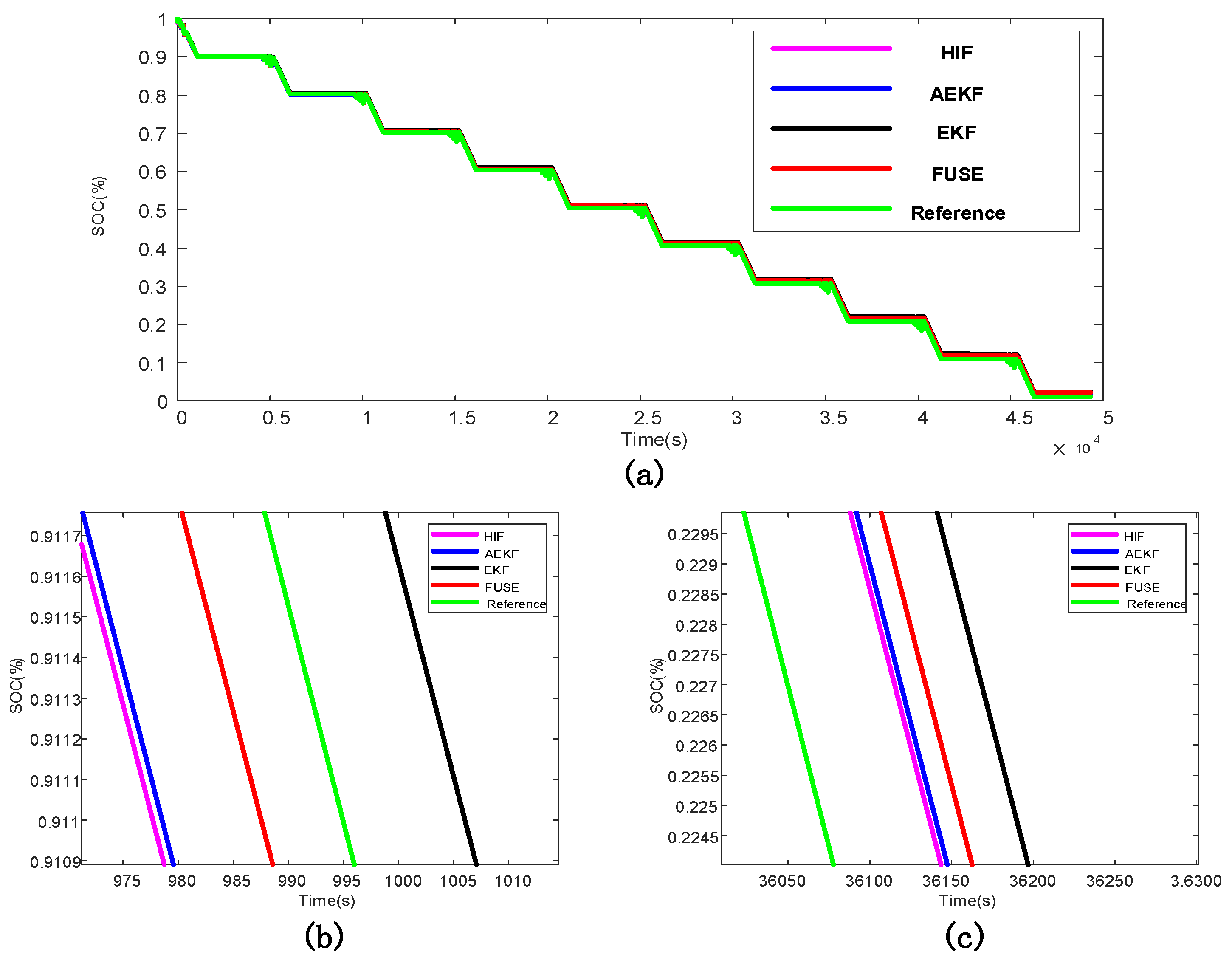
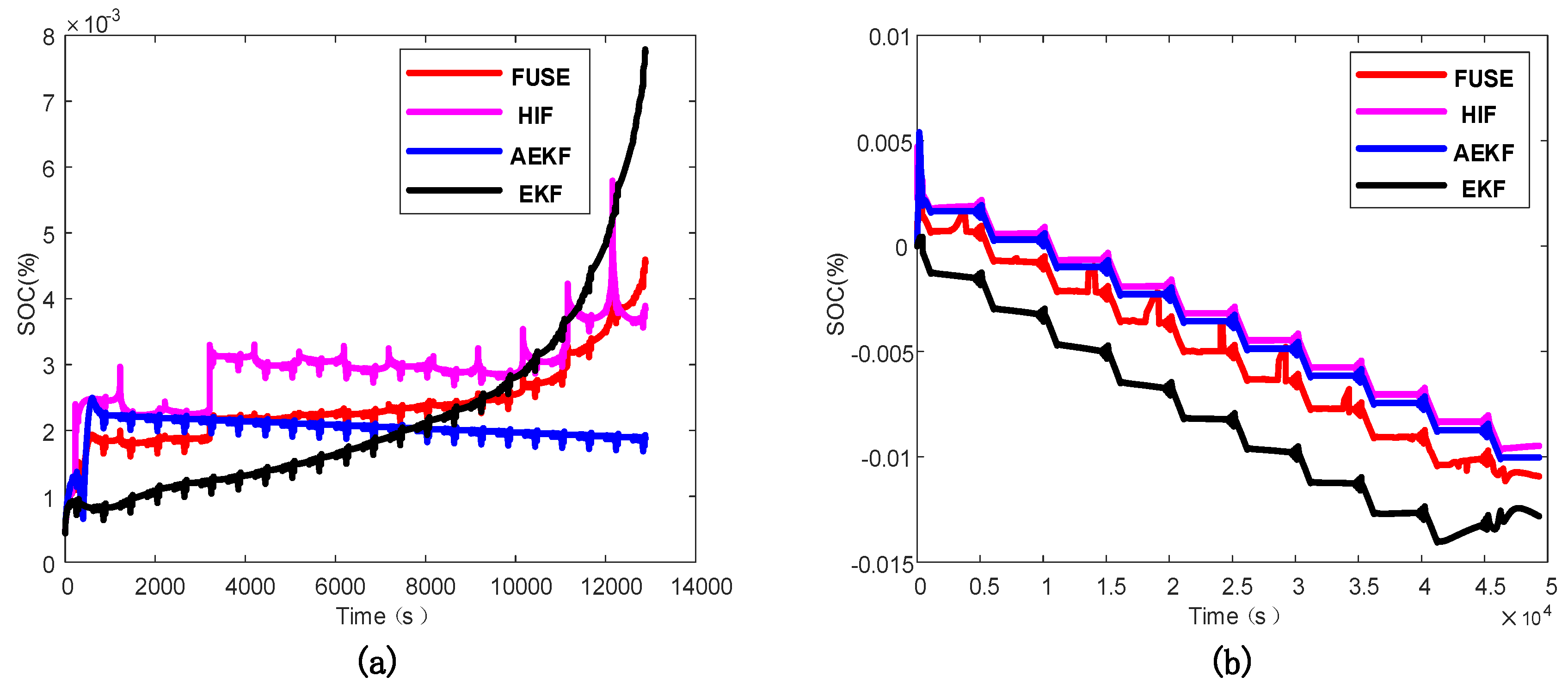
The estimated and real SOC values of each algorithm under DST are shown in Figure 4, and the estimated and real SOC values of each algorithm under HPPC conditions are shown in Figure 5. The SOC errors of the single algorithm estimation and multi-algorithm fusion estimation under DST are shown in Figure 6a, and the SOC errors of the single algorithm estimation and multi-algorithm fusion estimation under HPPC conditions are shown in Figure 6b. It can be clearly seen from the three figures that although the fusion algorithms in the two test environments cannot achieve the local optimization, it is robust in the whole process of SOC estimation. That is, the fusion algorithm has better robustness and estimation accuracy than the single algorithm.

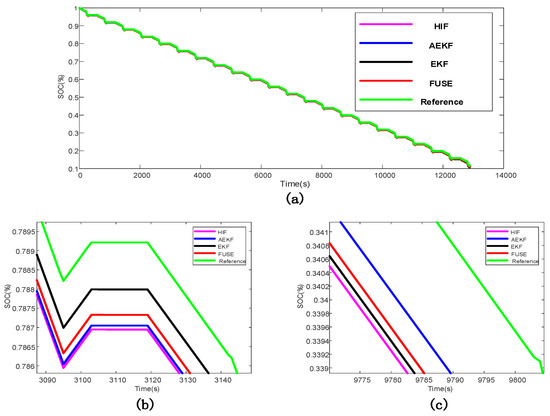
Figure 4. (a) SOC estimates under DST; (b) Local graph of SOC estimates under DST; (c) Local graph of SOC estimates under DST.

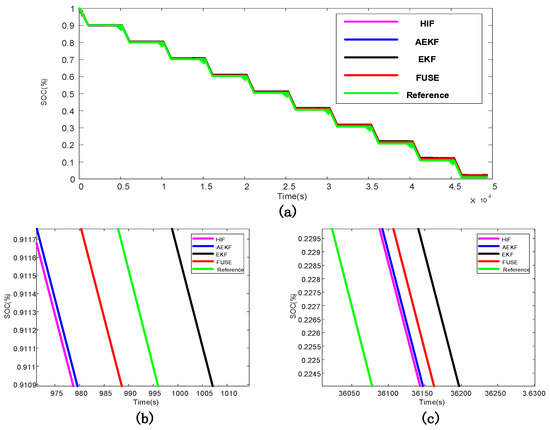
Figure 5. (a) SOC estimates under HPPC; (b) Local graph of SOC estimates under HPPC; (c) Local graph of SOC estimates under HPPC.

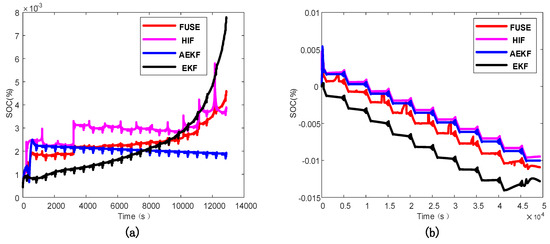
Figure 6. (a) SOC estimation errors under DST; (b) SOC estimation errors under HPPC.

When the initial soc is 1, the four algorithms are compared according to the statistical results of the relative errors of the algorithms. First, under DST (the specific results are shown in Table 3), the indicators of the fusion algorithm such as the maximum error, the mean error, and the root mean square of the error are only larger than those of the AEKF algorithm. Under HPPC (the specific results are shown in Table 4), the indicators of the fusion algorithm are close to the AEKF algorithm and the HIF algorithm and are better than the EKF algorithm. In other words, in the whole SOC estimation process, the fusion algorithm also has good estimation accuracy. The fusion algorithm is essentially a post-processing method of data processing with little computational burden. It can also be seen from the two tables that its running time is lower than that of the HIF algorithm and AEKF algorithm.

Table 3. SOC estimation errors of the four algorithms under DST.

Algorithms	ME (%)	MAE (%)	RMSE (%)	Run Time (ms)
EKF	0.97	0.27	0.30	75
HIF	0.58	0.29	0.30	141
AEKF	0.25	0.20	0.20	150
FUSE	0.46	0.23	0.24	103

Table 4. SOC estimation errors of the four algorithms under HPPC.

Algorithms	ME (%)	MAE (%)	RMSE (%)	Run Time (ms)
EKF	1.41	0.82	0.92	180
HIF	0.97	0.42	0.52	430
AEKF	1.01	0.45	0.55	455
FUSE	1.12	0.53	0.64	382

5. Conclusions

This paper presents a method of multi-algorithm fusion to estimate SOC. Through the establishment of a Thevenin model, the SOC estimation accuracy and algorithm running time of a single algorithm and the fusion algorithm are compared and verified under the tests of DST and HPPC. The experimental results show that the terminal voltage weighted fusion algorithm based on a Bayesian probability formula is more robust and accurate in SOC global estimation. In terms of algorithm time, as a data post-processing method, the computational burden of the fusion algorithm is small, lower than that of the HIF algorithm and AEKF algorithm. To realize the online application of the fusion algorithm in a real vehicle, multiple algorithms need to be loaded on BMS, which is not feasible at present. However, with the emergence of the cloud battery, the onboard BMS is no longer limited by storage and computing power. The fusion algorithm mentioned in this paper also has the possibility of real vehicle online application in the future.

In the next step, the author also plans to carry out the comparison test between the fusion algorithm and a single algorithm under different temperatures and different SOC initial values, and analyze the advantages of the fusion algorithm from the perspectives of battery capacity and impedance change.