IPTVisual: Visualisation of the Spatial Energy Flows in Inductive Power Transfer Systems with Arbitrary Winding Shapes
Abstract
:1. Introduction
2. Materials and Methods
2.1. Winding Modelling
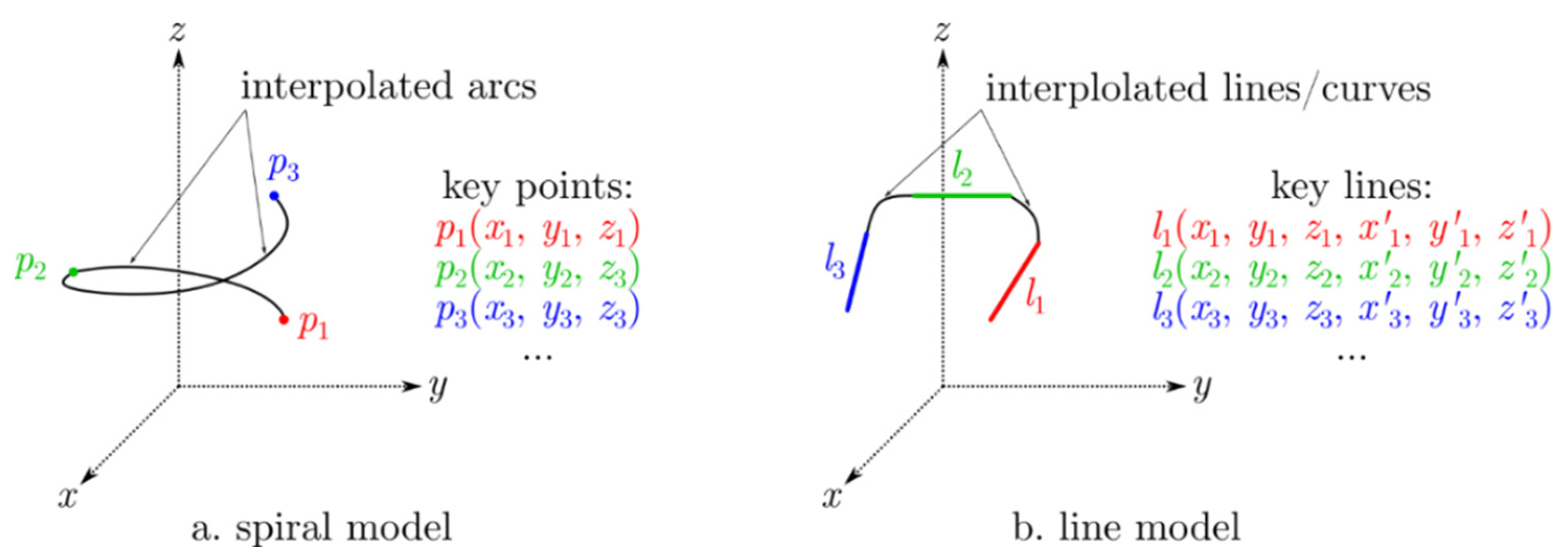
2.1.1. Spiral Type Windings
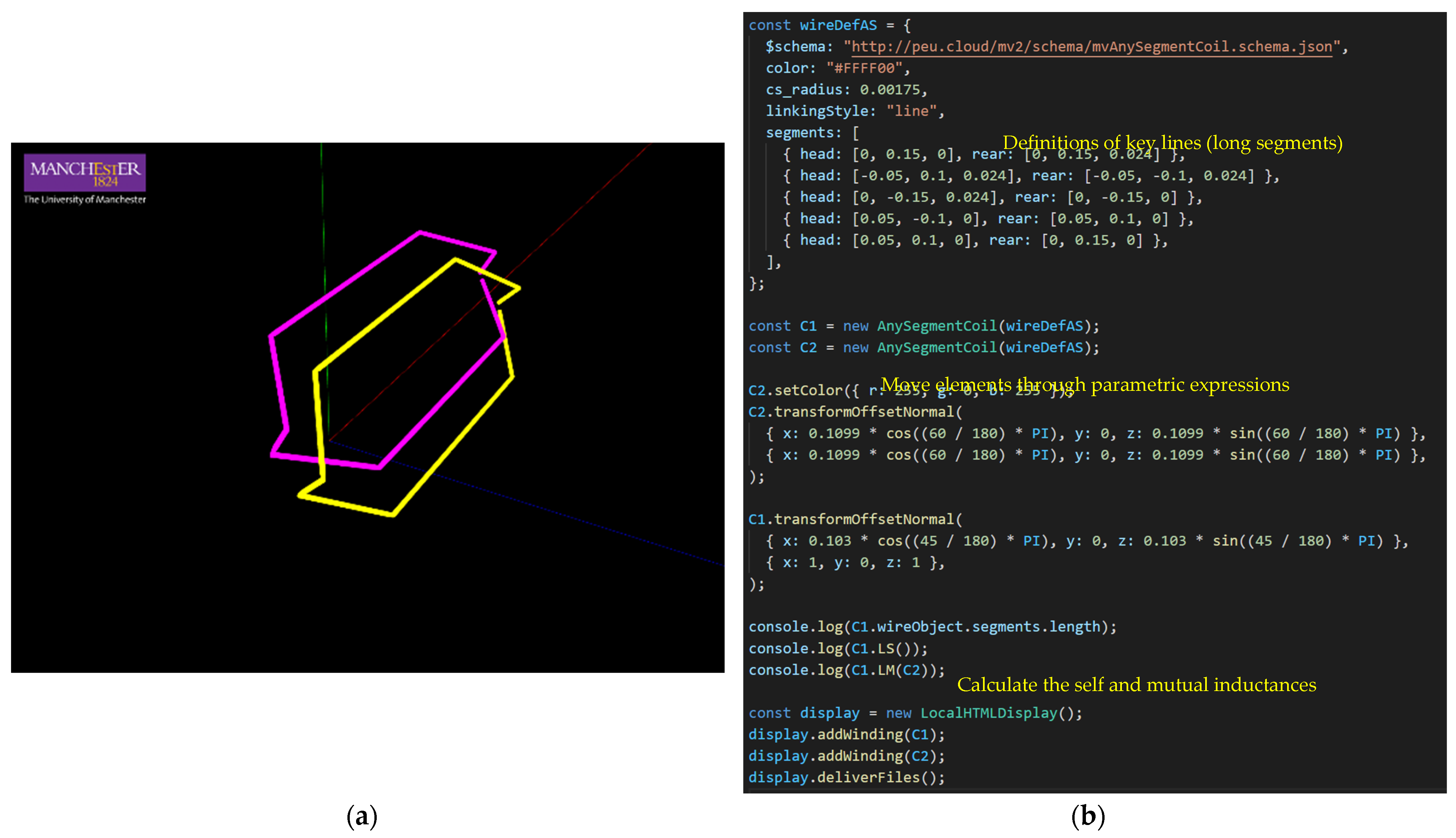
2.1.2. Straight Line Type Model
2.1.3. Preparations of the Winding Objects
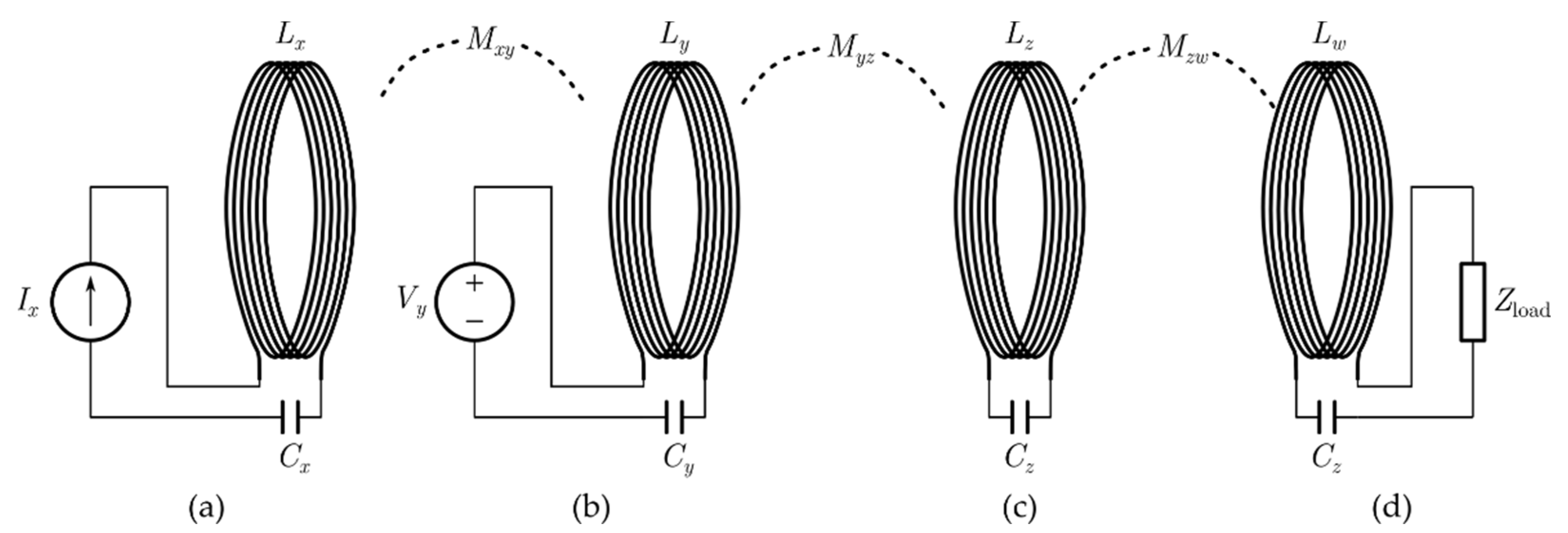
2.2. Circuit and System Modelling
2.3. Solver
3. Results and Discussions
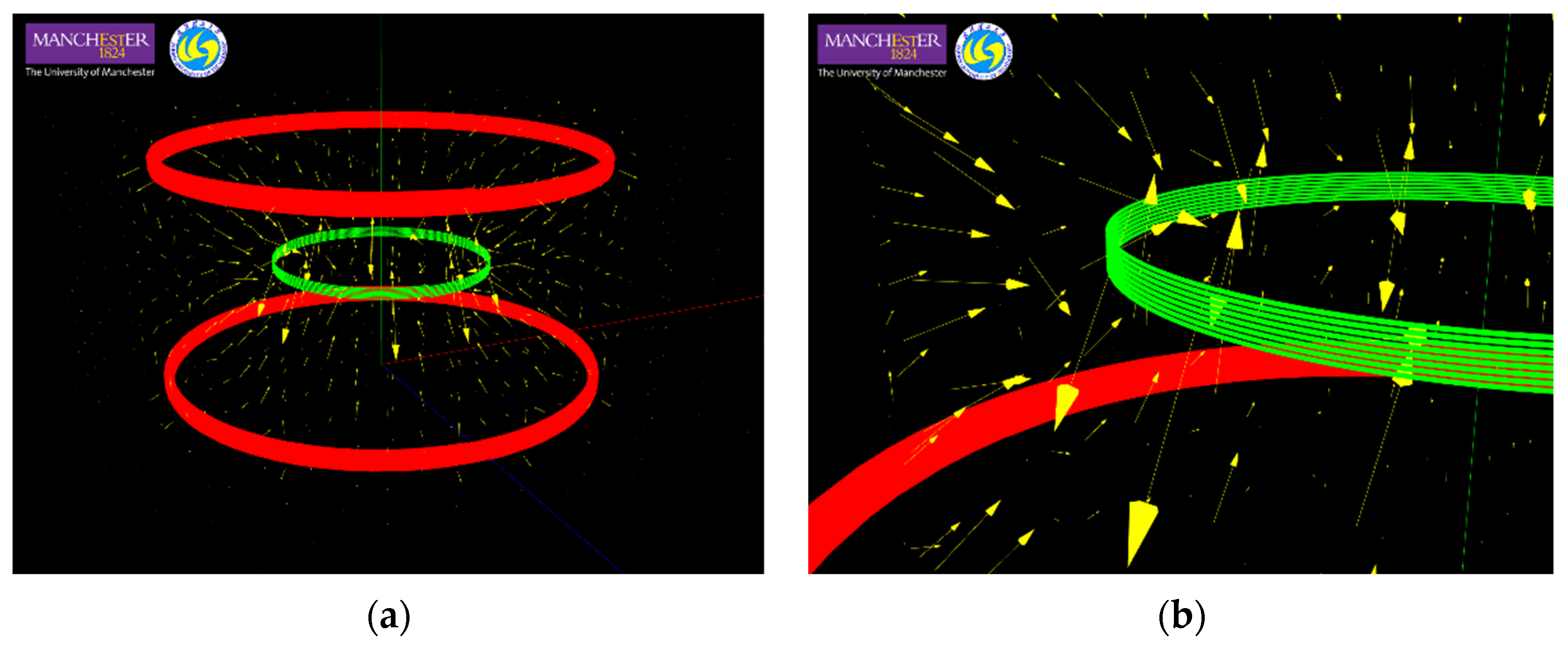
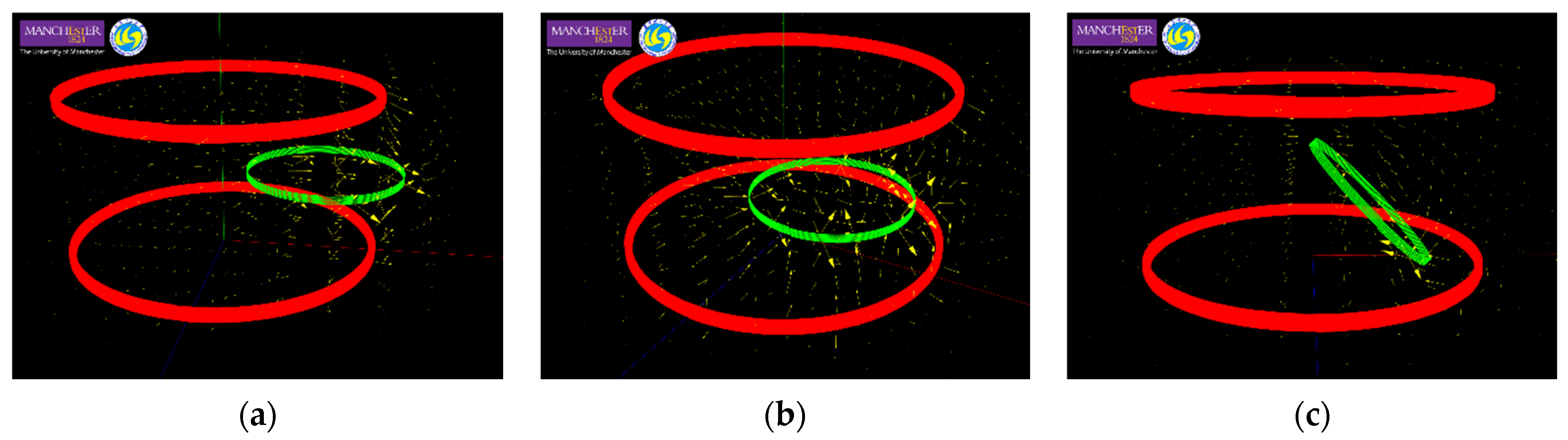
3.1. A Helmholtz Transmitter System
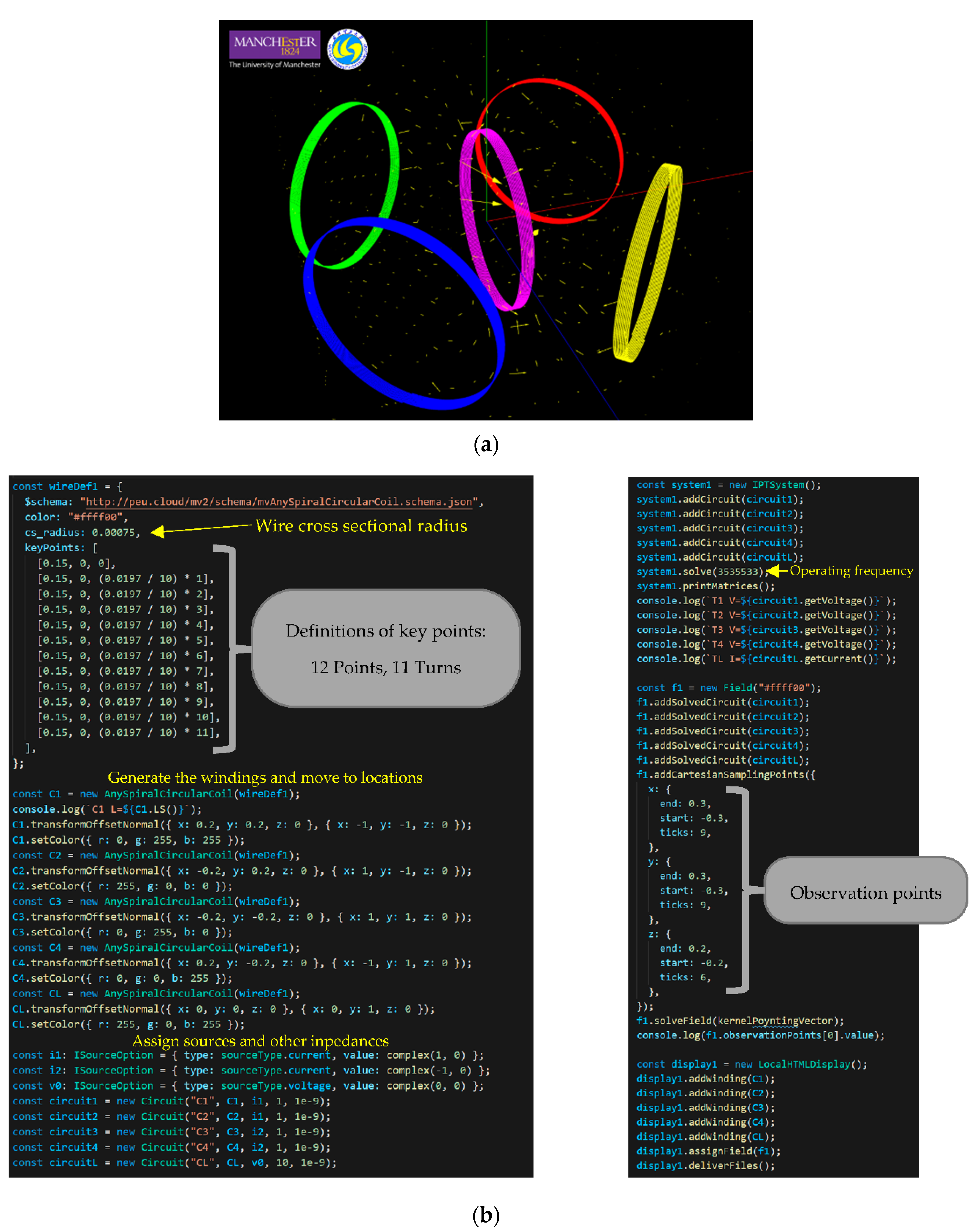
3.2. A Multi-Transmitter System
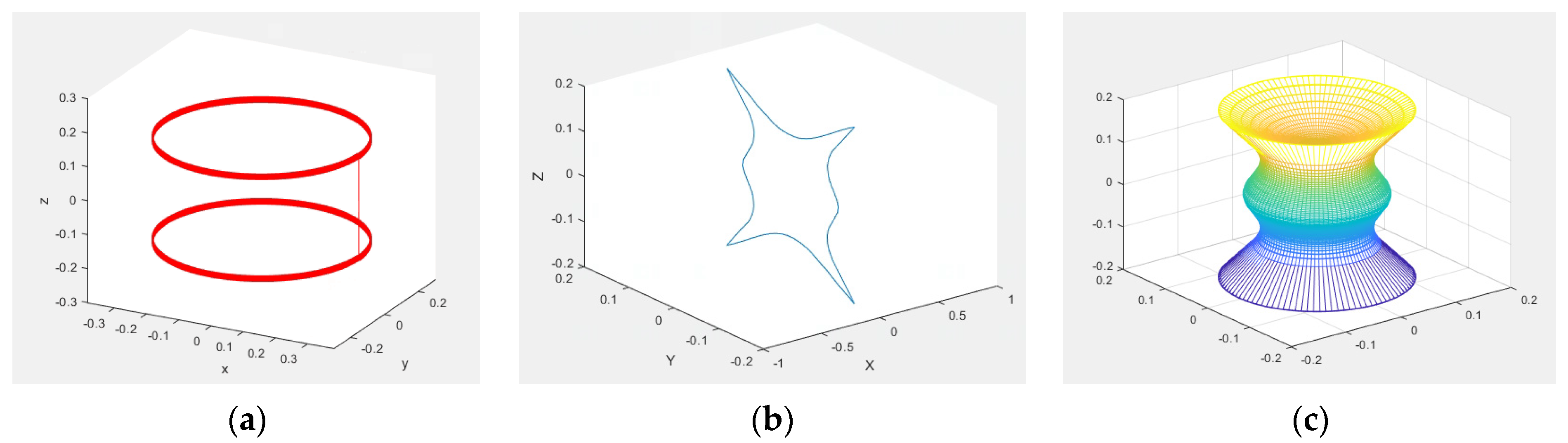
3.3. Line Windings Construction Used in Air-Core Electric Machines
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Verification of the Self- and Mutual-Inductance Calculation in IPTVisual
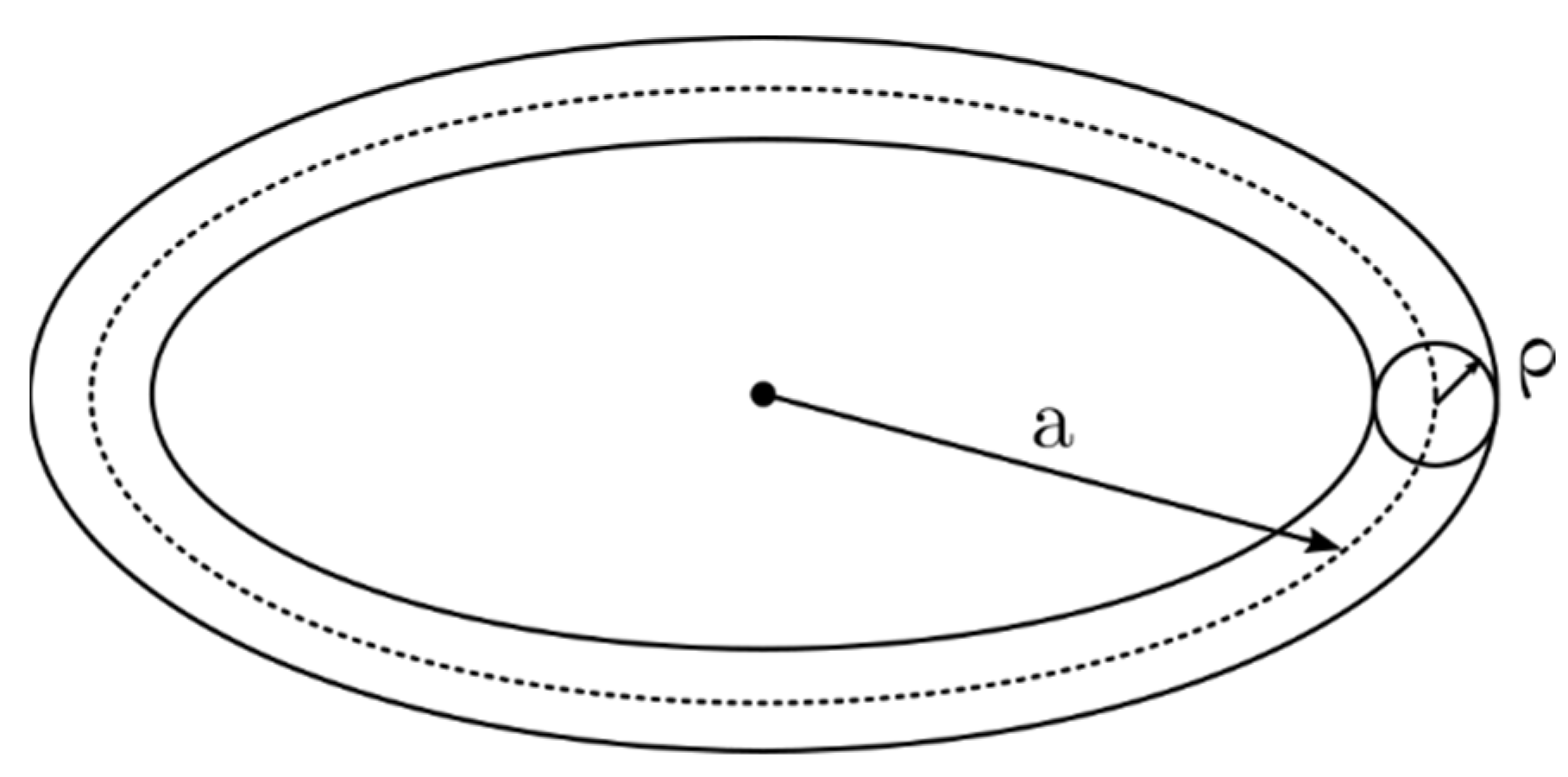
Appendix A.1. Self-Inductance of Circular Windings
| Model Parameters | Equation (A1) | ANSYS | IPTVisual (This Work, NodeJS) | |||||
|---|---|---|---|---|---|---|---|---|
| Time | Mem | Time | Mem | |||||
| 0.25 m | 0.5 mm | 2.056 μH | 1.8097 μH | 102 min | 3.2 GB | 2.058 μH | 0.24 s | 48 MB |
| 0.25 m | 5 mm | 1.333 μH | 1.0963 μH | 4.5 min | 2.3 GB | 1.323 μH | 0.20 s | 44 MB |
| 0.10 m | 10 mm | 331.4 nH * | 310.7 nH | 1.5 min | 1.7 GB | 315.3 nH | 0.20 s | 40 MB |
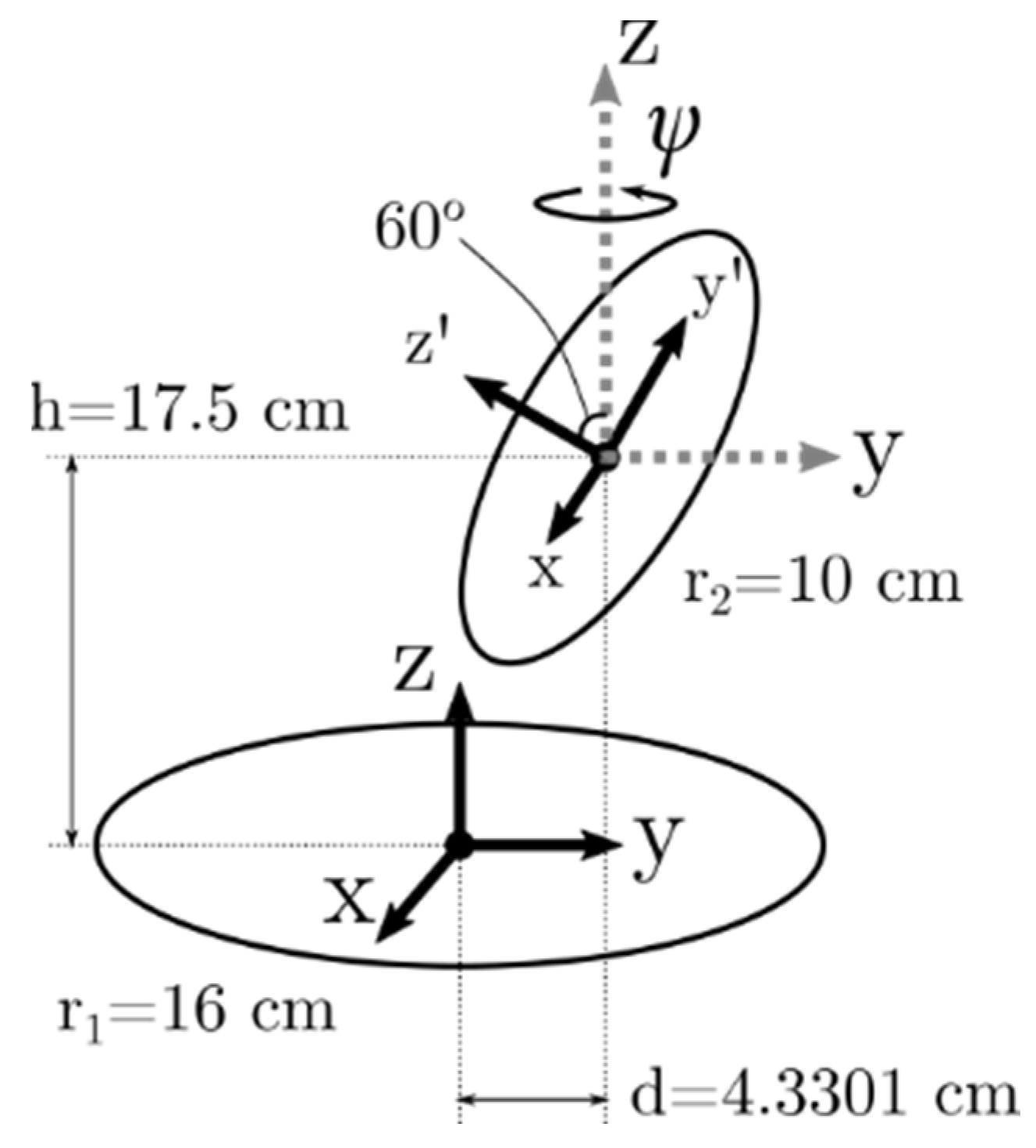
Appendix A.2. Mutual-Inductance between Two Circular Coils
- Cross-section radius: 5 μm … reference did not specify
- C1 Key-points: [(0.16, 0, 0), (0.16, 0, 0)] … a full circle (arc) with radius 16 cm
- C2 Key-points: [(0.10, 0, 0), (0.10, 0, 0)] … a full circle (arc) with radius 10 cm
- C2 transform offset: (0, 4.3301, 17.5)
- C2 transform normal: (sin(ψ)sin(60°), cos(ψ)sin(60°), cos(60°))
| Azimuth Angle * | Grover [23] | Babic [21] | FastHenry [22] | IPTVisual (This Work, NodeJS) |
| (nH) | (nH) | (nH) | (nH) | |
| 0 | 13.6113 | 13.6113 | 13.6162 | 13.6113 |
| π/6 | 14.4688 | 14.4688 | 14.4704 | 14.4683 |
| π/4 | 15.4877 | 15.4877 | 15.4932 | 15.4870 |
| π/3 | 16.8189 | 16.8189 | 16.8249 | 16.8181 |
| π/2 | 20.0534 | 20.0534 | 20.0604 | 20.0522 |
| 2π/3 | 23.3253 | 23.3253 | 23.3334 | 23.3238 |
| 3π/4 | 24.6936 | 24.6936 | 24.7022 | 24.6921 |
| 5π/6 | 25.7493 | 25.7493 | 25.7583 | 25.7478 |
| π | 26.6433 | 26.6433 | 26.6526 | 26.6419 |
References
- Consortium, W.P. Wireless Power Consortium. Available online: https://www.wirelesspowerconsortium.com/ (accessed on 25 February 2021).
- Rahman, M. Motorola Demos Wireless Charging Tech That Can Power Devices 100cm Away. Available online: https://www.xda-developers.com/motorola-no-contact-wireless-charging/ (accessed on 29 January 2021).
- Araque, J. Xiaomi Introduces a Wireless Charger That Can Charge Your Phone from Two Meters Away. Business Insider. 2 February 2021. Available online: https://www.businessinsider.com/xiaomi-charger-mobile-distance-wireless-remote-technology-smartwatch-testing-advance-mi-air (accessed on 25 February 2021).
- Cheah, W.; Watson, S.A.; Lennox, B. Limitations of wireless power transfer technologies for mobile robots. Wirel. Power Transf. 2019, 6, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Shin, J.; Song, B.; Lee, S.; Shin, S.; Kim, Y.; Jung, G.; Jeon, S. Contactless power transfer systems for On-Line Electric Vehicle (OLEV). In Proceedings of the 2012 IEEE International Electric Vehicle Conference, Greenville, SC, USA, 4–8 March 2012. [Google Scholar]
- Shinohara, N. Novel Beam-Forming Technology for WPT System to Flying Drone. In Proceedings of the 2020 IEEE Wireless Power Transfer Conference (WPTC), Seoul, Korea, 15–19 November 2020. [Google Scholar]
- Hui, R.S.Y.; Zhong, W.; Lee, C.K. A Critical Review of Recent Progress in Mid-Range Wireless Power Transfer. IEEE Trans. Power Electron 2014, 29, 4500–4511. [Google Scholar] [CrossRef] [Green Version]
- Energous Receives FCC Approval, Extending Charging Zone to up to 1 Meter for Groundbreaking Over-the-Air, Power-at-a-Distance Wireless Charging. Business Wire. 30 September 2020. Available online: https://www.businesswire.com/news/home/20200930005275/en/Energous-Receives-FCC-Approval-Extending-Charging-Zone-to-Up-to-1-Meter-for-Groundbreaking-Over-the-Air-Power-at-a-Distance-Wireless-Charging (accessed on 25 February 2021).
- Zhang, C.; Zhong, W.; Hui, R.S.Y.; Liu, X. A time-efficient methodology for visualizing time-varying magnetic flux patterns of mid-range wireless power transfer systems. In Proceedings of the 2013 IEEE Energy Conversion Congress and Exposition, Denver, CO, USA, 15–19 September 2013. [Google Scholar]
- Wang, H.; Zhang, C.; Hui, R.S.Y. Visualization of Energy Flow in Wireless Power Transfer Systems. In Proceedings of the 2019 IEEE Wireless Power Transfer Conference (WPTC), London, UK, 18–21 June 2019. [Google Scholar]
- Liu, Y.; Hu, A.P.; Madawala, U. Determining the power distribution between two coupled coils based on Poynting vector analysis. In Proceedings of the 2017 IEEE PELS Workshop on Emerging Technologies: Wireless Power Transfer (WoW), Chongqing, China, 20–22 May 2017. [Google Scholar]
- Faria, J.A.B. Poynting Vector Flow Analysis for Contactless Energy Transfer in Magnetic Systems. IEEE Trans. Power Electron. 2012, 27, 4292–4300. [Google Scholar] [CrossRef]
- Furusato, K.; Imura, T.; Hori, Y. Multi-band coil design for wireless power transfer at 85 kHz and 6.78 MHz using high order resonant frequency of short end coil. In Proceedings of the 2016 International Symposium on Antennas and Propagation (ISAP), Okinawa, Japan, 24–28 October 2016. [Google Scholar]
- Zhang, C.; Lin, D.; Hui, R.S.Y. Ball-Joint Wireless Power Transfer Systems. IEEE Trans. Power Electron. 2018, 33, 65–72. [Google Scholar] [CrossRef]
- Ho, G.K.Y.; Zhang, C.; Pong, B.M.H.; Hui, R.S.Y. Modeling and Analysis of the Bendable Transformer. IEEE Trans. Power Electron. 2016, 31, 6450–6460. [Google Scholar] [CrossRef]
- Schumaker, L.L. Spline Functions: Computational Methods; Society for Industry and Applied Mathematics: Philadelphia, PA, USA, 2015. [Google Scholar]
- Sullivan, C.R. Optimal choice for number of strands in a litz-wire transformer winding. IEEE Trans. Power Electron. 1999, 14, 283–291. [Google Scholar] [CrossRef] [Green Version]
- Zhang, C.; Lin, D.; Hui, R.S.Y. Efficiency optimization method of inductive coupling wireless power transfer system with multiple transmitters and single receiver. In Proceedings of the 2016 IEEE Energy Conversion Congress and Exposition (ECCE), Milwaukee, WI, USA, 18–22 September 2016. [Google Scholar]
- Jin, Z.; Iacchetti, M.F.; Smith, A.C.; Deodhar, R.P.; Komi, Y.; Abduallah, A.; Umemura, C. Winding Inductance Estimations in Air-Cored Resonant Induction Machines. In Proceedings of the 2020 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 11–15 October 2020. [Google Scholar]
- Rosa, E.B.; Cohen, L. On the self-inductance of circles. In Bulletin of the Bureau of Standards, Department of Commerce and Labor; US Department of Commerce and Labor: Washington, DC, USA, 1908; Volume 4. [Google Scholar]
- Babic, S.; Sirois, F.; Akyel, C.; Girardi, C. Mutual Inductance Calculation between Circular Filaments Arbitrarily Positioned in Space: Alternative to Grover’s Formula. IEEE Trans. Magn. 2010, 46, 3591–3600. [Google Scholar] [CrossRef]
- Kamon, M.; Tsuk, M.J.; White, J. FASTHENRY: A multipoleaccelerated 3-D inductance extraction program. IEEE Trans. Microw. Theory Tech. 1994, 42, 1750–1758. [Google Scholar] [CrossRef]
- Grover, F.W. Inductance Calculations; Dover: New York, NY, USA, 1964. [Google Scholar]


| Property | Type | Data | |
|---|---|---|---|
| Diameter | Number | a | |
| Number of coordinates | Number | N + 1 | |
| Coordinates | List | Address | Data |
| 0 | <0, 0, 0> | ||
| 1 | <a, 0, 0> | ||
| … | … | ||
| N | <Na, 0, 0> | ||
| Property | Type | Content |
|---|---|---|
| Winding | Object | Reference to winding object |
| Source Type | Enum | {CV|CI |Null} * |
| Source Value | Complex Number | Source amplitude and phase |
| Compensation Impedance | Complex Number | Total series impedance |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, C.; Chen, X.; Chen, K.; Lin, D. IPTVisual: Visualisation of the Spatial Energy Flows in Inductive Power Transfer Systems with Arbitrary Winding Shapes. World Electr. Veh. J. 2022, 13, 63. https://doi.org/10.3390/wevj13040063
Zhang C, Chen X, Chen K, Lin D. IPTVisual: Visualisation of the Spatial Energy Flows in Inductive Power Transfer Systems with Arbitrary Winding Shapes. World Electric Vehicle Journal. 2022; 13(4):63. https://doi.org/10.3390/wevj13040063
Chicago/Turabian StyleZhang, Cheng, Xiaoyun Chen, Kunyu Chen, and Deyan Lin. 2022. "IPTVisual: Visualisation of the Spatial Energy Flows in Inductive Power Transfer Systems with Arbitrary Winding Shapes" World Electric Vehicle Journal 13, no. 4: 63. https://doi.org/10.3390/wevj13040063
APA StyleZhang, C., Chen, X., Chen, K., & Lin, D. (2022). IPTVisual: Visualisation of the Spatial Energy Flows in Inductive Power Transfer Systems with Arbitrary Winding Shapes. World Electric Vehicle Journal, 13(4), 63. https://doi.org/10.3390/wevj13040063







