Abstract
The battery is the only power source of full electric vehicles, and the converter plays a key role in power and signal conversion; therefore, the stability and reliability of the converter determine the performance of the whole vehicle system. In order to improve the overall performance of the converter and optimize the function of the ID-NPC (improved diode neutral-point-clamped) topology with power allocation, the two-level topology is improved, and it is also a part of the ID-NPC topology. Based on the ID-NPC topology, the converter level can switch according to the proposed three-level and two-level modulation conversion strategies, which extends the fault-tolerant function of the converter. Finally, a simulation and experimental platform is built to verify the function of the improved topology and the feasibility of the proposed modulation strategy.
1. Introduction
Environmental and resource problems are two prominent contradictions that perplex the development of the automobile industry. The emergence of electric vehicles indicates the direction to solve these two problems [1]. The battery, converter, and driving motor are three important parts of an electric vehicle. Many scholars have conducted research on batteries, especially in the charge and discharge states [2,3]. Now, most drive motors use a permanent magnet synchronous motor. The power electronic converter is a more important component, and the topology has developed from two-level to multilevel.
The waveform quality of the output voltage is greatly improved by using a multilevel topology converter [4]. At present, the main structures of the multilevel converter are of the cascade type and NPC (neutral-point-clamped) type. The earliest NPC form of an element is the FC-NPC (flying-capacitor neutral-point-clamped) topology [5]. According to the structural characteristics of FC-NPC, a bidirectional switching power device is used to replace the capacitive devices as a neutral-point-clamped element, similar to the “T” shape, which is called the T topology [6]. The D-NPC (diode neutral-point-clamped) topology was proposed based on the T-NPC and FC-NPC topologies [7]. The D-NPC converter is featured by a simple main circuit, a flexible control mode, and easy control of the direction of the energy flow and power factor [8]. However, the inherent control and driving method of D-NPC are attributed to its uneven heat loss, increasing the design difficulty of a radiator, and limiting the power level, output current, and switching frequency. In order to improve the loss distribution, the A-NPC (active neutral-point-clamped) topology was proposed subsequently, but the added number of switching elements also brings about increased conduction loss and switching loss [9]. The comparison of four traditional topologies is shown in Table 1 [10]. As it can be seen from the table below, the switching loss of the two-level topology is large, but the heat distribution is balanced and different than that of the D-NPC topology.

Table 1.
The comparison of four traditional topologies.
2. D-NPC and ID-NPC Topology Converter and Loss Allocation Analysis
2.1. Traditional D-NPC (Diode Neutral-Point-Clamped) Topology
The D-NPC topology was proposed in 1980, which is more suitable for medium-voltage applications. The topological structure is shown in Figure 1 [11,12]. Each main bridge arm consists of four controllable switching elements and two clamped elements. The power supply is composed of two groups of DC sources with a single voltage of Vdc/2 in series, and the neutral point of the DC source is connected with the neutral point of the series diode. Taking the first group of main bridge arms as an example, when the first element T11 and the second element T12 of the four elements of main bridge arms are connected, the output voltage is Vdc/2 (called the positive-level state); when the second element T12 is connected with the third element T13, the output voltage is 0 (called the zero-level state); when the third element T13 is connected with the fourth element T14, the output voltage is −Vdc/2 (called the negative-level state). Four controllable switching elements turn on in turn to make the output present the three-level state. In the process of switching from the positive-level state to the zero-level state and from the zero-level state to the negative-level state, the second and third elements are in a repeated conduction state, that is, a continuous state, and the heat distribution on the single device is uneven [13,14]. Since each bridge arm has four elements, each element needs one driving circuit, and a set of converters needs 12 driving circuits [15,16].
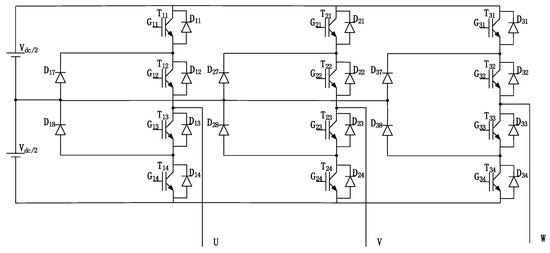
Figure 1.
Traditional D-NPC (diode neutral-point-clamped) topology.
2.2. D-NPC (Diode Neutral-Point-Clamped) Switching States
The switching states of the D-NPC topology are shown in Table 2. The switching table is explained by the U-phase.

Table 2.
D-NPC (diode neutral-point-clamped) switching table.
2.3. ID-NPC (Improved Diode Neutral-Point-Clamped) Topology
ID-NPC (improved diode neutral-point-clamped) is shown in Figure 2. Each bridge arm consists of six controllable switching elements and two clamped elements. The connection mode of the DC power supply and converter is the same as that of D-NPC. Taking the U-phase as an example, the six switching elements of the bridge arm are divided into three groups: T11 and T12, T13 and T14, and T15 and T16, and the driving ports are G11, G13, and G15, respectively. When the driving port G11 is connected, the output voltage is Vdc/2 (positive state); when the driving port G15 is connected, the output voltage is 0 (zero state); when the driving port G13 is connected, the output voltage is −Vdc/2 (negative state). Three groups of switching elements turn on to make the output voltage present the three-level state. During switching states, the positive state, zero state, and negative state are completed by independent components, with no overlapping, meaning the heat distribution is uniform. The three groups of elements need three driving circuits, and the converter needs nine driving circuits.
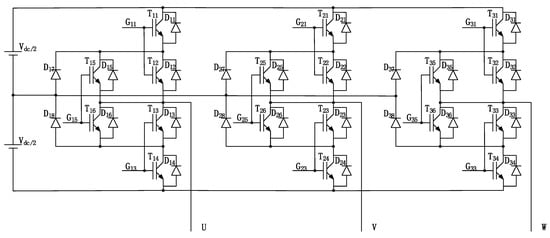
Figure 2.
The ID-NPC (improved diode neutral-point-clamped) topology.
2.4. ID-NPC (Improved Diode Neutral-Point-Clamped) Switching States
Corresponding to the ID-NPC topology, the switching states table is shown in Table 3. The switching states are simplified and more intuitive. The switching table is explained by the U-phase.

Table 3.
ID-NPC switching table.
2.5. Analysis of D-NPC (Diode Neutral-Point-Clamped) Switching Loss
It is also different that the different operating points and different modulation application schemes determine the loss and temperature distribution of each device. The following analysis takes the U-phase in three phases as an example [17].
The boundary of the D-NPC converter’s working area is the most critical working point. According to whether the reference direction of the current and the voltage is the same or not, the factor α is +1 or −1. The maximum modulation depth is M = 1.15, and the minimum is M ≈ 0. Based on these conditions, the switching process can be divided into four types: D1 (α =+1, M = 1.15), D2 (α = −1, M = 1.15), D3 (α = +1, M ≈ 0), and D4 (α = −1, M ≈ 0) [18].
For the D1 type (α = +1, M ≈ 0), α = +1, the voltage and current directions are the same, M = 1.15, and the converter state switches between “+” and “0”, as shown in Figure 3. T11 turns off and D17 turns on, and T12 bears the half-wave phase current in the whole switching process. In the case of maximum modulation M, T11 has on-loss at the beginning of switching and current loss at the end of switching. D17 has smaller conduction loss and self-loss after conduction. The solid line represents the current path direction in the “+” state, the dotted line represents the current path direction in the “0” state, and the thickness of the solid line and the dotted line represents the duty cycle.
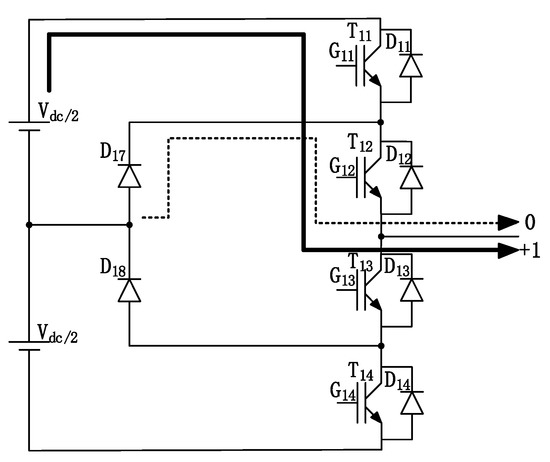
Figure 3.
D1 type (α = +1, M ≈ 0).
For D2(α = −1, M = 1.15), as shown in Figure 4, the actual current shifts 180 degrees from the direction shown in the figure, the converter switches between “0” and “−” states, and T12 and T13 have switching losses. After switching to the “−” state, the reverse diodes D13 and D14 are connected in series, and the two are on after switching, with negligible switching loss. When the state switches from “−” to “0” states, D14 or D13 has reverse recovery loss. T12 needs to turn the current on and off in the “0” to “−” states and bears a large on and off loss. When the reverse recovery loss occurs in D14, the loss scale for D14 and T12 also depends on the duty cycle of both. When the lower current is reversed, for T14, the internal switch and diode have loss, and the two also have an obvious junction temperature in the same housing.
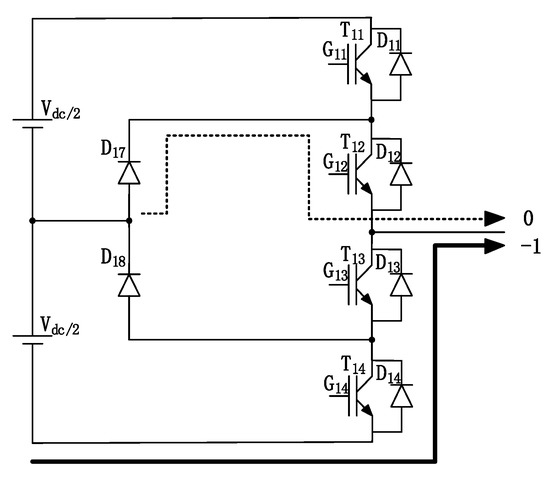
Figure 4.
D2 type (α = −1, M = 1.15).
For the case of the D3 type (α = +1, M ≈ 0), as shown in Figure 5, different from the D1 type, the conduction loss is different due to the change in the duty cycle. D17 has a negligible turn-on loss, directional recovery loss, and large duty cycle turn-on loss.
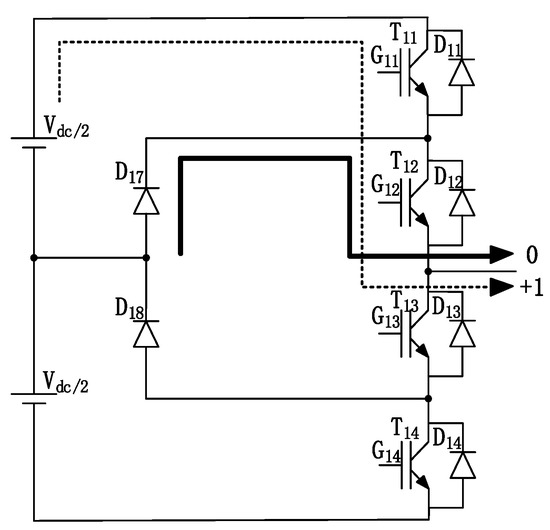
Figure 5.
D3 type (α = +1, M ≈ 0).
For the D4 type (α = −1, M ≈ 0), as shown in Figure 6, D17 and T12 have a current most of the time. T12 has conduction and turn-off loss. Due to the large duty cycle, the conduction loss is also large. D13 and D14 also bear reverse recovery losses when off.
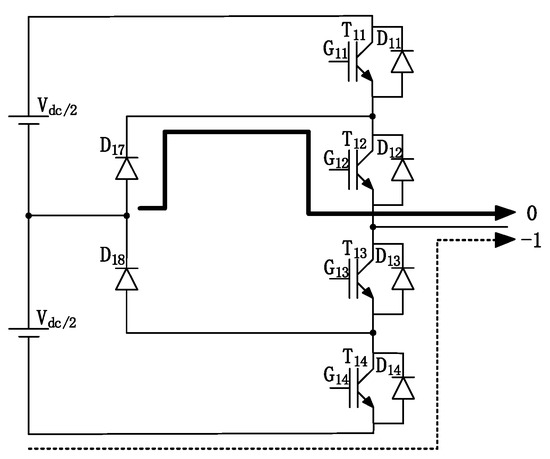
Figure 6.
D4 type (α = −1, M ≈ 0).
2.6. Analysis of ID-NPC (Improved Diode Neutral-Point-Clamped) Switching Loss
In order to facilitate the comparison with D-NPC switching loss, the working point setting of the ID-NPC converter is the same as that of D-NPC, and the analysis method is the same as above. The four types are marked as the ID1 type (α = +1, M = 1.15), ID2 type (α = −1, M = 1.15), ID3 type (α = +1, M ≈ 0), and ID4 type (α = −1, M ≈ 0) [19].
For the ID1 type (α = +1, M = 1.15), the state switches between “+” and “0”, as shown in Figure 7. T11 and T12 switch with D17 and T15. T11 and T12 are off and bear the turn-off loss. The mechanism is the same when opening, and the two pipes bear the turn-on loss. T15 bears the conduction loss. After conduction, T15 bears the half-wave phase current. The solid line represents the current path in the “+” state, the dotted line represents the current path in the “0” state, the thickness of the solid line and the dotted line indicates the duty cycle, and the arrow direction is the current direction. Compared with the type D1 switching loss in Figure 3, the circuit switching has one more on–off loss.
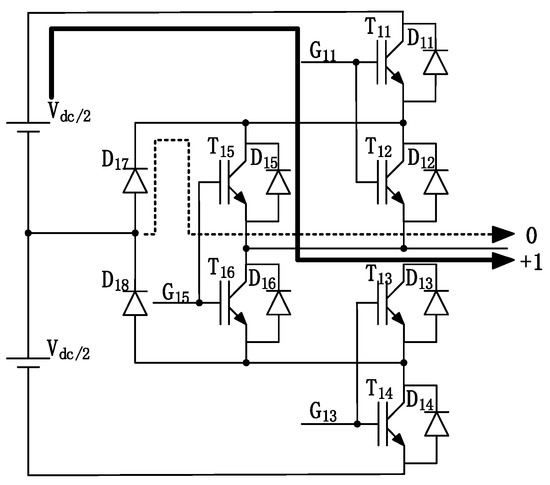
Figure 7.
ID1 type (α = +1, M = 1.15).
For the ID2 type (α = −1, M = 1.15), as shown in Figure 8, the actual current is also 180 degrees phase shifted with the direction shown in the figure, and the converter switches from “0” to “−” states. T15 is off, then D17 is off, and after the dead time, T13 and T14 are on. On the contrary, D13 and D16 or D14 bear large reverse recovery loss. T15 needs to turn the conduction current on and off when switching and bears the on–off loss. Due to the different duty cycles, for D13 and D16, D14 and T15, and D17, the loss is different.
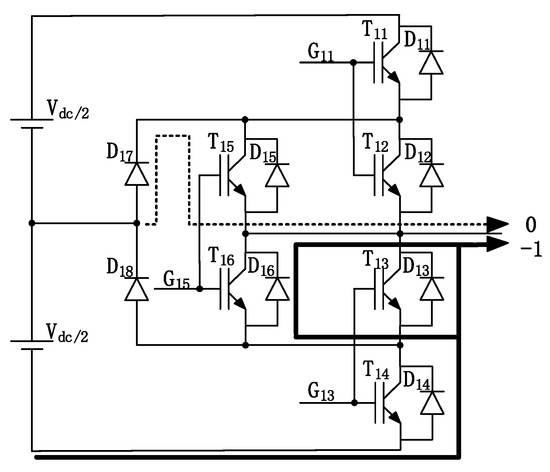
Figure 8.
ID2 type (α = −1, M = 1.15).
In the case of the ID3 type (α = +1, M ≈ 0), as shown in Figure 9, it switches from “+” to “0”, T11 and T12 turn off, and T15 turns on. In the switching process, T11 and T12 have on and off losses. Different from D3, T15 has on and off losses. Due to the different duty cycles, the conduction loss is also different.
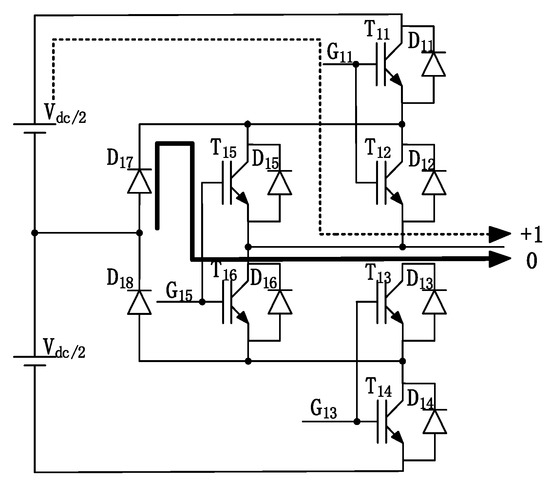
Figure 9.
ID3 type (α = +1, M ≈ 0).
For the ID4 type (α = −1, M ≈ 0), as shown in Figure 10, the difference compared with ID2 is that duty cycles lead to different conduction losses. In the “−1” state, because D14 is connected in series with D13 and D16, the three diodes conduct at the same time when they are on, and there are reverse recovery losses when they are off.
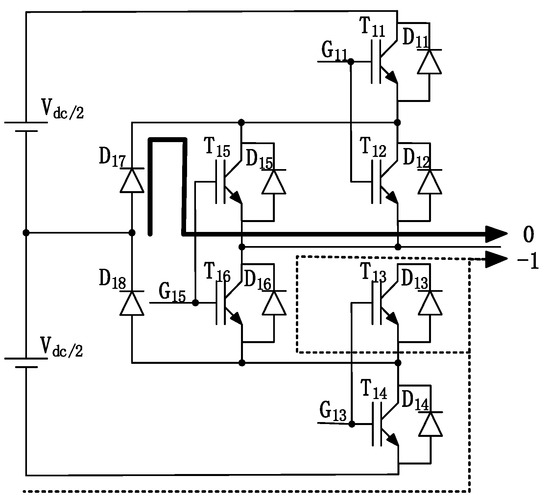
Figure 10.
ID4 type (α = −1, M ≈ 0).
2.7. Comparison and Analysis

Table 4.
D-NPC switching loss table.

Table 5.
ID-NPC switching loss table.
Comparing the switch loss tables, the conclusions are as follows:
- The ID-NPC topology only needs nine driving circuits.
- ID-NPC has two more elements per phase, and six more elements in three phases.
- The ID-NPC topology has more switching loss in no-load switching.
- The additional switching elements of ID-NPC can evenly distribute the heat generated by switching loss, and the heat distribution is relatively more uniform.
- ID-NPC can run in the two-level state, when G12 is zero (take the U-phase as an example). This is very suitable for the field of zero speed in the power drive system, and the characteristic is that the regulation system is low, and the frequency output is zero or near zero.
- In the ID-NPC topology, because the zero level is realized by independent components, although the switching loss is increased, the heat dissipation can be dispersed, and the switching frequency can be increased.
3. Three-Level and Two-Level Modulation Conversion Strategy Based on ID-NPC
3.1. I-TL (Improved Two-Level) Topology
The I-TL (improved two-level) topology is shown in Figure 11, and it is a part of the ID-NPC topology. Two groups of parallel switching elements are used on each bridge arm to improve the withstand voltage of the bridge arm. Two fast diodes are added to each bridge arm.
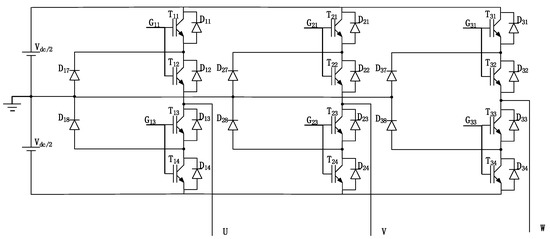
Figure 11.
Improved two-level topology.
There is a reverse current in the UVW phase during shutdown, and, at the same time, the lower half of the bridge arm is opened, namely, the (“−1” “−1” “−1”) state, G13, G23, and G33 are on, and the reverse current flows into the zero potential through T13 and D18, T23 and D28, and T33 and D38, which increases the return path and reduces the impact of the reverse current on the on–off components.
3.2. Region Order Algorithm
The rotating voltage vector produces a rotating flux linkage, where the clockwise order is II → VI → IV→V → I → III, and the counterclockwise order is III → I → V → IV → VI → II. For a PMSM (permanent magnet synchronous motor), it is not very important which sector the rotation vector starts from, but it can rotate sequentially from this sector. For sector judgment, only the angle order is needed, and the sector number is just an identification of the order. The corresponding relationship is shown in Table 6.

Table 6.
Corresponding relationship of sector, basic vector, αβ coordinate system region order, and RAM.
3.3. Optimization of Vector Action Time
The SVPWM (space vector pulse width modulation) algorithm contains trigonometric function calculation; therefore, the calculation of the basic voltage vector action time is more complex. The vector action time is completely determined by U1, U2, and U3, and some simple transformation can be conducted. Take the vector composition in the () region as an example, as shown in Figure 12.
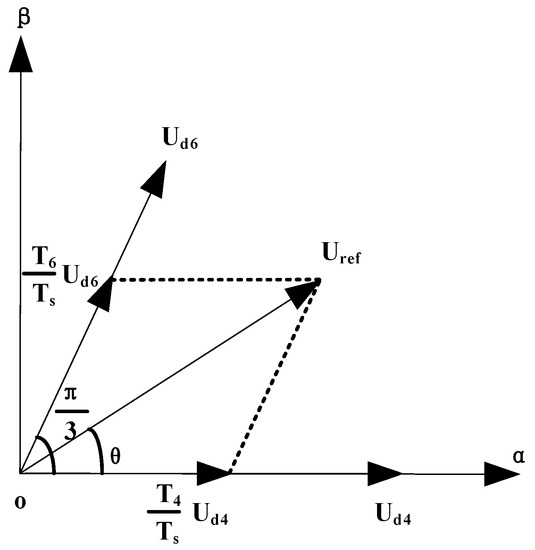
Figure 12.
The vector composition in the ) region.
According to Figure 12 and the volt-second balance principle, we obtain the following formula:
We can further launch
Similarly, the time of each basic voltage vector in other regions can be obtained. According to U1, U2, and U3, in Equation (2), the region of the reference voltage vector is determined. Then, by using the look-up table in the FPGA (field-programmable gate array), the action time of the basic voltage vector in the corresponding region can be obtained, and the relationship between the action time and the vector in the region is obtained, as shown in Table 7. In the table, K = 1.732Ts/Vdc, where Vdc represents the DC bus voltage.

Table 7.
Relationship between the sector action time and the sector.
Due to U1, U2, U3, and , is derived from and . For PMSM, the rotation vector does not need to be judged on which sector it is located in but can rotate sequentially counterclockwise or clockwise. Therefore, the RAM allocation value is used to directly express the sector action time. Equation (3) can be obtained:
and are stored in two 16-bit RAMs. The angle and action time are derived from Equation (2), and the relationship is shown in Table 8, K = 1.732Ts/Vdc.

Table 8.
The relationship between angle and action time.
3.4. Three–Two- and Two–Three-Level Modulation Conversion Strategy Based on Loss Allocation and Fault Tolerance
The number of winding phases is limited to three phases. Therefore, if one of the phase windings fails when a three-phase motor is driven by a D-NPC topology converter, the generated rotating magnetic field will be destroyed, inevitably leading to a difference between the winding currents of the other two phases without faults. In this case, a pulsed magnetic field will be generated, causing problems with the orientation of the rotor rotating magnetic field. In terms of the converter control system, the probability of a problem with the converter is greater than the probability of a problem with the motor winding, and the problem with a converter may easily expand to motor winding [20,21].
The improved ID-NPC increases the number of semiconductor switching elements and reduces the system economy. Moreover, the increase in the number of switching elements also brings about the decrease in the inherent reliability, but the increased switching elements can improve the heat loss distribution. When the neutral point potential balance is taken into account, the ID-NPC topology is composed of the positive level, negative level, and the independent zero level; therefore, it can work in the two-level state of the positive and negative levels, or in the three-level state of the positive, negative, and zero levels.
The short circuit and open circuit of switching elements are the main causes of converter fault. When only one is stuck open, the element shall be shorted or replaced. The two switching elements in the middle of the converter bridge arm of the traditional D-NPC topology are multiplexed elements, which suffer a higher fault probability and have a relatively short service life. If there is a short circuit between the two switching elements in the middle of the bridge arm, only one switching element remains in the part of the bridge arm where the short-circuit element is located, and when the other part of the bridge arm is turned on, the remaining switching element will withstand the full bus voltage, the breakdown probability will increase, and the entire bridge arm will be short-circuited.
In the ID-NPC topology, the upper positive and lower negative levels of the bridge arms are determined by two groups of parallel elements. When one of the two parallel elements in the bridge arm is short-circuited by a breakdown, or one element in the upper and lower parallel bridge arms is short-circuited by a breakdown, the converter can still operate in a three-level state.
In the ID-NPC topology, when one of the two parallel elements in the bridge arm is short-circuited by a breakdown, or one element in the upper and lower parallel bridge arms is short-circuited by a breakdown when the converter runs in the two-level state, it can still be in a two-level state.
Comparing with the traditional two-level converter, the D-NPC three-level converter has more conduction loss, and the switching loss is significantly reduced. When the switching frequency is higher (>10 Hz), the three-level topology converter has a higher conversion efficiency; therefore, a three–two-level modulation conversion strategy based on loss allocation and fault tolerance is proposed. When the driving frequency of PMSM is not greater than 10 Hz, the improved two-level SVPWM optimized modulation algorithm is adopted. When the frequency is greater than 10 Hz, the three-level SVPWM modulation algorithm is adopted. The conversion of the two modulation algorithms can help them complement each other to ensure that less heat is generated by loss and distributed uniformly, and that the neutral point potential deviation is controlled within the required range. The flowchart of modulation conversion is shown in Figure 13.
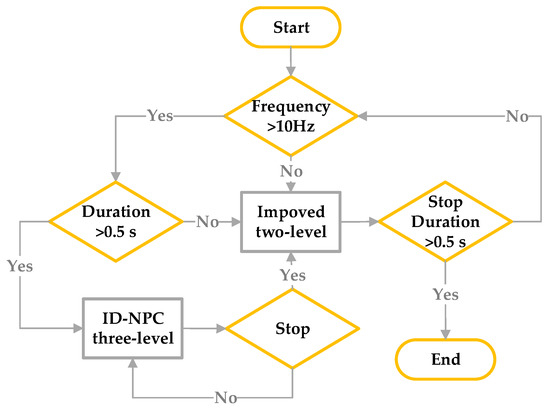
Figure 13.
The flowchart of modulation conversion.
4. Simulation Analysis
4.1. Simulation Comparison Based on Two Two-Level Topologies
The simulation conditions are shown in Table 9.

Table 9.
Simulation conditions.
The structures of the traditional two-level topology and the improved two-level topology based on ID-NPC are built. Under the same simulation conditions, the voltage waveforms are shown in Figure 14, where Uac1 and Ubc1 are the traditional two-level Uac and Ubc voltage waveforms, respectively, and Uac2 and Ubc2 are the improved two-level Uac and Ubc waveforms, respectively. Additionally, the x-axis is in seconds, and the y-axis is in volts.
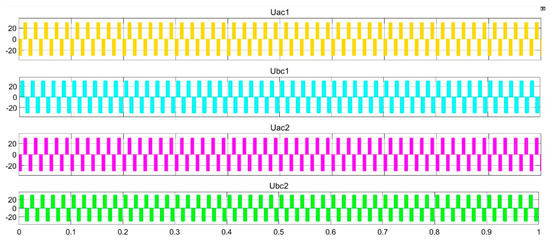
Figure 14.
The simulation waveforms based on two topologies.
It can be seen from Figure 14 above that the simulation waveform based on the two topologies is basically the same, and this shows that the structure of the improved two-level topology has the same function as that of the traditional two-level topology.
4.2. Simulation Analysis of Three-Level and Two-Level Modulation Conversion Strategies
Figure 15 is the simulation voltage waveform of three–two-level modulation conversion, and Figure 16 is the simulation voltage waveform of two–three-level modulation conversion. The units of Uac and Ubc are in volts. The simulation time is one second, and when the time is at 0.5 s, the level converts from three-level to two level or two-level to three-level. It can be seen from the below two figures that the voltage fluctuation is small, which indicates that the conversion influence is relatively small.
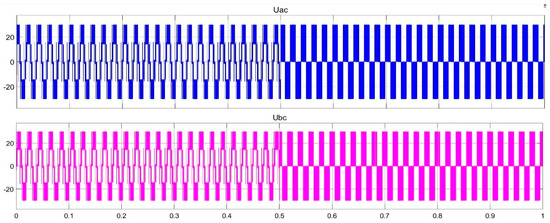
Figure 15.
The simulation voltage waveform of three–two-level modulation conversion.
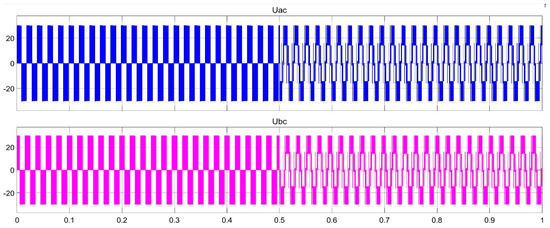
Figure 16.
The simulation voltage waveform of two–three-level modulation conversion.
Using a two-level start, a three-level operation, and a two-level stop, the Uac and Ubc simulation waveforms of the whole process are shown in Figure 17. The simulation time is 1.5 s. At 0.5 s, two-level (6.1 Hz) converts to three-level (48.8 Hz), and at 1.0 s, three-level (48.8 Hz) converts to two-level (6.1 Hz) until it stops. The feasibility of the three-level and two-level modulation conversion strategies based on loss allocation and fault tolerance is verified. The units of Uac and Ubc are in volts.

Figure 17.
The simulation voltage waveform of the whole conversion process.
5. Experimental Analysis
5.1. Experimental Comparison Based on Two Two-Level Topologies
The experimental parameters are consistent with the above simulation parameters, and the voltage waveforms are shown in Figure 18, where 1 and 2 are the traditional two-level Uac and Ubc voltage waveforms, respectively, and 3 and 4 are the improved two-level Uac and Ubc waveforms, respectively. The experimental waveform is basically consistent with the simulation waveform.
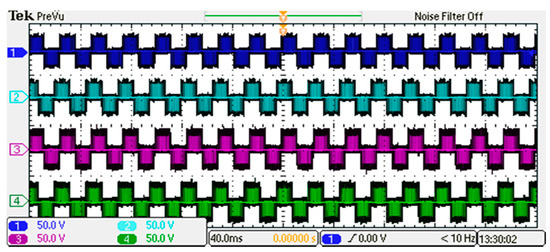
Figure 18.
The experimental waveforms of two topologies.
5.2. Experimental Analysis of Three-Level and Two-Level Modulation Conversion Strategies
The experimental waveform of three–two-level modulation conversion is shown in Figure 19. The experimental waveform of two–three-level modulation conversion is shown in Figure 20. The whole conversion process of the modulation strategy is shown in Figure 21. In those figures, 1 is the Uac voltage waveform, and 2 is the Ubc waveform.
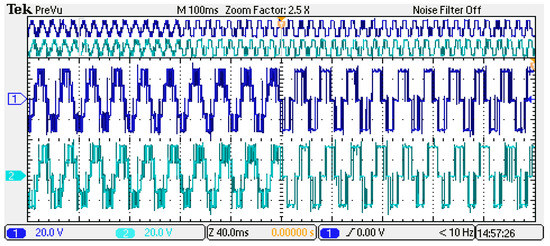
Figure 19.
The experimental waveform of three–two-level modulation conversion.
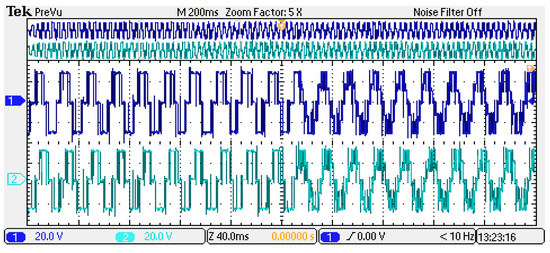
Figure 20.
The experimental waveform of two–three-level modulation conversion.
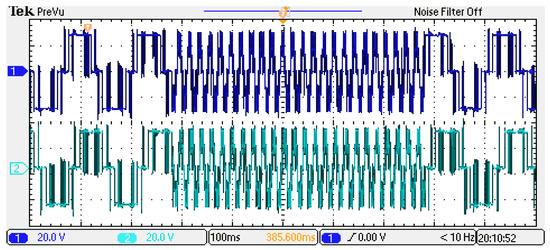
Figure 21.
The whole conversion process of the modulation strategy.
By comparing the conversion results of the three–two-level and two–three-level experiments, it can be seen from the figures that the experimental waveform reflects the simulation waveform, and the difference in waveforms has a relationship with the sampling time in the process of simulations and experiments.
6. Summary
The switching losses of the D-NPC and ID-NPC topologies were qualitatively compared and analyzed. In the ID-NPC topology, 18 IGBTs can make the heat distribution more uniform and prolong the service life of all IGBTs. Additionally, the circuit of the ID-NPC topology can also save three groups of driving elements. The improved two-level topology was used, where, on the one hand, the current return path was added and, on the other hand, the three-level and two-level conversion strategies were adopted to expand the fault-tolerant function of the system, and to improve the reliability. The simulation and experiment further verify the function integrity of the improved topology and the feasibility of the modulation conversion strategy.
Author Contributions
Conceptualization, Y.C. and X.Z.; methodology, Y.C. and X.Z.; software, Y.C.; validation, Y.C., X.Z., X.L., and Y.M.; formal analysis, Y.C. and X.Z.; investigation, X.Z.; resources, Y.C.; data curation, Y.C.; writing—original draft preparation, X.L.; writing—review and editing, X.L.; project administration, X.Z. and Y.M.; funding acquisition, X.Z. and Y.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Teaching Research and Reform Program of Cangzhou Jiaotong College, grant number: HBJY19014.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ghosh, A. Possibilities and Challenges for the Inclusion of the Electric Vehicle (EV) to Reduce the Carbon Footprint in the Transport Sector: A Review. Energies 2020, 13, 2602. [Google Scholar] [CrossRef]
- Bhattacharjee, A.; Mohanty, R.K.; Ghosh, A. Design of an Optimized Thermal Management System for Li-Ion Batteries under Different Discharging Conditions. Energies 2020, 13, 5695. [Google Scholar] [CrossRef]
- Chandran, V.; Patil, C.K.; Karthick, A.; Ganeshaperumal, D.; Rahim, R.; Ghosh, A. State of Charge Estimation of Lithium-Ion Battery for Electric Vehicles Using Machine Learning Algorithms. World Electr. Veh. J. 2021, 12, 38. [Google Scholar] [CrossRef]
- Zhang, J.; Wai, R.J. Design of New SVPWM Mechanism for Three-Level NPC ZSI via Line-Voltage Coordinate System. IEEE Trans. Power Electron. 2020, 35, 8593–8606. [Google Scholar] [CrossRef]
- Bennani-Ben Abdelghani, A.; Ben Abdelghani, H.; Richardeau, F.; Blaquiere, J.M.; Mosser, F.; Slama-Belkhodja, I. Versatile Three-Level FC-NPC Converter with High Fault-Tolerance Capabilities: Switch Fault Detection and Isolation and Safe Postfault Operation. IEEE Trans. Ind. Electron. 2017, 64, 6453–6464. [Google Scholar] [CrossRef]
- Xia, Y.; Zou, J.X.; Li, K.; Min, Z.S.; Du, L. Optimized Virtual Space Vector Modulation for Three-phase Three-level T-type Converter. Clust. Comput. J. Netw. Softw. Tools Appl. 2019, 22, 14679–14687. [Google Scholar] [CrossRef]
- Nabaf, A.; Takahashi, I.; Akagi, H. New Neutral-Point-Clamped PWM Inverter. IEEE Trans. Ind. Appl. 1981, IA-17, 518–523. [Google Scholar] [CrossRef]
- Choudhury, A.; Pillay, P.; Williamson, S.S. DC-Bus Voltage Balancing Algorithm for Three-Level Neutral-Point-Clamped (NPC) Traction Inverter Drive with Modified Virtual Space Vector. IEEE Trans. Ind. Appl. 2016, 52, 3958–3967. [Google Scholar] [CrossRef]
- Cai, H.H.; Tang, S.X.; Zhang, X.C. Loss Calculation and Balance Control Agorithm for NPC Three-level Inverter. Power Electron. Technol. 2015, 49, 10–14. [Google Scholar]
- Dargahi, V.; Corzine, K.A.; Sadigh, A.K. A New Three-Level Active Neutral-Point-Clamped (A-NPC) Multilevel Converter Topology. In Proceedings of the 45th Annual Conference of the IEEE Industrial Electronics Society (IECON), Lisbon, Portugal, 14–17 October 2019; IEEE: New York, NY, USA, 2019. [Google Scholar]
- Bruckner, T.; Bernet, S.; Guldner, H. The Active NPC Converter and Its Loss-balancing Control. IEEE Trans. Ind. Electron. 2005, 52, 855–868. [Google Scholar] [CrossRef]
- Celik, O.; Tan, A.; Inci, M.; Teke, A. Improvement of Energy Harvesting Capability in Grid-connected Photovoltaic Micro-inverters. Energy Sour. Part A Recover. Utlization Environ. Eff. 2020. [Google Scholar] [CrossRef]
- Xu, H.P.; Chen, Q.; Li, G.L.; Hu, C.G. Research on Neutral Point Potential Balance of NPC 3-L Inverter Based on SVPWM. In Proceedings of the 13th IEEE Conference on Industrial Electronics and Applications (ICIEA), Wuhan, China, 31 May–2 June 2018; IEEE: New York, NY, USA, 2018. [Google Scholar]
- Xu, S.Z.; He, F.Y. Thermal Equilibrium Dynamic Control Based on DPWM Dual-Mode Modulation of High Power NPC Three-Level Inverter. Math. Probl. Eng. 2016, 2016, 1–13. [Google Scholar] [CrossRef]
- Yuan, Q.Q.; Qian, J.Y.; Li, A. A Simplified Common-Mode Voltage Suppression and Neutral-Point Potential Control for the NPC Three-Level Inverter. J. Electr. Eng. Technol. 2019, 14, 2389–2398. [Google Scholar] [CrossRef]
- Porru, M.; Serpi, A.; Marongiu, I.; Damiano, A. Suppression of DC-link voltage unbalance in three-level neutral-point clamped converters. J. Frankin Inst. Eng. Appl. Math. 2018, 55, 728–752. [Google Scholar] [CrossRef]
- Bruckner, T.; Bernet, S. Loss Balancing in Three-level Voltage Source Inverters Applying Active NPC Switches. In Proceedings of the 32nd Annual Power Electronics Specialist Conference (PESC 2001), Vancouver, BC, Canada, 17–21 June 2001; IEEE: New York, NY, USA, 2001. [Google Scholar]
- Bruckner, T.; Holmes, D.G. Optimal Pulse-width Modulation for Three-level Inverters. IEEE Trans. Power Electron. 2005, 20, 82–89. [Google Scholar] [CrossRef]
- Rajapakse, A.D.; Gole, A.M.; Wilson, P.L. Electromagnetic Transients Simulation Models for Accurate Representation of Switching Losses and Thermal Performance in Power Electronic Systems. IEEE Trans. Power Deliv. 2005, 20, 319–327. [Google Scholar] [CrossRef]
- Jean, P.L. Chapter 7 Fault Tolerant Predictive Control of Synchronous Motor and Inverter. In Synchronous Motor Control; Zhu, X., Ed.; China Machine Press: Beijing, China, 2016; pp. 229–246. [Google Scholar]
- Martinez, B.L.C.; Ma, K.; Li, R.; Xu, D.H. Efficiency Analysis and Comparison of Three-level and Two-level Inverters. Power Electron. 2009, 43, 1–2. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).