Implementation Schemes for Electric Bus Fleets at Depots with Optimized Energy Procurements in Virtual Power Plant Operations
Abstract
1. Introduction
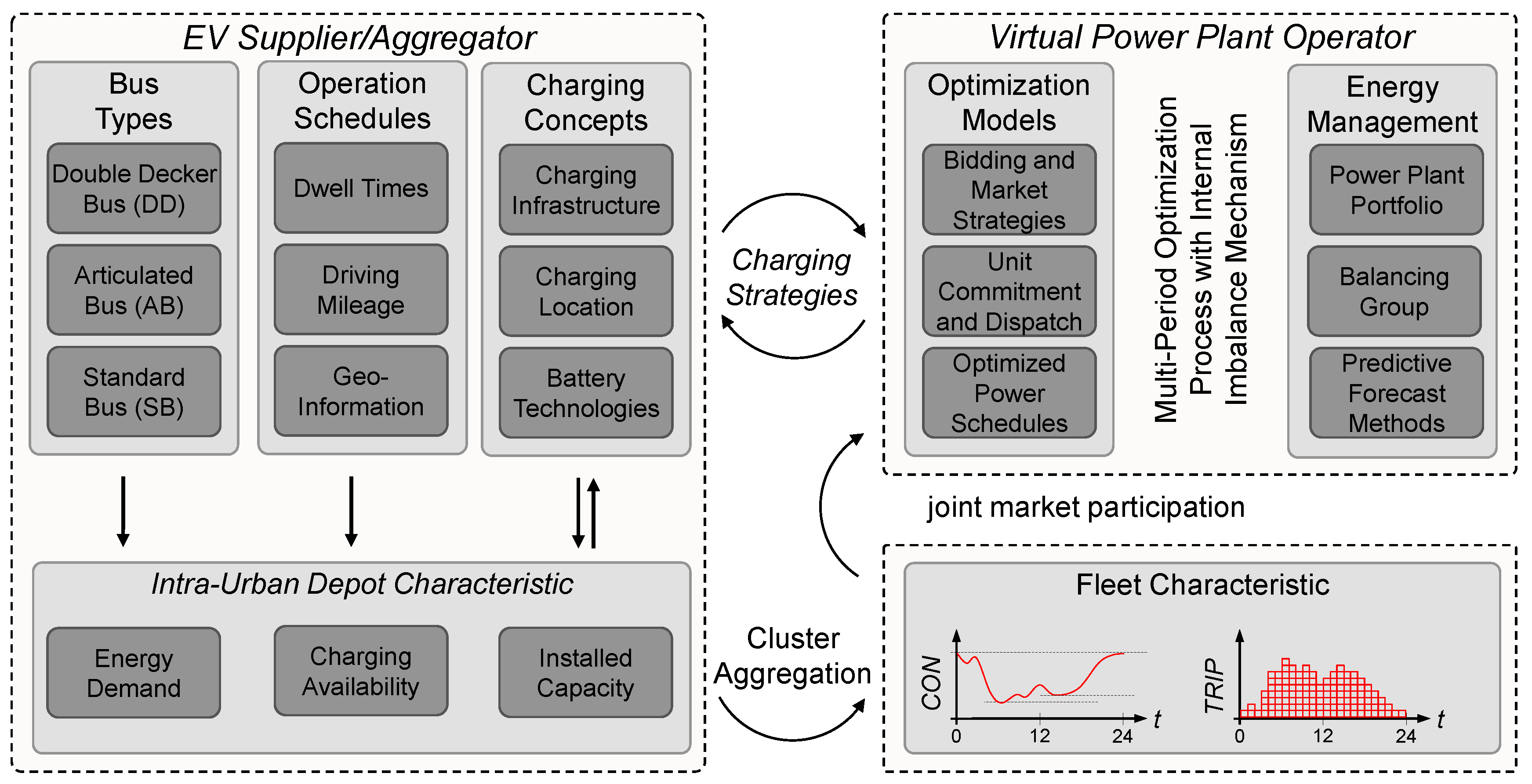
2. Framework Conditions and Operational Planning
2.1. Modeling Timetable-Based Driving Schedules
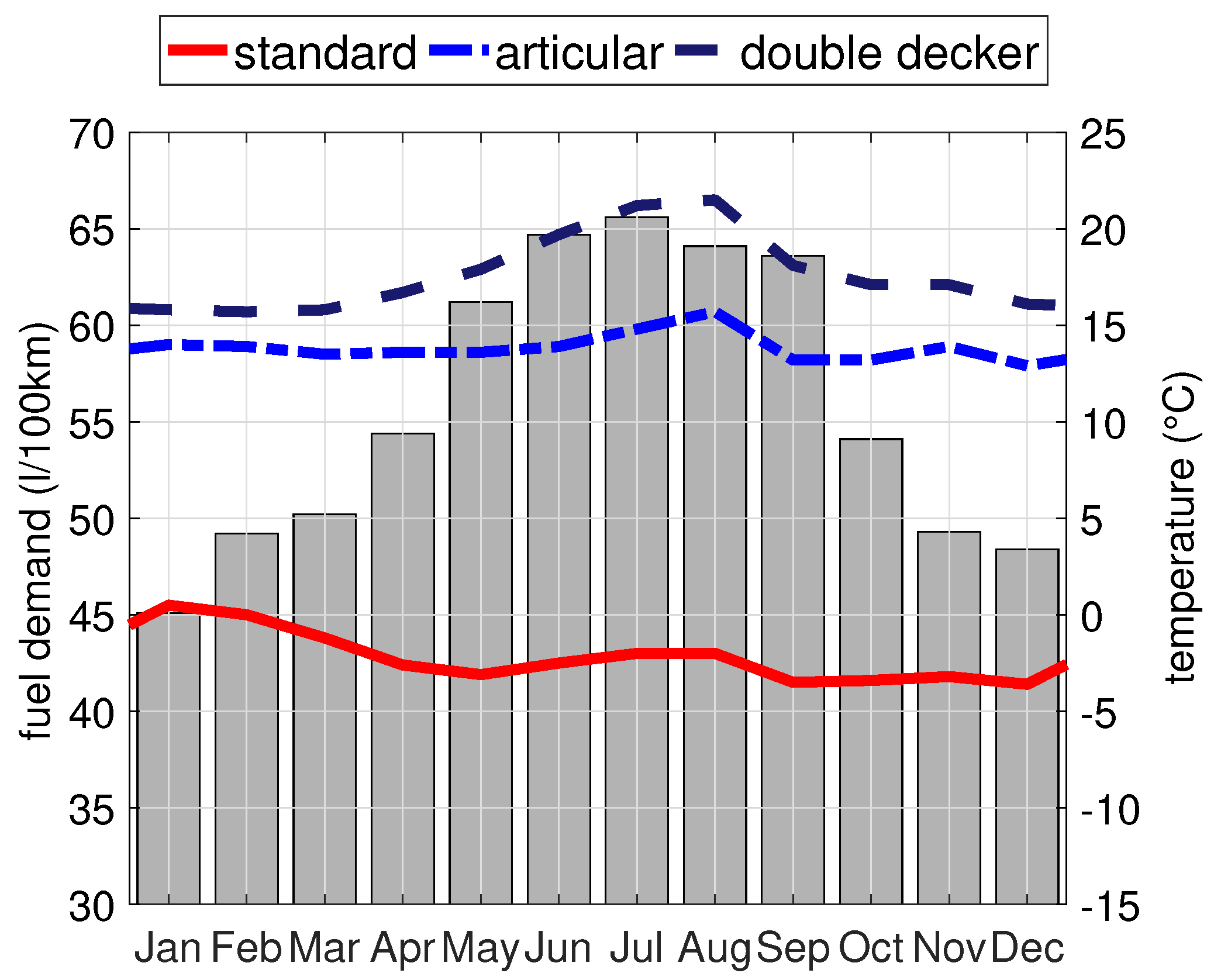
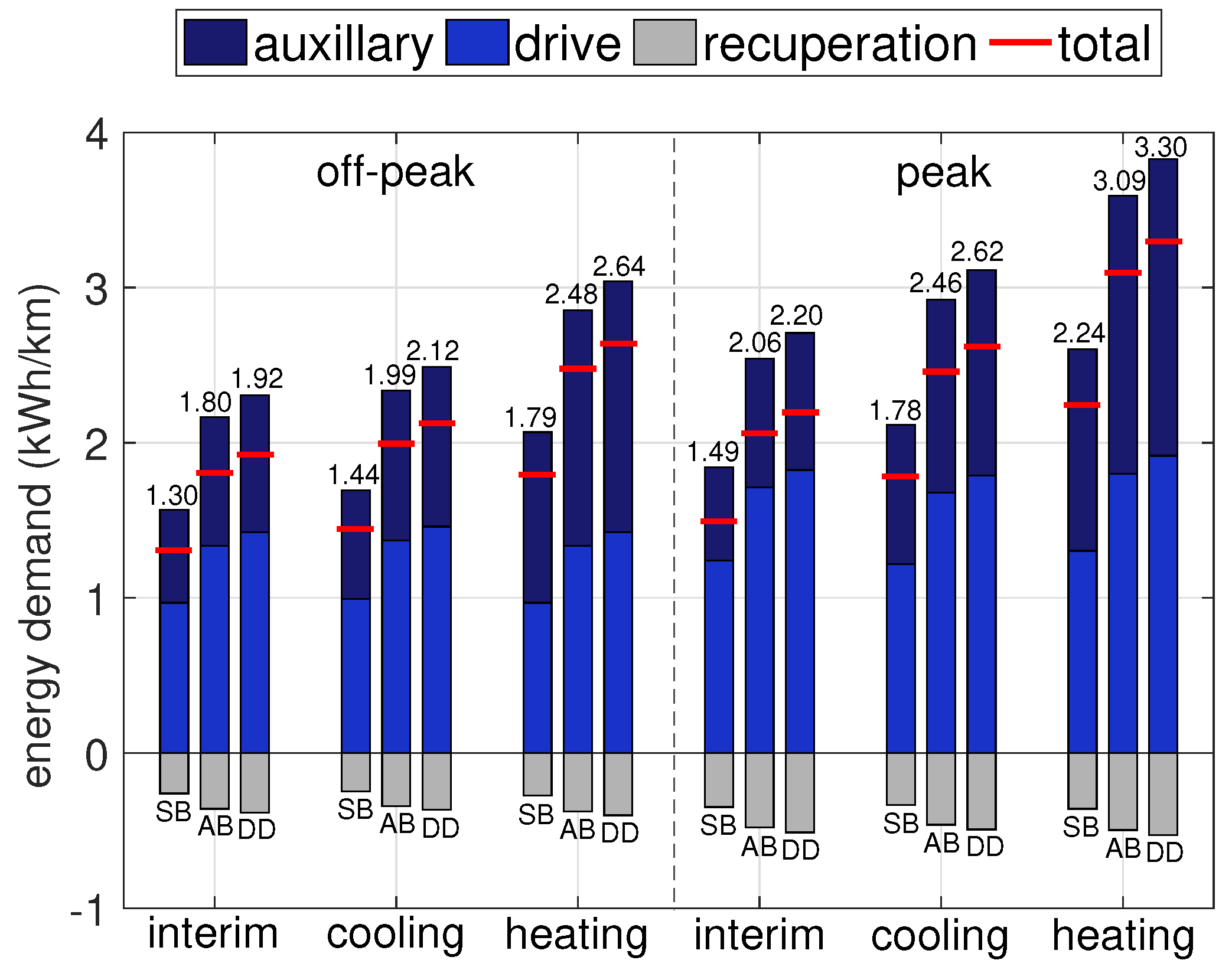
2.2. Energy Equivalence and Bus Type-Specific Models
2.3. Charging Concepts and Strategies
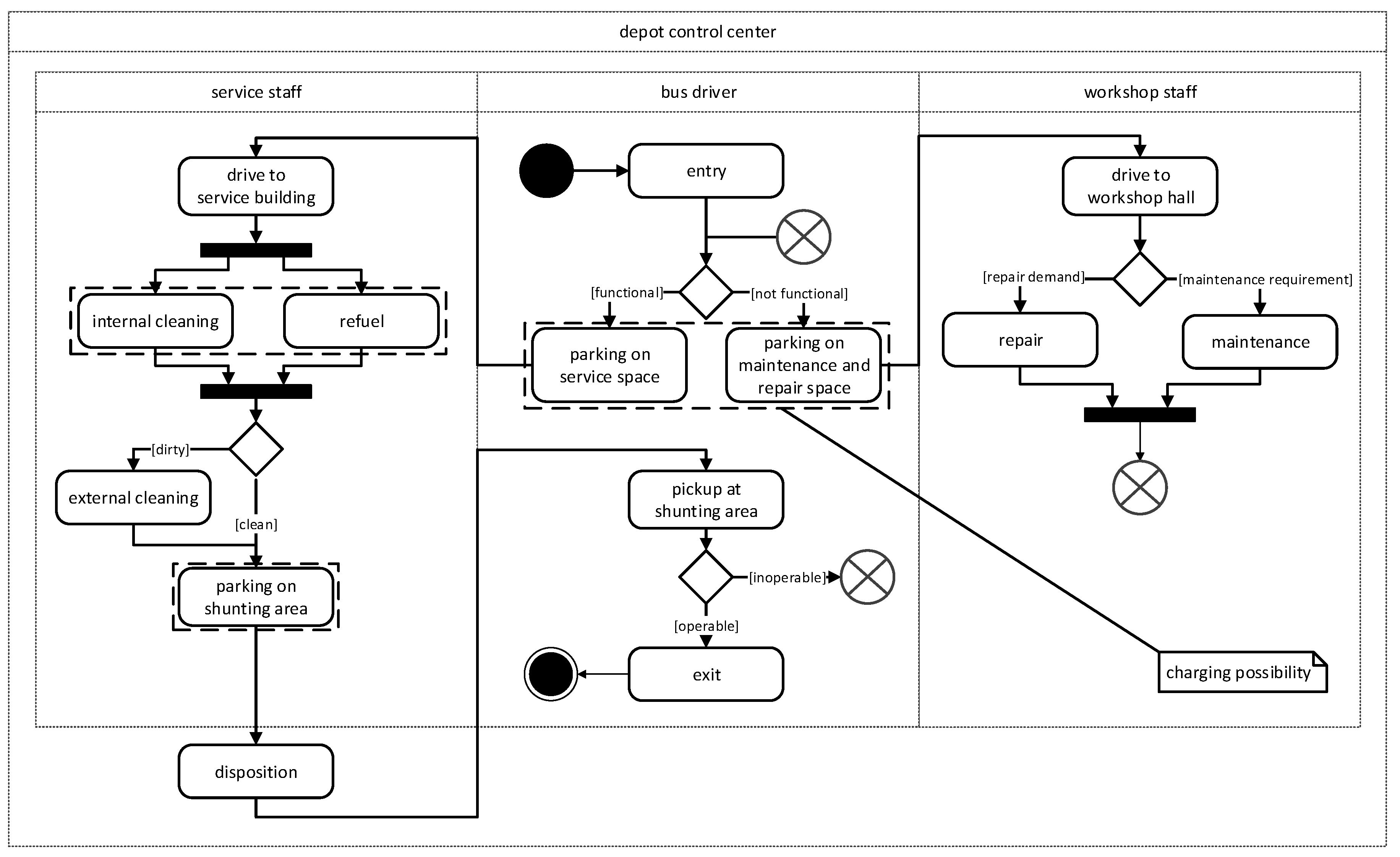
3. Operation Procedures and Depot Characteristics
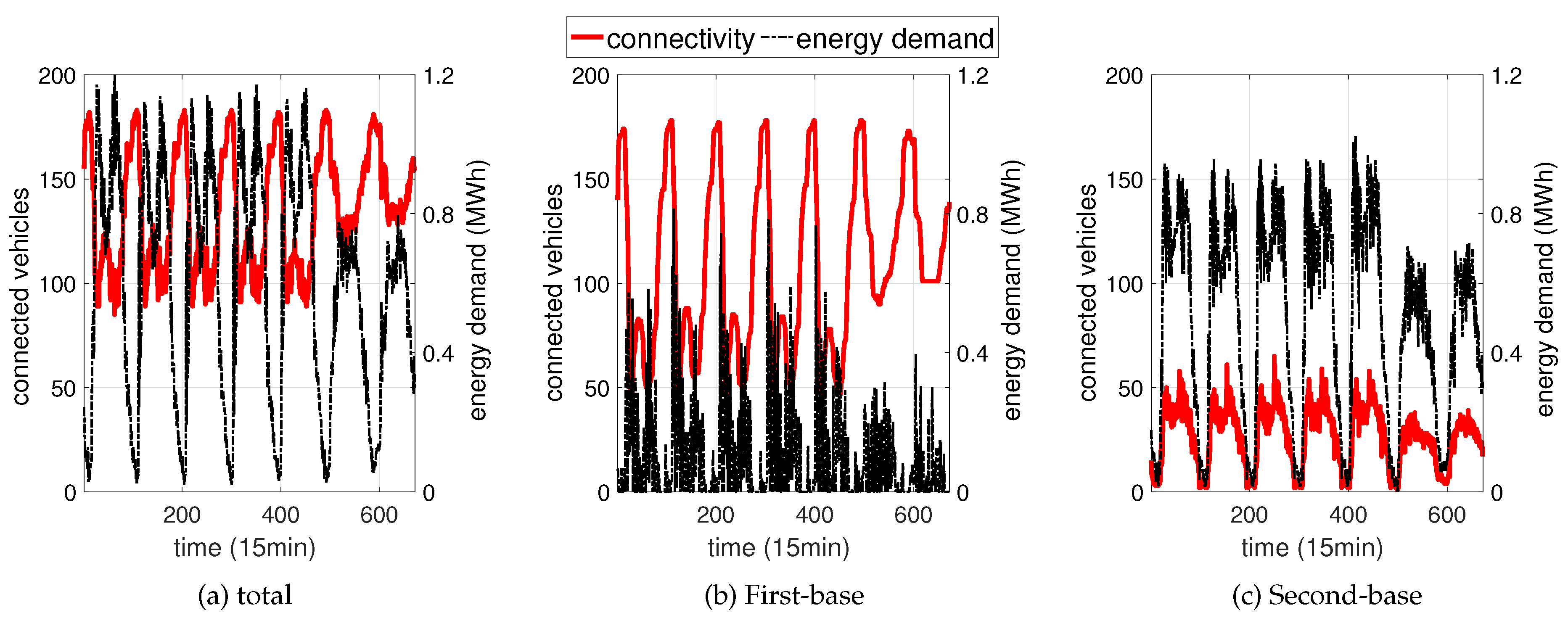
3.1. Analysis of Operation Processes and Schedules
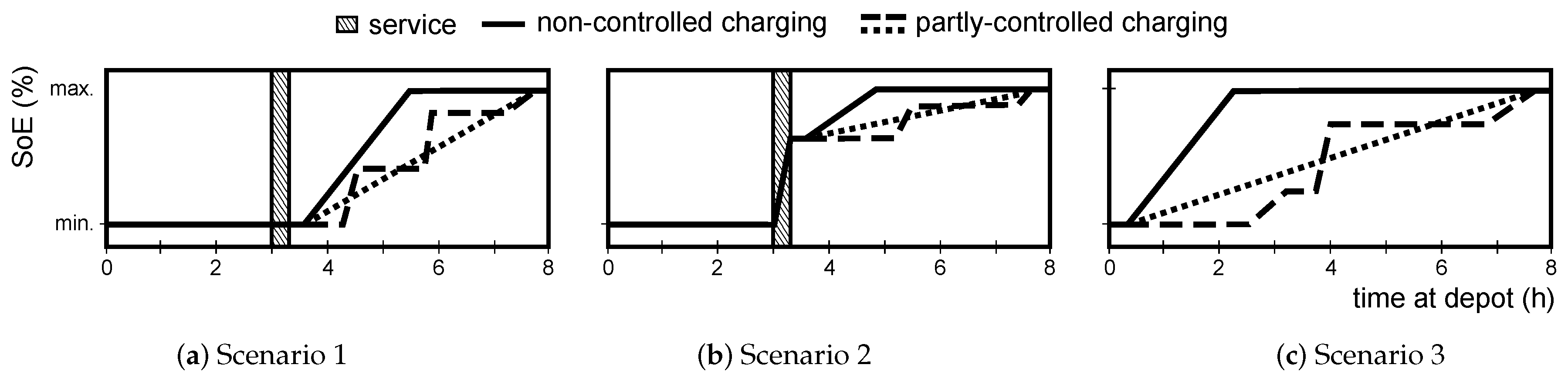
3.2. Charging Infrastructure and Process
4. Optimized Energy Procurements in VPP Operations
4.1. Implementation Model and Mathematical Formulation
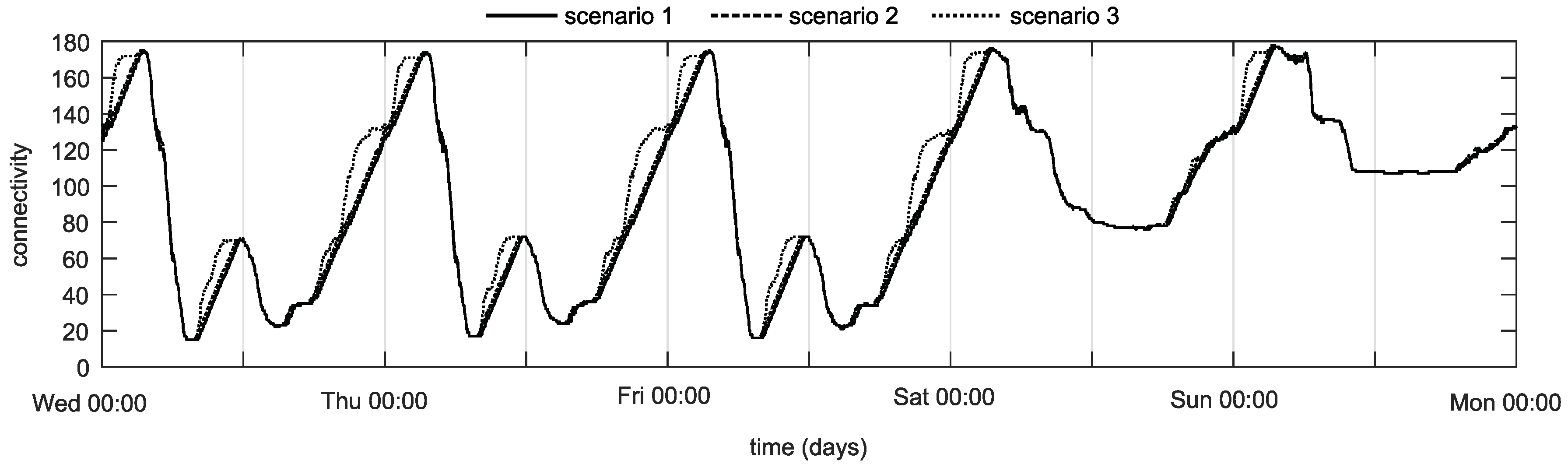
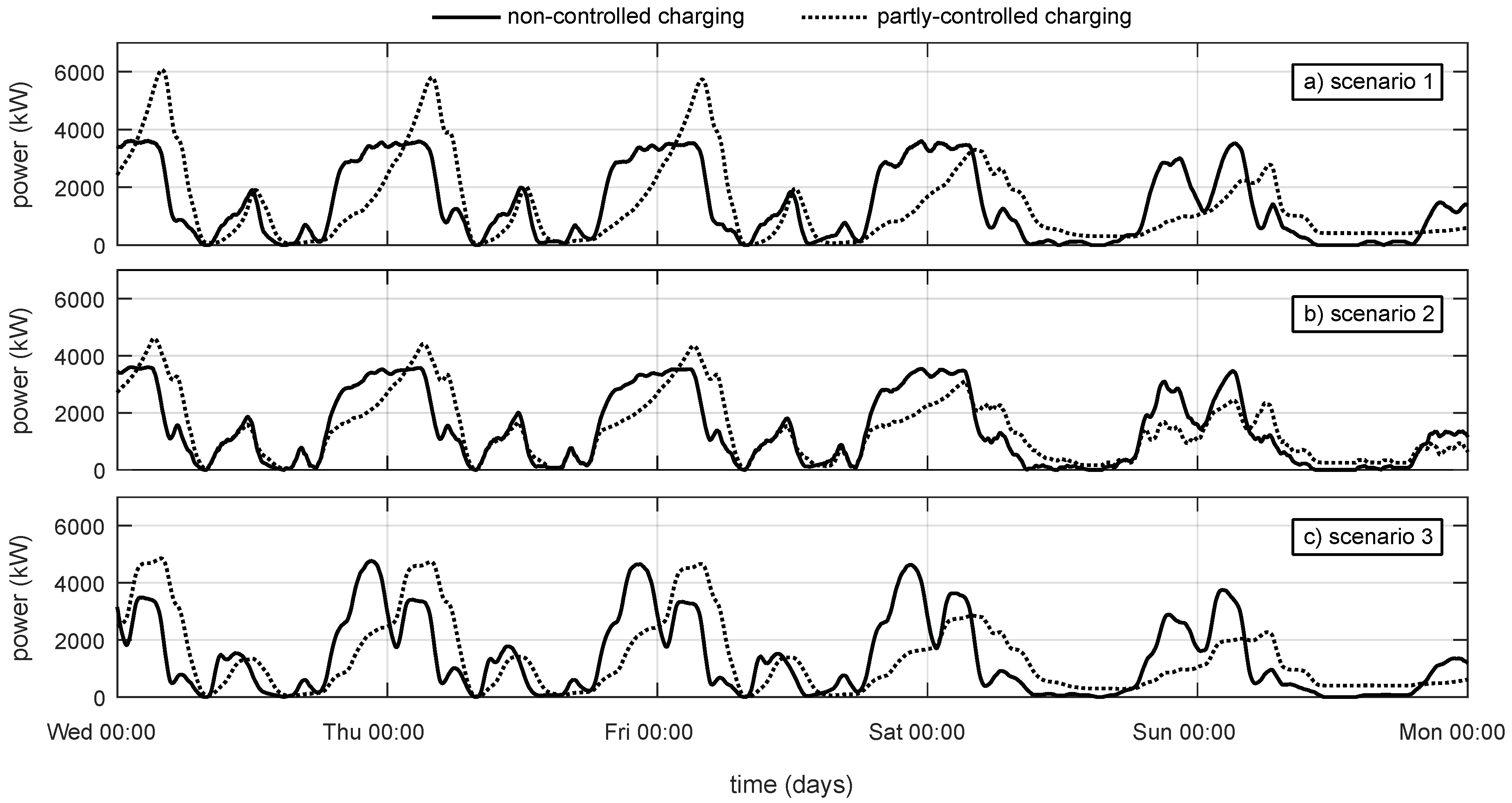
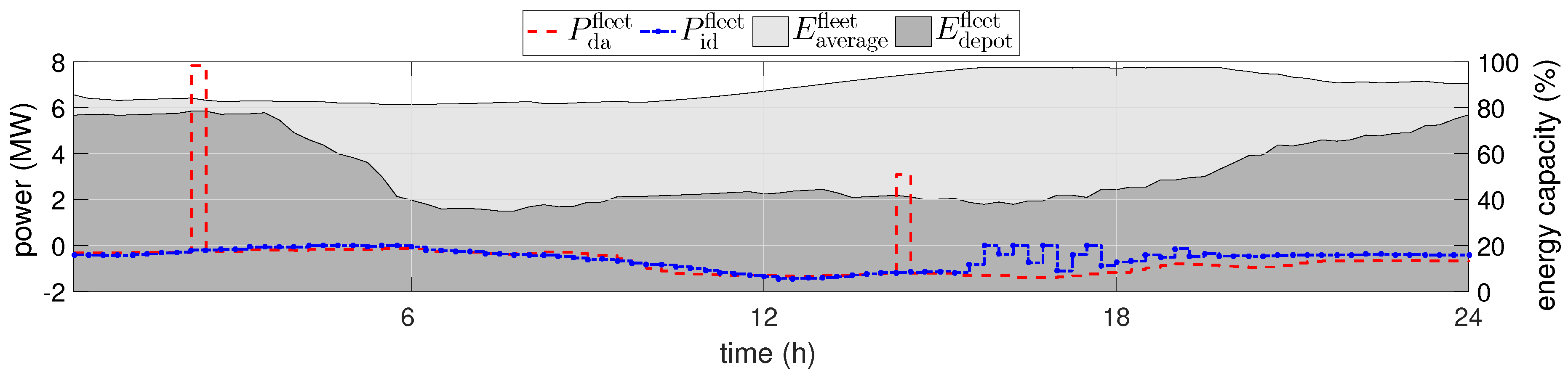
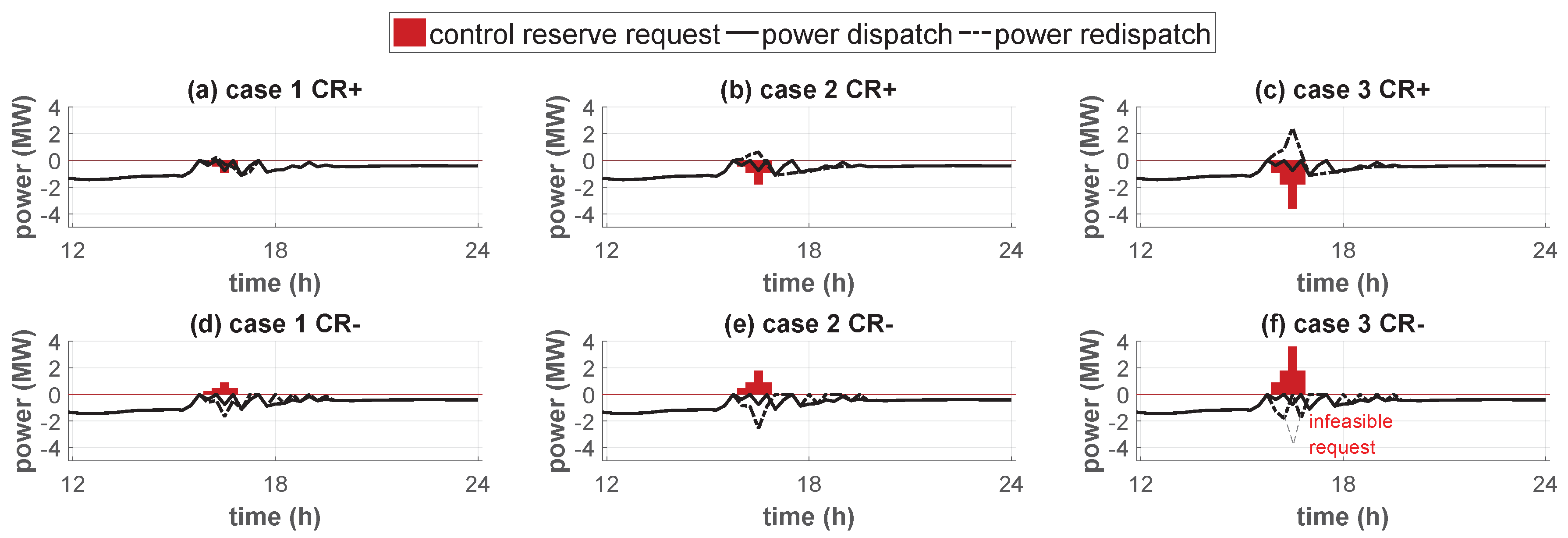
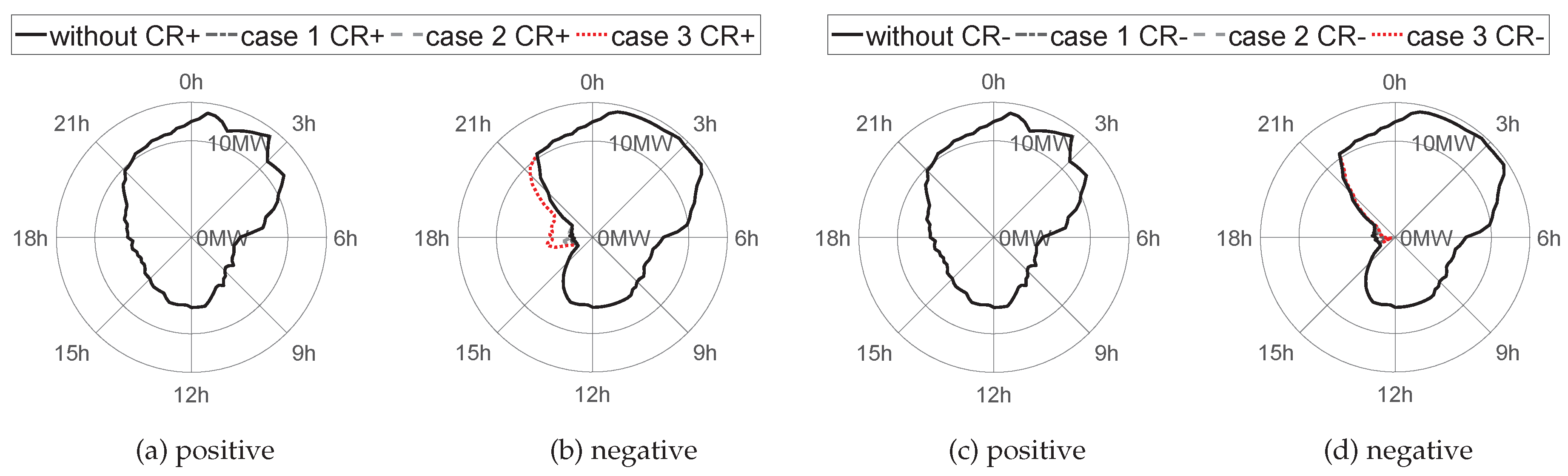
4.2. Computational Study and Dispatch Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| AB | articular bus |
| chp | combined heat and power plant |
| DD | double decker bus |
| dBus | diesel bus |
| eBus | electric bus |
| em | energy market |
| EV | electric vehicle |
| EVS/A | electric vehicle supplier/aggregator |
| ind | industrial load units |
| SB | standard bus |
| pv | photovoltaic power plant |
| VPP | virtual power plant |
| wind | wind power plant |
References
- Kunith, A.; Mendelevitch, R.; Göhlich, D. Electrification of a city bus network—An optimization model for cost-effective placing of charging infrastructure and battery sizing of fast-charging electric bus systems. Int. J. Sustain. Transp. 2017, 11, 707–720. [Google Scholar] [CrossRef]
- Göhlich, D.; Fay, T.A.; Jefferies, D.; Lauth, E.; Kunith, A.; Zhang, X. Design of urban electric bus systems. Des. Sci. 2018, 4, e15. [Google Scholar] [CrossRef]
- Baouche, F.; Billot, R.; Trigui, R.; Faouzi, N.E.E. Efficient Allocation of Electric Vehicles Charging Stations: Optimization Model and Application to a Dense Urban Network. IEEE Intell. Transp. Syst. Mag. 2014, 6, 33–43. [Google Scholar] [CrossRef]
- ZeEUS. eBus Report: An Overview of Electric Buses in Europe; International Association of Public Transport: Brussels, Belgium, 2016. [Google Scholar]
- Rogge, M.; Wollny, S.; Sauer, D.U. Fast Charging Battery Buses for the Electrification of Urban Public Transport—A Feasibility Study Focusing on Charging Infrastructure and Energy Storage Requirements. Energies 2015, 8, 4587–4606. [Google Scholar] [CrossRef]
- Bessa, R.J.; Matos, M.A. Economic and technical management of an aggregation agent for electric vehicles: A literature survey. Eur. Trans. Electr. Power 2012, 22, 334–350. [Google Scholar] [CrossRef]
- Mets, K.; D’hulst, R.; Develder, C. Comparison of intelligent charging algorithms for electric vehicles to reduce peak load and demand variability in a distribution grid. J. Commun. Netw. 2012, 14, 672–681. [Google Scholar] [CrossRef]
- Zheng, J.; Wang, X.; Men, K.; Zhu, C.; Zhu, S. Aggregation model-based optimization for electric vehicle charging strategy. IEEE Trans. Smart Grid 2013, 4, 1058–1066. [Google Scholar] [CrossRef]
- Shao, C.; Wang, X.; Wang, X.; Du, C.; Wang, B. Hierarchical Charge Control of Large Populations of EVs. IEEE Trans. Smart Grid 2016, 7, 1147–1155. [Google Scholar] [CrossRef]
- Wang, Y.; Ai, X.; Tan, Z.; Yan, L.; Liu, S. Interactive Dispatch Modes and Bidding Strategy of Multiple Virtual Power Plants Based on Demand Response and Game Theory. IEEE Trans. Smart Grid 2016, 7, 510–519. [Google Scholar] [CrossRef]
- Kang, Q.; Feng, S.; Zhou, M.; Ammari, A.C.; Sedraoui, K. Optimal Load Scheduling of Plug-In Hybrid Electric Vehicles via Weight-Aggregation Multi-Objective Evolutionary Algorithms. IEEE Trans. Intell. Transp. Syst. 2017, 18, 2557–2568. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, D.; Jia, H.; Djilali, N.; Zhang, W. Aggregation and Bidirectional Charging Power Control of Plug-in Hybrid Electric Vehicles: Generation System Adequacy Analysis. IEEE Trans. Sustain. Energy 2015, 6, 325–335. [Google Scholar] [CrossRef]
- Torzynski, S.; Göhlich, D.; Hahn, D.; Bryl-Radziemska, M. Demonstration of An Electric Bus Fleet Operated on Line 204 with Inductive Charging System in Berlin (EBus Berlin); Institut für Elektrische Anlagen und Energiewirtschaft: Aachen, Germany, 2016. [Google Scholar]
- Ye, M.; Bai, Z.F.; Cao, B.G. Energy Recovery for Battery Electric Vehicles. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2008, 222, 1827–1839. [Google Scholar] [CrossRef]
- Tsolakis, A.; Megaritis, A.; Wyszynski, M. Engine performance and emissions of a diesel engine operating on diesel-RME (rapeseed methyl ester) blends with EGR (exhaust gas recirculation). Energy 2007, 32, 2072–2080. [Google Scholar] [CrossRef]
- Emadi, A.; Lee, Y.J.; Rajashekara, K. Power Electronics and Motor Drives in Electric, Hybrid Electric, and Plug-In Hybrid Electric Vehicles. IEEE Trans. Ind. Electron. 2008, 55, 2237–2245. [Google Scholar] [CrossRef]
- Estima, J.O.; Cardoso, A.J.M. Efficiency Analysis of Drive Train Topologies Applied to Electric/Hybrid Vehicles. IEEE Trans. Veh. Technol. 2012, 61, 1021–1031. [Google Scholar] [CrossRef]
- Lauber, A.; Sax, E.; Wiedemann, M. Autonomous driving in public transportation depots. ATZ Worldwide 2018, 120, 68–71. [Google Scholar] [CrossRef]
- Kempton, W.; Tomić, J. Vehicle-to-Grid Power Fundamentals: Calculating Capacity and Net Revenue. J. Power Resour. 2005, 144, 268–279. [Google Scholar] [CrossRef]
- Pieltain Fernández, L.; Román, T.; Cossent, R.; Domingo, C.; Frias, P. Assessment of the Impact of Plug-in Electric Vehicles on Distribution Networks. IEEE Trans. Power Syst. 2011, 26, 206–213. [Google Scholar] [CrossRef]
- Raab, A.F. Operational Planning, Modeling and Control of Virtual Power Plants with Electric Vehicles. Ph.D. Thesis, Technische Universität Berlin, Berlin, German, 2018. [Google Scholar]
- Ausubel, L.M.; Cramton, P. Virtual Power Plant Auctions. Util. Policy 2010, 18, 201–208. [Google Scholar] [CrossRef]
| Unit Model | Energy Capacity (kWh) | Weekly Mileage of Driving (km) | Specific Energy Demand (kWh/km) | Daily Energy Demand (kWh) |
|---|---|---|---|---|
| SB | 175 | 1045/1147/1469 | 1.30/1.80/2.30 | 245–345 |
| AB | 225 | 1135/1231/1566 | 1.80/2.50/3.10 | 368–508 |
| DD | 250 | 1118/1231/1500 | 1.90/2.60/3.30 | 385–517 |
| Fleet Composition | |||||
|---|---|---|---|---|---|
| Total | SB | AB | DD | (MWh) | |
| 193 | 53 | 103 | 37 | 10.59 | 41.53 |
| Installed Capacities of Generation, Load and Storage Units (MW) | |||||
| Total | Wind | pv | chp | ev | ind |
| 25 | 6 | 2.5 | 1 | 14.5 | 1 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Raab, A.F.; Lauth, E.; Strunz, K.; Göhlich, D. Implementation Schemes for Electric Bus Fleets at Depots with Optimized Energy Procurements in Virtual Power Plant Operations. World Electr. Veh. J. 2019, 10, 5. https://doi.org/10.3390/wevj10010005
Raab AF, Lauth E, Strunz K, Göhlich D. Implementation Schemes for Electric Bus Fleets at Depots with Optimized Energy Procurements in Virtual Power Plant Operations. World Electric Vehicle Journal. 2019; 10(1):5. https://doi.org/10.3390/wevj10010005
Chicago/Turabian StyleRaab, Andreas F., Enrico Lauth, Kai Strunz, and Dietmar Göhlich. 2019. "Implementation Schemes for Electric Bus Fleets at Depots with Optimized Energy Procurements in Virtual Power Plant Operations" World Electric Vehicle Journal 10, no. 1: 5. https://doi.org/10.3390/wevj10010005
APA StyleRaab, A. F., Lauth, E., Strunz, K., & Göhlich, D. (2019). Implementation Schemes for Electric Bus Fleets at Depots with Optimized Energy Procurements in Virtual Power Plant Operations. World Electric Vehicle Journal, 10(1), 5. https://doi.org/10.3390/wevj10010005





