Intelligent Control Approaches for Warehouse Performance Optimisation in Industry 4.0 Using Machine Learning
Abstract
1. Introduction
2. Materials and Methods
2.1. Optimization Methods in Logistics
2.2. Machine Learning Models
- MAE: Mean Absolute Error
- MSE: Mean Squared Error
- R2: Coefficient of Determination
2.3. Dataset Introduction
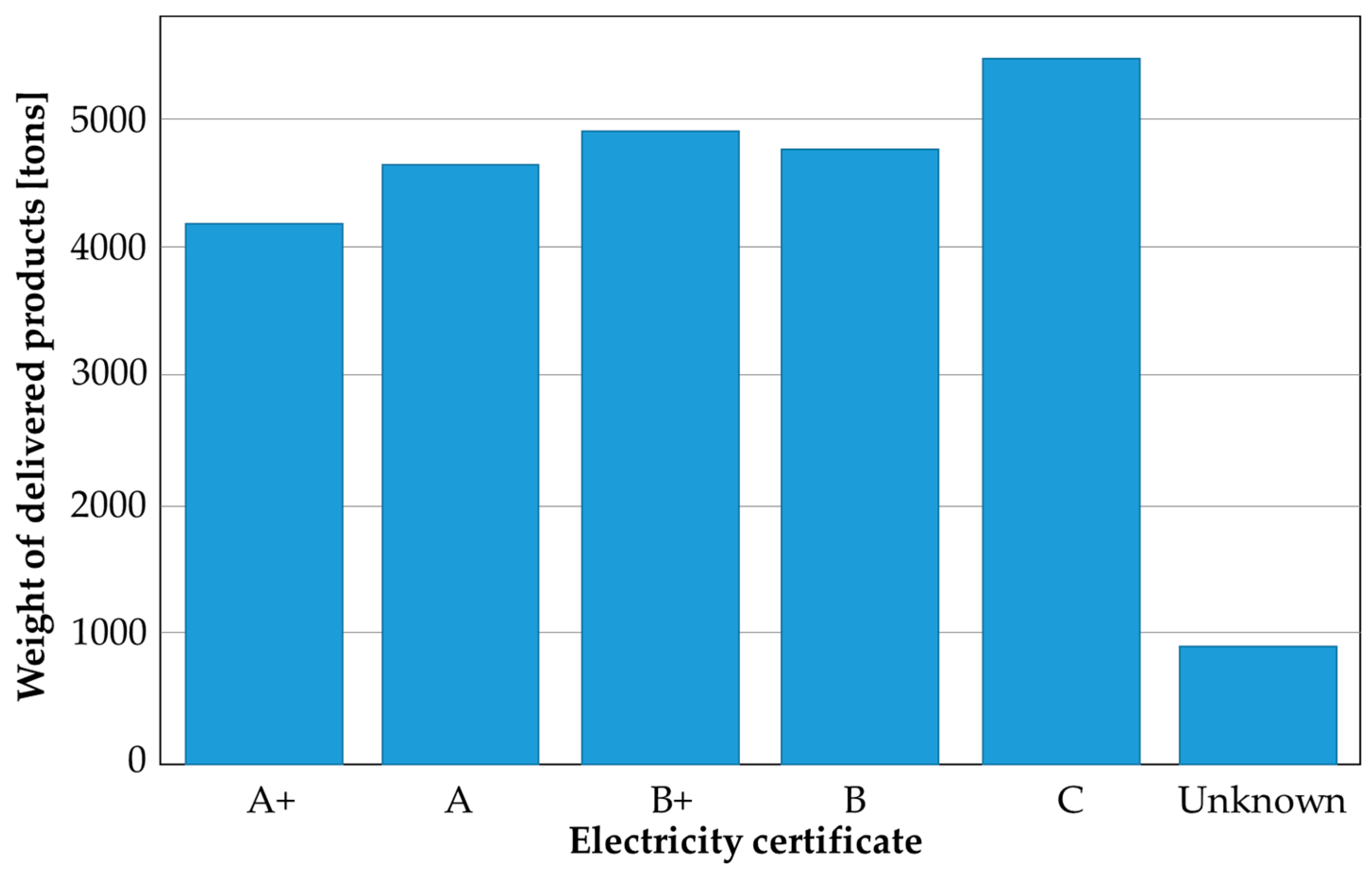
2.4. Exploratory Data Analysis
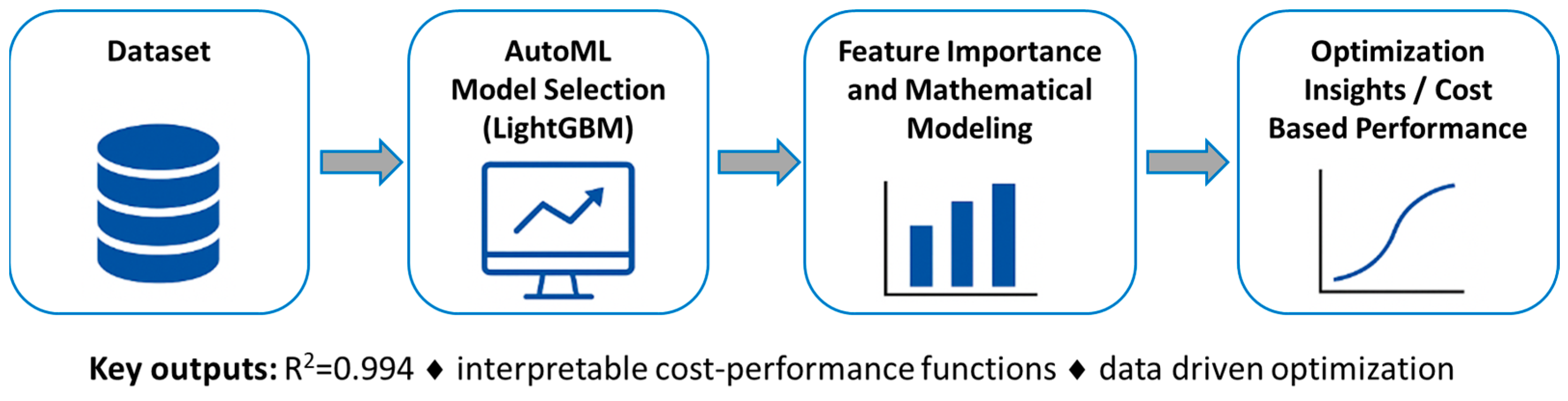
2.5. Applying of Automated Machine Learning
- The process starts with data preparation, which includes data collection, data cleaning, and data augmentation.
- Next comes feature engineering, where raw data is transformed into useful features. This involves feature selection, feature extraction, and feature construction. The outcome is the set of features used by the models.
- In model generation, the search space is defined: it can involve traditional models (e.g., SVM, KNN) or deep neural networks (e.g., CNN, RNN). Performance is improved through optimization methods such as hyperparameter optimization and architecture optimization. The process can also include Neural Architecture Search (NAS).
- Finally, in model estimation, efficient evaluation methods are applied to save computational resources: low-fidelity estimation, early stopping, surrogate models, and weight-sharing.
2.6. LightGBM Model
3. Results
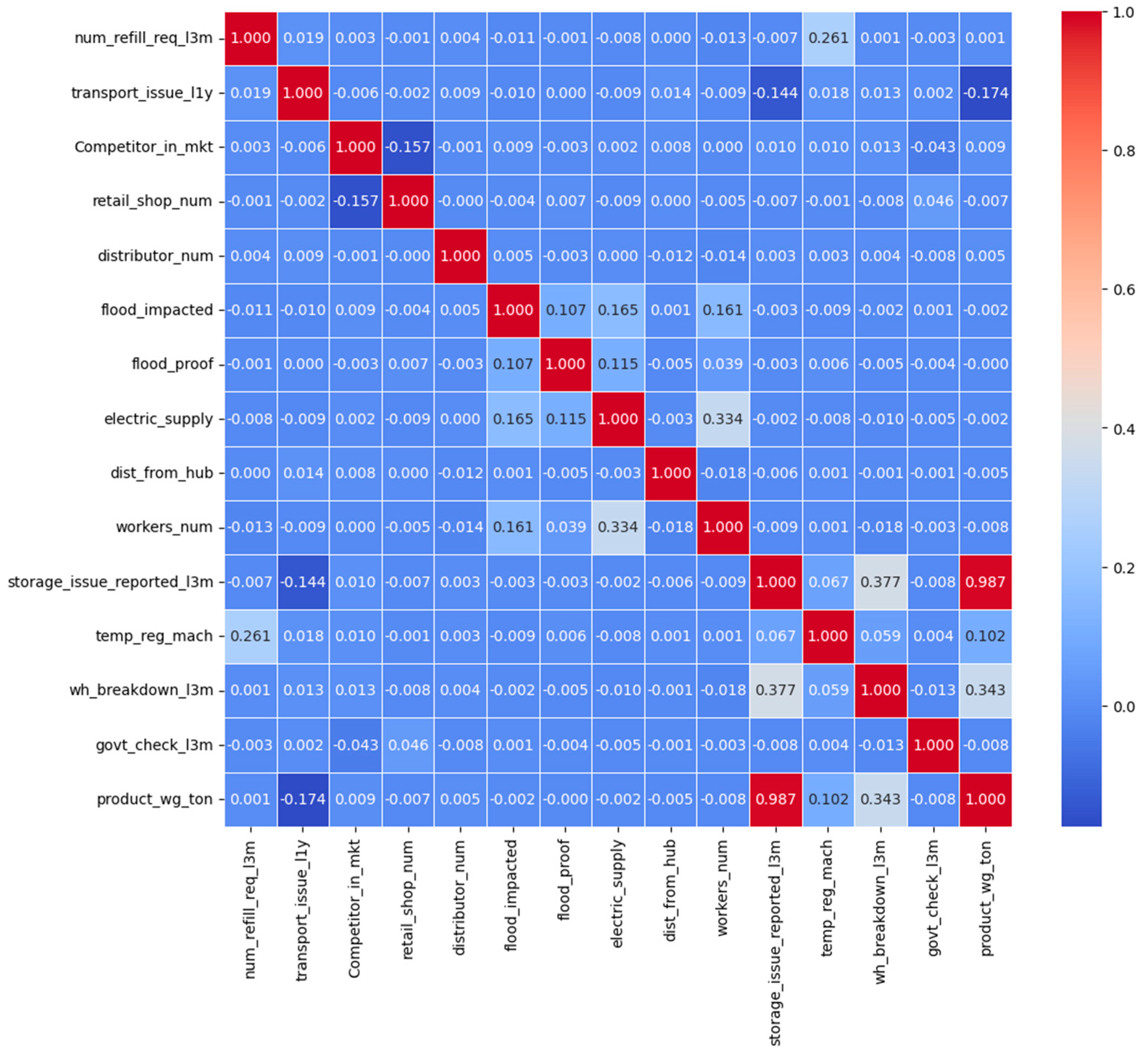
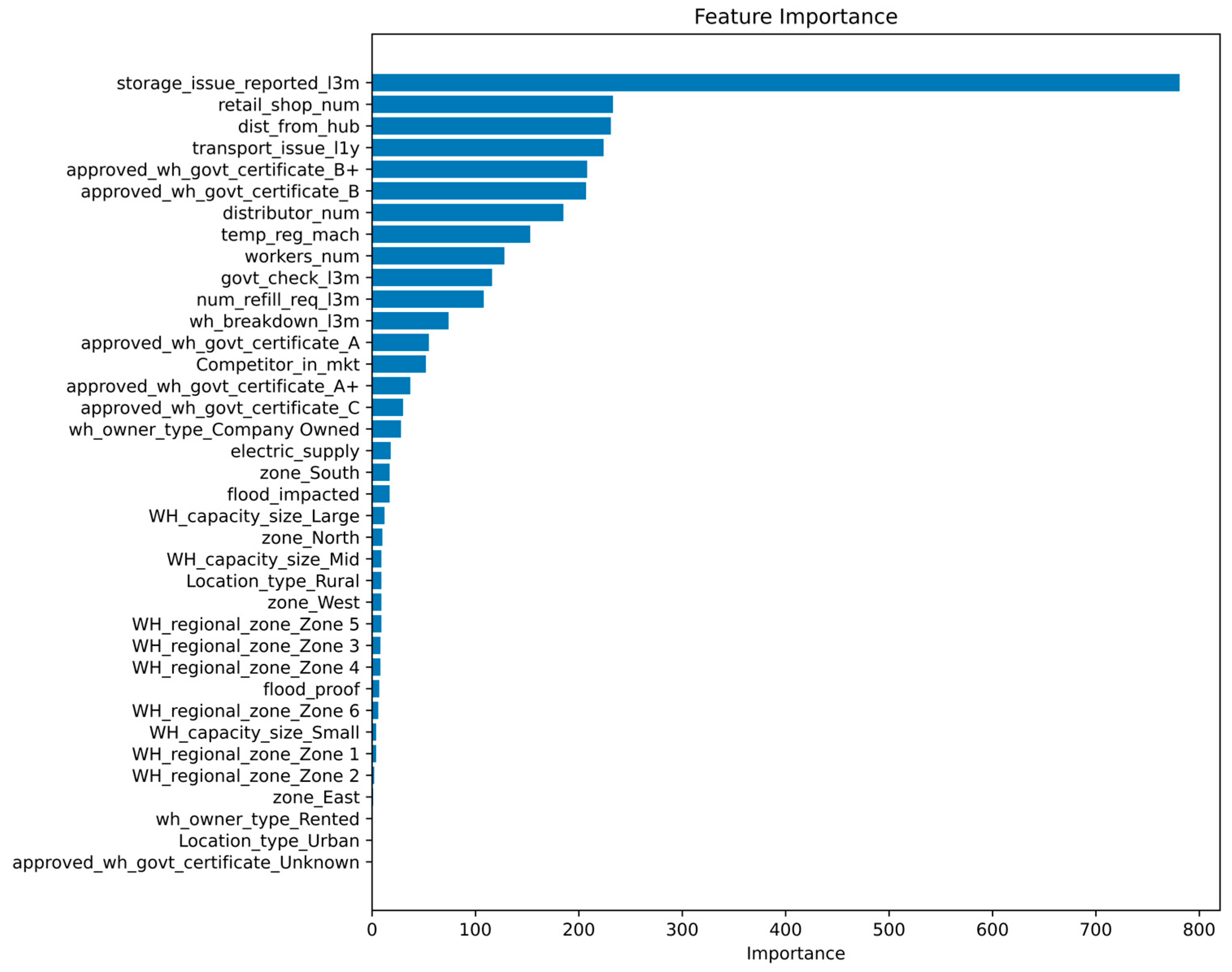
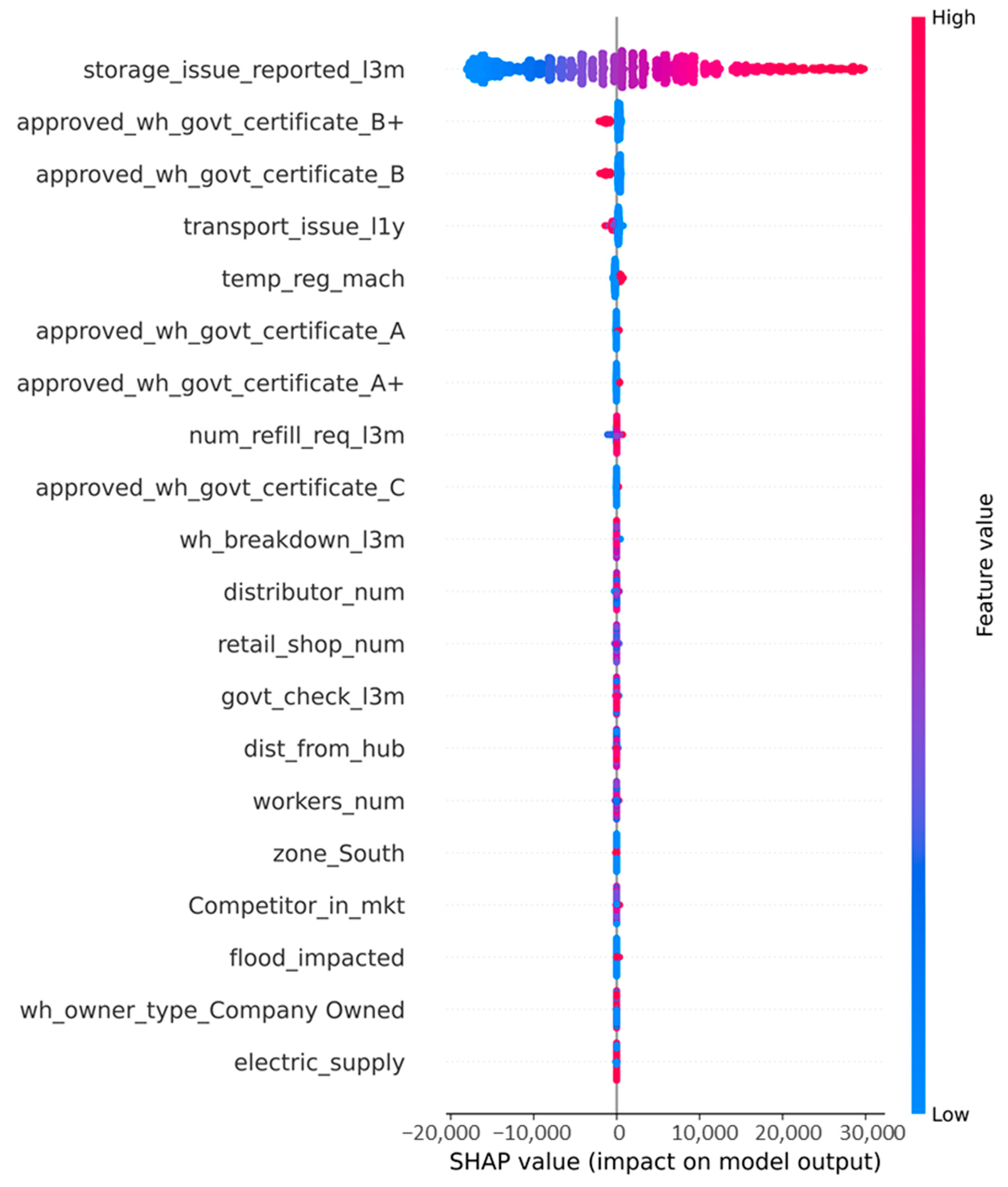
3.1. Feature Importance
- Filter Method: features are selected not based on model performance, but on some statistical or information-theoretic measure (correlation, mutual information, chi-squared test, ANOVA).
- Wrapped Method: a learning algorithm is wrapped into the feature selection process, which is evaluated based on various metrics, and the method selects the best method.
- Hybrid Method: a combination of filter and wrapped methods for feature selection on large data sets [43].
- Both methods consistently highlight overlapping key features.
- SHAP explains local, instance-level effects, while feature importance captures global trends.
- Normalization and averaging increase stability of results.
- Using two independent techniques reduces bias of a single method.
- Differences reflect complementary perspectives rather than contradictions.
- Cross-validation of results strengthens interpretability and trustworthiness.
- Robustness is enhanced because similar influential parameters appear under different assumptions.
- transport issue l1y;
- certificate;
- retail shop num;
- dist from hub;
- distributor num;
- temp reg mch;
- workers num.
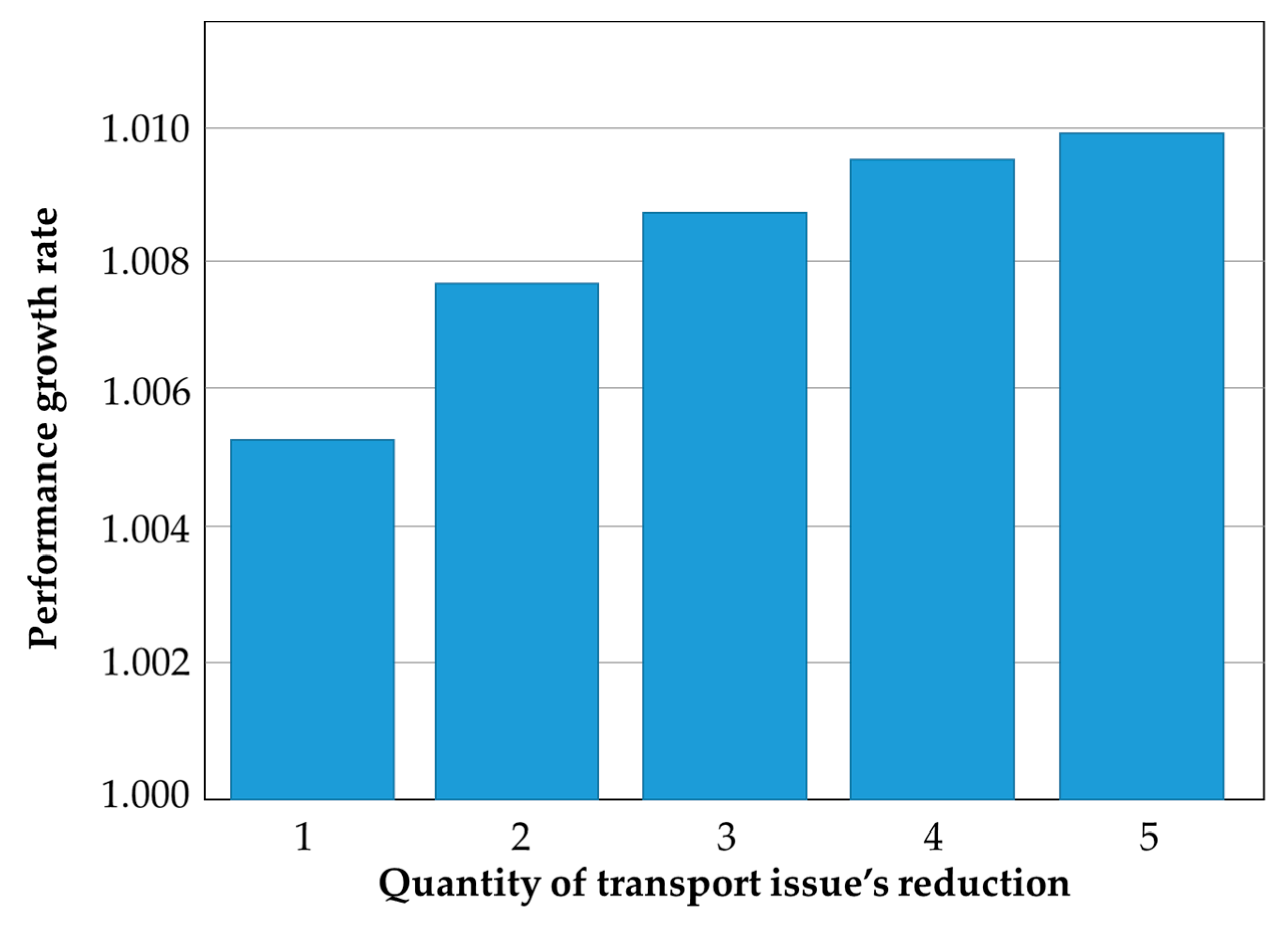
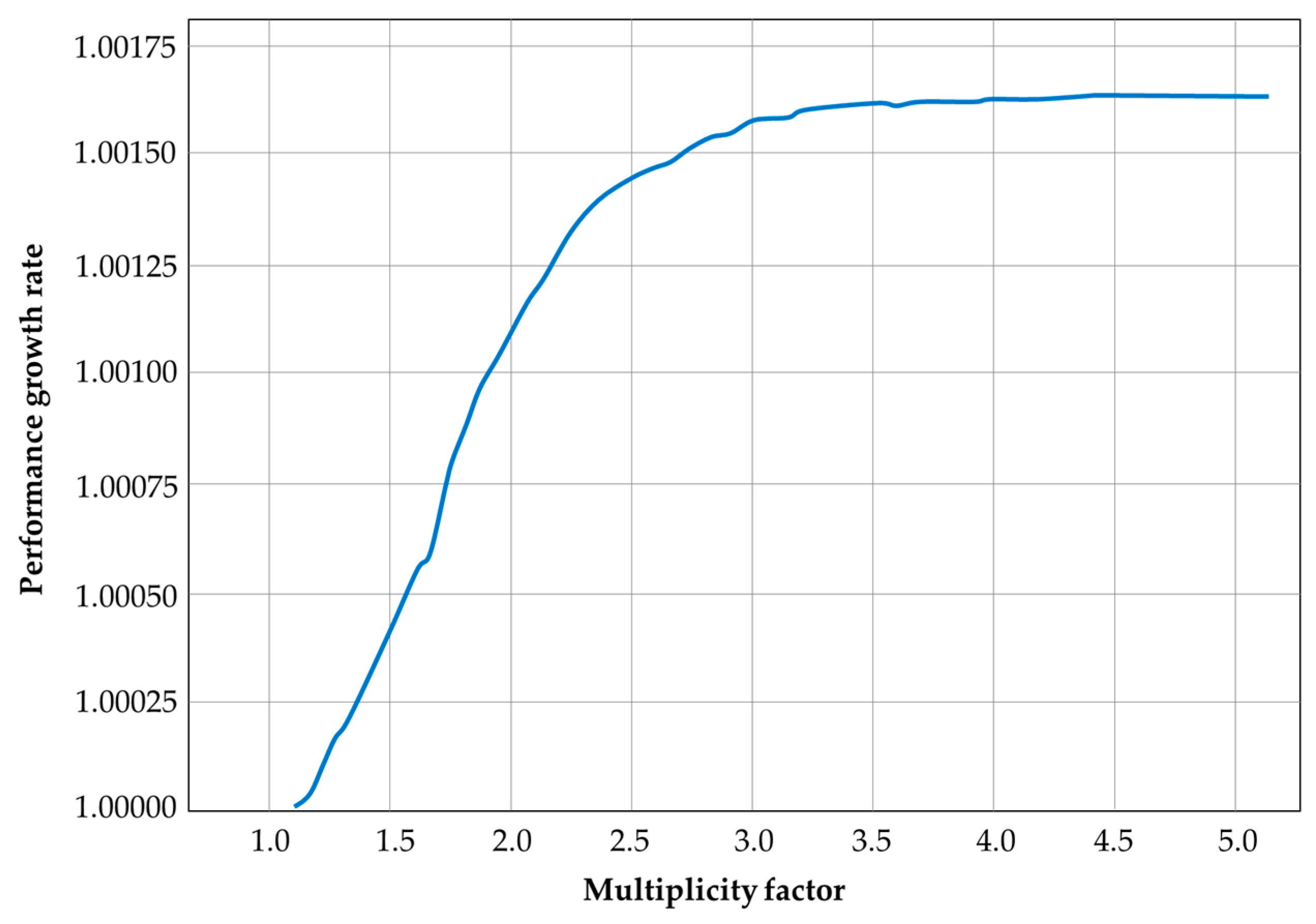
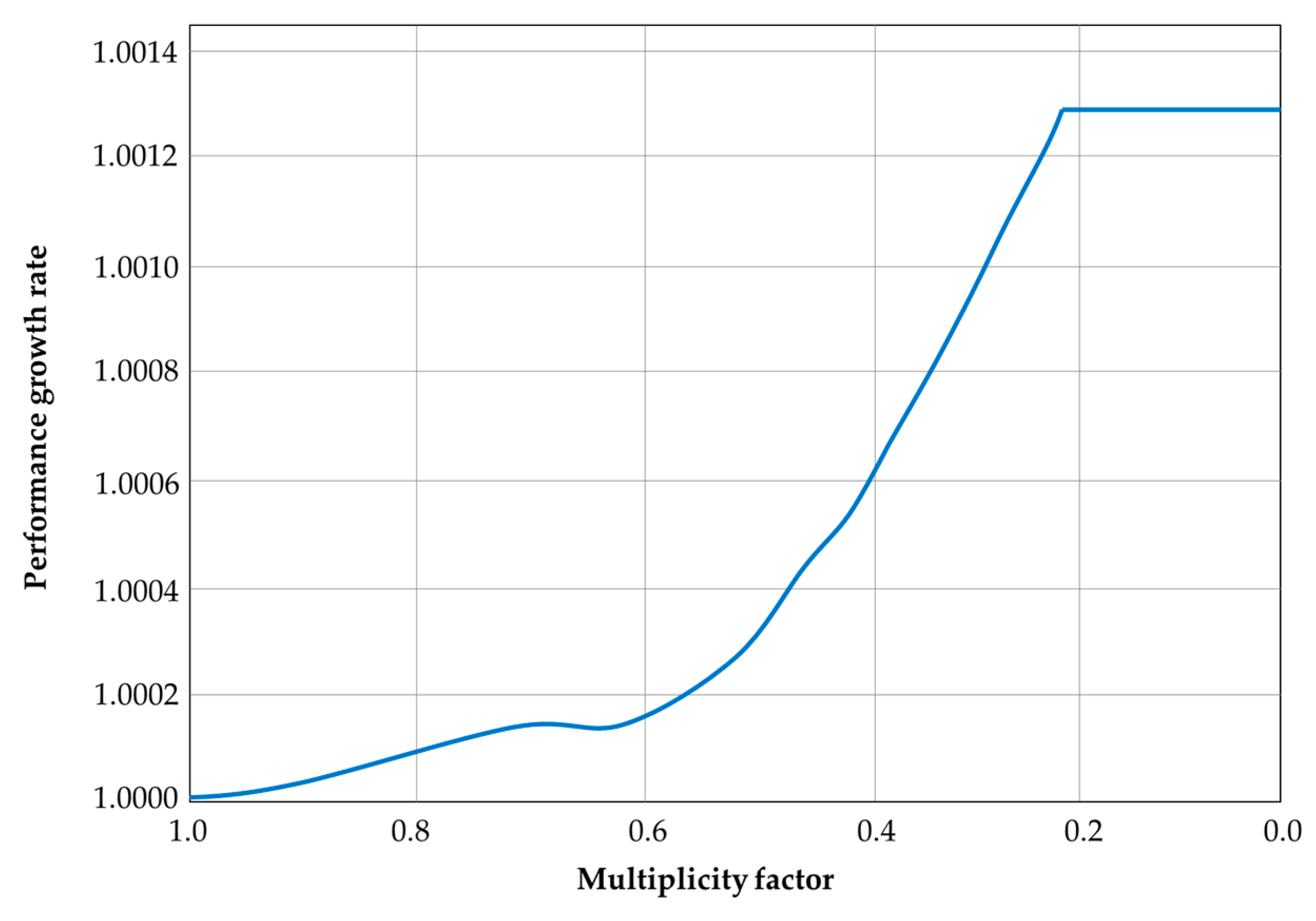
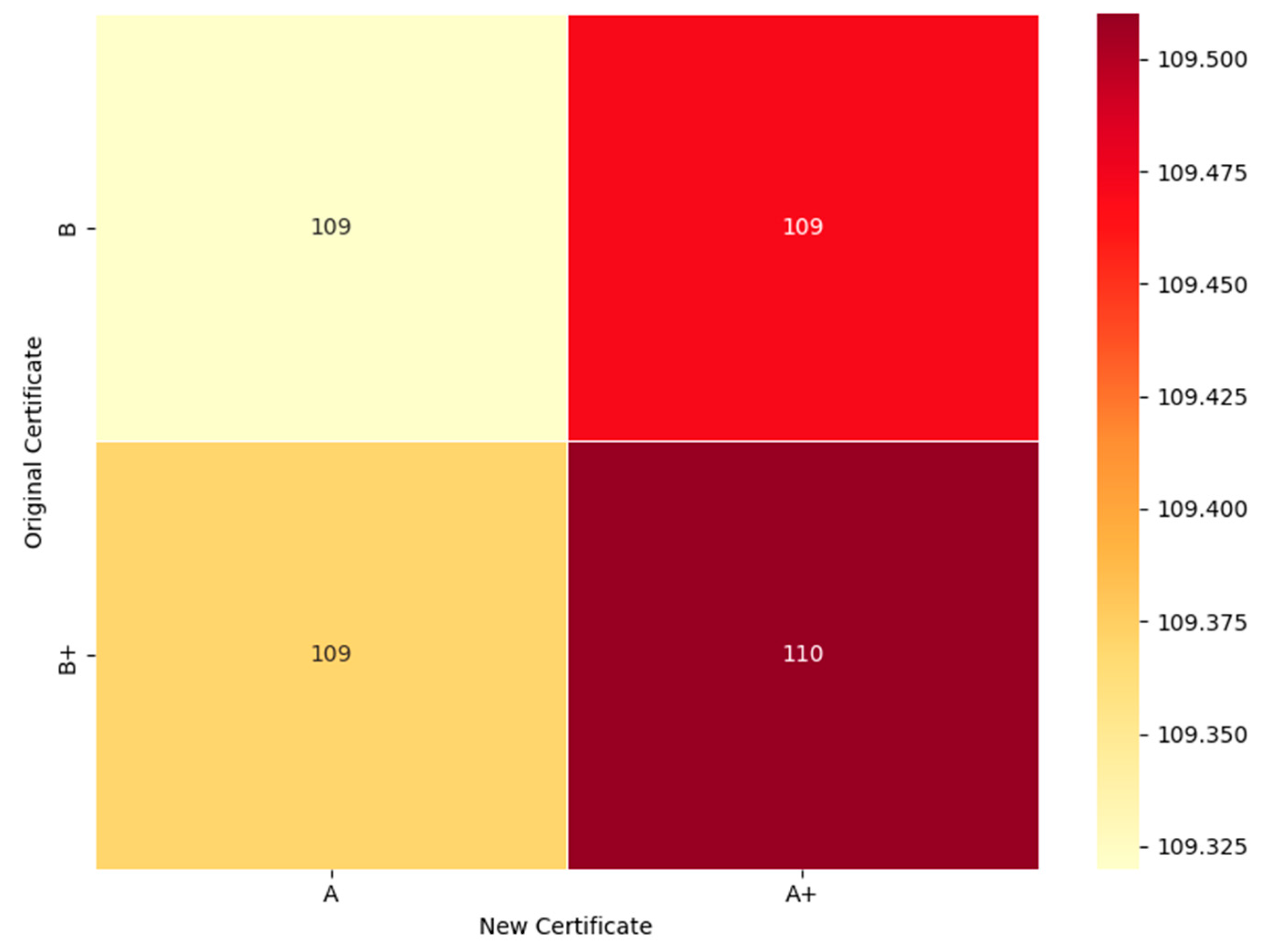
3.2. Parameter Value Changes
3.3. Mathematical Modelling
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ACO | Ant Colony Optimization |
| AGV | Automated Guided Vehicle |
| AI | Artificial Intelligence |
| ANOVA | Analysis of Variance |
| API | Application Programming Interface |
| AutoML | Automated Machine Learning |
| COI | Cube Per Order Index |
| DES | Discrete Event Simulation |
| DRL | Deep Reinforcement Learning |
| DSLAP | Dynamic Storage Location Assignment Problem |
| GA | Genetic Algorithms |
| GBM | Gradient Boosting Machine |
| IoT | Internet of Things |
| IT | Information Technology |
| MAE | Mean Absolute Error |
| MAPE | Mean Absolute Percentage Error |
| ML | Machine Learning |
| MSE | Mean Squared Error |
| OOS | Order Oriented Slotting |
| PDP | Partial Dependence Plot |
| RFID | Radio Frequency Identification |
| RMSE | Root Mean Squared Error |
| RMSLE | Root Mean Squared Logarithmic Error |
| SC | Supply Chain |
| SHAP | SHapley Additive exPlanations |
| SKU | Stock Keeping Unit |
References
- Negi, P.; Pathani, A.; Bhatt, B.C.; Swami, S.; Singh, R.; Gehlot, A.; Thakur, A.K.; Gupta, L.R.; Priyadarshi, N.; Twala, B.; et al. Integration of Industry 4.0 Technologies in Fire and Safety Management. Fire 2024, 7, 335. [Google Scholar] [CrossRef]
- Li, K. Optimizing Warehouse Logistics Scheduling Strategy Using Soft Computing and Advanced Machine Learning Techniques. Soft Comput. 2023, 27, 18077–18092. [Google Scholar] [CrossRef]
- Savaglio, C.; Mazzei, P.; Fortino, G. Edge Intelligence for Industrial IoT: Opportunities and Limitations. Procedia Comput. Sci. 2024, 232, 397–405. [Google Scholar] [CrossRef]
- Hu, Y.; Jia, Q.; Yao, Y.; Lee, Y.; Lee, M.; Wang, C.; Zhou, X.; Xie, R.; Yu, F.R. Industrial Internet of Things Intelligence Empowering Smart Manufacturing: A Literature Review. IEEE Internet Things J. 2024, 11, 19143–19167. [Google Scholar] [CrossRef]
- Hosseini, M.; Chalil Madathil, S.; Khasawneh, M.T. Reinforcement Learning-Based Simulation Optimization for an Integrated Manufacturing-Warehouse System: A Two-Stage Approach. Expert Syst. Appl. 2025, 290, 128259. [Google Scholar] [CrossRef]
- de Koster, R.; Le-Duc, T.; Roodbergen, K.J. Design and Control of Warehouse Order Picking: A Literature Review. Eur. J. Oper. Res. 2007, 182, 481–501. [Google Scholar] [CrossRef]
- Roodbergen, K.J. Layout and Routing Methods for Warehouses, 1st ed.; Erasmus University Rotterdam: Rotterdam, The Netherlands, 2001. [Google Scholar]
- Small Parts Order Picking: Design and Operation. Available online: https://www2.isye.gatech.edu/~mgoetsch/cali/Logistics%20Tutorial/order/article.htm (accessed on 12 August 2025).
- Hausman, W.H.; Schwarz, L.B.; Graves, S.C. Optimal storage assignment in automatic warehousing systems. Manag. Sci. 1976, 22, 629–638. [Google Scholar] [CrossRef]
- Schuur, P.C. The Cube Per Order Index Slotting Strategy, How Bad Can It Be? University of Twente: Enschede, The Netherlands, 2014. [Google Scholar]
- Mantel, R.J.; Schuur, P.C.; Heragu, S.S. Order oriented slotting: A new assignment strategy for warehouses. Eur. J. Ind. Eng. 2007, 1, 301. [Google Scholar] [CrossRef]
- De Koster, M.B.M.; Van der Poort, E.S.; Wolters, M. Efficient orderbatching methods in warehouses. Int. J. Prod. Res. 1999, 37, 1479–1504. [Google Scholar] [CrossRef]
- Tsige, M. Improving Order-Picking Efficiency Via Storage Assignments Strategies. Master’s Thesis, University of Twente, Enschede, The Netherlands, 2013. [Google Scholar]
- Waubert de Puiseau, C.; Nanfack, D.T.; Tercan, H.; Löbbert-Plattfaut, J.; Meisen, T. Dynamic Storage Location Assignment in Warehouses Using Deep Reinforcement Learning. Technologies 2022, 10, 129. [Google Scholar] [CrossRef]
- Seyedan, M.; Mafakheri, F. Predictive big data analytics for supply chain demand forecasting: Methods, applications, and research opportunities. J. Big Data 2020, 7, 53. [Google Scholar] [CrossRef]
- Aamer, A.; Eka Yani, L.; Alan Priyatna, I. Data Analytics in the Supply Chain Management: Review of Machine Learning Applications in Demand Forecasting. Oper. Supply Chain. Manag. Int. J. 2020, 14, 1–13. [Google Scholar] [CrossRef]
- Falatouri, T.; Darbanian, F.; Brandtner, P.; Udokwu, C. Predictive Analytics for Demand Forecasting—A Comparison of SARIMA and LSTM in Retail SCM. Procedia Comput. Sci. 2020, 200, 993–1003. [Google Scholar] [CrossRef]
- Douaioui, K.; Oucheikh, R.; Benmoussa, O.; Mabrouki, C. Machine Learning and Deep Learning Models for Demand Forecasting in Supply Chain Management: A Critical Review. Appl. Syst. Innov. 2024, 7, 93. [Google Scholar] [CrossRef]
- Omprakash, M.K. Optimizing Demand Forecasting and Inventory Management with AI in Automotive Industry. Master’s Thesis, Lappeenranta–Lahti University of Technology LUT, Lappeenranta, Finland, 2024. [Google Scholar]
- Umoren, J.; Utomi, E.; Adukpo, T. AI-powered Predictive Models for U.S. Healthcare Supply Chains: Creating AI Models to Forecast and Optimize Supply Chain. IJMR 2025, 11, 2455–3662. [Google Scholar]
- Srinivas, A. AI-Driven Demand Forecasting in Enterprise Retail Systems: Leveraging Predictive Analytics for Enhanced Supply Chain. Int. J. Sci. Technol. 2025, 16, 1–22. [Google Scholar] [CrossRef]
- Cergibozan, Ç.; Tasan, A.S. Genetic algorithm based approaches to solve the order batching problem and a case study in a distribution center. J. Intell. Manuf. 2022, 33, 137–149. [Google Scholar] [CrossRef]
- Azadnia, A.H.; Taheri, S.; Ghadimi, P.; Mat Saman, M.Z.; Wong, K.Y. Order Batching in Warehouses by Minimizing Total Tardiness: A Hybrid Approach of Weighted Association Rule Mining and Genetic Algorithms. Sci. World J. 2013, 2013, 246578. [Google Scholar] [CrossRef]
- de Koster, R.; van der Poort, E.; Roodbergen, K.J. When to apply optimal or heuristic routing of orderpickers. In Advances in Distribution Logistics, 1st ed.; Fleischmann, B., van Nunen, J.A.E.E., Speranza, M.G., Stähly, P., Eds.; Springer: Berlin, Germany, 1998; Volume 460, pp. 375–401. [Google Scholar] [CrossRef]
- Cano, J.A.; Correa-Espinal, A.A.; Gómez-Montoya, R.A. An Evaluation of Picking Routing Policies to Improve Warehouse Efficiency. Int. J. Ind. Eng. Manag. 2017, 8, 229–238. [Google Scholar] [CrossRef]
- Tufano, A.; Accorsi, R.; Manzini, R. A machine learning approach for predictive warehouse design. Int. J. Adv. Manuf. Technol. 2022, 119, 2369–2392. [Google Scholar] [CrossRef]
- Wang, Y.; Vasan, G.; Mahmood, R. Real-Time Reinforcement Learning for Vision-Based Robotics Utilizing Local and Remote Computers. arXiv 2022, arXiv:2210.02317. [Google Scholar] [CrossRef]
- Peyas, I.S.; Hasan, Z.; Tushar, M.R.R.; Musabbir, A.; Azni, R.M.; Siddique, S. Autonomous Warehouse Robot using Deep Q-Learning; IEEE: Piscataway, NJ, USA, 2022. [Google Scholar] [CrossRef]
- Vinod Chandra, S.S.; Anand, H.S. Nature inspired meta heuristic algorithms for optimization problems. Computing 2022, 104, 251–269. [Google Scholar] [CrossRef]
- Discrete Event Simulation (DES). Available online: https://www.ebsco.com/research-starters/mathematics/discrete-event-simulation-des (accessed on 1 September 2025).
- Georgescu, I. The early days of Monte Carlo methods. Nat. Rev. Phys. 2023, 5, 372. [Google Scholar] [CrossRef]
- Antony, J. Six Sigma for service processes. Bus. Process Manag. J. 2006, 12, 234–248. [Google Scholar] [CrossRef]
- Yao, J.F.; Yang, Y.; Wang, X.C.; Zhang, X.P. Systematic review of digital twin technology and applications. Vis. Comput. Ind. Biomed. 2023, 6, 10. [Google Scholar] [CrossRef]
- Dubey, V.; Kumari, P.; Patel, K.; Singh, S.; Shrivastava, S. Amalgamation of Optimization Algorithms with IoT Applications. In Sustainable Development in Industry and Society 5.0; IGI Global: Hershey, PA, USA, 2024; pp. 176–204. [Google Scholar] [CrossRef]
- Wen, X.; Liao, J.; Niu, Q.; Shen, N.; Bao, Y. Deep learning-driven hybrid model for short-term load forecasting and smart grid information management. Sci. Rep. 2024, 14, 13720. [Google Scholar] [CrossRef]
- Edozie, E.; Shuaibu, A.N.; John, U.K.; Sadiq, B.O. Comprehensive review of recent developments in visual object detection based on deep learning. Artif. Intell. Rev. 2025, 58, 277. [Google Scholar] [CrossRef]
- Ma, C.; Li, A.; Du, Y.; Dong, H.; Yang, Y. Efficient and scalable reinforcement learning for large-scale network control. Nat. Mach. Intell. 2024, 6, 1006–1020. [Google Scholar] [CrossRef]
- Supply Chain Optimization for a FMCG Company. Available online: https://www.kaggle.com/datasets/suraj9727/supply-chain-optimization-for-a-fmcg-company/data (accessed on 20 July 2025).
- He, X.; Zhao, K.; Chu, X. AutoML: A survey of the state-of-the-art. Knowl.-Based Syst. 2021, 212, 106622. [Google Scholar] [CrossRef]
- Bentéjac, C.; Csörgő, A.; Martínez-Muñoz, G. A comparative analysis of gradient boosting algorithms. Artif. Intell. Rev. 2021, 54, 1937–1967. [Google Scholar] [CrossRef]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.-Y. LightGBM: A Highly Efficient Gradient Boosting Decision Tree. In Proceedings of the 30th Conference on Neural Information Processing Systems (NeurIPS 2017), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- LightGBM Documentation. Available online: https://lightgbm.readthedocs.io/en/latest/Features.html# (accessed on 16 August 2025).
- Theng, D.; Bhoyar, K.K. Feature selection techniques for machine learning: A survey of more than two decades of research. Knowl. Inf. Syst. 2024, 66, 1575–1637. [Google Scholar] [CrossRef]
- Rodríguez-Pérez, R.; Bajorath, J. Interpretation of machine learning models using shapley values: Application to compound potency and multi-target activity predictions. J. Comput.-Aided Mol. Des. 2020, 34, 1013–1026. [Google Scholar] [CrossRef]
- Reducing Picker Travel Time: Enhancing Warehouse Efficiency with Automation and Smart Slotting. Available online: https://www.logiwa.com/blog/reducing-picker-travel-time-to-enhance-warehouse-efficiency (accessed on 17 August 2025).
- Transforming Logistics: The Rise of High-Power Warehouses and Smart Energy Systems. Available online: https://blog.intellimeter.com/transforming-logistics-the-rise-of-high-power-warehouse-and-smart-energy-systems (accessed on 17 August 2025).
- Korponai, J.; Bányai, Á.; Illés, B. The Effect of the Safety Stock on the Occurrence Probability of the Stock Shortage. Manag. Prod. Eng. Rev. 2017, 8, 69–77. [Google Scholar] [CrossRef]
- Borodavko, B.; Illés, B.; Bányai, Á. Role of Artificial Intelligence in Supply Chain. Acad. J. Manuf. Eng. 2021, 19, 75–79. [Google Scholar]
- Veres, P. A Comparison of the Black Hole Algorithm against Conventional Training Strategies for Neural Networks. Mathematics 2025, 13, 2416. [Google Scholar] [CrossRef]
- Veres, P. ML and Statistics-Driven Route Planning: Effective Solutions without Maps. Logistics 2025, 9, 124. [Google Scholar] [CrossRef]
- Veres, P. The Opportunities and Possibilities of Artificial Intelligence in Logistic Systems: Principles and Techniques. In Advances in Digital Logistics, Logistics and Sustainability; Tamás, P., Bányai, T., Telek, P., Cservenák, Á., Eds.; CECOL 2024. Lecture Notes in Logistics; Springer: Cham, Switzerland, 2024. [Google Scholar] [CrossRef]



| Approach | Main Focus | Limitations | Novelty |
|---|---|---|---|
| Layout design & distance minimisation [14,15,16,17] | Reduce travel distances of material handling equipment | Static, layout-specific, limited adaptability | Goes beyond static layouts by extracting dynamic patterns from data |
| Slotting strategies (COI, OOS) [18,19] | Product placement based on frequency or co-occurrence | Limited to order relations, ignores other factors | Considers multiple parameters simultaneously via regression |
| Batching & zoning [20,21] | Coordinating small orders, grouping SKUs | Limited overall impact on performance | Broader optimisation perspective using data-driven models |
| Metaheuristics (GA, hybrid models) [30,31] | Optimising picking and batching routes | High computational cost, less interpretable | Our approach emphasizes interpretability and cost functions |
| Routing heuristics (S-shape, Largest Gap, etc.) [32,33] | Picker route optimisation | Simplistic, not globally optimal | Proposes mathematical functions derived from ML for optimisation |
| Robotics + AI (RL, DL) [35,36] | Automation and real-time control | Requires heavy investment, complex integration | Provides a lightweight, interpretable alternative for optimisation |
| This research | Pattern recognition via regression models (AutoML + LightGBM) | Needs validation on real data, causality not guaranteed | Transforms regression from prediction to pattern extraction, formulating an optimisation-oriented, interpretable objective function |
| Model | MAE | MSE | RMSE | R2 | RMSLE | MAPE | |
|---|---|---|---|---|---|---|---|
| lightgbm | Light Gradient Boosting Machine | 678.8557 | 839,779.1779 | 916.0946 | 0.9938 | 0.0801 | 0.0438 |
| gbr | Gradient Boosting Regressor | 695.8355 | 869,759.6419 | 932.2677 | 0.9935 | 0.0837 | 0.0456 |
| rf | Random Forest Regressor | 712.245 | 934,943.3382 | 966.6337 | 0.9931 | 0.0834 | 0.0459 |
| xgboost | Extreme Gradient Boosting | 713.7591 | 937,255.2687 | 967.598 | 0.993 | 0.0876 | 0.0469 |
| et | Extra Trees Regressor | 730.8405 | 1,013,394.922 | 1006.1808 | 0.9925 | 0.0859 | 0.0469 |
| ridge | Ridge Regression | 884.6469 | 1,309,630.251 | 1144.0836 | 0.9903 | 0.1092 | 0.0611 |
| llar | Lasso Least Angle Regression | 883.8248 | 1,309,304.182 | 1143.9377 | 0.9903 | 0.1087 | 0.0609 |
| br | Bayesian Ridge | 884.6194 | 1,309,632.473 | 1144.0844 | 0.9903 | 0.1091 | 0.0611 |
| lasso | Lasso Regression | 884.0397 | 1,309,316.367 | 1143.9438 | 0.9903 | 0.1089 | 0.061 |
| lr | Linear Regression | 884.7628 | 1,309,630.904 | 1144.0847 | 0.9903 | 0.1093 | 0.0612 |
| dt | Decision Tree Regressor | 882.6388 | 1,773,604.005 | 1331.0611 | 0.9868 | 0.1127 | 0.056 |
| en | Elastic Net | 1152.8724 | 2,577,668.8 | 1604.7077 | 0.9809 | 0.2473 | 0.0773 |
| ada | AdaBoost Regressor | 1413.0806 | 3,132,509.587 | 1769.5949 | 0.9768 | 0.1617 | 0.1072 |
| huber | Huber Regressor | 1264.9622 | 3,142,596.727 | 1767.4949 | 0.9767 | 0.4595 | 0.0853 |
| omp | Orthogonal Matching Pursuit | 1353.6249 | 3,421,633.209 | 1849.2622 | 0.9746 | 0.3484 | 0.0895 |
| par | Passive Aggressive Regressor | 1587.6008 | 4,461,971.235 | 2078.8567 | 0.9668 | 0.3997 | 0.1086 |
| knn | K Neighbors Regressor | 6103.7732 | 60,215,414.01 | 7759.333 | 0.5534 | 0.4724 | 0.459 |
| dummy | Dummy Regressor | 9576.893 | 134,923,670.3 | 11,615.2979 | −0.0008 | 0.6743 | 0.7883 |
| lar | Least Angle Regression | 91,640.5912 | 1.116 × 1015 | 133,455.673 | −860.208 | 0.8561 | 6.2092 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Francuz, Á.; Bányai, T. Intelligent Control Approaches for Warehouse Performance Optimisation in Industry 4.0 Using Machine Learning. Future Internet 2025, 17, 468. https://doi.org/10.3390/fi17100468
Francuz Á, Bányai T. Intelligent Control Approaches for Warehouse Performance Optimisation in Industry 4.0 Using Machine Learning. Future Internet. 2025; 17(10):468. https://doi.org/10.3390/fi17100468
Chicago/Turabian StyleFrancuz, Ádám, and Tamás Bányai. 2025. "Intelligent Control Approaches for Warehouse Performance Optimisation in Industry 4.0 Using Machine Learning" Future Internet 17, no. 10: 468. https://doi.org/10.3390/fi17100468
APA StyleFrancuz, Á., & Bányai, T. (2025). Intelligent Control Approaches for Warehouse Performance Optimisation in Industry 4.0 Using Machine Learning. Future Internet, 17(10), 468. https://doi.org/10.3390/fi17100468








