Abstract
In this paper, we propose a fuzzy formulation of the classic Frankot–Chellappa algorithm by which surfaces can be reconstructed using normal vectors. In the fuzzy formulation, the surface normal vectors may be uncertain or ambiguous, yielding a fuzzy Poisson partial differential equation that requires appropriate definitions of fuzzy derivatives. The solution of the resulting fuzzy model is approached by adopting a fuzzy variant of the discrete sine transform, which results in a fast and robust algorithm for surface reconstruction. An adaptive defuzzification strategy is also introduced to improve noise handling in highly uncertain regions. In experiments, we demonstrate that our fuzzy Frankot–Chellappa algorithm achieves accuracy on par with the classic approach for smooth surfaces and offers improved robustness in the presence of noisy normal data. We also show that it can naturally handle missing data (such as gaps) in the normal field by filling them using neighboring information.
1. Introduction
The integration of surface normals to recover the corresponding surface in 3D space is a classic problem in computer vision [1,2,3]. Many methods have been proposed with the aim of achieving high accuracy, robustness to noise in the data, and computational efficiency; see, e.g., refs. [4,5,6,7] as well as the survey paper [8]. Even today, it remains challenging to devise a method that simultaneously meets all these criteria.
In terms of computational efficiency, the classic algorithm of Frankot and Chellappa [5] is still among the most powerful. It relies on solving a Poisson equation that arises naturally in the formulation of surface integration via a discrete sine transform. However, the Frankot–Chellappa (FC) algorithm does not explicitly handle noisy data, and accuracy issues may arise in the vicinity of steep surface gradients. Furthermore, the use of a discrete sine transform constrains the method to rectangular domains with complete data, making it challenging to deal with missing data in the normal field using the classic approach directly.
Recent advancements in surface reconstruction have focused on improving robustness and uncertainty quantification. Sellán and Jacobson [9] introduced Stochastic Poisson Surface Reconstruction, which models the reconstructed surface as a Gaussian process, enabling statistical reasoning about reconstruction uncertainty. Hou et al. [10] proposed iterative Poisson surface reconstruction, which refines surface orientation iteratively. More recently, Yu et al. [11] introduced Gaussian Opacity Fields—a method for direct surface and normal extraction from Gaussian splats, showing strong performance in unbounded scenes compared to classical Poisson methods. In general, unlike stochastic approaches such as Stochastic Poisson Surface Reconstruction, which rely on Gaussian processes to capture uncertainty, our method introduces fuzziness directly at the level of gradient fields. This enables uncertainty modeling without requiring probabilistic assumptions and integrates naturally with classical Poisson solvers via fuzzy arithmetic.
The concept of a fuzzy transform was introduced by I. Perfilieva et al. in [12,13] and was applied in image processing by Y. Nie et al. in [14]. The fuzzy transform (F-transform) provides direct and inverse operations that allow one to approximate a function using fuzzy basis functions. The authors of [13] showed that the inverse F-transform has good approximation properties and is relatively easy to use, even in the presence of noise. Meanwhile, fuzzy partial differential Equations (PDEs) were studied for problems like the Poisson equation in [15,16,17]. In particular, in 2018, Ghasemi Moghaddam et al. discussed a fuzzy Poisson equation with Dirichlet boundary conditions, proving the uniqueness and stability of its solution in [17], and a continuous fuzzy Fourier sine transform was applied to solve a fuzzy wave equation in [18].
We explored for the first time a fuzzified formulation of the discrete sine transform method and used it to solve the Poisson equation with fuzzy boundary conditions in [19]. Fuzzy logic provides a means to represent and process imprecise or uncertain information, which in the context of surface integration can arise from measurement noise or ambiguity in the normal data. By leveraging fuzzy concepts, the integration process can accommodate these uncertainties, potentially yielding more robust results. Here, we extend upon the previous method by providing more extensive experiments. Also, we include developments that further refine that approach by introducing a multiplicative fuzzification of input normals and an adaptive defuzzification strategy that dynamically adjusts reconstruction weights based on local uncertainty. Unlike a fixed defuzzification scheme, this method adjusts how the fuzzy solution is resolved to a crisp surface depending on the spread at each pixel.
We showed that this enhanced fuzzy FC method maintains the computational efficiency of the classical algorithm while improving noise resilience. This adaptive algorithm models the uncertainty of each pixel more accurately: in regions with low uncertainty (small fuzzy spread), it trusts the central value, whereas in regions with higher uncertainty, it incorporates more information from the range of possible values.
A distinctive contribution of this paper is the introduction of the fuzzy F-transform as a preprocessing mechanism for surface reconstruction with missing data. This is the first application of the F-transform to address the problem of gap reconstruction in surface normal integration. In contrast to classical methods like the FC scheme, which process input data uniformly and do not provide a framework to adapt to missing or uncertain regions, our approach uses the fuzzy F-transform to both smooth the gradient field and implicitly detect unreliable zones through attenuated membership values. This enables adaptive Poisson solving, where missing regions are reconstructed smoothly using information from neighboring confident areas, without the need for explicit boundary definitions or gap localization. As a result, our fuzzy FC algorithm (Algorithm 1) framework naturally produces coherent reconstructions, even under noisy or incomplete input.
Key contributions of this work include the following: (1) defining fuzzy-valued normal vectors and fuzzy partial derivatives in the context of surface integration; (2) demonstrating that solving the Poisson equation in the fuzzy domain yields a family of solutions that encompasses the classical solution as the central value, thereby not losing accuracy; (3) leveraging the fuzzy transform to filter out high-frequency noise during integration; and (4) providing a strategy to handle missing data (gaps) by treating unknown normals as fuzzy and letting the solution naturally interpolate those regions.
2. Fuzzy Concepts
In our framework, uncertainty in a value is represented using fuzzy numbers. A fuzzy number is typically described by its membership function , which maps each real number x to a value in indicating its degree of membership. We now recall a list of notations and several theoretical concepts useful in this paper. More information on related fuzzy concepts can be found in [20] and the references therein.
Definition 1
(Fuzzy set and -cut). A fuzzy set in is characterized by a membership function :. For , the α-cut of is defined as
Definition 2
(Triangular fuzzy number). A fuzzy number is defined as a fuzzy subset of the real numbers with a normalized, convex, and upper semi-continuous membership function : such that the support of is bounded and there exists exactly one point with membership degree 1.
In this work, we use triangular fuzzy numbers (TFNs). A triangular fuzzy number is defined by a triplet , with , where is the peak (core) and is the support.
Definition 3
(gH difference). Let be fuzzy numbers. Then the generalized Hukuhara difference is a fuzzy number such that one of the following holds:
where is defined as the symmetric of with respect to 0, i.e., if is a triangular fuzzy number (TFN), then .
Definition 4
(Fuzzy-valued function). Let be a fuzzy-valued function defined on a compact rectangular domain , where is the set of fuzzy numbers on , and denote the spatial coordinates. For each and , the function can be expressed in terms of α-cuts:
At each point , the output is a triangular fuzzy number (TFN) represented by the triple , where is the peak (core) and is the support.
Hence, the membership function of the output fuzzy number is defined as
Definition 5
(Fuzzy partial derivative using gH difference). Let be a fuzzy-valued function defined over domain D, where denotes the set of fuzzy numbers. The partial derivative of f with respect to u at the point is defined using the generalized Hukuhara (gH) difference as follows:
provided that this limit exists. Similarly, the partial derivative with respect to v is defined as
This definition generalizes the classical derivative to the fuzzy domain by replacing the usual difference with the gH difference. The result is a fuzzy number representing the derivative at a point.
Definition 6
(Defuzzification). In order to compare fuzzy-valued outputs with crisp ground-truth data or to visualize numerical results, it is necessary to convert fuzzy numbers into real numbers through defuzzification.
In this work, we use the midpoint method based on the support of the triangular fuzzy number (TFN). Given a fuzzy value with lower bound and upper bound (at ), the defuzzified (crisp) value is computed as
This corresponds to the centroid of the base of the TFN and coincides with the core value in the case of symmetric fuzzy numbers. This defuzzification strategy is consistently applied throughout our method to obtain final numerical surfaces from fuzzy results.
Additionally, an adaptive defuzzification strategy is proposed in Section 5.2 to improve performance under data-dependent uncertainty.
Definition 7
(Fuzzy partition). A fuzzy partition of an interval is a collection of fuzzy sets with membership functions that satisfy the following conditions:
- 1.
- , with for some ;
- 2.
- if , where ;
- 3.
- is continuous on ;
- 4.
- is strictly increasing on and strictly decreasing on ;
- 5.
- for all .
In an h-uniform fuzzy partition, the centers are equally spaced with step size . The membership functions are usually symmetric triangular functions and are often referred to as basic functions of the partition. These form the foundation for defining the fuzzy transform.
F-transform: The fuzzy transform (F-transform) is a technique to approximate a real-valued function using a fuzzy partition. It consists of the following: (i) a direct transform that computes fuzzy coefficients from data, and (ii) an inverse transform that reconstructs a smooth approximation from those coefficients.
Given a set of points and fuzzy sets forming a fuzzy partition, the discrete F-transform of f is the vector defined as
Each approximates the local average behavior of f around . The inverse transform reconstructs f as
This smooths out high-frequency components of f, effectively acting as a low-pass filter.
In two dimensions, let be defined on a grid , and let and be fuzzy partitions of and , respectively. The 2D F-transform is defined as
where and are membership functions. The inverse F-transform reconstructs the approximation:
Explicit properties of the F-transform [13] are as follows:
- Low-pass filtering: The F-transform acts as a low-pass filter. It suppresses high-frequency components (e.g., noise), retaining only the smooth trend of the original function.
- Local averaging: Each component of the F-transform represents a local average of the original function with respect to the support of a fuzzy basis function. This averaging provides noise resilience and locality.
- Smoothing and approximation: The inverse F-transform yields a smooth and continuous approximation of the original function. It effectively reconstructs the global behavior while suppressing irregularities.
- Stability to noise: The discrete version of the F-transform is stable under noisy input. As proven in [13], the method preserves signal similarity even under perturbations.
In fact, they proved that the inverse F-transform acts as filter: applying the F-transform and then the inverse F-transform to a noisy function yields a result almost free from that noise (provided the noise has negligible F-transform components). We leverage this filtering property in our fuzzy integration method when dealing with noisy data.
In particular, if the noise present in the data varies at a frequency higher than the scale of the fuzzy membership functions, that is, if it changes faster than the granularity of the fuzzy partition, then its contribution to the F-transform coefficients becomes negligible. Consequently, such noise will be largely suppressed during the reconstruction via the inverse F-transform, as the fuzzy basis functions act as a natural low-pass filter that emphasizes only the smooth, low-frequency components of the data.
3. Classic Frankot–Chellappa Surface Normal Integration
Let us briefly recall the classic Frankot–Chellappa method [5].
Given a normal field defined on domain (with ), we seek a surface such that is orthogonal to surface at each point. Equivalently,
In practice, the observed may not be exactly integrable (i.e., there may not exist a single-valued z whose gradient is g everywhere) due to noise or discretization. The Frankot–Chellappa solution is to find a function that minimizes the distance between and g in a least-squares sense:
The optimality condition for this minimization is the Poisson equation
with Dirichlet boundary conditions . Here, denotes the boundary of the computational domain . For instance, if , then consists of all points where either , , , or . The Dirichlet boundary condition on ensures compatibility with the discrete sine transform (sT), which implicitly assumes zero values at the domain boundaries. The right-hand side is the divergence of the gradient estimate.
We discretize the domain into an uniform grid with step sizes h. The continuous coordinates are given by , , where and .
For simplicity and without loss of generality, we assume a uniform square grid where the step sizes in both directions are equal also, that is, . To solve this numerically, one applies a 5-point finite difference stencil on a uniform grid of spacing h:
where the right-hand side is approximated using central differences:
Frankot and Chellappa observed that this discrete Poisson problem with zero Dirichlet boundary conditions can be efficiently solved via the sT. Let and denote the sT coefficients of and , respectively. Then
for and . The final surface is then recovered by applying the inverse sT.
Summary of the classical FC algorithm:
- Compute and from the normal field.
- Evaluate using finite differences.
- Apply the forward sT to f to obtain .
- Use the analytical solution in the frequency domain to compute .
- Apply the inverse sT to reconstruct .
This classical FC approach serves as the foundation for our fuzzy-enhanced integration method introduced in Section 4.
It is important to note that surface reconstruction from normal vectors is generally determined only up to an additive constant. This is because the gradient field corresponds to infinitely many surfaces differing by a constant vertical shift. In the classical formulation, this ambiguity is resolved by imposing Dirichlet boundary conditions (e.g., on the boundary ), which uniquely fix the reconstructed surface. In our fuzzy extension, we adopt the same boundary conditions.
4. Fuzzy Frankot–Chellappa Surface Normal Integration
We extend the classical Frankot–Chellappa (FC) surface normal integration method into a fuzzy framework by incorporating uncertainty into the surface normals and gradient fields using triangular fuzzy numbers (TFNs). This leads to a fuzzy Poisson equation, where the derivatives are defined in the gH-differentiability sense and solved using a discrete fuzzy finite difference scheme.
Let the fuzzy surface be denoted by and the divergence of the fuzzy gradient field be .
4.1. Fuzzy Discretization of Poisson Equation
Let be the unknown fuzzy-valued function to be determined and be a given fuzzy-valued source function:
We discretize the domain using a uniform grid of size with step size h, following the formulation presented by Abdi and Allahviranloo [17], the Fuzzy Poisson equation takes the form:
Then
The right-hand side is computed using central fuzzy differences:
4.2. Fuzzy Frankot–Chellappa Method
In the fuzzy domain, the surface reconstruction is governed by a fuzzy Poisson equation with Dirichlet boundary conditions, where the fuzzy gradient field is derived from uncertain normal vectors. The fuzzy Laplacian is discretized using the fuzzy finite difference scheme, and the solution is computed using a fuzzy variant of the discrete sine transform. The main novelty of this approach lies in the fact that it is applying the discrete fuzzy sine transform directly to obtain the solution of a fuzzy Poisson equation. We use the fuzzy inverse discrete sine transformation
and :
First we solve it only with a homogeneous Dirichlet condition for , where , in order to later determine the solution for problems with an inhomogeneous Dirichlet boundary conditions using the knowledge gained.
We assume Dirichlet boundary conditions (e.g., on ) for the fuzzy Poisson equation, as in the classic case. We seek a fuzzy solution satisfying , where is the fuzzy divergence of the fuzzy normal field. To solve this numerically, we follow a similar approach to the classical algorithm but operate on the fuzzy quantities.
First, we compute the discrete fuzzy Laplace equation analogous to Equation (9) by replacing z and f with and and using difference for subtraction in Equation (9). The resulting Equation (at each -cut) has the form
We again insert the inverse transform from (10) into the discrete Formula (11), leaving h undetermined:
Since the sine functions form an independent linear family, we can claim that the coefficients in the above equation are zero; in addition, we know .
All fuzzy operations, including addition, subtraction, multiplication, and division, are performed componentwise on each -cut representation of the fuzzy numbers. As a result, the mathematical manipulations reduce to interval arithmetic at each -level, avoiding the need for explicit definitions of fuzzy multiplication and division. This -cut approach guarantees that all transformations remain consistent with the properties of fuzzy numbers and ensures that the algorithm proceeds in a rigorous and computationally efficient manner. Then, we have
so
is obtained. If i and k are not in and j and l are not elements of , then can be reduced, with which we can obtain
then
where and are the discrete fuzzy sine transform of and and
This relation is applied to the fuzzy coefficients. The fuzzy surface is then obtained by inverse FsT:
Finally, we defuzzify by taking as described in Section 2.
| Algorithm 1: Fuzzy FC algorithm. |
Input: Normal map details Output: Defuzzified surface
|
4.3. Adaptive Strategy and Parameter Selection Strategy
Unlike the additive noise modeling in [8], we also introduce uncertainty in the gradient fields by scaling the perturbation relative to the magnitude of the gradient. For each pixel , we construct a fuzzy gradient as a symmetric triangular fuzzy number:
The scaling factor is selected based on the estimated noise level, allowing the fuzzification process to adaptively reflect the local uncertainty in the gradients.
In contrast to [8], where fixed averaging of fuzzy bounds used (i.e., ), here we introduce a context-aware defuzzification that dynamically adjusts weights depending on the local spread of the fuzzy surface solution. The defuzzified result is
where weights are dynamically determined by the local spread , with thresholds and defined as functions of the noise level.
This dual improvement leads to a fuzzy integration method that is more responsive to local variations and noise characteristics in the input data.
The adaptive defuzzification strategy employs threshold parameters and , where is the estimated noise level, and are tunable constants.
In this study, we determined these parameters empirically through grid search experiments over a validation set consisting of synthetic benchmark surfaces. The goal was to identify values that minimize RMSE while maintaining consistent performance across varying noise intensities. Note that using the noise level directly as a threshold (e.g., ) is not suitable due to differences in scale between the normalized noise metric and the actual spread in the fuzzy output. Therefore, we define adaptive thresholds as affine functions of , incorporating a base level a and a sensitivity coefficient , allowing better alignment with the expected range of spread values across different datasets and noise intensities.
5. Experimental Results
In this section, we investigate our basic method along with the adaptive version using several test surfaces and compare it to the classical method. We consider two main scenarios: (1) uncertain but noise-free normals (to test accuracy), and (2) normals with added noise (to test noise suppression). Additionally, we demonstrate the method’s ability to handle missing normal data.
We use several representative surfaces in our experiments. These surfaces exhibit a variety of smooth and sharp features. Each surface is sampled on a grid over the domain . The true surface height is known analytically for each case, so we can compute the exact normals and hence the ground-truth solution for integration.
Input description and normal field construction: In our experiments, the input to the reconstruction algorithm is a normal vector field , derived analytically from synthetic ground-truth surfaces shown in Figure 1.
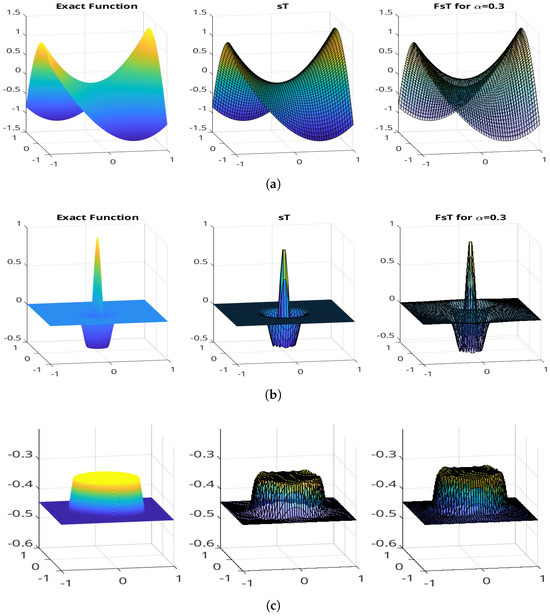
Figure 1.
(a–c) are for comparison of exact functions and and , discrete sine transformation approximation in classic FC method (sT), and -cut components of the fuzzy sine discrete transformation approximation (FsT) in fuzzified FC method, with for .
To compute the gradients required by the FC method, we extract the partial derivatives:
These gradient fields serve as the primary inputs to both the classical and the fuzzy FC reconstruction processes.
For experiments with noise, Gaussian perturbations are applied directly to p and q. For fuzzy experiments, these perturbed gradients are encoded as symmetric triangular fuzzy numbers, and , to model uncertainty.
Error reduction strategy evaluation: Here, to assess the performance of the proposed algorithm on surface reconstruction tasks, the following steps are undertaken:
- Ground-truth reconstruction: The original surface is computed.
- Clean reconstructions: Both the classical FC and fuzzified FC methods are used to reconstruct the surface from noise-free data.
- Noisy reconstructions: Reconstructions are performed for selected noise levels.
- RMSE analysis: RMSE values are computed using different noise levels for both classical FC and fuzzified FC methods.
To further highlight some advantages of the fuzzified approach, controlled noise was introduced into the normal vectors, thereby perturbing the computed gradients. We obtained 3D surface reconstructions using both the classical FC and fuzzy FC methods. In all cases, the fuzzy approach produces smoother reconstructions.
In this work, the noise level models the degree of uncertainty or perturbation introduced into the normal vector field due to measurement errors or external disturbances. Specifically, we assume the presence of Gaussian noise in the normal gradients, meaning that the observed noisy gradients are modeled as
where and are independent zero-mean Gaussian noise components:
The noise level, denoted as , is then defined as the ratio of the standard deviation of the noise to the maximum magnitude of the true gradient field:
This relative measure ensures that the noise intensity is expressed proportionally to the inherent scale of the gradients, making it invariant to absolute magnitudes.
Furthermore, in our fuzzified formulation, the spread of the fuzzy numbers and is dynamically adapted based on the estimated noise level.
5.1. Impact of Symmetric Perturbations
At first, we considered as in [11] that the modifications applied to the input data are symmetric around the original value. Consequently, the weighted average (which ultimately yields the fuzzy output) closely approximates the original value.
Our experiments are outlined as follows:
- Fuzzy perturbation of gradient data: In the simple implementation considered [11], the gradient data were perturbed to form three sets:representing a symmetric triangular fuzzy number characterized by the triplet . The same formulation applies to .
- Comparison of classical and fuzzified methods: To evaluate the accuracy of the classical and fuzzified solutions, we computed their deviation from the exact solution. For every , where , the root mean square error (RMSE) of was calculated. The classical solution was obtained using a sine discrete transform, whereas the defuzzified solution, denoted as , was derived using a fuzzy sine discrete transform.
- Defuzzification method: The defuzzification method used was assuming , , and in Equation (13).
Table 1 presents a comparison between the exact function and in Figure 1, the discrete sine transform approximation, and the fuzzy discrete sine transform approximation for several surfaces:

Table 1.
Comparison of classical and fuzzy FC methods: = and = .
The reconstruction is carried out under homogeneous Dirichlet boundary conditions, and we center the reconstructed surface by subtracting the mean height, if needed, to align it visually with the reference. This ensures fair visual and quantitative comparison despite the mismatch in boundary conditions.
Figure 1 illustrates 3D surface reconstructions obtained using the fuzzy FC method, which is better at suppressing noise than classic FC methods, as we can see their difference between errors. If the noise were of even higher frequency (or if we increased the fuzziness level to aggressively filter out more detail), the advantage of the fuzzy approach would likely become even more pronounced. Conversely, if the noise were very low frequency, both methods would reconstruct it similarly. Our results here focus on demonstrating that the fuzzy approach does no harm to the solution (the accuracy remains essentially the same for clean data).
5.2. Adaptive Fuzzification and Defuzzification Strategy
Modified fuzzification strategy: Here, we use a multiplicative fuzzification scheme in which the width of the fuzzy support is proportional to the magnitude of the value itself. The gradient data were perturbed to form three sets:
representing a symmetric triangular fuzzy number characterized by the triplet . The same formulation applies to . The fuzzification parameters control the spread of uncertainty around each gradient value. Larger values of introduce more fuzziness, improving robustness against noise but potentially oversmoothing the surface. In our experiments, we empirically found that yields a good trade-off between accuracy and stability. An adaptive selection of based on local gradient magnitude could be an interesting future direction. This approach enables adaptive uncertainty modeling: smaller values yield narrower fuzzy intervals, while larger values admit proportionally larger uncertainty ranges. This proportional fuzzification better reflects relative uncertainty in signals such as gradients and normals.
The adaptive defuzzification approach: To enhance robustness against noise, we adopt an adaptive approach in which the final reconstruction is calculated using Equation (13). The defuzzified value is determined by weighting the fuzzy bounds, with weights selected based on the local uncertainty (i.e., the spread of the fuzzy estimate).
To dynamically adjust these weights in response to noise, we define two adaptive thresholds and as functions of the noise standard deviation :
The constants are empirically set to control how sensitive the threshold values are to increasing noise. This formulation ensures that as the noise level rises, the thresholds increase accordingly, allowing the algorithm to adapt to greater uncertainty in the input data.
In this study, the variable noise level reflects the standard deviation of the Gaussian noise added to the gradient measurements. This noise level directly informs how the weights are computed in the defuzzification phase, ensuring a more reliable reconstruction.
The adaptive defuzzification is applied in three different regimes based on the magnitude of the local fuzzy spread:
- Low uncertainty (): The fuzzy number center is considered as the defuzzified values of the surface points:
- Moderate uncertainty (): A weighted sum of the lower, center, and upper fuzzy bounds is considered as the defuzzified values of the surface points:
- High uncertainty (): The weights of the two edges are halved because they are no longer trusted. The system prefers to rely more on the central z value, because that point is likely to be the closest representative of reality:
This adaptive scheme ensures that the combination of fuzzy outputs is guided by the level of local uncertainty. In areas with high noise or data gaps, the method compensates by adjusting weights to incorporate a broader contribution from the fuzzy bounds, thus maintaining a more stable and realistic reconstruction.
Table 2 presents a comparison of the exact function, the discrete sine transform approximation, and the fuzzy discrete sine transform approximation for several surfaces using the following new strategy: , , . As shown, the values and differ, with the new fuzzy approach resulting in a reduced error.

Table 2.
Comparison of classical and fuzzified FC methods: and .
To further demonstrate the advantages of the fuzzified approach, controlled noise is added to the normal vectors, thereby perturbing the computed gradients. Figure 2 illustrates 3D surface reconstructions obtained using the new fuzzified FC methods on ground truths. In each case, the fuzzified method yields smoother reconstructions with improved noise suppression.
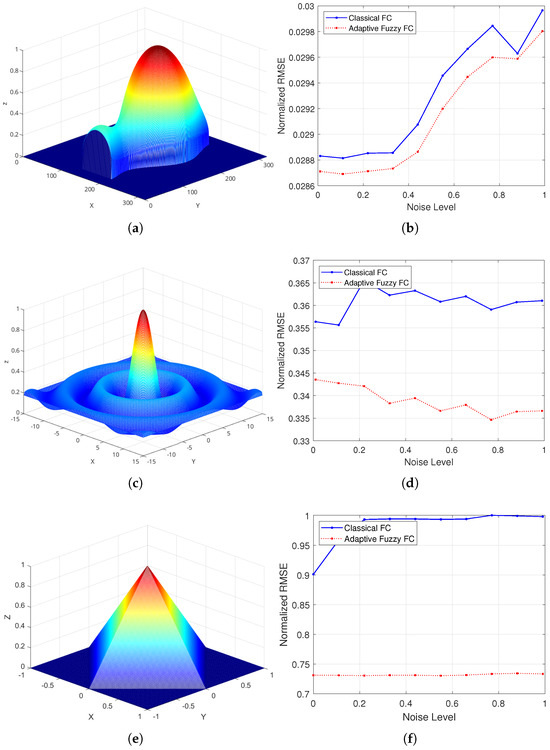
Figure 2.
Ground truth dataset and the RMSEs depending on the noise level increase. (a) Ground-truth surface of the vase model; (b) RMSE comparison of classical FC vs. fuzzified FC methods for the vase model under increasing noise levels; (c) Ground-truth surface of the sombrero model; (d) RMSE comparison of classical FC vs. fuzzified FC methods for the sombrero model under increasing noise levels; (e) Ground-truth surface of the pyramid model; (f) RMSE comparison of classical FC vs. fuzzified FC methods for the pyramid model under increasing noise levels.
Table 3 presents a comparison of the previous fuzzified formulation of FC in [19] and the new strategy as the fuzzy FC method for , , and surfaces. As shown, the values and differ, with the new fuzzy approach resulting in a reduced error.

Table 3.
Comparison of previous and new fuzzy FC method.
5.3. Comparison in Terms of Gap Reconstruction
Another advantage of fuzzy integration is its ability to handle missing data (gaps in the normal field) in a principled way. In classic integration, if some region has no valid normals, one must fill in those normals by interpolation or simply leave that area unreconstructed. In our fuzzy approach, we can interpret missing normals mathematically as extremely uncertain values and let the algorithm naturally fill in the gaps using neighboring information.
To simulate a gap, we removed the normals in a square region on each test surface. We then attempted to reconstruct the surface despite this missing data. In the fuzzy method, when computing differences in the discrete Poisson equation, we used the nearest available normals for the missing points. For example, if is inside the gap, we replaced with (the closest known neighbor in the i-direction) and with for the difference formula. In effect, this assumes the gradient in the gap is similar to the gradient just outside the gap, which is a reasonable assumption for a smooth surface.
Then in Equation (9) needs to be modified for points at the boundary of the gap: if is just inside the gap, then one of its neighbors is missing. We handled this by using a one-sided difference: e.g., if is missing, we use twice (essentially skipping the missing point, which is equivalent to taking a larger step of ). Concretely, we derived
for points where or are missing, so we used , which are just outside the gap. This essentially uses the nearest known data to approximate the derivative across the gap boundary.
Using these adjustments, we solved for as usual. What this achieves is a continuation of the surface into the gap. In other words, the gap is filled in a membrane-like or smoothest possible way, constrained by the boundary of the gap. This approach is analogous to classic hole-filling techniques (like treating it as a Dirichlet interior problem), but here it arose naturally by extending the fuzzy method.
Figure 3 shows the results of gap filling for two example surfaces. In each case, we display the ground-truth surface (with a visible hole where data is missing) and the reconstruction by using Equation (14) in the fuzzy FC method. We see that the fuzzy method successfully reconstructed the shape through the missing region; it yields a smooth fill consistent with surrounding slopes.
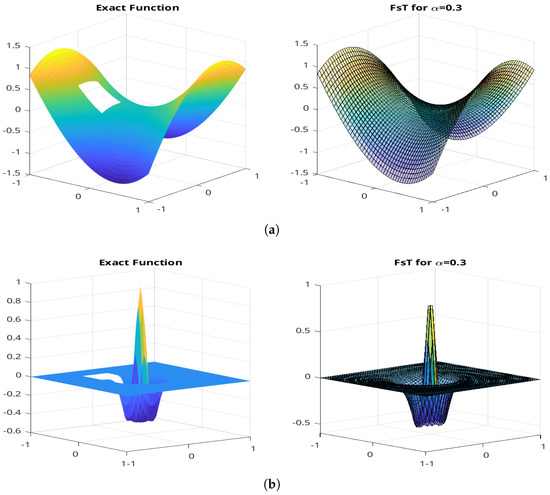
Figure 3.
Reconstructing surfaces with areas containing unknown normal vectors. (a) Left: Ground-truth surface with a visible gap (missing data region) for ; Right: Reconstruction using the fuzzy FC method, demonstrating smooth and coherent gap-filling based on neighboring slope information for ; (b) Left: Ground-truth surface with a visible gap (missing data region) for ; Right: Reconstruction using the fuzzy FC method, demonstrating smooth and coherent gap-filling based on neighboring slope information for ;
Additional clarification on gap filling: Unlike classical discrete methods such as the original Frankot–Chellappa algorithm, which process input data uniformly without awareness of missing regions, the proposed fuzzy extension inherently handles data gaps. Through the fuzzification stage, regions with missing or highly uncertain data naturally receive very low membership values, effectively reducing their influence in the F-transform computation. A simple thresholding strategy on the fuzzy membership map allows explicit identification of gap regions, enabling selective application of specialized reconstruction formulas in those areas. As a result, during surface reconstruction, gaps are treated adaptively without requiring external boundary condition definitions. Consequently, hole filling emerges from the fuzzy framework, producing smoother and more coherent reconstructions even in the presence of incomplete or noisy input data.
Role of the F-transform: The F-transform is not a reconstruction method, but it plays a critical preparatory role in the surface reconstruction pipeline. Its main contribution lies in the preprocessing stage and regularizing the input normal field before applying the fuzzy Frankot–Chellappa reconstruction step.
- Smoothing and noise reduction real: The F-transform, applied to the fuzzified gradient data, acts as a low-pass filter. This attenuates rapid variations (such as noise) while preserving the underlying shape characteristics. As a result, the gradient field fed into the Poisson solver becomes more regular, which improves the stability and accuracy of the reconstruction.
- Implicit gap identification: In addition to denoising, the F-transform naturally identifies unreliable regions. During the fuzzification step, input points with low confidence (due to occlusion, missing data, or inconsistency) receive reduced fuzzy membership. The resulting fuzzy coefficients in these areas become negligible. This behavior allows for implicit detection of gaps in the data without explicit labeling or manual segmentation.
- Enabling adaptive Poisson solving: The output of the F-transform is passed to the fuzzy Poisson solver. Regions with confident data retain their structure, while uncertain areas can be handled selectively, either by omission or by applying special gap-filling formulas. Thus, the F-transform prepares the problem domain for adaptive treatment in the reconstruction phase.
As a result, the F-transform acts as a smoothing, filtering, and data-awareness mechanism prior to fuzzy Poisson reconstruction. Its integration is essential to ensure robustness in noisy or incomplete settings and enables the subsequent fuzzified Frankot–Chellappa method to operate more reliably, as we can see in Figure 4.
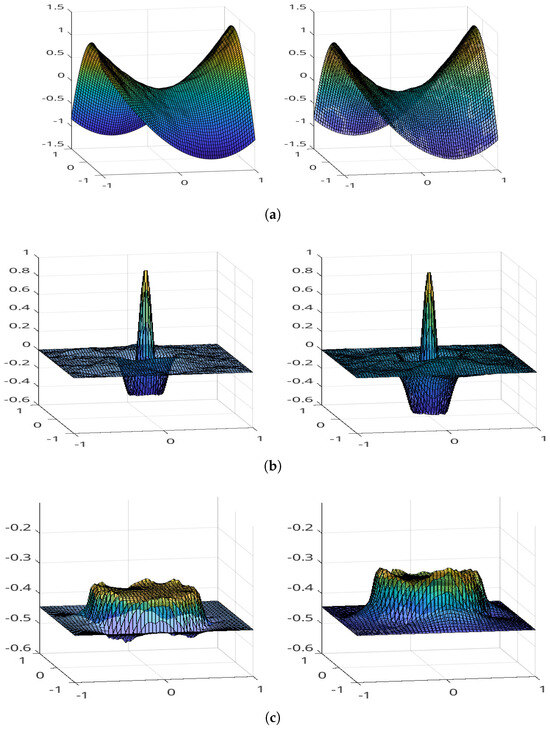
Figure 4.
The (left column) shows the approximation results obtained using the classical Frankot–Chellappa method with the discrete sine transform (sT), while the (right column) illustrates the corresponding approximations using the proposed fuzzy Frankot–Chellappa method based on the fuzzy discrete sine transform (FsT). In the fuzzy approach, the FsT is applied via a fuzzy partition (F-transform) for three representative functions from Table 1, using the -cut representation with . (a) ; (b) ; (c) .
6. Conclusions
We have presented a fuzzified Frankot–Chellappa method for surface normal integration, which incorporates fuzzy logic to handle uncertainty in the input normals. The fuzzy Poisson equation with Dirichlet boundary conditions was formulated and solved using a fuzzy discrete sine transform. The improved fuzzified Frankot–Chellappa method can reconstructs surfaces with normal vectors that are uncertain or noisy, with performance comparable to the classic method on clean data and improved behavior on noisy data. In terms of accuracy, for smooth surfaces, the defuzzified fuzzy solution is essentially equivalent to the classical solution. In terms of noise suppression, the use of fuzzy concepts (in particular the inherent filtering effect of the F-transform) led to reconstructions with slightly lower error than the classical approach.
Overall, the developed fuzzy Frankot–Chellappa algorithms represent a promising extension of the classical approach. They maintain the computational efficiency of the original algorithm while providing improved noise tolerance and resilience to missing or ambiguous data.
Empirical evaluations demonstrate that the proposed strategy consistently improves reconstruction accuracy in noisy scenarios compared to both the classical FC method and the original fuzzy approach in [19].
Despite its promising performance, the proposed fuzzy FC method has certain limitations. First, the current model relies on predefined fuzzy parameters () which are empirically tuned and may not adapt well to all types of noise distributions. Second, the method assumes a regular grid structure and Dirichlet boundary conditions, which might not generalize to arbitrary or irregular domains. Future work will focus on automatic tuning of fuzziness parameters (e.g., determining optimal spreads or thresholds based on data characteristics) and on extending the approach to non-rectangular domains or irregular integration regions, which would further enhance its applicability in real-world scenarios.
Author Contributions
The authors declare that the main idea and experiments were proposed by S.H. and M.B. and that the manuscript was written together with S.H. and M.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The authors declare that upon reasonable request, the data and the code are available from the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| TFNs | Triangular Fuzzy Numbers |
| gH | Generalized Hukuhara |
| PDEs | Partial Differential Equations |
| sT | Discrete Sine Transformation |
| FsT | Fuzzy Discrete Sine Transformation |
| FC | Frankot–Chellappa |
| RMSE | Root Mean Square Error |
References
- Cao, X.; Santo, H.; Shi, B.; Okura, F.; Matsushita, Y. Bilateral Normal Integration. In Proceedings of the European Conference on Computer Vision, ECCV 2022, Tel Aviv, Israel, 23–27 October 2022; pp. 552–567. [Google Scholar]
- Durou, J.D.; Aujol, J.F.; Courteille, F. Integrating the normal field of a surface in the presence of discontinuities. In Proceedings of the Energy Minimization Methods in Computer Vision and Pattern Recognition, EMMCVPR 2009, Bonn, Germany, 24–27 August 2009; pp. 261–273. [Google Scholar]
- Horn, B.K.P. Photometric Stereo. In Robot Vision; MIT Press: Cambridge, MA, USA; McGraw-Hill: London, UK, 1986; pp. 243–398. [Google Scholar]
- Bähr, M.; Breuß, M. An Improved Eikonal Method for Surface Normal Integration. In Proceedings of the 37th German Conference on Pattern Recognition, GCPR 2015, Aachen, Germany, 7–10 October 2015; pp. 274–284. [Google Scholar]
- Frankot, R.T.; Chellappa, R. A method for enforcing integrability in shape from shading algorithms. IEEE Trans. Pattern Anal. Mach. Intell. 1988, 10, 439–451. [Google Scholar] [CrossRef]
- Harker, M.; O’Leary, P. Least Squares Surface Reconstruction from Measured Gradient Fields. In Proceedings of the Conference on Computer Vision and Pattern Recognition, CVPR 2008, Anchorage, AK, USA, 23–28 June 2008. [Google Scholar]
- Simchony, V.F. Direct analytical methods for solving poisson equations in computer vision problems. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 12, 435–446. [Google Scholar] [CrossRef]
- Queau, Y.; Durou, J.-D.; Aujol, J.-F. Normal Integration: A survey. J. Math. Imaging Vis. 2018, 60, 576–593. [Google Scholar] [CrossRef]
- Sellan, S.; Jacobson, A. Stochastic Poisson Surface Reconstruction. In Proceedings of the SIGGRAPH Asia 2022, Daegu, Republic of Korea, 6–9 December 2022. [Google Scholar]
- Hou, F.; Wang, C.; Wang, W.; Qin, H.; Qian, C.; He, Y. Iterative Poisson Surface Reconstruction (iPSR) for Unoriented Points. Acm Trans. Graph. 2022, 41, 1–13. [Google Scholar] [CrossRef]
- Yu, Z.; Sattler, T.; Geiger, A. Gaussian Opacity Fields: Efficient Adaptive Surface Reconstruction in Unbounded Scenes. Acm Trans. Graph. 2024, 43, 1–13. [Google Scholar] [CrossRef]
- Perfilieva, I. Fuzzy transforms: Theory and applications. Fuzzy Sets Syst. 2006, 157, 993–1023. [Google Scholar] [CrossRef]
- Perfilieva, I.; Valášek, P. Fuzzy Transforms in Removing Noise. In Proceedings of the Computational Intelligence, Theory and Applications, International Conference 8th Fuzzy Days, Dortmund, Germany, 29 September–1 October 2004; pp. 221–230. [Google Scholar]
- Nie, Y.; Barner, K.E. The Fuzzy ransformation and Its Applications in Image Processing. In Proceedings of the IEEE Transactions on Image Processing, ICIP 2003, Barcelona, Spain, 14–17 September 2006; pp. 910–927. [Google Scholar]
- Allahviranloo, T. Difference methods for fuzzy partial differential equations. Comput. Methods Appl. Math. 2006, 2, 233–242. [Google Scholar] [CrossRef]
- Abdi, M.; Allahviranloo, T. Fuzzy finite difference method for solving fuzzy Poisson equation. J. Intell. Fuzzy Syst. 2019, 37, 5281–5296. [Google Scholar] [CrossRef]
- Ghasemi Moghaddam, R.; Allahviranloo, T. On the fuzzy Poisson equation. Fuzzy Sets Syst. 2018, 374, 105–128. [Google Scholar] [CrossRef]
- Allahviranloo, T.; Ghobadi, M.; Matinfar, M. A fuzzy solution of wave equation by FFS-transform. Numer. Methods Partial. Differ. Equ. 2024, 40, e22661. [Google Scholar] [CrossRef]
- Hajighasemi, S.; Breuß, M. Fuzzy Frankot-Chellappa Method for Surface Normal Integration. In Proceedings of the Central-European Conference on Scientific Computing, High Tatra Mountains, ALGORITMY 2024, Podbanské, Slovakia, 15–20 March 2024; pp. 245–254. [Google Scholar]
- Dubois, D.; Prade, H. Operations on fuzzy numbers. Int. J. Syst. Sci. 1978, 9, 613–626. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).