Abstract
Partial shading conditions lead to power mismatches among photovoltaic (PV) panels, resulting in the generation of multiple peak power points on the P-V curve. At this point, conventional MPPT algorithms fail to operate effectively. This research work mainly focuses on the exploration of performance optimization and harnessing more power during the partial shading environment of solar PV systems with a single-objective non-linear optimization problem subjected to different operations formulated and solved using recent metaheuristic algorithms such as Cat Swarm Optimization (CSO), Grey Wolf Optimization (GWO) and the proposed Chimp Optimization algorithm (ChOA). This research work is implemented on a test system with the help of MATLAB/SIMULINK, and the obtained results are discussed. From the overall results, the metaheuristic methods used by the trackers based on their analysis showed convergence towards the global Maximum Power Point (MPP). Additionally, the proposed ChOA technique shows improved performance over other existing algorithms.
1. Introduction
Solar energy has become increasingly important as an energy resource due to its inexhaustible nature, cleanliness, scalability in power generation and low maintenance requirements. As a country with high sunshine, India offers an exceptional opportunity for harnessing solar energy, which can significantly address our pollution problems. In recent times, photovoltaic systems have gained immense popularity due to their numerous advantages. These systems are known for their sustainability, low maintenance requirements, absence of complex parts and extended lifespan, among other benefits [1]. The PV systems are subjected to shading effects along with dynamically changing weather conditions due to the shadow of large buildings, passing clouds, birds’ shadows, etc. In the case of Partial Shading Condition (PSC), the PV modules get different irradiations and temperatures, leading to decreasing the power output obtained from the PV array and causing hot spots and loss of tracking efficiency. During shading, power variation with voltage characteristic plot possesses several peaks, one referred to as Global Maximum Power Point (GMPP), and others are well known as local maximum power points, as delineated in Figure 1.
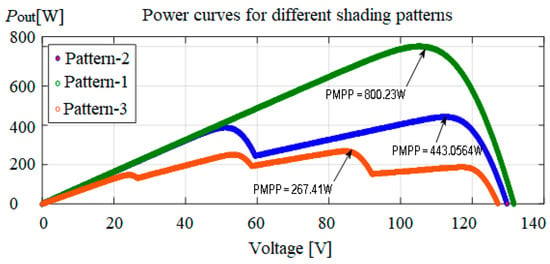
Figure 1.
P-V plot of PV module under changing shading conditions.
Most conventional MPPT approaches like Perturb and Observe (P&O), Incremental Conductance (INC) and Constant Voltage (CV) techniques can work efficiently when solar radiation and temperature are uniform but significantly fail when the weather conditions are varying. In order to address the mentioned challenge, researchers have utilized intelligent global search optimization algorithms which effectively tackle the global maximum power tracking (MPPT) problems. In the available literature, diverse MPPT techniques and alternative solutions have been employed to accurately identify the true global maximum power point amidst various local MPPs.
These popular intelligent algorithms include (a) Genetic Algorithm (GA), (b) Particle Swarm Optimization (PSO), (c) Ant Colony Optimization (ACO) and (d) Teaching learning-based optimization. Kulaksiz et al. [2] implemented the GA with an ANN-based tracking method for the standalone PV system. Genetic algorithm optimization was used in this algorithm to optimise the required number of neutrons in a multi-layer perception neural network, thereby tracking required power during uneven irradiance situations. Tajuddin et al. [3] suggested a superior Differential Evolution (DE) algorithm for changing solar environmental conditions to obtain global power output. Thangamani et al. [4] introduced an adaptive differential algorithm that can track MPP under swiftly changing climatic conditions. Ramli et al. [5] surveyed methods resembling artificial intelligence and hybrid algorithm for tracking MPP and summarized the finer points of various techniques understanding to increase the power output of the PV array.
Liu et al. [6] applied the PSO for various operating situations and reported the merits of the PSO algorithm, which includes ease of implementation, system independence and enhanced output. Ishaque et al. [7] discussed the PSO algorithm, which eliminates the need for the direct duty ratio method’s proportional-integral (PI) control block. Renaudineau et al. [8] used the PSO algorithm to control the gate pulse given to the boost converter to extract GMPP. Phimmasone et al. [9] used the PSO algorithm by taking additional specific coefficients of the algorithm to progress to the next step and get the global point of the PV. The usage of more specific parameters in PSO algorithms results in decreased tracking efficiency and increased uncertainty of the solution. Therefore, the desired operating point cannot be reached. To overcome these drawbacks, improved optimization algorithms were proposed by the researchers. Chao et al. [10] offered a modified PSO algorithm to harness GMPP from a PV system during a cloudy day. The adjustment practice fallouts to figure out the algorithm-specific parameters for the next step of acceleration. In [11], Chen et al. focused on applying an enhanced PSO algorithm for MPPT to enhance tracking efficiency, particularly under shading conditions. Chowdhury et al. [12] proposed the adaptive PSO to defeat the de-merits of a conventional PSO. Tobon et al. [13] implemented an Improved Pattern Search Method (IPSM) for MPPT, and the solution obtained by the pattern search technique succeeded in their convergence properties. Babu et al. [14] worked on the voltage-band-based improved PSO approach to improve the convergence of the PSO. Gavhane et al. [15] examined the studies on MPPT on cloudy days by applying Enhanced-Leader-Particle Swarm Optimization (EL-PSO), which was more efficient for implementation. Babu et al. [16] presented the benefits of the modified PSO algorithm, highlighting its nearly zero steady-state oscillations and faster dynamic response compared to traditional approaches. Husain et al. [17] commented on the various parameters of the PSO and elaborated on the numerous procedures for MPP tracking. Kalaiarasi et al. [18] proposed an enhanced PSO method for getting maximum benefits from solar-powered energy integrated through the Z-source inverter and observed various benefits of reduction in the steady state oscillations.
Dileep and Singh [19] gave an inclusive report on different computing methods (PSO and ACO) to get GMPP beneath diverse shading effects. Ahmed et al. [20] applied PSO, ACO, Cuckoo Search (CS) and DE for the simulation of the MPPT system during shading patterns, the provision of operation and merits, and the limitations of each optimization algorithm have been highlighted. Li et al. [21] considered a new GMPP tracking approach which depends on changes in power, besides analysing the nature of the activity. Rezk et al. [22] reviewed the various power extraction algorithms and concluded that PSO and CS algorithms have shown more convergence to the global maximum power tracking. Ahmed et al. [23] investigated the effectiveness of the Particle Swarm Optimization-Support Vector Regression (PSO-SVR) method in reducing the percentage of ripple content and minimizing oscillations in the power waveform around the MPP region. Gangwar et al. [24] studied the cat swarm optimization in a specific pattern well known as phyllotaxy in order to extract more solar power. Mohanty and Tripatty [25] presented a novel Teaching Learning Based Optimization (TLBO) algorithm, that was introduced for the optimal placement of distributed generation in a radial distribution network. This technique offers a unique approach to addressing the problem of determining the best locations for distributed generation sources within the network.
Hegazy and Fathy [26] carried out numerous simulations under different shading patterns using (FLC, PSO, and TLBO) and concluded that TLBO extracts GMPP more dynamically than others. Ahmed and Rezk [27] implemented a novel Mine Blast Algorithm (MBA) and applied different patterns of shadow. The obtained results were compared, thereby declaring MBA as superior to TLBO. Crepinsek et al. [28] observed that the TLBO algorithm showed better performance for maximum power point tracking among the optimisation algorithms. Sundareswaran et al. [29] found that Firefly Algorithm (FA) was one of the efficient approaches to harnessing maximum solar energy beneath partial shading conditions. Javed et al. [30] studied enhancing the FA algorithm; the study aimed to improve MPPT efficiency and mitigate the adverse effects of partial shading. Comparative analysis between the modified FA and PSO algorithms provided valuable insights into the effectiveness of the modified FA algorithm for achieving superior MPPT performance under partially shaded conditions. Mohanty et al. [31] proposed a hybrid maximum power point tracking technique using the P&O method with GWO for better MPPT from PV module strings beneath shading conditions. Eltamay et al. [32] applied the GWO algorithm with fuzzy logic controllers to eliminate the oscillation near GMPP. Mohanty et al. [33] examined the design of the MPPT circuit along with the GWO algorithm that mitigates the shortfalls of conventional tracking methods, such as poor performance in tracking, low efficiency and more oscillations near and around MPP.
The key distinctions among this approach include their effectiveness range, convergence speed, design complexity, sensor requirements, control parameters and hardware implementation costs. Consequently, selecting an appropriate algorithm is crucial when designing a photovoltaic (PV) system, as it depends on the intended application. After the selection of the optimization algorithm, the adaptation for the solved optimization task must be done.
This paper compares widely used MPPT techniques to mitigate the negative impact of partial shading, thereby enhancing maximum power output. It explores the advantages and disadvantages of these techniques and provides a general comparison of various solutions. This article particularly focuses on discussing different approaches for global maximum power point tracking (GMPPT) under partial shading conditions, with emphasis on recent advancements in the scientific literature.
The main contributions of this paper are as follows:
- A statistical investigation of modern heuristic optimization methods for (GMPPT) in photovoltaic (PV) systems under partial shading conditions has been presented;
- Comprehensive analysis of the challenges associated with heuristic optimization-based GMPPT techniques, focusing on their exploitative and explorative search capabilities;
- Introduction of a novel GMPPT method called Chimp Optimization Algorithm, which effectively balances the exploitative and explorative search capabilities;
- Statistical comparisons of different heuristic optimization-based GMPPT techniques in terms of tracking routines, accumulated energy and tracking efficiency.
Applications of Metaheuristics Algorithm
- ➢
- Metaheuristics algorithms offer a powerful approach to tackling complex optimization problems in diverse domains. Their flexibility, robustness and ability to find satisfactory solutions make them invaluable tools for real world problems as presented below.
- ➢
- Metaheuristics are widely used to tackle problems with a large number of possible combinations, such as the Traveling Salesman Problem, Knapsack Problem or Job Scheduling. Examples of metaheuristics for combinatorial optimization include GA, PSO, ACO and Simulated Annealing (SA).
- ➢
- Metaheuristics are used for optimizing the design parameters of complex systems. For example, they can optimize the shape of an aircraft wing, the layout of an electric circuit, electromagnetic device or the parameters of a chemical process.
- ➢
- Metaheuristics are utilized in optimizing transportation routes, vehicle routing problems and logistics planning. They help find efficient paths for deliveries, minimizing travel time and costs.
- ➢
- Metaheuristics can optimize production schedules, inventory management, and resource allocation in manufacturing processes.
- ➢
- Metaheuristics can be used to create computer programs that can play games effectively by finding near-optimal strategies.
2. Application of CSO-Based MPPT Controller for Solar PV Strings under Partial Shading Conditions
In the CSO algorithm, the natural behaviour of the cats is used to solve the optimization problem [34]. In this algorithm, the behaviour of cats is deciphered in two modes: seeking mode and tracing mode and used to move the virtual cats in the search space. A predetermined ratio, known as the Mixture Ratio (MR), determines how many cats participate in each iteration in tracing and seeking mode.
2.1. Seeking Mode
The virtual cat walks slowly while it follows the searching mode. In this seeking mode, the following four basic criteria are defined as follows:
- ➢
- Seeking memory pool (SMP);
- ➢
- Seeking range dimensions (SRD);
- ➢
- Counts of dimensions to change (CDC);
- ➢
- Self-position consideration (SPC).
Each cat’s size in the search pool is determined by the SMP value, which translates the points needed by the cat. SRD announces the boundary condition requirement for updating the dimensions as well as the Mixture Ratio (MR) of the preferred dimensions. The CDC is a key element of the searching mode that reports how many dimensions need to be modified. The SPC value plays a crucial role in determining whether the current candidate of the virtual cat can be deemed as a suitable choice within the search memory. The flow chart interpreting the CSO algorithm is shown in Figure 2. The sequential procedure involved in the Seeking approach is presented below.
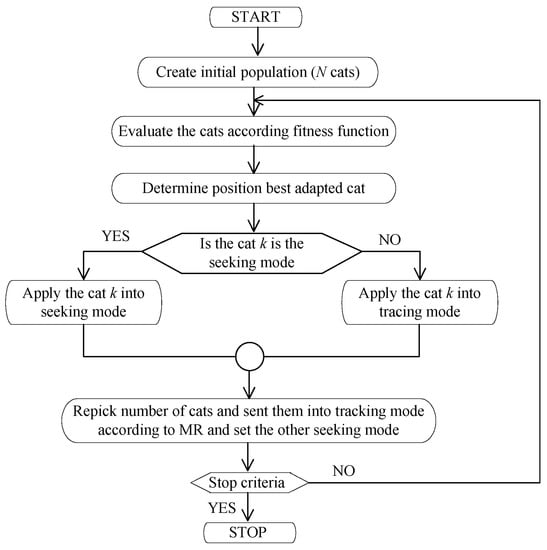
Figure 2.
The flow chart of the CSO algorithm.
Step 1: Let us consider “j” copy the current position of Cat k
where j = SMP if SPC = TRUE
Otherwise,
Step 2:
where r1 is the random number from range (0, 1)
Step 3: Determines fresh value of fitness for each cat.
Step 4: Find out the selection capability from Equation (2) whenever the fitness function value changes. If not, set each solution’s selection probability to 1.
Step 5:
where Pi is the probability of selection, FS is the fitness function value.
If the objective function is to minimize, then FSb = FSmax. Otherwise,
where FSmax is the largest fitness offered by the candidate, and FSmax is the smallest fitness offered by the candidate.
Step 6: Arrange the candidate’s cat by Pi and anyone can select to retain the co-ordinate cat k.
2.2. Tracing Mode
The virtual cats can imitate the movement of other cats to track their prey during the tracing mode. The mechanism of the tracing process can be described in Equations (3) and (4).
Step 1: Equation (3) represents the velocity of each cat updated in every dimension.
where d = 1, 2, …, M, r1 is the random number from range (0, 1), C1 is the constant number, and Xbest is the best adapted cat in population.
Step 2: The velocity of each cat is examined to determine if it falls within the permissible limits. In cases where the velocity exceeds the limit, it is adjusted to the maximum allowable velocity value.
Step 3: Determine the position of every cat by adding the current velocity of each cat.
where Xk,d old is the old coordinate of cat k, Xk,d new is the updated coordinate of cat, and Δt = 1 is the time step.
3. Application of GWO-Based MPPT Controller for Solar PV String under Shading Conditions
This section presents a mathematical model that describes the social hierarchy, tracking, encircling and attacking behaviour of predators toward their prey. The model aims to capture the dynamics and interactions between predators as they coordinate their actions to maximize their chances of capturing the prey [35].
3.1. Encircling the Prey
The following Equations (5) and (6) represent the behavioural model of wolves while encircling the prey [31].
where t is iteration number; D, A and C are the GWO parameters; Xp is the position of the prey.
To determine A and C, the following equations are used.
where r1 and r2 are the random numbers from range (0, 1).
The control parameter changes to the grey wolf optimization process, causing omega wolves to either approach or be free from the alpha beta, and delta-dominating wolves. While the iterations are being performed, the operating parameter is set to decrease linearly from a value of 2 to 0.
In the above equation, T indicates maximum iteration numbers.
3.2. Hunting Process (Updating of Wolf Position)
The alpha group of wolves, the leaders, usually directs the hunting process. They are followed by beta and delta group wolves, who occasionally engage in hunting. The surrounding wolves in the pack worry the delta and omega wolves. As a result, the alpha wolf is seen as the best option with solid information of where the prey is. The GWO algorithm indicates a superior balance between the exploitation and exploration phases because of these qualities. Moreover, by choosing while C considers the environment, GWO eliminates the local stuck.
Hence, the different wolf groups’ positions can be obtained from Equations (10) to (12) as follows:
Overall, the final grey wolves positioned in the iteration are obtained from Equation (13).
3.3. Attacking the Prey (Exploitation of Search Process)
Grey wolves attack their prey to end their hunt. This method of attack is described mathematically by lowering the value of a, which then modifies the value of . A is reduced from 2 to 0 and initially has a random value in the range [−a, a].
3.4. Searching the Prey
Figure 3 represents the flow chart of the GWO algorithm step-by-step process for the present research problem.
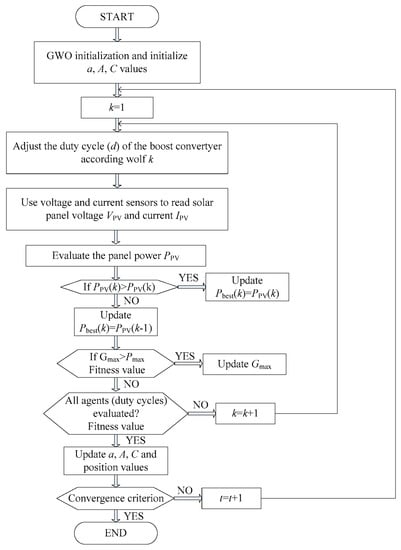
Figure 3.
GWO algorithm flow chart.
4. Application of ChOA-Based MPPT Controller for Solar PV Module under Shading Conditions
Exploration and exploitation are the two phases in which the hunting process is completed. Equations (14) and (15) are used for the design process of driving prey and chasing prey as presented below.
where m is chaotic vector, XChimp (t) is the chimp position at t-th iteration.
The values of a and C coefficient in each iteration Equations (16)–(18) are used.
where f is the dynamic vector [36].
In the exploration and exploitation stages of the iteration process, the value of f decreases nonlinearly from 2.5 to 0. Random vectors r1 and r2 vary within [0, 1] while regulation vectors are indicated by a and C. The distance between them is denoted as D. The chaotic vector (m) is calculated based on different maps to simulate the sexual motivation of chimps during the search process. In subsection C, a detailed report on the chaotic vector (m) is provided. Unlike conventional swarm intelligent optimization algorithms, where all particles (agents) behave similarly across the entire search space, the mathematical model incorporates various strategies for independent groups of chimps to revise their hunting approach. The behaviour of independent chimp groups in the ChOA is updated using a continuous function. Through the use of constant parameters, the independent process is iteratively refined. All these parameters are explicitly defined throughout the entire process, ensuring that f is decreased in successive iterations of the optimization process. Each self-determining group employs its model to explore both the global and local search spaces. The dynamic coefficient vector with different groups is delineated in Table 1. To enhance the search capability and precisely capture the search nature of the chimp’s independent groups, a dynamic coefficient of f is proposed and illustrated in Figure 4. Different curves and slopes are chosen for these dynamic coefficients (f) to facilitate the adjustment of the behaviour of the Chimp Optimization Algorithm’s independent groups.

Table 1.
Dynamic coefficient vector f.
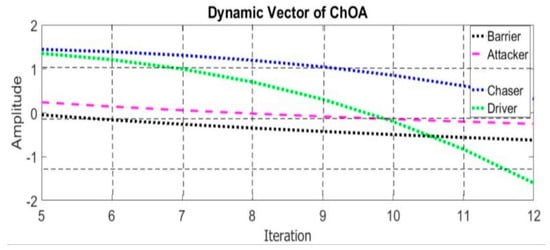
Figure 4.
Variation of dynamic coefficients vector with different groups of ChOA.
In the above table, T is the maximum number of iterations, and t is the current iteration.
4.1. Exploration Stage
When chimps are attacking, they are likely to search the prey’s local position by the use of diverse stages such as chasing, driving and blocking to enclose the prey. In general, attackers are managed by the chase process. In the initial iteration, since the optimal position of the prey is unknown, the attacker’s location is assumed to be the actual location of the prey. Then, the subsequent barrier, driver and chaser locations (denoted by C) are determined relative to the attacker’s position. The best position achieved is stored. However, the other chimps need to refine their positions based on the location of the most successful chimp. Mathematical equations are employed to model the process of encircling the prey by the chimps (19), (20) and (21), respectively.
where XAttacher is the best search agent, XBarrier is the second-best search agent, XChaser is the third-best search agent, and XDriver is the fourth-best search agent.
4.2. Attacking Approach (Exploitation Phase)
The mathematical model represents the attack process, where the value of f decreases linearly from 2.5 to 0. This linear reduction enhances the effectiveness of the attack and the exploitation of the prey’s location. To enhance the attacking and exploitation of the prey location, the mathematical model employs a linear reduction of the value of f from 2.5 to 0, representing the process of attack. Further, the scope of the vector is found to decrease like that of function f. The described vector is random within the range of −2f and 2f. All the time, a random value is selected for the vectors stretch-out within the range of [−1 and 1], and the value determines the next placement of the chimp, which can be at any location within the available position and conditions of the prey. Although there is mention of projected blocking, chasing and driving mechanisms that highlight the searching limits, there is a concern that the algorithm referred ChOA may get trapped in nearby minima. To address this, an additional operator is deemed necessary to enhance the searching ability during the exploitation period. In this approach, all the chimps embark on hunting the prey, as depicted in Figure 5. The value of “a” coefficient is mathematically modelled to align with the hunting behaviour. Consequently, the disparity among the chimps compels them to wander in pursuit of the prey, ultimately driving them to converge at the location of the prey.
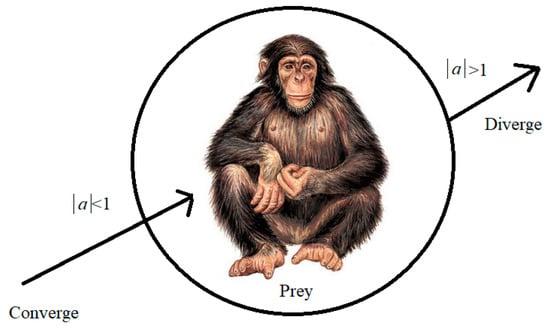
Figure 5.
Influence of a on refining the chimp’s location mechanism.
4.3. Chaotic Maps (Sexual Motivation)
Introducing chaotic behaviour in the optimization algorithm utilizing chimps helps address two key challenges in solving high-dimensional engineering application problems. Firstly, it helps alleviate the issue of getting trapped in local optima during the final stages of the optimization process. Local optima are suboptimal solutions that can hinder the algorithm from reaching the global optimum. By incorporating chaotic behaviour, the algorithm introduces randomness and exploration, allowing the chimps to venture into unexplored regions of the search space. This exploration enhances the chances of escaping local optima and discovering better globally optimal solutions. The mathematical model for this approach is presented in Equation (22).
where μ is random number within the range of [0, 1] [36].
The flow chart of the ChOA is delineated in Figure 6.
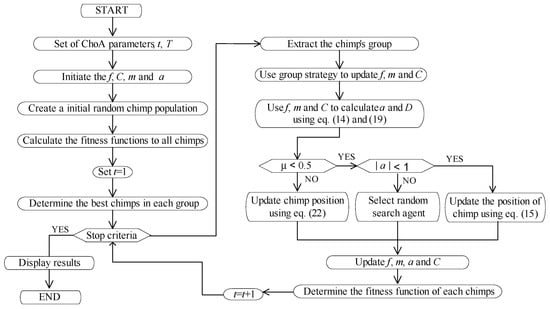
Figure 6.
ChOA flow chart.
5. Case Studies
Four cases are considered with four different shading patterns, as shown in Figure 7, and are proposed with different irradiance as mentioned in Table 2 to explore the PV characteristics under shading conditions.
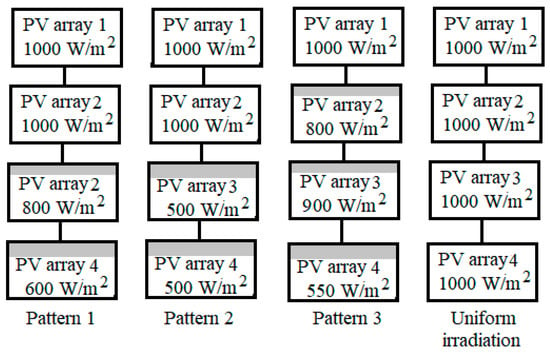
Figure 7.
Different irradiation patterns of PV system under shading conditions.

Table 2.
PV module with different partial shading patterns.
The performance of the PV string is evaluated under partial shading conditions for three cases considering three different shading patterns as shown in Table 2, using various optimization-based MPPT techniques. Figure 8 represents the simulation circuit of four series-connected PV modules by varying the irradiation levels, temperature at 25 °C with the PV module and converter circuit details listed in Table 3.
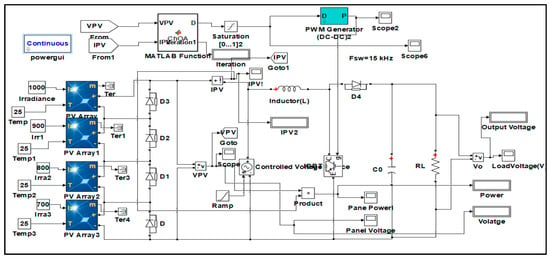
Figure 8.
Simulation circuit of four series-connected KC200GT PV module.

Table 3.
PV module and converter circuit details.
All characteristic parameters of the optimization algorithm are carefully selected to provide good convergence to the solved optimization task. The parameters used during simulations for CSO, GWO and ChoA algorithms are listed in Table 4.

Table 4.
Tuning parameters for metaheuristic algorithms.
In this case, the details of irradiance levels received on the modules in Pattern-1 and their P-V and P-I plots are discussed and presented in Figure 9. The voltage and current at GMPP under this shading condition are 544.12 W, 114.008 V and 4.7771 A, respectively.
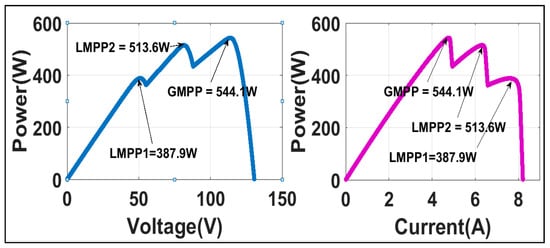
Figure 9.
P-V and P-I variations under the first shading pattern on PV string.
According to the simulation findings for Pattern 1 displayed in Figure 10, Figure 11 and Figure 12, the ChoA shows reduced oscillation during the MPP search process. Specifically, when shading occurs, the PV module power output rapidly converges to the MPP with very minimal fluctuations. However, based on the simulation results depicted in Figure 10 (Simulation results using CSO for Pattern-1), Figure 11 (Simulation results using GWO for Pattern-1) and Figure 12 (Simulation results using ChOA for pattern 1), the average convergence time of the GWO algorithm is relatively high. Even though the suggested chimp algorithm converges sufficiently quickly and catches only after a short period, the ability of ChOA, GWO and CSO algorithms to chase the GMPP under various shading situations is examined. It is observed from the simulation result that the output power obtained from the PV array using CSO is 521.41 W, using GWO is 527.44 W, and 531.198 W when ChoA is used.
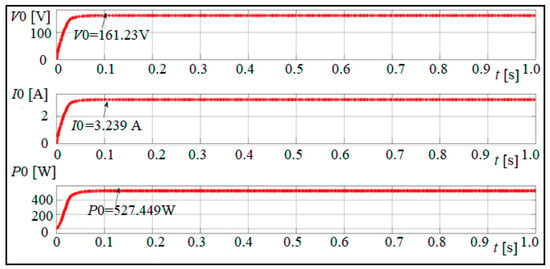
Figure 10.
Simulation result using CSO for the Patern-1.

Figure 11.
Simulation results using GWO for the Pattern-1.

Figure 12.
Simulation results using ChoA for the Pattern-1.
Figure 13 presents a performance comparison for the analysed metaheuristic algorithms.
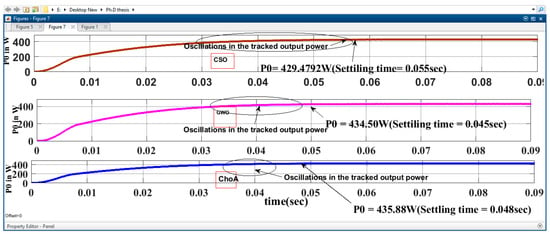
Figure 13.
Comparison of settling time for the CSO, GWO and ChoA algorithms.
The above Figure depicts the reduced oscillations and convergence time for the three algorithms, and it clearly shows that the proposed GWO have less oscillation and also less convergence time compared with the other algorithms, while the ChoA is slightly slower than the GWO algorithm.
ChOA, GWO and CSO algorithms are simulated in MATLAB/SIMULINK to validate their expected performance under various partial shade patterns (G1 to G6). Table 5 lists the outcomes of the statistical simulation. The variable power output with irradiation with different MPPT techniques under other shading patterns is presented in Figure 14. From Figure 14, G1 shading pattern will produce the solar photovoltaic system’s highest power. Due to its speed and confidence, the simulation results of the various shading situations showed that ChOA performed better than other optimization strategies under partial shading settings. The summarization of statistical simulation results like power, voltage and current of the PV module under other partial shading conditions is presented in Table 5.

Table 5.
Summarization of statistical simulation results like power, voltage, and current of PV module.
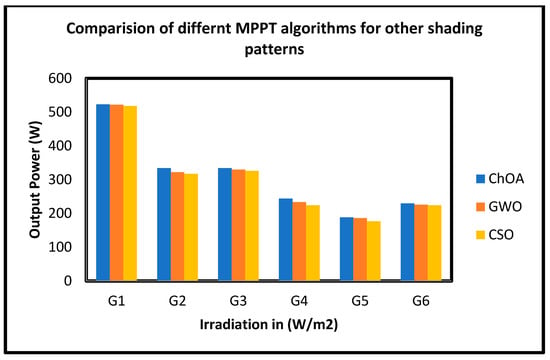
Figure 14.
Comparison of output power with different MPPT Algorithms under other shading patterns.
6. Conclusions
This research work presents a comprehensive study that analyses the challenges faced by three heuristic-optimization-based algorithms in the context of GMPPT. The focus is specifically on the search capabilities of these techniques, both in terms of exploitation and exploration. This article introduces a novel method called ChOA GMPPT to address these challenges. This method improves GMPPT performance by utilizing different deterministic starting points for exploitation and exploration. Simulation tests demonstrate that the proposed ChOA-based GMPPT achieves higher tracking accuracy and conversion efficiency compared to other tested methods. Additionally, it reduces computational complexity and is easy to implement. By providing a discussion and analysis of various heuristic optimization methods in the literature, along with the newly suggested ChoA-based GMPPT approach, this current work enables researchers to select the most suitable method based on their preferences and priorities.
In future research, the PSO, CSO, TLBO, GWO and ChOA variants are used to optimize the PV system performance under changing weather conditions. There is a possibility for the usage of recent algorithms as well as hybrid algorithms since a comparative study can be done.
Author Contributions
Conceptualization, T.N. and R.D.; methodology, T.N.; software, T.N. and R.D.; validation, T.N.; investigation resources, T.N. and R.D.; resources, T.N. and Ł.K.; writing—original draft preparation, T.N. and R.D.; writing—review and editing, Ł.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Poznan University of Technology, grant number [0212/SBAD/0594].
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| PV System | Photovoltaic system |
| MPPT | Maximum Power Point Tracking |
| GMPP | Global Maximum Power Point |
| PSC | Partial Shading Condition |
| CSO | Cat Swarm Optimization |
| GWO | Grey Wolf Optimization |
| ChoA | Chimp Optimization algorithm |
| PSO | Particle Swarm Optimization |
| TLBO | Teaching Learning Based Optimization |
| ACO | Ant Colony Optimization |
| P&O | Perturb and Observe |
| INC | Incremental Conductance |
| GA | Genetic Algorithm |
| DEA | Differential Evaluation Algorithm |
| FLC | Fuzzy Logic Controller |
| FA | Firefly Algorithm |
| SMP | Seeking Memory Pool |
| MBA | Mine Blast Algorithm |
References
- Available online: https://cea.nic.in/reports/monthly/executive%20summary/2020/exe_summary-02 (accessed on 1 March 2021).
- Novas, N.; Garcia, R.M.; Camacho, J.M.; Alcayde, A. Advances in Solar Energy towards Efficient and Sustainable Energy. Sustainability 2021, 13, 6295. [Google Scholar] [CrossRef]
- Kulaksız, A.A.; Akkaya, R. A genetic algorithm optimized ANN-based MPPT algorithm for a standalone PV system with induction motor drive. Solar Energy 2012, 86, 2366–2375. [Google Scholar] [CrossRef]
- Tajuddin, M.F.N.; Arif, M.S.; Ayob, S.M.; Salam, Z. Perturbative methods for maximum power point track-ing (MPPT) of photovoltaic (PV) systems: A review. Int. J. Energy Res. 2015, 39, 1153–1178. [Google Scholar] [CrossRef]
- Thangamani, K.; Manickam, M.L.; Chellaiah, C. An experimental study on photovoltaic module with opti-mum power point tracking method. Int. Trans. Electr. Energy Syst. 2020, 30, e12175. [Google Scholar] [CrossRef]
- Ramli, M.A.M.; Twaha, S.; Ishaque, K.; Al-Turki, Y.A. A review on maximum power point tracking for pho-tovoltaic systems with and without shading conditions. Renew. Sustain. Energy Rev. 2017, 67, 144–159. [Google Scholar] [CrossRef]
- Liu, Y.H.; Huang, S.C.; Liang, W.C. A particle swarm optimization –Based maximum power point tracking algorithm for PV systems operating under partially shaded conditions. IEEE Trans. Energy Convers. 2012, 27, 1027–1035. [Google Scholar] [CrossRef]
- KashifIshaquem, H.; Salam, Z. A direct control based maximum power point Tracking method for photovoltaic system under partial shading conditions using Particle Swarm optimization Algorithm. Appl. Energy 2012, 99, 414–422. [Google Scholar] [CrossRef]
- Renaudineau, H.; Donatantonio, F.; Fontchastagner, J.; Petrone, G. A PSO-Based Global MPPT Technique for Distributed PV Power Generation. IEEE Trans. Ind. Electron. 2015, 62, 1047–1058. [Google Scholar] [CrossRef]
- Phimmasone, V.; Kondo, Y.; Kamejima, T.; Miyatake, M. Evaluation of extracted energy from PV with PSO-based MPPT against various types of solar irradiation changes. In Proceedings of the 2010 International on Electrical Machines and Systems, Incheon, Republic of Korea, 10–13 October 2010; pp. 487–492. [Google Scholar]
- Chao, K.H.; Lin, Y.S.; Lai, U.D. Improved particle swarm optimization for maximum power point tracking in photovoltaic module arrays. Appl. Energy 2015, 158, 609–618. [Google Scholar] [CrossRef]
- Roy Chowdhury, S.; Saha, H. Maximum power point tracking of partially shaded solar Photovoltaic arrays. Sol. Energy Mater. Sol. Cells 2010, 94, 1441–1447. [Google Scholar] [CrossRef]
- Tobon, A.; Restrepo, J.; Ceballos, J.P.V.; Ibeas, A. Maximum Power Point Tracking of Photovoltaic Panels by Using Improved Pattern Search Methods. Energies 2017, 10, 1316. [Google Scholar] [CrossRef]
- Babu, T.S.; Sangeetha, K.; Rajasekar, N. Voltage band based improved particle. Swarm optimization technique for maximum power point tracking. in solar photovoltaic System. J. Renew. Sustain. Energy 2016, 8, 013106. [Google Scholar] [CrossRef]
- Gavhane, P.S.; Krishnamurthy, S.; Dixit, R.; Ram, J.P.; Rajasekar, N. EL-PSO based MPPT for solar PV. under partial shaded condition. Energy Procedia 2017, 117, 1047–1053. [Google Scholar] [CrossRef]
- Babu, T.S.; Rajasekar, N.; Sangeetha, K. Modified Particle Swarm optimization technique based Maximum Power Point Tracking for uniform and under partial shading condition. Appl. Soft Comput. 2015, 34, 13–624. [Google Scholar] [CrossRef]
- Husain, M.A.; Tariq, A.; Hameed, S.; Arif, M.S.B.; Jain, A. Comparative assessment of maximum power point tracking procedures for photovoltaic systems. Green Energy Environ. 2017, 2, 5–17. [Google Scholar] [CrossRef]
- Kalaiarasi, N.; Subranshu, D.; Sanjeevikumar, P.; Paramasivam, S. Maximum Power Point Tracking Implementation by DSPACE Controller Integrated through Z-Source Inverter Using PSO Technique for Photovoltaic Applications. Appl. Sci. 2018, 8, 145. [Google Scholar] [CrossRef]
- Dileep, G.; Singh, S.N. Application of soft computing techniques for maximum power point tracking of SPV system. Sol. Energy 2017, 141, 182–202. [Google Scholar] [CrossRef]
- Ahmed, J.; Salam, Z. A critical evaluation on maximum power point tracking methods for partial shading in PV systems. Renew. Sustain. Energy Rev. 2015, 47, 933–953. [Google Scholar] [CrossRef]
- Wen, H.; Chu, G.; Hu, Y.; Jiang, L. A novel power-increment based GMPPT algorithm for PV arrays under partial shading conditions. Sol. Energy 2018, 169, 353–361. [Google Scholar] [CrossRef]
- Rezk, H.; Fathy, A.; Abdelaziz, Y. A Comparision of different global MPPT techniques based on meta-heuristic algorithms for photovoltaic system subjected to partial Shading conditions. Renew. Sustain. Energy Rev. 2017, 74, 377–386. [Google Scholar] [CrossRef]
- Abokhalil, A. Maximum Power Point Tracking for a PV System using Tuned Support Vector Regression by Particle Swarm Optimization. J. Eng. Res. 2020, 8, 4. [Google Scholar] [CrossRef]
- Gangwar, P.; Singh, R.; Tripathi, R.P.; Singh, A.K. Effective solar power harnessing using a few novel solar tree designs and their performance assessment. Energy Sources Part A Recovery Util. Environ. Eff. 2019, 41, 1828–1837. [Google Scholar] [CrossRef]
- Mohanty, B.; Tripathy, S.A. Teaching learning based optimization technique for optimal location and size of DG in distribution network. J. Electr. Syst. Inf. Technol. 2016, 3, 33–44. [Google Scholar] [CrossRef]
- Rezk, H.; Fathy, A. Simulation of global MPPT based on Teaching-Learning based optimization technique for partially shaded PV system. Electr. Eng. 2017, 99, 847–859. [Google Scholar] [CrossRef]
- Fathy, A.; Rezk, H. A novel methodology for simulating maximum power point trackers using Mine blast optimization and teaching learning based optimization algorithm for partially shaded photovoltaic system. J. Renew. Sustain. Energy 2016, 8, 023503. [Google Scholar] [CrossRef]
- Crepinsek, M.; Liu, S.; Mernik, L. A note on teaching learning based optimization algorithm. Inf. Sci. 2012, 212, 79–93. [Google Scholar] [CrossRef]
- Sundareswaran, K.; Peddapati, S.; Palani, S. MPPT of PV Systems Under Partial Shaded Conditions through a Colony of Flashing Fireflies. IEEE Trans. Energy Convers. 2014, 29, 463–472. [Google Scholar] [CrossRef]
- Farzaneh, J.; Keypour, R.; Khanesar, M.A. A New Maximum Power Point Tracking Based on Modified Firefly Algorithm for PV System Under Partial Shading Conditions. Technol. Econ. Smart Grids Sustain. Energy 2018, 3, 9. [Google Scholar] [CrossRef]
- Mohanthy, S.; Subudhi, B.; Ray, P.K. A Grey wolf Assisted Perturb and Observe MPPT Algorithm for a PV system. IEEE Trans. Energy Conversat. 2017, 32, 340–347. [Google Scholar] [CrossRef]
- Eltamaly, A.M.; Farh, H.M.H. Dynamic global maximum power point tracking of the PV systems under variant partial shading using hybrid GWO-FLC. Sol. Energy 2019, 177, 306–316. [Google Scholar] [CrossRef]
- Mohanthy, S.; Subudhi, B.; Ray, P.K. A new MPPT design using Grey Wolf optimization technique for photovoltaic system under partial shading conditions. IEEE Trans. Sustain. Energy 2016, 7, 181–188. [Google Scholar] [CrossRef]
- Songyang, L.; Haipeng, Y.; Miao, W. Cat swarm optimization algorithm based on the information interaction of subgroup and the top-N learning strategy. J. Intell. Syst. 2022, 31, 489–500. [Google Scholar] [CrossRef]
- Knypiński, Ł. Constrained optimization of line-start PM motor based on the gray wolf optimizer. Eksploat. Niezawodn. Maint. Reliab. 2021, 23, 1–10. [Google Scholar] [CrossRef]
- Sadeghi, F.; Larijani, A.; Rostami, O.; Martín, D.; Hajirahimi, P. A Novel Multi-Objective Binary Chimp Optimization Algorithm for Optimal Feature Selection: Application of Deep-Learning-Based Approaches for SAR Image Classification. Sensors 2023, 23, 1180. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).