Abstract
The method of analyzing data known as Discrete Mathematical Analysis (DMA) incorporates fuzzy mathematics and logic. This paper focuses on applying DMA to study the morphology of time series by utilizing the language of fuzzy mathematics. The morphological characteristics of the time series, such as background, slopes, and vertices, are considered fuzzy sets within the domain of its definition. This allows for the use of fuzzy logic in examining the morphology of time series, ultimately leading to the detection of anomalies.
1. Introduction
Until recently, when working with a record (time series), a researcher could rely only on statistical methods of spectral–temporal analysis. Recently, the situation has changed. New methods for analyzing a record have appeared, associated with the development of artificial intelligence, and these methods allow researchers to take more active positions in relation to records, so that, in particular, they can express experience and knowledge at the formal level.
The subject of this work is one of these methods. Informally, the method is used when a researcher is interested in some property of a record of a local character. More precisely, he or she is interested in the dynamics of manifestation of a property in the record, because the investigator concerned believes that having this knowledge gives him or her an opportunity to better understand the nature of the process behind the record.
Thus, two things must be strictly understood: what a local property (hereinafter referred to as property) of a record is and what its dynamics are. All this is conducted on the basis of discrete mathematical analysis (DMA), which is a new approach to data analysis that focuses on the researcher and occupies an intermediate position between hard mathematical methods and soft analytical ones [1,2,3,4,5].
DMA in data analysis uses scenarios of classical mathematics, in which the fundamental foundations of the scenarios are replaced by fuzzy models of their discrete counterparts.
The solution of the problem within the DMA framework consists of two parts. The first part is informal, and consists of examining the logic of the researcher, introducing the necessary concepts, and explaining the scheme and principles of the solution. The second part has a formal character, wherein, with the help of the DMA apparatus, all concepts receive a strict definition within the framework of fuzzy mathematics (FM) and fuzzy logic (FL), and schemes and principles become algorithms. Guided by this, we turn to the concepts of Dynamics and Property.
Dynamics The informal first part of the dynamics concept in solving a problem is as follows. With a given relief and questions of a local morphological nature, we send the researcher on a journey through the relief and ask the researcher to answer the following question: “To what extent, being on the relief at a given moment in time, does he or she feel himself or herself to be on the relief’s surface, slope, peak, depression, and so on?”
Dynamics The formal second part of the dynamics concept in solving a problem involves formalizing the researcher’s answers by means of fuzzy logic. The result is a family of morphological measures that express the local morphological structure of the relief (background, trend, peak, depression, and so on).
Property The informal first part of the property concept in solving the problem involves the researcher sliding over the record, estimating by positive numbers the degree of manifestation of the property of interest to him or her in the same small fragments of the record. These scores are assigned by the researcher to the fragment centers. So, from the original record, the researcher arrives at a non-negative function, which is called straightening the record, with respect to the property of interest to the researcher.
Property The formal second part of the property concept in solving the problem is the third part of the article. The researcher researching a record can be interested in any property. Nevertheless, the reality, in regard to the stability of such interest, is that there is a circle of basic straightening that most researchers want to deal with. Behind each of the straightening is a fundamental mathematical concept. The paper presents the following rectifications: energy (dispersion, continuity), irregularity (frequency, length), and spread (Cauchy fundamentalism, continuity). The set is open to replenishment, which is dictated by practice, and provides greater flexibility to the analysis of a record within the framework of DMA.
Let us summarize the intermediate result. The researcher chooses a property, builds its rectification on the record and studies the dynamics of the manifestation of the property on the record through the morphology of its rectification.
Morphology is a collection of fuzzy structures in time associated with the morphological properties of straightening. In the simplest case, this is a set of fuzzy structures constructed in a work that are responsible for the simplest basic morphological properties of straightening. Further, NL makes it possible to express not only the complex property of one straightening, but also the properties related to several instances of straightening at the same time. In other words, it becomes possible to study a record based on the totality of their properties, in the form of their manifestations, on the record.
The purpose of the work is to create a morphological analysis of a record within the framework of DMA using NM and NL.
The structure of the work is based on two parts. The first part involves modeling in the form of fuzzy answer structures, analyzing the researcher’s record in regard to 16 questions concerning its local morphological structure (background, trend, top, bottom, and so on). The second part implements the systemic point of view on the record, connecting a system of rectifications with it, that quantitatively express the manifestation of one or another local property of the record.
Applying the first part with the second gives the main result. Let us formulate it.
The result of the work is a procedure for morphological analysis of a record based on a system of its rectifications, carried out using a family of fuzzy structures responsible for the simplest basic morphological properties of the rectification
Let us look at some examples.
Example 1.
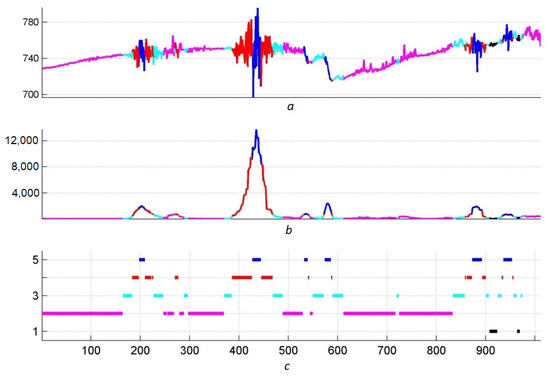
The more interesting (fundamental) the property behind the rectification, the more interesting its dynamic monitoring (dynamic analysis). This is exactly what the property is in this example. This is the local dispersion of a record, closely related to its continuity, and, therefore, to the regularity of the process behind it. Figure 1a shows the original record in black. The relief of its local dispersion is shown in Figure 1b. Four properties were chosen for its dynamic analysis: the surface of the relief, the boundary of the hill on it, its slope and top.

Figure 1.
Morphological parsing of the record, (a) is the original record, (b) is the local variance, (c) is the encoding The corridor in the first part of the figure provides dynamic (qualitative) understanding of the stochasticity of the record.
The fuzzy dynamic expressions are constructed according to the algorithms of the article, which serve as the basis for monitoring. The result is a morphological analysis of the variance, that is, its dynamic coding by a property that is most strongly fuzzy at the moment.
Figure 1c shows the result of such coding: 0 (lilac)—background, 1 (green)—border, 2 (blue)—slope, 3 (red)—peak. The colors help you understand what the encoding looks like on and through the rectifier of the original recording. The coloring of the stochastic corridor around the original record in Figure 1a shows its different stages and is useful for understanding what is happening on the record.
Example 2.
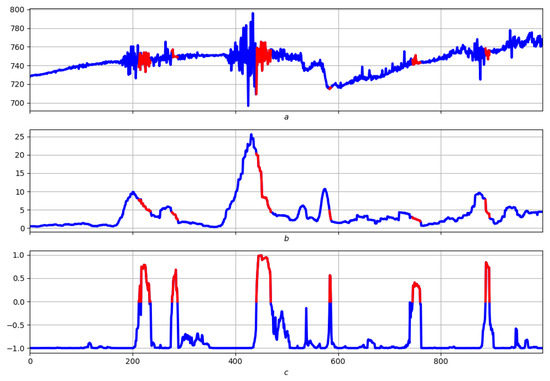
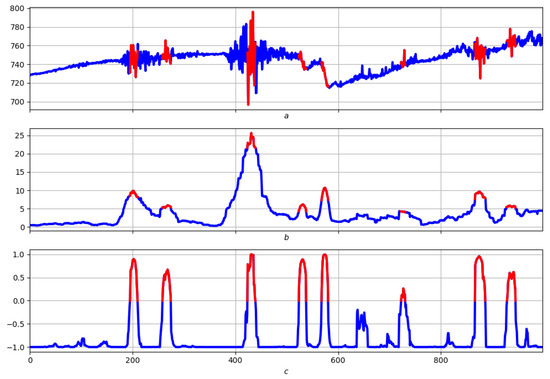
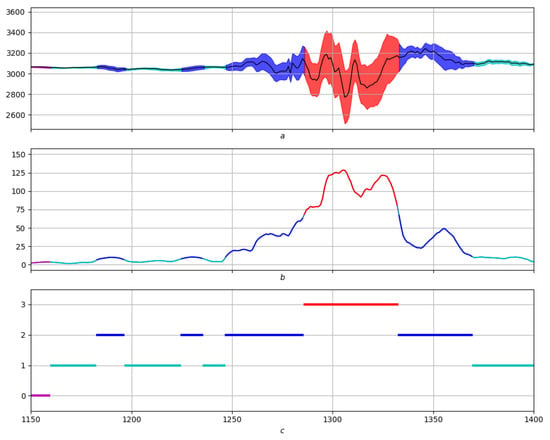
Here, the property is the local length of the record, as well as the dispersion, which are of fundamental importance, and depend on many factors. The most important factors are the local differential and spectral characteristics of the record. In this case, the basis for monitoring the straightening relief is its seven morphological properties, which are the following: the background and three groups of dual characteristics, left/right foot, left/right slope, top/bottom.
Fuzzy dynamic expressions are built for the above, acting as the basis for monitoring the “length" straightening on the original record. The background, left foot, right slope and top are shown in the third drawing in Figure 2, Figure 3, Figure 4 and Figure 5. The first two are the same (original notation and “length" straightening). The red color represents the region of the strongest manifestation of the corresponding property.

Figure 2.
(a)—record. (b)—the relief of the local length of the record. (c)—measure expressing the “background” on the relief of the local length of the record.

Figure 3.
(a)—record. (b)—the relief of the local length of the record. (c)—measure expressing the “beginning of a mountain” on the relief of the local length of the record.

Figure 4.
(a)—record. (b)—the relief of the local length of the record. (c)—measure expressing the “right slope” on the relief of the local length of the record.

Figure 5.
(a)—record. (b)—the relief of the local length of the record. (c)—measure expressing the “top of a mountain” on the relief of the local length of the record.
Example 3.
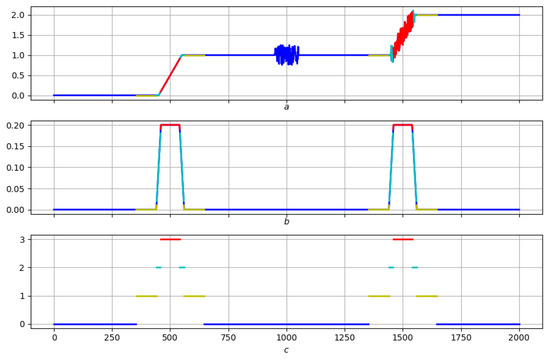
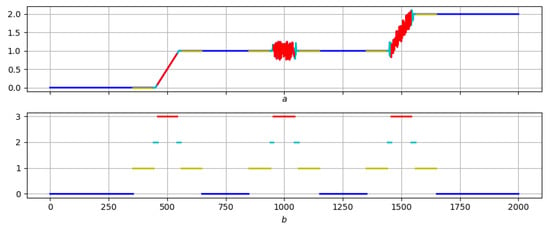
This example illustrates the possibilities of NL in morphological analysis. Figure 7 shows the morphological analysis of the “trend" property according to the analysis scenario of the Example 1, with colors 0 (blue)—background, 1 (yellow)—foot, 2 (cyan)—slope, 3 (red)—top.

Figure 7.
(a)—record; (b)—the relief of the local trend of the record; (c)—morphological analysis of the record and relief of the local trend.
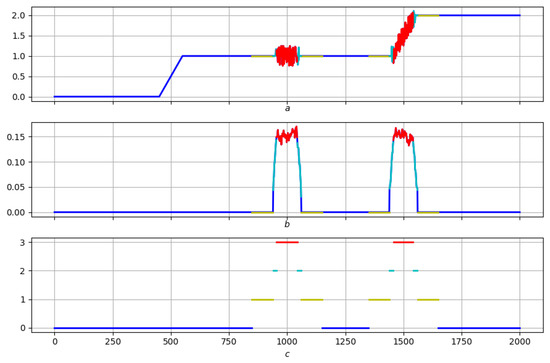
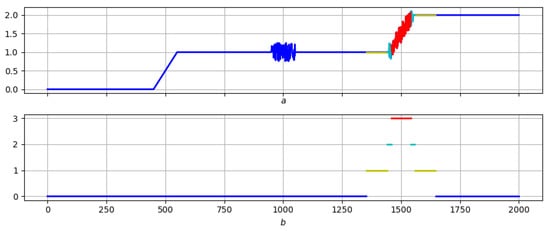
In accordance with the exact same scenario, and with the same colors. Figure 8 shows the result of a morphological analysis of the “length" property for the same record.

Figure 8.
(a)—record; (b)—the relief of the local length of the record; (c)—morphological analysis of the record and relief of the local length.
The fuzzy structures of both examples of monitoring, corresponding to the same morphological properties, can be interconnected using one or another fuzzy binary operation.
As a result, four fuzzy structures are obtained. These serve as the basis for the fuzzy binary operation, of one or another kind, in monitoring the original record, but by means of the properties “length" and “trend" at the same time. Figure 9 shows the result of joint monitoring, based on the disjunction “max", and Figure 10 shows the result of joint monitoring, based on the conjunction “min”.

Figure 9.
(a)—record; (b)—result of joint monitoring based on the disjunction “max”.

Figure 10.
(a)—record; (b)—result of joint monitoring based on the conjunction “min”.
The work can be conditionally attributed to fuzzy modeling. It is worth noting, however, that, today, fuzzy modeling is pragmatic, applied in nature and is mainly associated with decision-making in complex systems (economics, engineering, medicine, forecasting and market analysis). To a certain extent, this contradicts the aspirations of the authors, who need data analysis to obtain, mainly, scientific knowledge about the processes and phenomena behind them.
Such an analysis is mostly off-line in nature, and is cautious about simplifications and approximations, which are so popular in fuzzy modeling, thanks to the Zadeh principle, whereby simplifications are welcome only if they do not lead to emasculation and loss of knowledge. The authors believe that this is the morphological coding in the above examples.
In the future, the prognostic application of morphological analysis is of interest. It will require the creation of its online modification. At present, the main thing is the formation of global conclusions and knowledge based on morphological analysis, which has a local character.
These include the “color histogram” in the above examples, namely, the set of percentages of a particular color in morphological coding. Another example is related to the search for heights on a straightening and is addressed in this paper.
We compare our work to the most notable accomplishments in morphological analysis.
Mathematical morphology, created by Serra and Matheron [6,7,8,9], is a mathematical tool for the analysis and processing of geometric structures based on set theory.
It employs non-linear morphological filtering using structural elements for image analysis, such as pre-processing, structure enhancement, background selection, and quantitative description through morphological spectra [10,11,12].
According to Pyt’ev, mathematical morphology involves analyzing images under the assumption that they can be described by a particular class of transformations performed on an image, with the image’s shape obtained as the maximum invariant of this class [13,14,15,16].
The technical basis is convex analysis in Hilbert spaces, and aims to solve two types of problems: recognition of unknown objects on a known scene and dual search for known objects on an unknown scene.
The paper presents a fuzzy logic-based morphology of time series to analyze local properties of the time series, involving two stages: quantitative expression of a property and analysis of its morphology to understand its manifestation in dynamics on the time series.
The technical basis is DMA and fuzzy logic [17,18], and it differs from traditional morphological analysis options that focus on studying nonlocal characteristics, such as trends, seasonality, cyclicality, autocorrelations, and spectrum [19,20,21,22,23].
Similarly, fuzzy temporal analysis of time series has recently gained popularity, primarily focusing on complex series with many implicit relationships and factors such as those of the financial market and economy [24,25,26].
Finally, the authors have a positive experience in examining records for anomalies through straightening of their properties. Elevations on the straightening correspond to anomalies in the records. A natural continuation of research of this kind was a more thorough study of the morphology (geometry) of straightening, not limited to elevations.
If the properties behind the straightening are chosen correctly, then such a study is very meaningful, contributing greatly to understanding the morphology of the record, and, through this, about the process behind the record. The morphology of a record is closely related to the nature of the process that it expresses. Morphology allows you to encode, compress a record without losing its significant features, and effectively highlight the most significant features.
All of the above were motivations for this work. The work was carried out within the framework of DMA according to its scenarios and its technique. First, the informal logic of the study is addressed and, then, its exact implementation, without which the operation of the algorithms is impossible.
The result of the work has a high degree of novelty and differs from traditional variants of morphological analysis of records. In addition, it represents an approach to record analysis in which the researcher has an active position, because the choice of properties and parameters is up to the researcher. In its present form, the presented analysis requires knowledge of the entire record, that is, it has an off-line character and is intended mainly for scientific purposes.
2. Materials and Methods
2.1. DMA–Morphological Analysis: Nonformal Logic
The definition domain T of a record x is a finite regular set of nodes with the discretization parameter h:
Let denote the space of all records on T.
2.1.1. Elementary Measures
Suppose that, for any record at each node in the scale of the segment , we can answer the following four questions with the help of fuzzy structures, which we call elementary measures and denote by , , , :
Elementary measures must have an additional normalization. If is one of the elementary measures (), then the value of must be close to 1, when the property corresponding to at node t is satisfied, to record x strongly, or close to –1 to record weakly.
2.1.2. Morphological Measures
On the basis of four elementary measures and their fuzzy negations, using the fuzzy conjunction ⋀, sixteen measures are constructed that express more complex morphological aspects (features) of the original record x, and allow us to understand its geometry. Therefore, such measures are called morphological or geometric measures.
Let us define these as follows. Let us call the index a four-dimensional Boolean vector , where ∗ runs through the situations described in (1) and . In other words, with coordinates .
Using the fuzzy conjunction ⋀, each index i defines a fuzzy measure (structure) on T:
Let us present them more explicitly:
2.1.3. Conversion of the Geometry of One-Dimensional Relief into the Language of Fuzzy Logic
Let us first make two important remarks in regard to what follows:
- −
- It is difficult to say how geometric a record x appears in the region of node t with condition , but the situation is clear, which is “evenness” on the record x near node t in context ∗.
- −
- A large value of any measure (2) is equivalent to large values of all the terms included in its ⋀-conjunction.
Numerous studies, and this is referred to below, have provided grounds for the conclusion that, for any morphological measure , the relation , as a rule, is closely related to the well-defined local geometry P of the record x in the region of the node t.
Thus, the conversion of the geometry of one-dimensional relief into the language of fuzzy logic means that, if there is a geometry P near the node t on record x, then the corresponding measure at node t is close to 1.
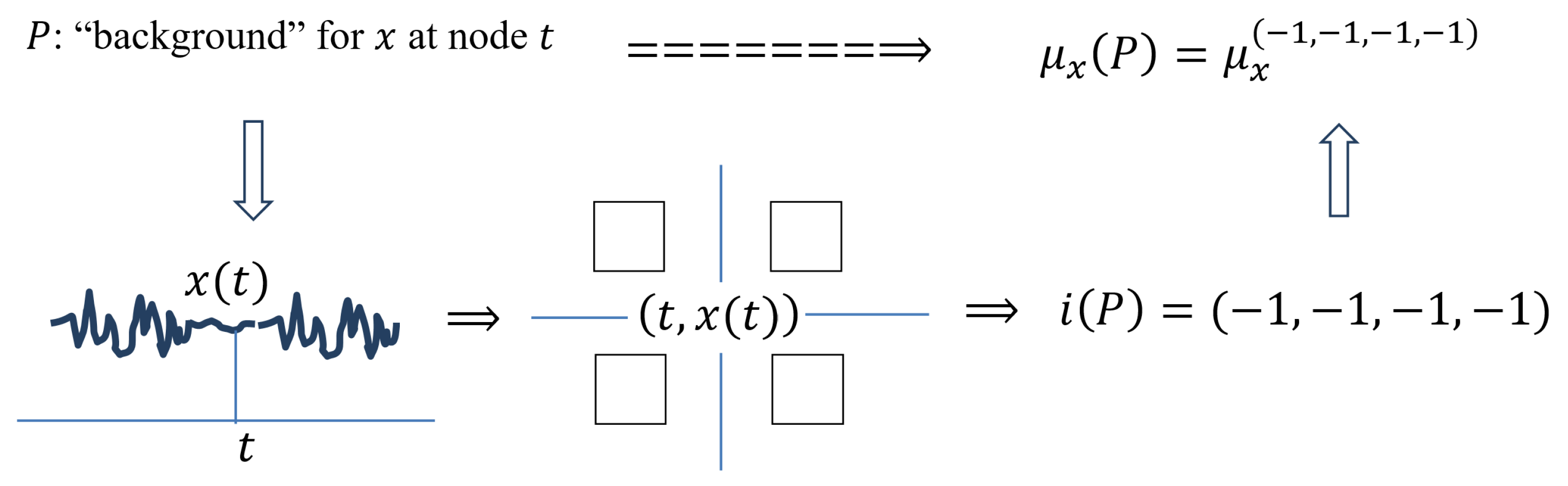
Figure 11 explains how such a conversion works. A graphical model, , is assigned to the geometric property P, and, then, to its Boolean perception with the help of squares. A full square is linked to, ↔, many of the graph in the corresponding square with the center in its point in context ∗, while an empty square ↔ few of the graph in the corresponding square with the center in its point in context ∗. helps to form the Boolean index , and, from it, the morphological measure is formed, representing property P.
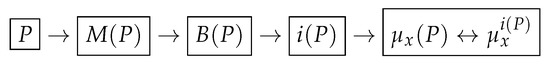
Figure 11.
Scheme for conversion of one-dimensional relief into the language of fuzzy logic.
P: “Background” for x at Node t
Taking into account the above remarks, a large value of the measure at a node t means that all elementary measures are weakly expressed in it, and, therefore, all of them must be small.
P: “Beginning of Growth (Mountain)” for x at Node t
In t for , minimality and maximality are weakly expressed on the left, while there is strongly expressed minimality and weakly expressed maximality on the right. Therefore, all elementary measures, excepting in t, must be small, while the exception is large.
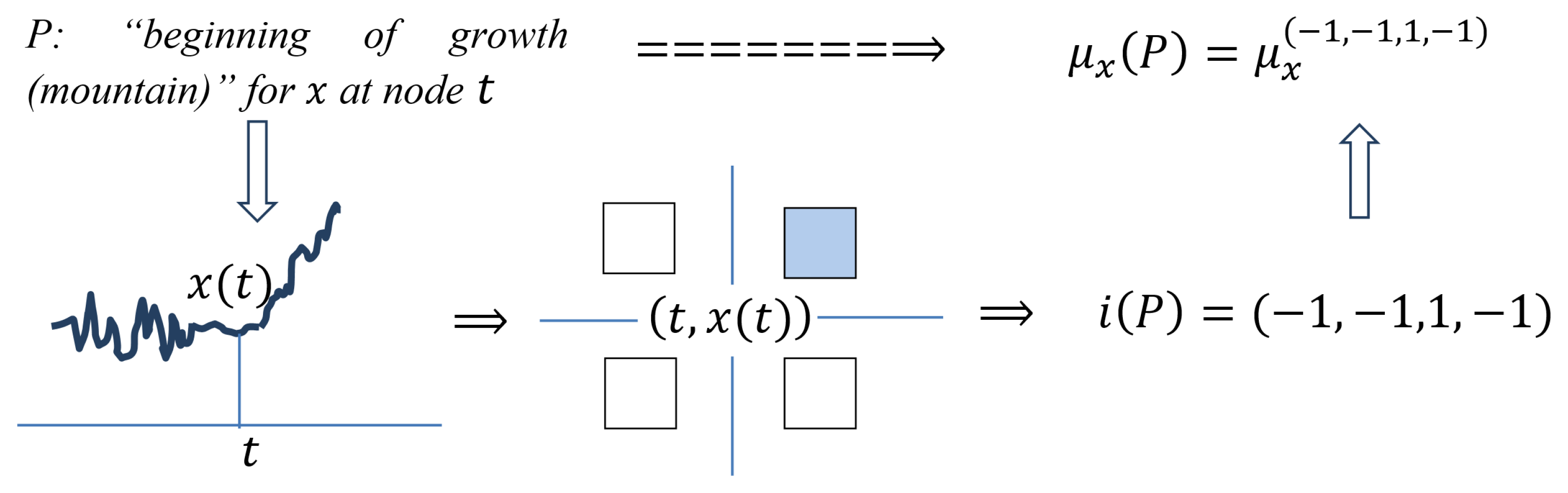
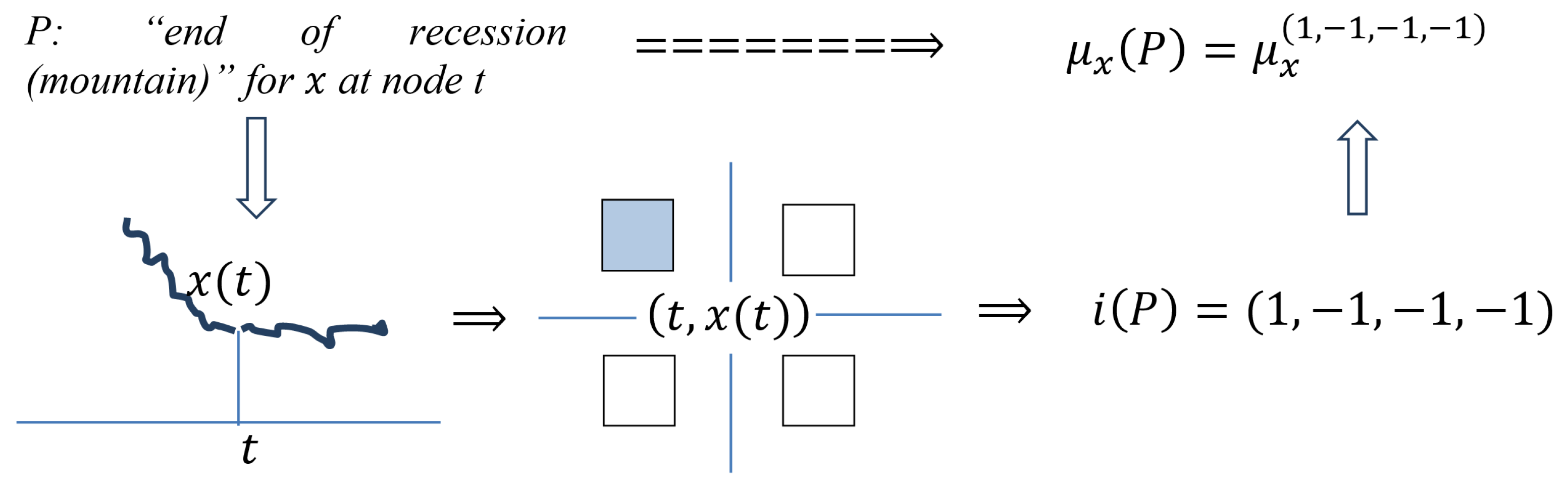
P: “End of Recession (Mountain)” for x at Node t
In t for the minimality and maximality are weakly expressed on the right, while the minimality is strongly expressed, and the maximality weakly expressed, on the left. Therefore, all elementary measures, excepting in t, must be small, while the exception is large.
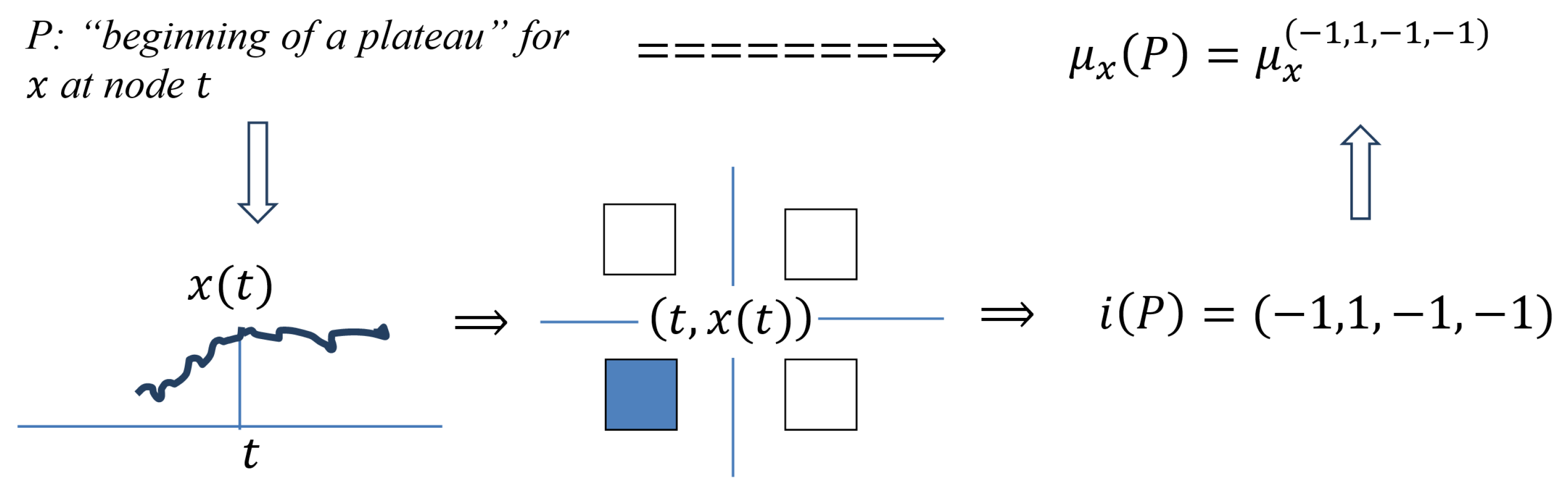
P: “Beginning of a Plateau” for x at Node t
In t for , the minimality is weakly expressed and the maximality strongly expressed on the left, while minimality and maximality are weakly expressed on the right. Therefore, all elementary measures, excepting in t, must be small, while the exception is large.
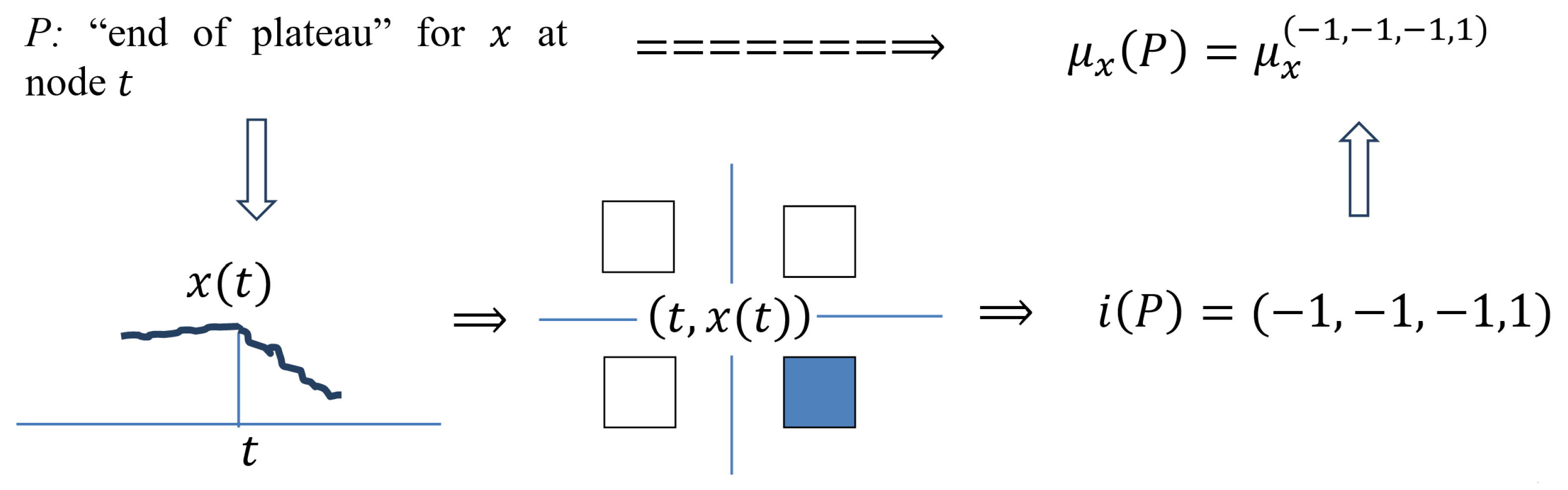
P: “End of Plateau” for x at Node t
In t for minimality and maximality are weakly expressed on the left, while minimality is weakly expressed, and maximality is strongly expressed, on the right. Therefore, all elementary measures, excepting in t, must be small, while the exception is large.
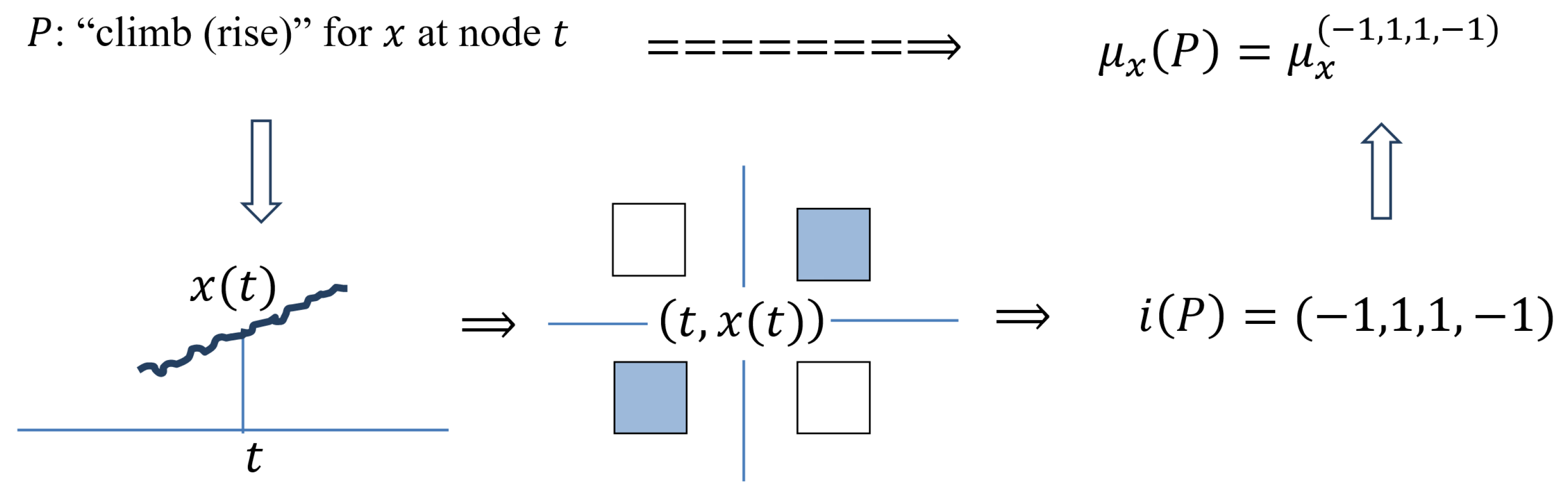
P: “Climb (Rise)” for x at Node t
In t, for , minimality is weakly expressed and maximality strongly expressed on the left, while the opposite is true on the right, where maximality is weakly expressed and minimality is strongly expressed. Therefore, the elementary measures and in t must be small, while the measures and are large.
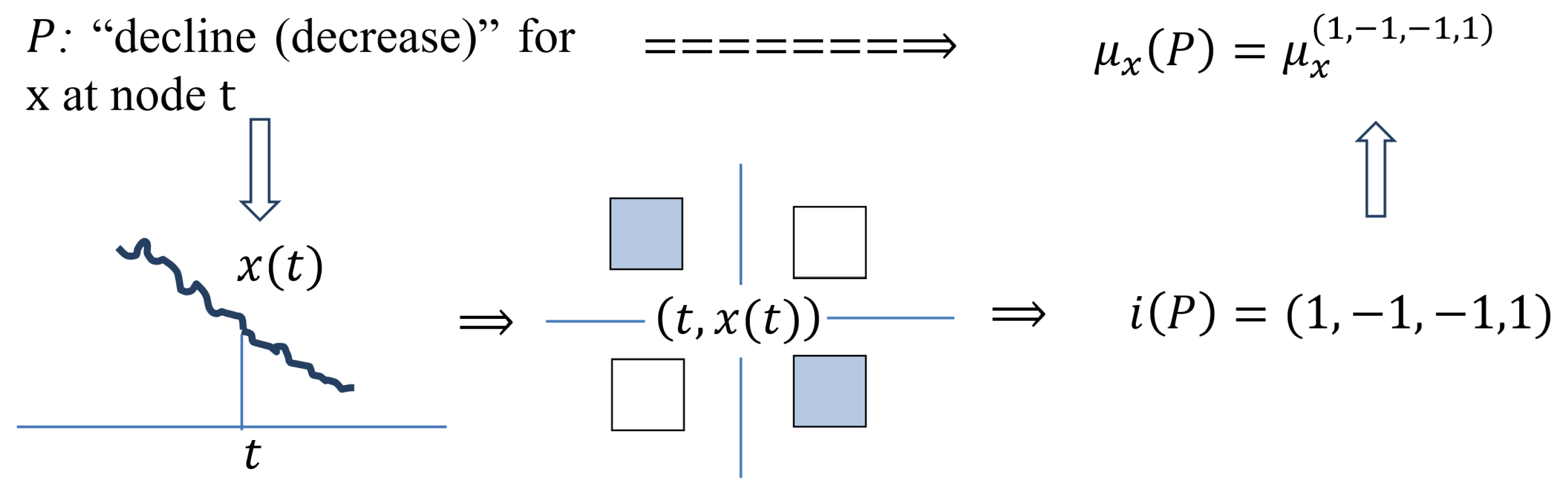
P: “Decline (Decrease)” for x at Node t
In t for , maximality is weakly expressed, and minimality is strongly expressed, on the left, while the opposite is true on the right, where minimality is weakly expressed and maximality is strongly expressed. Therefore, the elementary measures and in t must be large, while the measures and are small.
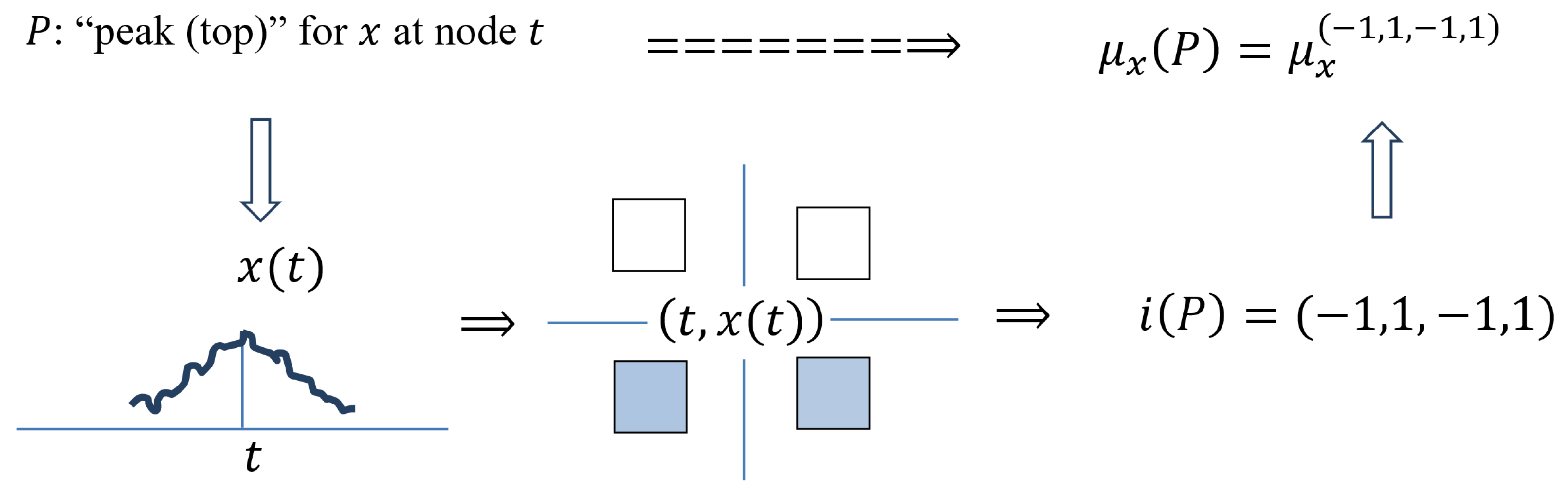
P: “Peak (Top)” for x at Node t
In t for , on the left and on the right, minimality is weakly expressed and maximality is strongly expressed. Therefore, the elementary measures and in t must be small, while the measures and are large.
P: “Depression (Bottom)” for x at Node t
In t for , on the left and on the right, there is weakly expressed maximality and strongly expressed minimality. Therefore, the elementary measures and in t must be small, while the measures and are large.
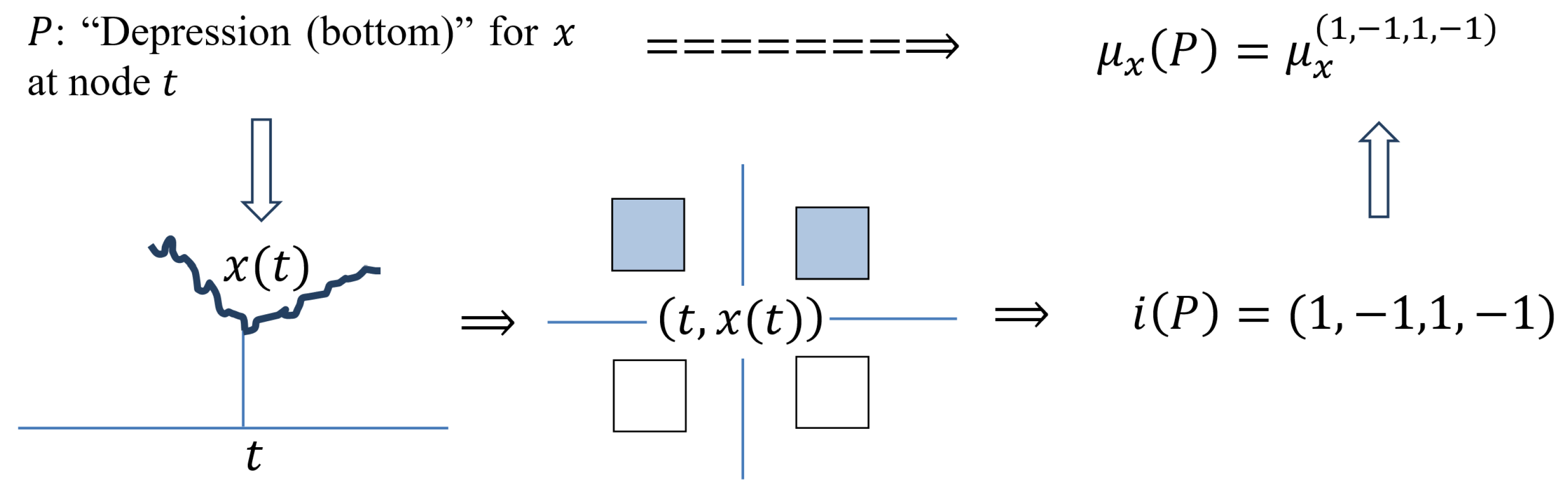
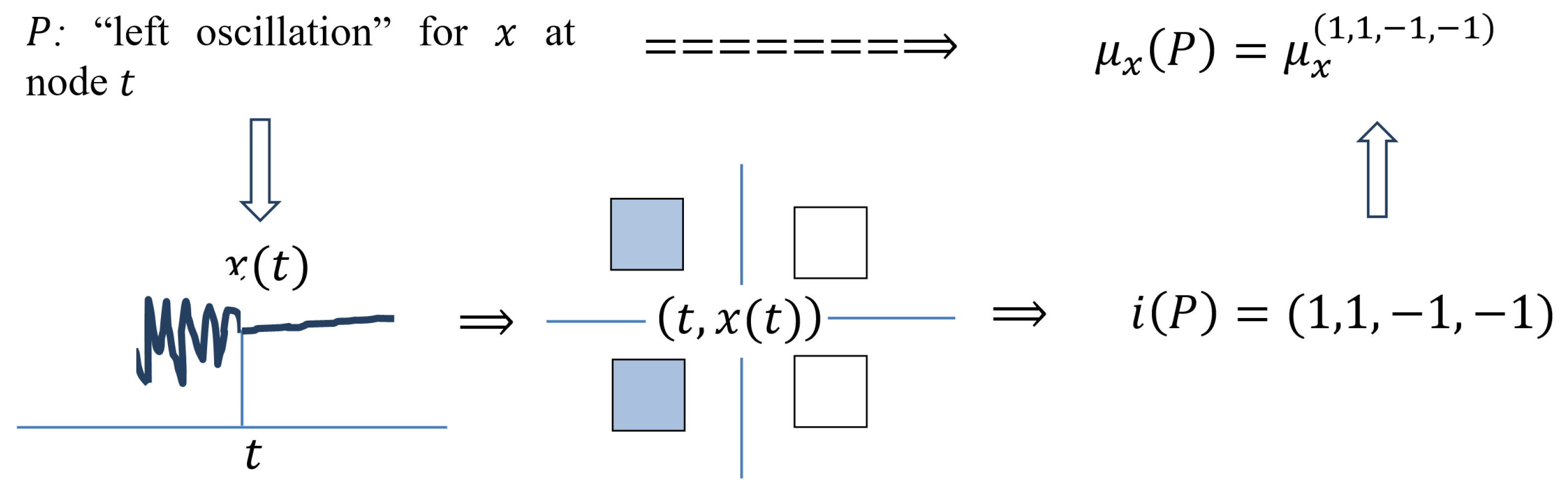
P: “Left Oscillation” for x at Node t
There is a significant oscillation to the left of t, and, therefore, the maximality and minimality with respect to are strongly expressed, while weakly so to the right. Therefore, the elementary measures and at t must be large, while the measures and are small.
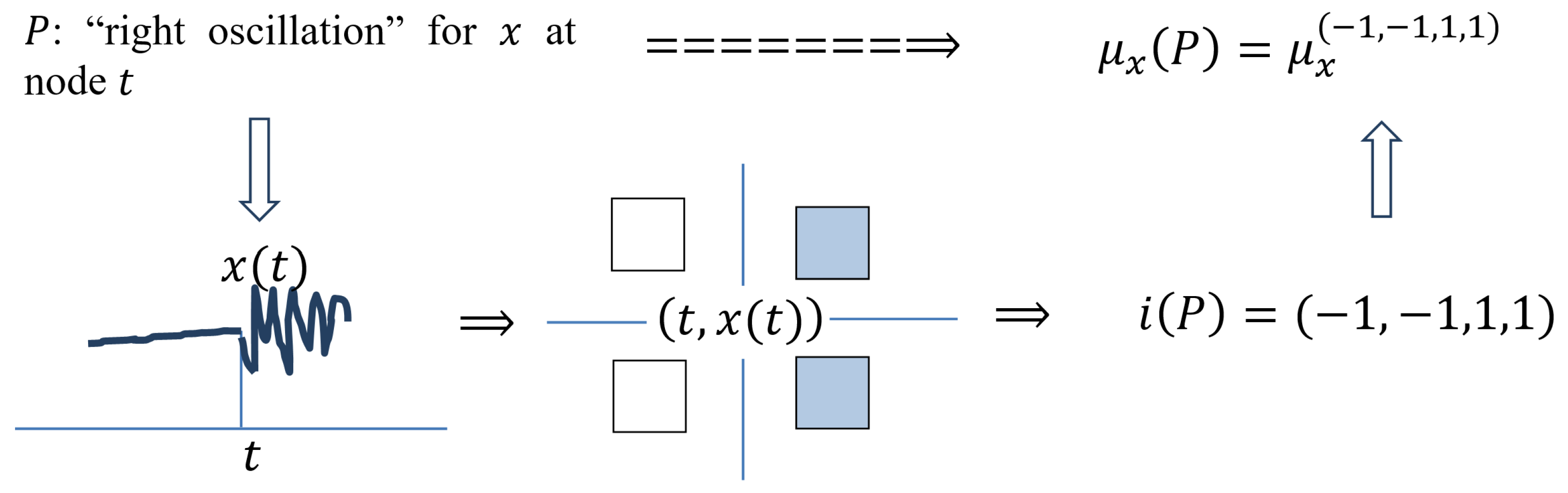
P: “Right Oscillation” for x at Node t
There is a significant oscillation to the right of t, and, therefore, the maximum and minimum , with respect to , are strongly expressed, while weakly so on the left. Therefore, the elementary measures and in t must be large, while the measures and are small.
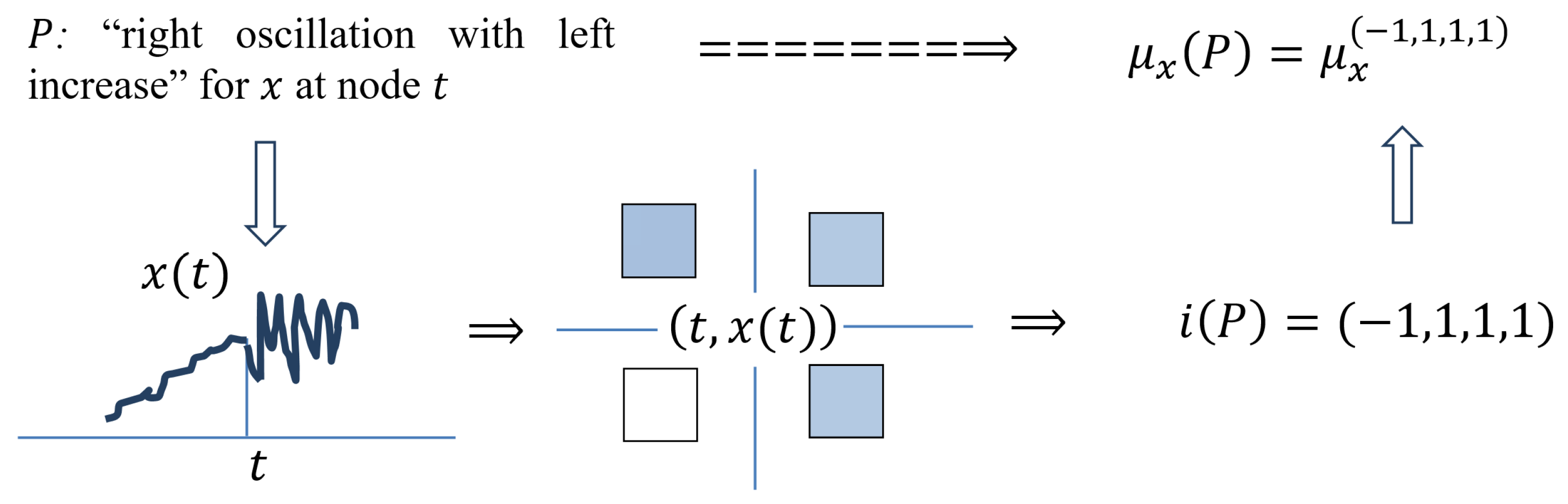
P: “Right Oscillation with Left Increase” for x at Node t
To the left of t, the minimality for is weakly expressed, and the maximality is strongly expressed, while on the right, both minimality and maximality for are strongly expressed. Therefore, all measures, excepting in t are large, and the exception is small.
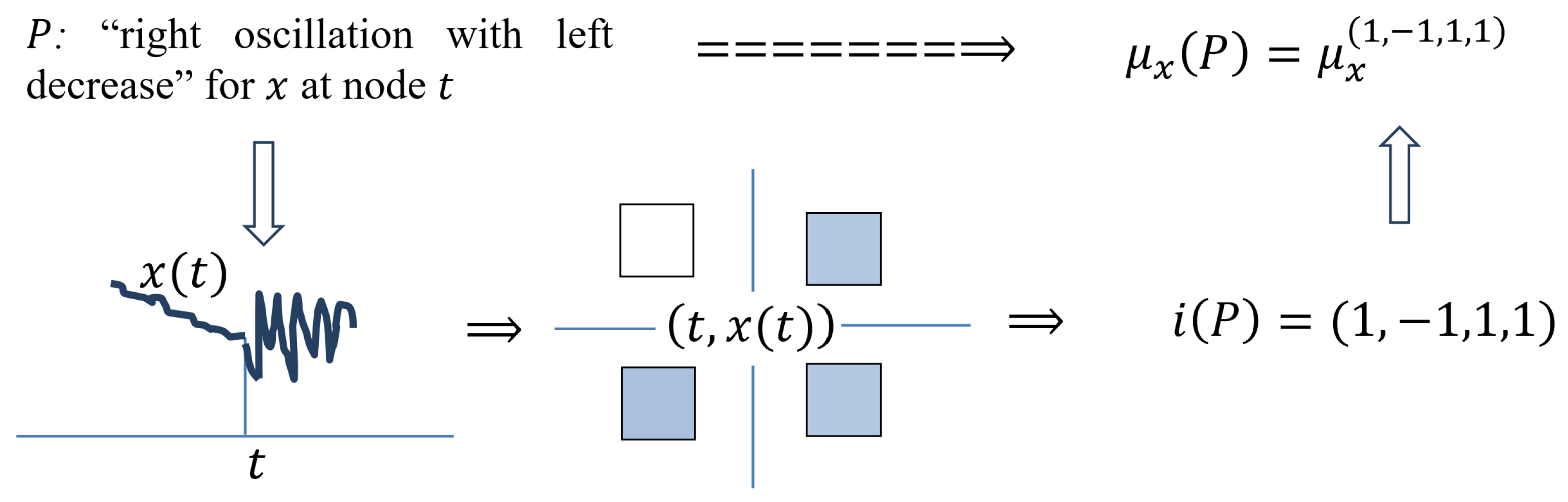
P: “Right Oscillation with Left Decrease” for x at Node t
To the left of t, minimality for is strongly expressed, and maximality is weakly expressed, while on the right, both minimality and maximality for are weakly expressed. Therefore, all measures, excepting in t, must be large, while the exception is small.
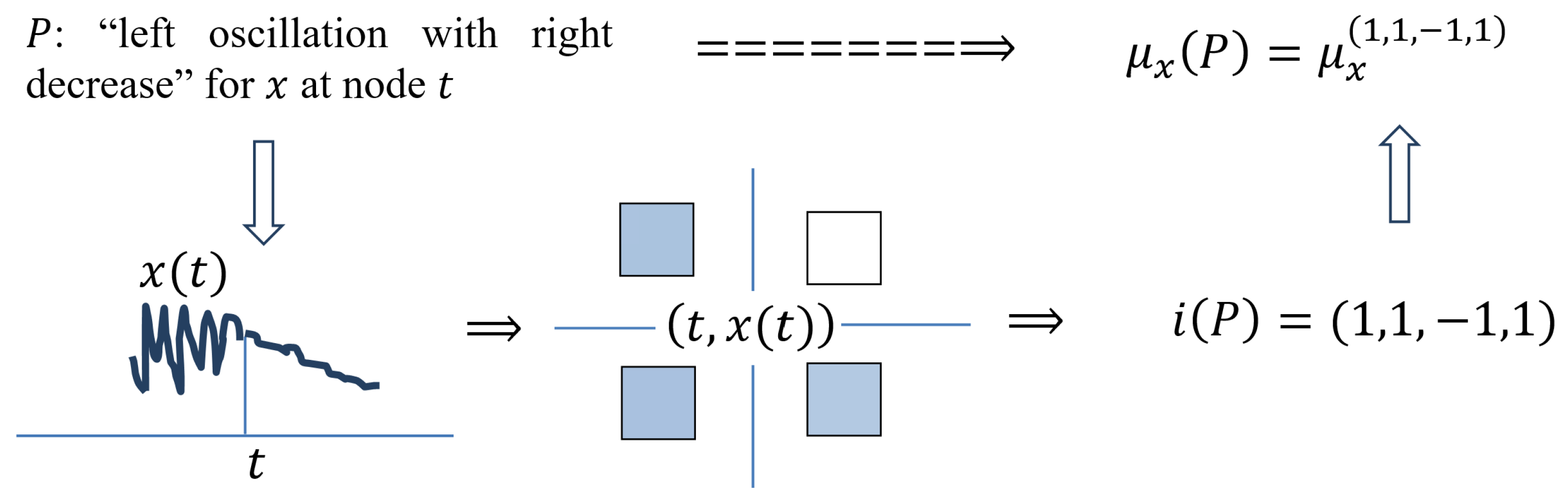
P: “Left Oscillation with Right Decrease for x at Node t
To the left of t, the maximality and minimality for are strongly expressed, while on the right, the minimality is weakly expressed and the maximality is strongly expressed. Therefore, all measures, excepting in t, must be large, while the exception is small.
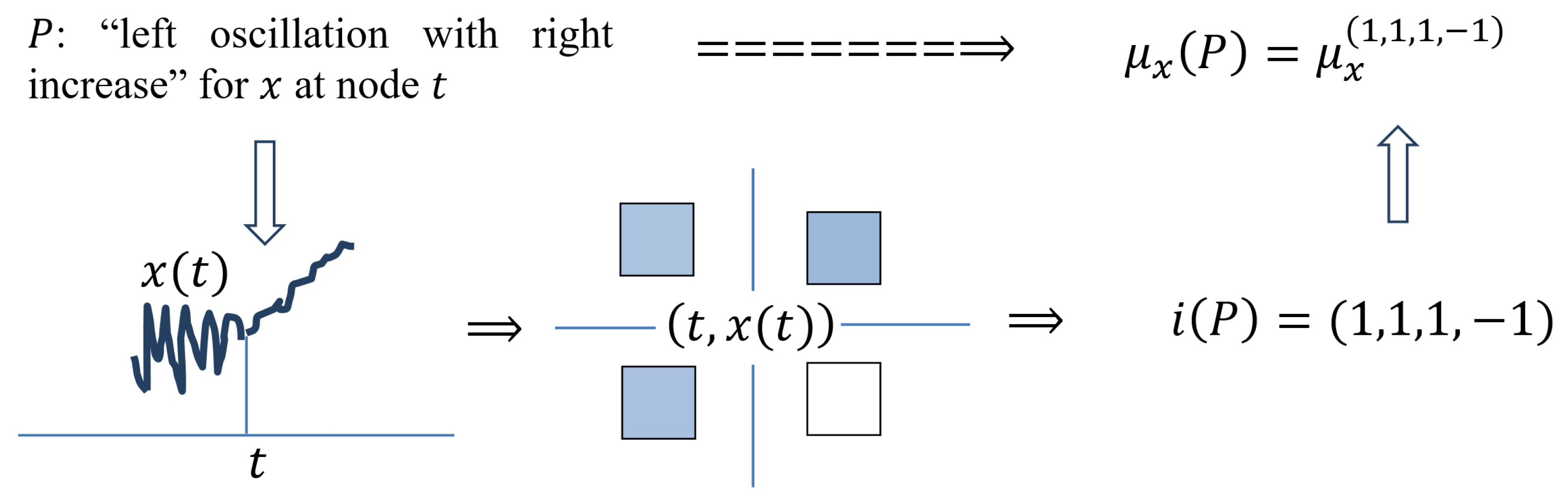
P: “Left Oscillation with Right Increase” for x at Node t
To the left of t, the maximality and minimality for are strongly expressed, while on the right, the minimality is strongly expressed, and the maximality is weakly expressed. Therefore, all measures, excepting in t, must be large, while the exception is small.
P: “Two-Way Oscillation” for x at Node t
In t, the minimality and maximality are strongly expressed, both on the left and on the right. Therefore, all elementary measures must be large.
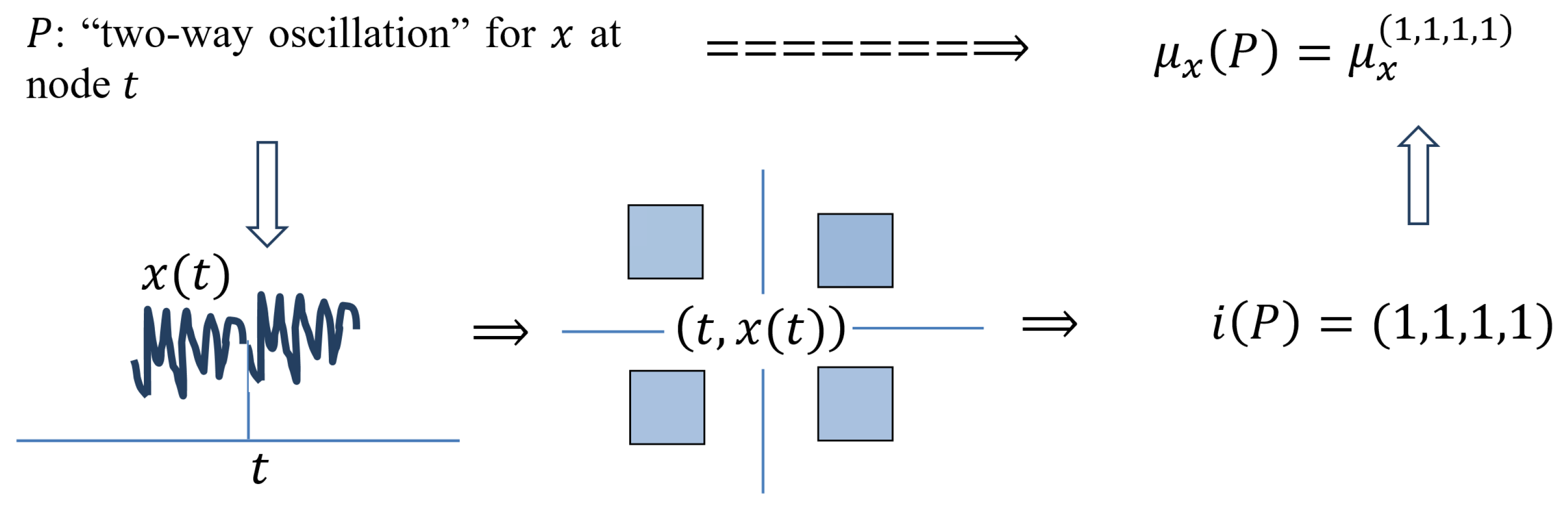
2.1.4. Conclusions
As stated in the introduction, DMA problem-solving involves two components: informal and formal. Our objective in this study was to develop a modified version of time series morphological analysis, and we completed the initial informal phase of the solution.
2.2. Next Steps
The next steps can be divided into three parts:
- −
- the first part involves extracting knowledge about the record by constructing morphological measures based on Section 2.1.3;
- −
- the second part focuses on improving the quality of conversion from one-dimensional relief geometry to fuzzy logic language according to the same Section 2.1.3;
- −
- the third part is similar to the first, but involves more complex scenarios where morphological measures are combined with other approaches to study the original record.
Let us start with the first one. Let us denote the set of all four-dimensional Boolean indices by I, and the set of all morphological measures by . Its value , at each node t, is, in the language of fuzzy sets, which is a representation of the fulfilment in t for x of the geometric properties corresponding to morphological measures.
The multivalued mapping , where is understood as the set of values , is complete, but complex. Therefore, it is necessary to start with the analysis of the measures , or their simple, but important, logical combinations. The analysis of the measures is certainly important, but it is appropriate in connection with one or another of the specific implementations and refers, rather, to the second part of further actions, which are discussed below. Much more interesting is a conversation about the logical combinations of the morphological measures, the analysis of which would provide much knowledge about the record x.
The first such combination, according to the authors, is the classical fuzzy disjunction
It is always non-negative, since, at each node t, there is at least one morphological measure that manifests itself non-negatively. Moreover, if the numerical set does not contain zero, then it contains an unique positive value , which naturally coincides with . The geometric property corresponding to the measure is defined for x in t.
Thus, on the support of the measure , a morphological encoding of the record x arises, which is very interesting for two reasons.
- −
- Reason one is that the kernel of the measure consists of exactly the nodes where at least one of the elementary measures . is equal to zero. In this way,
- −
- Reason two is that, in the general case, and taking into account the large number of nodes , and the stochasticity of x, we can conclude that the kernels are small (“measure zero”) in T, and, therefore, their union is small in T.
The support “almost everywhere” coincides with T, and, therefore, all sorts of statistical characteristics of the encoding and the measure itself are weighty characteristics of the record x and can serve as the basis for its comparison, in particular, in correlation with other records.
The very first and interesting characteristic of this kind ↔ is the histogram of morphological coding on 16 features.
The second part entails the specific implementation of Section 2.1.3. The analysis of the work of certain , in terms of their stability, and dependence on parameters, as well as the employment of techniques to enhance the quality of translation, such as pre-smoothing of record x.
The third part of the further actions is based on the second. Once the possibilities of a particular implementation are known, this knowledge is combined with other approaches to the record x. This allows us to obtain new results of a more general nature, and, in particular, of non-local nature. For instance, in Section 2.3, a specific implementation of Section 2.1 is built and, with the help of its measures of the beginning and end of the mountain, and , the measure of the peak in the fourth part is found and the elevations on the non-negative “smooth” reliefs are non-locally morphologically analyzed. As a consequence, there are very important results, in terms of anomalies on the record x by means of DMA methods (interpreter logic).
2.3. DMA-Morphological Analysis: Formalization
By utilizing DMA methods, it becomes feasible to construct various forms of elementary measures (1), and therefore, also take into account (2) morphological ones.
Moving forward, we need three types of localization at the node t:
where is the local view parameter.
Let us present a construction Q, expressing, in an elementary context ∗, the deviation of the record x from its value .
The series , quantifies the ∗-deviation of the record x from its value at node t. This is only the first half in the definition of the elementary measure at node t. The second half is the answer to the following question: “To what extent can ∗-deviation be considered large?”. The answer is obtained by comparing with the values at the remaining nodes , that is, with the pattern . In DMA, this is called the maximum measure of the series and is denoted as :
There are several of its designs. Here is one of them (-construction):
where
The next part of the work is devoted to the implementation of the scenario (5)–(8) on separate examples for the situations described in Section 2.1.3.
2.3.1. Background
The graph x at the top of Figure 12 has an area with a pronounced background. It is on this that the “background” measure (bottom row in Figure 12), is built for x, taking on the largest values (green dots).
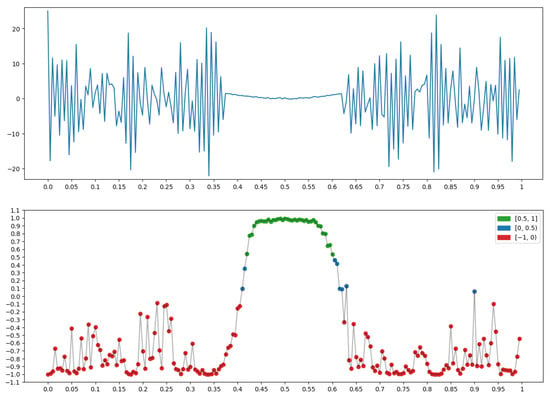
Figure 12.
Property P = “Background”: .
2.3.2. Beginning of Growth (Mountain)
The graph x at the top of Figure 13 has a pronounced rise beginning. It is on this that the “Beginning of the mountain” measure (bottom row in Figure 13), is built for x, taking on the largest values (green dots).
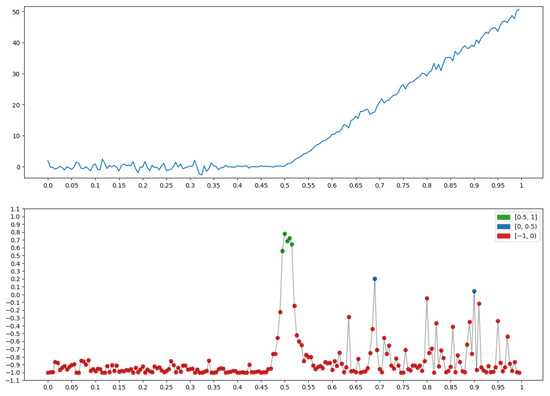
Figure 13.
Property P = “Beginning of growth (mountain)”: .
2.3.3. End of Descend (Mountain)
The graph x at the top of Figure 14 has a pronounced end of the descent. It is on this that the “End of the mountain” measure (bottom row in Figure 14), is built for x, taking on the largest values (green dots).
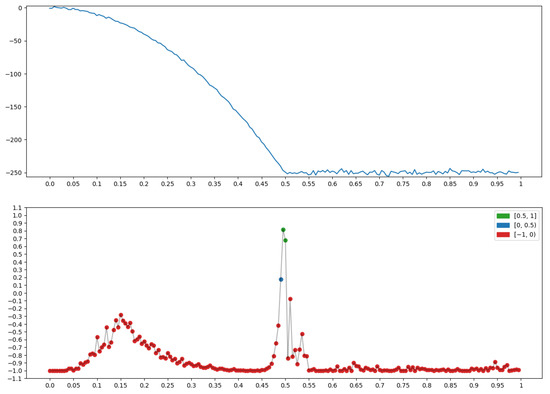
Figure 14.
Property P = “End of descend (mountain)”: .
2.3.4. Beginning of Plateau
The graph x at the top of Figure 15 has a pronounced beginning of the plateau. It is on this that the measure “Beginning of plateau” (Section 2.1.3) (bottom row in Figure 15), is built for x, taking on the largest values (green dots).
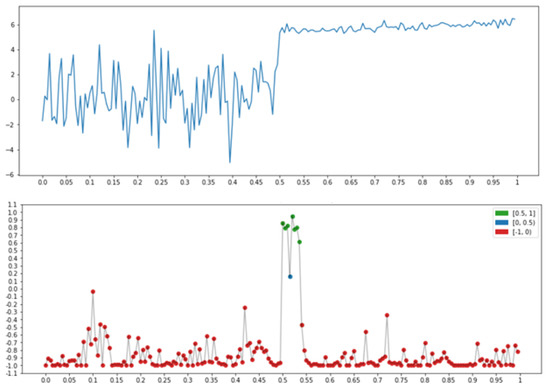
Figure 15.
Property P = “Beginning of plateau”: .
2.3.5. End of Plateau
The graph x at the top of Figure 16 has a pronounced plateau end. It is on this that the measure “End of plateau” (Section 2.1.3) (bottom row in Figure 16), is built for x, taking on the largest values (green dots).
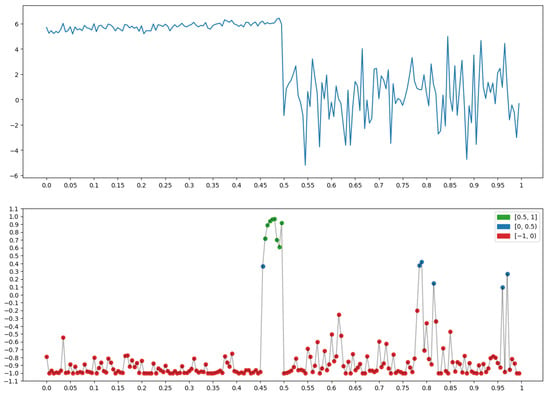
Figure 16.
Property P = “End of plateau”: .
2.3.6. Climb (Growth)
The graph x at the top of Figure 17 has a pronounced growth. It is on this that the measure "Growth" (Section 2.1.3) (bottom row in Figure 17), is built for x, taking on the largest values (green dots).
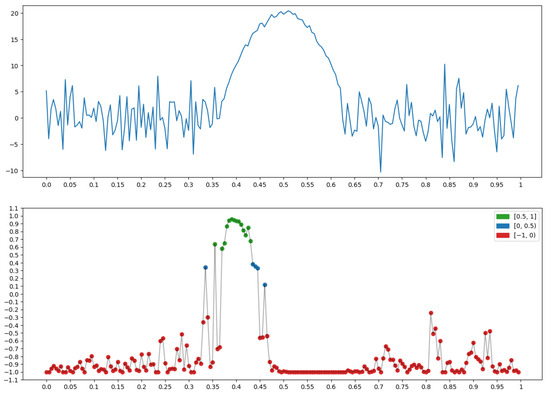
Figure 17.
Property P=“Climb (growth)”: .
2.3.7. Descending (Decreasing)
The graph x at the top of Figure 18 has a pronounced decline. It is on this that the measure "Descending" (Section 2.1.3) (bottom row in Figure 18), is built for x, taking on the largest values (green dots).
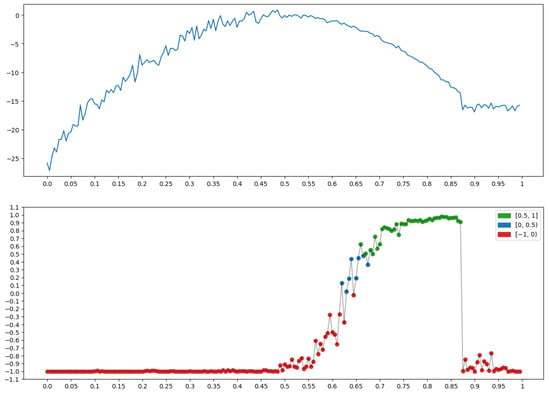
Figure 18.
Property P = “Descending (decreasing)”: .
2.3.8. Peak (Top)
The graph x at the top of Figure 19 has a pronounced peak. It is on this that the measure “Peak” (Section 2.1.3) (bottom row in Figure 19), is built for x, taking on the largest values (green dots).
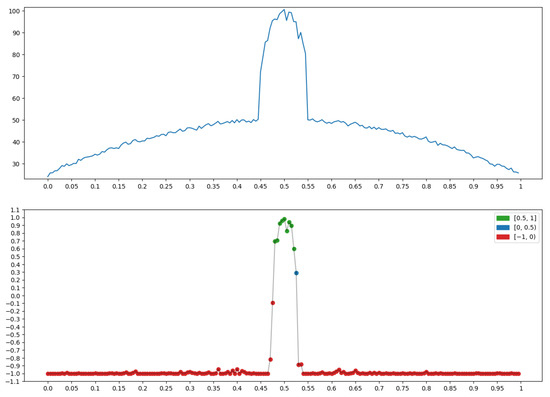
Figure 19.
Property P = “Peak (top)”: .
2.3.9. Depression (Bottom)
The graph x at the top of Figure 20 has a pronounced depression. It is on this that the measure “Depression” (Section 2.1.3) (bottom row in Figure 20), is built for x, taking on the largest values (green dots).
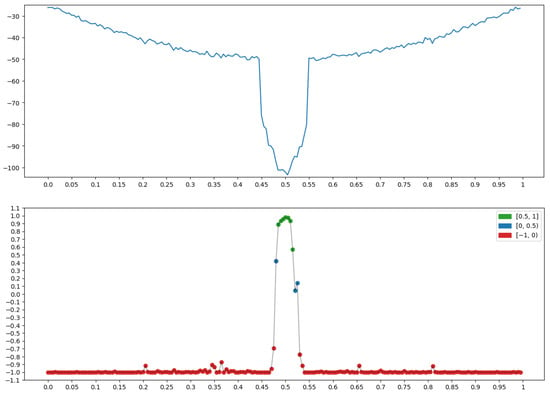
Figure 20.
Property P = “Depression (bottom)”: .
2.3.10. Left Oscillation
The graph x at the top of Figure 21 has a transition from left oscillation to a smooth background. It is on this that the measure “Left oscillation” (Section 2.1.3), is built for x, (bottom row in Figure 21), taking on the largest values (green dots).
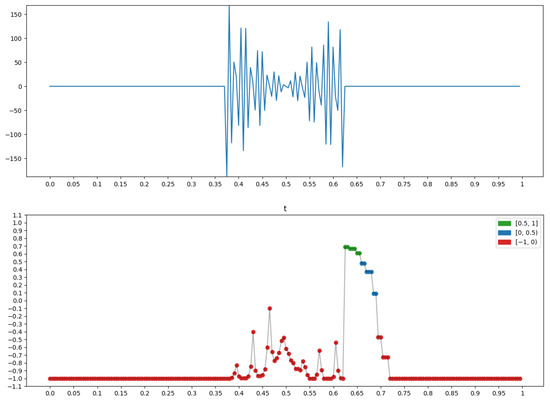
Figure 21.
Property P = “Left oscillation”: .
2.3.11. Right Oscillation
The graph x at the top of Figure 22 has a transition from a smooth background to a right oscillation. It is on this that the measure “Right oscillation” (Section 2.1.3), is built for x, (bottom row in Figure 22), taking on the largest values (green dots).
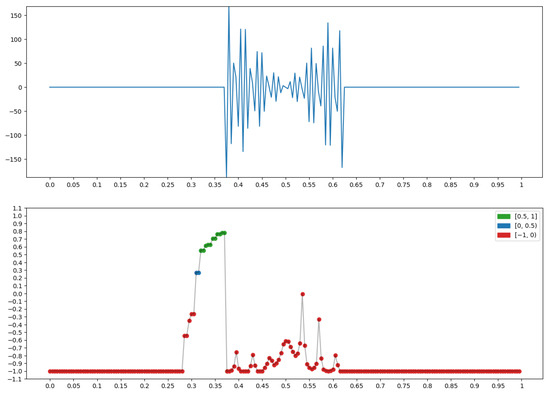
Figure 22.
Property P = “Right oscillation”: .
2.3.12. Right Oscillation with Left Increase
The graph x at the top of Figure 23 has a transition from a smooth increase to a right oscillation. It is on this that the measure “Right oscillation with left increase” (Section 2.1.3), is built for x, (bottom row in Figure 23), taking on the largest values (green dots).
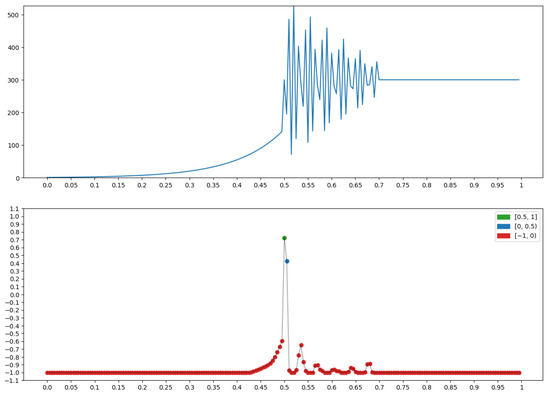
Figure 23.
Property P = “Right oscillation with left increase”: .
2.3.13. Right Oscillation with Left Decrease
The graph x at the top of Figure 24 has a transition from a smooth decrease to a right oscillation. It is on this that the measure “Right oscillation with left decrease” (Section 2.1.3), is built for x, (bottom row in Figure 24), taking the largest values (green dots).
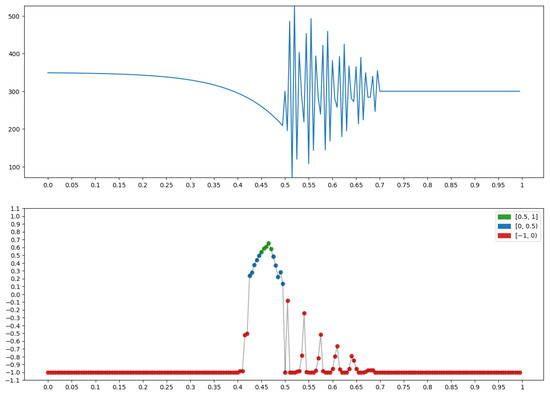
Figure 24.
Property P = “Right oscillation with left decrease”: .
2.3.14. Left Oscillation with Right Decrease
The graph x at the top of Figure 25 has a transition from left oscillation to right decreasing. It is on this that the measure “Left oscillation with right decrease” (Section 2.1.3), is built for x, (bottom row in Figure 25), taking the largest values (green dots).
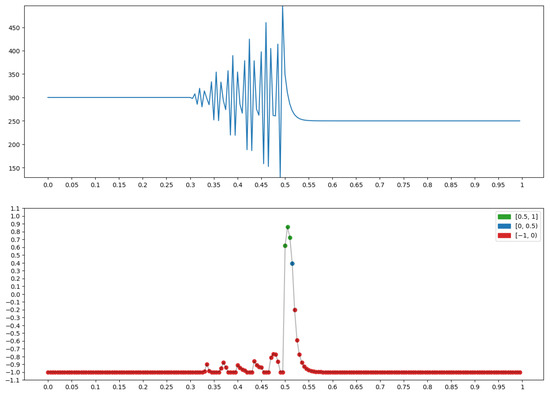
Figure 25.
Property P = “Left oscillation with right decrease”: .
2.3.15. Left Oscillation with Right Increase
The graph x at the top of Figure 26 has a transition from left oscillation to right increase. It is on this that the measure “Left oscillation with right increase” (Section 2.1.3), is built for x, (bottom row in Figure 26), taking on the largest values (green dots).
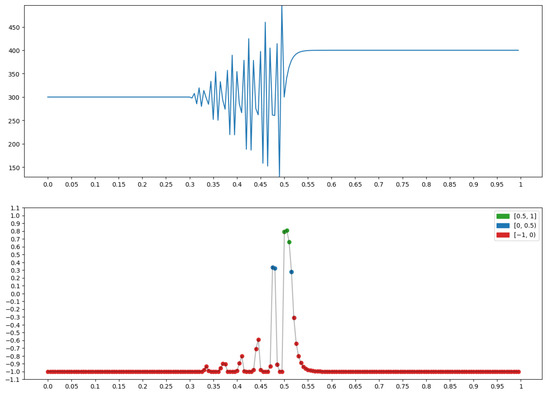
Figure 26.
Property P = “Left oscillation with right increase”: .
2.3.16. Two-Way Oscillation
The graph x at the top of Figure 27 has points with clearly expressed two-way oscillations. It is on this that the measure “Two-way oscillation” (Section 2.1.3), is built for x, (bottom row in Figure 27), taking on the largest values (green dots).
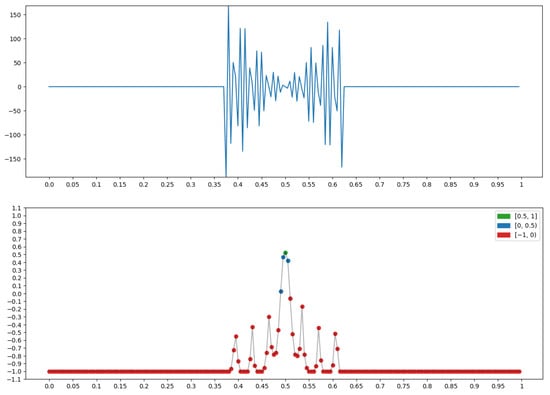
Figure 27.
Property P = “Two-way oscillation”: .
2.3.17. Morphological Analysis
Figure 28 shows an example of a morphological analysis of a fragment of a magnetic storm record using fuzzy disjunction of elementary measures (4).
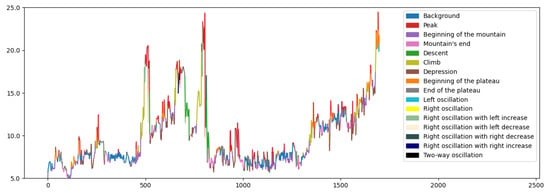
Figure 28.
An example of morphological analysis of a fragment of a magnetic storm record using fuzzy disjunction of elementary measures.
2.3.18. Conclusions
The given examples show the good work of morphological measures built according to the scenario (5)–(8) on synthetic examples. However, the scenario has the disadvantage of being unstable, due to direct dependence on value . Hence, the necessary requirement is that the value is “non-random” for any , that is, the record x is “globally smooth”.
The natural way out is a transition from the original record x to some kind of smoothing and, then, consideration of the corresponding morphological measure for as the morphological measure for the x record (this is an example of the second part of the further activity):
3. -Morphological Analysis
This is how the DMA analysis of records (time series) began. Its informal basis was the “interpreter logic”, this being the logic of an expert looking for anomalies on records [3,4]. Let us recall this logic in the following. An expert slides over the record, estimating the manifestation degree of his or her property of interest in identical small fragments of the record by positive numbers. The expert assigns these estimates to the centers of the fragments. So, from the original record, the expert goes to a non-negative function, which is called straightening the record with respect to the property of interest to the expert. The mountains on the straightening correspond to fragments that are already non-local on the record. They are of the most interest to the expert, who considers them to be anomalies. Thus, the expert operates on two levels: local straightening, and global searching for a mountain on straightening.
The formalization of this logic became the primary concern at the initial stage of DMA analysis of records. The DRAS and FCARS algorithms created at that time adequately competed with the classical spectral analysis algorithms in the search for anomalies [3,4]. DMA algorithms for anomaly search leave the expert free to understand (interpret) them through the choice of straightening. This offers great flexibility.
The mountains on straightening have stochastic nature. There are many large values, but there are also small ones. Only vertical considerations in their search are not enough. There must be horizontal ones too, and the latter must be non-local. It is also necessary to be able to combine those that are close to each other on straightening into a single whole mountain. Behind mountains on the record one large (long) signal is hidden, consisting of a sequence of short ones. Therefore, the search for mountains on non-negative reliefs is an important task in DMA. To date, the best solution is to use the DPS algorithm twice, but even this provides only the main part of the mountain on the straightening (respectively, anomalies on the record) without precise boundaries, initial and final stages, and explicit indications of slopes and peaks [1,5]. In other words, at present there is only recognition of mountains (anomalies) without their morphology.
Modern analysis of anomalies involves not only their recognition, but also their morphological analysis for subsequent classifications and encoding.
Now, we connect the morphological analysis with the logic of the interpreter, and then we receive and analyze the results of such a connection.
3.1. Record Straightening
Let us start with a rigorous definition.
3.1.1. Definition
- 1.
- The straightening construction R is a non-negative functional on T, parameterized by T:
- 2.
- The straightening of x, based on the construction R, is a non-negative function .
The value represents the value of and is understood as a quantitative assessment of the behavior of record x at node t with a local view of R for its dynamics locally, so the straightening construction is always connected to some fixed localization (5).
DMA allows an expert to choose the quantitative expression of the property he or she is interested in. However, the stability of using straightening has been proven. Most experts prefer to work within a range of basic straightening. Behind each of them is a fundamental mathematical concept, which confirms the correctness of the settings when creating DMA.
3.1.2. Conclusions
Straightening implements a systemic point of view on the original record, linking it with a system of derived records (its straightening), and quantitatively expresses the manifestation of one or another local property of the original record. This approach is very flexible and appropriate.
3.2. R-Morphological Measures
Basic straightening R has stochastic stability, so that the record can be considered “smooth”, and the application of morphological analysis (5)–(8) to it correct. This is how the DMA morphological analysis of the record x, begins, that is, through its stable straightening :
Such an analysis of the set is called R-morphological. It makes it possible to understand how the property of the record x behind the straightening is distributed in time on T.
The more fundamental the property behind R, the more interesting the R analysis is. So, for example, if R is the local variance of E, then E morphological analysis provides a dynamic understanding of the variance in the record x, which is closely related to continuity. If R is a local length L, then L morphological analysis provides a dynamic understanding of the length on the record x, closely related to the local frequency.
On the straightening , the most interesting are the elevations corresponding to R-anomalies on the record x, according to the logic of the interpreter. It is necessary not only to recognize them, but also to understand how they are constructed in order, in particular, to encode and be able to compare with other anomalies.
Below we solve this problem using morphological analysis on arbitrary non-negative reliefs and, as a consequence, conduct straightening of an arbitrary record.
4. Search for Elevations Using Morphological Measures
With the help of morphological measures of the beginning (end) Section 2.1.3 (Section 2.1.3) and peak Section 2.1.3, built on elementary measures in the implementation (8), on non-negative “smooth” reliefs, it is possible to determine the elevations and conduct a morphological analysis. The algorithm presented below is empirical, but is proven enough to be presented.
The search logic is consistently refined. Now, we give its first approximation. The mountain is a triad of foothills and a central part, which we recognize using the measures mentioned above.
4.1. Required Minimum: Designations, Definitions, Facts
Let us provide the necessary information for a thesis, a fully fledged story about the search for elevations using morphological measures.
4.1.1. Definition
A segment in , a subset (sequence) of nodes without gaps.
4.1.2. Statement
Any subset S in T is a disjoint union of its maximal segments.
4.1.3. Definition
System of segments in chain of maximal segments in S, following one after another.
4.1.4. Definition
subset of manifestation in T of the morphological measure .
4.1.5. Statement
.
4.1.6. Notations
4.1.7. Conclusions
The iscrete topological work conducted is necessary for such a formalization of elevation morphology. It is shown below.
4.2. Search Algorithm: Logic and Formalization
4.2.1. Construction of Elevation
Elevation construction ↔ initial stage (left foot), left slope, central part, right slope, final stage (right foot).
Next, we describe all the parts that make up the elevation according to the DMA method: first, the logic of the nonformal part, and then its algorithmic formalization. All of the above are shown step by step in the example shown in Figure 29.
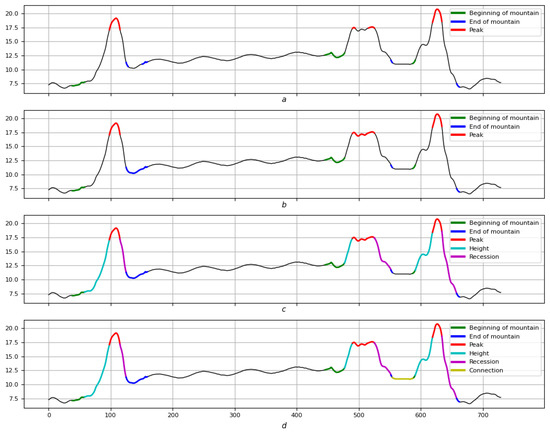
Figure 29.
(a) —maximum system of measure segments (green), (blue), (red); (b)—single continuous left foots (green), right foots (blue), central parts (red); (c)—left (cyan) and right (magenta) slopes; (d)—connection of nearby mountains (yellow).
4.2.2. Logic of the Initial Stage
The rise at the initial stage can occur with interruptions, which should not be significant, either vertically or descending. Interruptions are stochastic steps, not very high and they do not decrease much.
4.2.3. Formalization of the Initial Stage
The maximum system of measure segments , between which there are no measure segments of and the maximal in the union of the system of segments lying in . They are shown in green in Figure 29a. For further development, if necessary, these must be connected into a single continuous left foot. This is illustrated in Figure 29b.
4.2.4. End Stage Logic
Descending to the final stage may involve interruptions, which should not be significant, either vertically or ascending. Interruptions are stochastic right-hand steps that are not very high and are strongly non-increasing.
4.2.5. Formalization of the Final Stage
The maximum system of measure segments , between which there are no measure segments and the maximal in the union of the system of segments lying in . They are shown in blue in Figure 29a. For further development, if necessary, these are connected into a single continuous right foot. This is shown in Figure 29b.
4.2.6. The Logic of the Central Part
The system of peaks that is enclosed between the left and right foothill.
4.2.7. Formalization of the Central Part
4.2.8. Left Slope
Relief fragment connecting the end of the left foothill with the beginning of the central part. In Figure 29c, this is shown in light green.
4.2.9. Right Slope
Relief fragment connecting the end of the central part with the beginning of the right foothill. In Figure 29c, this is shown in purple.
4.2.10. Elevations and Their Chains
Let us sum up the intermediate result. The results of activity in Section 4.2.1, Section 4.2.2, Section 4.2.3, Section 4.2.4, Section 4.2.5, Section 4.2.6, Section 4.2.7, Section 4.2.8, Section 4.2.9 are fragments m on the relief x, defined by the triads , according to Section 4.2.2 and Section 4.2.3, Section 4.2.6 and Section 4.2.7, Section 4.2.4 and Section 4.2.5 (backbones m). Fragments m are called elevations (mountains) on relief x. All of them are disjunctive. Let us denote of their set by .
Among them there may be groups of elevations that are close to each other. Therefore, the set needs, in the general case, further clustering by combining elevations that are close to each other into single groups. We call such groups chains of elevations (mountain ranges) on relief x, and denote them by , and their totality by :
The transition is based on the proximity relation in :
In Figure 29d the connection of the central and right hills into a single circuit is shown in yellow.
4.2.11. Conclusions
A simple, but precise, description of the algorithm for finding hills on a non-negative relief using morphological measures is given.
4.3. Example: Morphological Analysis of a Magnetic Storm Record
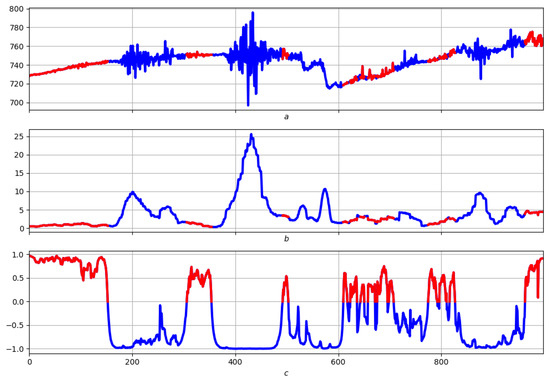
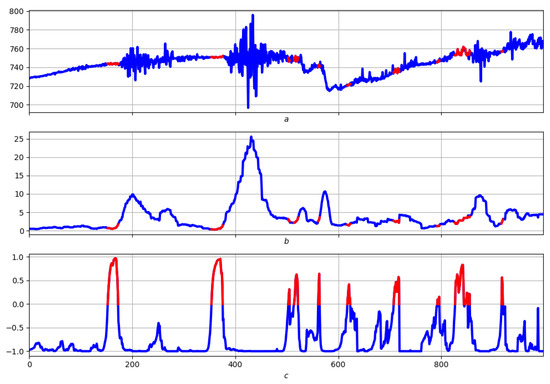
Figure 30, Figure 31, Figure 32 and Figure 33 show an example of a morphological analysis of a magnetic storm that occurred on 3–4 November, 2011. The component Y from the WSE (White Sea) observatory for the period 3–5 November (4320 points) was used as the record for study. “Energy” straightening with was used, and elementary measures were built with . Figure 30b presents a morphological analysis of the straightening for the entire period considered, and Figure 30a shows the corresponding anomalies. Figure 31a,b shows the morphological analysis of the storm.
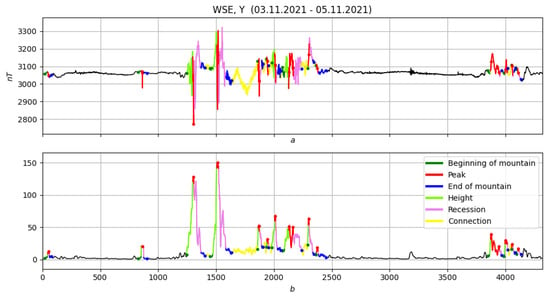
Figure 30.
Morphological analysis of straightening for the entire period considered. (a) original record, (b) straightening.
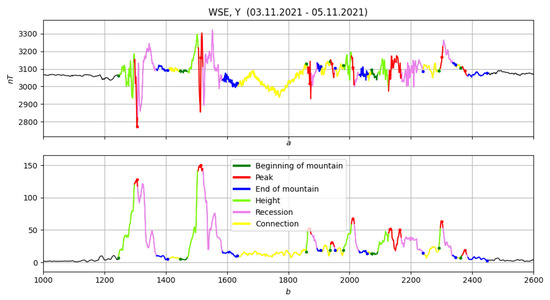
Figure 31.
Morphological analysis of the storm for the entire period considered. (a) original record, (b) straightening.
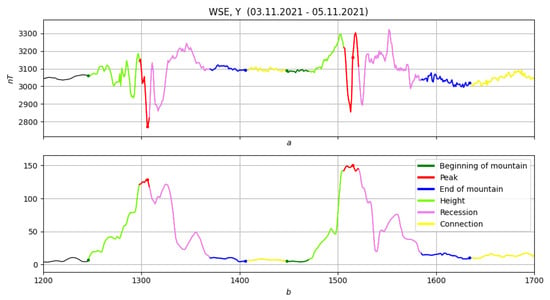
Figure 32.
Morphological analysis of the first part of the storm. (a) original record, (b) straightening.
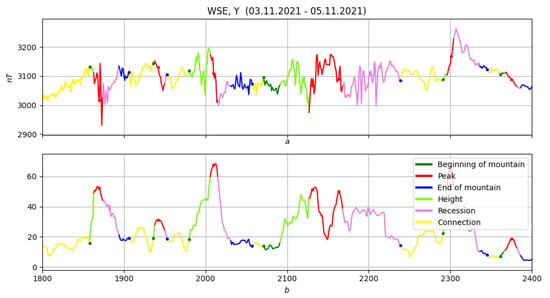
Figure 33.
Morphological analysis of the second part of the storm. (a) original record, (b) straightening.
Conclusions
The algorithm showed a result similar to the one above for a large number of examples. This was sufficient reason to consider it tested.
5. Conclusions
DMA comprises a set of algorithms designed to address various data analysis problems, such as clustering and tracing in multidimensional spaces, and time series analysis, including smoothing, searching for anomalies and trends, studying their morphology, and many more. These algorithms are built on a single formal basis and have a universal character.
DMA is based on the idea that human perception of form, discreteness, and stochasticity is more natural and stable than mathematical models. In turn, this is explained by a flexible, adaptive human perception of the fundamental concepts of proximity, continuity, connectedness, and others.
The technical basis of DMA, along with including classical mathematics, also includes fuzzy mathematics and fuzzy logic, since these are required as a means to model the actions of a person who thinks and operates not with numbers, but with fuzzy concepts [1,2].
All this was addressed in this work, The nonformal logic of our approach to the morphological analysis of the record presented in the first part is one of the possible answers for a person traveling along a graph to answer sixteen questions Section 2.1.3.
The formulation of such answers, proposed in the second part of the paper presented is especially effective for smooth time series, which, in particular, include the basic straightening of record . The R morphological analysis (third part) facilitates understanding of the dynamics of the manifestation of property R on the record . Despite the local nature of the straightening R, this conclusion is no longer local.
The same non-local character is the result of the final fourth part of the paper, concerning the search for mountains on the straightening , using the morphological measures of “beginning”, “peak” and “end”. Mountains are recognized with precise indications of boundaries, and initial and final stages, explicit indications of slopes and peaks (see Figure 6).
The morphological quality of the recognition of mountain passes to the R-anomalies corresponding to them on the records serves as the basis for their further classification and encoding (see Figure 6).
It is precisely because of these requirements for the recognition of extreme geomagnetic events that the MAGNUS (Monitoring and Analysis of Geomagnetic aNomalies in Unified Systems) is analytically complex [1], with an intellectual unit that includes DMA imposing formalization.
The authors suggest further research in three directions.
The first direction is to study the possibilities and properties of both elementary and morphological measures constructed in this paper (parameters, stability, and new logical connections in their constructions).
The second direction us the creation of new constructions of elementary measures and, on their basis, of morphological ones. In other words, the search for new scenarios of DMA morphological analysis described in this paper us proposed.
The third direction is to continue on from the results obtained in the present paper, applied to the analysis of magnetic storms, by seeking other, primarily physical, applications.
Author Contributions
All authors contributed to the study conception and design. Conceptualization, S.M.A., D.A.K., A.O.A. and B.V.D.; Data curation, S.R.B. and A.O.A.; Formal analysis, S.R.B. and A.O.A.; Methodology, D.A.K., S.R.B., A.O.A. and B.V.D.; Software, S.R.B. and A.O.A.; Validation, D.A.K., A.O.A. and B.V.D.; Writing—original draft, S.M.A.; Writing—review & editing, D.A.K., A.O.A. and B.V.D. All authors have read and agreed to the published version of the manuscript.
Funding
This work was conducted in the framework of budgetary funding of the Geophysical Center of RAS, adopted by the Ministry of Science and Higher Education of the Russian Federation.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Acknowledgments
This work employed data provided by the Shared Research Facility, the Analytical Geomagnetic Data Center of the Geophysical Center of RAS (http://ckp.gcras.ru/ accessed on: 23 January 2023).
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| DMA | Discrete Mathematical Analysis |
| FM | Fuzzy Mathematics |
| FL | Fuzzy Logic |
| DRAS | Difference Recognition Algorithm for Signals |
| FCARS | Fuzzy Comparison Algorithm for Recognition of Signals |
| MAGNUS | Monitoring and Analysis of Geomagnetic aNomalies in Unified System |
References
- Gvishiani, A.; Soloviev, A. Observations, Modeling and Systems Analysis in Geomagnetic Data Interpretation; Springer International Publishing: Cham, Switzerland, 2020. [Google Scholar] [CrossRef]
- Agayan, S.M.; Bogoutdinov, S.R.; Krasnoperov, R.I. Short introduction into DMA. Russ. J. Earth Sci. 2018, 18, 1–10. [Google Scholar] [CrossRef]
- Gvishiani, A.D.; Agayan, S.M.; Bogoutdinov, S.R.; Zlotnicki, J.; Bonnin, J. Mathematical methods of geoinformatics. III. Fuzzy comparisons and recognition of anomalies in time series. Cybern. Syst. Anal. 2008, 44, 309–323. [Google Scholar] [CrossRef]
- Gvishiani, A.D.; Agayan, S.M.; Bogoutdinov, S.R. Fuzzy recognition of anomalies in time series. Dokl. Earth Sci. 2008, 421, 838–842. [Google Scholar] [CrossRef]
- Agayan, S.; Bogoutdinov, S.; Soloviev, A.; Sidorov, R. The Study of Time Series Using the DMA Methods and Geophysical Applications. Data Sci. J. 2016, 15, 16. [Google Scholar] [CrossRef]
- Serra, J. Image Analysis and Mathematical Morphology; Academic Press: Cambridge, MA, USA, 1982; p. 610. [Google Scholar]
- Serra, J. Image Analysis and Mathematical Morphology, Volume 2: Theoretical Advances, 1st ed.; Academic Press: Cambridge, MA, USA, 1988; p. 411. [Google Scholar]
- Matheron, G. Random Sets and Integral Geometry; Wiley: New York, NY, USA, 1975; p. 261. [Google Scholar]
- Gonzalez, R.C.; Woods, R.E. Digital Image Processing, 4th ed.; Pearson: London, UK, 2017; p. 1192. [Google Scholar]
- Maragos, P. Pattern spectrum and multiscale shape representation. IEEE Trans. Pattern Anal. Mach. Intell. 1989, 11, 701–716. [Google Scholar] [CrossRef]
- Urbach, E.R.; Roerdink, J.; Michael Wilkinson, M.H.F. Connected Shape-Size Pattern Spectra for Rotation and Scale-Invariant Classification of Gray-Scale Images. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 29, 272–285. [Google Scholar] [CrossRef] [PubMed]
- Wilkinson, M.H.F. Generalized pattern spectra sensitive to spatial information. In Proceedings of the 16th International Conference on Pattern Recognition, Québec City, QC, Canada, 11–15 August 2002; Volume 1, pp. 21–24. [Google Scholar] [CrossRef]
- Kulichkov, S.N.; Chulichkov, A.I.; Demin, D.S. Morphological Analysis Infrasonic Signals in Acoustics; Novyi Akropol: Moscow, Russia, 2010; p. 132. (In Russian) [Google Scholar]
- Pyt’ev, Y.; Chulichkov, A. Morphological Methods for Image Analysis; Fiz-matlit Publisher: Moscow, Russia, 2010; p. 336. (In Russian) [Google Scholar]
- Pyt’ev, Y. Morphological image analysis. Pattern Recognit. Image Anal. 1993, 3, 19–28. (In Russian) [Google Scholar]
- Vizil’ter, Y.V.; Zheltov, S.Y.; Bondarenko, A.V.; Osokov, M.V.; Morzhin, A.V. Image Processing and Analysis in Machine Vision Problems. A Course of Lectures and Practical Exercises; Fizmatkniga: Moscow, Russia, 2010; p. 672. (In Russian) [Google Scholar]
- Zadeh, L.A. The Concept of a Linguistic Variable and its Application to Approximate Reasoning. In Learning Systems and Intelligent Robots; Springer: New York, NY, USA, 1974; pp. 1–10. [Google Scholar] [CrossRef]
- Novák, V.; Perfilieva, I.; Močkoř, J. Mathematical Principles of Fuzzy Logic; Springer: New York, NY, USA, 1999. [Google Scholar] [CrossRef]
- Box, G.E.P.; Jenkins, G.M. Time Series Analysis: Forecasting and Control; Holden-Day: San Francisco, CA, USA, 1976. [Google Scholar]
- Hamilton, J.D. Time Series Analysis; Princeton University Press: Princeton, NJ, USA, 1994. [Google Scholar] [CrossRef]
- Priestley, M.B. Spectral Analysis and Time Series; Academic Press Inc.: New York, NY, USA, 1981. [Google Scholar]
- Shumway, R.H.; Stoffer, D.S. Time Series Analysis and Its Applications; Springer International Publishing: Cham, Switzerland, 2017. [Google Scholar] [CrossRef]
- Woodward, W.A.; Gray, H.L.; Elliot, A.C. Applied Time Series Analysis; CRC Press: Boca Baton, FL, USA, 2012. [Google Scholar]
- Chen, S.M. Forecasting enrollments based on fuzzy time series. Fuzzy Sets Syst. 1996, 81, 311–319. [Google Scholar] [CrossRef]
- Novák, V.; Perfilieva, I.; Dvořák, A. Insight into Fuzzy Modeling; John Wiley & Sons, Inc.: New York, NY, USA, 2016. [Google Scholar] [CrossRef]
- Song, Q.; Chissom, B.S. Fuzzy time series and its models. Fuzzy Sets Syst. 1993, 54, 269–277. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).