Robustness of Single- and Dual-Energy Deep-Learning-Based Scatter Correction Models on Simulated and Real Chest X-rays
Abstract
:1. Introduction
2. Materials and Methods
2.1. COVID-19 CT Image Database
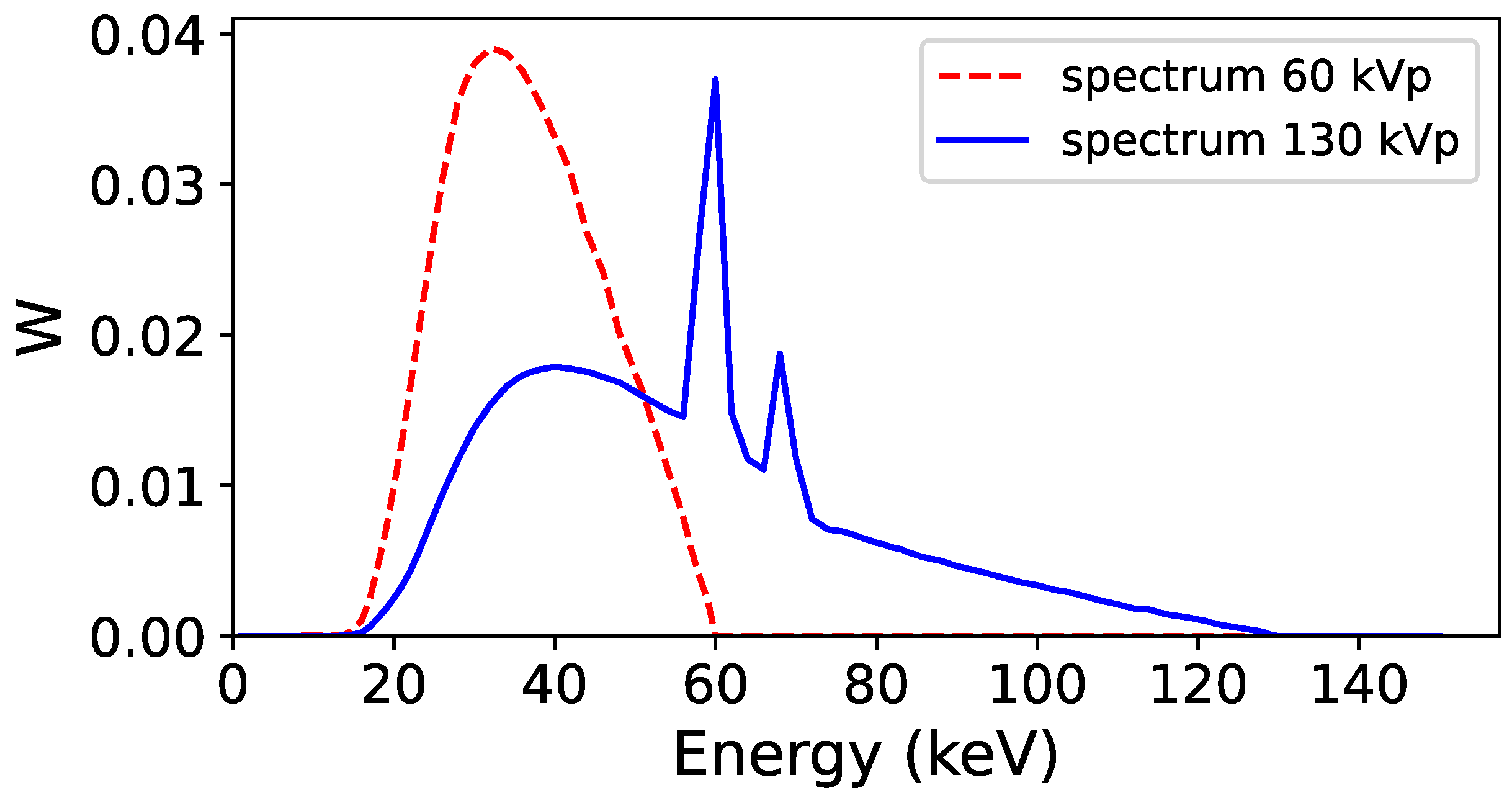
2.2. Monte Carlo Simulations to Generate Training and Validation Dataset
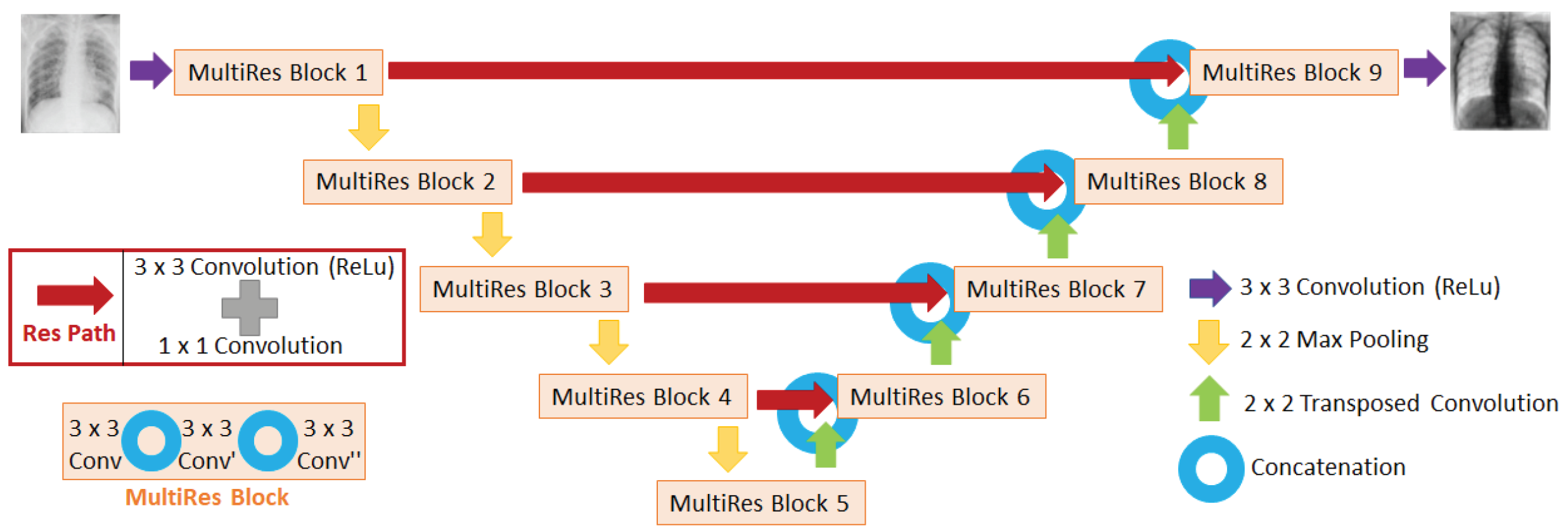
2.3. CNN Architecture
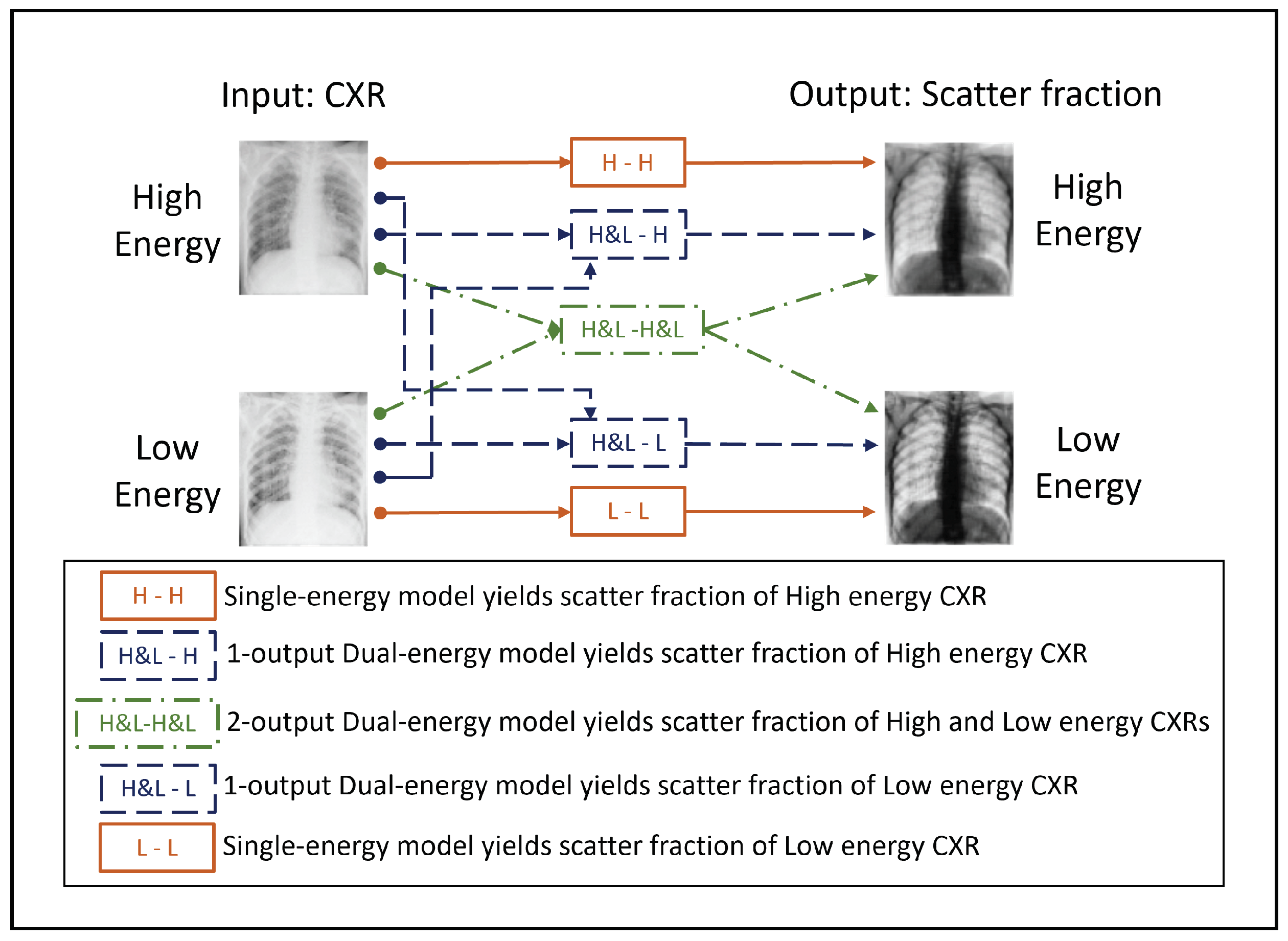
2.4. Evaluation of Scatter Estimation Models on Simulated CXRs
2.5. Evaluation of Scatter Correction on True CXRs
3. Results
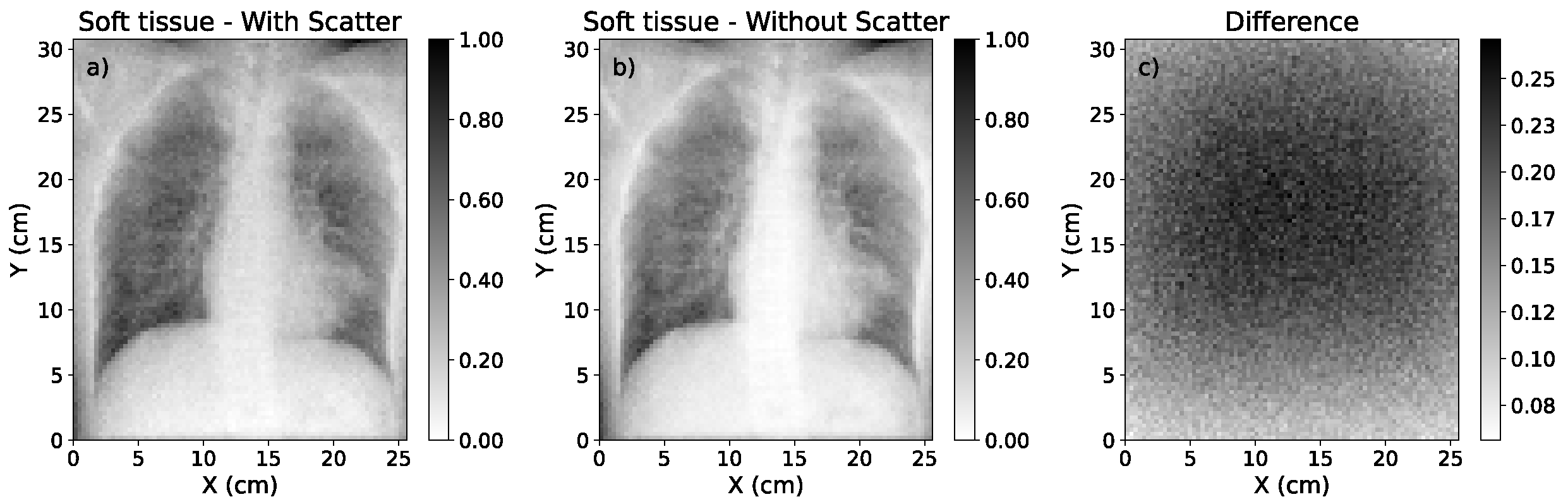
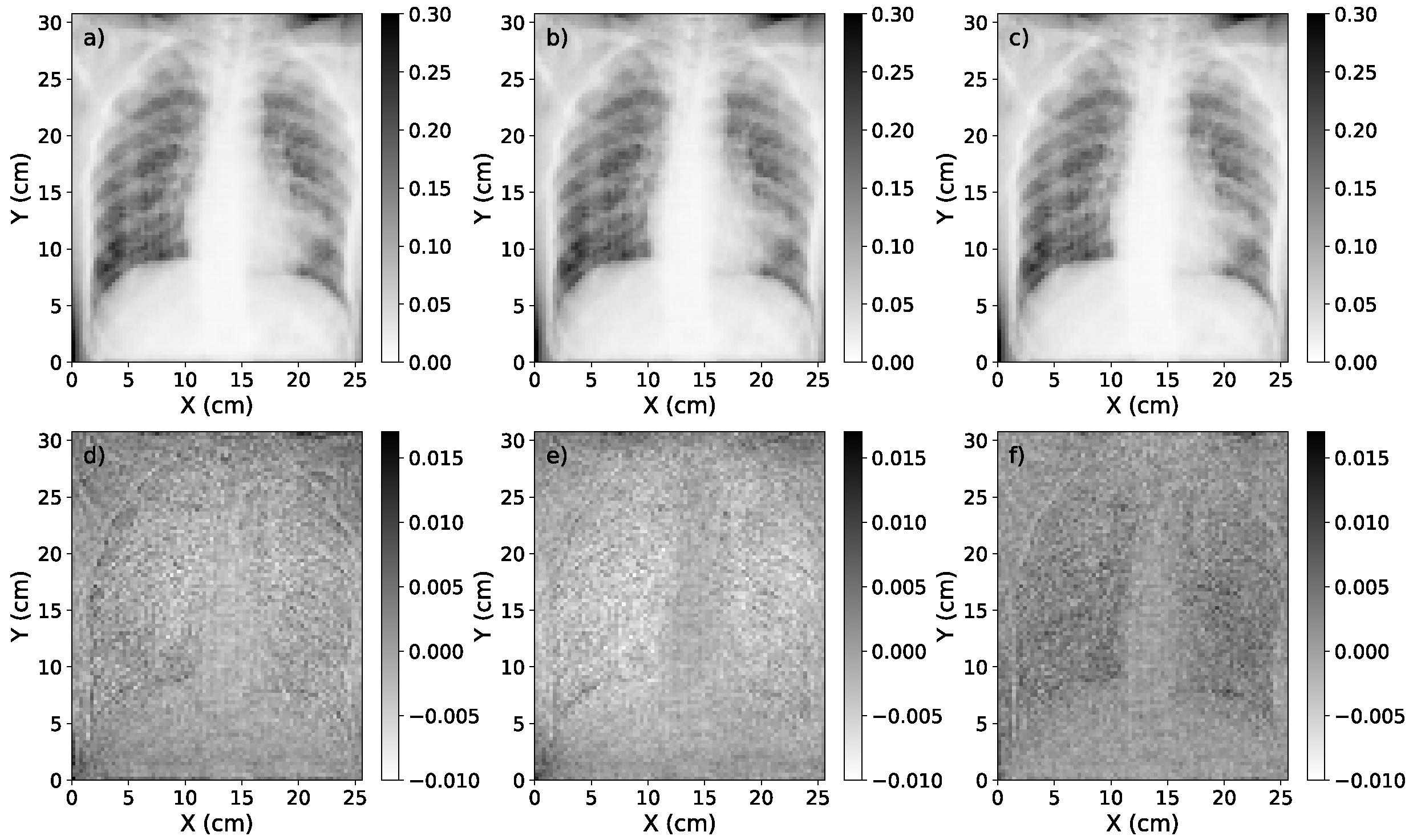
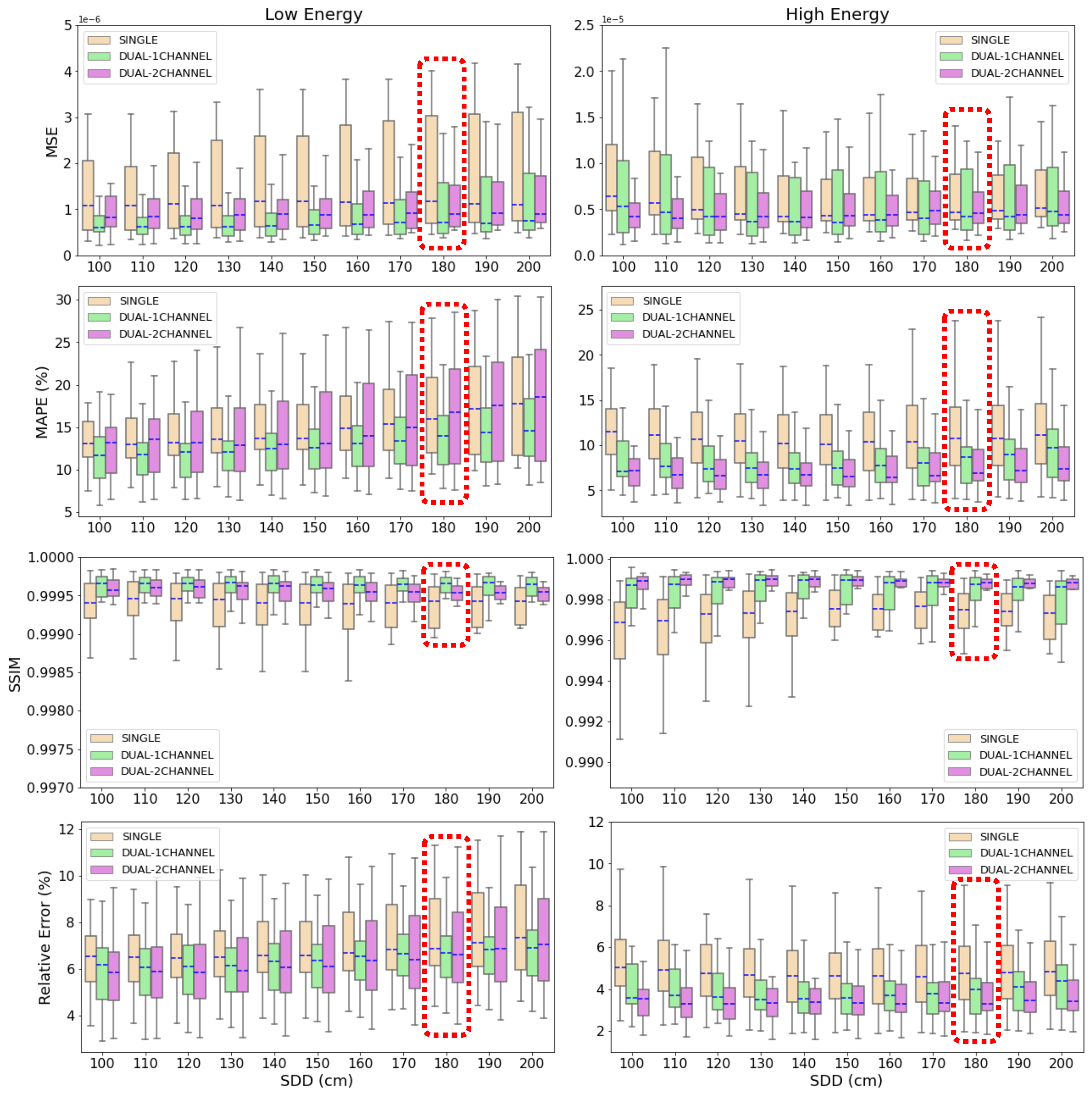
3.1. Accuracy of Scatter Correction on Simulated CXRs
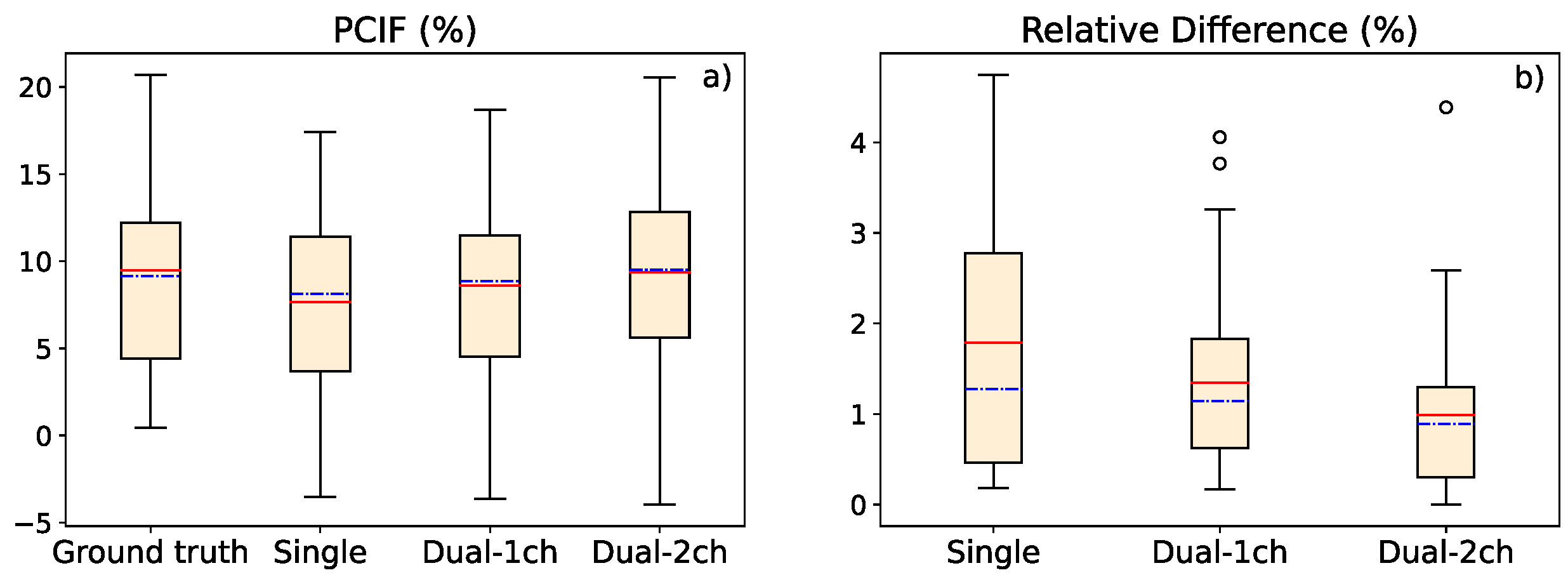
3.2. Study of Contrast Improvement after Scatter Correction
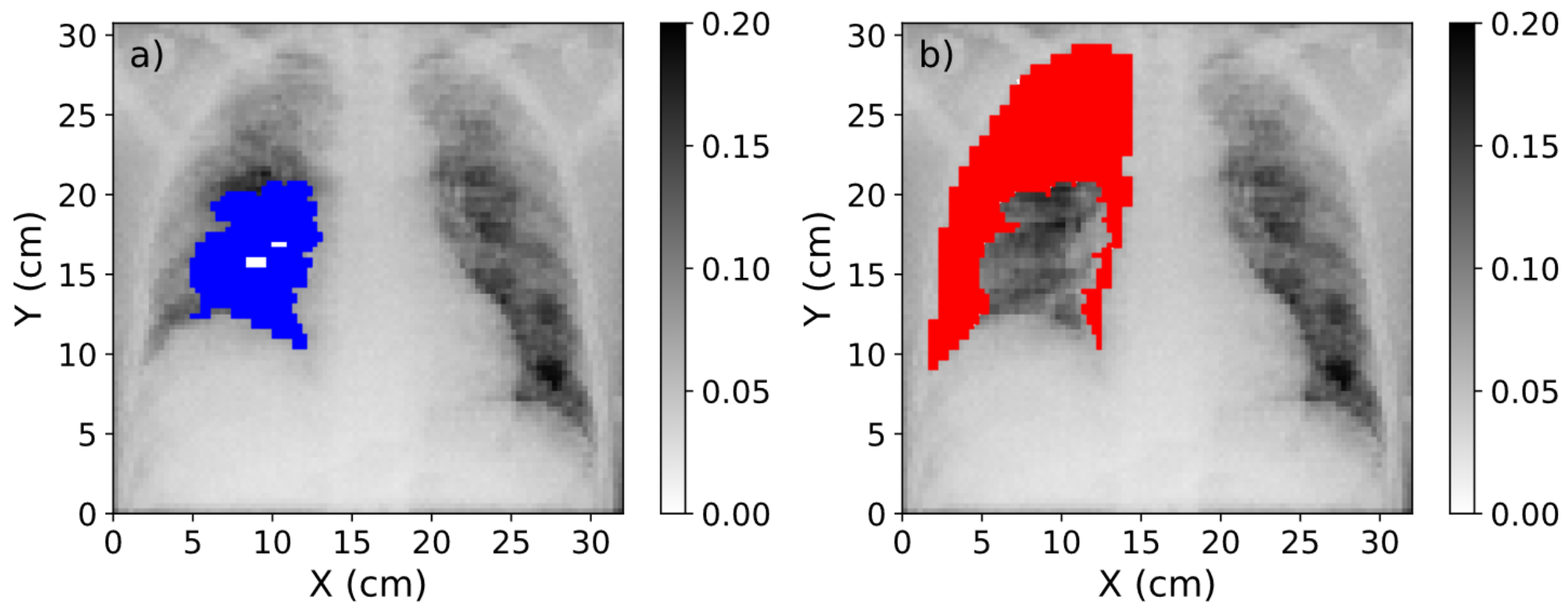
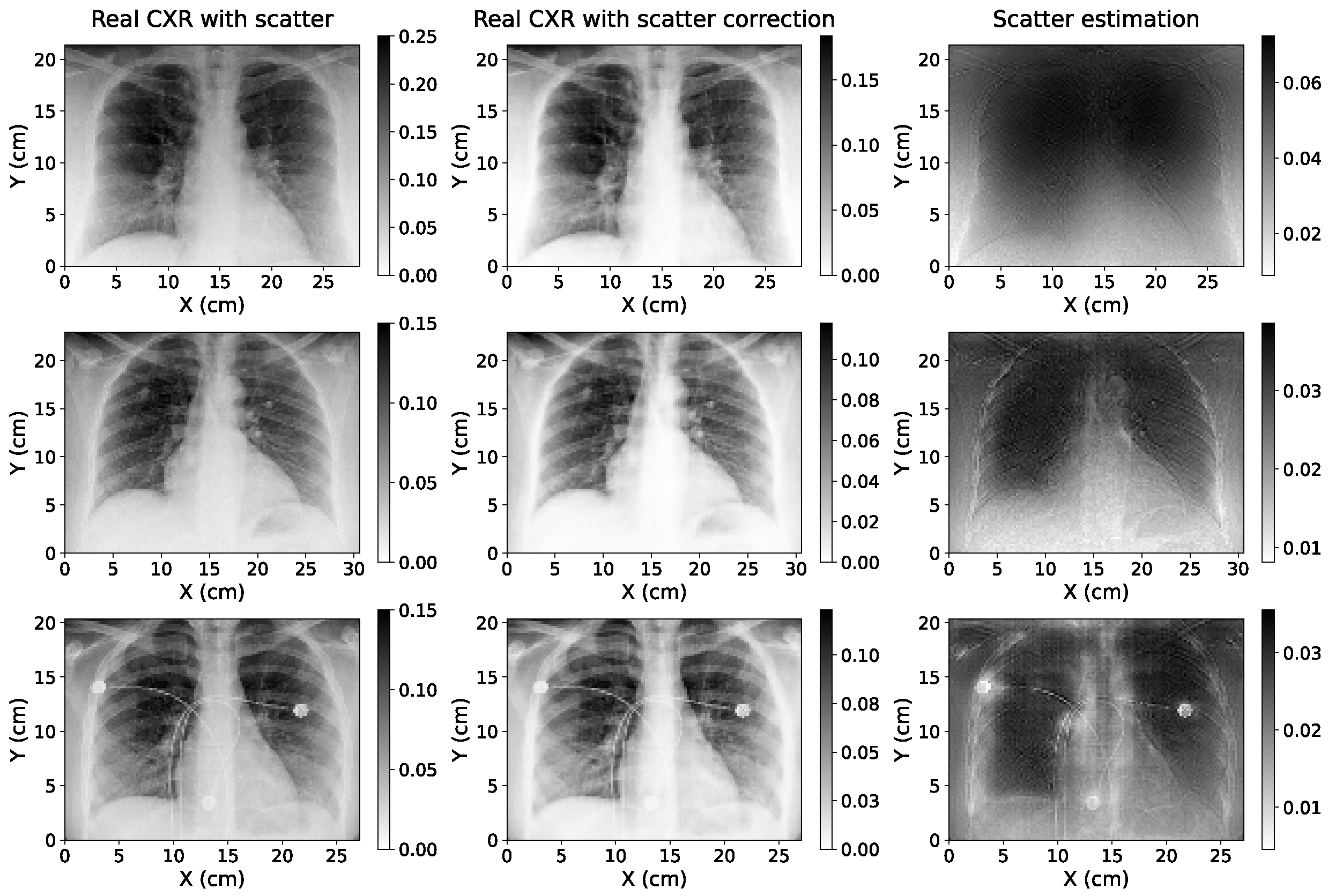
3.3. Study of Scatter Correction on True CXRs
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Patient | Ground Truth Uncorrected Image | Ground Truth Scatter-Corrected Image | Scatter-Corrected with Single Energy | Scatter-Corrected with 1-Output Dual Energy | Scatter-Corrected with 2-Output Dual Energy |
|---|---|---|---|---|---|
| Case 1 | 1.216 | 1.385 | 1.352 | 1.374 | 1.380 |
| Case 2 | 1.165 | 1.282 | 1.268 | 1.285 | 1.278 |
| Case 3 | 1.032 | 1.101 | 1.072 | 1.080 | 1.095 |
| Case 4 | 1.292 | 1.430 | 1.419 | 1.404 | 1.455 |
| Case 5 | 1.187 | 1.299 | 1.289 | 1.293 | 1.299 |
| Case 6 | 1.047 | 1.018 | 1.045 | 1.048 | 1.014 |
| Case 7 | 1.147 | 1.239 | 1.235 | 1.231 | 1.255 |
| Case 8 | 1.297 | 1.448 | 1.453 | 1.439 | 1.434 |
| Case 9 | 1.096 | 1.301 | 1.244 | 1.252 | 1.284 |
| Case 10 | 1.301 | 1.553 | 1.499 | 1.531 | 1.526 |
| Case 11 | 1.154 | 1.201 | 1.195 | 1.198 | 1.190 |
| Case 12 | 1.045 | 1.159 | 1.104 | 1.145 | 1.149 |
| Case 13 | 0.795 | 0.645 | 0.648 | 0.684 | 0.627 |
| Case 14 | 1.209 | 1.454 | 1.403 | 1.434 | 1.436 |
| Case 15 | 1.305 | 1.575 | 1.532 | 1.549 | 1.573 |
| Case 16 | 1.128 | 1.176 | 1.170 | 1.198 | 1.184 |
| Case 17 | 0.960 | 0.931 | 0.922 | 0.953 | 0.928 |
| Case 18 | 1.104 | 1.202 | 1.173 | 1.205 | 1.213 |
| Case 19 | 1.037 | 1.035 | 1.052 | 1.045 | 1.040 |
| Case 20 | 0.879 | 0.890 | 0.864 | 0.861 | 0.913 |
| Case 21 | 1.110 | 1.115 | 1.113 | 1.103 | 1.114 |
| Case 22 | 1.021 | 1.056 | 1.054 | 1.063 | 1.058 |
| Case 23 | 0.945 | 0.987 | 0.967 | 0.972 | 1.001 |
| Case 24 | 1.098 | 1.165 | 1.148 | 1.163 | 1.162 |
| Case 25 | 1.209 | 1.324 | 1.327 | 1.333 | 1.325 |
| Case 26 | 1.183 | 1.279 | 1.293 | 1.287 | 1.291 |
| Case 27 | 0.962 | 0.886 | 0.898 | 0.899 | 0.851 |
| Case 28 | 0.841 | 0.719 | 0.719 | 0.723 | 0.717 |
| Case 29 | 0.872 | 0.816 | 0.795 | 0.817 | 0.791 |
| Case 30 | 0.908 | 0.912 | 0.876 | 0.875 | 0.872 |
| Case 31 | 1.316 | 1.532 | 1.529 | 1.562 | 1.544 |
References
- Candemir, S.; Antani, S. A review on lung boundary detection in chest x-rays. Int. J. Comput. Assist. Radiol. Surg. 2019, 14, 563–576. [Google Scholar] [CrossRef] [PubMed]
- Gange, C.P.; Pahade, J.K.; Cortopassi, I.; Bader, A.S.; Bokhari, J.; Hoerner, M.; Thomas, K.M.; Rubinowitz, A.N. Social distancing with portable chest radiographs during the COVID-19 pandemic: Assessment of radiograph technique and image quality obtained at 6 feet and through glass. Radiol. Cardiothorac. Imaging 2020, 2, e200420. [Google Scholar] [CrossRef] [PubMed]
- Çallı, E.; Sogancioglu, E.; van Ginneken, B.; van Leeuwen, K.G.; Murphy, K. Deep learning for chest X-ray analysis: A survey. Med. Image Anal. 2021, 72, 102125. [Google Scholar] [CrossRef] [PubMed]
- Raoof, S.; Feigin, D.; Sung, A.; Raoof, S.; Irugulpati, L.; Rosenow, E.C., III. Interpretation of plain chest roentgenogram. Chest 2012, 141, 545–558. [Google Scholar] [CrossRef] [PubMed]
- Shaw, D.; Crawshaw, I.; Rimmer, S. Effects of tube potential and scatter rejection on image quality and effective dose in digital chest X-ray examination: An anthropomorphic phantom study. Radiography 2013, 19, 321–325. [Google Scholar] [CrossRef]
- Jones, J.; Murphy, A.; Bell, D. Chest Radiograph. Available online: https://radiopaedia.org/articles/chest-radiograph?lang=us (accessed on 7 February 2023).
- Mentrup, D.; Neitzel, U.; Jockel, S.; Maack, H.; Menser, B. Grid-Like Contrast Enhancement for Bedside Chest Radiographs Acquired without Anti-Scatter Grid; Philips SkyFlow: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Seibert, J.A.; Boone, J.M. X-ray imaging physics for nuclear medicine technologists. Part 2: X-ray interactions and image formation. J. Nucl. Med. Technol. 2005, 33, 3–18. [Google Scholar] [PubMed]
- Lee, H.; Lee, J. A deep learning-based scatter correction of simulated X-ray images. Electronics 2019, 8, 944. [Google Scholar] [CrossRef]
- Liu, X.; Shaw, C.C.; Lai, C.J.; Wang, T. Comparison of scatter rejection and low-contrast performance of scan equalization digital radiography (SEDR), slot-scan digital radiography, and full-field digital radiography systems for chest phantom imaging. Med. Phys. 2011, 38, 23–33. [Google Scholar] [CrossRef]
- Rührnschopf, E.P.; Klingenbeck, K. A general framework and review of scatter correction methods in X-ray cone-beam computerized tomography. Part 1: Scatter compensation approaches. Med. Phys. 2011, 38, 4296–4311. [Google Scholar] [CrossRef]
- Chan, H.P.; Lam, K.L.; Wu, Y. Studies of performance of antiscatter grids in digital radiography: Effect on signal-to-noise ratio. Med. Phys. 1990, 17, 655–664. [Google Scholar] [CrossRef]
- Roser, P.; Birkhold, A.; Preuhs, A.; Syben, C.; Felsner, L.; Hoppe, E.; Strobel, N.; Kowarschik, M.; Fahrig, R.; Maier, A. X-ray scatter estimation using deep splines. IEEE Trans. Med. Imaging 2021, 40, 2272–2283. [Google Scholar] [CrossRef] [PubMed]
- Gauntt, D.M.; Barnes, G.T. Grid line artifact formation: A comprehensive theory. Med. Phys. 2006, 33, 1668–1677. [Google Scholar] [CrossRef] [PubMed]
- Bernhardt, T.; Rapp-Bernhardt, U.; Hausmann, T.; Reichel, G.; Krause, U.; Doehring, W. Digital selenium radiography: Anti-scatter grid for chest radiography in a clinical study. Br. J. Radiol. 2000, 73, 963–968. [Google Scholar] [CrossRef] [PubMed]
- Roberts, J.; Evans, S.; Rees, M. Optimisation of imaging technique used in direct digital radiography. J. Radiol. Prot. 2006, 26, 287. [Google Scholar] [CrossRef] [PubMed]
- Moore, C.; Avery, G.; Balcam, S.; Needler, L.; Swift, A.; Beavis, A.; Saunderson, J. Use of a digitally reconstructed radiograph-based computer simulation for the optimisation of chest radiographic techniques for computed radiography imaging systems. Br. J. Radiol. 2012, 85, e630–e639. [Google Scholar] [CrossRef] [PubMed]
- Lifton, J.; Malcolm, A.; McBride, J. An experimental study on the influence of scatter and beam hardening in X-ray CT for dimensional metrology. Meas. Sci. Technol. 2015, 27, 015007. [Google Scholar] [CrossRef]
- Maier, J.; Sawall, S.; Knaup, M.; Kachelrieß, M. Deep scatter estimation (DSE): Accurate real-time scatter estimation for X-ray CT using a deep convolutional neural network. J. Nondestruct. Eval. 2018, 37, 1–9. [Google Scholar] [CrossRef]
- Swindell, W.; Evans, P.M. Scattered radiation in portal images: A Monte Carlo simulation and a simple physical model. Med. Phys. 1996, 23, 63–73. [Google Scholar] [CrossRef]
- Bhatia, N.; Tisseur, D.; Buyens, F.; Létang, J.M. Scattering correction using continuously thickness-adapted kernels. NDT Int. 2016, 78, 52–60. [Google Scholar] [CrossRef]
- Codella, N.C.; Gutman, D.; Celebi, M.E.; Helba, B.; Marchetti, M.A.; Dusza, S.W.; Kalloo, A.; Liopyris, K.; Mishra, N.; Kittler, H.; et al. Skin lesion analysis toward melanoma detection: A challenge at the 2017 international symposium on biomedical imaging (ISBI), hosted by the international skin imaging collaboration (ISIC). In Proceedings of the 2018 IEEE 15th International Symposium on Biomedical Imaging (ISBI 2018), Washington, DC, USA, 4 April 2018. [Google Scholar]
- Sermanet, P.; Eigen, D.; Zhang, X.; Mathieu, M.; Fergus, R.; LeCun, Y. Overfeat: Integrated recognition, localization and detection using convolutional networks. arXiv 2013, arXiv:1312.6229. [Google Scholar]
- Rouhi, R.; Jafari, M.; Kasaei, S.; Keshavarzian, P. Benign and malignant breast tumors classification based on region growing and CNN segmentation. Expert Syst. Appl. 2015, 42, 990–1002. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention—MICCAI 2015: 18th International Conference, Munich, Germany, 5 October 2015. [Google Scholar]
- Siddique, N.; Paheding, S.; Elkin, C.P.; Devabhaktuni, V. U-net and its variants for medical image segmentation: A review of theory and applications. IEEE Access 2021, 9, 82031–82057. [Google Scholar] [CrossRef]
- Moon, J.H.; Lee, H.; Shin, W.; Kim, Y.H.; Choi, E. Multi-modal understanding and generation for medical images and text via vision-language pre-training. IEEE J. Biomed. Health Inform. 2022, 26, 6070–6080. [Google Scholar] [CrossRef]
- Liu, C.; Cheng, S.; Chen, C.; Qiao, M.; Zhang, W.; Shah, A.; Bai, W.; Arcucci, R. M-FLAG: Medical vision-language pre-training with frozen language models and latent space geometry optimization. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention—MICCAI 2023: 26th International Conference, Vancouver, BC, Canada, 8 October 2023. [Google Scholar]
- Ibtehaz, N.; Rahman, M.S. MultiResUNet: Rethinking the U-Net architecture for multimodal biomedical image segmentation. Neural Netw. 2020, 121, 74–87. [Google Scholar] [CrossRef] [PubMed]
- Alvarez, R.E.; Macovski, A. Energy-selective reconstructions in X-ray computerised tomography. Phys. Med. Biol. 1976, 21, 733. [Google Scholar] [CrossRef]
- Sellerer, T.; Mechlem, K.; Tang, R.; Taphorn, K.A.; Pfeiffer, F.; Herzen, J. Dual-energy X-ray dark-field material decomposition. IEEE Trans. Med. Imaging 2020, 40, 974–985. [Google Scholar] [CrossRef] [PubMed]
- Fredenberg, E. Spectral and dual-energy X-ray imaging for medical applications. Nucl. Instrum. Methods Phys. Res. A 2018, 878, 74–87. [Google Scholar] [CrossRef]
- Martz, H.E.; Glenn, S.M. Dual-Energy X-ray Radiography and Computed Tomography; Technical Report; Lawrence Livermore National Lab (LLNL): Livermore, CA, USA, 2019.
- Marin, D.; Boll, D.T.; Mileto, A.; Nelson, R.C. State of the art: Dual-energy CT of the abdomen. Radiology 2014, 271, 327–342. [Google Scholar] [CrossRef]
- Manji, F.; Wang, J.; Norman, G.; Wang, Z.; Koff, D. Comparison of dual energy subtraction chest radiography and traditional chest X-rays in the detection of pulmonary nodules. Quant. Imaging Med. Surg. 2016, 6, 1. [Google Scholar]
- Vock, P.; Szucs-Farkas, Z. Dual energy subtraction: Principles and clinical applications. Eur. J. Radiol. 2009, 72, 231–237. [Google Scholar] [CrossRef] [PubMed]
- Yang, F.; Weng, X.; Miao, Y.; Wu, Y.; Xie, H.; Lei, P. Deep learning approach for automatic segmentation of ulna and radius in dual-energy X-ray imaging. Insights Imaging 2021, 12, 191. [Google Scholar] [CrossRef]
- Luo, R.; Ge, Y.; Hu, Z.; Liang, D.; Li, Z.C. DeepPhase: Learning phase contrast signal from dual energy X-ray absorption images. Displays 2021, 69, 102027. [Google Scholar] [CrossRef]
- Lee, D.; Kim, H.; Choi, B.; Kim, H.J. Development of a deep neural network for generating synthetic dual-energy chest X-ray images with single X-ray exposure. Phys. Med. Biol. 2019, 64, 115017. [Google Scholar] [CrossRef] [PubMed]
- Roth, H.R.; Xu, Z.; Tor-Díez, C.; Jacob, R.S.; Zember, J.; Molto, J.; Li, W.; Xu, S.; Turkbey, B.; Turkbey, E.; et al. Rapid artificial intelligence solutions in a pandemic—The COVID-19-20 lung CT lesion segmentation challenge. Med. Image Anal. 2022, 82, 102605. [Google Scholar] [CrossRef] [PubMed]
- Schneider, U.; Pedroni, E.; Lomax, A. The calibration of CT Hounsfield units for radiotherapy treatment planning. Phys. Med. Biol. 1996, 41, 111. [Google Scholar] [CrossRef] [PubMed]
- Ibáñez, P.; Villa-Abaunza, A.; Vidal, M.; Guerra, P.; Graullera, S.; Illana, C.; Udías, J.M. XIORT-MC: A real-time MC-based dose computation tool for low-energy X-rays intraoperative radiation therapy. Med. Phys. 2021, 48, 8089–8106. [Google Scholar] [CrossRef] [PubMed]
- Punnoose, J.; Xu, J.; Sisniega, A.; Zbijewski, W.; Siewerdsen, J. Technical note: Spektr 3.0—A computational tool for x-ray spectrum. Med. Phys. 2016, 43, 4711–4717. [Google Scholar] [CrossRef]
- Sisniega, A.; Desco, M.; Vaquero, J. Modification of the tasmip X-ray spectral model for the simulation of microfocus X-ray sources. Med. Phys. 2014, 41, 011902. [Google Scholar] [CrossRef]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In Proceedings of the International Conference on Machine Learning, Lille, France, 6 July 2015. [Google Scholar]
- Hara, K.; Saito, D.; Shouno, H. Analysis of function of rectified linear unit used in deep learning. In Proceedings of the 2015 International Joint Conference on Neural Networks (IJCNN), Killarney, Ireland, 12 July 2015. [Google Scholar]
- Carneiro, T.; Da Nóbrega, R.V.M.; Nepomuceno, T.; Bian, G.B.; De Albuquerque, V.H.C.; Reboucas Filho, P.P. Performance analysis of Google colaboratory as a tool for accelerating deep learning applications. IEEE Access 2018, 6, 61677–61685. [Google Scholar] [CrossRef]
- Bisong, E. Building Machine Learning and Deep Learning Models on Google Cloud Platform; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]
- Avanaki, A.N. Exact global histogram specification optimized for structural similarity. Opt. Rev. 2009, 16, 613–621. [Google Scholar] [CrossRef]
- Johnson, A.; Pollard, T.; Mark, R.; Berkowitz, S.; Horng, S. Mimic-CXR database. PhysioNet10 2019, 13026, C2JT1Q. [Google Scholar]
- Johnson, A.E.; Pollard, T.J.; Berkowitz, S.J.; Greenbaum, N.R.; Lungren, M.P.; Deng, C.Y.; Mark, R.G.; Horng, S. Mimic-CXR, a de-identified publicly available database of chest radiographs with free-text reports. Sci. Data 2019, 6, 317. [Google Scholar] [CrossRef]
- Swinehart, D.F. The Beer-Lambert law. J. Chem. Educ. 1962, 39, 333. [Google Scholar] [CrossRef]
- Benjamin, D.J.; Berger, J.O.; Johannesson, M.; Nosek, B.A.; Wagenmakers, E.J.; Berk, R.; Bollen, K.A.; Brembs, B.; Brown, L.; Camerer, C.; et al. Redefine statistical significance. Nat. Hum. Behav. 2018, 2, 6–10. [Google Scholar] [CrossRef]
- Di Leo, G.; Sardanelli, F. Statistical significance: p value, 0.05 threshold, and applications to radiomics–reasons for a conservative approach. Eur. Radiol. Exp. 2020, 4, 18. [Google Scholar] [CrossRef]
- Creswell, A.; White, T.; Dumoulin, V.; Arulkumaran, K.; Sengupta, B.; Bharath, A.A. Generative adversarial networks: An overview. IEEE Signal Process. Mag. 2018, 35, 53–65. [Google Scholar] [CrossRef]

| Parameter | Specification |
|---|---|
| Source-Detector Distance (cm) | 180 |
| X-ray Detector Size (cm) | |
| X-ray Detector Resolution (pixel) |
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | C10 | Avg | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Original | 2.71 | 1.66 | 1.36 | 1.11 | 1.35 | 1.16 | 1.71 | 1.47 | 1.28 | 1.59 | 1.54 |
| Scatter-corrected | 3.80 | 2.02 | 1.54 | 1.17 | 1.49 | 1.23 | 2.14 | 1.68 | 1.41 | 1.64 | 1.81 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Freijo, C.; Herraiz, J.L.; Arias-Valcayo, F.; Ibáñez, P.; Moreno, G.; Villa-Abaunza, A.; Udías, J.M. Robustness of Single- and Dual-Energy Deep-Learning-Based Scatter Correction Models on Simulated and Real Chest X-rays. Algorithms 2023, 16, 565. https://doi.org/10.3390/a16120565
Freijo C, Herraiz JL, Arias-Valcayo F, Ibáñez P, Moreno G, Villa-Abaunza A, Udías JM. Robustness of Single- and Dual-Energy Deep-Learning-Based Scatter Correction Models on Simulated and Real Chest X-rays. Algorithms. 2023; 16(12):565. https://doi.org/10.3390/a16120565
Chicago/Turabian StyleFreijo, Clara, Joaquin L. Herraiz, Fernando Arias-Valcayo, Paula Ibáñez, Gabriela Moreno, Amaia Villa-Abaunza, and José Manuel Udías. 2023. "Robustness of Single- and Dual-Energy Deep-Learning-Based Scatter Correction Models on Simulated and Real Chest X-rays" Algorithms 16, no. 12: 565. https://doi.org/10.3390/a16120565
APA StyleFreijo, C., Herraiz, J. L., Arias-Valcayo, F., Ibáñez, P., Moreno, G., Villa-Abaunza, A., & Udías, J. M. (2023). Robustness of Single- and Dual-Energy Deep-Learning-Based Scatter Correction Models on Simulated and Real Chest X-rays. Algorithms, 16(12), 565. https://doi.org/10.3390/a16120565







