Abstract
This paper presents a hybrid grasshopper optimization algorithm using a novel decoder and local search to solve instances of the open vehicle routing problem with capacity and distance constraints. The algorithm’s decoder first defines the number of vehicles to be used and then it partitions the clients, assigning them to the available routes. The algorithm performs a local search in three neighborhoods after decoding. When a new best solution is found, every route is locally optimized by solving a traveling salesman problem, considering the depot and clients in the route. Three sets containing a total of 30 benchmark problems from the literature were used to test the algorithm. The experiments considered two cases of the problem. In the first, the primary objective is to minimize the total number of vehicles and then the total distance to be traveled. In the second case, the total distance traveled by the vehicles is minimized. The obtained results showed the algorithm’s proficient performance. For the first case, the algorithm was able to improve or match the best-known solutions for 21 of the 30 benchmark problems. For the second case, the best-known solutions for 18 of the 30 benchmark problems were found or improved by the algorithm. Finally, a case study from a real-life problem is included.
1. Introduction
In recent years, the development of metaheuristic methodologies for the solution of complex optimization problems has increased, both in the continuous and discrete space versions. Some of the most significant metaheuristics are: particle swarm optimization (PSO) [1], ant colony optimization (ACO) [2], genetic algorithms (GA) [3], artificial bee colony algorithm (ABC) [4], tabu search (TS) [5], variable neighborhood search (VNA) [6], the bees algorithm (BA) [7], fish school search (FSS) [8], swallow swarm optimization (SSO) [9], hybrid particle swallow swarm optimization (HPSSO) [10], grasshopper optimization algorithm (GOA) [11], bat algorithm (BAT) [12], whale optimization algorithm (WOA) [13] just to mention a few. Within the metaheuristics mentioned above it can be observed that they are developed using two main ingredients: (1) the basic principles of physics such as velocity, the force of attraction and acceleration and (2) the behavior of certain groups of animals. There are many applications in which GOA has been used. Among such applications the most recent and relevant are [14,15,16,17,18].
The open vehicle routing problem (OVRP) is a variant of the classic vehicle routing problem (VRP) first introduced in [19]. Many variants of the VRP have been studied in the literature, and recent research focuses on modeling very specialized real-world variants of the VRP. Some of these recent specialized real-world variants can be found in [20,21,22,23,24,25,26,27,28,29].
Although new routing problems arise everyday, classic problems such as the OVRP are still studied thanks to their potential applications. The research presented in this paper was motivated by the case study presented in Section 5, which required the solution of OVRP instances.
The OVRP was formally introduced in [30], although the first work related to the problem was first presented in [31] for an air express courier problem. The OVRP is an NP-Hard combinatorial optimization problem (as mentioned in [32]), which makes it difficult to solve by exact methods. Therefore, many heuristic approaches have been developed to solve the problem. Among the most important heuristic algorithms used to solve the OVRP are those in [32,33,34,35,36,37,38,39].
The applications of the OVRP are not limited to the context of vehicle route design. In [31], the OVRP is used to solve an air express courier problem, and in [40], the train services planning at the Channel tunnel is made by solving an OVRP.
In this work, a novel hybrid grasshopper optimization algorithm with local search (HGOALS) method is used to solve instances of the open vehicle routing problem. To our knowledge, GOA has not been previously used for solving the OVRP. In fact, there is not much literature on GOA in the context of vehicle routing problems. The proposed solution method is based on the grasshopper optimization algorithm (GOA) and uses local search to improve solutions and accelerate the optimization process. The GOA is a swarm optimization algorithm that mimics the behavior of a grasshopper swarm to solve optimization problems.
The HGOALS combines the GOA framework with a decodification procedure and local search to obtain solutions for the OVRP instances. The decodification procedure incorporates a feasibility recovery phase in case the decoded solutions are infeasible. Once the solutions are feasible, the best ones are selected for improvement using local search. Every time a new best solution is found, it is subjected to an improvement phase. The algorithm finishes when two given stop criteria are reached.
To demonstrate the efficiency of the proposed methodology, experiments were carried out using 30 benchmark problems taken from the scientific literature and the results were compared against previous algorithms. The experiments considered two objective functions for the problem. The first is the hierarchical objective function, which has as a first goal the minimization of the total number of vehicles to be used, and as a second goal the minimization of the total traveling cost of such vehicles. In the second objective function, only the total traveling cost is minimized. The results show that the proposed methodology is competitive. Additionally, the algorithm was utilized to solve a case study from a security company, obtaining excellent results. The rest of this paper is organized as follows: Section 2 describes the OVRP, while Section 3 describes the proposed algorithm. The computational experiments are reported in Section 4, where the used benchmark instances, the corresponding numerical results and a numerical comparison concerning other algorithms are presented. Finally, conclusions and future research are discussed in Section 6.
2. Problem Description
As mentioned before, two types of objective functions have been taken from the literature for the problem: (i) the hierarchical one (minimize the number of routes and then minimize the total traveling cost) and (ii) the minimization of the total traveling cost.
Consider a complete directed graph , with the set of vertices and A the set of arcs. The reason to consider a directed graph is that in real-life applications, cost (distance) matrices are not symmetric (See Section 5). Notice that vertex 0 (depot) is the departure point of all vehicles. Each vertex (except the depot) , has an associated demand . Also, each arc , has an associated cost . Feasible solutions to the OVRP are open routes originated at the depot, that satisfy capacity and route length constraints.
Before formally defining the OVRP, some notation is introduced. Let denote a given set of open routes of G originated at the depot (0):
- , the set of vertices without the depot.
- Cost of R, .
- , the time required to service any client.
- First vertex, a vertex directly connected to 0 in R ().
- Subroute (), an open route in R originated at vertex .
- s-route (), a subroute originated at i, where i is the first vertex of .
- , the set of vertices that are part of subroute .
- , the sum of the demands of the vertices in .
- , the total length of .
The capacity constraints for the OVRP impose that for a given open route originated at 0 the total demand of any subroute can not exceed a given value . That is for any subroute of R. Open routes are also subjected to length constraints, which impose that route duration can not exceed a given value . That is for any subroute of R.
The OVRP can be defined as the problem of finding a set of open routes originated at the depot, visiting all clients and satisfying the capacity and route length constraints while minimizing one of the above mentioned objective functions.
Mathematical Formulation
As mentioned before the OVRP is a variant of the VRP and formulations for the VRP can be adapted to solve the OVRP. Following a formulation for the OVRP is presented. This formulation is useful for solving symmetric and asymmetric OVRP and considers capacity and route length constraints. It is based on a classic formulation of the VRP and the Miller–Tucker–Zemlin subtour elimination constraints for the VRP [41]. Therefore, the OVRP can be formulated using the following variables:
The hierarchical objective function is defined using the variables mentioned above, as follows:
where M is a large number. The first term in Equation (1) minimizes the total number of vehicles, while the second term minimizes the total traveling cost.
The second objective function only minimizes the total traveling cost and is defined as follows:
The following constraints are required to complete the model for the OVRP:
The constraints in Equation (3) guarantee that all clients are visited, and the constraints in Equation (4) guarantee that routes leave the client or finish the route at the client. Route capacity is controlled with the constraints in Equations (5) and (6). The constraints in Equations (7) and (8) control the route length. Note that the constraints in Equation (5) are the Miller–Tucker–Zemlin subtour elimination constraints for the VRP [41], and the constraints of Equation (7) are the same constraints adapted to control route length.
3. Hybrid Grasshopper Optimization Algorithm with Local Search
This section describes the proposed hybrid grasshopper optimization algorithm with local search (HGOALS) for solving OVRP’s instances. The grasshopper optimization algorithm (GOA) has been proposed initially in [11].
The behavior of a grasshopper’s swarm of size P can be simulated using , where is the current position of the member of the swarm, the effect of the wind on the grasshoppers movement, the gravity force and the social interaction between the grasshopper and the rest of the members of the swarm. The coefficients , and are random numbers in the interval used to introduce random behavior among the members of the swarm. As mentioned in [11], the problem with this model is that grasshoppers tend to stay in a comfort zone, which is not useful when solving optimization problems. Therefore the authors proposed to use:
In this equation, and are vectors containing respectively, the upper and lower bounds for the variables considered for optimization. T is the target solution, which is the best solution found so far by the algorithm, is the distance between grasshoppers i and j. Finally, the social interaction between grasshoppers is computed using , where f is the intensity of attraction, and l the attractive length scale. Constant determines how likely is the grasshopper to explore around the target T (equivalent to w in the PSO algorithm), balancing the exploration and exploitation of the area around T. Constant defines the attraction, repulsion and comfort zone among the grasshoppers. For a problem of dimension n, the position of the grasshopper on dimension h () is given by:
The movement of the grasshopper can be simulated in a multidimensional space using Equation (10). For further details about the GOA, the reader is encouraged to read [11].
Since the GOA is a continuous optimization algorithm, it is necessary to implement a decodification procedure in order to solve non-continuous optimization problems. Therefore, a decodification procedure is required to transform the continuous values from the GOA into solutions of the non-continuous problem.
3.1. HGOALS Description
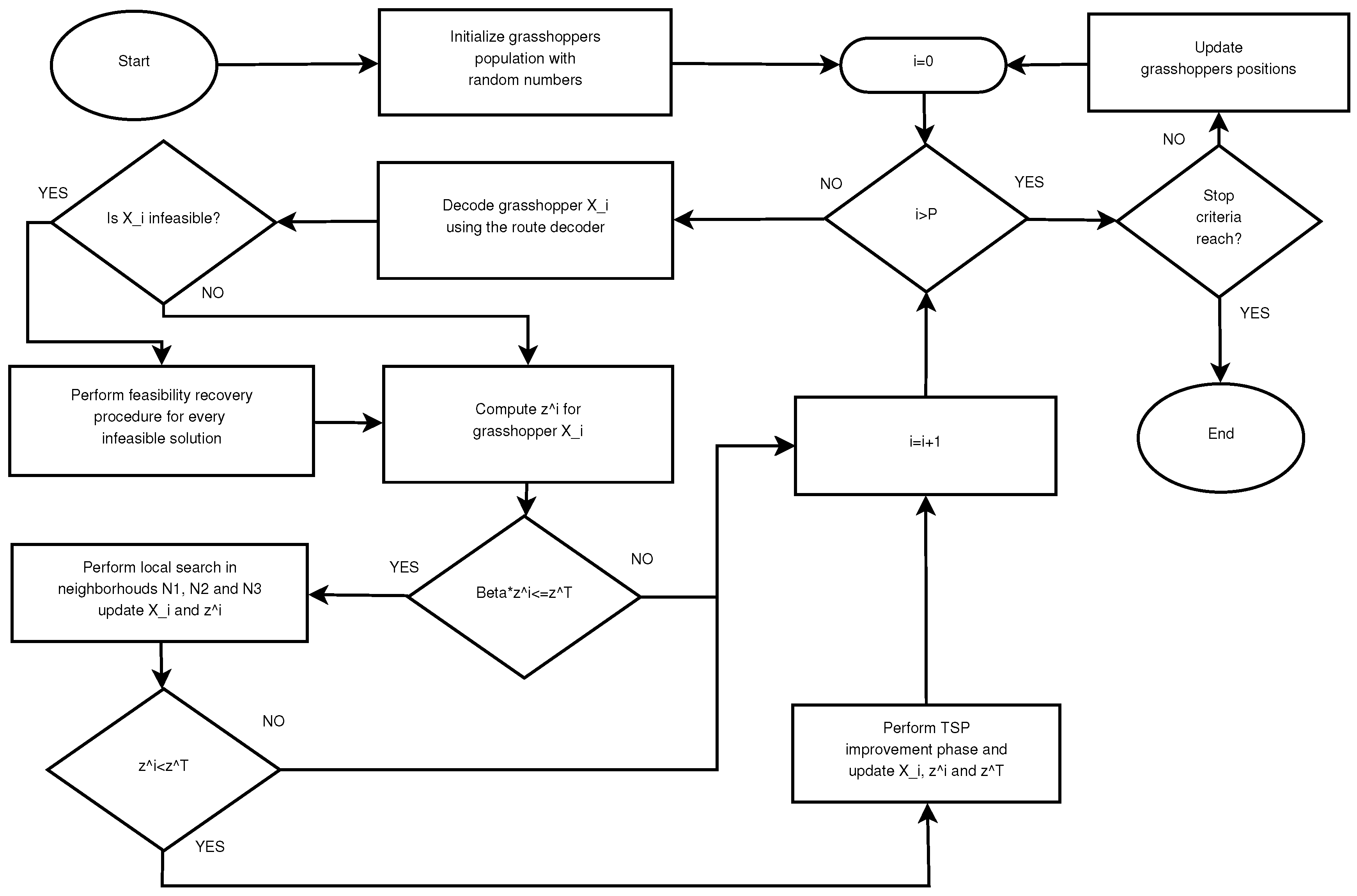
A mentioned previously, HGOALS combines the GOA framework with a decodification procedure and local search to solve OVRP instances. Figure 1 shows a flow diagram for the HGOALS. The proposed algorithm receives as an input graph , the associated cost matrix c, the service time parameter , the vehicle capacity parameter Q, the maximum length parameter L, the grasshopper population size P and the grasshopper dimension n. HGOALS has three essential components: (i) The route decoder (decodification procedure), (ii) the local search and (iii) the improvement phase. To facilitate comprehension the above mentioned components are described first, and the complete process of the proposed HGOALS algorithm is explained after.
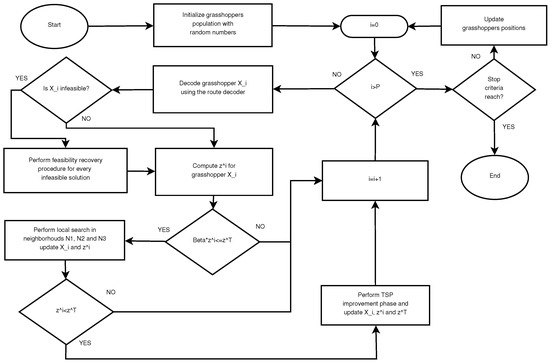
Figure 1.
Flow diagram for the hybrid grasshopper optimization algorithm with local search (HGOALS).
3.2. The Route Decoder
As mentioned before, the HGOALS requires the implementation of a decoder. Other decoders for similar problems have been previously proposed. The objective of proposing a new decoder is to find better results than those obtained by previous decoders and other metaheuristics. In this section, the new decoder is described.
The route decoder (RD) requires as input the associated cost to every arc , the random-key vector and the demand vector d. The random-key vector contains fractional values. , the first value in vector , is used to define the total number of vehicles available in the solution. The other n values are used to assign vertices to different vehicles. The decoder determines the total number of vehicles, by first computing the minimum number of vehicles required to deliver all the clients demand using:
where:
Using the random-key vector value the number of available vehicles in the solution is given by:
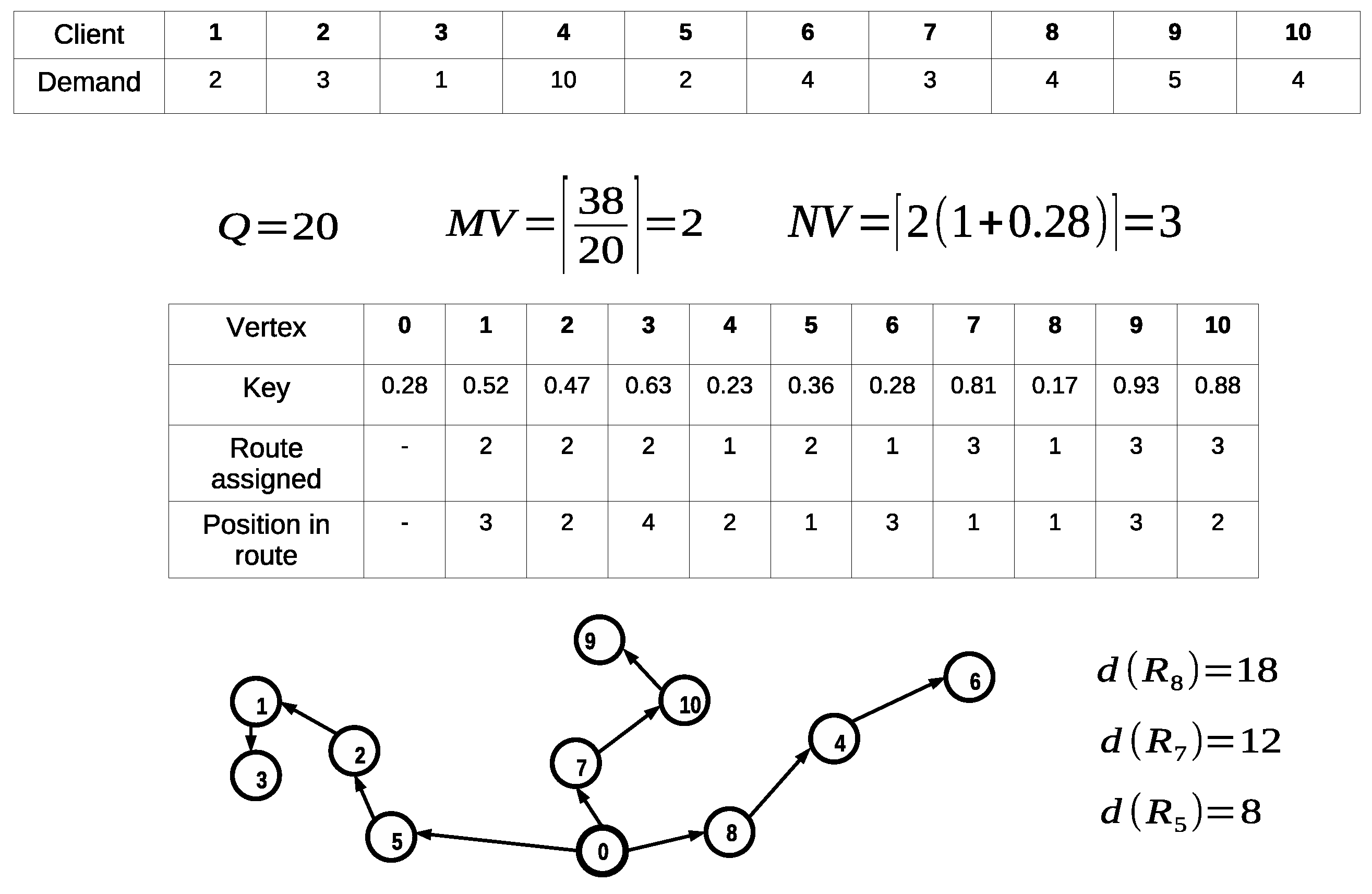
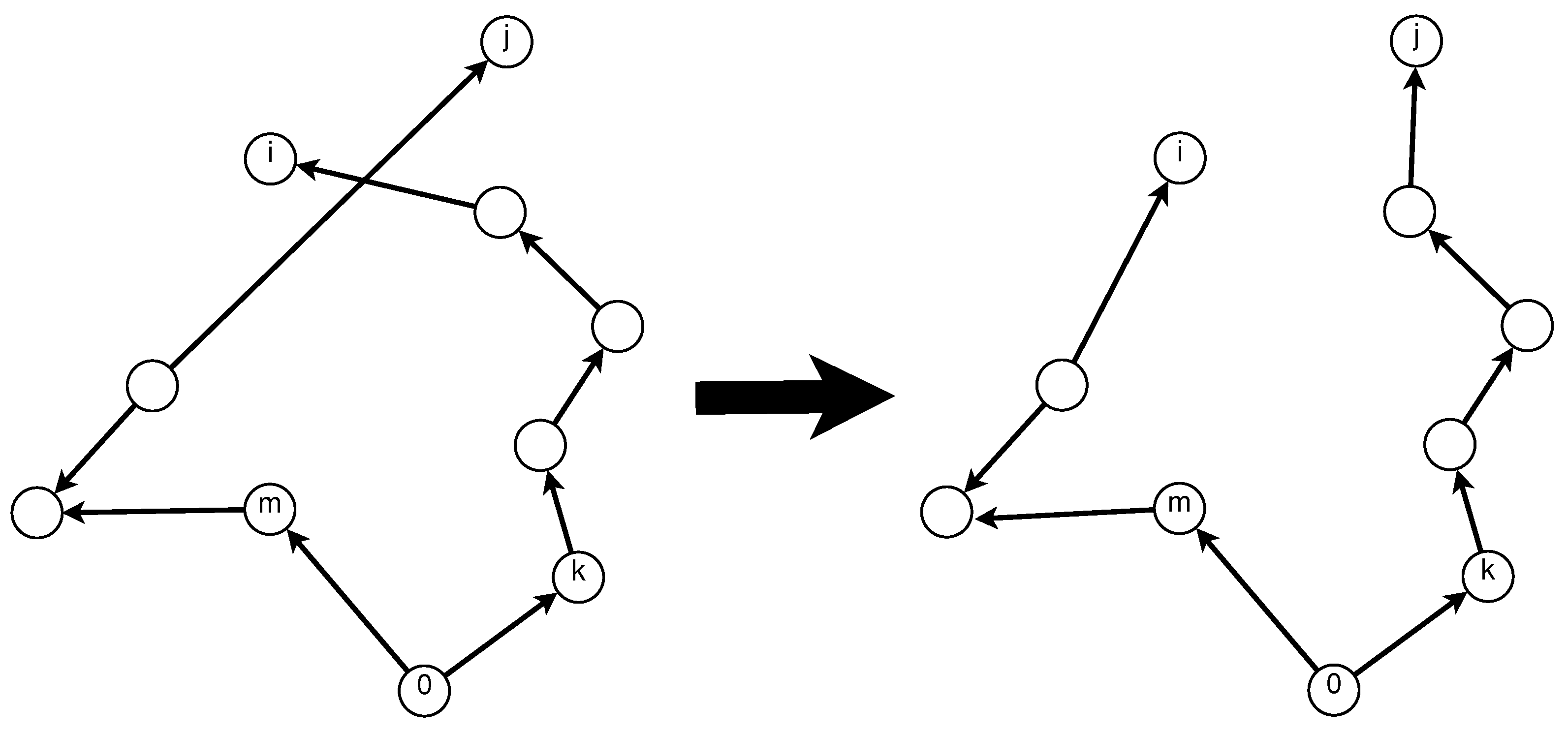
Then the interval is divided into subintervals. Each client is assigned to a vehicle using these subintervals and the keys associated with each client. Once all clients have been assigned to a vehicle, they are sorted in ascending order according to their key. The routes are built using the sorted keys. Figure 2 illustrates an example of how the proposed decodification procedure works. In this example, using the demand vector d, the capacity parameter and the first key-value , the minimum and the available number of vehicles are obtained: and respectively. Therefore, the interval is divided into three subintervals which are used to assign clients to vehicles. Clients 4, 6 and 8 are assigned to vehicle number 1; clients 1, 2, 3 and 5 are assigned to vehicle 2; and clients 7, 9 and 10 are assigned to vehicle number 3. For vehicle 1, the assigned vertices are transformed into the route ; for vehicle 2, the resulting route is . Finally, for vehicle 3, the resulting route is .
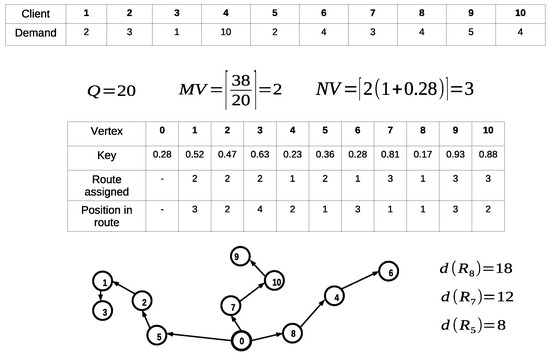
Figure 2.
Route decoder example.
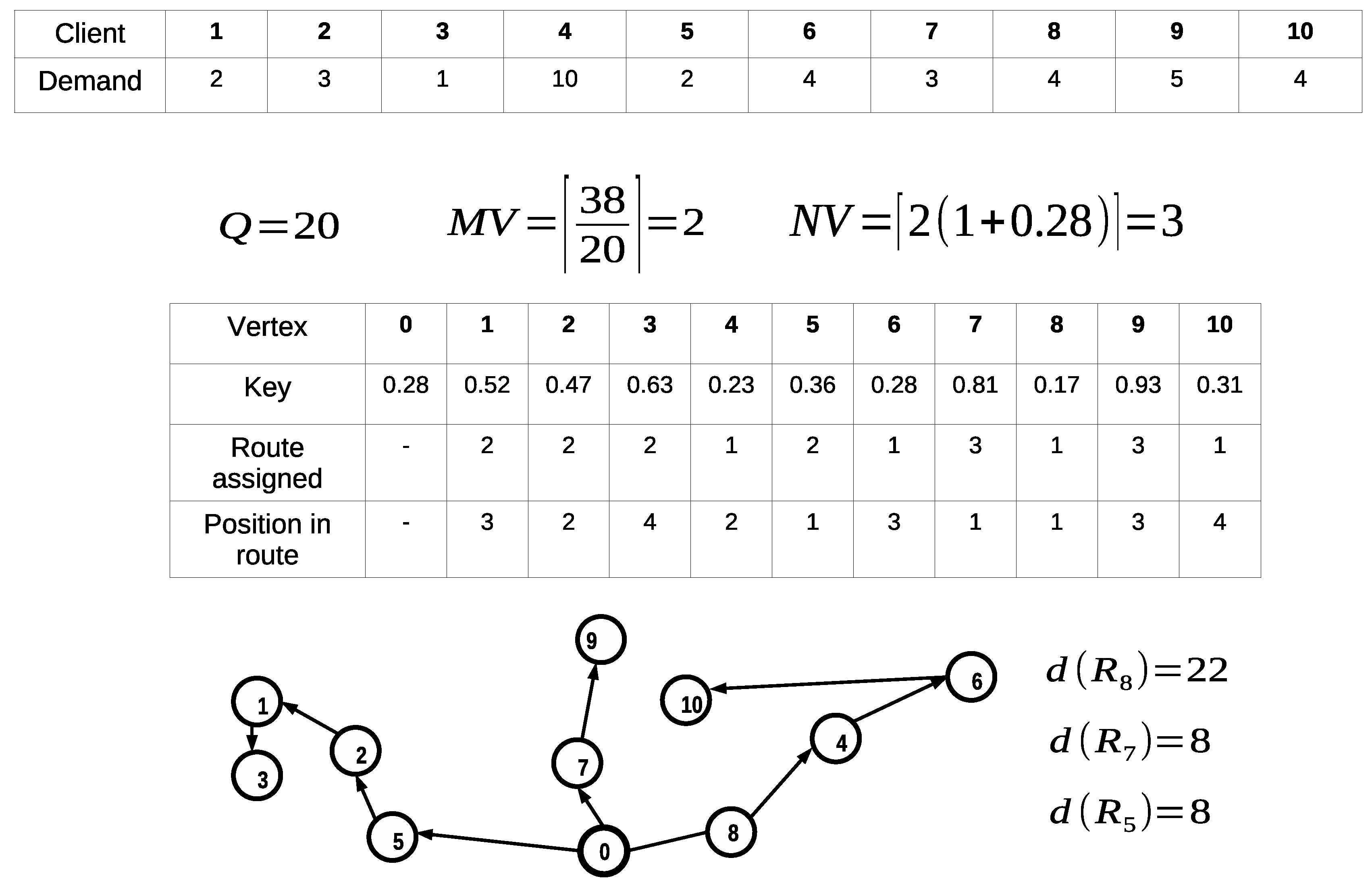
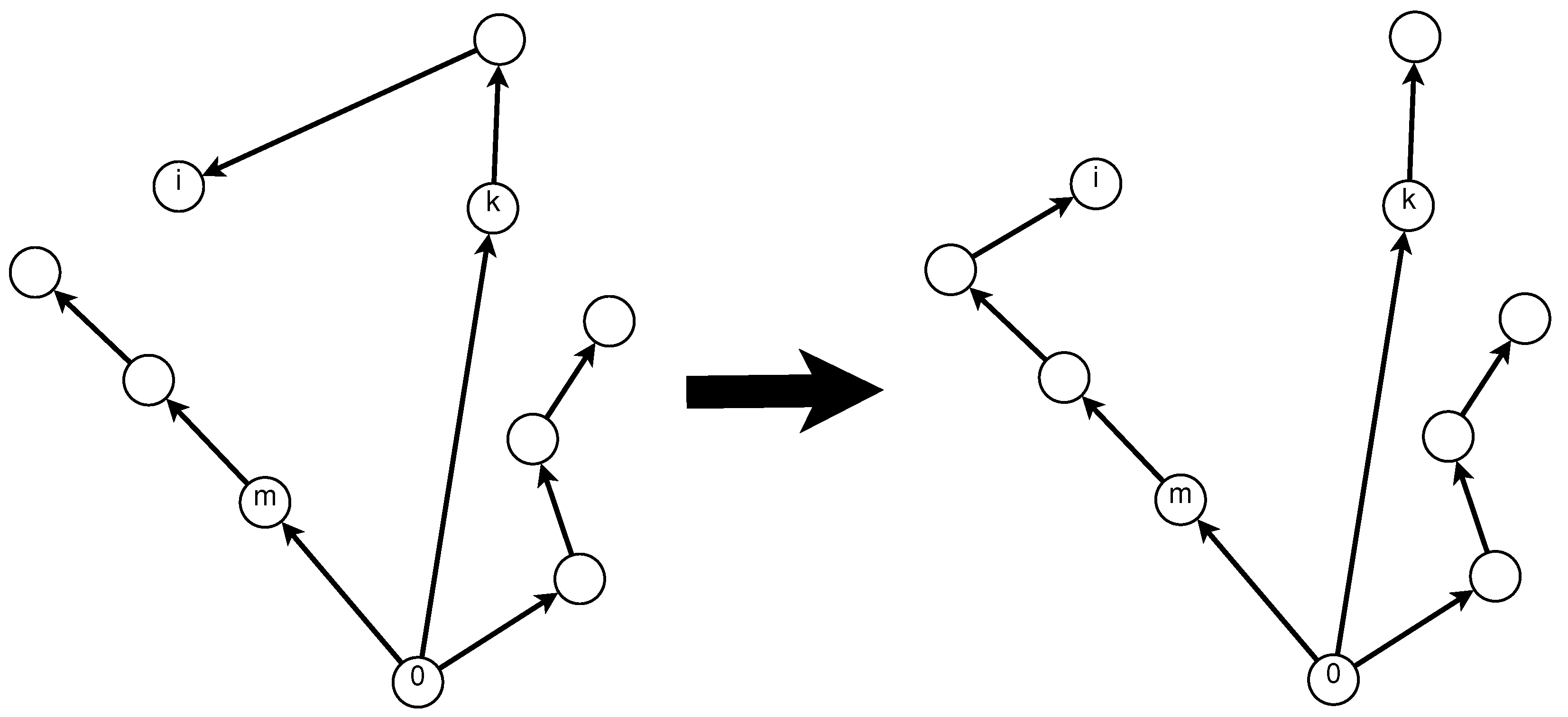
It is relevant to notice that this decodification/codification method can lead to infeasible solutions. In Figure 3, an example of an infeasible solution is presented. The violation is made over the capacity and maximum distance constraints since for s-route , and .
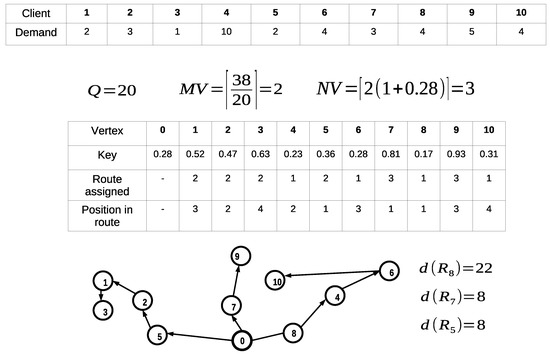
Figure 3.
Infeasible solution example.
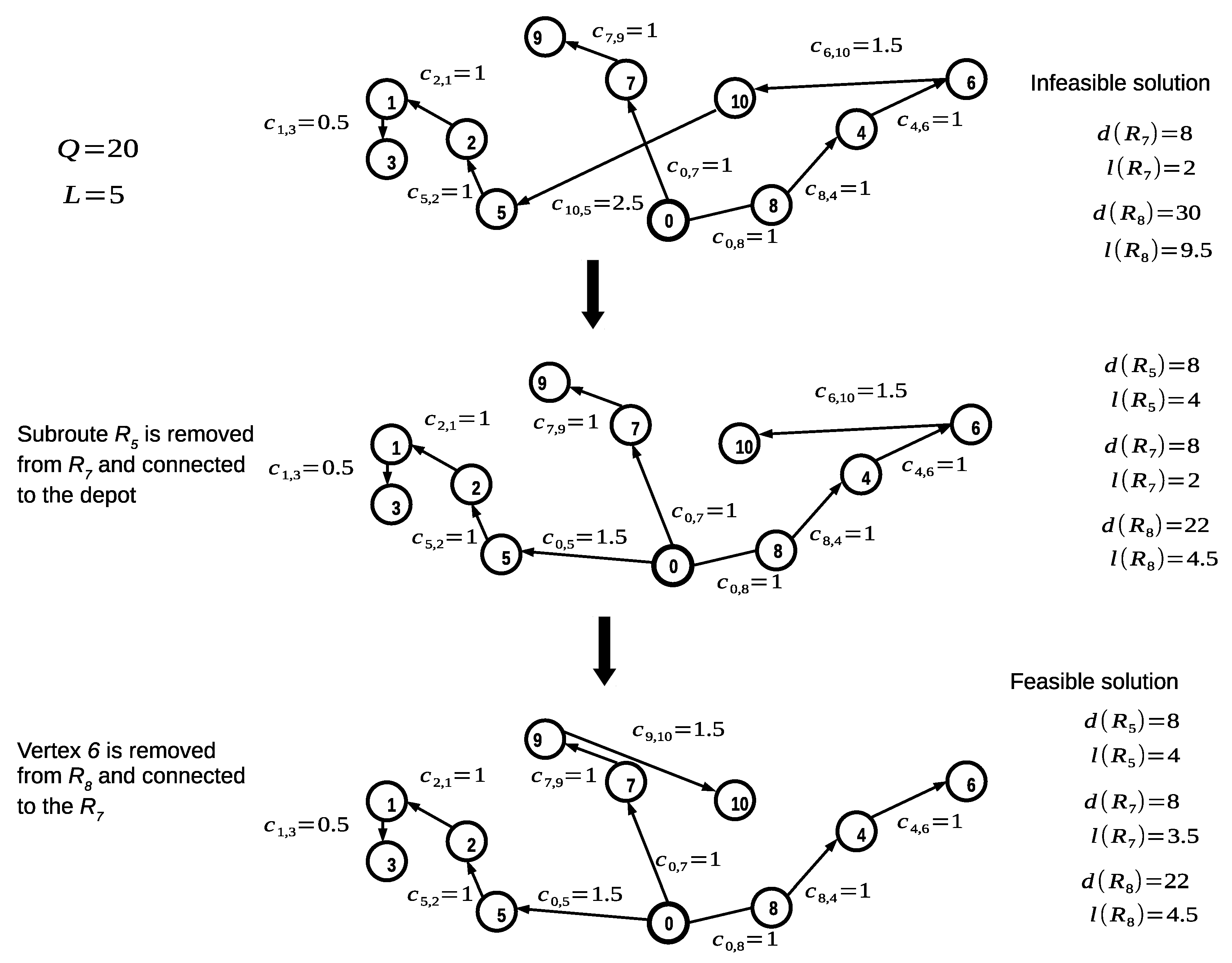
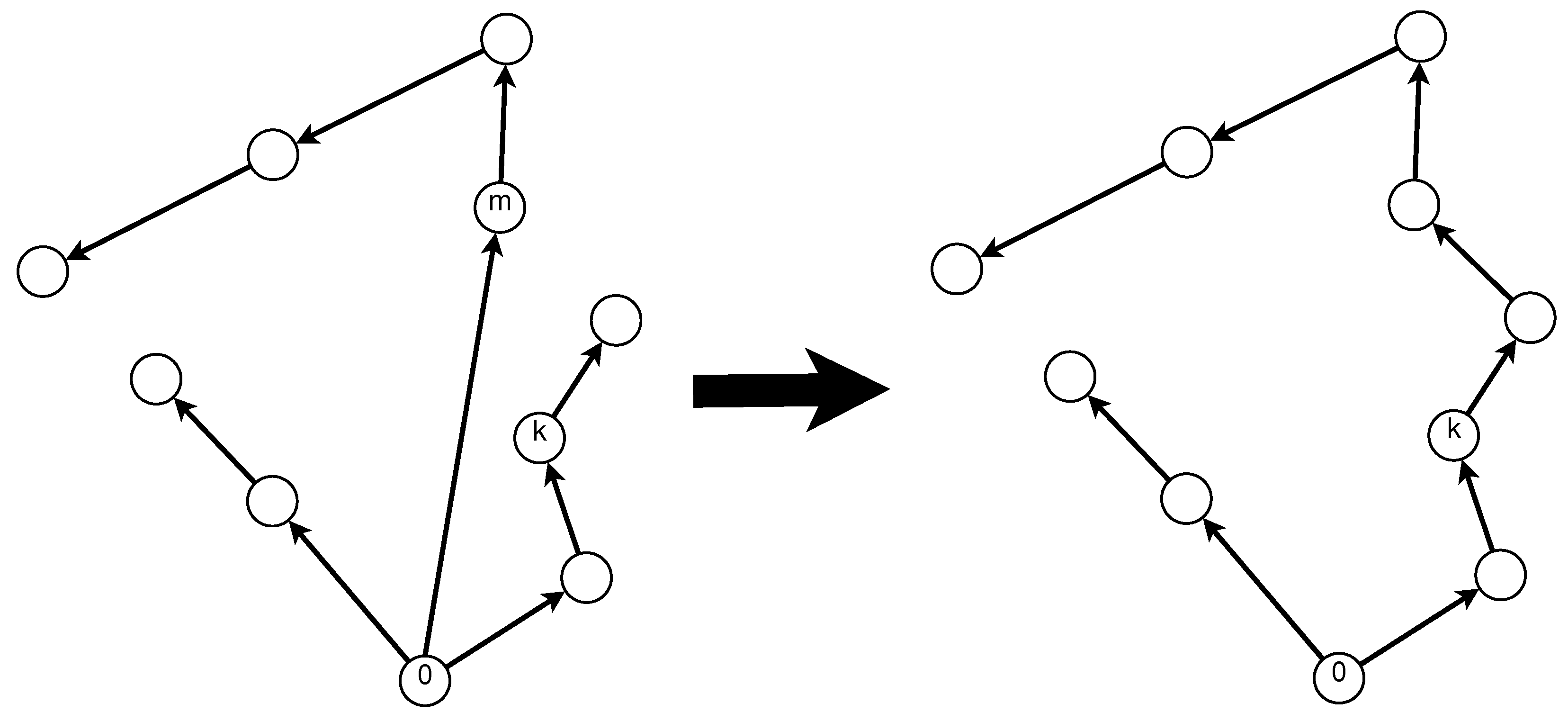
Whenever a solution is infeasible after decoding, it enters the feasibility recovery procedure. The feasibility recovery procedure reassigns subroutes or vertices from the infeasible route to other routes with available capacity and without violating the maximum length constraint. If there are no suitable routes for reassigning a given subroute or vertex, a new route is created by connecting such subroute or vertex directly to the depot. The reassignment is made by replacing arcs on the solution, using the cheapest available that reduces or eliminates the route’s infeasibility. Figure 4 shows how the feasibility recovery procedure repairs an infeasible solution. In this example, s-route violates the capacity and maximum distance constraints ( and ). For recovering feasibility, subroute is removed from . Since annexing to s-route will violate the maximum length constraint, is directly connected to the depot. At this point, only violates the capacity constraint. Therefore, vertex 10 is removed from and annexed to s-route , leading to a feasible solution.
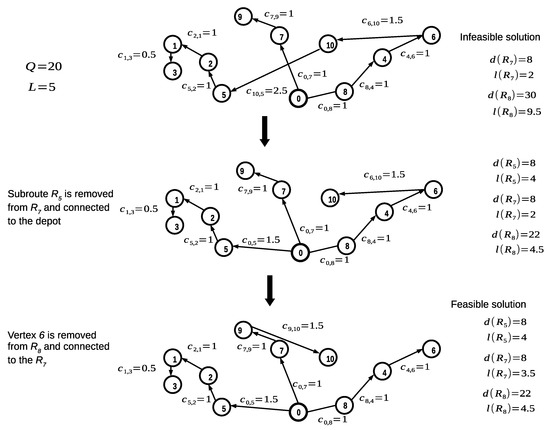
Figure 4.
Feasibility recovery procedure example of an infeasible solution.
3.3. Local Search
Once a solution is feasible, it is improved through a local search phase if its objective function value , is close to the objective function value of the current best solution T (, ). In the local search, three neighborhoods are explored: (i) vertex exchange, (ii) vertex reassignment and (iii) route merging. Consider two vertices i and j belonging respectively, to two different s-routes k and m. In the neighborhood, vertex i is removed from s-route k and connected to s-routes m, while vertex j is removed from s-route m and connected to s-routes k (Figure 5). The neighborhood is explored by removing vertex i from s-routes k and connecting i to s-route m (Figure 6). Finally, s-routes k and m are merged into one s-route (k) in the neighborhood (Figure 7). The three neighborhoods are explored sequentially () until no further improvement is found.
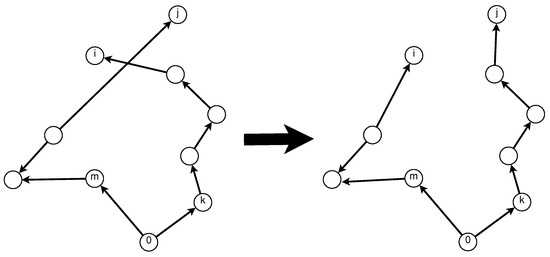
Figure 5.
Neighborhood , vertex exchange.
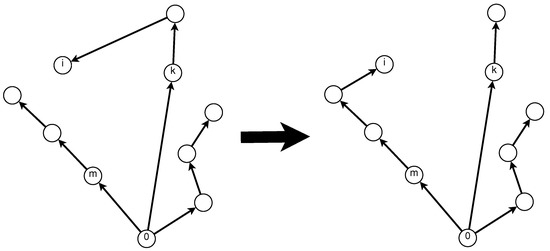
Figure 6.
Neighborhood , vertex reassignment.
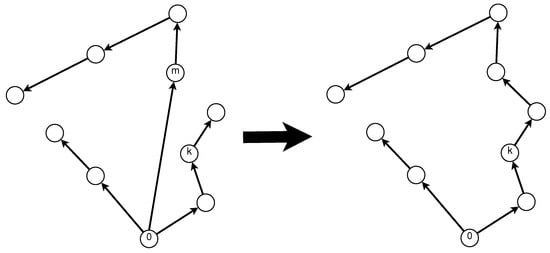
Figure 7.
Neighborhood , route merging.
3.4. Improvement of Best Solutions
If after the local search, the algorithm finds a new best solution, such a solution is subjected to an improvement phase. Consider the subset of vertices that contains the vertices assigned to a given s-route and the depot. Using and the associated subset of arcs , the sub-graph is built. Associated costs for every arc are obtained from the original problem. The cost for the remaining arcs are substituted using . Using and its associated costs, a traveling salesman problem (TSP) can be solved in order to minimize the cost of route since every route respects the capacity and maximum length constraints. Notice that the solution obtained by the TSP using graph and its associated costs are equivalent to an open route, since the costs for returning to the depot are equal to zero. Therefore, a TSP problem is solved for every s-route using the formulation in [41], leading to a locally optimized solution.
Since all HGOALS components have been explained, it is appropriate to describe the algorithm with the aid of the flow diagram presented in Figure 1. The first step is to initialize the P grasshoppers with continuous random values, and the target solution T’s objective function is initialized . Then, the algorithm enters a loop to transform grasshoppers into OVRP solutions. As every grasshopper enters the loop, the route decoder (comprehensively explained in Section 3.2) transforms the grasshopper’s continuous values to obtain OVRP solutions in a non-continuous space. If the obtained solution is infeasible, then it enters the feasibility recovery procedure. Once the solution is feasible, its objective function is computed. If the solution is among the best solutions (, ) then it enters local search. In the local search, three neighborhoods , and are explored sequentially. After the local search phase, the solution’s objective function is computed. If then T is updated with . The loop finishes once all grasshoppers have been decoded. At this point, the grasshoppers’ positions are updated using Equation (10), and the stop criteria are checked. The algorithm finishes when one stop criterion is reached.
4. Computational Experiments
In this Section, test instances are described first, and second, the results from the computational experiments for both of the objective functions previously mentioned are presented.
4.1. Test Instances
For testing the proposed algorithm, three sets of instances were used: group C, group O and group K. The first two sets of instances have been widely used in previous research, while the third set was only used in [42,43]. Table 1 shows the characteristics for every group of instances; n specifies the size of the instances in the group (excluding the depot), Q specifies the vehicle’s capacity and L specifies the range for the maximum length allowed for the routes.

Table 1.
Test instances.
Table 1 shows that instances C1–C5, C11–C12 and O1–O8 do not consider route length constraints, while instances C6–C10, C13–C14 and K01–K08 do. For instances C1–C10, O1–O8 and K01–K08 the depot is located at the center of the customers, while for instances C11–C14 the depot is located on an extreme side. Additionally, for instances C11–C14, clients are distributed in clusters over the plane. For instances C1–C10, clients are randomly distributed around the depot. Finally, clients for K and O instances follow a ring-like distribution over the plane.
4.2. Implementation Details
The proposed algorithm was implemented in Matlab. Two criteria were used to stop the algorithm. The first was set to a maximum running CPU time of 1000 s, while the second was to reach 25 iterations without improving the current best solution found. The machine used for the experiments was running Linux with an Intel Core2 Duo, a CPU clock speed of 3.1 GHz and 4 GB of RAM.
4.3. Results with the Hierarchical Objective Function
Table 2 presents the results obtained by the HGOALS for the benchmark problems using a hierarchical objective function. In this case, the first goal is to minimize the number of vehicles, and the second, the total traveling cost. Column n shows the size of the instance, Q shows the vehicles capacity, presents the number of vehicles and the best-known solution value. Column shows the average solution value after five runs, presents the value of the best solution value after five runs, shows the percentage difference between the best-known solution value and the best solution value obtained by the HGOALS, and presents the average CPU time per run in seconds, after five runs. Row presents the average for columns and . Results in bold format show that the algorithm found the best know solution for the instance. Results in bold and underlined show the algorithm improved the best-known solution for the benchmark problem. The symbol ‘**’ is used to indicate that the algorithm found solutions with a new minimum number of vehicles. When the number of vehicles from the best-known solution is different of the best solution obtained by the HGOALS, the number of vehicles used by the best-known solution is shown in column . The results show that the algorithm was able to improve the best-known solutions for seven instances in group C, five on group K and one in group O.

Table 2.
Results obtained by the HGOALS for all the test instances (hierarchical objective function).
Therefore, the HGOALS is capable of improving the best-known solution for 15 of the 30 benchmark problems. Notice that 11 of the improved best-known solutions where from instances considering route length constraints. The algorithm also finds the best-known solutions for the other five instances. Other relevant results are the new best solutions for instances C6, C13, C14 and O4 that use fewer vehicles (5, 10, 10 and 9, respectively) than the solutions found in previous research (6, 11, 11 and 10). Finally, the algorithm struggles with the C11 instance. The average percentage deviation from the best-known solution (gap) is the worst for all benchmark problems (). The reason is the cluster distribution of the clients and the tendency of the feasibility recovery procedure to create more routes than the minimum required. Note that instance C6 has a higher gap, but it uses fewer vehicles than the best-known solution.
The CPU times increase significantly as the benchmark problem size increases. The algorithm reached the 1000 s limit for seven of the benchmark instances, two from set O and five from set K. The algorithm performs the worst in the set O with an average deviation from the best-known solution of . For group C, the algorithm performs the best having an average deviation from the best-known solutions of , while for group K this metric is .
Table 3 compares the proposed algorithm with the results from previous research. Considering all instances in group C, the HGOALS outperforms the other algorithms. The Broad Local Search Algorithm (BLSA) performs better than the HGOALS in instances without route length constraints in this group. The HGOALS performs the best in instances with route length constraints, improving the best-known solutions for six of the seven instances. The HGOALS obtains new best solutions for C2, C6, C7, C9, C10, C13 and C14. For instances C6, C13 and C14 the algorithm found solutions using one less vehicle. Finally, it is relevant to mention that the algorithm struggles with C11 instance obtaining the largest gap (). The latter instance has a cluster like distribution.

Table 3.
Comparison between the HGOALS results and previous research for instances in group C (hierarchical objective function).
The comparison of the results with previous research for instances in group O is made in Table 4. In this set of instances, the BLSA performs the best obtaining the best-known solutions for six of the eight benchmark problems. On the other hand, the HGOALS performs better than the other algorithms (except BLSA), and finds a new best solution for instance O4 using nine vehicles instead of ten. Notice that test problems in this set do not consider route length constraints.

Table 4.
Comparison between route decoder and previous research for instances in group O (hierarchical objective function).
Finally, Table 5 compares results for instances in group K. The comparison is made with upper bounds obtained by the GRASP algorithm proposed in [42] and the BRKGA in [48]. The results show that the HGOALS outperforms the other two metaheuristics by obtaining six new best solutions for the eight instances in the set. In this set, all benchmark problems consider route length constraints.

Table 5.
Comparison between route decoder results and previous research for instances in group K (hierarchical objective function).
4.4. Results with the Traveling Cost Minimization Objective Function
The obtained results by the HGOALS for the benchmark problems with the second objective function of minimizing the total traveling cost are presented in Table 6. The results show that the algorithm was able to improve three of the 14 instances of group C, one of group O and five on group K. The HGOALS also reaches the best-known solutions for five instances in group C and one for group K.

Table 6.
Results obtained by the HGOALS for all the test instances (minimizing traveling cost).
The results show that the proposed algorithm is capable of improving the best-known solution in nine of the 30 instances used to test the algorithm. Notice that eight of these instances consider route length constraints. It is also capable of finding the best-known solutions in other nine test instances. In brief, the HGOALS matches or improves the best-known solutions for 18 of the 30 test instances. On the other hand, the CPU times required by the algorithm reach 1000 s for six instances in group O. It is also in this group where the algorithm performs the worst with an average deviation from the best solution of . For group K, the algorithm performs the best having an average deviation from the best solution of , while for group C this metric is of .
Table 7 compares the proposed algorithm with previous research for benchmark problems in group C. For instances with no route length constraints, the HGOALS performs worse than the BLSA and BRKGA but better than the other algorithms. For the benchmark problems including route length constraints, the HGOALS performs better than the rest of the algorithms obtaining new best solutions for instances C9, C10 and C13 and reaching the best-known solutions for instances C6, C7 and C14.

Table 7.
Comparison between the HGOALS and previous research for instances in group C (minimizing traveling cost).
The comparison of the results with previous research for instances of group O is made in Table 8. In this set of instances, the BLSA performs the best obtaining the best-known solutions for six of the eight instances, followed by the HGOALS obtaining the best-known solution for one of the eight instances.

Table 8.
Comparison between route decoder and previous research for instances in group O (minimizing traveling cost).
For the benchmark problems in group K, the comparison with results obtained in previous research is made in Table 9. The results show that the HGOALS outperforms the other two metaheuristics by obtaining five new best solutions for the eight instances in the group.

Table 9.
Comparison between the HGOALS results and previous research for instances in group K (minimizing traveling cost).
4.5. Comparison of Average CPU Times with Previous Research
Finally, a comparison of the computational effort required by each of the solution methods is presented in Table 10 and Table 11. Rows C, O and K present the mean for the different sets of test instances of the average CPU time per run reported by the different solutions methods. Row shows the number of best-known solutions found and the number of tested instances by each algorithm. Finally, row presents the CPU model used by each algorithm and row , the SPECint2000 (https://www.spec.org/cpu2000/results/) and SPECint2006 (http://www.spec.org/cpu2006/results/cint2006.html) base score, along with an estimate of the computing times reduction factor.

Table 10.
Average CPU times comparison for the different solution approaches (hierarchical objective function).

Table 11.
Average CPU times comparison for the different solution approaches (minimizing traveling cost).
In terms of CPU times, the HGOALS has slightly higher average CPU times, when compared with the BBMO, BLSA, HBMO and ORTR, although it obtains better results. It has lower average CPU times when compared with MVNS, HES, TSB, ALNS and BRKGA.
5. A Case Study
A security and alarm company requires its payment collection routes to be more efficient for two reasons: the first is to reduce the days required to collect payments, and the second is to reduce the fuel consumption used by the company representative. The company provides alarm and security services on a monthly or yearly basis. Customers choose the type of service they require and pay on the same basis. Therefore, at the beginning of each month, the company requires to collect payment from around 100 customers. Payment collection routes were decided by the company representative based on his experience and usually took between three to four weeks to be completed (15 to 20 working days). The company provided the addressees of customer required to pay in the next two months. They also set a maximum number of customers to be visited per day (15 per day) and a maximum of working hours per day (seven hours). Finally, they provided the routes planned by the company representative in charge of collecting the payments for the next two months. A geographic information system (GIS), customers’ addresses, and a web-based tool were used to build cost(distance) and time matrices to feed the algorithm. Such matrices were non-symmetric. The capacity parameter was set to , the service time was set to hours and the maximum route length to hours. The algorithm was run five times using this information and the best solution was chosen. The results are presented in Table 12, where columns Dist CRP, Days CRP, Dist HGOALS and Days HGOALS show the total distance and required days for the routes planned by the company representative and the routes obtained by the HGOALS respectively. Columns Dist % red and Days % red show the percentaje reduction in total distance and working days obtained with the use of HGOALS proposed routes instead of the planned routes by the company representative. Finally, column CPU denotes the CPU time in seconds required by the algorithm and column %gap the gap with the best solution obtained by using a modified version (directed) of the formulation in [49] on CPLEX. This last column was added to verify the performance of the algorithm on real-life instances. For the exact method, a maximum CPU time was set to s.

Table 12.
Case study results.
The results show a significant reduction in terms of total distance and working days. The routes obtained by the HGOALS are more efficient than those planned by the company representative. Moreover, fuel consumption is also importantly reduced due to the reduction in the total distance to be traveled. Note that the associated demand for each customer is the same (). Considering unitary demands helps the HGOALS reach the optimal solution with a small computational effort.
6. Concluding Remarks
A new hybrid grasshopper algorithm is presented and used to solve the open vehicle routing problem with capacity and maximum distance constraints. The OVRP is a variant of the classic VRP and has multiple applications, especially in transportation and distribution services. It is also a difficult combinatorial optimization problem of the NP-Hard type. The novel decoder first defines the number of vehicles to be used in the solution and then assigns clients to them. Such an approach allows the algorithm to find a balance between transmitting genetic information and allowing diversification of the population. The combination of the decoder with the local search and improvement phase grants robustness to the proposed heuristic. The last because the algorithm is capable of solving instances of up to 480 vertices without changing any parameter. The computational experiments considered two different objective functions. In the first, the prime objective is to minimize the number of vehicles to be used. In the second case, the total traveled distance is minimized. The results also show the excellent performance of the algorithm, especially in benchmark problems considering maximum distance constraints. For the first objective function, the algorithm improves or finds the best-known solutions for 21 of the 30 benchmark problems. For the second objective function, 18 of the 30 best-known solutions were found or improved by the algorithm. For the 30 benchmark problems considering distance constraints (including both objective functions), the algorithm found or improved the best-known solution for 21 of them. A comparison of the proposed algorithm with other heuristics in the literature shows its efficiency in terms of solutions quality, particularly in benchmark problems with maximum distance constraints. Additionally, the algorithm was used to solve instances in a case study with excellent results. Finally, in future research, the algorithm can incorporate constraints related to time windows, heterogeneous fleet or hiring costs, among others.
Author Contributions
Conceptualization, E.R.-y.-R. and V.S.-M.; methodology, E.R.-y.-R. and I.G.-C.; validation, V.S.-M., I.G.-C. and J.P.-T.; formal analysis, E.R.-y.-R.,V.S.-M. and I.G.-C.; investigation, E.R.-y.-R. and V.S.-M.; resources, J.P.-T.; writing—original draft preparation, V.S.-M. and E.R.-y.-R.; writing—review and editing, I.G.-C. and J.P.-T.; visualization, J.P.-T.; supervision, E.R.-y.-R.. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
The authors thank the Tecnológico Nacional de México/Instituto Tecnológico de Saltillo and Universidad Autónoma de Coahuila for their support during the development of this research project.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kennedy, J.; Eberhat, R. Particle swarm optimization. In Proceedings of the IEEE international conference on neural networks, Perth, WA, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Dorigo, M.; Maniezzo, V.; Colorni, A. Ant system: Optimization by a colony of cooperating agents. IEEE Trans. Syst. Man Cybern. Part B (Cybern.) 1996, 26, 29–41. [Google Scholar]
- Holland, J.H. Adaptation in Natural and Artificial Systems; University of Michigan Press: Ann Arbor, MI, USA, 1975. [Google Scholar]
- Karaboga, D. An Idea Based on Honey Bee Swarm for Numerical Optimization. 2005. Available online: https://pdfs.semanticscholar.org/015d/f4d97ed1f541752842c49d12e429a785460b.pdf (accessed on 20 March 2020).
- Glover, F.; Laguna, M. Tabu search. In Handbook of Combinatorial Optimization; Springer: New York, NY, USA, 1998; pp. 2093–2229. [Google Scholar]
- Mladenović, N.; Hansen, P. Variable neighborhood search. Comput. Oper. Res. 1997, 24, 1097–1100. [Google Scholar]
- Pham, D.; Ghanbarzadeh, A.; Koc, E.; Otri, S.; Rahim, S.; Zaidi, M. The Bees Algorithm Technical Note; Manufacturing Engineering Centre, Cardiff University: Cardiff, UK, 2005; p. 40. [Google Scholar]
- Filho, C.J.A.B.; de Lima Neto, F.B.; Lins, A.J.C.C.; Nascimento, A.I.S.; Lima, M.P. A novel search algorithm based on fish school behavior. In Proceedings of the IEEE International Conference on Systems, Man and Cybernetics, SMC 2008, Singapore, 12–15 October 2008; pp. 2646–2651. [Google Scholar]
- Neshat, M.; Sepidnam, G.; Sargolzaei, M. Swallow swarm optimization algorithm: A new method to optimization. Neural Comput. Appl. 2013, 23, 429–454. [Google Scholar]
- Kaveh, A.; Bakhshpoori, T.; Afshari, E. An efficient hybrid Particle Swarm and Swallow Swarm Optimization algorithm. Comput. Struct. 2014, 143, 40–59. [Google Scholar]
- Saremi, S.; Mirjailili, S.; Lewis, A. Grasshopper Optimisation Algorithm: Theory and application. Adv. Eng. Softw. 2017, 105, 30–47. [Google Scholar]
- Yang, X.S. A New Metaheuristic Bat-Inspired Algorithm. Nat. Inspired Coop. Strateg. Optim. 2010, 284, 65–74. [Google Scholar]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar]
- Cubukcuoglu, C.; Ekici, B.; Tasgetiren, M.F.; Sariyildiz, S. OPTIMUS: Self-Adaptive Differential Evolution with Ensemble of Mutation Strategies for Grasshopper Algorithmic Modeling. Algorithms 2019, 12, 141. [Google Scholar]
- Mafarja, M.; Aljarah, I.; Heidari, A.A.; Hammouri, A.I.; Faris, H.; Ala’M, A.Z.; Mirjalili, S. Evolutionary population dynamics and grasshopper optimization approaches for feature selection problems. Knowl.-Based Syst. 2018, 145, 25–45. [Google Scholar]
- Wu, J.; Wang, H.; Li, N.; Yao, P.; Huang, Y.; Su, Z.; Yu, Y. Distributed trajectory optimization for multiple solar-powered UAVs target tracking in urban environment by Adaptive Grasshopper Optimization Algorithm. Aerosp. Sci. Technol. 2017, 70, 497–510. [Google Scholar]
- Zhang, X.; Miao, Q.; Zhang, H.; Wang, L. A parameter-adaptive VMD method based on grasshopper optimization algorithm to analyze vibration signals from rotating machinery. Mech. Syst. Signal Process. 2018, 108, 58–72. [Google Scholar] [CrossRef]
- Barman, M.; Choudhury, N.D.; Sutradhar, S. A regional hybrid GOA-SVM model based on similar day approach for short-term load forecasting in Assam, India. Energy 2018, 145, 710–720. [Google Scholar] [CrossRef]
- Dantzig, G.B.; Ramser, J.H. The truck dispatching problem. Manag. Sci. 1959, 6, 80–91. [Google Scholar] [CrossRef]
- Goel, A.; Gruhn, V. A general vehicle routing problem. Eur. J. Oper. Res. 2008, 191, 650–660. [Google Scholar] [CrossRef]
- Sicilia, J.; Pellicer, E.L.; Agustin, B.R.; Finol, D.E. Siatema inteligente de planificación de rutas para la distribución de mercanciasías basado en las técnicas metaheurísticas, búsqueda de entorno variable y búsqueda tabú. DYNA 2013, 88, 414–423. [Google Scholar] [CrossRef]
- Sicilia, J.A.; Royo-Agustin, B.; Quemada-Mayoral, C.; Olivares-Colay, M.J.; Larrodé, E. A decision support system to long haul freight transportation by means of ant colony optimization. Transp. Syst. Technol. 2015. [Google Scholar] [CrossRef]
- Cassettari, L.; Demartini, M.; Mosca, R.; Revetria, R.; Tonelli, F. A multi-stage algorithm for a capacitated vehicle routing problem with time constraints. Algorithms 2018, 11, 69. [Google Scholar] [CrossRef]
- Sicilia, J.A.; Quemada, C.; Royo, B.; Escuín, D. An optimization algorithm for solving the rich vehicle routing problem based on Variable Neighborhood Search and Tabu Search metaheuristics. J. Comput. Appl. Math. 2016, 291, 468–477. [Google Scholar] [CrossRef]
- Nepomuceno, N.; Barboza Saboia, R.; Rogério Pinheiro, P. A Fast Randomized Algorithm for the Heterogeneous Vehicle Routing Problem with Simultaneous Pickup and Delivery. Algorithms 2019, 12, 158. [Google Scholar] [CrossRef]
- Ait Haddadene, S.R.; Labadie, N.; Prodhon, C. Bicriteria Vehicle Routing Problem with Preferences and Timing Constraints in Home Health Care Services. Algorithms 2019, 12, 152. [Google Scholar] [CrossRef]
- Zhao, M.; Lu, Y. A heuristic approach for a real-world electric vehicle routing problem. Algorithms 2019, 12, 45. [Google Scholar] [CrossRef]
- Juárez Pérez, M.A.; Pérez Loaiza, R.E.; Flores, Q.; Malaquias, P.; Atriano Ponce, O.; Flores Peralta, C. A Heuristic Algorithm for the Routing and Scheduling Problem with Time Windows: A Case Study of the Automotive Industry in Mexico. Algorithms 2019, 12, 111. [Google Scholar] [CrossRef]
- Liang, Y.C.; Minanda, V.; Gunawan, A.; Chen, A.H.L. Harmony search algorithm for time-dependent vehicle routing problem with time windows. J. Appl. Sci. 2013, 13, 633–638. [Google Scholar]
- Sariklis, D.; Powell, S. A heuristic method for the open vehicle routing problem. J. Oper. Res. Soc. 2000, 51, 564–573. [Google Scholar] [CrossRef]
- Schrage, L. Formulation and structure of more complex/realistic routing and scheduling problems. Networks 1981, 11, 229–232. [Google Scholar] [CrossRef]
- Brandão, J. A tabu search algorithm for the open vehicle routing problem. Eur. J. Oper. Res. 2004, 157, 552–564. [Google Scholar] [CrossRef]
- Tarantilis, C.D.; Ioannou, G.; Kiranoudis, C.T.; Prastacos, G.P. Solving the open vehicle routeing problem via a single parameter metaheuristic algorithm. J. Oper. Res. Soc. 2005, 56, 588–596. [Google Scholar] [CrossRef]
- Fleszar, K.; Osman, I.H.; Hindi, K.S. A variable neighbourhood search algorithm for the open vehicle routing problem. Eur. J. Oper. Res. 2009, 195, 803–809. [Google Scholar] [CrossRef]
- Li, F.; Golden, B.; Wasil, E. The open vehicle routing problem: Algorithms, large-scale test problems, and computational results. Comput. Oper. Res. 2007, 34, 2918–2930. [Google Scholar] [CrossRef]
- Repoussis, P.P.; Tarantilis, C.D.; Bräysy, O.; Ioannou, G. A hybrid evolution strategy for the open vehicle routing problem. Comput. Oper. Res. 2010, 37, 443–455. [Google Scholar] [CrossRef]
- Marinakis, Y.; Marinaki, M. A Bumble Bees Mating Optimization algorithm for the Open Vehicle Routing Problem. Swarm Evol. Comput. 2014, 15, 80–94. [Google Scholar] [CrossRef]
- Zachariadis, E.E.; Kiranoudis, C.T. An open vehicle routing problem metaheuristic for examining wide solution neighborhoods. Comput. Oper. Res. 2010, 37, 712–723. [Google Scholar] [CrossRef][Green Version]
- Salari, M.; Toth, P.; Tramontani, A. An ILP improvement procedure for the open vehicle routing problem. Comput. Oper. Res. 2010, 37, 2106–2120. [Google Scholar] [CrossRef][Green Version]
- Fu, Z.; Eglese, R.; Li, L.Y. A new tabu search heuristic for the open vehicle routing problem. J. Oper. Res. Soc. 2005, 56, 267–274. [Google Scholar] [CrossRef]
- Miller, C.E.; Tucker, A.W.; Zemlin, R.A. Integer programming formulation of traveling salesman problems. J. ACM (JACM) 1960, 7, 326–329. [Google Scholar] [CrossRef]
- Ruiz-y Ruiz, E.; Soto-Mendoza, V. A GRASP Algorithm for the Open Vehicle Routing Problem; Technical Report; Instituto Tecnológico de Saltillo: Saltillo, Mexico, 2017. [Google Scholar]
- Ruiz, E.; Soto-Mendoza, V.; Barbosa, A.E.R.; Reyes, R. Solving the Open Vehicle Routing Problem with Capacity and Distance Constraints with a Biased Random Key Genetic Algorithm. Comput. Ind. Eng. 2019, 133, 207–219. [Google Scholar] [CrossRef]
- Marinakis, Y.; Marinaki, M. A honey bees mating optimization algorithm for the open vehicle routing problem. In 2011 Genetic and Evolutionary Computation Conference; Taylor and Francis: Abingdon, UK, 2011. [Google Scholar]
- Pisinger, D.; Ropke, S. A general heuristic for vehicle routing problems. Comput. Oper. Res. 2007, 34, 2403–2435. [Google Scholar] [CrossRef]
- Li, X.; Tian, P.; Leung, S.C. An ant colony optimization metaheuristic hybridized with tabu search for open vehicle routing problems. J. Oper. Res. Soc. 2009, 60, 1012–1025. [Google Scholar] [CrossRef]
- Marinakis, Y.; Marinaki, M. A hybrid particle swarm optimization algorithm for the open vehicle routing problem. In International Conference on Swarm Intelligence; Springer: Berlin, Germany, 2012; pp. 180–187. [Google Scholar]
- Ruiz-y Ruiz, E.; Ruiz-Barbosa, A. A Cutting Plane Algorithm for the Open Vehicle Routing Problem with Capacity and Distance Constraints; Technical Report; Instituto Tecnológico de Saltillo: Saltillo, Mexico, 2019. [Google Scholar]
- Letchford, A.N.; Lysgaard, J.; Eglese, R.W. A branch-and-cut algorithm for the capacitated open vehicle routing problem. J. Oper. Res. Soc. 2007, 58, 1642–1651. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).