Abstract
This paper develops the generalized causality algorithm and applies it to a multitude of data from the fields of economics and finance. Specifically, our parameter-free algorithm efficiently determines the optimal non-linear mapping and identifies varying lead–lag effects between two given time series. This procedure allows an elastic adjustment of the time axis to find similar but phase-shifted sequences—structural breaks in their relationship are also captured. A large-scale simulation study validates the outperformance in the vast majority of parameter constellations in terms of efficiency, robustness, and feasibility. Finally, the presented methodology is applied to real data from the areas of macroeconomics, finance, and metal. Highest similarity show the pairs of gross domestic product and consumer price index (macroeconomics), S&P 500 index and Deutscher Aktienindex (finance), as well as gold and silver (metal). In addition, the algorithm takes full use of its flexibility and identifies both various structural breaks and regime patterns over time, which are (partly) well documented in the literature.
1. Introduction
Measuring similarities of time series possesses a long tradition in literature as well as in practice. Particularly in the fields of economics and finance, research aims at identifying sequences of data points that show a strong relationship over a historical period. The vast majority of existing studies utilize classic approaches to achieve this goal [1,2,3,4,5,6]. Concretely, these manuscripts quantify the similarity between two time series and by the distance
where specifies the distance at fixed time i (). Due to the definition, the measure outlined in Equation (1) is very sensitive to time shifts and misalignments—it is impossible to determine the dependency of two time series with a time delay [7]. This major disadvantage is eliminated by a model that allows an elastic adjustment of the time axis to identify similar but phase-shifted sequences. For this purpose, the co-moving between the time series and is quantified by the cost measure
where c defines the local cost and . The concept of dynamic time warping represents an efficient technique for determining the most appropriate non-linear mapping by minimizing the measure outlined in Equation (2). Following [8,9], this technique is able to handle time series of different lengths as well as being robust against migration, amplitude changes, and noise in the data.
Due to its outstanding flexibility and adaptability, research studies use dynamic time warping in a wide range of application areas. Initially, it is employed in speech recognition to eliminate non-linear time shifts between two speech patterns as a result of different pronunciation [10,11,12]. Recently, dynamic time warping is used mainly in the field of gesture recognition [13,14], chemistry [15,16], medicine [17,18,19], and finance [9,20,21]. Surprisingly, there exists only one academic study that provides a non-parametric methodology to avoid the criticism of arbitrariness and data sniffing: ref. [9] determines the optimal lead–lag structure between two time series under the assumption that there is no structural break in the data set. Following [22,23,24,25,26], regime switching models become increasingly important because they allow structural changes to be taken into account—this procedure leads to lower prediction errors due to more stable parameters.
In recent years, there has been a rapid development in similar fields of dynamic time warping. Measuring the impact of high frequency data on low frequency by a class of mixed frequency VAR models is presented by [27]. The manuscript of [28] compares mixed-data sampling and mixed frequency VAR approaches to model specification in the presence of mixed-frequency data. In the context of model selection and combination, the study of [29] considers the properties of weighted linear combinations of several prediction models, or linear pools, which are evaluated using the conventional log predictive scoring rule. In similar context, ref. [30] estimate time-varying weights in linear prediction pools and use it to investigate the relative forecasting performance with and without financial frictions. Finally, dynamic Bayesian predictive synthesis in time series forecasting is provided by developing a novel class of dynamic latent factor model [31,32].
This manuscript extends the existing research in several aspects. First, we introduce a new algorithm, which captures time-varying lead–lag structures between two time series. Therefore, we enlarge [9] by allowing structural breaks. In contrast to the existing literature, e.g., polynomial time algorithms, we use a parameter-free procedure. Our algorithm outputs the optimal causal path, the corresponding structural breaks, and the estimated lag of each sub-period. Second, we validate the algorithm with the aid of a large-scaled simulation study. The results show an outperformance in the vast majority of parameter constellations in terms of efficiency, robustness, and feasibility. Third, we apply the generalized causality algorithm to real data from the fields of macroeconomics, finance, and metal. In all three fields, the algorithm is able to detect causal relationships, e.g., between gross domestic product and consumer price index (macroeconomics), S&P 500 index and Deutscher Aktienindex (finance), as well as gold and silver (metal). Additionally, it finds structural breaks which correspond to major economic and political events. In our manuscript, the terms “causality” and “dynamic” are used in the sense of [33,34,35]. Specifically, “causality” means that one time series leads the second time series by a (time-varying) lag rather than on statistical tests based on the idea of Granger causality. In similar spirit, “dynamic” is used in the context of dynamic programming which is both a mathematical optimization method and a computer programming method.
The remainder of this paper is structured as follows. Section 2 describes the theoretical concept of causal paths with regard to the relevant literature. In Section 3, we introduce the generalized causality algorithm and conduct a simulation study to validate its performance. Section 4 applies the presented methodology in the areas of macroeconomics, finance, and metal. Finally, Section 5 concludes and provides suggestions for further research areas.
2. Theoretical Concept
Identifying non-linear lead–lag effects of time series data is based on the concept of causal paths. Specifically, we aim at determining the optimal relation structure of two given time series and . Following [36], a sequence of points with for () is called causal path (warping path) if it fulfills the following three characteristics:
- and (Boundary condition).
- and (Monotonicity condition).
- (Step size condition).
It is simple to recognize that the step size condition implies the monotonicity condition, which, however, is given for reasons of clarity. We define P as the set of all possible causal paths between the given time series x and y. Then, the total cost of a causal path p () is determined by
where c describes the local cost measure. As such, the term describes the gap between the realizations of x at time and y at time (). Usually, the cost measure is based on the Manhattan distance [9,35,37] or the Euclidean distance [38,39,40]. The optimal causal path between x and y possesses lowest total cost of any possible causal path:
We define the total cost of as , which is the sum of all local costs of (see Equation (3)). Figure 1 illustrates the local costs and the optimal causal path of two given time series x and y. The points of runs along a “valley” of low cost (light colors) and avoids “mountains” of high cost (dark color).
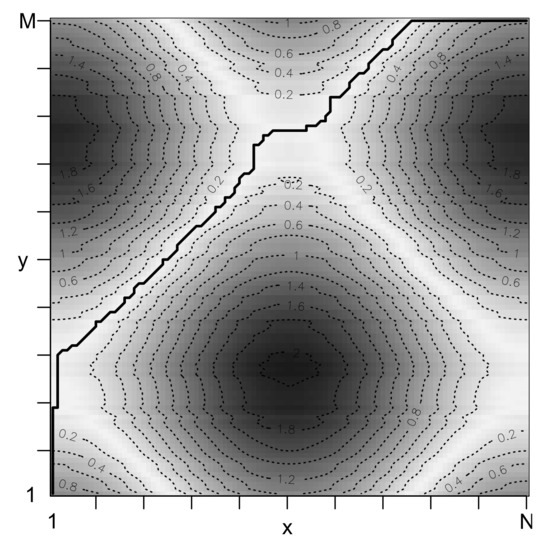
Figure 1.
Local costs of two time series and the identified optimal causal path (solid line). Regions of low cost (high cost) are marked by light colors (dark colors).
Finding the optimal causal path is a challenging and ambitious research objective. The naive approach would consider the total cost for all possible causal paths —a complexity of exponential order renders this approach impossible in practice. The most famous way to find the optimal causal path is dynamic programming, i.e., we divide the underlying problem into several sub-problems [41]. To be more specific, we simplify a complicated problem by breaking it down into simpler sub-problems in a recursive manner. Therefore, we first calculate the optimum solutions of the smallest sub-problems and then combine them to form a solution of the next larger sub-problem. This procedure is continued until the original problem is solved. Overall, achieved solutions are stored for future calculations resulting in a time complexity .
In addition to the three path conditions described above, academic studies establish global and local constraints with the primary purpose of accelerating computing time. Global constraints aim at limiting the deviation of a causal path from the diagonal—important representatives are the Sakoe–Chiba band [42] and the Itakura parallelogram [43] (see Figure 2). Local constraints alter the step size condition by changing the set of potential steps or preferring certain step directions (see [44,45,46,47]). However, we avoid global and local constraints, as both require additional parameter settings and produce inadequate results in most application areas (see [48]).
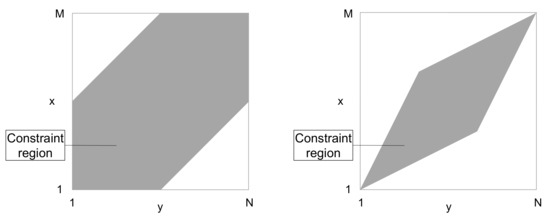
Figure 2.
Sakoe–Chiba band (left) and Itakura parallelogram (right). The constraint regions (grey) represent the environment in which the optimal causal path may run.
Although dynamic time warping measures a distance-like quantity between two given sequences, it doesn’t ensure the triangle inequality to hold [35]. We are talking about costs in the context of dynamic time warping because the triangle inequality is a necessary requirement for being a distance. In [49], the authors show that the corresponding estimator is asymptotically normal and converges to the true shift function as the sample size per subject goes to infinity. In case we observe structural breaks, things become more complex and the outlined statement cannot be kept.
In the 21st century, research has focused either on developing a generalized model framework or on optimizing the computation run time. With the exception of [9], the setting of model parameters plays a central role in all contributions—criticism of arbitrariness and data snooping is omnipresent.
Within the framework of generalization [33,34] universalize the optimal search by including the Boltzmann factor proportional to the exponent of the global imbalance of this path. In [50], the authors provide a symmetric variant for determining the time-dependent mapping. Finally, ref. [9] quantifies the optimal lead–lag structure between two time series under the assumption that there is no structural break in the data set.
Within the framework of optimization, ref. [51] implement a modification of the dynamic time warping, which uses a higher-order representation of data. In [48,52], the authors recursively project an alignment path calculated at a coarse resolution level to the next higher level and then refine it. In [53], the authors exploit the possible existence of inherent similarity between two time series. In [54], the authors present a memory-restricted alignment procedure and [55] use an upper bound estimation to prune unpromising warping alignments.
In recent times, machine learning methods are used to identify Granger causality, e.g., ref. [56] for univariate MIDAS regressions and [57] for VAR processes. Following [58], Granger causality and dynamic time warping are mechanisms to find possible causal links in temporal data. Of course, there also exist some differences between both [59,60]. First, Granger causality uses a statistical hypothesis test to judge whether a time series is causally affected by another time series based on predictability. In contrast, dynamic time warping is a method that calculates an optimal match between two given sequences with certain restriction and rules. Second, the Granger causality may lose its power in the context of structural breaks and drifts because the model residuals are not be stabilized. Dynamic time warping can handle such situations better. Third, Granger causality is a well-established method from econometrics that can identify relationships between temporally offset causes and effects when the offsets are fixed. In contrast, dynamic time warping addresses uneven temporal offsets.
3. Generalized Causality Algorithm
3.1. Methodology
This section introduces the “generalized causality algorithm” which captures time-varying lead–lag relations for two time series and . Specifically, Algorithm 1 outputs the optimal causal path, the corresponding structural breaks, and the estimated lag of each regime. For a pleasant visualization, the algorithm also provides the local costs.
Step A determines the 2-dimensional index of the time series x and y based on ascending local costs. Therefore, a double loop estimates all local costs between x and y, i.e., we calculate . If i equals j, we measure the distance between x and y at the same time points. Next, the algorithm creates the variable by rearranging the local costs in ascending order, e.g., the first row of I describes the combination of the indices of x and y with lowest local cost.
Step B specifies the optimal causal path that allows a time-varying lead–lag structure. For this purpose, we use a binary search algorithm, i.e., half of the solution space is eliminated in each iteration step. Specifically, our algorithm considers the first elements of I and uses the function to check whether the given set of points is capable of constructing a causal path. If a (no) subset of the regarded n data points depicts a causal path, we redefine n by (), where h describes the step size . Next, we conduct a similar process for the updated given set of n points, i.e., the algorithm checks whether the given set of n points is capable of constructing a causal path and redefines with step size . Repeating this procedure until the step size h is less than 1 leads to the optimal n, i.e., the lowest number of required elements of I that constitute a causal path. We note that there are many points in the first n elements of I that are not relevant for our causal path. Finally, we apply the function to the first n elements of I in order to find the shortest path—the result is the optimal causal path P. Using the binary search algorithm implicates two main advantages: our search runs in logarithmic time in the worst case and we know exactly the number of steps required for given N and M.
Step C identifies the optimal structural breaks and the corresponding lags of the optimal causal path P. Following [61,62], we estimate the structural breaks and the corresponding confidence bands by minimizing the sum of squared residuals. Furthermore, the model allows for lagged dependent variables and trending regressor. It should be noted that the number of structural breaks equals the number of sub-periods minus one. The algorithm determines the optimal lag of each sub-period by averaging the corresponding lags which could be disturbed by temporally noise terms. The algorithm returns (i) the local costs, (ii) the optimal causal path, (iii) the corresponding structural breaks, and (iv) the optimal lag of each sub-period.
| Algorithm 1 Generalized causality algorithm |
|
3.2. Simulation Study
In this section, we perform a simulation study with synthetic data to validate the generalized causality algorithm. Following [9], two stationary time series and are generated, whereby X leads Y—without loss of generality Y can also lead X. In contrast to the existing literature, our algorithm is able to handle time-varying lead–lag structures resulting in more flexible and realistic scenarios. From a mathematical point of view, we construct the stochastic process X through the following autoregressive process:
where and . The time series Y follows X and is given by
where and . The parameter indicates how much noise reduces the dependency between X and Y. The variable denotes the lead–lag structure of both processes at time t. In regime i, the stochastic process X leads Y by lags (), where r describes the number of regimes.
For a better understanding of the algorithm the following example is presented. First, we simulate the processes X and Y with three different lead–lag phases, i.e., . Specifically, the following subsets are constructed:
- The first phase () contains 100 data points () where X leads Y by 1 lag () with a “strength” of .
- The second phase () contains 100 data points () where X leads Y by 3 lags () with a “strength” of .
- The third phase () contains 100 data points () where X leads Y by 5 lags () with a “strength” of .
Summarizing, we create the stochastic processes X and Y of length with three different lead–lag structures. As already mentioned, our algorithm would be able to handle different lengths, but we renounce it for reasons of consistency with the existing literature and better comprehensibility. The other parameter values are set identical to [9], who assumes a constant lead lag structure—we set , , and . Furthermore, we define the local cost measure c as the absolute difference between and (), see Equation (3).
Figure 3 represents the corresponding simulated time series X and Y. In order to obtain reasonable results, X and Y are standardized, i.e., our time series start at value 1 and develop on the basis of the corresponding growth rates. We recognize that no lead–lag structures are visible to the naked eye. Furthermore, applying the classical lagged-cross correlation does not make sense for two reasons. First, it would be naive to associate the tiny peaks of the correlation function at 1, 3, and 5 to identify lags between the two time series. Second, finding structural breaks is impossible because the lagged-cross correlations are estimated over the whole time interval.
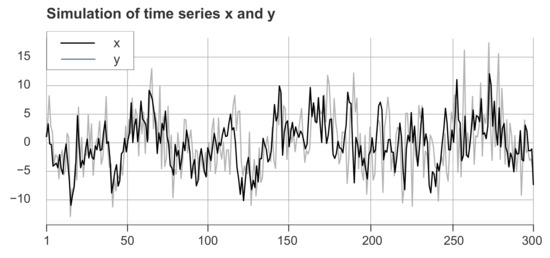
Figure 3.
Simulation of time series x and y with regimes and lead–lag relations , , and . Therefore, y follows x by 1 lag in the first phase, 3 lags in the second phase, and 5 lags in the third phase.
Figure 4 shows the results of applying our generalized causality algorithm. Specifically, we illustrate the local costs and the identified optimal causal path. Similar to Figure 1, the optimal causal path runs along a “valley” of low cost (light colors) and prevents “mountains” of high cost (dark color). On the x-axis, there are two identified structural breaks (large bars) with the corresponding 95 percent confidence interval (small bars). We observe that the optimal causal path represents a diagonal shifted by the number of lags , , and —a few outliers are explained by noise variations in the simulated time series.
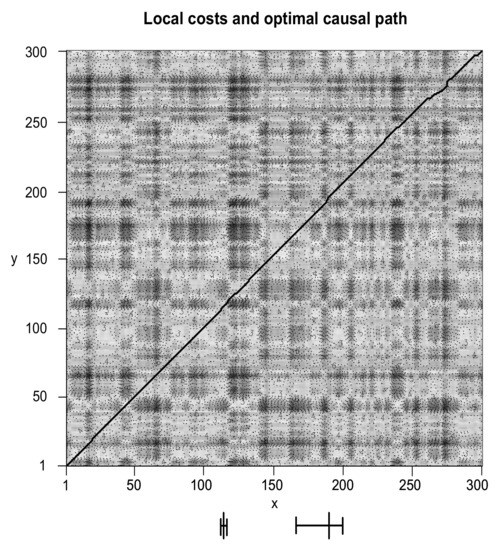
Figure 4.
Local costs and optimal causal path (solid line) of time series x and y. The large bars on the x-axis represent structural breaks with corresponding 95 percent confidence intervals (small bars).
Figure 5 depicts the detailed development of our estimated lags, i.e., the difference between the index of x and the index of y. We note that the length of the optimal causal path is greater than (see Section 2). The first regime possesses a length of around 110 and shows a constant course of 1, i.e., x leads y by 1 lag. The first structural break initiates the second sub-period, which exhibits a lag of 3 and is terminated with the second regime-switch. The third phase shows a time delay of 5 with a short-term outlier to lag 6. Since we have two time series with identical time period, the concept of causal paths, like any approach in this field of research, requires a burn-in period and a burn-out period.
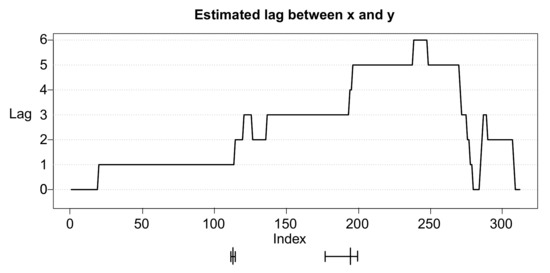
Figure 5.
Estimated lag between time series x and y. The estimated lag is the difference between the index of x and the index of y.
Summarizing, our algorithm performs very well for the simulated time series x and y. Whenever simulated time series generate remarkable results it arouses the suspicion of data snooping. Therefore, we conduct a large-scaled simulations study to validate the robustness of our generalized causality algorithm.
According to [9], this manuscript evaluates the performance of the generalized causality algorithm based on a two-stage procedure. First, the time series X and Y are generated whereby we vary ceteris paribus the sample size N, the coefficient a, and the noise level f—the other parameters remain the same because they do not directly influence the dependency between the two time series. Second, we apply our algorithm to identify the optimal causal path and to calculate the corresponding total cost. Following [63,64,65], we conduct 1000 repetitions for each parameter constellation. Figure 6 shows the resulting boxplots of the average total costs for varying the parameters N, a, and f.
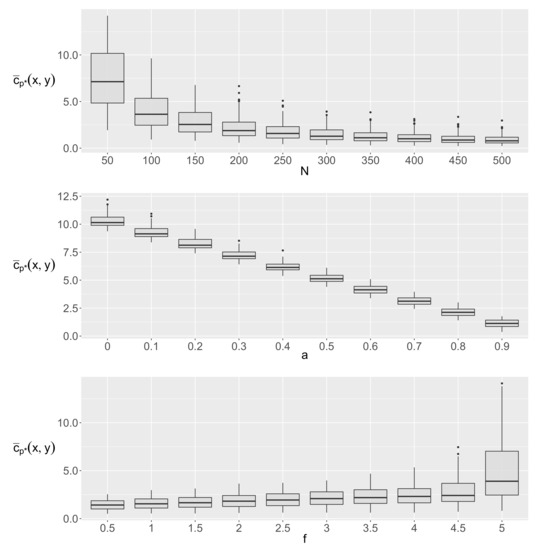
Figure 6.
Boxplots of the average total costs for varying the length of the time series N (first row), the coefficient a (second row), and the amount of noise f (third row).
First of all, we notice that an increasing sample size N results in lower average total costs —this fact is not surprising as outliers in the data set have less impact. At the same time, the total and interquartile ranges decrease towards zero, indicating predictive accuracy and robustness. As known from classical time series analysis, we achieve stable estimates from a data set of about 100 per lead–lag phase.
In addition, average total costs decline for ascending parameter a due to the fact that the dependency between both time series becomes stronger. The case possesses only misjudgements since this parameter constellation does not imply a direct relationship between the time series x and y.
Finally, we observe that increasing f causes rising average total costs . Furthermore, the boxplots show larger differences both between maximum and minimum as well as between upper and lower quartile. If and are at a similar level, we find a high precision of the estimations. In summary, the generalized causality algorithm outperforms in the vast majority of parameter constellations in terms of efficiency, robustness, and feasibility.
Of course, the optimal causal algorithm is not always able to estimate relation between two time series perfectly. Figure 7 shows two extreme situations where the algorithm comes up against limits. On the left, we observe a step function that represents an unusual curve function. In this case, the algorithm does not identify plausible relationships between x and y. On the right side, we get two optimal warping paths as a result of identical costs. Therefore, the concept does not provide an answer to the question of how two rank these optimal paths.
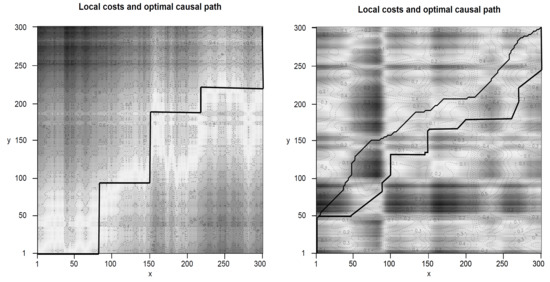
Figure 7.
Local costs and optimal causal path of time series x and y. The left side represents a step function in case the algorithm does not identify plausible relationships. The right side displays two optimal warping paths as a result of identical costs.
4. Applications to Real Data
4.1. Data set
In this section, we apply the generalized causality algorithm developed in the previous sections to real-world data to check for causality relations. Table 1 provides an overview of the self-assembled data set we use. For all time series, it shows the frequency, start and end points, as well as their source. We study three data subsets, namely macroeconomics, finance, and metal data.

Table 1.
Overview of the data subsets examined. The data are from the sources FRED (https://fred.stlouisfed.org/), Yahoo (https://de.finance.yahoo.com), Perth Mint (https://www.perthmint.com/), and Quandl (https://www.quandl.com/).
Regarding the first data subset, we examine macroeconomic data of the United States, using the following time series: consumer price index (CPI), gross domestic product (GDP), federal government tax receipts (FGT), and civilian unemployment rate (CUR). In addition, we use the economic policy uncertainty (EPU) index developed by [66]. According to the authors, EPU can be used as an indicator for economic uncertainty related to political events. As it is common for macroeconomic time series, most of the ones in this subset are of monthly or quarterly frequency. Our finance data subset comprises the S&P 500 index (S&P), the US federal funds rate (FFR), the Deutschen Aktienindex (DAX), the exchange rate between US Dollar and Euro (DEE), and the bitcoin price (BIT). Note that we could use the interest time series as part of the macroeconomic data subset as well, but the daily frequency fits better to the finance data. Lastly, we study the subset metal and use daily data on gold (GOL), silver (SIL), platinum (PLA), ruthenium (RUT), and palladium (PAL). The time period ranges from November 1994 until March 2019.
In [40], the authors motivate the attractiveness of dynamic time warping in the context of economics by different time periods until the same action has an impact. When an economic factor is released on the basis of its expectations, investors take a determined position, which leads to movements in share prices. At a certain point in the life of the financial markets, an announcement like the one mentioned above can have an impact within a short time frame, such as a week. Conversely, if you are in the presence of a high-volume trading period, the same news may have an impact for only an hour.
Our approach is the same for all three data subsets: We first find the common time period that all time series of one subset provide data for. Note that due to this approach, the length of the time series varies per subset. Within one subset, however, all time series have the same number of entries, which ensures comparability and facilitates interpretation. In a second step, we apply the generalized causality algorithm to all pairs and find the one with minimal local cost—details are discussed for this combination. We normalize the data before applying the algorithm to be able to reasonably compare the time series. To be more specific, we follow the vast majority of literature and determine the returns of each time series [9,67,68,69]. Following [70], returns can more easily be assumed to be invariant than prices.
4.2. Macroeconomics
The first data field we want to draw attention to is macroeconomics. The time series consumer price index (CPI), gross domestic product (GDP), federal government tax receipts (FGT), civilian unemployment rate (CUR), and economic policy uncertainty (EPU) cover the time period from January 1, 1985 to January 1, 2019 at monthly frequency, which means 137 entries per time series. The reason why our examined period of time starts in 1985 is that EPU was set up starting at that time only. The left-hand side of Figure 8 shows the development of the normalized data over the examined time period. We see that GDP and CPI follow an almost linear trend, whereas the other time series, such as FGT underlie more fluctuation. Furthermore there is a co-movement of CUR and EPU, with some peaks of EPU being followed by a similar development of CUR. The right-hand part of Figure 8 gives an overview of the distances between all time series after having applied the generalized causality algorithm. The two pairs with minimal total distance are (i) GDP and CPI as well as (ii) CUR and EPU. It is not surprising that GDP and CPI have small total distance. Their development over time is similar, as can be seen in Figure 8, and the variables mutually depend on one another. The small distance between CUR and EPU is an interesting finding, as unemployment usually is accompanied with uncertainty. Figure 9 and Figure 10 help to learn more about the causal relationship of these pairs. Please note that in this subsection as well as in Section 4.3 and Section 4.4, we will only consider figures of type Figure 4, because they contain more information than graphics such as Figure 5.
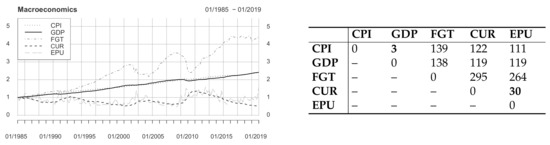
Figure 8.
Standardized macroeconomic time series of consumer price index (CPI), gross domestic product (GDP), federal government tax receipts (FGT), civilian unemployment rate (CUR), and economic policy uncertainty (EPU) (left) and pairwise distances applying the generalized causality algorithm (right). Numbers in bold symbol represent the lowest costs.
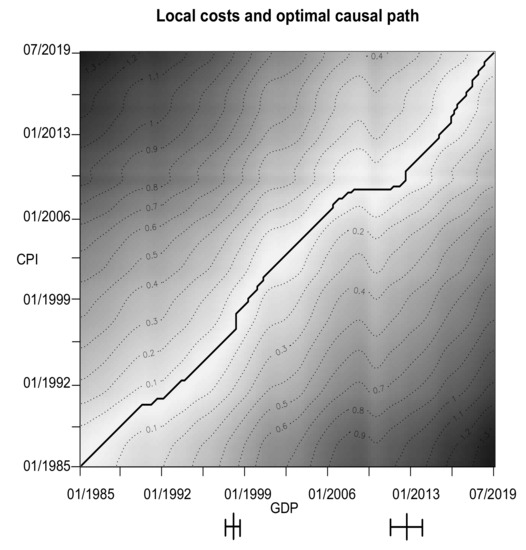
Figure 9.
Local costs and optimal causal path of gross domestic product (GDP) and consumer price index (CPI). The large bars on the x-axis represent structural breaks with corresponding 95 percent confidence intervals (small bars).
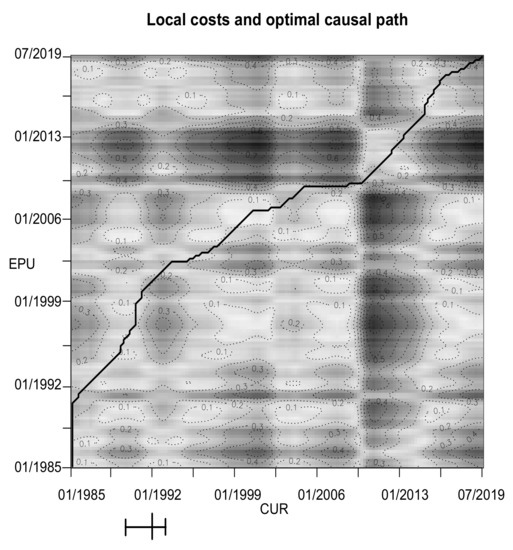
Figure 10.
Local costs and optimal causal path of civilian unemployment rate (CUR) and economic policy uncertainty (EPU). The large bar on the x-axis represent an structural break with corresponding 95 percent confidence interval (small bars).
Figure 9 shows that gross domestic product (GDP) and consumer price index (CPI) most of the time move almost perfectly together, with the lead switching regularly. However, the lag is never more than a few months. There are two structural breaks in the lead–lag structure approximately at the end of 1997 (from CPI to GDP as the leader) and around the second third of 2010 (back to CPI as the leader). Incidences that might have had an impact on this relationship are the Asian financial crisis in 1997–1998, which influenced other economies of the world as well [71,72] and the European financial crisis that was still prevalent in 2010 [73]. Taking a closer look at Figure 9, we see that there is an area of very low cost, i.e., a region of almost white color, approximately along the diagonal. This is not surprising if we look at the development of GDP and CPI over time as shown in the left part of Figure 8. The two time series move almost perfectly together, which means low cost along the diagonal. The similarity of the series is due to their (partial) mutual dependency. Since CPI is a measure of inflation and GDP naturally increases with higher prices (caused at least partly by inflation), rising prices imply larger values of both.
We also take a closer look at the pair yielding the second smallest total distance according to the generalized causality algorithm, namely civilian unemployment rate (CUR) and economic policy uncertainty (EPU). Figure 10 shows the causal path for the two variables. It is salient that the series do not move as smoothly together as GDP and CPI do in the aforementioned case, which is shown by the heterogeneous cost matrix with no clear area of small cost along the diagonal. CUR leads EPU throughout the entire period of time observed, which means that whenever unemployment is high, EPU will rise after some time and vice versa. The size of the lag varies, however, in the way that it becomes smaller over time and is almost zero between approximately the end of 2008 and 2014, before it increases again. There are significant moments to the lead–lag structure in mid-1992 and at the end of 2014. Reasons for this might be the reflation of the economy initiated by former U.S. president Clinton in 1992, which caused unemployment to drop [74] and hence lose its prompt impact on economic policy uncertainty. Furthermore, CUR achieves the lowest value since the beginning of the financial crisis in 2008 (see [75]).
To summarize Section 4.2, the generalized causality algorithm is able to detect interesting relationships between important macroeconomic variables. In both cases, the structural breaks go along with incisive economic and political events that might have had an influence on the lead–lag structure of the time series.
4.3. Finance
Our second study field of interest is finance, where we examine the time series S&P 500 index (S&P), federal funds rate (FFR), Deutscher Aktienindex (DAX), Dollar/Euro exchange rate (DEE), and bitcoin price (BIT). The series cover the time period from 17 July 2010 to 26 July 2019 at daily frequency, which means 2207 entries per time series because there is no data for weekends and holidays. The reason why our examined period of time starts in 2010 is that BIT was introduced in 2010 only. The left plots of Figure 11 show the development of the normalized data over the examined time period. Note that because BIT developed to extraordinarily high values, we display this series in a separate graph. Note also that FFR increased by the factor 13 approximately, from 0.19 percent in July 2010 to 2.4 percent at the end of July 2019. Furthermore, BIT develops to values larger than 200,000 although the original time series only reaches values slightly above 20,000 because it started with a value smaller than one. The right part of Figure 11 gives an overview of the distances between all time series after having applied the generalized causality algorithm. The pair with minimal distance is S&P and DAX. All pair combination with BIT show an enormous value implying that this time series has no similarity to the others.
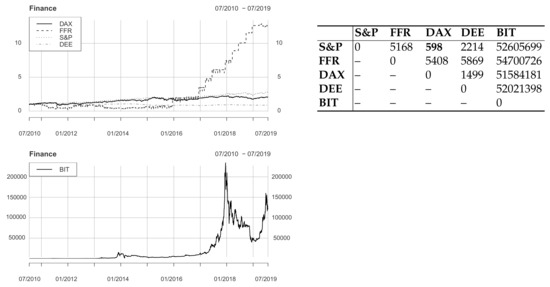
Figure 11.
Standardized finance time series of S&P 500 index (S&P), federal funds rate (FFR), Deutscher Aktienindex (DAX), Dollar/Euro exchange rate (DEE), and bitcoin (BIT) (left) and pairwise distances applying the generalized causality algorithm (right). The number in bold symbol represents the lowest cost.
Figure 12 shows the causal path and local costs for the Deutscher Aktienindex (DAX) and the S&P 500 index (S&P). We see that the time series move very well together, with the fact that the representative of the US stock exchange is leading the German counterpart—there are no changes in the lead–lag structure until the end of our observed period of time. Merely the size of the lag increases visibly from the fourth quarter of 2017 onward and shrinks again from mid-2019 onward. Important economic events that might have had an influence on these structural breaks could be the European debt crisis which was still at a peak in 2014 (see [76]). With this in mind, the increase of the lag between S&P and DAX could be caused by the slowly starting recovery of the European economy.
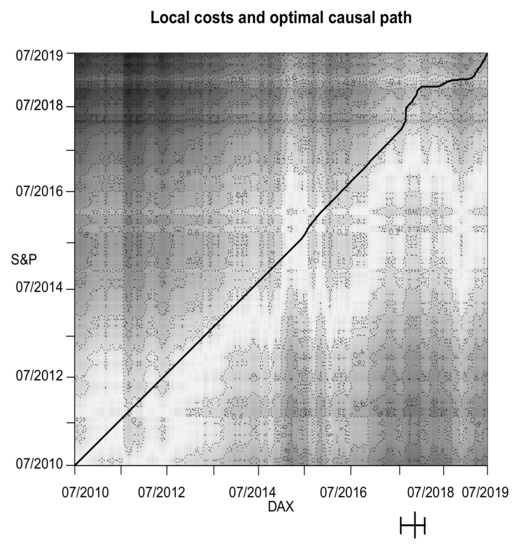
Figure 12.
Local costs and optimal causal path of Deutscher Aktienindex (DAX) and S&P 500 index (S&P). The large bar on the x-axis represents an structural break with corresponding 95 percent confidence interval (small bars).
To summarize Section 4.3, the generalized causality algorithm again finds an interesting causality between two of the most important stock indices of the world. The causal path shows less structural breaks than those for the macroeconomic data, yet they can still be attributed to economic events taking place at that time.
4.4. Metal
Our last data field of interest is the field of metal prices, in which we study the time series gold (GOL), silver (SIL), platinum (PLA), ruthenium (RUT), and palladium (PAL). Note that for all types of metal, we use average asking prices, which is in line with the literature (see [77]). All series cover the time period from November 17, 1994 to March 29, 2019 at daily frequency, which means each time series comprises 6060 entries. RUT depicts an enormous peak in 2006 and 2007 as a result of a price bubble. It was caused by a misinterpretation of the demand for ruthenium in the solar industry and the assumption that it could be used in medicine as an active ingredient for cancer therapy. The left-hand side of Figure 13 shows the development of the normalized data over the examined time period. The right-hand part of Figure 13 gives an overview of the distances between all time series after having applied the generalized causality algorithm. Gold and silver possesses minimal total distance.
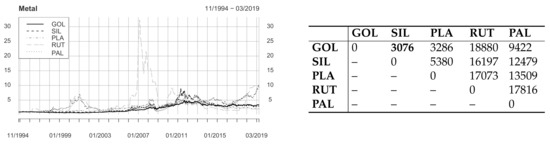
Figure 13.
Standardized metal time series of gold (GOL), silver (SIL), platinum (PLA), ruthenium (RUT), and palladium (PAL) (left) and pairwise distances applying the generalized causality algorithm (right). The number in bold symbol represents the lowest cost.
Figure 14 shows the causal path and local costs for the gold price (GOL) and the silver price (SIL). Again, the path wanders around the diagonal for the entire period of time we consider. In the last quarter of 2010, silver starts to lead gold until the end of the time period we study. One possible reason for this structural break is that the dollar was rather weak in 2010, which usually increases silver prices [78,79]. In contrast to [79,80], which see gold as a driving factor for silver prices, our generalized causality algorithm detects a contrary relationship. This finding is in line with other empirical evidence for silver driving gold prices (see [77]).
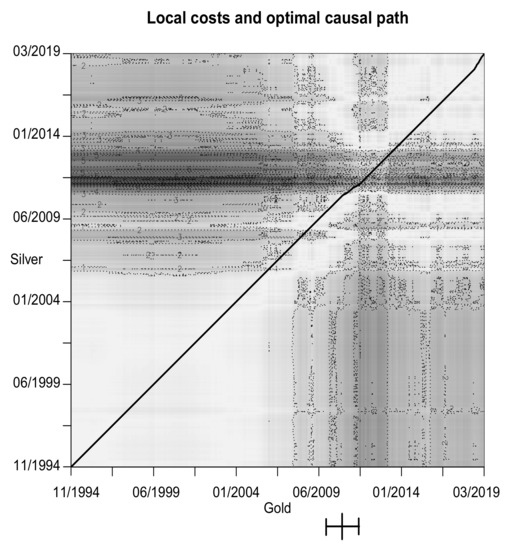
Figure 14.
Local costs and optimal causal path of gold (GOL) and silver (SIL). The large bar on the x-axis represents an structural break with corresponding 95 percent confidence interval (small bars).
To summarize Section 4.4, the generalized causality algorithm also performs well in the data field of metal prices. The pair yielding minimal total distance exhibits only one structural break in the causal path, which goes along in time with an economic event that might have had an influence on the structural break.
In general it can be said that the generalized causality algorithm outperforms in different areas of application, yielding sound results in line with economic and political events explaining occurring structural breaks.
5. Conclusions
This manuscript introduces the generalized causality algorithm and applies it to a variety of economic and finance data. In this respect, we make three main contributions to the existing literature.
The first contribution bears on the novel developed generalized causality algorithm, which captures time-varying lead–lag structures between two time series. Our parameter-free algorithm efficiently determines the optimal non-linear mapping and identifies varying lead–lag effects. Therefore, we are able to elastically adjust the time axis for finding similar but phase-shifted sequences—structural breaks in their relationship are also captured.
The second contribution refers to the large-scaled simulation study where we demonstrate the performance of the algorithm. The vast majority of parameter constellations lead to superior results in terms of efficiency, robustness, and feasibility. Furthermore, simulated structural breaks are always identified.
The third contribution relies on the application to macroeconomics, finance, and metal. In all three fields of application, the generalized causality algorithm performs well and detects causal relationships. Structural breaks can be justified with economic and political events that have an influence on the lead–lag structure.
For further investigations in this research area, a statistical arbitrage strategy may be built on the basis of the developed algorithm. Next, a multivariate framework could be implemented in order to account for common interactions between the variables. Finally, the generalized causality algorithm might be applied to other research areas, such as the recognition of human actions or robot programming.
Author Contributions
J.S. and K.A. conceived the research method. The experiments are designed by J.S. and performed by J.S. and K.A. The analyses were conducted and reviewed by J.S. and K.A. The paper was initially drafted by J.S. and revised by K.A. It was refined and finalized by J.S. and K.A. All authors have read and agreed to the published version of the manuscript.
Funding
We are grateful to the “Open Access Publikationsfonds”, which has covered 75 percent of the publication fees.
Acknowledgments
We are further grateful to two anonymous referees for many helpful discussions and suggestions on this topic.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gauthier, T.D. Detecting trends using Spearman’s rank correlation coefficient. Environ. Forensics 2001, 2, 359–362. [Google Scholar] [CrossRef]
- Mudelsee, M. Estimating Pearson’s correlation coefficient with bootstrap confidence interval from serially dependent time series. Math. Geol. 2003, 35, 651–665. [Google Scholar] [CrossRef]
- Gatev, E.; Goetzmann, W.N.; Rouwenhorst, K.G. Pairs trading: Performance of a relative-value arbitrage rule. Rev. Financ. Stud. 2006, 19, 797–827. [Google Scholar] [CrossRef]
- Batista, G.E.; Wang, X.; Keogh, E.J. A complexity-invariant distance measure for time series. In Proceedings of the 2011 SIAM International Conference on Data Mining; Liu, B., Liu, H., Clifton, C.W., Washio, T., Kamath, C., Eds.; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2011; pp. 699–710. [Google Scholar]
- Stübinger, J.; Endres, S. Pairs trading with a mean-reverting jump-diffusion model on high-frequency data. Quant. Financ. 2018, 18, 1735–1751. [Google Scholar] [CrossRef]
- Knoll, J.; Stübinger, J.; Grottke, M. Exploiting social media with higher-order factorization machines: Statistical arbitrage on high-frequency data of the S&P 500. Quant. Financ. 2019, 19, 571–585. [Google Scholar]
- Ding, H.; Trajcevski, G.; Scheuermann, P.; Wang, X.; Keogh, E.J. Querying and mining of time series data: Experimental comparison of representations and distance measures. In Proceedings of the VLDB Endowment; Jagadish, H.V., Ed.; ACM: New York, NY, USA, 2008; pp. 1542–1552. [Google Scholar]
- Wang, G.J.; Xie, C.; Han, F.; Sun, B. Similarity measure and topology evolution of foreign exchange markets using dynamic time warping method: Evidence from minimal spanning tree. Phys. A Stat. Mech. Its Appl. 2012, 391, 4136–4146. [Google Scholar] [CrossRef]
- Stübinger, J. Statistical arbitrage with optimal causal paths on high-frequency data of the S&P 500. Quant. Financ. 2019, 19, 921–935. [Google Scholar]
- Juang, B.H. On the hidden Markov model and dynamic time warping for speech recognition—A unified view. Bell Labs Tech. J. 1984, 63, 1213–1243. [Google Scholar] [CrossRef]
- Rath, T.M.; Manmatha, R. Word image matching using dynamic time warping. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition; Dyer, C., Perona, P., Eds.; IEEE: Danvers, MA, USA, 2003; pp. 521–527. [Google Scholar]
- Muda, L.; Begam, M.; Elamvazuthi, I. Voice recognition algorithms using mel frequency cepstral coefficient (MFCC) and dynamic time warping (DTW) techniques. J. Comput. 2010, 2, 138–143. [Google Scholar]
- Arici, T.; Celebi, S.; Aydin, A.S.; Temiz, T.T. Robust gesture recognition using feature pre-processing and weighted dynamic time warping. Multimed. Tools Appl. 2014, 72, 3045–3062. [Google Scholar] [CrossRef]
- Cheng, H.; Dai, Z.; Liu, Z.; Zhao, Y. An image-to-class dynamic time warping approach for both 3D static and trajectory hand gesture recognition. Pattern Recognit. 2016, 55, 137–147. [Google Scholar] [CrossRef]
- Jiao, L.; Wang, X.; Bing, S.; Wang, L.; Li, H. The application of dynamic time warping to the quality evaluation of Radix Puerariae thomsonii: Correcting retention time shift in the chromatographic fingerprints. J. Chromatogr. Sci. 2014, 53, 968–973. [Google Scholar] [CrossRef] [PubMed]
- Dupas, R.; Tavenard, R.; Fovet, O.; Gilliet, N.; Grimaldi, C.; Gascuel-Odoux, C. Identifying seasonal patterns of phosphorus storm dynamics with dynamic time warping. Water Resour. Res. 2015, 51, 8868–8882. [Google Scholar] [CrossRef]
- Rakthanmanon, T.; Campana, B.; Mueen, A.; Batista, G.; Westover, B.; Zhu, Q.; Zakaria, J.; Keogh, E.J. Searching and mining trillions of time series subsequences under dynamic time warping. In Proceedings of the 18th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining; Yang, Q., Ed.; ACM: New York, NY, USA, 2012; pp. 262–270. [Google Scholar]
- Fu, C.; Zhang, P.; Jiang, J.; Yang, K.; Lv, Z. A Bayesian approach for sleep and wake classification based on dynamic time warping method. Multimed. Tools Appl. 2017, 76, 17765–17784. [Google Scholar] [CrossRef]
- Stübinger, J.; Schneider, L. Epidemiology of coronavirus COVID-19: Forecasting the future incidence in different countries. Healthcare 2020, 8, 99. [Google Scholar] [CrossRef]
- Chinthalapati, V.L. High Frequency Statistical Arbitrage via the Optimal Thermal Causal Path; Working Paper; University of Greenwich: London, UK, 2012. [Google Scholar]
- Kim, S.; Heo, J. Time series regression-based pairs trading in the Korean equities market. J. Exp. Theor. Artif. Intell. 2017, 29, 755–768. [Google Scholar] [CrossRef]
- Ghysels, E. A Time Series Model with Periodic Stochastic Regime Switching; Université de Montréal: Montreal, QC, Canada, 1993. [Google Scholar]
- Bock, M.; Mestel, R. A regime-switching relative value arbitrage rule. In Operations Research Proceedings 2008; Fleischmann, B., Borgwardt, K.H., Klein, R., Tuma, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 9–14. [Google Scholar]
- Xi, X.; Mamon, R. Capturing the regime-switching and memory properties of interest rates. Comput. Econ. 2014, 44, 307–337. [Google Scholar] [CrossRef]
- Endres, S.; Stübinger, J. Regime-switching modeling of high-frequency stock returns with Lévy jumps. Quant. Financ. 2019, 19, 1727–1740. [Google Scholar] [CrossRef]
- Shi, Y.; Feng, L.; Fu, T. Markov regime-switching in-mean model with tempered stable distribution. Comput. Econ. 2019, 12, 105. [Google Scholar] [CrossRef]
- Ghysels, E. Macroeconomics and the reality of mixed frequency data. J. Econ. 2016, 193, 294–314. [Google Scholar] [CrossRef]
- Kuzin, V.; Marcellino, M.; Schumacher, C. MIDAS vs. mixed-frequency VAR: Nowcasting GDP in the euro area. Int. J. Forecast. 2011, 27, 529–542. [Google Scholar] [CrossRef]
- Geweke, J.; Amisano, G. Optimal prediction pools. J. Econ. 2011, 164, 130–141. [Google Scholar] [CrossRef]
- Del Negro, M.; Hasegawa, R.B.; Schorfheide, F. Dynamic prediction pools: An investigation of financial frictions and forecasting performance. J. Econ. 2016, 192, 391–405. [Google Scholar] [CrossRef]
- McAlinn, K.; West, M. Dynamic Bayesian predictive synthesis in time series forecasting. J. Econ. 2019, 210, 155–169. [Google Scholar] [CrossRef]
- McAlinn, K.; Aastveit, K.A.; Nakajima, J.; West, M. Multivariate Bayesian predictive synthesis in macroeconomic forecasting. J. Am. Stat. Assoc. 2019. [Google Scholar] [CrossRef]
- Sornette, D.; Zhou, W.X. Non-parametric determination of real-time lag structure between two time series: The “optimal thermal causal path” method. Quant. Financ. 2005, 5, 577–591. [Google Scholar] [CrossRef]
- Zhou, W.X.; Sornette, D. Non-parametric determination of real-time lag structure between two time series: The “optimal thermal causal path” method with applications to economic data. J. Macroecon. 2006, 28, 195–224. [Google Scholar] [CrossRef]
- Müller, M. Information Retrieval for Music and Motion; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Keogh, E.J.; Ratanamahatana, C.A. Exact indexing of dynamic time warping. Knowl. Inf. Syst. 2005, 7, 358–386. [Google Scholar] [CrossRef]
- Li, Q.; Clifford, G.D. Dynamic time warping and machine learning for signal quality assessment of pulsatile signals. Physiol. Meas. 2012, 33, 1491–1502. [Google Scholar] [CrossRef]
- Vlachos, M.; Kollios, G.; Gunopulos, D. Discovering similar multidimensional trajectories. In Proceedings of the 18th International Conference on Data Engineering; Agrawal, R., Dittrich, K., Eds.; IEEE: Washington, DC, USA, 2002; pp. 673–684. [Google Scholar]
- Senin, P. Dynamic Time Warping Algorithm Review; Working Paper; University of Hawaii at Manoa: Honolulu, HI, USA, 2008. [Google Scholar]
- Coelho, M.S. Patterns in Financial Markets: Dynamic Time Warping; Working Paper; NOVA School of Business and Economics: Lisbon, Portugal, 2012. [Google Scholar]
- Bellman, R. Dynamic programming. Science 1966, 153, 34–37. [Google Scholar] [CrossRef]
- Sakoe, H.; Chiba, S. Dynamic programming algorithm optimization for spoken word recognition. IEEE Trans. Acoust. Speech Signal Process. 1978, 26, 43–49. [Google Scholar] [CrossRef]
- Itakura, F. Minimum prediction residual principle applied to speech recognition. IEEE Trans. Acoust. Speech Signal Process. 1975, 23, 67–72. [Google Scholar] [CrossRef]
- Myers, C.; Rabiner, L.; Rosenberg, A. Performance tradeoffs in dynamic time warping algorithms for isolated word recognition. IEEE Trans. Acoust. Speech Signal Process. 1980, 28, 623–635. [Google Scholar] [CrossRef]
- Myers, C.; Rabiner, L. A level building dynamic time warping algorithm for connected word recognition. IEEE Trans. Acoust. Speech Signal Process. 1981, 29, 284–297. [Google Scholar] [CrossRef]
- Rabiner, L.; Juang, B.H. Fundamentals of Speech Recognition; Prentice Hall: Upper Saddle River, NJ, USA, 1993. [Google Scholar]
- Berndt, D.J.; Clifford, J. Using dynamic time warping to finder patterns in time series. In Knowledge Discovery in Databases: Papers from the AAAI Workshop; Fayyad, U.M., Uthurusamy, R., Eds.; AAAI Press: Menlo Park, CA, USA, 1994; pp. 359–370. [Google Scholar]
- Salvador, S.; Chan, P. Toward accurate dynamic time warping in linear time and space. Intell. Data Anal. 2007, 11, 561–580. [Google Scholar] [CrossRef]
- Wang, K.; Gasser, T. Alignment of curves by dynamic time warping. Ann. Stat. 1997, 25, 1251–1276. [Google Scholar]
- Meng, H.; Xu, H.C.; Zhou, W.X.; Sornette, D. Symmetric thermal optimal path and time-dependent lead-lag relationship: Novel statistical tests and application to UK and US real-estate and monetary policies. Quant. Financ. 2017, 17, 959–977. [Google Scholar] [CrossRef]
- Keogh, E.J.; Pazzani, M.J. Scaling up dynamic time warping for datamining applications. In Proceedings of the 6th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining; Ramakrishnan, R., Stolfo, S., Bayardo, R., Parsa, I., Eds.; ACM: New York, NY, USA, 2000; pp. 285–289. [Google Scholar]
- Müller, M.; Mattes, H.; Kurth, F. An efficient multiscale approach to audio synchronization. In Proceedings of the 7th International Conference on Music Information Retrieval; Tzanetakis, G., Hoos, H., Eds.; University of Victoria: Victoria, BC, Canada, 2006; pp. 192–197. [Google Scholar]
- Al-Naymat, G.; Chawla, S.; Taheri, J. SparseDTW: A novel approach to speed up dynamic time warping. In Proceedings of the 8th Australasian Data Mining Conference; Kennedy, P.J., Ong, K., Christen, P., Eds.; Australian Computer Society: Melbourne, Australia, 2009; pp. 117–127. [Google Scholar]
- Prätzlich, T.; Driedger, J.; Müller, M. Memory-restricted multiscale dynamic time warping. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing; Ding, Z., Luo, Z.Q., Zhang, W., Eds.; IEEE: Danvers, MA, USA, 2016; pp. 569–573. [Google Scholar]
- Silva, D.; Batista, G. Speeding up all-pairwise dynamic time warping matrix calculation. In Proceedings of the 16th SIAM International Conference on Data Mining; Venkatasubramanian, S.C., Wagner, M., Eds.; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2016; pp. 837–845. [Google Scholar]
- Babii, A.; Ghysels, E.; Striaukas, J. Estimation and HAC-Based Inference for Machine Learning Time Series Regressions; Working Paper; 2019. Available online: https://ssrn.com/abstract=3503191 (accessed on 16 April 2020).
- Basu, S.; Shojaie, A.; Michailidis, G. Network granger causality with inherent grouping structure. J. Mach. Learn. Res. 2015, 16, 417–453. [Google Scholar]
- Davis, P.K.; O’Mahony, A.; Pfautz, J. Social-Behavioral Modeling for Complex Systems; John Wiley & Sons: Hoboken, NJ, USA, 2019. [Google Scholar]
- Li, G.; Yuan, T.; Qin, S.J.; Chai, T. Dynamic time warping based causality analysis for root-cause diagnosis of nonstationary fault processes. IFAC-PapersOnLine 2015, 48, 1288–1293. [Google Scholar] [CrossRef]
- Sliva, A.; Reilly, S.N.; Casstevens, R.; Chamberlain, J. Tools for validating causal and predictive claims in social science models. Procedia Manuf. 2015, 3, 3925–3932. [Google Scholar] [CrossRef]
- Bai, J. Estimation of a change point in multiple regression models. Rev. Econ. Stat. 1997, 79, 551–563. [Google Scholar] [CrossRef]
- Bai, J.; Perron, P. Computation and analysis of multiple structural change models. J. Appl. Econ. 2003, 18, 1–22. [Google Scholar] [CrossRef]
- McFadden, D.; Train, K. Mixed MNL models for discrete response. J. Appl. Econ. 2000, 15, 447–470. [Google Scholar] [CrossRef]
- Ilzetzki, E.; Mendoza, E.G.; Végh, C.A. How big (small?) are fiscal multipliers? J. Monet. Econ. 2013, 60, 239–254. [Google Scholar] [CrossRef]
- Létourneau, P.; Stentoft, L. Refining the least squares Monte Carlo method by imposing structure. Quant. Financ. 2014, 14, 495–507. [Google Scholar] [CrossRef]
- Baker, S.R.; Bloom, N.; Davis, S.J. Measuring economic policy uncertainty. Q. J. Econ. 2016, 131, 1593–1636. [Google Scholar] [CrossRef]
- Badrinath, S.G.; Chatterjee, S. On measuring skewness and elongation in common stock return distributions: The case of the market index. J. Bus. 1988, 61, 451–472. [Google Scholar] [CrossRef]
- Frankel, R.; Lee, C.M. Accounting valuation, market expectation, and cross-sectional stock returns. J. Account. Econ. 1998, 25, 283–319. [Google Scholar] [CrossRef]
- Stübinger, J.; Schneider, L. Statistical arbitrage with mean-reverting overnight price gaps on high-frequency data of the S&P 500. J. Risk Financ. Manag. 2019, 12, 51. [Google Scholar]
- Meucci, A. Risk and Asset Allocation; Springer Science & Business Media: Berlin, Germany, 2009. [Google Scholar]
- The Economist. Ten Years on—How Asia Shrugged off its Economic Crisis. 2007. Available online: https://www.economist.com/news/2007/07/04/ten-years-on (accessed on 10 March 2020).
- Ba, A.D. Asian Financial Crisis. Encyclopaedia Britannica. 2013. Available online: https://www.britannica.com/event/Asian-financial-crisis (accessed on 10 March 2020).
- Elliott, L. Global Financial Crisis: Five Key Stages 2007–2011. The Guardian. 2011. Available online: https://www.theguardian.com/business/2011/aug/07/global-financial-crisis-key-stages (accessed on 10 March 2020).
- The Washington Post. A Brief History of U.S. Unemployment. The Washington Post. 2011. Available online: https://www.washingtonpost.com/wp-srv/special/business/us-unemployment-rate-history/??noredirect=on#21st-century (accessed on 10 March 2020).
- BBC News Service. US Unemployment Rate Hit a Six-Year Low in September. British Broadcasting Corporation. 2014. Available online: https://www.bbc.com/news/business-29479533 (accessed on 10 March 2020).
- Stübinger, J.; Mangold, B.; Krauss, C. Statistical arbitrage with vine copulas. Quant. Financ. 2018, 18, 1831–1849. [Google Scholar] [CrossRef]
- Chan, M.L.; Mountain, C. The interactive and causal relationships involving precious metal price movements: An analysis of the gold and silver markets. J. Bus. Econ. Stat. 1988, 6, 69–77. [Google Scholar] [CrossRef]
- Rich, M.; Ewing, J. Weaker Dollar Seen as Unlikely to Cure Joblessness. New York Times. 2010. Available online: https://www.nytimes.com/2010/11/16/business/economy/16exports.html (accessed on 10 March 2020).
- Scottsdale Bullion & Coin. 10 Factors that Influence Silver Prices. 2019. Available online: https://www.sbcgold.com/investing-101/10-factors-influence-silver-prices (accessed on 10 March 2020).
- Baur, D.G.; Tran, D.T. The long-run relationship of gold and silver and the influence of bubbles and financial crises. Empir. Econ. 2014, 47, 1525–1541. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).